Quantum double lock-in amplifier

Abstract

Quantum lock-in amplifiers have been proposed to extract an alternating signal from a strong noise background. However, due to the typical target signal has unknown initial phase, it is challenging to extract complete information about the signal’s amplitude, frequency, and initial phase. Here, we present a general protocol for achieving a quantum double lock-in amplifier by employing two quantum mixers operating under orthogonal pulse sequences. To demonstrate the practical implementation, we discuss the experimental feasibility using a five-level double-Λ coherent population trapping system with Rb atoms. Here, each Λ structure acts as a quantum mixer, and two applied dynamical decoupling sequences serve as orthogonal reference signals. Notably, the system significantly reduces the total measurement time by nearly half and mitigates time-dependent systematic errors compared to conventional two-level systems. Furthermore, our quantum double lock-in amplifier is robust against experimental imperfections. This study establishes a pathway to alternating signal measurement, thereby facilitating the development of practical quantum sensing technologies.

Introduction

The precise measurement of weak alternating signals in the presence of a noisy background is of great significance in both fundamental scientific research and practical applications. Typically, the desired signal is obscured by the noise, making detection challenging. To achieve a high signal-to-noise ratio, it is necessary to minimize the influence of noise while amplifying the response to the target signal. Lock-in amplifiers have been widely used in various fields^1,2,3,4,5,6 due to their ability to extract time-dependent alternating signals from highly noisy backgrounds. In essence, a lock-in amplifier employs a mixing process by multiplying the input signal with a reference signal, followed by detection through an adjustable low-pass filter. The filter effectively eliminates contributions from signals that do not share the same frequency as the reference signal, thereby selectively rejecting all other frequency components.

Typically, when dealing with time-dependent alternating signals of known initial phase, conventional lock-in techniques using a single reference signal can effectively extract the characteristics of the target signal. However, when the initial phase is unknown^7,8, extracting the complete characteristics, including amplitude, frequency, and initial phase, becomes challenging with a single reference signal alone. To address this issue, a double lock-in amplifier, also known as phase-sensitive detector⁹, has been proposed and widely used for signal measurement. In a double lock-in amplifier, the target signal is mixed with two orthogonal reference signals. The resulting signals from the two mixers pass through separate low-pass filters, generating two output signals that enable the extraction of the complete characteristics of the target signal. Quantum lock-in measurements, leveraging advancements in quantum control techniques, have been successfully demonstrated and widely employed for frequency measurement^10,11, magnetic field sensing¹⁰, vector light shift detection¹², and weak-force detection¹³. The key to realizing a quantum lock-in amplifier lies in identifying quantum analogs of mixing and filtering operations. By utilizing quantum probes, these processes can be achieved through non-commutative operations and time-evolution, respectively. Similar to the implementation of a quantum mixer^7,10,11,12, dynamical decoupling sequences can be employed as reference signals to realize a quantum lock-in amplifier. Notably, Carr-Purcell (CP) and periodic dynamical decoupling (PDD) sequences have been widely utilized in various quantum lock-in amplifiers, ranging from single-particle systems¹⁰ to many-body systems¹¹. However, these existing schemes only cater to target signals with known initial phases. Extracting the complete characteristics of a target signal using a single PDD or CP sequence becomes challenging when the initial phase is unknown. Similar to the classical double lock-in amplifier, the question arises as to whether a quantum counterpart can be developed to extract the complete characteristics of a target signal. Furthermore, how can a quantum double lock-in amplifier be realized using currently available experimental techniques?

In this article, we propose a general protocol for implementing a quantum double lock-in amplifier by combining double quantum interferometry with two orthogonal periodic multi-pulse sequences, characterized by orthogonal filter functions. In our protocol, each quantum interferometry using a specific periodic multi-pulse sequence serves as a single quantum lock-in amplifier. Specifically, we select the PDD and CP sequences as the two orthogonal periodic multi-pulse sequences. Additionally, the XY4-N sequences^{14,15,16,17,18}, with appropriate delays, can also be employed to realize the quantum double lock-in amplifier. Further, to demonstrate the feasibility of our protocol, we illustrate its implementation using a five-level double-Λ coherent population trapping (CPT) system consisting of ⁸⁷Rb atoms with PDD and CP pulse sequences. By appropriately adjusting the detuning, the five-level double-Λ system can be split into two Λ systems^19,20,21, serving as the quantum mixers for the quantum double lock-in amplifier. The utilization of the five-level system offers significant advantages, including a reduction of nearly half the total measurement time and the avoidance of additional time-dependent systematic errors compared to conventional two-level systems. Furthermore, we analyze the impact of finite pulse length and stochastic noise to demonstrate the experimental feasibility of our approach. Numerical results indicate that the quantum double lock-in amplifier exhibits robustness against these imperfections. Our scheme provides a practical pathway for accurately measuring the complete characteristics of an alternating signal within a strong noise background.

Results

General protocol

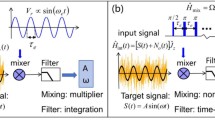
In this section, we introduce the general protocol of a quantum double lock-in amplifier, which aims to extract the complete characteristics of a target signal within strong noise background. In general, a conventional classical lock-in amplifier cannot effectively extract the phase information of the target signal. However, a classical double lock-in amplifier can solve this problem. By mixing the input signal V_S(t) = S(t) + N(t) with two orthogonal reference signals ${V}_{{{{{{{{\rm{r1}}}}}}}}}(t)=\sin ({\omega }_{m}t)$ and ${V}_{{{{{{{{\rm{r2}}}}}}}}}(t)=\cos ({\omega }_{m}t)$ respectively and integrating the two mixed signals over a certain time, the target signal can be extracted, see Fig. 1a. Here, $S(t)=A\sin (\omega t+\beta )$ is the target signal submerged in the noise N(t) and all three parameters (A, ω, β) are unknown to be measured and unchanged in measurements. The two multipliers, which are described by ${{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{r1}}}}}}}}}^{{{{{{{{\rm{mix}}}}}}}}}(t)={V}_{{{{{{{{\rm{S}}}}}}}}}(t)\times {V}_{{{{{{{{\rm{r1}}}}}}}}}(t)$ and ${{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{r2}}}}}}}}}^{{{{{{{{\rm{mix}}}}}}}}}(t)={V}_{{{{{{{{\rm{S}}}}}}}}}(t)\times {V}_{{{{{{{{\rm{r2}}}}}}}}}(t)$, are used for mixing input and reference signals. The integrator is used to filter out the components whose frequencies are different from the reference frequency ω_m. One can find that, at the lock-in point ω_m = ω, the two output signals are given as $I=\frac{AT}{2}\cos (\beta )$ and $Q=\frac{AT}{2}\sin (\beta )$. Therefore, at the lock-in point, one can obtain $A=2\sqrt{{I}^{2}+{Q}^{2}}/T$ and $\beta =\arctan (Q/I)$ for the target signal^22,23. In particular, if the noise spectral components are far from the reference frequency ω_m, the noise effects will be averaged out through the integration (see Supplementary Note 1 for more details).

Fig. 1: The schematic of classical and quantum double lock-in amplifiers.

a The classical double lock-in amplifier. V_s(t) = S(t) + N(t) is the input signal, where $S(t)=A\sin (\omega t+\beta )$ is the target signal submerged within the noise N(t). V_r1,2(t) are the two orthogonal reference signals. The amplitude A, frequency ω, and phase β can be extracted after mixing with a multiplier and filtering by integration. b The quantum double lock-in amplifier. There are two identical quantum mixers. For each quantum mixer, the coupling between the probe and the signal is described by ${\hat{H}}_{{{{{{{{\rm{int}}}}}}}}}=\frac{\hslash }{2}M(t){\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}$ where M(t) = S(t) + N(t) includes the target signal S(t) and the noise N(t). The mixing modulations ${\hat{H}}_{{{{{{{{\rm{ref1}}}}}}}}}=\frac{\hslash }{2}{\Omega }_{{{{{{{{\rm{PDD}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{x}}}}}}}}}$ and ${\hat{H}}_{{{{{{{{\rm{ref2}}}}}}}}}=\frac{\hslash }{2}{\Omega }_{{{{{{{{\rm{CP}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{x}}}}}}}}}$ (implemented by the periodic dynamical decoupling (PDD) and Carr-Purcell (CP) sequences respectively), which do not commute with ${\hat{H}}_{{{{{{{{\rm{int}}}}}}}}}$, are analog to the two reference signals V_r1(t) and V_r2(t). Each mixer obeys the Hamiltonian $\hat{H}={\hat{H}}_{{{{{{{{\rm{int}}}}}}}}}+{\hat{H}}_{{{{{{{{\rm{ref1,2}}}}}}}}}$, which can be regarded as a single quantum lock-in amplifier. The mixing process is achieved by non-commutating operations, and the filtering process is realized by time-evolution. The combination of the two quantum lock-in amplifiers forms a quantum double lock-in amplifier, which can extract the complete characteristics of the target signal $S(t)=A\sin (\omega t+\beta )$.

In analogy to a classical double lock-in amplifier, a quantum double lock-in amplifier can be realized by using two orthogonal multi-pulse sequences, which act the role of two orthogonal reference signals. Generally, to realize the quantum double lock-in amplifier, one can choose any two multi-pulse sequences whose filtering functions are orthogonal. The spacing of the adjacent π pulses is τ_m and one can define the carrier frequency ω_m = π/τ_m. As the applied multi-pulse sequences (acting as the reference signal) are non-commutating with the target signal^7,10,11, one can mix the input signal and the reference signal. And then the following time-evolution filters out the noise spectral components different from the reference frequency ω_m.

To illustrate our protocol, we consider two individual two-level systems such as NV center^7,8,14 and single trapped ion¹⁰ whose energy levels are labeled by $\left\vert \uparrow \right\rangle$ and $\left\vert \downarrow \right\rangle$. For each two-level system, the coupling between the probe and the external signal is described by the Hamiltonian ${\hat{H}}_{{{{{{{{\rm{int}}}}}}}}}=\frac{\hslash }{2}M(t){\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}$ with the Pauli operators ${\hat{\sigma }}_{{{{{{{{\rm{x,y,z}}}}}}}}}$. The external signal M(t) = S(t) + N(t) consists of the target signal $S(t)=A\sin (\omega t+\beta )$ and the stochastic noise N(t). Here, we consider the mixing term ${\hat{H}}_{{{{{{{{\rm{ref}}}}}}}}}=\frac{\hslash }{2}\Omega (t){\hat{\sigma }}_{{{{{{{{\rm{x}}}}}}}}}$, which does not commute with ${\hat{H}}_{{{{{{{{\rm{int}}}}}}}}}$. Thus, the whole Hamiltonian reads

$$\hat{H}={\hat{H}}_{{{{{{{{\rm{int}}}}}}}}}+{\hat{H}}_{{{{{{{{\rm{ref}}}}}}}}}=\frac{\hslash }{2}\left[M(t){\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}+\Omega (t){\hat{\sigma }}_{{{{{{{{\rm{x}}}}}}}}}\right].$$

(1)

The time-evolution obeys the Schrödinger equation,

$$i\frac{\partial {\left\vert \Psi (t)\right\rangle }_{{{{{{{{\rm{S}}}}}}}}}}{\partial t}=\frac{1}{2}\left[M(t){\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}+\Omega (t){\hat{\sigma }}_{{{{{{{{\rm{x}}}}}}}}}\right]{\left\vert \Psi (t)\right\rangle }_{{{{{{{{\rm{S}}}}}}}}},$$

(2)

where ${\left\vert \Psi (t)\right\rangle }_{{{{{{{{\rm{S}}}}}}}}}$ denotes the system state. In the interaction picture with respecting to ${\hat{H}}_{{{{{{{{\rm{ref}}}}}}}}}$ (See Supplementary Note 2 for more details), the time-evolution obeys

$$i\frac{\partial {\left\vert \Psi (t)\right\rangle }_{{{{{{{{\rm{I}}}}}}}}}}{\partial t}=\frac{1}{2}M(t)\left[\cos (\alpha (t)){\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}+\sin (\alpha (t)){\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}\right]{\left\vert \Psi (t)\right\rangle }_{{{{{{{{\rm{I}}}}}}}}}$$

(3)

with $\alpha (t)=\int\nolimits_{0}^{t}\Omega ({t}^{{\prime} })d{t}^{{\prime} }$. The instantaneous state at time t reads

$${\left\vert \Psi (t)\right\rangle }_{{{{{{{{\rm{I}}}}}}}}}=\hat{{{{{{{{\mathcal{T}}}}}}}}}{e}^{-i\frac{1}{2}\left[{\phi }_{{{{{{{{\rm{z}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}+{\phi }_{{{{{{{{\rm{y}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}\right]}{\left\vert \Psi (0)\right\rangle }_{{{{{{{{\rm{I}}}}}}}}},$$

(4)

where $\hat{{{{{{{{\mathcal{T}}}}}}}}}$ denotes the time-ordering operator, and ${\phi }_{{{{{{{{\rm{z}}}}}}}}}(t)=\int\nolimits_{0}^{t}{\omega }_{{{{{{{{\rm{z}}}}}}}}}({t}^{{\prime} })d{t}^{{\prime} }$ and ${\phi }_{{{{{{{{\rm{y}}}}}}}}}(t)=\int\nolimits_{0}^{t}{\omega }_{{{{{{{{\rm{y}}}}}}}}}({t}^{{\prime} })d{t}^{{\prime} }$ with angular frequencies ${\omega }_{{{{{{{{\rm{z}}}}}}}}}(t)=M(t)\cos (\alpha (t))$ and ${\omega }_{{{{{{{{\rm{y}}}}}}}}}(t)=M(t)\sin (\alpha (t))$. In our scheme, the time-dependent modulation Ω(t) is designed as a sequence of π pulses with equidistant spacings. This technique is mature and has been widely used in quantum sensing for measuring an oscillating signal in the presence of noises^{10,11,13,14,24,25,26}. In experiments, the π pulse sequences can usually be approximated as square waves,

$${\Omega }_{{{{{{{{\rm{S}}}}}}}}}(t,{T}_{\Omega })=\left\{\begin{array}{ll}\pi /{T}_{\Omega },\hfill &| t-{t}_{j}| < {T}_{\Omega }/2,\\ 0, &{{{{{{{\rm{others}}}}}}}},\hfill\end{array}\right.$$

(5)

where T_Ω denotes the pulse length. In the limit of T_Ω → 0, the π-pulse sequences can be described by hard pulses

$$\Omega (t)=\pi {\sum}_{{{{{{{{\rm{j=1}}}}}}}}}^{{N}_{p}}\delta [t-(j-\lambda ){\tau }_{m}],$$

(6)

with δ(t) being the Dirac δ function, N_p denoting the pulse number, τ_m describing the spacing of the adjacent π pulses, and the parameter λ determining the relative phase with respect to the target signal. Here, as an example for realizing our quantum double lock-in amplifier, we choose two orthogonal sequences: a PDD sequence (λ = 0) and a CP sequence (λ = 1/2)^15,27, which can be easily realized with current experimental techniques^10,11,15 (see Supplementary Note 2 for more details). In addition to the above sequences, the XY4-N sequences with suitable delay can also be applied to realize the quantum double lock-in amplifier. For hard π pulses, one can easily find $\alpha (t)=\int\nolimits_{{{{{{{{\rm{0}}}}}}}}}^{t}\Omega ({t}^{{\prime} })d{t}^{{\prime} }={N}_{p}\pi$, therefore we have $\sin [\alpha (t)]=0$. Initializing each quantum system into the state ${\left\vert \Psi \right\rangle }_{{{{{{{{\rm{in}}}}}}}}}=(\left\vert \uparrow \right\rangle +\left\vert \downarrow \right\rangle )/\sqrt{2}$, in the interaction picture, the instantaneous state at time t_n = nτ_m becomes

$${\left\vert \Psi ({t}_{n})\right\rangle }_{{{{{{{{\rm{I}}}}}}}}}= \, {e}^{-i\int\nolimits_{0}^{{t}_{n}}\frac{1}{2}M({t}^{{\prime} })\cos [\alpha ({t}^{{\prime} })]d{t}^{{\prime} }{\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}}{\left\vert \Psi \right\rangle }_{{{{{{{{\rm{in}}}}}}}}},\\ = \, \left(\left\vert \uparrow \right\rangle +{e}^{i{\phi }_{n}}\left\vert \downarrow \right\rangle \right)/\sqrt{2},$$

(7)

with n chosen as a even number to suppress DC noise¹⁵. For the results determined by the density matrix $\rho =\left\vert \Psi \right\rangle \left\langle \Psi \right\vert$, the global phase ${e}^{-i{\phi }_{n}/2}$ can be ignored. Back to the Schrödinger picture^10,11, the output state is

$$\begin{array}{rcl}{\left\vert \Psi ({t}_{n})\right\rangle }_{{{{{{{{\rm{S}}}}}}}}}&=&(\left\vert \uparrow \right\rangle +{e}^{i{(-1)}^{{N}_{p}}{\phi }_{n}}\left\vert \downarrow \right\rangle )/\sqrt{2},\end{array}$$

(8)

with the pulse number N_p. For PDD and CP sequences, the total accumulation phases are

$${\phi }_{n}^{{{{{{{{\rm{PDD}}}}}}}}}\, = \, \frac{2A}{\omega }\cos \left[\frac{n\omega \cdot ({\tau }_{m}-\tau )}{2}+\beta \right]\\ \times \cos \left[\frac{\omega \cdot ({\tau }_{m}-\tau )}{2}\right]\frac{\sin \left[n\omega \cdot ({\tau }_{m}-\tau )/2\right]}{\sin \left[\omega \cdot ({\tau }_{m}-\tau )/2\right]},$$

(9)

and

$${\phi }_{n}^{{{{{{{{\rm{CP}}}}}}}}}\,= \, \frac{2A}{\omega }\sin \left[\frac{n\omega \cdot ({\tau }_{m}-\tau )}{2}+\beta \right]\\ \times \left[1+\sin \left(\frac{\omega \cdot ({\tau }_{m}-\tau )}{2}\right)\right]\frac{\sin [n\omega \cdot ({\tau }_{m}-\tau )/2]}{\sin [\omega \cdot ({\tau }_{m}-\tau )/2]},$$

(10)

respectively (see Supplementary Note 2 for more details). Here τ = π/ω is the half period of the target signal. Obviously, given β = 0 (β = π/2), ${\phi }_{n}^{{{{{{{{\rm{PDD}}}}}}}}}$ is symmetric (anti-symmetric) and ${\phi }_{n}^{{{{{{{{\rm{CP}}}}}}}}}$ is anti-symmetric (symmetric) with respect to the lock-in point τ_m = τ, see Fig. 2. However, the symmetry of ${\phi }_{n}^{{{{{{{{\rm{PDD(CP)}}}}}}}}}$ will be destroyed when β ≠ 0 (or β ≠ π/2), see Fig. 2. Different from the classical lock-in amplifier, which defines the lock-in point based on the reference frequency ω_m, the lock-in point of our scheme is defined according to the half period of target signal τ¹⁰.

Fig. 2: The parameter dependence of the two total accumulation phases ${\phi }_{n}^{{{{{{{{\rm{PDD}}}}}}}}}$ and ${\phi }_{n}^{{{{{{{{\rm{CP}}}}}}}}}$.

a The variations of ${\phi }_{n}^{{{{{{{{\rm{PDD}}}}}}}}}$ versus (τ − τ_m) and β. b The variations of the phase ${\phi }_{n}^{{{{{{{{\rm{PDD}}}}}}}}}$ versus (τ − τ_m) with β = 0, π/6, π/2. The phase ${\phi }_{n}^{{{{{{{{\rm{PDD}}}}}}}}}$ is symmetric (or antisymmetric) with respect to the lock-in point τ = τ_m when β = 0 (or β = π/2), and is not symmetric with respect to the lock-in point τ = τ_m when β = π/6. c The variations of ${\phi }_{n}^{{{{{{{{\rm{CP}}}}}}}}}$ versus (τ − τ_m) and β. d The variations of ${\phi }_{n}^{{{{{{{{\rm{CP}}}}}}}}}$ versus (τ − τ_m) with β = 0, π/6, π/2. The phase ${\phi }_{n}^{{{{{{{{\rm{CP}}}}}}}}}$ is antisymmetric (or symmetric) with respect to the lock-in point τ = τ_m when β = 0(or β = π/2), and is not symmetric (or antisymmetric) with respect to the lock-in point τ = τ_m when β = π/6. Here, A = 1/100, ω = π and n = 50.

In the stage of signal extraction, an unitary operation $U={e}^{-i\frac{\pi }{4}{\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}}$ is applied for recombination and the readout state becomes ${\left\vert \Psi \right\rangle }_{{{{{{{{\rm{re}}}}}}}}}=\left[-i\sin (\frac{{\phi }_{n}^{{\prime} }}{2})\left\vert \uparrow \right\rangle +\cos (\frac{{\phi }_{n}^{{\prime} }}{2})\left\vert \downarrow \right\rangle \right]$ with ${\phi }_{n}^{{\prime} }={(-1)}^{{N}_{p}}{\phi }_{n}$. Hence the final probability of the probe in the state $\left\vert \uparrow \right\rangle$ are ${P}_{\uparrow ,n}^{{{{{{{{\rm{PDD}}}}}}}}}=[1-\cos ({\phi }_{n}^{{{{{{{{\rm{PDD}}}}}}}}})]/2$ and ${P}_{\uparrow ,n}^{{{{{{{{\rm{CP}}}}}}}}}=[1-\cos ({\phi }_{n}^{{{{{{{{\rm{CP}}}}}}}}})]/2$ respectively. The corresponding expectations of z-component Pauli operator are ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{PDD}}}}}}}}}=-\cos ({\phi }_{n}^{{{{{{{{\rm{PDD}}}}}}}}})$ and ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{CP}}}}}}}}}=-\cos ({\phi }_{n}^{{{{{{{{\rm{CP}}}}}}}}})$ respectively. For β = 0 (or β = π/2), ${P}_{\uparrow ,n}^{{{{{{{{\rm{PDD(CP)}}}}}}}}}$ and ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{PDD(CP)}}}}}}}}}$ are both symmetric with respect to the lock-in point τ = τ_m. Thus through modulating the pulse repetition period τ_m, one can determine the lock-in point from the pattern symmetry, and the amplitude can be extracted from Eq. (9) or Eq. (10) via a fitting procedure^{7,10,11,15,28}. However, when β ≠ 0 (or β ≠ π/2), the phase ${\phi }_{n}^{{{{{{{{\rm{PDD(CP)}}}}}}}}}$ is not symmetric with respect to the lock-in point τ = τ_m. Thus the symmetry of ${P}_{\uparrow ,n}^{{{{{{{{\rm{PDD(CP)}}}}}}}}}$ and ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{PDD(CP)}}}}}}}}}$ are destroyed, see Fig. 3. This means that one cannot determine the lock-in point from the spectrum and extract the target signal S(t) only by means of a single PDD or CP sequence. Below, we introduce how to solve this issue via the quantum double lock-in amplifier. To analyze our protocl analytically, we divide the target signals into two types: (i) the weak signals of $\frac{A}{\omega }\le \frac{1}{2n}$ and (ii) the strong signals of $\frac{A}{\omega } > \frac{1}{2n}$.

Fig. 3: Extraction of a weak target signal.

a, bThe variations of the measurement signals ${P}_{\uparrow ,n}^{{{{{{{{\rm{PDD}}}}}}}}}$ versus (τ_m − τ)/τ. The measurement signals ${P}_{\uparrow ,n}^{{{{{{{{\rm{PDD}}}}}}}}}$ is not symmetric with respect to the lock-in point τ_m = τ and it is well consistent with the analytically approximate result. c, d The variations of the measurement signals ${P}_{\uparrow ,n}^{{{{{{{{\rm{CP}}}}}}}}}$ versus (τ_m − τ)/τ. The measurement signals ${P}_{\uparrow ,n}^{{{{{{{{\rm{CP}}}}}}}}}$ is not symmetric with respect to the lock-in point τ_m = τ and it is well consistent with the analytically approximate result. e, f The variations of the measurement signals ${P}_{\uparrow ,n}^{{{{{{{{\rm{sum}}}}}}}}}$ versus (τ_m − τ)/τ. The measurement signals ${P}_{\uparrow ,n}^{{{{{{{{\rm{sum}}}}}}}}}$ is symmetric with respect to the lock-in point τ_m = τ and it is well consistent with the analytically approximate result Eq. (11). Here, we choose 2nA/ω = 0.1 [left: (a), (c), and (e)] and the critical case 2nA/ω = 1 [right: (b), (d), and (f)] with n = 100, β = − π/6 and ω = π.

For weak signals, i.e., $\frac{A}{\omega }\le \frac{1}{2n}$, we choose the sum of ${P}_{\uparrow ,n}^{{{{{{{{\rm{PDD}}}}}}}}}$ and ${P}_{\uparrow ,n}^{{{{{{{{\rm{CP}}}}}}}}}$ as a measurement signal to recover the spectrum symmetry, that is,

$${P}_{\uparrow ,n}^{{{{{{{{\rm{sum}}}}}}}}}= \, {P}_{\uparrow ,n}^{{{{{{{{\rm{PDD}}}}}}}}}+{P}_{\uparrow ,n}^{{{{{{{{\rm{CP}}}}}}}}}\\ \approx {\left(\frac{A}{\omega }\right)}^{2}{\left[\frac{\sin [n\omega \cdot ({\tau }_{m}-\tau )/2]}{\sin [\omega \cdot ({\tau }_{m}-\tau )/2]}\right]}^{2}.$$

(11)

Obviously, ${P}_{\uparrow ,n}^{{{{{{{{\rm{sum}}}}}}}}}$ is symmetric with respect to the lock-in point τ_m = τ again, see Fig. 3e, f. Thus, one can determine the lock-in point from the symmetric pattern of ${P}_{\uparrow ,n}^{{{{{{{{\rm{sum}}}}}}}}}$ versus (τ_m − τ), which can be obtained by adjusting the spacing τ_m of adjacent π pulses. Our analytical results are well consistent with the numerical ones, even for the case of $\frac{A}{\omega }=\frac{1}{2n}$. Once the value of ω is determined via the the lock-in point τ_m = τ, one can extract A from Eq. (11) via a fitting procedure^26,29. Moreover, due to the value of ω and A are both extracted, one can determine β from ${P}_{\uparrow ,n}^{{{{{{{{\rm{PDD}}}}}}}}}$ or ${P}_{\uparrow ,n}^{{{{{{{{\rm{CP}}}}}}}}}$. Thus the complete characteristics of the target signal can be obtained within our scheme.

For strong signals, i.e., $\frac{A}{\omega } > \frac{1}{2n}$, the Taylor expansion is no longer valid and one cannot obtain the target signal via the measurement signal ${P}_{\uparrow ,n}^{{{{{{{{\rm{sum}}}}}}}}}$. To resolve this problem, we choose the sum of ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{PDD}}}}}}}}}$ and ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{CP}}}}}}}}}$ as a new measurement signal, that is,

$${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{sum}}}}}}}}}\,= \, {\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{PDD}}}}}}}}}+{\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{CP}}}}}}}}}\\ = \, -\left[\cos ({\phi }_{n}^{{{{{{{{\rm{PDD}}}}}}}}})+\cos ({\phi }_{n}^{{{{{{{{\rm{CP}}}}}}}}})\right].$$

(12)

At the lock-in point τ_m = τ, it reads

$${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{n,{\tau }_{m} = \tau }^{{{{{{{{\rm{sum}}}}}}}}}=-\cos \left[\frac{2A}{\omega }\cos (\beta )\cdot n\right]-\cos \left[\frac{2A}{\omega }\sin (\beta )\cdot n\right],$$

(13)

which is an exactly bisinusoidal oscillation. By using a fast Fourier transform (FFT), one can determine the lock-in point by judging whether ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{sum}}}}}}}}}$ has bisinusoidal oscillatory pattern. In comparison to ${P}_{\uparrow ,n}^{{{{{{{{\rm{sum}}}}}}}}}$, the FFT of ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{sum}}}}}}}}}$ does not contain the zero-frequency component and it is easy to determine the lock-in point from the FFT. In our analysis, we consider a series of measurement results ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{sum}}}}}}}}}$ for different evolution times t_n = nτ_m. As shown in Fig. 4a, we give the FFT spectrum of ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{sum}}}}}}}}}$ versus τ_m. When τ_m = τ, the FFT spectrum has only four peaks and therefore we can determine the lock-in point via its inverse participation ratio (IPR)^{30,31,32,33,34}, which is defined as

$${{{{{{{\rm{IPR}}}}}}}}=\frac{{\sum}_{{{{{{{{\rm{k}}}}}}}} = 1}^{{n}_{m}/2}| {F}_{k}{| }^{4}}{{\left\vert {\sum}_{{{{{{{{\rm{k}}}}}}}} = 1}^{{n}_{m}/2}| {F}_{k}{| }^{2}\right\vert }^{2}},$$

(14)

with ${F}_{k}={\sum}_{{{{{{{{\rm{n}}}}}}}} = {2},{{{{{{{{\rm{even}}}}}}}}}}^{{n}_{m}}{\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{sum}}}}}}}}}{e}^{-i\left(\frac{2\pi }{{n}_{m}}nk\right)}$, ∣F_k∣ is the FFT amplitude corresponding to FFT angular frequency ${\omega }_{k}=k\frac{2\pi \omega }{{n}_{m}}\,$(k = 1, 2,⋯, n_m/2) and ${t}_{{n}_{m}}={n}_{m}{\tau }_{m}$ is the maximum sensing time. After some algebra, when ω(τ_m − τ) ≪ 1 and n_m → ∞, we have IPR = 1/4 for τ_m = τ and IPR = 0 for τ_m ≠ τ (see Supplementary Note 3 for more details). Given τ_m = τ, the four peaks appear at ${\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{CP}}}}}}}}}=2A| \sin (\beta )|$, ${\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{PDD}}}}}}}}}=2A| \cos (\beta )|$, ${\overline{\omega }}_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{PDD}}}}}}}}}=(\pi \omega -{\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{PDD}}}}}}}}})$ and ${\overline{\omega }}_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{CP}}}}}}}}}=(\pi \omega -{\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{CP}}}}}}}}})$ respectively, see Fig. 4c. In which, the two peaks at ${\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{CP}}}}}}}}}$ and ${\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{PDD}}}}}}}}}$ correspond to the two oscillation frequencies of the measurement signal ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{n}^{{{{{{{{\rm{sum}}}}}}}}}{| }_{{\tau }_{m} = \tau }$. Thus, the values of A and β are given as

$$A=\frac{1}{2}\sqrt{{({\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{PDD}}}}}}}}})}^{2}+{({\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{CP}}}}}}}}})}^{2}}$$

(15)

and

$$| \beta | =\arctan \left({\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{CP}}}}}}}}}/{\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{PDD}}}}}}}}}\right),$$

(16)

which is similar to a classical double lock-in amplifier. Moreover, one can determine the sign of parameters β from ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{PDD}}}}}}}}}$ or ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{CP}}}}}}}}}$. The sign of β can be uniquely determined by the derivation of ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{n}^{{{{{{{{\rm{PDD}}}}}}}}}$ or ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{n}^{{{{{{{{\rm{CP}}}}}}}}}$ with respect to the pulse repetition period τ_m for three different modulation periods τ_m = (τ − dτ), τ_m = τ and τ_m = (τ + dτ), in which dτ is the spacing of two adjacent pulse repetition periods (see Supplementary Note 2 for more details). Considering the coherence time of a quantum system is limited in experiments, we numerically calculate the systems under moderate n_m satisfying ${n}_{m}\le \frac{{T}_{2}}{\tau }$ with the coherence time T₂^7,10,19. It is shown that IPR ≈ 1/4 for τ_m = τ and IPR ≈ 0 for τ_m ≠ τ, thus we can still extract the frequency ω by finding the maximum of IPR, see Fig. 4b. Further, given the measurement signal ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{sum}}}}}}}}}{| }_{{\tau }_{m} = \tau }$, we can extract A and β via Eqs. (15) and (16), see Fig. 4d.

Fig. 4: Extraction of a strong target signal.

a The fast Fourier transform (FFT) spectrum of ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{sum}}}}}}}}}$ versus (τ_m − τ) with even positive integers n up to n_m = 400. Given τ = τ_m, the FFT spectrum just has four peaks and one can use it to determine the lock-in point. b The inverse participation ratio (IPR) versus (τ_m − τ). The maximum of IPR can be used to determine the lock-in point. c The inset for the local amplification region in (b) and denotes the shift of lock-in point D. d The FFT of ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{{{{{{{{\rm{n}}}}}}}}}^{{{{{{{{\rm{sum}}}}}}}}}$ at τ_m = τ. The four peaks locate at ${\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{CP}}}}}}}}}/\omega =\frac{2}{\omega }A| \sin (\beta )| =0.637$, ${\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{PDD}}}}}}}}}/\omega =\frac{2}{\omega }A| \cos (\beta )| =1.103$, ${\overline{\omega }}_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{PDD}}}}}}}}}/\omega =(\pi -{\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{PDD}}}}}}}}}/\omega )$ and ${\overline{\omega }}_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{CP}}}}}}}}}/\omega =(\pi -{\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{CP}}}}}}}}}/\omega )$ respectively. e The variation of the shift D versus the maximum sensing scanning time n_m. Here, we choose A = 2, β = −π/6, and ω = π.

In experiments, the coherence time T₂ is finite and thus the value of n_m should satisfy T₂ > n_mτ. Given the value of n_m, the frequency ω_FFT can only take discrete values ${\omega }_{k}=k\frac{2\pi \omega }{{n}_{m}}$(k = 1, 2,⋯, n_m/2), and thus the lock-in point may be shifted. In Fig. 4c, we show the frequency shift D of the lock-in point. We numerically calculate how the frequency shift D varies with n_m and find that the envelop of D decreases with n_m due to the resolution ratio of FFT frequency ω_FFT is $({\omega }_{{{{{{{{\rm{k+1}}}}}}}}}-{\omega }_{k})=\frac{2\pi \omega }{{n}_{m}}\propto 1/{n}_{m}$, see Fig. 4e.

Experimental feasibility

Our quantum double lock-in amplifier can be realized via a double-Λ CPT system, in which each Λ system is employed as a quantum mixer. As shown in Fig. 5a, the double-Λ CPT system can be realized by simultaneously coupling two independent two-level systems ($\{\left\vert 1\right\rangle ,\left\vert 2\right\rangle \}$ and $\{\left\vert 3\right\rangle ,\left\vert 4\right\rangle \}$) with a common excited state ($\left\vert 5\right\rangle$), which has been extensively observed in alkali atoms such as Cs^3,35,36 and Rb^19,37,38. Moreover, such a system can be divided into two single-Λ systems by splitting the Zeeman sublevels of their ground states^19,39, which provide the two independent physical channels. For every single-Λ structure, the population of the excited state reflects the coherence information of two ground states^19,20,21. Therefore, for this double-Λ CPT system, the population of the common excited state includes two groups of ground states coherence information, and it may act the role of the sum of two-level systems with PDD and CP sequence modulation¹⁹. The simultaneous coupling of these two physical channels can be achieved by lin∣∣lin CPT scheme, in which two CPT light fields are linearly polarized to the same direction and orthogonal to the applied magnetic field^19,20,21.

Fig. 5: Schematic of the quantum double lock-in amplifier via five-level double-Λ coherent population trapping (CPT) in ⁸⁷Rb.

a Five-level double-Λ configuration of ⁸⁷Rb atom which includes $\left\vert 1\right\rangle =\left\vert F=1,{m}_{F}=-1\right\rangle$, $\left\vert 2\right\rangle =\left\vert F=2,{m}_{F}=-1\right\rangle$, $\left\vert 3\right\rangle =\left\vert F=1,{m}_{F}=1\right\rangle$, $\left\vert 4\right\rangle =\left\vert F=2,{m}_{F}=1\right\rangle$ and $\left\vert 5\right\rangle =\left\vert {F}^{{\prime} }=1,{m}_{F}=0\right\rangle$. b Realization of the quantum double lock-in amplifier. Initialization: preparing the two dark states as the initial states. Sensing: coupling the two ground states $\{\left\vert 1\right\rangle ,\left\vert 2\right\rangle \}$ and $\{\left\vert 3\right\rangle ,\left\vert 4\right\rangle \}$ through the periodic dynamical decoupling (PDD) and Carr-Purcell (CP) sequences respectively. Here, T_Ω denotes the π pulse length, τ_m is the pulse repetition periods and the total sensing time is t_n = nτ_m. Detection: a CPT pulse with 2 μs is imposed to detect the common excited state population via fluorescence or transmission spectrum.

In general, for a single-Λ system, the CPT lasers will pump the atoms into a dark state which is a coherent superposition of two ground states^20,36,40. To achieve our quantum double lock-in amplifier, we can simultaneously prepare two dark states as the initial states of two physical channels by a CPT pulse with just one laser and a fiber-coupled electro-optic modulator (EOM) for different tones and such a CPT system has been realized in several laboratories⁴¹. After the initialization via CPT pulse, the prepared two dark states can independently accumulate phases under the control of PDD and CP sequences, respectively. During the signal interrogation process, the applied PDD and CP sequences only couple the ground states in the same quantum mixer, see Fig. 5a. Due to the action times of PDD and CP sequence pulses are different, one can utilize just one microwave synthesizer or just a laser beam to realize π pulses via the microwave or Raman lasers, which are both very mature with current experimental technology^42,43,44. In comparison to the protocol via separately applying different sequences on the same two-level system^{7,10,11,14,26}, in our protocol with a five-level system, the two orthogonal sequences are applied simultaneously and thus one can save near a half of the total measurement times. Meanwhile, the relative phase of the two orthogonal sequences in five-level system can be tuned easily. Then through applying the CPT pulse, the coherent property of ground states becomes proportional to the population of the common excited state, which can be experimentally detected by fluorescence or transmission spectrum^{19,20,21,45,46}. In particular, the summed signal in our quantum double lock-in amplifier can be directly obtained by only one single measurement on the common excited-state population. In the following, we show an example of quantum double lock-in amplifier via a five-level double-Λ system constructed by the D1 line of ⁸⁷Rb atoms. The involved energy levels include two groups of magneto-sensitive states $\{\left\vert 1\right\rangle =\left\vert F=1,{m}_{F}=-1\right\rangle ,\left\vert 2\right\rangle =\left\vert F=2,{m}_{F}=-1\right\rangle \}$ and $\{\left\vert 3\right\rangle =\left\vert F=1,{m}_{F}= 1\right\rangle ,\left\vert 4\right\rangle = \left\vert F= 2,{m}_{F}= 1\right\rangle \}$ coupling with a common excited state $\left\vert 5\right\rangle =\left\vert {F}^{{\prime} }=1,{m}_{F}=0\right\rangle$, as shown in Fig. 5a. Their eigen frequencies are respectively labeled as ω_j(j = 1, 2, 3, 4, 5). The total decay rate from the excited state ($\left\vert 5\right\rangle$) to the four ground states is Γ = 2π × 5.746 MHz. To perform the simultaneous coupling, the CPT pulse should contain four frequency components (ω_L1, ω_L2, ω_L3, ω_L4) with Rabi frequencies (Ω₁, Ω₂, Ω₃, Ω₄), which can be generated by modulating a single laser with a fiber-coupled EOM. For convenience, one can set the four Rabi frequencies Ω_j = Ω are real and the four decay rates γ_j = Γ/4 (j = 1, 2, 3, 4)^19,20. The time-evolution obeys the Lindblad master equation²⁰,

$$\frac{\partial \hat{\rho }}{\partial t}=-\frac{i}{\hslash }\left[\hat{H},\hat{\rho }\right]+{\sum }_{{{{{{{{\rm{j=1}}}}}}}}}^{4}\frac{\Gamma }{4}\left({\hat{L}}_{j}\hat{\rho }{\hat{L}}_{j}^{{{{\dagger}}} }-\frac{1}{2}{\hat{L}}_{j}^{{{{\dagger}}} }{\hat{L}}_{j}\hat{\rho }-\frac{1}{2}\hat{\rho }{\hat{L}}_{j}^{{{{\dagger}}} }{\hat{L}}_{j}\right),$$

(17)

where ${\hat{L}}_{j}=\left\vert j\right\rangle \left\langle 5\right\vert$ is the Lindblad operator, and $\hat{\rho }$ is the density matrix. In the rotating frame, the Hamiltonian matrix is given as

$$\hat{H}\,=\,\hslash \,\left(\begin{array}{ccccc}-{\delta }_{1}\,-\,\frac{{\Delta }_{1}}{2}&0\,&0\,&0\,&{\Omega }^{* }\\ 0&-{\delta }_{1}\,+\,\frac{{\Delta }_{1}}{2}\,&0\,&0\,&{\Omega }^{* }\\ 0\,&0\,&{\delta }_{2}\,-\,\frac{{\Delta }_{2}}{2}\,&0\,&{\Omega }^{* }\\ 0\,&0\,&0\,&{\delta }_{2}\,+\,\frac{{\Delta }_{2}}{2}\,&{\Omega }^{* }\\ \Omega \,&\Omega \,&\Omega \,&\Omega \,&0\end{array}\right),$$

(18)

where Δ₁ = (ω₂ + ω_L2) − (ω₁ + ω_L1) and Δ₂ = (ω₄ + ω_L4) − (ω₃ + ω_L3) are the two-photon detunings, and δ₁ = [ω₅ − (ω₂ + ω_L2 + ω₁ + ω_L1)/2] and δ₂ = [(ω₄ + ω_L4 + ω₃ + ω_L3)/2 − ω₅] are the average detunings.

In order to realize the quantum double lock-in amplifier, we input two dark states $\left\vert {D}_{{{{{{{{\rm{12}}}}}}}}}\right\rangle =(\left\vert 1\right\rangle -\left\vert 2\right\rangle )/\sqrt{2}$ and $\left\vert {D}_{{{{{{{{\rm{34}}}}}}}}}\right\rangle =(\left\vert 3\right\rangle -\left\vert 4\right\rangle )/\sqrt{2}$ as two probe states which can be prepared via CPT procedure. In experiments, one can prepare the two dark states via setting a big gap between the average detunings δ₁ and δ₂ which satisfy the far detuning condition: δ₂ = δ₁ ≫ {Ω, Δ_1,2}, see Fig. 5b. Thus the corresponding density matrix reads ${\hat{\rho }}_{D}=\frac{1}{2}\left(\left\vert {D}_{{{{{{{{\rm{12}}}}}}}}}\right\rangle \left\langle {D}_{{{{{{{{\rm{12}}}}}}}}}\right\vert +\left\vert {D}_{{{{{{{{\rm{34}}}}}}}}}\right\rangle \left\langle {D}_{{{{{{{{\rm{34}}}}}}}}}\right\vert \right)$. During the signal interrogation process, due to the two physical channels have different resonance frequencies and there is a strong bias field magnetic field B_bias, the two dark states $\left\vert {D}_{{{{{{{{\rm{12}}}}}}}}}\right\rangle$ and $\left\vert {D}_{{{{{{{{\rm{34}}}}}}}}}\right\rangle$ will independently accumulate phases ${\phi }_{n}^{{{{{{{{\rm{PDD}}}}}}}}}$ and ${\phi }_{n}^{{{{{{{{\rm{CP}}}}}}}}}$ under the corresponding PDD and CP sequences (see Supplementary Note 4 for more details).

In our calculations, the two physical channels $\{\left\vert 1\right\rangle ,\left\vert 2\right\rangle \}$ and $\{\left\vert 3\right\rangle ,\left\vert 4\right\rangle \}$ are decoupled in the whole process due to the far detuning condition, and the detunings are set as δ₁ = δ₂ = 2π × 1 MHz. At time t_n = nτ_m before detection, the density matrix is ${\hat{\rho }}_{f}=\left(\left\vert {\Psi }_{{{{{{{{\rm{12}}}}}}}}}({t}_{n})\right\rangle \left\langle {\Psi }_{{{{{{{{\rm{12}}}}}}}}}({t}_{n})\right\vert + \left\vert {\Psi }_{{{{{{{{\rm{34}}}}}}}}}({t}_{n})\right\rangle \left\langle {\Psi }_{{{{{{{{\rm{34}}}}}}}}}({t}_{n})\right\vert \right)/2$ with $\left\vert {\Psi }_{{{{{{{{\rm{12}}}}}}}}}({t}_{n})\right\rangle =(\left\vert 1\right\rangle -{e}^{i{\phi }_{n}^{{{{{{{{\rm{PDD}}}}}}}}}}\left\vert 2\right\rangle )/\sqrt{2}$ and $\left\vert {\Psi }_{{{{{{{{\rm{34}}}}}}}}}({t}_{n})\right\rangle =(\left\vert 3\right\rangle -{e}^{i{\phi }_{n}^{{{{{{{{\rm{CP}}}}}}}}}}\left\vert 4\right\rangle )/\sqrt{2}$. At last, a CPT query pulse of 2 μs is imposed to obtain the population of the common excited state. Here, the transmission of CPT light can be converted as the transmission signal (TS) via a photodetector^19,20, which is proportional to (1 − ρ₅₅), i.e., the absorption is proportional to the excited-state population ρ₅₅. Moreover, the common excited-state population can be expressed as

$${\rho }_{{{{{{{{\rm{55,n}}}}}}}}}\approx \frac{{\Omega }^{2}}{{\Gamma }^{2}}\left[1+2\Re ({\rho }_{{{{{{{{\rm{12,n}}}}}}}}})+2\Re ({\rho }_{{{{{{{{\rm{34,n}}}}}}}}})\right]\\ \approx \frac{{\Omega }^{2}}{{\Gamma }^{2}}\left[1-\frac{\cos ({\phi }_{n}^{{{{{{{{\rm{PDD}}}}}}}}})}{2}-\frac{\cos ({\phi }_{n}^{{{{{{{{\rm{CP}}}}}}}}})}{2}\right],$$

(19)

where ℜ(x) denotes the real part of x and ρ_ij,n is the density matrix element at time t_n reflecting the coherence of ρ_12,n and ρ_34,n (see Supplementary Note 4 for more details). Further, according to Eq. (19), for a weak signal, we have the common excited-state population

$$\begin{array}{r}{\rho }_{{{{{{{{\rm{55,n}}}}}}}}}\approx \frac{{\Omega }^{2}}{{\Gamma }^{2}}{\left(\frac{A}{\omega }\right)}^{2}{\left[\frac{\sin [n\omega \cdot ({\tau }_{m}-\tau )/2]}{\sin [\omega \cdot ({\tau }_{m}-\tau )/2]}\right]}^{2},\end{array}$$

(20)

which is proportional to the measurement signal ${P}_{\uparrow ,n}^{{{{{{{{\rm{sum}}}}}}}}}$ given in Eq. (11). According to Eq. (20), one can extract the weak signal from the common excited-state population ρ_55,n, which is proportional to the CPT light absorption and can be detected via a photodetector^19,47. For a strong signal, we define

$${\tilde{\rho }}_{55,{{{{{{{\rm{n}}}}}}}}}= \, {\rho }_{55,{{{{{{{\rm{n}}}}}}}}}-\frac{1}{({n}_{m}/2)}{\sum}_{{{{{{{{{\rm{n}}}}}}}}}^{{\prime} }=2,{{{{{{{\rm{even}}}}}}}}}^{{n}_{m}}{\rho }_{55,{{{{{{{{\rm{n}}}}}}}}}^{{\prime} }}\\ \approx -\frac{{\Omega }^{2}}{2{\Gamma }^{2}}\left[\cos ({\phi }_{n}^{{{{{{{{\rm{PDD}}}}}}}}})+\cos ({\phi }_{n}^{{{{{{{{\rm{CP}}}}}}}}})\right]$$

(21)

which is proportional to ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{n}^{{{{{{{{\rm{sum}}}}}}}}}$ given in Eq. (12). At the point of τ_m = τ, we have ${\tilde{\rho }}_{{{{{{{{\rm{55,n}}}}}}}}}\approx -\frac{{\Omega }^{2}}{2{\Gamma }^{2}}\left[\cos \left(\frac{2A}{\omega }\cos (\beta )\cdot n\right)+\cos \left(\frac{2A}{\omega }\sin (\beta )\cdot n\right)\right]$, which can be used to extract the strong signal (see Supplementary Note 4 for more details).

Therefore, according to Eqs. (19) and (20), one can successfully extract the target signal from the population of the common excited-state in a five-level double-Λ CPT system. In experiment, one can obtain the common excited-state population ρ_55,n and further obtain ${\tilde{\rho }}_{{{{{{{{\rm{55,n}}}}}}}}}$ by adjusting the spacing τ_m of adjacent π pulses. In our consideration, we chose $\{\left\vert 1\right\rangle ,\left\vert 2\right\rangle \}$ and $\{\left\vert 3\right\rangle ,\left\vert 4\right\rangle \}$ to form two groups of magneto-sensitive transitions with gyromagnetic ratios γ₁₂ = −γ₃₄ = γ_g = −(g₂ − g₁)μ_B/ℏ = −1.0014 × 2π × 1.4 MHz/G, where μ_B is the Bohr magneton, {g₁, g₂} are the Landég factors for ground states F = {1, 2}, and μ_B/ℏ = 2π × 1.4 MHz/G and (g₂ − g₁) = 1.0014. Below, for a target AC magnetic field in form of ${B}_{0}\sin (\omega t+\beta )$, we use A = γ_gB₀ to denote its amplitude. Based upon currently available experimental techniques, we set the frequency ω = 2π × 50 kHz, the initial phase β = −π/6, the π pulse length T_Ω = 2 μs, and the Rabi frequencies $\Omega =0.035\times \frac{\Gamma }{4}$ for simulation^{18,19,42,48,49}. To split the Zeeman sublevels, a bias magnetic field B_bias = 0.143 mT is applied while the two-photon detunings are set as Δ₁ = Δ₂ ≈ 0, leading to the average detunings δ₁ = δ₂ ≈ 2π × 1 MHz.

Our numerical results from the Lindblad master equation (17) are well consistent with the analytical ones given by Eqs. (19) and (21), see Fig. 6. For a weak target signal, such as a magnetic field of B₀ = 2 × 10⁻⁹ T satisfying $\frac{A}{\omega }\le \frac{1}{2n}$, one can obtain the information of the target signal by measuring ρ_55,n, see Fig. 6a. Based upon the numerical simulation of Lindblad master equations, the normalized common excited-state population (ρ₅₅/a with the normalization coefficient $a \, \approx \, \frac{{\Omega }^{2}}{{\Gamma }^{2}}$) given by a five-level double-Λ system (red dashed line) fit well with the sum of excited-state populations given by two independent Λ systems (blue line). Moreover, these numerical results are both well consistent with the analytical ones of Eq.(19) (green dotted line). Thus one can determine the lock-in point to extract the frequency ω from the common excited-state population. In addition, one can determine the initial phase via only performing extra independent CP or PDD measurements for three specific modulation periods τ_m = (τ − dτ), τ_m = τ and τ_m = (τ + dτ) (see Supplementary Note 2 for more details). For a strong target signal, such as a magnetic field B₀ = 2 × 10⁻⁶ T satisfying $\frac{A}{\omega } > \frac{1}{2n}$, one can determine the value of ω via the IPR given by the FFT spectrum of the measurement signal ${\tilde{\rho }}_{{{{{{{{\rm{55,n}}}}}}}}}$, see in Fig. 6b. Therefore one can extract A and β from the FFT spectrum of ${\tilde{\rho }}_{{{{{{{{\rm{55,n}}}}}}}}}$ at the lock-in point τ_m = τ, see Fig. 6c. Similarly, we find the numerical results are well consistent with the analytical ones, see Fig. 6b, c. The little deviation of numerical between analytical results is because that the pulse is not a ideal Dirac δ function but a square pulse of a finite length T_Ω = 2 μs. Overall, comparing with the protocol with two-level systems, our protocol with five-level double-Λ system can dramatically reduce the total measurement times and avoid additional time-dependent systematic errors (see Supplementary Note 4 for more details). In addition, a single NV center in diamond is a system with electron spin (S = 1) and nuclear spin (I = 1), thus it may be able to realize the double-Λ five-level via delicate design^50,51.

Fig. 6: Numerical results of the quantum double lock-in amplifier via five-level double-Λ coherent population trapping (CPT) in ⁸⁷Rb.

a Locking of a weak target signal via the normalized common excited-state population ρ₅₅ versus (τ_m − τ). The numerical results of ρ₅₅/a (dashed red line) fit well with the sum of excited-state populations given by two independent Λ configurations (solid blue line), and they are both consistent with the analytical approximation (dotted green line). Here, B₀ = 1 nT, n = 200, ω = 2π × 50 kHz (τ = 10 μs), β = − π/6, and T_Ω = 2 μs. b Locking of a strong target signal via the IPR versus (τ_m − τ). The inverse participation ratio (IPR) approach its maximum at the lock-in point τ_m = τ. c The fast Fourier transform (FFT) spectrum of ${\tilde{\rho }}_{{{{{{{{\rm{55,n}}}}}}}}}$ for τ_m = τ. The first two peaks are 0.587 and 0.968 which are very close to the theoretical ones ${\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{CP}}}}}}}}}/\omega =2A| \sin (\beta )| /\omega =0.561$ and ${\omega }_{{{{{{{{\rm{FFT}}}}}}}}}^{{{{{{{{\rm{PDD}}}}}}}}}/\omega =2A| \cos (\beta )| /\omega =0.971$. Here, B₀ = 2 μT, n = 2, 4,⋯, 400, ω = 2π × 50 kHz(τ = 10 μs), β = − π/6, and T_Ω = 2 μs.

Robustness

In experiments, there are many imperfections that may influence the lock-in signal. Below we discuss two key imperfections: the finite pulse length T_Ω and the stochastic noises^18,48,49. Firstly, we consider square pules and analyze the influence of their pulse length T_Ω on our scheme. According to Eq. (4), for a weak target signal, we can ignore the time-ordering operator $\hat{{{{{{{{\mathcal{T}}}}}}}}}$, that is, ${\left\vert \Psi (t)\right\rangle }_{{{{{{{{\rm{I}}}}}}}}}={e}^{-i\frac{1}{2}\left[{\phi }_{{{{{{{{\rm{z}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}+{\phi }_{{{{{{{{\rm{y}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}\right]}{\left\vert \Psi (0)\right\rangle }_{{{{{{{{\rm{I}}}}}}}}}$ with ${\left\vert \Psi (0)\right\rangle }_{{{{{{{{\rm{I}}}}}}}}}=\frac{\left\vert \uparrow \right\rangle +\left\vert \downarrow \right\rangle }{\sqrt{2}}$. Hence, after an unitary operation $U={e}^{-i\frac{\pi }{4}{\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}}$ for readout, the population in the state $\left\vert \uparrow \right\rangle$ reads

$${P}_{\uparrow ,n}\approx \frac{1-\cos \left(\sqrt{{\phi }_{{{{{{{{\rm{y}}}}}}}}}{({t}_{n})}^{2}+{\phi }_{{{{{{{{\rm{z}}}}}}}}}{({t}_{n})}^{2}}\right)}{2}.$$

(22)

The analytical results of Eq. (22) are well consistent with the corresponding numerical ones (see Supplementary Note 5 for more details). To show the influences of the pulse length T_Ω, we numerically calculate the common exited-state population ρ_55,n in double-Λ system with T_Ω = {0, 0.2 τ, 0.4τ}. It indicates that the finite pulse length T_Ω almost has no effects on the lock-in point, see Fig. 7a. For a strong target signal, one can still extract the frequency via the periodicity of the measurement signal ${\langle {\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\rangle }_{n}^{{{{{{{{\rm{sum}}}}}}}}}$. When τ_m = τ, we have $\hat{H}(t+2{\tau }_{m})=\hat{H}(t)$ and the IPR reaches its maximum. We also numerically verify that the pulse length T_Ω indeed does not affect the lock-in point, as shown in Fig. 7b. Moreover, we numerically calculate the FFT spectrum for different T_Ω at the lock-in point τ_m = τ, see Fig. 7c. In addition, in order to estimate the influence of the pulse length T_Ω, we numerically calculate the relative deviation of the amplitude B₀ and the phase β for different T_Ω. They are $\delta {B}_{0}^{{{{{{{{\rm{est}}}}}}}}}=\left({B}_{0}^{{{{{{{{\rm{est}}}}}}}}}-{B}_{0}\right)$ and $\delta | \beta {| }^{{{{{{{{\rm{est}}}}}}}}}=\left(| \beta {| }^{{{{{{{{\rm{est}}}}}}}}}-| \beta | \right)$. In general, the pulse length need satisfy 0 < T_Ω < τ to avoid the mixing term become a continuous driving. Here, B₀ and ∣β∣ denote the exact values, and ${B}_{0}^{{{{{{{{\rm{est}}}}}}}}}$ and ∣β∣^est correspond to the estimated values according to Eqs. (15) and Eq. (16), respectively. Our numerical results show that the effect of pulse length T_Ω is small enough to be ignored when T_Ω≤ 0.4 τ, as shown in Fig. 7d.

Fig. 7: The influence of finite pulse length on the quantum double lock-in amplifier.

a For the weak target signal measurement, the normalized excited state population ρ₅₅/a versus (τ_m − τ) with different pulse length T_Ω = 0 (solid blue line), T_Ω = 2 μs (dashed red line) and T_Ω = 4 μs (dotted green line). It indicates that the pulse length does not affect the lock-in point when T_Ω≤ 0.4 τ. Here,B₀ = 1 nT, ω = 2π × 50 kHz (τ = 10 μs), β = −π/6, n = 200 (nτ = 2 ms). b For the strong target signal measurement, the inverse participation ratio (IPR) versus (τ_m − τ) with different pulse length T_Ω = 0 (solid blue line), T_Ω = 2 μs (dashed red line) and T_Ω = 4 μs (dotted green line). It also indicates that the pulse length does not affect the lock-in point. c The fast Fourier transform (FFT) results of ${\tilde{\rho }}_{{{{{{{{\rm{55,n}}}}}}}}}$ in the case of τ_m = τ with different pulse length T_Ω = 0 (solid blue line), T_Ω = 2 μs (dashed red line) and T_Ω = 4 μs (dotted green line). d The relative error relative deviation of the amplitude B₀ and the phase β versus the pulse length T_Ω. The effect of pulse length T_Ω can be ignored if T_Ω≤ 0.4 τ. Here, B₀ = 2 μT, ω = 2π × 50 kHz (τ = 10 μs), β = −π/6 and n = 0, 2, 4,⋯, n_m(n_m = 400, n_mτ = 4 ms).

Below we will illustrate the robustness of our quantum double lock-in amplifier against stochastic noise. In experiments, one of the most common and most dominant types of noise is white noise. The white noise is a random signal equably distributed in the whole frequency domain and it is also called f₀ noise for its constant power spectral density. Due to the PDD and CP sequences can enhance the part with frequency ${f}_{k}=\frac{(2k+1)}{2{\tau }_{m}}(k=0,1,2,\cdots )$¹⁵, the signal-to-noise ratio (SNR) can be effectively improved by these two sequences (see more details in Supplementary Note 8). Here, we consider the signal and the noise couple to the probe through the same channel, that is, the system obeys the Hamiltonian $\hat{H}(t,{T}_{\Omega },\sigma )=\frac{\hslash }{2}A\left[\sin (\omega t+\beta )+{N}_{(0,\sigma )}(t)\right]{\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}+\frac{\hslash }{2}\Omega (t){\hat{\sigma }}_{{{{{{{{\rm{x}}}}}}}}}$. Here, N_(0, σ)(t) = σN_(0,1)(t) denotes the Gaussian random noise with the time-averaged value $\overline{{N}_{(0,\sigma )}(t)}=0$, and σ = N/S is the standard deviation. Thus, we have the corresponding SNR = − 10lg(N/S) dB^52,53. To illustrate the robustness of our scheme, we numerically calculate the two measurement signals versus the modulation period τ_m under different noise strengths. For a weak target signal, we calculate the population ρ_55,n versus the difference (τ_m − τ) for different noise strengths σ = 0, σ = 100, and σ = 300, as shown in Fig. 8a. The stochastic noise almost do not affect the lock-in point even under a large noise strength σ = 100. Our protocol is still hold for SNR ≥ −20 dB after averaging over 20 times. For a strong target signal, we calculate the IPR versus (τ_m − τ) and the FFT spectra of ${\tilde{\rho }}_{{{{{{{{\rm{55,n}}}}}}}}}$ for different noise strengths σ = 0, σ = 5, and σ = 10, see Fig. 8b. Our results show that the maximum IPR and the FFT amplitude decrease with the noise strength. When SNR≥ −10 dB, one can still determine the lock-in point via the IPR and extract the target signal via performing FFT on ${\tilde{\rho }}_{{{{{{{{\rm{55,n}}}}}}}}}$ (averaging over 20 times), see Fig. 8c. In addition, our scheme is also robust against decoherence phenomenon causing by the population decay, the depolarization noise arising from the optical pumping effect (see Supplementary Note 6 for more details) and 50 Hz noise which originates from the electrical power for a lab (see Supplementary Note 7 for more details).

Fig. 8: Robustness of the quantum double lock-in amplifier against white noises.

The parameters for the target signal are chosen as ω₀ = 2π × 50 kHz (τ = 10 μs) and β = −π/6. a For a weak target signal with B₀ = 1 nT, the normalized common excited-state population ρ₅₅/a after 200 π-pulses versus (τ_m − τ) under different signal-to-noise ratio (SNR = −10lg(N/S) dB) with N/S = 0 (solid blue line, without noise), N/S = 100 (dashed red line) and N/S = 300 (dotted green line). b For a strong target signal with B₀ = 2 μT, the inverse participation ratio (IPR) versus (τ_m − τ) under different SNR N/S = 0 (solid blue line, without noise), N/S = 5 (dashed red line) and N/S = 10 (dotted green line). c The fast Fourier transform (FFT) spectrum of ${\tilde{\rho }}_{{{{{{{{\rm{55,n}}}}}}}}}$ in the case of τ_m = τ under different SNR N/S = 0 (solid blue line, without noise), N/S = 5 (dashed red line) and N/S = 10 (dotted green line). In (b) and (c), the pulse number is chosen as n = 0, 2, 4,⋯,400.

In general, different quantum systems have different environments and therefore different noise sources. For trapped-ion system, except for the white noise and 50 Hz noise, the 150 Hz noise is also one of the most common noise and can limit the ultimate measurement precision^54,55. For the NV centers, the photon shot noise always exists and can affect the the measurement⁸. Moreover, since the NV centers near the surface, the interaction with external materials and spins also can affect the ultimate measurement precision^56,57. Their influences within our scheme are worthy studied in future.

Discussion

In conclusion, we propose a comprehensive framework for implementing a quantum double lock-in amplifier utilizing two orthogonal dynamical decoupling sequences: PDD and CP sequences. This scheme establishes a quantum counterpart to the classical double lock-in amplifier. We mathematically derive a general formula for measuring an AC signal in the presence of strong noise using our quantum double lock-in amplifier, which relies on two quantum mixers subjected to orthogonal modulations. Our protocol enables the extraction of the complete characteristics, including frequency, amplitude, and initial phase, of the target AC signal. In the case of a weak target signal, the lock-in point can be determined by exploiting the symmetry of the combined measurement signal, allowing for subsequent extraction of the amplitude and, the phase through a fitting procedure. For a strong target signal, the target signal can be extracted from the FFT spectrum of the combined measurement signal. We also compare the measurement sensitivity of the amplitude A achieved by two methods for weak and strong signals at the lock-in point (see supplementary Note 9). In the previous scheme⁸, the frequency is measured via sweeping MW strength Ω firstly, and then measure the amplitude and the phase via Rabi oscillation. Differently, our scheme measures the frequency via modulating the pulse repetition period τ_m and can extract complete information about the signal’s amplitude, frequency, and initial phase simultaneously.

Furthermore, we illustrate the realization of a quantum double lock-in amplifier using a five-level double-Λ CPT system of ⁸⁷Rb as an example. In this five-level double-Λ CPT system, the common excited state population can be measured to obtain two measurement signals: ρ_55,n and ${\tilde{\rho }}_{{{{{{{{\rm{55,n}}}}}}}}}$. Compared to implementations using two-level systems, our experimental proposal based on a five-level system can significantly reduce the total measurement time and avoid additional time-dependent systematic errors. Moreover, the system control complexity does not increase appreciably and all necessary techniques are compatible with current experimental capabilities. Our scheme also demonstrates strong robustness against finite pulse length and stochastic noise. Owing to the highly developed quantum control methods, various physical systems are well-suited for realizing quantum double lock-in amplifiers. These include Bose condensed atoms^58,59,60,61, trapped ions^{62,63,64,65,66}, nitrogen-vacancy centers in diamond^{56,67,68,69,70}, doped spins in semiconductors^71,72, and even “artificial atoms” like superconducting qubits^27,73,74 and so on. Meanwhile, how to realize the five-level structure in other quantum systems for achieving our scheme still have open questions, and should be carefully analyzed and studied in future. Furthermore, our protocol could enable the development of practical quantum sensors, such as magnetometers^{11,75,76,77,78}, atomic clocks^79,80,81, weak-force detectors¹³, and noise spectroscopy detector^27,81,82.

Methods

Calculation of the common excited-state population

According to Eqs. (17) and (18), we can obtain the time-evolution of the density matrix ρ (see Supplementary Note 4 for more details). After the adiabatic elimination ($t \, \gg \, \frac{1}{\Gamma }$ and $\frac{\partial }{\partial t}{\rho }_{{{{{{{{\rm{55}}}}}}}}}=0$) and assuming the four Rabi frequencies satisfy Ω_j = Ω and {Ω, δ} ≪ Γ, we can derive the common excited-state population

$${\rho }_{{{{{{{{\rm{55}}}}}}}}}\approx \frac{{\Omega }^{2}}{{\Gamma }^{2}}\left(1+\mathop{\sum}_{i,j=1;i\ne j}^{4}\Re ({\rho }_{ij})\right).$$

(23)

In our consideration, ρ₁₃, ρ₁₄, ρ₂₃, and ρ₂₄ are almost 0 before detection, hence the population ρ₅₅ can be approximately given as Eq. (19). Due to the two Λ configurations $\left\{\left\vert 1\right\rangle ,\left\vert 2\right\rangle ,\left\vert 5\right\rangle \right\}$ and $\left\{\left\vert 3\right\rangle ,\left\vert 4\right\rangle ,\left\vert 5\right\rangle \right\}$ have their density matrix elements satisfying ${\rho }_{{{{{{{{\rm{21}}}}}}}}}^{{\prime} }=2{\rho }_{{{{{{{{\rm{21}}}}}}}}}$ and ${\rho }_{{{{{{{{\rm{34}}}}}}}}}^{{\prime} }=2{\rho }_{{{{{{{{\rm{34}}}}}}}}}$, we have

$${\rho }_{{{{{{{{\rm{55}}}}}}}}}\approx \frac{{\Omega }^{2}}{2{\Gamma }^{2}}\left[\left(1+\Re ({\rho }_{{{{{{{{\rm{12}}}}}}}}}^{{\prime} })+\Re ({\rho }_{{{{{{{{\rm{21}}}}}}}}}^{{\prime} })\right)+\left(1+\Re ({\rho }_{{{{{{{{\rm{34}}}}}}}}}^{{\prime} })+\Re ({\rho }_{{{{{{{{\rm{43}}}}}}}}}^{{\prime} })\right)\right],\\ = \frac{{\Omega }^{2}}{{\Gamma }^{2}}\left(1+2\Re ({\rho }_{{{{{{{{\rm{12}}}}}}}}})+2\Re ({\rho }_{{{{{{{{\rm{34}}}}}}}}})\right).$$

(24)

According to the above equation, we find that the five-level double Λ configuration can be divided to such two Λ configurations.

Dyson expansion of quantum evolution

In order to simplify the calculation of the time-ordering operator $\hat{{{{{{{{\mathcal{T}}}}}}}}}$ in Eq. (4), we consider the case of $At\le \frac{\pi }{2}$ and utilize the Dyson expansion

$$\hat{U}({t}_{0},t)= \, \hat{{{{{{{{\mathcal{T}}}}}}}}}\exp \int\nolimits_{{t}_{0}}^{t}\frac{\hat{H}({t}^{{\prime} })}{i\hslash }d{t}^{{\prime} }\\ = \,1\,+\,\,{\sum }_{n=0}^{\infty }\,{\left(\frac{-i}{\hslash }\right)}^{n}\,\,\int\nolimits_{{t}_{0}}^{t}\,\,\,d{t}_{1}\,\,\int\nolimits_{{t}_{0}}^{{t}_{1}}\,\,\,\,d{t}_{2}\,\cdots \,\,\,\int\nolimits_{{t}_{0}}^{{t}_{{{{{{{{\rm{n-1}}}}}}}}}}\,\,\,d{t}_{n}\hat{H}(\,{t}_{1})\,\hat{H}(\,{t}_{2})\,\cdots \,\hat{H}(\,{t}_{n}),$$

(25)

with $\hat{H}({t}^{{\prime} })=\frac{\hslash }{2}\left[{\omega }_{{{{{{{{\rm{z}}}}}}}}}({t}^{{\prime} }){\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}+{\omega }_{{{{{{{{\rm{y}}}}}}}}}({t}^{{\prime} }){\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}\right]$. In units of ℏ = 1, one can obtain

$$\hat{U}(0,t)\, \approx \, 1-\frac{i}{2}[{\phi }_{{{{{{{{\rm{z}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}+{\phi }_{{{{{{{{\rm{y}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}] \\ -\frac{1}{4}\,\left[\int\nolimits_{{{{{{{{\rm{0}}}}}}}}}^{t}\,{\omega }_{{{{{{{{\rm{z}}}}}}}}}({t}_{1}){\phi }_{{{{{{{{\rm{z}}}}}}}}}({t}_{1})d{t}_{1}{\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}^{2}+\int\nolimits_{{{{{{{{\rm{0}}}}}}}}}^{t}{\omega }_{{{{{{{{\rm{y}}}}}}}}}({t}_{1}){\phi }_{{{{{{{{\rm{y}}}}}}}}}({t}_{1})d{t}_{1}{\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}^{2}\right]\\ -\frac{1}{4}\left[\int\nolimits_{{{{{{{{\rm{0}}}}}}}}}^{t}{\omega }_{{{{{{{{\rm{y}}}}}}}}}({t}_{1}){\phi }_{{{{{{{{\rm{z}}}}}}}}}({t}_{1})d{t}_{1}{\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}{\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}+\int\nolimits_{{{{{{{{\rm{0}}}}}}}}}^{t}\,{\omega }_{{{{{{{{\rm{z}}}}}}}}}({t}_{1}){\phi }_{{{{{{{{\rm{y}}}}}}}}}({t}_{1})d{t}_{1}\,{\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}{\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}\right]\\ +{{{{{{{\mathcal{O}}}}}}}}({\phi }^{3})\\ \, \approx \, 1-\frac{i}{2}[{\phi }_{{{{{{{{\rm{z}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}+{\phi }_{{{{{{{{\rm{y}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}]-\frac{1}{8}[{\phi }_{{{{{{{{\rm{z}}}}}}}}}^{2}(\,t)+{\phi }_{{{{{{{{\rm{y}}}}}}}}}^{2}(t)]\\ -\frac{1}{4}{\phi }_{{{{{{{{\rm{z}}}}}}}}}(t){\phi }_{{{{{{{{\rm{y}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}{\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}-\frac{1}{4}\int\nolimits_{{{{{{{{\rm{0}}}}}}}}}^{t}{\omega }_{{{{{{{{\rm{z}}}}}}}}}({t}_{1}){\phi }_{{{{{{{{\rm{y}}}}}}}}}({t}_{1})d{t}_{1}[{\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}},{\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}]\\ +{{{{{{{\mathcal{O}}}}}}}}({\phi }^{3})$$

(26)

and

$${\hat{U}}_{{{{{{{{\rm{g}}}}}}}}}(0,t)= \exp \int\nolimits_{{t}_{0}}^{t}\frac{\hat{H}({t}^{{\prime} })}{i\hslash }d{t}^{{\prime} }\\ \approx 1-\frac{i}{2}\left[{\phi }_{{{{{{{{\rm{z}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}+{\phi }_{{{{{{{{\rm{y}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}\right]\\ -\frac{1}{8}\left[{\phi }_{{{{{{{{\rm{z}}}}}}}}}^{2}(t){\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}^{2}+{\phi }_{{{{{{{{\rm{y}}}}}}}}}^{2}(t){\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}^{2}+{\phi }_{{{{{{{{\rm{y}}}}}}}}}(t){\phi }_{{{{{{{{\rm{z}}}}}}}}}(t)\{{\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}},{\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}\}\right]+{{{{{{{\mathcal{O}}}}}}}}({\phi }^{3})\\ \approx 1-\frac{i}{2}[{\phi }_{{{{{{{{\rm{z}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{z}}}}}}}}}+{\phi }_{{{{{{{{\rm{y}}}}}}}}}(t){\hat{\sigma }}_{{{{{{{{\rm{y}}}}}}}}}]-\frac{1}{8}[{\phi }_{{{{{{{{\rm{z}}}}}}}}}^{2}(t)+{\phi }_{{{{{{{{\rm{y}}}}}}}}}^{2}(t)]\,+{{{{{{{\mathcal{O}}}}}}}}({\phi }^{3}).$$

(27)

Thus, through using $\{{\hat{\sigma }}_{{{{{{{{\rm{I}}}}}}}}},{\hat{\sigma }}_{j}\}={\hat{\sigma }}_{{{{{{{{\rm{I}}}}}}}}}{\hat{\sigma }}_{j}+{\hat{\sigma }}_{j}{\hat{\sigma }}_{{{{{{{{\rm{I}}}}}}}}}=2{\delta }_{{{{{{{{\rm{i,j}}}}}}}}}(i,j=x,y,z)$, the time-ordering operator $\hat{{{{{{{{\mathcal{T}}}}}}}}}$ in Eq. (26) can be removed when $\phi \le 2n\frac{A}{\omega }\le 1$ corresponding to $At\le \frac{\pi }{2}$.