1 Introduction

High-precision measurement of weak alternating signals is a ubiquitous issue in fundamental science and a critical task in practical technologies [1–6]. In practise, the target signal to be measured is generally submerged in a noisy background, which makes it hard to be detected. To obtain a high signal-to-noise ratio (SNR), one has to suppress the effect of noise and enhance the response to the target signal, which are often in conflict. Lock-in measurement is usually used in high-efficiency classical detector to extract a signal from noises, which can be achieved via nonlinear devices [7, 8]. In essence, a classical lock-in amplifier performs a mixing process via generating the instantaneous product of the target signal and the reference signal, and then applies an adjustable low-pass filter for detection.

In analogy to the classical lock-in amplifier, quantum lock-in amplifier can be realized by making use of quantum non-commutativity [9, 10]. Utilizing the quantum lock-in measurement, one can also extract the weak alternating signal from noise with a high SNR. Originated for protecting qubits from decoherence, dynamical decoupling (DD) method becomes one of the well-known quantum control techniques [11–21] and has been extensively used to realize the quantum lock-in measurement [10, 18, 22–27]. The first quantum lock-in amplifier with a single trapped \(\mathrm{Sr} ^{+}\) ion has been demonstrated [9], in which DD manipulations are performed to decouple the quantum probe from noise while enhancing its response to the target signal. Meanwhile, the single-particle quantum lock-in amplifier has recently been used to frequency measurement [9, 10], magnetic field sensing [9], vector light shift detection [28] and weak-force detection [24]. For quantum lock-in measurement, the DD manipulations act as the reference signal, and the subsequent time-evolution act as the filter which can filter out the noise spectral components different from the reference frequency.

It is well known that many-body quantum entanglement can improve the measurement precision. The quantum lock-in measurement has also been developed from single-particle system to many-body system [10]. Using multiple entangled particles, one can realize the entanglement-enhanced lock-in amplifier to achieve Heisenberg-limited detection for weak alternating signals.

In this review, we present the protocols of achieving quantum lock-in amplifier via multi-pulse quantum interferometry to improve the SNR, from single particle system to many-body system. In Sect. 2, we introduce the general protocol for achieving quantum lock-in measurement in analogy to a classical lock-in amplifier. In Sect. 3, we review the protocol of single-particle quantum lock-in amplifier, and its application in high-precision magnetometers, as well as weak force sensors. In Sect. 4, we introduce the general protocol of many-body quantum lock-in amplifier and show how to achieve the Heisenberg-limited quantum lock-in amplifier via the many-body quantum entanglement. Finally, we give a brief summary and outlook in Sect. 5.

2 Quantum lock-in measurement

Lock-in measurement can be used to efficiently extract a weak alternating signals with high SNR from an extremely noisy environment, which is widely used in precision measurement and sensing. Usually, a lock-in measurement mainly includes a mixing process and a filtering process. For classical lock-in measurement, multiplier and integrator are used to realize the mixing and filtering, respectively. While for quantum lock-in measurement, the mixing and filtering are achieved via quantum non-commutativity modulation and time-evolution of the wavefunction. In this section, we first introduce the basic on classical lock-in measurement, and then show the principle of quantum lock-in measurement.

2.1 Classical lock-in measurement

Classical lock-in amplifiers were invented in the 1930’s [29–31] and are capable of extracting a weak alternating signals in extremely noisy environments. The classical lock-in amplifiers has been used as precision AC voltage and AC phase meters, noise measurement units, impedance spectroscopes, network analyzers, spectrum analyzers and phase detectors in phase-locked loops [7, 8]. In general, the input signal in a classical lock-in amplifier can be written as

$$ V _{s}(t)=S (t)+N _{o}(t), $$
(1)

and the reference signal is

$$ V _{r}(t)=\sin (\omega _{m} t). $$
(2)

Here, \(S (t)= A\sin (\omega t)\) is the target signal with A the strength of the signal and ω the oscillation frequency. \(N _{o}(t)\) is the noise signal. The two time-independent parameters \((A,\omega )\) are unknown to be measured. A classical lock-in amplifier generates the output signal via a mix-down process. The input signal \(V _{s}(t)\) is multiplied by the reference signal \(V _{r}(t)\) by an analog multiplier, and then integrated over an integration time T. Eventually after a low pass filter, the target signal can be extracted from the output signal

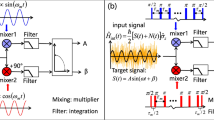
$$ I(T)= \int _{0}^{T}V _{s}(t)\times V _{r}(t)\,dt\approx \frac{AT}{2} \frac{\sin [(\omega -\omega _{m})T]}{(\omega -\omega _{m})T}, $$
(3)

as shown in Fig. 1 (a). Obviously, if the two frequencies ω and \(\omega _{m}\) are equal, the average value reaches the maximum, which is equal to half of the target signal amplitude. However, if ω and \(\omega _{m}\) are different, the average tends to zero. Meanwhile, if the frequencies of noise spectral components are far from reference signal, the negative effect will be averaged out in the integration. This is the basic of a classical lock-in amplifier.

Figure 1
figure 1

(color online). The schematic of classical lock-in amplifier and quantum lock-in amplifier. (a) The classical lock-in amplifier. \(V_{s}(t)=S (t)+N _{o}(t)\) is the input signal, where \(S (t)=A\sin (\omega t)\) is the target signal submerged within the noise \(N _{o}(t)\). \(V_{r}(t)\) is a known reference signal. Inputting the two signals through the classical lock-in amplifier, the signal \(V_{s}(t)\) can be extracted. The amplitude A and frequency ω can be extracted after mixing with a multiplier and filtering by integration. (b) The quantum lock-in amplifier. The coupling between the probe and the signal is described by \(\hat{H}_{\textrm{int}}= [S (t)+N _{o}(t) ] \hat{J}_{z}\) with the target signal \(S (t)\) and the stochastic noise \(N _{o}(t)\). The oscillating modulation term \({\hat{H}}_{\textrm{mix}}\), which is analogue to the reference signal \(V_{r}(t)\), does not commute with \(\hat{H}_{\textrm{int}}\). Hence the mixing process is achieved by such non-commutating operations, and the filtering process is realized by time-evolution. Thus the quantum probe, obeying the Hamiltonian \(\hat{H}=\hat{H}_{\textrm{int}}+\hat{H}_{\textrm{mix}}\), can be used to realize a quantum lock-in amplifier for extracting the signal \(S (t)\)

Full size image

2.2 Lock-in measurement via quantum non-commutativity

The mix-down process is essential for the classical lock-in measurement, which is used for generating the instantaneous product of the target signal with reference signal. It is usually achieved by nonlinear electronic devices. Correspondingly, one can realize a quantum counterpart of lock-in measurement in quantum systems. The key is to find a quantum analogue of the mix-down process. Due to the linearity of Schrödinger’s equation, nonlinear dynamics of the wavefunction cannot be introduced directly. However, the wavefunction dynamics will be proportional to a product of Hamiltonian terms if the total Hamiltonian does not commute with itself at different times [9, 10, 32]. Thus, the quantum mix-down process can be achieved by quantum non-commutativity, and quantum lock-in measurement can be achieved, see Fig. 1 (b).

To illustration the principle of quantum lock-in measurement, we consider an ensemble of N identical two-state bosonic particles, which includes the cases from single-particle (\(N=1\)) to many-body systems (\(N>1\)). The two states can be selected as any desired two levels labeled as spins \(| {\uparrow} \rangle \) and \(| {\downarrow} \rangle \), respectively. The system states can be well characterized by the collective spin operators: \(\hat{J}_{x}=\frac{1}{2}(\hat{a}^{\dagger}\hat{b}+\hat{a}\hat{b}^{\dagger})\), \(\hat{J}_{y}=\frac{1}{2i}(\hat{a}^{\dagger}\hat{b}-\hat{a}\hat{b}^{\dagger})\), \(\hat{J}_{z}=\frac{1}{2}(\hat{a}^{\dagger}\hat{a}-\hat{b}^{\dagger}\hat{b})\), where â and b̂ denote annihilation operators for spins \(| {\uparrow} \rangle \) and \(| {\downarrow} \rangle \), respectively. The system states can be represented in terms of the Dicke basis \(\{| J,m\rangle \}\), where \(\hat{J}_{z} | J,m\rangle = m| J,m\rangle \) with \(J=\frac{N}{2}\) and \(m = -J,-J + 1, \ldots, J-1, J\).

The coupling between the probe system and the external field can be described by the Hamiltonian (we set \(\hbar =1\) hereafter),

$$ {\hat{H}}_{\textrm{int}}(t)=M(t) \hat{J}_{z}, $$
(4)

where the external field \(M(t)=S (t)+N _{o}(t)\) consists of the target signal \(S (t)=A\sin (\omega t)\) and the stochastic noise \(N _{o}(t)\). The noise couple to the probe through the same physical channel and will lead to random energy shifts of the transitions. To implement the quantum lock-in measurement, one can mix the system with an induced modulation signal that does not commute with \({\hat{H}}_{\textrm{int}}(t)\). For the signal term \(\hat{J}_{z}\), one can choose \(\hat{J}_{x}\), \(\hat{J}_{y}\), or other operators that do not commute with \(\hat{J}_{z}\) as the mixing term. Here, without loss of generality, we consider the mixing term is \(\hat{H}_{\textrm{mix}}(t)=\Omega ({t})\hat{J}_{x}\) and the whole Hamiltonian becomes

$$ {\hat{H}}={\hat{H}}_{\textrm{int}}(t)+ \hat{H}_{\textrm{mix}}(t)= M(t) \hat{J}_{z} + \Omega ({t})\hat{J}_{x}. $$
(5)

The Hamiltonian (5) does not commute with itself at different times. The non-commutativity of the two modulation terms \({\hat{H}}_{\textrm{int}}\) and \({\hat{H}}_{\textrm{mix}}\) play an important role for lock-in measurement. The time-evolution of system state \(| {\Psi (t)}\rangle \) obeys the Schrödinger equation,

$$ i\frac{\partial{| {\Psi (t)}}\rangle}{\partial{t}}= \bigl[M(t) \hat{J}_{z}+\Omega ({t})\hat{J}_{x} \bigr]{\big| {\Psi (t)}\big\rangle }. $$
(6)

For convenience, we move into the interaction picture respect to \({\hat{H}_{\textrm{mix}}}\), and the time-evolution is described by

$$\begin{aligned} i\frac{\partial{| {\Psi (t)}}\rangle _{I}}{\partial{t}}= M(t) \bigl[\cos (\alpha ) \hat{J}_{z}+\sin (\alpha )\hat{J}_{y} \bigr]{\big| {\Psi (t)} \big\rangle _{I}}, \end{aligned}$$
(7)

where \(| \Psi (t)\rangle _{I} =e^{i\int ^{t}_{0}{\hat{H}_{\textrm{mix}}(t')} \,\textrm{d}t'}{| {\Psi (t)}\rangle}\) and \(\alpha =\int ^{t}_{0} \Omega (t')\,dt'\). At time T, the system state is

$$\begin{aligned} \big| \Psi (T)\big\rangle _{I} = \hat{\mathcal{T}} e^{-i (\varphi _{1} \hat{J}_{z}+\varphi _{2}\hat{J}_{y} )}\big| {{\Psi}}(0)\big\rangle _{I}, \end{aligned}$$
(8)

with the time-ordering operator \(\hat{\mathcal{T}}\), the initial state \(| {\Psi (0)}\rangle _{I}=| \Psi (0)\rangle \), and the two phase factors

$$ \varphi _{1} = A \int _{0}^{T} \sin (\omega t)\cos (\alpha ) \,\textrm{d}t + \int _{0}^{T} N _{o}(t)\cos (\alpha )\,\textrm{d}t, $$
(9)

and

$$ \varphi _{2} = A \int _{0}^{T} \sin (\omega t)\sin (\alpha ) \,\textrm{d}t + \int _{0}^{T} N _{o}(t)\sin (\alpha )\,\textrm{d}t. $$
(10)

According to Eq. (9) and Eq. (10), it is obvious that if one apply a suitable modulation \(\Omega (t)\) to make \(\cos (\alpha )\) and \(\sin (\alpha )\) periodic and synchronized with the signal \(S (t)\), the phase accumulated owing to \(S (t)\) can adds up coherently and subsequently measured, whereas the phase accumulated owing to stochastic noise \(N _{o}(t)\) can be averaged away. Especially, if the frequencies of the noise spectral components is far from the signal frequency ω, the noise spectral components can be disappeared in the long-time integration. Thus the SNR of the output can be significantly improved via the quantum lock-in measurement.

In quantum control, DD method is a well-developed technique, which can be used to decouple a quantum probe from noise. In the past few years, the DD method has been used in quantum lock-in measurement to improve the SNR of quantum sensors for weak alternating signals [9, 13–16, 19–21, 24, 25, 28, 33–41]. In the following, we will introduce show to use the DD method to realize the quantum lock-in amplifier.

3 Single-particle quantum lock-in amplifier

Single two-level quantum probes are widely used for performing measurements with high sensitivity and precision, including a single nitrogen-vacancy center in diamond [25, 42–47], a single trapped ion [9, 24, 48–52] and so on. Utilizing the quantum lock-in measurement, single-particle quantum lock-in amplifier can be realized and have been widely used for frequency metrology, magnetic field sensing [10, 53–56], vector light shift detection [24], and force detection for the quantum motion of magnetic mechanical resonators [57–59]. In this section, we will first introduce the general framework of single-particle quantum lock-in amplifier [9, 24]. Then, we will review some experimental demonstrations on single-particle quantum lock-in amplifier for high-precision magnetometers and force sensors.

3.1 General protocol

For a single-particle two-level quantum probe, the coupling between the probe and the external signal is described by the Hamiltonian \(\hat{H}_{\textrm{int}}=\frac{1}{2}M (t)\hat{\sigma}_{z}\). Initially, the probe is prepared in the state \(| {\Psi}\rangle _{\textrm{in}}=({| {\uparrow}\rangle +| { \downarrow}}\rangle )/{\sqrt{2}}\), which is a vector along the x axis on the Bloch sphere. In general, under the Hamiltonian \(\hat{H}_{\textrm{int}}\), states \(| {\uparrow} \rangle \) and \(| {\downarrow} \rangle \) acquire a relative phase, which is oscillating back and forth as a result of the signal and is randomly varying owing to the effect of noise. According to the theory in Sect. 2.2, one can realize the quantum lock-in measurement via mixing the system with an induced modulation signal \(\hat{H}_{\textrm{mix}}(t)=\Omega ({t})\hat{J}_{x}\), which does not commute with \({\hat{H}}_{\textrm{int}}\). Here, we consider the modulation \(\Omega (t)\) is a sequence of equidistant sharp π pulses and it written as

$$ \Omega (t)= \pi \sum_{l=1}^{L} \delta (t-l\tau _{e}) $$
(11)

with \(\delta (t)\) is the Dirac δ function, L is the pulse number. Ignoring the noise signal \(N _{o}(t)\), and according to Eq. (8) ∼ (10), at time \(T_{n}=n\tau _{e}\), the output state in the Schrödinger picture is

$$\begin{aligned} | {\Psi (T_{n})}\rangle =e^{i(-1)^{L-1}\phi _{n}(\omega )/2}\bigl({ | { \uparrow}\rangle +e^{i(-1)^{L}\phi _{n}(\omega )}| { \downarrow}}\rangle \bigr)/{\sqrt{2}}. \end{aligned}$$
(12)

Here, the phase \(\phi _{n}(\omega )\) is

$$\begin{aligned} \phi _{n}(\omega ) =&\frac{2A}{\omega}\cos \biggl[ \frac{n\omega \cdot (\tau _{e}-\tau )}{2} \biggr] \\ &{}\times \cos \biggl[\frac{\omega \cdot (\tau _{e}-\tau )}{2} \biggr] \frac{\sin [n\omega \cdot (\tau _{e}-\tau )/2 ]}{\sin [\omega \cdot (\tau _{e}-\tau )/2 ]}. \end{aligned}$$
(13)

where \(\tau =\pi /\omega \) is the half period of the target signal. Obviously, \(\phi _{n}\) is symmetric with respect to the lock-in point \(\tau _{e}=\tau \). Thus through modulating the pulse repetition period \(\tau _{e}\), one can determine the lock-in point from the pattern symmetry, and the amplitude can be extracted from Eq. (13) via a fitting procedure [9]. Especially, in Ref. [9], the target signal is a square waveform, see Fig. 2(b). In general, the rectangular waveform signal can be divided into a sum of weighted sin functions by the Fourier series expansion. Here, we denote phase \(\phi _{n}(\omega )\) as \(\phi _{\textrm{lock-in}}\), and it is

$$\begin{aligned} \phi _{\textrm{lock-in}} =&\frac{2}{\pi}\sum _{k=1,\textrm{odd}}^{ \infty}\frac{1}{k}\phi _{n}(k \omega ) \\ \approx & \frac{AT_{n}}{2}\sum_{k=1,\textrm{odd}}^{\infty} \frac{1}{k^{2}}\textrm{sinc}\bigl[nk\omega (\tau -\tau _{e})\bigr], \end{aligned}$$
(14)

with \(\textrm{sinc}(x)=\frac{\sin (x)}{x}\). Obviously, \(\phi _{\textrm{lock-in}}\) is symmetric with respect to the lock-in point \(\tau _{e}=\tau \), as shown in Fig. 2(f). Similarly, through modulating the pulse repetition period \(\tau _{e}\), one can determine the lock-in point from the pattern symmetry, and the amplitude can be extracted from Eq. (14) via a fitting procedure [9].

Figure 2
figure 2

(color online). The measurement scheme and results of single-ion quantum lock-in amplifier. (a) Level diagram of a \({}^{88}\mathrm{Sr} ^{+}\) ion. (b) The quantum lock-in measurement pulse scheme. (c) Probability of finding the ion in the \(| {\uparrow} \rangle \) state versus \(\phi _{rf}\) at a lock-in period of \(2\tau _{e}=2\) ms. (d) Fringe contrast C versus half lock-in modulation period, \(\tau _{e}\), in the absence of any modulated signal. (e) The columns are lock-in fringe scans, similar to that in (c), for different values of \(\tau _{e}\). (f) Lock-in signal, \(\phi _{\textrm{lock--in}}\), versus \(\tau _{e}\), extracted from (e) as explained in (c). Reproduced from Ref. [9]

Full size image

3.2 Experiment realization

In the past few years, single-particle quantum lock-in amplifier have been widely used in quantum sensing, it includes high-precision magnetometers [9, 25], light shift measurements [9, 28], as well as weak force measurements [24]. Especially, the quantum lock-in measurement was also used to evaluate the phase-noise spectral density of an optical atomic clock [24].

The first quantum lock-in amplifier has been proposed and demonstrated with trapped \(\mathrm{Sr} ^{+}\) ion for high-precision magnetometry [9]. Using this technique, they have measured frequency shifts with a sensitivity of 0.42 Hz\(^{-1/2}\) corresponding to a magnetic field measurement sensitivity of 15 pTHz\(^{-1/2}\). They also perform light shift spectroscopy of a narrow optical quadrupole transition as an application of quantum lock-in amplifier. In the experiment, the two spin states of the electronic ground level of a single \({}^{88}\mathrm{Sr} ^{+}\) ion, \(| {\uparrow}\rangle =| {5s_{1/2},J=1/2,M_{J}=1/2}\rangle \) and \(| {\downarrow}\rangle =| {5s_{1/2},J=1/2,M_{J}=-1/2}\rangle \) are served as a two-level quantum probe, see Fig. 2(a). State initialization and measurement are performed by optical pumping and state-selective fluorescence, respectively. The initial state \(| {\Psi}\rangle _{\textrm{in}}= (| {\uparrow}\rangle + | {\downarrow}\rangle )/\sqrt{2}\) are prepared by a \(\pi /2\) pulse onto \(| {\downarrow}\rangle \). To modulate the ion probe, a train of π pulses equally spaced \(\tau _{e}\) apart are applied, which can be expressed as Eq. (11). Especially, at the lock-in point with \(\tau _{e}=\tau \), according to Eq. (14), \(\phi _{\textrm{lock-in}}\) is proportional to the signal magnitude A. To measure the probe phase \(\phi _{\textrm{lock-in}}\), an additional \(\pi /2\) rotation following the sequence are imposed with a relative phase \(\phi _{rf}\) with respect to the initial \(\pi /2\) pulse. At last, one can evaluate \(\phi _{\textrm{lock-in}}\) by detecting the probability of the ion in the state \(| {\uparrow} \rangle \) with \(P_{\uparrow}=\frac{1}{2}+\frac{C}{2} \cos (\phi _{rf}-\phi _{ \textrm{lock-in}})\). By scanning \(\phi _{rf}\), \(\phi _{\textrm{lock-in}}\) and the fringe contrast C can be retrieved via a fitting procedure, see Fig. 2 (c). Ideally \(C=1\), but in practice, the cosine fringe is reduced in the process of averaging noise term: \(C=\langle \cos (\phi _{N_{o}})\rangle \) with \(\phi _{N_{o}}=\int N _{o}(t)\cos [\alpha (t)]\,dt\), where angle brackets denote an average over different noise. Assuming the noise is composed mainly of discrete frequency components, \(f_{k}=\omega _{k}/2\pi \), with corresponding amplitudes \(B_{k}\), the fringe contrast C can be written as

$$\begin{aligned} C(n,\tau _{e}) =&\prod_{k} J_{0} \biggl(\frac{-4g\mu _{B}}{\hbar} \frac{B_{k}}{\omega _{k}}\sin ^{2} \biggl( \frac{\omega _{k}\tau _{e}}{2} \biggr) \\ &{}\times \frac{\sin ((n-1)\omega _{k}\tau _{e})}{\sin (\omega _{k}\tau _{e})} \biggr). \end{aligned}$$
(15)

Here \(J_{0}(x)\) is the zeroth Bessel function of the first kind, g is the Landé g-factor and \(\mu _{B}\) is the Bohr magneton. For a lock-in sequence with \(n=18\), the experimental results of C (filled circles) and a best fit to Eq. (15) (solid line) are shown in Fig. 2 (d). The lock-in measurement of a small modulated square signal are shown in Fig. 2 (e) and (f).

Meanwhile, the quantum lock-in amplifier also has been used for weak force measurement with trapped \(\mathrm{Sr} ^{+}\) ion [24]. Using the quantum lock-in measurement, they were able to measure force magnitude of \(8.64\pm 0.03\times 10^{-19} \text{ N}\), at frequency of 1 kHz, three orders of magnitude below the trap resonance. In particular, it was reported that the frequency force detection sensitivity can be as low as \(2.8\times 10^{20}\) NHz\(^{1/2}\). An optical atomic clock transition \(S^{1/2}-D^{5/2}\) is used for force measurement, \(| {\downarrow}\rangle =| {S,-\frac{1}{2}}\rangle \) and \(| {\uparrow}\rangle =| {D,\frac{1}{2}}\rangle \) are served as a two-level quantum probe, as shown in Fig. 3 (a). In experiment, the ion is initialized in an equal superposition of the clock states via a \(\pi /2\) pulse onto \(| {\downarrow}\rangle \), i.e., \(| {\Psi}\rangle _{\textrm{in}}= (| {\uparrow}\rangle + | {\downarrow}\rangle )/\sqrt{2}\). Subsequently, the modulation sequence of n echo pulses is applied as shown in Fig. 3(b). After the modulation sequence, a second clock laser \(\pi /2\) pulse with laser phase \(\phi _{rf}\) relative to the initial \(\pi /2\) pulse phase is applied to conclude the sequence. After the Ramsey process, the ion state was detected using state-selective fluorescence. Similarly, the probability of finding the ion in the state \(| {D,\frac{1}{2}}\rangle \) is \(P_{\uparrow}=\frac{1}{2}+\frac{C}{2} \cos (\phi _{rf}-\phi _{n})\) and one can obtain the \(\phi _{n}\) by scanning \(\phi _{rf}\).

Figure 3
figure 3

(color online). The weak-force measurement scheme of single-ion quantum lock-in amplifier. (a) Level diagram of a \({}^{88}\mathrm{Sr} ^{+}\) ion. (b) The quantum lock-in measurement pulse scheme. Reproduced from Ref. [24]

Full size image

Motivated by the concept of quantum lock-in measurement, one can realize quantum heterodyne (Qdyne) detection to achieve high frequency resolution beyond the constraints of the sensor’s coherence time [25, 47]. In the Qdyne detection scheme, the qubit sensor probes an ac signal \(X (t)=A\cos (\omega t)\) in intervals of the sampling period \(T_{s} = T_{a} + T_{r} + T_{d}\), as shown in Fig. 4 (a). Each sampling instance k consists of sensor initialization (green), a phase measurement using quantum lock-in detection (red pulses), and sensor readout (yellow). At time stamp \(T_{k}=kT_{s}\), the sensor output \(Y_{k}\) is proportional to the quantum phase \(\Phi _{k}\) and the instantaneous value of \(X (T_{k})\) (blue dots). In the meantime, the under-sampled signal \(X (t)\) (gray oscillation) is contained in the time trace \(\{Y_{k}\}_{k=1}^{N}\) of sensor outputs. At every measurement time \(T_{k}\), the sensor phase is \(\Phi _{k}=\frac{2AT_{a}}{\pi}\cos [\delta (T_{k}-T_{s}) ]\), where \(\delta =\omega -\omega _{e}\) and \(\omega _{e}(T_{s})\) is a function of \(T_{s}\). The measurement time \(T_{k}\) is independent of the qubit probe and limited by the stability of local oscillator which determines the accuracy of ω. The Qdyne detection has been demonstrated with nitrogen–vacancy (NV) centers for high-precision frequency estimation [25, 47]. In addition, by applying an 880 nT magnetic field oscillating near 1 MHz to a NV center and then recording the magnetic spectrum via Qdyne detection, one can observe a spectrum with a linewidth of 607 μHz, which is just limited by the stability of a quartz crystal oscillator [25], as shown in Fig. 4 (b). Especially, the precision of frequency estimation scaling with time as \(T^{-3/2}\) for classical oscillating fields, as shown in Fig. 4 (c). The Qdyne detection method allows for the detection of an oscillating magnetic field with a frequency precision of 70 microhertz across a bandwidth of one megahertz. Additionally, it achieves an SNR exceeding 104 when measuring a 170 nT test signal for a duration of one hour. In addition, one also can use Qdyne detection to obtain clear nuclear magnetic resonance (NMR) spectra with high resolution. In experiment [60], NMR spectral resolution of about one hertz and NMR scalar couplings in a micrometre-scale sample volume of approximately ten picolitres are both observed.

Figure 4
figure 4

(color online). The quantum heterodyne (Qdyne) detection with a single NV center. (a) Qdyne detection scheme. The qubit sensor stroboscopically probes an ac signal \(X(t)\) in intervals of the sampling period \(T_{s}\). Reproduced from Ref. [47]. Each sampling instance k consists of three stags: sensor initialization (green), a phase measurement using quantum lock-in detection (red pulses), and sensor readout (yellow). (b) Spectroscopy of magnetic fields with a single NV center by applying Qdyne detection. (c) The precision of frequency estimation with Qdyne detection, which scales as \(T^{-3/2}\). Reproduced from Ref. [25]

Full size image

4 Many-body quantum lock-in amplifier

It is well known that many-body quantum entanglement is a useful resource to offer a significant enhancement of measurement precision [39, 61–66]. For N individual particles, such as spin coherence state (SCS), the measurement precision just scales as the standard quantum limit (SQL) i.e., \(\propto 1/\sqrt{N}\). However, the SQL can be surpassed by using entangled multiparticle states. Especially, entangled non-Gaussian states (ENGSs), such as spin cat states or even Greenberger-Horne-Zeilinger (GHZ) states, which set a benchmark for beating the SQL in quantum metrology. The measurement precision can be increased to the Heisenberg limit, i.e., \(\propto 1/{N}\). In this section, we introduce the quantum lock-in amplifier in many-body quantum systems [10]. Firstly, we give the general protocol of the many-body quantum lock-in amplifier. Then, we introduce how to realize the entanglement-enhanced quantum lock-in amplifier. At last, we discuss the experiment feasibility with cold atoms.

4.1 General protocol

The coupling between the probe and the signal is described by the Hamiltonian (4). For an AC magnetic field, \(A=\gamma B\), where B corresponds to the magnetic field amplitude and γ is the gyromagnetic ratio. The goal is to determine the frequency ω and the amplitude B via a many-body quantum lock-in amplifier. According to the theory in Sect. 2.2, one can realize the quantum lock-in measurement via mixing the system with an induced modulation signal \(\hat{H}_{\textrm{mix}}(t)=\Omega ({t})\hat{J}_{x}\), which does not commute with \({\hat{H}}_{\textrm{int}}\). Similar to single-particle quantum lock-in amplifier, the many-body quantum lock-in amplifier can be implemented via use of a sequence of π pulses with equidistant spacing \(\tau _{e}\), which can be expressed as Eq. (11). The carrier frequency \(\omega _{e} \equiv \frac{\pi}{\tau _{e}}\) is analogous to the carrier frequency for the classical lock-in amplifier. When \(\omega _{e}=\omega \), the π pulses are applied at every peak and valley of the target signal \(A=\gamma B\) resulting in a tiny accumulated phase, which can be used for frequency locking. Meanwhile, the phase accumulated owing to the stochastic noise \(N_{o}(t)\) can be averaged away. Through modulating the carrier frequency \(\omega _{e}\), one can extract the frequency ω of the AC magnetic field from the measurement. For a given frequency \(\omega _{e}\), one can use a many-body quantum interferometry to obtain the measurement information. Here, the many-body quantum interferometry includes three stages: (i) initialization, (ii) interrogation, and (iii) readout (see Fig. 5). In the initialization stage, an input state \(| \Psi \rangle _{\textrm{in}}\) is prepared. Then, the input state undergoes an interrogation stage for signal accumulation. At this stage, the system state interacts with the signal field \(S(t)\), and a train of π-pulses with an equidistant spacing are applied at the same time. In the readout stage, a certain unitary operation Û is applied for recombination, and the half-population difference is measured. To describe the protocol intuitively, one can change our description from the Schrödinger picture to the interaction picture. The two pictures are connected via a unitary transformation \(U_{\textrm{{Tr}}}=e^{i\alpha \hat{J}_{x}}=e^{iL\pi \hat{J}_{x}}\). Thus, the final state in the interaction picture before half-population difference measurement can be written as

$$\begin{aligned} | \Psi \rangle _{\textrm{final}}=\hat{U}e^{-i\phi \hat{J}_{z}} | \Psi \rangle _{\textrm{in}}, \end{aligned}$$
(16)

with the accumulated phase \(\phi =\frac{2\gamma B}{\pi} \frac{1-\cos [(\omega -\omega _{e}) T ]}{\omega -\omega _{e}}\). The expectation of the half-population difference measurement on final state is

$$\begin{aligned} \langle \hat{J}_{z}\rangle _{\text{f}}=_{\text{final}} \langle{\Psi} | \hat{J}_{z} | {\Psi}\rangle _{\text{final}}. \end{aligned}$$
(17)

Furthermore, to eliminate the influence of the pulse number, one can define a measurement signal \(J_{z}\) as

$$\begin{aligned} J_{z}=(-1)^{K}\langle \hat{J}_{z} \rangle _{\text{f}}. \end{aligned}$$
(18)

with \(K = 0\) for even L and \(K = 1\) for odd L. According to Eq. (18), When \(\omega -\omega _{e} \rightarrow 0\), the accumulated phase \(\phi \rightarrow \frac{\gamma B (\omega -\omega _{e})T^{2}}{\pi} \approx 0\), the values of \(J_{z}\) is time-independent, while \(J_{z}\) is time-dependent for \(\omega -\omega _{e} \neq 0\). Thus, the pattern of half-population difference measurement at the time \(t=T\) versus the detuning \(\omega -\omega _{e}\) can tell us the lock-in point \(\omega =\omega _{e}\) (the red cross in Fig. 5). Similar to a classical amplifier, one can determine the lock-in point from the pattern of the time-integral of half-population difference measurement, that is

$$\begin{aligned} \tilde{{J}_{z}}=\frac{1}{T_{2}-T_{1}} \int _{T_{1}}^{T_{2}}{J}_{z}\,dt. \end{aligned}$$
(19)

These patterns depend on the input states and will have influences on the measurement precisions. In the next subsection, we discuss how to realize a entanglement-enhanced many-body lock-in amplifier within this framework.

Figure 5
figure 5

(color online). The general protocol of a many-body quantum lock-in amplifier for detecting an AC magnetic field. (a) The many-body quantum interferometry consists of three stages: (i) preparation, (ii) signal interrogation, and (iii) readout. In the initialization stage, an input state \(| \Psi \rangle _{\textrm{in}}\) is prepared. Then, the input state undergoes an interrogation stage for signal accumulation. At this stage, the system state interacts with the magnetic field, and a train of π-pulses with specific equidistant spacing \(\tau _{i}\) is applied. In the readout stage, a certain unitary operation Û is applied for recombination, and the half-population difference is measured. (b) The half-population difference versus the detuning \(\omega -\omega _{e}\) can tell the lock-in point \(\omega =\omega _{e}\). Reproduced from Ref. [10]

Full size image

4.2 Entanglement-enhanced many-body lock-in amplifier

Here, we show the measurement precisions of the many-body quantum lock-in amplifier and show how quantum entanglement can improve the measurement precisions. For individual particles without entanglement, the measurement precisions can just approach the SQL. For entangled particles in a spin cat state, the measurement precisions can be improved to the Heisenberg limit.

For individual particles without any entanglement, suppose all N particles are prepared in the spin coherent state (SCS) \(| \Psi \rangle _{\textrm{SCS}}=e^{-i\frac{\pi}{2}\hat{J}_{y}}| {N/2,-N/2} \rangle \). In this situation, one can choose \(\hat{U}=e^{-i\frac{\pi}{2}{\hat{J}_{y}}}\). Thus, according to Eq. (18), the measurement signal \(J_{z}\) is given as

$$\begin{aligned} J_{z} = \frac{N}{2}\cos (\phi ). \end{aligned}$$
(20)

Further, one can obtain the time-averaged signal \(\tilde{{J}_{z}}\). As shown in Fig. 6(a), (d), (g), the two measurement signals \(J_{z}\) and \(\tilde{{J}_{z}}\) both are exactly symmetric with respect to the lock-in point \(\omega -\omega _{e}=0\). Thus one can determine the lock-in point from the pattern symmetry, and the amplitude can be extracted via a fitting procedure. Utilizing the error propagation formula [1, 67–69], one can obtain the measurement precisions for ω and B via the half-population difference measurement. However without entanglement, the optimal measurement precisions Δω and ΔB only exhibit the SQL scaling, as shown in Fig. 7 (a). For entangled particles, one can use spin cat states to realize the entanglement-enhanced quantum many-body lock-in amplifier. Spin cat state, as a kind of non-Gaussian entangled state, is one of the promising candidates for entanglement-enhanced metrology [64, 70–74].

Figure 6
figure 6

(color online). The lock-in signal of the many-body quantum lock-in amplifier. The measurement signal \(J_{z}\) versus the detuning \(\omega -\omega _{e}\) for (a)(d) SCS, (b)(e) spin cat state \({|\Psi (\theta =\pi /8)}\rangle_{\textrm{CAT}}\), and (c)(f) GHZ state \({|\Psi (\theta =0)}\rangle_{\textrm{CAT}}\) under different evolution times T. The time-averaged signal \(\tilde{{J}_{z}}=\frac{1}{T_{2}-T_{1}}\int _{T_{1}}^{T_{2}}{J}_{z}\,dt\) versus the detuning \(\omega -\omega _{e}\) for (g) SCS, (h) spin cat state \({|\Psi (\theta =\pi /8)}\rangle_{\textrm{CAT}}\), and (i) GHZ state \({|\Psi (\theta =0)}\rangle_{\textrm{CAT}}\), with \(T_{1}=\pi \) and \(T_{2}=3\pi \). Both \(J_{z}\) and \(\tilde{{J}_{z}}\) are symmetric (or antisymmetric) with respect to the lock-in point \(\omega -\omega _{e}=0\) which are also consistent with the analytic expressions

Full size image
Figure 7
figure 7

(color online). Log-log scaling of the optimal measurement precisions (a) Δω and (b) ΔB versus total particle number. The circles are the results for a SCS. The squares and triangles denote the results for spin cat state \(|{\Psi (\theta =\pi /8)}\rangle_{\textrm{CAT}}\) and GHZ state \({|\Psi (\theta =0)}\rangle_{\textrm{CAT}}\), respectively. The lines are the corresponding fitting curves. Reproduced from Ref. [10]

Full size image

Under some conditions, the spin cat states can be written as

$$\begin{aligned} | {\Psi (\theta )}\rangle _{\textrm{CAT}} = \frac{1}{\sqrt{2}} \Biggl[\sum_{m=-J}^{J}c_{m}^{J}( \theta ) (| {J,m}\rangle +| {J,-m} \rangle ) \Biggr]. \end{aligned}$$
(21)

where \(c_{m}^{J}(\theta )=\sqrt{\frac{(2J)!}{(J+m)!(J-m)!}}\cos ^{J+m}( \frac{\theta}{2})\sin ^{J-m}(\frac{\theta}{2})\). Especially when \(\theta =0\), the spin cat state \(| \Psi (0)\rangle _{\textrm{CAT}}=\frac{1}{\sqrt{2}} (| J,J \rangle + | {J,-J}\rangle )\) corresponds to the well-known GHZ state. In this situation, one can choose \(\hat{U}=e^{i\frac{\pi}{2}\hat{J}_{x}}e^{i\frac{\pi}{2}{\hat{J}_{z}^{2}}}e^{i \frac{\pi}{2}\hat{J}_{x}}\). After some algebra, the measurement signal \(J_{z}\) is

$$\begin{aligned} J_{z}=-\sum_{m=-J}^{m=J}(-1)^{J-m}m | c_{m}^{J}(\theta )| ^{2} \sin (2m\phi ). \end{aligned}$$
(22)

Due to the entanglement, the oscillation of the measurement signal \(J_{z}\) becomes related to 2m. When \(\theta =0\), the measurement signal for the GHZ state is \(J_{z} = -\frac{N}{2}\textrm{sin}(N\phi )\). Similarly, one can obtain the time-averaged signal \(\tilde{{J}_{z}}\). As shown in Fig. 6(b), (c), (e), (f), (h), (i), the two measurement signals \(J_{z}\) and \(\tilde{{J}_{z}}\) both are exactly antisymmetric with respect to the lock-in point \(\omega -\omega _{e}=0\). Thus, one can determine the values of ω and B via the two measurement signals. Further, the optimal measurement precisions for spin cat states can exhibit the Heisenberg-limited scaling, as shown in Fig. 7 (b).

4.3 Robustness against stochastic noise

The goal of quantum lock-in amplifier is to detect time-dependent signal from stochastic noise \(N_{o}(t)\). For white noises, \(N_{o}(t)\in [-\eta , \eta ]\) with η denoting the maximum fluctuation strength of the fluctuating field, their long-time integration \(\overline{N_{o}(t)}=0\). Consider a set of sharp π pulses, we have \(\alpha =\int ^{t}_{0}\Omega (t')\,dt'=L\pi \), this means that \(\cos (\alpha )=\pm 1\) and \(\sin (\alpha )=0\). Thus we have \(\int _{0}^{T}N_{o}(t)\cos (\alpha )\,dt \approx 0\), \(\varphi _{1}\approx \phi \) and \(\varphi _{2} =0\). This means that the effect of stochastic noise \(N_{o}(t)\) is canceled out through the time integral. However, the contribution of the target signal \(S(t)\) is imprinted into the phase ϕ. In Fig. 8 (a) ∼ (c), the measurement precision of Δω versus detuning under different stochastic noises \(N_{o}(t)\) is shown. Even though stochastic noise exists, the quantum many-body lock-in amplifier can still be used for weak alternating signal detection with a high SNR.

Figure 8
figure 8

(color online). The robustness of the many-body quantum amplifiers against stochastic noise. The measurement precision Δω versus versus the detuning \(\omega -\omega _{e}\) for (a) SCS, (b)spin cat state \(| \Psi (\theta =\pi /8)\rangle _{\textrm{CAT}}\), and (c) GHZ state \(| \Psi (\theta =0)\rangle _{\textrm{CAT}}\). The blue solid line are the results without stochastic noise (\(\eta =0\)). The red dashed line and green dotted line are the results under stochastic noise with \(\eta =5\gamma B\) and \(\eta =25\gamma B\), respectively. These results are averaged over 20 times. Reproduced from Ref. [10]

Full size image

From another perspective, the noise \(N_{o}(t)\) coupled to the probe through the same physical channel of \(S(t)\) would result in random shifts of the probe’s transition frequency. These random shifts caused by \(N_{o}(t)\) lead to dephasing in the many-body system and may influence the measurement precision. Dephasing is one of the main types of decoherence [75–78], which can be caused by many noise sources such as stray fields, collisions, and laser instabilities. Recent experimental breakthroughs with closely spaced particles such as atoms in optical lattices, ions stored in linear Paul traps [79–81] show that the correlated dephasing is one of the major sources of decoherence in quantum sensing systems.

When the noise \(N_{o}(t)\) uniformly affects all particles in the probe in the same way as Eq. (4), the dephasing is correlated. The influences of correlated dephasing can be well described by the master equation [75–78]. In some circumstances, the time evolution of density matrix under correlated dephasing is equivalent to the ones using unitary dynamical evolution \(e^{-i\hat{H} t}\) under Hamiltonian of Eq. (4) with \(N_{o}(t)\) being a stochastic noise [75–78], which is the cases studied in Fig. 8. That is, the many-body quantum lock-in amplifier in noisy environment is somehow closely related to the many-body Ramsey interferometry under correlated dephasing. According to the results of robustness against stochastic noise, one can find that the quantum many-body lock-in amplifier measurement that using periodic pulses is effective and robust against correlated dephasing.

When the noise \(N_{o}(t)\) is not uniformly coupled to all of the particles in the probe, the resultant dephasing is uncorrelated. This is also commonly observed in systems like trapped-ion and spin-based sensors. Differently, the uncorrelated dephasing independently affects the particles within a probe. However, how the uncorrelated dephasing influences the performance of a many-body quantum lock-in amplifier is still an open question. The effect of uncorrelated dephasing on quantum many-body lock-in amplifier can also be studied via adding an inhomogeneous noise or solving the master equation [75–78], which is deserved further investigation. However, from the results of many-body interferometry under dephasing, one may deduce the influences of uncorrelated dephasing. It was shown that using a GHZ state for typical Ramsey interferometry, the decoherence timescale of evolved state are different for correlated and uncorrelated dephasing [75]. For uncorrelated dephasing, the decoherence timescale is proportion to \(1/N\). While for correlated dephasing, the decoherence timescale is proportion to \(1/N^{2}\), which also called ‘superdecoherence’ [75]. That is, the influence comes form the correlated dephasing is in principle more negative than the ones with uncorrelated dephasing. Since the many-body quantum lock-in amplifier is robust against correlated dephasing, it is believed that the many-body quantum lock-in amplifier would also be robust against uncorrelated dephasing. But this should be carefully analyzed and studied in future.

4.4 Experiment feasibility

Finally, we discuss the experimental feasibility of achieving the many-body quantum lock-in amplifier. To realize the quantum lock-in amplifier, one has to apply multiple rapid π pulses in the interrogation stage. The precise implementation of π pulses is a mature technology in quantum control [16, 20, 33, 39, 40, 82, 83]. In further, to achieve a entanglement-enhanced many-body quantum lock-in amplifier, the preparation of the desired spin cat state and the implementation of an interaction-based readout are two key processes. Owing to the well-developed techniques in quantum control, various multi-particle entangled states have been generated in several systems, including nitrogen-vacancy defect centers [84], Bose condensed atoms [36, 85–88] and ultracold trapped ions [39, 89].

As an example, for an ensemble of Bose condensed atoms occupying two hyperfine levels, it is feasible to prepare the desired spin cat state via dynamical evolution [36, 85, 86, 90] or adiabatic process [63, 64, 66, 87, 88, 91, 92], and achieve the interaction-based readout via tuning the atom-atom interaction. The system can be described by a symmetric two-mode Bose-Josephson Hamiltonian \(\hat{H}_{\textrm{twist}}=\chi \hat{J}_{z}^{2}+\Omega \hat{J}_{x}\). The non-negative parameter Ω is the Josephson coupling strength, and χ denotes the nonlinear atom-atom interaction. The strength and the sign of the nonlinearity χ can be tuned by adjusting the spatial overlap between different spin components via applying a spin-dependent force [90, 93], or by modifying the s-wave scattering lengths via a Feshbach resonance [36, 90, 94].

5 Conclusion and outlook

In this review, we have given an introduction on the principle and implementation of quantum lock-in measurements from single-particle to many-body system. In analogy to a classical lock-in amplifier, a quantum lock-in amplifier can extract weak alternating signals with high SNR from an extremely noisy environment. Using quantum non-commutativity and time-evolution, one can realize quantum lock-in measurements. In particular, quantum lock-in amplifier can be realized via quantum interferometry under a periodic multi-pulse sequence. Further, utilizing suitable quantum entanglement, one can realize entanglement-enhanced quantum lock-in amplifier and achieve the Heisenberg-limited measurements of alternating signals. Based on the state-of-the-art techniques, the quantum sensing protocols with quantum lock-in measurement pave a practical way to achieve high-precision time-dependent signal measurements, which can be widely applied in the field of frequency metrology [9, 16, 25], magnetic field sensing [9], vector light shift detection [28], and force detection [24].

There are still many open problems in the field of quantum lock-in measurements. First, a target alternating signal usually has an unknown initial phase, it is generally hard to extract complete information of amplitude, frequency and phase of a target signal. For classical probes, one can resolve this issue via a double lock-in amplifier. How to realize a quantum counterpart to the classical double lock-in amplifier for alternating signals measurement? Further, how to realize the quantum double lock-in amplifier based on the typical synthetic quantum systems such as cold atoms and trapped ions? Second, vector alternating signal estimation is yet another crucial problem for practical sensing technology. A main challenge for a vector alternating signal estimation is the incompatibility of optimal measurements for different vector components. How to realize vector alternating signal estimation with the aid of quantum lock-in measurement? Third, there are many different types of noise in realistic experiments, such as color noise, depolarization noise, radio frequency noise and so on. How to resist different types of noise via applying suitable quantum non-commutative modulations? The exploration of these problems will hopefully promote the development of practical quantum sensing technologies in the near future.