Introduction

Geometries of microwave passive components become continuously more involved to fulfil the performance requirements of various application areas (wireless communications including 5G and 6G1,2, internet of things3, wireless sensing4, microwave imaging5, wearable devices6, autonomous vehicles7, etc.). In particular, many of these applications require specific functionalities such as multi-band operation8, harmonic suppression9, customized phase characteristics10, reconfigurability11, often combined with limitations on the physical size of the devices12,13,14,15. Due to their inherent complexity, microwave structures designed to meet these and other requirements typically feature considerably increased numbers of design variables than conventional circuits, whereas their design process has to account for several objectives and constraints imposed on their electrical characteristics. Adequate parameter tuning of such circuits requires rigorous numerical optimization16,17,18,19,20. At the same time, the adjustment process has to be carried out at the level of full-wave electromagnetic (EM) simulations to account for effects such as EM cross-couplings, or dielectric and radiation losses. These cannot be properly quantified using analytical or equivalent network models, yet are important for the operation of modern circuits implemented using techniques such as transmission line folding21, defected ground structures22, the employment of slow-wave phenomena (e.g., compact microstrip resonant cells, CMRCs23), or the incorporation of geometrical modifications (stubs24, slots25, shorting pins26). Although imperative from the standpoint of ensuring design quality, EM-driven design optimization is computationally expensive, even in the case of local tuning27, let alone global28 or multi-objective search29, or statistical design30.

Given the importance of simulation-based design, substantial research efforts have been aimed at addressing the underlying challenges, primarily in terms of improving the computational efficiency of the optimization procedures. In the case of local gradient-based search, the major bottleneck is the evaluation of the system response gradients, which can be accelerated using adjoint sensitivities31,32, by restricting the finite-differentiation-based updates33,34,35, or utilization of mesh deformation techniques36. In some cases, the cost of simulation-driven design may be reduced by the employment of fast dedicated solvers37. Another option is the exploration of the specific structure of the system response (e.g., the allocation of resonances, in-band ripples, etc.) using techniques such as response feature technology38,39, or cognition-driven design40. Notwithstanding, one of the most popular approaches in the recent years have become surrogate-assisted methods20,41,42. Therein, most of the operations are carried out at the level of fast surrogates, with costly EM simulations only executed occasionally, to validate the designs produced using the metamodels or to obtain the data necessary for model refinement. Among the two major classes of surrogate modelling methods, the physics-based ones are more often used for local search purposes (space mapping43, response correction44,45,46), whereas data-driven models (kriging47, Gaussian process regression, GPR48, artificial neural networks49,50,51, support vector regression52, polynomial chaos expansion53) are perceived as more generic, and suitable for global and multi-criterial design54,55,56, as well as uncertainty quantification57,58,59,60. Related methods include machine learning techniques61,62,63, as well as surrogate-assisted frameworks involving variable-resolution models (two-level GPR64, co-kriging65).

While the methods outlined in the previous paragraph mainly focus on reducing the CPU costs, reliability of simulation-based design procedures is just as important consideration. In practice, the lack of sufficiently good initial design may lead to a failure of local parameter tuning, with the alternative being the involvement of much more expensive global search algorithms. A typical situation is dimension scaling (re-design of a circuit to meet different operating parameters, e.g., the centre frequency or dielectric substrate), or design of miniaturized components employing CMRCs66. Although global search may be accelerated using surrogate-assisted methods67,68, these methods are incapable of handling structures featuring large number of parameters69.

An attempt to address the reliability issues pertinent to local search procedures has been made in a recently introduced design requirement management procedure70. Therein, the design goals for a given iteration of the optimization algorithm are set up having in mind the actual operating parameters of the circuit at hand. In particular, the goals (e.g., target operating frequencies) are relocated automatically to ensure their attainability through local tuning. As the optimization process progresses, the objectives step-by-step converge to their initial values. The method of Koziel et al.70 has been shown to significantly enhance the immunity of the gradient-based algorithms to inferior-quality starting points at the expense of a certain increase of the computational cost. In this paper, we describe a novel procedure, which is an advancement over70 in terms of improving the computational efficacy of the search process. The latter is achieved via the incorporation of variable-fidelity EM models, selected from a continuous spectrum of the assumed resolutions. A priori knowledge concerning the range of admissible model resolutions is necessary to set up the proposed optimization framework, and it has to be provided by the user. Typically, this range is assessed through grid convergence studies, i.e., visual inspection of the families of component responses at various fidelities. The lowest-fidelity simulations are utilized at the onset of the optimization process, which allows for parameter space exploration at minimum CPU expenses. During the algorithm course, the problem-specific knowledge (in the form of the actual operating parameters of the current design) is extracted from the EM-simulated components response at this design, and, similarly as in Koziel et al.70, is subsequently utilized to adjust the design goals at the current iteration, as well as the EM model fidelity. As the design goals (according to the scheme adopted from70) become closer to their original values, and the algorithm starts to converge—as measured by the relocation of the design and iteration-wise objective function differences—the model fidelity increases, to eventually attain the high-fidelity level near the conclusion of the run. The proposed knowledge-based procedure has been verified using three microstrip circuits, including two couplers and a dual-band power divider. The obtained results demonstrate a significant improvement of the computational efficiency with the average savings of 55 percent over the single-fidelity procedure of Koziel et al.70, and essentially no detrimental effects on the design quality. The presented algorithm offers improved reliability under difficult design scenarios (e.g., poor initial conditions), as well as reduced running costs. The former feature extends the applicability of local search procedures by reducing the need to default to global routines, which is of significant practical importance. The aforementioned advantages of the introduced procedure, i.e., its enhanced reliability and increased computational efficacy, have been achieved by employing two mechanisms, automated design requirement management and knowledge-based adjustment of the simulation model fidelity.

The novelty and the technical contribution of this work can be summarized as follows: (1) development and implementation of a variable-resolution design optimization framework algorithm with design requirement management, (2) association of the model fidelity management scheme with the discrepancy between the target and actual operating frequencies of the component under design, (3) verifying reliability and low computational cost of the introduced algorithm under demanding scenarios, especially inferior-quality starting points operating at frequencies severely misaligned with the targets. The presented algorithm combines the computational efficiency and robustness, which are integrated in a single optimization procedure. To the authors’ best knowledge, no comparable algorithm for design optimization of microwave components has been reported in the literature thus far.

Adaptive design requirements for reliability improvement

This section briefly summarizes the adaptive performance specification method of Koziel et al.70, which is one of the two major ingredients of the optimization framework proposed in the paper. The other, variable-fidelity model management, will be elaborated on in “Variable-fidelity models for optimization cost reduction” section.

Automated adaptation of design requirements for local search enhancement

The design requirement management scheme of Koziel et al.70 will be explained using a design problem in which the N-band circuit at hand is to work at the target frequencies fk, k = 1. We denote by x a vector of design parameters, and by S(x) the EM-evaluated outputs (normally, the scattering parameters). The frequencies fk are gathered into a target vector F = [f1 … fN]T. The aim is to find

$${\boldsymbol{x}}^{*} = \arg \mathop {\min }\limits_{{\boldsymbol{x}}} U({\boldsymbol{S}}({\boldsymbol{x}}),{\boldsymbol{F}})$$
(1)

with U being a merit function (or objective function). For additional clarification, consider an equal-split coupler, which is to run at the operating frequency f0; the device is supposed to minimize both input matching and port isolation at f0. Given the above, the characteristics of interest are S-parameters Sj1, j = 1, …, 4. The function U can take the form of

$$\begin{gathered} U({\boldsymbol{S}}({\boldsymbol{x}}),{\boldsymbol{F}}) = U\left( {[S_{11} ({\boldsymbol{x}},f),S_{21} ({\boldsymbol{x}},f),S_{41} ({\boldsymbol{x}},f),S_{41} ({\boldsymbol{x}},f)],[f_{0} ]} \right) = \\ \max \left\{ {|S_{11} ({\boldsymbol{x}},f_{0} )|,|S_{41} ({\boldsymbol{x}},f_{0} )|} \right\} + \beta \left[ {|S_{21} ({\boldsymbol{x}},f_{0} )| - |S_{31} ({\boldsymbol{x}},f_{0} )|} \right]^{2} \\ \end{gathered}$$
(2)

Note that the objectives are categorized: minimization of |S11| and |S41| is the primary goal; the equal power split condition is an equality constraint, ensured by the penalty term proportional to the penalty coefficient β. It should be emphasized that (2) is only an illustrative example, whereas the overall concept outlined here is generic and applicable to other EM-driven tasks.

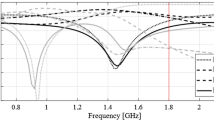
Figure 1 shows the example of a branch-line coupler, which is intended to work at 1.8 GHz. Local search starting from the design indicated using black lines will succeed, whereas optimization from the design shown using the grey lines will fail because of a significant discrepancy between the target and existent operating frequencies.

Figure 1
figure 1

S-parameters of a compact branch-line coupler. Vertical line indicates the intended operating frequency of 1.8 GHz, which is reachable by a local optimizer if launched from the design marked black. Yet, it cannot be reached from the design marked grey due to the operating frequency overly distant from the intended one.

Full size image

The automated adaptive specification management scheme70 addresses the above issue by relocating the targets throughout the optimization run so that they are reachable at each stage of the process. The amount of relocation depends on the detected discerned discrepancy between the existent and desired operating frequencies. A graphical illustration of the specification management procedure has been provided in Fig. 2.

Figure 2
figure 2

The concept of the design requirement adjustment on the example of a branch-line coupler of Fig. 1. The starting point (marked gray) and the intended operating frequency (marked using vertical line) are identical to that of Fig. 1: (a) target frequency shifted near the actual operating frequency of the initial design to make sure that the ongoing specifications (dashed line) may be reached from this very design, (b) intermediate step with the current design and specs shown, (c) ultimate optimization step: the intended operating frequency restored to its assumed value, (d) final design meeting the original requirements.

Full size image

Automated adaptation of design requirements: prerequisites and implementation

The design specification management scheme operates based on the following prerequisites: (i) the necessary relocation of the target frequencies should be identified using the actual operating conditions at the current design, and (ii) the relocated goals should be reachable through local search.

In the following, J(x) will represent the sensitivity matrix of the system outputs S(x). Assuming that the optimization procedure is iterative and yields approximate designs x(i), i = 0, 1, …, to the optimum solution x* of (1) (x(0) denotes the starting point), we utilize the first-order linear expansion model LS(i)(x) of S(x) at x(i)

$$L_{S}^{(i)} ({\boldsymbol{x}}) = {\boldsymbol{S}}({\boldsymbol{x}}^{(i)} ) + {\boldsymbol{J}}({\boldsymbol{x}}^{(i)} ) \cdot ({\boldsymbol{x}} - {\boldsymbol{x}}^{(i)} )$$
(3)

Also, consider an auxiliary sub-problem

$${\boldsymbol{x}}^{tmp} = \arg \mathop {\min }\limits_{{||{\boldsymbol{x}} - {\boldsymbol{x}}^{(i)} || \le D}} U(L_{S}^{(i)} ({\boldsymbol{x}}),{\boldsymbol{F}})$$
(4)

where the search radius D is typically set to D = 1, whereas xtmp denotes the temporary design.

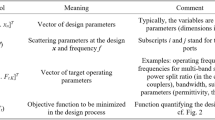
The automated alteration of design specs is based on the factors described in Table 170.These guide the decision-making process and are used to define the conditions gathered in Table 2, satisfaction of which decides upon modification of the design goals with respect to their original values aggregated in the target vector F. In particular, satisfaction of any of the conditions is considered an indication that the performance requirements are unlikely to be attained and should be relaxed accordingly.

Table 1 Adaptive performance specifications: decision factors.
Full size table
Table 2 Design specification adjustment conditions&.
Full size table

The thresholds Fr.min (for improvement factor) and Dc.max (for distance between the actual and target operating frequencies) of Table 2 are generally problem dependent, and should be set up having in mind the typical (or expected) operating bandwidths of the circuit at hand. A simple procedure for adjusting these values has been described in Koziel et al.70.

Having defined the decision factors and adjustment conditions, we can now summarize the design specification management procedure. The target operating frequencies for the (i + 1)th iteration of the optimization algorithm will be denoted as Fcurrent(a) = [fcurrent.1(a) … fcurrent.N(a)]T, where 0 ≤ a ≤ 1. The individual frequencies fcurrent.k are obtained as

$$f_{current.k} (a) = (1 - a)f_{c.k} + af_{k} \quad for\quad k = 1, \ldots ,N$$
(5)

where fc.k are the existent operating frequencies at x(i) (we also have the vector of current operating frequencies Fc = [fc.1 … fc.N]T). The value of the factor a is determined as the maximal value a ≤ 1 so that Fr ≥ Fr.min and Dc ≤ Dc.max at the design xtmp obtained through minimizing (cf. (4))

$${\boldsymbol{x}}^{tmp} = \arg \mathop {\min }\limits_{{||{\boldsymbol{x}} - {\boldsymbol{x}}^{(i)} || \le 1}} U(L_{S}^{(i)} ({\boldsymbol{x}}),{\boldsymbol{F}}_{current} (a))$$
(6)

In practice, a is found using an auxiliary numerical optimization process, in which it is gradually reduced (starting from a = 1) so that Fr ≥ Fr.min and Dc ≤ Dc.max for xtmp produced by (6). Satisfaction of both conditions means that the current targets are reachable from x(i). In the course of the optimization run, the adjusted specs will ultimately converge to the assumed values (which is equivalent to satisfying both Fr ≥ Fr.min and Dc ≤ Dc.max for a = 1), assuming that that initial specs are attainable. Otherwise, the algorithm will terminate when getting as close to the targets as achievable.

The described decision-making procedure is executed before each iteration of the search process. Consequently, the design targets are continuously adjusted to account for the current discrepancies between the actual and desired operating parameters. An important observation is that the modification process incurs no extra computational costs (in terms of additional EM evaluations), because it is based on the sensitivity data already evaluated during routine working of the optimization procedure.

Variable-fidelity models for optimization cost reduction

In this work, the primary tool incorporated to enhance computational efficacy of the optimization process is the incorporation of variable-fidelity EM simulation models. This section explicates the introduced knowledge-based model fidelity management procedure, which is based on two factors: (1) the detected discrepancy between the current and original design targets, and (2) the convergence indicators of the algorithm.

Variable-fidelity EM simulations

Computational models of microwave devices can be implemented using full-wave EM analysis71, or circuit theory tools (equivalent networks72, analytical descriptions73). In this work, it is assumed that the primary (high-fidelity) representation of the circuit of interest is in the form of (high-fidelity) EM simulation, whereas lower-fidelity models are obtained through EM analysis executed at lower discretization density of the structure. This is a versatile and easy to control way, which also ensures a sufficiently good correlation between the models of different resolutions. Other simplification factors (e.g., neglecting losses, reducing computational domain74) will not be considered here. Utilization of multi-fidelity models can be beneficial for computational efficiency of the CAD procedures, e.g., space mapping75, response correction45,46, co-kriging76. Typically, two levels of fidelity are employed (coarse/low-fidelity, fine/high-fidelity)77), which raises some practical issues related to appropriate model selection and setup78.

Model fidelity can be modified using the parameters controlling the meshing algorithms, e.g., lines-per-wavelength (LPW) of CST Microwave Studio. Figure 3 provides an example of a dual-band power divider and the relationship between LPW and the average simulation times of the structure. The minimum model fidelity (here, denoted as Lmin) should be selected to ensure that the corresponding circuit responses are still representative, i.e., not excessively distorted with respect to the maximum fidelity (here, denoted as Lmax). The latter, corresponding to the high-fidelity model, should render the circuit response of the accuracy considered sufficient for practical purposes. Observe that in our work, the model accuracy is understood as the accuracy of the EM simulation model implemented is CST Microwave Studio, and it depends on the mesh density. In general, the higher the density, the better the model accuracy.

Figure 3
figure 3

Dual-band power divider with multi-fidelity EM simulations: (a) average simulation time vs model resolution (controlled by LPW, i.e., lines-per-wavelength parameter), (b) certain S-parameters for the chosen LPW values. The vertical lines denote resolutions of the fine (high-fidelity) model (—), and the coarse (low-fidelity) model (---).

Full size image

The computational model fidelity L is selected from the admissible range Lmin ≤ L ≤ Lmax. At the initial phase of the optimization procedure, L is set to Lmin so as to accelerate the optimization process. Towards the end of the run, L gradually converges to Lmax to ensure reliability. The resolution at any given iteration of the optimization algorithm is governed by the discrepancy between the original and current values of the target operating frequencies (cf. “Knowledge-based model fidelity adjustment based on performance specifications”section), and by the algorithm convergence status (cf. “Model fidelity adjustment based on convergence status”section).

Knowledge-based model fidelity adjustment based on performance specifications

Here, we propose to adjust the model fidelity at the initial phase of the optimization run based on the distance Dcr =||Fcr − F|| between the target operating vector Fcr at the current iteration point and the target F. It should be noted that Dcr is similar to Dc (cf. Table 1), but evaluated using the modified targets instead of the current operating frequencies Fc. Further, we denote Dcr(0) as the value of Dcr after the initial adjustment of the targets, which will be the point of reference for subsequent fidelity modifications. At this point, the fidelity parameter L is set to Lmin (i.e., the optimization process is initiated with the lowest-fidelity model). The model fidelity L(i) at the ith iteration is set according using the formula

$$L^{(i)} = L_{\min } + \alpha \left( {L_{\max } - L_{\min } } \right)\left[ {1 - \frac{{D_{cr}^{(i)} }}{{D_{cr}^{(0)} }}} \right]$$
(7)

where Fcr denotes the target operating vector at the current iteration point, \(D_{cr}^{(i)} = ||{\boldsymbol{F}}_{cr}^{(i)} - {\boldsymbol{F}}||\); here, and Fcr(i) stands for the target operating frequencies modified for iteration i. The scalar coefficient α ∈ [0, 1] controls the maximum model fidelity used until Fcr(i) reaches F (for the experiments of “Verification case studies” section, we set α = 0.5).

Model fidelity adjustment based on convergence status

The increase of the model fidelity is continued after reducing Dcr(i) to zero, i.e., after Fcr(i) becomes equal to F. This second stage is governed by the procedure discussed in79. It is also assumed that the optimization process is concluded if one of the two conditions is met: (i) ||x(i+1) − x(i)||< εx (convergence in argument), or |U(x(i+1)) − U(x(i))|< εU (convergence in the merit function value). Therein, εx and εU are the termination thresholds, set to εx = 10−3 and εU = 10−2, in the numerical experiments of “Verification case studies” section. Let us also consider the convergence factor79

$$Q^{(i)} (\varepsilon_{x} ,\varepsilon_{U} ) = \max \left\{ {\varepsilon_{x} /||{\boldsymbol{x}}^{(i + 1)} - {\boldsymbol{x}}^{(i)} ||,\varepsilon_{U} /|U_{P} ({\boldsymbol{x}}^{(i + 1)} ) - U_{P} ({\boldsymbol{x}}^{(i)} )|} \right\}$$
(8)

It is employed to decide upon the model fidelity level L(i+1) for the (i + 1)th algorithm iteration. We have

$$L^{(i + 1)} = \left\{ \begin{gathered} L_{cr} \;\;{\text{if}}\;\;Q^{(i)} (\varepsilon_{x} ,\varepsilon_{U} ) \le M \hfill \\ \max \left\{ {L^{(i)} ,L_{cr} + \left( {L_{\max } - L_{cr} } \right)\left[ {1 - \frac{{\log (Q^{(i)} (\varepsilon_{x} ,\varepsilon_{U} )}}{\log M}} \right]} \right\} \hfill \\ \end{gathered} \right.$$
(9)

where Lcr is the model fidelity when the actual frequency Fcr(i) first reached the target F. The parameter M determined the convergence level for initiating fidelity adjustment (set M = 102εx, as recommended in79). Furthermore, the fidelity is obligatorily set to Lmax near the convergence if the highest L(i) was below Lmax. In such case, the search region size (cf. “Trust-region-embedded gradient-search” section) is additionally extended by a multiplier Md (we use, Md = 10), and the search continues with L(i+1) = Lmax79.

The final acceleration mechanism is to evaluate the Jacobian matrices of the circuit at hand through finite differentiation executed at iteration i at lower level of fidelity LFD (model fidelity for carrying out finite differentiation), rather than L(i). Here, LFD = max{Lmin, λL(i)}, with λ = 2/3 (cf.79). It has been observed that this typically results in reducing the overall computational cost (due to good correlation of sensitivities for models of different resolutions), even though the optimization may require a slightly larger number of iterations.

Complete optimization framework

Here, we put together the algorithmic components discussed in “Adaptive design requirements for reliability improvement” and “Variable-fidelity models for optimization cost reduction” sections, and summarize the operation of the entire procedure proposed in this work. The core optimization procedure is a gradient-based routine with numerical derivatives, which will be recalled in “Trust-region-embedded gradient-search” section. “Optimization algorithm” section provides the pseudocode of our algorithm, along with the flow diagram thereof.

Trust-region-embedded gradient-search

The algorithmic components oriented towards improving the reliability (“Adaptive design requirements for reliability improvement” section) and computational efficiency of the search process (“Variable-fidelity models for optimization cost reduction” section) can be incorporated into any iterative optimization procedure. In this work, the core routine is the trust-region (TR) gradient search80. The design task is the minimization problem (1). The TR algorithm works iteratively and yields a series of approximations x(i), i = 0, 1, …, to the optimum design x* as

$${\boldsymbol{x}}^{(i + 1)} = \arg \mathop {\min }\limits_{{||{\boldsymbol{x}} - {\boldsymbol{x}}^{(i)} || \le d^{(i)} }} U(L_{S}^{(i)} ({\boldsymbol{x}}),{\boldsymbol{F}}_{cr}^{(i)} )$$
(10)

In (10), L(i) is a linear expansion model (3) established at the current design x(i). Recall that Fcr(i) is the current vector of assumed operating frequencies. Throughout the optimization run, the update of the TR search radius d(i) is performed iteratively by taking into account the gain ratio r = [U(S(x(i+1)),Fcr(i)) − U(S(x(i)),Fcr(i))]/[U(LS(i)(x(i+1)),Fcr(i)) − U(LS(i)(x(i)),Fcr(i))], which quantifies the actual improvement of the objective function (based on EM analysis) versus the estimated improvement (based on the linear model prediction). In case of improvement (r > 0), the design x(i+1) is accepted. Also, if r > 0.75, d(i+1) is increased to 2d(i); if r < 0.25, d(i+1) is reduced to d(i)/3. Rejection of the design (r < 0) results in repeating the iteration with a reduced TR size.

Optimization algorithm

The kernel of the knowledge-based optimization procedure introduced in this paper is the TR algorithm briefly discussed in “Trust-region-embedded gradient-search” section. The automated design requirement management strategy of “Adaptive design requirements for reliability improvement” section, and the variable-fidelity model adjustment scheme of “Variable-fidelity models for optimization cost reduction” section, are simultaneously incorporated therein. In particular, both the design goals and the model fidelity are adjusted before each iteration of the TR routine. The goals are modified based on the decision factors of Table 1 and conditions of Table 2, whereas the model fidelity is altered using the coefficient Dcr (cf. “Knowledge-based model fidelity adjustment based on performance specifications” section), and the convergence indicator Q(i) (cf. “Model fidelity adjustment based on convergence status” section). Figure 4 shows the pseudocode of the entire procedure, whereas Fig. 5 provides its flow diagram. The designer needs to supply the following information:

  • Initial design x(0),

  • Analytical formula for the objective function U,

  • Target vector F,

  • The range of EM model fidelities Lmin and Lmax.

Figure 4
figure 4

Pseudocode of the proposed optimization algorithm with design requirement management and variable-fidelity EM models.

Full size image
Figure 5
figure 5

Flow diagram of the introduced optimization algorithm with design requirement adjustment and variable-fidelity EM models.

Full size image

Also, the termination condition discussed in “Model fidelity adjustment based on convergence status” section (argument and objective function convergence) needs to be complemented by an additional condition specific to the trust region frameworks, i.e., d(i) < εx (reduction of the TR size).

Verification case studies

The algorithm introduced in “Adaptive design requirements for reliability improvement” through “Complete optimization framework” sections is verified here with the use of three examples of microstrip circuits: two branch-line couplers (a single- and dual-band one), and a dual-band power divider. All circuits are optimized from inferior-quality initial designs, i.e., such whose operating frequencies are away from the design targets. This setup allows us to demonstrate the relevance of the reliability improvements achieved through the adaptive performance requirement approach. At the same time, we investigate computational savings that can be obtained using the variable-fidelity mechanisms incorporated into our procedure. All the simulations were performed on Intel Xeon 2.1 GHz dual-core CPU with 128 GB RAM.

Circuit I: compact branch-line coupler (BLC)

The first example is a compact branch-line coupler shown in Fig. 6a. Figure 6b provides the relevant data, including designable parameters, computational models, initial design, and performance specifications. The circuit is to be optimized to minimize its matching and port isolation, as well as to provide equal power split at the center frequency of 1.0 GHz. The results obtained using the proposed algorithm, standard gradient-based optimization (cf. "Trust-region-embedded gradient-search" section), as well as adaptive design requirements technique70, have been gathered in Table 3. The S-parameters of the circuit at the initial design as well as design obtained using the presented approach can be found in Fig. 7. The optimized parameter values are x* = [0.99 0.65 8.59 13.2 1.00 0.94 0.85 0.62 4.02 0.24]T mm. It can be noted (cf. Table 3) that the designs obtained using the algorithm discussed in this work and the method of Koziel et al.70 are of similar quality. Moreover, the computational speedup achieved through the incorporation of variable-fidelity EM simulations is significant: the total cost of the parameter tuning process corresponds to only 97 high-fidelity circuit analyses (51 percent savings over70). As indicated in Table 3, conventional gradient-based search failed to identify a satisfactory design. The evolution of the design targets and model fidelity has been illustrated in Fig. 8. Note that the major part of the optimization process has been carried out using lower-fidelity models, the high-fidelity simulations are only applied at the latest stages of the algorithm, which translated into the aforementioned speedup.

Figure 6
figure 6

Compact branch-line coupler (Circuit I): (a) geometry81; (b) main parameters and design objectives.

Full size image
Table 3 Optimization results for Circuit I.
Full size table
Figure 7
figure 7

Compact branch-line coupler: circuit responses at the initial design (grey lines), and the optimal design rendered by the introduced framework with design specification adaptation and variable-fidelity models (black lines). Vertical line marks target operating frequency.

Full size image
Figure 8
figure 8

Compact branch-line coupler: (a) history of the target operating frequency (horizontal line marks the initial target); (b) evolution of the model resolution.

Full size image

Circuit II: dual-band branch-line coupler

As the second verification case, consider a dual-band branch-line coupler of Fig. 9a. The important parameters of the circuit have been listed in Fig. 9b. In this case, the design objective is to minimize the matching |S11| and isolation |S41|, and to achieve equal power split at the operating frequencies of 1.2 GHz and 2.7 GHz. Table 4 gathers the optimization results for the introduced and the benchmark methods. Figure 10 shows the coupler S-parameters at the initial and the final design, x* = [42.0 10.0 0.85 2.56 1.50 1.33 0.60 0.44 2.01]T mm, found by the algorithm of "Verification case studies" section. Similarly as for the first example, the utilization of variable-fidelity simulations leads to considerable computational savings of 61 percent over the adaptive design specification method of Koziel et al.70. The cost reduction is achieved without compromising the design quality as indicated in Table 4. In absolute terms, optimization cost corresponds to 94 EM analyses of the coupler using highest resolution. Figure 11 illustrates the evolution of design goals and model fidelity.

Figure 9
figure 9

Dual-band branch-line coupler (Circuit II): (a) geometry82; (b) main parameters and design objectives.

Full size image
Table 4 Optimization results for Circuit II.
Full size table
Figure 10
figure 10

Dual-band branch-line coupler: circuit responses at the initial design (grey lines), and the optimal design rendered by the introduced framework with design specification adaptation and variable-fidelity models (black lines). Vertical lines mark target operating frequencies.

Full size image
Figure 11
figure 11

Dual-band branch-line coupler: (a) history of the target operating frequency (horizontal lines mark the initial targets); (b) evolution of the model resolution.

Full size image

Circuit III: dual-band power divider

The final verification case is a dual-band power divider shown in Fig. 12a. The essential circuit parameters have been provided in Fig. 12b. The aim is to minimize the input and output matching (|S11|, |S22|, |S33|) and port isolation |S23| simultaneously at the operating frequencies 2.4 GHz and 3.8 GHz, as well as to obtain equal power division ratio. The latter is implied by the circuit symmetry, therefore, does not have to be explicitly handled in the optimization process. The numerical results are provided in Table 5. The algorithm performance is in accordance with that of the previous examples. On the one hand, we observed considerable computational savings of 54 percent over the single-fidelity procedure of Koziel et al.70. On the other hand, the quality of design produced by the presented method is similar to the benchmark. It should also be noted that the conventional gradient search fails due to severe misalignment between operating frequencies of the coupler at the initial design and the assumed ones. The optimized parameter vector is x* = [26.3 5.09 20.6 5.12 1.0 0.60 4.34]T. The remaining results can be found in Fig. 13 (circuit responses at the initial and optimal designs), and Fig. 14 (evolution of the design specifications and model fidelity).

Figure 12
figure 12

Dual-band power divider (Circuit III): (a) geometry83; (b) main parameters and design objectives.

Full size image
Table 5 Optimization results for Circuit III.
Full size table
Figure 13
figure 13

Dual-band power divider: circuit responses at the initial design (grey lines), and the optimal design rendered by the introduced framework with design specification adaptation and variable-fidelity models (black lines). Vertical lines mark target operating frequencies.

Full size image
Figure 14
figure 14

Dual-band power divider: (a) history of the target operating frequency (horizontal lines mark the initial targets); (b) evolution of the model resolution.

Full size image

The introduced approach is an accelerated version of the algorithm proposed in Koziel et al.70. In contrast to70, where only single-fidelity EM model of the component under design is employed, here, we utilize EM models of various fidelities belonging to the continuous range of admissible resolutions. This is a source of the computational benefits of our procedure over that proposed in Koziel et al.70. The reliability of our procedure is excellent: it has been capable of yielding the designs fulfilling the required design specifications in all the considered cases, even though the starting points have been to a large extent misaligned with the targets. At the same time, the speedup over the single-fidelity framework70 is around fifty-five percent on average (from fifty to sixty percent across the benchmark set).

Conclusion

In this work, we proposed a new technique for computationally-efficient and improved-reliability parameter tuning of microwave passive components. The presented approach combines two distinct algorithmic tools, the automated design requirement management scheme, and the knowledge-based adaptively-adjusted EM simulation fidelity mechanism. The former allows for a considerable improvement of the optimization process reliability. In particular, it enables successful local tuning even under challenging conditions (e.g., poor starting point). The latter results in a significant computational speedup with respect to the standard, single-fidelity optimization. Both mechanisms are implemented to work simultaneously. More specifically, the decision-making procedure governing model fidelity setup for a given iteration of the optimization algorithm depends on the current discrepancy between the observed and target operating parameters of the circuit at hand, as well as the convergence status of the search process. The proposed framework is intended to work with full-wave simulation models (e.g., finite-difference time-domain (FDTD), or finite element method (FEM)), but also dedicated solvers that permit a control over discretization density of the structure under simulation. The prerequisite is that the utilized computational models should be evaluated using the same simulation engine, and differ solely by mesh density to ensure satisfactory correlation between the models of different resolutions. Whereas this level of correlation is not possible to achieve with circuit-theory models (or equivalent circuits, or else analytical models). The methodology proposed in this work has been validated using three microstrip components, including two couplers and a power divider. In all cases, it demonstrated superior performance, both in terms of successful allocation of the operating frequencies of the considered circuits despite of poor initial designs, and computational efficiency. The average CPU savings over the recent technique involving adaptively adjusted design specifications are as high as 55 percent. The speedup has been shown not to be detrimental to the design quality. The optimization strategy introduced in this paper has a potential to replace or complement traditional methods, especially in situations where local optimization is likely to fail due to the lack of good starting points or the necessity of re-designing the circuit over broad frequency ranges, whereas the involvement of global search routines is questionable because of the incurred computational expenses.