Introduction

One of the fundamental properties for designing gas absorption and stripping columns in chemical industries is the solubility of gases in liquids1. While the basic principles of solubility thermodynamics are well known, it is still a challenging issue to accurately predict solubility for important industrial systems applying molecular thermodynamics alone. Nowadays, hydrogen is an eminent substance in the industry. Hydrogen plays a substantial role in industrial processes, hence the solubility of it in various hydrocarbon solutions such as fuels is very important for designing and optimal operating of these processes2. Hydrogen is a useful compound in the chemical and petroleum industries. The quality of heavy petroleum fractions can be upgraded through hydrovisbreaking or hydrocracking processes by adding hydrogen to them and increase the hydrogen to carbon ratio (H/C). The production of low sulfur fuels in the oil refining industry is such that large amounts of hydrogen are used for desulfurization plants3,4,5. Design and operating processes such as hydrogenation and hydrocracking, along with corresponding kinetic models, require hydrogen solubility data6. Pressure, temperature, and composition of solvents can remarkably affect the hydrogen solubility as a thermodynamic quantity. Increasing pressure and temperature have an increasing impact on the solubility of gases. Also, from the molar fraction point of view, as hydrocarbon carbon number increases, hydrogen solubility increases as demonstrated by experimental tests2,7,8,9. It is well known that traditional equations of state (EOSs) are limited in accurately predicting the solubility of hydrogen for the modeling of hydrogenation processes. There is a potential for energy waste and even a potential safety hazard in the hydrogenation process due to the overuse of hydrogen. Therefore, solubility data is very significant to predict the optimal amount of hydrogen in this process and can lead to improved plant safety. Performing experiments for heavy hydrocarbons due to the complexity of them is particularly difficult. Also, the risks associated with high-pressure or/and high-temperature conditions in industrial processes do not make extensive testing an attractive choice. Hence, modeling based on experimental data can be a good alternative.

The methods for predictions of hydrogen solubility in solvents such as hydrocarbons or petroleum mixture are mostly based on the application of empirical and semi-empirical models such as EOSs and are alike to those applied for solubility of other gases such as methane and CO210,11,12,13,14,15. Shaw16 proposed a correlation for measuring the solubility of hydrogen in hydrocarbon solvents including heterocyclic, aromatic, and alicyclic type, by applying corresponding state theory16. Yuan et al.17 used molecular dynamics simulations to estimate the hydrogen solubility in heavy hydrocarbons for a range of pressures and temperatures. They concluded that a combination of the EOSs and molecular dynamics simulations can lead to more accurate and practical predictions for the hydrogen solubility at high pressures and temperatures17. Riazi and Roomi5 proposed a method for predicting the hydrogen solubility in hydrocarbons and their mixtures based on regular solution theory. Their procedure was based on calculating the parameter of hydrogen solubility according to the type of solvents or their molecular weight. The advantage of their method was that, unlike EOSs or other models, critical properties of solvent were not needed to calculate the hydrogen solubility. However, the need for other calculations in this method can still be considered a negative point5. Torres et al.18 applied the augmented Grayson Streed method19 to better model the solubility of hydrogen in heavy oil cuts. However, they noted that the homogeneous EOSs models could provide better results. The solubility of hydrogen in n-alcohols has been measured and modeled by d’Angelo and Francesconi20. Also, in their work, individual correlations as pseudo-Henry’s constants were used to better estimate hydrogen solubility20. Luo et al.21 experimentally investigated the hydrogen solubility in coal liquid and several hydrocarbons. They also proposed a mathematical model based on Henry’s law and the Pierotti method21. Yin and Tan22 obtained hydrogen solubility data in toluene in the presence of CO2 (i.e., ternary system H2 + toluene + CO2). An EOS named Peng–Robinson associated with the van der Waals mixing rule was used to model the vapor–liquid equilibrium (VLE) data22. Qian et al.23 used Peng–Robinson EOS to model a large dataset of various hydrogen-containing binary systems with the implementation of the group-contribution method for calculating temperature-dependent binary interaction parameters23. This method was previously been proposed by Jaubert and Mutelet to predict the VLE of hydrocarbons binary mixtures24. The solubility of hydrogen in several heavy normal alkanes has measured and modeled by Florusse et al.2. They used statistical associating fluid theory (SAFT) approach to model the hydrogen solubility after experiments. However, this method is a complex method due to the adjustable parameters and parameters required for any potential function2. Perturbed-Chain SAFT (PC-SAFT) EOS25 is another method that can be used to estimate the solubility of hydrogen in hydrocarbons. This method has been utilized to propose several models for prognostication of the solubility of hydrogen in hydrocarbons and heavy oils6,26,27,28. The classical EOSs, activity models, etc. require adjustable parameters, proper mixing rules, iterative calculations, etc. Traditional EOSs are only reliable in specific temperature and pressure ranges and have bounded flexibility for substances used.

Complex calculations in chemical and petroleum sciences have been facilitated by artificial intelligence (AI) methods in recent years. Regarding the use of artificial intelligence in the case of hydrogen solubility, Safamirzaei et al.29 have considered the hydrogen solubility in primary n-alcohols and after that, they applied artificial neural networks (ANNs) to overcome EOSs and simple correlations constraints in achieving best modeling29. Nasery et al.30 implemented Adaptive Neuro-Fuzzy Inference System (ANFIS) to estimate the solubility of hydrogen in heavy oil fractions30. Safamirzaei and Modarress31 modeled hydrogen solubility in heavy n-alkanes (C46H94, C36H74, C28H58, C16H34, and C10H22) by ANNs31. As can be seen in the literature studies, the issue of modeling hydrogen solubility in different solvents especially hydrocarbons has always been the focus of researchers. Also, according to the classification scheme of van Konynenburg and Scott32 and the updated version by Privat and Jaubert33, hydrogen-containing systems systematically show type III phase behavior, and such systems are acknowledged to be particularly difficult to correlate. Hence, there is a window for developing a more general model to estimate hydrogen solubility in hydrocarbons using AI methods, which accounts more influential variables, with higher precision. Due to the nature of data-driven soft computing techniques, such a comprehensive model can be developed by combining more data points and various operating conditions.

In the current work, we apply a total of 919 experimental hydrogen solubility data points for 26 different hydrocarbons accumulated at different operating conditions1,2,8,11,14,21,34,35,36,37,38,39,40,41,42,43,44. Advanced machine learning methods namely extreme gradient boosting (XGBoost), adaptive boosting support vector regression (AdaBoost-SVR), gradient boosting with categorical features support (CatBoost), light gradient boosting machine (LightGBM), and multi-layer perceptron (MLP) optimized by Levenberg–Marquardt (LM) algorithm are utilized to develop models for estimating the hydrogen solubility in hydrocarbons. Moreover, the validity of the proposed models is checked by applying statistical parameters and graphical error analyses. Also, several hydrogen solubility systems are estimated by the models developed in this work and five EOSs including Soave–Redlich–Kwong (SRK), Peng–Robinson (PR), Redlich–Kwong (RK), Zudkevitch–Joffe (ZJ), and perturbed-chain statistical associating fluid theory (PC-SAFT) to make a comparison between these models and EOSs.

Data gathering

To accurately model hydrogen solubility in hydrocarbons, 919 experimental hydrogen solubility data were gathered from the literature1,2,8,11,14,21,34,35,36,37,38,39,40,41,42,43,44. Table 1 represents the sources of the experimental hydrogen solubility data used in this work along with the pressure range, temperature range, and uncertainty values for each system. Since the type of hydrocarbon dictates hydrogen solubility, a broad range of hydrocarbons was selected with properties represented in Table S1. Hydrocarbon families used in this study include alkane, alkene, cycloalkane, aromatic, polycyclic aromatic, and terpene.

Table 1 Hydrogen solubility database used for modeling in this work.
Full size table

To model hydrogen solubility in hydrocarbons, thermodynamic properties were considered for model development. In this work, molecular weight, critical pressure, and critical temperature of solvents along with pressure and temperature were selected as input parameters to the models. The hydrogen solubility (in terms of mole fraction) at different pressures and temperatures is set to be the model output. Moreover, a short statistical description of input and target parameters of the data bank applied for modeling is listed in Table 2. Using the uncertainty values of the experimental data in data-driven modeling can make the model really reliable. However, because uncertainty values (for test conditions and results of solubility tests) were not reported or fully reported in some papers, it was not possible to use them in modeling.

Table 2 Statistical information about the collected databank in this paper.
Full size table

It is very important to apply different systems to achieve a comprehensive model for predicting hydrogen solubility in hydrocarbons. The characterization data for the 26 various hydrocarbons from 6 hydrocarbon families utilized for modeling are presented in Table S1. A databank including 919 data points was gathered from 48 different systems of the literature1,2,8,11,14,21,34,35,36,37,38,39,40,41,42,43,44, the statistical information of which is reported in Table 2. The carbon number of hydrocarbons is ranging from 4 to 46 corresponding to a molecular weight range of 58.12–647.2 g/mol. Also, the experimental hydrogen solubility data were collected in a broad range of operating temperatures, 213–623 (K) and pressures, 0.1–25.5 (MPa). According to the statistics reported in Table 2, the variation range and distribution of model input parameters are wide enough to provide a general model for estimating hydrogen solubility in hydrocarbons.

Models implementation

Extreme gradient boosting (XGBoost)

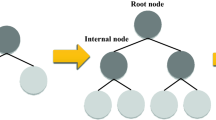
The main idea behind a tree-based ensemble technique is to utilize an ensemble of classification and regression trees (CARTs) such that the training data is fitted by the minimization of a regularized objective function. XGBoost is one of these tree-based models under the framework of gradient boosting decision tree (GBDT). To elaborate on the CART’s structure, every cart consists of (I) a root node, (II) internal nodes, and (III) leaf nodes as shown in Fig. 1. According to the binary decision practice, the root node which embodies the whole data set is subjected to be split into internal nodes, while the leaf nodes represent the ultimate classes. In order to build a robust ensemble in gradient boosting, a series of base CATRs are consecutively constructed where the weight of every individual CART needs to be tuned through the training process45.

Figure 1
figure 1

Level-wise tree growth in XGboost.

Full size image

To model the output y for a given dataset where m and n are dimension features and examples, respectively, an ensemble of n tress needs to be trained:

$$\begin{gathered} \hat{y}_{i} = \sum\limits_{{k = 1}}^{N} {f_{k} \left( {X_{i} } \right)} , \quad f_{k} \in f \hfill \\ With\; f = \left\{ {f(X) = \omega _{{q(x)}} } \right\},(q:\mathbb{R}^{m} \to T,\omega \;\in \mathbb{R}^{T} ) \hfill \\ \end{gathered}$$
(1)

where the example × is mapped by the decision rule q(x) to the binary leaf index. In Eqs. (1) and (2), f represents the space of regression trees, fk is the kth independent tree, T denotes the number of leaves on the tree, and ω is the weight of the leaf.

The determination of the ensemble of trees is performed by the minimization of regularized objective function L:

$$\begin{gathered} L = \sum _{i}^{n} l(\hat{y}_{{_{i} }} ,y_{{_{i} }} ) + \sum _{k}^{N} \Omega (f_{k} ) \hfill \\ With\;\Omega (f) = \gamma T + \frac{1}{2}\lambda \left\| \omega \right\|^{2} \hfill \\ \end{gathered}$$
(2)

where Ω is the regularization term limiting the model intricacy, assisting the reduction of the overfitting; l denotes a differentiable convex loss function; γ stands for the minimum loss reduction which is needed to split a new leaf, and λ shows the regulation coefficient. It should be noted that γ and λ in these sets of equations help to soar the model variance and decrease the overfitting46.

In the gradient boosting approach, the objective function for every individual leaf is minimized through which more branched will be added iteratively.

$$L^{{(t)}} = \sum\limits_{{i = 1}}^{n} {\left\{ {l(y_{i} ,\hat{y}_{i} ^{{(t - 1)}} ) + f_{t} (X_{i} )} \right\}} + \Omega (f_{t} )$$
(3)

where t represents the t-th iteration in the aforementioned training process. To notably ameliorate the ensemble model, the XGBoost’s approach greedily adds the space of regression trees which is usually referred to as “greedy algorithm”. Therefore, the model output is iteratively updated through the minimization of the objective function:

$$\hat{y}_{i}^{{(t)}} = \hat{y}_{i}^{{(t - 1)}} + f_{t} (X_{i} )$$
(4)

The XGBoost benefits from the shrinkage strategy in which newly added weights are scaled after every step of boosting by a learning factor rate. This helps to diminish the effects of future new trees on every existing individual tree, thereby reducing the risk of overfitting47.

Light gradient boosting machine (LightGBM)

Another new gradient learning framework built up upon the idea of the decision tree is LightGBM48. The salient features of LightGBM which dominates XGBoost are consuming less memory, utilizing a leaf-wise growth approach with depth restrictions, and benefiting from a histogram-based algorithm that expedites the training process49. Using the aforementioned histogram algorithm, LightGBM discretizes continuous floating-point eigenvalues into k bins, hence leading to building a k-width histogram. In addition, extra storage of pre-sorted results is not required in the histogram algorithm and values can be stored in an 8-bit integer after the feature discretization that reduces the memory consumption to 1/8. Nevertheless, this rough partitioning approach does decrease the model accuracy. LightGBM also uses a leaf-wise approach which is more effective than the traditional growth strategy named level-wise. The rationale behind this inefficiency in level-wise strategy is that the leaves from the same layer are considered at each step, thereby leading to a gratuitous memory allocation. Instead, the leaves with the highest branching gain are found at every step in the leaf-wise approach after which the algorithm continues to the branching cycle. Thus, the errors can be diminished and higher precision is achieved with the same number of segmentations compared to the horizontal direction. In Fig. 2, the strategy of leaf-wise tree growth is depicted. The downside of leaf orientation is growing deeper decision trees which unavoidably results in overfitting. However, LightGBM precludes this overfitting while furnishing high efficiency by applying a maximum depth limit to the leaf top48,49.

Figure 2
figure 2

Leaf-wise tree growth in LightGBM.

Full size image

In the followings, calculations for LightGBM are shown50:

For a given training dataset \(X = \left\{ {(x_{i} ,y_{i} )} \right\}_{{_{i = 1} }}^{m}\), LightGBM searches an approximation \(\widehat{f}(x)\) to the function f*(x) to minimize the expected values of specific loss functions L(y, f (x)):

$$\mathop f\limits^{ \wedge } \left( x \right) = \arg \mathop {\min }\limits_{f} E_{y,x} L(y,f(x))$$
(5)

LightGBM ensembles many T regression trees \(\sum_{t=1}^{T}{f}_{t }(x)\) to approximate the model. The regression trees are defined as wq(x), \(q \in \left\{ {1, \, 2,...,N} \right\}\), where w shows a vector representing the sample weights of leaf nodes, N stands for the number of tree leaves, and q represents the decision rule of trees. The model is trained in the additive form at step t:

$$G_{t} \cong \sum\limits_{i = 1}^{N} {L(y_{i} ,F_{t - 1} (x_{i} ) + f_{t} (x_{i} ))}$$
(6)

Newton's approach is used to approximate the objective function.

Gradient boosting with categorical features support (CatBoost)

For categorical boosting, categorical columns are used in CatBoost which uses permutation techniques such as one_hot_max_size (OHMS) and target-based statistics. In this technique, a greedy method is used for each new split of the current tree which enables CatBoost to find the exponential growth of the feature combination51. The following steps are applied in CatBoost for every feature possessing more categories compared to OHMS:

  1. 1.

    Random subset formation of the records

  2. 2.

    Label conversion to integers

  3. 3.

    Categorical feature transformation to numeric, as follows:

    $$avgT\arg et = \frac{countInClass + prior}{{totalCount + 1}}$$
    (7)

where countInClass counts targets with the value of one for a given categorical feature, and totalCount counts previous objects (the starting parameters determine the prior to count the objects)52,53.

Adaptive boosting (AdaBoost)

For supervised classification, Freund and Schapire54 have suggested the AdaBoost system. In this model, reweighted data, that the eights are chosen reliability refers to the consistency of the output of the learners, are sequentially assumed in the week learners. This trick reduces the inexperienced learner in order to concentrate on the hard cases55. The following represent the key steps of the Adaboost technique:

  • Defining Weights: \({w}_{j}=\frac{1}{n}, j=\mathrm{1,2},\dots .,n\) ;

  • For each i, set the training data to a weak learner \({Wl}_{i}(x)\) using weights and obtain the weighted error

    $${Err}_{i}=\frac{{\sum }_{j=1}^{n}{w}_{j}I({t}_{j}\ne {wl}_{i}\left(x\right))}{{\sum }_{j=1}^{n}{w}_{j}}, I\left(x\right)=\{\begin{array}{c}0 if x=false \\ 1 if x=true\end{array}$$

  • For each i, determine weights for predictors as: \({\beta }_{i}=log\left(\frac{(1-{Err}_{i})}{{Err}_{i}}\right)\)

  • Modified data wights for each i to N ( N denotes the number of learners);

  • Adjust weak learner for data test (x) as output.

In this study, support vector regressors (SVR) were applied as the weak learners in Adaboost systems.

Support vector regression (SVR)

Support Vector machine (SVM) is a group of similar supervised machine learning algorithms that can be applied for both regression and clustering tasks56. SVR is a systematic technique for soft computation, with a well-established mathematical formulation. As it has been shown to be very stable for modeling multiple complex structures, this approach has gained significant interest. In the literature, the fundamental concept behind SVR is commonly presented57. Therefore, we present a short description of the SVR conception for the sake of brevity. SVR attempts to obtain a regression function f(x) for a given dataset \([\left({x}_{1}, {y}_{1}\right),\dots ..,\left({x}_{n}, {y}_{n}\right)]\) with \(x\in {R}_{d}\) as the d-dimensional input space and \(y\in R\) as the output vector dependent on the input data to estimate the output as below:

$$f(x) = w.\phi (x_{i} ) + b$$
(8)

where \(b\) denotes bias vectors, \(w\) shows the weight, and \(\phi \left(x\right)\) refers to the function of the kernel. The following minimization problem proposed by Vapnik should be solved in order to achieve the right values of the weight and bias vectors58:

$$\begin{gathered} minimize\frac{1}{2}w^{T} w + C\sum\limits_{j = 1}^{N} {(\zeta_{j}^{ - } + \zeta_{j}^{ + } )} \hfill \\ \hfill \\ \left\{ \begin{gathered} (w.\phi (x_{i} ) + b) - y_{i} \le \varepsilon + \zeta_{j}^{ - } \hfill \\ y_{i} - (w.\phi (x_{i} ) + b) \le \varepsilon + \zeta_{j}^{ + } \hfill \\ \zeta_{j}^{ + } ,\zeta_{j}^{ - } \ge 0,i = 1,2,...,m \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$
(9)

where \(T\) represents the transpose operator, \(\varepsilon\) shows the error tolerance, C represents a positive regularization parameter that defines the variance from \(\varepsilon\), \({\zeta }_{j}^{+}\) and \({\zeta }_{j}^{-}\) consider positive parameters, attempting to point out the lower and higher excess variations, respectively.

By means of the Lagrange multipliers, the previously discussed constrained optimization problem is taken into a dual function. This move then leads to the final solution, which is presented as follows:

$$f(x) = \sum\limits_{j = 1}^{n} {(a_{k} - a_{k}^{*} )K(x_{k} ,x_{l} ) + } b$$
(10)

where \(K({x}_{k},{x}_{l})\) represents the kernel function; \({a}_{k}\) and \({a}_{k}^{*}\) represent the Lagrange multipliers that follow the 0 k and k C constraints.

Multilayer perceptron (MLP) neural network

MLP is a class of feedforward ANNs that consists of various layers. The primary layer which is pertinent to the input data is the input layer, the last layer which corresponds to the output of the model is the output layer and the middle layers which process the information are hidden layers59. In the hidden layers, each neuron will connect to every neuron in the next and prior layers. The manner of calculating the value of every neuron in the output or hidden layers is as follows: the amount of every neuron in the prior layer which is multiplying in its corresponding particular weight is summed together and a bias factor is appended to these values. Then, the resulting value passes through an activation function60. Table S2 summarizes different activation functions along with their corresponding mathematical equations. The number of hidden layers and neurons in any hidden layer should be optimized to acquire a highly efficient and accurate model, usually using the empirical method. The performance of the MLP model depends on the optimization algorithms such as Levenberg–Marquardt (LM)61 applied to train this intelligent model. In this work, the MLP model which is developed on the basis of the LM optimization algorithm is dubbed MLP-LM . Figure 3 represents a schematic of the developed MLP in this work.

Figure 3
figure 3

A schematic of the developed MLP neural network.

Full size image

The procedure of model development

For developing each model and take care of overfitting, we used grid search for optimizing hyperparameters of models. The hyperparameters used in grid search for each model were different, the importance of the hyperparameters was based on theoretical and practical aspects. The following hyperparameters were used for each model:

  • For XGBoost: max_depth, n_estimators, learning_rate, min_child_weight, base_score.

  • For LightGBM: Boosting type, objective, metric, learning rate, feature fraction, bagging fraction.

  • For AdaBoost-SVR: learning rate, loss, epsilon, n_estimators, γ, C.

  • For CatBoost: n_estimators, max_depth, learning rate.

  • For MLP-LM: learning rate, Epoches.

The empirical method is also applied to determine the optimal number of hidden layers and neurons in any hidden layer for the MLP neural network.

In this work, we used k-fold cross-validation on our train dataset because it cares that every observation from the dataset has the chance of appearing in training and validation. For all models, we did use KFold 6 (as we know Kfold should not be too small or too high, and it depends on data size) so the value is picked up based on our data. It means we split the train data randomly into 6 folds and then fit the model using K-1 (which is 5 folds) and validate the model using the remaining fold.

Equations of state (EOSs)

The analytical description of the relationship between volume, temperature, and pressure of a substance can be expressed by an EOS. The vapor–liquid–equilibria (VLE), volumetric behavior, and thermal properties of mixtures and pure substances can be described by this expression. The phase behavior of petroleum fluids is widely predicted by EOSs. As already mentioned, traditional EOSs offer poor predictions for the solubility of gases in solvents, especially in complex operating conditions. In this study, four cubic EOSs including SRK, PR, RK, and ZJ along with PC-SAFT as a type of SAFT EOSs are implemented to measure the hydrogen solubility in hydrocarbons and their precision in estimating the hydrogen solubility is compared with the proposed machine learning models. Conventional van der Waals one-fluid mixing rules are utilized in cubic EOSs. Table S3 shows the PVT relationships of the cubic EOSs and PC-SAFT equation in terms of the residual Helmholtz free energy. Furthermore, the parameters and mixing rules for the EOSs are presented in Table S4. Also, the pure-component PC-SAFT parameters for the substances used in this work are reported in Table S5. The binary interaction parameter (kij) in van der Waals mixing rules characterizing molecular interactions between molecules of two components, can be a key parameter in estimating the solubility of a solute in a solvent in cubic EOSs. A similar kij parameter is introduced by applying the van der Waals one-fluid mixing rules to the perturbation terms in PC-SAFT EOS that corrects the segment-segment interactions of unlike chains. The optimized values of kij parameter for all EOSs in different hydrogen solubility systems are reported in Table S6.

Model assessment

Statistical error analysis

The following definitions have been implemented for the statistical parameters of standard deviation (SD), average absolute percent relative error (AAPRE), root mean square error (RMSE), coefficient of determination (R2), and average percent relative error (APRE) to assess the validation and accuracy of the models:

$$SD = \sqrt {\frac{1}{N - 1}\sum\limits_{i = 1}^{N} {\left( {\frac{{HS_{i,e} - HS_{i,p} }}{{HS_{{i,{\text{e}} }} }}} \right)}^{2} }$$
(11)
$$RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {HS_{{i,{\text{e}} }} - HS_{i,p} } \right)}^{2} }$$
(12)
$$AAPRE = \frac{100}{N}\sum\limits_{i = 1}^{N} {\left| {\frac{{HS_{{i,{\text{e}} }} - HS_{i,p} }}{{HS_{{i,{\text{e}} }} }}} \right|}$$
(13)
$$APRE = \frac{100}{N}\sum\limits_{i = 1}^{N} {\left( {\frac{{HS_{{i,{\text{e}} }} - HS_{i,p} }}{{HS_{{i,{\text{e}} }} }}} \right)}$$
(14)
$$R^{2} = 1 - \frac{{\sum\limits_{i = 1}^{N} {(HS_{{i,{\text{e}} }} - HS_{i,p} )^{2} } }}{{\sum\limits_{i = 1}^{N} {(HS_{i,p} - \overline{{HS_{{i,{\text{e}} }} }} )^{2} } }}$$
(15)

In these formulas, HSi,e, HSi,p, and N, respectively, represent the experimental hydrogen solubility data and predicted values of hydrogen solubility in hydrocarbons by developed models, and the number of data points. The coefficient of determination which is represented almost everywhere by the R2 is one of the most well-known criteria for the goodness of fit of a model. R2 is an important statistical parameter that shows how well the model output corresponds to the experimental data and how valid the model is. If the R2 value is closer to 1, the fit of the model response to the experimental values is greater. The data scattering around zero deviation is assessed by RMSE. APRE and AAPRE measure the relative deviation and the relative absolute deviation from the target data, respectively. The measure of scattering is assessed by SD, which less value of it demonstrates a lower grade of dispersion.

Graphical error analysis

Besides the statistical error analysis that has already been mentioned, visual graphical analysis can also help to understand the validity of the models developed in this work. The significant items are classified as follows:

Crossplot: in this graph, the estimated values of a model are plotted versus experimental values. If the finest fit line of the model estimation has no deviation from the 45° line and the computed data are mostly concentrated nearest to the unit slope line (Y = X), the performance of the model is excellent.

Error distribution plot: the presence or absence of error trend is checked by measuring the error scattering around the zero-error line. Here, the relative error (Ei) is calculated through Eq. (16):

$${\text{E}}_{{\text{i}}} = \left[ {\frac{{HS_{{i,{\text{e}} }} - HS_{i,p} }}{{HS_{{i,{\text{e}} }} }}} \right] \times100 {\text{i }} = 1,2,3,...,n$$
(16)

Cumulative frequency graph: the cumulative frequency of data is sketched versus absolute relative error (Ea). The higher cumulative frequency curve reveals that most of the estimations fall within the usual error range. In other words, the closer the curve to the vertical axis, the model error in estimating the high percentage of data is less. In this work, the Ea is calculated through Eq. (17):

$${\text{E}}_{a} = \left| {\frac{{HS_{{i,{\text{e}} }} - HS_{i,p} }}{{HS_{{i,{\text{e}} }} }}} \right| \times 100{\text{i }} = 1,2,3,...,n$$
(17)

Group error diagram: the data are divided into diverse ranges and their error at each range is calculated and sketched.

Trend plot: in this diagram, both target data and estimated values by the proposed model are sketched against the index of data points and their coverage and trend are tracked.

Results and discussion

Description of model development

The optimal values of the important hyperparameters along with the search interval of the hyperparameters tuned for the machine learning models implemented in this work are presented in Table 3.

Table 3 Optimal features for implemented models.
Full size table

In Table 3, n_estimators show the number of trees; subsample is subsample ratio of the training instance; C denotes a degree of importance that is given to misclassifications; max_depth represents maximum depth of a tree; min_child_weight is the minimum sum of instance weight (hessian) needed in a child; bagging_fraction shows the fraction of data to be used for each iteration; feature_fraction is parameters randomly selected in each iteration for building trees; learning_rate controls the impact of each tree on the final outcome; base_score represents the initial prediction score of all instances; epsilon is a parameter affect the number of support vectors applied to construct the regression function; γ shows kernel coefficient, and epochs show the number of times that the learning algorithm is passed through a full training dataset.

Statistical assessment of the developed models

To identify the most accurate model, we should compare the developed models using statistical factors including, R2, AAPRE (%), SD, APRE (%), and RMSE. The calculated values for these parameters are reported in Table 4. The results reveal that among all developed models, XGBoost provides the most accurate predictions, followed by AdaBoost-SVR, LightGBM, CatBoost, and MLP−LM models, respectively. Based on Table 4, AAPRE values of 2.14% for the testing set, 1.71% for the training set, and 1.81% for the total set of data, suggest that the XGBoost model has the most accurate estimation of hydrogen solubility in hydrocarbons. However, Table 4 reveals that other models also display good accuracy.

Table 4 Statistical error analysis for the models developed in this work.
Full size table

For a comparative evaluation of the models developed in this work with five EOSs, 30 hydrogen solubility data points in three different systems including hydrocarbons with low, medium, and high molecular weight collected from the literature8,11,39 were estimated by these models. Predictions of models along with the results calculated by the EOSs are presented in Table 5. The AAPRE reported in Table 5 is much higher for the EOSs than the machine learning models. ZJ EOS with an AAPRE of 15.78% has the best calculations for hydrogen solubility in hydrocarbons among the other cubic EOSs. Also, PC-SAFT as a modern type of EOSs shows good estimates with AAPRE of 9.56% and has superior performance compared to traditional cubic EOSs. All machine learning models have good predictions and show a significant advantage over EOSs. XGBoost model has the best performance among all models and EOSs with an AAPRE of 1.92%. It is noteworthy that uncertainty values are different for different systems. According to our studies, AAPRE values reported in Table 5 can vary about 5–10% due to uncertainty values, but it is better to trust the reported experimental values in the literature.

Table 5 Comparison of proposed models’ performance in this work with EOSs.
Full size table

To further evaluate the validity and reliability of the XGBoost model, an external validation dataset containing 413 hydrogen solubility data in 18 different hydrocarbons, including 6 new hydrocarbons (i.e. ethane, propane, ethene, 1-hexene, 1-heptene, and diphenylmethane) over a wide range of operating temperatures (98–701 K) and pressures (1.03–78.45 MPa), were collected from the literature. The properties of all hydrocarbons used in this work are presented in Table S1. Table 6 describes this validation dataset of hydrogen solubility data. This dataset is completely outside the training and testing sets used for modeling in this paper. Hence, it allows evaluating the performance of the model outside the modeling data sets. AAPRE values for each system are calculated using experimental data and predictions of the XGBoost model. The AAPRE values reported in Table 6 show that the XGBoost model has good predictions for all systems, even for new hydrocarbons not used in modeling. Overall AAPRE of 1.78% for this validation dataset shows the high validity of the XGBoost model in predicting hydrogen solubility in hydrocarbons.

Table 6 Validation dataset for evaluation of XGBoost model.
Full size table

Visual error analysis

For a more detailed assessment of the accuracy of the proposed models, visual analysis applying the crossplot of predicted hydrogen solubility against the corresponding experimental values was depicted in Fig. 4. Besides, Fig. 5 presented the error distribution diagram for each of the two testing and training sets of all models. Figure 4 demonstrates that the high concentration of data points surrounding the 45° line for all models. However, the XGBoost model performs much better than other models, indicating its high reliability for predicting hydrogen solubility in hydrocarbons. The relative errors among experimental hydrogen solubility and estimated values by the proposed models versus the experimental data for the test and training sets are illustrated in Fig. 5. This figure demonstrates that the relative errors of XGBoost and AdaBoost-SVR models are highly near the zero-error line, but the errors of the predictions of CatBoost, LightGBM, and MLP-LM models are not as low as the XGBoost and AdaBoost-SVR models. The maximum percent relative error among the estimated hydrogen solubility values and the experimental data for the XGBoost model is 19%. Figures 4 and 5 reflect the significant extent of agreement between the experimental hydrogen solubility data and the XGBoost model predictions.

Figure 4
figure 4

Crossplot of prediction of hydrogen solubility in hydrocarbons by the models versus experimental data.

Full size image
Figure 5
figure 5

Error distribution graphs of the proposed models for test and training sets.

Full size image

Figure S1 represents the trend plot of the predicted values of hydrogen solubility in hydrocarbons for all proposed models and the experimental hydrogen solubility data versus the index of data points. As demonstrated in Fig. S1 in the Supplementary file, all models show good overlap between the estimated hydrogen solubility data and the experimental values, but the degree of overlap is excellent for the XGBoost model.

Figure S2 depicts the cumulative frequency of the data versus Ea for all developed models. Based on this figure, more than 70% of estimated hydrogen solubility by the XGBoost model have an absolute relative error < 1.3%, as well as more than 90% of the estimated data, have an absolute relative error < 3.6%. However, for the AdaBoost-SVR, LightGBM, CatBoost, and MLP-LM models respectively 81%, 79%, 73%, and 48% of predicted hydrogen solubility data have an absolute relative error < 3.6%, indicating the high validity of the XGBoost model.

Operating pressure and temperature greatly affect the solubility of hydrogen in hydrocarbons. As mentioned earlier, predicting hydrogen solubility under high-pressure/ igh-temperature conditions in various industries, is very important and the safety and efficiency of industrial processes depend on it. Figure 6 presents the validity of models at selected values of pressure and temperature ranges by applying the group error plots. It is worth noting that the group error analysis is performed by splitting all data into various ranges of pressure (i.e. 0–5 MPa, 5–10 MPa, 10–15 MPa, 15–20 MPa, and 20–25 MPa) and temperature (i.e. 210–294 K, 294–378 K, 378–462 K, 462–546 K, and 546–630 K) to investigate the validity of the proposed models at various ranges of these important parameters. AAPRE was calculated for the mentioned intervals and plotted in Fig. 6a for pressure parameter and Fig. 6b for temperature parameter. As can be seen in Fig. 6, LightGBM and MLP-LM models have relatively higher errors in low and high pressures and temperatures. Also, CatBoost and AdaBoost-SVR models have relatively higher errors in low pressures and temperatures. XGBoost model has the lowest error among all models for different temperature and pressure operating conditions, which proves the previous claims of good performance of this model.

Figure 6
figure 6

Graph of Group error for all models for various ranges of (a) pressure and (b) temperature.

Full size image

Trend analysis

At the next stage, several different analyses were performed to assess the performance of the XGBoost model in different systems of hydrogen solubility in hydrocarbons. First, the impact of pressure on the hydrogen solubility in n-Decane at a high temperature of 432 K2 is evaluated in Fig. 7. The hydrogen solubility values predicted by the XGBoost model for this system along with the values calculated by the EOSs are demonstrated in Fig. 7. As indicated in this figure, at high-temperature conditions, the deviation between traditional RK EOS calculations and experimental data is high, but the other EOSs and XGBoost model predict experimental data excellently. As expected, the solubility of hydrogen in the n-Decane increases with increasing pressure. However, cubic EOSs slightly overestimate or underestimate the increase in solubility with increasing pressure at high temperatures, while the XGBoost model follows the trend very well. PC-SAFT EOS also has good predictions with low deviation from experimental data and outperforms traditional cubic EOSs.

Figure 7
figure 7

Estimated hydrogen solubility in n-Decane at a high-temperature of 432 K.

Full size image

Next, the hydrogen solubility data in a hydrocarbon named diphenylmethane76 with a molecular weight of 168.23 and a carbon number of 13 are predicted by the XGBoost model at high temperature and pressure conditions (Fig. 8). Again, as depicted in Fig. 8, the XGBoost model correctly detects data trends and provides excellent forecasts. As can be seen, the effect of temperature increase along with increasing pressure on hydrogen solubility is correctly predicted by the XGBoost model.

Figure 8
figure 8

Experimental data with XGBoost model predictions of hydrogen solubility in diphenylmethane under different operating conditions.

Full size image

As mentioned earlier, the solubility of hydrogen increases with an increasing carbon number of hydrocarbons2,7,8,9. Therefore, the predictions of the XGBoost model for the solubility of hydrogen in several hydrocarbons with different carbon numbers (decane, eicosane, octacosane, and hexatriacontane) at a temperature of 373 K, which have been studied experimentally in literature8, are presented in Fig. 9. In this case, as well, the estimations of the XGBoost model are in good agreement with the reported experimental hydrogen solubility data for all these hydrocarbons.

Figure 9
figure 9

The solubility of hydrogen in several hydrocarbons with different carbon numbers for the XGBoost model with experimental data.

Full size image

Conclusions

In this work, five robust machine learning models were introduced for estimating the hydrogen solubility in hydrocarbons as a function of critical pressure, critical temperature, and molecular weight of solvents along with pressure and temperature operating conditions. A databank including 919 data points gathered from 48 different systems of the 26 various hydrocarbons was applied to model the hydrogen solubility. Implementing the techniques of XGBoost, CatBoost, LightGBM, AdaBoost-SVR, and MLP-LM revealed that the estimations of hydrogen solubility in hydrocarbons from the five proposed models reached the AAPRE of 1.81%, 3.40%, 3.52%, 4.70%, and 6.01% for XGBoost, AdaBoost-SVR, LightGBM, CatBoost, and MLP-LM , respectively. XGBoost is introduced as the best-proposed model in this work based on graphical and statistical error analysis. Evaluation of the XGBoost model with an external validation dataset containing 413 hydrogen solubility data in 18 different hydrocarbons over a wide range of operating temperatures (98–701 K) and pressures (1.03–78.45 MPa) also proved the validity and reliability of the XGBoost model in predicting hydrogen solubility in hydrocarbons. Also, the calculation of hydrogen solubility in hydrocarbons for several different systems by EOSs showed that PC-SAFT has the best predictions for hydrogen solubility in hydrocarbons among the other EOSs. However, ZJ EOS also outperformed another cubic EOSs.