The Effects of Intra-membrane Viscosity on Lipid Membrane Morphology: Complete Analytical Solution

Abstract

We present a linear theory of lipid membranes which accommodates the effects of intra-membrane viscosity into the model of deformations. Within the Monge parameterization, a linearized version of the shape equation describing membrane morphology is derived. Admissible boundary conditions are taken from the existing non-linear model but reformulated and adopted to the present framework. We obtain a complete analytical expression illustrating the deformations of lipid membrane subjected to the influences of intra-membrane viscosity. The result predicts wrinkle phenomena in the event of membrane-substrate interactions. Finally, we mention that the obtained solutions reduce to those from the classical shape equation when the viscosity effects are removed.

Introduction

Lipid membranes are composed of transversely oriented lipid molecules (phospholipids) containing hydrophilic head groups and hydrophobic tails. These phospholipids arrange themselves into a two-layered sheet (a bilayer) with opposing orientations that effectively shield the tail groups from the surrounding aqueous solution. It was found by Evert Gorter and F. Grendel¹ that a lipid bilayer constitutes cell membrane and later, in 1959, David Robertson² justified that the bilayer structure is characteristic of all biological membranes (biomembranes). They are quite fragile and negligibly thin (typically 512610 nm) but represent a critically important interface within biological cells mediating interactions between cells and their surrounding environment through cellular processes such as fission, fusion and budding^3,4. These cellular functions are facilitated by the membranes morphological transition which is also dependent on the membrane forces and surrounding viscous flows^5,6. Therefore, the study of the morphological aspects of membranes is crucial to the understanding of a wide range of essential cellular functions.

Due to the delicate and complex nature of lipid membranes, the study of the various mechanical responses of lipid bilayers can be, most often, practiced with the use of an artificial ‘model’. This also includes the development of continuum-based models in the description of the behavior of lipid bilayers, typically based on the Cosserat theory of elastic surfaces (see⁷, and the reference therein). Within this context, the work in⁸ reveals that intra-membrane viscosity has considerable effects on the deformation of lipid membranes. The authors in⁹ develop the non-linear models of membranes which incorporates intra-membrane viscosity through the adjustment of the equilibrium and boundary conditions based on the conventional theory of elastic surfaces. There the authors further corroborate the relations between lipid flow and membrane shape via the numerical analysis of the resulting coupled PDEs. However, the analysis presented in⁹ is limited to the case of a rectangular portion of lipid membranes whereas membrane morphology is oftentimes affected by external forces such as interactions between membranes and substrates. In addition, it seems necessary to develop a linear theory in order to facilitate further researches on the related subjects.

In the present work, we reformulate the non-linear governing equations of membranes directly from the membrane free-energy density function within the frame work of tensor analysis of surfaces. A compatible linear theory is then developed by employing the principles of superposed incremental deformations. More importantly, we obtained complete analytical solutions which describes the deformations of lipid membranes subjected to intra-membrane viscous flow. Emphasis is placed on the assimilation of the complex nature of boundary forces and the film/substrate interaction conditions, while maintaining the rigor and sufficient generality in the derivation of linearized shape equations and boundary conditions. The obtained linear model predicts the straining effects when a rectangular portion of membranes is subjected to intra-membrane viscous flow. The result is also aligned with the numerical study conducted under the compatible settings⁹. In particular, we find that the viscous flows give rise to wrinkle phenomena when the membrane makes contact with a circular substrate. Quantitative comparison is made by assimilating the experimental results reported in¹⁰ where we find that the number of wrinkles is sensitive to the thickness of membranes and the radius of interacting substrates. A phenomenologically compatible result is also reported in the work of^11,12. We believe that the results may provide an important breakthrough in the study of relevant problems such as the effects of wrinkles on the vesicle fusion/diffusion processes¹³ and a wrinkle-caused disease of human eyes (e.g. a macular pucker/epiretinal membrane)¹⁴. Lastly, we note that our solution also accommodates the scenarios presented in^15,16 in the limit of vanishing viscous flow.

Throughout the paper, we make use of a number of well-established symbols and conventions. Thus, unless otherwise stated, Greek indices take the values 1 and 2. Einstein summation is applied for the repeated indices.

Prerequisite

The theoretical formulation of a lipid membrane which accounts for the effects of intra-membrane viscosity is presented in⁹. There the authors obtain the constitutive relation from the theory of an elastic surface via the relation W = ρF and later by substituting viscosity terms in the resulting formulae. In this section, we reformulate the results directly from the membrane free-energy density W = W(H, K, ρ) for the sake of consistency and completeness.

Inviscid lipid membranes

The equilibrium state of a purely elastic surface, subjected to normal pressure p, is given by¹⁷

$${{\bf{T}}}_{;\alpha }^{\alpha }+p{\bf{n}}=0,$$

(1)

where T^α and n are the stress vectors and the local surface unit normal, respectively. The semi-colon denotes the surface covariant differentiation associated with the Levi-Civita contraction of the surface metric a_αβ = a_α · a_β, where a_α = r_,α(θ^α, t) = ∂r/∂θ^α. For instance, a_α;β is defined by¹⁸

$${{\bf{a}}}_{\alpha ;\beta }={{\bf{a}}}_{\alpha ,\beta }-{{\rm{\Gamma }}}_{\alpha \beta }^{\lambda }{{\bf{a}}}_{\lambda }.$$

(2)

Here ${{\rm{\Gamma }}}_{\alpha \beta }^{\lambda }={{\bf{a}}}_{\alpha ,\beta }\cdot {{\bf{a}}}^{\lambda }$ are the Christoffel symbols induced by the local surface coordinate ${\bf{n}}({\theta }^{\alpha })=\tfrac{1}{2}{\varepsilon }^{\alpha \beta }{{\bf{a}}}_{\alpha }\times {{\bf{a}}}_{\beta }$ such that n is a unit-vector field and a_α and a_β are the tangent vectors on the deformed surface ω. ${\varepsilon }^{\alpha \beta }={e}^{\alpha \beta }/\sqrt{a}$ refers to the permutation tensor with a = det(a_αβ). Thus, for example, we evaluate e^αβ as e¹¹ = e²² = 0, e¹² = −e²¹ = 1. The matrix a_αβ of the surface metric is a positive-definite, with a > 0, leading to the existence of dual metric a^αβ which is the inverse of the surface metric (i.e. a^αβ = (a_αβ)⁻¹). Hence the to the dual basis is given as a^α = a^αβa_β. The energy induced on the membranes’ deformations can be expressed via the two primary parameters: the coefficient of the first fundamental form a_αβ (the surface metric); and the second fundamental form b_αβ (the curvature) defined by b_αβ = n · a_α,β. For example, in the case of the surface with energy density W = W(a_αβ, b_αβ), T^α take the following compact form¹⁷

$${{\bf{T}}}^{\alpha }=({\sigma }^{\beta \alpha }+{b}_{\mu }^{\beta }{M}^{\mu \alpha }){{\bf{a}}}_{\beta }-{M}_{;\beta }^{\alpha \beta }{\bf{n}},$$

(3)

where

$${\sigma }^{\beta \alpha }=\rho (\tfrac{\partial \tfrac{1}{\rho }(W-\gamma )}{\partial {a}_{\alpha \beta }}+\tfrac{\partial \tfrac{1}{\rho }(W-\gamma )}{\partial {a}_{\beta \alpha }})\,{\rm{and}}\,{M}^{\beta \alpha }=\frac{\rho }{2}(\tfrac{\partial \tfrac{1}{\rho }(W-\gamma )}{\partial {b}_{\alpha \beta }}+\tfrac{\partial \tfrac{1}{\rho }(W-\gamma )}{\partial {b}_{\beta \alpha }}).$$

(4)

In the above, ρ and γ are the surface mass density and the constitutively-indeterminate Lagrange-multiplier field, respectively. For lipid membranes whose free-energy density is expressed by the mean and Gaussian curvatures through a_αβ and b_αβ (i.e. W = W(H, K, ρ;a_αβ, b_αβ)), the expressions of σ^βα and M^βα can be obtained by using chain rules $({\rm{e}}.\,{\rm{g}}.\,\frac{\partial W}{\partial {a}_{\alpha \beta }}=\frac{\partial W}{\partial \rho }\frac{\partial \rho }{\partial {a}_{\alpha \beta }}+\frac{\partial W}{\partial H}\frac{\partial H}{\partial {a}_{\alpha \beta }}+\frac{\partial W}{\partial K}\frac{\partial K}{\partial {a}_{\alpha \beta }})$. To see this, we evaluate

$$\begin{array}{rcl}\rho \frac{\partial \frac{1}{\rho }(W-\gamma )}{\partial {a}_{\alpha \beta }} & = & \rho [\,-{\rho }^{-2}\frac{\partial \rho }{\partial {a}_{\alpha \beta }}W+\frac{1}{\rho }({W}_{\rho }\frac{\partial \rho }{\partial {a}_{\alpha \beta }}+{W}_{H}\frac{\partial H}{\partial {a}_{\alpha \beta }}+{W}_{K}\frac{\partial K}{\partial {a}_{\alpha \beta }})\\ & & +\,{\rho }^{-2}\frac{\partial \rho }{\partial {a}_{\alpha \beta }}\gamma -\frac{1}{\rho }\frac{\partial \gamma }{\partial \rho }\frac{\partial \rho }{\partial {a}_{\alpha \beta }}],\end{array}$$

(5)

where the expressions of H and K are given explicitly as¹⁸

$$H=\tfrac{1}{2}{a}^{\alpha \beta }{b}_{\alpha \beta }\,{\rm{and}}\,K=\tfrac{1}{2}{\varepsilon }^{\alpha \beta }{\varepsilon }^{\lambda \mu }{b}_{\alpha \lambda }{b}_{\beta \mu }.$$

(6)

The derivatives of ρ, H and K with respect to a_αβ can be evaluated as¹⁷

$$\frac{\partial \rho }{\partial {a}_{\alpha \beta }}=-\,\frac{\rho }{2}{a}^{\alpha \beta },\,\frac{\partial H}{\partial {a}_{\alpha \beta }}=-\,\frac{1}{2}{b}^{\alpha \beta }\,{\rm{and}}\,\frac{\partial K}{\partial {a}_{\alpha \beta }}=-\,K{a}^{\alpha \beta },$$

(7)

Accordingly, Eq. (5) reduces to

$$\begin{array}{rcl}\rho \frac{\partial \frac{1}{\rho }(W-\gamma )}{\partial {a}_{\alpha \beta }} & = & \rho [\frac{1}{2\rho }{a}^{\alpha \beta }W-\frac{1}{2}{a}^{\alpha \beta }{W}_{\rho }-\frac{1}{2\rho }{b}^{\alpha \beta }{W}_{H}\\ & & -\,\frac{1}{\rho }{W}_{K}K{a}^{\alpha \beta }-\frac{1}{2\rho }{a}^{\alpha \beta }\gamma +{\gamma }_{\rho }\frac{1}{2}{a}^{\alpha \beta }].\end{array}$$

(8)

Now using F_ρ = (W/ρ − γ/ρ)_,ρ $({\rm{i}}.\,{\rm{e}}.\,{W}_{\rho }=\rho {F}_{\rho }+\frac{W}{\rho }+{\gamma }_{\rho }-\frac{\gamma }{\rho })$, we obtain

$$\begin{array}{rcl}\rho \frac{\partial \frac{1}{\rho }(W-\gamma )}{\partial {a}_{\alpha \beta }} & = & [\,-\,\frac{1}{2}{b}^{\alpha \beta }{W}_{H}-{W}_{K}K{a}^{\alpha \beta }-\frac{1}{2}{a}^{\alpha \beta }{\rho }^{2}{F}_{\rho }]\\ & = & -\,\frac{1}{2}\gamma {a}^{\alpha \beta }-({W}_{H}H+{W}_{K}K){a}^{\alpha \beta }+\frac{1}{2}{W}_{H}{\tilde{b}}^{\alpha \beta },\end{array}$$

(9)

where F_ρ is defined via the relation ρ²F_ρ = γ¹⁷ and ${b}^{\alpha \beta }=2H{a}^{\alpha \beta }-{\tilde{b}}^{\alpha \beta }$. Thus,

$${\sigma }^{\beta \alpha }=(\lambda +W){a}^{\alpha \beta }-(2{W}_{H}H+2{W}_{K}K){a}^{\alpha \beta }+{W}_{H}{\tilde{b}}^{\alpha \beta },$$

(10)

and

$$\lambda =-\,(\gamma +W).$$

(11)

Similarly, by using

$$\frac{\partial \rho }{\partial {b}_{\alpha \beta }}=0,\,\frac{\partial H}{\partial {b}_{\alpha \beta }}=\frac{1}{2}{a}^{\alpha \beta }\,{\rm{and}}\,\frac{\partial K}{\partial {b}_{\alpha \beta }}={\tilde{b}}^{\alpha \beta },$$

(12)

Eq. (4)₂ yields

$${M}^{\beta \alpha }=\frac{1}{2}{W}_{H}{a}^{\alpha \beta }+{W}_{K}{\tilde{b}}^{\alpha \beta }.$$

(13)

Consequently, by substituting Eq. (3) into (1), we have

$${({\sigma }^{\beta \alpha }+{b}_{\mu }^{\beta }{M}^{\mu \alpha })}_{;\alpha }{{\bf{a}}}_{\beta }+({\sigma }^{\beta \alpha }+{b}_{\mu }^{\beta }{M}^{\mu \alpha }){{\bf{a}}}_{\beta ;\alpha }-{({M}_{;\beta }^{\alpha \beta })}_{;\alpha }{\bf{n}}-{M}_{;\beta }^{\alpha \beta }{{\bf{n}}}_{,\alpha }+p{\bf{n}}={\bf{0}}.$$

(14)

Applying Euclidean dot products in normal n and tangential a_α directions and invoking Gauss and Weingarten equations¹⁸ a_β;α = b_βαn and n_,α = −b_αβa^β, Eq. (14) becomes

$$({\sigma }^{\beta \alpha }+{b}_{\mu }^{\beta }{M}^{\mu \alpha }){b}_{\beta \alpha }-{({M}_{;\beta }^{\alpha \beta })}_{;\alpha }+p={\bf{0}},$$

(15)

and

$${({\sigma }^{\beta \alpha }+{b}_{\mu }^{\beta }{M}^{\mu \alpha })}_{;\alpha }+{M}_{;\mu }^{\alpha \mu }{b}_{\alpha }^{\beta }={\bf{0}}.$$

(16)

Eq. (15) is often referred to as a membrane shape equation when used in conjunction with Helfrich potential¹⁹.

Viscous lipid membranes

Viscous stress arises due to the straining effects of the fluid and can be accommodated by the time derivative of the evolving surface metric²⁰. In a typical environment, where lipid membranes are subjected to morphological transitions, the reference velocity of the system is low and therefore the corresponding Reynolds numbers are sufficiently small^21,22. Further, it is widely accepted that lipid membranes are relatively stiff against areal dilation in comparison with bending or shear motions^23,24. Thus, in the forthcoming derivations, we adopt the assumption of incompressible fluid and thereby find the expression of the corresponding stress as

$${\sigma }^{\alpha \beta }=-\,\gamma {a}^{\alpha \beta }+\nu {a}^{\alpha \lambda }{a}^{\beta \mu }{\dot{a}}_{\lambda \mu },$$

(17)

where ν is the intra-membrane shear viscosity and the superscript dot $(\dot{\ast })$ refers to the time derivative. Since a_αβ = a_α · a_β, we find

$${\dot{a}}_{\lambda \mu }=({{\bf{a}}}_{\lambda }\cdot {{\bf{a}}}_{\mu }\dot{)}={\dot{{\bf{a}}}}_{\lambda }\cdot {{\bf{a}}}_{\mu }+{{\bf{a}}}_{\lambda }\cdot {\dot{{\bf{a}}}}_{\mu }\mathrm{.}$$

(18)

In convected coordinates, ${\dot{{\bf{a}}}}_{\lambda }$ is defined as¹⁷ ${\dot{{\bf{a}}}}_{\lambda }=\partial {\bf{u}}{\boldsymbol{/}}\partial {\theta }^{\lambda }={{\bf{u}}}_{,\lambda }$ where ${\bf{u}}=\dot{{\bf{r}}}={v}^{\alpha }{{\bf{a}}}_{\alpha }+w{\bf{n}}$ is the velocity of a material point on the initial surface. It is now trivial to show that

$$\begin{array}{rcl}{\dot{{\bf{a}}}}_{\lambda } & = & {{\bf{u}}}_{,\lambda }={({v}^{\alpha }{{\bf{a}}}_{\alpha }+w{\bf{n}})}_{,\lambda }={v}_{,\lambda }^{\alpha }{{\bf{a}}}_{\alpha }+{v}^{\alpha }{{\bf{a}}}_{\alpha ,\lambda }+{w}_{,\lambda }{\bf{n}}+w{{\bf{n}}}_{,\lambda }\\ & = & ({v}_{\alpha ;\lambda }-w{b}_{\alpha \lambda }){{\bf{a}}}^{\alpha }+({v}^{\alpha }{b}_{\alpha \lambda }+{w}_{,\lambda }){\bf{n}},\,\because {v}_{\alpha ;\beta }={v}_{\alpha ,\beta }-{v}_{\beta }{{\rm{\Gamma }}}_{\alpha \beta }^{\lambda }\mathrm{.}\end{array}$$

(19)

Now, in view of Eqs (18 and 19), we find

$${\dot{a}}_{\lambda \mu }={v}_{\mu ;\lambda }+{v}_{\lambda ;\mu }-2w{b}_{\lambda \mu }$$

(20)

Further, from Eqs (10), (11), (17) and (20), the expression of the viscous stress can be derived as

$$\begin{array}{rcl}{\sigma }^{\beta \alpha } & = & (\lambda +W){a}^{\beta \alpha }-\mathrm{(2}{W}_{H}H+2{W}_{K}K){a}^{\beta \alpha }+{W}_{H}{\tilde{b}}^{\beta \alpha }\\ & & +\,\nu [{a}^{\beta \lambda }{a}^{\alpha \mu }({v}_{\mu ;\lambda }+{v}_{\lambda ;\mu })-4wH{a}^{\beta \alpha }+2w{\tilde{b}}^{\beta \alpha }],\end{array}$$

(21)

where we also use the relations: a^αλa^βμb_λμ = b^αβ and ${b}^{\alpha \beta }=2H{a}^{\alpha \beta }-{\tilde{b}}^{\alpha \beta }$. The equation of motion (normal direction) of the lipid membrane in the presence of intra-membrane viscosity effects is therefore obtianed from Eqs (13), (15) and (21)

$$\begin{array}{rcl}p & = & -\,(\lambda +W){a}^{\beta \alpha }{b}_{\beta \alpha }+({W}_{H}H+{W}_{K}K){a}^{\beta \alpha }{b}_{\beta \alpha }-\frac{1}{2}{W}_{H}{\tilde{b}}^{\beta \alpha }{b}_{\beta \alpha }\\ & & +\,{[\frac{1}{2}{({W}_{H})}_{;\beta }{a}^{\beta \alpha }+{({W}_{K})}_{;\beta }{\tilde{b}}^{\beta \alpha }]}_{;\alpha }-\nu [{a}^{\beta \lambda }{a}^{\alpha \mu }({v}_{\mu ;\lambda }+{v}_{\lambda ;\mu })\\ & & -\,4wH{a}^{\beta \alpha }+2w{\tilde{b}}^{\beta \alpha }]{b}_{\beta \alpha }\mathrm{.}\end{array}$$

(22)

Utilizing the identities $H=\tfrac{1}{2}{a}^{\alpha \beta }{b}_{\alpha \beta }$, ${b}_{\beta \alpha }={b}_{\alpha }^{\mu }{a}_{\mu \beta }$, ${a}^{\alpha \lambda }{a}_{\lambda \beta }={\delta }_{\beta }^{\alpha }$ and ${a}^{\beta \alpha }K={b}_{\mu }^{\beta }{\tilde{b}}^{\mu \alpha }$ and knowing the fact that covariant derivatives of the dual metric and the covariant cofactor identically vanish $({\rm{i}}.\,{\rm{e}}{\rm{.}}\,{a}_{;\beta }^{\alpha \beta }=0,\,{\tilde{b}}_{;\beta }^{\alpha \beta }=0)$, the above equation further reduces to

$$\begin{array}{rcl}p & = & {W}_{H}(2{H}^{2}-K)+2H({W}_{K}K-W)-2\lambda H\\ & & +\,{\rm{\Delta }}(\frac{1}{2}{W}_{H})+{({W}_{K})}_{;\alpha \beta }{\tilde{b}}^{\alpha \beta }-2\nu [\frac{1}{2}{b}^{\alpha \beta }({v}_{\alpha ;\beta }+{v}_{\beta ;\alpha })-2w(2{H}^{2}-K)],\end{array}$$

(23)

where Δ is the Laplace-Beltrami operator (i.e. Δϕ = ϕ_;αβa^αβ), defined on the surface.

Similarly, by substituting Eqs (13) and (21) into Eq. (16), we obtain

$$\begin{array}{l}-\,({\gamma }_{,\alpha }+{W}_{K}{K}_{,\alpha }+{W}_{H}{H}_{,\alpha }){a}^{\beta \alpha }-4\nu w{H}_{,\alpha }{a}^{\beta \alpha }\\ \,+\,2\nu [\frac{1}{2}{a}^{\beta \lambda }{a}^{\alpha \mu }{({v}_{\mu ;\lambda }+{v}_{\lambda ;\mu })}_{;\alpha }-{w}_{,\alpha }{b}^{\beta \alpha }]=0,\end{array}$$

(24)

where ${({v}_{\mu ;\lambda }+{v}_{\lambda ;\mu })}_{;\alpha }={({v}_{\mu ;\lambda }+{v}_{\lambda ;\mu })}_{,\alpha }-({v}_{\beta ;\lambda }+{v}_{\lambda ;\beta }){{\rm{\Gamma }}}_{\mu \alpha }^{\beta }-({v}_{\beta ;\mu }+{v}_{\mu ;\beta }){{\rm{\Gamma }}}_{\lambda \alpha }^{\beta }$. Invoking ${b}^{\beta \alpha }={b}_{\lambda }^{\alpha }{a}^{\lambda \beta }$ and γ_,α = −λ_,α − W_KK_,α − W_HH_,α, Eq. (24) further reduces to

$${a}^{\beta \alpha }[{\lambda }_{,\alpha }-4vw{H}_{,\alpha }+2\nu \{\frac{1}{2}{a}^{\lambda \mu }{({v}_{\mu ;\alpha }+{v}_{\alpha ;\mu })}_{;\lambda }-{w}_{,\lambda }{b}_{\alpha }^{\lambda }\}]=0.$$

Since a^βα ≠ 0, the above becomes

$${\lambda }_{,\alpha }-4vw{H}_{,\alpha }+2\nu [\frac{1}{2}{a}^{\lambda \mu }{({v}_{\mu ;\alpha }+{v}_{\alpha ;\mu })}_{;\lambda }-{w}_{,\lambda }{b}_{\alpha }^{\lambda }]=0,$$

(25)

which serves as the tangential equations of motion.

In the case of uniform membranes of the Helfrich type, the energy density W is defined by

$$W=k{H}^{2}+\bar{k}K,$$

(26)

where k and $\bar{k}$ are empirical constants (the bending moduli). It is noted here that, within the framework of the forgoing model, membranes with continuously distributed proteins can be accommodated through the energy density function: $W=k(\sigma ){H}^{2}+\bar{k}(\sigma )K;\sigma ({\theta }^{\alpha },t)$, where σ(θ^α, t) describes the areal concentration of proteins on the membrane surface. However, the case is excluded from the present study in an effort to obtain mathematically tractable equations. Now, Eqs (23) and (26) yield

$$p=k[{\rm{\Delta }}H+2H({H}^{2}-K)]-2\lambda H-2[\nu \frac{1}{2}{b}^{\alpha \beta }({v}_{\alpha ;\beta }+{v}_{\beta ;\alpha })-2w(2{H}^{2}-K)],$$

(27)

while Eq. (25) remains intact. From the incompressibility condition $\dot{J}/J=\frac{1}{2}{a}^{\alpha \beta }{a}_{\alpha \beta }=0$²⁵ together with Eqs (6) and (20), we also find

$${v}_{;\alpha }^{\alpha }-2wH=0.$$

(28)

Finally, admissible boundary conditions (e.g., boundary forces f and moments M on ∂ω) of Eq. (27) are derived in detail in⁹ and¹⁵. In the case of uniform viscous Helfrich membranes, these are given by

$$\begin{array}{rcl}M & = & \frac{1}{2}k({\kappa }_{\nu }+{\kappa }_{\tau })+\bar{k}\tau ,\,{f}_{n}=\bar{k}\tau ^{\prime} -k{H}_{,\nu }\\ {f}_{\nu } & = & \frac{1}{4}k({\kappa }_{\nu }^{2}-{\kappa }_{\tau }^{2})-\bar{k}{\tau }^{2}+\lambda \\ & & +\,\nu [{a}^{\beta \lambda }{a}^{\alpha \mu }({v}_{\mu ;\lambda }+{v}_{\lambda ;\mu })-4wH{a}^{\beta \alpha }+2w{\tilde{b}}^{\beta \alpha }]{\nu }_{\beta }{\nu }_{\alpha },\\ {f}_{\tau } & = & \nu [{a}^{\beta \lambda }{a}^{\alpha \mu }({v}_{\mu ;\lambda }+{v}_{\lambda ;\mu })-4wH{a}^{\beta \alpha }\\ & & +\,2w{\tilde{b}}^{\beta \alpha }]{\nu }_{\beta }{\nu }_{\alpha }-\frac{1}{2}k\tau {\kappa }_{\nu }-(\frac{1}{2}k+\bar{k})\tau {\kappa }_{\tau },\end{array}$$

(29)

and corner forces

$${{\bf{f}}}_{i}=\bar{k}{[\tau ]}_{i}{\bf{n}},$$

(30)

where

$${\kappa }_{\nu }={b}_{\alpha \beta }{\nu }^{\alpha }{\nu }^{\beta },\,{\kappa }_{\tau }={b}_{\alpha \beta }{\nu }^{\alpha }{\nu }^{\beta },\,\tau ={b}_{\alpha \beta }{\nu }^{\alpha }{\tau }^{\beta }$$

(31)

are the normal curvatures of ω in the direction of ν and τ and τ is the twist of w on the (ν, τ) axes with τ = n × ν. We note here that the normal force remains intact in the presence of intra-membrane viscosity effects.

Monge Representation and Superposed Incremental Deformations

In order to study the responses of the membrane, we use the Monge representation with space vector r(θ^α, t) representing material points on the membrane surface w, which is given by

$${\bf{r}}({{\boldsymbol{\theta }}}^{\alpha },t)={\boldsymbol{\theta }}+z({\boldsymbol{\theta }},t){\bf{k}},$$

(32)

where θ(θ^α) is position on a plane defined by the unit normal k and z(θ, t) is height function that describes the bilayer membrane mid-plane shape. The Monge representation is an approximation of out-of-plane deformations in which no folds of the membrane are allowed, and hence, z(θ, t) is restricted to a single-valued function. For instance, the membrane surface can be represented by orthonormal Cartesian basis θ = θ^αe_α and, unless otherwise specified, the subscripts of the surface coordinates are dropped and replaced by 1 = x, 2 = y for convenience. Within this setting, we compute

$$\begin{array}{rcl}{{\bf{r}}}_{,t} & = & {z}_{,t}{\bf{k}},\,{{\bf{a}}}_{\alpha }={{\bf{e}}}_{\alpha }+{z}_{,\alpha }{\bf{k}},\\ & & \,\,\,\,\,\,a={\rm{\det }}({a}_{\alpha \beta })\\ & & \,\,\,\,\,\,\,\,=[1+{({z}_{,1})}^{2}+{({z}_{,2})}^{2}],\\ & & \,\,{a}^{\alpha \beta }={\delta }_{\alpha \beta }+{z}_{,\alpha }{z}_{,\beta },\\ H & = & \frac{(1+{z}_{\mathrm{,2}}^{2}){z}_{\mathrm{,11}}+(1+{z}_{\mathrm{,1}}^{2}){z}_{\mathrm{,22}}-2{z}_{\mathrm{,1}}{z}_{\mathrm{,2}}{z}_{\mathrm{,12}}}{2{a}^{\mathrm{3/2}}},\,K=\frac{({z}_{\mathrm{,11}}{z}_{\mathrm{,22}}-{z}_{\mathrm{,12}}^{2})}{{a}^{2}},\\ {\bf{n}} & = & \frac{({\bf{k}}-\nabla z)}{\sqrt{a}}\,{\rm{and}}\,{\bf{b}}=\frac{{z}_{,\alpha \beta }}{\sqrt{a}}({{\bf{a}}}^{\alpha }\otimes {{\bf{a}}}^{\beta }),\end{array}$$

(33)

where is δ_αβ Kronecker delta, $\nabla z={z}_{,\alpha }{{\bf{e}}}_{\alpha }$ is the gradient evaluated on the surface and is b curvature tensor with components ${b}_{\alpha \beta }={z}_{,\alpha \beta }/\sqrt{a}$,

$$\begin{array}{rcl}{{\bf{a}}}^{1} & = & \frac{1}{a}[(1+{z}_{\mathrm{,2}}^{2})\,({{\bf{e}}}_{1}+{z}_{\mathrm{,1}}{\bf{k}})-{z}_{\mathrm{,1}}{z}_{\mathrm{,2}}({{\bf{e}}}_{2}+{z}_{\mathrm{,2}}{\bf{k}})],\,{\rm{and}}\\ {{\bf{a}}}^{2} & = & \frac{1}{a}[(1+{z}_{\mathrm{,1}}^{2})\,({{\bf{e}}}_{2}+{z}_{\mathrm{,2}}{\bf{k}})-{z}_{\mathrm{,1}}{z}_{\mathrm{,2}}({{\bf{e}}}_{1}+{z}_{\mathrm{,1}}{\bf{k}})]\mathrm{.}\end{array}$$

(34)

Further, the normal velocity and the Christoffel symbols are computed as

$$w={{\bf{r}}}_{,t}\cdot {\bf{n}}={z}_{,t}/\sqrt{a},\because {{\bf{r}}}_{,t}=w{\bf{n}},$$

(35)

and

$${{\rm{\Gamma }}}_{\alpha \beta }^{\lambda }={z}_{,\lambda }{z}_{,\alpha \beta }/\sqrt{a},$$

(36)

respectively.

The evaluation of the resulting shape equation Eq. (27) in terms of Eqs (33–36) furnishes a highly nonlinear PDE system, which most often requires heavy computational resources. Instead, a means of ‘admissible linearization’ can be employed to make the system mathematically tractable with minimum loss of generality. The concept of the superposed incremental deformations has been widely and successfully adopted in the relevant subject of studies (see, for example^15,26,27,28). Within this prescription, the derivatives of z(θ, t) of all orders are considered to be ‘small’ (e.g. ${z}_{,\alpha }\ll 1.$), and therefore, their products can be neglected. Accordingly, using the notation ‘$\simeq$’ to identify equations to the leading order in z, we have

$$\begin{array}{l}a\simeq \mathrm{1,}\,w\simeq {z}_{t},\,{\bf{n}}={\bf{k}}-{\nabla }_{p}z,\,{{\bf{a}}}^{\alpha }\simeq {{\bf{a}}}_{\alpha }={{\bf{e}}}_{\alpha }+{z}_{,\alpha }{\bf{k}},\,{{\rm{\Gamma }}}_{\alpha \beta }^{\lambda }\simeq \mathrm{0,}\,{\bf{n}}\cdot {\bf{r}}\simeq z-{z}_{,\alpha }{\theta }^{\alpha },\\ {\bf{b}}\simeq {\nabla }_{p}^{2}z,\,H\simeq \frac{1}{2}{{\rm{\Delta }}}_{p}z\,{\rm{and}}\,K\simeq \mathrm{0,}\end{array}$$

(37)

where the subscript ${(\ast )}_{p}$ refers to the projected counterparts of $(\,\ast \,)$ on the coordinate plane ω_p, ${\nabla }_{p}^{2}z={z}_{,\alpha \beta }$ ${{\bf{e}}}_{\alpha }\otimes {{\bf{e}}}_{\beta }$ is the second gradient and ${{\rm{\Delta }}}_{p}z=tr({\nabla }_{p}^{2}z)$ is the corresponding Laplacian, respectively. In particular, the straining (20), viscous stress (17) and incompressibility condition (28) can be approximated as:

$${\dot{a}}_{\alpha \beta }\simeq {v}_{\alpha ,\beta }+{v}_{\beta ,\alpha },$$

(38)

$${\sigma }^{\alpha \beta }\simeq -\,\frac{1}{2}\gamma {\delta }_{\alpha \beta }+\nu ({v}_{\alpha ,\beta }+{v}_{\beta ,\alpha }),$$

(39)

and

$${v}_{\alpha ,\alpha }\simeq 0.$$

(40)

Further, the equations of motion in normal and tangential directions (Eqs (25) and (27)) can be approximated as

$$\frac{1}{2}k{{\rm{\Delta }}}_{p}({{\rm{\Delta }}}_{p}z)-\lambda {{\rm{\Delta }}}_{p}z-\nu {z}_{,\alpha \beta }({v}_{\alpha ,\beta }+{v}_{\beta ,\alpha })\simeq p,\,{\rm{and}}\,{\lambda }_{,\alpha }+v{({v}_{\lambda ,\alpha }+{v}_{\alpha ,\lambda })}_{,\lambda }\simeq 0.$$

(41)

In view of, Eqs (38) and (40) (e.g. z_,αβ = z_,βα, ${v}_{\lambda ,\alpha \lambda }={v}_{\lambda ,\lambda \alpha }\ldots$), the above are equivalent to

$$\frac{1}{2}k{{\rm{\Delta }}}_{p}({{\rm{\Delta }}}_{p}z)-\lambda {{\rm{\Delta }}}_{p}z-2\nu {z}_{,\alpha \beta }{v}_{\alpha ,\beta }\simeq p\,{\rm{and}}\,{\lambda }_{,\alpha }+v{{\rm{\Delta }}}_{p}{v}_{,\alpha }\simeq 0.$$

(42)

To obtain simplified edge conditions, let r(S, t) = r(θ(S), t), where θ(S) is the arc length parameterization of the projected curve ∂ω_p on the plane ω_p. Thus, under the Monge representation, we obtain

$${\bf{r}}(S)^{\prime} =\frac{d{\bf{r}}}{dS}=\frac{d({\boldsymbol{\theta }}+z({\boldsymbol{\theta }}){\bf{k}})}{dS}=\frac{d{\boldsymbol{\theta }}}{dS}+(\frac{z({\boldsymbol{\theta }})}{d{\boldsymbol{\theta }}}\cdot \frac{d{\boldsymbol{\theta }}}{dS}){\bf{k}}={\tau }_{p}+({\nabla }_{p}z\cdot {\tau }_{p}){\bf{k}};\frac{d{\boldsymbol{\theta }}}{dS}\equiv {\tau }_{p}\mathrm{.}$$

(43)

Eq. (43) is equivalent to

$${\bf{r}}(S)^{\prime} =\frac{d{\bf{r}}(s)}{ds}\frac{ds}{dS}=\tau |{\bf{r}}(s)^{\prime} |;\frac{d{\bf{r}}(s)}{ds}\equiv \tau \,{\rm{and}}\,\frac{ds}{dS}\equiv |{\bf{r}}(s)^{\prime} \mathrm{|.}$$

(44)

Accordingly, Eqs (43 and 44). yield

$${\bf{r}}(S)^{\prime} =\tau |{\bf{r}}(s)^{\prime} |={\tau }_{p}+({\nabla }_{p}z\cdot {\tau }_{p}){\bf{k}},\,{\rm{and}}$$

(45)

$$|{\bf{r}}(s)^{\prime} |=|{\tau }_{p}+({\nabla }_{p}z\cdot {\tau }_{p}){\bf{k}}|=\sqrt{1+{({\nabla }_{p}z\cdot {\tau }_{p})}^{2}}\cong 1.$$

(46)

Comparing the right sides of Eqs (45 and 46) and referring Eq. (37), we have

$$\tau \cong {\tau }_{p}+({\nabla }_{p}z\cdot {\tau }_{p}){\bf{k}},\,{\rm{and}}$$

(47)

$$\nu =\tau \times {\bf{n}}\simeq [{\tau }_{p}+({\nabla }_{p}z\cdot {\tau }_{p}){\bf{k}}]\times ({\bf{k}}-{\nabla }_{{\bf{p}}}{\bf{z}})={\nu }_{p}+{\nabla }_{p}z\times {\tau }_{p},$$

(48)

where ν_p = τ_p × k is the unit normal to the projected curve. Consequently,

$${\nu }_{\alpha }={{\bf{a}}}_{\alpha }\cdot \nu \simeq {({\nu }_{\alpha })}_{p}+{e}_{\alpha \beta }{z}_{,\beta }\,{\rm{and}}\,{\tau }_{\alpha }={{\bf{a}}}_{\alpha }\cdot \tau \simeq {({\tau }_{\alpha })}_{p},$$

(49)

where (ν_α)_p = e_α · v_p and (ν_α)_p = e_α · τ_p and e_αβ is the unit alternator defined by e₁₂ = −e₂₁ = 1 and e₁₁ = e₂₂ = 0. Also, invoking Eqs (31), (37), (47) and (48), becomes

$${\kappa }_{\nu }=\nu \cdot {\bf{b}}\nu \simeq ({\nu }_{p}+{\nabla }_{p}z\times {\tau }_{p})\cdot {\nabla }_{p}^{2}z({\nu }_{p}+{\nabla }_{p}z\times {\tau }_{p})\simeq {\nu }_{p}\cdot ({\nabla }_{p}^{2}z){\nu }_{p},$$

(50)

and similarly for

$${\kappa }_{\tau }\simeq {\tau }_{p}\cdot ({\nabla }_{p}^{2}z){\tau }_{p}\,{\rm{and}}\,\tau \simeq {\tau }_{p}\cdot ({\nabla }_{p}^{2}z){\nu }_{p}.$$

(51)

Therefore, it follows from Eqs (29)_1–3 and (49–51) that

$$M\simeq \frac{1}{2}k{{\rm{\Delta }}}_{p}z+\bar{k}{\tau }_{p}\cdot ({\nabla }_{p}^{2}z){\tau }_{p},\,{f}_{\nu }\simeq \lambda +\nu ({v}_{\alpha ,\beta }+{v}_{\beta ,\alpha }){\nu }_{\beta }{\nu }_{\alpha }\,{\rm{and}}\,{f}_{\tau }\simeq \nu ({v}_{\alpha ,\beta }+{v}_{\beta ,\alpha }){\tau }_{\beta }{\nu }_{\alpha },$$

(52)

and

$${\nu }_{\alpha }{\nu }_{\beta }\simeq {({\nu }_{\alpha }{\nu }_{\beta })}_{p}+{e}_{\alpha \lambda }{z}_{,\lambda }{({\nu }_{\beta })}_{p}+{e}_{\beta \lambda }{z}_{,\lambda }{({\nu }_{\alpha })}_{p}\,{\rm{and}}\,{\tau }_{\beta }{\nu }_{\alpha }\simeq {({\tau }_{\beta }{\nu }_{\alpha })}_{p}+{e}_{\alpha \lambda }{z}_{,\lambda }{\tau }_{\beta }.$$

(53)

Now, the normal force is given by

$${f}_{n}=\overline{k}\tau ^{\prime} (s)-k{H}_{,\nu },$$

(54)

where ${(\ast )}_{,\nu }$ is the normal derivatives on ∂ω. By Eq. (46), the arclength derivatives satisfies the approximation

$$\tau ^{\prime} (S)=\frac{d\tau (s)}{ds}\frac{ds}{dS}=\tau ^{\prime} (s)|{\bf{r}}(s)^{\prime} |\simeq \tau ^{\prime} (s\mathrm{).}$$

(55)

Here $\tau ^{\prime} (S)=\frac{d\tau }{dS}=\frac{d\tau }{d{\boldsymbol{\theta }}}\cdot \frac{d{\boldsymbol{\theta }}}{dS}={\nabla }_{p}\tau \cdot {\tau }_{p}$ is the arclength derivative on the projected curve. In addition, H_,ν can be re-written as

$${H}_{,\nu }=(\frac{\partial H}{\partial {\theta }^{\alpha }})\,(\frac{\partial {\theta }^{\alpha }}{\partial {\bf{r}}})\cdot \frac{\partial {\bf{r}}}{\partial \nu }={{\bf{a}}}^{\alpha }{H}_{,\alpha }\cdot (\frac{\partial {\bf{r}}}{\partial {\theta }^{\alpha }})\,(\frac{\partial {\theta }^{\alpha }}{\partial \nu })={{\bf{a}}}^{\alpha }{H}_{,\alpha }\cdot {{\bf{a}}}_{\beta }{v}^{\beta }=\nu \cdot {{\bf{a}}}^{\alpha }{H}_{,\alpha },$$

(56)

Consequently, by substituting Eqs (37) and (48) into Eq. (56), the leading order expression of H_,α can be evaluated on the projected plane as

$$\begin{array}{rcl}{H}_{,\nu } & = & \nu \cdot {{\bf{a}}}^{\alpha }{H}_{,\alpha }=[{\nu }_{p}+{\nabla }_{p}z\times {\tau }_{p}+\ldots ]\cdot [{{\bf{e}}}_{\alpha }+{z}_{,\alpha }{\bf{k}}+\ldots ]{H}_{,\alpha }\\ & \simeq & {\nu }_{p}\cdot ({{\bf{e}}}_{\alpha }{H}_{,\alpha })={\nu }_{p}\cdot {\nabla }_{p}H,\end{array}$$

(57)

and therefore, we obtain

$${f}_{n}\simeq \overline{k}{\nabla }_{p}\tau \cdot {{\boldsymbol{\tau }}}_{p}-k{{\boldsymbol{\nu }}}_{p}\cdot {\nabla }_{p}H.$$

(58)

Solutions to the Linearized Systems

Consider the case where the membrane flows over a rectangular portion of the plane $(\frac{-\,a}{2}\le x\le \frac{a}{2},\frac{-\,b}{2}\le y\le \frac{b}{2})$. Driven by the controlled force, lipid molecules are flowing in through the boundary, while the boundary remains clamped. The corresponding kinematic edge conditions are

$$z=0\,{\rm{and}}\,{\bf{n}}={\bf{k}}.$$

(59)

In view of Eq. (37), the later implies that $\nabla z=0$ and thus both z_,α and the normal derivative z_,ν = ν^αz_,α vanish on the boundary. Accordingly, the edge moment acting on the boundary Eq. (52)₁ becomes

$$M\simeq \frac{1}{2}k{{\rm{\Delta }}}_{p}z\mathrm{.}$$

(60)

It is suggested that the kinetic conditions lead to the particular set of the tangential and normal force (i.e. f_τ = 0, f_ν = −q), where q is prescribed surface pressure (see, for example⁹ and²⁹). Thus, Eq. (52)_2–3 furnishes

$$({v}_{\alpha ,\beta }+{v}_{\beta ,\alpha })\,{({\tau }_{\beta }{\nu }_{\alpha })}_{p}\simeq 0\,{\rm{and}}\,-\,(q+\lambda )\simeq \nu ({v}_{\alpha ,\beta }+{v}_{\beta ,\alpha })\,{({\nu }_{\beta }{\nu }_{\alpha })}_{p},$$

(61)

where the approximations have been made via Eq. (53). We note here that, up to leading order, membrane shape has negligible effects on the surface flow, whereas shape is influenced by the flow via the viscosity term in the shape equation (41). Admissible linearization thus reduces the non-linear, fully coupled equations to a system of PDEs with one-way coupling. Further, the present model incorporates the purely elastic theory of lipid membranes in the limit of vanishing viscosity $\nu \simeq 0$;

$$\frac{1}{2}k{{\rm{\Delta }}}_{p}({{\rm{\Delta }}}_{p}z)-\lambda {{\rm{\Delta }}}_{p}z\simeq p,$$

(62)

while the kinetic boundary conditions remain intact (i.e. z = 0 and ${\nabla }_{p}z=0$). This observation, in turn, suggests that the decay of a dynamic solution to a purely elastic solution can be investigated by assigning q(t) on the boundary in a way that

$$q({\theta }^{\alpha },t)=q(t)\,{\rm{and}}\,\bar{\lambda }=\lambda +q,$$

(63)

where q(θ^α, t) is understood as a uniform function assigned in the interior (i.e. q(θ^α, t) = q(θ^α)) at each sequential step. Then the equations of motion Eq. (42) and boundary conditions Eq. (61) become

$$\frac{1}{2}k{{\rm{\Delta }}}_{p}({{\rm{\Delta }}}_{p}z)-\lambda {{\rm{\Delta }}}_{p}z-2\nu {z}_{,\alpha \beta }{v}_{\alpha ,\beta }\simeq p,\,{\bar{\lambda }}_{,\alpha }+v{{\rm{\Delta }}}_{p}{v}_{,\alpha }\simeq 0,\,{v}_{\alpha ,\alpha }\simeq 0,$$

(64)

and

$$({v}_{\alpha ,\beta }+{v}_{\beta ,\alpha })\,{({\tau }_{\beta }{\nu }_{\alpha })}_{p}\simeq 0\,{\rm{and}}\,-\,\bar{\lambda }\simeq \nu ({v}_{\alpha ,\beta }+{v}_{\beta ,\alpha })\,{({\nu }_{\beta }{\nu }_{\alpha })}_{p},$$

(65)

respectively, where q is prescribed.

Within the domain of interest (a rectangular portion), we now create a particular set of intra-surface viscous flow as

$${v}_{x}=-\,Ax\,{\rm{and}}\,{v}_{y}=Ay.$$

(66)

Since v_x,x + v_y,y = A − A = 0 and either τ_xν_y or τ_yν_x vanishes on the boundary (e.g. for $x=\frac{a}{2}$ boundary, ν_p = −v_xe₁ and τ_p = −τ_ye₂ so that v_y = τ_x = 0), Eqs (64)₃ and (65)₁ are automatically satisfied. Similarly, it follows from Eqs (65 and 66) that

$$\bar{\lambda }\simeq 0\,{\rm{and}}\,\lambda \simeq -\,q,$$

(67)

which agree with the elastic boundary condition in the limit as discussed in^{25,26,27,28,29} (i.e. λ = −q). In addition, Eq. (64)₂ is also satisfied because both ${\bar{\lambda }}_{,\gamma }$ and Δv_γ vanish identically (e.g. Δv_x = Δ(Ax) = 0 and ${\bar{\lambda }}_{,x}=0.$). Consequently, the systems of coupled PDEs (64-65) now reduces to

$$\frac{1}{2}k{{\rm{\Delta }}}_{p}({{\rm{\Delta }}}_{p}z)-\lambda {{\rm{\Delta }}}_{p}z-2\nu {z}_{,\alpha \beta }{v}_{\alpha ,\beta }\simeq p,z=0,\nabla z=0\,{\rm{and}}\,\frac{1}{2}k{{\rm{\Delta }}}_{p}({{\rm{\Delta }}}_{p}z)=M\,{\rm{on}}\,\partial {\omega }_{p}.$$

(68)

In the case of vanishing p, the solution of the above is obtained by³⁰

$$\begin{array}{rcl}z(x\mathrm{,\ }y) & = & \sum _{n\mathrm{=1}}^{\infty }\,\{({A}_{n}\,\cosh \,\sqrt{-\,P+\sqrt{{P}^{2}-4Q}}x\\ & & +\,{B}_{n}\,\cosh \,\sqrt{-\,P-\sqrt{{P}^{2}-4Q}}x)\,\cos \,\beta y\\ & & +\,({C}_{n}\,\cosh \,\sqrt{-\,T+\sqrt{{T}^{2}-4U}}y\\ & & +\,{D}_{n}\,\cosh \,\sqrt{-\,T-\sqrt{{T}^{2}-4U}}y)\,\cos \,\alpha x\},\end{array}$$

(69)

where

$$\begin{array}{rcl}\alpha & = & \frac{n\pi }{a},\,\beta =\frac{n\pi }{b},\,P=-\,{\beta }^{2}+{\mu }^{2}+\frac{4A\nu }{k},\,Q={\beta }^{4}-({\mu }^{2}+\frac{4A\nu }{k}){\beta }^{2},\\ T & = & -\,{\alpha }^{2}+{\mu }^{2}+\frac{4A\nu }{k}\,{\rm{and}}\,U={\alpha }^{4}-({\mu }^{2}-\frac{4A\nu }{k}){\alpha }^{2}\mathrm{.}\end{array}$$

(70)

By imposing boundary conditions (68)_2–4, the unknown constants (e.g. A_n, B_n etc…) can be completely determined. Here, we omit details for the sake of conciseness which can be found in¹⁶. The value of intramembrane surface viscosity ν = 10⁻⁴ pN · s/nm and the bending modulus of the membrane k = 82 pN · nm are adopted from the work of³¹ and³², respectively. We also note that the data are obtained under the normalized setting unless otherwise specified. It is clear from Fig. 1 that membrane shape is influenced by the viscous flow via the viscosity term in the shape equation (64)₁. More precisely, the applied flow gives rise to straining effects on the membrane shape (Fig. 1) in lateral direction. The corresponding transverse deflections (Fig. 2) decrease with the increasing velocity field of viscous flow. In addition, Fig. 2a illustrates that the obtained solutions accommodate those presented in¹⁶ in the limit of vanishing viscous flow. This can also be seen by the reduction of Eq. (64)₁ to the classical shape equation (see, for example^15,16) in the absence of viscous flow (i.e. v_α = 0) and so too the corresponding solutions.

Figure 1

Membrane shape evolutions in the presence of intra-membrane viscosity: A = 10⁻⁵ and 10⁻⁹.

Figure 2

Deflections of lipid membrane with respect to intra-membrane viscous flows.

Membrane-Substrate Interactions in the Presence of Viscous Flow

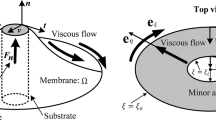
In light of the foregoing discussions, we now investigate a membrane-substrate interaction problem under the influence of intra-membrane viscosity. Driven by the bi-normal (transverse direction) force f_n, the interaction occurs on the boundary r = a of an annular portion of the membrane, while it remains clamped (i.e. z = 0 and n = k). Under a polar-coordinate parametrization of the Monge plane, Eq. (32) is replaced by

$${\bf{r}}({\theta }^{\alpha },t)=r{{\bf{e}}}_{r}(\theta )+z(r,\theta ,t){\bf{k}},$$

(71)

where r is the radius and θ is the azimuth; e_r is the usual radial unit vector at azimuth θ. We take {θ¹, θ²} = {r, θ} and recast Eq. (33) as

$$\begin{array}{rcl}{{\bf{r}}}_{,t} & = & {z}_{,t}{\bf{k}},\,{{\bf{a}}}_{1}={{\bf{e}}}_{r}(\theta )+{z}_{,r}(r,\theta ){\bf{k}},\\ & & \,\,\,{{\bf{a}}}_{2}=r{{\bf{e}}}_{\theta }(\theta )+{z}_{,\theta }(r,\theta ){\bf{k}},\\ & & \,\,\,\,\,a={\rm{\det }}({a}_{\alpha \beta })\\ & & \,\,\,\,\,\,\,\,={r}^{2}\mathrm{(1}+{z}_{,r}^{2})+{z}_{,\theta }^{2},\\ {a}^{11} & = & \frac{{r}^{2}+{z}_{,\theta }^{2}}{a},\,{a}^{22}=\frac{1+{z}_{,r}^{2}}{a},\,{a}^{12}={a}^{21}=-\,\frac{{z}_{,r}{z}_{,\theta }}{a},\\ H & = & \frac{1}{2{a}^{\mathrm{3/2}}}[{r}^{3}{z}_{,rr}+{r}^{2}{z}_{,r}+{r}^{2}{z}_{,r}^{3}+r{z}_{,rr}{z}_{,\theta }^{2}-2r{z}_{,r\theta }{z}_{,r}{z}_{,\theta }+r{z}_{,\theta \theta }+r{z}_{,\theta \theta }{z}_{,r}^{2}+2{z}_{,r}{z}_{,\theta }^{2}],\\ K & = & \frac{1}{{a}^{2}}[{r}^{3}{z}_{,r}{z}_{,rr}+{r}^{2}{z}_{,rr}{z}_{,\theta \theta }-{r}^{2}{z}_{,r\theta }^{2}+2r{z}_{,r\theta }-{z}_{,\theta }^{2}]\,{\rm{and}}\\ & & {\bf{n}}=\frac{1}{\sqrt{a}}(\,-\,{z}_{,\theta }{{\bf{e}}}_{\theta }-r{z}_{,r}{{\bf{e}}}_{r}+r{\bf{k}}\mathrm{).}\end{array}$$

(72)

Further, the normal velocity and the curvature tensor are given by

$$w={{\bf{r}}}_{,t}\cdot {\bf{n}}=r{z}_{,t}/\sqrt{a}\,{\rm{and}}\,{\bf{b}}={b}_{\alpha \beta }({{\bf{a}}}^{\alpha }\otimes {{\bf{a}}}^{\beta }),$$

(73)

where

$$\begin{array}{rcl}{b}_{11} & = & {z}_{,rr}{\bf{k}},\,{b}_{12}={b}_{21}=\frac{1}{\sqrt{a}}(r{z}_{,r\theta }-{z}_{,\theta }),\,{b}_{22}=\frac{1}{\sqrt{a}}({r}^{2}{z}_{,r}+r{z}_{,\theta \theta }),\\ {{\bf{a}}}^{1} & = & \frac{1}{a}[({r}^{2}+{z}_{,\theta }^{2}){{\bf{e}}}_{r}-r{z}_{,r}{z}_{,\theta }{{\bf{e}}}_{\theta }+{r}^{2}{z}_{,r}{\bf{k}}],\,{\rm{and}}\\ {{\bf{a}}}^{2} & = & \frac{1}{a}[\,-\,r{z}_{,r}{z}_{,\theta }{{\bf{e}}}_{r}+r\mathrm{(1}+{z}_{,r}^{2}){{\bf{e}}}_{\theta }+{z}_{,\theta }{\bf{k}}\mathrm{].}\end{array}$$

(74)

By extracting leading order terms, Eqs (72–74) yield

$$\begin{array}{rcl}a & \simeq & {r}^{2},\,w\simeq r{z}_{,t},\,{\bf{n}}\simeq {\bf{k}}-{\nabla }_{p}z,\,{{\bf{a}}}^{1}\simeq {{\bf{e}}}_{r}+{z}_{,r}{\bf{k}},\,{{\bf{a}}}^{2}\simeq \frac{1}{r}{{\bf{e}}}_{\theta }+\frac{1}{{r}^{2}}{z}_{,\theta }{\bf{k}}\\ {\bf{b}} & \simeq & {\nabla }_{p}^{2}z,\,H\simeq \frac{1}{2}{{\rm{\Delta }}}_{p}z\,{\rm{and}}\,K\simeq \mathrm{0,}\end{array}$$

(75)

and the incompressibility condition Eq. (28) becomes

$$0\simeq {v}_{\alpha ,\alpha }={\rm{div}}\,v={v}_{r,r}+\frac{{v}_{\theta ,\theta }}{r}+\frac{{v}_{r}}{r}.$$

(76)

The equations of motion (42) and boundary conditions (61) are approximated as

$$\frac{1}{2}k{{\rm{\Delta }}}_{p}({{\rm{\Delta }}}_{p}z)-\lambda {{\rm{\Delta }}}_{p}z-2\nu {z}_{,\alpha \beta }{v}_{\alpha ,\beta }\simeq p,\,{\bar{\lambda }}_{,\alpha }+v{{\rm{\Delta }}}_{p}{v}_{,\alpha }\simeq \mathrm{0,}\,{v}_{\alpha ,\alpha }\simeq \mathrm{0,}$$

(77)

and

$$({v}_{\alpha ,\beta }+{v}_{\beta ,\alpha })\,{({\tau }_{\beta }{\nu }_{\alpha })}_{p}\simeq 0\,{\rm{and}}\,-\,\bar{\lambda }\simeq \nu ({v}_{\alpha ,\beta }+{v}_{\beta ,\alpha })\,{({\nu }_{\beta }{\nu }_{\alpha })}_{p}\mathrm{.}$$

(78)

Lastly, on the interacting boundary, we have from¹⁵ and²⁸ that

$$\sigma ={f}_{n}\simeq \overline{k}{\nabla }_{p}\tau \cdot {{\boldsymbol{\tau }}}_{p}-k{{\boldsymbol{\nu }}}_{p}\cdot {\nabla }_{p}H,$$

(79)

where σ is an empirical wetting constant. In the present case (i.e. ν_p = −e_r and τ_p = e_θ), the above condition reduces to

$${({{\rm{\Delta }}}_{p}z)}_{,r}=\frac{2\sigma }{k}.$$

(80)

Example 1: Circumferentially dominant viscous flow

We consider a case in which

$${v}_{\theta }=A\,{\rm{and}}\,{v}_{r}=\frac{A}{r},$$

(81)

so that (77)_2–3 are met and thus yield $\bar{\lambda }\simeq 0$ and $\lambda \simeq -\,q$. Accordingly, in the case of vanishing p, Eqs (77 and 78) become

$$\begin{array}{l}({z}_{,rrrr}+\frac{2{z}_{,rrr}}{r}+\frac{{z}_{,rr}}{{r}^{2}}+\frac{2{z}_{,rr\theta \theta }}{{r}^{2}}+\frac{2{z}_{,r\theta \theta }}{{r}^{3}}+\frac{{z}_{,\theta \theta \theta \theta }}{{r}^{4}})\\ \,-\,{\mu }^{2}({z}_{,rr}+\frac{{z}_{,r}}{r}+\frac{{z}_{,\theta \theta }}{{r}^{2}})-\frac{8A\nu }{k}\frac{r{z}_{,r}+{z}_{,\theta \theta }}{{r}^{4}}\simeq 0,\end{array}$$

(82)

subjected to

$$z=0,\,{\nabla }_{p}z=0\,{\rm{and}}\,{z}_{,rrr}+\frac{{z}_{,rr}}{r}-\frac{{z}_{,r}}{{r}^{2}}-\frac{2{z}_{,\theta \theta }}{{r}^{3}}+\frac{{z}_{,\theta \theta r}}{{r}^{2}}=\frac{2\sigma }{k},$$

(83)

where ${\mu }^{2}=\frac{2\lambda }{k}$. A complete analytical solution of the above PDEs is available via the method presented in^33,34,35,36 and is obtained by

$${z}_{1}(r,\theta )={z}_{11}(r,\theta )+{z}_{12}(r,\theta ),$$

(84)

$$\begin{array}{rcl}{z}_{11} & = & \sum _{m=0}^{\infty }\,{K}_{n}(\frac{\mu }{\sqrt{2}}r)\,[{A}_{m}+{B}_{m}\theta +{C}_{m}\,\sin \,m\theta +{D}_{m}\,\cos \,m\theta ]\\ & & +\,{K}_{n}(\frac{\mu }{\sqrt{2}}r)\,[{A}_{0}+{B}_{0}\theta +{D}_{0}]\\ & & +\,\sum _{m=1}^{\infty }\,{K}_{n}(\frac{\mu }{\sqrt{2}}r)[{A}_{m}+{B}_{m}\theta +{C}_{m}\,\sin \,m\theta +{D}_{m}\,\cos \,m\theta ],\end{array}$$

(85)

and

$$\begin{array}{rcl}{z}_{12} & = & \sum _{m=0}^{\infty }[{C}_{m}{I}_{q}(\frac{\mu }{\sqrt{2}}r)+{D}_{m}{K}_{q}(\frac{\mu }{\sqrt{2}}r)\\ & & +\,{E}_{m}{J}_{q}(\frac{\mu }{\sqrt{2}}r)+{F}_{m}{Y}_{q}(\frac{\mu }{\sqrt{2}}r)]\,[{A}_{m}\,\sin \,m\theta +{B}_{m}\,\cos \,m\theta ]\\ & & +\,{r}^{\sqrt{\frac{{\mu }^{2}}{2}}}[{C}_{0}{I}_{0}(\frac{\mu }{\sqrt{2}}r)+{D}_{0}{K}_{0}(\frac{\mu }{\sqrt{2}}r)\\ & & +{E}_{0}\,{J}_{0}(\frac{\mu }{\sqrt{2}}r)+{F}_{0}{Y}_{0}(\frac{\mu }{\sqrt{2}}r)]\,[{B}_{0}]\\ & & +\,\sum _{m=0}^{\infty }\,{r}^{\sqrt{\frac{{\mu }^{2}}{2}}}[{C}_{m}{I}_{q}(\frac{\mu }{\sqrt{2}}r)+{D}_{m}{K}_{q}(\frac{\mu }{\sqrt{2}}r)\\ & & +{E}_{m}{J}_{q}(\frac{\mu }{\sqrt{2}}r)+{F}_{m}{Y}_{q}(\frac{\mu }{\sqrt{2}}r)]\,[{A}_{m}\,\sin \,m\theta +{B}_{m}\,\cos \,m\theta ],\end{array}$$

(86)

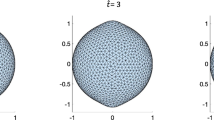
where ${n}^{2}=\frac{4A\nu }{k}+\frac{{m}^{2}}{2}$ and ${q}^{4}=\frac{8{m}^{2}A\nu }{k}$. The solutions are the first and second kinds of the modified Bessel functions and usual Bessel functions of the order n and q with parameter μ, denoted conventionally by, I_n, K_n, J_n, and Y_n, respectively³⁷. Similarly as in the rectangular case, it is found that the intra-membrane viscosity, in the case of circumferentially dominant flow, leads to straining effects on the membrane (Fig. 3) and the resulting transverse deflection is reduced with increasing velocity of viscous flow (Fig. 4a). More importantly, the viscous flow gives rise to wrinkling phenomena when $\frac{A\nu }{\lambda }\ge {10}^{-9}$. Based on our analysis of a rectangular portion of membranes and the observations from⁹ where no interactions are considered, we infer that the interaction forces between the membrane and the substrate give rise to wrinkling phenomena. Further clarification of such phenomena is, however, beyond the scope of present study due to the paucity of available data. It is shown in Fig. 4(a) that both the amplitude of wrinkles and the magnitude of transverse deflections decay away as they approach to far field boundary. Also, Fig. 4(b) illustrates that the solutions from the proposed model (dot lines) reduce to those predicted by the existing model (solid lines)¹⁵ in the limit of vanishing viscous flow (i.e. $A\simeq 0$). In other words, the presented solution is general enough to accommodate the particular solution where the viscous effects are not integrated.

Figure 3

Membrane shape evolutions with intra-membrane viscosity (Circumferential): A = 10⁻⁵ and 10⁻⁷.

Figure 4

Deflections of lipid membrane with respect to intra-membrane viscous flows.

Example 2: Radially dominant flow

In this section, radially dominant flow is considered where we have

$${v}_{\theta }=-\,A\theta \,{\rm{and}}\,{v}_{r}=A.$$

(87)

Similar to the previous case, Eqs (77 and 78), together with the above yield

$$\begin{array}{l}({z}_{rrrr}+\frac{2{z}_{rrr}}{r}+\frac{{z}_{rr}}{{r}^{2}}+\frac{2{z}_{rr\theta \theta }}{{r}^{2}}+\frac{2{z}_{r\theta \theta }}{{r}^{3}}+\frac{{z}_{\theta \theta \theta \theta }}{{r}^{4}})\\ \,-\,{\mu }^{2}({z}_{rr}+\frac{{z}_{r}}{r}+\frac{{z}_{\theta \theta }}{{r}^{2}})-\frac{8A\nu }{k}{z}_{rr}=0.\end{array}$$

(88)

Again, using the methods in^33,34,35,36, the solution of Eq. (88) is obtained by the following explicit form;

$${z}_{2}(r,\theta )={z}_{21}(r,\theta )+{z}_{22}(r,\theta ),$$

(89)

$$\begin{array}{rcl}{z}_{21} & = & \sum _{m=0}^{\infty }\,{K}_{s}(\frac{\mu }{\sqrt{2}}r)\,[{A}_{m}+{B}_{m}\theta +{C}_{m}\,\sin \,m\theta +{D}_{m}\,\cos \,m\theta ]\\ & & +\,{K}_{0}(\frac{\mu }{\sqrt{2}}r)[{A}_{0}+{B}_{0}\theta +{D}_{0}]\\ & & +\,\sum _{m=1}^{\infty }\,{K}_{s}(\frac{\mu }{\sqrt{2}}r)[{A}_{m}+{B}_{m}\theta +{C}_{m}\,\sin \,m\theta +{D}_{m}\,\cos \,m\theta ],\end{array}$$

(90)

and

$$\begin{array}{rcl}{z}_{22} & = & \sum _{m=0}^{\infty }\,{r}^{\sqrt{\frac{{\mu }^{2}}{2}}}[{C}_{m}{I}_{t}(\frac{\mu }{\sqrt{2}}r)+{D}_{m}{K}_{t}(\frac{\mu }{\sqrt{2}}r)+{E}_{m}{J}_{t}(\frac{\mu }{\sqrt{2}}r)\\ & & +\,{F}_{m}{Y}_{t}(\frac{\mu }{\sqrt{2}}r)]\,[{A}_{m}\,\sin \,m\theta +{B}_{m}\,\cos \,m\theta ]\\ & & +\,{r}^{\sqrt{\frac{{\mu }^{2}}{2}}}[{C}_{0}{I}_{0}(\frac{\mu }{\sqrt{2}}r)+{D}_{0}{K}_{0}(\frac{\mu }{\sqrt{2}}r)\\ & & +\,{E}_{0}\,{J}_{0}(\frac{\mu }{\sqrt{2}}r)+{F}_{0}{Y}_{0}(\frac{\mu }{\sqrt{2}}r)]\,[{B}_{0}]\\ & & \sum _{m=0}^{\infty }\,[{C}_{m}{I}_{t}(\frac{\mu }{\sqrt{2}}r)+{D}_{m}{K}_{t}(\frac{\mu }{\sqrt{2}}r)+{E}_{m}{J}_{t}(\frac{\mu }{\sqrt{2}}r)\\ & & +\,{F}_{m}{Y}_{t}(\frac{\mu }{\sqrt{2}}r)]\,[{A}_{m}\,\sin \,m\theta +{B}_{m}\,\cos \,m\theta ],\end{array}$$

(91)

where and ${s}^{2}=\frac{{m}^{2}}{2}$ and t² = mμ. Similar to the circular case, radially arranged wrinkles begin to form as the parameter exceeds the critical value of $\frac{A\nu }{\lambda }\ge 3\times {10}^{-10}$ and they vanish at the remote boundary. The number of radial wrinkles increases with the growing effects of viscous flow (Fig. 5) and with larger radius of an inner circle. A similar tendency can be found in the work of¹⁰ (See, Fig. 6) where the authors measure the number of wrinkles on thin polymer films under the compatible settings as considered in the present work. In addition, we assimilate the experiments in¹⁰ by using the proposed analytical model and present the results in Fig. 7. Although, the obtained model is not intended for the analysis of thin polymer films, it still provides reasonable agreement with the results in¹⁰ (see, Fig. 7) that the number of wrinkles is sensitive to both the thickness ‘t’ (inversely proportional) and the inner radius ‘a’ (proportional). The results are also align with the theoretical developments regarding to finely wrinkled states of the membrane via the minimization of the strain-energy function and by its quasi-convexification^11,12. Potential applications to biomechanics may include monitoring vesicle thickness and enhancing vesicle fusion processes. However, prior to these applications, it would be necessary to further clarify and/or justify the obtained results by employing the aforementioned theory.

Figure 5

Number of wrinkles on lipid membranes with respect to A and μa (inner radius).

Figure 6

Number of wrinkles on thin polymer films¹⁰. From [Huang, J. et al. 50–653 (2007)]. Reprinted with permission from AAAS.

Figure 7

Comparison with the experimental result in¹⁰.

Data acquisition

Figures in the manuscript are prepared by visualizing analytical solutions presented in the manuscript. For the purpose, a commercial software (MATLAB) is used.

Ethics statement

This work did not involve any collection of human data.