Introduction

Computational high-throughput screening techniques have accelerated catalyst discovery, primarily by facilitating rapid identification of promising candidate materials for rigorous additional testing through detailed experiments and simulations. Computational approaches have also enabled in-operando catalyst structure prediction, wherein the stable structure(s) may vary based on reaction conditions. However, when the materials space under investigation is exceedingly complex, brute-force enumeration and evaluation of target properties becomes intractable using first principles methods such as density functional theory (DFT). Machine learning (ML)-based surrogate models have been proposed as a possible alternative to navigate these complex phase spaces at a fraction of the computational cost of first principles methods1. In particular, graph convolutional neural network (GCN) models2,3, including the crystal graph convolutional neural network (CGCNN)4 approach, have been explored as effective non-linear maps between a material’s crystal structure, featurized as graphs, and one or more desired target properties. GCNs, benchmarked against DFT data, have been demonstrated to work as reliable surrogates for DFT for many classes of materials and prediction tasks5,6,7,8,9,10,11,12,13,14. However, for an ML surrogate to effectively discover new materials and catalysts via high-throughput screening, it must be able to provide reliable predictions outside the training space, where DFT data are not necessarily available. It is therefore necessary to provide reliable estimates of the uncertainty in the surrogate model’s predictions.

A multitude of uncertainty quantification (UQ) techniques have been used in recent years to address this issue, including Gaussian process regression (GPR) models15 query-by-committee16, latent space distance17, Bayesian neural networks18, and dropout neural networks19. In general, a surrogate model with UQ can provide not only an estimate of the target property but also an associated uncertainty, and recently, Tran et al. 20 provided a comparison of UQ techniques and various metrics used to judge them. Since the uncertainty estimates are often associated with candidate materials outside the training space, improved model predictions may be found by iteratively sampling candidates that show either desired values of the target property or high uncertainty, and then retraining the surrogate model with these candidates included in the training data. Such an active learning workflow has been demonstrated to work well for the discovery of Ir-oxides21, transition metal complexes22, intermetallics23, transition metal dichalcogenides24, solid-state electrolytes25, and high melting temperature alloys26, among many others. In each of these cases, the active learning workflow is geared towards the optimization of a particular target property of interest along with improvement in model predictions.

The optimization approach described above can become challenging when the system of interest is complex and the target property depends on a large number of variables, often on the order of thousands or more. In most cases, however, the intrinsic behavior of such systems in fact depends on only a subset of the available quantities27. Theoretically-motivated approaches exist for correspondingly reducing the dimensionality of a system, including the well-known Buckingham Pi theorem28, which seeks to combine relevant physical quantities, often identified through intuition, into dimensionless groups that capture system behavior more parsimoniously. Such methods rely on prior analytical knowledge about the system of interest, which usually allows one to preserve physical interpretability of the reduced model. However, knowledge of a system’s inner workings is not always available, and data-driven methods are required for cases involving a black box. There is a variety of techniques for representing high-dimensional data in a reduced space that retain only the information deemed necessary for describing the system of interest. These include well-known, linear methods such as principal component analysis (PCA)29,30 and more advanced, nonlinear techniques such as diffusion maps (DMaps)31 and variational autoencoders32. Dimensionality reduction may be used to ascertain the intrinsic dimensionality of a dataset that describes experimental results for one or more properties of interest. Discovering the intrinsic geometry of the input data can, in turn, simplify the task of optimizing a target property by lowering the number of variables needed to learn the relationship between inputs and output. Techniques such as DMaps help find which combinations of variables matter, in the sense of contributing to the functional behavior of the target property. These data-driven effective coordinates may not correspond directly to individual variables, but it is possible to check for a one-to-one relationship between the discovered data-driven coordinates and a collection of physically meaningful quantities33.

High-entropy alloys (HEAs) are a class of disordered, multimetallic alloys that are stabilized due to their configurational entropy of mixing and represent a complex materials space characterized by many variables34,35,36. As such, they can be considered to be an ideal materials science testbed for some of the techniques described above. HEAs have shown promising activity and stability as catalysts for various electrochemical reactions, such as the oxygen reduction reaction (ORR)37,38, the CO2 reduction reaction (CO2RR)39, the oxygen evolution reaction (OER)40, and thermal catalytic reactions including ammonia decomposition41,42 and ammonia oxidation43. While the vast design space of HEAs, consisting of multiple elements and configurations, provides ample opportunities for tailoring catalytic properties, it also presents a challenge in terms of computational tractability. Additionally, the properties of interest that predict HEA stability—for instance, the free energy of formation—are all functions of an ensemble of configurations, rather than of a single structure, and estimation of these properties depends on the method of sampling the ensemble. Usually, it is infeasible to sample the entire configuration space; so statistical sampling methods are used to infer the ensemble property from a reduced subset of configurations. However, this approach introduces an additional sampling error in the estimation of the property of interest. Traditional active learning paradigms may not be ideally suited to elucidating such properties since they involve acquisition of single candidates, as opposed to ensembles of candidates, and they do not typically involve a treatment of sampling error.

Motivated by the above considerations, we present a modified active learning workflow for the identification of HEAs with an optimal target property—in this case, the formation free energy—calculated through ensemble-averaging of properties of individual HEA configurations. We consider a ternary alloy system consisting of the elements Pd, Pt, and Sn. The choice of these elements is based on their utility as catalysts in a host of reactions such as propane dehydrogenation and electrochemical nitrate reduction, among many others44,45,46,47,48,49. Further, we utilize a dropout graph convolutional network (dGCN) as a surrogate model to predict formation energies, with associated uncertainties, of binary and ternary HEA configurations in this ternary alloy system. We train the dGCN on an initial dataset consisting of only binary configurations, and then improve the model’s prediction in the ternary space by iteratively sampling ternary configurations that are grouped into ensembles. We compare two versions of our proposed workflow, which differ primarily in how ensembles are formed. The first is motivated by physical first principles and groups configurations according to their composition. The second takes a more data-driven approach and forms groups for the configurations using K-means clustering on the dGCN’s internal representations in a lower dimensional space discovered by DMaps. Further, we derive an acquisition function by combining probability theory with a simple formalism for the canonical ensemble of statistical mechanics that accepts ensembles of target properties and uncertainties as inputs and suggests new candidate ensembles as outputs. Additionally, we show that a physically significant parameter from the original formalism, temperature, transforms into an exploration-exploitation tradeoff parameter, providing more flexibility to our acquisition function.

Using this acquisition function, we select ensembles of ternary configurations, representing either ternary compositions in the physics-driven approach or clusters in DMaps space in the data-driven approach, randomly sample ~100 ternary configurations from the selected ensemble, and perform DFT calculations to evaluate their formation energies. These ternary configurations are then added to the training set, and the dGCN model is retrained, completing one iteration of the active learning cycle. We perform six iterations of this active learning cycle and compare predictions of the active learned-models (from both approaches) with a high-fidelity model trained on a larger set of DFT calculations. Broadly, we find that the formation free energy predictions of the active learned-models converge to ‘true’ values, as predicted by the high-fidelity model, in the central region of composition space, where most of the sampling occurs. Additionally, we find that the convergence behavior is different for the two approaches—the physics-based strategy performs more akin to a depth-first approach whereas the data-driven strategy is more like a breadth-first approach.

Our approach provides a novel acquisition strategy to sample alloy structures from an ensemble based on thermodynamic stability criteria. This strategy permits iterative improvement of the predictions of a model of ternary alloy formation energies—initially trained only on binary alloy structures—by sampling using physics-informed and data-informed schemes, the latter based on dimensionality reduction with Diffusion Maps. These two active learning schemes are able improve the prediction accuracy of formation free energies in ternary composition space to a level comparable to what is achieved with a high-fidelity model trained on nearly five times more ternary alloy structures. The results demonstrate that significant dimensionality reduction, and consequent gains in efficiency, are possible in thermodynamic sampling problems when suitable active learning schemes are employed.

Results

Workflow

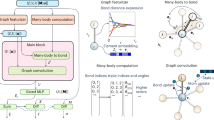
Here, we provide an overview of the proposed active learning scheme (Fig. 1), with further details given below and in the Supplementary Information (SI). As mentioned previously, we introduce two distinct methods of selecting optimization coordinates: a physically motivated approach that uses bulk composition as the main variables, and a data-driven approach involving latent coordinates computed from the manifold learning technique known as Diffusion Maps (DMaps). For ease of comparison, in each case we group crystal structures into ensembles—either compositions, or clusters in the space of DMaps coordinates—and we minimize an acquisition function inspired by statistical mechanics for the ensembles to determine the one with the most stable configurations for further investigation. The two approaches follow the same overall workflow, except that the ensembles formed in each consist of different subsets of all available crystal structures.

Fig. 1: The active learning workflow.
figure 1

First, binary crystal configurations are sampled from the edges of the ternary phase diagram and input to the DFT code to evaluate formation energies. The dGCN (central block) is trained on these binary alloy formation energies, converting an input crystal into a graph, on which convolution and pooling operations are performed to convert it to a 42-element embedding vector representing the crystal. This vector is then fed to a feed-forward neural network with dropout to predict the formation energy and corresponding uncertainty. In the physics-informed scheme, ternary configurations are sampled from a particular composition for which the acquisition function is minimized and input to the DFT code for evaluation. In the data-driven scheme, the 42-element embedding vector is input to the DMaps algorithm (lower block) to discover latent coordinates. The acquisition function is computed on clusters formed in this lower dimensional space through k-means clustering, and ternary configurations are sampled from the selected cluster and input to the DFT code for evaluation. The dGCN is then retrained on a dataset containing these additional sampled ternary crystals.

Full size image

We use our in-house code HEAT (High-Entropy Alloy Toolbox) to generate an initial training set composed solely of binary alloy configurations having all possible compositions that can be represented using a 16-atom unit cell. The choice of this unit cell is a balance between having a high composition-space resolution and computational cost. For each of these sets, we perform DFT calculations to evaluate formation energies, storing the relaxed structures and corresponding formation energy values in a training database. Next, we convert the relaxed structures into equivalent graph representations for training our dropout graph convolutional network (dGCN) to predict formation energies from crystal configurations. We use dropout not only during network training, but also during prediction, which enables us to obtain concomitant uncertainty estimates, as well. This trained network becomes the basis of our surrogate model acquisition function construction.

To start the process of selecting the subsequent candidate sample points, we use HEAT to generate ternary crystal configurations from all ternary compositions that can be represented using a 16-atom unit cell. For each composition, 1% of the total number of possible configurations are sampled to maintain computational tractability and a reasonable database size. We show in Supplementary Section 3.1 that the error in formation free energy, which we use to estimate stability, due to this reduced sampling can be eliminated with a simple scaling factor. At this point, we do not perform any DFT calculations, but instead use the current optimization iteration’s version of the dGCN to predict formation energies and the corresponding uncertainty estimates for all of the generated ternary configurations, storing the results in a prediction database. As a part of the dGCN architecture, discussed in Methods, we also obtain in this prediction phase a 42-dimensional vector representation of each generated crystal at this iteration of the optimization.

Next, we group the ternary configurations in the prediction database into ensembles. Here, the two approaches diverge. For the physics-informed approach, the ensembles correspond to different bulk compositions. In the case of the data-driven approach, DMaps is used to compute lower dimensional representations of the 42-dimensional embeddings. K-means clustering is then used to group ternary configurations into ensembles based on proximity in this DMaps space.

Now, we proceed to optimize our acquisition function. The acquisition function is derived from a modified partition function for the Helmholtz free energy of formation. The function is designed to pick clusters in which structures have low formation energies \(({\bar{U}}_{{ij}})\) and/or high uncertainties \(({s}_{{ij}})\), as predicted by the dGCN. The inverse temperature \((\beta )\), which is a physical parameter in the Helmholtz free energy expression, transforms into an exploitation-exploration tradeoff parameter, such that low values of β (or high temperatures) lead to exploitation, and vice versa. For each ensemble i, we input the formation energies and uncertainties of ternary configurations in that ensemble (predicted by the dGCN) from the prediction database to estimate the corresponding value of our acquisition function, which is given by

$${A}_{i}=-\frac{1}{\beta }\log \left[\mathop{\sum }\limits_{j=1}^{{J}_{i}}\exp \left(-\beta {\bar{U}}_{{ij}}+\frac{{\beta }^{2}{s}_{{ij}}^{2}}{2}\right)\right]$$
(1)

(see Supplementary Section 3 for derivation and additional discussion). We select as our next candidate the ensemble with the lowest computed value for Ai, randomly choose ~100 crystals from this ensemble, and use DFT to calculate the associated formation energy values. We add the results to our training database and repeat the procedure. We note that, for completeness, in addition to the two approaches mentioned above, we also add one more method of parametrizing the database: instead of a finite number of discrete DMaps clusters, we also optimized in continuum DMaps space (see Supplementary Section 6 for a brief discussion of this alternative strategy).

The Initial Model

The first step in the workflow involves training the surrogate model on DFT calculations of all symmetrically distinct binary alloy configurations in a 16-atom cell. This initial dataset comprises ~2000 binary alloy configurations across the Pd-Sn, Pt-Sn, and Pd-Pt pairs. The data are partitioned into training, validation, and test sets (60:20:20 split). The training set is used to update the model weights and biases, while the validation set is used to assess the model predictions at the end of every epoch using a collection of metrics that includes the mean absolute error (MAE) and the root mean square error (RMSE). At the end of the training procedure, we select the model with the lowest validation error for evaluations on the test set. This validation-based early stopping technique50 is used to prevent overfitting of the dGCN. We keep the test set hidden from the model during the entire training procedure and only used it to judge the model’s fidelity at the end of training.

We test the performance of the dGCN by making a parity plot (Fig. 2a) and computing three metrics for the test set: mean absolute error (MAE), root mean squared error (RMSE), and coefficient of determination (R2). The MAE of the model is 0.019 eV per atom which is comparable to that reported for the CGCNN model in Xie et al. 4 (0.039 eV per atom). We also plot a distribution of the dropout-based uncertainties (Fig. 2b) and calculate three metrics to judge the performance of our UQ method: sharpness, coefficient of variation, and calibration (miscalibration error). We find that the sharpness is 0.027 eV per atom, the coefficient of variation is 0.331 (Fig. 2b), and the miscalibration error is 0.057 (Supplementary Figure 15). According to an analysis of UQ methods in Tran et al. 20, these values indicate that the uncertainties are reasonably sharp and well-calibrated.

Fig. 2: Evaluation of the model trained exclusively on binary alloys.
figure 2

a Parity plot of dGCN-calculated formation energies and DFT-calculated formation energies of Pd-Sn, Pt-Sn, and Pd-Pt binary alloy configurations in the initial training test set. Each binary pair is represented by a different color. b Distribution of standard deviations predicted using dGCN with the sharpness and coefficient of variation (Cv). c Plot of mean relaxation distance against absolute error for randomly sampled configurations from four different ternary compositions in the benchmark set. d Composition-averaged mean relaxation distance and absolute error for compositions in the benchmark set.

Full size image

Next, we test the performance of the network on a benchmark set of ternary structures sampled from Pd-rich (Pd10Pt2Sn4), Pt-rich (Pd4Pt10Sn2), Sn-rich (Pd3Pt2Sn11), and near-equimolar (Pd6Pt5Sn5) compositions. We sample 100 structures from each composition, perform DFT relaxations on them, and calculate their relaxed-state formation energies. We compare these values to the formation energies predicted by the binary-trained dGCN model on the unrelaxed ternary structures and calculate an absolute error, which we designate as the ‘benchmark set error’. We then plot this absolute error against a mean relaxation distance, which we define as the absolute difference between the mean nearest-neighbor distances of the relaxed and unrelaxed ternary structures in the benchmark set (Fig. 2c). We also plot composition-averaged quantities in Fig. 2d. We find that, in general, structures and compositions that possess a higher mean relaxation distance also have a higher benchmark set error, indicating that the more a structure relaxes, the more difficult it is for the dGCN to predict its relaxed-state energy correctly. Ultimately, it is the relaxed-state formation energies that are of interest, since those correspond to ground state geometries. However, it is only the initial, unrelaxed geometries that are available to the dGCN. To resolve this apparent paradox, we train the network to predict relaxed-state energies from unrelaxed geometries, so for any additional ternaries introduced to the training set, we provide the unrelaxed structure but label it with the relaxed-state formation energy.

As shown in Fig. 2d, there is a close association between the composition of the ternary alloys, the degree of relaxation, and the average error of the dGCN model in the benchmark set, and we will return to this composition-based, physically motivated analysis below. At the same time, one could envision using the 42-dimensional representations obtained from our dGCN to characterize the configurations, with additional simplifications provided by using DMaps to represent the network’s internal description of each crystal in terms of fewer coordinates. To this end, we compute DMaps on the data and find that the first two eigenvectors represent intrinsic coordinates for a low-dimensional manifold embedded in the 42-dimensional space of dCGN representations. These diffusion space coordinates, illustrated in Fig. 3, are a dimensionally reduced representation of the original crystal lattice data. Notice that the intrinsic geometry of the data bear certain resemblances to physical intuition. For example, there is a small cluster of Pd-Pt binary crystals at a short distance from the remainder of the data. These crystals are formed as fcc structures, rather than the bcc structures used for crystals that contain Sn, and DMaps distinguishes between the two packing geometries without any explicit information about this principle. In addition, we note that the larger cluster of data is roughly triangular, corresponding to the traditional shape of ternary composition plots, and there are three general regions of the cluster where crystals rich in each element tend to be located. Using this DMaps representation of crystal lattice space, we form 153 clusters via k-means, matching the number of distinct compositions available for ternary alloys with 16-atom unit cells. The acquisition function is further evaluated for these clusters. We note that the clusters generated using DMaps computed on the latent space of the model trained exclusively on binaries are used (without modification) for subsequent steps of the active learning procedure. DMaps are not iteratively recomputed on active-learned models trained on ternary structures, since we find that there is no significant change in the latent space structure on the addition of ternaries (see Supplementary Section 7 for a detailed discussion).

Fig. 3: Binary and ternary alloy structures in DMaps space.
figure 3

The first two DMaps coordinates as computed for our cluster-based approach are plotted. The same values are plotted in each subfigure, colored by composition (lighter is higher) (first three) and by whether the corresponding crystal was binary or ternary (rightmost). We used k-means to partition these data into 153 clusters, which were used analogously to the compositions in the physically motivated approach.

Full size image

Comparison of active learning schemes

The network trained on only binary alloy structures, discussed above, is considered to be a ‘low-fidelity’ model. Now, we iteratively retrain this model by sampling additional ternary alloy structures in order to (1) improve the value of the target property—the free energy of formation—in the region of interest, and (2) improve predictions of the model in regions of high uncertainty. To balance between these objectives, we evaluate the ensemble acquisition function (discussed in Supplementary Section 3). We predetermine a computational budget and an optimization schedule: 600 ternary alloy structures spread evenly over six iterations, with the first two focused on exploration, the next two with a balanced focus, and the last two centered on exploitation. This is achieved by setting the temperature to T = 100 K, T = 2000 K, and T = 6000 K, respectively. We note that it is possible to vary both the computational budget and optimization schedule based on the system being studied and desired target property being optimized. In our illustrative example, we stop at six iterations (600 datapoints) since we find that the maximum errors in formation free energies (compared to a high-fidelity model, discussed below) in the stable region of composition space drop below the MAE (0.019 eV per atom) of the initial model trained on binary configurations.

The selection of 100 ternary alloy structures to be sampled per iteration can be made using either of the optimization approaches discussed above. In the physically informed approach, structures are sampled from a single composition in each iteration. In the data-informed approach, structures are sampled from clusters that we initially construct using k-means clustering in low-dimensional DMaps space. For every iteration, we evaluate the ensemble acquisition function on each composition or cluster and randomly select 100 structures from the composition or cluster with the minimum value among those not previously sampled. We use DFT to evaluate the formation energies of these sampled structures and transfer the candidates from the predict set to the training set. The network is retrained with this modified training set, and predictions on the predict set are updated to identify the next composition or cluster to be sampled.

Next, we compare the relative stability of different compositions by evaluating the formation free energy for each composition through a partition function approach (see Supplementary Section 3.1 for details). Fig. 4 shows the free energy landscapes before and after six iterations of active learning using the two approaches. Both approaches yield similar shifts in the free energy minimum compared to the initial predictions based on the binary alloys alone. However, the magnitudes of the changes in free energy are relatively modest at all compositions, indicating that the initial model trained only on binary alloy structures is a qualitatively reasonable model for giving approximate predictions on ternary alloy structures. As such, this active learning cycle can be conceptualized as a scheme to add quantitative corrections to a qualitatively correct model.

Fig. 4: Comparison of free energy landscapes predicted by the dGCN.
figure 4

Free energy landscapes (a) based on binary training data only, (b) after six iterations of the composition-based active learning scheme, and (c) after six iterations of the DMaps cluster-based scheme.

Full size image

To compare the performance of the two sampling approaches in more detail, we create a larger set of DFT-optimized structures and energies, with 3478 ternary alloy structures representing 38 compositions evenly sampled across the full ternary composition space such that sufficient Pd-rich, Pt-rich, Sn-rich, and equimolar compositions are included. Although the full ternary space cannot be exhaustively assessed with DFT calculations, this ‘high-fidelity’ data set is nevertheless considerably larger than the 600 DFT-analyzed ternary alloy structures and can therefore serve as a proxy for the full space.

First, we analyze the compositions that each approach selects for DFT computation. These are summarized in Fig. 5. The physically informed scheme samples configurations from only a single composition at each iteration, so a total of six compositions are sampled by the end of the active learning cycle. At every iteration, the composition with the lowest acquisition function value that is at least two composition steps away from currently sampled compositions is selected. We add the latter criterion to efficiently sample training data based on our analysis in Supplementary Section 5.2 that shows that the dGCN is able to generalize at least one composition step away from sampled compositions. In the data-driven scheme, configurations across multiple compositions may be sampled in each iteration. In Fig. 5, we illustrate the identity of sampled compositions (marked with circles) and the number of configurations sampled from each (sizes of circles). Although the two approaches sample configurations in a different manner, we find a significant overlap in the regions of composition space that they explore. This region contains compositions that have the lowest free energies, i.e., those that are most stable. Overall, we find that both versions of the active learning scheme explore a region of composition space characterized by roughly equimolar compositions, with some preference toward Pd-rich structures.

Fig. 5: Analysis of the compositions of ternary crystals sampled during the composition-based and cluster-based approaches.
figure 5

The ternary plot illustrates the 27 locations within composition space at which more than five configurations were sampled (red circles, size indicates number of configurations at the corresponding composition) and the six locations sampled during the composition-based approach (black crosses). The two methods, though distinct, explore the same region of composition space.

Full size image

Second, we analyze the order in which compositions and clusters are suggested by the acquisition function in the workflow. The first two iterations of our DMaps cluster-based scheme are exploratory and select clusters on the edge of the region covered by our data, which initially have high predictive uncertainty. Upon shifting to a balance between exploration and exploitation, the scheme begins to prefer clusters closer to the center of the data. At the sixth iteration, when we focus on exploitation and prioritize favorable predicted formation energies, the scheme chooses the cluster that overlaps the origin in diffusion coordinate space. We illustrate the first and last iteration of this approach in Fig. 6, and the remaining iterations are provided in Supplementary Section 4. Similarly, in the composition-based scheme, the exploration-to-exploitation approach leads to a selection of compositions on the edge of the composition space, followed by those in the center of the ternary phase diagram. We show in Supplementary Figure 12 that changing the temperature in the acquisition function from low to high, corresponding to a shift from exploration to exploitation, effectively corresponds to a changes in its minimum from the edge of the composition space to its center.

Fig. 6: Choice of ensembles in the cluster-based and composition-based approaches.
figure 6

Illustration of the clusters chosen for (a) the first and (b) the sixth iterations of our DMaps cluster-based approach. Initially, the focus is on exploration, and clusters at the edge of the data set are selected; for this iteration, we needed to combine the six lowest-acquisition value clusters to form a collection of at least 100 crystals. In the final iterations, the focus is on exploitation, and a cluster near the center of the data is selected. Grey points represent crystals in other clusters not selected for the current iteration. c Phase diagram and table highlighting the compositions chosen in the physics-based approach.

Full size image

Finally, we compare the errors between free energy predictions of the DFT-based high-fidelity model (3478 entries) and our initial low-fidelity model, based on binary alloys alone, in Fig. 7a. We find that Pd2Pt5Sn9, and nearby compositions, show the highest error in free energy. More generally, compositions exhibiting the highest errors (> 0.1 eV per atom) contain a majority of Sn, which may be explained by the fact that configurations in Sn-rich compositions have a higher mean-relaxation distance, which makes it more challenging for the dGCN to predict their relaxed-state formation energies without any ternary data (consistent with Fig. 2d). After the active learning has been completed, however, we find that errors are significantly reduced, particularly in the central region of composition space, where most of the sampling occurs. The maximum error in that region falls from 0.06 eV per atom to 0.01 eV per atom for both the physically informed and data informed models. Overall, the number of ternary compositions having an error of greater than 0.1 eV per atom in their formation free energies falls from 19 to 11 (for the physically informed model) and 8 (for the data-informed model).

Fig. 7: Comparison of active-learned models with the high-fidelity model.
figure 7

a Ternary heatmaps showing the errors in free energies for all ternary compositions between a particular model (top: initial, center: physics-informed, bottom: data-informed) and the high-fidelity model. b The error in formation energies of three selected compositions (compared to the high-fidelity model) predicted by various active-learned models (red: data-informed, blue: physics-informed) at every iteration.

Full size image

In Fig. 7b, we show both methods’ convergence to the ‘true’ free energy value, as predicted by the high-fidelity model, with three illustrative compositions, Pd3Pt6Sn7, Pd8Pt2Sn6, and Pd6Pt5Sn5. For all three compositions, we find that the convergence to the value predicted by the high-fidelity model is gradual for the data-informed model. In contrast, the convergence of the physics-informed model is uneven, with no clear monotonic trend. For Pt3Pt6Sn7, we find that the data-informed model is able to reduce the error in formation energy from about 0.1 eV per atom to less than 0.02 eV per atom within the six-iteration cycle, whereas the physics-informed model reduces the error to about 0.04 eV per atom. In the case Pd8Pt2Sn6 (the composition with the lowest free energy as predicted by the high-fidelity model), the error is reduced to less than 0.01 eV per atom from 0.05 eV per atom using both schemes. The convergence of the data-informed scheme is, again, more monotonic as compared to the physics-informed scheme, which only begins converging after an adjacent composition (i.e., Pd7Pt3Sn6) is sampled at the fifth iteration. Similarly, in the case of Pd6Pt5Sn5, both the schemes reduce the error to less than 0.01 eV per atom from 0.03 eV per atom, but the convergence is more oscillatory for the physics-informed approach. Here, too, the physics-informed scheme starts converging rapidly when a surrounding composition is sampled in the fifth iteration. Based on these results, the difference between the two approaches may be likened to the contrast between depth-first and breadth-first strategies. The physically informed approach prioritizes depth and appears to learn a more accurate local representation that improves predictions in a narrow region of composition space at each iteration. The data-driven approach, on the other hand, prioritizes breadth and appears to learn a more holistic representation, but lacks enough data to make an accurate prediction initially. This dearth in training data is progressively mitigated with more active learning iterations, leading to a gradual convergence to the true value.

Discussion

We present an active learning framework to identify stable compositions in a Pd-Pt-Sn ternary alloy system. In this framework, a dGCN is used as a surrogate model to predict the target property, i.e., the formation energy, as well as the associated uncertainty for binary and ternary bulk alloy structures. The initial dGCN model is trained on the DFT-predicted formation energies of binary structures only and shows reasonable parity on the test set consisting of binaries. When this model is tested on a benchmark set of ternary structures, we find that the error varies significantly based on the ternary composition, and this error is, in turn, dependent on how much the ternary structure relaxes, which we quantify using a ‘mean relaxation distance’ metric.

Considering the enormity of the ternary crystal configuration space \(\left(O\left({10}^{7}\right)\right)\), we use active learning to improve the predictions of the dGCN on ternary structures. First, we sample 1% of the total number of ternary structures for each composition that can be represented using a 16-atom unit cell. To determine stability, we evaluate the formation free energy via the canonical partition function for each ternary composition, modified to account for the limited sampling. Further, we derive an acquisition function based on the modified partition function that is used to sample ensembles by balancing both exploitation (of formation energy) and exploration (of dGCN uncertainty). This approach allows us to select stable candidate structures from ensembles of structures, which is convenient for our chosen application since HEA properties, like stability, are functions of ensemble averages.

We use two philosophically different approaches to create ensembles and sample ternary structures for the subsequent calculations: a physically informed approach, with ensembles being equivalent to compositions, and a data-informed approach, with clusters created in DMaps space using k-means clustering as ensembles. For both approaches, we perform six iterations of our active learning workflow, during each of which we sample about 100 structures from the ensemble with the minimum value of the acquisition function. DFT calculations are performed for these structures, which are added to the training set before the dGCN is retrained. We demonstrate that, with both sampling strategies, this active learning workflow achieves comparable predictive capability to a more accurate data set consisting of five times as many DFT calculations. However, the manner in which these two strategies lead to improved models is different—the physically motivated strategy appears akin to a depth-first approach, wherein the model improves predictions in a local region of composition space where sampling occurs during each iteration. In contrast, the data-informed strategy is more akin to a breadth-first approach, such that it samples a broader and more diverse subset of the space and builds a model with globally improved predictions every iteration. Additionally, in the data-informed scheme, DMaps lends interpretability to the dGCN’s predictions by highlighting certain features of the low-dimensional manifold that align with physical intuition.

Through our framework, we systematically extrapolate from a materials space that can be sufficiently evaluated using DFT, comprising binary alloys, to an exponentially larger materials space consisting of ternary alloys, which is challenging to sufficiently sample and evaluate using only DFT. The results demonstrate that significant dimensionality reduction, and consequent gains in efficiency, are possible in thermodynamic sampling problems when suitable active learning schemes are employed. Moreover, this framework shows that both physically motivated and data-driven optimization strategies can be useful for computational materials design applications. To further explore the tradeoffs between these strategies, it would be useful to extend the analysis to a wider space of alloys with differing elements, including high entropy alloys with at least five elements per alloy unit. Another interesting possibility would be to train the dGCN model with data representing surface sites. This analysis would provide information on target properties of surfaces, such as the binding energy of a reaction intermediate, which can assist the discovery of new catalytically active sites.

Methods

Density functional theory

In order to systematically enumerate, prune, and meaningfully generate binary and ternary alloy structures, we utilize our in-house code HEAT (High-Entropy Alloy Toolbox) that leverages the Python Atomic Simulation Environment (ASE)51, Python Materials Genomics (Pymatgen)52, and Vienna Ab-initio Simulation Package (VASP)53 codes for high-throughput alloy calculations. We prescribe the resolution of the composition space by selecting a 16-atom cubic unit cell as our template. Initially, to populate the training space, we enumerate all combinatorically possible discrete binary compositions in the Pd-Pt-Sn alloy system and generate all the unique unrelaxed configurations for each composition. The Pd-Sn and Pt-Sn binary configurations are modeled as body centered cubic (bcc) structures while the Pt-Pd binary configurations are modeled as face centered cubic (fcc) structures. These structures are relaxed using DFT, and the relaxed structures are used in the training set.

Further, we systematically enumerate all possible ternary compositions at 16-atom unit cell resolution and generate unrelaxed face-centered cubic (fcc) configurations for each composition having a lattice constant calculated using Vegard’s law54, which assumes that the lattice constant, ax, for an alloy with composition \({\boldsymbol{x}}=\left({x}_{{Pd}},{x}_{{Pt}},{x}_{{Sn}}\right)\), is the composition-weighted sum of the pure-metal fcc lattice constants:

$${a}_{{\boldsymbol{x}}}={x}_{{Pd}}{a}_{{Pd}}+{x}_{{Pt}}{a}_{{Pt}}+{x}_{{Sn}}{a}_{{Sn}}$$
(2)

To keep the analysis tractable, we sample only 1% of the total number of configurations for each ternary composition. We perform a convergence test to verify that there is negligible sampling error for this sampling percentage (see Supplementary Section 3.1 for details).

We convert the generated binary and ternary configurations into equivalent graph representations, in which each node represents an atom in the crystal structure, and each edge represents a bond (adjacency relationship) between two atoms4. The nodes are characterized by atom-feature vectors consisting of chemical and physical properties, and edges are characterized by bond-features consisting of one-hot encoded vectors signifying the distance between two atoms. The node features are a subset of those used in Xie et al. 4, namely, electronegativity, covalent radius, valence electrons, and first ionization energy. The bond feature vectors are computed using a one-hot encoding of the bond distances. Further discussion regarding node and bond feature vectors is provided in Supplementary Section 5.3 and Ghanekar et al. 13.

Bulk structures are relaxed using periodic density functional theory calculations performed using VASP. The Kohn-Sham orbitals are expanded in terms of a basis of planewave functions to an energy cutoff of 400 eV. The frozen core approximation is used to model the core electron states, which are expressed using the projector augmented wave (PAW)55 method. The Perdew-Burke-Enzerhof (PBE)56 exchange-correlation functional is used to model effects of electron correlation and exchange. The Brillouin zone is sampled using a K-point density of 30/Å3 using the Monkhorst-Pack scheme57. Electron states above the Fermi level are populated at 0 K using a first-order Methfessel-Paxton smearing method58 with a width of 0.2 eV. The electronic self-consistent field (SCF) iterations are carried out until the electronic energy differences between subsequent iterations are below 1 × 10−6 eV. Geometric optimization of the bulk structures is terminated when the Hellman-Feynmann forces are below 1 × 10−3 eV/Å. Bulk relaxation is performed in two steps. First, the volume of the unit cell is relaxed, and next, a geometric relaxation of atom positions at a fixed volume is performed on the converged structure from the first step.

Dropout Graph Convolutional Networks

Our dGCN model is based on the crystal graph convolutional neural network (CGCNN) framework4 developed by Xie et al., which we outline here. Beginning with a crystal graph as the model input, a sequence of convolutional layers updates each atom feature vector vi according to the information contained in feature vectors of neighboring atoms and the corresponding bonds. In the notation of Xie et al.,

$${v}_{i}^{\left(t+1\right)}={v}_{i}^{\left(t\right)}+\mathop{\sum}\limits_{j,k}\sigma \left({z}_{{\left(i,j\right)}_{k}}^{\left(t\right)}{W}_{f}^{\left(t\right)}+{b}_{f}^{\left(t\right)}\right)\odot g\left({z}_{{\left(i,j\right)}_{k}}^{\left(t\right)}{W}_{s}^{\left(t\right)}+{b}_{s}^{\left(t\right)}\right)$$
(3)

where \({z}_{{\left(i,j\right)}_{k}}^{\left(t\right)}={v}_{i}^{\left(t\right)}\oplus {v}_{j}^{\left(t\right)}\oplus {u}_{{\left(i,j\right)}_{k}}\) represents vector concatenation; the symbol \(\odot\) indicates an elementwise product; and \({W}_{f}^{\left(t\right)}\), \({W}_{s}^{\left(t\right)}\), \({b}_{f}^{\left(t\right)}\), and \({b}_{s}^{\left(t\right)}\) are weights and biases. Additional hidden layers are used to refine the network’s learned representation of the local crystal structure at each atom. Finally, the atom feature vectors are pooled, through a mean pooling function, to produce a 42-dimensional latent space13 vector that is fed to the hidden layers in the network. These vectors, one for each crystal graph, are also stored separately for subsequent dimensionality reduction using DMaps.

We modify the hidden layers in the network to incorporate dropout using the Dropout layer in PyTorch59 with a 0.35 dropout probability. The network is trained on the formation energy of each alloy structure predicted using DFT. The training is performed for 500 epochs using the ADAM optimizer60 with the early stopping criterion50; the model with the lowest validation error is chosen. In the prediction phase, the output is predicted 30 times for each input, and the mean and variance of this sample are used as parameters for each structure’s subsequent UQ. We perform a sensitivity analysis for hyperparameters that control the size of the network, namely, the hidden layer size, number of hidden layers, and number of convolutional layers, and find that the errors (MAE and RMSE) are most sensitive to the hidden layer size (see Supplementary Section 5.3 for further details).

The binary input data are first divided randomly into train, validation, and test sets in a 60:20:20 ratio and subsequently passed through the network. The (unrelaxed) ternary alloy structures are classified into a predict set that is not used for training because no DFT data are initially available for these structures. In the retraining procedure of the workflow, ternary alloy structures from the predict set for which DFT energies have been evaluated are labelled and added to the train, validation, and test sets in a 60:20:20 split. The model training procedure outlined above is repeated for this new dataset. See Supplementary Section 5 for additional details on calibration and generalizability of our dGCN model.

Diffusion Maps

Inasmuch as diffusion maps may be thought of as a nonlinear analogue of PCA, a brief explanation of the latter may be helpful in describing the former. Given a cloud of points in some high-dimensional space, PCA first identifies the direction in which the data exhibit the greatest variance, followed by a sequence of further maximal-variance directions constrained to be orthogonal to all previous such directions. If the data lie (at least approximately) on a low-dimensional hyperplane, the sequence of variances corresponding to these so-called principal component directions will show a sharp decrease after exhausting the dimensionality of the hyperplane29. By discarding those principal components with sufficiently small variance, it is possible to represent the data with fewer effective coordinates and to reconstruct the original data to a level of accuracy that depends on how many components were retained.

Although PCA is powerful even in its simplicity, it suffers from the limitation of only being able to describe linear relationships in the data it is given. Diffusion maps, on the other hand, can parameterize both linear and nonlinear manifolds. The DMaps algorithm uses a kernel function to quantify pairwise similarity of the points in a data set, usually a Gaussian kernel, which has the form

$$k({\boldsymbol{x}},{\boldsymbol{x}}^{\prime})=\exp \left[-\frac{{\Vert {\boldsymbol{x}}-{\boldsymbol{x}}^{\prime}\Vert }^{2}}{{\varepsilon }^{2}}\right]$$
(4)

where ε is a scale parameter chosen by the user. From the pairwise similarity values, DMaps approximates the eigenfunctions of the Laplace-Beltrami operator on the manifold from which the data are sampled31. These eigenfunctions form a Fourier-like basis that includes functions which are higher harmonics of other basis members as, for example, \(\cos (k{x}_{1})\) for k a positive integer61. From the perspective of parameterizing a manifold, these higher harmonics do not provide any new information beyond that contained in the lowest-frequency member of the sequence, so dimensionality reduction requires the practitioner to identify a minimal set of informative eigenvectors that does not contain unnecessary redundancy. By determining which approximated eigenfunctions to use, one can build a parameterization for the manifold of interest that uses the minimal required number of coordinates. Details about this process and further exposition on DMaps are provided in Supplementary Section 1.

Gaussian process regression

Formally, a Gaussian process (GP) is a collection of random variables, \({\left\{{Y}_{x}\right\}}_{x\in {X}}\), any finite subset of which possesses a multivariate normal distribution15. It is also common to describe GPs as random functions in the sense that fixing a value \(\omega \in \Omega\) from the underlying sample space determines the observed value \(f\left(x|\omega \right)={Y}_{x}\left(\omega \right)\) at each \(x\in {X}\). GPs are a common choice for uncertainty quantification because they allow one to compute a predictive distribution, rather than a point estimate, for function outputs at unevaluated input locations. Given a set of observed input-output pairs, \({\left\{\left({{\boldsymbol{x}}}_{i},{y}_{i}\right)\right\}}_{i=1}^{n}\), Gaussian process regression (GPR) computes a posterior distribution for the output \({y}^{\star }\) at a new input \({{\boldsymbol{x}}}^{\star }\). As in DMaps, this process involves a kernel function that characterizes how strongly two outputs are correlated based on their corresponding inputs. Kernel functions are more varied for GPR and are chosen for the functional properties (e.g., differentiability or periodicity) they provide to the resulting regression model. For example, an analogous form of the Gaussian kernel corresponds to infinitely differentiable functions and is given by

$$k({\boldsymbol{x}},{\boldsymbol{x}}^{\prime})={\rm{Cov}}\left[f({\boldsymbol{x}}),f({\boldsymbol{x}}^{\prime})\right]={\sigma }^{2}\exp \left[-\frac{{\Vert {\boldsymbol{x}}-{\boldsymbol{x}}^{\prime}\Vert }^{2}}{{\ell }^{2}}\right]$$
(5)

where \(\ell ,{\sigma }^{2}\, > \,0\) are hyperparameters whose values must be determined from the training data.

Given an objective function, \(f:{{\mathbb{R}}}^{d}{\to}{\mathbb{R}}\), Bayesian optimization (BO) seeks a global minimizer by using sequentially updated GP models to select subsequent search locations. This procedure replaces the original, difficult optimization problem with a sequence of simpler ones involving an acquisition function62, chosen by the user to balance the competing interests of searching in locations with desirable predicted outputs (exploitation) and those with high predictive uncertainty (exploration). One common family of acquisition functions is the lower confidence bound

$${\alpha }_{{LCB}}\left({\boldsymbol{x}}\right)=\mu \left({\boldsymbol{x}}\right)-\beta \sigma \left({\boldsymbol{x}}\right)$$

where μ and σ represent the predictive mean and standard deviation, respectively, of the current GP model and β ≥ 0 controls the amount of exploration. Each iteration of a BO algorithm uses an acquisition function to choose a new point \({{\boldsymbol{x}}}^{\star }\) for objective evaluation, adds the observation \(\left({{\boldsymbol{x}}}^{\star },f\left({{\boldsymbol{x}}}^{\star }\right)\right)\) to the training data, and updates the GP model. Further details, including a discussion of approaches to GPR designed for cases with noisy measurements, are provided in Supplementary Section 2.