Solution of Dynamic Deformation Problems for Prestressed Laminated Plates Based on the Three-Dimensional Theory of Elasticity

Abstract

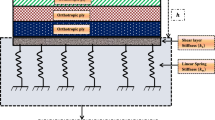
A three-dimensional analytical solution describing forced harmonic vibrations of prestressed laminated plates is found for the case of a hinged support. The solution is based on the analytical separation of variables. It is assumed that the prestressed state is homogeneous, subcritical, linear, and momentless and that the vibration amplitudes are small. A solution based on a model with a polynomial approximation of the required displacement functions across the plate thickness is also considered. These functions are found on the front surfaces of the structure. This allows us to solve the problem both in the continuous and discrete structural approaches. In the continuous structural approach, the order of the resolving system of equations is independent of the number of layers. In the discrete structural approach, for rigid contact of layers with similar boundary conditions at the plate end face, an algorithm can be introduced which reduces significantly the number of operations required for realization of the model proposed. In the numerical examples presented, both rigid and sliding contacts of layers and various prestressed conditions are considered. Both approaches give results that agree well.