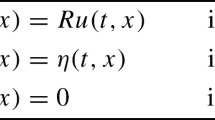Skip to main content
SpringerLink
Log in

Application of the Augmented Lagrangian-SQP Method to Optimal Control Problems for the Stationary Burgers Equation

  • Published:
Computational Optimization and Applications Aims and scope Submit manuscript

Abstract

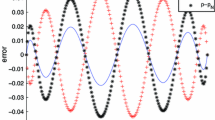
In this paper optimal control problems for the stationary Burgers equation are analyzed. To solve the optimal control problems the augmented Lagrangian-SQP method is applied. This algorithm has second-order convergence rate depending upon a second-order sufficient optimality condition. Using piecewise linear finite elements it is proved that the discretized augmented Lagrangian-SQP method is well-defined and has second-order rate of convergence. This result is based on the proof of a uniform discrete Babuška-Brezzi condition and a uniform second-order sufficient optimality condition.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. E.L. Allgower, K. Böhmer, F.A. Potra, and W.C. Rheinboldt, “A mesh-independence principle for operator equations and their discretizations,” SIAM J. Numer. Anal., vol. 23, no. 1, February 1986.

  2. R.A. Adams, Sobolev Spaces, Academic Press, 1975.

  3. J.-P. Aubin, Approximation of Elliptic Boundary-Value Problems, vol. 26 of Pure and Applied Mathematics, Wiley-Interscience, 1972.

  4. F. Brezzi and M.Fortin, Mixed and Hybrid Finite Element Methods, vol. 15 of Springer Series in Computational Mathematics, Springer-Verlag, 1991.

  5. J.M. Burgers, “Application of a model system to illustrate some points of the statistical theory of free turbulence,” Nederl. Akad. Wefensh. Proc., vol. 43, pp. 2–12, 1940.

    Google Scholar 

  6. J.M. Burgers, “A mathematical model illustrating the theory of turbulence,” Adv. in Appl. Mech., vol. 1, pp. 171–199, 1948.

    Google Scholar 

  7. J.D. Cole, “On a quasi-linear parabolic equation occuring in aerodynamics,” Quarterly of Applied Mathematics, vol. IX, no. 3, pp. 225–236, 1951.

    Google Scholar 

  8. J.B. Conway, A Course in Functional Analysis, vol. 96 of Graduate Texts in Mathematics, Springer-Verlag, 1978.

  9. D. Gilbarg and N.S. Trudinger, Elliptic Differential Equations of Second Order, Springer-Verlag, 1977.

  10. W. Hackbusch, Elliptic Differential Equations. Theory and Numerical Treatment, Springer-Verlag, 1992.

  11. J.W. Heidel, “A second-order nonlinear boundary value problem,” J. Math. Anal. & Appl., vol. 48, pp. 493–503, 1974.

    Google Scholar 

  12. K. Ito and K. Kunisch, “Augmented Lagrangian-SQP-methods for nonlinear optimal control problems of tracking type,” SIAM J. Control and Optimization, vol. 34, no. 3, pp. 874–891, May 1996.

    Google Scholar 

  13. K. Ito and K. Kunisch, “Augmented Lagrangian-SQP-methods in Hilbert spaces and application to control in the coefficient problems,” SIAM J. on Optimization, vol. 6, no. 1, pp. 96–125, February 1996.

    Google Scholar 

  14. E. Kreyszig, Introductory Functional Analysis with Applications, John Wiley & Sons, 1978.

  15. K. Kunisch and S. Volkwein, “Augmented Lagrangian-SQP techniques and their approximations,” in Optimization Methods in Partial Differential Equations, vol. 209 of Contemporary Mathematics, S. Cox and I. Lasiecka (Eds.), 1997, pp. 147-159.

  16. D.G. Luenberger, Optimization by Vector Space Methods, John Wiley & Sons, Inc., 1969.

  17. H. Maurer and J. Zowe, “First and second order necessary and sufficient optimality conditions for infinite-dimensional programming problems,” Math. Programming, vol. 16, pp. 98–110, 1979.

    Google Scholar 

  18. M.H. Protter and H.F. Weinberger, Maximum Principles in Differential Equations, Prentice-Hall, Inc., 1967.

  19. E. Sachs and S. Volkwein, “Augmented Lagrange-SQP methods with Lipschitz-continuous Lagrange multiplier updates,” Submitted, October 1998.

  20. R. Temam, “Navier-Stokes Equations,” Studies in Mathematics and its Applications, North-Holland, 1979.

  21. S. Volkwein, “Mesh-independence of an augmented Lagrangian-SQP method in Hilbert spaces and control problems for the Burgers equation,” PhD thesis, Department of Mathematics, Technical University of Berlin, October 1997.

  22. S. Volkwein, “Mesh-Independence for an Augmented Lagrangian-SQP method in Hilbert spaces,” To appear SIAM J. Control and Optimization, 2000.

Download references

Author information

Authors and Affiliations

  1. Karl-Franzens-Universiät Graz, Heinrichstraße 36, A-8010, Graz, Austria

    S. Volkwein

Authors
  1. S. Volkwein
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Volkwein, S. Application of the Augmented Lagrangian-SQP Method to Optimal Control Problems for the Stationary Burgers Equation. Computational Optimization and Applications 16, 57–81 (2000). https://doi.org/10.1023/A:1008777520259

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1008777520259

Search

Navigation