1 Introduction

Developing rapid and effectual communication systems requires the use of optical fibers, which are currently utilized in local area networks (LANs) and for transmitting data at very high speeds over the internet [1, 2]. For high-bandwidth long-distance communication systems operating at gigabit speeds per second and higher, optical transport is the preferred method. Three primary shortcomings of optical fibers are dispersion, nonlinearity, and attenuation. For the first time, losses greater than 1000 dB/km were observed in optical fibers in 1966. Within the 1.55 μm wavelength range, attenuation of single mode fiber was just 0.2 dB/km [3]. Dispersion is the term for the imperfections that restrict a fiber’s bandwidth. As light pulses travel through optical fiber, they experience chromatic dispersion, which causes them to spread out.

In order to send large amounts of data rapidly, wavelength division multiplexing (WDM) systems were first made commercially available in the latter part of the 1990s as a high-capacity telecommunications solution. The distribution problem is solved by WDM, which combines multiple channels to achieve high combined data rates while maintaining the communication rate of each channel at a very low level (e.g., 10 Gb/s) [4]. Not all laser and LED lights have a single color. Consonants are commonly audible near the elementary frequency. Group velocity dispersion (GVD) is the phenomenon that arises when scattered spectral components of a light pulse have marginally different group velocities. The propagation of pulses causes an overlap at the receiver, known as inter-signal interference (ISI), limiting the transmission of high data rates. Data loss and errors could come from this. A higher-order group velocity distribution and a first-order group velocity distribution make up GVD. The intrinsic GVD is one of the key elements limiting the communication length of high-speed optical communication systems. Fiber networks or dispersion-compensated fiber can be used to remove primary GVD. The higher-order (second-order) scattering effect increases with increasing driving speed. The shape, width, propagation, and inter-symbol interference of a pulse are all determined by the third-order dispersion [5].

Fiber networks spanning more than 100 km in length necessitate substantial transmission power for each channel, resulting in nonlinearities like self-phase modulation (SPM) and cross-phase modulation (XPM). Connecting networks to a WDM approach can be very challenging if interference occurs. The performance of arithmetic and corresponding fiber optic transmission approaches is limited by these nonlinear effects [6, 7]. The pursuit of continually increasing fiber rates faces the challenge of fiber group velocity distortion (GVD), which limits bit rates. Additionally, as the channel dimensions, absolute optical power, bit rate, and total number of wavelength networks increase in WDM systems, XPM becomes a more important nonlinear effect, limiting system performance [8,9,10]. Recent studies have examined changes in the linear and nonlinear consequences of optical fibers in optical transmission systems. Several studies have evaluated the impact of XPM nonlinearity on BER, cross-correlation, and network modeling without first-order GVD. In high bit rate and long-distance systems, secondary GVD can have a detrimental effect on the optical transmission scheme. There are few studies on the impact of XPM in WDM systems in terms of connectivity, considering the presence of primary and secondary GVD [11, 12]. Therefore, the impact of XPM and pulse width capacity in second and third-order dispersion on the WDM approach needs to be researched and developed using analytical and numerical methods.

In this work, we use standard single mode fiber (SSMF) to assess the validity of the results at various data rates and input powers across the propagation space compared to the large effective area fiber (LEAF). When it comes to pulse amplification, the strength of the XPM and second and third-order dispersion are crucial factors. Even at small distances and depleted values, the consequence of secondary GVD is not large, but while the speed upsurges, this consequence increases and affects the scheme execution. Data speed and fiber span appear to have a greater influence on pulse width than input impact. Consequences were calculated using analytical differentiation of SSMF, LEAF, and Fourier numerical simulations by dividing through measurements of the same data and input energy. The effect of XPM and GVD was found to be more effective on SSMF fibers than on LEAF fibers.

2 Literature review

Extensive research has been conducted on the profound influence of nonlinearity and linearity of fibers in optical transmission networks. XPM and GVD are the key factors affecting system performance and bit rates in WDM optical transmission systems. Plansinis et al. [13] exhibit a complementary panorama of XPM involves the pump pulse generating a travelling refractive-index margin within a dispersive nonlinear medium. This action causes the probe pulse to separate into two individual fragments, each with its optical continuums.

Jiang et al. [14] demonstrate how to adjust the light spectrum, make it broader, and compress it in the ultraviolet range by utilizing the cross-phase modulation between a strong near-infrared pulse and its third harmonic, both traveling together in a gas-filled hollow-core fiber. The ultraviolet pulses with negative chirp lead to self-density through to 6 fs during dissemination in air and have an energy of more than 10 µJ.

Lassagni et al. [15], present a general expression for the cross-arrangement territory of the XPM variance with an arbitrary mode dispersion degree in order to expand the ergodic Gaussian noise model.

Bouhadda et al. [16] created a two-frequency mutual coherence function (MCF) on-axis for disseminative pulses traveling through uncertain atmospheric disorder, highlights the significance of having BER brought on by pulse broadening as the propagation distance is increased.

Schelte et al. [17] conducted both theoretical and experimental research on the effects of third-order dispersion (TOD) in a coordination of paired optical microcavities. Asymmetrically emerging scattering-encouraged beat outposts disrupt the mode-locking regime.

Liao et al. [18] clarifies the TOD and free carrier spreading in a wideband silicon photonic crystal waveguide with minimally atypical dispersion are used to pretend high-order sequential soliton firmness.

Kassegne et al. [19] explores the effects of nonlinear trends, namely the XPM while considering input power. Simulation results for the studied power range show that system performance increases with input power when nonlinear effects are removed.

Chakkour et al. [20] developed an optical mode to amend the efficacy of WDM optical transmission systems. Increases in the transmitted signal amplitudes were accompanied by notable decreases in nonlinear effects and chromatic dispersion compensation.

Singh et al. [21] utilized the coupled and Schrödinger equations to compare the non-linear crosstalk caused by XPM in the subcarrier WDM transmission system due to the TOD parameter.

After analyzing the information and conducting a thorough literature assessment, we discovered that most research studies have examined the affect of nonlinearity XPM on bit error rate (BER), crosstalk, and eye diagrams. These studies have considered the presence or absence of first-order GVD in their evaluations. Conversely, second-order GVD may affect long-haul and elevated bit-rate optical transmission approaches. There has been only one published study on the influence of XPM in a WDM system when both first- and second-order GVD are present simultaneously. Therefore, it is crucial to investigate and develop how the performance of the analytical and numerical pulse broadening factors in WDM systems is affected by XPM with first- and second-order GVD.

3 Methods

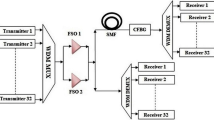
The XPM effect is demonstrated in Fig. 1 and is caused when an optical wave’s optical intensity modulates the phase of other co-propagating optical signals while it is propagating through a fiber. As a result, interference may arise from multiple channels interacting with one another as they travel down an optical fiber. The spreading of signal pulses during their descent through the fiber is called dispersion. The receiver’s capacity to discern between discrete signal pulses can be impacted by dispersion.

Fig. 1
figure 1

Demonstration of XPM consequence in WDM fiber optic communication system

Full size image

3.1 Pulse expanding factor caused by the XPM consequence of first-order GVD

Second and third-order dispersion consequences preserve be implicated by including second- and third-order derivative provisions to the leftward of the nonlinear Schrödinger equation (NLSE). The NLSE that takes linearity and variance into account is expressed as [22,23,24,25].

$$i\frac{\partial {A}_{1}}{\partial z}=-i\frac{\alpha }{2}{A}_{1}+\frac{{\beta }_{2}}{2}\frac{{\partial }^{2}{A}_{1}}{\partial {t}^{2}}+i\frac{{\beta }_{3}}{6}\frac{{\partial }^{3}{A}_{1}}{\partial {}^{3}}-i{\gamma }_{1}\left({\left|{A}\right|}^{2}+2{\left|{A}_{2}\right|}^{2}\right){A}_{1},$$
(1)

where the complex amplitudes of the fields are \(A_{1} (z,t)\) and \(A_{2} (z,t)\) that vary slowly over time, and the propagation direction z, time t, attenuation coefficient α, the first order GVD \(\beta_{2}\), second order GVD \(\beta_{3}\). \(\gamma_{1} \left( { = \frac{{n_{2} \omega_{0} }}{{CA_{eff} }}} \right)\) is a nonlinear constraint, \(n_{2}\) is the nonlinear index, \(\omega_{0}\) is the frequency, \(C\) is the light velocity and \(A_{eff}\) is the effective area of the fiber. The fiber nonlinearity is the cause of the final twofold on the right side of Eq. (1). SPM is the result of the first term, and XPM is the result of the second. The two pulses are coupled by the XPM term.

Both GVD and XPM significantly contribute to an optical pulse width \(T_{0}^{{}}\), the walk of length \(L_{W}\), dispersion length \(L_{D}\), and fiber length \(L\) if \(L_{W} \le L\) and \(L_{D} \le L\), with XPM affecting the spectrum and the pulse shape. Now considering \(L < < L_{D}\) \(L_{W} \le L\), if the attenuation constant and dispersion terms are ignored, the Eq. (1) becomes

$$\frac{\partial {A}_{1}}{\partial z}=-i{\gamma }_{1}\left({\left|{A}_{1}\right|}^{2}+2{\left|{A}_{2}\right|}^{2}\right){A}_{1}.$$

The precise retort is contained in the NLSE.

$${A}_{1}\left(z,t\right)={A}_{1}(0,t){exp}\left[-i{\gamma }_{1}\left({\left|{A}_{1}\right|}^{2}+2{\left|{A}_{2}\right|}^{2}\right){L}_{eff}\right],$$
$$\Rightarrow {A}_{1}\left(z,t\right)={A}_{01}{f}_{1}(t) {exp}\left[-{\theta }_{1m}{f}_{1}^{2}(t)-{\theta }_{2m}{f}_{2}^{2}(t)\right],$$

where both fields are launched, \({A}_{1}\left(0,t\right)={A}_{01}(0,t){f}_{1}(t)\), \({A}_{2}\left(0,t\right)={A}_{02}(0,t){f}_{2}(t)\), \(A_{01}\) and \(A_{02}\) represent the pulse amplitude, \(f_{1} (t)\) and \(f_{2} (t)\) represent the pulse shape, \({\theta }_{1m}=i{\gamma }_{1}{A}_{01}^{2}{L}_{eff}\), \({\theta }_{2m}=i{\gamma }_{1}{A}_{02}^{2}{L}_{eff}\) and \({L}_{eff}=\frac{1- {exp}\left(\alpha z\right)}{z}\) is the effective distance of the fiber and \(\alpha\) attenuation constant. The modified pulsate therefore makes two collisions. XPM is to blame for the second term, while SPM is to blame for the first. Because of the group velocity mismatch, XPM’s contribution varies with fiber length. The Fourier transform can produce the field equivalency in the frequency sphere at a distance z for the XPM-based first order GVD.

$${A}_{1}\left(z,\omega \right)=F\left[{A}_{01}{f}_{1}(t){exp}\left[-{\theta }_{1m}{f}_{1}^{2}(t)-{\theta }_{2m}{f}_{2}^{2}(t)\right]\right]\times {exp}\left(\frac{i}{2}{\beta }_{2}{\omega }^{2}z\right),$$

As input for both fields, the Gaussian pulse has been taken into consideration so that the field equation becomes

$${A}_{1}(z,\omega )=F\left[{A}_{01}{exp}\left(\frac{{t}^{2}}{2{T}_{o}^{2}}\right){exp}\left[-i\left({\theta }_{1m} {exp}\left(-\frac{2{t}^{2}}{2{T}_{o}^{2}}\right)+{\theta }_{2m}{exp}\left(-\frac{2{t}^{2}}{2{T}_{o}^{2}}\right)\right)\right]\right]{exp}\left(\frac{i}{2}{\beta }_{2}{\omega }^{2}z\right).$$

Let spectral width,

$$\Psi (\omega ))=F\left\{{exp}(-\frac{{t}^{2}}{2{T}_{o}^{2}})\times {exp}\left[-i\left({\theta }_{1m} {exp}(-\frac{2{t}^{2}}{2{T}_{o}^{2}})+{\theta }_{2m} {exp}(-\frac{2{t}^{2}}{2{T}_{o}^{2}})\right)\right]\right\}.$$

So, the field equation can be written \({A}_{1}\left(z,\omega \right)=\psi \left(\omega \right) {exp}\left(\frac{i}{2}{\beta }_{2}{\omega }^{2}z\right)\)

Thus, the frequency domain solution of the field equation is as

$${A}_{1}\left(z,\omega \right)={A}_{01}{exp}\left[-\frac{1}{2}.\frac{{\omega }^{2}{T}_{o}^{2}}{\left[1+\frac{4}{3\sqrt{3}}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right]}\right]\times {exp}\left(\frac{i}{2}{\beta }_{2}{\omega }^{2}z\right).$$
(2)

By inverse Fourier transform the time domain can be obtained from Eq. (2)

$${A}_{1}\left(z,t\right)=\frac{{A}_{01}}{\sqrt{2\pi }}\frac{ {exp}\left(-\frac{{t}^{2}\left[9+4\sqrt{3}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right]}{9{T}_{o}^{2}-i{\beta }_{2}z\left(9+4\sqrt{3}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right)}\right)}{{\left[9{T}_{o}^{2}-i{\beta }_{2}z\left(9+4\sqrt{3}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right)\right]}^\frac{1}{2}}\times {\left[9+4\sqrt{3}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right]}^\frac{1}{2},$$
(3)

Equation (3), can be simplified as,

$$Q\left(z,t\right)=\frac{{A}_{01}}{\sqrt{2\pi }}\frac{{\left[9+4\sqrt{3}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right]}^\frac{1}{2}}{{\left[9{T}_{o}^{2}-i{\beta }_{2}z\left(9+4\sqrt{3}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right)\right]}^\frac{1}{2}},$$
$$h\left(z,t\right)= {exp}\left(-\frac{1}{2}\frac{{t}^{2}\left[9+4\sqrt{3}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right]}{9{T}_{o}^{2}-i{\beta }_{2}z\left(9+4\sqrt{3}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right)}\right).$$

Thus, Eq. (3) can be transmuted as,

$${A}_{1}\left(z,t\right)=Q(z,t).h(z,t).$$
(4)

The root mean square (RMS) value of the pulse width can therefore be found using the following equation:

$$\Delta t\left(z\right)=\frac{{T}_{0}}{\sqrt{2}}\frac{{\left[27+27{L}^{2}+24\sqrt{3}{L}^{2}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}+16{L}^{2}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{4}\right]}^\frac{1}{2}}{{\left[3\left\{9+4\sqrt{3}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right\}\right]}^\frac{1}{2}},$$
(5)

Pulse broadening factor for the initial RMS value becomes,

$$U=\frac{{\left[1+{L}^{2}+\frac{24}{9\sqrt{3}}{L}^{2}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}+\frac{16}{27}{L}^{2}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{4}\right]}^\frac{1}{2}}{{\left[3\left\{9+4\sqrt{3}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right\}\right]}^\frac{1}{2}},$$
(6)

Equation (6) determines the first Gaussian pulse propagation coefficient to satisfy the first-order effects of XPM and SPM on the GVD while propagating through the WDM optical fiber transmission system at the same time.

3.2 Pulse expanding factor caused by XPM effects of second order GVD

It is required to complement the first- and second-order GVD (\({\partial A}_{1}/\partial z=-i{\beta }_{3}{\omega }^{3}{A}_{1}/6\)) in the pulse expanding factor as of XPM-based first- and second-order GVD. As a result, the field equivalency for the first- and second-order consequences of XPM appears in the time domain as follows.

$${A}_{1}\left(z,t\right)=\frac{1}{2\pi }{A}_{01}{\int }_{-\infty }^{\infty } {exp}\left[-\frac{1}{2}.\frac{{\omega }^{2}{T}_{0}^{2}}{\left[1+\frac{4}{3\sqrt{3}}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right]}\right]. {exp}\left[i\left[\left(\omega t-\frac{1}{2}{\beta }_{2}{\omega }^{2}z-\frac{1}{6}{\beta }_{3}{\omega }^{3}z\right)\right]\right]d\omega.$$
(7)

In order to simplify, it does the following

$${F}_{1}(z,\omega )= {exp}\left(-{\omega }^{2}\left(\frac{{T}_{o}^{2}}{\left[1+\frac{4}{3\sqrt{3}}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right]}+i\frac{1}{2}{\beta }_{2}z\right)\right),$$

and \({F}_{2}(z,\omega )= {exp}\left(-{\omega }^{3}\left(i\frac{1}{6}{\beta }_{3}z\right)\right).\)  

Considering \({F}_{1}(z,\omega )\) to be the Fourier transform of the functions \({f}_{1}(z,\tau )\) and \({F}_{2}(z,\omega )\). The convolution theorem is applied as the Fourier Transform of a function given as \({f}_{2}(z,t-\tau )\).

$${f}_{1}\left(z, \tau \right)={\left(\frac{1}{4\pi \left(\frac{{T}_{o}^{2}}{\left[1+\frac{4}{3\sqrt{3}}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right]}\right)+\frac{1}{2}{\beta }_{2}z}\right) {exp}\left(-\frac{{\tau }^{2}}{4\left(\frac{{T}_{o}^{2}}{\left[1+\frac{4}{3\sqrt{3}}{\left({\theta }_{1m}+2{\theta }_{2m}\right)}^{2}\right]}+i\frac{1}{2}{\beta }_{2}z\right)}\right)}^\frac{1}{2},$$

and \({f}_{2}\left(z,t-\tau \right)=\frac{1}{3}\frac{1}{{\left(-i\left(i\frac{1}{6}{\beta }_{3}z\right)\right)}^\frac{1}{3}}{\left(\frac{t-\tau }{i{\left(i\frac{1}{6}{\beta }_{3}z\right)}^\frac{1}{3}}\right)}^\frac{1}{2}\frac{1}{\pi }\times bessel{k}_\frac{1}{3}\left(\frac{2}{9}{3}^\frac{1}{2}{\left(-\frac{t-\tau }{{\left(-\frac{1}{6}{\beta }_{3}z\right)}^\frac{1}{3}}\right)}^\frac{3}{2}\right).\)  

The Eq. (8) was obtained by MATLAB, solving \(ifourier( {exp}(-ja{\omega }^{3}))\), where, \(a=i\frac{1}{6}{\beta }_{3}z\), \(bessel{k}_{\pm \frac{1}{3}}(l)=\pi \left(\frac{3}{\gamma }\right)Ai(\gamma )\), \(l=\frac{2}{9}{3}^\frac{1}{2}{\left(-\frac{t-\tau }{{\left(-\frac{1}{6}{\beta }_{3}z\right)}^\frac{1}{3}}\right)}^\frac{3}{2},\) and \(\gamma ={\left(\frac{3}{2}l\right)}^\frac{2}{3}\).

$$A\left(z,t\right)=\frac{1}{2\pi }{A}_{o}{\int }_{-\infty }^{\infty }\left(\frac{1}{4\pi \left(\frac{{T}_{o}^{2}}{2\left(1-iC\right)}+i{\beta }_{2}z\right)}\right)\frac{1}{3}\frac{1}{{\left(\frac{1}{6}{\beta }_{3}z\right)}^\frac{1}{3}}{\left(-\frac{t-\tau }{{\left(-\frac{1}{6}{\beta }_{3}z\right)}^\frac{1}{3}}\right)}^\frac{1}{2}\times {\left(\frac{3}{{\left(\frac{3}{2}l\right)}^\frac{3}{2}}\right)}^\frac{1}{2}Ai\left({\left(\frac{3}{2}l\right)}^\frac{2}{3}\right)\partial \tau .$$
(8)

The XPM-induced first- and second-order GVD pulse broadening coefficients are acquired by numerically resolving the NLSE utilizing the stepwise Fourier organization in MATLAB. The split-step Fourier method (SSFM) is a pseudo-spectral numerical scheme for calculating NLSE caused by XPM, based on first- and second-order GVD. To estimate the actual pulse propagation, one must separately apply the effects of fiber propagation and nonlinearity over a small portion of the transmission distance, and then combine the two effects [26, 27]. This is the key to SSFM. NLSE has been described as,

$$\frac{\partial {A}_{1}(t,z)}{\partial z}=-\frac{\alpha }{2}{A}_{1}(t,z)-\frac{j}{2}{\beta }_{2}(z)\frac{{\partial }^{2}{A}_{1}(t,z)}{\partial {t}^{2}}+\frac{j}{6}{\beta }_{3}(z)\frac{{\partial }^{3}{A}_{1}(t,z)}{\partial {t}^{3}}+j\gamma \left(\left|{A}_{1}(t,z{)}^{2}\right|+2\left|{A}_{2}(t,z{)}^{2}\right|\right){A}_{1}(t,z).$$

So, \(\frac{{\partial A_{1} \left( {t,z} \right)}}{\partial z} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} } \right)\)where \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}\) is a nonlinear operator that is primarily responsible for fiber nonlinearities and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L}\) interpretations for dispersion that absorb in a linear medium. The operators are shown by \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} = - \alpha /2 - j\beta_{2} /2\left( {\partial^{2} /\partial^{2} t} \right) + j\beta_{3} /6(\partial^{3} /\partial^{3} t)\) and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} = j\gamma \left( {\left| {A_{1} \left( {t,z} \right)} \right|^{2} + 2\left| {A_{2} \left( {t,z} \right)} \right|^{2} } \right)\). Figure 2 shows the proportionate SSFM in action.

Fig. 2
figure 2

Demonstration of balanced split step Fourier method

Full size image

Table 1 lists various system attributes for LEAF and SSMF fibers [28]. The MATLAB (R2023a) simulation software is used for simulation.

Table 1 values of the theoretically computed parameters
Full size table

4 Results

4.1 Impact of XPM-based second order GVD on SSMF fiber pulse broadening

To calculate the pulse broadening factor for SSMF owing to XPM with second-order GVD in MATLAB, the NLSE is numerically solved using the SSFM. The second-order GVD-induced pulse expansion for input powers of 30 mW and 90 mW and data rates of 10 Gbps and 40 Gbps is shown in Fig. 3 as a function of fiber length.

Fig. 3
figure 3

Pulse broadening factor for the constant powers but changed data rates

Full size image

As illustrated in Fig. 3, XPM and second-order GVD cooperate to cause the pulse to broaden. After 12 km, oscillations and ripples appear, and the broadening factor rises with fiber length. Asymmetric spectral broadening is caused by these effects, which also limit the transmission distance. When second-order GVD is evident, the XPM-induced chirp causes the probe pulse to rapidly oscillate close to the trailing edge, producing an asymmetric shape. The non-linear features of the fused chirp causes distinct parts of the pulse to broadcast at various rates. Since XPM and second-order GVD work together, changes in data rates have a major impact on the pulse expansion. For example, when the data rate is 40 Gbps, the pulse extending is 530 at a fiber length of 0.2 km, and 40 at the same fiber length when the bit rate is 10 Gbps. This demonstrates that the pulse broadening factor increases with data tariffs.

The pulse expansion for a SSMF with input powers of P1 = 10 mW, P2 = 10 mW, and P1 = 300 mW, P2 = 300 mW at the same 40 Gbps data rate is displayed on the graph in Fig. 4. It shows that in a WDM transmission system with XPM and second-order GVD, changes in input powers have negligible effects on pulse broadening.

Fig. 4
figure 4

Pulse broadening factor for different input powers with the same data rate = 40 Gbps in SSMF

Full size image

4.2 Impact of XPM-based second order GVD on LEAF fiber pulse broadening

In LEAF fiber, the pulse broadening factor resulting from XPM with second-order GVD increases in tandem with an increase in data rate. When XPM with second-order GVD is present, the pulse expansion in LEAF fiber is less affected by changes in input power.

Table 2 lists various system attributes for LEAF and SSMF fibers [29].

Table 2 Key parameters of LEAF and SSMF
Full size table

Figure 5 displays the pulse expansion component against fiber length in the circumstance of the XPM appearance. In SSMF the curve oscillates after 10 km to produce multiple waves, while in LEAF fiber it oscillates after 12 km to produce multiple waves. Representing the similar data rate of 40 Gbps with response power P1 and P2 are 10 mW and 30 mW respectively. The quantity of pulse enlargement for dual diverse optical fibers is dissimilar since they have altered dispersion identities.

Fig. 5
figure 5

Output pulsation of XPM with third-order dispersion for SSMF and LEAF

Full size image

4.3 Pulse broadening facto in SSMF in comparison to GVD first order and GVD second order with XPM

In Fig. 6, the pulse expanding owed to the appearance of XPM with second-order GVD and the consequence of XPM with first-order GVD are shown and compared for the same data rate and input powers.

Fig. 6
figure 6

Pulse broadening factor due to XPM-based first- and second-order GVD in SSMF

Full size image

The two curves are compared, and it is found that the pulse expanding affected by XPM with second-order GVD upsurges significantly in the length from 9 to 10 km, while the pulse increases with XPM from GVD. The first degree occurs. little by little When using XPM with a second-order GVD over a 10 km fiber, the pulse broadening factor is 600, while XPM causes a first-order GVD of up to 1. After the fiber length reaches 10 km, the pull factor begins. to fluctuate owed to the interaction of the second-order GVD and the XPM and to form multiple waves, while the XPM causes a disproportionate increase to the original GVD. Consequently, the pulse expansion feature of the XPM with second-order GVD is greater than that of the XPM with first-order GVD. Asymmetric pulse expansion results from vibrational waves produced by the interaction of XPM with the second order of GVD.

4.4 Impact of XPM-based first- and second-order GVD on output pulse

A Gaussian pulse is introduced into the fiber to initiate transmission, as shown in Fig. 7. The transmitting pulse caused by the combination of second-order GVD and XPM is shown in Figs. 8, 9 and 10.

Fig. 7
figure 7

Conception of an input Gaussian pulse

Full size image
Fig. 8
figure 8

Conception of output pulse in XPM-base second-order GVD at input powers of 30 mW and data rates of 10 Gbps

Full size image
Fig. 9
figure 9

Conception of output pulse in XPM-base second-order GVD at input powers of 60 mW and data rates of 10 Gbps

Full size image
Fig. 10
figure 10

Conception of output pulse in XPM-base second-order GVD at 40 Gbps

Full size image

The appearance of a change in the input powers on the output pulse can be examined and illustrated by contrasting Figs. 8 and 9. Normalized output pulses for a settled data rate are found to remain relatively similar when P1 (input power) is changed from 30 to 60 mW and P2 (10 mW to 30 mW). For XPM and TOD, this means that with WDM transmission systems, variations in input powers have less of an effect on transmitting pulses. The second-order GVD can significantly change the transmitting pulse’s behavior in the presence of XPM, transforming the Gaussian pulse into multiple-shaped pulses at an extreme data rate of 40 Gbps, as shown in Fig. 10. The distorted spines are the result of the output pulse.

5 Discussion

The combined effects of GVD and XPM, which affect high data rates, channel capacity, and final optical power, severely limit the performance of WDM systems. Thus, this study’s main goal was to look into how XPM affected system performance as primary and secondary GVD were being developed. The pulse expansion coefficients of primary and secondary GVD pulses affected by XPM in WDM optical communication systems are studied through a thorough analysis and numerical research.

The spectral pulse broadening seen in WDM systems is primarily caused by the interaction between first-order XPM and GVD. The expansion factor is found to increase with data rate, input power, and fiber length. Nonetheless, the input power has less of an consequence on the pulse broadening factor than the data rate and fiber length. System performance is significantly affected by second-order GVD at very high data rates. Asymmetric pulse broadening and multiple ripples are the results of combining XPM with second-order GVD. Data rate and fiber length have an increasing impact on the pulse expansion due to GVD and second-order XPM. When second-order GVD is used instead of first-order GVD, XPM behaves differently and has a better pulse broadening factor.

5.1 Limitation

This work uses the SSFM to resolve the NLSE. Because the dispersal of computational grid points along the fiber has a significant impact on the practical efficiency of the SSFM, an effective adaptive step-size control strategy is obligatory, for completing the SSFM for NSLE solution with all the mathematical precision necessary to guarantee a thorough comprehension of the subject.

We hope that our findings will also have a qualitative effect on other scenarios, like optical pulses and interactions between light waves traveling at different frequencies and modes, even though our research has only looked at how nonlinearities affect homochromous light roaming in a single mode. This implies that accurate modeling and design of these components require second-order nonlinear approaches and that a wide variety of nonlinear slow-light devices can be significantly impacted by second-order terms.

6 Conclusions and future works

In the WDM regime, the pulse spectral broadening is based on first-order GVD and the XPM effect. It is believed that as input power, fiber length, and data rate increase, so does the supplementary factor. However, the pulse width factor is more affected by data rate and fiber length than by power. At high bit rates, second-order GVD effects are critical to system performance. Second GVD is caused by multi-channel asymmetric pulse amplification arising from XPM. The impact of second-order GVD-based XPM on pulse gain increases with both data rate and fiber length. According to the pulse enhancement factor, second-order GVD is more proficient and exhibits distinct behavior when paired with XPM and first-order GVD. The effect of XPM with first- and second-order GVD on the pulse propagation factor is similar to that of XPM with third-order dispersion, since the effect of second-order GVD domination is different from XPM at better data levels. Whereas the amplified output pulse of XPM only has first-order GVD, the second-order GVD of XPM causes the output pulse to be amplified and form multiple waveforms. The presence of second-order GVD asymmetric behavior in the XPM is indicated by the increased pulsation. Third-order dispersion and XPM in SSMF fibers are more effective than in LEAF fibers. In terms of pulse broadening, SPM with CD is not as effective as XPM with first-order GVD.

We have examined inter-channel XPM in a two-channel WDM system. Subsequent investigations could examine the intra-channel XPM effect across a vast array of channels (> 16) with diverse channel spacing, extending as low as 0.1 nm. Investigating the strategies and tactics for making up for the XPM impairment is also crucial. The performance limitations resulting from nonlinear phenomena could be accurately represented by considering additional nonlinear effects.