1 Introduction

Propelled by the rapidly growing demand for function incorporation and performance improvement, various freeform specular components with complex structured surfaces are broadly applied in numerous optical imaging and display systems [1–3]. Form accuracy of the structured surfaces directly impacts the specular components’ functioning. Point scanning technologies represented by the coordinate measuring machine (CMM) and stylus profiler [4, 5] are common methods in the industry today to measure specular surfaces. These solutions are time-consuming and impractical for on-machine measuring applications due to the large system volume and heavy weight of the measurement systems. Interferometry is another widely applied technique in specular surface measurement, but this technique is sensitive to environmental disturbances [6, 7].

Phase measuring deflectometry (PMD) is an optical technology developed for the 3D measurement of freeform specular surfaces [8–10] with advantages of good accuracy, low cost, full field of view, and non-contact measurement. PMD systems generally have a simple configuration and small system volume, and are lightweight; therefore this technique can be easily applied in in-situ measurements [11–13]. PMD works based on the law of reflection. When regular fringe patterns are reflected by a measured specular surface, the reflected fringes are deformed due to the modulation of the shape of the surface. The shape of the measured surface can be extracted from the deformed patterns by applying a series of algorithms, such as the phase-shifting algorithm [14, 15], phase unwrapping algorithm [16, 17], and depth reconstruction algorithm [18, 19]. In recent years, several PMD techniques have been studied for measuring specular surfaces with complex structures, such as direct phase measuring deflectometry (DPMD) and segmentation phase measuring deflectometry (SPMD). DPMD [20, 21] establishes the relationship between phase data and depth variation based on a mathematical model and reconstructs form information of the measured surfaces through phase value. Since DPMD calculates form data from the phase directly and cannot obtain gradient data, significant phase noise is introduced to the measurement result. Therefore, the measurement accuracy of DPMD is limited compared with gradient-based PMD [22–25]. To increase the measurement accuracy, Zhang et al. [26] proposed stereo direct phase measurement deflectometry by using stereo imaging sensors in the DPMD system to calculate gradient data to improve the surface reconstruction accuracy. A DPMD system comprises two fringe-displaying screens and requires that the screens remain parallel. In contrast, SPMD [27] only needs one screen and has more flexible configuration relationships. SPMD introduces the concept of segmentation in topology into PMD and separates a structured specular surface into several continuous segments. SPMD reconstructs each segment based on gradient data and therefore can achieve a better form accuracy compared with DPMD. Then, the reconstructed segments are fused together based on absolute depth data calculated through the triangular relationship between the two imaging sensors in the system. Feng et al. [28] studied segmentation algorithms to achieve automatic segmentation for SPMD. Techniques based on SPMD have been investigated to reduce the system volume for embedded measurement and to decrease the influence of structure shadows on the measurement result [13].

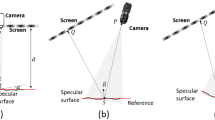
In modern optical engineering arenas, a number of specular surfaces are applied and designed to have types of structures with different scales and importance of functions. Therefore, the structures usually require different measurement demands in scale, lateral resolution and accuracy, which would be difficult to satisfy by a single PMD system. An example is shown in Fig. 1. \(S_{1}\) in Fig. 1(a) denotes a surface whose field is covered by an image sensor. The black square lattice represents sampling points in the measurement field under a certain sensor resolution. A structured surface consisting of surface \(S_{1}\) and surface \(S_{2}\) is illustrated in Fig. 1(b). The area of surface \(S_{2}\) is k times that of surface \(S_{1}\). If we do not change the imaging sensor, a wider measurement field is required to cover the overall structured surface, as shown in the black square lattice in Fig. 1(b). In this case, the sampling points on surface \(S_{1}\) in Fig. 1(b) are dramatically reduced compared with those in Fig. 1(a). A new imaging sensor with k times the resolution of the old sensor (shown in Fig. 1(c)) can be used to obtain the same sampling points on surface \(S_{1}\) as those in Fig. 1(a). However, there are several drawbacks of applying sensors with large resolution. One is that the measurement speed will be significantly decreased. An experiment with a camera (XIMEA, MC050MG-SY) was conducted to study the relationship between capture speed and camera resolution. The experimental results are summarized in Fig. 1(d). At the same exposure time (3.62 ms), the capture speed is 241.9 frames per second (fps) when the resolution is 1232 × 1028 pixels. The speed drops down to 61.5 fps at a resolution of 2464 × 2056 pixels. Moreover, the resolution of current industry cameras is limited and the cameras cannot be manufactured infinitely large. This means that the sampling requirement of the small-scale surfaces can not be satisfied when k is quite large. In addition, the price of a super-high-resolution camera is especially expensive. Instead of using sensors with large resolution, multi-scale sensors can be applied to solve this problem, as displayed in Fig. 1(e). A sensor with a wide measurement field covers the overall structured surface. At the same time, small measurement field can be achieved by using another sensor, as the purple square lattice shown in Fig. 1(e). This solution is flexible enough to meet the resolution requirements of surfaces with different scales. Since this solution does not need a sensor with higher resolution and parallel acquisition can be achieved between sensors, its impact on capture speed can be almost negligible. However, on the other hand, applying multiple sensors brings technical challenges in system design, calibration, and data fusion.

Figure 1
figure 1

Illustration of the advantages of applying multiscale sensors. (a) A small-scale surface covered by an image sensor; (b) a large-scale structured surface covered by an image sensor; (c) a large-scale structured surface covered by an image sensor with high resolution; (d) relationship between capture speed and camera resolution; (e) a large-scale structured surface covered by multiscale sensors

Full size image

A multiscale deflectometry that contains two sub-SPMD systems is proposed in this paper. Each sub-system works as a single SPMD system and can be designed to have different measurement scales, lateral resolutions, and accuracies to meet the measurement demands of the targeted surfaces. Two imaging sensors in the proposed system cover the measured full-scale surfaces and establish the spatial relationship of the continuous segments based on the principle of SPMD. The third imaging sensor is a camera with a long working distance that only captures the field of the small-scale structures to improve the resolution and accuracy of the reconstruction data of the small-scale structures. The reconstructed small-scale structures and the other surface parts are stitched together through the proposed fusion technique. Section 2 describes the principle, configuration, calibration method, and fusion method of the proposed technique. The experiment verifies the effectiveness of the system by measuring a concave mirror with small-scale structures in Sect. 3. The conclusion is addressed in Sect. 4.

2 Method and principle

2.1 Measurement principle

Figure 2 illustrates the measurement principle of the proposed multiscale form measurement technique for structured specular surfaces. S in Fig. 2 denotes a surface point on a small-scale structure of the measured surface. Our aim is to obtain the 3D coordinates of S and its normal data (expressed as n). During a measurement process, a series of phase-shifting sinusoidal fringe patterns in the vertical and horizontal directions are generated by a computer and displayed on a screen. Based on the sinusoidal fringe patterns, two mutually perpendicular absolute phase maps are obtained by using phase shifting and phase unwrapping algorithms. With knowledge of the relationship between the phase value and physical pixels of the screen, the accurate location of a point on the screen can be calculated based on its vertical and horizontal phase data (as \(P_{v}\) and \(P_{h}\) shown in Fig. 2). The sinusoidal fringe patterns displayed on the screen are captured by three imaging sensors through the reflection of the measured surface. Two wide-field (WF) cameras cover the whole measured surface. A long working-distance (LW) camera with a small field-of-view (FOV) only captures the targeted small-scale structures on the measured surfaces. Image points of S in the cameras are denoted by \(C_{1}\), \(C_{2}\) and \(C_{3}\), respectively. With known vertical and horizontal absolute phase values of \(C_{1}\), \(C_{2}\) and \(C_{3}\), corresponding points \(Q_{1}\), \(Q_{2}\) and \(Q_{3}\) on the display screen can be obtained. If we treat WF Camera 1 as the master camera and choose an arbitrary coordinate on the ray of \(C_{1}O_{1}\) as the position of S (\(O_{1}\) is denoted as the optical center of WF Camera 1), an equivalent normal vector of S can be obtained based on \(C_{1}\), S and \(Q_{1}\) according to the law of reflection. Then, a calculated point (\(\widehat{Q_{2}}\)) on the screen can be obtained with \(C_{2}\), S, and the equivalent normal vector. Using \(d_{2}\) to express the difference between \(Q_{2}\) and \(\widehat{Q_{2}}\), an accurate 3D coordinate of S with its normal data n can be calculated by searching points along the ray of \(C_{1}O_{1}\) and finding the point at which \(d_{2}\) achieves the minimum. By using the measurement principle described above, the 3D coordinates of the measured full-scale surface and its gradient data can be obtained based on WF Camera 1 and WF Camera 2. In order to reconstruct the measured structured specular surface, we treat the surface as a combination of several continuous segments. The obtained 3D coordinates can establish the absolute position of the continuous segments in space. Since it has been verified that the accuracy of the absolute 3D form acquired by PMD is far less accurate than a reconstructed form based on gradient data [22], continuous segments of the surface are reconstructed based on gradient data to improve surface quality.

Figure 2
figure 2

Measurement principle of the multiscale form measurement technique

Full size image

Based on the same principle, absolute 3D coordinates and gradient data of the small-scale structures on the measured surface can be obtained if we treat the LW Camera as the master camera and WF Camera 1 as the slave camera. There are two significant advantages to using the LW Camera. One is to improve the measurement accuracy of the small-scale structures and to enhance the lateral resolution of the measurement system by increasing the number of sampling points on the structures. The other is to improve the reconstruction accuracy of continuous sections by enhancing gradient calculation accuracy. Based on a previous study [29], the relationship between gradient uncertainty δn and position uncertainty of imaging point δC can be expressed as

$$ \delta \boldsymbol{n}=\delta C/(2L_{C}), $$
(1)

where \(L_{C}\) is the working distance of the camera in PMD. It is obvious that increasing the working distance of the camera can restrain the influence of the position error of the imaging point on the gradient calculation accuracy. A simulation has been conducted to verify this point, as Fig. 3(a) illustrates that the simulated deflectometer is based on triple imaging sensors. Changing the length of \(L_{C}\) from 100 mm to 1400 mm, the variation of form error of the reconstructed surface based on the gradient calculated by the system is demonstrated in Fig. 3(b). It is obvious that the measurement error decreases with increasing LW Camera working distance, especially when the working distance is less than 300 mm.

Figure 3
figure 3

Simulation for analysing the influence of the working distance of imaging sensors on gradient calculation accuracy. (a) The simulated deflectometry system; (b) relationship between the working distance of the imaging sensors and the form error of reconstructed surface based on the gradient. PV refers to peak value and RMS refers to root mean square

Full size image

2.2 Compact configuration and calibration

Figure 4(a) demonstrates the system configuration developed based on the measurement principle of the proposed multiscale form measurement technique. In order to meet all optical constraints of the measurement principle, the screen and the cameras have a dispersed distribution on opposite sides of the normal of the sample under test (SUT), which leaves a largely useless space between the screen and the cameras. This configuration leads to a large system volume and considerable disadvantages for portable and embedded measurement. In order to decrease system volume, an advanced configuration with a beam splitter is developed in Fig. 4(b) based on the study in our previous work [13]. A plate beam splitter (BS) is placed in front of the SUT with an approximately 45-degree angle. Fringe patterns from the screen are successfully reflected by the BS and the SUT, and then go through the BS and are captured by the cameras. The size of the configuration in Fig. 4(b) is significantly reduced compared with that in Fig. 4(a). However, the application of the LW camera still requires a large system volume. Therefore, a more compact configuration is proposed in Fig. 4(c). This configuration is derived from Fig. 4(b) but uses an optical flat to reflect the light of the LW camera and thus reverse the position of the LW camera in the system. It is obvious that the system size is further decreased compared with Fig. 4(b).

Figure 4
figure 4

Illustration of the configuration development of the proposed technique. (a) Initial configuration; (b) an advanced configuration with a beam splitter; (c) the compact configuration by adding a beam splitter and an optical flat. SUT refers to sample under test and BS refers to beam splitter

Full size image

Since the proposed technique operates based on geometrical optical principles, it requires the relative positions of system components in space to be known accurately in advance. This step is called calibration. In addition, because the multiscale measurement data in the proposed technique are obtained in terms of multiple camera coordinate systems, calibration is also a basic step to support the data transfer between multiple coordinate systems in the subsequent data fusion process. A calibration method is studied based on a pin-hole imaging model as demonstrated in Fig. 5. \(\{ \boldsymbol{S}\}\) represents the 3D coordinate system of the equivalent screen of the real display screen after the reflection of the BS. The coordinate system of WF Camera 1, WF Camera 2, and the equivalent camera of the LW Camera after the reflection of the optical flat is denoted by \(\{ \boldsymbol{C^{1}}\}\), \(\{\boldsymbol{C^{2}}\}\), and \(\{ \boldsymbol{C^{3}}\}\). Rotation matrix and translation matrix from \(\{ \boldsymbol{S}\}\) to each camera coordinate system are expressed as \(\boldsymbol{R^{i}}\) and \(\boldsymbol{T^{i}}\), respectively (i represents the index of cameras and ranges from 1 to 3). \(\{\boldsymbol{P^{1}}\}\), \(\{ \boldsymbol{P^{2}}\}\), and \(\{\boldsymbol{P^{3}}\}\) are the two-dimensional (2D) pixel coordinate system of WF Camera 1, WF Camera 2, and the equivalent LW Camera, respectively. Imaging mapping from \(\{\boldsymbol{C^{i}}\}\) to \(\{\boldsymbol{P^{i}}\}\) is represented with \(\boldsymbol{A^{i}}\). A display screen is used as a phase target [30] to calibrate the deflectometry system by displaying phase-shifting fringe patterns in the vertical and horizontal directions. Note that, fringe patterns captured by the LW Camera should do mirror reverse to calibrate the equivalent LW Camera. Placing a flat mirror at an arbitrary position, imaging sensors can capture the phase target through the reflection of the flat mirror. Changing the position of the flat mirror several times during the calibration process, \(\boldsymbol{A^{i}}\), \(\boldsymbol{R^{i}}\) and \(\boldsymbol{T^{i}}\) can be obtained based on the previous method [31] and be optimized through bandage adjustment by minimizing the following function:

$$ \sum_{i=1}^{3}\sum _{j=1}^{k} \bigl\Vert m^{i}-\widehat{m} \bigl( \boldsymbol{A^{i}},\boldsymbol{R^{i}}, \boldsymbol{T^{i}}, \boldsymbol{n}_{j},d^{i}_{j},M^{i}_{j} \bigr) \bigr\Vert ^{2}, $$
(2)

where k represents the movement number of the flat mirror during calibration. \(\boldsymbol{n}_{j}\) is normal of the flat mirror located at position j. \(d^{i}_{j}\) is the distance between the flat mirror and optical center of camera i. \(m^{i}\) represents camera pixels of camera i. \(M^{i}_{j}\) represents corresponding points on the display screen that can be observed by \(m^{i}\) through the reflection of the flat mirror. m̂ denotes reprojection pixels calculated based on \(\boldsymbol{A^{i}}\), \(\boldsymbol{R^{i}}\), \(\boldsymbol{T^{i}}\), \(\boldsymbol{n}_{j}\), \(d^{i}_{j}\), and \(M^{i}_{j}\).

Figure 5
figure 5

Illustration of coordinate systems in terms of the proposed deflectometer

Full size image

2.3 Data fusion

Data fusion is an important step in the proposed multiscale form measurement technique. One task of data fusion is to establish the spatial relationship of the reconstructed continuous segments. That is because the reconstructed surfaces after the gradient integral are relative values, the absolute positions of the reconstructed segments in space must be known to stitch them together. Another task is to transfer multiscale data obtained by multiple sensors into a common coordinate system. To complete these tasks, a fusion strategy is developed for the proposed deflectometer, as illustrated in Fig. 6.

Figure 6
figure 6

Diagram of the developed data fusion strategy

Full size image

Three cameras in the multiscale form measurement capture the deformed fringe patterns through the reflection of the measured surface. Mutually perpendicular absolute phase data can be calculated based on the captured fringe patterns of the cameras by applying phase-shifting algorithms and phase unwrapping algorithms. Treating LW Camera as master camera and WF Camera 1 as slave camera, absolute 3D coordinates and gradient data of targeted small-scale structures on the measured surface in terms of the coordinate system of LW Camera can be obtained through segmentation [27], calibration, and the spatial point searching algorithm presented in Sect. 2.1. Similarly, we can compute absolute 3D coordinates and gradient data of all continuous segments of the measured surface by using WF Camera 1 as the master camera and WF Camera 2 as the slave camera. Because the accuracy of the absolute 3D coordinates is seriously affected by phase error, it commonly can only reach the level of tens of micrometers [20]. Therefore, it is quite important to reconstruct the data in z direction of continuous segments based on gradient data and x, y coordinates of the segments to improve the form accuracy. However, on the other hand, the constructed data after the gradient integral result in the loss of absolute depth information of the continuous segments. Thus, we use a technique based on the least-square method to recalculate the absolute depth data of the constructed segments according to Equation (3). The absolute location of the reconstructed segments can be obtained by compensating for the depth difference between the reconstructed data and the data’s absolute 3D coordinates according to Equation (3):

$$ \textstyle\begin{cases} \boldsymbol{H}=\boldsymbol{P}-\boldsymbol{S}, \\ \widehat{\boldsymbol{S}} =\boldsymbol{S}-\overline{H},\end{cases} $$
(3)

where S represents depth values of the reconstructed segments and P denotes the absolute 3D coordinates of the segments under the same x, y coordinates of S. H̅ means the average of H. The reconstructed segments with absolute location (denoted as \(\widehat{\boldsymbol{S}}\)) can be found by compensating with H̅. By using this method, we can obtain absolute 3D coordinates of the reconstructed small-scale structure surfaces in terms of the LW Camera system and absolute 3D coordinates of all reconstructed continuous segments in terms of the WF Camera 1 system. The next step is to transfer the data in the LW Camera system and the data in the WF Camera 1 system to a common coordinate system. This step can be conducted based on the relationship between the camera coordinate system of WF Camera 1 and the camera coordinate system of LW Camera since the relationship can be obtained through calibration. Therefore, the absolute 3D coordinates of the reconstructed small-scale structure surfaces in the LW Camera system can be transferred to the WF Camera 1 system. However, the transformation is usually inaccurate because of calibration errors. Therefore, a method is studied to optimize the transformation parameter for improving the transformation accuracy. Using \(\boldsymbol{R}_{lw}\) and \(\boldsymbol{T}_{lw}\) to represent the rotation matrix and translation matrix from the camera coordinate system of LW Camera to the camera coordinate system of WF Camera 1. \(\boldsymbol{R}_{lw}\) and \(\boldsymbol{T}_{lw}\) are calculated from the calibration result and then can be optimized based on the iteration algorithm by minimizing the following function:

$$ \sum_{j=1}^{k} \bigl\Vert M^{j}_{wf}-\widehat{M}\bigl(\boldsymbol{R}_{lw}, \boldsymbol{T}_{lw},M^{j}_{lw}\bigr) \bigr\Vert ^{2}, $$
(4)

where \(M_{wf}\) expresses sampling surface points in the WF Camera 1 system. \(M_{lw}\) represents surface points in the LW Camera system. M̂ denotes the transferred surface points from the LW Camera system to the WF Camera 1 system based on \(\boldsymbol{R}_{lw}\) and \(\boldsymbol{T}_{lw}\). j is the number of sampling points. Finally, accurate measurement data of the full-scale surface and small-scale structures can be obtained by combining all continuous segments based on absolute 3D coordinate data in the WF Camera 1 system and replacing the data of small-scale structures with the surface data transferred from the LW Camera.

3 Experiment and discussion

A portable prototype is developed based on the proposed multiscale form measurement technique, as displayed in Fig. 7. The system volume of the prototype is 335 mm in length, 250 mm in width, and 200 mm in height. A 7-inch screen (model: Feelworld FW279) with a resolution of 1920 × 1200 pixels is used to display fringe patterns. BS in the prototype is from Edmund with stock number 46-583. The BS is 3 mm thick. The peak value (PV) and root mean square (RMS) of its flatness are 7.41 μm and 1.51 μm, respectively, which were measured using LuphoScan 260HD of Taylor Hobson. Three cameras in the prototype are from XIMEA with the MC050MG-SY model. The resolution of the cameras is 2464 × 2056 pixels. A 16 mm fixed focal length camera lens (Edmund, stock number 15-643) is mounted on the WF cameras to cover the full-scale SUT. The working distance of the WF cameras is approximately 180 mm. The LW camera is equipped with a 50 mm fixed focal length lens (Edmund, stock number 15-666). A 2” square optical flat from Thorlabs (Model: PFSQ20-03-G01) is located at the end of the prototype and is used to reflect the light of the LW camera according to the configuration design of Fig. 4(c). The application of the optical flat can benefit the system volume from a reduction of approximately 220 mm in length. PV of the flatness of the optical flat is 79.13 nm, as given by the Thorlabs. The equivalent working distance of the LW camera after the reflection of the optical flat is approximately 500 mm. The prototype was calibrated based on the proposed calibration method by placing an optical flat (Thorlabs, PFSQ20-03-G01) at 10 arbitrary positions within the measurement field. Figure 8 demonstrates the calibration results after optimizing the imaging parameters of the prototype by minimizing Equation (2). Figure 8(a), Fig. 8(b), and Fig. 8(c) are the reprojection error between camera pixels and reprojected pixels calculated based on imaging parameters obtained by calibration in WF Camera 1, WF Camera 2, and LW Camera, respectively. It can be seen from the results that most of the calibration errors in the cameras are within ± 1 pixel.

Figure 7
figure 7

A portable prototype developed based on the proposed multiscale form measurement technique. SUT refers to sample under test and BS refers to beam splitter

Full size image
Figure 8
figure 8

Calibration results. Color represents the result calculated under different optical flat positions (a) Reprojection error of WF Camera 1; (b) reprojection error of WF Camera 2; (c) reprojection error of LW Camera

Full size image

A sample with four small-scale structures was measured by the prototype to test the measurement ability, as shown in Fig. 7. The small-scale structures are marked as \(S1, S2, \ldots, S4\) in the figure. The sample was measured by Mitutoyo FormTracer as a benchmark. The small-scale structures are spheres with a radius of 400 mm. The PV of the structure’s surface error is approximately 70 nm. The other part of the sample excluding the four structures is a sphere with a radius of 600 mm and its PV surface error is 0.21 μm. An example of absolute phase data of the sample obtained by the developed prototype is demonstrated in Fig. 9. Figure 9(a), Fig. 9(b), and Fig. 9(c) are the calculated horizontal absolute phase data in WF Camera 1, WF Camera 2, and LW Camera, respectively. Here, we focus on discussing three parameters of the prototype that mainly determine the system measurement accuracy. The first is the transformation error between the LW Camera system and WF Camera 1 system; the second is the absolute 3D coordinate calculation error in the WF Camera 1 system; and the third is the reconstruction error based on the gradient integral in LW Camera and WF Camera 1. Figure 10 shows the transformation error from the camera coordinate system of LW Camera to the camera coordinate system of WF Camera 1. A comparison is conducted in the figure. First, absolute surface data obtained in LW Camera is transferred to the WF Camera 1 system based on the transformation parameters obtained directly from calibration. Second, we sampled the transferred surface points and the absolute surface data obtained in the WF Camera 1 with the same lateral coordinate. Then we compared the difference in depth direction between the transferred surface points from the LW Camera system and the corresponding surface data in the WF Camera 1 system, as presented in Fig. 10(a). The average value of the difference is −0.23 mm as drawn in the red line of Fig. 10(a), while the difference is decreased dramatically when calculating under the optimized transformation parameters using the proposed method by minimizing function (4), as shown in Fig. 10(b). The average value of the difference is 78.0 nm as drawn in the red line of Fig. 10(b). It is demonstrated that the transformation accuracy has a dramatic improvement after optimization of the transformation parameters. Absolute 3D coordinates of the sample can be calculated based on WF Camera 1 and WF Camera 2 by using the presented technique in Sect. 2.1. This value is important because all reconstructed segments after the gradient integral will be fused together by finding their absolute positions in a common coordinate system based on the value. In order to verify the accuracy of the absolute 3D coordinate calculation, we compared the obtained absolute 3D coordinate data after removing the structures with the benchmark offered by Mitutoyo FormTracer. The residual between these two measurement techniques is illustrated in Fig. 11(a). The RMS of the residual is 38.0 μm. Figure 12 demonstrates a comparison of the reconstruction error of S1 between WF Camera 1 and LW Camera. Please note that the sub-system composed of the stereo WF camera is a traditional stereo PMD system whose configuration is designed based on our previous study [29]. The surface of S1 is reconstructed based on the gradient data obtained in WF Camera 1 and the gradient data obtained in LW Camera, respectively, and then compared with the benchmark offered by Mitutoyo FormTracer. Figure 12(a) shows the residual between the bench and the surface reconstructed based on the gradient data of WF Camera 1. The PV and RMS of the residual are 408 nm and 79.3 nm, respectively. Figure 12(b) shows the residual between the bench and the surface reconstructed based on the gradient data of LW Camera. The PV and RMS of the residual are 342 nm and 61.1 nm, respectively. Similarly, we also compared the reconstruction error of S2, S3, and S4 between WF Camera 1 and LW Camera, as shown in Fig. 13. Figure 13(a) compared PV of reconstruction error. The values of WF Camera 1 are 375 nm, 469 nm, and 357 nm for S2, S3, and S4 respectively. While the corresponding value in LW Camera is 361 nm, 412 nm, and 343 nm for S2, S3, and S4, respectively. Figure 13(b) compared RMS of reconstruction error. These values in WF Camera 1 are 69.9 nm, 81.7 nm, and 65.9 nm for S2, S3, and S4 respectively, while the corresponding values in LW Camera are 57.3 nm, 66.2 nm, and 56.5 nm for S2, S3, and S4, respectively. Details of the comparisons are listed in Table 1 and Table 2. It is obvious from the comparisons that using the LW Camera can increase the reconstruction accuracy of small-scale structures. Finally, the reconstructed surface of the small-scale structures in the LW Camera can be transferred to the WF Camera 1 system, finding their absolute position in the system according to absolute 3D coordinate data, and then replacing the corresponding data in WF Camera 1. The final surface data after fusing the reconstructed structured surface transferred from LW Camera and absolute 3D coordinates in WF Camera 1 can be seen in Fig. 11(b).

Figure 9
figure 9

The calculated horizontal absolute phase data of the sample. (a) Phase data calculated based on WF Camera 1; (b) phase data calculated based on WF Camera 2; (c) phase data calculated based on LW Camera

Full size image
Figure 10
figure 10

Transformation error from the LW Camera system to the WF Camera 1 system. (a) The difference in depth direction between sampled surface points in the WF Camera 1 system and the transferred surface points from the LW Camera system based on the transformation parameters calculated from calibration; (b) the difference in depth direction between sampled surface points in the WF Camera 1 system and the transferred surface points from the LW Camera system based on the transformation parameters optimized by the proposed method

Full size image
Figure 11
figure 11

Absolute 3D coordinate calculation error in WF Camera 1 and the surface fusion result based on the absolute 3D coordinate data. (a) The residual between the calculated absolute 3D coordinates in the WF Camera 1 system and the benchmark; (b) the surface data by fusing the reconstructed structured surface transferred from the LW Camera and absolute 3D coordinates in WF Camera 1

Full size image
Figure 12
figure 12

Comparison of the reconstruction error of a structure between WF Camera 1 and LW Camera. (a) The residual of measurement data of S1 between the bench and the surface reconstructed based on the gradient data of WF Camera 1; (b) the residual of measurement data of S1 between the bench and the surface reconstructed based on the gradient data of LW Camera. PV refers to peak value and RMS refers to root mean square

Full size image
Figure 13
figure 13

Comparison of the reconstruction error of the structures between WF Camera 1 and LW Camera. (a) Comparison between WF Camera 1 and LW Camera in PV of reconstruction error; (b) comparison between WF Camera 1 and LW Camera in RMS of reconstruction error. PV refers to peak value and RMS refers to root mean square

Full size image
Table 1 Comparison of the peak value of the reconstruction error between WF Camera and LW Camera (unit: nm)
Full size table
Table 2 Comparison of the root mean square of the reconstruction error between WF Camera and LW Camera (unit: nm)
Full size table

4 Conclusions

In this paper, a multiscale form measurement technique based on triple-sensor deflectometry is introduced for the 3D form measurement of specular surfaces with small-scale structures. Cameras with a wide field of view are used to calculate the absolute position data of all measured surfaces. A long working-distance camera is applied to improve the reconstruction accuracy of small-scale structures. The proposed measurement principle, configuration, calibration technique, and data fusion method have been verified through a developed prototype. The knowledge is also applicable to the development of multiscale deflectometry systems with greater field differences. The developed technique has the advantages of non-contact detection, good accuracy, full-field measurement, and small system volume. The technique has the potential to be applied in online and embedded measurements. The beam splitter and the optical flat in the proposed technique play very important roles in reducing the system volume. However, they could cause measurement errors due to manufacturing errors and refraction. Further study on quantitative analyses of the measurement error and compensation method is necessary.