1 Introduction

High-pressure die casting (HPDC) is widely utilized for manufacturing automobile and machine components because of its high productivity in high-accuracy casting processes for nonferrous alloys, such as aluminum alloys [1]. However, the HPDC process is unsuitable for the manufacture of low-volume spare parts after the end of high-volume production because of the inefficiency of low-volume production and the costs of long-term storage of the molds. Additive manufacturing (AM) is an alternative method for the fabrication of low-volume spare parts [2, 3]. However, the manufacturing speeds of metal AM processes such as laser powder bed fusion (PBF-LB/M), or selective laser melting (SLM) are lower than those of most other processes. For the typical aluminum alloy AlSi10Mg, in AM processes, accelerating PBF-LB/M by changing the process parameters, such as the layer thickness and scanning speed, often causes porosity formation [2, 4,5,6,7,8,9,10,11]. Porosity negatively affects the mechanical properties of additively manufactured AlSi10Mg products [5, 9, 10, 12] and significantly promotes their fatigue failure [2, 13,14,15,16,17,18].

Nonetheless, HPDC products typically exhibit porosity [19]. This suggests that additively manufactured products have excessively high quality. A recent study on AlSi10Mg additively manufactured via PBF-LB/M indicated that there is a relationship between the cross-sectional pore area ratio and the fatigue strength and that the fatigue strength of AlSi10Mg with a pore area ratio of <4% is close to or higher than those of JIS (Japanese Industrial Standards) ADC12 (similar to AA A383.0, ASTM 383.0, and ISO AlSi11Cu3(Fe)) castings manufactured via HPDC [2]. These findings indicate that the PBF-LB/M of AlSi10Mg can be accelerated. Furthermore, for additively manufactured AlSi10Mg with a constant layer thickness, the pore area ratio increased and then decreased with an increase in the energy density (radiation energy per unit volume) [2]. The mechanism underlying these tendencies is unclear. Because direct observation and instantaneous temperature measurement of the PBF-LB/M process are difficult, clarification of the mechanism via computer-aided engineering is required. For example, the effects of melting and/or solidification conditions, such as the solidification velocity and temperature gradient, on the formation of pores have been considered [20]. Although these factors may be correlated with the pore area ratio through machine learning [21, 22], it may be possible that none of them affects the pore area ratio. Sparse modeling, which is a machine-learning method, is effective for cases where only a few explanatory variables affect the target variable (most explanatory variables do not affect the target variable) [23].

In this study, we conducted a melting and solidification simulation replicating the PBF-LB/M of AlSi10Mg. Sparse modeling was performed with the cross-sectional pore area ratio of AlSi10Mg as the target variable and the process parameters of the PBF-LB/M and the simulated melting and solidification conditions of AlSi10Mg as the explanatory variables. Using the results, we investigated the dominant factors affecting the pore area ratio of AlSi10Mg manufactured via PBF-LB/M and the mechanisms underlying porosity formation.

2 Numerical methods

2.1 Thermodynamic calculations

The enthalpy curve, liquidus and solidus temperatures, specific and latent heat, and density of AlSi10Mg (Al-10 wt% Si-0.35 wt% Mg [2]) were thermodynamically calculated using a commercial thermodynamic calculation software program (Thermo-Calc Software AB, Thermo-Calc version 2017b) and an aluminum alloy database (Thermo-Calc Software AB, TCAL4) via the CALPHAD method [24]. For these calculations, all available phases in the database—except for the gas phases—were considered, and the molecular volume data of aluminum alloys included in the database were used to calculate the density. In this study, the average specific heat in the temperature ranges of 200 °C to the solidus temperature and the liquidus temperature to 1000 °C was used as the constant specific heat, which did not depend on the temperature, for simplicity. The average density in the temperature range of 200–1000 °C was used as the constant density. The latent heat was obtained by removing the enthalpy corresponding to the total specific heat in the solidification temperature range from the difference in enthalpy at the liquidus and solidus temperatures.

2.2 Melting and solidification simulation

Figure 1 and Table 1 present a schematic of the melting and solidification simulation model and the process parameters for the PBF-LB/M of AlSi10Mg [2], respectively. In this study, the simple two-dimensional model replicating the PBF-LB/M shown in Fig. 1 with a constant layer thickness of t = 0.15 mm (2.5 times larger than the standard thickness) and the process parameters presented in Table 1 [2] was employed, which corresponds to the cross-section of the laser-radiation part vertical to the laser scanning direction. The energy densities (E) presented in Table 1 were calculated using Eq. (1), which gives the energy per unit volume.

Fig. 1
figure 1

Schematic of the two-dimensional melting and solidification simulation model replicating PBF-LB/M of AlSi10Mg

Full size image
Table 1 Process parameters and cross-sectional pore area ratios of AlSi10Mg manufactured via PBF-LB/M with a layer thickness of 0.15 mm [2]
Full size table
$$E=\frac{P}{v\bullet s\bullet t}$$
(1)

Here, P represents the laser power (the setting value in the PBF-LB/M), v represents the scanning speed, and s represents the hatch distance. In the model shown in Fig. 1, heat conduction from the melted area that was used for the calculation of E (the area with width s and height t) to the previously solidified preceding layers causes partial remelting of the preceding layers. The interfacial heat transfer between the calculated area of E or the preceding layers and the surrounding powder bed was neglected for simplicity because of the realistic impossibility of an accurate input of the actual initial temperature distribution, which significantly depends on the product shape and the scan path of the laser. The interfacial heat transfer between the calculated area of E or the preceding layers and the atmosphere (high-purity argon) was neglected because of the rapid heat conduction to the preceding layers. Owing to the geometric symmetry, a 1/2-symmetric model was employed.

Table 2 presents the physical properties and initial temperatures of the AlSi10Mg alloys. The physical properties of the calculated area of E and the preceding layers were not distinguished for simplicity, as shown in Table 2. Because the thermal conductivity cannot be obtained from the thermodynamic calculations, the average of the horizontal and vertical thermal conductivities at 20 °C after the AM process [25] was used as the thermal conductivity for simplicity, which was independent of the temperature. The latent heat was uniformly allocated to the solidification temperature range. The initial temperature of the calculated area of E was estimated according to the added heat, which depended on the process parameters and the thermodynamically calculated enthalpy curve. The energy (heat) per unit weight added to the calculated area of E under the assumption of no attenuation of P is calculated by dividing E by the density of AlSi10Mg. For the preceding layers, the initial temperature of the target area (1.05 mm × 1 mm) of the simulation was assumed to be 150 °C for simplicity, which was equal to the initial base plate temperature for PBF-LB/M. The outside of the target area was also set to a constant temperature of 150 °C. Melting and solidification simulations were conducted using the finite volume method, in which latent heat release was simulated using the temperature recovery method. The computational elements that did not contact the line of symmetry were set to be square, with side lengths of 0.01 mm. The computational elements that contacted the line of symmetry were set as rectangular, with a height of 0.01 mm and a width of 0.005 mm. The timestep was set as 0.00001 s (a value satisfying the stability condition of the simulations). A solid fraction (0.5) was used for identifying the state (melting or solidification) of the computational elements. The cooling rates and temperature gradients of the computational elements at a solid fraction of 0.5 during solidification were also obtained.

Table 2 Physical properties and initial temperatures of AlSi10Mg
Full size table

2.3 Sparse modeling

Figure 2 shows the examples of the polished central vertical cross-sections of the AlSi10Mg (10 mm × 10 mm × 10 mm) additive manufactured via PBF-LB/M under various process parameters, which were used for the calculation of the cross-sectional pore area ratios (total area of the pore of more than 500 μm2 per cross-sectional area) by the image analysis [2]. These experimentally measured cross-sectional pore area ratios of the additively manufactured AlSi10Mg under various process parameters are presented in Table 1 [2]. In this study, sparse modeling with the standardized pore area ratio as the target variable, the standardized process parameters (Table 1), and the standardized melting and solidification conditions of AlSi10Mg obtained via the melting and solidification simulation as the explanatory variables was conducted through lasso regression and backward elimination. Lasso regression is a machine-learning (supervised learning) method in which multiple linear regression is used to minimize the sum of squared errors and the regularization term [23]. The regularization term is the product of the hyperparameter and the sum of the absolute values of the intercept and partial regression coefficients. Consequently, the partial regression coefficients of the explanatory variables remotely related to the target variable have values of zero [23]. For the lasso regression, R (version 4.1.2) and the glmnet package (version 4.1-4) were used under the random seed specified by the “set.seed” function (set.seed(1)), where the reproducible intercept and the reproducible partial regression coefficients under the optimum hyperparameter based on cross validation for enhanced generalization performance were obtained. Backward elimination was performed by manually removing partial data of the explanatory variables from the dataset for lasso regression. The obtained multiple regression equations were evaluated according to the plots of the relationships between the measured pore area ratios and the ratios estimated via the equations, as well as the calculated mean squared errors (MSEs) for the relationships.

Fig. 2
figure 2

Polished central vertical cross-sections of the additively manufactured AlSi10Mg under process parameters of a No. C-4, b No. D-1, c No. D-4, and d No. F-2 [2]

Full size image

3 Results and discussion

3.1 Initial temperature of calculated area of energy density

Figure 3 shows the thermodynamically calculated enthalpy curve, providing an estimation example of the initial temperature of the calculated area of energy density (E) in AlSi10Mg under the assumptions of no vaporization and no latent heat of vaporization. The unmelted powder was not observed in AlSi10Mg manufactured via LB-PBF under the process parameters presented in Table 1 [2], as shown in Fig. 2. Thus, the initial temperature of the calculated area of E should be higher than the liquidus temperature of AlSi10Mg, as shown in Fig. 3. When all the energy (heat) was added to the calculated area of E at a temperature of 150 °C before the heat addition, the temperatures of the area after the heat addition were within the range of 6100–30,000 °C. These temperatures are distant because the boiling temperature of aluminum is 2520 °C. Table 3 presents the estimated initial temperatures of the calculated area of E under an absorption rate of 20%. When 20% of the energy was added to the calculated area of E at a temperature of 150 °C, the initial temperatures of the area were within the range of 1000–5700 °C, as shown in Table 3. Although a uniform absorption rate of 20% is adequate according to the relationship between the incidence angle of the laser and the absorption rate of aluminum (in the range of approximately 0%–30%) [26] and simulations of laser welding (10% and 16%) [26, 27], some initial temperatures in the calculated area of E were higher than the boiling temperature of aluminum. In fact, most of the melted AlSi10Mg remained without vaporization (a small portion became fumes) [2] under the process parameters shown in Table 1, where the PBF-LB/M of AlSi10Mg was not prevented by significant vaporization. This suggests that instantaneous heating and cooling in PBF-LB/M actually lead to superheating (opposite of supercooling) of AlSi10Mg at temperatures higher than the boiling temperature and that the assumptions of no vaporization and no latent heat of vaporization in the melting and solidification simulation are valid.

Fig. 3
figure 3

Thermodynamically calculated enthalpy curve showing an estimation example of the initial temperature of the calculated area of energy density in AlSi10Mg under the assumptions of no vaporization and no latent heat of vaporization

Full size image
Table 3 Estimated initial temperatures of the calculated area of energy density
Full size table

3.2 Melting and solidification conditions

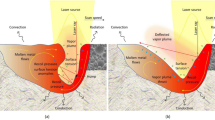
Figure 4 presents examples of the temperature distributions of AlSi10Mg obtained via the melting and solidification simulation, where Fig. 4a, b show the distributions under the minimum and maximum E values [process parameters No. D-1 and No. F-4, respectively (Table 1)]. In the case of No. D-1, the preceding layers were not melted, as shown in Fig. 4a. However, for No. F-4, the preceding layers melted significantly, as shown in Fig. 4b. Figure 5 shows a typical example of the classification of the melted area (under process parameters No. E-4). The melt-pool depth (maximum height of the melted area) was determined, as shown in Fig. 5. In addition, the melted areas were classified into four categories, as shown in Fig. 5. Melted areas 1 and 3 corresponded to the area remelted by the laser scan of the next layer and the area that may have been remelted by the laser scan of the next hatch, respectively. Melted area 4 corresponded to the area that may have been the measurable heat-transfer effect of the product shape and scan path of the laser on the melting and solidification behavior. Thus, the medians of the cooling rate (R) and temperature gradient (G) between their averages for the melted areas 2 and 3 and for the area 2 were obtained. Subsequently, the solidification velocity (\(\dot{X}\)= R/G) and the NIYAMA parameter G/\(\sqrt{R}\) (= \(\sqrt{{G}^{2}/R}\)) were calculated. In general, R, G, \(\dot{X}\), and G/\(\sqrt{R}\) affect the solidification microstructure [28]. Table 4 presents the simulated melting and solidification conditions for each process parameter. The melt-pool depths exceeded the layer thicknesses (0.15 mm), as shown in Table 4, which is consistent with the cross-sectional microstructures, where the unmelted powder was not observed as shown in Fig. 2 [2]. The magnitude of the melt-pool depths can also correspond to the actual spacing of the scaly melted boundaries in the microstructures owing to PBF-LB/M [2]. In addition, the cooling rates were in the range of 140,000–230,000 K/s, which is suitable for PBF-LB/M [29].

Fig. 4
figure 4

Temperature distribution of AlSi10Mg after 0.001 s obtained via melting and solidification simulation under process parameters a No. D-1 and b No. F-4 (unit: °C)

Full size image
Fig. 5
figure 5

Classification of the melted areas under process parameters No. E-4

Full size image
Table 4 Simulated melting and solidification conditions
Full size table

3.3 Lasso regression and backward elimination

Table 5 presents the partial regression coefficients obtained via lasso regression and the MSE for the relationships between the measured pore area ratios and the ratios estimated via the obtained multiple regression equations under combinations of the various explanatory variables consisting of the process parameters listed in Table 1 and the melting and solidification conditions listed in Table 3. Most of the partial regression coefficients obtained were nonzero, and the MSE tended to decrease with an increase in the number of explanatory variables, as shown in Table 5. This suggests that the multicollinearity between the explanatory variables and/or overfitting in the lasso regression reduced the accuracy of the results. Thus, reasonable combinations of the explanatory variables (combinations that do not significantly increase the MSE with a reduction in the number of explanatory variables) were searched through manual backward elimination by sequentially removing a few explanatory variables that were remotely related to the target variable. Figure 6a–c show the relationships between the measured pore area ratio and the ratio estimated via the obtained multiple regression equations under the combinations of explanatory variables No. 4, 19, and 22 presented in Table 5, which led to the minimum MSE in the combinations of six, three, and two variables, respectively. Although the MSE for Nos. 19 and 22 exceeded that for No. 4, the linearity of the relationship between the measured pore area ratio and the estimated ratio for Nos. 19 and 22 was similar to that for No. 4, where the determination coefficient (R2) for No. 4 is not significantly smaller than that for Nos. 19 and 22, as shown in Fig. 6. Thus, the search for a reasonable combination of a few explanatory variables indicated that E and the melt-pool depth were the dominant factors affecting the pore area ratio. Energy density is an important process parameter in AM. The melt-pool depth is also important for industrial melting and solidification processes, such as continuous casting and welding. In addition, the obtained partial regression coefficients of E and melt-pool depth were consistently negative and positive, respectively, regardless of the combination of explanatory variables. These results confirmed that E and the melt-pool depth significantly affected the pore area ratio.

Table 5 Partial regression coefficients obtained via lasso regression and the MSE for the relationships between the measured pore area ratios and the ratios estimated via the regression equations under various combinations of explanatory variables (N/A: excluded from explanatory variables)
Full size table
Fig. 6
figure 6

Relationships between the measured pore area ratio and the ratio estimated via multiple regression equations under the following combinations of explanatory variables: a No. 4, b No. 19, and c No. 22

Full size image

3.4 Effects of dominant factors on porosity formation

Figure 7 shows the relationships among the initial temperature in the calculated area of E, the melt-pool depth, and E. Here, the upside-down vertical axis for the initial temperature was used because the partial regression coefficient of E was negative, and there was a linear correlation between E and the initial temperature (because of the calculation method for the initial temperature shown in Fig. 3). Although the relationship between E and the initial temperature in the calculated area of E was linear, the relationship between E and the melt-pool depth was curvilinear; the melt-pool depth under a high E of more than 53.3 J/mm3 that corresponded to the maximum pore area ratio [2] slowly increased with an increase in E, as shown in Fig. 7. Figure 8 shows the relationship between the pore area ratio and E [2], along with the dominant factors affecting the ratio, which are based on Fig. 7. The tendencies of the relationships shown in Fig. 7 indicate not only that the pore area ratio increased with increases in the energy density and melt-pool depth but also that the pore area ratio decreased with an increase in the energy density or a decrease in the change rate of the pool depth under the range of the slow increase in the pool depth with an increase in the energy density, as shown in Fig. 8.

Fig. 7
figure 7

Relationships among the initial temperature in the calculated area of energy density, melt-pool depth, and energy density

Full size image
Fig. 8
figure 8

Relationship between the cross-sectional pore area ratio and the energy density [2], indicating the dominant effect of the latter on the former

Full size image

The observed pores of the additively manufactured AlSi10Mg were spherical, regardless of the process parameters presented in Table 1 [2]. Spherical porosity is generally caused by the trapping of bubbles of dissolved hydrogen in the powder [7], generated fumes, and atmospheric gas. The trapping is caused by convective flow in the melt pool [2, 30] and/or keyhole-mode melting [26, 27, 31]. The effects of an increase in E, the initial temperature in the calculated area of E, and the melt-pool depth on the increase in the pore area ratio are mediated by the promotion of convective flow in the melt pool and/or keyhole-mode melting, as well as the increase in fume generation. However, the slow increase in the melt-pool depth under a high E leads to a low R and/or \(\dot{X}\) in the melted area. This corresponds to the result in which the three reasonable principal explanatory variables of No. 19 shown in Table 5 include \(\dot{X}\) with a positive partial regression coefficient. Meanwhile, the observed maximum diameter of the pores tended to increase monotonically with an increase in E, as shown in Fig. 2 [2, 8]. This suggests that the effects of the increase in E under a low R and/or \(\dot{X}\) on the decrease in the pore area ratio are mediated by the promotion of not only the remelting of the preceding layer but also the coalescence and flotation separation of the bubbles. Thus, the mechanisms of porosity formation and the dominant factors affecting the pore area ratio depend on the process parameters, confirming the hypothesis regarding the variation in the pore area ratio [2]. Meanwhile, the actual melt-pool depth may exceed the simulated depth because of the promotion of vertical heat conduction due to convective flow [32] and/or keyhole-mode melting [26, 27, 31] in the pool. This suggests that assumptions such as the athermalization of the powder bed surrounding the calculated area of E and neglecting the vaporization in the melting and solidification simulation were appropriate for obtaining reasonable magnitude relationships of the melting and solidification conditions under the process parameters presented in Table 1.

Table 6 presents the recommended standard process parameters for the PBF-LB/M of AlSi10Mg and the pore area ratio of the additively manufactured AlSi10Mg under these process parameters [2], which is also shown in Fig. 8. The relationship between the pore area ratio and E under the standard process parameters listed in Table 6 was not located on the approximated curve of the relationships under the process parameters listed in Table 1 [2], as shown in Fig. 8. This indicates that the pore area ratio depends on explanatory variables other than E and the melt-pool depth. In fact, there are reports of relationships between E and the pore area ratio or relative density [30, 33, 34] that are opposite to the relationship shown in Fig. 8. These imply that the contribution of the melt-pool depth significantly depends on the layer thickness and that the normalized melt-pool depth, e.g., the pool depth divided by the layer thickness, may be an effective explanatory variable for the sparse modeling of the dataset under various layer thicknesses.

Table 6 Standard process parameters and cross-sectional pore area ratio of AlSi10Mg manufactured via PBF-LB/M [2]
Full size table

4 Conclusions

In this study, a melting and solidification simulation replicating the PBF-LB/M of AlSi10Mg based on sparse modeling with the cross-sectional pore area ratio of AlSi10Mg as the target variable and the process parameters of PBF-LB/M and the simulated melting and solidification conditions of AlSi10Mg as the explanatory variables was conducted. According to the obtained results, the dominant factors affecting the pore area ratio in PBF-LB/M of AlSi10Mg and the mechanisms of porosity formation were investigated. The following conclusions are drawn.

  1. (1)

    The combination of a few explanatory variables that did not significantly increase the MSE obtained through lasso regression and backward elimination indicated that the energy density (one of the process parameters) and melt-pool depth (one of the melting conditions) were the dominant factors affecting the pore area ratio.

  2. (2)

    The obtained partial regression coefficients of the energy density and melt-pool depth were negative and positive, respectively. The relationship between the energy density and melt-pool depth was curvilinear.

  3. (3)

    These results suggest not only that the pore area ratio increases with the energy density and melt-pool depth but also that it decreases with an increase in the energy density or a decrease in the change rate of the pool depth under the range of the slow increase in the pool depth with an increase in the energy density.

  4. (4)

    The mechanisms of porosity formation, as well as the dominant factors affecting the pore area ratio, depend on the process parameters.

  5. (5)

    Assumptions such as the athermalization of the powder bed surrounding the laser-radiation part (the calculated area of energy density) and neglecting the vaporization of AlSi10Mg in the melting and solidification simulation are appropriate for analyzing the tendencies of the melting and solidification conditions in PBF-LB/M.