Introduction

Electrical propulsion systems for satellites have long been popular due to their high efficiencies, with specific impulses of up to 10 000 seconds for plasma-based systems [1]. One particular type of plasma thruster that recently has garnered a lot of attention is the helicon plasma thruster, which has been the subject of many recent studies worldwide, with research carried out at e.g., Canberra [2], Tohoku University [3], Stuttgart [4], Auckland University [5], Madrid university [6], and Padova University [7]. Research has also been carried out at the University of Bologna, e.g., [1, 7,8,9,10].

The thruster operates by injecting a gas into a dielectric tube that is wrapped with either magnets or coils which produce a quasi-axial static magnetic field [1]. This magnetic field serves both to confine the plasma within the tube, and more importantly allows for helicon waves in the plasma, which leads to higher ionization efficiency and better performance [1]. The magnets (or coils) also form a magnetic nozzle through which the plasma is expelled to generate thrust.The tube is surrounded by a radiofrequency antenna that imparts power into the gas which ionizes it. The antenna then heats the resulting plasma further to increase thruster performance. Thus, a helicon plasma thruster does not have any electrodes, neutralizers or grids. This simplifies the design and makes the thruster ideally suited for cubesats and other small spacecraft [1].

To achieve an efficient helicon plasma thruster, it is important to maximize the power deposited by the radiofrequency antenna into the plasma. Helicon plasma thrusters typically operate at frequencies in the order of MHz which means that the power deposited into the plasma can be approximated as equal to the power supplied to the antenna \(P_A\) [11]. \(P_A\) is defined as

$$\begin{aligned} P_A = \frac{1}{2} Re(Z_A) \vert I_A \vert ^2 \end{aligned}$$
(1)

where is \(I_A\) the current over the antenna and \(Z_A\) the impedance of the antenna [12]. Maximum power transfer, according to the maximum power transfer theorem, occurs when

$$\begin{aligned} Z_L = Z^*_S \end{aligned}$$
(2)

is fulfilled, with \(Z_L\) being the impedance of the load (i.e., the antenna), and \(Z_S\) being the impedance of the source (i.e., the generator) [13]. To achieve this a matching network has to be designed, which makes the load and the source see each other as having the same impedance through the use of capacitors and inductors [14]. To design this matching network it is thus paramount to know the impedance of the antenna. The impedance can be calculated, for example, by using a computer program called Adamant [12]. However, just like many other numerical tools, Adamant is a slow and computer-resource-demanding program, making it unwieldy for assessing small design changes or for use in large parametric studies. Therefore, the objective of this work is to study the potential of training a machine learning model on data generated by Adamant to predict the impedance is investigated. Similar research was carried out in [15], where the authors demonstrated the superiority of deep neural networks (DNN) over classical algorithms for predicting energy deposition in helicon sources, highlighting DNN’s enhanced stability and accuracy. Schuckla et al., explored the use of Decision Tree and Random Forest algorithm to predict the density of plasma within a hydrogen fed Helicon discharge as well as linear regression techniques and Deep Learning to predict the potential variation along the discharge axis [16,17,18].

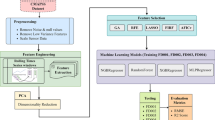
In this study, six different machine learning models implemented in MATLAB [19] are evaluated, their hyperparameters optimized using Bayesian hyperoptimization and their performance evaluated using both nested k-fold cross-validation to calculate the root mean square error (RMSE), and a test set to calculate point-to-point errors. Finally, the models are also subjected to a practical test by testing their predictions on input data that is outside of the training data domain. The objective is to find a model with less than 5% maximum point-to-point error.

Machine learning

Machine learning is used in everything from signal processing to translation [20] and is prevalent in many aspects of life today, even though the end user might not always be aware of it. In [21] three different categories of problems that can be solved with machine learning are presented: classification, clustering and prediction. If the algorithm should sort the presented data into different categories, it is a classification problem. If the algorithm sorts the data into clusters with different clusters containing data of similar type, with the algorithm sometimes even having to define the clusters by itself, it is a clustering problem. Finally, if the problem is to find patterns in the data and then try to predict what the result would be when presented with new data of the same type, the problem is a prediction problem, which is the type of problem that is to be solved in this study.

There are also different types of machine learning models, which [21] classifies as supervised, semi-supervised, unsupervised, or reinforcement learning models. In supervised learning the model is fed with both the input and the corresponding output, in unsupervised learning the model has to figure out what the output should be by itself and find patterns in the data, and semi-supervised learning is a mix of both previous types [21]. Reinforcement learning is another type and is used in for example self-driving cars [21]. All the models in this work belong to the supervised learning category.

Models

The models evaluated in this work were the following: decision trees, ensembles, support vector machines (SVM), Gaussian process regressions (GPR), generalized additive models (GAM), and artificial neural networks (ANN) [22].

The decision tree gets its name from the structure of the algorithm. It is based on so-called nodes that are connected through edges. While each node can potentially connect to an unlimited number of other nodes, the most common structure is to have each node connected to two other nodes further downstream, in what is called a binary decision tree [21]. It works as follows: in each node, some property of the data is investigated, and a question is posed. Depending on the answer it then sends the data further down to another node, which looks at some other property. Eventually, enough evaluations will have been made for the tree to decide what class the data belongs to, or what numerical value the data should lead to in the regression case. The final decision is made by the nodes at the bottom of the tree, which are called leaves [21]. An example of a decision tree for fruit types is shown in Fig. 1. The structure resembles an upside-down tree.

Fig. 1
figure 1

Example of decision tree to classify fruits

Full size image

The main difficulty when building the decision tree is to decide what information each split should be based on, and what split should be made in which node [21]. For regressions the CART method is often used [23].

Ensembles are technically not machine learning models per se, but rather it is a method to congregate the results from many different models and perform the prediction using some kind of averaging of all the results [24]. In MATLAB the ensemble function uses decision trees as its base [25]. By using the combined results the ensemble method can avoid overfitting, expand the solution space and also decrease the risk of the model becoming stuck in local optima [24]. The methods used to perform the averaging vary. A common method is boosting, where many so-called weak learners are trained on different subsets of the training data, with weak here referring to the fact that they on their own are only able to find very basic prediction rules and thus are useless on their own [26]. The output of the ensemble is then an aggregation of all the results from the weak learners, where majority voting is used to determine the final result [26]. Each learner is assigned a weight to make the learners whose prediction rules are more important for the result have more say in the final output [26].

An SVM performs classification or regression by dividing the data set according to its characteristics using a hyperplane. The hyperplane is chosen using the maximum-margin method, meaning that the hyperplane is placed such that it is at maximum distance from all data points [27]. In the case that the data points are not easily separable, which is often the case in real-world applications, soft margins may be used that allow some of the data to fall on the “wrong” side of the hyperplane to allow it to be fitted [27, 28]. Another defining characteristic of the SVM is the kernel function. The kernel function is used to both increase the generalisability of the model and to allow data to be fitted. The latter function is because the kernel works the data into higher dimensions where it might be possible to find a hyperplane that can separate the data neatly even if that wasn’t possible with the original dimensionality [27, 28]. This does not necessarily mean that soft margins are not required as well, as the time and resources required to fit the SVM increase exponentially with the number of dimensions [28]. Using too many dimensions might also lead to overfitting [27].

The GPR model is, as the name implies, built on Gaussian processes. A Gaussian process is defined by a mean function m(x) and a kernel function k(x,x’), i.e.,

$$\begin{aligned} f(\textbf{x} \sim GP(m(\textbf{x},k(\textbf{x},\textbf{x}')). \end{aligned}$$
(3)

Rasmussen and Williams [29]. In machine learning, the process starts by prescribing a prior, which is then updated using Bayesian inference according to the training data [30]. This gives a posterior Gaussian process from which predictions can be obtained. An important part of the training is choosing relevant and appropriate mean and kernel functions, as that will have a large impact on the performance. This is generally done by optimization after first making an initial guess regarding what function would be appropriate given some data [30].

Generalized additive models are a continuation of generalized linear models [31]. Whereas the standard linear regression is on the form

$$\begin{aligned} E(Y\vert X_1, X_2...,X_p) = \beta _0 +\beta _1X_1+...+\beta _pX_p \end{aligned}$$
(4)

where \(\beta _i\) are some coefficients, the GAM instead takes the form

$$E(Y\vert X_1, X_2...,X_p) = f_0 + \sum\limits_{j=1}^p f_j(X_j)$$
(5)

where \(f_j\) are so-called smooth functions [31]. These functions must be estimated during training.

The ANN has become a very popular machine learning model since its introduction in 1958 [20]. An ANN consists of multiple layers: the input layer, a number of hidden layers, and the output layer. Each layer is built out of perceptrons, or neutrons [20]. The connections between the neurons and layers differ depending on the type of ANN, but in the case of the implementation in MATLAB a feed-forward type network is used, where information flows only in one direction, from the input layer through the hidden layers until the output layer [20, 32]. An example schematic of a feed-forward ANN is shown in Fig. 2.

Fig. 2
figure 2

An example schematic of an ANN

Full size image

As shown in Fig. 2 the number of inputs and outputs do not have to correspond. Each neuron has a so-called activation function f which is often an S-shaped function such as a hyperbolic or sigmoid function [20]. The output of each neuron is then \(y = f(w_0+\textbf{w}^T\textbf{x})\), where \(w_i\) are weights that are altered during the training process in order to make the neural network perform as well as possible, while \(\textbf{x}\) is a vector with inputs.

Selecting hyperparameters - Bayesian hyperparameter optimization

There are many different methods for choosing the hyperparameters of a model. Three of the most prominent ones are grid search, random search, and Bayesian hyperparameter optimization. Grid search is the most basic of the concepts, simply using a predetermined grid with different hyperparameters for training the models. It then selects the hyperparameters that resulted in the best performing model. This method will invariably find the optimal hyperparameters but the computational load is high [22]. Random search is shown to give better results than grid search [33], as it selects sets of hyperparameters using random sampling, but it cannot be guaranteed that it will find the most optimal hyperparameters [22]. Bayesian hyperparameter optimization, while also a function that exploits sampling, works much better [34], and it is thus the method chosen for this work.

In short, the Bayesian optimization algorithm is similar to the GPR machine learning model, in that the Bayesian optimization algorithm starts out knowing nothing about the algorithm it is supposed to optimize. Thus, it prescribes a prior that it then updates with information from evaluating the model using a certain set of hyperparameters. This creates the Bayesian posterior, a statistical model of the function that should be evaluated [35]. To decide what set of hyperparameters should be evaluated next in order to improve the results the most, acquisition functions are used [36]. There are a plethora of acquisition functions, but the most common one is the expected improvement function [36]. The expected improvement, in the absence of noise, is defined as

$$\begin{aligned} EI_n(x):= E_n [[f(x)-f_n^*]^+] \end{aligned}$$
(6)

where n represents the number of iterations and \(f^*_n = max_{m \le n} f(x_m)\) [36], i.e. the point for which f takes its maximum value [36]. Then, the next point to be evaluated is

$$\begin{aligned} x_{n+1} = argmax EI_n(x) \end{aligned}$$
(7)

which the point that the posterior distribution indicates would give maximum improvement [36]. Figure 3 shows the process, with the evaluated points and the point that is to be evaluated next clearly marked. The impact of the optimization is shown in Fig. 4, where it is clear that the optimized model using tuned hyperparameters perform much better than the non-optimized model.

Fig. 3
figure 3

The Bayesian optimization model process for the SVM

Full size image
Fig. 4
figure 4

The loss function value for different iterations of hyperparameters

Full size image

The parameters that were optimized, and the options for each hyperparameter, are shown in Table 1.

Table 1 Table of all optimized hyperparameters for each model
Full size table

Cross-validation

To solve the problem that evaluating the machine learning models on data it has already seen will give a highly biased result, different methods can be used. One is cross-validation. Fundamentally, all cross-validation models divide the data into a training set, which is used only for training the model, and a test set, which is used for testing the model. This is also called the single hold-out method [38]. There is also the k-fold method which is a bit more involved. As shown in Fig. 5, the data set is divided into k different folds, each fold using a different subset of the data for testing and for training. By calculating the root mean square error (RMSE) of the model that is trained using the data division in each fold and then calculating the average RMSE, a reasonable value of error for the final model trained on the whole training data set can be obtained [38].

Fig. 5
figure 5

A visual depiction of the k-fold method

Full size image

A more intricate version of the k-fold method is the nested k-fold method, a schematic of which is shown in Fig. 6.

Fig. 6
figure 6

Visual depiction of the nested k-fold method. Note that the procedure would normally include more hyperparameter sets and that this only depicts one iteration of the outer loop

Full size image

As is shown in Fig. 6, for each outer fold, several hyperparameter sets are tested and the resulting model performance is evaluated using the k-fold method. Then the model that performed the best in the inner loop is sent out to be trained on the whole training set of the outer loop and tested [39]. The RMSE for that outer fold is kept, and the outer loop proceeds to the next fold. Once all folds have been evaluated the average RMSE is calculated to get an estimate of the model’s performance. The final model that is used is trained with one run of the inner loop using all data available.

This work used a combination of the hold-out method and the nested k-fold method. First, the entire data set was divided randomly into two sets, with 20% going into the test set and the rest going to the training set. The nested k-fold method was then applied for the training data set, while the test set was kept separate. The reason for keeping a test set was the performance target which was set on a point-to-point error basis, which would have been impossible to evaluate in a non-biased manner if all available data had been used in training the model.

Model performance evaluation

This work uses the RMSE [40] as the primary evaluation metric in the hyperparameter selection. It is given by

$$RMSE = \sqrt{\frac{\sum\nolimits_{i=1}^N (y_i'-y_i) ^2}{N}}$$
(8)

where \(y_i\) is the impedance from Adamant, \(y_i'\) is the impedance as predicted by the machine learning model, and N is the number of observations.

Another metric is the point-to-point error in percentage. As the values of impedance are less than 1, this leads to very high percentages of error even if the absolute value is tiny. This becomes misleading as the machine learning model is in reality very close to the target, so instead the percentage is calculated using the span of the data instead of the point data value in the denominator. The point deviation PD is thus calculated as

$$\begin{aligned} PD [\%] = 100 \frac{\vert y_i-y_i' \vert }{max(y)-min(y)} \end{aligned}$$
(9)

In addition to the PD the mean PD is also reported, calculated as

$$\text{Mean}\ PD\ [\%] = \frac{\sum _{i} PD_i }{N}$$
(10)

with N being the total number of observations and \(PD_i\) the individual point-to-point errors.

Another metric is the integral deviation. The integral value is defined as

$$\begin{aligned} I = \int _{n_e} Z d n_e \end{aligned}$$
(11)

i.e., the integral value of the impedance over the electron density. The integral deviation is then

$$\text{Integral deviation}\ [\%] = 100 \left| \frac{I_{target} - I_{model}}{I_{model}} \right| .$$
(12)

It is used to get an additional metric of how well the overall fit of the model is over the whole data range.

Finally, the variance of the fit is also interesting, and therefore the R-squared value [41] is calculated as

$$\begin{aligned} R^2 = 1 - \frac{\sum _i(y_i'-y_i)^2}{\sum _i (\bar{y} - y_i)^2} \end{aligned}$$
(13)

where \(\bar{y}\) is the mean impedance of the testing data. A negative R-squared value indicates that the fit is worse than it would be for a simple line, while a perfect fit has an R-squared of 1 [41].

Relative input importance & training data sensitivity

The relative input importance (RII) and training data sensitivity are not performance metrics per se, but they can reveal interesting characteristics about the trained models, such as overfitting and potential over-dependence on input parameters, which is why they are implemented for this work.

The relative input importance indicates how much impact each input parameter has on the model output. There are many different methods to calculate it, in this case a sensitivity input analysis was used [42, 43]. A schematic of the method is shown in Fig. 7.

Fig. 7
figure 7

Schematic of how the relative input importance is calculated. Note that there is also a -10% variation for all parameters that is not depicted here, and that RMSE\(_i\) would actually be the RMSE of both +10% and -10% summed for each input parameter

Full size image

The figure shows part of the process. Each input is varied ±10%, the RMSE between that output and the output for the model fed with unmodified data is calculated, and all RMSEs are summed. Then, the RII is calculated as

$$\text {RII}\ [\%] = 100*\frac{RMSE_i}{RMSE_{tot}}$$
(14)

where \(RMSE_i\) is the total RMSE for input parameter i.

The training data sensitivity is a measure of how sensitive the model results are to what data is in the training set and in the test set. To explore this one run of a k-fold loop is performed, but the RMSE for each fold is calculated by evaluating the model on the test set that was kept away from the training data. The mean, maximum and minimum RMSEs are then presented to give an indication of how the variation of training data affects the model.

Adamant & data generation

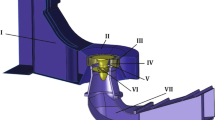
Adamant was developed at the University of Padova [12], and can be used for a multitude of purposes, although in this work only its capability of calculating the impedance on the radiofrequency antenna is used. It uses coupled volume integral equations to simulate the plasma domain, while the antenna surface is simulated using surface integral equations [12]. In this work, the plasma domain was modelled using a volume (3D) mesh as a 10 cm long cylinder with a radius of 2 cm, while the chosen antenna, the Nagoya III [12], was modelled using a surface mesh (2D) with a radius of 3 cm and a width of 6 cm. The Nagoya III antenna was selected for its good performance in the range of electron densities and magnetic field strengths that were used in this work [11]. The meshes of both the antenna and the plasma are shown in Fig. 8.

Fig. 8
figure 8

Mesh of the plasma computational domain with the Nagoya III antenna

Full size image

A small study was conducted to decide the mesh size for the plasma domain. As is shown in Fig. 9, the impedance value fluctuates due to numerical noise. Since the computer resource demands for smaller mesh sizes than depicted in the graph were impossible to meet, the decision was taken to use the mesh with 10800 triangles, as the value of the impedance seems to be approximately close to the asymptotic value that the graph indicates that the program is converging toward.

Fig. 9
figure 9

Impedance values for different mesh sizes as calculated by Adamant

Full size image

Four input parameters were included: the electron density \(n_e\), the magnetic field strength \(B_0\), the electron temperature \(T_e\) and the static pressure \(P_0\). Due to computer resource constraints, two sets of data were created and combined, with each set using a slightly different combination of input parameters. The average CPU time per simulation required by ADAMANT for generating the data set is \(3.7x10^3\) s. Calculations are done on a 3.67-GHz machine. In total, 1179 data points were generated. The values are shown in Table 2 and Fig. 10.

Table 2 Parameter values for the generated data. Note that \(P_0\) and \(T_e\) were the same for both sets
Full size table
Fig. 10
figure 10

All values of \(n_e\) in the generated data set

Full size image

From the combined data set 80% of the points were randomly selected to be in the training set, while the remaining 20% formed the test set. A small extra test set, containing 16 points in total, was also generated to explore the generalization abilities of the models in practice. Table 3 shows the input parameter values for that set.

Table 3 Parameter values for the extra test set
Full size table

The resulting impedance values for the training set are shown in Fig. 11.

Fig. 11
figure 11

Overview of the data from Adamant excluding the extra test set. Note that for each point there are also three variations of \(T_e\) and three variations of \(P_0\)

Full size image

Results & discussion

The optimized hyperparameters for each model are shown in Table 4.

Table 4 Table of all optimized hyperparameters for each model
Full size table

Looking at Table 5 the GPR and the ANN have the lowest and second-lowest RMSEs respectively, while the ensemble has an RMSE that is not much higher. The rest of the models perform much worse, with the difference being at least an order of magnitude.

Table 5 Cross-validated mean RMSE for each model
Full size table

The results from the test set are shown in Table 6, with the results mostly validating the results of the cross-validation. The GPR scores the lowest RMSE, max and mean point deviation and has the highest R-squared value, although its integral deviation is somewhat higher than that of the decision tree. Overall though, it is the clear winner here, but both the ANN, the ensemble and the decision tree score well too.

Table 6 Error metrics for all models when evaluated on the test set
Full size table

The correlation of the decision tree is shown in Fig. 12. On the training set it shows excellent adherence to the target line, and while the errors are slightly larger on the test set, they are still in such range that they can be classed as acceptable. The same conclusions can be drawn for the ensemble model, whose correlation is shown in Fig. 13.

Fig. 12
figure 12

Correlation for the decision tree model

Full size image
Fig. 13
figure 13

Correlation for the ensemble model

Full size image

Figure 14 shows a distinctly different correlation to the decision tree and the ensemble. It is clear that the SVM fails to accurately predict both the training set and the test set data, which indicates that it has failed to find a reasonable relationship between the input parameters and the output parameters.

Fig. 14
figure 14

Correlation for the SVM

Full size image

The GPR shows the best correlation of all, as shown in Fig. 15. The data points fall almost perfectly on the target line on both the training set and the test set, indicating a very good fit.

Fig. 15
figure 15

Correlation for the GPR model

Full size image

As shown in Fig. 16, the correlation of the GAM is more similar to that of the SVM than to that of the other models, with neither training nor test set points being accurately reproduced.

Fig. 16
figure 16

Correlation for the GAM

Full size image
Table 7 Error metrics for all models when evaluated on on the extra test set
Full size table

On the extra test set the results are rather different from the results on the test set. As seen in Table 7, the ANN is now the model that performs the best across all different metrics, and with some margin too, with for example an RMSE of only 0.0059 while the GPR’s RMSE is much higher at 0.0213. The only exception is that the SVM scores lower on the integral deviation, which is a very surprising result considering its overall performance. The GAM also scores very well in integral deviation but looking at the other metrics it can be said that it also shows a subpar overall performance. Looking at Fig. 17, the low integral deviation is most likely because the errors coincidentally are spread out on both sides of the zero line, meaning that the integral value is close to zero despite the actual magnitude of the errors being very large.

Fig. 17
figure 17

Errors for all models on the extra test set

Full size image

Figure 18 immediately makes it clear that the GAM’s attempts at predicting the impedance on the extra test are futile, but the other models do manage to predict at least some of the impedance values quite accurately, although their overall performance is hampered by having at least one large outlier where the error is much larger than for the other points. The ANN is the only exception to this rule.

Fig. 18
figure 18

Correlation for all models on the extra test set

Full size image

In Fig. 19 the residuals for each model on the extra test set is shown. The decision tree and ensemble have similar results, both with an error of approximately 0.1 for a target impedance of around 0.57, while the errors are much smaller for the other targets. The SVM is shown to perform remarkably well, but has an error of 0.1 for a target impedance of about 0.82. The GPR shows very small errors for all target impedances, while the GAM shows large errors for both the lowest and highest target impedances. The ANN, finally, exhibits an almost perfect zero-error score across the range.

Fig. 19
figure 19

Residuals for all models on the extra test set

Full size image

Relative input importance

Figure 20 shows the model relative input importance for all models. It is strongly indicated that the \(n_e\) and \(B_0\) parameters are the only input parameters that are taken into account by the majority of the models, and none of those who do take \(T_e\) and \(P_0\) into account ascribe any significant importance to them. This is a finding that is corroborated by the parametric analysis presented in [11] in which Melazzi et al., show that both \(T_e\) and \(P_0\) plays a negligible effect on the real part of the impedance when a Nagoya III type antenna is considered and plasma density lies in the range of \(10^{16} - 10^{19}\) \(m^{-3}\) for magnetic field intensities that goes from 10 to 100 mT. Nevertheless, these parameters were still included for the sake of completeness. In fact, when further investigations were made by training the ANN, the GPR and the decision tree models using only the \(B_0\) and \(n_e\) input parameters, the GPR’s result on the extra test set improved drastically, as is shown in Table 8.

Fig. 20
figure 20

Input sensitivity for all models

Full size image
Table 8 Error metrics for the three best performing models when evaluated on the extra test set. Results using only \(n_e\) and \(B_0\)
Full size table

For the decision tree and the ANN, however, there was no significant change in the results, and while the GPR did improve the ANN still outperformed it on every metric. Thus the test did not affect the outcome of this work but underscored the robustness of the ANN model in capturing the complex relationships among the selected inputs. However, it might be worth exploring excluding the electron temperature and pressure as input parameters in any future work.

Training data sensitivity

Figure 21 shows the impact that using different partitioning of the data set into training and test sets has on the output of the trained models. The models with the least variation between folds are the GPR, the ensemble and the ANN. The decision tree has a slightly higher mean RMSE but shows a larger variation between minimum and maximum RMSE than the aforementioned models. Meanwhile, the SVM and the GAM show both high mean and high variation. This indicates that there is a need to ensure that the data set is as balanced as possible when training those models, and that the results for those models might be improved by using some method of dividing the training data that takes the characteristics of the input parameters into account, such as the stratified k-fold method which was not used in this work because of its higher complexity, and time constraints. In the end, the ANN, GPR and ensemble models still perform much better than the GAM and SVM, making it somewhat of a moot point.

Fig. 21
figure 21

Variation in RMSE arising from different training data partitioning for the different models. The squares represent the mean RMSE and the bars the maximum and minimum RMSE

Full size image

When comparing all the models it is clear that the ANN or the GPR would be best suited for actual use. Both achieve a low RMSE using cross-validation, their point-to-point error on the test set is less than 5% and if the \(T_e\) and \(P_0\) parameters are excluded for the GPR, both models achieve less than 5% also on the extra test set. However, since the ANN seems to have better generalization ability, based on the fact that it does not need to exclude any inputs to achieve a good result on the extra test set, it is deemed to be the prime candidate. There are still many things that could be done to improve the performance further. Chief among them would naturally be to use a larger data set, as the size of the available data set for this work was constrained by time and computer resource availability. A larger data set could potentially improve the results for all the models. Looking specifically at the ANN, MATLAB’s fitrnet function uses only one type of solver algorithm [32], but it is entirely possible that using some other function that would allow for different algorithms could result in even better predictions, as evidenced by the findings of [18, 44, 45].

Conclusion & next steps

In conclusion, following the study and the creation of a Design of Experiments (DoE) for the development of the training dataset, six different machine learning models were implemented in MATLAB to determine the impedance of an antenna in an helicon plasma thruster. Different hyperparameters of the models were optimized using nested cross-validation. Additionally, to assess the predictive capability of the models and their prospective application to the specific case study, two distinct test datasets were employed, and point-to-point errors were evaluated. An additional outcome of the study demonstrated that electron temperature (Te) and pressure (P0) are not only redundant but even detrimental to the performance, at least of the GPR model and possibly others as well. The most effective model is deemed to be the artificial neural network (ANN), with a cross-validated RMSE of \(6.5801 \times 10^{-5}\), a maximum point-to-point error of 3.98%, an R-squared value of 0.9993 on the test dataset, and only a 1.78% maximum point-to-point error with an R-squared of 0.9994 on the additional test dataset. Consequently, the results highlight the feasibility of utilizing these models in lieu of Adamant for minor design evaluations and similar tasks, thereby significantly reducing the time required for such assessments. Future endeavors will concentrate on generating a more extensive training dataset, encompassing various antenna shapes and dimensions to broaden the model’s applicability. Moreover, further considerations regarding the implementation of diverse solver algorithms for the artificial neural network will be explored to enhance the model’s performance. Nevertheless, the ANN model produced by this study already meets the performance requirements, which is regarded as a highly positive outcome.