Abstract
Plasma instabilities in the plume of hollow cathodes have been extensively researched in particular for high-current operation. The rise of plume mode ionization-like instability leads to a degradation of cathode’s performance along with the emergence of highly energetic ions that can produce sputtering of various cathode’s surfaces. Numerical simulations using 2D fluid or hybrid codes brought forward an interesting correlation between the evolution of ion acoustic turbulence (IAT) and emergence of plume mode oscillations. Such numerical findings were proven to be true by experimental measurements of wave dispersion and plume mode-IAT correlation in the plume of cathodes emitting currents >10 A. This study brings forward evidence of the correlation between plume mode oscillations and IAT in the plume of low-current cathodes operating with Kr at sub-ampere current levels. It is shown that at <1 A the plume mode instability is highly correlated with the IAT and the anomalous electron collision drives the electron transport in the cathode plume. The fluctuations in IAT wave energy lead to large temperature oscillations which then drive fluctuations in the density via ionization.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Thermionic hollow cathode operating at sub-ampere (<1 A) current levels remain instrumental for the operation of low-power (<250 W) Hall thrusters. Such devices create highly dense plasmas, \(n_{e}\sim \mathcal {O}(10^{19}-10^{22})\) m −3, that expand into collisionless plumes in the cathode-anode space with large gradients in the neutral and electron density. Two modes of operation were observed, i.e. spot and plume, with spot-to-plume mode transition taking place at larger discharge currents or insufficient propellant flow rates [1, 2]. Both modes and the mode transition were observed to occur also at currents below 1 A [3, 4]. The mode transition comes with the distinct change in plume morphology, i.e. bright spot-like structure next to the cathode in the case of spot mode and divergent diffuse plume attached to the anode in the case of plume mode. Moreover, the plume mode is characterized by the emergence of low-frequency oscillations in the range 10-250 kHz as seen in the discharge current spectra. The cathode discharge stability influences the efficiency of the propulsion system and operation in plume mode is detrimental to the lifetime of the cathode due to the emergence of high energy ions that sputter the surface of the cathode and accelerate erosion. Therefore, understanding the mechanism that triggers the spot-to-plume mode transition and the underlying phenomena that sustain and enhance plume mode operation remains an important issue for the electric propulsion community.
Over the years, several studies focused on the origin of plume mode [1, 2, 5, 6]. The widely accepted interpretation suggests an ionization related process with a predator-prey relation between the neutral and electron density [7]. The plume mode waves are believed to be driven unstable by large fluctuations in the electron temperature and plasma potential. Furthermore, the unusually large values for the electron temperature and plasma potential along the cathode-anode gap when the cathode operates in plume mode could be explained by a primarily anomalous elecron transport as suggested by numerical results [8–10]. The anomalous electron Ohmic heating was attributed to ion acoustic turbulence (IAT). The coexistence of low-frequency plume mode ionization instability and high-frequency IAT content in the plume of such devices was experimentally proved [11–19]. Nevertheless, the mentioned studies, except for the one of Tsikata et al. [19], were conducted with cathodes operating at high-current in excess of 10 A. In their recently published study, Tsikata et al. employed the coherent Thomson scattering method to evaluate the plasma wave content in the plume of a cathode operating with a Hall thruster at 1 A. The cathode was not in self-sustained mode and operated in the magnetic field environment of the thruster. Their study showed the presence of MHz IAT waves propagating towards the thruster and the cathode, along and across the magnetic field lines, as well as kHz fluctuations which may be attributed to drift-driven instabilities in the plane perpendicular to the magnetic field.
The present work tries to answer the following questions: i) does the plume mode oscillation have the same structure at sub-ampere current operation in comparison to high-current operation? ii) is IAT present in the plume of hollow cathodes operating at <1 A? iii) is there still a correlation between the IAT and plume mode oscillation? and finally iv) quantitatively, are the oscillations amplitudes in the same order of magnitude as compared to high-current operation? Here, Kr is used as propellant due to the increasingly interest for this gas driven by its much lower cost as compared to Xe, making it the ideal fuel for large constellations.
This communication brings novel insights on the ionization instability in a low-current hollow cathode’s plume where ion saturation probes are used to construct a better understanding of the main wave phenomena. Theory of the ionization instability and IAT section includes a brief presentation of the ionization instability and IAT theory. The experimental setup and methods used here are described in Experimental setup and methods section and the main results and discussion are included in Results and discussion section which comprises of: a macroscopic depiction of the correlation between the two aforementioned classes of instabilities in Macroscopic correlation of low- and high-frequency oscillations section, a study of the plume plasma wave dispersion in Plume plasma wave dispersion section, evidence of temporal and spatial correlation of low- and high-frequency waves in Correlation of ionization instability and IAT section, and the evolution of plasma parameters over the plume mode oscillation time-scale in Plasma parameters evolution over the ionization instability time-scale section. In the end, Conclusions section outlines the conclusions.
Theory of the ionization instability and IAT
The cathode discharge stability when operated in diode mode with an external anode or keeper electrode can be assessed by analyzing the temporal evolution of the discharge/anode current, Id, and potential, Vd, and their respective power spectral densities (PSDs) [20, 21]. Spot mode operation is characterized by quiescent, less energetic spectra, with no distinct frequency peaks or harmonics. Plume mode is expected to be characterized by noisy and energetic spectra, with higher amplitudes and distinct frequency peaks and harmonics in the low-frequency range 10-150 kHz for Xe [20, 21]. Moreover, the plume mode instability shows large scale and amplitude (up to 100% of the average) oscillations that can be observed in the discharge current, plasma density, and potential. The oscillations are quasi-coherent and propagate mainly in longitudinal direction. Due to their large amplitude, there is a common acceptance that such oscillations must be related to ionization, hence, their name of ionization-like instabilities [7]. Nevertheless, in the presence of an applied magnetic field that simulates the thruster environment, the amplitude of the ionization instability decreases with higher field strengths [22] and other instabilities arise in the plasma, such as the drift instability propagating azimuthally across the magnetic field lines [19, 22, 23] and the kink instability at large discharge current [24].
Due to the strongly drifting electrons in the plume of hollow cathodes, the growth of high-frequency turbulence such as IAT can be facilitated through inverse electron Landau damping [25]. Such waves propagate mainly in the direction of the electron current and are known to induce non-classical resistivity acting on electrons [12] and non-classical ion heating [14]. They have low amplitudes and present an incoherent and broadband continuous spectrum from 200 kHz up to 10 MHz, with cut-off at low frequency and decaying power with increasing frequency. Being a current-driven oscillation, IAT is strongly dependent on discharge current, mass flow rate, and facility pressure [26, 27]. Increased charge exchange events at higher flow rate or facility pressure tend to damp the IAT.
The plume of a hollow cathode is characterized by a low collisional environment with large electron drifts that challenge the assumption of Maxwellian plasmas. Therefore, numerical fluid approaches fail to predict the experimentally observed trends in plasma potential and electron temperature in this region. Non-classical behaviors, such as the IAT anomalous resistivity, are usually added to fluid codes to match the trend and magnitude of plasma parameters in the cathode plume to the experimentally observed ones. The most striking result of the implementation of IAT contribution to the cathode plume plasmadynamics is far from being the high fidelity prediction of the plasma temperature and potential, but the emergence of low-frequency oscillations in the cathode plume, similar to the experimentally found plume mode instability [9, 10, 28]. This suggests that the cathode plume plasma is primarily described by non-classical effects of acoustic turbulence, where there may be a correlation between the IAT and the plume mode instability.
Assuming the frequency of the waves in the IAT spectrum are much lower than the ion plasma frequency, ωpi, the following expressions are found for the real and imaginary parts of the dispersion relation of IAT [22]:
where k is the wavevector, ui and ue are the ion and electron drift velocities respectively, \(c_{s}=\sqrt {eT_{e}/M}\) is the ion sound speed with M the ion mass and e the elementary charge, vg is the group velocity, ve is the electron thermal velocity, and Me the electron Mach number. Equation 2 can be seen as the electron contribution to the IAT growth rate and shows that the source of energy for the IAT growth is the electron drift velocity.
An established approach in modeling the anomalous collision frequency induced by the IAT follows a proportionality law [29, 30]. Assuming that the IAT energy density scales with the thermal energy density of the plasma [31] and that the plasma potential fluctuations, \(\tilde {\phi }_{p}\), can be correlated to the fluctuations in electron density, \(\tilde {n}_{e}\), the following expression can be obtained [16]:
where m is the electron mass and ne is the electron density.
However, in simulation context, a priori knowledge of the IAT spectrum is needed to implement an anomalous collision frequency as described thus far. To alleviate this caveat, fluid-like approximations for νan are used to self-consistently solve plasma parameters in the plume region. Georgin and Jorns [17] give a comprehensive review of the main closure models used for IAT anomalous frequency in fluid codes and subject them to a comparison with experimental data. One of the established models was introduced by Mikellides et al. and gives the following expression for νan [8]:
where the proportionality constant αIAT is typically \(\mathcal {O} (10^{-2})\) and ωpe is the electron plasma frequency. The ion temperature, Ti, is usually assumed to be 0.1 〈Te〉.
It was shown for a high-current cathode operating at >15 A that the IAT amplitude is modulated on the time-scale of the plume mode instability with a correlation between the two classes of instability [22]. The phase difference observed between the IAT and density might imply a causal relation. Moreover, the IAT oscillations are correlated with the plasma parameters where the anomalous collision frequency leads in phase the electron temperature, which then leads the electron density, suggesting an ionization process. In the presence of IAT-driven resistivity, a predator-prey wave oscillates near the ionization frequency and grows when the temperature is above a critical threshold and fluctuating [22], suggesting a link between the IAT-driven non-classical electron transport and the low-frequency ionization instability.
The current hypothesis that the ionization-like waves are driven unstable by non-classical effects such as enhanced resistivity and electron Ohmic heating induced by the growth of IAT is explored in the following section for hollow cathodes operated with Kr at <1 A and in the absence of a magnetic field.
Experimental setup and methods
In this section, a brief description of the vacuum facility, cathode, and probe array used for this work is presented.
Cathode and vacuum facility
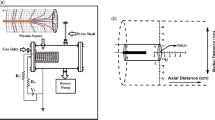
The PSAC-KE cathode is used in the following investigations [4]. The cathode has an 2 mm diameter open-end cylindrical LaB6 emitter with a 45 ∘ knife-edge, as shown in Fig. 1a. The total emission area is 0.66 cm2. The emitter is connected to the cathode’s stainless steel base via a tantalum gas tube and a graphite holder. The heater comprises of two ceramic parts encapsulating a tungsten-rhenium filament. Two thermal shields made of tantalum foil are placed around the heater and at the base of the cathode respectively to improve the device’s thermal design. The keeper electrode is made of stainless steel with a tantalum orifice plate welded at its extremity. The keeper orifice has a diameter of 2rko=1 mm. A 6 mm thick complex boron nitride ceramic part (BN-ZrO2) insulates the keeper from the cathode base.
Figure 1b shows the general I−V characteristics of the PSAC-KE cathode operated at various Kr mass flow rates in self-sustained mode (i.e. no heating and keeper powers) with the disk anode. The anode potential, Va, varies from 68 to 135 V, increasing with lower mass flow rates and decreasing with higher anode current, Ia. The overall power consumption of the cathode ranges between 40 and 86 W. Nevertheless, in order to ensure stable discharges, a small keeper current Ik∼0.05 A is applied throughout the following measurements.
The experimental setup is depicted in Fig. 2 and the main testing conditions are summarized in Table 1. The experiments are performed in the CEVAC chamber [3]. The chamber is a stainless steel cylindrical enclosure with a diameter of 0.4 m and a height of 0.3 m equipped with a dry rotary pump and a turbomolecular pump with a capacity of 600 l s−1 for light gases. Inside the CEVAC, the pressure can reach 5×10−6 mbar-N2. The chamber is accessed through a 0.4 m diameter hatch. For single point investigations at specific locations in the plume, the cathode is firstly tested with a 30 mm-diameter disk anode placed at Lca≈9 mm downstream of the keeper orifice, whereas a second 51 mm-diameter cylindrical anode at Lca≈22 mm is used for a complete plume swipe along the cathode-anode centerline.
Probe array and estimation of plasma parameters
The probe array consists of two cylindrical Langmuir probes made of 0.15 mm-diameter tungsten wires with a length of 1.5 mm and one emissive probe made of 0.15 mm-diameter tungsten wires with a length of 3.6 mm. All three probes are protruding from a single four-bore alumina tube that provides mechanical support and the electrical insulation between the probes. The distance between the two cylindrical Langmuir probes is Δx=1.5 mm. Furthermore, the distance between the emissive probe loop and the two Langmuir probes is also 1.5 mm, leading to a measuring volume of 1.5 mm ×1.5 mm ×1.5 mm. The probes are inserted orthogonally to the plasma flow as shown in Fig. 2, with one Langmuir probe closer to the cathode and the second one closer to the anode.
The two Langmuir probes can be i) both in ion saturation mode, when they are biased at -36 V by using a pack of batteries to collect ion saturation currents across 1 k Ω resistors or ii) one can be in ion saturation mode while the second one is left floating to measure the local floating potential, ϕf, using a high-voltage oscilloscope probe. A 1.8 A current is passed through the emissive probe bringing it to electron emission, while the floating potential of the hot probe, ϕem, is collected by a high-voltage oscilloscope probe and used to approximate the local plasma potential, ϕp.
Experimentally, electron densities from around 1×1017 to 3×1018 m −3 and electron temperatures <2 eV are measured in the cathode plume at Id<1 A. This leads to Debye lengths in the range 6-30 μm, which are at least one order of magnitude smaller than the probes’ diameter. By assuming quasi-neutrality, i.e. ni=ne, the thin sheath limited theory can be applied to compute the electron density, ne, in [m −3] [16]:
where Isat is the ion saturation current collected by one of the Langmuir probes, Ap is the probe collection area, and Te is the electron temperature in [eV]. Here, to compute ne, the ion current collected by the Langmuir probe closer to the cathode, Isat,1, is used.
The floating potential of the hot emissive probe, ϕem, can be used to estimate the plasma potential, ϕp, as follows [16]:
Due to sheath effects near the surface of a hot emissive probe, in Eq. 6 a correction parameter, α, is included and is typically between 1 and 1.5. This suggests that the plasma potential is 1 Te to 1.5 Te above the floating potential of the probe [32]. In this study, α=1.
Finally, for the electron temperature, the following expression stands [33]:
where ϕf is the floating potential of the Langmuir probe closer to the anode.
The oscillations in the anode/discharge current are also recorded using a Pearson wideband current monitor and this signal is used as a trigger reference when computing time-resolved analyses.
The probes’ and the discharge current signals are recorded by an oscilloscope for 100 ms at 12.5 MHz, allowing for a cut-off frequency of 6.25 MHz.
Uncertainty in plasma parameter measurements
The electrostatic probes used in this study are known to induce plasma perturbations [34] and affect to a certain extent the plasma parameter measurements. The changes in plasma conditions can be linked to changes in the anode voltage when the probe array is inserted in the plasma. For the following results, the anode voltage during probe array insertion in the plasma drifted by 2-3 V, which amounts to a maximum of ±5% change in the operating conditions. This uncertainty is ultimately found in the plasma parameter measurements.
A previous study showed that the amplitude of the IAT waves can be affected by the electrostatic probes [35]. The study suggested that if the cross-sectional area of the probe surpasses 10% of the size of the plasma, the amplitude of the drift waves is affected. In the present setup, assuming a conical expansion of the plasma plume from the keeper orifice to the anode, as shown in Fig. 2, the probe is more likely to influence the IAT spectrum amplitude for locations closer to the cathode where the plume cross-sectional area is smaller. For the current setup, the nearest locations to the cathode probed are z=2.5 mm, in the case of disk anode, and z=3.5 mm, in the case of cylindrical anode. At these locations, the plume cross-sectional area can be calculated as follows:
where θ is the plume expansion angle. Given the 0.15 mm-diameter of the ion saturation probes and the 1.5 mm-diameter of the entire probe array, their corresponding cross-sectional areas remain below 2.5% of the plume cross-sectional area at locations near the cathode. This suggests minimal influence of the probe array on the IAT spectrum amplitude.
In summary, apart from the uncertainty induced by the statistical variations in the measurements, the perturbations induced by the probes to the plasma are the main contributor to the systematic error. Conservatively, in the results herein the following total uncertainty levels are considered: 50% for ne, 30% for Te, and 10% for ϕp [21, 36–38].
Results and discussion
The following sections present several sets of results that are intended to support the hypothesis of the correlation between the ionization instability, i.e. plume mode instability and IAT at sub-ampere cathode operation. Time-averaged spectral properties of the parameters collected by the probes are shown and a cross-correlation technique is used to investigate wave propagation behavior at a single location in the plume as well as its spatial development in the cathode-anode space. Furthermore, the temporal evolutions of the IAT, ionization instability, as well as of plasma parameters are explored.
Macroscopic correlation of low- and high-frequency oscillations
The Fourier amplitude of the anode current oscillations, \(\left (\tilde {I}_{a}/I_{a,0}\right)^{2}_{\omega }\), where \(\tilde {I}_{a}\) is the fluctuation in the anode current around its mean value, Ia,0, offers a macroscopic picture of the main oscillatory phenomena in the cathode plume and their response to the change in anode current or flow rate. As shown in Fig. 3 for Kr, both quasi-coherent modes characteristic of the ionization/plume mode instability and turbulent content underlying the existence of IAT are present in the anode current spectra. Moreover, the general observed trends suggest an increase in both low-, <250 kHz, and high-frequency contents with higher Ia or lower \(\dot {m}\). This simple picture also suggests a correlation between the low-frequency modes and higher frequency oscillations: they both tend to increase or decrease in tandem for a given cathode operational point, with larger amplitudes at higher current or lower mass flow rate as expected.
Next, using the signal collected by the Langmuir probe closer to the cathode and operated in ion saturation mode, the contribution of low- and high-frequency fluctuations to the total spectrum of the saturation current is dissociated and their correlation is investigated. The total spectrum energy of the low-frequency plume mode fluctuations can be computed as follows:
and the IAT wave spectrum energy is given by:
with the cut-off frequency ωc=250 kHz for Kr. The sum over the low-frequency spectrum is performed from 10 kHz to ωc, while for the high-frequency part of the spectrum from ωc to 2 MHz. Experimentally, it is observed that for Kr, the plume mode fluctuations tend to have a frequency content extending beyond the 150 kHz usually assumed for Xe [25] and in this study the cut-off frequency is set at 250 kHz.
The results for various locations within the cathode-anode space and on the cathode centerline are shown in Fig. 4. The trends observed previously in the anode current spectra are seen for the ion saturation current as well, both at low- and high-frequency. In general, the waves amplitudes, Aiz and AIAT, tend to increase with higher Ia and lower \(\dot {m}\). Moreover, the waves amplitudes increase further downstream the cathode orifice. The increasing IAT wave amplitude with the distance from the cathode could be explained by higher electron temperatures in a less collisional environment which leads to higher IAT growth rates as dictated by Eq. 2. At z=2.5 mm, due to the proximity of the probe to the keeper orifice the plasma is perturbed to a greater extent, particularly at low anode current operation, as suggested by the reversed trends at 0.5 A and 0.7 A.
Now, to show that the two classes of waves are indeed correlated, the bivariate coefficient and p-value are computed for data sets corresponding to individual Ia values and across the mass flow rate range and z of 2.5, 4.5, and 6.5 mm. This technique was employed by Georgin [22] for high-current cathode operation. The data are shown in Fig. 5 as a response plot between Aiz and AIAT for three values of Ia. The dotted lines are linear fits to data at 0.5 A, 0.7 A, and 1 A. The bivariate coefficient for two data sets is given by \(\phantom {\dot {i}\!}\rho _{A_{iz},A_{IAT}}=\) cov\(\phantom {\dot {i}\!}(A_{iz},A_{IAT})/(\sigma _{A_{iz}}\sigma _{A_{IAT}})\), where cov is the covariance between the parameters of the two data sets and σ is the standard deviation for each data set. Values of \(\phantom {\dot {i}\!}\rho _{A_{iz},A_{IAT}}\) closer to 1 suggest a positive, linear correlation between Aiz and AIAT, while values closer to -1 suggest negative, linear correlations. If \(\phantom {\dot {i}\!}\rho _{A_{iz},A_{IAT}}\) is close to 0, the two quantities are most probably uncorrelated. To add more certainty to this statistical analysis, the p-value is also computed for each data set under the statistical test hypothesis that the two quantities are not correlated. Under such an assumption, a small p-value (∼0.05 [22]) suggests that it is highly improbable to compute such results if the quantities in the data sets are not correlated, whereas a high p-value signifies that the results can be produced even if the two quantities are uncorrelated.
Table 2 summarizes the results of the statistical analysis for the data sets shown in Fig. 5. At the lowest anode current, Ia=0.5 A, the weakest correlation is found, \(\phantom {\dot {i}\!}\rho _{A_{iz},A_{IAT}}=0.27\), with a large p-value, 0.52. At higher anode currents, Ia=0.7 A and Ia=1 A, relatively high bivariate coefficients are found, above 0.75, with small p-values, below 0.05. This confirms that the growth in the plume mode oscillations amplitude is correlated with the growth in the IAT waves spectrum amplitude. The low correlation observed at 0.5 A could be explained by weaker manifestation of the plume mode oscillations and IAT and confirms the current-driven nature of the plume mode-IAT phenomena. Moreover, a higher level of plasma perturbation induced by the probe is observed at low anode current which could result in spurious results. Nevertheless, the results confirm a high level of correlation between low- and high-frequency oscillations in the plume of a Kr-fed hollow cathode operated at sub-ampere levels and suggests a mainly current-driven mechanism for the emergence of predator-prey ionization instability.
Plume plasma wave dispersion
To enter deeper into the fabric of cathode plume instabilities, the ion saturation currents collected by the two probes are used to estimate the wave dispersion, S(ω,k), with ω the frequency and k the wavenumber of a plane wave. To achieve this, the cross-correlation technique introduced by Ili\(\acute {c}\) [39] and Beall et al. [40] is used, where the Fourier decompositions of the two ion saturation currents, \(\mathcal {F}\left (I_{sat,1}\right)\) and \(\mathcal {F}\left (I_{sat,2}\right)\), lead to the calculation of the dispersion power:
Furthermore, the wavenumber can be found from the cross-phase as follows:
with Δx=1.5 mm being the inter-probe separation. The physical dimensions of the probe array induce limitations to the current technique. For instance, the highest frequencies that this technique can measure cannot overpass the ion plasma frequency. Moreover, the smallest wavelength that this technique can unambiguously detect is equal to the inter-probe separation, which in this case is λmin=1.5 mm, leading to a maximum wavenumber of kmax=2090 m −1.
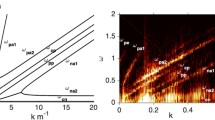
The aforementioned technique allows a simple visualization of the wave dispersion in the ω−k space in two-dimensional histograms. The entire domain is first discretized in 5 kHz frequency bins and 10 m −1 wavenumber bins, while to each bin the average Fourier amplitude computed using Eq. 11 is assigned. To reduce the noise, the analysis is averaged over 500 data sets. In the following analysis, the data are collected at z=2.5 mm at Ia=0.5 A and \(\dot {m}=0.12\) mg s −1-Kr. Under these operational conditions, the measured plasma density is ne=2.83×1018 m −3 and the electron temperature is Te=1.44 eV. The Debye length is then λD=5.3×10−6 m and the ion plasma frequency is ωpi≈31 MHz. Therefore, the measurements shown herein are restricted to frequencies well below ωpi.
As shown in Fig. 6a, a linear dispersion relation, ∝ω/k, is observed for frequencies below 1 MHz. Given that the relation characterizes fairly high frequencies, the observed features are attributed to IAT waves with their dispersion relation given by Eq. 1. The group velocity of those high-frequency waves is approximated to vIAT=3.7±0.5 km s −1, which is commensurate with previous measurements for high-current cathodes [15]. The dispersion relation for IAT states that the group velocity of such waves estimates the sum of ion sound speed and ion drift velocity, vIAT=cs+ui. Here, the ion sound speed is cs≈1.1 km s −1 which leads to an ion drift velocity of ui≈2.6 km/s, similar to measurements of ion velocity using laser-induced fluorescence spectroscopy in the plume of low- [41] and high-current cathodes [42, 43].
For this particular example, distinctive frequency peaks were observed in the discharge current and ion saturation current spectra at 35 kHz, 70 kHz, and 140 kHz, as shown in Fig. 7. Figure 6b shows a close-up saturated view on the wave dispersion histogram at frequencies below 300 kHz and makes more evident the higher amplitude around 35, 70, and 140 kHz. The results show that these lower frequency modes, most probably related to the plume mode ionization instability, have a phase velocity viz=5.5±0.5 km/s.
The results presented thus far depict a clearer picture of the coexistence of both low-frequency ionization-like waves and high-frequency IAT content in the plume of a Kr-fed cathode operated at sub-ampere current levels. Both classes of instabilities are propagating towards the anode with the ionization instability waves having a larger velocity. The IAT group velocity suggests an ion drift velocity commensurate with the one experimentally measured for higher current cathodes. From a quantitative perspective, albeit the anode current here being 1 to 1.5 orders of magnitude lower than in similar studies, the high operating mass flow rate leads to comparable electron densities and temperatures in the cathode plume and thus, similar ion and electron behaviors to the ones observed for higher current cathodes. The following sections further explore the relationship between the two classes of instabilities along with their influence on the temporal evolution of plasma parameters.
Correlation of ionization instability and IAT
The last two sections shown that both the ionization instability and IAT coexist in the plume of hollow cathodes operated at currents <1 A, while showing similar features to the high-current cathodes operation. Moreover, a first attempt at proving their correlation showed that the average amplitude of the coherent plume mode oscillations is indeed correlated with the average amplitude of the IAT spectrum as depicted in Figs. 4 and 5. Nevertheless, a temporal analysis of their correlation can bring more insights on the mechanism that links the two classes of oscillations. Here, single-point and spatial correlation along the cathode-anode gap are presented.
Herein, the technique described by Georgin et al. [15] is used, where the average amplitude of the IAT spectrum, AIAT defined in Eq. 10, is monitored on the time-scale scale of the low-frequency ionization instability. To capture the low-frequency coherent part of the spectrum, the time-averaged ion saturation current is computed, 〈Isat〉τ. The measurements take place over one temporal cycle of the plume mode oscillation, 1/f0, defined by the frequency peak, f0, observed in the anode current spectra. The ion current signal collected by one probe together with the anode current signal are used to perform peak-triggered averages, since both signals show the same characteristic oscillations. First, the anode current signal is filtered using a bandpass filter to keep only the low-frequency oscillations below ωc which is set to 250 kHz. Then, the ion saturation current signal is high-pass filtered for frequencies above ωc. Next, the ion saturation current signal for one period of the ionization instability is divided in smaller intervals each with the time width τ=1/(5f0). For each interval, the average ion saturation current, 〈Isat〉τ, is computed and a fast Fourier transform is applied to compute AIAT. To increase the signal-to-noise ratio of the results, around 5000 averages are performed.
In Fig. 8, the time variations of the IAT, \(\tilde {A}_{IAT}/A_{IAT,0}\), and ionization, \(\left \langle \tilde {I}_{sat}\right \rangle _{\tau }/I_{sat,0}\), contents in the ion saturation probe signal are shown, with AIAT,0 and Isat,0 being the time-averaged values. Three cycles over the ionization instability time-scale are shown. The analysis led to highly correlated fluctuations in IAT and ion saturation current over the time-scale of the ionization instability. The fluctuation in IAT tends to be higher than the one in the ion current and both quantities are up to two orders of magnitude lower than the ones reported for high-current cathodes using the same analysis technique [15]. This can be explained by the much lower discharge current, 0.5 A, as compared to 22.5 A, and ten times lower mass flow rates, ∼0.1 mg s−1 against 1 mg s−1. The growth in IAT leads the coherent component in phase and since \(\left \langle \tilde {I}_{sat}\right \rangle /I_{sat,0}\propto {\tilde {n}_{e}/n_{e,0}}\) it can be inferred that the fluctuations in IAT lead to fluctuations in plasma density. For this example, the IAT leads the density in phase by 118.6 ∘.
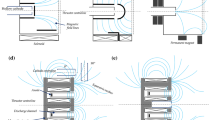
The results presented in Fig. 8 are representative of a single location in the cathode-anode space. It is important to prove that this behavior remains consistent throughout the plume or in other words the IAT and ion saturation current fluctuations are correlated spatially along the cathode’s discharge plume. Figure 9 depicts the evolutions of \(\tilde {A}_{IAT}/A_{IAT,0}\) and \(\left \langle \tilde {I}_{sat}\right \rangle _{\tau }/I_{sat,0}\) along the cathode discharge axis when the cathode operates at Ia=0.5 A and \(\dot {m}=0.088\) mg s −1-Kr together with the disk anode. The color maps show that the IAT and the coherent oscillations are correlated in time and space along the cathode discharge axis, with the IAT leading in phase the fluctuation in ion saturation current. Furthermore, the velocity of the IAT is measured to be around v=3.4±1.12 km s −1 and shows a displacement towards the anode as depicted in Fig. 9a, while the structures observed for the density fluctuation in Fig. 9b seem to move towards the anode with a similar velocity, v=3±1.12 km s −1. The results are commensurate with the IAT velocity revealed by the dispersion plot in Fig. 6a, where the cathode is operated at the same anode current but a slightly higher mass flow rate. On top of that, the results show that the level of fluctuations for both the IAT and coherent structure seem to increase in the far-field plume, towards the anode, if one ignores the high fluctuation in IAT measured at z=2.5 mm which may be a spurious result due to higher plume perturbation by the probe array. This features are different from the ones reported in literature [15] for cathode operation with a cylindrical anode, where both the IAT and the coherent fluctuations decrease in intensity towards the anode. It is possible that the disk anode used in this study induces higher neutral and plasma densities in the far-field plume which may sustain a higher turbulent content at the anode proximity. In the next section, results with a cylindrical anode are presented.
Oscillatory behavior of a IAT and b ion saturation current over the ionization instability time-scale for Kr at Ia=0.5 A and \(\dot {m}=0.088\) mg s −1 along the cathode-anode space on the discharge centerline. The cathode is operated with the disk anode placed at Lca≈9 mm from the cathode orifice. The maps show three concatenated waveforms
Plasma parameters evolution over the ionization instability time-scale
Plume mode ionization-like instability is related to ionization processes in the cathode plume. Thus far, it was shown that a periodic fluctuation in the IAT content modulated over the ionization instability time-scale induces fluctuations in the coherent content of the signal collected by an ion saturation probe. It was also shown that the two fluctuations are correlated in time and space, with the IAT leading in phase the coherent oscillations. Therefore, it is important to investigate how other plasma parameters such as density and temperature respond to the temporal variation in the IAT and coherent oscillations. The collisional environment is explored here in terms of total electron collision frequency and its spatial and temporal evolution over the ionization instability time-scale.
For this study, the cathode is operated with the cylindrical anode as shown in Fig. 2b. Based on the collected data, the plasma density, ne, and electron temperature, Te, are calculated using Eqs. 5 and 7. Next, the electron behavior in the cathode plume can be modeled by the generalized Ohm’s law for electron momentum:
where νe is the total electron collision frequency, E=−∇ϕp is the electric field with ϕp the local measured plasma potential computed using Eq. 6, and ue is the electron drift velocity. The total electron collision frequency can be written as the sum of the Coulomb collision frequency, νei, electron-neutral collision frequency, νen, which are both considered as classical collisions, while the ionization frequency, νiz, tends to have a much lower contribution to the electron dynamics [16].
The classical collision frequencies are found using the following equations for νei:
where the Coulomb logarithm is:
and for νen:
where σen is the electron-neutral collision cross section. The electron-neutral scattering cross section as a function of electron temperature for Kr, σen(Te) [m2], is given by (for Te>0.4 eV) [44]:
Next, the ionization frequency is estimated by νiz=nnUiz, where the ionization reaction rate for Kr, Uiz, given by (for Te<5 eV) [44]:
and the neutral density is taken as (assuming a conically expanding plume from the keeper orifice to the anode):
where Az is the plume cross-sectional area at the location z computed using Eq. 8 and \(v_{n}=\sqrt {8k_{B}T_{g}/(\pi {M})}\) is the neutral velocity with Tg≈Ti≈0.1〈Te〉.
Finally, the contribution of the IAT to the total electron collision frequency, known as the anomalous collision frequency, \(\nu _{an}^{IAT}\), can be computed using Eq. 3. However, in an experimental context the next approximation can be made \(\tilde {n}_{e}/\left \langle n_{e}\right \rangle \approx \tilde {I}_{sat}/I_{sat,0}\) [16], where Isat is the ion saturation current collected by the probe with its mean value Isat,0. With this, Eq. 3 becomes:
where 0.25≤ωr≤2 MHz.
Figure 10 shows the time-averaged results. When the cathode operates with Kr at Ia=0.8 A and \(\dot {m}=0.145\) mg s −1, a distinct frequency peak is observed in the anode current PSD at f0=85 kHz. The fluctuations in the IAT and coherent content as measured by the ion saturation probe show a high degree of correlation, with the IAT leading in phase the density as depicted by Fig. 10a-b. As opposed to the disk anode, for the cylindrical anode case the two parameters tend to decrease with the distance from the cathode’s keeper orifice. The density fluctuations in Fig. 10b, seem to emerge from two distinct locations in the plume: around z=6 mm and moving towards the cathode and the anode with a velocity around v=3.57±1.12 km s −1 and at z=14 mm and moving towards the anode at a slightly lower velocity of v=2.92±1.12 km −1. The time-averaged plasma parameters along the cathode discharge axis are shown in Fig. 10c. The electron density drops almost one order of magnitude from slightly over 1.2×1018 m −3 to 1.8×1017 m −3 and depicts two distinct changes in gradient at z=6 mm and z=14 mm, in correspondence to the higher fluctuations in saturation current shown in Fig. 10b. The electron temperature follows a slightly increasing trend from 1.3 eV at z=3.5 mm to 1.76 eV at the anode. The two parameters are used to approximate the gradient ∇(neeTe) as well as the other quantities used to compute the various collision frequencies. As presented in Fig. 10d, the sum of classical collision frequencies is orders of magnitude lower than the total electron collision frequency computed using Ohm’s law of electron momentum. Moreover, νen+νei shows a monotonically decreasing trend further away from the cathode, while νe seems to slightly increase before reaching a plateau. The ionization frequency, νiz, is the lowest contributor, decreasing with the distance from the cathode due to lower collisionality and steep drop in neutral density. This parameter shows a slight increase after z=14 mm, in correlation with the high fluctuations in ion saturation current at this location. The results prove that the main contributor to the electron dynamics in the plume of a sub-ampere hollow cathode operated with Kr remains the anomalous collision frequency, \(\nu _{an}^{IAT}\), which estimates both the magnitude and spatial evolution trend in the total electron collision frequency. Figure 10d depicts also the estimated anomalous collision frequency at the Sagdeev-Galeev limit, \(\nu _{an}^{SG}\), computed using Eq. 4 where the electron drift velocity at a given location z can be estimated with ue≈Ia/(eneAz) and the electron thermal velocity is given by \(v_{e}=\sqrt {8eT_{e}/(\pi {m})}\). This parameter follows closely the classical components, showing a decreasing trend most probably due to the rapid decay in plasma electron frequency, ωpe, and it is apparent that a coefficient αIAT=0.01 and the assumption of Te/Ti≈10 does not capture the magnitude of the total electron collision frequency especially for locations beyond z=6 mm towards the anode.
Oscillatory behavior of a IAT and b ion saturation current over the ionization instability time-scale. Time-averaged plasma parameters: c plasma density, ne, and electron temperature, Te, and d evolution of the various collision frequencies as functions of location on the cathode discharge axis. The cathode is operated with Kr at Ia=0.8 A and \(\dot {m}=0.145\) mg s −1 with the cylindrical anode placed at Lca≈22 mm from the cathode orifice
The next set of results presented in Fig. 11 offer information on the temporal variation of plasma parameters such as density, electron temperature, IAT collision frequency, and electron drift velocity with respect to the anode current phase, φ. A peak-triggered average technique similar to the one described in Correlation of ionization instability and IAT section is used here, where the anode current is bandpass-filtered below ωc=250 kHz, and its peaks are used to define averaging intervals. Each interval is further divided into 20 points. In this way, the fluctuation in each parameter is reconstructed over the ionization instability time-scale, which in this case is 11.76 μs (f0=85 kHz). Three cycles are concatenated to produce the plots in Fig. 11 for two locations in the cathode plume at z=9 mm in Fig. 11a and at z=22 mm in Fig. 11b. At both locations, the results show that the IAT wave energy, represented as \(\nu _{an}^{IAT}\), leads the electron temperature in phase by 36 ∘ at z=9 mm and by 126 ∘ at the anode location. The electron temperature leads then the density in phase by around 55 ∘ at both locations. This behavior was observed at high-current cathode operation [15] and suggests that the plume mode is indeed an ionization related process where the IAT growth in the plume heats the electrons which then induce increased ionization. The density and the electron drift velocity are out of phase, with the velocity leading the density by 270 ∘ at 9 mm and 200 ∘ at the anode location. This is expected since this lag allows current continuity, whereas the synchronized parts of the two waveforms are responsible for the fluctuations in the anode current. The anomalous collision frequency is correlated with the total electron collision frequency showing oscillations of similar amplitudes. The large oscillations in the total electron collision frequency, led by the anomalous component, induce large temperature oscillations, up to 20% nearer to the cathode and 10% at the anode location. Moreover, at the anode, the density and electron drift velocity show much larger fluctuations as compared to the location closer to the cathode. Nevertheless, here the out-of-phase relationship between the two parameters leads to lower fluctuations in Ia, of 10% as compared to 20% at z=9 mm. The complex structures of the waveforms at the location nearer to the cathode and the more cnoidal evolution of the parameters at the anode are proof of the nonlinear inter-dependance between the plasma oscillations, plasma parameters, and macroscopic discharge parameters such as the anode current.
Summary
The results presented in the previous sections bring more insights on the various oscillatory content found in the plume of a low-current hollow cathode operated with Kr. The correlation between the high-frequency IAT content and low-frequency coherent oscillations is visible macroscopically in both anode and ion saturation current spectra respectively and its sensitivity to the increase in anode current or flow rate suggests an underlying ionization-related process. The dispersion plot proved the existence of both classes of waves in the cathode plume, with the low-frequency component traveling towards the anode at velocities higher than the IAT. Interestingly, the ion drift velocities for sub-ampere operation are comparable to high-current cathode operation. As the anomalous collision frequency dictates the electron dynamics as shown by the results in Fig. 10d, the large oscillations in the IAT wave energy over the ionization instability time-scale plotted in Fig. 11 are most probably responsible for the anomalous electron heating given the lag in the electron temperature. The density lags behind the electron temperature, supporting the hypothesis of a predator-prey mechanism for the ionization instability at very low current too. Low anode currents induce low electron drift velocities, while relatively large plasma potentials lead to collision frequencies comparable to the ones obtained in the plume of high-current cathode, \(\mathcal {O}(10^{8}-10^{10})\) Hz.
Conclusions
This work provided an investigation on the main instabilities in the plume generated by low-current hollow cathodes operated with Kr. It was shown that the nature of the plume mode for low-current operation remains similar to the one of high-current cathodes: predator-prey relation between the temperature and density. The onset of such instability is still intrinsically related to the growth of IAT in the cathode plume. Both IAT and coherent fluctuations reside in the plume of a cathode operating in plume mode as observed in the dispersion plot and are highly correlated especially at larger currents, suggesting a current-driven process. The dispersion plot suggested that the ionization instability traveled towards the anode at velocities in the order of viz∼5 km s −1. The same dispersion plot showed that the IAT waves traveled also towards the anode at velocities in the order of vIAT∼4 km s −1, implying that the ion drift velocities were ui∼2.5 km s −1, commensurate to ion velocities measured in the plume of higher-current cathodes. The growth and damping of the IAT is still modulated in time over the time-scale of the coherent low-frequency oscillation. The correlation remains valid throughout the plume where the IAT leads the fluctuation in temperature in phase, which then leads the density, suggesting a possible ionization-related process. Nevertheless, quantitatively at sub-ampere levels, the coherent wave energy and the IAT energy are 1.5-2 orders of magnitude lower than in the case of high-current cathode operation and proportional to the discharge current ratio between the two classes of cathodes. The results presented here are meant to expand the understanding of plasma instabilities and the link between the plume mode oscillations and IAT from high-current to low-current cathode operation. They can help the effort for higher fidelity cathode numerical modeling at sub-ampere operation.
References
Csiky GA (1969) Measurements of some properties of a discharge from a hollow cathode. NASA Technical Note D-4966.
Kaufman HR (1974) Technology of electron-bombardment ion thrusters. Adv Electron Electron Phys 36:265–373.
Potrivitu G-C, Xu L, Huang S, Rohaizat MWAB, Xu S (2019) Discharge mode transition in a krypton-fed 1 A-class LaB 6 cathode for low-power Hall thrusters for small satellites. J Appl Phys 127:064501.
Potrivitu G-C, Xu S (2021) A low-current LaB 6 open-end knife-edge emitter hollow cathode for low-power Hall thrusters. Plasma Sources Sci Technol 30:085012.
Rehn L, Kaufman HR (1978) Correlation of inert gas hollow cathode performance In: Proceedings of the 13th International Electric Propulsion Conference (IEPC paper 1978-707).. Electric Rocket Propulsion Society, San Diego.
Mandell MJ, Katz I (1994) Theory of hollow cathode operation in spot and plume modes In: Proceedings of the 30th Joint Propulsion Conference (AIAA paper 94-3134).. AIAA/ARC, Indianapolis.
Goebel DM, Katz I (2008) Fundamentals of Electric Propulsion: Ion and Hall Thrusters (JPL Space Science and Technology Series). Wiley, New Jersey.
Mikellides IG, Katz I, Goebel DM, Jameson KK (2007) Evidence of nonclassical plasma transport in hollow cathodes for electric propulsion. J Appl Phys 101:063301.
Sary G, Garrigues L, Boeuf J-P (2017) Hollow cathode modeling: I. A coupled plasma thermal two-dimensional model. Plasma Sources Sci Technol 26:055007.
Sary G, Garrigues L, Boeuf J-P (2017) Hollow cathode modeling: II. Physical analysis and parametric study. Plasma Sources Sci. Technol. 26:055008.
Jorns BA, Mikellides IG, Goebel DM (2014) Ion acoustic turbulence in a 100-A LaB 6 hollow cathode. Phys Rev E 90:063106.
Jorns BA, Dodson C, Goebel DM, Wirz R (2017) Propagation of ion acoustic wave energy in the plume of a high-current LaB 6 hollow cathode. Phys Rev E 96:023208.
Dodson C, Jorns BA, Wirz RE (2017) Ion acoustic wave propagation and heating in a high-current hollow cathode plume In: Proceedings of the 35th International Electric Propulsion Conference (IEPC paper 2017-398).. Electric Rocket Propulsion Society, Atlanta.
Dodson C, Perez-Grande D, Jorns BA, Goebel DA, Wirz R (2018) Ion heating measurements on the centerline of a high-current hollow cathode plume. J Propuls Power 34:1225–1234.
Georgin MP, Jorns BA, Gallimore AD (2019) Correlation of ion acoustic turbulence with self-organization in a low-temperature plasma. Phys Plasmas 26:082308.
Georgin MP, Jorns BA, Gallimore AD (2020) Transient non-classical transport in the hollow cathode plume I: measurements of time-varying electron collision frequency. Plasma Sources Sci Technol 29:105010.
Georgin MP, Jorns BA (2019) Transient non-classical transport in the hollow cathode plume II: evaluation of models for the anomalous collision frequency. Plasma Sources Sci Technol 29:105011.
Georgin MP, McDonald MS (2021) Experimental evaluation of the 2D nonclassical ohmic transport model for electrons in the hollow cathode plume. J Appl Phys 130:203301.
Tsikata S, Hara K, Mazouffre S (2021) Characterization of hollow cathode plasma turbulence using coherent Thomson scattering. J Appl Phys 130:243304.
Joussot R, Grimaud L, Mazouffre S (2017) Examination of a 5 A-class cathode with a LaB 6 flat disk emitter in the 2 A-20 A current range. Vacuum 146:52–62.
Potrivitu G-C, Joussot R, Mazouffre S (2018) Anode position influence on discharge modes of a LaB 6 cathode in diode configuration. Vacuum 151:122–132.
Georgin MP (2020) Ionization instability of the hollow cathode plume. Ph.D. thesis, University of Michigan, MI, USA.
Jorns BA, Hofer RR (2014) Plasma oscillations in a 6-kW magnetically shielded Hall thruster. Phys Plasmas 21:053512.
Becatti G, Goebel DM, Zuin M (2021) Observation of rotating magnetohydrodynamic modes in the plume of a high-current hollow cathode. J Appl Phys 129:033304.
Lev DR, Mikellides IG, Pedrini D, Goebel DM, Jorns BA, McDonald MS (2019) Recent progress in research and development of hollow cathodes for electric propulsion. Rev Mod Plasma Phys 3:6.
Jorns BA, Mikellides IG, Goebel DA, Ortega AL (2015) Mitigation of energetic ions and keeper erosion in a high-current hollow cathode In: Proceedings of the 34th International Electric Propulsion Conference (IEPC paper 2015-134).. Electric Rocket Propulsion Society, Hyogo-Kobe.
Mikellides IG, Ortega AL, Goebel DM, Becatti G (2020) Dynamics of a hollow cathode discharge in the frequency range of 1-500 kHz. Plasma Sources Sci Technol 29:035003.
Mikellides IG, Guerrero P, Ortega AL, Polk JE (2018) Spot-to-plume mode transition investigations in the HERMeS hollow cathode discharge using coupled 2-D axisymmetric plasma-thermal simulations In: Proceedings of the 2018 Joint Propulsion Conference (AIAA paper 2018-4722).. AIAA/ARC, Cincinnati.
Sagdeev RZ, Galeev A (1969) Nonlinear Plasma Theory. W. A. Benjamin, New York.
Davidson RC, Krall NA (1977) Anomalous transport in high-temperature plasmas with applications to solenoidal fusion systems. Nucl Fusion 17:1313–1372.
Jorns BA, Dodson C, Anderson J, Goebel DM, Hofer RR, Sekerak M, Ortega AL, Mikellides IG (2016) Mechanisms for pole piece erosion in a 6-kW magnetically-shielded Hall thruster In: Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference (AIAA paper 2016-4839), Salt Lake City.
Sheehan JP, Hershkowitz N (2011) Emissive probes. Plasma Sources Sci Technol 20:063001.
Chen FF (2003) Langmuir probe diagnostics In: IEEE-ICOPS Meeting (Mini-Course on Plasma Diagnostics).. IEEE Xplore, Jeju.
Grimaud L, Pétin A, Vaudolon J, Mazouffre S (2016) Perturbations induced by electrostatic probe in the discharge of Hall thrusters. Rev Sci Instrum 87:043506.
Ito T, Cappelli MA (2009) Electrostatic probe disruption of drift waves in magnetized microdischarges. Appl Phys Lett 94:211501.
Herman DA, Gallimore AD (2005) Discharge cathode electron energy distribution functions in a 40-cm next-type ion engine In: Proceedings of the 2005 Joint Propulsion Conference (AIAA paper 2005-4252).. AIAA/ARC, Tucson.
Reid BM, Gallimore AD (2008) Langmuir probe measurements in the discharge channel of a 6-kW Hall thruster In: Proceedings of the 2008 Joint Propulsion Conference (AIAA paper 2008-4920), Hartford.
Popov TK, Dimitrova M, Ivanova P, Hasan E, Horáček J, Dejarac R, Stöckel J, Weinzettl V, Kovačič J (2014) Langmuir probe evaluation of the plasma potential in tokamak edge plasma for non-maxwellian EEDF. Contrib Plasma Phys 54(3):267–272.
B.Ilić D (1977) Spectra of ion acoustic plasma instability. Phys Fluids 20:1717–1727.
Beall JM, Kim YC, Powers EJ (1982) Estimation of wavenumber and frequency spectra using fixed probe pairs. J Appl Phys 53:3933–3940.
Morishita T, Tsukizaki R, Nishiyama K, Kuninaka H (2022) Plasma parameter measured inside and outside a microwave-discharge-based plasma cathode using laser-indusced fluorescence spectroscopy. J Appl Phys 131:013301.
Williams GJ, Smith TB, Domonkos MT, Gallimore AD, Drake RP (2000) Laser-induced fluorescence characterization of ions emitted from hollow cathodes. IEEE T Plasma Sci 28:1664–1675.
Potrivitu G-C, Mazouffre S, Grimaud L, Joussot R (2019) Anode geometry influence on LaB 6 cathode discharge characteristics. Phys Plasmas 26:113506.
Potrivitu G-C, Xu S (2022) Phenomenological plasma model for open-end emitter with orificed keeper hollow cathodes. Acta Astronaut 191:293–316.
Acknowledgments
The authors would like to thank Dr M. P. Georgin and Dr S. Tsikata for their valuable support and suggestions.
Funding
This work was supported by OSTIn-SRP/EDB through the National Research Foundation and in part by the Ministry of Education Singapore through MOE AcRF (RP6/16XS). G.-C.P. acknowledges the support from the National Institute of Education Singapore through the NIE PhD Scholarship.
Declarations
Author information
Authors and Affiliations
Contributions
G.-C.P. managed the conceptualization of the article and the preparation of the manuscript, the definition of methodologies, and data collection, processing, and analysis. S.X. supervised the entire process. Both authors reviewed the manuscript.
Corresponding author
Ethics declarations
Consent for publication
The authors give their consent for publication.
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Potrivitu, GC., Xu, S. Evidence of the ionization instability and ion acoustic turbulence correlation in sub-ampere hollow cathodes. J Electr Propuls 1, 6 (2022). https://doi.org/10.1007/s44205-022-00005-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s44205-022-00005-y