1 Introduction

Probability distributions have become a fundamental component of any scientific inquiry. These probability models describe a variety of real-world random events [1]. Various lifetime probability distributions are available in the literature to analyze data sets from different fields, including engineering, medicine, actuarial sciences, and economic and social sciences. The Topp-Leone distribution [2] is among the most often used continuous distributions. It is commonly utilized to analyze unit interval datasets alternative to renowned bounded distributions Beta and Kumaraswamy distributions. Since its development, several scholars have researched the distribution, see for example [3,4,5,6,7,8].

Neutrosophy statistics is an extension of classical statistics. The Neutrosophy term was originally presented by [9] and it is the generality of Fuzzy logic. Neutrosophy logic guides the investigation of false or true propositions that are uncertain, neutral, inconsistent, or somewhere in between [10, 11]. Every subject in mathematics has a neutrosophic element or the feature of indeterminacy. Smarandache was the first to use the neutrosophic approach in calculus, precalculus, and statistics to address imprecision in study variables [12]. Neutrosophic statistics has thus led to the emergence of study fields that address the impact of indeterminacy in statistical models. The neutrosophic principle of statistical modeling has recently been described in the literature for the first time [13]. Ref. [14] discusses neutrosophic measurements of probability and descriptive statistics. Neutrosophic Cramer Mises goodness-of-fit test was proposed by [15]. Recently some neutrosophic probability distributions have been introduced and studied. Some examples are; neutrosophic Rayleigh distribution [16], neutrosophic beta [17], neutrosophic Exponential distribution [18], neutrosophic Kumaraswamy distribution [19], and neutrosophic Weibull distribution [20].

In this work, a unique extension of the Topp-Leone distribution is developed for modeling uncertain data regarding research variables. We call this distribution that is obtained the "Neutrosophic Topp-Leone distribution-(NTLD)." To the best of my knowledge, the Topp-Leone model's neutrosophic calculus has not been covered in any published work. It is therefore one of the things that spurs us on to keep working.

2 Neutrosophic Topp-Leone Distribution and Its Properties

Definition 1: Let the \({Y}_{N}=d+uI;uI\in \left[{Y}_{L},{Y}_{U}\right]\) where \({Y}_{L}\) and \({Y}_{U}\) are lower and upper values of the neutrosophic Topp-Leone random variable having determined part \(d\) and indeterminate part \(uI;uI\in \left[{I}_{L},{I}_{U}\right]\). Note that the neutrosophic Topp-Leone distribution (NTLD) reduces to classical Tope-Leone distribution when \({Y}_{L}={Y}_{U}\). The neutrosophic probability density (npdf) of NTLD has a Neutrosophic shape parameter \({\alpha }_{N}\in \left[{\alpha }_{L},{\alpha }_{U}\right]\) is defined by.

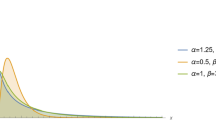
$${f}_{N}\left(y;{\alpha }_{N}\right)=2{\alpha }_{N}{y}^{{\alpha }_{N}-1}\left(1-y\right){\left(2-y\right)}^{{\alpha }_{N}-1}, 0\le y\le 1, {\alpha }_{N}>0.$$
(1)

Some plots of npdf are offered in Fig. 1.

Fig. 1
figure 1

Neutrosophic probability density for NTL distribution

Full size image

Figure 1 shows that NTLD is a flexible distribution with only one parameter. It has a variety of forms, including exponentially decreasing and unimodal.

The corresponding neutrosophic cumulative distribution function (ncdf) is

$${F}_{N}\left(y;{\alpha }_{N}\right)={y}^{{\alpha }_{N}}{\left(2-y\right)}^{{\alpha }_{N}}.$$
(2)

Some plots of ncdf for selected value parameters are presented in Fig. 2.

Fig. 2
figure 2

Neutrosophic cumulative distribution function plots for NTL distribution

Full size image

3 Statistical Properties

In this section, some statistical properties of Neutrosophic Topp-Leone distribution are derived including moments, quantile function, and reliability characteristics.

3.1 Moments

Theorem 1. The ordinary moments of NTL distribution are

$${\mu }_{rN}^{\prime}={2}^{r+2{\alpha }_{N}}{\alpha }_{N}\left[\mathrm{\rm B}\left(\frac{1}{2},r+{\alpha }_{N},{\alpha }_{N}\right)-2\mathrm{\rm B}\left(\frac{1}{2},r+{\alpha }_{N}+1,{\alpha }_{N}\right)\right]$$
(3)

Proof: By definition, the rth moments of NTL distribution can be obtained as

$$\begin{array}{c}{\mu }_{rN}^{\prime}={\int }_{0}^{1}{y}^{r}{f}_{N}\left(y\right)dy\\ =2{\alpha }_{N}{\int }_{0}^{1}{y}^{{r+\alpha }_{N}-1}\left(1-y\right){\left(2-y\right)}^{{\alpha }_{N}-1}dy\\ {\mu }_{rN}^{\prime}=2{\alpha }_{N}{\int }_{0}^{1}{y}^{r+{\alpha }_{N}-1}{\left(2-y\right)}^{{\alpha }_{N}-1}dy-2{\alpha }_{N}{\int }_{0}^{1}{y}^{{r+\alpha }_{N}}{\left(2-y\right)}^{{\alpha }_{N}-1}dy\end{array}$$

Making substitution \(\left(\frac{y}{2}\right)=x\), we get

$${\mu }_{rN}^{\prime}={2}^{2{\alpha }_{N}+r-1}{\alpha }_{N}{\int }_{0}^\frac{1}{2}{x}^{r+{\alpha }_{N}-1}{\left(1-x\right)}^{{\alpha }_{N}-1}dx-{2}^{2{\alpha }_{N}+r}{\alpha }_{N}{\int }_{0}^\frac{1}{2}{x}^{r+{\alpha }_{N}}{\left(1-x\right)}^{{\alpha }_{N}-1}dx$$

After some computations, we get the moment’s final form

$${\mu }_{rN}^{\prime}={2}^{r+2{\alpha }_{N}-1}{\alpha }_{N}\left[\mathrm{\rm B}\left(\frac{1}{2},r+{\alpha }_{N},{\alpha }_{N}\right)-2\mathrm{\rm B}\left(\frac{1}{2},r+1+{\alpha }_{N},{\alpha }_{N}\right)\right]$$

where \(B\left(a,y\right)={\int }_{0}^{y}{x}^{a-1}{\left(1-x\right)}^{a-1}dx\) is an incomplete beta function.

3.2 Quantile function and associated measures

The neutrosophic quantile function of NTL distribution is

$${M}_{pN}=1\pm \sqrt{\left(1-{p}^{\frac{1}{{\alpha }_{N}}}\right)}$$
(4)

First, second, and third neutrosophic quantiles

$$\begin{array}{c}{M}_{1N}=\left[\begin{array}{cc}\left\{1\pm \sqrt{1-{\left(\frac{1}{4}\right)}^{\frac{1}{{\alpha }_{L}}}}\right\} ,& \left\{1\pm \sqrt{1-{\left(\frac{1}{4}\right)}^{\frac{1}{{\alpha }_{U}}}}\right\}\end{array}\right].\\ {M}_{2N}=\left[\begin{array}{cc}\left\{1\pm \sqrt{1-{\left(\frac{1}{2}\right)}^{\frac{1}{{\alpha }_{L}}}}\right\} ,& \left\{1\pm \sqrt{1-{\left(\frac{1}{2}\right)}^{\frac{1}{{\alpha }_{U}}}}\right\}\end{array}\right].\\ {M}_{3N}=\left[\begin{array}{cc}\left\{1\pm \sqrt{1-{\left(\frac{3}{4}\right)}^{\frac{1}{{\alpha }_{L}}}}\right\} ,& \left\{1\pm \sqrt{1-{\left(\frac{3}{4}\right)}^{\frac{1}{{\alpha }_{U}}}}\right\}\end{array}\right].\end{array}$$

3.3 Some Reliability Properties

The survival and hazard functions of NTLD are, respectively

$${S}_{N}\left(y\right)=1-{y}^{{\alpha }_{N}}{\left(2-y\right)}^{{\alpha }_{N}}.$$
(5)

And

$${h}_{N}\left(y\right)=\frac{2{\alpha }_{N}{y}^{{\alpha }_{N}-1}\left(1-y\right){\left(2-y\right)}^{{\alpha }_{N}-1}}{1-{y}^{{\alpha }_{N}}{\left(2-y\right)}^{{\alpha }_{N}}}.$$
(6)

The reversed hazard function is

$${r}_{N}\left(y\right)=\frac{2{\alpha }_{N}{y}^{{\alpha }_{N}-1}\left(1-y\right){\left(2-y\right)}^{{\alpha }_{N}-1}}{{y}^{{\alpha }_{N}}{\left(2-y\right)}^{{\alpha }_{N}}}=\frac{2{\alpha }_{N}\left(1-y\right)}{y\left(2-y\right)}$$
(7)

The cumulative hazard is

$$\begin{array}{c}{H}_{N}\left(y\right)=-\mathit{log}\left({S}_{N}\left(y\right)\right),\\ =-\mathit{log}\left[1-{y}^{{\alpha }_{N}}{\left(2-y\right)}^{{\alpha }_{N}}\right].\end{array}$$
(8)

The Mills Ratio

$$\begin{array}{c}M=\frac{{S}_{N}\left(y\right)}{{f}_{N}\left(y\right)},\\ =\frac{1-{y}^{{\alpha }_{N}}{\left(2-y\right)}^{{\alpha }_{N}}}{2{\alpha }_{N}{y}^{{\alpha }_{N}-1}\left(1-y\right){\left(2-y\right)}^{{\alpha }_{N}-1}}.\end{array}$$
(9)

4 Parameter Estimation

The neutrosophic maximum likelihood estimation technique is utilized to calculate the parameter of the NTL distribution. Let \({y}_{N1}, {y}_{N2},{y}_{N3},\dots ,{y}_{Nn}\) be a random sample from NTL distribution, then the ML estimator of \({\alpha }_{N}\), is obtained by maximizing the log-likelihood function given below

$$l\left({\alpha }_{N}\right)=n{\text{log}}2{\alpha }_{N}+{(\alpha }_{N}-1)\sum_{i=1}^{n}{\text{log}}{y}_{Ni}+\sum_{i=1}^{n}{\text{log}}\left(1-{y}_{Ni}\right)+{(\alpha }_{N}-1)\sum_{i=1}^{n}{\text{log}}\left(2-{y}_{Ni}\right)$$

Partially differentiate with respect to \({\alpha }_{N}\)

$$\frac{\partial l\left({\alpha }_{N}\right)}{\partial {\alpha }_{N}}=\frac{n}{{\alpha }_{N}}+\sum_{i=1}^{n}{\text{log}}{y}_{Ni}+\sum_{i=1}^{n}{\text{log}}\left(2-{y}_{Ni}\right).$$
(10)

Equating Eq. (10) and some algebraic simplification

$${\widehat{\alpha }}_{N}= -n{\left\{\sum_{i=1}^{n}{\text{log}}{y}_{Ni}+\sum_{i=1}^{n}{\text{log}}\left(2-{y}_{Ni}\right)\right\}}^{-1}.$$
(11)

The analytical results of the NTL distribution for moments and associated measures have been validated using Monte Carlo simulation also in this section. To assess the validity of theory-based results, the NTL distribution may be easily simulated in R software. For this purpose, consider the set of neutrosophic parameters \(\alpha =\left[\mathrm{0.1,0.5}\right], \left[\mathrm{1.5,2.0}\right]\) and \(\left[\mathrm{2.0,3.0}\right]\) in the NTL distribution and 10,000 samples are generated from the Uniform distribution \(U\left[\mathrm{0,1}\right]\). The assessment of the parameter estimates is carried out using the following measures (AB) (absolute bias), MRE (mean relative error), and MSE (mean square error). Table 1 displays the values of AB, MRE, and MSE.

Table 1 Simulation results of NTL distribution
Full size table

5 Application

In this section, we utilized a real dataset related to the monthly low and high temperatures of Lahore, Pakistan for the last five years (2016–2020). The data observations are collected from World Weather Online. The data observations are given in Table 2.

Table 2 Minimum and maximum temperature for Lahore data
Full size table

Data having values in unit intervals can be of several types, such as proportions and percentages. Based on positive evidence \({x}_{N1}, {x}_{N2},\dots ,{x}_{Nn}\), phenomena can be described by a random variable U, with the theoretical support approximated by \(m={\text{sup}}\left({x}_{N1}, {x}_{N2},\dots ,{x}_{Nn}\right)\) or a higher value. Next, we may consider the random variable \(X=U/m\), present in (0, 1). By multiplying by m, we can a posteriori rebuild the distribution of U in every scenario. To get data between 0 and 1, we now perform a normalization technique by dividing these numbers by 120.

The method of neutrosophic maximum likelihood estimation is used to estimate the model parameter. The maximum likelihood estimates and model selection measures, neutrosophic Akaike Information Criteria (NAIC), neutrosophic Bayesian Information Criteria (NBIC), and neutrosophic Kolmogorov–Smirnov (NKS) test are presented in Table 3. All the numerical computations were performed via R software. The fitted PDF is shown in Fig. 3.

Table 3 Estimates and Goodness-of-fit measures
Full size table
Fig. 3
figure 3

Fitted pdf (left panel) and cdf (right panel) over empirical data

Full size image

6 Conclusion

This study proposes the NTL distribution, a novel representation of the Topp-Leone statistical model. The structural features of the suggested model in the neutrosophic environment are addressed in detail. For neutrosophic variance, neutrosophic mean, and other related values, analytical formulas are obtained. The neutrosophic reliability properties are derived. We estimate the parameters by applying the neutrosophic maximum likelihood method. A simulation study was conducted to verify the accuracy of the calculated neutrosophic parameter. The simulated results show that indeterminate sample data with a large size estimate the unknown parameter efficiently. An application example of the NTLD is considered, primarily for processing indeterminacies in lifetime data.