1 Introduction

Since the World Health Organization declared the Corona virus (COVID-19) pandemic outbreak a public health crisis and of international concern in 2020, approximately 704,241,673 cases and 7,006,177 deaths have been recorded worldwide as of 19 March 2024 [1]. Between 2020 and 2021, when the pandemic was at its peak, several efforts were made to develop and identify COVID-19 prevention methods. Despite global efforts to develop vaccines and cures, the primary strategy used to contain the spread was social distancing, isolation, personal and community hygiene, and mass testing. Prior to the advent of effective vaccines, a number of alternative methods were proposed to combat the pandemic. Most of these strategies were only able to reduce the spread of the disease through the use of personal hygiene measures such as face and nose masks, social distancing, patient quarantine, social isolation, mass testing and lockdown. Irrespective of the measures taken to limit the transmission of the pandemic, social distancing and isolation, as well as general lockdown measures, were all reported to be successful in reducing the spread of the virus [2,3,4].

The development and comparisons of life models (distributions) curves are always of key importance in modelling and predicting the outbreak of the disease. This is because if the data on the outbreak can be well modelled, the evolution of the disease can be traced, and then the spread can be prevented by studying the dynamics of the disease in the model. A good model in this resguard can be very helpful in decision-making by survival analysts and health authorities. The exponentiated-G class was first proposed by [5], who raised the cumulative distribution function (cdf) to a positive power parameter. Thus, becoming one of many methods proposed by statisticians where parameters are added to distributions. A number of techniques for creating new families of distributions have been investigated by [6]. New families of probability distributions that expand well-known distributions are frequently created to offer flexibility when modeling data in practice. In other words, distributions have been built by expanding popular families of continuous distributions. By enhancing the original model with at least one shape or scale parameter, these generalized distributions offer greater versatility. Additionally, statisticians create families of distributions so that distributions can be skewed to the right, left, unimodal, J or reversed J shape to provide consistently better fits, which equip other distributions with the same underlying model. In fact, a large number of families of continuous probability distributions have been developed with one or two parameters, such as the Marshall-Olkin-G [7], beta generalized-G [8], exponentiated generalized-G [9], exponentiated Gompertz using informative prior [10], Burr X-G distribution [11], generalized odd generalized exponential family [12], Lomax-G [13], mixture of Lomax distribution [14], Type I general exponential class of distributions by [15], transmuted Weibull-G family of distributions [16], and generalized odd generalized exponential family [17].

To obtain a better fit of the models, this article proposes the inclusion of new parameters and provides evidence that the use of two parameters provides a better fit compared to the original distributions. The Topp-Leone Exponentiated-G and Pareto distribution functions are used to generate a new distribution, the Topp-Leone Exponentiated Pareto (TLetP), and the mathematical properties are defined. The proposed Topp-Leone Exponentiated Pareto (TLEtP) distribution has an exceptional probability density function (pdf) due to its ability to model both positively and negatively skewed data with significant tails and symmetric data sets, making it a more flexible model. It can also be used to model increasing, decreasing and bathtub hazard and survival rates. These characteristics make the proposed model a novel distribution for modelling life data, including survival, reliability engineering and biomedical life testing. The proposed model is then applied to two real COVID-19 datasets to illustrate the properties and flexibility of the distribution. The first example is daily confirmed COVID-19 cases recorded in Pakistan and the results are compared with those obtained by [18] and the second example uses data from the COVID-19 pandemic in South Africa. The rest of the paper is organised as follows: Section 2 explains the procedure for generating the Topp Leonne Exponentiated Pareto (TLetP) distribution and develops its mathematical properties. Section 3 shows how the proposed distribution is applied to a real data set and section 4 contains the conclusion.

2 Methods

A four-parameter distribution, the Topp Leone Exponentiated-G Family of Distributions, is proposed by [19] with the probability density function (pdf) and cumulative distribution function (cdf) of the family are given as:

$$\begin{aligned} F(x; \alpha , \theta ) = \{ 1 - [ 1 - (G(x, \psi ))^{\alpha }]^{2} \}^{\theta } \end{aligned}$$
(1)

and

$$\begin{aligned} f(x; \alpha , \theta ) = 2 \alpha \theta g(x; \psi ) G(x; \psi )^{\alpha - 1} \{1 - [ G(x; \psi ) ]^{\alpha } \} \{ 1 - [ 1 - (G(x, \psi ))^{\alpha }]^{2} \}^{\theta } \end{aligned}$$
(2)

where \(\psi\) is the vector of parameters of the baseline distribution. The cdf and pdf of the baseline distribution correspond to the Pareto distribution.

$$\begin{aligned} G(x, \beta , \lambda ) = 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \end{aligned}$$
(3)

and

$$\begin{aligned} g(x; \beta , \lambda ) = \lambda \beta ^{\lambda } x^{-(\lambda + 1)} \end{aligned}$$
(4)

Some properties like moments, moment generating function, quantile, hazard function, survival function, odd function, distribution of order statistics, and estimate of the parameters using the method of maximum likelihood are described.

2.1 The Proposed Topp-Leone Exponentiated Pareto (TLEtP) distribution

In this sub-section, a new Topp-Leone exponentiated Pareto distribution is derived. To obtain the the new distribution, (3) is inserted into (1) to give the cumulative distribution function (cdf) of TLEtP as:

$$\begin{aligned} F (x; \alpha , \theta , \lambda , \beta ) = \Biggl \{ 1 - \biggl [ 1 - \biggl ( 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \biggl )^{\alpha } \biggl ]^{2} \Biggl \}^{\theta } \end{aligned}$$
(5)

On differentiation Eq. (3) with respect x, we have the pdf given as:

$$\begin{aligned} \frac{\partial F (x; \alpha , \theta )}{\partial x} = 2 \alpha \theta \lambda \beta ^{\lambda } x^{-(\lambda + 1)} \Bigl [ 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \Bigl ]^{\alpha - 1} \Biggl \{1 - \Bigl [ 1- \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \Bigl ]^{\alpha } \Biggl \} \Biggl \{ 1 - \biggl [ 1 - \biggl ( 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \biggl )^{\alpha } \biggl ]^{2} \Biggl \}^{\theta - 1} \end{aligned}$$

Therefore,

$$\begin{aligned}{} & {} f(x; \alpha , \theta , \lambda , \beta ) = 2 \alpha \theta \lambda \beta ^{\lambda } x^{-(\lambda + 1)} \Bigl [ 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \Bigl ]^{\alpha - 1}\nonumber \\{} & {} \quad \Biggl \{1 - \Bigl [ 1- \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \Bigl ]^{\alpha } \Biggl \} \Biggl \{ 1 - \biggl [ 1 - \biggl ( 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \biggl )^{\alpha } \biggl ]^{2} \Biggl \}^{\theta - 1} \end{aligned}$$
(6)

Where \(x \ge 0\), \(\beta > 0\) is the scale parameters and \(\alpha , \theta , \lambda > 0\) are the shape parameters.

We can represent the distribution using binomial expansion on (6) as:

$$\begin{aligned} (1 - Z)^{b - 1} = \sum _{i=0}^{x} (-1)^{i} \left( {\begin{array}{c}b-1\\ i\end{array}}\right) Z^{i} \end{aligned}$$

Then,

$$\begin{aligned}{} & {} \Biggl \{ 1 - \biggl [ 1 - \biggl ( 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \biggl )^{\alpha } \biggl ]^{2} \Biggl \}^{\theta - 1} = \sum _{i=0}^{x} (-1)^{i} \left( {\begin{array}{c}\theta - 1\\ i\end{array}}\right) \biggl [ 1 - \biggl ( 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \biggl )^{\alpha } \biggl ]^{2i} \\{} & {} \quad \biggr [ 1 - \biggl ( 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \biggl )^{\alpha } \biggr ]^{2i + 1} = \sum _{j=0}^{x} (-1)^{j} \left( {\begin{array}{c}2i + 1\\ j\end{array}}\right) \Bigl [ 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \Bigl ]^{\alpha j} \\{} & {} \quad \biggl [ 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \biggl ]^{\alpha (1 + j) - 1} = \sum _{k=0}^{x} (-1)^{k} \left( {\begin{array}{c}\alpha (1+j) - 1\\ k\end{array}}\right) \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda k} \end{aligned}$$

Therefore,

$$\begin{aligned}{} & {} f(x; \alpha , \theta , \lambda , \beta ) = 2 \alpha \theta \lambda \beta ^{(\lambda + \lambda k)} \nonumber \\{} & {} \quad \sum _{i,j,k=0}^{\infty } (-1)^{i+j+k} \left( {\begin{array}{c}\theta -1\\ i\end{array}}\right) \left( {\begin{array}{c}21+1\\ j\end{array}}\right) \left( {\begin{array}{c}\alpha (1+j)-1\\ k\end{array}}\right) x^{-(\lambda + 1 + \lambda k)} \nonumber \\{} & {} f(x; \alpha , \theta , \lambda , \beta ) = \sum _{i,j,k = 0}^{x} \gamma _{i}x^{-(\lambda + 1 + \lambda k)} \end{aligned}$$
(7)

and

$$\begin{aligned} \gamma _{i} = 2 \alpha \theta \lambda \beta ^{(\lambda + \lambda k)} \sum _{i,j,k=0}^{\infty } (-1)^{i+j+k} \left( {\begin{array}{c}\theta -1\\ i\end{array}}\right) \left( {\begin{array}{c}21+1\\ j\end{array}}\right) \left( {\begin{array}{c}\alpha (1+j)-1\\ k\end{array}}\right) \end{aligned}$$

We can also represent the distribution using binomial expansion on (5) as:

$$\begin{aligned}{} & {} \Biggl \{ 1 - \biggl [ 1 - \biggl ( 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \biggl )^{\alpha } \biggl ]^{2} \Biggl \}^{\theta h} = \displaystyle \sum _{m=0}^{\theta h} (-1)^{m} \left( {\begin{array}{c}\theta h\\ m\end{array}}\right) \biggl [ 1 - \biggl ( 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \biggl )^{\alpha } \biggl ]^{2m} \nonumber \\{} & {} \quad \biggl [ 1 - \biggl ( 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \biggl )^{\alpha } \biggl ]^{2m} = \displaystyle \sum _{q=0}^{\infty } (-1)^{q} \left( {\begin{array}{c}2m\\ q\end{array}}\right) \Biggl [ 1 - \Bigl ( \frac{\beta }{x}\Bigl )^{\lambda } \Biggl ]^{\alpha q} \nonumber \\{} & {} \quad \Bigl [ 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \Bigl ]^{\alpha q} = \displaystyle \sum _{w=0}^{\infty } (-1)^{w} \left( {\begin{array}{c}\alpha q\\ w\end{array}}\right) \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda w} \nonumber \\{} & {} \quad F(x; \alpha , \theta , \lambda , \beta ) = \beta ^{\lambda w} \displaystyle \sum _{q, w=0}^{\infty } (-1)^{m + q + w} \left( {\begin{array}{c}\theta h\\ m\end{array}}\right) \left( {\begin{array}{c}2m\\ q\end{array}}\right) \left( {\begin{array}{c}\alpha q\\ w\end{array}}\right) x^{-\lambda }\nonumber \\{} & {} F(x; \alpha , \theta , \lambda , \beta ) = \displaystyle \sum _{q, w=0}^{\infty } \psi _{j} x^{- \lambda } \end{aligned}$$
(8)

and

$$\begin{aligned} \psi _{j} = \displaystyle \sum _{m=0}^{\theta h} \left( {\begin{array}{c}\theta h\\ m\end{array}}\right) \left( {\begin{array}{c}2m\\ q\end{array}}\right) \left( {\begin{array}{c}\alpha q\\ w\end{array}}\right) \end{aligned}$$

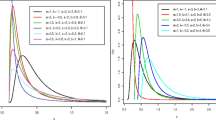
Figure 1a and b show the cdf and pdf of the proposed distribution with different simulated parameters.

Fig. 1
figure 1

The cdf and pdf of TLEtP distribution with different parameter values

Full size image

Using Eqs. (7) and (8), various properties of the TLEtP distribution are presented in section (2.2).

2.2 Mathematical properties

2.2.1 Moments

$$\begin{aligned}&\mu _{r} = E(X^{r}) = \int \limits _{\beta }^{\infty } x^{r} f(x) dx \nonumber \\&\quad \mu _{r} = \int \limits _{\beta }^{\infty } x^{r} \displaystyle \sum _{i,j,k = 0}^{\infty } \gamma _{i} x^{-(\lambda + 1 + \lambda k)} dx \nonumber \\&\quad = \displaystyle \sum _{i,j,k = 0}^{\infty } \gamma _{i} \int \limits _{\beta }^{\infty } x^{-(\lambda +1 + \lambda k) + r} dx \nonumber \\&\quad = \displaystyle \sum _{i,j,k = 0}^{\infty } \gamma _{i} \Biggl [ \frac{x^{-(\lambda + 1 + \lambda k)+r+1}}{(\lambda + 1 + \lambda k) + r+ 1} \Biggl ]_{\beta }^{\infty } \nonumber \\&\quad \mu _{r} = \displaystyle \sum _{i,j,k = 0}^{\infty } \gamma _{i} \Biggl [ \frac{\beta ^{-(\lambda + 1 + \lambda k)+r+1}}{(\lambda + 1 + \lambda k) + r+ 1} \Biggl ] \end{aligned}$$
(9)

2.3 Moment Generating Function (mgf)

The moment-generating function of X can be obtained using the following equation.

$$\begin{aligned} M_{x} (t) = \displaystyle \sum _{i,j,k=0}^{\infty } \displaystyle \sum _{m=0}^{\infty } \frac{t^{m}}{m!} \gamma _{i} \Biggl [ \frac{\beta ^{-(\lambda +1 + \lambda k)+m+1}}{(\lambda +1 + \lambda k)+m+1} \Biggl ] \end{aligned}$$

2.4 Quantile Function

The TLEtP distribution is simply approximated by inverting (5). If \(\mu\) has a uniform \(U \sim (0,1)\) distribution, then the equation’s solution is:

$$\begin{aligned} \Biggl \{ 1 - \Biggl [ 1 - \Biggl ( 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \Biggl )^{\alpha } \Biggl ]^{2} \Biggl \}^{\theta }&= \mu \nonumber \\ \mu ^{\frac{1}{\theta }}&= 1 - \Biggl [ 1 - \Biggl ( 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \Biggl )^{\alpha } \Biggl ]^{2} \nonumber \\ 1 - \mu ^{\frac{1}{\theta }}&= \Biggl [ 1 - \Biggl ( 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \Biggl )^{\alpha } \Biggl ]^{2} \nonumber \\ \Biggl (1 - \mu ^{\frac{1}{\theta }}\Biggl )^{\frac{1}{2}}&= 1 - \Biggl [ 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \Biggl ]^{\alpha } \nonumber \\ 1 - \Biggl (1 - \mu ^{\frac{1}{\theta }}\Biggl )^{\frac{1}{2}}&= \Biggl [ 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \Biggl ]^{\alpha } \nonumber \\ \Biggl [1 - \Biggl (1 - \mu ^{\frac{1}{\theta }}\Biggl )^{\frac{1}{2}} \Biggl ]^{\frac{1}{\alpha }}&= 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \nonumber \\ 1 - \Biggl [1 - \Biggl (1 - \mu ^{\frac{1}{\theta }}\Biggl )^{\frac{1}{2}} \Biggl ]^{\frac{1}{\alpha }}&= \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \nonumber \\ \Biggl \{ 1 - \Biggl [1 - \Biggl (1 - \mu ^{\frac{1}{\theta }}\Biggl )^{\frac{1}{2}} \Biggl ]^{\frac{1}{\alpha }} \Biggl \}^{\frac{1}{\lambda }}&= \frac{\beta }{x} \nonumber \\ x&= \frac{\beta }{\Biggl \{ 1 - \Biggl [1 - \Biggl (1 - \mu ^{\frac{1}{\theta }}\Biggl )^{\frac{1}{2}} \Biggl ]^{\frac{1}{\alpha }} \Biggl \}^{\frac{1}{\lambda }}} \end{aligned}$$
(10)

Equation (10) is the quantile function of the Topp-Leone exponentiated Pareto distribution and Eq. (11) is the median for the Topp-Leone exponential Pareto distribution.

$$\begin{aligned} x = \frac{\beta }{\Biggl \{ 1 - \Biggl [1 - \Biggl (1 - 0.5^{\frac{1}{\theta }}\Biggl )^{\frac{1}{2}} \Biggl ]^{\frac{1}{\alpha }} \Biggl \}^{\frac{1}{\lambda }}} \end{aligned}$$
(11)

2.5 Hazard Function

The hazard function is defined by:

$$\begin{aligned} H(x; \alpha , \theta , \beta , \lambda ) = \frac{f(\alpha , \theta , \beta , \lambda )}{1 - F(\alpha , \theta , \beta , \lambda )} \end{aligned}$$

Considering the definition above, the hazard function of TLEtP distribution is given as:

$$\begin{aligned} H(x; \alpha , \theta , \beta , \lambda ) = \frac{2 \alpha \theta \lambda \beta ^{\lambda } x^{-(\lambda + 1)} \Biggl [ 1 - \Bigl ( \frac{\beta }{x} \Bigl )^{\lambda } \Biggl ]^{\alpha - 1} \Biggl \{ 1 - \Bigg [ 1 - \Bigg ( \frac{\beta }{x}\Bigg )^{\lambda } \Bigg ]^{\alpha } \Biggl \} \Biggl \{ 1 - \Bigg [ 1 - \Bigg ( 1 - \Big ( \frac{\beta }{x} \Big )^{\lambda } \Bigg )^{\alpha } \Bigg ]^{2} \Biggl \}^{\theta -1}}{1-\Biggl \{ 1 - \Bigg [ 1 - \Bigg ( 1 - \Big ( \frac{\beta }{x} \Big )^{\lambda } \Bigg )^{\alpha } \Bigg ]^{2} \Biggl \}^{\theta }} \end{aligned}$$
(12)

Figure 2 shows the hazard function with different parameter values.

Fig. 2
figure 2

Hazard function plot of TLEtP distribution with different parameter values

Full size image

2.6 Survival Function

The survival function, which is the probability of an item not failing prior to some time, can be defined as:

$$\begin{aligned} S(x; \alpha , \theta , \beta , \lambda ) = 1 - F(x; \alpha , \theta , \beta , \lambda ) \end{aligned}$$

So, the survival function for the TLEtP distribution is given as:

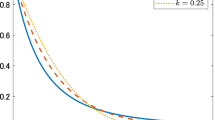
$$\begin{aligned} S(x;\alpha , \theta , \beta , \lambda ) = 1-\Biggl \{ 1 - \Bigg [ 1 - \Bigg ( 1 - \Big ( \frac{\beta }{x} \Big )^{\lambda } \Bigg )^{\alpha } \Bigg ]^{2} \Biggl \}^{\theta } \end{aligned}$$

And, the survival function plot can be seen in Fig. 3.

Fig. 3
figure 3

Survival function plot of TLEtP distribution with different parameter values

Full size image

2.7 Odds Function

The odds function is obtained using the relation:

$$\begin{aligned} O(x;\alpha , \theta , \beta , \lambda ) = \frac{F(x; \alpha , \theta , \beta , \lambda )}{1 - F(x; \alpha , \theta , \beta , \lambda )} \end{aligned}$$

The odds function of TLEtP distribution is given as:

$$\begin{aligned} O(x;\alpha , \theta , \beta , \lambda ) = \frac{\Biggl \{ 1 - \Bigg [ 1 - \Bigg ( 1 - \Big ( \frac{\beta }{x} \Big )^{\lambda } \Bigg )^{\alpha } \Bigg ]^{2} \Biggl \}^{\theta }}{1-\Biggl \{ 1 - \Bigg [ 1 - \Bigg ( 1 - \Big ( \frac{\beta }{x} \Big )^{\lambda } \Bigg )^{\alpha } \Bigg ]^{2} \Biggl \}^{\theta }} \end{aligned}$$

2.8 Distribution of Order Statistics

Let \(X_{1}, X_{2}, \dots , X_{n}\) be n independent random variable from the TLEtP distribution and let \(X_{(1)}, X_{(2)}, \cdots , X_{(n)}\) be their corresponding order statistics. Let \(F_{r:n}(x)\) and \(f_{r:n}(x)\), \(r=1,2,3, \dots , n\) denote the cdf and pdf of the \(r^{th}\) order statistics \(X_{r:n}\) respectively. The pdf of the \(r^{th}\) order statistics of \(X_{r:n}\) is given as:

$$\begin{aligned} f_{r:n} (x; \alpha , \theta , \lambda , \beta ) = \frac{1}{B(r, n-r+1)} \displaystyle \sum _{v=0}^{n-r} \displaystyle \sum _{i,j,k=0}^{\infty } \displaystyle \sum _{q,w=0}^{\infty } \gamma _{i} \psi _{j} x^{-(\lambda +1 + \lambda k + \lambda d)} \end{aligned}$$
(13)

Where

$$\begin{aligned} \gamma _{i} = 2 \alpha \theta \lambda \beta ^{(\lambda + \lambda k)} \left( {\begin{array}{c}\theta - 1\\ i\end{array}}\right) \left( {\begin{array}{c}2i + 1\\ j\end{array}}\right) \left( {\begin{array}{c}\alpha (1+j)-1\\ k\end{array}}\right) \end{aligned}$$

and

$$\begin{aligned} \psi _{j} = \displaystyle \sum _{m=0}^{\theta (v+r-1)} \left( {\begin{array}{c}\theta (v+r-1)\\ m\end{array}}\right) \left( {\begin{array}{c}2m\\ q\end{array}}\right) \left( {\begin{array}{c}\alpha q\\ w\end{array}}\right) \end{aligned}$$

The maximum order statistics is obtained by setting \(r = n\) in Eq. (13) as:

$$\begin{aligned} f_{n:n} = (x; \alpha , \theta , \lambda , \beta ) = n \sum _{i,j,k=o}^{\infty } \sum _{q,w=o}^{\infty } \gamma _{i} \psi _{j} x^{-(\lambda + 1 + \lambda k + \lambda d)} \end{aligned}$$
(14)

And, the minimum order statistics is obtained by setting \(r=1\) in Eq. (13).

$$\begin{aligned} f_{1:n} = (x; \alpha , \theta , \lambda , \beta ) = n \displaystyle \sum _{v=0}^{n-1} \sum _{i,j,k=o}^{\infty } \sum _{q,w=o}^{\infty } \gamma _{i} \psi _{j} x^{-(\lambda + 1 + \lambda k + \lambda d)} \end{aligned}$$
(15)

Now

$$\begin{aligned} \psi _{j} = \displaystyle \sum _{m=0}^{\theta v} \left( {\begin{array}{c}\theta v)\\ m\end{array}}\right) \left( {\begin{array}{c}2m\\ q\end{array}}\right) \left( {\begin{array}{c}\alpha q\\ w\end{array}}\right) \end{aligned}$$

2.9 Parameter Estimation

Since maximum likelihood estimators give the maximum information about the population parameters, this section presents the maximum likelihood estimates (MLEs) of the parameters that are inherent within the distribution function.

Let \(X_{1}, X_{2}, \dots , X_{n}\) be random variables of the TLEtP distribution of size n. The log-likelihood function of the TLEtP distribution is obtained as:

$$\begin{aligned} l(\phi )&= n log(2) + n log(\alpha ) + n log( \theta ) + nlog(\lambda ) + n \lambda log(\beta ) - (\lambda + 1) \displaystyle \sum _{i=1}^{n} log(x) + \nonumber \\&\quad \displaystyle \sum _{i=1}^{n} log \Biggl \{1 - \biggl [1 - \Bigl (\frac{\beta }{x_{i}} \Bigl )^{\lambda } \biggl ]^{\alpha } \Biggl \} + (\theta - 1) \displaystyle \sum _{i=1}^{n} log \Biggl \{1 - \biggr [1 - \biggl ( 1- \Bigl (\frac{\beta }{x_{i}} \Bigl )^{\lambda } \biggl )^{\alpha } \biggr ]^{2} \Biggl \} \end{aligned}$$
(16)

Deriving the Eq. (16), we have:

$$\begin{aligned}{} & {} \frac{\partial L(\phi )}{\partial \alpha } = \frac{n}{\alpha } - \displaystyle \sum _{i=1}^{n} \frac{\Biggl [1 - \biggl (\frac{\beta }{x_{i}}\biggl )^{\lambda } \Biggl ]^{\alpha } log \Biggl [1 - \biggl (\frac{\beta }{x_{i}}\biggl )^{\lambda } \Biggl ]}{\Biggl \{ 1 - \biggl [1 - \bigl (\frac{\beta }{x_{i}}\bigl )^{\lambda } \biggl ]^{\alpha } \Biggl \}} - \nonumber \\{} & {} (\theta - 1) \displaystyle \sum _{i=1}^{n} \frac{\Biggl \{ 1 - \biggl [1 - \bigl (\frac{\beta }{x_{i}}\bigl )^{\lambda } \biggl ]^{\alpha } \Biggl \} \biggl [1 - \bigl (\frac{\beta }{x_{i}}\bigl )^{\lambda } \biggl ]^{\alpha } log \biggl [1 - \bigl (\frac{\beta }{x_{i}}\bigl )^{\lambda } \biggl ]}{\Biggl \{1 - \biggr [1 - \biggl ( 1- \Bigl (\frac{\beta }{x_{i}} \Bigl )^{\lambda } \biggl )^{\alpha } \biggr ]^{2} \Biggl \}} \end{aligned}$$
(17)
$$\begin{aligned}{} & {} \frac{\partial L(\phi )}{\partial \theta } = \frac{n}{\theta } - \displaystyle \sum _{i=1}^{n} log \Biggl \{ 1 - \biggl [ 1 - \Bigl (1 - \Bigl (\frac{\beta }{x_{i}} \Bigl )^{\lambda } \Bigl )^{\alpha } \biggl ]^{2} \Biggl \} \end{aligned}$$
(18)
$$\begin{aligned}{} & {} \frac{\partial L(\phi )}{\partial \lambda } = \frac{n}{\lambda } + n log( \beta ) - \displaystyle \sum _{i=1}^{n} log(x_{i})\nonumber \\{} & {} \quad - \displaystyle \sum _{i=1}^{n} \frac{ \alpha \Biggl [ 1 - \biggl (\frac{\beta }{x_{i}}\biggl )^{\lambda } \Biggl ]^{\alpha - 1} \Biggl [ 1 - \biggl (\frac{\beta }{x_{i}}\biggl )^{\lambda } \Biggl ] log \Biggl [ 1 - \biggl (\frac{\beta }{x_{i}}\biggl )^{\lambda } \Biggl ]}{ \Biggl \{ 1 - \biggl [ 1 - \Bigl ( \frac{\beta }{x_{i}} \Bigl )^{\lambda } \biggl ]^{\alpha } \Biggl \} } \nonumber \\{} & {} \quad - (\theta - 1) \displaystyle \sum _{i=1}^{n} \alpha \frac{ \Biggl \{1 - \biggl [ 1 - \Bigl (\frac{\beta }{x_{i}} \Bigl )^{\lambda } \biggl ]^{\alpha } \Biggl \} \biggl [ 1 - \Bigl (\frac{\beta }{x_{i}} \Bigl )^{\lambda } \biggl ]^{\alpha -1} \Biggl [ 1 - \biggl (\frac{\beta }{x_{i}} \biggl )^{\lambda } \Biggl ] log \Biggl [ 1 - \biggl (\frac{\beta }{x_{i}} \biggl )^{\lambda } \Biggl ]}{\Biggl \{1 - \biggr [1 - \biggl ( 1- \Bigl (\frac{\beta }{x_{i}} \Bigl )^{\lambda } \biggl )^{\alpha } \biggr ]^{2} \Biggl \}} \end{aligned}$$
(19)
$$\begin{aligned}{} & {} \frac{\partial L(\phi )}{\partial \beta } = \frac{n \lambda }{\beta } + \displaystyle \sum _{i=1}^{n} \frac{\alpha \lambda \Biggl [ 1 - \biggl ( \frac{\beta }{x_{i}} \biggl )^{\lambda } \Biggl ]^{\alpha - 1} \biggl ( \frac{\beta }{x_{i}} \biggl )^{\lambda - 1} \frac{1}{x_{i}}}{\Biggl \{ 1 - \biggl [1 - \bigl (\frac{\beta }{x_{i}}\bigl )^{\lambda } \biggl ]^{\alpha } \Biggl \}} - \nonumber \\{} & {} \quad (\theta - 1)\displaystyle \sum _{i=1}^{n} \frac{\alpha \lambda \Biggl \{ 1 - \biggl [ 1 - \Bigl (\frac{\beta }{x_{i}} \Bigl )^{\lambda } \biggl ]^{\alpha } \Biggl \} \biggl [ 1 - \Bigl (\frac{\beta }{x_{i}} \Bigl )^{\lambda } \biggl ]^{\alpha - 1} \Bigl (\frac{\beta }{x_{i}} \Bigl )^{\lambda - 1} \frac{1}{x_{i}} }{\Biggl \{1 - \biggr [1 - \biggl ( 1- \Bigl (\frac{\beta }{x_{i}} \Bigl )^{\lambda } \biggl )^{\alpha } \biggr ]^{2} \Biggl \}} \end{aligned}$$
(20)

Equations (17), (18), and (20) do not have a simple form and are intractable. As a result, we have to resort to using interactive procedures to estimate the parameters.

3 Application Using Real-Life Data Sets

The application of the TLEtP distribution is demonstrated using two data sets. The performance of the distribution with regards to providing reasonable parametric fit to the data sets was compared to Topp-Leone Pareto type I(TLPI) and Pareto (P) distributions using the Akaike information criterion (AIC) and Bayesian information criterion (BIC), respectively. The model with a minimum value of AIC and BIC is chosen as the best model to fit the data set.

3.1 Example 1

The first data set as listed in the Table 1 represents the daily confirmed COVID-19 cases recorded in Pakistan from March 24 to April 28, 2020, previously used by Al-Marzouki, et al. (2020).

Table 1 Positive cases recorded in Pakistan from March 24 to April 24, 2020 (Al-Marzouki et al. 2020)
Full size table

The TLEtP distribution provides a better fit for the data set compared to the TLPI model. From Table 2, the TLEtP distribution has the highest log-likelihood and the smallest AIC and BIC values compared to the other fitted models. This fit can also be seen in Figs. 4 and 5.

Table 2 The MLEs and information criteria of the models based on confirmed COVID-19 cases recorded in Pakistan from March 24 to April 28, 2020
Full size table
Fig. 4
figure 4

Fitted pdfs for the TLEtP, TLPI, and Pareto distribution based on confirmed COVID-19 cases recorded in Pakistan from March 24 to April 28, 2020

Full size image
Fig. 5
figure 5

Fitted cdf, pdf, Q-Q and P-P plots of confirmed COVID-19 cases recorded in Pakistan from March 24 to April 28, 2020 for the TLEtP distribution

Full size image

3.1.1 Example 2

The second data set as listed in the Table 3 represents the active COVID-19 cases per day in South Africa from March 11 to August 31, 2020.

Table 3 Active COVID-19 cases per day in South Africa from March 11 to August 31, 2021
Full size table

The analysis of the data from South Africa showed similar results that of Pakistan, i.e., the model with the TLEtP distribution showed a better fit compared to other models. From Table 4, the TLEtP distribution has the highest log-likelihood and the smallest AIC and BIC. This fit can be seen in Figs. 6 and 7.

Table 4 The MLEs and information criteria of the models based on confirmed COVID-19 cases per day in South Africa from March 11 to August 31, 2020
Full size table
Fig. 6
figure 6

Fitted pdfs for the TLEtP, TLPI, and Pareto distribution based on confirmed COVID-19 cases per day in South Africa from March 11 to August 31, 2020

Full size image
Fig. 7
figure 7

Fitted cdf, pdf, Q-Q, and P-P plots of confirmed COVID-19 cases per day in South Africa from March 11 to August 31, 2020 for the TLEtP distribution

Full size image

4 Conclusion

Recently, statisticians have increasingly created extended distributions from families of existing distributions. We have successfully created the novel Topp-Leone Exponentiated Pareto (TLEtP) family of distributions. Furthermore, some mathematical characteristics of the newly developed distribution are derived. By analyzing the COVID-19 outbreak in Pakistan and South Africa and comparing the data with two members of the Topp-Leone Pareto type I (TLPI) and Pareto (P) families of distributions, we show the adaptability and applicability of the new distributions. Compared to (TLPI) and (P) distributions, the proposed distribution (TLEtP) provides a better fit for the data set. As a result, we anticipate that the proposed distributions (TLEtP) will be useful in a variety of domains, particularly in reliability studies when the hazard rate is increasing.