Properties and Applications of A New Attractive Distribution

Abstract

We provide a new, flexible model called the Odd Kappa-Exponential (OK-E) distribution. The shape of its hazard rate function (hrf) might be constant, declining, growing, inverted-J, bathtub, or inverted-bathtub. The probability density function (pdf) and the cumulative distribution function (cdf) have both been expressed as linear expansions. Bonferroni and Lorenz curves, ordinary and incomplete moments, the quantile function, the mean residual life, the mean waiting time, and the entropy are all defined. The maximum likelihood method is used to estimate the values of the model’s unknown parameters. To verify the precision of the estimate, we ran a simulation study. The attractiveness and adaptability of the Odd Kappa-Exponential model were shown using four real-world examples from the fields of economics, engineering, and the environment.

1 Introduction

In the fields of reliability modeling and life testing analysis, the univariate exponential distribution is by far the most popular and extensively utilized continuous one-parameter distribution. Independent events occur at a constant average rate in a Poisson point process, hence the time between them is assumed to follow an exponential distribution. This distribution may be thought of as a special case of the gamma distribution. This distribution may be thought of as a no-memory, continuous variant of the geometric distribution. It’s not only for studying Poisson point processes; there are many applications. The cdf and pdf for the exponential distribution are defined as:

$$\begin{aligned} G\left( t;\beta \right)&=1-e^{-\beta t} \quad \text {and} \end{aligned}$$

(1)

$$\begin{aligned} g\left( t;\beta \right)&=\beta e^{-\beta t}, \end{aligned}$$

(2)

where $\beta >0$ is a rate parameter. Predictions of when something will happen are often made using the exponential distribution. It is often used to track radioactive decay in the field of physics; in engineering, time-to-defect analysis is used to determine how long a production line must wait to acquire a faulty product, and it is often used to predict the likelihood of a portfolio’s next default in finance. The exponential distribution is often used to estimate the time remaining before an event happens. For instance, an exponential distribution may be found in the period (from now on) until an earthquake occurs. Other examples are the life of a vehicle battery in months or the duration of a long-distance business call in minutes. New generalizations and applications of the exponential distribution include [2, 3, 18, 27]. These are but a few examples of when the exponential distribution might be handy. Additionally, owing to space limitations, further details related to exponential distribution cannot be given.; Readers interested in learning more might go to resources like [4, 17, 35] and the references found within them.

The Kappa distribution, suggested by [44] and [45], is a desirable positive-skew asymmetric distribution. Because it may be used to compare rainfall, streamflow, and wind speed data, this distribution is gaining increased interest in hydrological research. The well-known gamma and log-normal distributions have been used to fit historical rainfall data. However, these distributions are computationally problematic since there are no closed forms for computing their cdf and quantile functions. On the other hand, the Kappa distribution’s formulae are closed algebraic expressions that can be readily evaluated. The cdf of three-parameter Kappa(Kappa3) distribution ( [45]) is

$$\begin{aligned} R\left( t\right) =\frac{{\left( \frac{t}{b }\right) }^{\lambda }}{{\left[ a +{\left( \frac{t}{b }\right) }^{a\lambda }\right] }^{\left( \frac{1}{a }\right) }}\ \textrm{for}\ t,a ,b \ \textrm{and}\ \lambda >0,{} & {} \end{aligned}$$

(3)

where a and $\lambda$ are shape parameters and b is a scale parameter. Furthermore, the pdf of three-parameter Kappa(Kappa3) distribution is

$$\begin{aligned} r\left( t\right) =\frac{a\lambda }{b }\ \ {\left( \frac{t}{b }\right) }^{\lambda -1}\ {\left[ a +{\left( \frac{t}{b }\right) }^{a\lambda }\right] }^{-\left( \frac{a +1}{a }\right) }\ \textrm{for}\ t,a ,b \ \textrm{and}\ \lambda >0. \end{aligned}$$

(4)

Keep in mind that the Kappa(Kappa3) distribution with three parameters becomes the Kappa(Kappa1) distribution with just one parameter if $\lambda =b =1$. In addition, if $\lambda =1$, the Kappa(Kappa3) distribution with three parameters becomes the Kappa(Kappa2) distribution with just two parameters.

Many fields, including demography, economics, finance, insurance, biological research, medicine, engineering, the environment, and actuarial science, have employed various classical distributions to model data throughout the last few decades. However, flexible distributions are constantly required to describe, explain, and predict the phenomena investigated in these areas. No one kind of distribution can adequately characterize skewed data under all conditions. The options for studying a variety of tail weights and skewnesses are widened when one or more shape parameters are added to the baseline distribution. Therefore, researchers have explored several methods for generating new families of distributions that are either more adaptable or better reflect certain practical situations.

An exciting method for creating a new, more versatile family of distributions was proposed by [42], which included adding a new parameter to an existing distribution. Their method results in an extended distribution that encompasses the baseline distribution as a special case and hence may be used to more precisely explain a wider range of data. Parameter addition by exponentiation, on the other hand, may be traced back to [31], who exponentiated the extreme value distribution to graduate mortality tables [5].

Reference [29] proposed a new family of distributions with roots in the beta distribution. By replacing the cdf of a normal distribution with $F\left( x\right)$, they came up with the beta-normal distribution. Several new distributions have been defined and studied using this approach. Beta-generated distributions and other generalizations were summarized by [39]. References [24] and [36] expanded the beta-generated method by substituting the Kumaraswamy distribution [38] for the beta distribution. In addition, Ref. [8] used the Topp-Leone distribution to create the Topp-Leone family of distributions (for additional information, see see [49] and [62]). Additionally, Ref. [6] extended the beta and hypergeometric distributions to create new generalized statistical probability distributions.

Other popular generators, to mention a few, include Weibull-G by [19], logistic-G by [64], exponentiated half logistic generated family by [23], McDonald-G (Mc-G) by [9], gamma-G type 1 by [65], gamma-G type 2 by [55], gamma-G type 3 by [63] and log-gamma-G by [14], Transformed-Transformer (T-X) by [11], exponentiated (T-X) by [13], T-X$\{$Y$\}$-quantile based approach by [10], T-R$\{$Y$\}$ by [12]. alpha power transformation introduced by [41]. For discussions of further examples of generators see [30, 37, 39, 60, 61].

Several modifications were made to the original Kappa distribution. Reference [33] proposed the Kumaraswamy generalized Kappa (KGK), the exponentiated generalized Kappa (EGK), and the McDonald generalized Kappa (McGK) as three generalized forms of the Kappa distribution. The author looked into the different statistical features of these innovative extended forms, used several methods to estimate their unknown parameters, and applied the models to real-world data. The Kumaraswamy generalized Kappa (KGK) distribution was suggested by [52] (derived from [33]), whereas [34] proposed the Marshall-Olkin Kappa (MOK) distribution. Many features were examined, unknown parameters were calculated, and examples from real-world data sets were given to show how their proposed allocations would work.

Although many studies have generalized some existing distributions, there is a lack of research on the extension of Kappa distribution. This research gap limits our understanding of the usefulness of Kappa extension. Reference [7] introduced a novel flexible family of distributions, the Odd Kappa-G family, with its cdf defined as:

$$\begin{aligned} F\left( x;a ,b ,\lambda ,\varvec{\vartheta }\right)&=\frac{{\left( \frac{G(x;\varvec{\vartheta })}{b\left[ 1-G(x;\varvec{\vartheta })\right] }\right) }^{\lambda }}{{\left[ a +{\left( \frac{G(x;\varvec{\vartheta })}{b\left[ 1-G(x;\varvec{\vartheta })\right] }\right) }^{a\lambda }\right] }^{\left( \frac{1}{a }\right) }}\ \ ,\ \ x\in R. \end{aligned}$$

Therefore, our contribution to this study aims to explore the flexibility of our Odd Kappa family of distributions by studying the Odd Kappa-Exponential (OK-E) distribution as a member of this family that can be applied to real-life phenomena. This study will present and extensively examine the OK-E distribution.

The remaining sections of the paper are structured as follows. The novel Odd Kappa-Exponential (OK-E) distribution is presented in Sect. 2. We show the asymptotic and shapes of this distribution’s pdf and hrf in Sect. 3. In Sect. 4, we provide an applicable linear form for the pdf and cdf of this distribution. This model’s quantile function is derived in Sect. 5. Moments, both ordinary and incomplete, as well as the mean residual life (MRL) and the mean waiting time (MWT), are reported in Sect. 6. Section 7 introduces the concept of entropy. Maximum likelihood parameter estimation is discussed in Sect. 8. In Sect. 9, we provide simulation results that evaluate the efficacy of the maximum likelihood estimation strategy. In Sect. 10, we show the flexibility of the new distribution with four examples drawn from actual data. In Sect. 11, we provide some concluding remarks.

2 Odd Kappa-Exponential (OK-E) Distribution

We assume an exponential distribution as the starting point, with the cdf and pdf specified by equations (1) and (2), respectively. In that case, the OK-E cdf, pdf, and hrf are as follows:

$$\begin{aligned} F\left( x;a ,b ,\lambda ,\beta \right)&={\left[ \frac{{\left( \frac{e^{\beta x}-1}{b }\right) }^{a\lambda }}{a +{\left( \frac{e^{\beta x}-1}{b }\right) }^{a\lambda }}\right] }^{\left( \frac{1}{a }\right) } , \end{aligned}$$

(5)

$$\begin{aligned} f\left( x;a ,b ,\lambda ,\beta \right)&=\left( \frac{a\lambda \beta \ e^{\beta x}}{b }\right) \ {\left( \frac{e^{\beta x}-1}{b }\right) }^{\lambda -1}{\left[ a +{\left( \frac{e^{\beta x}-1}{b }\right) }^{a\lambda }\right] }^{-\left( \frac{a +1}{a }\right) } , \end{aligned}$$

(6)

$$\begin{aligned} h\left( x;a ,b ,\lambda ,\beta \right)&=\frac{\left( \frac{a\lambda \beta \ e^{\beta x}}{b }\right) \ {\left( \frac{e^{\beta x}-1}{b }\right) }^{\lambda -1}{\left[ a +{\left( \frac{e^{\beta x}-1}{b }\right) }^{a\lambda }\right] }^{-1}}{{\left[ a +{\left( \frac{e^{\beta x}-1}{b }\right) }^{a\lambda }\right] }^{\left( \frac{1}{a }\right) }-\ {\left( \frac{e^{\beta x}-1}{b }\right) }^{\lambda }} ,{} & {} \end{aligned}$$

(7)

where$\ x>0$ and $a,b,\lambda ,\beta >0$.

Fig. 1

Plots of the pdf and hrf of the OK-E distribution, respectively, for the selected parameter values

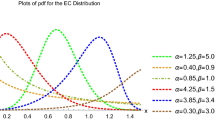
Several different pdf types, such as unimodal, monotonically decreasing, symmetrical, and right-skewed, are shown in Fig. 1 to be generated by the OK-E distribution. The hrf shapes produced by this distribution may be constant, monotonically decreasing, increasing, bathtub, upside-down bathtub, or even reversed-J. Therefore, the OK-E distribution may be pretty effective in fitting various data sets.

3 Asymptotics and Shapes

Proposition 1

The asymptotics of cdf, pdf and hrf when $x\rightarrow 0$ are given by

$$\begin{aligned}&F\left( x\right) \ \sim \ \frac{{\left[ 1-e^{-\beta x}\right] }^{\lambda }}{{b }^{\lambda }\ {a }^{\left( \frac{1}{a }\right) }}, \\&f\left( x\right) \ \sim \ \frac{\lambda \beta \ {\left[ 1-e^{-\beta x}\right] }^{\left( \lambda -1\right) }}{{b }^{\lambda }\ {a }^{\left( \frac{1}{a }\right) }}, \\&h\left( x\right) \ \sim \ \frac{\lambda \beta \ {\left[ 1-e^{-\beta x}\right] }^{\left( \lambda -1\right) }}{{b }^{\lambda }\ {a }^{\left( \frac{1}{a }\right) }}. \end{aligned}$$

Proposition 2

The asymptotics of cdf, pdf and hrf when $x\rightarrow \infty$ are given by

$$\begin{aligned}&1-F\left( x\right) \ \sim \ {\left[ b \ e^{-\beta x}\right] }^{\left( a\lambda \right) }, \\&\ \ \ \ \ f\left( x\right) \ \sim \ {ab\lambda \beta \ e^{-\beta x}\ \left[ b \ e^{-\beta x}\right] }^{\left( a\lambda -1\right) }, \\&\ \ \ \ \ h\left( x\right) \ \sim \ a\lambda \beta . \end{aligned}$$

The Shapes of the pdf and hrf can be described analytically. The critical points of the OK-E’s pdf are the roots of the equation:

$$\begin{aligned} \frac{d \log \left[ f\left( x\right) \right] }{dx}&=-\beta \left( \frac{a \lambda +e^{-\beta x}}{1-e^{-\beta x}}\right) + a b\lambda \left( a +1\right) \left( \frac{\beta e^{-\beta x}}{1-e^{-\beta x}}\right) \nonumber \\&\qquad \times \frac{{\left( be^{-\beta x}\right) }^{\left( a \lambda -1\right) }}{\left[ a {\left( be^{-\beta x}\right) }^{\left( a \lambda \right) }+{\left( 1-e^{-\beta x}\right) }^{\left( a \lambda \right) }\right] }=0 , \end{aligned}$$

(8)

that corresponds to points where $f^{\prime }\left( x\right) =0$. There may be more than one root to this equation.

Let $\tau \left( x\right) =\frac{d^2 \log \left[ f\left( x\right) \right] }{{dx}^2}$. We get

$$\begin{aligned} \tau \left( x\right)&=\frac{\left( a \lambda +1\right) \ \beta ^2 e^{-\beta x}}{{\left[ 1-e^{-\beta x}\right] }^2}+ a b\lambda \left( a +1\right) \left\{ \frac{{\left( be^{-\beta x}\right) }^{\left( a \lambda -1\right) }}{\left[ a {\left( be^{-\beta x}\right) }^{\left( a \lambda \right) }+{\left( 1-e^{-\beta x}\right) }^{\left( a \lambda \right) }\right] } \right. \nonumber \\&\qquad \times \left( \frac{\left( -\beta ^2 e^{-\beta x}\right) }{1-e^{-\beta x}}-{\left[ \frac{\beta e^{-\beta x}}{1-e^{-\beta x}}\right] }^2\right) - b \left( \frac{{\left[ \beta e^{-\beta x}\right] }^2}{1-e^{-\beta x}}\right) {\left( be^{-\beta x}\right) }^{\left( a \lambda -2\right) } \nonumber \\ {}&\qquad \times \left\{ \frac{\left( a \lambda -1\right) \left[ a {\left( be^{-\beta x}\right) }^{\left( a \lambda \right) }+{\left( 1-e^{-\beta x}\right) }^{\left( a \lambda \right) }\right] }{{\left[ a {\left( be^{-\beta x}\right) }^{\left( a \lambda \right) }+{\left( 1-e^{-\beta x}\right) }^{\left( a\lambda \right) }\right] }^2}\right. \nonumber \\&\qquad + \left. \left. \frac{a\lambda \ e^{-\beta x}\left[ {\left( 1-e^{-\beta x}\right) }^{\left( a \lambda -1\right) }-a b{\left( be^{-\beta x}\right) }^{\left( a \lambda -1\right) }\right] }{{\left[ a {\left( be^{-\beta x}\right) }^{\left( a \lambda \right) }+{\left( 1-e^{-\beta x}\right) }^{\left( a \lambda \right) }\right] }^2}\right\} \right\} \end{aligned}$$

(9)

If $x=c$ is a root of the equation (8) then it refers to a local maximum if $\tau \left( x\right) >0$ for all $x<c$ and $\tau \left( x\right) <0$ for all $x>c$. In addition, it corresponds to a local minimum if $\tau \left( x\right) <0$ for all $x<c$ and $\tau \left( x\right) >0$ for all $x>c$. Moreover, it gives an inflexion point if either $\tau \left( x\right) >0$ for all $x\ne c$ or $\tau \left( x\right) <0$ for all $x\ne c$.

Similarly, the roots of the equation are the critical points of the OK-E’s hrf:

$$\begin{aligned} \frac{d \log \left[ h\left( x\right) \right] }{dx}&=-\beta \left( \frac{a\lambda +e^{-\beta x}}{1-e^{-\beta x}}\right) + a\lambda \left( a +1\right) \left( \frac{\beta }{1-e^{-\beta x}}\right) \ \nonumber \\&\qquad \times \frac{{\left( be^{-\beta x}\right) }^{\left( a\lambda \right) }}{\left[ a{\left( be^{-\beta x}\right) }^{\left( a\lambda \right) }+{\left( 1-e^{-\beta x}\right) }^{\left( a\lambda \right) }\right] }+ a\lambda \left( \frac{\beta }{1-e^{-\beta x}}\right) \ \nonumber \\&\qquad \times {\left[ 1-e^{-\beta x}\ {\left( be^{-\beta x}\right) }^{a }\right] }^{\lambda } \nonumber \\&\qquad \div \left\{ {\left[ a{\left( be^{-\beta x}\right) }^{\left( a\lambda \right) }+{\left( 1-e^{-\beta x}\right) }^{\left( a\lambda \right) }\right] }^{\left( \frac{a +1}{a }\right) } \right. \nonumber \\&\qquad - \left. a{\left[ 1-e^{-\beta x}\ {\left( be^{-\beta x}\right) }^{a }\right] }^{\lambda }-{\left( 1-e^{-\beta x}\right) }^{\lambda \left( a +1\right) }\right\} =0, \end{aligned}$$

(10)

that corresponds to points where $h^{\prime }\left( x\right) =0$. There may be more than one root to this equation.

Let $\varphi \left( x\right) =\frac{d^2 \log \left[ h\left( x\right) \right] }{{dx}^2}$. We get

$$\begin{aligned} \varphi \left( x\right)&=\frac{\left( a\lambda +1\right) \ \beta ^2 e^{-\beta x}}{{\left[ 1-e^{-\beta x}\right] }^2}-\frac{a \ b\lambda \left( a +1\right) \ \beta ^2 e^{-\beta x}\ {\left( 1-e^{-\beta x}\right) }^{\left( a\lambda -2\right) }\ {\left( be^{-\beta x}\right) }^{\left( a\lambda -1\right) }}{{\left[ a \ {\left( be^{-\beta x}\right) }^{\left( a\lambda \right) }+{\left( 1-e^{-\beta x}\right) }^{\left( a\lambda \right) }\right] }^2} \nonumber \\&\qquad \times \Bigg \{a\lambda \left( 1-2e^{-\beta x}\right) + e^{-\beta x} \left[ a{\left( \frac{be^{-\beta x}}{1-e^{-\beta x}}\right) }^{\left( a\lambda \right) }+1\right] \Bigg \} \nonumber \\&\qquad + \left\{ \left\{ a b \lambda \beta ^2 \left( \frac{e^{-\beta x}}{1-e^{-\beta x}}\right) \ {\left( be^{-\beta x}\right) }^{a -1}\ {\left[ \left( 1-e^{-\beta x}\right) \ {\left( be^{-\beta x}\right) }^{a }\right] }^{\lambda -1}\right\} \right. \nonumber \\&\qquad \div \left[ {\left[ a \ {\left( be^{-\beta x}\right) }^{\left( a\lambda \right) }+{\left( 1-e^{-\beta x}\right) }^{\left( a\lambda \right) }\right] }^{\left( \frac{a +1}{a }\right) }-a \ {\left[ \left( 1-e^{-\beta x}\right) \ {\left( be^{-\beta x}\right) }^{a }\right] }^{\lambda } \right. \nonumber \\&\qquad - \left. \left. {\left( 1-e^{-\beta x}\right) }^{\lambda \left( a +1\right) }\right] ^2 \right\} \times \Bigg \{\left( -e^{-\beta x}+\lambda \left( 1-\left( a +1\right) \ \left( 1-e^{-\beta x}\right) \right) \right) \Bigg [ \bigg [ \nonumber \\&\qquad {a {\left( be^{-\beta x}\right) }^{\left( a\lambda \right) } + {\left( 1-e^{-\beta x}\right) }^{\left( a\lambda \right) }\bigg ]}^{\left( \frac{a +1}{a }\right) }-a \ {\left[ \left( 1-e^{-\beta x}\right) \ {\left( be^{-\beta x}\right) }^{a }\right] }^{\lambda } \nonumber \\&\qquad - {\left( 1-e^{-\beta x}\right) }^{\lambda \left( a +1\right) }\Bigg ] - \lambda \ \left( 1-e^{-\beta x}\right) \ e^{-\beta x} \Bigg [\left( a +1\right) \left( {\left( 1-e^{-\beta x}\right) }^{\left( a\lambda -1\right) } \right. \nonumber \\&\qquad - \left. a b {\left( be^{-\beta x}\right) }^{\left( a\lambda -1\right) }\right) \bigg [a \ {\left( be^{-\beta x}\right) }^{\left( a\lambda \right) } + {\left( 1-e^{-\beta x}\right) }^{\left( a\lambda \right) }{\bigg ]}^{\left( \frac{1}{a }\right) } - a b {\left( be^{-\beta x}\right) }^{a -1}\nonumber \\&\qquad \times \left( 1-\left( a +1\right) \ \left( 1-e^{-\beta x}\right) \right) {\left[ \left( 1-e^{-\beta x}\right) \ {\left( be^{-\beta x}\right) }^{a }\right] }^{\lambda -1} \nonumber \\&\qquad - \left( a +1\right) {\left( \left( 1-e^{-\beta x}\right) \right) }^{\lambda \left( a +1\right) -1}\Bigg ]\Bigg \} \end{aligned}$$

(11)

If $x=d$ is a root of the equation (10) then it corresponds to a local maximum if $\varphi \left( x\right) >0$ for all $x<d$ and $\varphi \left( x\right) <0$ for all $x>d$. Moreover, it corresponds to a local minimum if $\varphi \left( x\right) <0$ for all $x<d$ and $\varphi \left( x\right) >0$ for all $x>d$. Furthermore, it refers to an inflexion point if either $\varphi \left( x\right) >0$ for all $x\ne d$ or $\varphi \left( x\right) <0$ for all $x\ne d$.

Most symbolic computing software platforms, such as Mathematica, Maple, Matlab, SageMath, Maxima, and others, may be used to find the local minimums and maximums, as well as inflexion points, for these equations.

The plots of equations (8)-(11) for the OK-E distribution are shown at (a) through (d) in Fig. 2. We observe that cases (1), (2) and (4) at (a) and (b) in Fig. 2 have $\frac{d}{dx} \log \left[ f\left( x\right) \right] <0$ which implies f(x) is a decreasing function. However, case (4) starts with concave-up since $\tau \left( x\right) =\frac{{d}^{2}}{{dx}^{2}} \log \left[ f\left( x\right) \right] >0$ for $x < c$ then becomes concave-down since $\tau \left( x\right) =\frac{{d}^{2}}{{dx}^{2}} \log \left[ f\left( x\right) \right] <0$ for $x > c$ which implies that c is the inflection point and equals 0.5493. Moreover, curves of $\frac{d}{dx} \log \left[ f\left( x\right) \right]$ in cases (3) and (5) at (a) and (b) in Fig. 2 cut the horizontal axis and $\tau \left( x\right) =\frac{{d}^{2}}{{dx}^{2}} \log \left[ f\left( x\right) \right] <0$. This implies that f(x) is log-concave and unimodal with the existence of a local maximum equals 0.7815 for case (3) or 1.053 for case (5).

On the other hand, case (1) at (c) and (d) in Fig. 2 has $\frac{d}{dx} \log \left[ h\left( x\right) \right] <0$ and $\varphi \left( x\right) =\frac{{d}^{2}}{{dx}^{2}} \log \left[ h\left( x\right) \right] >0$ where this indicates that h(x) is a decreasing and concave up function, respectively. However, case (2) at (c) and (d) in Fig. 2 has $\frac{d}{dx} \log \left[ h\left( x\right) \right] =0$ implying that h(x) is a constant for all x. Moreover, curves of $\frac{d}{dx} \log \left[ h\left( x\right) \right]$ in cases (3) and (5) at (c) and (d) in Fig. 2 cut the horizontal axis and $\varphi \left( x\right) =\frac{{d}^{2}}{{dx}^{2}} \log \left[ h\left( x\right) \right] <0$. In these cases, h(x) is log-concave and unimodal with the existence of a local maximum equals 1.3725 for case (3) or 1.754 for case (5). In addition, h(x) is log-convex with a local minimum equals 0.3155 in case (4) since the curve of $\frac{d}{dx} \log \left[ h\left( x\right) \right]$ at (c) and (d) in Fig. 2 cuts the horizontal axis and $\varphi \left( x\right) =\frac{{d}^{2}}{{dx}^{2}} \log \left[ h\left( x\right) \right] >0$.

Fig. 2

Plots of the ${1}^{st}$ and ${2}^{nd}$ derivatives of the log of both pdf {(a) & (b)} and hrf {(c) & (d)} for the OK-E distribution, respectively

4 Expansions of Both cdf and pdf of OK-E

In the event that you round off numbers incorrectly, for instance, it might be difficult to determine some mathematical aspects of the OK-E distribution using numerical integration. Therefore, using established algebraic expansions to determine particular characteristics. In most practical situations, we may substitute a big positive integer, say ten or more, for the sum’s “infinite” limit. The following Proposition is derived from [7]’s work, specifically Sect. 5.

Proposition 3

The OK-E distribution’s cdf and pdf may be stated, respectively, as

$$\begin{aligned}&F\left( x;a ,b ,\lambda , \beta \right) =\sum ^{\infty }_{j=0}{w_j\ \left( 1-e^{(-\beta x)}\right) ^j}\ \nonumber \\&and \end{aligned}$$

(12)

$$\begin{aligned}&f\left( x;a ,b ,\lambda , \beta \right) =\beta e^{(-\beta x)} \sum ^{\infty }_{j=0}{j \ w_j\ \left( 1-e^{(-\beta x)}\right) ^{(j-1)}}\ \end{aligned}$$

(13)

$$\begin{aligned}&where \nonumber \\&w_j=\sum ^{\infty }_{i=0}{{\left( -1\right) }^i a^i b^{a \lambda i} \left( \genfrac{}{}{0.0pt}{}{\frac{1}{a }}{i}\right) d_{j,i}} . \end{aligned}$$

(14)

Proof

Due to space limitations, all proofs have been excluded; nevertheless, interested readers may find them in [7] or by contacting the author personally. $\square$

Therefore, the main findings of this study are presented in Proposition 3. Thus, the OK-E distribution’s cdf and pdf may be expressed as an infinite linear combination of exponentiated-exponential cdf and pdf, respectively. The ordinary moments, incomplete moments, and residual life functions, among other mathematical aspects of the proposed distribution, may be derived from Proposition 3. Among others, [32, 47], and [50] address several features of the exp-G distributions.

5 Quantile Function

Proposition 4

The quantile function (qf) of the OK-E distribution is obtained as

$$\begin{aligned} x_{\tau }=Q_X\left( \tau ;a ,b ,\lambda ,\beta \right) =\left( \frac{1}{\beta }\right) ln\left\{ 1+b {\left[ \frac{a{\tau }^{a }}{1-{\tau }^{a }}\right] }^{\left( \frac{1}{a\lambda }\right) }\right\} , \end{aligned}$$

(15)

where $\tau \sim \text {uniform}\left( 0,1\right)$.

6 Moments

Several properties of the OK-E distribution are obtained in this section, including the (reversed) residual life, skewness, kurtosis, and ordinary and incomplete moments.

6.1 Ordinary Moments

Proposition 5

The ${r}^{th}\ (r=1,2,...)$ non-central moments of the OK-E distribution is given by

$$\begin{aligned} {\mu }^{'}_r&=r\ {\beta }^{\left( -r\right) }\ \sum ^{\infty }_{j=0}{\sum ^{\infty }_{k=0}{\sum ^k_{s=0}{\frac{{\left( -1\right) }^{k+s} j\ w_j}{\left( r-s\right) \ \left( j+r+k\right) } {k \atopwithdelims ()s} {k-r \atopwithdelims ()k}\ p_{s,k}}}} , \end{aligned}$$

(16)

where $p_{s,0}=1\,\ p_{s,k}=\frac{1}{k}\sum ^k_{m=1}{\left[ m\left( s+1\right) -k\right] \ q_m \ p_{s,k-m}}\ \ and\ \ q_m=\frac{{\left( -1\right) }^m}{m+1}$ and $w_j$ is defined in equation (14).

Remark 1

The ${s}^{th}$ central moments of the OK-E distribution, say ${\mu }_s$, may be derived using the relationship between non-central and central moments as follows:

$$\begin{aligned} {\mu }_s=E{\left( X-\mu \right) }^s=\sum ^s_{r=0}{\left( \genfrac{}{}{0.0pt}{}{s}{r}\right) \ {\left( -{\mu }^{\prime }_1\right) }^{s-r}\ {\mu }^{\prime }_r} \ \ for\ s=1,2,... ,{} & {} \end{aligned}$$

(17)

where ${\mu }^{\prime }_r$ is defined in Proposition 5. Furthermore, ${\mu }_0={\mu }^{\prime }_0=1$, ${\mu }_1=0$, ${\mu }_2={\mu }^{\prime }_2-{\left( {\mu }^{\prime }_1\right) }^2={\sigma }^2$, ${\mu }_3={\mu }^{\prime }_3-3{\mu }^{\prime }_2{\mu }^{\prime }_1+2{\left( {\mu }^{\prime }_1\right) }^3$, ${\mu }_4={\mu }^{\prime }_4-4{\mu }^{\prime }_3{\mu }^{\prime }_1+6{\mu }^{\prime }_2{\left( {\mu }^{\prime }_1\right) }^2-3{\left( {\mu }^{\prime }_1\right) }^4$, etc.

For some arbitrary choices of the distribution parameters, some numerical values for the mean($\mu ={\mu }^{\prime }_1$) and variance(${\sigma }^2={\mu }^{\prime }_2-{\left( {\mu }^{\prime }_1\right) }^2$) of the OK-E($a,b,\lambda ,\beta$) distribution are displayed in Table 1. As the values of the parameters($a,\lambda \ and\ \beta$) increase, it is observed that both the mean and variance decrease. Whereas the values of the parameter(b) increase, the mean and variance increase as well.

Table 1 Mean and variance for some arbitrary parameter values

6.2 Skewness and Kurtosis

To make skewness and kurtosis independent of data units, it is typically to divide ${\mu }_3$ and ${\mu }_4$ by ${\left( {\mu }_2\right) }^{\left( 3/2\right) }$ and ${\left( {\mu }_2\right) }^2$, respectively. Hence, kurtosis = ${\mu }_4/{\left( {\mu }_2\right) }^2$ and skewness = ${\mu }_3/{\left( {\mu }_2\right) }^{\left( 3/2\right) }$, see [22].

Figure 3 shows the behavior of the skewness and kurtosis of the OK-E($a,b,\lambda ,\beta$) defined in equation (6) with respect to a and $\lambda$ when $b =2$ and $\beta =1$. Based on this Figure, we can infer that changes in the parameters a and $\lambda$ have a significant influence on the skewness and kurtosis of the OK-E distribution, indicating higher flexibility for OK-E.

Fig. 3

Skewness and kurtosis plots for the Odd Kappa-exponential($a,b,\lambda ,\beta$) when $b =2$ and $\beta =1$

The Moors coefficient of kurtosis $\left( K \right)$ and Bowley coefficient of skewness $\left( S \right)$ are considered to be robust statistics. These coefficients are, respectively, given as

$$\begin{aligned} K=\frac{Q_X\left( 7/8;a ,b ,\lambda ,\beta \right) -Q_X\left( 5/8;a ,b ,\lambda ,\beta \right) +Q_X\left( 3/8;a ,b ,\lambda ,\beta \right) -Q_X\left( 1/8;a ,b ,\lambda ,\beta \right) }{IQR}. \end{aligned}$$

and

$$\begin{aligned} S=\frac{\left( Q_3-Q_2\right) -\left( Q_2-Q_1\right) }{IQR},{} & {} \end{aligned}$$

where the three quartiles of the OK-E distribution are defined by $Q_1=Q_X\left( 1/4;a,b,\lambda ,\beta \right) ,\ Q_2=Q_X\left( 1/2;a,b,\lambda ,\beta \right) =Median(M)\ and\ Q_3=Q_X\left( 3/4;a,b,\lambda ,\beta \right)$ where $Q_X\left( \cdot \right)$ is defined in equation (15). In addition, the inter-quartile range is given by $IQR=Q_3-Q_1$.

See [20] and [46] for more details on these coefficients, respectively.

Table 2 Values of $Q_1,\ M,\ Q_3,\ S\ and\ K$ of the Odd Kappa-exponential(OK-E) distribution for some parameter values

We observe in Table 2 that the effects of $a,b,\lambda \ and\ \beta$ on the quartiles are significant. The spread of the distribution increases as the value of a, $\lambda$ or $\beta$ decreases. However, the spread of the distribution increases as the value of b increases. In addition, we always have moderate variations for K. Furthermore, the distribution is approaching negatively-skewed shape (i.e. $S<0$) when all values of the distribution parameters start to be greater than one; otherwise, the shape of the distribution becomes right-skewed.

6.3 Incomplete Moments

Proposition 6

the first incomplete moment of the OK-E distribution is given by

$$\begin{aligned} m_{\textrm{1}}\left( y\right)&= \int ^y_0{x\mathrm{\ }f\left( x\right) }dx=\left( \frac{1}{\beta }\right) \sum ^{\infty }_{j=0}{\sum ^{\infty }_{k=1}{j w_j \frac{{\left[ 1-e^{-\beta y}\right] }^{j+k}}{k\ \left( j+k\right) }\ }} \end{aligned}$$

(18)

where $w_j$ is defined in equation (14).

Remark 2

Empirical descriptions of the form of many distributions and measures of inequality, such as the Lorenz and Bonferroni curves, may benefit from incomplete moments. Because of this, the Lorenz and Bonferroni curves (see [25]) are thought to be the most widely utilized inequality indicators in the distribution of income and wealth. The following is the Lorenz curve for a certain probability, $\pi$:

$$\begin{aligned} L_X\left( \pi \right) \mathrm {=}\frac{\int ^q_0{t\mathrm {\ }f\left( t\right) }dt}{E\left( X\right) } \mathrm {=}\frac{\int ^\pi _0{F^{\mathrm {-}\textrm{1}}_X\mathrm {(}u \mathrm {)}}du}{E\left( X\right) } \mathrm {=}\frac{m_{\textrm{1}}\left( q\right) }{E\left( X\right) }, \end{aligned}$$

(19)

where

$$\begin{aligned} q\mathrm {=}Q_X\mathrm {(}\pi \mathrm {)=}F^{\mathrm {-}\textrm{1}}_X\mathrm {(}\pi \mathrm {)} \ and \ m_{\textrm{1}}\left( q\right) \text {is defined in equation } 18. \end{aligned}$$

Also, the Bonferroni curve as follows:

$$\begin{aligned} B_X\left( \pi \right) \mathrm {=}\frac{\int ^q_0{t\mathrm {\ }f\left( t\right) }dt}{\pi \ E\left( X\right) } \mathrm {=}\frac{\int ^\pi _0{F^{\mathrm {-}\textrm{1}}_X\mathrm {(}u \mathrm {)}}du}{\pi \ E\left( X\right) } \mathrm {=}\frac{m_{\textrm{1}}\left( q\right) }{\pi \ E\left( X\right) }\mathrm {=}\frac{L_X\left( \pi \right) }{\pi }.{} & {} \end{aligned}$$

(20)

Plots of the Lorenz and Bonferroni curves for some parameter values are depicted in Fig. 4.

Fig. 4

Lorenz($L_X\left( \pi \right)$) and Bonferroni($B_X\left( \pi \right)$) curves for the Odd Kappa-exponential($a,b,\lambda ,\beta$) for some parameter values

In economics, if $\pi =F_{X}\left( q\right)$ is the proportion of units with incomes less than or equal to q, $L_{X}\left( \pi \right)$ gives the proportion of total income volume accumulated by the set of units with an income lower than or equal to q. In a similar manner, the Bonferroni curve $B_{X}\left( \pi \right)$ calculates the ratio of this group’s mean income to the population’s mean income.

6.4 (Reversed) Residual Life Function

The use of (reversed) residual life random variables is widespread in reliability analysis and risk theory. We propose mean residual life (MRL) and mean waiting time (MWT) as special cases in the following Proposition:

Proposition 7

Let X follows the OK-E distribution then the first moment of residual life of X, say $M_1\left( t\right) =E\left[ X-t|X>t\right] \ for\ t>0$ and the first moment of reversed residual life of X, say $M^*_1\left( t\right) =E\left[ t-X|X\le t\right] \ for\ t>0$, uniquely determine $F\left( x\right)$ (see [51]) are expressed respectively as:

$$\begin{aligned} M_1\left( t\right)&=\frac{\textrm{1}}{\overline{F\left( t\right) }}\sum ^{\infty }_{i=0}{w_i}\left\{ t\left( {\left[ 1-e^{\left( -\beta t\right) }\right] }^i-1\right) + \left( \frac{i}{\beta }\right) \sum ^{\infty }_{k=1} \frac{1}{k\ \left( i+k\right) } \right. \times \nonumber \\ {}&\left. \qquad \qquad \qquad \qquad \left\{ 1-{\left[ 1-e^{-\beta t}\right] }^{i+k}\right\} \right\} ,{} & {} \end{aligned}$$

(21)

and

$$\begin{aligned} M^{*}_1\left( t\right)&=\frac{\textrm{t}}{F\left( t\right) }\sum ^{\infty }_{i=0}{w_i\left\{ {\left[ 1-e^{\left( -\beta t\right) }\right] }^i-\left( \frac{i}{\beta }\right) \sum ^{\infty }_{k=1}{\frac{{\left[ 1-e^{-\beta t}\right] }^{i+k}}{k\ \left( i+k\right) }\ }\right\} } , \end{aligned}$$

(22)

Remark 3

The extra life expectancy if a component survives until time t is reflected in the mean residual life (MRL) which is a function of t in equation (21). The following is one interpretation of the MRL: If anything survives this far, what is the estimated length of time for it to live? MRL provides an answer to this query.

Remark 4

The mean waiting time (MWT), which is sometimes referred to as the mean past lifetime, the mean reversed residual life function, or the mean inactivity time (MIT), may be expressed as follows in equation (22): Think about the following situation: We have discovered that a device has malfunctioned at some point in the past, let’s say t. When estimating the precise moment of a device breakdown, the MWT is a valuable metric. In biomedicine, the length of a patient’s remission, or disease-free survival time, is used to evaluate how effective a treatment is while dealing with recurrent diseases. The actual size of the remission is often uncertain since it takes a significant amount of money and time to maintain constant patient monitoring. In such cases, the real remission time may be estimated using a MWT function.

For some arbitrary choices of the OK-E distribution parameters at the time points $t=1,\ 2,\ 3$ and 5, some numerical values for the mean residual life and the mean waiting time of the Odd Kappa-Exponential($a,b,\lambda ,\beta$) distribution are, respectively, displayed in Tables 3 and 4. As the values of the parameters($a,b,\ \lambda$ and $\beta$) become smaller than one, it is observed in Table 3 that the mean residual life increases with increasing the time points t. However, the mean residual life decreases with increasing the time points t as the values of the parameters($a,b,\ \lambda$ and $\beta$) become equal or greater than one. On the other hand, Table 4 shows that the mean waiting time increases with increasing the time points t as the values of the parameters($a,b,\ \lambda$ and $\beta$) increase.

Table 3 Mean residual life for some arbitrary parameter values

Table 4 Mean reversed residual life for some arbitrary parameter values

7 Entropy

Entropy is a measure of unpredictability or randomness used in many research fields, including engineering, hydrology, statistical mechanics, physics, molecular imaging of cancer, and sparse kernel density estimation. The Rényi entropy ( [54]) and the Shannon entropy ( [58]) are two standard entropy metrics. Creating a Rényi entropy expression is important because it allows one to compare the shapes and tails of many widely used densities and characterize the shape of a distribution (see [59] for more information).

Proposition 8

The Rényi entropy for the OK-E distribution is given by

$$\begin{aligned} I_R\left( \delta \right)&=\frac{{\beta }^{\delta -1 }}{1-\delta } \ \log \left\{ \sum ^{\infty }_{i=0}\sum ^{\infty }_{j=0}\sum ^{\infty }_{k=0}{\left( -1\right) }^k {k+\delta +i-1 \atopwithdelims ()k} \ \frac{a^{-\delta -i-k}}{b^{ka\lambda }} \ \omega \left( i,j\right) \right. \times \nonumber \\ {}&\left. Beta\left( \delta -ka\lambda ,j+ka\lambda -\delta +1\right) \right\} , \end{aligned}$$

(23)

where $\delta>0\,\ \delta \ne 1 \, \ \omega \left( i,j\right) ={\left( -1\right) }^{i+j}\ {\lambda }^{\delta }\ {a }^{\left( \delta +i\right) } \ {\frac{\delta }{a} \atopwithdelims ()i} \ {-\delta \atopwithdelims ()j} \, \ j+ka\lambda +1>\delta \ >ka\lambda$, and $Beta\left( s,t\right) =\int ^1_0{u^{s-1}\ {\left( 1-u\right) }^{t-1}}du$ for $s>0\ and\ t>0$.

The Shannon entropy is a special case of the Rényi entropy in Proposition 8 when $\delta \rightarrow 1$.

Proposition 9

The Shannon entropy for the OK-E distribution is given by

$$\begin{aligned} E\left\{ - \log \left[ f\left( X\right) \right] \right\}&=- \log \left[ a\right] - \log \left[ \lambda \right] +\lambda \ \log \left[ b\right] - \log \left[ \beta \right] +\sum ^{\infty }_{j=1}{w_j}\left\{ \frac{\left( \lambda -1\right) }{j}+ \right. \\&\qquad \left[ \psi \left( 1\right) -\psi (j+1)\right] - \lambda j\left( \frac{a+1}{a}\ \right) \sum ^{\infty }_{k=1}\sum ^k_{s=0}\sum ^s_{t=0}{\ }\frac{{\left( -1\right) }^{2k-s}}{k\ b^{a\lambda t}} \times \\&\left. \qquad \qquad {k \atopwithdelims ()s} {s \atopwithdelims ()t} a^{s-t}\ Beta\left( j+a\lambda t,1-a\lambda t\right) \right\} \end{aligned}$$

where $a\lambda t<1 \, \ \psi \left( x\right) =\frac{d \log \left[ \Gamma \left( x\right) \right] }{dx}$ is the psi function or the digamma function which is the logarithmic derivative of the gamma function and $w_j$ is defined in equation (14).

Some numerical values for the Rényi and Shannon entropies of the OK-E($a,b,\lambda ,\beta$) distribution for some several choices of the distribution parameters are displayed in Table 5. We observe that the model parametrs have an important impact on the amount of information quantified by the entropy. Therefore, both the Rényi and Shannon entropies decrease as the values of the parameter($\beta$) increase. Moreover, the Shannon entropy decreases as the values of the parameters($a \ or\ \lambda$) increase. Whereas the values of the parameter(b) increase, both the Rényi and Shannon entropies increase, too. However, the Rényi entropy increases as the values of the parameter(a) increase toward 0.7 then it starts to decrease as the values of the parameter(a) become greater than 0.7 (holding $b=0.5,\ \lambda =1\ and\ \beta =3$). Similarly, the Rényi entropy increases as the values of the parameter($\lambda$) increase toward 1.5 then it starts to decrease as the values of the parameter($\lambda$) become greater than 1.5 (holding $a=0.5,\ b=1\ and\ \beta =3$). Some values of the entropy are negatives which may be interpreted as loss of information (see [56] and [16]).

Table 5 Rényi and Shannon entropies for several arbitrary parameter values

8 Estimation

The most popular technique for estimating parameters is the maximum likelihood approach (see [22]). In this part, we use complete samples to get the maximum likelihood estimates (MLEs) of the unknown parameters in the OK-E distribution. Let $x={\left( x_1,\dots ,x_n\right) }^T$ be a random sample of size n from the OK-E distribution with parameters a, b, $\lambda$, and $\beta$. Let the $\mathrm {p\times 1}$ parameter vector be $\varvec{\xi }\mathrm {=}{\left( a \mathrm {,\ }b,\lambda \mathrm {,\ }{\beta }\right) }^{\textrm{T}}$. The total log-likelihood function for $\varvec{\xi }$ is ${\ell }_n={\ell }_n\left( \varvec{\xi }\right) =\sum ^n_{i=1}{{\ell }^{\left( i\right) }}$, where ${\ell }^{\left( i\right) }$ is the log likelihood for the ith observation ($i=1,\dots ,n$). Then, ${\ell }_n$ is given by

$$\begin{aligned} {\ell }_n&={n\ \log \left[ a \right] \ }+{n\ \log \left[ \lambda \right] \ }+{n\ \log \left[ \beta \right] \ }+{n\ a\lambda \ \log \left[ b \right] \ }+\beta \lambda \sum ^n_{i=1}{x_i}+\left( \lambda -1\right) \times \nonumber \\ {}&\quad \quad \sum ^n_{i=1}{ \log \left[ 1-e^{-\beta x_i}\right] }-\left( \frac{a +1}{a }\right) \ \sum ^n_{i=1}{ \log \left[ a \ {b }^{a\lambda }+{\left( e^{\beta x_i}-1\right) }^{a\lambda }\right] } . \end{aligned}$$

(24)

In order to maximize ${\ell }_n$, we must differentiate equation (24) and then solve the resulting nonlinear likelihood equations. However, it is not possible to solve these equations analytically. Because of this, they may be solved by statistical software employing iterative techniques like Newton-type algorithms. A few examples include the MaxBFGS in Ox (see [26]), the PROC NLMIXED Procedure in SAS/STAT (see [57]), and optim in R (see [53]).

The components of the score function $U_n\left( \varvec{\xi }\right) ={\left( U_{a },\ U_{b },\ U_{\lambda },\ U_{\beta }\right) }^T=$ ${\left( \mathrm {\partial }{\ell }_n/\partial a \mathrm {,\ }\mathrm {\partial }{\ell }_n/\partial b \mathrm {,\ }\mathrm {\partial }{\ell }_n/\partial \lambda \textrm{,}\mathrm {\partial }{\ell }_n/\partial \beta \right) }^{\textrm{T}}$ are

$$\begin{aligned} U_{a }&=\frac{\mathrm {\partial }{\ell }_n}{\partial a }\mathrm {=}\frac{n}{a }+\left( \frac{1}{{a }^2}\right) \sum ^n_{i=1}{ \log \left[ a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right] }\mathrm {-}\left( \frac{a +1}{a }\right) \\ {}&\qquad \qquad \times \sum ^n_{i=1}{\frac{1+\lambda \ \log \left[ \frac{e^{\beta x_i}-1}{b }\right] {\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }}{a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }}} \\ U_{b }&=\frac{\mathrm {\partial }{\ell }_n}{\partial b }\mathrm {=-}\frac{n\ \lambda }{b }+\left( \frac{\lambda \left( a +1\right) }{b }\right) \ \sum ^n_{i=1}{{\left[ 1+a \ {\left( \frac{e^{\beta x_i}-1}{b }\right) }^{-a\lambda }\right] }^{-1}} \\ U_{\lambda }&=\frac{\mathrm {\partial }{\ell }_n}{\partial \lambda } \mathrm {=}\frac{n}{\lambda }\mathrm {-}{n\ \log \left[ b \right] \ }+\sum ^n_{i=1}{ \log \left[ 1-e^{-\beta x_i}\right] }+\beta \sum ^n_{i=1}{x_i}-\left( a +1\right) \\ {}&\qquad \qquad \times \sum ^n_{i=1} \log \left[ \frac{e^{\beta x_i}-1}{b }\right] {\left[ 1+a \ {\left( \frac{e^{\beta x_i}-1}{b }\right) }^{-a\lambda }\right] }^{-1} \\ U_{\beta }&=\frac{\mathrm {\partial }{\ell }_n}{\partial \beta }\mathrm {=}\frac{n}{\beta }\mathrm {+}\sum ^n_{i=1}{x_i}+\left( \lambda -1\right) \ \sum ^n_{i=1}{\frac{x_i}{\left( 1-e^{-\beta x_i}\right) }}-\left( \frac{\lambda \left( a +1\right) }{b }\right) \times \\ {}&\qquad \qquad \sum ^n_{i=1}{\frac{x_i{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{\left( a\lambda -1\right) }}{e^{-\beta x_i}\left[ a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right] }}. \end{aligned}$$

Solving the equations $U_n\left( \varvec{\xi }\right) ={\left( U_{a },\ U_{b },\ U_{\lambda },\ U_{\beta }\right) }^T=\textbf{0}$ simultaneously gives the maximum likelihood estimate (MLE) $\widehat{\varvec{\xi }}\mathrm {=}{\left( {\widehat{a}},{\widehat{b}},\widehat{\lambda },{\widehat{\beta }}\right) } ^{\textrm{T}}$ of $\varvec{\xi }\mathrm {=}{\left( a, b,\lambda ,\beta \right) }^{\textrm{T}}$.

The Fisher information matrix must be constructed to test hypotheses and provide parameter interval estimates, which may be done by utilizing the second partial derivatives of the log-likelihood function about each parameter (see 1). For parameter MLEs, the asymptotic variance-covariance matrix may be obtained by inverting the Fisher information matrix. This procedure’s evaluation might be challenging at times. Therefore, it may be estimated using the observed Fisher’s information matrix.

9 Simulation

We may evaluate the Odd Kappa-Exponential MLEs in terms of their performance as a function of sample size n by using these steps:

• 1. Generate $B=10000$ samples of size n by using the inversion method to get $x_{\tau }=\frac{1}{\beta } \log \left[ 1+b {\left[ \frac{a \ {\tau }^{a }}{1-{\tau }^{a }}\right] }^{\left( \frac{1}{a\lambda }\right) }\right]$ where $\tau$ is uniform(0,1) (see Proposition 4).

• 2. Compute the MLEs for the B samples, say ${\widehat{\xi }}_i={{\widehat{a}}}_i,{{\widehat{b}}}_i,{\widehat{\lambda }}_i,{{\widehat{\beta }}}_i$ for $i=1,\dots ,B$.

• 3. Compute the standard errors of the MLEs by inverting the observed information matrices for the B samples, say ${se}_{{{\widehat{\xi }}}_i}$ for $i=1,\dots ,B$.

• 4. Compute the biases and the mean squared errors given by Bias(${\widehat{\xi }}$)=$\mathrm {\ }\frac{\textrm{1}}{\textrm{B}}\sum ^{\textrm{B}}_{\mathrm {i=1}}{\left( {\widehat{\xi }}_{\textrm{i}}\mathrm {-}\xi \right) }$ and MSE($\widehat{\xi }$)= $\frac{\textrm{1}}{\textrm{B}}\sum ^{\textrm{B}}_{\mathrm {i=1}}{{\left( {\widehat{\xi }}_{\textrm{i}}\mathrm {-}\xi \right) }^{\textrm{2}}}$ Also, $\overline{\widehat{\xi }}\mathrm {=}\frac{\textrm{1}}{\textrm{B}}\sum ^{\textrm{B}}_{\mathrm {i=1}}{{\widehat{\xi }}_{\textrm{i}}}$ where $\xi =a,b,\lambda ,\beta$.

• 5. Repeat steps(1-4) for the combinations of n and $\xi$.

Table 6 gives empirical findings on the performance of model parameters, and from these results, we learn the following:

• Biases decrease as sample size increases.

• MSE decreases as sample size increases.

• As sample sizes increases, estimates of model parameters are closer to true values.

Table 6 Biases and MSEs of MLEs (${\widehat{a}},{\widehat{b}},\widehat{\lambda },{\widehat{\beta }}$) versus n for different values of the true parameters ($a,b,\lambda ,\beta$)

10 Applications

This section examines the fitting of competing models and the odd Kappa-Exponential (OK-E) to four actual data sets. The first data set that is explained below and examined by [52, 34], and [45] provides the reason for selecting almost all of these competing models, as seen in Table 7. The exponential and attractive Weibull models are added to Table 7. Therefore, the thirteen selected models presented in Table 7 are: exponential(Exp($\beta$)), gamma($\alpha ,\beta$), log-normal(lognormal($\alpha ,\beta$)) and weibull($\alpha ,\beta$) distributions, one-parameter Kappa(Kappa1($\alpha$)), two-parameter Kappa(Kappa2 ($\alpha ,\beta$)) and three-parameter Kappa(Kappa3($\alpha ,\beta ,\theta$)) distributions, exponentiated Kappa Lehmann type I (EK-L1($a,\alpha ,\beta ,\theta$)) and exponentiated Kappa Lehmann type II (EK-L2($b,\alpha ,\beta ,\theta$)) distributions, Marshall-Olkin Kappa(MOK ($\lambda ,\alpha ,\beta ,\theta$)) distribution, Kumaraswamy generalized Kappa(KGK ($a,b,\alpha ,\beta ,\theta$)), exponentiated generalized Kappa(EGK ($b,\lambda ,\alpha ,\beta ,\theta$)) and McDonald generalized Kappa(McGK (a,b,$\lambda$,$\alpha$,$\beta$,$\theta$)) distributions.

To compare these models, the estimated negative log-likelihood values ($-l\left( \cdot \right)$), goodness of fit statistics based on empirical distribution function (Kolmogorov-Smirnov(KS), Anderson-Darling(A${}^{*}$), Cramer–von-Mises(W${}^{*}$), and Sum of Squares(SS)), and goodness of fit statistics based on information criteria (AIC, AICc, cAIC, BIC, and HQIC) will be used. Based on goodness-of-fit statistics across four actual data sets, these competitive models will be compared against the Odd Kappa-Exponential (OK-E($a,b,\lambda ,\beta$)).

Typically, the best model is characterized by possessing the highest p-value in KS and lower values for the $-l\left( \cdot \right)$, AIC, AICc, cAIC, BIC, SS, W${}^{*}$, A${}^{*}$ and KS. All calculations are derived using the R program ( [53]).

Table 7 Selected distributions and corresponding pdfs $f\left( x\right)$

10.1 Data Set 1: Stream Flow Amounts Data

The data set pertains to environmental or geological information and comprises 35 stream flow quantities (measured in 1000 acre-feet). These observations were gathered between 1936 and 1970 from the surface water records maintained by the US Geological Survey (USGS), specifically from the gaging station identified as 9-3425. The data obtained corresponds to the period spanning from April 1st to August 31st of each year (see [44]). This data set was also investigated by [34, 45], and [52]. For convenience, the data are 192.48, 303.91, 301.26, 135.87, 126.52, 474.25, 297.17, 196.47, 327.64, 261.34, 96.26, 160.52, 314.6, 346.3, 154.44, 111.16, 389.92, 157.93, 126.46, 128.58, 155.62, 400.93, 248.57, 91.27, 238.71, 140.76, 228.28, 104.75, 125.29, 366.22, 192.01, 149.74, 224.58, 242.19, 151.25.

The estimated values and their corresponding standard errors, included in parentheses, may be found in Table 8 for the parameters of the OK-E distribution and the competitive models. Table 9 presents the lowest values of the negative log-likelihood function $-l\left( \cdot \right)$ and the goodness of fit statistics derived from both information criteria and the empirical distribution function. These values are obtained for all distributions examined using the first data set. In the study conducted by [34], the Anderson-Darling (A${}^{*}$) and Cramer–von-Mises (W${}^{*}$) statistics were used as metrics to assess the relative performance of different distributions. Other researchers in reputable scientific publications widely adopt this approach. By employing the same measures, as well as the negative log-likelihood function $-l\left( \cdot \right)$, the sum of squares (SS), and the Kolmogorov-Smirnov (KS) statistic along with its corresponding p-value, it becomes evident that the OK-E distribution exhibits the lowest values for $-l\left( \cdot \right)$, SS, W${}^{*}$, A${}^{*}$, and KS, as well as the highest p-value when compared to the other distributions listed in Table 9.

Table 8 MLEs and their standard errors (in parentheses) for stream flow amounts data

Table 9 Performance indices for stream flow amounts data

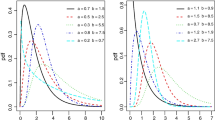
The total time on the test (TTT) and hrf plots are shown in Fig. 5. For more comprehensive information on using the TTT plot in data analysis, please see reference [1]. The concave shape of the TTT curve is seen in both graphs shown in Fig. 5, supporting the suitability of a monotonic increasing hrf, as suggested by [1]. Therefore, it can be concluded that the OK-E distribution is a suitable model for accurately representing this particular data set.

Fig. 5

Empirical and fitted scaled TTT-transforms and hrf for the first data set, respectively

To demonstrate the existence of a singular solution in the parameters, we generate profile log-likelihood plots for the parameters of the OK-E distribution using the provided dataset. Figure 6 provides empirical evidence supporting the model’s distinctive characteristics under consideration.

Fig. 6

The log-likelihood as a function of parameters of OK-E for the first data set

The relative histogram with the fitted densities and the empirical with the fitted distribution functions are shown in Fig. 7, respectively. The plots confirm the findings in Table 9 and show that the OK-E distribution is the best-fitting model out of all the models considered.

Fig. 7

Plots of Estimated cdfs and pdfs for the first data set, respectively

As a result, the following is the estimated variance-covariance matrix for the OK-E$(a, b, \lambda , \beta )$ distribution:

$$\begin{aligned}\left[ \begin{array}{cccc} \mathrm{1.49761}\times {10}^{-10} &{} \mathrm{\ -1.888665}\times {10}^{-6} &{} \mathrm{-1.827728} &{} \mathrm{-4.662012}\times {10}^{-9} \\ \mathrm{-1.888665}\times {10}^{-6} &{} \mathrm{1.70992} &{} -23877.78 &{} 0.00423608 \\ \mathrm{-1.827728} &{} -23877.78 &{} \textrm{23946940000} &{} -58.93456 \\ \mathrm{-4.662012}\times {10}^{-9} &{} 0.00423608 &{} -58.93456 &{} \mathrm{1.064683}\times {10}^{-5} \end{array}\right] \end{aligned}$$

The $95\%$ confidence intervals for a, b, $\lambda$, and $\beta$ are $[0,\mathrm{3.518907\times }{10}^{-5}]$, [0, 3.9661], [0, 444973.9698], and [0, 0.0117], respectively.

The LR test statistic for testing $H_0: OK-E(1,1,1,\beta ) \equiv Exp(\beta )$ against $H_1: OK-E(a,b,\lambda ,\beta )$ is 34.3124 with the associated p-value = $\mathrm{1.702032\times }{10}^{-7}$. Therefore, it is concluded that there is strongly significant difference between $OK-E(a,b,\lambda ,\beta )$ and $Exp(\beta )$ distributions.

The last three data sets, which will be discussed next, demonstrate the adaptability of OK-E as a member of this family of distributions and the effectiveness of our model (OK-E) in contrast to the other models listed in Table 7.

10.2 Data Set 2: Failure Times of 50 Components y

The provided data set pertains to electrical engineering and includes 50 observations about the failure times of 50 components measured per 1000 h. This information may be found in [48], page 180. [43, 15] and [28] also investigated this data collection. The data are 0.036, 0.058, 0.061, 0.074, 0.078, 0.086, 0.102, 0.103, 0.114, 0.116, 0.148, 0.183, 0.192, 0.254, 0.262, 0.379, 0.381, 0.538, 0.570, 0.574, 0.590, 0.618, 0.645, 0.961, 1.228, 1.600, 2.006, 2.054, 2.804, 3.058, 3.076, 3.147, 3.625, 3.704, 3.931, 4.073, 4.393, 4.534, 4.893, 6.274, 6.816, 7.896, 7.904, 8.022, 9.337, 10.940, 11.020, 13.880, 14.730, 15.080.

The table labeled "Table 10" presents the estimates and their corresponding standard errors in parentheses for the parameters of the OK-E distribution and the competitive models. Table 11 displays the lowest values of the negative log-likelihood function $-l\left( \cdot \right)$, the goodness of fit statistics derived from the information criterion, and the empirical distribution function. Among all measures except cAIC, it is evident that the OK-E distribution exhibits the highest p-value for the KS. Additionally, the $-l\left( \cdot \right)$, AIC, AICc, BIC, SS, W${}^{*}$, A${}^{*}$, and KS values for the OK-E distribution are comparatively less than those of the other distributions shown in Table 11. Hence, this model is deemed the most suitable for accurately representing the given data set. In contrast, it is worth noting that the remaining data sets consistently prefer the OK-E distribution across all measures without any exceptions, as will be shown subsequently.

Table 10 MLEs and their standard errors (in parentheses) for failure times of 50 components data

Table 11 Performance indices for failure times of 50 components data

The total time on the test (TTT) and hrf graphs are shown in Fig. 8. Figure 8 displays two charts that demonstrate the convexity of the TTT curve, suggesting that a hrf that decreases monotonically is sufficient. Due to the aforementioned reasons, the OK-E distribution may be considered a suitable model for the present data set.

Fig. 8

Empirical and fitted scaled TTT-transforms and hrf for the second data set, respectively

To demonstrate the existence of only one solution in the parameters, we provide a graphical representation of the profile log-likelihood functions for the parameters associated with the OK-E distribution in the second data set. Figure 9 provides evidence supporting the uniqueness of the parameters within our model.

Fig. 9

The log-likelihood as a function of parameters of OK-E for the second data set

Figure 10 displays the relative histogram with the fitted densities and the empirical with the fitted distribution functions. Therefore, the plots demonstrate that the OK-E distribution is the most suitable model among all the models under consideration, aligning with the findings in Table 11.

Fig. 10

Plots of Estimated cdfs and pdfs for the second data set, respectively

Hence, the variance-covariance matrix for the OK-E$(a, b, \lambda , \beta )$ distribution may be expressed as:

$$\begin{aligned}\left[ \begin{array}{cccc} \mathrm{2.358872}\mathrm{\times }{10}^{-11} &{} \mathrm{\ }\mathrm{-1.650457}\mathrm{\times }{10}^{-8} &{} \mathrm{-8.027292} &{} \mathrm{-1.203496}\mathrm{\times }{10}^{-8} \\ \mathrm{-1.650457}\mathrm{\times }{10}^{-8} &{} \mathrm{0.0565875} &{} -5650.431 &{} 0.03429593 \\ \mathrm{-8.027292} &{} -5650.431 &{} \textrm{2735810000000} &{} -4113.108 \\ \mathrm{-1.203496}\mathrm{\times }{10}^{-8} &{} 0.03429593 &{} -4113.108 &{} \mathrm{0.0295696} \end{array}\right] \end{aligned}$$

The $95\%$ confidence intervals for a, b, $\lambda$, and $\beta$ are $[0,\mathrm{1.061779\times }{10}^{-5}]$, [0, 0.8237], [0, 3615971.3572], and [0.1539, 0.8279], respectively.

The LR test statistic for testing $H_0: OK-E(1,1,1,\beta ) \equiv Exp(\beta )$ against $H_1: OK-E(a,b,\lambda ,\beta )$ is 25.5144 with the associated p-value = $\mathrm{1.205227\times }{10}^{-5}$. Therefore, it may be inferred that there is a considerable difference in the distributions of $OK-E(a,b,\lambda ,\beta )$ and $Exp(\beta )$.

10.3 Data Set 3: Gross Domenstic Product Data

The provided dataset consists of 196 observations, including the gross domestic product (GDP) per capita of various nations worldwide in 2007. The World Bank facilitated the initial dissemination of this data via their database at http://data.worldbank.org/data-catalog/world-development-indicators. In addition, the R program ( [53]) offers a convenient means of acquiring the necessary information. This may be achieved by using the “gdp” data frame, which is included inside the R package “rpanel” ( [21]) and consists of 216 rows and 48 columns.

Table 12 presents the estimated parameters of the OK-E distribution and the competitive model and their corresponding standard errors included in parentheses. Table 13 displays the lowest values of the negative log-likelihood function $-l\left( \cdot \right)$ for each distribution applied to the third data set. Additionally, the table includes goodness-of-fit statistics derived from information criteria and the empirical distribution function. Upon comparing the OK-E distribution with the other distributions listed in Table 13, it becomes evident that the former exhibits the highest p-value for the KS and the lowest values for the $-l\left( \cdot \right)$, AIC, AICc, cAIC, BIC, SS, W${}^{*}$, A${}^{*}$, and KS metrics. This implies that the model under consideration is the most suitable choice for the given data set.

Table 12 MLEs and their standard errors (in parentheses) for gross domenstic product data

Table 13 Performance indices for gross domenstic product data

Figure 11 illustrates the hrf plots and the total time on the test (TTT). Both graphs shown in Fig. 11 demonstrate that the TTT curve has a convex form, providing more support for the notion that a nearly monotonically increasing or unimodal hrf is satisfactory. The OK-E distribution may suitably characterize the data collection.

Fig. 11

Empirical and fitted scaled TTT-transforms and hrf for the third data set, respectively

Based on the third data set, the profile log-likelihood functions of the parameters of the OK-E distribution demonstrate that the likelihood equations possess a singular solution for the parameters. Figure 12 provides evidence of the parameters’ uniqueness in the OK-E model.

Fig. 12

The log-likelihood as a function of parameters of OK-E for the third data set

Figure 13 shows the fitted distribution functions on the empirical and the fitted densities on the relative histogram. In line with the findings in Table 13, the plots demonstrate that the OK-E distribution provides the most excellent overall fit.

Fig. 13

Plots of Estimated cdfs and pdfs for the third data set, respectively

Given this, we can write down the OK-E$(a, b, \lambda , \beta )$ distribution’s estimated variance-covariance matrix as

$$\begin{aligned}\left[ \begin{array}{cccc} \mathrm{1.967753}\mathrm{\times }{10}^{-9} &{} \mathrm{\ }\mathrm{-7.463711}\mathrm{\times }{10}^{-9} &{} \mathrm{-20.80279} &{} \mathrm{-2.185061}\mathrm{\times }{10}^{-12} \\ \mathrm{-7.463711}\mathrm{\times }{10}^{-9} &{} \mathrm{0.001785329} &{} -80.082 &{} 4.755158\mathrm{\times }{10}^{-7} \\ \mathrm{-20.80279} &{} -80.082 &{} \textrm{219955100000} &{} -0.02110061 \\ \mathrm{-2.185061}\mathrm{\times }{10}^{-12} &{} 4.755158\mathrm{\times }{10}^{-7} &{} -0.02110061 &{} \mathrm{1.5}\textrm{66888}\mathrm{\times }{10}^{-10} \end{array}\right] \end{aligned}$$

The $95\%$ confidence intervals for a, b, $\lambda$, and $\beta$ are $[0,\mathrm{9.411654\times }{10}^{-5}]$, [0.0511, 0.2167], [0, 995056.467], and $[\mathrm{3.028068\times }{10}^{-5},\mathrm{7.934854\times }{10}^{-5}]$, respectively.

With a p-value of 0, the LR test statistic for comparing $H_0: OK-E(1,1,1,\beta ) \equiv Exp(\beta )$ against $H_1: OK-E(a,b,\lambda ,\beta )$ is 122.416. Therefore, we infer that the $OK-E(a,b,\lambda ,\beta )$ and $Exp(\beta )$ distributions are distinct from one another in a very significant way.

10.4 Data Set 4: Carbon Dioxide Data

The following dataset provides 196 observations of carbon dioxide (CO2) emissions, measured in metric tons per capita, for nations worldwide in 2003. Carbon dioxide (CO2) emissions are primarily generated via the production of cement and the combustion of fossil fuels. The emissions include carbon dioxide (CO2) generated from the combustion of gaseous, liquid, and solid fuels, as well as the process of gas flaring. The World Bank facilitated the initial provision of this data through the database accessible at http://data.worldbank.org/data-catalog/world-development-indicators. Moreover, the “co2.emissions” data frame, including 216 rows and 48 columns, may be readily accessed from the R program ( [53]) under the “rpanel” package ( [21]).

The parameter estimates and their corresponding standard errors for the OK-E distribution and the competitive models are shown in Table 14. Table 15 presents the lowest values of the negative log-likelihood function $-l\left( \cdot \right)$ and goodness of fit statistics derived from information criteria and the empirical distribution function for all the investigated distributions under study on the fourth data set. After considering all metrics, it becomes evident that the OK-E distribution exhibits the highest p-value for the KS while displaying lowest values for the $-l\left( \cdot \right)$, AIC, AICc, cAIC, BIC, SS, W${}^{*}$, A${}^{*}$, and KS in comparison to the other distributions shown in Table 15. Hence, it can be concluded that this model is the most optimal choice for accurately representing the given data set.

Table 14 MLEs and their standard errors (in parentheses) for carbon dioxide data

Table 15 Performance indices for carbon dioxide data

In this study, we offer empirical and fitted scaled TTT-transforms and hrf plots for the fourth data set, as seen in Fig. 14. Both figures demonstrate that the TTT curve is convex, proving that a monotonically declining hrf is appropriate. Hence, it can be concluded that the OK-E distribution is an approach suitable for fitting the given data set.

Fig. 14

Empirical and fitted scaled TTT-transforms and hrf for the fourth data set, respectively

The profile log-likelihood functions of the parameters of the OK-E distribution for the fourth data set are shown in Fig. 15. This display demonstrates that the likelihood equations possess a unique solution in the parameters. Therefore, Fig. 15 provides evidence of the uniqueness in the parameter support for our OK-E model.

Fig. 15

The log-likelihood as a function of parameters of OK-E for the fourth data set

The figure labeled 16 displays the empirical with the fitted distribution functions and the relative histogram with the fitted densities, respectively. The plots effectively illustrate that the OK-E distribution is the most suitable model among the several competing models, hence corroborating the findings shown in Table 15.

Fig. 16

Plots of Estimated cdfs and pdfs for the fourth data set, respectively

Therefore, the estimated variance covariance matrix for the OK-E$(a, b, \lambda , \beta )$ distribution is given by:

$$\begin{aligned}\left[ \begin{array}{cccc} \mathrm{1.143188}\mathrm{\times }{10}^{-5} &{} \mathrm{\ }\mathrm{-2.914239}\mathrm{\times }{10}^{-5} &{} \mathrm{-0.3990852} &{} \mathrm{-1.392578}\mathrm{\times }{10}^{-5} \\ \mathrm{-2.914239}\mathrm{\times }{10}^{-5} &{} \mathrm{0.06689471} &{} -1.0475857 &{} 0.01647857 \\ \mathrm{-0.3990852} &{} -1.0475857 &{} \mathrm{14040.5532152} &{} -0.1320393 \\ \mathrm{-1.392578}\mathrm{\times }{10}^{-5} &{} 0.01647857 &{} -0.1320393 &{} \mathrm{0.005692087} \end{array}\right] \end{aligned}$$

The $95\%$ confidence intervals for a, b, $\lambda$, and $\beta$ are [0, 0.0099], [0.1785, 1.1924], [0, 346.7002], and [0.2808, 0.5765], respectively.

The LR test statistic for testing $H_0: OK-E(1,1,1,\beta ) \equiv Exp(\beta )$ against $H_1: OK-E(a,b,\lambda ,\beta )$ is 50.7044 with the associated p-value = $\mathrm{5.655454\times }{10}^{-11}$. Hence, it is concluded that there is very strongly significant difference between $OK-E(a,b,\lambda ,\beta )$ and $Exp(\beta )$ distributions.

11 Concluding Remarks

This research study presents a novel and adaptable distribution known as the Odd Kappa-Exponential (OK-E) distribution. This paper presents an introduction to certain mathematical features of the OK-E distribution. Through empirical evidence, we have established that this probability distribution may effectively simulate a diverse range of heavy-tailed, skewed, and extreme datasets across several domains. The OK-E model has proven to be a valuable tool for analyzing environmental, engineering, and economic data frequently encountered in practical scenarios. Hence, we use four real data sets to provide empirical evidence of the efficacy of our novel flexible distribution from this particular family compared to other existing models documented in the literature. In subsequent investigations, more distributions belonging to this specific family will be explored in the context of complete and censored data.

Appendices

Appendix>

Second Partial Derivatives of the OddKappa-Exponential Distribution

$$\begin{aligned} \frac{{\mathrm {\partial }}^{\textrm{2}}{\ell }_n}{{\partial a }^2}&\mathrm {=-}\frac{n}{{a }^2}-\sum ^n_{i=1}{log\left[ a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right] ^{\left( \frac{2}{{a }^3}\right) }}\mathrm {+}\sum ^n_{i=1}\frac{1+\lambda \ log\left[ \frac{e^{\beta x_i}-1}{b }\right] {\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }}{{a^2 \left[ a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right] }^2} \times \nonumber \\ {}&\left\{ a \left( a +3\right) +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\left[ 2+a\lambda \left( a +1\right) \ log\left[ \frac{e^{\beta x_i}-1}{b }\right] \right] \right\} -\left( \frac{{\lambda }^2\left( a +1\right) }{a }\right) \times \nonumber \\&\sum ^n_{i=1}{{\left( log\left[ \frac{e^{\beta x_i}-1}{b }\right] \right) }^2{\left[ 1+a \ {\left( \frac{e^{\beta x_i}-1}{b }\right) }^{-a\lambda }\right] }^{-1}} \\{} & {} \frac{{\mathrm {\partial }}^{\textrm{2}}{\ell }_n}{\partial a \partial b }\mathrm {=}\left( \frac{\lambda }{b }\right) \sum ^n_{i=1} \frac{\left\{ {\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }+log\left[ \frac{e^{\beta x_i}-1}{b }\right] ^{a\lambda \left( a +1\right) }-1\right\} }{\left[ 1+a{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{-a\lambda }\right] } \\&\frac{{\mathrm {\partial }}^{\textrm{2}}{\ell }_n}{\partial a \partial \lambda }\mathrm {=}\sum ^n_{i=1}{\frac{log\left[ \frac{e^{\beta x_i}-1}{b }\right] {\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }}{{\left[ a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right] }^2}}\left\{ 1-{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }-a\lambda \left( a +1\right) log\left[ \frac{e^{\beta x_i}-1}{b }\right] \right\} \\&\frac{{\mathrm {\partial }}^{\textrm{2}}{\ell }_n}{\partial a \partial \beta }\mathrm {=}\lambda \sum ^n_{i=1}{\frac{x_i{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{\left( a\lambda -1\right) }}{e^{-\beta x_i}{\left[ a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right] }^2}}\left\{ \mathrm {1-}{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }-a\lambda \left( a +1\right) log\left[ \frac{e^{\beta x_i}-1}{b }\right] \right\} \\ \frac{{\mathrm {\partial }}^{\textrm{2}}{\ell }_n}{{\partial b }^2}&\mathrm {=}\frac{n\ \lambda }{{b }^2}\mathrm {-}\frac{\lambda \left( a +1\right) }{{b }^2}\sum ^n_{i=1}{\frac{{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }}{{\left[ a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right] }^2}}\left\{ \left( 1+a\lambda \right) \left( a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right) -\right. \nonumber \\ {}&\left. a\lambda {\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right\} \\&\frac{{\mathrm {\partial }}^{\textrm{2}}{\ell }_n}{\partial b \partial \lambda }\mathrm {=-}\frac{n}{b }\mathrm {+}\frac{\left( a +1\right) }{b }\sum ^n_{i=1}{\frac{{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }}{{\left[ a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right] }^2}}\mathrm {*}\left\{ a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }+{a }^2 \lambda log\left[ \frac{e^{\beta x_i}-1}{b }\right] \right\} \\&\frac{{\mathrm {\partial }}^{\textrm{2}}{\ell }_n}{\partial b \partial \beta }\mathrm {=}\left( a +1\right) \ {\left( \frac{a\lambda }{b }\right) }^{\textrm{2}}\sum ^n_{i=1}{\frac{x_i\ {\left( \frac{e^{\beta x_i}-1}{b }\right) }^{\left( a\lambda -1\right) }}{e^{-\beta x_i}\ {\left[ a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right] }^2}} \\&\frac{{\mathrm {\partial }}^{\textrm{2}}{\ell }_n}{{\partial \lambda }^2}\mathrm {=-}\frac{n}{{\lambda }^2}\mathrm {-}{a }^{\textrm{2}}\left( a +1\right) \ \sum ^n_{i=1}{\frac{{\left( log\left[ \frac{e^{\beta x_i}-1}{b }\right] \right) }^2\ {\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }}{{\left[ a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right] }^2}} \\&\frac{{\mathrm {\partial }}^{\textrm{2}}{\ell }_n}{\partial \lambda \partial \beta }&\mathrm {=}\sum ^n_{i=1}{\frac{x_i}{\left( 1-e^{-\beta x_i}\right) }}\mathrm {-}\left( \frac{\left( a +1\right) }{b }\right) \sum ^n_{i=1}{\frac{x_i\ {\left( \frac{e^{\beta x_i}-1}{b }\right) }^{\left( a\lambda -1\right) }}{e^{-\beta x_i}\ {\left[ a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right] }^2}} \times \nonumber \\ {}&\left\{ a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }+{a }^2\ \lambda \ log\left[ \frac{e^{\beta x_i}-1}{b }\right] \right\} \\&\frac{{\mathrm {\partial }}^{\textrm{2}}{\ell }_n}{{\partial \beta }^2}&\mathrm {=-}\frac{\textrm{1}}{{\beta }^{\textrm{2}}}\sum ^n_{i=1}{\left[ \beta \ x_i\left( 2-\beta x_i\right) \ +{\left( 1-\beta x_i\right) }^2\right] }+\ \sum ^n_{i=1}\frac{1}{{\left[ e^{-\beta x_i}\left( 1-e^{-\beta x_i}\right) \right] }^2} \times \nonumber \\ {}&\left\{ e^{-\beta x_i}\left( 1-e^{-\beta x_i}\right) \left[ 2\left( {\left( x_i\ e^{-\beta x_i}\right) }^2-\left( 1-e^{-\beta x_i}\right) \left( {x_i}^2\ e^{-\beta x_i}\right) \right) - \right. \right. \nonumber \\ {}&\left. \left. \frac{\left( {x_i}^2\ e^{-\beta x_i}\right) }{\left( \lambda -1\right) ^{-1}}\right] - \frac{\left( 1-2\left( 1-e^{-\beta x_i}\right) \right) \left( \lambda -1+2\left( 1-e^{-\beta x_i}\right) \right) }{{\left( x_i\ e^{-\beta x_i}\right) }^{-2}}\right\} -\lambda \left( a +1\right) \times \nonumber \\ {}&\sum ^n_{i=1}{\frac{\left( \frac{1}{e^{-4\beta x_i}}\right) {\left( \frac{e^{\beta x_i}-1}{b}\right) }^{\left( a\lambda -2\right) }}{b^2 {\left[ a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right] }^2}}\Bigg \{{\left( x_i\ e^{-\beta x_i}\right) }^2\Bigg [a \left( a\lambda -1\right) +2\ a \left( 1-e^{-\beta x_i}\right) + \nonumber \\ {}&\left( 2\left( 1-e^{-\beta x_i}\right) -1\right) {\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\Bigg ]-e^{-\beta x_i}\left( 1-e^{-\beta x_i}\right) \left( {x_i}^2\ e^{-\beta x_i}\right) \times \\ {}&\left( a +{\left( \frac{e^{\beta x_i}-1}{b }\right) }^{a\lambda }\right) \Bigg \} \end{aligned}$$