1 Introduction

Statistical distributions have long been used to represent data for goals such as prediction and decision-making. Life cycle analysis, reliability, life expectancy, insurance, engineering, finance, economics, biological sciences, extreme events, medicine, agricultural engineering, actuarial science, demography, administration, sports, and materials science are all examples of their applications. Numerous statistical distributions consist of additional parameters to well-established continuous distributions in order to provide them new and intriguing functions. The most notorious of these families are Exponential-G family [1], beta-G family [2], gamma-G family [3]. Recent promising families include the Kumaraswamy-G family [4], half-logistic-G family of type II [5], generalized odd log-logistic Poisson family [6], odd Frechet-G family of distributions [7], Garhy-generated family of distributions [8], generalized transmuted Poisson-G family [9], Topp-Leone family [10, 11], Topp-Leone-Weibull [12], power Lambert uniform distribution [13], Gemeay–Zeghdoudi distribution [14], step stress and partially accelerated life testing [15], Burr III-Topp-Leone-G family of distributions [16], Fréchet Topp-Leone-G [17], Topp-Leone G transmuted [18], Topp-Leone Inverse Lomax [19], new power Topp-Leone-G Family [20], Generalized Topp-Leone-Weibull [12], Topp-Leone-Marshall-Olkin-G family [21], Topp-Leone generalized Rayleigh distribution [22, 23], Topp-Leone inverse Rayleigh distribution [24], truncated exponential Topp Leone Rayleigh distribution [25]. In addition to these previous works, recent advancements in the field of statistical distributions have introduced promising newcomers, including a novel extension of the Fréchet distribution [26], an efficient estimators of population variance in two-phase successive sampling under random non-response [27], and the half-normal model using informative priors under Bayesian Structure [28].

Most statistical distributions face limitations when it comes to adapting to various types of data sets. Indeed, certain datasets exhibit specific characteristics like high skewness, kurtosis, heavy tails, inverted J-shapes, multimodality, and more. Distribution generators offer the capability to manage and manipulate these dataset characteristics effectively. In this research, our objective is to create a novel set of distributions by merging the Topp-Leone and Cauchy distribution families, and showing how distributions from the created family offer a large possibility of adapting to real life data. The Topp-Leone distributions are extensively employed due to their advantageous attributes, such as mathematical simplicity and the versatility of their probabilistic functions. Its cumulative distribution function (CDF) is given by:

$$\begin{aligned} F(x;\alpha )=x^\alpha (2-x)^\alpha , \end{aligned}$$
(1)

where \(\alpha >0\) and \(0\le x \le 1\) and the pdf is:

$$\begin{aligned} f(x;\alpha )=2\alpha x^{\alpha -1}(1-x)(2-x)^{\alpha -1}. \end{aligned}$$
(2)

The Topp-Leone-G distribution family emerges from the fusion of (1) and P, where P represents a CDF. It is precisely this CDF that defines the distinguishing features of this distribution family.

$$\begin{aligned} F(x;\alpha ,\tau )= \left[ P(x;\tau )\right] ^{\alpha }\left[ 2-P(x,\tau ) \right] ^{\alpha }. \end{aligned}$$
(3)

\(P( x; \tau ) \in \left[ 0, 1 \right] , \alpha > 0 \), and \(P( x; \tau )\) is a basic continuous distribution’s CDF depending on \(\tau =( \tau _1,\ldots, \tau _n)\).

One way to define the Cauchy distribution is by its CDF, which is given by:

$$\begin{aligned} H(x;a,b)=\frac{1}{\pi }\arctan \left(\frac{x-b}{a}\right)+ \frac{1}{2}, \end{aligned}$$
(4)

where \(a>0\) represents a scale parameter, b a position parameter, and \(x \in \left] 0; +\infty \right[\). By combining \(P(x, \tau )\) and the Cauchy distribution’s CDF (4), we get:

$$\begin{aligned} H(x;a,b,\tau )=\frac{1}{\pi }\arctan \left(\frac{P(x,\tau )-b}{a}\right)+ \frac{1}{2} \end{aligned}$$
(5)

By merging the Topp-Leone distribution family (3) with the Cauchy distribution (5), we will create the new family. The representation of the CDF of the Topp-Leone distribution family (3) can be restated as:

$$\begin{aligned} F(x;\alpha ,\tau )= \left[ 1-\left( 1-P(x;\tau )\right) ^2\right] ^{\alpha } \end{aligned}$$
(6)

By combining expressions (5) and (6), we get the new family’s CDF which is defined by:

$$\begin{aligned} F(x;\nu )=\left\{1-\left[ \frac{1}{2}-\frac{1}{\pi }\arctan\left( \frac{x( {P(x;\tau )+m)-b}}{a}\right) \right]^2 \right \}^\alpha\end{aligned}$$
(7)

\(\nu = (\alpha , a, b, \tau, m )\) and \(\alpha , a,\tau, m >0\) and \(x\in \,-\infty;+\infty \).

The development of this novel distribution family is driven by several motivations. First, it aims to offer increased flexibility compared to traditional statistical distributions like the normal or exponential, which often have limited parameters, making them less suitable for modeling highly variable real-world data. This new family introduces more parameters, enhancing its ability to adapt to complex phenomena. Second, it extends beyond the restricted value ranges commonly seen in classic distributions, making it applicable to a wider range of fields where data may lack predefined bounds. Additionally, it seeks to model diverse real-world phenomena more accurately, accounting for behaviors such as heavy tails, asymmetries, and extreme values. Finally, its versatility allows for application across various disciplines, from environmental sciences to medicine and engineering. Ultimately, the overarching goal is to improve the quality of statistical model fitting to real data, leading to more precise and reliable results across diverse research and application domains.

From this new family of distributions, several are the special members with very interesting properties. Within this family, we have introduced a distinct member where the basic distribution is represented by the CDF G. This yields the Topp-Leone Cauchy Rayleigh distribution, which encompasses four parameters. To evaluate its effectiveness, we have applied this distribution to two actual datasets and compared its performance against other existing competing models.

2 A Special Member: The TLCAR Distribution

The TLCA-G family encompasses various distributions, and the process of discovering a new distribution within this family parallels the process of discovering a new base distribution. In this work, the TLCAR distribution is established by utilizing the Rayleigh distribution with a positive shape parameter \(\theta\) as the foundational distribution. The CDF of the Rayleigh distribution can be expressed as:

$$\begin{aligned} L(x;\theta )= 1-e^{\left( \frac{-x^2}{2\theta ^2}\right) }, \end{aligned}$$

where \(\theta > 0\) et \(x \in [ 0,+\infty [.\)

The associated probability density function (PDF) and hazard rate function (HRF) are given respectively, by:

$$\begin{aligned} l(x;\theta )=\frac{xe^{\left( \frac{-x^2}{2\theta ^2}\right) }}{\theta ^2}, \end{aligned}$$

and

$$\begin{aligned} hrf(x;\theta )=\frac{1}{\theta ^2}x. \end{aligned}$$

The CDF that defines the TLCAR distribution is expressed as follows:

$$\begin{aligned} F(x;\nu )=\left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }\arctan \frac{1-e^{\left( \frac{-x^2}{2\theta ^2}\right) } -b}{a}\right) ^2\right] ^\alpha , \end{aligned}$$
(8)

where \(\alpha , a, \theta > 0\). The associated PDF and HRF of (8) are respectively:

$$\begin{aligned} f(x;\nu )=\frac{2\alpha }{\pi a\theta ^2}&\times \left[ \frac{xe^{\frac{-x^2}{2\theta ^2}}}{1+\left( \frac{1-e^{\frac{-x^2}{2\theta ^2}} -b}{a}\right) ^2}\right] \nonumber \\&\times \left[ \frac{1}{2}-\frac{1}{\pi } \arctan\frac{1-e^{\frac{-x^2}{2\theta ^2}} -b}{a}\right] \nonumber \\&\times \left[ 1-\left( \frac{1}{2}-\frac{1}{\pi } \arctan\frac{1-e^{\frac{-x^2}{2\theta ^2}} -b}{a}\right) ^2\right] ^{\alpha -1}, \end{aligned}$$
(9)

and

$$\begin{aligned} h(x;\nu )=\frac{f(x;\nu )}{1-\left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }arctan\frac{1-e^{\frac{-x^2}{2\theta ^2}} -b}{a}\right) ^2\right] ^\alpha }. \end{aligned}$$
(10)

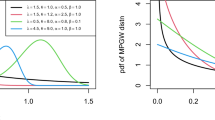
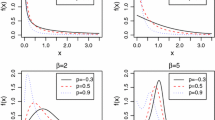
Figure 1 displays a graphical representation of the PDF of the TLCAR distribution, while Fig. 2 illustrates its HRF. Notably, Fig. 1 highlights the potential for the PDF to display a positive asymmetry and a shape of type J inverted. The PDF can exhibit diverse shapes, including increasing, decreasing, inverted, or bathtub-shaped patterns. This observation aligns with previous findings documented in the literature. These curvature characteristics are well known to be useful for developing versatile statistical models.

Fig. 1
figure 1

Probability density functions of the TLCAR distribution

Full size image
Fig. 2
figure 2

TLCAR distribution’s hazard rate functions

Full size image

3 Several Mathematical Properties of the TLCAR Distribution

This section highlights several important mathematical characteristics of the TLCAR distribution.

3.1 Serial Development of f

Proposition 1

The serial development of f is given by:

$$\begin{aligned} f(x)=\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j} \times k(x;\nu ) \times K_{j-1}(x;\nu ), \end{aligned}$$
(11)

where

$$\begin{aligned} T_{i,j}=\left( -1\right) ^{i+j} \times j \times \left( {\begin{array}{c}\alpha \\ i\end{array}}\right) \left( {\begin{array}{c}2i\\ j\end{array}}\right) \left( \frac{1}{2}\right) ^{2i-j}\left( \frac{1}{\pi }\right) ^j, \end{aligned}$$
(12)

and

$$\begin{aligned} K_{j-1}= & {} \left[ K(x;\nu )\right] ^{j-1}, k(x,\nu )=(K(x;\nu ))' \hspace{0.2cm}, \end{aligned}$$
(13)
$$\begin{aligned} K(x;\nu )= & {} \arctan \left( \frac{1-e^{\frac{-x^2}{2\theta ^2}}-b}{a}\right) . \end{aligned}$$
(14)

Proof

According to (8), \(F(x;\nu )=\left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }\arctan \frac{1-e^{\frac{-x^2}{2\theta ^2}} -b}{a}\right) ^2\right] ^\alpha\),

Considering \(K(x;\nu ) =\arctan \left( \frac{1-e^{\frac{-x^2}{2\theta ^2}}-b}{a}\right)\),

and

$$\begin{aligned} F(x;\nu )=\left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }K(x;\nu )\right) ^2 \right] ^\alpha , \end{aligned}$$
(15)

Using the binomial formula, we have:

$$\begin{aligned} \left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }K(x;\nu )\right) ^2\right] ^\alpha =\sum _{i=0}^{\alpha }\left( -1\right) ^i\left( {\begin{array}{c}\alpha \\ i\end{array}}\right) \left[ \frac{1}{2}-\frac{1}{\pi }K(x;\nu )\right] ^{2i}, \end{aligned}$$

and

$$\begin{aligned} \left[ \frac{1}{2}-\frac{1}{\pi }K(x,\sigma )\right] ^{2i} =\sum _{j=0}^{2i}(-1)^{j}\left( {\begin{array}{c}2i\\ j\end{array}}\right) \left( \frac{1}{2}\right) ^{2i-j}\left( \frac{1}{\pi }\right) ^j\times \left[ K(x,\nu )\right] ^j, \end{aligned}$$

So we get:

$$\begin{aligned} F(x)=\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}(-1)^{i+j}\left( {\begin{array}{c}\alpha \\ i\end{array}}\right) \left( {\begin{array}{c}2i\\ j\end{array}}\right) \left( \frac{1}{2}\right) ^{2i-j}\left( \frac{1}{\pi }\right) ^j\times \left[ K(x,\nu )\right] ^j. \end{aligned}$$
(16)

By deriving the expression (16) of F(x) with x, we obtain the serial development (11) of f(x). \(\square\)

3.2 Rényi Entropy

The Rényi entropy associated with the distribution is given by:

$$\begin{aligned} ER(X)=\frac{1}{1-\gamma }log\left\{ \sum _{i=0}^{\gamma (\alpha -1)}\sum _{j=0}^{2i+\gamma }L_{i,j,\gamma }I_{j,\gamma }(x,\nu )\right\} , \end{aligned}$$
(17)

where

$$\begin{aligned} L_{i,j,\gamma }=\frac{(-1)^{i+j}}{i!j!}&\times \frac{\Gamma (\gamma (\alpha -1)+1)\Gamma (2i+\gamma +1)}{\Gamma (\gamma (\alpha -1)-i+1)\Gamma (2i+\gamma -j+1)} \nonumber \\&\times \left( \frac{1}{2}\right) ^{2i+\gamma -j}\left( \frac{1}{\pi }\right) ^{j} \left( \frac{2\alpha }{\pi }\right) ^{\gamma }, \end{aligned}$$
(18)

and

$$\begin{aligned} I_{j,\gamma }(x,\nu )= & {} \int _{\mathbb {R}}k(x;\nu )^{\gamma }K(x;\nu )^jdx, \end{aligned}$$
(19)
$$\begin{aligned} K_{j-1}= & {} \left[ K(x;\nu )\right] ^{j-1}, k(x;\nu )=(K(x;\nu ))', \end{aligned}$$
(20)
$$\begin{aligned} K(x;\nu )= & {} \arctan \left( \frac{1-e^{\frac{-x^2}{2\theta ^2}}-b}{a}\right) \end{aligned}$$
(21)

Proof

The Rényi entropy of X for a continuous random variable can be defined by:

$$\begin{aligned} ER(X)= & {} \frac{1}{1-\gamma }\log \left\{ \int _{\mathbb {R}}f(x,\nu )^\gamma dx \right\} ,\gamma \ne 1, \gamma > 0, \\ f(x;\nu )^{\gamma }= & {} \left[ \frac{2\alpha }{\pi }\right] ^{\gamma }\times \left[ k(x;\nu )\right] ^{\gamma } \times \left[ \frac{1}{2}-\frac{1}{\pi }K(x;\nu )\right] ^{\gamma }\\{} & {} \times \left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }K(x;\nu )\right) ^2\right] ^{\gamma (\alpha -1)}, \end{aligned}$$

       So we have:

$$\begin{aligned} f(x;\nu )^{\gamma }&=\sum _{i=0}^{\gamma (\alpha -1)}\sum _{j=0}^{2i+\gamma }(-1)^{i+j}\left( {\begin{array}{c}\gamma (\alpha -1)\\ i\end{array}}\right) \left( {\begin{array}{c}2i+\gamma \\ j\end{array}}\right) \\& \quad \times \left( \frac{1}{2}\right) ^{2i+\gamma -j}\left( \frac{1}{\pi }\right) ^j\left( \frac{2\alpha }{\pi }\right) ^{\gamma }\left[ k(x;\nu )\right] ^{\gamma }\left[ K(x;\nu )\right] ^j, \end{aligned}$$

Therefore, the Renyi entropy is given by:

$$\begin{aligned} ER(X)=\frac{1}{1-\gamma }\log\left\{ \sum _{i=0}^{\gamma (\alpha -1)}\sum _{j=0}^{2i+\gamma }L_{i,j,\gamma }I_{j,\gamma }(x,\nu )\right\} , \end{aligned}$$

\(\square\)

3.3 Moments

At this point, we will take a closer look at the moments of our distribution. Moment is a key statistical measure that allows us to characterize the shape of the distribution and to better understand its properties and behavior.

Proposition

The moment of order s associated with our distribution is given by:

$$\begin{aligned} M_s=\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j} \times S_s(x;\nu ), \end{aligned}$$
(22)

where \(T_{i,j}\) is defined in (12)

$$\begin{aligned} S_{s}(x;\nu )=\int _{0}^{+\infty } x^s \times k(x;\nu ) \times K_{j-1}(x;\nu ) dx, \end{aligned}$$
(23)

Proof

The moment of order s of a variable is determined by:

$$\begin{aligned} M_s=\mathbb {E}(X^s), \end{aligned}$$

so

$$\begin{aligned} M_s=\int _{0}^{\infty } x^s \times f(x) dx, \end{aligned}$$

By using the serial development (11), we have:

$$\begin{aligned} M_s&=\int _{0}^{+\infty } x^s \times \sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j} \times k(x;\nu ) \times K_{j-1}(x;\nu ) dx \\&= \sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j}\int _{0}^{+\infty } x^s \times k(x;\nu ) \times K_{j-1}(x;\nu ) dx, \end{aligned}$$
$$\begin{aligned} M_s=\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j} \times S_s(x;\nu ), \end{aligned}$$

where \(S_s(x;\nu )\) is defined in (23). \(\square\)

3.4 Moment Generating Function

Proposition

The moment generating function is given by:

$$\begin{aligned} M_{X}(t)= \sum _{l=0}^{+\infty }\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j}\times \frac{t^l}{l!}\times S_{l}(x;\nu ), \end{aligned}$$
(24)

Proof

The moment generating function is determined by:

$$\begin{aligned} M_{X}(t)=\mathbb {E}(e^{tx}). \end{aligned}$$

By using the serial development of exponential function, we have:

$$\begin{aligned} e^{tx}=\sum _{r=0}^{+\infty }\frac{(tx)^r}{r!}, \end{aligned}$$

So we can write:

$$\begin{aligned} M_{X}(t)&=\mathbb {E}( \sum _{r=0}^{+\infty }\frac{(tx)^r}{r!}) \nonumber \\&=\sum _{r=0}^{+\infty }\mathbb {E}(\frac{(tx)^r}{r!})\nonumber \\&=\sum _{r=0}^{+\infty }\frac{(t)^r}{r!}\mathbb {E}(x^r), \end{aligned}$$
(25)

\(\mathbb {E}(x^r)\) represents the order moment r of the distribution. So,

$$\begin{aligned} M_r&=\mathbb {E}(x^r) \nonumber \\&=\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j,\alpha } \times S_r(x;\nu ), \end{aligned}$$
(26)

By replacing (26) in (25), we obtain:

$$\begin{aligned} M_{X}(t)= \sum _{r=0}^{+\infty }\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j}\times \frac{t^r}{r!}\times S_{r}(x;\nu ), \end{aligned}$$

where

$$\begin{aligned} S_{r}(x;\nu )=\int _{0}^{+\infty } x^r \times k(x;\nu ) \times K_{j-1}(x;\nu ) dx. \end{aligned}$$

\(\square\)

3.5 Incomplete Moments

The incomplete moment of TLCAR distribution can be obtained as:

$$\begin{aligned} M_s(y)&=\mathbb {E}(X^sY_y) ,\\&= \int _{-\infty }^{y} x^s \times f(x;\nu ) dx , \end{aligned}$$

By considering the expression obtained with the moment in (22), we have:

$$\begin{aligned} M_s(y)=\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j} \times S_{s,y}(x;\nu ), \end{aligned}$$

where \(T_{i,j}\) is defined in (12)

$$\begin{aligned} S_{s,y}(x;\nu )=\int _{-\infty }^{y} x^s \times k(x,\nu ) \times K_{j-1}(x;\nu ) dx. \end{aligned}$$

3.6 Moment-Weighted Probabilities (MWP)

The MWP is defined by:

$$\begin{aligned} M_{r,s}=\sum _{i=0}^{\alpha (s+1)-1}\sum _{j=0}^{2i+1}J_{i,j,s}I_{j}(x;\nu ), \end{aligned}$$

where

$$\begin{aligned} J_{i,j,s}&=(-1)^{i+j}\left( {\begin{array}{c}\alpha (s+1)-1\\ i\end{array}}\right) \left( {\begin{array}{c}2i+1\\ j\end{array}}\right) (-1)^{i+j}\nonumber \\& \quad \times \left( \frac{1}{2}\right) ^{2i+1-j}\left( \frac{1}{\pi }\right) ^{j}\left( \frac{2\alpha }{\pi }\right) , \end{aligned}$$
(27)

and

$$\begin{aligned} I_{j}(x,\nu )=\int _{0}^{+\infty }x^rk(x;\nu )K(x;\nu )^jdx, \end{aligned}$$
(28)

Proof

Let put \(\varphi (x)=f(x) \times F^s(x)\),

$$\begin{aligned} f(x)&=\left( \frac{2\alpha }{\pi }\right) \times k(x;\nu )\times \left( \frac{1}{2}-\frac{1}{\pi }K(x;\nu )\right) \nonumber \\ {}& \quad \times \left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }K(x;\nu )\right) ^2\right] ^{\alpha -1} , \nonumber \\ F^s(x)&=\left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }K(x;\nu )\right) ^2\right] ^{\alpha \times s} , \end{aligned}$$
(29)

so

$$\begin{aligned} \varphi (x)&=\left( \frac{2\alpha }{\pi }\right) \times k(x;\nu )\times \left( \frac{1}{2}-\frac{1}{\pi }K(x;\nu )\right) \\ {}& \quad \times \left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }K(x;\nu )\right) ^2\right] ^{\alpha (s+1)-1} , \end{aligned}$$

By using the binomial formula, we have:

$$\begin{aligned} \varphi (x)&=\sum _{i=0}^{\alpha (s+1)-1} \sum _{j=0}^{2i+1}(-1)^{i+j}\left( {\begin{array}{c}\alpha +s-1\\ i\end{array}}\right) \left( {\begin{array}{c}2i+1\\ j\end{array}}\right) \nonumber \\ {}& \quad \times \left( \frac{1}{2}\right) ^{2i+1-j}\left( \frac{1}{\pi }\right) ^{j}\left( \frac{2\alpha }{\pi }\right) k(x;\nu ) \times K(x;\nu )^j, \end{aligned}$$
(30)

The moment generating function is determined by:

$$\begin{aligned} M_{r,s}=E\left[ X^rF^s(x)\right] =\int _{0}^{+\infty }x^r\varphi (x)dx, \end{aligned}$$

Therefore:

$$\begin{aligned} M_{r,s}=\sum _{i=0}^{\alpha (s+1)-1}\sum _{j=0}^{2i+1}J_{i,j,s}I_{j}(x;\nu ), \end{aligned}$$

where \(J_{i,j,s}\) and \(I_j(x;\nu )\) are defined respectively in (27) and (28). \(\square\)

3.7 Quantile Function

In this section, we will give with justification the quantile function.

Proposition

The quantile function associated with the distribution is defined by:

$$\begin{aligned} Q(y;\nu )=\theta \sqrt{2\ln \left[ \frac{1}{1-a\tan \left(\frac{1}{2}-\sqrt{1-y^{\frac{1}{\alpha }}}\right)\pi -b}\right] }. \end{aligned}$$

Proof

Let us put

$$\begin{aligned} x_y = Q(y;\nu ) \hspace{0.5cm} \forall \hspace{0.2cm} y \in \left[ 0, 1\right] ; \end{aligned}$$

Then by the definition of the quantile function, \(x_y\) satisfies the nonlinear equation:

$$\begin{aligned} y = F(x;\tau ) \end{aligned}$$

So

$$\begin{aligned} y=\left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }\arctan \frac{P(x;\tau )-b}{a}\right) ^2\right] ^\alpha , \end{aligned}$$
(31)

By raising each member of Eq> (31) to the power \(\frac{1}{\alpha }\) we have:

$$\begin{aligned} y^{\frac{1}{\alpha }}=1-\left[ \frac{1}{2}-\frac{1}{\pi }\arctan (\frac{P(x;\tau )-b}{a}\right] ^2, \end{aligned}$$

Let put

$$\begin{aligned} \arctan \left(\frac{(P(x;\tau )-b)}{a}\right)= K \end{aligned}$$
(32)

We get:

$$\begin{aligned}{} & {} y^{\frac{1}{\alpha }} =1-\left(\frac{1}{2}-\frac{1}{\pi }K\right)^2, \\{} & {} \quad K=(\frac{1}{2}-\sqrt{1-y^{\frac{1}{\alpha }}})\pi , \end{aligned}$$

Considering the expression (32), we can write:

$$\begin{aligned}{} & {} \arctan \left( \frac{P(x;\tau )-b}{a}\right) =\left( \frac{1}{2}-\sqrt{1-y^{\frac{1}{\alpha }}}\right)\pi , \\{} & {} \quad P(x;\tau )=a\left[ \tan \left( \frac{1}{2}-\sqrt{1-y^{\frac{1}{\alpha }}}\right) \pi \right] +b, \end{aligned}$$

In our case, \(P(x;\theta )= 1-e^{\left( \frac{-x^2}{2\theta ^2}\right) }\),

So we have:

$$\begin{aligned} e^{\left( \frac{-x^2}{2\theta ^2}\right) } &=1-a\left[ \tan \left(\frac{1}{2}-\sqrt{1-y^{\frac{1}{\alpha }}}\right)\pi \right] -b \\ x &=\theta \sqrt{-2\ln \left(1-a\left[ \tan \left(\frac{1}{2}-\sqrt{1-y^{\frac{1}{\alpha }}}\right)\pi \right] -b\right)}, \end{aligned}$$

Therefore, the quantile function is given by:

$$\begin{aligned} Q(y,\sigma )=\theta \sqrt{2\ln \left[ \frac{1}{1-a\tan \left(\frac{1}{2}-\sqrt{1-y^{\frac{1}{\alpha }}}\right)\pi -b}\right] } \end{aligned}$$

\(\square\)

3.8 Survival Function

The survival function of TLCAR distribution is given by:

$$\begin{aligned} suf(x)= & {} 1-F(x), \\ suf(x)= & {} 1-\left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }\arctan \frac{1-e^{\frac{-x^2}{2\theta ^2}} -b}{a}\right) ^2\right] ^\alpha . \end{aligned}$$

3.9 Hazard Function

The hazard function of TLCAR distribution is defined as:

$$\begin{aligned} haf(x)= & {} \frac{f(x)}{suf(x)}, \\ haf(x)= & {} \frac{f(x)}{1-\left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }\arctan \frac{1-e^{\frac{-x^2}{2\theta ^2}} -b}{a}\right) ^2\right] ^\alpha }, \end{aligned}$$

3.10 Cumulative Hazard Function (Cf)

The cumulative hazard function is defined by the following expression:

$$\begin{aligned} Cf(x)=-\log (suf(x)), \end{aligned}$$

So, the TLCAR distribution’s cumulative hazard function is given by:

$$\begin{aligned} Cf(x)=-\log \left\{ 1-\left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }\arctan \frac{1-e^{\frac{-x^2}{2\theta ^2}} -b}{a}\right) ^2\right] ^\alpha \right\} \end{aligned}$$

3.11 Reserve Hazard Function

We use the following expression to determine the reserve hazard function:

$$\begin{aligned} Rf(x)=\frac{f(x)}{F(x)}, \end{aligned}$$

Therefore, the reserve hazard function of TLCAR distribution is given by:

$$\begin{aligned} Rf(x)=\frac{f(x)}{\left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }\arctan \frac{1-e^{\frac{-x^2}{2\theta ^2}} -b}{a}\right) ^2\right] ^\alpha } \end{aligned}$$

3.12 Mean Waiting Time

The mean waiting time refers to the average time one has to wait for an event or an outcome to occur. It is a measure of central tendency that quantifies the typical or average duration of waiting. It is defined as:

$$\begin{aligned} mt(x)=x-\left[ \frac{1}{F(x)}\int _0^xx \times f(x)dx\right] , \end{aligned}$$

By using the expression (11) of f(x), we have:

$$\begin{aligned} mt(x)&=x-\frac{1}{F(x)}\int _{0}^{x}\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j} k(x;\nu ) K_{j-1}(x;\nu ) x dx \\&=x-\frac{1}{F(x)}\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j} \int _0^x k(x;\nu ) K_{j-1}(x;\nu ) x dx , \end{aligned}$$

So, the mean waiting time of TLCAR distribution is given by:

$$\begin{aligned} mt(x)=x-\frac{1}{F(x)}\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j,\alpha } M_x(x;\nu ), \end{aligned}$$

where

$$\begin{aligned} M_x(x,\nu )=\int _0^x k(x;\nu ) \times K_{j-1}(x;\nu ) \times x dx. \end{aligned}$$
(33)

3.13 Mean Residual Life

The mean residual life is a concept that pertains to survival analysis and the study of lifetime or duration data. It is a measure that provides information about the average remaining lifetime of an individual or system given that it has already survived up to a certain point. The mean residual life function (mr) is defined as:

$$\begin{aligned} mr(x)=\frac{1}{1-F(x)}\int _0^{\infty }xf(x)dx -x, \end{aligned}$$

By using the serial development (11) of f(x), we have:

$$\begin{aligned} mr(x)=\frac{1}{1-F(x)}\int _0^{\infty }\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j} k(x;\nu ) K_{j-1}(x;\nu ) x dx -x, \end{aligned}$$

So, the mean residual life of TLCAR distribution is given by:

$$\begin{aligned} mr(x)=\frac{1}{1-F(x)}\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,ja}M_\infty (x;\nu ) -x, \end{aligned}$$

where

$$\begin{aligned} M_\infty (x;\nu )=\int _0^\infty k(x;\nu ) \times K_{j-1}(x;\nu ) \times x dx \end{aligned}$$

3.14 Mean Deviation About Mean

The mean deviation about the mean (also known as the mean absolute deviation or simply the average deviation) is a measure of the average distance between each data point in a dataset and the mean of that dataset. It provides a measure of the dispersion or spread of the data. Suppose X has TLCAR distribution with a mean of \(\mu\). The mean absolute deviation is expressed as follows:

$$\begin{aligned} MAD(\mu )=\mathbb {E}(|X-\mu |) \end{aligned}$$
(34)

By using (34), we have:

$$\begin{aligned} MAD(\mu )&=\int _0^\infty |x-\mu |\times f(x)dx \\&=\int _0^\mu |x-\mu |\times f(x)dx+\int _\mu ^\infty |x-\mu |\times f(x)dx\\&=2\mu F(\mu ) - 2\int _{0}^\mu x \times f(x)dx\\&=2\mu F(\mu ) - 2\int _{0}^\mu \sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j} k(x;\nu ) K_{j-1}(x;\nu ) x dx\\&=2\mu F(u)-2\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j} \int _{0}^\mu k(x;\nu ) K_{j-1}(x;\nu ) x dx , \end{aligned}$$

So, the mean absolute deviation is given by:

$$\begin{aligned} MAD(\mu )=2\mu F(\mu )-2\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j}M_\mu (x;\nu ), \end{aligned}$$

where

$$\begin{aligned} M_\mu (x;\nu )=\int _{0}^\mu k(x;\nu ) K_{j-1}(x;\nu ) x dx \end{aligned}$$

3.15 Mean Deviation About Median

The mean deviation about the median is a measure of the average distance between each data point in a dataset and the median of that dataset. It is similar to the mean deviation about the mean, but instead of using the mean as the central measure, the median is used. Let consider the TLCAR distribution’s random variable X has a median value of Me. The mean deviation about median can be expressed as:

$$\begin{aligned} MDM(\mu )=\mathbb {E}(|X-Me|), \end{aligned}$$
(35)

By using (35), we have:

$$\begin{aligned} md(Me)&=\int _0^\infty |x-Me|f(x)dx \\&=\int _0^{Me} |x-Me|f(x)dx +\int _{Me}^\infty |x-Me|f(x)dx \\&=\mu - 2\int _{0}^{Me} xf(x)dx\\&=\mu - 2\int _{0}^{Me} \sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j} k(x;\nu ) K_{j-1}(x;\nu ) x dx\\&=\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j} \int _{0}^{Me}k(x;\nu ) K_{j-1}(x;\nu ) x dx , \end{aligned}$$

So, the mean absolute deviation is given by:

$$\begin{aligned} md(Me)=\mu -2\sum _{i=0}^{\alpha }\sum _{j=0}^{2i}T_{i,j}M_{m}(x,\nu ), \end{aligned}$$

where

$$\begin{aligned} M_{m}(x;\nu )=\int _{0}^M k(x;\nu ) K_{j-1}(x;\nu ) x dx \end{aligned}$$

4 Estimation

Let \(x_1, x_2,\ldots, x_n\) be a random sample of size n of a variable X. Then, using the pdf in (9), the likelihood function is given by:

$$\begin{aligned} L(\alpha ,a,b,\theta )=\prod _{k=1}^n f(x_{k}), \end{aligned}$$

So we have:

$$\begin{aligned} L(\alpha ,a,b,\theta )&=\left( \frac{2\alpha }{\pi a\theta ^2}\right) ^n\prod _{k=1}^n\left[ \frac{x_ke^{\frac{-x_k^2}{2\theta ^2}}}{1+\left( \frac{1-e^{\frac{-x_k^2}{2\theta ^2}}-b}{a}\right) ^2}\right] \left[ \frac{1}{2}-\frac{1}{\pi }\arctan \frac{1-e^{\frac{-x_k^2}{2\theta ^2}} -b}{a}\right] \\ {}& \quad \times \left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }\arctan \frac{1-e^{\frac{-x_k^2}{2\theta ^2}} -b}{a}\right) ^2\right] ^{\alpha -1}. \end{aligned}$$

The log-likelihood function is defined as:

$$\begin{aligned} l(\alpha ,a,b,\theta )= \ln \left[ L(\alpha ,a,b,\theta ))\right] , \end{aligned}$$

We obtain:

$$\begin{aligned} l(\alpha ,a,b,\theta )&= n\ln 2+n\ln \alpha -n\ln \pi -n\ln a-2n\ln \theta \\ &\quad +\sum _{k=1}^{n}\ln x_k-\sum _{k=1}^{n}\frac{x_k^2}{2\theta ^2}-\sum _{k=1}^{n}\ln \left[ 1+\left( \frac{1-e^{\frac{-x_k^2}{2\theta ^2}}-b}{a}\right) ^2\right] \\ {}&\quad +\sum _{k=1}^n\ln \left[ \frac{1}{2}-\frac{1}{\pi }\arctan \left( \frac{1-e^{\frac{-x_k^2}{2\theta ^2}} -b}{a}\right) \right] \\ &\quad +(\alpha -1)\sum _{k=1}^n\ln \left[ 1-(\frac{1}{2}-\frac{1}{\pi }\arctan \left( \frac{1-e^{\frac{-x_k^2}{2\theta ^2}} -b}{a}\right) ^2\right] . \end{aligned}$$

Defining the maximum likelihood estimators \(\hat{\alpha }\), \(\hat{a}\), \(\hat{b}\) and \(\hat{\theta }\), we satisfy:

\(l(\hat{\alpha },\hat{a},\hat{b},\hat{\theta })= max_{ (\alpha ,a,b,\theta ) \in \left[ 0,+\infty \right] ^{4}} l(\alpha ,a,b,\theta )\)

Let’s put:

$$\begin{aligned} Z_k=\frac{1-e^{\frac{-x_k^2}{2\theta ^2}} -b}{a} \end{aligned}$$

We have:

$$\begin{aligned}{} {} \frac{\partial Z_k}{\partial \alpha } &= 0 \\ {} \frac{\partial Z_k}{\partial a} &= -\frac{1}{a^2}\left[ 1-e^{\frac{-x_k^2}{2\theta ^2}} -b\right] = -\frac{Z_k}{a} \\{} \frac{\partial Z_k}{\partial b} &= -\frac{1}{a} \\{} \frac{\partial Z_k}{\partial \theta } &= -\frac{1}{a}\frac{x_k^2}{\theta ^3}\exp ^{-\frac{x_k^2}{2\theta ^2}} \end{aligned}$$

The log-likelihood function can therefore be rewritten as follows:

$$\begin{aligned} l(\alpha ,a,b,\theta )&= n\ln 2+n\ln \alpha -n\ln \pi -n\ln a-2n\ln \theta \\ & \quad +\sum _{k=1}^{n}\ln x_k-\sum _{k=1}^{n}\frac{x_k^2}{2\theta ^2}-\sum _{k=1}^{n}\ln \left[ 1+Z_k^2\right] \nonumber \\ {}&\quad +\sum _{k=1}^n\ln \left[ \frac{1}{2}-\frac{1}{\pi }\arctan Z_k\right] \\ & \quad +(\alpha -1)\sum _{k=1}^n\ln \left[ 1-\left(\frac{1}{2}-\frac{1}{\pi }\arctan Z_k^2\right)\right] . \end{aligned}$$
(36)

The first partial derivatives of \(l(\hat{\alpha },\hat{a},\hat{b},\hat{\theta })\) to be set to zero are provided as follows:

$$\begin{aligned} \frac{\partial l}{\partial \alpha }= & {} \frac{n}{\alpha }+\sum _{k=1}^n\ln \left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }\arctan Z_k\right) ^2\right] , \end{aligned}$$
(37)
$$\begin{aligned} \frac{\partial l}{\partial a} &=-\frac{n}{a}-\sum _{k=1}^{n}\frac{2Z_k^2}{a\left( 1+Z_k^2\right) }+\sum _{k=1}^{n}\frac{Z_k}{\pi a\left( 1+Z_k^2\right) \left( \frac{1}{2}-\frac{1}{\pi }\arctan Z_k\right) } \\ & \quad +\sum _{k=1}^{n}\frac{2(\alpha -1)Z_k\left( \frac{1}{2}-\frac{1}{\pi }\arctan Z_k\right) }{\pi a\left( 1+Z_k^2\right) \left[ 1-\left( \frac{1}{2}-\frac{1}{\pi }\arctan Z_k\right) ^2\right] }, \end{aligned}$$
(38)
$$\begin{aligned} \frac{\partial l}{\partial b} &=\sum _{k=1}^{n}\frac{2Z_k}{a(1+Z_k^2)}+\sum _{k=1}^{n}\frac{1}{\pi a^2(1+Z_k^2)(\frac{1}{2}-\frac{1}{\pi }\arctan Z_k)} \\ & \quad +\sum _{k=1}^{n}\frac{2(\alpha -1)(\frac{1}{2}-\frac{1}{\pi }\arctan Z_k)}{\pi a^2(1+Z_k^2)\left[ 1-(\frac{1}{2}-\frac{1}{\pi }\arctan Z_k)^2\right] }, \end{aligned}$$
(39)
$$\begin{aligned}\frac{\partial l}{\partial \theta } &=-\frac{2n}{\theta }+\sum _{k=1}^{n}\frac{x_k^2}{\theta ^3}-\sum _{k=1}^{n}\frac{x_k^2}{a\theta ^3}e^{-\frac{x_k^2}{2\theta ^2}}\frac{Z_k}{1+Z_k^2} +\sum _{k=1}^{n}\frac{x_k^2e^{-\frac{x_k^2}{2\theta ^2}} }{\pi a \theta ^3 (1+Z_k^2)(\frac{1}{2}-\frac{1}{\pi }\arctan Z_k)}\\& \quad -\sum _{k=1}^{n}\frac{2(\alpha -1)x_k^2e^{-\frac{x_k^2}{2\theta ^2}}(\frac{1}{2}-\frac{1}{\pi }\arctan Z_k)}{\pi a \theta ^3(1+Z_k^2)(1-(\frac{1}{2}-\frac{1}{\pi }\arctan Z_k)^2)} \end{aligned}$$
(40)

5 Simulation Study

To assess the consistency of maximum likelihood estimators (MLEs) within the context of our hybrid TLCAR distribution, a comprehensive simulation study is conducted in this section using the R package ’stats4.’ We generate one thousand independent samples, each with varying sizes of \(n=80, 100, 200, 300\), and 400, drawn from the TLCAR distribution. For each of the 1000 replications, we computed the MLEs for the parameters of interest. Subsequently, we assessed two fundamental statistical metrics: the average bias (Bias) and the root mean square error (RMSE). These metrics were used to evaluate the precision and consistency of the estimated parameters. The results of these calculations are documented in Table 1. This simulation-based approach provides a robust framework for scrutinizing the performance of MLEs and offers valuable insights into their consistency under various sample size scenarios within the unique context of the TLCAR distribution.

Table 1 Results from Monte Carlo simulations for the TLCAR distribution: Calculations of Mean, RMSE, and Mean Bias
Full size table

6 Data Analysis

To test the performance of our distribution in real life situations, we will apply it with two appropriate data sets and compare its performance to the existing competing models below:

  1. 1.

    Topp-Leone Compound Rayleigh (TLCR) [29].

  2. 2.

    On Type II Topp Leone Inverse Rayleigh Distribution (TIITIR) [30].

  3. 3.

    Rayleigh distribution [31].

We used Mathematica to determine the estimated values of the density function parameters and Matlab to plot them. The analysis of the results will allow us to determine whether the distribution lives up to its promise in real-life situations.

Dataset I:

The provided dataset exhibits failure times (measured in hours) obtained from an accelerated life test involving 59 conductors. The data are presented below [32, 33]: 6.545, 9.289, 7.543, 6.956, 6.492, 5.459, 8.120, 4.706, 8.687, 2.997, 8.591, 6.129, 11.038, 5.381, 6.958, 4.288, 6.522, 4.137, 7.459, 7.495, 6.573, 6.538, 5.589, 6.087, 5.807, 6.725, 8.532, 9.663, 6.369, 7.024, 8.336, 9.218, 7.945, 6.869, 6.352, 4.700, 6.948, 9.254, 5.009, 7.489, 7.398, 6.033, 10.092, 7.496, 4.531, 7.974, 8.799, 7.683, 7.224, 7.365, 6.923, 5.640, 5.434, 7.937, 6.515, 6.476, 6.071, 10.941, 5.923. Table 2 displays the estimated values for the dataset I. The information criteria obtained from different models on the dataset I are presented in Table 3. Moreover, empirical PDFs and CDFs for dataset I can be visualized in Fig. 3.

Table 2 Estimated values for the dataset I
Full size table
Table 3 The information criteria results for the hailing time data (dataset I)
Full size table
Fig. 3
figure 3

Visualization of Empirical PDFs and CDFs for dataset I

Full size image

Dataset II:

The dataset consists of observations on the fracture toughness of silicon nitride, measured in units of MPa \(m^{\frac{1}{2}}\) [16]. The set is consisted of 119 observations which are: 5.5, 5, 4.9, 6.4, 5.1, 5.2, 5.2, 5, 4.7, 4, 4.5, 4.2, 4.1, 4.56, 5.01, 4.7, 3.13, 3.12, 2.68, 2.77, 2.7, 2.36, 4.38, 5.73, 4.35, 6.81, 1.91, 2.66, 2.61, 1.68, 2.04, 2.08, 2.13, 3.8, 3.73, 3.71, 3.28, 3.9, 4, 3.8, 4.1, 3.9, 4.05, 4, 3.95, 4, 4.5, 4.5, 4.2, 4.55, 4.65, 4.1, 4.25, 4.3, 4.5, 4.7, 5.15, 4.3, 4.5, 4.9, 5, 5.35, 5.15, 5.25, 5.8, 5.85, 5.9, 5.75, 6.25, 6.05, 5.9, 3.6, 4.1, 4.5, 5.3, 4.85, 5.3, 5.45, 5.1, 5.3, 5.2, 5.3, 5.25, 4.75, 4.5, 4.2, 4, 4.15, 4.25, 4.3, 3.75, 3.95, 3.51, 4.13, 5.4, 5, 2.1, 4.6, 3.2, 2.5, 4.1, 3.5, 3.2, 3.3, 4.6, 4.3, 4.3, 4.5, 5.5, 4.6, 4.9, 4.3, 3, 3.4, 3.7, 4.4, 4.9, 4.9, 5. Table 4 displays the estimated values for the dataset II. The information criteria obtained from different models on the dataset II are presented in Table 5. From Fig. 4, we can see the empirical PDFs and CDFs for dataset II.

Table 4 Estimated values for the dataset II
Full size table
Table 5 Results of information criteria for hailing time Data (dataset II)
Full size table
Fig. 4
figure 4

Visualization of empirical PDFs and CDFs for dataset II

Full size image

After analyzing the Tables 2, 3, 4, 5, and Figs. 3, 4, it can be deduced that the TLCAR model demonstrates a more robust compatibility with the datasets I and II examined in comparison to the rival models. The TLCAR model possesses the advantage of flexibility, enabling its application to both industrial and artificial intelligence data. Hence, it can be concluded that the TLCAR model is the preferable option for modeling these datasets, owing to its superior performance and versatility in accommodating diverse data types.

7 Conclusion

Our study focused on the creation and use of a distribution to simulate data. We implemented a rigorous methodology and were able to create a reliable distribution based on empirical data and precise statistical calculations. The simulations performed with this distribution showed results very close to the real data, thus demonstrating the relevance and efficiency of our approach.

Furthermore, we emphasized the relevance of assessing the suitability of statistical models to the data by comparing simulation outcomes to real-world data and employing visualization tools like histograms and density functions.

Finally, our study has shown that the creation of custom distributions can be an efficient approach to simulate data in different fields such as finance, biology, industry or physics.

We hope that our work will serve as a foundation for future research and contribute to the advancement of knowledge in these areas.

8 Future Work and Coming

This research intends to focus on various areas of exploration in the future. One of these topics will include investigating transformations as TX among others in order to create a new distribution for predicting unknown lifetime occurrences. This new distribution will provide a more sophisticated statistical model for studying and predicting lifetimes, as well as it has the potential to be employed in a wide range of applications. Another area of research will be the creation of a bivariate distribution, which will allow us to evaluate and forecast the interaction of two variables. We will also investigate copulas and other aspects of this novel distribution to better understand its behavior and applicability.

Last but not least, we also intend to use the new distribution with engineering and accelerated data to investigate the reliability function’s behavior utilizing calibrated data. This will help to establish the new distribution’s potential utility in industry and other sectors by providing insights into how it might be utilized in real-world circumstances. Overall, our future research will concentrate on the development of advanced statistical models and the analysis of their behavior in a variety of applications. We are excited about the possible insights and breakthroughs that these investigations may yield.