The Extended Birnbaum–Saunders Distribution Based on the Scale Shape Mixture of Skew Normal Distributions

Abstract

In this article, a large class of univriate Birnbaum–Saunders distributions based on the scale shape mixture of skew normal distributions is introduced which generates suitable subclasses for modeling asymmetric data in a variety of settings. The moments and maximum likelihood estimation procedures are disscused via an ECM-algorithm. The observed information matrix to approximate the asymptotic covariance matrix of the parameter estimates is then derived in some subclasses. A simulation study is also performed to evaluate the finite sample properties of ML estimators and finally, a real data set is analyzed for illustrative purposes.

1 Introduction

The two-parameter Birnbaum Saunders (BS) distribution, as a life type distribution, was originally introduced by Birnbaum and Saunders [8] in a failure model due to cracks, see Miner [31]. This distribution is related with normal distribution by means of a very simple functional relationship, and is based on a physical argument of cumulative damage that produces fatigue in the materials. The BS distribution, as a skew distribution, has been frequently applied in last few years; to biological model by Desmond [14], to medical field by Leiva et al. [26] and Barros et al. [5], to the forestry and environmental sciences by Podaski [32], Leiva et al. [28] and Vilca et al. [37], to fatigue life model by Cordeiro et al. [12], and to genetic model by Hassani et al. [20].

However, the BS model may suffer from a lack of robustness in the presence of extreme outlying observations. To allay this problem, several extensions of the BS distribution have been proposed in the literature, see e.g. Diaz-Garcia and Leiva [15], Sanhueza et al. [36], Leiva et al. [27], Gomez et al. [17], Vilca et al. [38], Hashemi et al. [25], Poursadeghfard et al. [33], Reyes et al.[34], and Mahbudi et al. [29], Benkhalifa [7],

The skew normal (SN) distribution proposed by Azzalini [2, 3] has been widely used in many applications to accommdate data with skewness. For more flexibilities, several extension of the SN model have been still considered. Branco and Dey [9] discussed the family of scale mixtures the skew-normal (SMSN) distributions. The random variable Y is said to have the univariate SMSN model when it has the following representation

$$\begin{aligned} Y\mid \tau \overset{d}{=}SN\left( \varepsilon ,\sigma ^{2}\tau ^{-1},\lambda \right) , \end{aligned}$$

where $\tau$ is a positive random variable with cumulative distribution function (cdf) $H(\tau ;\upsilon ).$ The cdf $H(\tau ;\upsilon )$ is known as the mixing scale distribution. The univarite skew-t ([4]) and skew-slash ([39]) distributions are two special cases of SMSN distributions. Jammalizadeh et al. (2017) consider a more general class of scale-shape mixtures of skew normal (SSMSN) distributions and applied the EM-type algorithm for the computation of maximum likelihood estimates of parameters. This model includes SMSN model as a special case. Further, any model of the form $\frac{2}{\sigma }f\left( \frac{y-\xi }{\sigma }\right) G\left( \lambda \left( \frac{y-\xi }{\sigma }\right) \right) ,$ for which f and G are scale mixtures of the normal distributions, belongs to this class. For example, the skew t normal (STN) distribution discussed by Gomez et al. [18] and Cabral et al. [11] is a special case of SSMSN distributions.

In this paper, we introduce a new extension class of the BS distributions based on the SSMSN class, named the scale shape mixture of skew nomal- Birnbaum Saunders (SSMSN-BS) class. It includes the STN-BS distributions in Poursadeghfard et al. [33], the SNT-BS distributions in Hashemi et al. [25] and the SN-BS distributions in Vilca et al. (38) as the special cases. According to more felxibility of the class of SSMSN-BS distributions, they are attractive for modeling skewed and positive data sets in a much wider range, and we hope they have a better fit to compare the gamma, lognormal, weibull and exponential distributions as the lifetime distributions. However, a direct likelihood maximization for this class is dificult to compute due to the complexity of the likelihood function. To overcome this hurdle, we propose the ECM algorithm to estimate the parameters based on a convenient stochastic representation.

The rest of this paper is structured as follows. In Sect. 2, a useful stochastic representation of the SSMSN-BS class and its subclasses is presented, and basic properties of them are studied. In Sect. 3, the ECM-type algorithms for calculating ML estimates of parameters are provided. The information matrix for obtaining the asymptotic covariance matrix of the ML estimates are calculated in Sect. 4. Finally, a simulation study is presented in Sect. 5, where the proposed methodology through a real data set is also illustrated.

2 The Class of SSMSN-BS Distributions

In this section, we present the definition and some simple properties of the SSMSN-BS distributions. Some important asymmetric distributions generated from SSMSN-BS are also studied. Suppose $Z_{1}$ and $Z_{2}$ be two independent copies from $N\left( 0,1\right)$, and $\varvec{\tau } =\left( \tau _{1},\tau _{2}\right) ^{T}$ be a positive bivariate random variable, i.e. $P\left( \tau _{1}>0,\tau _{2}>0\right) =1,$ with probability density function (pdf) $h\left( \varvec{\tau ,\eta }\right)$ where $\varvec{\eta }$ is a vector of parameters. Further, we assume that both $\mathbf {Z}=\left( Z_{1},Z_{2}\right) ^{T}$ and $\varvec{\tau }=\left( \tau _{1},\tau _{2}\right) ^{T}$ are independent. A random variable Y is said to have the scale shape mixture of skew normal $\left( SSMSN\right)$ distribution, denoted by $Y\thicksim SSMSN\left( \lambda ,\varvec{\eta } \right)$, if

$$\begin{aligned} Y\mid \left( \tau _{1},\tau _{2}\right) \overset{d}{=}SN\left( 0,\tau _{1}^{-1},\lambda \left( \frac{\tau _{1}}{\tau _{2}}\right) ^{-\frac{1}{2} }\right) . \end{aligned}$$

(1)

By using the stochastic representation in $\left( 1\right)$ the random variable Y has following useful representation

$$\begin{aligned} Y\overset{d}{=}\left( \frac{\tau _{1}^{-\frac{1}{2}}f^{\frac{1}{2}}}{\sqrt{ f+\lambda ^{2}}}Z_{2}+\frac{\lambda \tau _{1}^{-\frac{1}{2}}}{\sqrt{ f+\lambda ^{2}}}\left| Z_{1}\right| \right) , \end{aligned}$$

(2)

with $f=\frac{\tau _{1}}{\tau _{2}}.$ Denoting by $\gamma =\sqrt{\tau _{1}^{-1}\left( f+\lambda ^{2}\right) }\left| Z_{1}\right| ,$ a further hierarchical representation of the SSMSN distribution can be written as

$$\begin{aligned} Y&\mid&\left( \gamma ,\tau _{1},\tau _{2}\right) \overset{d}{=}N\left( \frac{\lambda \gamma }{f+\lambda ^{2}},\frac{f}{\tau _{1}\left( f+\lambda ^{2}\right) }\right) ,\nonumber \\ \text { }\gamma&\mid&\left( \tau _{1},\tau _{2}\right) \overset{d}{=} TN\left( 0,\frac{f+\lambda ^{2}}{\tau _{1}};\left( 0,+\infty \right) \right) , \end{aligned}$$

(3)

where TN $\left( \mu ,\sigma ^{2};\left( a,b\right) \right)$ represents the truncated normal distribution for $N\left( \mu ,\sigma ^{2}\right)$ lying within the truncated interval $\left( a,b\right) ,$ see Jammalizadeh and Lin (2017) for more details.

The cdf and pdf of a BS random variable, denoted by T $\thicksim BS\left( \alpha ,\beta \right) ,$ are given by

$$\begin{aligned} F_{BS}\left( t;\alpha ,\beta \right)\,=\, & {} \Phi \left( a\left( t;\alpha ,\beta \right) \right) ,\nonumber \\ f_{BS}\left( t;\alpha ,\beta \right)=\, & {} \phi \left( a\left( t;\alpha ,\beta \right) \right) A\left( t;\alpha ,\beta \right) ,t>0, \end{aligned}$$

(4)

where

$$\begin{aligned} a\left( t;\alpha ,\beta \right)=\, & {} \frac{1}{\alpha }\left( \sqrt{\frac{t}{ \beta }}-\sqrt{\frac{\beta }{t}}\right) ,\nonumber \\ A\left( t;\alpha ,\beta \right)=\, & {} \frac{da\left( t;\alpha ,\beta \right) }{ dt}=\frac{t+\beta }{2\alpha \sqrt{\beta }\sqrt{t^{3}}}, \end{aligned}$$

(5)

and $\alpha >0$ and $\beta >0$ are shape and scale parameters, and $\Phi$ and $\phi$ denote the cdf and pdf of the standard normal distribution, respectively.

The stochastic representation of T is

$$\begin{aligned} T=\frac{\beta }{4}\left[ \alpha Z+\sqrt{\left( \alpha Z\right) ^{2}+4}\right] ^{2},\text { }Z\thicksim N\left( 0,1\right) . \end{aligned}$$

(6)

See Birnbaum and Saunders [8].

Definition 2.1

If $Z\thicksim SSMSN\left( \lambda ,\varvec{ \eta }\right)$ in (6), then T is said to have a BS distribution based on SSMSN distribution with parameter$\left( \alpha ,\beta ,\lambda , \varvec{\eta }\right) .$ It is denoted by $T\thicksim \text {SSMSN-BS}\left( \alpha ,\beta ,\lambda ,\varvec{\eta }\right) .$

From (3), (5) and (6), the joint pdf T,  $\gamma$ and $\varvec{\tau } =\left( \tau _{1},\tau _{2}\right)$ is given by

$$\begin{aligned} f\left( t,\gamma ,\varvec{\tau }\right)= & {} \frac{1}{\pi }\exp \left( - \frac{1}{2}\tau _{2}\gamma ^{2}+\tau _{2}\lambda \gamma \tau a\left( t;\alpha ,\beta \right) -\frac{1}{2}\tau _{2}\lambda ^{2}a^{2}\left( t;\alpha ,\beta \right) -\frac{1}{2}\tau _{1}a^{2}\left( t;\alpha ,\beta \right) \right) \nonumber \\&\times \sqrt{\tau _{1}\tau _{2}}h(\varvec{\tau };\varvec{\eta } )A\left( t;\alpha ,\beta \right) . \end{aligned}$$

(7)

By integrating on $\gamma$ in (7), we get

$$\begin{aligned} f\left( t,\varvec{\tau }\right) =2\phi \left( \sqrt{\tau _{1}}a\left( t;\alpha ,\beta \right) \right) \Phi \left( \lambda \sqrt{\tau _{2}}a\left( t;\alpha ,\beta \right) \right) \sqrt{\tau _{1}}h(\varvec{\tau ;\eta }). \end{aligned}$$

(8)

The marginal density of T is then given by

$$\begin{aligned} f\left( t\right) =\int _{0}^{\infty }\int _{0}^{\infty }f\left( t,\tau _{1},\tau _{2}\right) d\tau _{1}d\tau _{2}. \end{aligned}$$

(9)

Dividing (7) by (8) gives

$$\begin{aligned} f\left( \gamma \mid t,\tau _{1},\tau _{2}\right) =\sqrt{\tau _{2}}\frac{\phi \left( \sqrt{\tau _{2}}\left( \gamma -\lambda a\left( t;\alpha ,\beta \right) \right) \right) }{\Phi \left( \lambda \sqrt{\tau _{2}}a\left( t;\alpha ,\beta \right) \right) }=f\left( \gamma \mid t,\tau _{2}\right) , \end{aligned}$$

(10)

implying that $\gamma$ and $\tau _{1}$ are conditionally independent given $T=t$ and $\tau _{2}.$ From (10), it is clear that

$$\begin{aligned} \gamma \mid \left( t,\tau _{2}\right) \thicksim TN\left( \lambda a\left( t;\alpha ,\beta \right) ,\frac{1}{\tau _{2}},\left( 0,\infty \right) \right) . \end{aligned}$$

(11)

The conditional pdf of $\varvec{\tau }=\left( \tau _{1},\tau _{2}\right)$ given $T=t$ is also given by

$$\begin{aligned} f\left( \tau _{1},\tau _{2}\mid t\right) =\frac{2\phi \left( \sqrt{\tau _{1}} a\left( t;\alpha ,\beta \right) \right) \Phi \left( \lambda \sqrt{\tau _{2}} a\left( t;\alpha ,\beta \right) \right) \sqrt{\tau _{1}}h(\varvec{\tau ;\eta })}{f\left( t\right) }. \end{aligned}$$

(12)

Proposition 2.1

Let $T\thicksim \text {SSMSN-BS}$, then the mean, variance, coefficient of variation, skewness and kurtosis of T are given by

$$\begin{aligned} E[T]= & {} E[T_{1}]+\frac{\alpha \beta }{2}\omega _{1},\nonumber \\ V[T]= & {} V[T_{1}]+\left[ \frac{\alpha \beta }{2}\right] ^{2}\alpha _{\omega }, \nonumber \\ \gamma [T]= & {} \gamma [T_{1}]\frac{\sqrt{1+\frac{\alpha ^{2}\beta ^{2}\alpha _{\omega }}{V(2T_{1})}}}{1+\frac{\alpha \beta \omega _{1}}{E[2T_{1}]}},\nonumber \\ \alpha _{3}[T]= & {} \alpha _{3}[T_{1}]\left[ \frac{\alpha ^{2}(2ET^{*4}-E^{2}T^{*2})+4ET^{*2}}{\alpha ^{2}(2ET^{*4}-E^{2}T^{*2})+4ET^{*2}+\alpha \omega }\right] ^{\frac{3}{2}}\nonumber \\&+\frac{2[a_{0}+a_{1}\alpha +a_{2}\alpha ^{2}]}{[\alpha ^{2}(2ET^{*4}-E^{2}T^{*2})+4ET^{*2}+\alpha _{\omega }]^{\frac{3}{2}}},\nonumber \\ \alpha _{4}[T]= & {} \left[ \alpha _{4}[T_{1}]+\frac{b_{0}+b_{1}\alpha +b_{2}\alpha ^{2}+b_{3}\alpha ^{3}}{(\alpha ^{2}(2ET^{*4}-E^{2}T^{*2})+4ET^{*2})^{2}}\right] \nonumber \\&\frac{[\alpha ^{2}(2ET^{*4}-E^{2}T^{*2})+4ET^{*2}]^{2}}{ [\alpha ^{2}(2ET^{*4}-E^{2}T^{*2})+4ET^{*2}+\alpha _{\omega }]^{2}}, \end{aligned}$$

(13)

respectively, where

$$\begin{aligned} E[T_{1}]= & {} \frac{\beta }{2}\left[ \alpha ^{2}ET^{*^{2}}+2\right] ,\nonumber \\ V[T_{1}]= & {} \frac{\beta ^{2}\alpha ^{2}}{4}\left[ \alpha ^{2}(2ET^{*^{4}}-E^{2}T^{*^{2}})+4ET^{*^{2}}\right] , \nonumber \\ \gamma [T_{1}]= & {} \frac{\alpha \sqrt{\alpha ^{2}(2ET^{*^{4}}-E^{2}T^{*^{2}})+4ET^{*^{2}}}}{\left[ \alpha ^{2}ET^{*^{2}}+2\right] }, \nonumber \\ \alpha _{3}[T_{1}]= & {} \frac{1}{\left[ V[T_{1}]\right] ^{\frac{3}{2}}}\frac{ \beta ^{3}\alpha ^{4}}{8}\left[ \alpha ^{2}(4ET^{*^{6}}-6ET^{*^{4}}ET^{*^{2}}+2E^{3}T^{*^{2}})+12ET^{*^{4}}-12E^{2}T^{*^{2}}\right] , \nonumber \\ \alpha _{4}[T_{1}]= & {} \frac{1}{\left[ V[T_{1}]\right] ^{2}}\frac{\beta ^{4}\alpha ^{4}}{8}[\alpha ^{4}(8ET^{*^{8}}-16ET^{*2}ET^{*^{6}}+12ET^{*^{4}}E^{2}T^{*2}-3E^{4}T^{*2}) \nonumber \\&+\alpha ^{2}(32ET^{*^{6}}-48ET^{*^{4}}ET^{*2}+24E^{3}T^{*^{3}})+16ET^{*^{4}}], \end{aligned}$$

(14)

with $T^{*}\left( \upsilon _{1}\right) \overset{d}{=}\tau _{1}^{-\frac{1 }{2}}\left( \upsilon _{1}\right) Z\left( 0,1\right) ,ET^{*2}=E\tau _{1}^{-1},ET^{*4}=3E\tau _{1}^{-2},ET^{*6}=15E\tau _{1}^{-3},ET^{*^{8}}=105E\tau _{1}^{-4},$ and

$$\begin{aligned} \alpha _{\omega }=\, & {} 2\alpha (\omega _{3}-\omega _{1}ET^{*2})-\omega _{1}^{2},\nonumber \\ a_{0}=\, & {} \omega _{1}^{3}-6\omega _{1}ET^{*2}+2\omega _{3}, \nonumber \\ a_{1}=\, & {} 3\omega _{1}^{2}ET^{*2}-3\omega _{1}\omega _{3}, \nonumber \\ a_{2}=\, & {} 2\omega _{5}-3\omega _{3}ET^{*2}-3\omega _{1}ET^{*4}+3\omega _{1}E^{2}T^{*2}, \nonumber \\ b_{0}=\, & {} -3\omega _{1}^{4}-16\omega _{1}\omega _{3}+24\omega _{1}^{2}ET^{*2}, \nonumber \\ b_{1}=\, & {} 16\omega _{5}-16\omega _{3}ET^{*2}-48\omega _{1}ET^{*2}+48\omega _{1}E^{2}T^{*2}+12\omega _{1}^{2}\omega _{3}-12\omega _{1}^{3}ET^{*2}, \nonumber \\ b_{2}=\, & {} -16\omega _{1}\omega _{5}+12\omega _{1}^{2}ET^{*4}-18\omega _{1}^{2}E^{2}T^{*2}+24\omega _{1}\omega _{3}ET^{*2}, \nonumber \\ b_{3}=\, & {} 8\omega _{7}-16\omega _{1}ET^{*6}-16\omega _{5}ET^{*2}+12\omega _{3}E^{2}T^{*2}+24\omega _{1}ET^{*2}ET^{*4}-12\omega _{1}E^{3}T^{*2}, \nonumber \\ \omega _{k}=\, & {} E[Y^{k}\sqrt{\alpha ^{2}Y^{2}+4}],k=1,3,5,7,\text { \ \ } Y\thicksim SSMSN\left( \lambda ,\varvec{\eta }\right) . \end{aligned}$$

(15)

In the following subsections, some asymmetric distributions generated by $SSMSN-BS$ are studied.

2.1 The Skew t$_{1}$t$_{2}$-BS Distribution

Let $\tau _{1}$ and $\tau _{2}$ be two independent gamma random variables with shape and rate parameters equal to $\frac{\upsilon _{i}}{2},$ namely $\Gamma \left( \frac{\upsilon _{i}}{2},\frac{\upsilon _{i}}{2}\right)$ for $i=1,2,$ with the following joint density

$$\begin{aligned} h\left( \varvec{\tau ;\eta }\right) =f\left( \tau _{1};\frac{\upsilon _{1}}{2},\frac{\upsilon _{1}}{2}\right) f\left( \tau _{2};\frac{\upsilon _{2} }{2},\frac{\upsilon _{2}}{2}\right) , \end{aligned}$$

(16)

where $\varvec{\eta }=\left( \upsilon _{1},\upsilon _{2}\right)$ and f denotes the pdf of the gamma distribution, then Y in (2) and (3), is said to have the skew t$_{\text {1}}$t$_{\text {2}}$ distribution with parameter $\left( \lambda ,\varvec{\eta }\right) ,$ and will be denoted by $Y\sim ST_{\upsilon _{1}}T_{\upsilon _{2}}\left( \lambda ,\upsilon _{1},\upsilon _{2}\right) .$ Now we define the skew

t$_{\text {1}}$t$_{\text {2}}$-BS distribution as follows:

Definition 2.2

If $Y\overset{d}{=}Z\sim ST_{\upsilon _{1}}T_{\upsilon _{2}}\left( \lambda ,\upsilon _{1},\upsilon _{2}\right)$ in (6), we say that the random variable T follows the $ST_{\upsilon _{1}}T_{\upsilon _{2}}\text {-BS}$ distribution with the following pdf

$$\begin{aligned} f_{ST_{\upsilon _{1}}T_{\upsilon _{2}}-BS}(t;\alpha ,\beta ,\lambda ,\upsilon _{1},\upsilon _{2})= & {} 2t(a(t;\alpha ,\beta );\upsilon _{1})T(\lambda a(t;\alpha ,\beta );,\upsilon _{2})\nonumber \\ & \times {}\, A(t;\alpha ,\beta ),\text {\ }t,\text { } \alpha ,\text { }\beta ,\text { }\upsilon _{1},\text { }\upsilon _{2}>0,\text { } \lambda \in R\text {.} \end{aligned}$$

(17)

where $t\left( .;\upsilon _{1}\right) ,$ $T\left( .;\upsilon _{2}\right)$ denote the pdf and cdf of the Student-t distribution with degree of freedom $\upsilon _{1},$ $\upsilon _{2}$ respectively.

We shall write $T\sim ST_{\upsilon _{1}}T_{\upsilon _{2}}\text {-BS}(\alpha ,\beta ,\lambda ,\upsilon _{1},\upsilon _{2})$ to denote that T follows the $ST_{\upsilon _{1}}T_{\upsilon _{2}}\text {-BS}$ distribution with pdf in (17). The mean, variance and measures of skewness and kurtosis coefficients of T follows from the equations in (13)–(15), for which, we have

$$\begin{aligned} T^{*}\left( \upsilon _{1}\right) \overset{d}{=}\Gamma ^{-\frac{1}{2} }\left( \frac{\upsilon _{1}}{2},\frac{\upsilon _{1}}{2}\right) Z\left( 0,1\right) , \end{aligned}$$

(18)

with

$$\begin{aligned} ET^{*2}=\, & {} \frac{\upsilon _{1}}{\upsilon _{1}-1},\ \upsilon _{1}>2, \\ ET^{*4}= \,& {} \frac{3\upsilon _{1}^{2}}{(\upsilon _{1}-1)(\upsilon _{1}-4)} ,\upsilon _{1}>4, \\ ET^{*6}= \,& {} \frac{15\upsilon _{1}^{3}}{(\upsilon _{1}-1)(\upsilon _{1}-4)(\upsilon _{1}-6)},\upsilon _{1}>6, \\ ET^{*8}= \,& {} \frac{105\upsilon _{1}^{4}}{(\upsilon _{1}-1)(\upsilon _{1}-4)(\upsilon _{1}-6)(\upsilon _{1}-8)},\upsilon _{1}>8,\\ Y\sim & {} ST_{\upsilon _{1}}T_{\upsilon _{2}}\left( \lambda ,\upsilon _{1},\upsilon _{2}\right) . \end{aligned}$$

From (12), the conditional pdf of $\tau _{1}$ given $T=t$ is

$$\begin{aligned} \left( \tau _{1}\mid T=t\text { }\right) \thicksim \Gamma \left( \frac{ \upsilon _{1}+1}{2},\frac{\upsilon _{1}+a^{2}(t;\alpha ,\beta )}{2}\right) , \end{aligned}$$

(19)

and the conditional pdf of $\tau _{2}$ given $T=t$ is

$$\begin{aligned} f\left( \tau _{2}\mid T=t\text { }\right) =\frac{\left( \frac{\upsilon _{2}}{2 }\right) ^{\frac{\upsilon _{2}}{2}}\tau _{2}^{^{\frac{\upsilon _{2}}{2} -1}}\exp \left( -\frac{\upsilon _{2}}{2}\tau _{2}\right) \Phi \left( \lambda \sqrt{\tau _{2}}a(t;\alpha ,\beta )\right) }{T\left( \lambda a(t;\alpha ,\beta );\upsilon _{2}\right) }. \end{aligned}$$

(20)

So, we have

$$\begin{aligned} E\left( \tau _{1}\mid T=t\right)= \,& {} E\left( \tau _{1}\mid T=t\right) =\frac{ \upsilon _{1}+1}{\upsilon _{1}+a^{2}(t;\alpha ,\beta )},\nonumber \\ E\left( \log \tau _{1}\mid T=t\right)=\, & {} DG\left( \frac{\upsilon _{1}+1}{2} \right) -\log \left( \frac{\upsilon _{1}+a^{2}(t;\alpha ,\beta )}{2}\right) , \nonumber \\ E\left( \tau _{2}\mid T=t\right)= \,& {} \frac{T\left( \lambda a(t;\alpha ,\beta ) \sqrt{\frac{\upsilon _{2}+2}{\upsilon _{2}}};\upsilon _{2}+2\right) }{ T\left( \lambda a(t;\alpha ,\beta );\upsilon _{2}\right) }, \nonumber \\ E\left( \log \tau _{2}\mid T=t\right)= \,& {} \frac{T\left( \lambda a(t;\alpha ,\beta )\sqrt{\frac{\upsilon _{2}+2}{\upsilon _{2}}};\upsilon _{2}+2\right) }{T\left( \lambda a(t;\alpha ,\beta );\upsilon _{2}\right) }-\log \left( \frac{\upsilon _{2}}{2}\right) -1+DG\left( \frac{\upsilon _{2}+1}{2}\right) \nonumber \\&+\frac{1}{T\left( \lambda a(t;\alpha ,\beta );\upsilon _{2}\right) } \int _{-\infty }^{\lambda a(t;\alpha ,\beta )}\frac{x^{2}-1}{\left( \upsilon _{2}+x\right) }t\left( x;\upsilon _{2}\right) dx. \nonumber \\ E\left( \gamma \tau _{2}\mid T=t\right)= \,& {} \frac{1}{T\left( \lambda a(t;\alpha ,\beta );\upsilon _{2}\right) }\lambda a(t;\alpha ,\beta )T\left( \lambda a(t;\alpha ,\beta )\sqrt{\frac{\upsilon _{2}+2}{\upsilon _{2}}} ;\upsilon _{2}+2\right) \nonumber \\&+\frac{1}{T\left( \lambda a(t;\alpha ,\beta );\upsilon _{2}\right) }\frac{ \Gamma \left( \frac{\upsilon _{2}+1}{2}\right) \left( \frac{\upsilon _{2}}{2} \right) ^{\frac{\upsilon _{2}}{2}}}{\Gamma \left( \frac{\upsilon _{2}}{2} \right) \left( \lambda ^{2}a^{2}(t;\alpha ,\beta )+\upsilon _{2}\right) ^{\left( \frac{\upsilon _{2}+1}{2}\right) }}, \end{aligned}$$

(21)

where $DG\left( x\right) =\frac{\Gamma ^{\prime }\left( x\right) }{\Gamma \left( x\right) }$ is the digamma function.

Remark: If $\upsilon _{1}=\upsilon _{2}=\upsilon ,$ then $T\sim ST_{\upsilon }T_{\upsilon }\thicksim BS(\alpha ,\beta ,\lambda ,\upsilon ).$

It should be noted that SSMSN-BS class includes some special distributions. In the following, some special cases are given.

(I) The skew t normal-BS (STN-BS) distribution formulated by taking $\tau _{1}\thicksim \Gamma \left( \frac{\upsilon }{2},\frac{\upsilon }{2}\right)$ and $\tau _{2}=1$ with probability 1. The pdf is

$$\begin{aligned}&f_{STN-BS}(t;\alpha ,\beta ,\lambda ,\upsilon )=2t(a(t;\alpha ,\beta );\upsilon )\Phi (\lambda a(t;\alpha ,\beta ))A(t;\alpha ,\beta )\nonumber \\&\quad \text { \ \ \ \ }t,\text { }\alpha ,\text { }\beta ,\text { }\upsilon >0,\text { }\lambda \in R\text {.} \end{aligned}$$

(22)

See Poursadeghfard et al. (2016).

(II) The skew normal t-BS (SNT-BS) distribution formulated by $\tau _{1}=1$ with probability 1 and $\tau _{2}\thicksim \Gamma \left( \frac{ \upsilon }{2},\frac{\upsilon }{2}\right) .$ The pdf is

$$\begin{aligned}&f_{SNT-BS}(t;\alpha ,\beta ,\lambda ,\upsilon )=2\phi (a(t;\alpha ,\beta ))T(\lambda a(t;\alpha ,\beta );\upsilon )A(t;\alpha ,\beta )\nonumber \\&\quad \text { \ \ \ \ } t,\text { }\alpha ,\text { }\beta ,\text { }\upsilon >0,\text { }\lambda \in R \text {.} \end{aligned}$$

(23)

See Hashemi et al. [25].

(III) The skew normal-BS (SN-BS) distribution obtained by taking $\tau _{1}=\tau _{2}=1$ with probability 1. The pdf is

$$\begin{aligned} f_{SN-BS}(t;\alpha ,\beta ,\lambda )=2\phi (a(t;\alpha ,\beta ))A(t;\alpha ,\beta )\text { \ \ \ \ }t,\text { }\alpha ,\text { }\beta >0,\text { }\lambda \in R\text {.} \end{aligned}$$

(24)

See Vilca et al. [38].

Figure 1 displays the graph of the densities, BS, SN-BS, STN-BS, SNT-BS, $ST_{\upsilon }T_{\upsilon }\text {-BS}$ with $\alpha =0.5,$ $\beta =0.8$, $\lambda =3$ and four different degrees of freedom $\upsilon =1,$ 3,  5 and 15.

Fig. 1

The graph of densities, BS, SN-BS, STN-BS, SNT-BS, and $ST_{ \upsilon }T_{\upsilon }\text {-BS}$, for the selected of values of parameters

2.2 The Skew t-BS Distribution

Let $\tau _{1}=\tau _{2}=\tau$ with probability 1 be a one gamma random variable with shape and rate parameters equal to $\frac{\upsilon }{2},$ with the following pdf

$$\begin{aligned} h\left( \varvec{\tau } ;\upsilon \right) =f\left( \varvec{\tau } ;\frac{ \upsilon }{2},\frac{\upsilon }{2}\right) . \end{aligned}$$

(25)

Then Y in (2) is said to have the skew t distribution with parameter $\left( \lambda ,\upsilon \right) ,$ and will be denoted by Y $\sim ST\left( \lambda ,\upsilon \right) .$

Definition 2.3

If $Y\overset{d}{=}Z\sim ST\left( \lambda ,\upsilon \right)$ in (6) we say that the random variable T follows the ST-BS distribution with pdf

$$\begin{aligned} f_{ST-BS}(t;\alpha ,\beta ,\lambda ,\upsilon )= & {} 2t(a(t;\alpha ,\beta );\upsilon )T(\lambda a(t;\alpha ,\beta )\sqrt{\frac{\upsilon +1}{ a^{2}(t;\alpha ,\beta )+\upsilon }},\upsilon +1) \nonumber \\\times & {} A(t;\alpha ,\beta )\text {\ \ }t,\text { }\alpha ,\text { }\beta ,\text { }\upsilon >0,\text { }\lambda \in R\text {.} \end{aligned}$$

(26)

we shall write T $\sim ST-BS(\alpha ,\beta ,\lambda ,\upsilon )$ to denote that T follows the $ST-BS$ distribution.

The mean, variance and measures of skewness and kurtosis coefficients of T follows equations in (13)–(15), (18). In addition $Y\sim ST\left( \lambda ,\upsilon \right) .$

From (12), the conditional pdf of $\tau$ given $T=t$ is

$$\begin{aligned} f\left( \tau \mid T=t\text { }\right)= & {} \left( \frac{a^{2}(t;\alpha ,\beta )+\upsilon }{2}\right) ^{\left( \frac{\upsilon +1}{2}\right) }\frac{1}{ \Gamma \left( \frac{\upsilon +1}{2}\right) T\left( \lambda a(t;\alpha ,\beta )\sqrt{\frac{\upsilon +1}{a^{2}(t;\alpha ,\beta )+\upsilon }};\upsilon +1\right) } \nonumber \\&\times \exp \left( -\frac{\tau }{2}\left( a^{2}(t;\alpha ,\beta )+\upsilon \right) \right) \Phi \left( \sqrt{\tau }\lambda a(t;\alpha ,\beta )\right) \tau ^{\frac{\upsilon -1}{2}}, \end{aligned}$$

(27)

and so the conditional expectation of $\tau$ and $\log \tau$ given $T=t$ are

$$\begin{aligned} E\left( \tau \mid T=t\right)= \,& {} \frac{\upsilon +1}{a^{2}(t;\alpha ,\beta )+\upsilon }\frac{T\left( \lambda a(t;\alpha ,\beta )\sqrt{\frac{\upsilon +3 }{a^{2}(t;\alpha ,\beta )+\upsilon }};\upsilon +3\right) }{T\left( \lambda a(t;\alpha ,\beta )\sqrt{\frac{\upsilon +1}{a^{2}(t;\alpha ,\beta )+\upsilon }};\upsilon +1\right) },\nonumber \\ E\left( \log \tau \mid T=t\right)=\, & {} DG\left( \frac{\upsilon +1}{2}\right) -\log \left( \frac{a^{2}(t;\alpha ,\beta )+\upsilon }{2}\right) \nonumber \\&+\frac{\upsilon +1}{a^{2}(t;\alpha ,\beta )+\upsilon }\left( \frac{T\left( \lambda a(t;\alpha ,\beta )\sqrt{\frac{\upsilon +3}{a^{2}(t;\alpha ,\beta )+\upsilon }};\upsilon +3\right) }{T\left( \lambda a(t;\alpha ,\beta )\sqrt{ \frac{\upsilon +1}{a^{2}(t;\alpha ,\beta )+\upsilon }};\upsilon +1\right) } -1\right) \nonumber \\&+\lambda a(t;\alpha ,\beta )\frac{a^{2}(t;\alpha ,\beta )-1}{\sqrt{\left( \upsilon +1\right) \left( a^{2}(t;\alpha ,\beta )+\upsilon \right) ^{3}}}\nonumber \\&\quad \frac{t\left( \lambda a(t;\alpha ,\beta )\sqrt{\frac{\upsilon +1}{ a^{2}(t;\alpha ,\beta )+\upsilon }};\upsilon +1\right) }{T\left( \lambda a(t;\alpha ,\beta )\sqrt{\frac{\upsilon +1}{a^{2}(t;\alpha ,\beta )+\upsilon }};\upsilon +1\right) } \nonumber \\&+\frac{1}{T\left( \lambda a(t;\alpha ,\beta )\sqrt{\frac{\upsilon +1}{ a^{2}(t;\alpha ,\beta )+\upsilon }};\upsilon +1\right) }\nonumber \\&\quad \int _{-\infty }^{\lambda a(t;\alpha ,\beta )\sqrt{\frac{\upsilon +1}{a^{2}(t;\alpha ,\beta )+\upsilon }}}g\left( x;\upsilon \right) t\left( x;\upsilon +1\right) dx, \end{aligned}$$

(28)

respectively, where $g\left( x;\upsilon \right) =DG\left( \frac{\upsilon +2}{ 2}\right) -DG\left( \frac{\upsilon +1}{2}\right) -\log \left( 1+\frac{x^{2}}{ \upsilon +1}\right) +\frac{\left( \upsilon +1\right) x^{2}-\upsilon -1}{ \left( \upsilon +1\right) \left( \upsilon +1+x^{2}\right) }.$ Also

$$\begin{aligned} E\left( \gamma \tau \mid T=t\right)= & {} \lambda a(t;\alpha ,\beta )E\left( \tau \mid T=t\right) +\frac{\Gamma \left( \frac{\upsilon +2}{2}\right) }{ \Gamma \left( \frac{\upsilon +1}{2}\right) }\frac{1}{\sqrt{\pi }}\frac{1}{ T\left( \lambda a(t;\alpha ,\beta )\sqrt{\frac{\upsilon +1}{a^{2}(t;\alpha ,\beta )+\upsilon }};\upsilon +1\right) } \\&\frac{1}{\left( \lambda ^{2}a^{2}(t;\alpha ,\beta )+a^{2}(t;\alpha ,\beta )+\upsilon \right) ^{\left( \frac{\upsilon +2}{2}\right) }}\left( a^{2}(t;\alpha ,\beta )+\upsilon \right) ^{\left( \frac{\upsilon +1}{2} \right) }. \end{aligned}$$

Note that in the case of $\tau =1$ with probability 1, the SN-BS distribution is obtained. Figure  2 displays the graph of the densities, BS, ST-BS with $\alpha =0.5,$ $\beta =0.8,$ $\lambda =3$ and four different degrees of freedom $\upsilon =1,$ 3,  5,  15.

Fig. 2

The graph of densities, BS, ST-BS, for the selected of values of parameters

2.3 The Skew Generalized Laplace Normal-BS Distribution

A random variable Y is said to have a generalized Laplace $\left( GL\right)$ distribution, denote by $Y\sim GL\left( \upsilon \right) ,$ if it has the pdf

$$\begin{aligned} f_{GL}\left( y;\upsilon \right) =\frac{1}{\sqrt{2\pi }2^{\upsilon -1}\Gamma \left( \upsilon \right) }\left| y\right| ^{\upsilon -\frac{1}{2} }k_{.5-\upsilon }\left( \left| y\right| \right) , \end{aligned}$$

(29)

where $k_{r}\left( x\right)$ denotes the modified Bessel function of third kind of order $r\in R$ defined by

$$\begin{aligned} k_{r}\left( x\right) =\frac{1}{2}\int _{0}^{\infty }y^{r-1}\exp \left( -\frac{ x}{2}\left( y+\frac{1}{y}\right) \right) dy,\text { \ \ }x>0. \end{aligned}$$

(30)

The first derivative of (30) with respect to r is

$$\begin{aligned} k_{r}^{\prime }\left( x\right) =\frac{dk_{r}\left( x\right) }{dr}=\frac{1}{2} \int _{0}^{\infty }\left( \log y\right) y^{r-1}\exp \left( -\frac{x}{2}\left( y+\frac{1}{y}\right) \right) dy,\text { \ \ }x>0. \end{aligned}$$

(31)

Let $\tau _{1}\sim \frac{1}{\chi _{\left( 2\upsilon \right) }^{2}},$ $\tau _{2}=1$ with probability 1 in (2) , where $\chi _{\left( 2\upsilon \right) }^{2}$ denotes the chi squared distribution with df $2\upsilon ,$ then Y is said to have the skew generalized Laplace normal distribution with pdf given by

$$\begin{aligned} f_{SGLN}(y;\lambda ,\upsilon )=2f_{GL}(y;\upsilon )\Phi (\lambda y), \end{aligned}$$

(32)

and will be denoted by $Y\sim SGLN\left( \lambda ,\upsilon \right)$. See Jammalizadeh and Lin (2016).

Definition 2.4

If $Y\overset{d}{=}Z\sim SGLN\left( \lambda ,\upsilon \right)$ in (6), we say that the random variable T follows the SGLN-BS distribution with pdf

$$\begin{aligned}&f_{SGLN-BS}(t;\alpha ,\beta ,\lambda ,\upsilon )=2f_{GL}(a(t;\alpha ,\beta );\upsilon )\Phi (\lambda a(t;\alpha ,\beta ))A(t;\alpha ,\beta )\ \ \ \ t,\alpha ,\beta ,\upsilon >0,\lambda \in R. \end{aligned}$$

(33)

We write $T\sim \text {SGLN-BS}\left( \alpha ,\beta ,\lambda ,\upsilon \right)$ to denote that T follows the $SGLN-BS$ distribution. The mean, variance and measures of skewness and kurtosis coefficients of T follows from equation in (13)–(15), for which, we have

$$\begin{aligned} T^{*}\left( \upsilon \right) \overset{d}{=}\sqrt{\chi ^{2}\left( 2\upsilon \right) }Z\left( 0,1\right) , \end{aligned}$$

(34)

with

$$\begin{aligned} ET^{*2}=\, & {} 2\upsilon , \\ ET^{*4}= \,& {} 12\upsilon (\upsilon +1), \\ ET^{*6}= \,& {} 120\upsilon (\upsilon +1)(\upsilon +2), \\ ET^{*8}= \,& {} 1680\upsilon (\upsilon +1)(\upsilon +2)(\upsilon +3),\\ Y\sim & {} SGLN\left( \alpha ,\beta ,\lambda ,\upsilon \right) . \end{aligned}$$

From (12), we can show that the conditional pdf of $\tau$ given $T=t$ is

$$\begin{aligned} \tau \mid T=t\sim GIG\left( \upsilon =\frac{1}{2}-\alpha , \varkappa =1, \psi =a^{2}(t; \alpha , \beta )\right) , \end{aligned}$$

(35)

where GIG is the Generalized Inverse Gaussian distribution, see Jørgensen [21].

So we obtain

$$\begin{aligned} E\left( \tau \mid T=t\right)= & {} \left| a(t;\alpha ,\beta )\right| ^{-1}\frac{k_{\upsilon +1}\left( \left| a(t;\alpha ,\beta )\right| \right) }{k_{\upsilon }\left( \left| a(t;\alpha ,\beta )\right| \right) }, \nonumber \\ E\left( \log \tau \mid T=t\right)= & {} -\log \left| a(t;\alpha ,\beta )\right| +\frac{k_{\upsilon }^{\prime }\left( \left| a(t;\alpha ,\beta )\right| \right) }{k_{\upsilon }\left( \left| a(t;\alpha ,\beta )\right| \right) }. \end{aligned}$$

(36)

Figure 3 displays several density functions of T with $\alpha =0.5,$ $\beta =0.8,$ $\lambda =3$ and four different $\upsilon =1,$ 3,  5 and 15.

Fig. 3

The graph of densities, SGLN-BS, for the selected of values

Remark: Some special cases are as follows:

(I) If $\tau _{1\text { }}=1$ with probability 1 and $\tau _{2\text { }}\sim \frac{1}{\chi _{\left( 2\upsilon \right) }^{2}},$ then $T\sim \text {SNGL-BS}\left( \alpha ,\beta ,\lambda ,\upsilon \right)$ with density function

$$\begin{aligned} f_{SNGL-BS}(t)=2\phi (a(t;\alpha ,\beta ))F_{GL}(\lambda a(t;\alpha ,\beta ))A(t;\alpha ,\beta ), \end{aligned}$$

(II) If $\tau _{1\text { }}\sim \frac{1}{\chi _{\left( 2\upsilon _{1}\right) }^{2}},$ $\tau _{2\text { }}\sim \Gamma \left( \frac{\upsilon _{2}}{2},\frac{ \upsilon _{2}}{2}\right) ,$ then $T\sim SGLT-BS\left( \alpha ,\beta ,\lambda ,\upsilon _{1},\upsilon _{2}\right)$ with density function

$$\begin{aligned} f_{SGLT-BS}(t)=2f_{GL}(a(t;\alpha ,\beta );\upsilon _{1})T(\lambda a(t;\alpha ,\beta );\upsilon _{2})A(t;\alpha ,\beta ), \end{aligned}$$

(III) If $\tau _{1\text { }}\sim \Gamma \left( \frac{\upsilon _{1}}{2},\frac{ \upsilon _{1}}{2}\right) ,$ $\tau _{2\text { }}\sim \frac{1}{\chi _{\left( 2\upsilon _{1}\right) }^{2}},$ then $T\sim STGL-BS\left( \alpha ,\beta ,\lambda ,\upsilon _{1},\upsilon _{2}\right)$ with density function

$$\begin{aligned} f_{STGL-BS}(t)=2t(a(t;\alpha ,\beta );\upsilon _{1})F_{GL}(\lambda a(t;\alpha ,\beta );\upsilon _{2})A(t;\alpha ,\beta ). \end{aligned}$$

where $F_{GL}(.;\upsilon _{2})$ is the cdf of the generalized Laplace distribution.

2.4 The Skew Slash Normal-BS Distribution

Let $\tau _{1}\sim$ $Beta\left( \frac{\upsilon }{2},1\right) ,$ $\tau _{2}=1$ with probability in (2), then we obtain the pdf of the skew slash normal distribution with shape parameter $\upsilon$ and skewness parameter $\lambda ,$ denoted by Y $\sim SSN\left( \upsilon ,\lambda \right) .$ The pdf is given by

$$\begin{aligned} f_{SSN}\left( y;\upsilon ,\lambda \right) =2f_{s}\left( y;\upsilon \right) \Phi \left( \lambda y\right) , \end{aligned}$$

(37)

where $f_{s}\left( .;\upsilon \right)$ is the pdf of the slash distribution with shape parameter $\upsilon .$

$$\begin{aligned} f_{s}\left( y;\upsilon \right) =\left\{ \begin{array}{cc} \frac{\upsilon \Gamma \left( \frac{\upsilon +1}{2}\right) 2^{\frac{\upsilon }{2}-1}G\left( \frac{y^{2}}{2},\frac{\upsilon +1}{2}\right) }{\sqrt{\pi } \left| y\right| ^{\upsilon +1}} &{} y\ne 0, \\ \frac{\upsilon }{\sqrt{2\pi }(\upsilon +1)} &{} y=0, \end{array} \right. \end{aligned}$$

(38)

where $G(.;\alpha )$ denotes the cdf of gamma distribution with scale parameter 1 and shape parameter $\alpha .$ See Rogers and Tukey [35].

Definition 2.5

If $Y\overset{d}{=}Z\sim SSN\left( \upsilon ,\lambda \right)$ in (6), we say that the random variable T follows the SSN-BS with pdf

$$\begin{aligned} f\left( t;\alpha ,\beta ,\lambda ,\upsilon \right) =2f_{s}\left( a(t;\alpha ,\beta );\upsilon \right) \Phi \left( \lambda a(t;\alpha ,\beta )\right) A(t;\alpha ,\beta )\text { \ \ \ \ }t\text { },\text { }\alpha ,\text { }\beta , \text { }\upsilon _{2}>0,\text { }\lambda \in R\text {.} \end{aligned}$$

(39)

We write $T\sim \text {SSN-BS}\left( \alpha ,\beta ,\lambda ,\upsilon \right)$ to denote that T follows the SSN-BS distribution.

Figure 4 displays several density functions of T $\sim \text {SSN-BS}\left( \alpha ,\beta ,\lambda ,\upsilon \right)$ with $\alpha =0.5,$ $\beta =0.8,$ $\lambda =3$ and four different $\upsilon =1,$ 3,  5,  15.

Fig. 4

The graph of the densities, SSN-BS, for selected values of parameters

The mean, variance and measures of skewness and kurtosis coefficients of T follows equations in (13), (14), (15), for which we have

$$\begin{aligned} T^{*}\left( \upsilon \right) \overset{d}{=}Beta^{-\frac{1}{2}}\left( \frac{\upsilon }{2},1\right) Z\left( 0,1\right) , \end{aligned}$$

(40)

$$\begin{aligned} ET^{*2}= \,& {} \frac{\upsilon }{\upsilon -2}, \\ ET^{*4}= \,& {} 3\frac{\upsilon }{\upsilon -4}, \\ ET^{*6}=\, & {} 15\frac{\upsilon }{\upsilon -6}, \\ ET^{*^{8}}=\, & {} 105\frac{\upsilon }{\upsilon -8}, Y\sim SSN\left( \upsilon ,\lambda \right) . \end{aligned}$$

From (12), we can show that the conditional pdf of $\tau$ given $T=t$ is

$$\begin{aligned} f\left( \tau \mid T=t\right) =\left\{ \begin{array}{cc} \frac{\left| a(t;\alpha ,\beta )\right| ^{\upsilon +1}\tau ^{\frac{ \upsilon -1}{2}}\exp \left( -\frac{1}{2}a^{2}(t;\alpha ,\beta )\right) }{ \Gamma \left( \frac{\upsilon +1}{2}\right) 2^{\frac{\upsilon +1}{2}}G\left( \frac{a^{2}(t;\alpha ,\beta )}{2};\frac{\upsilon +1}{2}\right) } &{} t\ne \beta \\ \frac{\upsilon +1}{2}\tau ^{\frac{\upsilon +1}{2}-1} &{} t=\beta \end{array} \right. , \end{aligned}$$

(41)

and the conditional expectation of $\tau$ and $\log \left( \tau \right)$ given $T=t$ is

$$\begin{aligned} E\left( \tau \mid T=t\right)=\, & {} \left\{ \begin{array}{cc} \frac{(\upsilon +1)G\left( a^{2}(t;\alpha ,\beta );\frac{\upsilon +3}{2} \right) }{a^{2}(t;\alpha ,\beta )G\left( \frac{a^{2}(t;\alpha ,\beta )}{2}; \frac{\upsilon +1}{2}\right) } &{} t\ne \beta \\ \frac{\upsilon +1}{\upsilon +3} &{} t=\beta \end{array} \right. ,\nonumber \\ E\left( \log \tau \mid T=t\right)=\, & {} \left\{ \begin{array}{cc} \log \frac{2}{a^{2}(t;\alpha ,\beta )}+\frac{\int _{0}^{\frac{a^{2}(t;\alpha ,\beta )}{2}}\left( \log x\right) x^{\frac{\upsilon -1}{2}}\exp \left( -x\right) dx}{\Gamma \left( \frac{\upsilon +1}{2}\right) G\left( \frac{ a^{2}(t;\alpha ,\beta )}{2};\frac{\upsilon +1}{2}\right) } &{} t\ne \beta \\ -\frac{2}{\upsilon +1} &{} t=\beta \end{array} \right. . \end{aligned}$$

(42)

3 Maximum Likelihood Estimation

In this section, we derive the ML estimation parameters of SSMSN-BS distributions via modification of the EM-algorithm (ECM-algorithm). The ECM algorithm modifies the EM Algorithm by replacing its Maximization step by a sequence of conditional maximization steps. For more details about EM and ECM algorithms, see Dempster et al. [13] and Meng and Rubin [30].

3.1 The General Case

Let $T_{1},$ $T_{2},$ $\ldots ,$ $T_{n}$ are random samples from $SSMSN-BS\left( \alpha ,\text { }\beta ,\text { }\lambda ,\text { }\varvec{\eta }\right)$ with the following hierarchical formulation

$$\begin{aligned} f\left( T_{i}=t_{i}\mid \left( \gamma _{i},\tau _{1i},\tau _{2i}\right) \right)= & {} \phi \left( \sqrt{\tau _{2i}\left( f_{i}+\lambda ^{2}\right) } \left( a(t;\alpha ,\beta )\right) -\frac{\sqrt{\tau _{2i}}\lambda \gamma }{ \sqrt{f_{i}+\lambda ^{2}}}\right) \nonumber \\&\times \sqrt{\tau _{2i}\left( f_{i}+\lambda ^{2}\right) }A\left( t;\alpha ,\beta \right) ,\nonumber \\ \gamma _{i},&\mid&\left( \tau _{1i},\tau _{2i}\right) \sim TN\left( 0, \frac{f_{i}+\lambda ^{2}}{\tau _{1i}};\left( 0,\infty \right) \right) , \end{aligned}$$

(43)

where $\gamma _{i}=\sqrt{\tau _{1i}\left( f_{i}+\lambda ^{2}\right) } \left| Z_{1}\right| ,$ $f_{i}=\frac{\tau _{1i}}{\tau _{2i}},$ and $\varvec{\tau }_{i}=\left( \tau _{1i},\tau _{2i}\right) ^{T}$ are n bivariate positive random samples with pdf $h\left( \tau _{1i},\tau _{2i}; \varvec{\eta }\right) .$

Set the observed data by $\mathbf {t}=\left( t_{1},\ldots ,\text { } t_{n}\right) ^{T},$ the missing data $\varvec{\gamma }=\left( \gamma _{1},\ldots ,\text { }\gamma _{n}\right) ^{T}$ and $\varvec{\tau } =\left( \varvec{\tau }_{1},\ldots ,\text { }\varvec{\tau } _{n}\right) ^{T}$ and the complete data by $\mathbf {t}^{c}=\left( \mathbf {t} ^{T},\varvec{\gamma }^{T},\varvec{\tau }^{T}\right) ^{T}$. Then from (43), and $h\left( \varvec{\tau }_{i}\varvec{,\eta }\right)$ we can construct the complete data log-likelihood function of $\varvec{\theta } =\left( \alpha ,\beta ,\lambda ,\varvec{\eta }\right)$ given complete data $\mathbf {t}^{c}=\left( t,\gamma ,\tau _{1},\tau _{2}\right) .$ By ignoring the additive constant terms, the log-likelihood function is given by

$$\begin{aligned} \mathbf {\ell }^{(c)}(\varvec{\theta }&\mid&\mathbf {t} ^{(c)})=\sum _{i=1}^{n}\mathbf {\ell }_{i}^{(c)}(\varvec{\theta }\mid (t_{i},\tau _{1i},\tau _{2i},\gamma _{i}))\nonumber \\= & {} -\frac{1}{2}\sum _{i=1}^{n}\tau _{2i}\gamma _{i}^{2}+\frac{\lambda }{ \alpha }\sum _{i=1}^{n}\tau _{2i}\gamma _{i}\varepsilon (t_{i};\beta )-\frac{1 }{2}\frac{\lambda ^{2}}{\alpha ^{2}}\sum _{i=1}^{n}\tau _{2i}\varepsilon ^{2}(t_{i};\beta )-\frac{1}{2\alpha ^{2}}\sum _{i=1}^{n}\tau _{1i}\varepsilon ^{2}(t_{i};\beta ) \nonumber \\&+\sum _{i=1}^{n}\log \frac{t_{i}+\beta }{\sqrt{\beta }}-n\log (\alpha )+\sum _{i=1}^{n}\log \left( \sqrt{\tau _{1i}\tau _{2i}}h\left( \tau _{1i},\tau _{2i};\varvec{\eta } \right) \right) , \end{aligned}$$

(44)

where $\varepsilon (t_{i};\beta )=\sqrt{\frac{t_{i}}{\beta }}-\sqrt{\frac{ \beta }{t_{i}}}.$ Suppose $\widehat{\varvec{\theta }}^{(r)}=( \widehat{\alpha }^{(r)},\widehat{\beta }^{(r)},\widehat{\lambda }^{(r)}, \widehat{\varvec{\eta }}^{(r)})$ is the current estimate (in the rth iteration) of $\varvec{\theta }$. Based on the ECM algorithm principle, in the E-step, we should first form the following conditional expectation

$$\begin{aligned} \mathbf {Q(\varvec{\theta }}\mathbf {\mid }\widehat{ \varvec{\theta }}^{(r)})= \,& {} E(\mathbf {\ell }^{(c)}( \varvec{\theta }\mid t^{(c)})) \nonumber \\= \,& {} \frac{\lambda }{\alpha }\sum _{i=1}^{n}\widehat{S}_{3i}^{(r)}\varepsilon (t_{i};\beta )-\frac{1}{2}\frac{\lambda ^{2}}{\alpha ^{2}}\sum _{i=1}^{n} \widehat{S}_{2i}^{(r)}\varepsilon ^{2}(t_{i};\beta ) \nonumber \\&-\frac{1}{2\alpha ^{2}}\ \sum _{i=1}^{n}\widehat{S}_{1i}^{(r)}\varepsilon ^{2}(t_{i};\beta )+\sum _{i=1}^{n}\log \frac{t_{i}+\beta }{\sqrt{\beta }} -n\log (\alpha ) \nonumber \\&+\sum _{i=1}^{n}\left[ E\left( \log \left( \sqrt{\tau _{1i}\tau _{2i}} h\left( \tau _{1i},\tau _{2i};\varvec{\eta }\right) \right) \mid t_{i}, \widehat{\varvec{\theta }}^{(r)}\right) \right] , \end{aligned}$$

(45)

where

$$\begin{aligned} \widehat{S}_{1i}^{(r)}= & {} E(\tau _{1i}\mid t_{i},\widehat{\varvec{\theta }}^{(r)}), \nonumber \\ \widehat{S}_{2i}^{(r)}= & {} E(\tau _{2i}\mid t_{i},\widehat{\varvec{\theta }}^{(r)}), \nonumber \\ \widehat{S}_{3i}^{(r)}= & {} E(\tau _{2i}\gamma _{i}\mid t_{i},\widehat{ \varvec{\theta }}^{(r)}). \end{aligned}$$

(46)

Then the ECM algorithm is done as follows:

E-step: Given $\varvec{\theta }=\widehat{ \varvec{\theta }}^{(r)}$, compute $\widehat{S}_{1i}^{(r)},\widehat{S} _{2i}^{(r)},\widehat{S}_{3i}^{(r)}$, for $i=1,\ldots ,n.$

CM-step 1: Fix $\beta =\widehat{\beta }^{(r)}$ and update $\widehat{ \alpha }^{(r)},\widehat{\lambda }^{(r)}$ by maximizing (45) over $\alpha$ and $\lambda$, which leads to

$$\begin{aligned} \widehat{\lambda }^{(r+1)}=\, & {} \frac{\widehat{\alpha }^{(r+1)}\sum _{i=1}^{n} \varepsilon (t_{i};\widehat{\beta }^{(r)})\widehat{S}_{3i}^{(r)}}{ \sum _{i=1}^{n} \varepsilon ^{2}(t_{i};\beta )\widehat{S}_{2i}^{(r)}},\nonumber \\ \widehat{\alpha }^{2(r+1)}= \,& {} \frac{1}{n}\sum _{i=1}^{n}\varepsilon ^{2}(t_{i};\widehat{\beta }^{(r)})\widehat{S}_{1i}^{(r)}. \end{aligned}$$

(47)

CM-step 2: Updating $\widehat{\varvec{\eta }}^{(r)}$ is strongly related to form of the $h\left( \tau _{1i},\tau _{2i};\varvec{ \eta }\right)$ said to the next section.

CM-step 3: Fix $\alpha =\widehat{\alpha }^{(r+1)},\lambda =\widehat{ \lambda }^{(r+1)},\mathbf {\eta }=\widehat{\varvec{\eta }}^{(r+1)}$ and update $\widehat{\beta }^{(r)}$ using

$$\begin{aligned} \widehat{\beta }^{(r+1)}=\arg \max Q(\widehat{\alpha }^{(r+1)},\beta , \widehat{\lambda }^{(r+1)},\widehat{\varvec{\eta }}^{(r+1)}\mid \widehat{ \varvec{\theta }}^{(r)}). \end{aligned}$$

(48)

Note that the CM-step 3 requires a one-dimensional search for the root of $\beta ,$ which can be easily obtained by using the optimize function in the statistical software R.

3.2 ECM-Estimation for the $ST_{\upsilon _{1}}T_{ \upsilon _{2}}\text {-BS}$ Distribution

For the $ST_{\upsilon _{1}}T_{\upsilon _{2}}\text {-BS}$ distribution, we recall equation (16)

$$\begin{aligned} h\left( \varvec{\tau }_{i};\varvec{\eta }\right) =f\left( \tau _{1i}; \frac{\upsilon _{1}}{2},\frac{\upsilon _{1}}{2}\right) f\left( \tau _{2i}; \frac{\upsilon _{2}}{2},\frac{\upsilon _{2}}{2}\right) \text { \ }\varvec{ \eta }=\left( \upsilon _{1},\upsilon _{2}\right) , \end{aligned}$$

(49)

from (45), the E-step involves the calculation of two additional conditional expectations, given by

$$\begin{aligned} \widehat{S}_{4i}^{(r)}= & {} E(\log \tau _{1i}\mid t_{i},\widehat{\varvec{ \theta }}^{(r)}), \nonumber \\ \widehat{S}_{5i}^{(r)}= & {} E(\log \tau _{2i}\mid t_{i},\widehat{\varvec{ \theta }}^{(r)}), \end{aligned}$$

(50)

which can be calculated by using (21). Now, rewrite

CM-step 2: Fix $\alpha =\widehat{\alpha }^{(r+1)},\lambda =\widehat{ \lambda }^{(r+1)},$ $\beta =\widehat{\beta }^{(r)}$ and update $\widehat{ \upsilon }_{1}^{(r)}$ and $\widehat{\upsilon }_{2}^{(r)}$ by maximizing (45) over $\upsilon _{1},$ $\upsilon _{2}$ which leads to solve the root of the following equations

$$\begin{aligned} \log \frac{\upsilon _{1}}{2}-DG\left( \frac{\upsilon _{1}}{2}\right) +1+ \frac{1}{n}\sum _{i=1}^{n}\left( \widehat{S}_{3i}^{(r)}-\widehat{S} _{1i}^{(r)}\right)= & {} 0,\nonumber \\ \log \frac{\upsilon _{2}}{2}-DG\left( \frac{\upsilon _{2}}{2}\right) +1+ \frac{1}{n}\sum _{i=1}^{n}\left( \widehat{S}_{3i}^{(r)}-\widehat{S} _{1i}^{(r)}\right)= & {} 0. \end{aligned}$$

(51)

3.3 ECM-Estimation for the ST-BS Distribution

For the ST-BS distribution, we recall equation (25)

$$\begin{aligned} h\left( \tau _{i};\upsilon \right) =f\left( \tau _{i};\frac{\upsilon }{2}, \frac{\upsilon }{2}\right) , \end{aligned}$$

(52)

The E-step (46) converts to

$$\begin{aligned} \widehat{S}_{1i}^{(r)}= & {} \widehat{S}_{2i}^{(r)}=\widehat{S} _{i}^{(r)}=E(\tau _{i}\mid t_{i},\widehat{\varvec{\theta }} ^{(r)}),\nonumber \\ \widehat{S}_{3i}^{(r)}= & {} E(\gamma _{i}\mid t_{i},\widehat{\varvec{ \theta }}^{(r)}), \end{aligned}$$

(53)

and one additional conditional expectation, given by

$$\begin{aligned} \widehat{S}_{4i}^{(r)}=E(\log \tau _{i}\mid t_{i},\widehat{\varvec{ \theta }}^{(r)}), \end{aligned}$$

(54)

which can be calculated by using (26). Now, we rewrite

CM-step 2: Updating $\widehat{\upsilon }^{(r)}$ leads to solve the root of the following equation

$$\begin{aligned} \log \frac{\upsilon }{2}-DG\left( \frac{\upsilon }{2}\right) +1+\frac{1}{n} \sum _{i=1}^{n} \left( \widehat{S}_{4i}^{(r)}-\widehat{S}_{1i}^{(r)}\right) =0. \end{aligned}$$

(55)

3.4 ECM-Estimation for the SGLN-BS Distribution

As mentioned in Sect. 2.3, the SGLN-BS distribution can be generated from SSMSN-BS by taking $\tau _{1i}=\tau _{i}\overset{d}{=}\frac{1}{\chi _{\left( 2\upsilon \right) }^{2}}$ and $\tau _{2i}=1$ with probability 1 for $i=1,$ $\ldots ,$ n. and so we have

$$\begin{aligned} h\left( \varvec{\tau }_{i};\varvec{\eta }\right) =h\left( \tau _{i};\upsilon \right) =\frac{1}{2^{\upsilon }\Gamma \left( \upsilon \right) } \tau _{i}^{-\left( \upsilon +1\right) }\exp \left( \frac{1}{2\tau _{i}} \right) . \end{aligned}$$

(56)

Then the E-step (46) converts to

$$\begin{aligned} \widehat{S}_{1i}^{(r)}= & {} E(\tau _{i}\mid t_{i},\widehat{\varvec{\theta } }^{(r)}),\nonumber \\ \widehat{S}_{2i}^{(r)}= & {} 1, \nonumber \\ \widehat{S}_{3i}^{(r)}= & {} E(\gamma _{i}\mid t_{i},\widehat{\varvec{ \theta }}^{(r)}), \end{aligned}$$

(57)

and additional conditional expectation

$$\begin{aligned} \widehat{S}_{4i}^{(r)}=E(\log \tau _{i}\mid t_{i},\widehat{\varvec{ \theta }}^{(r)}), \end{aligned}$$

(58)

which can be calculated via (36). Now we rewrite

CM-step 2: Updating $\widehat{\upsilon }^{(r)}$ leads to solve the root of the following equation

$$\begin{aligned} \log 2+DG\left( \upsilon \right) +\frac{1}{n}\sum _{i=1}^{n} \widehat{S} _{4i}^{(r)}=0. \end{aligned}$$

(59)

3.5 ECM-Estimation for the SSN-BS Distribution

As shown in Sect. 2.4, the SSN can be considered as a special case of SSMSN-BS by taking

$\tau _{1i}=\tau _{i}\overset{d}{=}Beta\left( \upsilon ,1\right)$ and $\tau _{2i}=1$ with probability 1 for $i=1,$ $\ldots ,$ $n.$ So we have

$$\begin{aligned} h\left( \varvec{\tau } _{i};\varvec{\eta } \right) =h\left( \tau _{i};\upsilon \right) =\upsilon \tau _{i}^{\upsilon -1}. \end{aligned}$$

(60)

The E-step (46) converts to

$$\begin{aligned} \widehat{S}_{1i}^{(r)}= & {} E(\tau _{i}\mid t_{i},\widehat{\varvec{\theta } }^{(r)}), \nonumber \\ \widehat{S}_{2i}^{(r)}= & {} 1, \nonumber \\ \widehat{S}_{3i}^{(r)}= & {} E(\gamma _{i}\mid t_{i},\widehat{\varvec{ \theta }}^{(r)}), \end{aligned}$$

(61)

and additional conditional expectation

$$\begin{aligned} \widehat{S}_{4i}^{(r)}=E(\log \tau _{i}\mid t_{i},\widehat{\varvec{ \theta }}^{(r)}). \end{aligned}$$

(62)

which can be calculated via (42). Now we rewrite

CM-step 2: Update $\widehat{\upsilon }^{(r)}$ by

$$\begin{aligned} \widehat{\upsilon }^{(r+1)}=-\frac{n}{\widehat{S}_{4i}^{(r)}}. \end{aligned}$$

(63)

3.6 The Information Matrix

Under some regularity condition, the asymptotic covariance matrix of the ML estimates can be approximated by inverse of the observed information matrix, given by

$$\begin{aligned} I_{0}(\widehat{\varvec{\theta }}\mid \mathbf {t})=\frac{-\partial ^{2}\ell (\varvec{\theta }\mid t)}{\partial \varvec{\theta } \partial \varvec{\theta }^{T}}\mathbf {\mid }_{\varvec{\theta }=\widehat{\varvec{\theta }}\text { }}, \end{aligned}$$

where $\ell (\varvec{\theta }\mid t)$ is the observed log-likelihood function on the basis of observations $T=\left( t_{1},\ldots ,t_{n}\right) ^{T}.$

Following Basford et al. [6], we obtain

$$\begin{aligned} I_{0}(\widehat{\varvec{\theta }}\mid \mathbf {t})=\sum _{i=1}^{n} \widehat{\mathbf {S}}_{i}\widehat{\mathbf {S}}_{i}^{T}, \end{aligned}$$

where

$$\begin{aligned} \widehat{\mathbf {S}}_{i}=\frac{\partial \mathbf {\ell }_{i}( \varvec{\theta }\mid t_{i})}{\partial \varvec{\theta }}\mid _{ \varvec{\theta }=\widehat{\varvec{\theta }}}=(\widehat{ \mathbf {S}}_{i,\alpha },\widehat{\mathbf {S}}_{i,\beta },\widehat{\mathbf {S}} _{i,\lambda },\widehat{\mathbf {S}}_{i,\upsilon })^{T}, \end{aligned}$$

is the individual score statistic corresponding to the single observation $t_{i}$ $\left( i=1,\ldots ,n\right) .$ Explicit expression for the elements of $\widehat{\mathbf {S}}_{i}$ are summerized below.

$\left( i\right)$ For the $ST_{\upsilon _{1}}T_{\upsilon _{2}}-BS$ distribution, the elements of $\widehat{\mathbf {S}}_{i}$ contain

$$\begin{aligned} \widehat{\mathbf {S}}_{i,\alpha }= & {} -\left( \frac{\widehat{\upsilon _{1}}+1}{ \widehat{\upsilon _{1}}}\right) \left( 1+\frac{a^{2}(t_{i};\widehat{\alpha },\widehat{ \beta })}{\widehat{\upsilon }_{1}}\right) ^{-1}a(t_{i};\widehat{\alpha },\widehat{ \beta })\frac{\partial }{\partial \alpha }a(t_{i};\widehat{\alpha },\widehat{ \beta }) \\&+\frac{t(\widehat{\lambda }a(t_{i};,\widehat{\alpha },\widehat{\beta }), \widehat{\upsilon _{2}})}{T(\widehat{\lambda }^{(r)}a(t_{i};,\widehat{\alpha }^{(r)},\widehat{\beta }^{(r)}),\widehat{\upsilon _{2}})}\frac{\widehat{ \lambda }\partial }{\partial \alpha }a(t_{i};\widehat{\alpha },\widehat{ \beta })+\frac{\frac{\partial }{\partial \alpha }A(t_{i},\widehat{\alpha }, \widehat{\beta })}{A(t_{i},\widehat{\alpha },\widehat{\beta })},\\ \widehat{\mathbf {S}}_{i,\beta }= & {} -\left( \frac{\widehat{\upsilon _{1}}+1}{ \widehat{\upsilon _{1}}}\right) \left( 1+\frac{a^{2}(t_{i};\widehat{\alpha },\widehat{ \beta })}{\widehat{\upsilon _{1}}}\right) ^{-1}a(t_{i};\widehat{\alpha },\widehat{ \beta })\frac{\partial }{\partial \beta }a(t_{i};\widehat{\alpha },\widehat{ \beta }) \\&+\frac{t(\widehat{\lambda }a(t_{i};,\widehat{\alpha },\widehat{\beta }), \widehat{\upsilon _{2}})}{T(\widehat{\lambda }^{(r)}a(t_{i};,\widehat{\alpha }^{(r)},\widehat{\beta }^{(r)}),\widehat{\upsilon _{2}})}\frac{\widehat{ \lambda }\partial }{\partial \beta }a(t_{i};\widehat{\alpha },\widehat{\beta })+\frac{\frac{\partial }{\partial \beta }A(t_{i},\widehat{\alpha },\widehat{ \beta })}{A(t_{i},\widehat{\alpha },\widehat{\beta })},\\ \widehat{\mathbf {S}}_{i,\lambda }= & {} \frac{t(\widehat{\lambda }a(t_{i};, \widehat{\alpha },\widehat{\beta }),\widehat{\upsilon _{2}})}{T(\widehat{ \lambda }^{(r)}a(t_{i};,\widehat{\alpha }^{(r)},\widehat{\beta }^{(r)}), \widehat{\upsilon _{2}})}a(t_{i};\widehat{\alpha },\widehat{\beta }),\\ \widehat{\mathbf {S}}_{i,\upsilon _{1}}= \,& {} \frac{1}{2}DG\left( \frac{\widehat{ \upsilon _{1}}+1}{2}\right) -\frac{1}{2}DG\left( \frac{\widehat{\upsilon _{1} }}{2}\right) -\frac{1}{2}\widehat{\upsilon _{1}}^{-1}-\frac{1}{2}\ln \left( 1+\frac{a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })}{\widehat{\upsilon _{1}}}\right) \nonumber \\&+\frac{a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })\left( \widehat{\upsilon _{1}}+1\right) }{2\widehat{\upsilon _{1}}\left( \widehat{ \upsilon _{1}}+a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })\right) },\\ \widehat{\mathbf {S}}_{i,\upsilon _{2}}= \,& {} \frac{1}{2}DG\left( \frac{\widehat{ \upsilon _{1}}+1}{2}\right) -\frac{1}{2}DG\left( \frac{\widehat{\upsilon _{1} }}{2}\right) -\frac{1}{2}\widehat{\upsilon _{1}}^{-1}+\frac{1}{2} \int _{-\infty }^{\lambda a(t;\alpha ,\beta )} (-\ln \left( 1+\frac{x^{2}}{ \widehat{\upsilon _{2}}}\right) \nonumber \\&+\frac{x^{2}\left( \widehat{\upsilon _{2}} +1\right) }{2\widehat{\upsilon _{2}}\left( \widehat{\upsilon _{2}} +x^{2}\right) })t\left( x;\widehat{\upsilon _{2}}\right) dx. \end{aligned}$$

In the case of $\upsilon _{1}=\upsilon _{2}=\upsilon ,$ we have $\widehat{ \mathbf {S}}_{i,\upsilon }=\widehat{\mathbf {S}}_{i,\upsilon _{1}}+\widehat{ \mathbf {S}}_{i,\upsilon _{2}}.$

$\left( ii\right)$ For the ST-BS distribution, the elements of $\widehat{ \mathbf {S}}_{i}$ are obtained by

$$\begin{aligned} \widehat{\mathbf {S}}_{i,\alpha }= & {} -\left( \frac{\widehat{\upsilon }+1}{\widehat{ \upsilon }}\right) \left( 1+\frac{a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })}{ \widehat{\upsilon }}\right) ^{-1}a(t_{i};\widehat{\alpha },\widehat{\beta })\frac{ \partial }{\partial \alpha }a(t_{i};\widehat{\alpha },\widehat{\beta }) \\&+\frac{t(\widehat{\lambda }a(t_{i};,\widehat{\alpha },\widehat{\beta }) \sqrt{\frac{\widehat{\upsilon }+1}{a^{2}(t_{i};\widehat{\alpha },\widehat{ \beta })+\widehat{\upsilon }}};\widehat{\upsilon }+1)\widehat{\lambda }\frac{ \partial a(t_{i};\widehat{\alpha },\widehat{\beta })}{\partial \alpha }}{T( \widehat{\lambda }^{(r)}a(t_{i};,\widehat{\alpha }^{(r)},\widehat{\beta } ^{(r)})\sqrt{\frac{\widehat{\upsilon }+1}{a^{2}(t_{i};\widehat{\alpha }, \widehat{\beta })+\widehat{\upsilon }}},\widehat{\upsilon }+1)}\left( \sqrt{\frac{ \widehat{\upsilon }+1}{a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })+ \widehat{\upsilon }}} \right. \\&\left. -a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })\sqrt{\frac{\widehat{ \upsilon }+1}{(a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })+\widehat{ \upsilon })^{3}}}\right) +\frac{\frac{\partial }{\partial \alpha }A(t_{i},\widehat{ \alpha },\widehat{\beta })}{A(t_{i},\widehat{\alpha },\widehat{\beta })},\\ \widehat{\mathbf {S}}_{i,\beta }= & {} -\left( \frac{\widehat{\upsilon }+1}{\widehat{ \upsilon }}\right) \left( 1+\frac{a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })}{ \widehat{\upsilon }}\right) ^{-1}a(t_{i};\widehat{\alpha },\widehat{\beta })\frac{ \partial }{\partial \beta }a(t_{i};\widehat{\alpha },\widehat{\beta }) \\&+\frac{t(\widehat{\lambda }a(t_{i};,\widehat{\alpha },\widehat{\beta }) \sqrt{\frac{\widehat{\upsilon }+1}{a^{2}(t_{i};\widehat{\alpha },\widehat{ \beta })+\widehat{\upsilon }}};\widehat{\upsilon })\widehat{\lambda }\frac{ \partial a(t_{i};\widehat{\alpha },\widehat{\beta })}{\partial \beta }}{T( \widehat{\lambda }^{(r)}a(t_{i};,\widehat{\alpha }^{(r)},\widehat{\beta } ^{(r)})\sqrt{\frac{\widehat{\upsilon }+1}{a^{2}(t_{i};\widehat{\alpha }, \widehat{\beta })+\widehat{\upsilon }}},\widehat{\upsilon }+1)}\left( \sqrt{\frac{ \widehat{\upsilon }+1}{a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })+ \widehat{\upsilon }}}\right. \\&\left. -a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })\sqrt{\frac{\widehat{ \upsilon }+1}{(a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })+\widehat{ \upsilon })^{3}}}\right) +\frac{\frac{\partial }{\partial \beta }A(t_{i},\widehat{ \alpha },\widehat{\beta })}{A(t_{i},\widehat{\alpha },\widehat{\beta })},\\ \widehat{\mathbf {S}}_{i,\lambda }=\, & {} \frac{t(\widehat{\lambda }a(t_{i};, \widehat{\alpha },\widehat{\beta })\sqrt{\frac{\widehat{\upsilon }+1}{ a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })+\widehat{\upsilon }}}, \widehat{\upsilon }+1)}{T(\widehat{\lambda }^{(r)}a(t_{i};,\widehat{\alpha } ^{(r)},\widehat{\beta }^{(r)})\sqrt{\frac{\widehat{\upsilon }+1}{a^{2}(t_{i}; \widehat{\alpha },\widehat{\beta })+\widehat{\upsilon }}},\widehat{\upsilon } +1)}a(t_{i};\widehat{\alpha },\widehat{\beta })\sqrt{\frac{\widehat{\upsilon }+1}{a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })+\widehat{\upsilon }}},\\ \widehat{\mathbf {S}}_{i,\upsilon }=\, & {} \frac{1}{2}DG\left( \frac{\widehat{ \upsilon }+1}{2}\right) -\frac{1}{2}DG\left( \frac{\widehat{\upsilon }}{2} \right) -\frac{1}{2}\widehat{\upsilon }^{-1}-\frac{1}{2}\ln \left( 1+\frac{ a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })}{\widehat{\upsilon }}\right) \\&+\frac{a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })\left( \widehat{ \upsilon }+1\right) }{2\widehat{\upsilon }\left( \widehat{\upsilon } +a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })\right) } \\&+\frac{1}{2}DG\left( \frac{\widehat{\upsilon }+2}{2}\right) -\frac{1}{2} DG\left( \frac{\widehat{\upsilon }+1}{2}\right) \\&-\frac{1}{2}\frac{\int _{-\infty }^{\lambda a(t_{i};,\widehat{\alpha }, \widehat{\beta })\sqrt{\frac{\widehat{\upsilon }+1}{a^{2}(t_{i};\widehat{ \alpha },\widehat{\beta })+\widehat{\upsilon }}}}\left( -\ln \left( 1+\frac{ x^{2}}{\widehat{\upsilon }+1}\right) +\frac{x^{2}\left( \widehat{\upsilon } +2\right) }{\left( \widehat{\upsilon }+1\right) \left( \widehat{\upsilon } +1+x^{2}\right) }\right) t\left( x,\widehat{\upsilon }+1\right) dx.}{T\left( \widehat{\lambda }a(t_{i};,\widehat{\alpha },\widehat{\beta })\sqrt{\frac{ \widehat{\upsilon }+1}{a^{2}(t_{i};\widehat{\alpha },\widehat{\beta })+ \widehat{\upsilon }}},\widehat{\upsilon }+1\right) }. \end{aligned}$$

$\left( iii\right)$ For the SGLN-BS distribution, the elements of $\widehat{\mathbf {S}}_{i}$ are obtained by

$$\begin{aligned} \widehat{\mathbf {S}}_{i,\alpha }= & {} \left( \widehat{\upsilon }-\frac{1}{2} \right) \frac{\frac{\partial }{\partial \alpha }a(t_{i};\widehat{\alpha }, \widehat{\beta })}{a(t_{i};\widehat{\alpha },\widehat{\beta })}+\frac{ k^{\prime }{}_{0.5-\widehat{\upsilon }}\left( \left| a(t_{i};\widehat{ \alpha },\widehat{\beta })\right| \right) }{k_{0.5-\widehat{\upsilon } }\left( \left| a(t_{i};\widehat{\alpha },\widehat{\beta })\right| \right) }\frac{a(t_{i};\widehat{\alpha },\widehat{\beta })\frac{\partial }{ \partial \alpha }a(t_{i};\widehat{\alpha },\widehat{\beta })}{\left| a(t_{i};\widehat{\alpha },\widehat{\beta })\right| } \\&+\frac{\phi (\widehat{\lambda }a(t_{i};,\widehat{\alpha },\widehat{\beta } ))}{\Phi (\widehat{\lambda }^{(r)}a(t_{i};,\widehat{\alpha }^{(r)},\widehat{ \beta }^{(r)}))}\frac{\widehat{\lambda }\partial }{\partial \alpha }a(t_{i}; \widehat{\alpha },\widehat{\beta })+\frac{\frac{\partial }{\partial \alpha } A(t_{i},\widehat{\alpha },\widehat{\beta })}{A(t_{i},\widehat{\alpha }, \widehat{\beta })},\\ \widehat{\mathbf {S}}_{i,\beta }= & {} \left( \widehat{\upsilon }-\frac{1}{2} \right) \frac{\frac{\partial }{\partial \beta }a(t_{i};\widehat{\alpha }, \widehat{\beta })}{a(t_{i};\widehat{\alpha },\widehat{\beta })}+\frac{ k^{\prime }{}_{0.5-\widehat{\upsilon }}\left( \left| a(t_{i};\widehat{ \alpha },\widehat{\beta })\right| \right) }{k_{0.5-\widehat{\upsilon } }\left( \left| a(t_{i};\widehat{\alpha },\widehat{\beta })\right| \right) }\frac{a(t_{i};\widehat{\alpha },\widehat{\beta })\frac{\partial }{ \partial \beta }a(t_{i};\widehat{\alpha },\widehat{\beta })}{\left| a(t_{i};\widehat{\alpha },\widehat{\beta })\right| } \\&+\frac{\phi (\widehat{\lambda }a(t_{i};,\widehat{\alpha },\widehat{\beta } ))}{\Phi (\widehat{\lambda }a(t_{i};,\widehat{\alpha },\widehat{\beta }))} \frac{\widehat{\lambda }\partial }{\partial \beta }a(t_{i};\widehat{\alpha }, \widehat{\beta })+\frac{\frac{\partial }{\partial \beta }A(t_{i},\widehat{ \alpha },\widehat{\beta })}{A(t_{i},\widehat{\alpha },\widehat{\beta })},\\ \widehat{\mathbf {S}}_{i,\lambda }= & {} \frac{\phi (\widehat{\lambda }a(t_{i};, \widehat{\alpha },\widehat{\beta }))}{\Phi (\widehat{\lambda }a(t_{i};, \widehat{\alpha },\widehat{\beta }))}a(t_{i};\widehat{\alpha },\widehat{ \beta }), \\ \widehat{\mathbf {S}}_{i,\upsilon }= & {} -\ln 2-DG(\widehat{\upsilon })+\ln \left| a(t_{i},\widehat{\alpha },\widehat{\beta })\right| -\frac{ k^{\prime }{}_{0.5-\widehat{\upsilon }}\left( \left| a(t_{i};\widehat{ \alpha },\widehat{\beta })\right| \right) }{k_{0.5-\widehat{\upsilon } }\left( \left| a(t_{i};\widehat{\alpha },\widehat{\beta })\right| \right) }. \end{aligned}$$

$\left( iv\right)$ For the SSN-BS distribution, the elements of $\widehat{ \mathbf {S}}_{i}$ are obtained by

$$\begin{aligned} \widehat{\mathbf {S}}_{i,\alpha }=\, & {} \frac{\left( a(t_{i};\widehat{\alpha }, \widehat{\beta })\right) ^{\widehat{\upsilon }}\exp \left( -a^{2}(t_{i}; \widehat{\alpha },\widehat{\beta })\right) \frac{\partial }{\partial \alpha } a(t_{i};\widehat{\alpha },\widehat{\beta })}{\Gamma \left( \frac{\widehat{ \upsilon }+1}{2}\right) G\left( \frac{a^{2}(t_{i};\widehat{\alpha },\widehat{ \beta })}{2},\frac{\widehat{\upsilon }+1}{2}\right) }-\frac{\left( \widehat{ \upsilon }+1\right) \frac{\partial }{\partial \alpha }a(t_{i};\widehat{ \alpha },\widehat{\beta })}{a(t_{i};\widehat{\alpha },\widehat{\beta })} \\&+\frac{\phi (\widehat{\lambda }a(t_{i};,\widehat{\alpha },\widehat{\beta } ))}{\Phi (\widehat{\lambda }^{(r)}a(t_{i};,\widehat{\alpha }^{(r)},\widehat{ \beta }^{(r)}))}\frac{\widehat{\lambda }\partial }{\partial \alpha }a(t_{i}; \widehat{\alpha },\widehat{\beta })+\frac{\frac{\partial }{\partial \alpha } A(t_{i},\widehat{\alpha },\widehat{\beta })}{A(t_{i},\widehat{\alpha }, \widehat{\beta })},\\ \widehat{\mathbf {S}}_{i,\beta }= \,& {} \frac{\left( a(t_{i};\widehat{\alpha }, \widehat{\beta })\right) ^{\widehat{\upsilon }}\exp \left( -a^{2}(t_{i}; \widehat{\alpha },\widehat{\beta })\right) \frac{\partial }{\partial \beta } a(t_{i};\widehat{\alpha },\widehat{\beta })}{\Gamma \left( \frac{\widehat{ \upsilon }+1}{2}\right) G\left( \frac{a^{2}(t_{i};\widehat{\alpha },\widehat{ \beta })}{2},\frac{\widehat{\upsilon }+1}{2}\right) }-\frac{\left( \widehat{ \upsilon }+1\right) \frac{\partial }{\partial \beta }a(t_{i};\widehat{\alpha },\widehat{\beta })}{a(t_{i};\widehat{\alpha },\widehat{\beta })} \\&+\frac{\phi (\widehat{\lambda }a(t_{i};,\widehat{\alpha },\widehat{\beta } ))}{\Phi (\widehat{\lambda }a(t_{i};,\widehat{\alpha },\widehat{\beta }))} \frac{\widehat{\lambda }\partial }{\partial \beta }a(t_{i};\widehat{\alpha }, \widehat{\beta })+\frac{\frac{\partial }{\partial \beta }A(t_{i},\widehat{ \alpha },\widehat{\beta })}{A(t_{i},\widehat{\alpha },\widehat{\beta })},\\ \widehat{\mathbf {S}}_{i,\lambda }= \,& {} \frac{\phi (\widehat{\lambda }a(t_{i};, \widehat{\alpha },\widehat{\beta }))}{\Phi (\widehat{\lambda }a(t_{i};, \widehat{\alpha },\widehat{\beta }))}a(t_{i};\widehat{\alpha },\widehat{ \beta }),\\ \widehat{\mathbf {S}}_{i,\upsilon }= \,& {} \frac{1}{\widehat{\upsilon }}+\frac{\log 2 }{2}+\frac{\int _{0}^{\frac{a^{2}(t;\alpha ,\beta )}{2}}\left( \log x\right) x^{\frac{\widehat{\upsilon }+1}{2}-1}\exp \left( -x\right) dx}{2\Gamma \left( \frac{\widehat{\upsilon }+1}{2}\right) G\left( \frac{a^{2}(t_{i}; \widehat{\alpha },\widehat{\beta })}{2},\frac{\widehat{\upsilon }+1}{2} \right) }-\log \left| a(t_{i};\widehat{\alpha },\widehat{\beta } )\right| . \end{aligned}$$

The covariance matrix can be useful for studying the asymptotic behavior of $\widehat{\varvec{\theta }}=[\widehat{\alpha },\widehat{\beta }, \widehat{\lambda },\widehat{\upsilon }]$ by its asymptotic normality. The statistical inference about $\varvec{\theta }=\left[ \alpha ,\beta ,\lambda ,\upsilon \right]$ can be then made.

4 Simulation Study and an Illustrative Example

4.1 Simulation Study

We perform a simulation study to evaluate the finite sample properties of ML estimators described in Sect. 3. To conduct the experimental study, we generate different sample of sizes $n=50,$ 100,  200,  400,  800 from the STN-BS, SGLN-BS, SSN-BS models. The true parameters are supposed to b $\varvec{\theta }=\left[ \alpha ,\beta ,\lambda ,\upsilon \right] =\left[ 1,1,2,2\right]$ and $\varvec{\theta }=\left[ \alpha ,\beta ,\lambda ,\upsilon \right] =\left[ 0.5, 1, 2, 2\right] .$ Each simulate data set was fitted via the ECM algorithm under the same generated model using $M=5000$ replications. To examine the performance of the ML estamates, for each sample size and for each estimate, $\widehat{\varvec{\theta }}=[\widehat{\alpha },\widehat{\beta },\widehat{\lambda },\widehat{ \upsilon }],$ we compute the mean, $E[\widehat{\theta }_{i}],$ the root mean square error,  $\sqrt{MSE},$ and the relative bias in absolute value,  RB,  defined as

$$\begin{aligned} \sqrt{MSE}= & {} \sqrt{E\left( \widehat{\theta }_{i}-\theta _{i}\right) ^{2},}\\ RB= & {} \left| \frac{E\left( \widehat{\theta }_{i}\right) -\theta _{i}}{ \theta _{i}}\right| , \end{aligned}$$

respectively, such that $\theta _{1}=\alpha ,$ $\theta _{2}=\beta ,$ $\theta _{3}=\lambda ,$ $\theta _{4}=\upsilon .$ Tables 1, 2, 3 present the mean, $\% RB,$ and $\sqrt{MSE}$ of the ML estimates of the parameters $\theta _{i}$ $i=1,2,3,4$ for STN-B, SGLN-BS and SSN-BS models.

Table 1 Parameter estimates for STN-BS model, when $\beta =1,$ $\lambda =2,$ $\upsilon =2$

Table 2 Parameter estimates for SGLN-BS model, when $\beta =1,$ $\lambda =2,$ $\upsilon =2$

Table 3 Parameter estimates for SSN-BS model, when $\beta =1,$ $\lambda =2,$ $\upsilon =2$

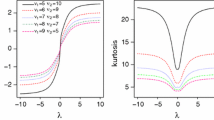
Figures 5, 6, 7 and 8 show the graphical representations of RB and $\sqrt{ MSE}$ of the four parameter estimates as a function of sample size n,  respectively. Clearly, the $\sqrt{MSE}$ and RB values converge to zero when n increases.

Fig. 5

RB values in parameter estimates when $\alpha =0.5,$ $\beta =1,$ $\lambda =2,$ $\upsilon =2$

Fig. 6

MSE root values in parameter estimates when $\alpha =0.5,$ $\beta =1,$ $\lambda =2,$ $\upsilon =2$

Fig. 7

RB values in parameter estimates when $\alpha =1,$ $\beta =1,$ $\lambda =2,$ $\upsilon =2$

Fig. 8

MSE root values in parameter estimates when $\alpha =1,$ $\beta =1,$ $\lambda =2,$ $\upsilon =2$

4.2 An Illustrative Example

In this section, we consider the results in preceding sections by analyzing a data set originally reported by Bjerkedal [10] and analyzed by Kundu et al. [23]. Table 4 displays the summary of these data including sample median, mean, standard deviation (SD),  coefficient of variation (CV),  coefficient of skewness (CS),  coefficient of kurtosis (CK),  range, minimum, maximum and the sample size (n). As it is observed, the data comes from a positively skewed distribution with a kurtosis greater than three. So we propose that these data set can be suitable to modeling some kind of SSMSN-BS distributions listed in Table 5.

Table 4 Descriptive statistics for the data

Estimation and model checking are provided in Table 5. We first obtain the ML estimation of the parameters via ECM algorithm described in Sect. 3. Then to assess the fitting performance, we use the maximized log-likelihood $\mathbf {\ell }\left( \widehat{\varvec{\theta }}\right) ,$ the Akaike $\left( AIC\right)$ and AIC with a correction (AICc) information criteria which defined as

$$\begin{aligned} AIC= & {} 2m-2\mathbf {\ell }\left( \widehat{\varvec{\theta } }\right) , \\ AICc= & {} AIC+\frac{2m\left( m+1\right) }{n-m-1}, \end{aligned}$$

where m is the number of the model parameters.

Table 5 The ML estimates and information criteria based on the SSMSN-BS distributions

According to the AIC and AICc we find that the $ST_{\upsilon _{1}}T_{\upsilon _{2}}-BS$ distribution provides the best fit.

The PP plots and empirical and theoretical cdf plots given in Figures 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 confirm again the appropriateness of the $ST_{\upsilon _{1}}T_{\upsilon _{2}}-BS$ distribution.

Fig. 9

The PP plot (left) and empirical versus theoretical c.d.f. (right) for the BS model

Fig. 10

PP plot (left) and empirical versus theoretical c.d.f. (right) for the T-BS model

Fig. 11

PP plot (left) and empirical versus theoretical c.d.f. (right) for the SGLNT-BS model

Fig. 12

PP plot (left) and empirical versus theoretical c.d.f. (right) for the SSN-BS model

Fig. 13

PP plot (left) and empirical versus theoretical c.d.f. (right) for the ST-BS model

Fig. 14

PP plot (left) and empirical versus theoretical c.d.f. (right) for the SN-BS model

Fig. 15

PP plot (left) and empirical versus theoretical c.d.f. (right) for the SNT-BS model

Fig. 16

PP plot (left) and empirical versus theoretical c.d.f. (right) for the STN-BS model

Fig. 17

PP plot (left) and empirical versus theoretical c.d.f. (right) for the $\text {ST}_{ \upsilon }T_{ \upsilon }\text {-BS}$ model

Fig. 18

PP plot (left) and empirical versus theoretical c.d.f. (right) for the $\text {ST}_{ \upsilon _{1}}T_{ \upsilon _{2}}\text {-BS}$ model

Also we use known distributions such as gamma, lognormal, weibull, exponential to compare the competition models. For the ML estimates we use fitdistr function in package MASS in the statistical software R. see Table 6. Again $\text {ST}_{\upsilon _{1}}T_{\upsilon _{2}}\text {-BS}$ distribution seems to be the best.

Table 6 The ML estimates and information criteria on the four distributions

5 Concluding Remarks

In this paper, an extension of the Birnbaum-Saunders distribution, called scale shape mixture of skew normal Birnbaum–Saunders (SSMSN-BS) distribution and its subclasses, are introduced. The parameters estimation via ECM algorithm are discussed and the utility of models is shown by means of simulation and real data set. The SSMSN-BS distributions can be in modeling different types of data due to their properties and their flexibility.

The study of the bivariate SSMSN-BS class (see [22]), or more general, the study of the multivariate $SSMSN-BS$ class (see [1]) are interesting problems that remain to be studied. These works are currently under progress and we hope to report our findings in a future paper.