1 Introduction

For the advancement of high technology, the investigation and discovery of novel natural laws, and the gathering of crucial data, weak signal detection is a crucial tool. has numerous applications at the moment in a variety of fields, including bio-medicine [1, 2], earth sciences [3], microelectronic physics [4], etc. The main application scenario of this technique is to extract useful, weak signals that are submerged in noise. In addition, there are various detection methods for different application scenarios, commonly time domain detection methods and frequency domain detection methods [5,6,7]. Both of these techniques typically rely on linear theory, which can cause the signal to be detected to be lost while filtering out the noise. As a result, nonlinear systems have gained popularity as a detection technique in recent years [8,9,10,11,12]. This detection technique transforms signals and noise into nonlinear system features, then employs these features to assess signals and carry out detection.

A typical non-linearity system in which chaotic phenomena occur is referred to as a chaotic system, also known as a chaotic oscillator. They occur in deterministic dynamical systems that exhibit motion that appears random due to sensitivity to initial values. The Logistic model [13], Duffing model [14], Lorenz model [15], Chua model [16], etc. are examples of common chaotic oscillators. The Duffing chaotic oscillator is a nonlinear vibration model derived from a straightforward physical model, but its model is typical. This oscillator can be used to represent a wide variety of mathematical models for nonlinear vibration issues encountered in engineering practice [17, 18]. In [17], This paper reviews eight major types of nonlinear vibration energy harvesting reported over the past decade, covering underlying principles, advantages and disadvantages, and application-specific guidance for researchers and designers. In the past decade, there has been a rapid expansion in research of vibration energy harvesting into various nonlinear vibration principles such as Duffing non-linearity, bi-stability, parametric oscillators, stochastic oscillators and other nonlinear mechanisms. In [18], they investigate the complex dynamics of a rotating pendula arranged into a simple mechanical scheme. Three nodes forming the small network are coupled via the horizontally oscillating beam and the springs. These models can be summarized as Duffing models. In addition, there are also many chaotic applications that directly use Duffing oscillators. In [19], Haibo Liu advanced a new weak sinusoidal signal detection scheme that used the Duffing oscillator state transition from big-cycle motion to chaotic motion. In [20], Cong Chao introduces a detection scheme for the state of a qubit that is based on resonant few-photon transitions in a driven nonlinear resonator, which is a Duffing oscillator. In [21], V. Leyton introduces a detection scheme for the state of a qubit that is based on resonant few-photon transitions in a driven nonlinear resonator. The latter is parametrically coupled to the qubit and is used as its detector. In addition, as a pathway into chaos, intermittent chaos has also been studied in many papers, such as [22,23,24,25,26,27],. However, when the parameters are fixed, the intermittent chaos phenomenon that changes with the time of iterations in the chaotic state has never been found in integer-order Duffing chaotic systems before, which is only in incommensurate fractional-order Duffing systems.

The fractional-order Duffing system is one of the many improved forms of Duffing oscillators, and it has been extensively studied [28,29,30]. It is more accurate than the integer-order Duffing system in describing physical phenomena and also has a larger control range in chaos control theory. Additionally, we have found that in incommensurate fractional-order Duffing systems, there is an intermittent chaotic phenomenon in our previous work [31], this paper [31] explains that incommensurate fractional Duffing systems would exhibit intermittent chaos regardless of the definition of fractional calculus or the choice of different approximate solving algorithms. The fractional derivatives of different orders can exhibit a perturbation-like effect, etc. the phenomenon of intermittent chaos. However, the intermittent dynamical properties of fractional-order Duffing chaotic systems affected by the driving force have not been successfully applied to weak signal detection, and the majority of studies continue to use the properties of integer-order chaotic systems retained by fractional-order chaotic systems [32,33,34,35,36].

In this paper, weak signals will be detected using the new intermittent chaos phenomenon of a fractional-order incommensurate Duffing oscillator. Design a time series-based judgment method that successfully separates chaotic, intermittent chaotic, and limit-cycle states. This enables the detection of weak signals using intermittent chaotic states. When the frequency of the signal to be measured is known, the fast phase change characteristic of the intermittent chaotic state to the limit cycle state is used to determine the amplitude of the weak signals. When the signal’s amplitude is known, the detection system’s frequency change will cause it to exhibit various intermittent chaotic properties, and the frequency range of the signal that can be detected is determined by these intermittent chaotic properties. The simulation results demonstrate that the fractional-order system is more complex than the integer-order system dynamics characteristics and can have more applications scenarios due to the new intermittent chaos phenomenon. This paper’s innovation lies in its ability to detect weak signal frequency by using a single chaotic oscillator, and integer-order chaotic detection systems cannot complete the detection.

In Sect. 2, the model of a fractional-order incommensurate Duffing oscillator is introduced to identify weak signals. In Sect. 3, we describe how to use time series data to identify intermittent chaos, how to identify weak signals using the identified intermittent chaotic characteristics, and how to detect the amplitude parameter and frequency parameter of weak signals, respectively. In Sect. 4, conclusions are provided.

2 Duffing Oscillator Model

The Duffing oscillator, one of the most popular models for studying chaos, demonstrates a wealth of nonlinear dynamical properties. The Duffing oscillator’s equation is typically as follows:

$$\begin{aligned} \ddot{x}\left( t\right) +\delta \dot{x}\left( t\right) +\beta x\left( t\right) +\alpha x\left( t\right) ^3 = \gamma cos \left( \omega t\right) . \end{aligned}$$
(1)

In Eq. 1, the physical meaning of x is displacement and y is the derivative of x, which has the physical meaning of velocity. Typically, it can also be written as:

$$\begin{aligned} \dot{x}\left( t\right)&= y\left( t\right) \nonumber \\ \ddot{y}\left( t\right)&= -\delta \dot{x}\left( t\right) -\beta x\left( t\right) -\alpha x\left( t\right) ^3+\gamma cos \left( \omega t\right) . \end{aligned}$$
(2)

where \(\delta\) is the damping radio, \(-\beta x\left( t\right) -\alpha x\left( t\right) ^3\) is the nonlinear term, \(\alpha\) represents the spring force’s non-linearity, and \(\beta\) stands for toughness. The periodic driving force is \(\gamma cos\left( \omega t\right)\), and the driving force’s amplitude and angular frequency are represented by \(\gamma\) and \(\omega\), respectively. The Duffing oscillator can be flexibly controlled by the driving force because the entire driving force term \(\gamma cos\left( \omega t\right)\) can be controlled as an applied signal. It has been shown that with increasing values of \(\gamma\), the Duffing oscillator goes from a period-doubling bifurcation into chaos and finally into a limit cycle state. The Duffing oscillator is used to detect weak signals when the chaotic oscillator’s state is between chaotic and limit-cycle states. This is because even a small change in the parameter \(\gamma\) will result in a rapid change in the chaotic oscillator’s state.

To create the fractional order Duffing chaotic system, the fractional order differential is added to equation ref Eq. 2. Let the order value of the fractional-order differentiation be less than one but near one at this point since the attributes of the integer-order Duffing system must be kept for weak signal detection. This paper uses a value of 0.9. The fractional-order Duffing chaos detection system equation is finally:

$$\begin{aligned} \frac{d^{q_1} x\left( t\right) }{d^{q_1} t}&= y\left( t\right) \nonumber \\ \frac{d^{q_2} y\left( t\right) }{d^{q_2} t}&= -\delta y\left( t\right) -\beta x\left( t\right) -\alpha x\left( t\right) ^3+\gamma cos \left( \omega t\right) . \end{aligned}$$
(3)

where \(\frac{d^{q_1} x\left( t\right) }{d^{q_1} t}\) is the \(q_1\) order differential of x, \(\frac{d^{q_2} y\left( t\right) }{d^{q_2} t}\) is the \(q_2\) order differential of y, The equation is said to be commensurate when \(q_1\) and \(q_2\) are equal, and incommensurate when \(q_1\) and \(q_2\) are not equal. The remaining parameters’ definitions are compatible with Eq. 2. The fractional-order derivative can be defined in a variety of ways, including those proposed by Caputo, Riemann–Liouville, and Grünwald–Letnikov, among others [37]. The form of the Riemann–Liouville definition is as follows:

$$\begin{aligned} D^q = \frac{d^q x\left( t\right) }{d^q t} = \frac{d}{dt}\left[\frac{1}{\Gamma (1-q)} \int _{0}^{t}(t-\tau )^{-q} x(\tau ) d\tau \right],0<q\le 1. \end{aligned}$$
(4)

where \(D^q\) is the fractional derivative operator of order q. q is the order of the fractional derivative operator. \(\Gamma\) is a gamma function, When q=1, the fractional derivative operator is equivalent to the first derivative operator.

Consider Eqs. 2 and 3 for weak signal detection. The integer-order Duffing oscillator in Eq. 2 only exhibits chaos when the driving force’s frequency is low. When the frequency of the weak signal is significantly different from the frequency of the driving force, the detecting system will quickly classify the weak signal as noise and disregard it. The integer-order Duffing oscillator is changed into the fractional-order oscillator, which likewise has this characteristic. Therefore, we have modified Eq. 3 using the method described in the literature [38], at this time the chaotic system’s driving force frequency can be changed at will while still retaining its intermittent chaotic properties. The equations for the oscillator of fractional order are as follows:

$$\begin{aligned} \frac{d^{q_1} x\left( t\right) }{d^{q_1} t}&= y\left( t\right) \nonumber \\ \frac{d^{q_2} y\left( t\right) }{d^{q_2} t}&= - k_2 \delta y\left( t\right) +k_1 k_2\left( -\beta x\left( t\right) -\alpha x\left( t\right) ^3+\gamma cos \left( \omega t\right) \right) \end{aligned}$$
(5)

where \(k_1=D^{q_1}\left( 1/\Omega \right)\), \(k_2=D^{q_2}\left( 1/\Omega \right)\), When intermittent chaos occurs, the Duffing oscillator’s parameters are \(\alpha\), \(\beta\), and \(\delta\), the chaotic detection system’s critical threshold is \(\gamma\), and its frequency is \(\Omega\). When utilizing Eq. 5 to identify weak signals, Add noise and weak signal respectively. With \(\gamma _1 cos\left( \Omega _1 t\right)\) being the weak signal to be measured, \(\gamma _1\) represents the weak signal’s amplitude, and \(\Omega _1\) is its frequency. White Gaussian noise is represented by WGN, and its power is indicated by \(P_W\). At this time, the detecting system’s expression can be written as:

$$\begin{aligned} \frac{d^{q_1} x\left( t\right) }{d^{q_1} t}&= y\left( t\right) \nonumber \\ \frac{d^{q_2} y\left( t\right) }{d^{q_2} t}&= - k_2 \delta y\left( t\right) + k_1 k_2\left( -\beta x\left( t\right) - \alpha x\left( t\right) ^3 + \gamma cos \left( \Omega t\right) + \gamma _1 cos \left( \Omega _1 t\right) + WGN \right) \end{aligned}$$
(6)

A simulation model based on Eq. 6 is shown in Fig. 1.

Fig. 1
figure 1

Simulation model of fractional-order incommensurate Duffing chaotic system for detecting weak signals

Full size image

In the model of Fig. 1, the Signal generator is used to generate the driving force term, and White Gaussian Noise is used to generate the input noise. Sine Wave is the input signal to be measured, Sum is the adder, and XY Graph for generating the attractor graphs. X Scope is used to display time series. \(\alpha\), \(\beta\), \(\gamma\), \(\delta\), and \(\omega\) are used to adjust the corresponding parameters in the equation. \(fractional-order integrator 1\) represents the fractional order integrator of order \(q_1\). Where diffY represents the first order derivative of y. Here the integration is used to achieve the iteration of x values and thus obtain the approximate solution of the fractional order chaos equation. Using a method described in the literature [39] that uses an arbitrary precision integer-order approximation equation for the transfer function, we approximate the solution of the fractional-order integral. It should be emphasized that there are drawbacks to utilizing this strategy to resolve fractional-order chaotic systems [40]. However, when performing applications for weak signal detection, it is not necessary to employ the precise numerical solution of the fractional-order Duffing equation; the method is used for circuit implementation of chaotic systems for weak signal detection. In applications, the value of \(\gamma\) in the \(\gamma cos \left( \Omega t\right)\) term value is raised from 0, and the fractional-order chaotic system can be employed for weak signal detection when intermittent chaos occurs. In this paper,the intermittent chaos phenomena appear in the transition states from the chaotic states to periodic state, and the results are shown in Fig. 2.

Fig. 2
figure 2

The time series diagram of variables (x) in the chaotic system established based on Eq. 5, where \(\gamma\) =0.980 dBV in (a), \(\gamma\) =0.982 dBV in (b), \(\gamma\) =0.984 dBV in (c), \(\gamma\) =0.986 dBV in (d). The remaining parameters are \(q_1\)=1, \(q_2\)=0.9, \(\Omega _1\)=1 rad/s, \(\delta\)=0.5, \(\beta\)=1, \(\alpha\)=-1, and the initial conditions are \(x_0\)=\(y_0\)=0.1

Full size image

Figure 2 shows that the closer the amplitude of the driving force is to the critical threshold, the fewer chaotic windows there are in the time series. Conversely, the more chaotic windows there are, the more chaotic phenomena there are. The general definition of intermittent chaos refers to the chaotic state that changes with the amplitude of the driving force. However, a new phenomenon that this paper focuses on is that when the amplitude of the driving force is fixed within a specific range, the chaotic state will change with simulation time. This phenomenon did not previously occur in integer-order Duffing equations or proportional fractional-order Duffing equations.

3 Incommensurate Fractional-Order Duffing Oscillator for Weak Signal Detection

Because sine and cosine signals can be used to make any signal and they can be turned into one another, sine and cosine signal identification is a crucial step in the theory of weak signal detection. Additionally, the Duffing system uses a cosine-shaped driving term. As a result, detecting the amplitude and frequency of weak cosine signals becomes crucial for weak signal detection that uses chaotic systems. In this section, we’ll use a fractional-order incommensurate chaotic detection system to do just that. The intermittent chaos phenomenon that arises in fractional-order incommensurate Duffing systems has gone unmentioned in the many studies [41]. Conversely, other fractional-order chaotic systems have also been observed to exhibit intermittent chaos phenomena [42, 43]. Firstly, this section shows a time-series-based approach put forth to detect intermittent chaotic phenomena. This approach can be used to differentiate between chaotic, intermittent, and limit cycle states. Secondly, we show how to use the recently found intermittent chaotic phenomenon in fractional-order incommensurate Duffing systems for amplitude detection of weak signals. Thirdly we use the intermittent chaotic detection approach to detect weak signal frequencies.

3.1 Discriminatory Method of Intermittent Chaos

In this paper, we distinguish between intermittent chaos state and limit cycle state using the proportion of limit cycle windows and the number of chaotic windows in the time series plot. This is because the intermittent chaotic windows in the intermittent chaotic phenomena in the chaotic oscillators used in this paper are small, and the length of the periodic orbit in the limit cycle state accounts for most of the time series. The following are the steps of the method:

Step 1 We first select a time series with a particular length in the chaotic system’s limit cycle state and determine its maximum and minimum values. These two values are multiply by two-thirds to determine the central value \(C_+\) and \(C_-\).To represent the repeated orbits of the limit cycle state and to distinguish it from the intermittent chaotic state, we count the number of points in the time series that is close to the central value as L.

Step 2 Using the same central value in the intermittent chaos state, we count the number of points in the time series that is close to the central value as I. and compare I with L to distinguish the intermittent chaos state.

Step 3 The proportion of limit cycle windows is equal to I/L, and the number of chaotic windows is equal to the absolute value of \(L-I\). This is due to our belief that repeating time series fill the time series graph while the chaotic system is in the limit cycle state, whereas intermittent chaos causes the repetitive time series to decrease when chaotic windows arise.

Step 4 The aforementioned approach, however, is susceptible to inaccuracies, particularly when the chaotic window’s chaotic trajectory lies precisely close to the central value, which can result in a bigger I than L. As a result, Altering the time series that was chosen and choosing more central values can successfully lower the inaccuracy. The closer the central value is to the most value, the less the calculated error.

When the detection system is in the limit cycle state, it is clear that the number of chaotic windows is 0 and the proportion of limit cycle windows is 100%, whereas the number of chaotic windows rises and the proportion of limit cycle windows falls when the detection system is in the intermittent chaotic state. Weaker intermittency is indicated by a lower proportion of chaotic windows and a higher proportion of limit cycle windows, whereas stronger intermittency is indicated by the reverse. The window of limit cycles does not emerge when the intermittency of chaos is too high, and the chaotic system then acts like a typical chaotic phenomenon. Therefore, too much or too little intermittency will cause intermittent chaotic phenomena to vanish.

3.2 Amplitude Detection of Weak Signals

The driving force frequency \(\Omega\) of the adjustment detection system is consistent with the weak signal frequency \(\Omega _1\) when the frequency of the weak signal is known but the amplitude is unknown. The detecting system’s equation in this case is:

$$\begin{aligned} \frac{d^{q_1} x\left( t\right) }{d^{q_1} t}&= y\left( t\right) \nonumber \\ \frac{d^{q_2} y\left( t\right) }{d^{q_2} t}&= - k_2 \delta y\left( t\right) +k_1 k_2\left( -\beta x\left( t\right) -\alpha x\left( t\right) ^3+\left( \gamma +\gamma _1 \right) cos \left( \Omega _1 t\right) + WGN \right) \end{aligned}$$
(7)

We start by thinking about the scenario in which there is no noise, namely WGN=0. The remaining parameters are \(q_1\)=1, \(q_2\)=0.9, \(\Omega _1\)=1 rad/s, \(\delta\)=0.5, \(\beta\)=1, \(\alpha\)=-1, and the initial conditions are \(x_0\)=\(y_0\)=0.1. Let \(\gamma _0\)=\(\gamma + \gamma _1\) represent the amplitude of the driving force under the joint action of the detection system itself and the weak signal when the frequency is known. By adjusting this value, the chaotic system is in the critical intermittent chaotic state and the limit cycle state.

Fig. 3
figure 3

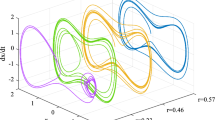
The attractors diagram of variables (x) (y) and time series diagram of variables (x) in the weak signal detection system established based on Eq. 7, where \(\gamma _0\) =0.986 dBV in (a), (b), \(\gamma _0\) =0.987 dBV in (c, d)

Full size image

Figure 3a and c shows how quickly the chaotic system’s state transitions from the intermittent chaotic state to the limit cycle state when \(\gamma _0\) is changed from 0.986 to 0.987. As a result, we can set the detection system’s driving force amplitude \(\gamma\) to 0.986. At this time, if there is no signal to be measured that is, \(\gamma _1\)=0, then \(\gamma _0\)=\(\gamma\)+\(\gamma _1\)=0.986, the chaotic detection system behaves as an intermittent chaotic state, and if there is a signal to be measured that is, \(\gamma _1\)=0.001, then \(\gamma _0\)=0.987 and the chaotic detection system behaves as a limit cycle state. The various states of the chaotic detection system can then be used to determine if there are any weak signals present or not. When the chaotic system reaches the limit cycle state, we can reduce \(\gamma\) by further control and allow the chaotic state to intermittently resurface. At this moment, \(\gamma _0\) is once more equal to 0.986, and the value of \(\gamma\) the applied control’s reduction is the weak signal’s amplitude, which is \(\gamma _1\). We can therefore conclude that, given the parameters used in this paper, the minimum discernible weak signal amplitude is 0.001 dBV.

Due to the nonlinear terms in its equations, the chaotic detection system can withstand noise interference. However, if the noise’s power is too large, it will destroy the chaotic detection system’s critical intermittent chaos state and would fail detecting weak signals. To investigate the impact of noise on the fractional-order chaotic detection system, we will add noise with various powers to the detection system with \(\gamma _0\)=0.986.

Fig. 4
figure 4

The attractors diagram of variables (x) (y) and time series diagram of variables (x), P is the power of WGN in Eq. 7, where P=10 mW in (a, b), P=50 mW in (c, d)

Full size image

As can be seen in Fig. 4, the attractors of the chaos detection system remain relatively unchanged, but the intermittent chaotic state represented by the time series changes after introducing noise of 10 mW and 50 mW power, respectively. Therefore, we intercept the time series of the appropriate length by the chosen conditions and determine that the number of chaotic windows corresponding Fig. 3b is 3 and the proportion of limit cycle windows is 97.26%, the number of chaotic windows corresponding to Fig. 4b is 10 and the proportion of limit cycle windows is 90.54%, and the number of chaotic windows corresponding to Fig. 4d is 37 and the proportion of limit cycle windows is 67.83%.

Next, the noise of different power is added to the detection system, obtained the number of chaotic windows and the proportion of limit cycle windows of the time series, and then determine the maximum noise that the detection system can withstand, as shown in Fig. 5.

Fig. 5
figure 5

Number of chaotic windows and Proportion of limit cycle windows for intermittent chaotic phenomenon after adding different power noise in the detection system

Full size image

Figure 5 illustrates how the intermittent chaos of the detection system gradually loses its intermittent nature as the noise level gradually rises. The intermittent nature of intermittent chaos has vanished when the number of chaotic windows exceeds 24 and the proportion of limit cycle windows is less than 84%, at this time,the time series is an ordinary chaotic phenomenon. This makes it possible to distinguish between chaotic, intermittent chaotic, and limit cycle states using the number of chaotic windows and the proportion of limit cycle windows.

The detection system used in this paper can withstand a maximum noise power of 21 mW to guarantee the effectiveness of the system. A weak signal that has resisted the noise is added to the detection system to get the minimum detectable signal-to-noise ratio of the detection system. To bring the detection system’s state into the limit cycle, again adjust the noise power. The detection theory then states that the detection system transitions from a limit cycle state to an intermittent chaotic state when gamma is reduced by 0.001. The results show that the minimum detectable signal-to-noise ratio is \(-\)13.26 dB, and the small signal \(\gamma _1\) has an amplitude of 0.001 dBV.

3.3 Frequency Detection of Weak Signals

The main idea behind using an integer-order chaotic system to determine the range of weak signal frequencies is that when the frequency of a weak signal is close to the detection system’s frequency, it leads to intermittent chaos in a detection system without intermittent chaos [44, 45]. However, a weak signal with a different frequency from the detection system will affect the properties of the intermittent chaos and, as a result, also be able to detect the frequency of the weak signal for a fractional-order incommensurate Duffing detection system that already has intermittent chaos. We use the detection of common hydro-acoustic signals as an example. When it is necessary to determine the frequency of weak signals, the detection system’s parameters are set as follows: \(q_1\)=1, \(q_2\)=0.9, \(\gamma\)=0.801, \(\beta\)=-1, \(\alpha\)=1, \(\gamma _1\)=0.001 dBV, and \(\Omega\)=200 rad/s. Small signals of various frequencies are then added to the system under test, and the system’s intermittent chaotic characteristics are examined.

Fig. 6
figure 6

The proportion of limit cycle windows and the quantity of chaotic windows when the weak signal’s frequency is very close to the detecting system’s. The detection system’s operating frequency is 200 rad/s

Full size image

According to Fig. 6, there are 6 chaotic windows and the proportion of limit cycle windows is 0.9570 when the frequency of the signal to be monitored and the driving frequency of the detecting system are the same. When the detection system’s intermittent chaotic characteristics change as the frequency difference increases, the proportion of limit cycle windows gradually decreases and the number of chaotic windows gradually rises when the frequency difference between the signal to be measured and the detection system is less than 1 rad/s. When the frequency difference is more than 1 rad/s, the detecting system’s intermittent chaotic characteristics stabilize when the frequency difference is more than 1 rad/s.

When this phenomenon occurs in an integer-order chaotic detection system, it is sometimes thought that weak signals are being mistaken for noise because the frequency difference between the detection system and the little signal is too great at this moment. In contrast, we think that small signals can still be recognized in fractional-order chaotic detection systems because the intermittent chaotic properties of the detection system may still be analyzed. Figure 7 illustrates an intriguing shift in the intermittent chaotic properties of the detecting system as the frequency difference increases.

Fig. 7
figure 7

The proportion of limit cycle windows and the quantity of chaotic windows when the weak signal’s frequency is very differences to the detecting system’s. The detection system’s operating frequency is 200 rad/s

Full size image

Figure 7 shows that when the frequency of the weak signal is less than 200 rad/s, the quantity of chaotic windows rapidly drops. When the frequency of the weak signal is between 200 rad/s and 1250 rad/s, the number of chaotic windows increases quickly and then stays within a specific range. However, when the frequency of the weak signal exceeds 1250 rad/s, the detection system’s chaotic window count begins to decline once more. Additionally, when the frequency of the weak signal rises, the intermittent chaotic feature of the detection system will become much weaker than it would be in the absence of the weak signal, making detection impossible.

Based on the aforementioned phenomenon, we think that the frequency of the weak signal can be estimated to be close to the driving force frequency of the detection system in the case where the intermittent chaos in the fractional-order detection system becomes stronger. Additionally, the fractional-order detection system’s frequency detectable range is substantially wider than the integer-order detection system’s. In this study, the selected condition of the detection system driving force frequency is 200 rad/s, and the highest detectable frequency difference of the fractional-order Duffing oscillator is 1050 rad/s.

4 Conclusions

In this paper, the method is based on the intermittent chaotic properties of fractional-order incommensurate Duffing systems, and can detect weak signals in the background of white Gaussian noise. Only fractional-order incommensurate Duffing systems exhibit the intermittent chaotic feature, this feature can not occur in commensurate or integer-order Duffing systems. Thus, it demonstrates that fractional-order chaotic systems can have more complex dynamic characteristics than integer-order systems and have more application scenarios. Firstly, a fractional-order incommensurate Duffing chaotic system is rewritten as a detection system that can measure weak signals at any frequency. Secondly, a time-series-based judgment method is proposed for identifying the intermittent chaos displayed by the detection system. The effectiveness of a single-detection oscillator for detecting weak signals is finally examined. When the weak signal’s frequency is known, its amplitude can be determined utilizing the intermittent chaos of a single-detection oscillator’s quick phase transition characteristics. In this case, the minimum discernible signal-to-noise ratio is \(-\)13.25 dB. When the weak signal’s amplitude is known, the driving force of the detection system’s frequency can be changed. If the difference between the driving force’s frequency and the weak signal’s frequency does not exceed 1050 rad/s, the intermittent chaos of the detection system will change, allowing the weak signal’s frequency to be detected. The findings of this study support the applicability of fractional-order chaotic systems to the detection of weak signals by demonstrating that the intermittent chaotic phenomenon of these systems is more suitable for doing so.