1 Introduction

Weak signal identification is widely used in many fields, such as universe exploration, fault diagnosis, medical diagnosis, life search, etc. How to identify it from strong noise has always been a research hotspot in the academic field. The characteristics of weak harmonic signals are amplitude, frequency and phase. There are many research results on the identification of these parameters. At present, weak signal identification systems adopt continuous systems, such as Duffing system [1,2,3], the variable scale Duffing system [4, 5], the Vanderpol-Duffing system [6], the dual coupling Duffing system [7], L-Y system [8,9,10], the time-delay Mathieu-Duffing system [11], Lorenz system [12], etc. But there are many shortcomings: (1) The calculation process of the Melnikov function of the continuous system is more complicated; (2) The calculation of the chaotic threshold often adopts necessary conditions, and the result is not accurate enough.

Moreover, many scholars have made a lot of achievements in the study of non-smooth systems. Kunze et al. [13] introduced plane non-smooth systems comprehensively. Du et al. [14] proposed homoclinic bifurcation Melnikov function of non-smooth systems and subharmonic Melnikov functions of non-smooth periodic orbits on the first and second kinds. Battelli and Feckan [15] gave Melnikov method for a class of high-dimensional discontinuous systems. Granados et al. [16] considered a two-dimensional piecewise smooth system divided into two regions by a transformation manifold. Granados et al. [17] studied the scattering maps of two coupled piecewise smooth systems, and their numerical applications on rocking blocks and Melnikov method. Tian et al. [18] used the pendulum as a model to study the chaotic thresholds under different pulse excitations when the pendulum collided with a rigid wall by using the non-smooth Melnikov method. Li et al. [19] studied a two-dimensional piecewise smooth system divided into four regions by two conversion surfaces. At present, there is no paper studying weak signal identification based on non-smooth system. Hence, it is the main task of this paper to find a non-smooth system with simple Melnikov function and accurate expression of chaotic threshold.

Consider the limit system of smooth and discontinuous (SD) oscillator which first proposed by Cao et al. [20]

$$\ddot{x} + [x - {\rm sign}(x)] = 0.$$
(1)

Many scholars have studied system (1) [21,22,23,24,25]. It can be seen that the limit system of the SD oscillator has an abundant of dynamic behavior transitions. From its simple non-smooth equation form, the calculation process of Melnikov will be simpler. So, we will consider the limit system of the SD oscillator as the identification system.

In this paper, when the variable scale limit system of SD oscillator without considering the phase is used as the identification system to identify weak signal parameters, the paper is organized as follows. In the next section, the limit system of SD oscillator with Gaussian white noise is adopted as the basic identification system. By using the non-smooth stochastic subharmonic-like Melnikov method, according to the necessary and sufficient condition that Melnikov function has a simple zero point in the mean square sense, the analytical expression of chaotic threshold of the identification system is given. The influence of noise intensity on the identification system is studied by making phase diagrams and Poincaré section diagrams. In Sect. 3, the expression of chaotic threshold of the identification system with signals to be detected is determined. Non-smooth variable-scale-convex-peak frequency identification method is used to identify the frequency of the signal to be detected. The amplitude of the signal to be detected is identify by using the bifurcation diagram of the amplitude of the reference signal. Determine the optimal value range of the parameter of the identification system. In Sect. 4, the electronic circuit is designed, which verifies the feasibility of the above method. In Sect. 5, the effectiveness of the above method is verified by an example of early fault of wheelset bearing in high-speed train.

2 Parameter Identification Model

Consider the limit system of SD oscillator with Gaussian white noise

$$\left\{ \begin{gathered} \dot{x} = y, \hfill \\ \dot{y} = - x + {\rm sign}(x) + \varepsilon ( - 2\mu y + f\cos (\omega t) + \sigma n(t)),(x,y) \ne (0,0), \hfill \\ \end{gathered} \right.$$
(2)

where \(- x + {\rm sign}(x)\) is the nonlinear term, \(\mu^{{}}\) is the damping coefficient, \(f\cos (\omega t)\) is the reference signal, \(\sigma n(t)^{{}}\) is Gaussian white noise with intensity \(\sigma^{{}}\) and power spectral density \(S_{n} (\omega ) = K = \frac{{\sigma^{2} }}{2\pi }\).

The undisturbed system of system (2) is

$$\left\{ \begin{gathered} \dot{x} = y, \hfill \\ \dot{y} = - x + {\rm sign}(x),(x,y) \ne (0,0). \hfill \\ \end{gathered} \right.$$
(3)

System (3) has three singularities \((0,0),( \pm 1,0)\). Because system (3) is discontinuous at \((0,0)\), and the Jacobian matrix does not exist, the topological structure near the saddle-like point \((0,0)\) is similar to the saddle point. The Jacobian matrix is \(J_{( \pm 1,0)} = \left( {\begin{array}{*{20}c} 0 & 1 \\ { - 1} & 0 \\ \end{array} } \right)\) at \(( \pm 1,0)\), and its eigenvalue is \(\lambda_{1,2} = \pm i\). So \(( \pm 1,0)\) is the center.

The piecewise Hamilton function of system (3) is

$$H(x,y) = \frac{{y^{2} }}{2} + U = \frac{{y^{2} }}{2} + \frac{{x^{2} }}{2} - \left| x \right|$$
(4)

where \(U = \frac{{x^{2} }}{2} - \left| x \right|\) is the potential energy function, as shown in Fig. 1.

Fig. 1
figure 1

The potential energy function of Eq. (4)

Full size image

When \(H(x,y) = 0^{{}}\), the homoclinic-like orbits of system (3) yield (5), as shown in Fig. 2.

$$q_{ \pm } = (x_{ \pm } (t),y_{ \pm } (t)) = ( \pm \cos t \pm 1, \mp \sin t),t \in [ - \pi ,\pi ].$$
(5)
Fig. 2
figure 2

Saddle-like point and homoclinic-like orbits

Full size image

The stochastic subharmonic-like Melnikov function of system (2) is

$$M_{ + } (t_{0} ) = \int_{ - \pi }^{\pi } {y_{ + } (t)[ - 2\mu y_{ + } (t) + f\cos (\omega (t + t_{0} )) + \sigma n(t + t_{0} )]dt} = - M + \overline{M}(t_{0} ) + \tilde{M}(t_{0} ),$$
(6)

where \(M = 2\mu \int_{ - \pi }^{\pi } {y_{ + }^{2} (t)dt} = 2\mu \pi\), \(\overline{M}(t_{0} ) = f\int_{ - \pi }^{\pi } {y_{ + } (t)\cos [\omega (t + t_{0} )]dt} = \frac{2}{{1 - \omega^{2} }}\,\,f\sin (\omega \pi )\sin (\omega t_{0} )\). \(\tilde{M}(t_{0} )\) is the random part of the stochastic subharmonic-like Melnikov function. The characteristics of \(\tilde{M}(t_{0} )\) considered below. Since \(n(t + t_{0} )\) is a stationary random process as the input, the output of \(\tilde{M}(t_{0} )\) is also a stationary random process. Therefore, the statistical characteristics of the stochastic Melnikov function can be completely determined by knowing the first and the second moment.

The first moment of \(\tilde{M}(t_{0} )\) is

$$E[\tilde{M}(t_{0} )] = E\Bigg[\int_{ - \pi }^{\pi } {\sigma y_{ + } (t)n(t + t_{0} )} dt\Bigg] = \int_{ - \pi }^{\pi } {\sigma y_{ + } (t)E[n(t + t_{0} )]} dt = 0.$$
(7)

Since \(E[\tilde{M}(t_{0} )] = 0\), the first moment ignores the influence of noise on the chaos threshold. Hence, the second moment of \(M_{ + } (t_{0} )\) must be considered.

The second moment of \(\tilde{M}(t_{0} )\) is

$$E[\tilde{M}^{2}(t_{0} ) ] = \int_{ - \pi }^{\pi } {|H(\omega )|^{2} S_{n} (\omega )d\omega } ,$$
(8)

where \(H(\omega )\) is the transfer function. Impulse response function \(h(t) = \sigma y_{ + }^{{}} (t)\) and \(H(\omega )\) form a Fourier transform pair, and we have

$$H(\omega ) = \int_{ - \pi }^{\pi } {h(t)e^{ - i\omega t} dt} = - \sigma \int_{ - \pi }^{\pi } {\sin (t)e^{ - i\omega t} dt} = \frac{2i\sigma }{{1 - \omega^{2} }}\sin (\omega \pi ),$$
(9)

then

$$E[\tilde{M}^{2}(t_{0}) ] = \int_{ - \pi }^{\pi } {\left| {H(\omega )} \right|^{2} S_{n} (\omega )d\omega } = 8K\sigma^{2} \int_{0}^{\pi } {\frac{{\sin^{2} (\omega \pi )}}{{(1 - \omega^{2} )^{2} }}d\omega } = 8K\sigma^{2} A,$$
(10)

where \(A = \int_{0}^{\pi } {\frac{{\sin^{2} (\omega \pi )}}{{(1 - \omega^{2} )^{2} }}d\omega }\). In the mean square sense, the necessary and sufficient conditions for the stochastic subharmonic-like Melnikov function of system (2) to have a simple zero point are

$$\left\{ {\begin{array}{*{20}c} {E[M{}_{+}^{2} (t_{0} )] = - (2\mu \pi )^{2} + \Bigg(\frac{2}{{1 - \omega^{2} }}f\sin (\omega \pi )\sin (\omega t_{0} )\Bigg)^{2} + 8K\sigma^{2} A = 0,} \\ {\frac{{dE[M{}_{ + }^{2} (t_{0} )]}}{{dt_{0} }} = \frac{8\omega }{{(1 - \omega^{2} )^{2} }}f^{2} \sin^{2} (\omega \pi )\sin (\omega t_{0} )\cos (\omega t_{0} ) \ne 0.\quad \quad \quad } \\ \end{array} } \right.$$
(11)

The chaotic threshold of system (2) is

$$f_{d} = \frac{{(1 - \omega^{2} )\sqrt {(\mu \pi )^{2} - 2K\sigma^{2} A} }}{{\sin (\omega \pi )\sin (\omega t_{0} )}},$$
(12)

satisfied \(\omega \ne k\), \(t_{0} \ne k\pi /\omega\), \(t_{0} \ne (2k\pi + \pi /2)/\omega\), \(k = 0, \pm 1, \pm 2, \ldots , \pm n, \ldots\).

Let \(\mu = 0.1,t_{0} = 2\). Accroding to Eq. (12), make the function diagram of the chaotic threshold \(f_{d}\) with respect to reference signal frequency \(\omega^{{}}\) and noise intensity \(\sigma^{{}}\) as shown in Fig. 3.

Fig. 3
figure 3

The function diagram of chaotic threshold \(f_{d}\) with respect to reference signal frequency \(\omega^{{}}\) and noise intensity \(\sigma^{{}}\)

Full size image

If \(f > f_{d}\),\(\varepsilon > 0\) and it is sufficiently small, system (2) may appear chaos. From the point of view of the calculation process, the calculation of the Melnikov function is simpler than that of the Duffing system. When solving the chaos threshold, the necessary and sufficient conditions are used, which are more accurate than the necessary conditions.

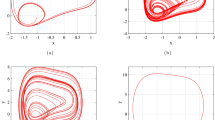
It can be seen from Eq. (12) that noise has an impact on the threshold which is verified by numerical simulation. Let \(\mu = 0.1,f = 0.6,\omega = 1.2\) make the phase diagram and Poincaré section diagram of system (2) with different noise intensity \(\sigma^{{}}\), as shown in Fig. 4.

Fig. 4
figure 4

Phase diagram and Poincaré section diagram of system (2) with different noise intensity

Full size image

It can be seen from Fig. 4a that system (2) have periodic five motion when \(\sigma = 0\), and the phenomenon of dissipation will appear with the increase of the noise intensity. Figure 4b, c show the multiply periodic motion when \(\sigma = 0.01\) and \(\sigma = 0.05\). Figure 4d becomes chaotic motion when \(\sigma = 0.5\). Figure 4e shows the Poincaré section diagram of system (2) when \(\sigma = 0.5\).

3 Parameter Identification of Weak Signal

3.1 Parameter Identification System

The signal to be detected without considering the phase is added into system (2) to obtain

$$\left\{ \begin{gathered} \dot{x} = y, \hfill \\ \dot{y} = - x +{\rm sign}(x) + \varepsilon ( - 2\mu y + f\cos (\omega t) + r\cos (\omega_{1} t) + \sigma n(t)),(x,y) \ne (0,0), \hfill \\ \end{gathered} \right.$$
(13)

where \(r\cos (\omega_{1} t)^{{}}\) is the signal to be detected.

Using the same method as in Ref. [5], making scale transformation on system (13), we get the following identification system

$$\left\{ \begin{gathered} \dot{x} = \omega y, \hfill \\ \dot{y} = \omega ( - x + {\rm sign}(x) + \varepsilon ( - 2\mu y + f\cos (\omega t) + r\cos (\omega_{1} t) + \sigma n(t))),(x,y) \ne (0,0). \hfill \\ \end{gathered} \right.$$
(14)

When \(\omega = \omega_{1}\), the chaotic threshold of systems (13) and (14) are same and yields

$$f^{\prime}_{d} = \frac{{(1 - \omega^{2} )\sqrt {(\mu \pi )^{2} - 2K\sigma^{2} A} }}{{\sin (\omega \pi )\sin (\omega t_{0} )}} - r,$$
(15)

where \(\omega \ne k\), \(t_{0} \ne k\pi /\omega\), \(t_{0} \ne (2k\pi + \pi /2)/\omega\), \(k = 0, \pm 1, \pm 2, \ldots , \pm n, \ldots\).

So, the amplitude of the weak signal to be detected is

$$r = f^{\prime}_{d} - f_{d} .$$
(16)

When \(\omega \ne \omega_{1}\), set \(\omega_{1} = \omega + \Delta \omega\), consider the chaotic threshold of system (13), we have

$$\begin{gathered} E[M_{ + }^{2} (t_{0} )] = - M^{2} + \overline{M}^{2} (t_{0} ) + E[\tilde{M}^{2} (t_{0} )] \hfill \\ = - (2\mu \pi )^{2} + 2\left\{ {\frac{f}{{1 - \omega^{2} }}\sin (\omega \pi )\sin (\omega t_{0} ) + \frac{r}{{1 - \omega_{1}^{2} }}\sin (\omega_{1} \pi )\sin [(\omega + \Delta \omega )t_{0} ]} \right\}^{2} + 8K\sigma^{2} A \hfill \\ = - (2\mu \pi )^{2} + 8K\sigma^{2} A + 2\Bigg\{ [\frac{f}{{1 - \omega^{2} }}\sin (\omega \pi ) + \frac{r}{{1 - \omega_{1}^{2} }}\sin (\omega_{1} \pi )\cos (\Delta \omega t_{0} )]\sin (\omega t_{0} ) \hfill \\ \quad + \frac{r}{{1 - \omega_{1}^{2} }}\sin (\omega_{1} \pi )\sin (\Delta \omega t_{0} )\cos (\omega t_{0} ))\Bigg\} \hfill \\ = - (2\mu \pi )^{2} + 8K\sigma^{2} A + 2F\sin (\omega t_{0} + \theta ), \hfill \\ \end{gathered}$$
(17)

where

\(F = \sqrt {\Bigg(\frac{f}{{1 - \omega^{2} }}\sin (\omega \pi ) + \frac{r}{{1 - \omega_{1}^{2} }}\sin (\omega_{1} \pi )\cos (\Delta \omega t_{0} )\Bigg)^{2} + \Bigg(\frac{r}{{1 - \omega_{1}^{2} }}\sin (\omega_{1} \pi )\sin (\Delta \omega t_{0} )\Bigg)^{2} }\), \(\theta = \tan \frac{{\frac{r}{{1 - \omega_{1}^{2} }}\sin (\omega_{1} \pi )\sin (\Delta \omega t_{0} )}}{{\frac{f}{{1 - \omega^{2} }}\sin (\omega \pi ) + \frac{r}{{1 - \omega_{1}^{2} }}\sin (\omega_{1} \pi )\cos (\Delta \omega t_{0} )}}\).

The chaotic threshold of system (13) is

$$f^{\prime}_{d} = \frac{{(1 - \omega^{2} )}}{\sin (\omega \pi )}\left( {\frac{1}{{\sin (\omega t_{0} + \theta )}}\sqrt {(\mu \pi )^{2} - 2K\sigma^{2} A} - \frac{r}{{1 - \omega_{1}^{2} }}\sin (\omega_{1} \pi )} \right),$$
(18)

satisfied \(\omega \ne k\), \(t_{0} \ne k\pi /\omega\), \(t_{0} \ne (2k\pi + \pi /2)/\omega\), \(k = 0, \pm 1, \pm 2 \cdots , \pm n, \cdots\).

The chaotic threshold of systems (14) is the same as that of (13), and the roof is similar to that of (13), which is omitted here.

Let \(\mu = 0.1,f = 0.6,r = 0.02,\omega_{1} = 0.7\), the bifurcation diagrams of systems (13) and (14) of the reference signal frequency \(\omega^{{}}\) are shown in Fig. 5.

Fig. 5
figure 5

The bifurcation diagram of different systems of reference signal frequency \(\omega^{{}}\)

Full size image

From Fig. 5, it can be seen that there is not a convex peak at \(\omega = 0.7\) of system (13), while there is an obvious convex peak at \(\omega = 0.7\) of the variable scale system (14). So, the variable scale system can be used to identify weak signals. This paper uses the variable scale system (14) to identify weak signal frequency and amplitude.

3.2 Frequency Identification of Weak Signal

Let \(\mu = 0.1,f = 0.6,r = 0.02,\omega_{1} = 1\), the bifurcation diagram of system (14) of reference signal frequency \(\omega^{{}}\) is shown in Fig. 6.

Fig. 6
figure 6

Bifurcation diagram of system (14) of reference signal frequency \(\omega^{{}}\)

Full size image

As can be seen from Fig. 6, there is a convex peak phenomenon at \(\omega = 1\), which shows that the frequency of the signal to be detected is \(\omega_{1} = 1\). The method of identifying frequencies based on a non-smooth variable-scale system by making a frequency bifurcation diagram of the signal to be detected is called a non-smooth variable-scale convex peak frequency identification method.

3.3 Amplitude Identification of Weak Signal

Let \(\mu = 0.05,r = 0.02,\omega = \omega_{1} = 1.06066\) bifurcation diagrams of the reference signal amplitude \(f\) of systems (2) and (14) are shown in Fig. 7.

Fig. 7
figure 7

Bifurcation diagram of different system of the reference signal amplitude \(f\)

Full size image

It can be seen from Fig. 7a that the chaotic threshold of system (2) is \(f_{d} = 0.1\) (shown by the blue line), which is obviously different from \(f^{\prime}_{d} = 0.0805\) of system (14) in Fig. 7b (shown by the red line). So, the amplitude of the weak signal to be detected is \(r^{\prime} = f_{d} - f^{\prime}_{d} = 0.0195\), which is same as hypothesis \(r = 0.02\). The absolute error is 0.0005 and the relative error is 2.5%.

The phase diagram of system (2) changing with the reference signal amplitude \(f\) are shown in Fig. 8a–c. The phase diagram of system (14) changing with the reference signal amplitude \(f\) are shown in Fig. 8d–f.

Fig. 8
figure 8

a–c Phase diagrams of system (2) about different amplitudes \(f\); d–f phase diagram of the system (14) about different amplitudes \(f\)

Full size image

Figure 8a–c show that system (2) changes from periodic motion to chaotic motion, and the chaotic threshold is \(f_{d} = 0.1\). Figure 8d–f show that system (14) changes from periodic motion to the chaotic motion, and the chaotic threshold is \(f^{\prime}_{d} = 0.08\). So, the amplitude of the signal to be detected is \(r^{\prime} = f_{d} - f^{\prime}_{d} = 0.02\), which verifies the correctness of the bifurcation diagram to identify the amplitude. After verification by numerical simulation, the optimal value range of system (14) is shown in Table 1.

Table 1 The optimal value range of the parameter of the identification system (14)
Full size table

From Table 1 we can see, the phenomenon of convex peak appears when \(r_{\min } = 0.02\) and \(\sigma_{\max } = 0.18\), so the signal-to-noise ratio of system (14) is

$${S \mathord{\left/ {\vphantom {S N}} \right. \kern-\nulldelimiterspace} N} = 10\lg \frac{{r_{\min }^{2} }}{{2\sigma_{\max }^{2} }} = - 50.8757\;{\text{dB}}{.}$$
(19)

4 Circuit Design and Simulation

The nonlinear analog circuit is constructed by Multisim software. Operational amplifier TL082 and analog multiplier AD633JN are shown in Fig. 9. Module V1 represents the reference signal, module V2 represents the signal to be detected and module V3 represents Gaussian white noise. Operational amplifier U2A and resistor \(R_{1} ,R_{2}\) constitute a zero-crossing comparator, which together with resistor \(R_{3} ,R_{4}\) and operational amplifier U2B are equivalent to a sign function.

Fig. 9
figure 9

Analog circuit diagram of system (14)

Full size image

A bifurcation diagram about the frequency and amplitude of the reference signal is made by using Fig. 9 to verify the feasibility of identifying the frequency and amplitude of the signal to be detected by using this bifurcation diagram. According to the theoretical results, suppose the damping coefficient \(\mu = 0.1\), the amplitude of the signal to be detected \(r = 0.05\), the noise intensity \(\sigma = 0.{0}1\), the reference signal amplitude \(f = 0.6\), the frequency to be detected \(\omega_{1} = 1.2\), the bifurcation diagram of the frequency \(\omega\) of the signal to be detected of system (14) is shown in Fig. 10a. Suppose the reference signal frequency \(\omega = 1.2\), the bifurcation diagram of the reference signal amplitude \(f\) of system (14) is shown in Fig. 10b. As can be seen from Fig. 10, Fig. 9 can be used to identify the frequency and amplitude of weak signals.

Fig. 10
figure 10

a Bifurcation diagram of system (14) of the frequency \(\omega\) of the signal to be detected; b bifurcation diagram of system (14) of the reference signal amplitude \(f\)

Full size image

5 Experimental Verification of Parameter Identification for Early Fault Signal of Wheelset Bearing in High-speed Train

The experimental data come from Shijiazhuang Tiedao University State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures. The bearing type is FAG F-80781109 Tarol 130/240-b-TVP. The outer diameter, inner diameter, roller diameter, roller number and pressure angle are 240 mm, 130 mm, 26.5 mm, 17, 10° respectively. The outer ring of the bearing has a machining failure with length 5 mm, width 1 mm, high 0.7 mm. The speed of bearing is 1200r/min. This experiment contains \(1.5 \times 10^{5}\) data. The weak fault signal is submerged in strong noise completely in the waveform diagram (Fig. 11).

Fig. 11
figure 11

Layout of measuring points of wheelset bearings

Full size image

The theoretical failure frequency calculated according to bearing parameters and rotational speed are shown in Table 2.

Table 2 Theoretical calculation of fault frequency
Full size table

5.1 Experimental Verification of Frequency Identification for Early Fault Signal

Input the fault experimental data of the bearing into system (14) to make the bifurcation diagram of the reference signal frequency \(\omega^{{}}\) of the signal to be detected, as shown in Fig. 12.

Fig. 12
figure 12

Bifurcation diagram of system (14) about the frequency \(\omega^{{}}\) of the signal to be detected

Full size image

5.2 Experimental Verification of Amplitude Identification for Early Fault Signal

Input the fault-free experimental data of the bearing into system (2) to make the bifurcation diagram of the reference signal amplitude \(f\), as shown in Fig. 13a. Input the fault experimental data of the bearing into system (14) to make the bifurcation diagram of the reference signal amplitude \(f\), as shown in Fig. 13b.

Fig. 13
figure 13

Bifurcation diagram of different system of the reference signal amplitude \(f\)

Full size image

It can be seen from Fig. 13a that the amplitude of the reference signal is \(f_{e} = 0.1778\) when there is no fault in the bearing; it can be obtained from Fig. 13b that the amplitude of the reference signal is \(f^{\prime}_{e} = 0.1651\) when there is a fault in the bearing. Then, the amplitude of the signal to be detected is \(r_{e} = f_{e} - f^{\prime}_{e} = 0.0127\).

6 Conclusion

In this paper, the limit system of SD oscillator without considering the phase is selected as the identification system. According to the random subharmonic-like Melnikov method, the analytical expression of the chaotic threshold is given. The calculation process of random subharmonic Melnikov function of non-smooth system is simpler and more concise than that of continuous system, which is more suitable for parameter identification of weak signal. More importantly, using the sufficient and necessary conditions for the existence of simple zeros of the random subharmonic-like Melnikov function of the non-smooth system, a more accurate chaotic threshold is obtained, which lays a theoretical foundation for the identification of frequency and amplitude. Furthermore, it is clarified that the limit system of the variable-scale SD oscillator can be used as a frequency identification system. The non-smooth variable scale convex peak frequency identification method is used to identify the frequency of the signal to be detected, and the signal-to-noise ratio is − 50.8757 dB. Through numerical simulation, the results obtained by identifying the amplitude of the signal to be measured using the amplitude bifurcation diagram of the reference signal are the same as those obtained by determining the amplitude through the phase diagram. The absolute error is 0.0195 and the relative error is 2.5%.The electronic circuit is designed to verify the feasibility of the bifurcation diagram to identify the amplitude and the convex peak method to identify the frequency. The optimal value range of the parameters of the identification system is determined. Taking an early bearing fault of a high-speed train wheel set as an example. In frequency identification, it is judged that the bearing outer ring may fail by observing the center value of the convex peak with the absolute error of 31.5 rad/s and the relative error of 3.44%, which fully verifies the effectiveness of the above method. In amplitude bifurcation, the amplitude of the weak signal can be accurately identified by the amplitude difference in the amplitude bifurcation diagram of the reference signal. The results show that the non-smooth system can identify the frequency and amplitude of the weak signal submerged in strong noise. The Melnikov function is simple to be calculated. The non-smooth variable scale-convex-peak frequency identification method has higher accuracy and is more widely used than continuous systems.