The Dynamic Bifurcation for the Granulation Convection in Cylindrical Coordinates

Abstract

This work formulates the simplified governing equations for granulation convection system in cylindrical coordinates by using the differential operator theory on Riemann manifold. We consider the case where the granulation convection system is under the influence of the control parameters R and E, Where R depends on the temperature difference and E is related to the magnetic field. Furthermore, we show that the simplified governing equations bifurcate from a trivial steady state solution, as the control parameters cross certain critical values. Notably, we are able to derive a RE-phase diagram in the case of two control parameters R and E, compared with the system without the influence of the control parameter E. In addition, our research shows that the difference of temperature and the magnetic field both accelerates the granulation convection.

1 Introduction

The atmosphere around the sun and earth are rotating geophysical fluids, which are important components of the climate system. The motion and states of the atmosphere system are derived using basic hydrodynamic and thermodynamic laws, together with laws for the diffusion of atmosphere, see among others [1, 2].

In this paper, we consider the atmospheric circulation of the sun. When we try to observe the atmosphere of sun with the best resolution possible, we see a structure, called granulation [3], as is shown in Fig. 1.

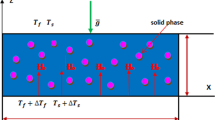
The granulation can be explained by circulation cells of materials, called convection zones. Convection is the form of energy transport in which matter actually moves from one place to another. For example, strong convection on the earth is responsible for the updrafts that produce thunderstorms; A pot of boiling water also has energy transport by convection. As to granulation convection, the fluid is heavier at the top and lighter at the bottom because of the thermal expansion. As the temperature difference between the lower and upper fluid exceeds a critical level, a convective motion sets in, as is shown in Fig. 2.

Fig. 1

Granulation in the sun. Remember the darker areas are not really dark. They are only a little cooler than the bright areas

There have been numerous studies concerning the stability and instability of the convective flows. A detailed discussion can be found in [4,5,6,7].

External magnetic fields change the characteristics of this convection significantly for electrically well conducting fluids. First, it is well known that the critical Rayleigh number increases with an increasing Chandrasekhar number Q for the onset of convection. Second, the existence of a magnetic field allows both the steady and oscillatory convection, see [8].

The equations governing the atmospheric circulation with magnetic field are the following magnetohydrodynamics (MHD) equations [9,10,11].

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial u}{\partial t}+(u\cdot \nabla )u =\nu \triangle u-\frac{1}{\rho _{0}}\nabla p-g\textbf{k}[1-\alpha (T-T_{0})] + \frac{1}{\rho _{0}}(\nabla \times H)\times H, \\ {}&\frac{\partial T}{\partial t}+(u \cdot \nabla )T=\kappa \triangle T, \\ {}&\frac{\partial H}{\partial t}=\nabla \times (u\times H)+\eta \triangle H+\nabla \Phi , \\ {}&\text {div} u=0, \\ {}&\text {div} H=0. \end{aligned} \right. \end{aligned}$$

(1)

Fig. 2

The structure of granulation

Note that the MHD convection problem also have been considered by several authors including Wang [12] and Sengul [13].There are several features of this work that distinguishes it from the other studies.

First, we adopt the following approximations: since the aspect ratio between the vertical scale and the horizontal scale is small, the spherical shell that the air occupies is treated as local cylindrical coordinates. This approximation is extensively adopted in geophysical fluid dynamics. Second, we study the case where there are two control parameters instead of one control parameter in [12]. Third, a crucial step in simplifying governing equations in cylindrical coordinates is the differential operator theory on Riemann manifold. Based on the definitions of curl and cross products on a $3-$D Riemann manifold $(M, g_{{ij}})$, we give the MHD equation in cylindrical coordinates.

In this paper, our main focus is on the stability and transition of the magnetic granulation convection in cylindrical coordinates. The technical methods for the analysis are the dynamic bifurcation theory and the phase transition dynamics theorem, developed by Ma and Wang in [14,15,16,17,18]. As is well known, for the magnetohydrodynamics (MHD) equations [19], due to non-selfadjoint operator, the transition can be caused by a finite set of real or complex eigenvalues crossing the imaginary axis. So we consider the real eigenvalues and complex eigenvalues.

Next, we study the case where there are two control parameters. We get the RE-phase diagram of granulation , where R is the Rayleigh number, which is related to the difference of temperature $T_{1}-T_{0}$, and E is a dimensionless parameter, which is related to the magnetic field H. The transition takes place as the parameter (R, E) crosses the critical curve L from region I to region II, see Fig. 3.

Fig. 3

The RE-phase diagram($R_{c}=\sigma _{c}$)

The rest of the article is organized as follows: in Section 2 the differential operator theory on Riemann manifold is introduced. And in Section 3, magnetohydrodynamics (MHD) equations in cylindrical coordinate are given. In Section 4 and Section 5 we state the perturbed dimensionless equations and functional setting. We give the main theorems in Section 6. In Section 7, physical remarks and conclusions are discussed

2 Preliminaries

Now, we will introduce the differential operator theory on Riemann manifold, which was given by the authors Wang [20] and Ma [21] recently.

Let $(M, g_{ij})$ be a $3-D$ Riemann manifold with metric

$$\begin{aligned} (ds)^{2}=g_{ij}dx^{i}dx^{j},\quad (i,j=1,2,3), \end{aligned}$$

(2)

where $(x_{i},x_{j})$ are local coordinate system on the Riemann manifold M, $g^{ij}$ are the inverse of $g_{ij}$. For simplicity, we use the Einstein summation convention in this paper. Then, the differential operators are crucial in studying the granulation of solar as shown in this section.

Let $u=(u_{1},u_{2},u_{3})$ and $H=(H_{1},H_{2,},H_{3})$ be smooth vector fields. From Ma [21], we immediately get the formulate:

• 1. The divergence of vector fields u is

  $$\begin{aligned} \text {div} u = \frac{\partial u^{k}}{\partial x^{k}} + \Gamma _{kj}^{k}u^{j} = \frac{1}{\sqrt{g}} \frac{\partial (\sqrt{g} u^{k})}{\partial x^{k}}, \end{aligned}$$

  (3)

  here $g=\text {det}(g_{ij})$, $\Gamma ^{i}_{kj}$ is the Levi-Civita connection and can be expressed as

  $$\begin{aligned} \Gamma _{kj}^{i} = \frac{1}{2}g^{il}\bigg (\frac{\partial g_{kl}}{\partial x^{j}} + \frac{\partial g_{jl}}{\partial x^{k}} - \frac{\partial g_{kj}}{\partial x^{l}}\bigg ). \end{aligned}$$

  (4)

• 2. The gradient operator $\nabla$ is

  $$\begin{aligned} \nabla p = \bigg (g^{11}\frac{\partial p}{\partial x^{1}},\cdots ,g^{nn}\frac{\partial p}{\partial x^{n}}\bigg ). \end{aligned}$$

  (5)

• 3. ${\Delta }$ is the Laplace-Beltrami operator, which is defined as $\triangle u=(\triangle u_{i}),i=1,2,3$, and

  $$\begin{aligned} \Delta u^{i}&= \text {div}{\nabla }u^{i} + g^{ij}R_{js}u^{s}, \end{aligned}$$

  (6)

  where $\text {div}{\nabla }u^{i}$ is expressed as the divergence of gradient and is a linear operator taking functions into functions:

  $$\begin{aligned} \text {div}{\nabla }u^{i}&= g^{kl}\bigg [\frac{\partial }{\partial x^{l}}\bigg (\frac{\partial u^{i}}{\partial x^{k}} + \Gamma _{kj}^{i} u^{j}\bigg ) + \Gamma _{lj}^{i}\bigg ( \frac{\partial u^{j}}{\partial x^{k}} + \Gamma _{ks}^{j} u^{s}\bigg ) \\ {}&- \Gamma _{kl}^{j}\bigg ( \frac{\partial u^{i}}{\partial x^{j}} + \Gamma _{js}^{i} u^{s}\bigg )\bigg ]. \nonumber \end{aligned}$$

  (7)

  Moreover, $R_{ij}$ in (6) is the Ricci Curvature Tensor, and is proposed as

  $$\begin{aligned} R_{ij}&=\frac{1}{2} g^{kl}\bigg (\frac{\partial ^{2}g_{kl}}{\partial x^{i}\partial x ^{j}} + \frac{\partial ^{2}g_{ij}}{\partial x^{k}\partial x ^{l}} - \frac{\partial ^{2}g_{kj}}{\partial x^{i}\partial x ^{l}} - \frac{\partial ^{2}g_{li}}{\partial x^{j}\partial x^{k}} \bigg )\nonumber \\ {}&+ g^{kl}g_{rs}\bigg (\Gamma _{kl}^{r}\Gamma _{ij}^{s}- \Gamma _{il}^{r}\Gamma _{kj}^{s}\bigg ). \end{aligned}$$

  (8)

• 4. The remove acceleration $(u\cdot {\nabla })u$ is

  $$\begin{aligned} \nonumber (u \cdot \nabla )u&= (u^{i}D_{i}u^{1},u^{i}D_{i}u^{2},u^{i}D_{i}u^{3}), \\ {}&\nonumber =( u^{1}D_{1}u^{1}+u^{2}D_{2}u^{1}+u^{3}D_{3}u^{1}, \\ {}&\nonumber \quad u^{1}D_{1}u^{2}+u^{2}D_{2}u^{2}+u^{3}D_{3}u^{2}, \\ {}&\quad u^{1}D_{1}u^{3}+u^{2}D_{2}u^{3}+u^{3}D_{3}u^{3}), \end{aligned}$$

  (9)

  where $D_{i}u^{k}$ is the covariant derivative:

  $$\begin{aligned} D_{i}u^{k}&= \frac{\partial u^{k}}{\partial x^{i}} + \Gamma _{ij}^{k}u^{j}. \end{aligned}$$

  (10)

• 5. The curl operator for the vector fields is given by

  $$\begin{aligned} \nonumber \text {rot} u =\nabla \times u&= \big ( \frac{\sqrt{g_{11}}}{\sqrt{g}}(\frac{\partial (u^{3}\sqrt{g_{33}})}{\partial x^{2}}- \frac{\partial (u^{2}\sqrt{g_{22}})}{\partial x^{3}}), \\ {}&\quad \frac{\sqrt{g_{22}}}{\sqrt{g}}(\frac{\partial (u^{1}\sqrt{g_{11}})}{\partial x^{3}}- \frac{\partial (u^{3}\sqrt{g_{33}})}{\partial x^{1}}), \\ {}&\nonumber \quad \frac{\sqrt{g_{33}}}{\sqrt{g}}(\frac{\partial (u^{2}\sqrt{g_{22}})}{\partial x^{1}}- \frac{\partial (u^{1}\sqrt{g_{11}})}{\partial x^{2}})\big ). \end{aligned}$$

  (11)

Remark 1

From Eq. 11, we immediately get the following formula for $(\nabla \times H){\times } H$ and ${\nabla }\times (u\times H)$, which are very useful for our equation.

• 1.
  $$\begin{aligned} \nonumber (\nabla \times H)\times H&=\big (\frac{\sqrt{g_{22}}}{\sqrt{g}}(\frac{\partial (H^{1}\sqrt{g_{11}})}{\partial x^{3}}- \frac{\partial (H^{3}\sqrt{g_{33}})}{\partial x^{1}}) H^{1} \\ {}&\nonumber - \frac{\sqrt{g_{33}}}{\sqrt{g}}(\frac{\partial (H^{2}\sqrt{g_{22}})}{\partial x^{1}}- \frac{\partial (H^{1}\sqrt{g_{11}})}{\partial x^{2}})H^{2}, \\ {}&\nonumber \frac{\sqrt{g_{33}}}{\sqrt{g}}(\frac{\partial (H^{2}\sqrt{g_{22}})}{\partial x^{1}}- \frac{\partial (H^{1}\sqrt{g_{11}})}{\partial x^{2}})H^{1} \\ {}&-\frac{\sqrt{g_{11}}}{\sqrt{g}}(\frac{\partial (H^{3}\sqrt{g_{33}})}{\partial x^{2}}- \frac{\partial (H^{2}\sqrt{g_{22}})}{\partial x^{3}})H^{3}, \\ {}&\nonumber \frac{\sqrt{g_{11}}}{\sqrt{g}}(\frac{\partial (H^{3}\sqrt{g_{33}})}{\partial x^{2}}- \frac{\partial (H^{2}\sqrt{g_{22}})}{\partial x^{3}})H^{2} \\ {}&\nonumber -\frac{\sqrt{g_{22}}}{\sqrt{g}}(\frac{\partial (H^{1}\sqrt{g_{11}})}{\partial x^{3}}- \frac{\partial (H^{3}\sqrt{g_{33}})}{\partial x^{1}})H^{1} \big ). \end{aligned}$$

  (12)
• 2.
  $$\begin{aligned} \nonumber \nabla \times (u\times H)=&\big ( \frac{\sqrt{g_{11}}}{\sqrt{g}}(\frac{\partial ((u^{2}H^{3}-u^{3}H^{2})\sqrt{g_{33}})}{\partial x^{2}}- \frac{\partial ((u^{3}H^{1}-u^{1}H^{3})\sqrt{g_{22}})}{\partial x^{3}}), \\ {}&\nonumber \quad \frac{\sqrt{g_{22}}}{\sqrt{g}}(\frac{\partial ((u^{2}H^{3}-u^{3}H^{2})\sqrt{g_{11}})}{\partial x^{3}}- \frac{\partial ((u^{1}H^{2}-u^{2}H^{1})\sqrt{g_{33}})}{\partial x^{1}}), \\ {}&\quad \frac{\sqrt{g_{33}}}{\sqrt{g}}(\frac{\partial ((u^{3}H^{1}-u^{1}H^{3})\sqrt{g_{22}})}{\partial x^{1}}- \frac{\partial ((u^{2}H^{3}-u^{3}H^{2})\sqrt{g_{11}})}{\partial x^{2}})\big ). \end{aligned}$$

  (13)

3 The Expression of MHD Equation in Cylindrical Coordinates

In this section, we will give the specific expression in cylindrical coordinates.

Let $X=(x,y,z)\in R^{3}$, $r^{2}=x^{2}+y^{2}+z^{2}$. Then, in the cylindrical coordinates, the metric is

$$ds^{2}=dr^{2}+r^{2}d\theta ^{2}+dz^{2}.$$

Obviously, we have

$$\begin{aligned} \left\{ \begin{aligned}&g_{11}=1, \quad g_{22}=r^{2}, \quad g_{33}=1, \\ \quad&g_{ij}=0, \; (i\ne j),\\&g^{kk}=\frac{1}{g_{kk}},(k=1,2,3),\\&\sqrt{g}=r. \end{aligned} \right. \end{aligned}$$

(14)

From Eqs. 4 and 8, it is easy to get the following Levi-Civita connection $\Gamma _{kj}^{i}$ and the Ricci curvature tensor $R_{js}$.

$$\begin{aligned} \left\{ \begin{aligned}&\Gamma _{21}^{2}=\Gamma _{12}^{2}=\frac{1}{r},\\&\Gamma _{22}^{1}=-r,\\&\Gamma _{kj}^{i}=0,\quad \text {others},\\&R_{js}=0. \end{aligned} \right. \end{aligned}$$

(15)

We obtain from Eqs. 3–11 and 14, 15 the following differential operators in the cylindrical coordinates for the Granulation Convection:

$$\begin{aligned} \nabla p=(\frac{\partial p}{\partial r}, \frac{1}{r^{2}}\frac{\partial p}{\partial \theta },\frac{\partial p}{\partial z}), \end{aligned}$$

(16)

$$\begin{aligned} \text {div}u=\frac{1}{r}\frac{\partial }{\partial r}(ru_{r})+\frac{\partial u_{\theta }}{\partial \theta }+\frac{\partial u_{z}}{\partial z}, \end{aligned}$$

(17)

$$\begin{aligned} \Delta u_{r}=\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial u_{r}}{\partial r})+\frac{1}{r^{2}} \frac{\partial ^{2}u_{r}}{\partial \theta ^{2}}+\frac{\partial ^{2}u_{r}}{\partial z^{2}}- \frac{2}{r}\frac{\partial u_{\theta }}{\partial \theta }-\frac{u_{r}}{r^{2}}, \end{aligned}$$

(18)

$$\begin{aligned} \Delta u_{\theta }=\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial u_{\theta }}{\partial r})+\frac{1}{r^{2}} \frac{\partial ^{2}u_{\theta }}{\partial \theta ^{2}}+\frac{\partial ^{2}u_{\theta }}{\partial z^{2}}- \frac{1}{r^{2}}u_{\theta }+\frac{2}{r^{3}}\frac{\partial u_{r}}{\partial \theta }, \end{aligned}$$

(19)

$$\begin{aligned} \Delta u_{z}=\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial u_{z}}{\partial r})+\frac{1}{r^{2}} \frac{\partial ^{2}u_{z}}{\partial \theta ^{2}}+\frac{\partial ^{2}u_{z}}{\partial z^{2}}, \end{aligned}$$

(20)

$$\begin{aligned} \Delta T=\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial T}{\partial r})+\frac{1}{r^{2}} \frac{\partial ^{2}T}{\partial \theta ^{2}}+\frac{\partial ^{2}T}{\partial z^{2}}, \end{aligned}$$

(21)

$$\begin{aligned} (u\cdot {\nabla } ) u={} & {} \big (u_{r}\frac{\partial u_{r}}{\partial r}+u_{\theta }\frac{\partial u_{r}}{\partial \theta }+u_{z}\frac{\partial u_{r}}{\partial z}-ru_{\theta }^{2}, \nonumber \\{} & {} u_{r}\frac{\partial u_{\theta }}{\partial r}+u_{\theta }\frac{\partial u_{\theta }}{\partial \theta }+u_{z}\frac{\partial u_{\theta }}{\partial z}+ \frac{2}{r}u_{r}u_{\theta }, \nonumber \\{} & {} u_{r}\frac{\partial u_{z}}{\partial r}+u_{\theta }\frac{\partial u_{z}}{\partial \theta }+u_{z}\frac{\partial u_{z}}{\partial z}\big ), \end{aligned}$$

(22)

$$\begin{aligned} (\nabla \times H)\times H=&\big (H_{z}(\frac{\partial H_{r}}{\partial {z}}-\frac{\partial H_{z}}{\partial r})- \frac{H_{\theta }}{r}(H_{\theta }+r\frac{\partial H_{\theta }}{\partial r}-\frac{\partial H_{r}}{\partial \theta }) ,\nonumber \\&\frac{H_{r}}{r}(\frac{\partial (r H_{\theta })}{\partial r}-\frac{\partial H_{r}}{\partial \theta })-\frac{H_{z}}{r}(\frac{\partial H_{z}}{\partial \theta }-r\frac{\partial H_{\theta }}{\partial z}), \nonumber \\&\frac{H_{\theta }}{r} (\frac{\partial H_{z}}{\partial \theta }-r\frac{\partial H_{\theta }}{\partial z})- H_{r}(\frac{\partial H_{r}}{\partial {z}}-\frac{\partial H_{z}}{\partial r}) \big ), \end{aligned}$$

(23)

$$\begin{aligned} \nonumber \nabla \times (u\times H)=&\big (\frac{1}{r}(\frac{\partial (u_{r}H_{\theta }-u_{\theta }H_{r})}{\partial \theta })-\frac{\partial (r(u_{z}H_{r}-u_{r}H_{z}))}{\partial z} , \\ {}&\nonumber \frac{\partial (u_{\theta }H_{z}-u_{z}H_{\theta })}{\partial z}-\frac{\partial ( u_{r}H_{\theta }-u_{\theta }H_{r})}{\partial r}, \\ {}&\frac{1}{r}(\frac{\partial (r(u_{z}H_{r}-u_{r}H_{z}))}{\partial r}-\frac{\partial (u_{\theta }H_{z}-u_{z}H_{\theta })}{\partial \theta } ) \big ), \end{aligned}$$

(24)

In an idealized case, the meridional component of velocity $u_{z}$ and the magnetic field $H_{z}$ vanishes, which implies that the granulation convection is the invariant circulation in the vertical direction. In this case, the study of transition of Eq. 1 is of special importance to understand the transverse circulation. so we restricted the equation on $z=0$ and the meridional component of velocity $u_{z}$ and the magnetic field $H_{z}$ are set to zero. To make the equation non-dimensional, we need a simple transformation $u_{\theta }=\frac{1}{r}u_{\theta ^{'}}, H_{\theta }=\frac{1}{r}H_{\theta ^{'}}$, Omitting the primes, by Eqs. 16–24, the equation (1) reads

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial u_{r}}{\partial t}+u_{r}\frac{\partial u_{r}}{\partial r}+\frac{u_{\theta }}{r}\frac{\partial u_{r}}{\partial \theta } -\frac{u^{2}_{\theta }}{r}=\nu (\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial u_{r}}{\partial r})+\frac{1}{r^{2}} \frac{\partial ^{2}u_{r}}{\partial \theta ^{2}}- \frac{2}{r^{2}}\frac{\partial u_{\theta }}{\partial \theta }-\frac{u_{r}}{r^{2}}) \\ {}&\quad \quad \quad \quad -\frac{1}{\rho _{0}}\frac{\partial p}{\partial r}-\frac{1}{\rho _{0}}\frac{H_{\theta }}{r^{2}}(\frac{H_{\theta }}{r}+\frac{\partial H_{\theta }}{\partial r}-\frac{\partial H_{r}}{\partial \theta })-g[1-\alpha (T-T_{0})], \\ {}&\frac{\partial u_{\theta }}{\partial t}+u_{r}\frac{\partial u_{\theta }}{\partial r}+\frac{u_{\theta }}{r}\frac{\partial u_{\theta }}{\partial \theta } +\frac{2}{r}u_{r}u_{\theta }= \nu (\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial u_{\theta }}{\partial r})+\frac{1}{r^{2}} \frac{\partial ^{2}u_{\theta }}{\partial \theta ^{2}}- \\ {}&\quad \quad \quad \quad \quad \frac{1}{r^{2}}u_{\theta }+\frac{2}{r^{2}}\frac{\partial u_{r}}{\partial \theta }) -\frac{1}{\rho _{0}r}\frac{\partial p}{\partial \theta }+\frac{H_{r}}{\rho _{0}}(\frac{\partial H_{\theta }}{\partial r}-\frac{\partial H_{r}}{\partial \theta }), \\ {}&\frac{\partial T}{\partial t}+u_{r}\frac{\partial T}{\partial r}+\frac{1}{r}u_{\theta }\frac{\partial T}{\partial \theta }= \kappa (\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial T}{\partial r})+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}}), \\ {}&\frac{\partial H_{r}}{\partial t}=\eta (\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial H_{r}}{\partial r})+\frac{1}{r^{2}} \frac{\partial ^{2}H_{r}}{\partial \theta ^{2}}- \frac{2}{r^{2}}\frac{\partial H_{\theta }}{\partial \theta }-\frac{H_{r}}{r^{2}})+ \frac{1}{r^{2}}\frac{\partial (u_{r}H_{\theta }-u_{\theta }H_{r})}{\partial \theta }+\frac{\partial \Phi }{\partial r}, \\ {}&\frac{\partial H_{\theta }}{\partial t}=\eta (\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial H_{\theta }}{\partial r})+\frac{1}{r^{2}} \frac{\partial ^{2}H_{\theta }}{\partial \theta ^{2}}+ \frac{2}{r^{2}}\frac{\partial H_{r}}{\partial \theta }-\frac{H_{\theta }}{r^{2}})-\frac{\partial (u_{r}H_{\theta }-u_{\theta }H_{r})}{\partial \theta } +\frac{1}{r}\frac{\partial \Phi }{\partial \theta }, \\ {}&\text {div} u=\frac{1}{r}\frac{\partial }{\partial r}(ru_{r})+\frac{\partial u_{\theta }}{\partial \theta }=0, \\ {}&\text {div} H=\frac{1}{r}\frac{\partial }{\partial r}(rH_{r})+\frac{\partial H_{\theta }}{\partial \theta }=0, \end{aligned} \right. \end{aligned}$$

(25)

The problem is supplemented with the natural periodic boundary condition in the $\theta$-direction:

$$\begin{aligned} (u,T,H)(r,\theta )=(u,T,H)(r,\theta +2k\pi ). \end{aligned}$$

(26)

Different combinations of top and bottom boundary conditions are normally used in different physical setting such as rigid-rigid, rigid-free, free-rigid, and free-free. For instance, we have

• 1. Dirichlet boundary condition (rigid-rigid):

  $$\begin{aligned} \left\{ \begin{aligned}&u_{r}=0, u_{\varphi }=0, H_{r}=H_{0}, H_{\varphi }=0,T=T_{0}, r=r_{0},\\&u_{r}=0, u_{\varphi }=0,H_{r}=0,H_{1},T=T_{1}, r=r_{0}+d.\\ \end{aligned} \right. \end{aligned}$$

  (27)

• 2. Free-free boundary condition:

  $$\begin{aligned} \left\{ \begin{aligned}&u_{r}=0, H_{r}=H_{0},T=T_{0},\frac{\partial {u_\varphi }}{\partial r}=\frac{\partial H_{\varphi }}{\partial r}=0, r=r_{0},\\&u_{r}=0, H_{r}=H_{1},T=T_{1},\frac{\partial {u_\varphi }}{\partial r}=\frac{\partial H_{\varphi }}{\partial r}=0, r=r_{0}+d.\\ \end{aligned} \right. \end{aligned}$$

  (28)

• 3. Free-rigid boundary condition:

  $$\begin{aligned} \left\{ \begin{aligned}&u_{r}=0, u_{\varphi }=0, H_{r}=H_{0}, H_{\varphi }=0,T=T_{0}, r=r_{0},\\&u_{r}=0, H_{r}=H_{1},T=T_{1},\frac{\partial {u_\varphi }}{\partial r}=\frac{\partial H_{\varphi }}{\partial r}=0, r=r_{0}+d.\\ \end{aligned} \right. \end{aligned}$$

  (29)

4 Perturbed Dimensionless Equations

We determine the basic flow by following assumptions:

• 1. $U=(u_{r},u_{\theta },T,H_{r} ,H_{\theta })=(0,0,\tilde{T}(r),\tilde{H}_{r},0)$, $p=\tilde{p}(r), \Phi =0$; that is, only the pressure, the temperature and the magnetic field in r-direction are not zero, and they only depend on r.

• 2. There is no doubt that $\tilde{T}(r)$, $\tilde{H}(r)$, $\tilde{p}(r)$ satisfy:

  $$\begin{aligned} \left\{ \begin{aligned}&-\frac{1}{\rho _{0}}\frac{\partial \tilde{p}}{\partial r}-g[1-\alpha (\tilde{T}-T_{0})]=0, \\ {}&\frac{\partial ^{2}\tilde{T}}{\partial r^{2}}+\frac{1}{r}\frac{\partial \tilde{T}}{\partial r}=0, \\ {}&\frac{\partial ^{2}\tilde{H}}{\partial r^{2}}+\frac{1}{r}\frac{\partial \tilde{H}}{\partial r}-\frac{1}{r^{2}} \tilde{H}=0, \\ {}&\text {div} \widetilde{H}=0. \end{aligned} \right. \end{aligned}$$

• 3. Based on the boundary condition (27), The value of basic flow at boundary is as follows

  $$\begin{aligned} \begin{aligned}&\tilde{H_{r}}=H_{0}, \tilde{T }=T_{0}, r=r_{0}, \\ {}&\tilde{H_{r}}=H_{1}, \tilde{T }=T_{1},r=r_{0}+d. \end{aligned} \end{aligned}$$

We derive them from above assumptions that the basic flow is defined by

$$\quad \tilde{T}=C_{1}lnr+C_{2},$$

$$\tilde{H}=\frac{K_{2}}{r},$$

$$\tilde{p}=\int ^{r_{0+d}}_{r_{0}}-\rho _{0}g[1-\alpha (\tilde{T}-T_{0})]dr,$$

where

$$\begin{aligned} C_{1}=\frac{T_{0}-T_{1}}{lnr_{1}-lnr_{0}},\quad \quad C_{2}=\frac{T_{0}lnr_{1}-T_{1}}{lnr_{1}-lnr_{0}}, \end{aligned}$$

(30)

$$\begin{aligned} K_{2}=r_{1}H_{1}. \end{aligned}$$

(31)

In the following, in order to get the perturbation equations related to the variables r and $\theta$, we make the translation:

$$p=p'+\tilde{p},\quad T=T'+\tilde{T},\quad H_{r}=H_{r}'+\tilde{H_{r}}.$$

Omitting the primes, the equations (25) can be written as:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial u_{r}}{\partial t}+u_{r}\frac{\partial u_{\theta }}{\partial r}+\frac{u_{\theta }}{r}\frac{\partial u_{r}}{\partial \theta } -\frac{u^{2}_{\theta }}{r}=\nu (\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial u_{r}}{\partial r})+\frac{1}{r^{2}} \frac{\partial ^{2}u_{r}}{\partial \theta ^{2}}- \frac{2}{r^{2}}\frac{\partial u_{\theta }}{\partial \theta }-\frac{u_{r}}{r^{2}}) \\ {}&\quad \quad \quad \quad -\frac{1}{\rho _{0}}\frac{\partial p}{\partial r}-\frac{1}{\rho _{0}}\frac{H_{\theta }}{r^{2}}(\frac{H_{\theta }}{r}+\frac{\partial H_{\theta }}{\partial r}-\frac{\partial H_{r}}{\partial \theta })+g\alpha T, \\ {}&\frac{\partial u_{\theta }}{\partial t}+u_{r}\frac{\partial u_{\theta }}{\partial r}+\frac{u_{\theta }}{r}\frac{\partial u_{\theta }}{\partial \theta } +\frac{2}{r}u_{r}u_{\theta }= \nu (\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial u_{\theta }}{\partial r})+\frac{1}{r^{2}} \frac{\partial ^{2}u_{\theta }}{\partial \theta ^{2}}- \\ {}&\quad \quad \quad \quad \quad \frac{1}{r^{2}}u_{\theta }+\frac{2}{r^{2}}\frac{\partial u_{r}}{\partial \theta }) -\frac{1}{\rho _{0}r}\frac{\partial p}{\partial \theta }+\frac{H_{r}}{\rho _{0}}(\frac{\partial H_{\theta }}{\partial r}-\frac{\partial H_{r}}{\partial \theta })+\frac{1}{\rho _{0}}\frac{K_{2}}{r}(\frac{\partial u_{\theta }}{\partial r}-\frac{\partial u_{r}}{\partial \theta }), \\ {}&\frac{\partial T}{\partial t}+u_{r}\frac{\partial T}{\partial r}+\frac{1}{r}u_{\theta }\frac{\partial T}{\partial \theta }= \kappa (\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial T}{\partial r})+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}}), \\ {}&\frac{\partial H_{r}}{\partial t}=\eta (\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial H_{r}}{\partial r})+\frac{1}{r^{2}} \frac{\partial ^{2}H_{r}}{\partial \theta ^{2}}- \frac{2}{r^{2}}\frac{\partial H_{\theta }}{\partial \theta }-\frac{H_{r}}{r^{2}})+ \frac{1}{r^{2}}\frac{\partial (u_{r}H_{\theta }-u_{\theta }H_{r})}{\partial \theta }+\frac{\partial \Phi }{\partial r}, \\ {}&\frac{\partial H_{\theta }}{\partial t}=\eta (\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial H_{\theta }}{\partial r})+\frac{1}{r^{2}} \frac{\partial ^{2}H_{\theta }}{\partial \theta ^{2}}+ \frac{2}{r^{2}}\frac{\partial H_{r}}{\partial \theta }-\frac{H_{\theta }}{r^{2}})-\frac{\partial (u_{r}H_{\theta }-u_{\theta }H_{r})}{\partial \theta } +\frac{1}{r}\frac{\partial \Phi }{\partial \theta }, \\ {}&\text {div} u=\frac{1}{r}\frac{\partial }{\partial r}(ru_{r})+\frac{\partial u_{\theta }}{\partial \theta }=0, \\ {}&\text {div} H=\frac{1}{r}\frac{\partial }{\partial r}(rH_{r})+\frac{\partial H_{\theta }}{\partial \theta }=0. \end{aligned} \right. \end{aligned}$$

(32)

In general, it is tough to get exact expressions of the first eigenvalue and the corresponding first eigenvector for a linear partial differential operator with non-constant coefficients. Some additional assumptions are necessary to get the simplified equations with constant coefficients. So we introduce the following approximations and assumptions:

First, the radius of sun is about $6.95\times 10^{5}$km and the photosphere is about 500km. Since the ration between the thickness of photosphere and the radius of sun is small, we adopt the approximations that $\frac{1}{r}=\frac{1}{r_{0}}.$

Second, for simplicity, we assume $\frac{\nu }{\kappa }=1$.

Third, since $\varphi$ is the angle, we denote $(\theta ^{'}, r^{'})=(r_{0}\theta , r)$.

Then,we start with the non-dimensional form of equation. Let

$$u=\frac{\kappa }{d}u',\quad r=dr',\quad T=\frac{T_{0}-T_{1}}{\sqrt{R}}T',\quad p=\frac{\rho _{0}\kappa ^{2}}{d^{2}}p',$$

$$H=H_{0}H',\quad \Phi =H_{0}\frac{\kappa }{d}\Phi ',\quad t=\frac{d^{2}}{\kappa }t',$$

where R is a non-dimensional parameter, called the Rayleigh number and $R=\frac{g\alpha (T_{0}-T_{1})}{\kappa \nu }d^{3}.$ Under the above simplification, omitting the primes, we get the following equations:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial u_{r}}{\partial t}+u_{r}\frac{\partial u_{\theta }}{\partial r}+ u_{\theta }\frac{\partial u_{r}}{\partial \theta } -\frac{u^{2}_{\theta }}{r_{0}^{2}}=\frac{\partial ^{2}u_{r}}{\partial r^{2}}+\frac{\partial ^{2}u_{\theta }}{\partial \theta ^{2}}- \frac{2}{r_{0}}\frac{\partial u_{\theta }}{\partial \theta } -\frac{u_{r}}{r^{2}} \\ {}&\quad \quad \quad \quad -\frac{\partial p}{\partial r}-\frac{1}{\rho _{0}\kappa ^{2}}H_{0}^{2}\frac{1}{r_{0}^{2}}H_{\theta }(\frac{H_{\theta }}{r_{0}} +\frac{\partial H_{\theta }}{\partial r})+\frac{1}{\rho _{0}\kappa ^{2}}H_{0}^{2}H_{\theta } \frac{\partial H_{r}}{\partial \theta } +\sqrt{R}T, \\ {}&\frac{\partial u_{\theta }}{\partial t}+u_{r}\frac{\partial u_{\theta }}{\partial r}+u_{\theta }\frac{\partial u_{\theta }}{\partial \theta } +\frac{2}{r_{0}}u_{r}u_{\theta }=\frac{\partial ^{2}u_{\theta }}{\partial r^{2}}+\frac{\partial ^{2}u_{\theta }}{\partial \theta ^{2}} -\frac{u_{\theta }}{r^{2}_{0}}+\frac{2}{r_{0}}\frac{\partial u_{r}}{\partial \theta }-\frac{\partial p}{\partial \theta } \\ {}&\quad \quad \quad \quad \quad +\frac{H_{0}^{2}d}{\rho _{0}\kappa ^{2}}H_{r}(\frac{\partial H_{\theta }}{\partial r}-\frac{\partial H_{r}}{\partial \theta }) +\frac{H_{0}^{2}d}{\rho _{0}\kappa ^{2}}\frac{\kappa ^{2}}{dr_{0}}(\frac{\partial H_{\theta }}{\partial r}-\frac{\partial H_{r}}{\partial \theta }), \\ {}&\frac{\partial T}{\partial t}+u_{r}\frac{\partial T}{\partial r}+u_{\theta }\frac{\partial T}{\partial \theta }= \frac{\partial ^{2}T}{\partial r^{2}}+\frac{\partial ^{2}T}{\partial \theta ^{2}}+d\sqrt{R}u_{r}, \\ {}&\frac{\partial H_{r}}{\partial t}=\frac{\partial ^{2}H_{r}}{\partial r^{2}}+ \frac{\partial ^{2}H_{r}}{\partial \theta ^{2}}- \frac{2}{r_{0}^{2}}\frac{\partial H_{\theta }}{\partial \theta }-\frac{H_{r}}{r_{0}^{2}})+ \frac{1}{r_{0}}\frac{\partial (u_{r}H_{\theta }-u_{\theta }H_{r})}{\partial \theta } \\ {}&\quad \quad \quad \quad \quad \quad \quad \quad -\frac{K_{2}}{d^{2}r_{0}^{2}}\frac{1}{H_{0}}\frac{\partial u_{\theta }}{\partial \theta } +\frac{\partial \Phi }{\partial r}, \\ {}&\frac{\partial H_{\theta }}{\partial t}=\frac{\partial ^{2}H_{\theta }}{\partial r^{2}}+ \frac{\partial ^{2}H_{\theta }}{\partial \theta ^{2}} +\frac{1}{r_{0}^{2}}(\frac{\partial H_{r}}{\partial \theta }-\frac{H_{\theta }}{r_{0}^{2}})-\frac{\partial (u_{r}H_{\theta }-u_{\theta }H_{r})}{\partial r} +\frac{K_{2}}{dr_{0}}\frac{\partial u_{r}}{\partial \theta }+ \frac{\partial \Phi }{\partial \theta }, \\ {}&\text {div} u=\frac{\partial u_{r}}{\partial r}+\frac{\partial u_{\theta }}{\partial \theta }=0, \\ {}&\text {div} H=\frac{\partial H_{r}}{\partial r}+\frac{\partial H_{\theta }}{\partial \theta }=0. \end{aligned} \right. \end{aligned}$$

(33)

The non-dimensional domain is $\Omega =[0,L]\times [r_{0},r_{0}+1]\subset R^{2}$. For simplicity, we proceed in this article with the set of boundary conditions given by Eqs. 26 and 28, and similar results hold true as well for other combinations of boundary conditions.

And, the boundary conditions become

$$\begin{aligned} \left\{ \begin{aligned}&(u,T,H)(\varphi ,r)=(u,T,H)(\varphi +L, r), \\ {}&u_{r}=0, H_{r}=0, T=0, \frac{\partial u_{\varphi }}{\partial r}=\frac{\partial H_{\varphi }}{\partial r}=0, r=r_{0}, \\ {}&u_{r}=0, H_{r}=0, T=0, \frac{\partial u_{\varphi }}{\partial r}=\frac{\partial H_{\varphi }}{\partial r}=0,r=r_{0}+1. \end{aligned} \right. \end{aligned}$$

(34)

Where $L=2\pi r_{0}$.

5 Functional Setting

Now we will show that the equations (33) have an operator form. Since the velocity field u and the magnetic field H on M are divergence-free, there exist stream functions $f_{1}$and $f_{2}$, such that:

$$u_{\theta }=\frac{\partial f_{1}}{\partial r},\quad \quad u_{r}=-\frac{\partial f_{1}}{\partial r};$$

$$H_{\theta }=\frac{\partial f_{2}}{\partial r},\quad \quad H_{r}=-\frac{\partial f_{2}}{\partial r};$$

satisfying the given boundary condition. Therefore the following two vector fields

$$(\frac{2}{r_{0}}\frac{\partial u_{r}}{\partial \theta }, -\frac{2}{r_{0}}\frac{\partial u_{\theta }}{\partial \theta }) =-\frac{2}{r_{0}}\nabla \frac{\partial f_{1}}{\partial \theta },$$

$$(\frac{2}{r_{0}}\frac{\partial H_{r}}{\partial \theta }, -\frac{2}{r_{0}}\frac{\partial H_{\theta }}{\partial \theta }) =-\frac{2}{r_{0}}\nabla \frac{\partial f_{2}}{\partial \theta },$$

are gradient fields, which can be balanced by $\nabla p$ and $\nabla \Phi$ in Eq. 33. Hence (33) are equivalent to the following equations

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial u_{r}}{\partial t}+(u\cdot {\nabla })u_{r} -\frac{u^{2}_{\theta }}{r_{0}^{2}}={\Delta } u_{r} -\frac{u_{r}}{r_{0}^{2}} -\frac{\partial p}{\partial r}-\frac{1}{\rho _{0}\kappa ^{2}}H_{0}^{2}\frac{1}{r_{0}^{2}}H_{\theta }(\frac{H_{\theta }}{r_{0}} +\frac{\partial H_{\theta }}{\partial r}) \\ {}&\quad \quad \quad \quad +\frac{1}{\rho _{0}\kappa ^{2}}H_{0}^{2}H_{\theta } \frac{\partial H_{r}}{\partial \theta } +\sqrt{R}T, \\ {}&\frac{\partial u_{\theta }}{\partial t}+(u\cdot {\nabla }) u_{\theta } +\frac{2}{r_{0}}u_{r}u_{\theta }={\Delta } u_{\theta } -\frac{u_{\theta }}{r^{2}_{0}}-\frac{\partial p}{\partial \theta } +\frac{H_{0}^{2}d}{\rho _{0}\kappa ^{2}}H_{r}(\frac{\partial H_{\theta }}{\partial r}-\frac{\partial H_{r}}{\partial \theta }) \\ {}&\quad \quad \quad \quad \quad +\frac{H_{0}^{2}d}{\rho _{0}\kappa ^{2}}\frac{\kappa ^{2}}{dr_{0}}(\frac{\partial H_{\theta }}{\partial r}-\frac{\partial H_{r}}{\partial \theta }), \\ {}&\frac{\partial T}{\partial t}+(u\cdot {\nabla })T= {\Delta } T+d\sqrt{R}u_{r}, \\ {}&\frac{\partial H_{r}}{\partial t}={\Delta } H_{r}- -\frac{H_{r}}{r_{0}^{2}}+ \frac{1}{r_{0}}\frac{\partial (u_{r}H_{\theta }-u_{\theta }H_{r})}{\partial \theta } -\frac{K_{2}}{d^{2}r_{0}^{2}}\frac{1}{H_{0}}\frac{\partial u_{\theta }}{\partial \theta } +\frac{\partial \Phi }{\partial r}, \\ {}&\frac{\partial H_{\theta }}{\partial t}={\Delta } H_{\theta } -\frac{H_{\theta }}{r_{0}^{2}}-\frac{\partial (u_{r}H_{\theta }-u_{\theta }H_{r})}{\partial r} +\frac{K_{2}}{dr_{0}}\frac{\partial u_{\theta }}{\partial r} +\frac{\partial \Phi }{\partial \theta }, \\ {}&\text {div} u=\frac{\partial u_{r}}{\partial r}+\frac{\partial u_{\theta }}{\partial \theta }=0, \\ {}&\text {div} H=\frac{\partial H_{r}}{\partial r}+\frac{\partial H_{\theta }}{\partial \theta }=0, \end{aligned} \right. \end{aligned}$$

(35)

where $(u\cdot \nabla )$, $\text {div}$ and ${\Delta }$ are as usual differential operators:

$$(u\cdot \nabla )=u_{\varphi }\frac{\partial }{\partial \varphi }+u_{r}\frac{\partial }{\partial r},\quad {\Delta } =\frac{\partial ^{2}}{\partial \varphi ^{2}}+\frac{\partial ^{2}}{\partial r ^{2}}, \quad \text {div}u=\frac{\partial u_{\varphi }}{\partial \varphi }+\frac{\partial u_{r}}{\partial r}.$$

For the problem (35) with conditions (34), we set the spaces

$$H=\{(u,T,H)\in L^{2}(\Omega , R^{5})\mid \text {div} u= \text{ div } H=0,(u,T,H) \;\text {is periodic in} \;\varphi \text {-direction}\},$$

$$H_{1}=\{(u,T,H)\in H^{2}(\Omega ,R^{5})\cap H\mid (u,T,H)\;\text{ satisfy } \;(34)\}.$$

Let the operators $G:H_{1}\rightarrow H$, and $L_{\lambda }=-A+B_{\lambda }:H_{1}\rightarrow H$ be defined by

$$\begin{aligned} AU+BU={} & {} -P({\Delta } u_{r} -\frac{u_{r}}{r_{0}^{2}}+\sqrt{R}T,\quad {\Delta } u_{\theta } -\frac{u_{\theta }}{r^{2}_{0}} + \frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}E (\frac{\partial H_{\theta }}{\partial r}-\frac{\partial H_{r}}{\partial \theta }), \\{} & {} {\Delta } T+d\sqrt{R}u_{r},\quad {\Delta } H_{r}-\frac{H_{r}}{r_{0}^{2}} -\frac{E}{H_{0}r_{0}d}\frac{\partial u_{\theta }}{\partial \theta }+\frac{\partial \Phi }{\partial r}, \\{} & {} {\Delta } H_{\theta }-\frac{H_{\theta }}{r_{0}^{2}} +E\frac{\partial u_{\theta }}{\partial r}+\frac{\partial \Phi }{\partial \theta })^{T}, \\ GU= P(-{} & {} (u\cdot \nabla )u_{r}+\frac{u_{\theta }^{2}}{r_{0}}-\frac{1}{\rho _{0}\kappa ^{2}}H_{0}^{2}\frac{1}{r_{0}^{2}}H_{\theta }(\frac{H_{\theta }}{r_{0}}+\frac{\partial H_{\theta }}{\partial r}) +\frac{1}{\rho _{0}\kappa ^{2}}H_{0}^{2}H_{\theta } \frac{\partial H_{r}}{\partial \theta },\\{} & {} -(u\cdot \nabla )u_{\theta }- \frac{2}{r_{0}}u_{r}u_{\theta }+ \frac{H_{0}^{2}d}{\rho _{0}\kappa ^{2}}H_{r} (\frac{\partial H_{\theta }}{\partial r}-\frac{\partial H_{r}}{\partial \theta }),\quad \quad -(u\cdot \nabla )T,\\{} & {} \frac{1}{r_{0}}\frac{\partial (u_{r}H_{\theta }-u_{\theta }H_{r})}{\partial \theta },\quad -\frac{\partial (u_{r}H_{\theta }-u_{\theta }H_{r})}{\partial r} )^{T}, \end{aligned}$$

for any $U=(u_{r},u_{\theta },T,H_{r},H_{\theta })$. Here $E=\frac{K_{2}}{dr_{0}}$, and P the Leray projection to $L^{2}$ fields.

Under the above definitions, the problem (33) with boundary conditions (34) are equivalent to the following abstract equation:

$$\begin{aligned} \frac{dU}{dt}=L_{\lambda }U+GU, \end{aligned}$$

(36)

where $\lambda =(R,E)$ is the parameter.

6 Bifurcation of the Granulation Convection

6.1 The Eigenvalue Problem

To study the phase transition of the granulation convection (33) and (34), it is necessary to consider the eigenvalue problem of its linearized equation.

Let $L_{\lambda }$ be the linear operator defined by Eq. 36, we consider the following eigenvalue problem

$$\begin{aligned} L_{\lambda }U=\beta _{\lambda }U,\quad \quad \text {for} \quad U=(u_{r},u_{\theta },T,H_{r},H_{\theta })\in H_{1}. \end{aligned}$$

(37)

By definition, the abstract form (37) is equivalent to the following eigenvalue equations with boundary condition (34):

$$\begin{aligned} \left\{ \begin{aligned}&{\Delta } u_{r}-\frac{1}{r_{0}^{2}}u_{r}-\frac{\partial p}{\partial r}+\sqrt{ R}T=\beta u_{r}, \\ {}&{\Delta } u_{\theta } -\frac{u_{\theta }}{r^{2}_{0}} + \frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}E (\frac{\partial H_{\theta }}{\partial r}-\frac{\partial H_{r}}{\partial \theta })=\beta u_{\theta }, \\ {}&{\Delta } T+ d\sqrt{R}u_{r}=\beta T, \\ {}&{\Delta } H_{r}-\frac{H_{r}}{r_{0}^{2}} -\frac{E}{H_{0}r_{0}d}\frac{\partial u_{\theta }}{\partial \theta }+\frac{\partial \Phi }{\partial r}=\beta H_{r}, \\ {}&{\Delta } H_{\theta }-\frac{H_{\theta }}{r_{0}^{2}} +E\frac{\partial u_{\theta }}{\partial r}+\frac{\partial \Phi }{\partial \theta }\beta H_{\theta }, \\ {}&\text {div}u=\text {div}H=0. \end{aligned} \right. \end{aligned}$$

(38)

Under the constraint (34), for $U=(u_{r},u_{\theta },T,H_{r},H_{\theta })\in H_{1}$, the eigenvectors of Eq. 38 have the separation of variables as follows

$$\begin{aligned} \begin{aligned}&\Psi : \left\{ \begin{aligned}&u_{\varphi }= \cos a_{k}\varphi \cdot h^{'}_{k}(r), \\ {}&u_{r}=a_{k}\sin a_{k}\varphi \cdot h_{k}(r), \\ {}&T=\sin a_{k}\varphi \cdot T_{k}(r), \\ {}&H_{\varphi }=\cos a_{k}\varphi \cdot g^{'}_{k}(r), \\ {}&H_{r}=a_{k}\sin a_{k}\varphi \cdot g_{k}(r), \end{aligned} \right. \end{aligned} \end{aligned}$$

(39)

$$p=p_{k}(r)\sin a_{k}\varphi ,\quad \Phi =\Phi _{k}(r)\sin a_{k}\varphi ,\quad a_{k}=\frac{2k\pi }{L}.$$

$$\begin{aligned} \begin{aligned}&\tilde{\Psi }: \left\{ \begin{aligned}&u_{\varphi }= \sin a_{k}\varphi \cdot h^{'}_{k}(r), \\ {}&u_{r}=-a_{k}\cos a_{k}\varphi \cdot h_{k}(r), \\ {}&T=-\cos a_{k}\varphi \cdot T_{k}(r), \\ {}&H_{\varphi }=\sin a_{k}\varphi \cdot g^{'}_{k}(r), \\ {}&H_{r}=-a_{k}\cos a_{k}\varphi \cdot g_{k}(r), \end{aligned} \right. \end{aligned} \end{aligned}$$

(40)

$$\tilde{p}=-p_{k}(r)\cos a_{k}\varphi ,\quad \tilde{\Phi }=-\Phi _{k}(r)\cos a_{k}\varphi ,\quad a_{k}=\frac{2k\pi }{L}.$$

Putting $(\Psi ,p,\Phi )$ and $(\tilde{\Psi },\tilde{p},\tilde{\Phi })$ into Eq. 38 respectively, we deduce from Eqs. 38, 39 and 40 that $(h_{k},g_{k},T_{k},p_{k},\Phi _{k})$ satisfy eigenvalue problems,

$$\begin{aligned} \left\{ \begin{aligned}&a_{k}D^{*}h_{k}-\frac{a_{k}}{r_{0}^{2}}h_{k}-Dp_{k}+\sqrt{R}T_{k}=\beta a_{k}h_{k}, \\ {}&D^{*}Dh_{k}-\frac{1}{r_{0}^{2}}Dh_{k}-a_{k}p_{k}+\frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}E D^{*} g_{k}=\beta Dh_{k}, \\ {}&D^{*}T_{k}+d\sqrt{R}a_{k}h_{k}=\beta T_{k}, \\ {}&a_{k}D^{*}g_{k}-\frac{1}{r_{0}^{2}}a_{k}g_{k}+\frac{E}{H_{0}r_{0}d}a_{k}Dh_{k}+D\Phi _{k}=\beta a_{k}g_{k}, \\ {}&D^{*}Dg_{k}-\frac{1}{r_{0}^{2}}Dg_{k}+ED^{2}h_{k}+a_{k}\Phi _{k}=\beta D g_{k}, \end{aligned} \right. \end{aligned}$$

(41)

for any $k\in Z$, with $k\ne 0$, where

$$D=\frac{d}{dr},\quad D^{*}=D^{2}-a_{k}^{2}. $$

We infer from Eq. 41 that

$$\begin{aligned} {\begin{matrix} a_{k}(D^{*}-\beta )(a_{k}D^{*}-\beta -\frac{1}{r_{0}^{2}})h_{k}-(D^{*}-\beta )(D^{*}-\beta -\frac{1}{r_{0}^{2}})D^{2}h_{k} \\ -\frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}E (D^{*}-\beta )D^{*}Dg_{k}-dRa_{k}^{2}Dh_{k}=0,\quad \quad \quad \quad \quad \end{matrix}} \end{aligned}$$

(42)

$$\begin{aligned} D^{*}(\frac{1}{r_{0}^{2}}+\beta -D^{*})g_{k}=(ED^{3}-Fa_{k}^{2}D)h_{k}. \end{aligned}$$

(43)

If $h_{k}\ne 0$, the Eqs. 42 and 43 can be reduced to a single equation

$$\begin{aligned} {\begin{matrix} -(D^{*}-\frac{1}{r_{0}^{2}}-\beta )^{2} ((D^{*}-\beta )D^{*}h_{k}-\varepsilon D(D^{*}-\beta ) (Fa_{k}^{2}D-ED^{3}h_{k}) \\ -dRa_{k}^{2}(D^{*}-\frac{1}{r_{0}^{2}}-\beta )h_{k}=0.\quad \quad \quad \quad \quad \end{matrix}} \end{aligned}$$

(44)

It is clear that the solution of Eq. 42 are sine functions

$$\begin{aligned} h_{kl}=sin l\pi (r-r_{0}). \end{aligned}$$

(45)

Substituting (45) into Eq. 44, we see that the corresponding eigenvalues $\beta$ of problem (41) satisfy the cubic equation

$$\begin{aligned} {\begin{matrix} -(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}}+\beta )(\alpha _{kl}^{2}+\beta )\alpha _{kl}^{2}+\varepsilon {(\alpha _{kl}^{2}+\beta )(-El^{4}\pi ^{4}-Fa_{k}^{2}l^{2}\pi ^{2}) } \\ +dRa_{k}^{2}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}}+\beta )=0.\quad \quad \quad \quad \quad \end{matrix}} \end{aligned}$$

(46)

where

$$\alpha _{kl}^{2}=a_{k}^{2}+l^{2}\pi ^{2}, \quad \varepsilon \cdot \frac{K_{0}^{2}d}{\rho _{0}\kappa ^{2}}=E.$$

Moreover, to determine $T_{k},g_{k},p_{k},\Phi _{k}$, we derive from Eq. 41 that

$$\begin{aligned} \left\{ \begin{aligned}&-(\alpha _{kl}^{2}+\beta )T_{k}=-d\sqrt{R}a_{k}h_{k}, \\ {}&-\alpha _{kl}^{2} (\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})g_{k}=(-El^{2}\pi ^{2}-Fa_{k}^{2})Dh_{k} , \\ {}&a_{k}p_{k}=(-\alpha _{kl}^{2}-\beta -\frac{1}{r_{0}^{2}})Dh_{k}-\varepsilon \alpha _{kl}^{2} g_{k}, \\ {}&a_{k}\Phi _{k}=(\beta +\alpha _{kl}^{2} +\frac{1}{r_{0}^{2}})Dg_{k}+El^{2}\pi ^{2}h_{k}. \end{aligned} \right. \end{aligned}$$

(47)

With the above calculations, all eigenvalues and eigenvectors of Eq. 38 can be derived and are given in the following three groups:

• 1. For $(k,l)=(0,l)$, we have

  $$\beta _{0l}^{1}=-l^{2}\pi ^{2},$$
  $$\Psi _{0l}=(0,0,\sin l\pi (r-r_{0}),0,0),\quad \tilde{\Psi _{0l}}=(0,0,\cos l\pi (r-r_{0}),0,0),$$

• 2. For $(k,l)=(k,0)$, the eigenvalues and eigenvectors are given by

  $$\beta _{k0}=-a_{k}^{2}-\frac{1}{r_{0}^{2}},$$
  $$\Psi _{k0}=(\sin a_{k}\varphi , 0,0,0,0),\quad \tilde{\Psi }_{k0}=(\cos a_{k}\varphi ,0,0,0,0,).$$

• 3. For $k\ne 0$ and $l\ne 0$, it is known that all solutions of equation (46) are eigenvalues. Let $\beta _{kl}^{1}(R)\;(1\le i\le 3)$ be three zeros of Eq. 46 such that

  $$Re\beta _{kl}^{1}\ge Re\beta _{kl}^{2}\ge Re\beta _{kl}^{3}.$$

  Then, by Eqs. 41, 45 and 47, the eigenvectors $\Psi _{kl}^{i},(i=1,2,3)$ corresponding to $\beta _{kl}^{i}$ can be written as

  $$\begin{aligned} \begin{aligned}&\Psi _{kl}^{i}=\left\{ \begin{aligned}&a_{k}\sin a_{k}\theta \cdot \sin l\pi (r-r_{0}), \\ {}&l\pi \cos a_{k}\theta \cdot \cos l\pi (r-r_{0}) , \\ {}&T_{kl}^{i}\sin a_{k}\theta \cdot \sin l\pi (r-r_{0}), \\ {}&g_{kl}^{i}a_{k} \sin a_{k}\theta \cdot \cos l\pi (r-r_{0}), \\ {}&-l\pi g_{kl}^{i}a_{k} \cos a_{k}\theta \cdot \sin l\pi (r-r_{0}), \end{aligned} \right. \end{aligned} \end{aligned}$$

  (48)
  $$\begin{aligned} \begin{aligned}&\tilde{\Psi }_{kl}^{i}=\left\{ \begin{aligned}&-a_{k}\cos a_{k}\theta \cdot \sin l\pi (r-r_{0}), \\ {}&l\pi \sin a_{k}\theta \cdot \cos l\pi (r-r_{0}) , \\ {}&-T_{kl}^{i}\cos a_{k}\theta \cdot \sin l\pi (r-r_{0}), \\ {}&-g_{kl}^{i}a_{k} \cos a_{k}\theta \cdot \cos l\pi (r-r_{0}), \\ {}&l\pi g_{kl}^{i}a_{k} \sin a_{k}\theta \cdot \sin l\pi (r-r_{0}), \end{aligned} \right. \end{aligned} \end{aligned}$$

  (49)

  where

  $$T_{kl}^{i}=\frac{d\sqrt{R}}{-\alpha _{kl}^{i}-\beta _{kl}^{i}},$$
  $$g_{kl}^{i}=\frac{El^{3}\pi ^{3}+Fa^{2}l\pi }{\alpha _{kl}^{2}(\frac{1}{r_{0}^{2}}+\beta _{kl}^{i}+\alpha _{kl}^{2})}.$$

The adjoint equation of Eq. 41 are given by

$$\begin{aligned} \left\{ \begin{aligned}&{\Delta } u_{r}^{*}-\frac{1}{r_{0}^{2}}u_{r}^{*}-\frac{\partial p^{*}}{\partial r}+d\sqrt{ R}T^{*}=\beta u_{r}^{*}, \\ {}&{\Delta } u_{\theta }^{*} -\frac{u_{\theta }^{*}}{r^{2}_{0}} + E\frac{\partial H_{\theta }^{*}}{\partial r}-\frac{F}{H_{0}}\frac{\partial H_{r}^{*}}{\partial \theta }-\frac{\partial p^{*}}{\partial \theta }=\beta u_{\theta }^{*}, \\ {}&{\Delta } T^{*}+ \sqrt{R}u_{r}^{*}=\beta T^{*}, \\ {}&{\Delta } H_{r}^{*}-\frac{H_{r}^{*}}{r_{0}^{2}} -\varepsilon \frac{\partial u_{\theta }^{*}}{\partial \theta }+\frac{\partial \Phi ^{*}}{\partial r}=\beta H_{r}^{*}, \\ {}&{\Delta } H_{\theta }^{*}-\frac{H_{\theta }^{*}}{r_{0}^{2}} +\varepsilon \frac{\partial u_{\theta }^{*}}{\partial r}+\frac{\partial \Phi ^{*}}{\partial \theta }=\beta H_{\theta }^{*}, \\ {}&\text {div}u^{*}=\text {div}H^{*}=0. \end{aligned} \right. \end{aligned}$$

(50)

Thus, the conjugate eigenvector $\Psi _{kl}^{i*}$ of Eq. 50 corresponding to $\beta _{kl}^{i}$ are as follows

$$\begin{aligned} \begin{aligned}&\Psi _{kl}^{i*}=\left\{ \begin{aligned}&a_{k}\sin a_{k}\theta \cdot \sin l\pi (r-r_{0}), \\ {}&l\pi \cos a_{k}\theta \cdot \cos l\pi (r-r_{0}) , \\ {}&T_{kl}^{i*}\sin a_{k}\theta \cdot \sin l\pi (r-r_{0}), \\ {}&g_{kl}^{i*}a_{k} \sin a_{k}\theta \cdot \cos l\pi (r-r_{0}), \\ {}&-l\pi g_{kl}^{i*} \cos a_{k}\theta \cdot \sin l\pi (r-r_{0}), \end{aligned} \right. \end{aligned} \end{aligned}$$

(51)

$$\begin{aligned} \begin{aligned}&\tilde{\Psi }_{kl}^{i*}=\left\{ \begin{aligned}&-a_{k}\cos a_{k}\theta \cdot \sin l\pi (r-r_{0}), \\ {}&l\pi \sin a_{k}\theta \cdot \cos l\pi (r-r_{0}) , \\ {}&-T_{kl}^{i*}\cos a_{k}\theta \cdot \sin l\pi (r-r_{0}), \\ {}&-g_{kl}^{i*}a_{k} \cos a_{k}\theta \cdot \cos l\pi (r-r_{0}), \\ {}&l\pi g_{kl}^{i*} \sin a_{k}\theta \cdot \sin l\pi (r-r_{0}), \end{aligned} \right. \end{aligned} \end{aligned}$$

(52)

where

$$T_{kl}^{i*}=\frac{d\sqrt{R}a_{k}}{\alpha _{kl}^{i}+\beta _{kl}^{i}},$$

$$g_{kl}^{i*}=\frac{\varepsilon }{\frac{1}{r_{0}^{2}}+\beta _{kl}^{i}+\alpha _{kl}^{2}}.$$

Thus, all eigenvectors of Eq. 41 consist of $\Psi _{0l},{\tilde{\Psi }_{0l}},\Psi _{k0},\tilde{\Psi }_{k0}$. All conjugate eigenvectors of Eq. 50 consist of $\Psi _{0l}^{*}=\Psi _{0l}, \tilde{\Psi }_{0l}^{*}=\tilde{\Psi }_{0l}, \Psi _{k0}^{*}=\Psi _{k0}, \tilde{\Psi }_{k0}^{*}=\tilde{\Psi }_{k0}$, and $\Psi _{kl}^{i*}, \tilde{\Psi }_{kl}^{i*}$ as in (51), (52).

6.2 The Critical Parameter R

The linear stability and instability are precisely determined by the critical-crossing of the first eigenvalues of Eq. 41, which is often called PES. For this purpose, we only need to study the solution $\beta$ of Eq. 46, which is equivalent to the following form

$$\begin{aligned} {\begin{matrix} \alpha _{kl}^{2}\beta ^{3}+(3\alpha _{kl}^{4}+\alpha _{kl}^{2}\cdot \frac{2}{r_{0}^{2}})\beta ^{2}+[2\alpha _{kl}^{4} (\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})+ \alpha _{kl}^{2}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})^{2}\quad \quad \\ +\frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}E^{2}(l^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l^{4}\pi ^{4}) -dRa^{2}]\beta +\frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}(l^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l^{4}\pi ^{4})\\ \alpha _{kl}^{2}E^{2}- da^{2}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})R+\alpha _{kl}^{4}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})^{2}=0.\quad \quad \quad \quad \end{matrix}} \end{aligned}$$

(53)

Let

$$b_{0}= \frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}\cdot \frac{1}{ \alpha _{kl}^{2}} (l^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l^{4}\pi ^{4}) E^{2}- \frac{da^{2}}{\alpha _{kl}^{2}}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})R +\alpha _{kl}^{2}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})^{2},$$

$$b_{1}=2\alpha _{kl}^{2} (\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})+ (\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})^{2} +\frac{1}{\alpha _{kl}^{2}}\cdot \frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}E^{2}(l^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l^{4}\pi ^{4}) - \frac{dRa^{2}}{\alpha _{kl}^{2}},$$

$$b_{2}=3\alpha _{kl}^{2}+\frac{2}{r_{0}^{2}}.$$

As we shall see, both real and complex eigenvalues can occur. The real eigenvalues often lead to transition to steady solution, and the complex eigenvalues give rise oscillation. As we mentioned in the introduction, these solutions are related to low frequency variabilities of the atmospheric circulation system and oceanic system.

First, we discuss the critical-crossing of real eigenvalues. It is clear that $\beta =0$ is a zero of Eq. 53 if and only if $b_{0}=0$.

In this case, we have $\sigma =R$ and

$$\sigma _{kl}= \frac{\frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}(l^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l^{4}\pi ^{4}) \alpha _{kl}^{2}E^{2}+\alpha _{kl}^{4}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})^{2}}{da^{2}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})}.$$

Let

$$\begin{aligned} \sigma _{c}=\min _{(k,l)} \frac{\frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}(l^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l^{4}\pi ^{4}) \alpha _{kl}^{2}E^{2}+\alpha _{kl}^{4}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})^{2}}{da^{2}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})}=\sigma _{k_{1}l_{1}}, \end{aligned}$$

(54)

where $\sigma _{c}$ is called the critical R-Rayleigh number.

Next, we consider the critical-crossing of the complex eigenvalues.In this case, we use $\eta$ to represent the Rayleigh number-R. Let $i\rho _{0}(\rho _{0}\ne 0)$ be a zero of Eq. 53. Then we have

$$\rho _{0}^{2}=\frac{2\alpha _{kl}^{4} (\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})+ \alpha _{kl}^{2}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})^{2} +\frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}E^{2}(l^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l^{4}\pi ^{4}) -dRa^{2}}{\alpha _{kl}^{2}},$$

$$\rho _{0}^{2}=\frac{\frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}(l^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l^{4}\pi ^{4}) \alpha _{kl}^{2}E^{2}- da^{2}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})R+\alpha _{kl}^{4}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})^{2}}{3\alpha _{kl}^{4}+\alpha _{kl}^{2}\cdot \frac{2}{r_{0}^{2}}}.$$

Therefore, equation (53) has a pair of purely imaginary solution $\pm i\rho _{0}$ if and only if the following condition hold true

$$\begin{aligned} b_{0}=b_{1}b_{2}. \end{aligned}$$

(55)

It follows from Eq. 55 that

$$\begin{aligned} {\begin{matrix} \eta _{kl}= \frac{ 2\alpha _{kl}^{4}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})(3\alpha _{kl}^{2}+\frac{2}{r_{0}^{2}}) +\alpha _{kl}^{2}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})^{2}(3\alpha _{kl}^{2}+\frac{2}{r_{0}^{2}})}{da^{2}(2\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})}+\\ \frac{\frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}E^{2}(l^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l^{4}\pi ^{4}) (3\alpha _{kl}^{2}+\frac{2}{r_{0}^{2}})}{da^{2}(2\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})}\quad \quad \quad \\ -\frac{\frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}(l^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l^{4}\pi ^{4}) \alpha _{kl}^{2}E^{2}+\alpha _{kl}^{4}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})^{2}}{da^{2}(2\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})}. \end{matrix}} \end{aligned}$$

(56)

Hence, we defined the critical R-Rayleigh number by

$$\begin{aligned} {\begin{matrix} \eta _{c}=\min _{(k,l)}\big [ \frac{ 2\alpha _{kl}^{4}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})(3\alpha _{kl}^{2}+\frac{2}{r_{0}^{2}}) +\alpha _{kl}^{2}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})^{2}(3\alpha _{kl}^{2}+\frac{2}{r_{0}^{2}})}{da^{2}(2\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})}+\\ \frac{\frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}E^{2}(l^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l^{4}\pi ^{4}) (3\alpha _{kl}^{2}+\frac{2}{r_{0}^{2}})}{da^{2}(2\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})}\quad \quad \quad \\ -\frac{\frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}(l^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l^{4}\pi ^{4}) \alpha _{kl}^{2}E^{2}+\alpha _{kl}^{4}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})^{2}}{da^{2}(2\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})}\big ]= \eta _{k_{2}l_{2}}. \end{matrix}} \end{aligned}$$

(57)

The following theorem provides a criterion to determine the first critical Rayleigh number for $\sigma _{c}$ and $\eta _{c}$.

Theorem 1

Let $(k_{1},l_{1})$ satisfy (54) and $(k_{2},l_{2})$ satisfy (57), then we have the following assertions:

• 1. If $\sigma _{c} <\eta _{c}$,then the number $\sigma _{c}$ is the first critical Rayleigh number, and

  $$\begin{aligned} \begin{aligned}&\beta _{k_{1}l_{1}}^{1}\left\{ \begin{aligned}&<0,\;if \sigma <\sigma _{c} , \\ {}&=0,\;if \sigma =\sigma _{c}, \\ {}&>0,\;if \sigma >\sigma _{c}, \end{aligned} \right. \end{aligned} \end{aligned}$$

  (58)
  $$\beta _{kl}^{i}<0,\;\forall (k,l,i)\ne (k_{1},l_{1},1).$$

• 2. If $\sigma _{c} >\eta _{c}$,then the number $\eta _{c}$ is the first critical Rayleigh number, and

  $$\begin{aligned} \begin{aligned}&Re\beta _{k_{2}l_{2}}^{1}=Re\beta _{k_{2}l_{2}}^{2}\left\{ \begin{aligned}&<0,\;if \eta <\eta _{c} , \\ {}&=0,\;if \eta =\eta _{c}, \\ {}&>0,\;if \eta >\eta _{c}, \end{aligned} \right. \end{aligned} \end{aligned}$$

  (59)
  $$Re\beta _{kl}^{i}<0,\;\forall (k,l,i)\ne (k_{2},l_{2},1),(k_{2},l_{2},2).$$

  .

This theorem provides a precise criteria on if the first unstable mode corresponds either to multiple equilibrium modes or to oscillatory modes, corresponding to steady state patterns or to spatiotemporal patterns.

Proof

The equation (53) can be written as

$$\begin{aligned} \beta ^{3}+b_{2}\beta ^{2}+b_{1}\beta +b_{0}=0. \end{aligned}$$

(60)

It is easy to see that

$$\begin{aligned} b_{2}(\sigma _{c})=3\alpha _{k_{0}l_{{0}}}^{2}+\frac{2}{r_{0}^{2}}>0. \end{aligned}$$

(61)

We shall show that

$$\begin{aligned} {\begin{matrix} b_{1}(\sigma _{c})=2\alpha _{k_{0}l_{0}}^{2} (\alpha _{k_{0}l_{0}}^{2}+\frac{1}{r_{0}^{2}})+ (\alpha _{k_{0}l_{0}}^{2}+\frac{1}{r_{0}^{2}})^{2}\quad \quad \quad \\ +\frac{1}{\alpha _{k_{0}l_{0}}^{2}}\cdot \frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}E^{2}(l_{0}^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l_{0}^{4}\pi ^{4}) - \frac{dRa^{2}}{\alpha _{k_{0}l_{0}}^{2}}>0. \end{matrix}} \end{aligned}$$

(62)

Assume that Eq. 62 is not true, we will consider the case

$$\begin{aligned} {\begin{matrix} b_{1}(\sigma _{c})=2\alpha _{k_{0}l_{0}}^{2} (\alpha _{k_{0}l_{0}}^{2}+\frac{1}{r_{0}^{2}})+ (\alpha _{k_{0}l_{0}}^{2}+\frac{1}{r_{0}^{2}})^{2}\quad \quad \quad \\ +\frac{1}{\alpha _{k_{0}l_{0}}^{2}}\cdot \frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d}E^{2}(l_{0}^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l_{0}^{4}\pi ^{4}) - \frac{dRa^{2}}{\alpha _{k_{0}l_{0}}^{2}}<0. \end{matrix}} \end{aligned}$$

(63)

Note that the solution $\beta (\sigma )=\beta _{k_{1}l_{1}}^{1}(\sigma )$ is continuous on $\sigma$, and $\beta (\sigma _{c})=0$. Hence

$$\begin{aligned} \beta (\sigma )\rightarrow 0,\quad \text {as} \quad \sigma \rightarrow \sigma _{c}. \end{aligned}$$

(64)

Thus, near $\sigma = \sigma _{c}$ the equation (53)can be written as

$$\begin{aligned} \beta (\sigma )=-\frac{b_{0}(\sigma )}{b_{1}(\sigma )} +0(\beta (\sigma )) . \end{aligned}$$

(65)

It follows from Eqs. 63, 64, 65 that

$$\begin{aligned} \begin{aligned}&\beta (\sigma )\left\{ \begin{aligned}&<0,\;if \sigma>\sigma _{c} , \\ {}&=0,\;if \sigma =\sigma _{c}, \\ {}&>0,\;if \sigma <\sigma _{c}, \end{aligned} \right. \end{aligned} \end{aligned}$$

(66)

for $\sigma$ near $\sigma _{c}$. We write the equation (53) in the following form

$$\begin{aligned} \beta ^{3}+b_{2}\beta ^{2}+b_{1}(\sigma )\beta +b_{0}(\sigma )=0. \end{aligned}$$

(67)

Meanwhile, $b_{2}>0$, and it is easy to see that

$$b_{0}(\sigma )\rightarrow +\infty ,\quad b_{1}(\sigma )\rightarrow +\infty , \text {as} \quad \sigma \rightarrow -\infty .$$

It implies that when $\sigma$ is sufficiently small, the real solution of Eq. 67 must be negative. Thus, by Eq. 66 there exist a number $\sigma _{0}<\sigma _{c}$ such that the solution $\beta (\sigma )$ of Eq. 53 vanishes to zero at $\sigma =\sigma _{0}$. Which is contradiction to that $b_{0}(\sigma )\ne 0$. Thus, we derive $b_{}(\sigma )\ge 0$. By Eq. 61, we can obtain (58).

In the following, we shall prove that

$$\begin{aligned} \beta _{kl}^{i}(\sigma _{c})<0,\quad \forall (k,l,i)\ne (k_{1},l_{1},1). \end{aligned}$$

(68)

Let$\beta _{m}=\beta _{kl}^{i}(\sigma _{c})$ be a solution of Eq. 53 at $\sigma =\sigma _{c}$. Now, we consider the coefficients of Eq. 53 at $\sigma =\sigma _{c}$ . It is easy to show

$$b_{2}(\sigma _{c})>0,$$

$$b_{0}(\sigma _{c})=\frac{\rho _{0}\kappa ^{2}}{H_{0}^{2}d} \frac{1}{\alpha _{kl}^{2}} (l^{4}\pi ^{4}+\frac{dr_{0}^{2}}{H_{0}}a^{2}l^{4}\pi ^{4}) E^{2} +\alpha _{kl}^{2}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})^{2} -\frac{da^{2}}{\alpha _{kl}^{2}}(\alpha _{kl}^{2}+\frac{1}{r_{0}^{2}})\sigma _{c}>0.$$

Thanks to Eq. 62, we have $b_{1}>0$. Hence, the coefficients of Eq. 53 at $\sigma =\sigma _{c}$ are nonnegative, and strictly positive positive provided that $\sigma \ne \sigma _{c}$. It follows that

$$\beta _{m}=\beta _{kl}^{i}(\sigma _{c})<0,\quad \forall (k,l,i)\ne (k_{1},l_{1},1).$$

Thus, we proved (58), and the proof of Eq. 59 is similar to Eq. 58, so we omit it here. $\square$

6.3 The Critical Parameter Curves and ER-phase Diagram

In this section, we consider the critical parameter R, which is related to temperature difference, and E, which is related to magnetic field. It is clear that $\beta =0$ is a zero of Eq. 53 if and only if

$$d_{k_{1}l_{1}}-e_{k_{1}l_{1}}R+f_{k_{1}l_{1}}E^{2}=0,$$

where

$$ d_{k_{1}l_{1}}=\alpha _{k_{1}l_{1}}^{4}(\alpha _{k_{1}l_{1}}^{2}+\frac{1}{r_{0}^{2}})^{2},\quad e_{k_{1}l_{1}}=da^{2}(\alpha _{k_{1}l_{1}}^{2}+\frac{1}{r_{0}^{2}}),\quad f_{k_{1}l_{1}}=\alpha _{k_{1}l_{1}}^{2},$$

And $k_{1},l_{1}$ are defined as Eq. 54. So we get the the critical parameter curve in the figure

$$L=\{(E,R)\in R^{2}_{+}\mid d_{{k_{1}l_{1}}}-e_{{k_{1}l_{1}}}R+f_{{k_{1}l_{1}}}E^{2}=0 \}.$$

The following theorem describe the critical-crossing for the eigenvalues of Eq. 41:

Theorem 2

Let $(k,l)=({{k_{1},l_{1}}})$ minimize the right hand side of Eq. 54 and assume the zero $\beta _{{k_{1}l_{1}}}^{1}$ of Eq. 21 is a real single eigenvalue of Eq. 14 near curve L. Then $\beta _{{k_{1}l_{1}}}^{1}$ satisfies that

$$\begin{aligned} \nonumber \begin{aligned}&\beta _{{k_{1}l_{1}}}^{1}\left\{ \begin{aligned}&<0,\;(E,R)\in \text {I} , \\ {}&=0,\;(E,R)\in L, \\ {}&>0,\;(E,R)\in \text {II }, \end{aligned} \right. \end{aligned} \end{aligned}$$

$\beta _{kl}^{i}<0,\;\forall (k,l)\ne ({k_{1}l_{1}})$, when (E, R) in region $\text {I}$ or in region $\text {II}$ near the curve L, as is shown in Fig. 3.

In summary, with the above analysis and the dynamic transition theory, we arrive at the following theorem:

Theorem 3

The critical parameters curve L divides the ER-plane into two regions $\text {I}$ and $\text {II }$(see Fig. 3), such that the following conclusions hold true:

• 1. If $(E,R)\in \text {I}$, the problem (36) don’t have bifurcation, and the basic flow is stable;

• 2. If $(E,R)\in \text {II}$, there exists a bifurcation solution;

• 3. The transition takes place as the control parameter (E, R) crosses the critical curve L from region $\text {I}$ into $\text {II}$ .

7 Conclusions

We end this paper with a few remarks:

First,we consider the three-dimensional granulation convection. Compared with two-dimensional polar coordinates, the three-dimensional cylindrical coordinates can more easily consider the influence of magnetic fields. In the two-dimensional polar coordinates system, only the radial and tangential components are usually considered, and the magnetic field in the vertical direction cannot be directly described. However, in cylindrical coordinates system, the components of the magnetic field in three directions can be described by three variables: radius, angle, and height, allowing for a more comprehensive consideration of the influence of the magnetic field.

Second, as mentioned above, we considered the effect of magnetic fields on bifurcation in three-dimensional cylindrical coordinates. The results show that magnetic field differences can accelerate bifurcation.

Finally, the production of granulation convection is illustrated by Theorem 2 and Fig. 3, where ${R_{c}}$ is the critical Rayleigh number. As is shown in the Fig. 3, when the difference of temperature and magnetic are small enough, the point (R, E) are below the critical curve L and in region I, the gas is in a static state. When they become greater than the curve L, the gas suddenly breaks into regular circulation cells, which is granulation convection. From both the mathematical and physical points of view, the results are valuable to understand the phase transition in fluid dynamics. It would be interesting to extend the current research to the convection problems in porous media, which can be found in our future work.