Optimal Control of Non-linear Volterra Integral Equations with Weakly Singular Kernels Based on Genocchi Polynomials and Collocation Method

Abstract

We consider a problem of finding the best way to control a system, known as an optimal control problem (OCP), governed by non-linear Volterra Integral Equations with Weakly Singular kernels. The equations are based on Genocchi polynomials. Depending on the applicable properties of Genocchi polynomials, the considered OCP is converted to a non-linear programming problem (NLP). This method is speedy and provides a highly accurate solution with great precision using a small number of basis functions. The convergence analysis of the approach is also provided. The accuracy and flawless performance of the proposed technique and verification of the theory are examined with some examples.

1 Introduction

Spectral methods have been widely employed to solve mathematical models that arise in various fields, such as heat conduction, quantum mechanics, and fluid dynamics [1]. These methods use different infinitely differentiable orthogonal functions as trial functions, which lead to various spectral approaches [1, 2]. The high accuracy of these approaches has led to their widespread use in solving many problems in applied mathematics and engineering, such as those encountered in heat conduction, boundary-layer heat transfer, chemical kinetics, and superfluidity [3,4,5,6]. In studying many non-linear problems in these fields, we are often confronted with singular Volterra integral equations that pose significant challenges in finding real solutions. In this essay, we present a numerical approach for solving OCP governed by non-linear Volterra integral equations with weakly singular kernels. The authors in [7] investigate the local convergence of a Sequential quadratic programming method for non-linear optimal control of weakly singular Hammerstein integral equations. They also discussed sufficient conditions for local quadratic convergence of their propounded approach. In [8], an optimal control problem for the non-linear weakly singular Volterra integral equation is considered, and second order sufficient optimality condition has been established for it. No numerical results are listed in this article. A kind of OCP governed by a system of weakly singular variable-order fractional integral equation has been established in [9], and a numerical approach with the Chebyshev cardinal function and its operational matrix of integration has been introduced. This method is also examined through several examples. In [10], numerical approaches for optimal control governed by the integro-differential system with singular kernels are presented. The method is designed to minimizes the difference between the optimal state and target function within a specific time frame. In this article, Genocchi polynomials and their operational matrices have been utilized to dissolve OCP governed by non-linear Volterra integral equations with weakly singular kernels of the following form:

$$\begin{aligned} \mathcal {J}(x,u,t)=\int _{0}^{T}\mathcal {F}(x,u,t)dt, \end{aligned}$$

(1)

subject to

$$\begin{aligned} x(t)=f(t)-\int _{0}^{t}\frac{s^{\nu }}{(t-s)^{\mu }}G(x(s),u(s))ds, \qquad t>0, \end{aligned}$$

(2)

where $f(t)\in L^2[0,T]$ and G are locally Lipchitz continuous, smooth, and a Hammerstein non-linear function; and $\mu$ and $\nu$ are real positive numbers. There are many multiple applications of OCP governed by non-linear Volterra integral equations with weakly singular Kernels, in various areas, such as mathematical economy, chemistry, and physics, like the scattering of waves and particles, heat conduction, semiconductors, population dynamics, and fluid flow [11, 12].

The article is formatted in the following way: This article presents some necessary basic definitions of Genocchi polynomials in Sect. 2. Section 3 demonstrates a numerical suggested technique based on Genocchi polynomials. This article approximates the error analysis of our proposed method in Sect. 4. Section 5 examines some examples to demonstrate the performance and precision of the proposed scheme. Section 6 provides the conclusion of the study.

2 Properties of the Genocchi Polynomials

Genocchi polynomials and numbers have been widely used in various branches of applied sciences, such as complex analytic number theory, homotopy theory, differential topology, and quantum groups [13, 15]. In terms of approximating unknown functions, Genocchi polynomials can be used to construct a linearly independent set of functions that can be used as a basis for approximating other functions. This is useful because it allows us to approximate a wide range of functions using a relatively small number of basis functions because of orthogonality property.

In addition, Genocchi polynomials can be used for numerical integration and function approximation [14]. The Genocchi polynomials $G_n(x)$ and numbers $G_n$ are usually expressed utilizing the exponential generating functions $\mathcal {Q}(t,x)$ and $\mathcal {Q}(t)$, respectively, as follows [13, 15]:

$$\begin{aligned} \mathcal {Q}(t)= & {} \frac{2t}{e^t+1}=\sum _{n=0}^{\infty }G_n\frac{t^n}{n!},(|t|<{\pi }) \end{aligned}$$

(3)

$$\begin{aligned} \mathcal {Q}(t,x)= & {} \frac{2t}{e^t+1}=\sum _{n=0}^{\infty }G_n(x)\frac{t^n}{n!},\ \ \ \ (|t|<{\pi }). \end{aligned}$$

(4)

$G_n(x)$ is the Genocchi polynomial of order n, and is defined as follows:

$$\begin{aligned} G_n(x)=\sum _{k=0}^{n}\displaystyle {n\atopwithdelims ()k}{G}_{n-k}x^k, \end{aligned}$$

(5)

where $G_{n-k}$ is the Genocchi number, which can be calculated from

$$\begin{aligned} G_n=2\left( 1-2^n\right) B_n, \end{aligned}$$

(6)

$B_n$ is Bernoulli numbers. For more awareness about the Genocchi polynomials, you can refer to references [13, 15,16,17]. Suppose that f(t) is an arbitrary function belonging to $L^2[0,1]$. We can approximate it as follows:

$$\begin{aligned} f(t)\approx \sum _{i=1}^{N}c_iG_i(t)=C^TG(t)=C^TG\mathcal {X}_t, \end{aligned}$$

(7)

in which $C=[c_1,c_2,\ldots ,c_N]^T$ is unknown vectors; $\mathcal {X}_t=[1,t,t^2,\ldots ,t^N]^T$ and $G(t)=[G_1(t),G_2(t),\cdots ,G_N(t)]$.

3 Implementation of Genocchi Polynomials Collocation Method

So far, various methods have been given to solve optimal control problems with different constraints. Some of these methods obtain necessary optimal conditions by using Pontryagin’s maximum principle [18, 19]. Applying the collocation method based on Genocchi Polynomials involves the discretization of both the cost function (1) and the controlled integral equation with weakly singular kernels (2). Firstly, we implement a spectral approach based on the Genocchi polynomials to solve equation (2). We compute the following integral for $m=0,1,\ldots$ to apply the propounded approach for approximating the system dynamics in (2)

$$\begin{aligned} \int _{0}^{t}\frac{s^m}{(t-s)^{\mu }}ds=\frac{\Gamma (1-\mu ) \Gamma (m+1)}{\Gamma (m-\mu +2)}s^{m-\mu +1}. \end{aligned}$$

(8)

We assume

$$\begin{aligned} z(s)=g(x(s),u(s)). \end{aligned}$$

(9)

According to relation (2), we have

$$\begin{aligned} z(t)=g\left( x(t),u(t)\right) =g\left( f(t)-\int _{0}^{t} \frac{s^{\nu }}{(t-s)^{\mu }}g(x(s),u(s))ds,u(t)\right) . \end{aligned}$$

(10)

We approximate z(t) and u(t) in Eq. (10) as follows:

$$\begin{aligned} {C}^TG(t)=g\left( f(t)-\int _{0}^{t}\frac{s^{\nu }}{(t-s)^{\mu }} C^TG\mathcal {X}_sds,U^TG(t)\right) . \end{aligned}$$

(11)

So, we obtain

$$\begin{aligned} C^TG(t)=g\left( f(t)-C^TG\int _{0}^{t} \frac{s^{\nu }}{(t-s)^{\mu }}\mathcal {X}_sds,U^TG(t)\right) . \end{aligned}$$

(12)

We write the integral part of (12) in matrix form as follows:

$$\begin{aligned} \int _{0}^{t}\frac{s^\nu }{(t-s)^{\mu }}\mathcal {X}_sds=\left[ \begin{array}{ccccc} \int _{0}^{t}\frac{s^\nu }{(t-s)^{\mu }}ds,&\int _{0}^{t}\frac{s^{\nu +1}}{(t-s)^{{\mu }}}ds,&\cdots ,&\int _{0}^{t}\frac{s^{\nu +N}}{(t-s)^{{\mu }}}ds \end{array} \right] ^T, \end{aligned}$$

(13)

in which $X_s=[1,s,s^2,\ldots ,s^N].$ From (8), we obtain

$$\begin{aligned} \int _{0}^{t}\frac{s^{\nu +m}}{(t-s)^{\mu }}dt=\frac{\Gamma (1-\mu ) \Gamma (m+1)}{\Gamma (m-\mu +1)}t^{m-\mu +1}.\ \ \ m=0,1,2,\cdots . \end{aligned}$$

(14)

By utilizing (14), (13) is converted to

$$\begin{aligned} \int _{0}^{t}\frac{s^\nu }{(t-s)^{\mu }}\mathcal {X}_sds=\left[ \begin{array}{cccc} \frac{\Gamma (1-\mu )\Gamma (\nu +1)}{\Gamma (\nu -\mu +2)}t^{\nu -\mu +1},&\frac{\Gamma (1-\mu )\Gamma (\nu +2)}{\Gamma (\nu -\mu +3)}t^{\nu -\mu +2},&\ldots ,&\frac{\Gamma (1-\mu )\Gamma (\mu +\nu +1)}{\Gamma (\nu +n-\mu +2)}t^{\nu +m-\mu +1} \end{array} \right] ^T. \end{aligned}$$

(15)

By considering $\kappa _{m,m}=\frac{\Gamma (1-\mu )\Gamma (\mu +\nu +1)}{\Gamma (\nu +{m}-\mu +2)}$, Equation (15) can be converted to matrix form as follows

$$\begin{aligned} \int _{0}^{t}\frac{s^{\nu +m}}{(t-s)^{\mu }}\mathcal {X}_sdt=\underbrace{ \left[ \begin{array}{cccccc} \kappa _{0,0} &{} 0 &{} 0 &{} \ldots &{} 0 &{} \ldots \\ 0 &{} \kappa _{1,1} &{} 0 &{} 0 &{} 0 &{} \ldots \\ 0 &{} 0 &{} \kappa _{2,2} &{} 0 &{} 0 &{} \ldots \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \\ 0 &{} 0 &{} 0 &{} \ldots &{} \kappa _{m,m} &{} \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} &{}\ddots \end{array} \right] }_{\psi }\underbrace{\left[ \begin{array}{c} t^{\mu -\nu +1} \\ t^{\mu -\nu +2} \\ \vdots \\ t^{\mu +m-\nu +1}\\ \vdots \end{array} \right] }_{\phi }=\psi \phi . \end{aligned}$$

(16)

$\psi$ is an infinite diagonal matrix, and $\phi$ is an infinite vector. By approximating each element of vector $\phi$ by Genocchi polynomials, we obtain

$$\begin{aligned} t^{\alpha +m-\nu +1}=\sum _{i=1}^{\infty }p_{m,i}G_i(t)=P_m G\mathcal {X}_t,P_m=\left[ p_{m,i},p_{m,i},\ldots \right] ,m=0,1,\ldots , \end{aligned}$$

(17)

Then, we have

$$\begin{aligned} \phi =\left[ {P_1}G\mathcal {X}_t,{P_2}G\mathcal {X}_t,\ldots ,{P_m}G\mathcal {X}_t\right] ^T=\gamma G\mathcal {X}_t, \gamma =\left[ P_1,P_2,\ldots ,P_m,\ldots \right] ^T. \end{aligned}$$

(18)

By substituting (18) in (16), we will have Eq. (12) as follows:

$$\begin{aligned} C^TG(t)=g\left( f(t)-C^TG\psi \gamma G\mathcal {X}_t,U^TG(t)\right) .\ \ 0\le t\le 1. \end{aligned}$$

(19)

By utilizing N nodal points of the Newton–Cotes rule $t_s=\frac{2s-1}{2N}, s=1,2,\ldots , N$, we collocate (19) as follows

$$\begin{aligned} C^TG(t_s)=g\left( f(t_s)-C^TG\psi \gamma G\mathcal {X}_{t_s},U^TG\mathcal {X}_{t_s} \right) . \end{aligned}$$

(20)

For approximating the cost function given in (2), the Gauss Legendre (GL) quadrature has been applied after the appropriate interval transformation.

$$\begin{aligned}{} & {} \int _{0}^{T}\mathcal {F}(x,u,t)dt=\frac{T}{2}\int _{-1}^{1}\mathcal {F} \left( x(\frac{T(\tau +1)}{2}),u(\frac{T(\tau +1)}{2}),\frac{T(\tau +1)}{2}\right) d\tau , \end{aligned}$$

(21)

$$\begin{aligned}{} & {} \approx \sum _{j=1}^{N}w_{j}^{'}\mathcal {F}\left( x\left( \tau _j^{'}\right) ,u\left( \tau _j^{'}\right) ,\tau _j^{'}\right) , \end{aligned}$$

(22)

where $w_{j}^{'}=\frac{T}{2}w_j$ and $\tau _j^{'}=\frac{T(\tau _j+1)}{2}$. $\tau _j$’s are the GL nodes, zeros of Legendre polynomial $L_N(t)$ in $[-1, 1]$, and $w_j$’s are the corresponding weights. The quadrature weights, $w_j$, can be obtained by the following relation [20]:

$$\begin{aligned} w_j=\frac{2}{(1-\tau _{j} ^{2})\left[ L_{N}^{'}\left( {\tau }_j\right) \right] ^2}. \end{aligned}$$

(23)

By substituting $u(t)=U^TG(t)$ and $x(t)=f(t)-C^TG\psi \gamma G\mathcal { X}_{t}$ in (22), we have

$$\begin{aligned} \bar{\mathcal {J}}(C,U,t)=\sum _{j=1}^{N}w_{j}^{'}\mathcal {F}\left( f\left( \tau _{j}^{'}\right) -C^T\psi \gamma G \mathcal {X}_s\tau _{j}^{'},U^TG\left( \tau _{j}^{'}\right) ,\tau _{j}^{'}\right) . \end{aligned}$$

(24)

Finally, OCP given in (1) and (2), is approximated and converted to the following NLP

$$\begin{aligned} \min \bar{\mathcal {J}}(C,U,t) \end{aligned}$$

(25)

subject to

$$\begin{aligned} C^TG(t_s)=g\left( f(t_s)-C^TG\psi \gamma G\mathcal { X}_{t_s},U^TG(t_s)\right) , \ \ s=1,2,\ldots ,N. \end{aligned}$$

(26)

After calculating unknown vectors C and U by solving the resulted NLP given in (25) and (26), we use the following Equations to obtain x(t) and u(t)

$$\begin{aligned} x(t)\approx \hat{x}_N(t)=f(t)-C^TG\psi \gamma G\mathcal {X}_{t}, \ \ \ u(t)\approx \hat{u}_N(t)=U^TG(t). \end{aligned}$$

(27)

4 Error Analysis

The theory of approximation is instrumental in solving various integral and differential equations. Using the following theorem, we can apply the proposed approach to calculate an arbitrary function approximation.

Theorem 1

Let $\mathcal {P}=span\{G_1(t),G_2(t),\ldots ,G_N(t)\}\subset L^{2}[0,1]$. It is obvious that $\mathcal {P}$ is a subspace of the $L^2[0,1]$ whose dimension is finite, and so, f(t), as an arbitrary function in $L^2[0,1]$, has a unique best approximation in $\mathcal {P}$, is named for example. $f^*(t)$, such that

$$\begin{aligned} \left| \left| f(t)-f^*(t)\right| \right| _2\le \left| \left| f(t)-g(t)\right| \right| _2:\forall g(t)\in \mathcal {P}. \end{aligned}$$

(28)

that unique coefficients $c_n$, for $0\le n\le N$ can be used to express any arbitrary function f(x) in terms of the Genocchi polynomials

$$\begin{aligned} f(t)\approx f^*(t)=\sum _{n=1}^{N}c_{n}G_n(t)=C^TG(t), \end{aligned}$$

(29)

where C consisting of the unique coefficient is called the Genocchi coefficient matrix C is given by the following:

$$\begin{aligned} C^T=\mathcal {L}^T T^{{(0,1)}^{-1}}, \end{aligned}$$

(30)

where $L=\{\int _{0}^{1}f(t){G}_{m}(t)dt\}, m=0,1,\ldots , N$ is a $N-dimensional$ matrix and $\mathcal {T}^{(0,1)}=\left[ \int _{0}^{1}G_n(t)G_m(t)dt\right] _{N\times N}$ is a square matrix. The method of calculating $\mathcal {F}$ and $\mathcal {T}^{(0,1)}$ is explained in [17].

Theorem 2

Let $f(t)\in C^{n+1}[0,1]$ and $\mathcal {P}=span\{G_1(t),G_2(t),\ldots ,G_N(t)\}$, if $C^TG(t)$ is the best approximation of f(t) out of the set of polynomials $\mathcal {P}$ then [13]

$$\begin{aligned} \left| \left| f(t)-C^TG(t)\right| \right| \le \frac{h^{\frac{2n+3}{2}}\mathcal {A}}{(n+1)!\sqrt{2n+3}},\ \ \ t\in \left[ t_i,t_{i+1}\right] \subset [0,1],\ \ \ i=1,2,\ldots ,n. \end{aligned}$$

(31)

where

$$\begin{aligned} \mathcal {R}=\underset{t\in [0,1]}{max}\left| f^{(n+1)}(t)\right| . \end{aligned}$$

(32)

According to Theorem 2, The estimation $C^TG(t)$ converges to f(t) as n goes to infinity.

The functions x and u are called admissible if, by putting them in (2), they satisfy in this equation. The set of admissible pairs is described as follows:

$$\begin{aligned} \mathcal {B}=\left\{ (x,u)|x(t)=f(t)-\int _{0}^{t}\frac{s^\nu }{(t-s)^{\mu }}G(x(s),u(s))ds,\right\} \end{aligned}$$

(33)

The errors of $\hat{x}$ and $\hat{u}$ described in (27) are proven to be bounded above by

$$\begin{aligned} ||x(t)-\hat{x}(t)||_2= & {} \int _{0}^{1}\left| x(t)-\hat{x}(t)\right| ^2dt \nonumber \\= & {} \int _{0}^{1}\left| f(t)-\int _{0}^{t}\left( \frac{s^{\nu }}{(t-s)^{\mu }} G(x(s),u(s))ds\right) -f(t)+\right. \end{aligned}$$

(34)

$$\begin{aligned}{} & {} \int _{0}^{t}\left| \left( \frac{s^{\nu }}{(t-s)^{\mu }}G(\hat{x}(s), \hat{u}(s))ds\right) \right| ^2dt\nonumber \\= & {} \int _{0}^{1}\left| \int _{0}^{t}\frac{s^{\nu }}{(t-s)^{\mu }} \left( G(x(s),u(s))-G(\hat{x}(s),\hat{u}(s))\right) ds\right| ^2dt. \end{aligned}$$

(35)

On the other hand, G is locally Lipschitz concerning $(x(t),u(t))\in \mathcal {B}$; therefore, there is a constant $Q_1>0$ such that

$$\begin{aligned} |G(x(s),u(s))-G(\hat{x}(s),\hat{u}(s))|\le Q_1\left( |x(s)-\hat{x}(s)|+|u(s)-\hat{x}(s)|\right) . \end{aligned}$$

(36)

By utilizing equations (36) and (35), we obtain

$$\begin{aligned} ||x(t)-\hat{x}(t)||_{2}^{2}\le & {} \int _{0}^{1}\left( \int _{0}^{t}\frac{s^{\nu }}{(t-s)^{\mu }}Q_1(|x(s) -\hat{x}(s)|+|u(s)-\hat{u}(s))|ds\right) ^2dt.\nonumber \\= & {} \int _{0}^{1}\left( \int _{0}^{t}\frac{s^{\nu }}{(t-s)^{\mu }}\left( Q_1|x(s)- \sum _{n=1}^{N}c_nG_n(s)|+Q_1|u(s)-\sum _{n=1}^{N}u_nG_n(s)|\right) ds\right) ^2dt\nonumber \\= & {} \int _{0}^{1}\left( \int _{0}^{t}\frac{s^{\nu }}{(t-s)^{\mu }}\left( Q_1| \sum _{n=N+1}^{\infty }c_nG_n(s)|+Q_1|\sum _{n=N+1}^{\infty }u_nG_n(s)|\right) ds\right) ^2dt\nonumber \\\le & {} \int _{0}^{1}\left( \int _{0}^{t}\frac{s^{\nu }}{(t-s)^{\mu }}(Q_1\sum _{n=N+1}^{\infty }|c_n||G_n(s)|\right. \nonumber \\{} & {} \left. +Q_1\sum _{n=N+1}^{\infty }|u_n||G_n(s)|ds\right) ^2dt \end{aligned}$$

(37)

By substituting (5) in (37), we get

$$\begin{aligned}\le & {} \int _{0}^{1}\left( \int _{0}^{t}\frac{s^{\nu }}{(t-s)^{\mu }}(Q_1\sum _{n=N+1}^{\infty }|c_n||\sum _{k=0}^{n}\displaystyle {n\atopwithdelims ()k}{G}_{n-k}s^k|+Q_1\sum _{n=N+1}^{\infty }|u_n||\sum _{k=0}^{n}\displaystyle {n\atopwithdelims ()k}{G}_{n-k}s^k|)ds\right) ^2dt\nonumber \\ \le \int _{0}^{1}\left( \int _{0}^{t}\frac{s^{\nu }}{(t-s)^{\mu }}\left( Q_1\sum _{n=N+1}^{\infty }|c_n| \sum _{k=0}^{n}\displaystyle {n\atopwithdelims ()k}|{G}_{n-k}|s^k+Q_1\sum _{n=N+1}^{\infty }|u_n|\sum _{k=0}^{n} \displaystyle {n\atopwithdelims ()k}|{G}_{n-k}|s^k\right) ds\right) ^2dt\nonumber \\\le & {} \int _{0}^{1} \left( Q_1\sum _{k=0}^{n}\sum _{n=N+1}^{\infty }|c_n| \displaystyle {n\atopwithdelims ()k}|{G}_{n-k}|\int _{0}^{t}\frac{s^{\nu +k}}{(t-s)^{\mu }}ds +Q_1\sum _{k=0}^{n}\sum _{n=N+1}^{\infty }|u_n|\displaystyle {n\atopwithdelims ()k} |{G}_{n-k}|\int _{0}^{t}\frac{s^{\nu +k}}{(t-s)^{\mu }}ds\right) ^2dt \end{aligned}$$

(38)

we define $\eta (t,\nu ,\mu )$ as follows

$$\begin{aligned} \eta (t,\nu ,\mu )=\int _{0}^{t}\frac{s^{\nu }}{(t-s)^{\mu }}ds= B(1-\mu ,1+\nu )t^{1-\mu +\nu }. \end{aligned}$$

(39)

$B(\mu ,\nu )$ is a beta function, which is defined as follows

$$\begin{aligned} B(\mu ,\nu )=\int _{0}^{1}\tau ^{\mu -1}(1-\tau )^{\nu -1}d\tau . \end{aligned}$$

(40)

By utilizing inequality (38) and (40), we get

$$\begin{aligned} ||x(t)-\hat{x}(t)||_{2}^{2}\le \int _{0}^{1} \left( Q_1B(1-\mu ,1+\nu +k)t^{1-\mu +\nu +k}\sum _{k=0}^{n}\sum _{n=N+1}^{\infty }(|c_n|+|u_n|) \displaystyle {n\atopwithdelims ()k}|{G}_{n-k}|\right) ^2dt, \end{aligned}$$

(41)

and

$$\begin{aligned} ||x(t)-\hat{x}(t)||_{2}\le \sqrt{\int _{0}^{1} \left( Q_1B(1-\mu ,1+\nu +k)\sum _{k=0}^{n}\sum _{n=N+1}^{\infty }(|c_n|+|u_n|) \displaystyle {n\atopwithdelims ()k}|{G}_{n-k}|\right)^2dt}. \end{aligned}$$

(42)

We can establish an upper bound for $||u(t)-\hat{u}(t)||$ from Theorem 2.

Let $\hat{x}_N$ and $\hat{u}_N$ are defined as in equation (27), then we set

$$\begin{aligned} \mathcal {A}_N=\{(\hat{x}_N,\hat{u}_N)|C^TG(t)=g\left( f(t)-C^T\mathcal {G}\psi \gamma GX_t,U^TG(t)\right) ,\ \ 0\le t\le 1\}. \end{aligned}$$

(43)

Theorem 3

Let $\bar{\mathcal {J}}_{N}^{*}=\inf _{\mathcal {A}_N}J$ and $J^*=\inf _{\mathcal {B}}J$ and $J^*$, also $J^*$ is finite and unique, then the following inequality holds.

$$\begin{aligned} \bar{\mathcal {J}_{1}}^{*}\ge \bar{\mathcal {J}_{2}}^{*}\ge \cdots \bar{\mathcal {J}_{r}}^{*}\ge \cdots \ge \mathcal {J}^{*} =\inf _{\mathcal {B}}\mathcal {J}(t,x,u). \end{aligned}$$

(44)

Proof: It is evident that the relation

$$\begin{aligned} \mathcal {A}_1\subset \mathcal {A}_2\subset \mathcal {A}_3 \subset \cdots \subset \mathcal {A}_{N}\subset \mathcal {B}. \end{aligned}$$

(45)

is satisfied, so $\mathcal {J}_{i}^{*}$ is a non-increasing sequence that is bounded and convergent to $\mathcal {J}^{*}$

5 Illustrative Examples

To examine the efficiency of the propounded collocation approaches, some examples are given in this section. All computations utilize Mathematica 10.4 on a PC with AMD A6-4400 M APU with Radeon(tm) HD Graphics, CPU @ 2.70 GHz and 4.0 GB of RAM. To verify the error of the propounded approach, the following notations are taken into consideration:

$$\begin{aligned} e_{u^*}=\left| \hat{u}^*-u^*\right| ,\ \ \ \ \ \ \ e_{x^*}=\left| \hat{x}^*-x^*\right| . \end{aligned}$$

(46)

where $u^*$ and $x^*$ are exact optimal control and state solutions in OCP described in (1) and (2) and $\hat{u}^*$ and $\hat{x}^*$ are approximate optimal control and state solutions in the resulted NLP given in (25) and (26). The absolute errors of optimal objective functional $\mathcal {J}^*$ are also defined as follows:

$$\begin{aligned} E_{\mathcal {J}^*}=\left| \mathcal {J}^*(x,u,t)-\bar{\mathcal {J}}^*(C,U,t)\right| . \end{aligned}$$

(47)

Example 1

Consider the following OCP governed by non-linear Volterra integral equation

$$\begin{aligned} \min \int \left( x(t)-t^5\right) ^2+\left( u(t)-Cos(t)\right) ^2dt, \end{aligned}$$

(48)

subject to

$$\begin{aligned} x(t)=f(t)-\int _{0}^{t}\frac{s^{1.5}}{(t-s)^{0.5}}x(s)u(s)ds, \end{aligned}$$

(49)

where

$$\begin{aligned} f(t)=t^5+ 0.6581 t^7.\textit{HypergeometricPFQ}[\{4.25,3.75\},\{4.5, 4., 1/2\}, -(t^2/4)]. \end{aligned}$$

(50)

$HypergeometricPFQ[\{a_1,\cdots ,a_p\},\{b_1,\ldots ,b_q\},z]$ is mathematical Notation of traditional Notation ${^{\scriptscriptstyle {\mathrm {}}}_{p}\mathop {{\mathop {{\text {F}}}\nolimits ^{}_{q}}}\nolimits }(a_1,\ldots ,a_p,b_1,\ldots ,b_q;z)= \sum _{k=0}^{\infty }\frac{\prod \nolimits _{j=1}^{p}(a_j)_k z^k}{\prod \limits _{j=1}^{q}(b_j)_kk!}$, where $q\le {p}$ or $q=p-1$ and $|z|<1$ or $q=p-1$ and $|z|=1$ and $Re[\sum _{j=1}^{p-1}b_j-\sum _{j=1}^{p}a_j]>0$. The exact solution of this OCP is $x^*(t)=t^5$ and $u^*(t)=Cos(t)$. The plots of approximate state and control functions for $N=5$ are given in Figs. 1 and 2. The exact and approximate solutions overlap with each other, which demonstrates the exactness and correctness of the propounded method. The exact solutions are shown with continuous lines, and approximate solutions are shown with dots. The optimal value of objective function for different values of N is shown in Table 1. The absolute errors of control and state functions for various values of points in interval [0, 1] are given in Table 2. The graphs of absolute errors are given in Figs. 3 and 4.

Fig. 1

The exact and approximate state function with $N=5$ for example 1

Fig. 2

The exact and approximate control function with $N=5$ for example 1

The absolute error of control function with $N=4$ for example 1

Fig. 3

The absolute error of control function with $N=4$ for example 1

Fig. 4

The absolute error of state function with $N=4$ for example 1

Table 1 The value of $J^{*}$, for example 1

Table 2 Absolute errors of state and control functions for $m=5$ in example 1

Example 2

Consider

$$\begin{aligned} \min \int _{0}^{1}\left( x(t)-t\sin (t)\right) ^2+\left( u(t)-\cos (t)\right) ^2dt{,} \end{aligned}$$

(51)

with the dynamical system

$$\begin{aligned} x(t)=f(t)-\int _{0}^{t}\frac{s^{1.5}}{(t-s)^{0.5}}(x(s)+u(s))ds{,} \end{aligned}$$

(52)

in which

$$\begin{aligned} f(t)= 0.8590 t^4.HypergeometricPFQ[{2.75, 2.25}, {3., 2.5, 1.5}, -t^2] + t \sin (t). \end{aligned}$$

(53)

where $x^*(t)=t\sin (t)$ and $u^*(t)=cos(t)$.

Fig. 5

The exact and approximate state function with $N=4$ for example 2

Fig. 6

The exact and approximate control function with $N=4$ for example 2

Fig. 7

The absolute error of control function with $N=4$ for example 2

Fig. 8

The absolute error of state function with $N=4$ for example 2

Table 3 The value of $J^{*}$ for example 2

Table 4 Absolute errors of state and control functions for $N=4$ in example 2

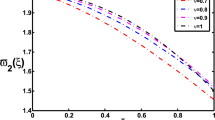
Figures 5 and 6 show the exact and approximate optimal control and state for $N = 4$. It is obvious that the exact and approximate solutions completely overlap. The exact and approximate solutions are shown respectively with, continuous orange line and black dots. In Table 3, the optimal value of $J^*$ is given for $N=2,3,4.$ Absolute errors of optimal state and control solutions in different value of t is also demonstrated in Table 4. The graphs of absolute errors are given in Figs. 7 and 8.

6 Conclusions

The main objective of this paper is to present an effective method that uses the collocation method based on Genocchi polynomials to solve OCP governed by non-linear Volterra integral equations with weakly singular kernels. The propounded approach efficiently and simply reduces the considered system to an NLP. The generated optimization problem is solved by NMinimize function in Mathematica software. The proposed method has been analyzed for convergence. Some illustrative examples have been provided to demonstrate the scheme’s easy applicability and good accuracy. It should be noted that the method can be used in the same way to solve OCP governed by integral equations which have kernels containing both points, endpoint and an Abel-type singularity, with exact solutions being typically non-smooth that have many engineering applications. We hope to refer to problems of this type in a later study. For subsequent research, we can utilize other polynomials like Legendre, Chebyshev, Bernoulli, etc. Due to substantial applications of the first kind of Volterra integral equations with singular kernels in load leveling problems and power engineering systems, the propounded approach can also be utilized for solving OCP governed with these equations for subsequent works.