1 Introduction

In a wide variety of technical applications, the non-Newtonian fluid flow is essential and plays a key role. Non-Newtonian fluids (NNFs) behave in a complicated and nonlinear way as opposed to Newtonian fluids, which show a linear relationship between shear stress and shear rate. Their flow qualities can be precisely controlled because of this special feature, which makes them important in a variety of sectors. NNFs are widely used in the food and beverage industry to produce goods with certain textures and consistencies, such as sauces, dressings, and dairy products. These liquids are also used in the pharmaceutical and cosmetics sectors to create creams, lotions, and gels. NNFs also have a significant impact on the oil and gas industry, where they improve oil recovery by altering fluid properties during the drilling and production processes. It has become clear that NNF flow is a crucial area of research with wide-ranging practical ramifications. The study and understanding of NNF flow have opened the way for creative solutions and breakthroughs in a variety of sectors [1]. Stress causes different reactions in NNFs, with some becoming more solid-like and others becoming more fluid-like. Depending on the intensity and duration of the applied stress, these fluids’ characteristics can alter. Distinct categories exist for NNFs based on their unique properties, and the increasing number of these fluids has piqued the interest of researchers. Various types of NNF models have been examined, such as the power-law model [2], viscoelastic model [3], Carreau model [4], Maxwell model [5], Williamson model [6], micropolar model [7], Powell-Eyring model [8], and Sisko model [9].

A well-known class of NNF models that has attracted great interest in both academic and practical contexts is the Casson fluid model (CFM). It can be recognized by its distinctive behavior, which is the need for a minimum yield stress to start flow. The CFM behaves like a solid when the stress is below this limit; but, when the stress surpasses the yield stress, it changes into a fluid-like behavior. The Casson model is particularly helpful in explaining materials having semi-solid or gel-like characteristics because of its yield stress property. The CFM has been used in many different contexts, including biomedical engineering, the food industry, and the petroleum industry. In these contexts, it is used to accurately represent the flow behavior of complicated fluids including blood, emulsions, and drilling muds. The CFM is essential for understanding and predicting the flow behavior of NNFs in real-world applications because it can take into account both shear-thinning and yield stress properties. When the applied shear stress is less than the yield stress, the CFM model behaves similarly to a solid. Researchers have shown a great deal of interest in this unusual quality, particularly given the variety of uses for CFMs. China clay [10], pigments, coal in water suspensions, synthetic lubricants, and the manufacture of biological fluids are a few of these applications. The adaptability of CFMs in various sectors emphasizes their practical significance and encourages further research and comprehension of their rheological characteristics. The literature [11, 12] demonstrates that many intriguing works have been published investigating the flow behavior of the CFM. These investigations into several facets of Casson fluid flow have illuminated its properties and offered insightful information regarding its uses and behavior in diverse contexts.

Due to their wide-ranging use in multiple applications in fluid mechanics, viscoelasticity, biology, physics, and engineering, ODEs and PDEs have been thoroughly investigated. Due to the prominence of ODEs, and PDEs in these domains, there has been a significant amount of study done to better understand their characteristics, solve them quickly, and understand their consequences for different phenomena and systems. As a result, the solutions of ODEs of physical relevance have received a lot of attention [13]. The spectral collocation method (SCM) based on the Chebyshev polynomials of the sixth-kind (CP\(_{6}s\)) [14] was used to solve the nonlinear ODEs that regulate the physical problem quantitatively. This study is unique in that it is the first of its type to solve the given model numerically by using the proposed numerical method in a pioneering manner.

Following prior research, numerous researchers have effectively implemented various numerical approaches in this particular field. One of these numerical approaches is the spectral collocation method, which serves as a general approximate analytical technique to obtain the approximate solution for differential equations. The SCM offers several advantages when dealing with this type of problems, as the Chebyshev coefficients for the solution can be readily obtained through the utilization of any available numerical program. Consequently, this method outperforms others in terms of speed. Chebyshev polynomials, well-known orthogonal polynomials defined on the interval \([-1,1]\), are frequently employed due to their favorable properties in function approximation. Additionally, this method is characterized by high accuracy, making it a reliable numerical technique. By guaranteeing accurate computations and reliable outcomes, the method ensures rapid convergence rates and user-friendly implementation across both finite and infinite domains for diverse problem scenarios [15, 16]. It demonstrates fast convergence, enabling accurate solutions with minimal terms or iterations, thereby saving computational time and resources. Additionally, its numerical stability reduces the likelihood of errors, even when tackling complex or challenging problems. Moreover, the technique’s versatility allows for its application in differential equations, and optimization problems, making it valuable across various fields. Atta et al. [17] employed a collocation technique to solve fractional differential equations with multiple terms. Similarly, in [18], the authors utilized a collocation approach to tackle specific non-linear fractional integro-differential equations. The tau method, on the other hand, has been employed for solving a variety of differential equations. For example, Abd-Elhameed et al. [19] applied the tau method to address the non-linear Fisher equation, while Youssri [20] utilized the tau method to solve the fractional Bagley-Torvik equation.

The study of ordinary and partial fractional differential equations has received significant attention due to their widespread occurrence in diverse fields such as fluid mechanics, visco-elasticity, biology, physics, and engineering. Consequently, there has been considerable focus on finding solutions for these physically relevant fractional differential equations (FDEs). Since most FDEs lack exact solutions, approximate and numerical techniques [21,22,23,24,25,26] are necessary for their analysis and resolution.

Definition 1

The Caputo fractional derivative \(D^{\nu }\) of order \(\nu \) of a function \(\varphi (x)\) is defined in the form:

$$\begin{aligned} D^{\nu }\varphi (x) = \frac{1}{\Gamma (1-\nu )}\,\int _{0}^{x}\frac{\varphi ^{'}(\tau )}{(x-\tau )^{\nu }}d\tau , \quad x>0,\quad 0<\nu \le 1. \end{aligned}$$

Caputo fractional derivative operator is a linear operation:

$$\begin{aligned} D^{\nu }\,(c_{1} \,f(x)+c_{2}\, g(x))=c_{1}\, D^{\nu }\,f(x)+c_{2} \,D^{\nu }\,g(x), \end{aligned}$$

where \(c_{1}\) and \(c_{2}\) are constants. For the Caputo’s derivative we have [27]:

$$\begin{aligned} D^{\nu }\,C= & {} 0,\quad \hbox {C is a constant}, \end{aligned}$$
(1)
$$\begin{aligned} D^{\nu }\,x^{n}= & {} \left\{ \begin{array}{ll} 0, &{} \quad \quad \hbox {for}\quad n\in {\mathbb {N}}_{0} \hbox { and }n<\lceil \nu \rceil ; \\ \frac{\Gamma (n+1)}{\Gamma (n+1-\nu )}\,x^{n-\nu }, &{} \quad \quad \hbox {for}\quad n\in {{\mathbb {N}}}_{0} \hbox { and }n\ge \lceil \nu \rceil . \\ \end{array} \right. \end{aligned}$$
(2)

For more details on fractional derivatives definitions and its properties see [28, 29].

The novelty of this research is revealed through a thorough exploration of slip velocity and thermal slip phenomena, which significantly influence the flow characteristics of Casson fluid. It is noteworthy that this study considers the important aspects of viscous dissipation and Ohmic dissipation, thereby contributing to a deeper understanding of the system’s dynamics. However, the innovation extends beyond these findings. The introduction of a new numerical technique (SCM based on Chebyshev approximations of the sixth kind) represents a substantial advancement in the field, as it is the first time such an approach has been employed in similar problems. By enhancing the precision and dependability of the obtained results, this pioneering numerical method becomes a valuable asset for future research endeavors in related domains.

2 Mathematical Formulation

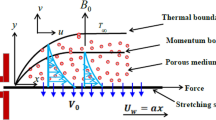
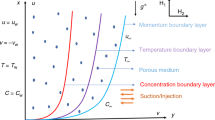
In a two-dimensional steady state, this study investigates the laminar magnetohydrodynamic flow of a non-Newtonian Casson fluid due to a vertically stretched sheet. The effects of thermal radiation, Ohmic dissipation, thermal slip, and viscous dissipation are all taken into account in the study. By incorporating slip velocity, thermal slip, thermal radiation, and Ohmic viscous dissipation into the investigation of Casson fluid flow, researchers seek to enhance their understanding of the fluid’s behavior, heat transfer properties, and energy dissipation mechanisms. This inclusion of crucial factors allows for a more holistic analysis of the system. The acquired knowledge holds significant implications for various disciplines including fluid mechanics, heat transfer, and process engineering, as it facilitates the development of more efficient systems and the optimization of industrial processes. By taking measurements along axes that are orthogonal to the stretched sheet and are inside the plane at \(y=0\), it is possible to see the flow, as shown in the schematic diagram (Fig. 1). The varying thermal conductivity properties are taken into consideration by the energy equation. The sheet is thought to be magnetized by a consistent, transverse magnetic field \(B_{0}\) that is pointed in the positive direction of \(y-\)axis. The sheet’s velocity is calculated as \(U_{w}=ax\) along the \(x-\)axis. The variables u and v are used to represent the velocity components in the x and y directions, respectively. Similarly, the density of the Casson fluid is denoted by the symbol \(\rho \). The following equations for momentum and energy regulate the steady motion of a viscous incompressible fluid taking all of the above into account:

Fig. 1
figure 1

Schematic diagram of the problem

Full size image
$$\begin{aligned}{} & {} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}= \nu \left( 1+\frac{1}{\beta }\right) \frac{\partial ^{2} u}{\partial y^{2}} +\frac{\sigma }{\rho }\left( E_{0} B_{0}-B_{0}^{2} u\right) +g \delta (T-T_{\infty }), \end{aligned}$$
(4)
$$\begin{aligned}{} & {} u \frac{\partial T}{\partial x}+v \frac{\partial T}{\partial y}=\frac{1}{\rho c_{p}}\frac{\partial }{\partial y} \left( \kappa \frac{\partial T}{\partial y}\right) -\frac{1}{\rho c_{p}}\frac{\partial q_{r}}{\partial y}\nonumber \\{} & {} \quad +\frac{\sigma }{\rho c_{p}}\left( u B_{0}-E_{0}\right) ^{2} +\frac{\mu }{\rho c_{p}} \left( 1+\frac{1}{\beta }\right) \left( \frac{\partial u}{\partial y}\right) ^{2}, \end{aligned}$$
(5)

where \(\beta \) is the Casson parameter, \(E_{0}\) is the electric field intensity, \(T_{\infty }\) is the ambient fluid temperature, \(\mu \) is the fluid viscosity, \(\kappa \) is the thermal conductivity, \(\sigma \) is the electrical conductivity of the fluid, \(B_{0}\) is the magnetic field strength, T is the temperature of the fluid, \(c_{p}\) is the specific heat, \(\nu \) is the kinematic viscosity, g is the gravitational acceleration, \(\delta \) is the coefficient of thermal expansion and \(q_{r}\) is the radiative heat flux. The following expression is used to calculate the radiative heat flow \(q_{r}\) within the Roseland approximation [30]:

$$\begin{aligned} q_{r}=-\frac{4\sigma ^{*}}{3k^{*}}\frac{\partial T^{4}}{\partial y}. \end{aligned}$$

In this case, \(k^{*}\) stands for the mean absorption constant, and \(\sigma ^{*}\) is the Stefan–Boltzmann constant. The Taylor series expansion of the equation, ignoring higher-order elements, results in the following formula under the assumption that the temperature differential within the flow is minimal.

$$\begin{aligned} T^{4}\cong 4T^{3}_{\infty }T-3T^{4}_{\infty }. \end{aligned}$$

The following are the boundary conditions taken into consideration for this study [31]:

$$\begin{aligned}{} & {} u=U_{w}+\lambda _{1}\left( 1+\frac{1}{\beta }\right) \frac{\partial u}{\partial y}, \quad \quad v=0, \quad \quad T=T_{w}+ \Omega \frac{\partial T}{\partial y}, \quad \quad \text { at }\,\, y=0, \end{aligned}$$
(6)
$$\begin{aligned}{} & {} u\rightarrow 0, \quad \quad T \rightarrow T_{\infty }, \quad \quad \text{ as } \,\,y \rightarrow \infty , \end{aligned}$$
(7)

where \(T_{w}\) is the sheet temperature, \(\lambda _{1}\) is the slip velocity coefficient, and \(\Omega \) is the thermal slip coefficient. The following transformations allow us to arrive at a conclusion that applies to both velocity and temperature and is not dependent on any a particular unit of measurement:

$$\begin{aligned} \eta= & {} \left( \frac{a}{\nu }\right) ^{\frac{1}{2}} y,\quad \quad u=a x f^{\prime }(\eta ), \quad \quad v=-\left( a\nu \right) ^{\frac{1}{2}} f(\eta ), \end{aligned}$$
(8)
$$\begin{aligned} \theta (\eta )= & {} \frac{T-T_{\infty }}{T_{w}-T_{\infty }}, \end{aligned}$$
(9)

where \(f(\eta )\) is the dimensionless stream function, a is a constant, and \(\theta (\eta )\) is the dimensionless temperature. The continuity Eq. (3) is satisfied by Eq. (8). The governing equations can be stated in the following ways when we use the relations (6)–(7):

$$\begin{aligned}{} & {} \left( 1+\frac{1}{\beta }\right) f^{\prime \prime \prime }+f f^{\prime \prime }-f^{\prime 2}+M^{2}\left( E_{1}- f^{\prime }\right) +\Delta \theta =0, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \frac{1}{Pr}\left( (1+R+\varepsilon \theta )\theta ''+\varepsilon \theta '^{2}\right) +M^{2}Ec\left( f^{\prime }-E_{1}\right) ^{2}+f \theta ^{\prime } +Ec\left( 1+\frac{1}{\beta }\right) f''^{2}=0. \end{aligned}$$
(11)

The previously mentioned governing equations can also be represented in their extended structure, taking into consideration the following appropriate boundary constraints, when taking into account the pertinent boundary conditions:

$$\begin{aligned}{} & {} f'(0)=1+\lambda \left( 1+\frac{1}{\beta }\right) f''(0),\quad \quad \quad f(0)=0,\quad \quad \quad \theta (0)=1+\Lambda \theta ^{\prime }(0), \end{aligned}$$
(12)
$$\begin{aligned}{} & {} \theta (\eta )\rightarrow 0,\quad \quad f'(\eta )\rightarrow 0,\quad \quad \hbox {as}\,\,\eta \rightarrow \infty , \end{aligned}$$
(13)

where \(\Delta =\frac{g \delta }{a(T_{w}-T_{\infty })}\) is the mixed convection parameter, \(\lambda =\lambda _{1}\sqrt{\frac{a}{\nu }}\) is the slip velocity parameter, \(E_{1}=\frac{E_{0}}{aB_{0}x}\) is the local electric parameter, \(\Lambda =\Omega \left( \frac{a \rho }{\mu }\right) ^{\frac{1}{2}}\) is the thermal slip parameter, \(M^{2}=\frac{\sigma B_{0}^{2}}{\rho a}\) is the magnetic parameter, \(Pr=\frac{\mu \,c_{p}}{\kappa _{\infty }}\) is the Prandtl number, \(\kappa _{\infty }\) is the ambient thermal conductivity, \(R=\frac{16 \sigma ^{*}T_{\infty }^{3}}{3k^{*}\kappa _{\infty }}\) is the radiation parameter, \(Ec=\frac{U_{w}^{2}}{c_{p}(T_{w}-T_{\infty })}\) is the Eckert number, and \(\varepsilon \) is the thermal conductivity parameter. The skin-friction coefficient (SFC), and local Nusselt number (LNN), which are physical quantities of importance in this study, are defined as follows:

$$\begin{aligned} C_{f}Re_{x}^{\frac{1}{2}}=- \left( 1+\frac{1}{\beta }\right) f''(0), \quad \quad \quad Nu_{x}Re_{x}^{\frac{-1}{2}}=-(1+\varepsilon )\theta '(0), \end{aligned}$$

where \(Re_{x}=\frac{U_{w} x}{\nu }\) is the local Reynolds number.

Furthermore, the study’s main goal is to investigate the numerical solution of the same model that takes fractional-order derivatives (\(2<\alpha \le 3,\,1<\delta \le 2,\,0<\gamma \le 1\)) into account as follows:

$$\begin{aligned}{} & {} \left( 1+\frac{1}{\beta }\right) D^{\alpha }f+f D^{\delta }f-(D^{\gamma }f)^{2}+M^{2}\left( E_{1}- D^{\gamma }f\right) +\Delta \theta =0, \end{aligned}$$
(14)
$$\begin{aligned}{} & {} \frac{1}{Pr}\left( (1+R+\varepsilon \theta )D^{\delta }\theta +\varepsilon (D^{\gamma }\theta )^{2}\right) \nonumber \\{} & {} \quad +M^{2}Ec\left( D^{\gamma }f-E_{1}\right) ^{2} +f D^{\gamma }\theta +Ec\left( 1+\frac{1}{\beta }\right) (D^{\delta }f)^{2}=0, \end{aligned}$$
(15)
$$\begin{aligned}{} & {} f'(0)=1+\lambda \left( 1+\frac{1}{\beta }\right) f''(0),\quad \quad \quad f(0)=0,\quad \quad \quad \theta (0)=1+\Lambda \theta ^{\prime }(0), \end{aligned}$$
(16)
$$\begin{aligned}{} & {} \theta (\eta )\rightarrow 0,\quad \quad f'(\eta )\rightarrow 0,\quad \quad \hbox {as}\,\,\,\,\eta \rightarrow \infty . \end{aligned}$$
(17)

3 Procedure of Solution Using SCM

3.1 Some Properties of the CP\(_{6}\)s and Approximate the Solution

In this subsection, we are going to present some of the main definitions and properties of the shifted Chebyshev polynomials of the sixth-kind (CP\(_{6}\)s) to suit their use in solving the problem presented here for study in the domain \([0,\hbar ]\).

The CP\(_{6}\)s, \(T_{k}(z)\) are orthogonal polynomials on \([-1,1]\) under the following formula [32, 33]:

$$\begin{aligned} \int _{-1}^{1}\,w(z)\,T_{i}(z)\,T_{j}(z)dz=\lambda _{i}\delta _{ij}, \end{aligned}$$

where the weight function \(w(z)=z^{2}\sqrt{1-z^{2}}\), but the factor \(\lambda _{i}\) and the Kronecker delta \(\delta _{ij}\) are defined by:

$$\begin{aligned} \lambda _{i}=\frac{\pi }{2^{2i+3}}\left\{ \begin{array}{ll} 1,\quad &{}i\,\,\, \hbox {even;} \\ \frac{i+3}{i+1},\quad &{} i\,\,\,\hbox {odd.} \end{array} \right. \quad \quad \quad \delta _{ij}=\left\{ \begin{array}{ll} 1, &{}\quad i=j; \\ 0, &{}\quad i\ne j. \end{array} \right. \end{aligned}$$
(18)

The polynomials \(T_{k}(z)\) can be generated by using the following recurrence relation:

$$\begin{aligned} T_{k}(z)=z\,T_{k-1}(z)-\left( \frac{(-1)^{k}(2k+1)+k(k+1)+1}{4k(k+1)}\right) T_{k-2}(z),\,\, T_{0}(z)=1,\,\,T_{1}(z)=z,\,\,\, k=2,3,.... \end{aligned}$$

The shifted CP\(_{6}\)s on \([0,\hbar ]\), \(\hbar >0\) can be defined with the help of the linear transformation \(z=(2/\hbar )\eta -1\) as \({{\mathbb {T}}}_{k}(\eta )=T_{k}((2/\hbar )\eta -1)\) [34]. We can construct these polynomials \(\{{{\mathbb {T}}}_{k}(\eta )\}_{k=0}^{\infty }\) by the following recursive formula:

$$\begin{aligned} {{\mathbb {T}}}_{k}(\eta )=((2/\hbar )\eta -1)\,{{\mathbb {T}}}_{k-1}(\eta )-\left( \frac{(-1)^{k}(2k+1)+k(k+1)+1}{4k(k+1)}\right) {{\mathbb {T}}}_{k-2}(\eta ),\quad \,\,\, k=2,3,.... \end{aligned}$$

where \({{\mathbb {T}}}_{0}(\eta )=1,\,\,{{\mathbb {T}}}_{1}(\eta )=(2/\hbar )\eta -1\). These polynomials hold the following orthogonality relation:

$$\begin{aligned} \int _{0}^{\hbar }(2\eta -\hbar )^{2}\,\sqrt{\hbar \,\eta -\eta ^{2}}\,{{\mathbb {T}}}_{i}(\eta ){{\mathbb {T}}}_{j}(\eta )d\eta =0.25\hbar ^{4}\lambda _{i}\delta _{ij}, \end{aligned}$$

where \(\lambda _{i}\) and \(\delta _{ij}\) are defined in (18). The analytic formula of \({{\mathbb {T}}}_{k}(\eta )\) is given by ([34, 35]):

$$\begin{aligned} {{\mathbb {T}}}_{k}(\eta )=\sum _{i=0}^{k}c_{i,k}\,\eta ^{i}, \end{aligned}$$
(19)

where

$$\begin{aligned} c_{i,k}=\frac{2^{2i-k}}{\hbar ^{i}(2i+1)!}\left\{ \begin{array}{ll} \sum _{r=\lfloor \frac{i+1}{2}\rfloor }^{\lfloor \frac{k}{2}\rfloor }\frac{(-1)^{0.5k+r+i}(2r+i+1)!}{(2r-i)!}, &{}\quad \hbox {if}\,\,\, k\,\,\, \hbox {even},\\ \sum _{r=\lfloor \frac{i}{2}\rfloor }^{\lfloor \frac{k-1}{2}\rfloor }\frac{2(-1)^{0.5(k+1)+r+i}(r+1)(2r+i+2)!}{(k+1)(2r-i+1)!}, &{}\quad \hbox {if}\,\,\, k\,\,\, \hbox {odd}.\\ \end{array} \right. \end{aligned}$$

The function \(\psi (\eta )\in L_{2}[0,\hbar ]\) may be defined as an infinite series sum as follows:

$$\begin{aligned} \psi (\eta )=\sum _{\ell =0}^{\infty }\zeta _{\ell }\,{{\mathbb {T}}}_{\ell } (\eta ). \end{aligned}$$
(20)

We take the first \((m+1)\)-terms of (20) to obtain the following approximation form:

$$\begin{aligned} \psi _{m}(\eta )=\sum _{\ell =0}^{m}\,\zeta _{\ell }\,{{\mathbb {T}}}_{\ell }\,(\eta ). \end{aligned}$$
(21)

The approximate formula of the fractional derivative for the approximated function \(\psi _{m}(\eta )\) may be defined as in the following theorem.

Theorem 1

Let \(\psi (\eta )\) be approximated by CP\(_{6}\)s as (21) and also suppose \(\nu > 0,\) then:

$$\begin{aligned} D^{\nu }(\psi _{m}(\eta ))\simeq \sum _{i=\lceil \nu \rceil }^{m}\,\sum _{k=\lceil \nu \rceil }^{i} \zeta _{i}\,\chi _{i,\,k,\nu }\,\eta ^{k-\nu }, \end{aligned}$$
(22)

where \(c_{i,k}\) is defined in (19), but \(\chi _{i,\,k,\nu }\) is given by:

$$\begin{aligned} \chi _{i,\,k,\nu }=\frac{\Gamma (k+1)}{\Gamma (k+1-\nu )}\,c_{i,k}. \end{aligned}$$
(23)

Proof

Since Caputo’s fractional differentiation is a linear operation we have:

$$\begin{aligned} D^{\nu }(\psi _{m}(\eta ))=\sum _{i=0}^{m}\zeta _{i}\,D^{\nu }({{\mathbb {T}}}_{i}(\eta )). \end{aligned}$$
(24)

Employing Eqs. (1)–(2) we have:

$$\begin{aligned} D^{\nu }\,{{\mathbb {T}}}_{i}(\eta )=0,\quad \quad i=0,1,...,\lceil \nu \rceil -1,\quad \nu >0. \end{aligned}$$
(25)

Also, for \(i = \lceil \nu \rceil ,...,m,\) by using Eqs.(1)-(2), we get:

$$\begin{aligned} \begin{aligned} D^{\nu }\,({{\mathbb {T}}}_{i}(\eta ))&=\sum _{k=\lceil \nu \rceil }^{i}\,c_{i,k}\,D^{\nu }\,\eta ^{k} = \sum _{k=\lceil \nu \rceil }^{i}\,c_{i,k}\,\frac{\Gamma (k+1)}{\Gamma (k+1-\nu )}\,\eta ^{k-\nu }. \end{aligned} \end{aligned}$$
(26)

A combination of Eqs. (24), (25) and (26) leads to the desired result. \(\square \)

The following theorem is devoted to investigating some details about the error of the approximation by using the CP\(_{6}\)s.

Theorem 2

Consider the approximation \(\psi _{m}(\eta )\) of the function \(\psi (\eta )\) which is defined in (21). Then the truncation error \(\varepsilon _{m}=|\psi (\eta )-\psi _{m}(\eta )|\) is estimated as follows:

$$\begin{aligned} \varepsilon _{m}\le 2^{-m}. \end{aligned}$$

Proof

For the proof, one can be referred to [18]. \(\square \)

3.2 Approximate the Solution with a Numerical Scheme

We will implement the SCM to solve the system (14)–(15) numerically. We approximate \(f(\eta )\), and \(\theta (\eta )\) by \(f_{m}(\eta )\), and \(\theta _{m}(\eta )\), respectively as follows:

$$\begin{aligned} f_{m}(\eta )=\sum _{\ell =0}^{m}a_{\ell }\,{{\mathbb {T}}}_{\ell }(\eta ),\quad \quad \quad \theta _{m}(\eta )=\sum _{\ell =0}^{m}b_{\ell }\,{{\mathbb {T}}}_{\ell }(\eta ). \end{aligned}$$
(27)

By using Eqs. (14)–(15), (27) and the formula (22), we can obtain:

$$\begin{aligned}{} & {} \begin{aligned}&\left( 1+\frac{1}{\beta }\right) \left( \sum _{\ell =3}^{m}\,\sum _{k=3}^{\ell }\,a_{\ell }\,\chi _{\ell ,\,k,\,\alpha }\,\eta ^{\ell -\alpha }\right) +\left( \sum _{\ell =0}^{m}\,a_{\ell }\,{{\mathbb {T}}}_{\ell }(\eta )\right) \left( \sum _{\ell =2}^{m}\,\sum _{k=2}^{\ell }\,a_{\ell }\,\chi _{\ell ,\,k,\,\delta }\,\eta ^{\ell -\delta }\right) \\&-\left( \sum _{\ell =1}^{m}\,\sum _{k=1}^{\ell }\,a_{\ell }\,\chi _{\ell ,\,k,\,\gamma }\,\eta ^{\ell -\gamma }\right) ^{2}\\ {}&\quad + M^{2}\,\left( E_{1}-\sum _{\ell =1}^{m}\,\sum _{k=1}^{\ell }\,a_{\ell }\,\chi _{\ell ,\,k,\,\gamma }\,\eta ^{\ell -\gamma }\right) +\Delta \left( \sum _{\ell =0}^{m}\,b_{\ell }\,{{\mathbb {T}}}_{\ell }(\eta )\right) =0, \end{aligned} \end{aligned}$$
(28)
$$\begin{aligned}{} & {} \begin{aligned} \left( \frac{1}{Pr}\right)&\left[ \left( 1+R+\varepsilon \,\left( \sum _{\ell =0}^{m}\,b_{\ell }\,{{\mathbb {T}}}_{\ell }(\eta )\right) \right) \left( \sum _{\ell =2}^{m}\,\sum _{k=2}^{\ell }\,b_{\ell }\,\chi _{\ell ,\,k,\,\delta }\,\eta ^{\ell -\delta }\right) \right. \\ {}&\quad \left. +\varepsilon \, \left( \sum _{\ell =1}^{m}\,\sum _{k=1}^{\ell }\,b_{\ell }\,\chi _{\ell ,\,k,\,\gamma }\,\eta ^{\ell -\gamma }\right) ^{2}\right] \\ {}&+M^{2}Ec\,\left( \sum _{\ell =1}^{m}\,\sum _{k=1}^{\ell }\,a_{\ell }\,\chi _{\ell ,\,k,\,\gamma }\,\eta ^{\ell -\gamma }-E_{1}\right) ^{2}+ \left( \sum _{\ell =0}^{m}\,a_{\ell }\,{{\mathbb {T}}}_{\ell }(\eta )\right) \\ {}&\quad \left( \sum _{\ell =1}^{m}\,\sum _{k=1}^{\ell }\,b_{\ell }\,\chi _{\ell ,\,k,\,\gamma } \,\eta ^{\ell -\gamma }\right) \\ {}&+Ec\left( 1+\frac{1}{\beta }\right) \left( \sum _{\ell =2}^{m}\,\sum _{k=2}^{\ell }\,a_{\ell }\,\chi _{\ell ,\,k,\,\delta }\,\eta ^{\ell -\delta }\right) ^{2}=0. \end{aligned} \end{aligned}$$
(29)

The previous Eqs. (28)–(29) will be collocated at m of nodes \(\eta _{p}\) as follows:

$$\begin{aligned}{} & {} \begin{aligned}&\left( 1+\frac{1}{\beta }\right) \left( \sum _{\ell =3}^{m}\,\sum _{k=3}^{\ell }\,a_{\ell }\,\chi _{\ell ,\,k,\,\alpha }\,\eta _{p}^{\ell -\alpha }\right) +\left( \sum _{\ell =0}^{m}\,a_{\ell }\,{{\mathbb {T}}}_{\ell }(\eta _{p})\right) \left( \sum _{\ell =2}^{m}\,\sum _{k=2}^{\ell }\,a_{\ell }\,\chi _{\ell ,\,k,\,\delta }\,\eta _{p}^{\ell -\delta }\right) \\ {}&-\left( \sum _{\ell =1}^{m}\,\sum _{k=1}^{\ell }\,a_{\ell }\,\chi _{\ell ,\,k,\,\gamma }\,\eta _{p}^{\ell -\gamma }\right) ^{2}+ M^{2}\,\left( E_{1}-\sum _{\ell =1}^{m}\,\sum _{k=1}^{\ell }\,a_{\ell }\,\chi _{\ell ,\,k,\,\gamma }\,\eta _{p}^{\ell -\gamma }\right) \\&\quad +\Delta \left( \sum _{\ell =0}^{m}\,b_{\ell }\,{{\mathbb {T}}}_{\ell }(\eta _{p})\right) =0, \end{aligned} \end{aligned}$$
(30)
$$\begin{aligned}{} & {} \begin{aligned} \left( \frac{1}{Pr}\right)&\left[ \left( 1+R+\varepsilon \,\left( \sum _{\ell =0}^{m}\,b_{\ell }\,{{\mathbb {T}}}_{\ell }(\eta _{p})\right) \right) \left( \sum _{\ell =2}^{m}\,\sum _{k=2}^{\ell }\,b_{\ell }\,\chi _{\ell ,\,k,\,\delta }\,\eta _{p}^{\ell -\delta }\right) \right. \\ {}&\quad \left. +\varepsilon \, \left( \sum _{\ell =1}^{m}\,\sum _{k=1}^{\ell }\,b_{\ell }\,\chi _{\ell ,\,k,\,\gamma }\,\eta _{p}^{\ell -\gamma }\right) ^{2}\right] \\ {}&+M^{2}Ec\,\left( \sum _{\ell =1}^{m}\,\sum _{k=1}^{\ell }\,a_{\ell }\,\chi _{\ell ,\,k,\,\gamma }\,\eta _{p}^{\ell -\gamma }-E_{1}\right) ^{2}+ \left( \sum _{\ell =0}^{m}\,a_{\ell }\,{{\mathbb {T}}}_{\ell }(\eta _{p})\right) \\&\quad \left( \sum _{\ell =1}^{m}\,\sum _{k=1}^{\ell }\,b_{\ell }\,\chi _{\ell ,\,k,\,\gamma }\, \eta _{p}^{\ell -\gamma }\right) \\ {}&+Ec\left( 1+\frac{1}{\beta }\right) \left( \sum _{\ell =2}^{m}\,\sum _{k=2}^{\ell }\,a_{\ell }\,\chi _{\ell ,\,k,\,\delta }\,\eta _{p}^{\ell -\delta }\right) ^{2}=0. \end{aligned} \end{aligned}$$
(31)

In addition, the boundary conditions (16)–(17) can be expressed by substituting from Eq. (27) in (16)–(17) to find the following equations:

$$\begin{aligned}{} & {} \sum _{\ell =0}^{m}\,(-1)^{\ell }\,a_{\ell }=0,\quad \quad \quad \sum _{\ell =0}^{m}\,a_{\ell }\,\left( {{\mathbb {T}}}_{\ell }^{'}(0)-\lambda \left( 1+\frac{1}{\beta }\right) {{\mathbb {T}}}_{\ell }^{''}(0)\right) =1, \end{aligned}$$
(32)
$$\begin{aligned}{} & {} \sum _{\ell =0}^{m}\,(-1)^{\ell }\,b_{\ell }=1+\Lambda \sum _{\ell =0}^{m}\,b_{\ell }\,{{\mathbb {T}}}_{\ell }^{'}(0),\quad \quad \quad \sum _{\ell =0}^{m}\,a_{\ell }\,{{\mathbb {T}}}_{\ell }^{'}(\hbar )=0,\quad \quad \quad \sum _{\ell =0}^{m}\,b_{\ell }=0. \end{aligned}$$
(33)

Equations (30)–(31), together with Eqs. (32)–(33), give a system of \(2(m+1)\) algebraic equations. This system will solve for the unknowns \(a_{\ell },\,b_{\ell },\) \( \ell =0,1,...,m,\) by using the Newton iteration method.

4 Main Results

In this section, we present a comparison of the local Nusselt number findings with Khan and Pop’s earlier results [36], and the comparison is shown in Table 1. The results show a striking resemblance between the acquired findings and the published results, demonstrating a high degree of agreement between the two sets of data. The consistency of the acquired results with the reported findings lends support to the accuracy and precision of the existing mathematical formulation as well as the numerical solutions used in the study with \(m=8,\,\alpha =1+\delta =2+\gamma =3\) in the domain [0, 6].

Table 1 Comparison of results for reduced Nusselt number \(-\theta '(0)\) with findings of Khan and Pop [36] for various values of Pr when \(M^{2}=\Delta =\lambda =\Lambda =Ec=R=E_{1}=\varepsilon =0.0\) and \(\beta \rightarrow 0\)
Full size table

In addition, we have presented graphical representations of the temperature \(\theta (\eta )\) and fluid velocity \(f'(\eta )\) solutions obtained from the proposed model with \(m=8,\,\alpha =1+\delta =2+\gamma =3\) in the domain [0, 6]. Additionally, we have provided a table for displaying the values of friction drag and the LNN. These results were obtained by considering the smallest appropriate values of key flow parameters, including the mixed convection parameter, slip velocity parameter, local electric parameter, thermal slip parameter, magnetic parameter, Eckert number, thermal conductivity parameter, and radiation parameter. Figure 2(Left) shows that when subjected to greater magnetic numbers, the fluid velocity is significantly suppressed. This phenomenon develops as a result of the reduced fluid flow brought on by an enhanced drag force brought on by a stronger magnetic field. At larger magnetic number values, as seen in Fig. 2(Right), it is expected that this augmented drag force will have a more noticeable effect on the thermal field. Physically, the decrease in fluid velocity caused by a magnetic field can be attributed to the interaction between the fluid and the magnetic field. When a magnetic field is present, it exerts a force on the charged particles in the fluid, known as the Lorentz force. This force acts perpendicular to both the magnetic field and the fluid’s direction of flow, creating resistance to the fluid’s motion. As the strength of the magnetic field increases, the influence of the Lorentz force becomes more pronounced, counteracting the fluid’s movement and resulting in a decrease in velocity.

Fig. 2
figure 2

(Left) \(f'(\eta )\) for picked M         (Right) \(\theta (\eta )\) for picked M

Full size image

The effects of the local electric parameter \(E_{1}\) on the \(f'(\eta )\) and \(\theta (\eta )\) profiles are shown in Fig. 3(Left and Right). These graphs’ observed trend shows that raising the local electric parameter causes the momentum and temperature fields in the Casson fluid to rise. Consequently, the boundary layer thickness increases when the local electric parameter is increased. This suggests that the local electric parameter is a key factor in determining the thermal and hydrodynamic motion of the Casson fluid, with bigger values producing stronger momentum and temperature fields and thicker boundary layers.

Fig. 3
figure 3

(Left) \(f'(\eta )\) for picked \(E_{1}\) (Right) \(\theta (\eta )\) for picked \(E_{1}\)

Full size image

Figure 4 illustrates the impact of the mixed convection parameter \(\Delta \) on both the momentum field and the thermal field. It demonstrates how different values of the parameter affect these fields. Specifically, in Fig. 4(Left), it is evident that higher values of the mixed convection parameter result in velocity curves that ascend within the boundary layer region. Additionally, Fig. 4(Right) indicates that the thermal field experiences a slight reduction caused by the same parameter \(\Delta \). Physically, as the mixed convection parameter rises, forced convection becomes less significant relative to natural convection. When there are large temperature gradients in the system, buoyancy-driven flow may result. As a result, the fluid velocity rises, particularly in the area of the boundary layer where convection effects are most pronounced.

Fig. 4
figure 4

(Left) \(f'(\eta )\) for picked \(\Delta \) (Right) \(\theta (\eta )\) for picked \(\Delta \)

Full size image

The effect of the Casson parameter \(\beta \) on the temperature field \(\theta (\eta )\) and the velocity field \(f'(\eta )\) is shown in Fig. 5. When the Casson parameter is increased, the Casson fluid behaves in a way that is more similar to a Newtonian fluid. The velocity and temperature fields consequently drop when the Casson parameter \(\beta \) is increased. The fluid behaves more like a typical fluid that adheres to Newton’s law of viscosity as the Casson parameter rises. The distributions of velocity and temperature within the fluid are impacted by this shift in behavior. In particular, both the velocity and temperature fields exhibit a falling trend or drop in their magnitudes as the Casson parameter is increased.

Fig. 5
figure 5

(Left) \(f'(\eta )\) for picked \(\beta \) (Right) \(\theta (\eta )\) for picked \(\beta \)

Full size image

The behavior of \(\theta (\eta )\) and \(f'(\eta )\) as affected by the slip velocity parameter \(\lambda \) is shown in Fig. 6. Raising the slip velocity parameter’s values causes the fluid layers to produce more resistance forces. The result is that these resistive forces help to lower the fluid velocity \(f'(\eta )\) while somewhat raising the temperature \(\theta (\eta )\). Stronger resistance is induced within the fluid layers when the \(\lambda \) is greater. The fluid properties are impacted by this higher resistance in two ways. The flow slows down as a result of the first effect, which is a reduction in \(f'(\eta )\). Second, \(\theta (\eta )\) shows a tiny increase, indicating a slight temperature rise. Physically, these data suggest that the slip velocity parameter influences the \(\theta (\eta )\) and \(f'(\eta )\). The resistive forces increase with \(\lambda \) value, which causes a decrease in \(f'(\eta )\) and a slight increase in \(\theta (\eta )\).

Fig. 6
figure 6

(Left) \(f'(\eta )\) for picked \(\lambda \) (Right) \(\theta (\eta )\) for picked \(\lambda \)

Full size image

The thermal conductivity parameter \(\varepsilon \), which indirectly affects the energy equation, is shown to have a negligible impact on the velocity field on the left side of Figs. 7. The outcomes show that \(\theta (\eta )\) is improved by raising the thermal conductivity parameter. Additionally, the thermal boundary layer thickens (TBLT) when these values are steadily raised. Physically, a system’s internal temperature distribution is improved by increasing its thermal conductivity parameter. It becomes more desirable in particular by improving the temperature profile and raising the thermal conductivity value.

Fig. 7
figure 7

(Left) \(f'(\eta )\) for picked \(\varepsilon \) (Right) \(\theta (\eta )\) for picked \(\varepsilon \)

Full size image

Figure 8 (Left) show how variations in the Eckert number Ec affect the thermal field. The outcomes show that the distribution of temperature is improved by raising the Eckert number. When this parameter was gradually increased, the thermal boundary layer also gets thicker. In simpler terms, this figure demonstrates how altering the Eckert number Ec will impact the thermal field. Physically, the distribution of internal temperatures inside the system is made more favorable by increasing the value of this parameter. Its increased desirability is specifically attributed to increasing the Eckert number and enhancing the temperature profile. The results from Fig. 8 (Right) emphasize that increasing the thermal radiation parameter R causes the thermal boundary layer to expand and the temperature distribution to improve. The expanded temperature distribution caused by an increase in the radiation parameter has a physical explanation for the improved heat transfer by radiation. A method of heat transmission that uses electromagnetic waves is called radiation. Increased radiation parameter values indicate that radiation plays a larger role in the overall heat transfer process. This may occur, for instance, when there are objects or surfaces with higher emissions or when there are significant temperature changes between surfaces.

Fig. 8
figure 8

(Left) \(\theta (\eta )\) for picked Ec (Right) \(\theta (\eta )\) for picked R

Full size image

The relationship between the temperature distribution and the two parameters, Prandtl number Pr and the thermal slip parameter \(\Lambda \) is further explained in Fig. 9. It indicates that while the thermal slip parameter exhibits the opposite pattern, the temperature distribution falls as the Prandtl number rises. Figure 9 shows how changes in the thermal slip parameter and Prandtl number affect the temperature distribution. The temperature distribution reduces as the Prandtl number rises, indicating a more localized or concentrated thermal profile. The temperature distribution, on the other hand, exhibits the reverse behavior, i.e., spreads out or gets more dispersed, as the thermal slip parameter rises.

Fig. 9
figure 9

(Left) \(\theta (\eta )\) for picked Pr (Right) \(\theta (\eta )\) for picked \(\Lambda \)

Full size image
Fig. 10
figure 10

(Left) \(D^{\gamma }f(\eta )\) for picked \(\alpha ,\,\delta ,\,\gamma \) (Right) \(\theta (\eta )\) for picked \(\alpha ,\,\delta ,\,\gamma \)

Full size image

Figure 10 is presented to show the numerical behavior of the velocity distribution (Left), and the temperature distribution (Right), respectively with different values of the fractional orders \(\alpha , \delta \) and \(\gamma \) at \(m=7\) to the proposed model. We take \(M=\beta =R=Ec=0.5, \,E_{1}=\lambda =0.1,\,\Delta =\Lambda =\varepsilon =0.2,\,Pr=2\). Here in this figure, we take \(\alpha =1+\delta =2+\gamma =3,\,2.95,\,2.9,\,2.85\). From Fig. 10, we can see that the behavior of the numerical solution is dependent on the values of fractional derivatives’s order; and this confirms that the given method is implemented in a good way for solving the present model in its fractional form.

Table 2 Values for  \(C_{f}Re_{x}^{\frac{1}{2}}\) and \(Nu_{x}Re_{x}^{\frac{-1}{2}}\) for various values of M, \(E_{1}\), \(\Delta \), \(\beta \), \(\lambda \), \(\varepsilon \) and Ec with \(Pr=2.0,\,R=0.5,\,\Lambda =0.1\)
Full size table

To observe the behavior of parameters affecting the skin-friction coefficient and the local Nusselt number, Table 2 is formulated. This table makes it abundantly clear that the SFC, and LNN have inverse relationships with the magnetic number. The Nusselt number decreases as the magnetic number rises, yet the skin-friction coefficient upsurges. Additionally, the local Nusselt number rises together with the value of the thermal conductivity parameter, whereas the skin-friction coefficient declines. The skin-friction coefficient also decreases when the Eckert number rises, as does the LNN. Additionally, the SFC decreases, but the LNN increases when the local electric, mixed convection, Casson, and slip velocity parameters are improved.

5 Conclusions and Remarks

When thermal radiation, thermal slip, Ohmic dissipation, and slip velocity conditions are present, a non-Newtonian Casson fluid’s mixed convection flow is investigated using numerical analysis. A numerical method based on sixth-kind Chebyshev polynomials known as the spectral collocation method is used to analyze how the flow velocities and temperature respond to changes in the physical parameters within their appropriate limits. The following is a summary of the major findings:

  1. 1.

    Elevated local temperatures and the Nusselt number are the results of an increase in the local electric parameter.

  2. 2.

    The LNN and SFC decrease as the Eckert number values rise.

  3. 3.

    The heat transfer rate increases while the local SFC reduces for high values of the Casson and mixed convection parameters.

  4. 4.

    By raising the value of the slip velocity parameter, the temperature distribution is enhanced with little changes in TBLT.

  5. 5.

    The presence of the magnetic field enhances the local SFC, but it also limits fluid flow and raises the fluid temperature.

  6. 6.

    There is a modest drop in temperature across the boundary layer, as opposed to the mixed convection parameter and the Casson parameter.