Many-Objective Whale Optimization Algorithm for Engineering Design and Large-Scale Many-Objective Optimization Problems

Abstract

In this paper, a novel Many-Objective Whale Optimization Algorithm (MaOWOA) is proposed to overcome the challenges of large-scale many-objective optimization problems (LSMOPs) encountered in diverse fields such as engineering. Existing algorithms suffer from curse of dimensionality i.e., they are unable to balance convergence with diversity in extensive decision-making scenarios. MaOWOA introduces strategies to accelerate convergence, balance convergence and diversity in solutions and enhance diversity in high-dimensional spaces. The prime contributions of this paper are—development of MaOWOA, incorporation an Information Feedback Mechanism (IFM) for rapid convergence, a Reference Point-based Selection (RPS) to balance convergence and diversity and a Niche Preservation Strategy (NPS) to improve diversity and prevent overcrowding. A comprehensive evaluation demonstrates MaOWOA superior performance over existing algorithms (MaOPSO, MOEA/DD, MaOABC, NSGA-III) across LSMOP1-LSMOP9 benchmarks and RWMaOP1-RWMaOP5 problems. Results validated using Wilcoxon rank sum tests, highlight MaOWOA excellence in key metrics such as generational distance, spread, spacing, runtime, inverse generational distance and hypervolume, outperforming in 71.8% of tested scenarios. Thus, MaOWOA represents a significant advancement in many-objective optimization, offering new avenues for addressing LSMOPs and RWMaOPs’ inherent challenges. This paper details MaOWOA development, theoretical basis and effectiveness, marking a promising direction for future research in optimization strategies amidst growing problem complexity.

1 Introduction

In recent years, the focus on many-objective optimization problems (MaOPs), a subset of multi-objective optimization problems (MOPs) with more than three objectives [1], has significantly increased within the evolutionary multi-objective optimization community [2], as evidenced by numerous studies [3]. These MaOPs are relevant to various real-life scenarios like routing [4], pattern mining [5] analysis of complex networks [6] etc. A typical MaOP can be defined as follows,

$$\begin{array}{c}min f(x)=({f}_{1}(x),{f}_{2}(x),...,{f}_{M}(x))\\ s.t. x\in X\end{array}$$

(1)

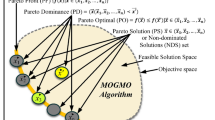
where $M$ symbolizes the total number of objectives; ${\varvec{x}}$ denotes the decision vector comprising n decision variables; and X ⊆ ℝn represents the decision space. Given the inherently conflicting nature of these objectives, it is impossible for a single solution to simultaneously optimize all objectives. Therefore, the ideal outcome is not a singular solution but a collection of compromise solutions, known as the Pareto optimal set (PS), located in the decision space. This set corresponds to the Pareto optimal front (PF) within the objective space shown in Fig. 1.

Fig. 1

Many-objective all definitions in search space of MaO-problem

Conversely, most multi-objective evolutionary algorithms (MOEAs) that rely on the Pareto-dominance relation encounter diminished selection pressure toward the Pareto front (PF) when dealing with an increased number of objectives, as the population solutions tend to be mostly non-dominated [7]. To address this issue, numerous methods have been devised to enhance MOEAs’ efficacy in tackling many-objective optimization problems (MaOPs). These methods can be broadly classified into three categories [3].

The first category encompasses decomposition-based methods, which are further split into two distinct decomposition techniques. The initial technique involves breaking down a MaOP into a series of single-objective subproblems. An exemplar in this category is MOEA/D [8], which utilizes a predefined array of weight vectors to transform a MaOP into several scalarizing subproblems, achieving notable convergence. Building upon MOEA/D framework, various adaptations have been proposed for MaOPs, including a revised replacement strategy in I-DBEA [9], a novel neighborhood definition based on solutions in MOEA/D-DU [10] and combined dominance and decomposition strategies in MOEA/DD [11]. In addition, RVEA [12] employs reference vectors to segment the objective space and introduces an angle penalized distance as a scalarization function for solution selection. The second technique segments a MaOP into multiple multi-objective subproblems. This approach, initially pioneered by MOEA/D-M2M for MOPs [13], has inspired a plethora of strategies for MaOPs, such as an objective space division using the K-means clustering method in NSGA-III-OSD [14], a clustering-ranking method in crEA [15] and a reference direction-based density estimator in SPEA/R [16]. However, to achieve optimal distribution performance, both decomposition methods must carefully consider the configuration of reference vectors, particularly for problems with irregular PFs.

The second category involves indicator-based approaches, which use a single metric to steer population evolution. the ɛ-indicator [17], hypervolume indicator [18] and R2 indicator [19]. The hypervolume indicator, in particular, is widely utilized due to its strict monotonic relationship with Pareto dominance, as seen in algorithms like the fast hypervolume-based evolutionary algorithm (HypE) [18], the Lebesgue indicator-based evolutionary algorithm (LIBEA) [20] and the hypervolume adaptive grid algorithm (HAGA) [21]. Nonetheless, the exponentially increasing computational complexity of calculating hypervolume renders it less feasible for MaOPs.

The third classification in enhancing MOEAs for many-objective optimization problems (MaOPs) involves Pareto-based approaches, which focus on augmenting convergence and fostering diversity. Convergence enhancement primarily aims to differentiate Pareto non-dominated solutions. This is typically achieved by altering the Pareto-dominance relation through methods like fuzzy dominance [22], grid dominance [23] and strengthened dominance [24]. The primary limitation of these methods is their reliance on one or more adjustable parameters, which must be tuned heuristically. Another strategy involves incorporating an additional convergence criterion. For instance, SPEA2 + SDE [25] employs a shift-based density estimation (SDE) tactic that uses a straightforward coordinate transformation to relocate poorly-converged solutions to denser areas. In KnEA [26], the concept of a knee point is introduced, calculated by the perpendicular distance of an individual from a hyperplane, thereby enhancing the selection pressure.

Diversity promotion, another crucial aspect, counters the loss of selection pressure. A prime example is Non-Dominated Sorting Genetic Algorithm-III (NSGA-III) [27], Many-Objective Particle Swarm Optimizer (MaOPSO) [28] and Many-Objective Artificial Bee Colony (MaOABC) [29], which uses an array of widely distributed reference points to preserve diversity, with each solution linked to a reference line. The MaOEA-DDFC [30] approach measures directional diversity by evaluating projection points on a hyperplane using k-nearest neighborhood distance. However, these methods can overly focus on promoting diversity at the expense of convergence.

Recent studies suggest that diversity estimation based on angles is more effective for MaOPs, as angles can more accurately represent diversity and integrate with convergence information [31]. For example, MaOEA-CSS [31] identifies a pair of solutions in a population with the minimal angle and calculates the variance in their Euclidean distances, thereby reducing the conflict between convergence and diversity. However, setting an appropriate distance threshold remains challenging. VaEA [32] introduces the maximum-vector-angle-first principle for diversity maintenance and a worse-elimination principle for convergence improvement. Yet, the angle threshold setting assumes a uniform distribution of PFs across the entire objective space, which requires more careful adjustment for irregular Pareto fronts [33]. Several other interesting studies on MaOPs have been carried out recently [34,35,36]. Notable metaheuristics like PSO [37], Sine–Cosine Algorithm [38], MOEA/D [39], WOA [40] etc. have also been used to develop MaOPs. Based on the discussion, indicator-based methods might struggle with complex Pareto fronts (PFs) [41, 42] such as disconnected or degenerated ones. The directional search they employ can lose diversity if the distribution of pre-set reference vectors does not align with the true PF. Research on many-objective optimization algorithms explores the intricate interplay between climate change impacts to contribute to mitigation efforts [43], uses hyperspectral data for disease recognition [44], examines socioeconomic factors and environmental outcomes [45], enhances machine learning models [46] and advances image processing techniques [47].

The evolution of optimization algorithms for addressing MOPs and particularly LSMOPs, has witnessed significant contributions from various researchers. Studies have extensively explored in Table 1 that provides an overview of these methodologies, summarizing the contributions, strengths, weaknesses and specific relevance of each algorithm to the development of the Many-Objective Whale Optimization Algorithm (MaOWOA).

Table 1  Comparative analysis of many-objective algorithms with relevance to MaOWOA

This paper introduces the MaOWOA, a novel approach designed to bridge this gap. For the evaluation of MaOWOA two types of datasets are used—synthetic benchmarks and real-world engineering design problems. The synthetic benchmarks include LSMOP1-LSMOP9, designed to test the algorithm performance across various dimensions and objectives. These benchmarks simulate large-scale optimization problems with 100 M decision variables, where M represents the number of objectives, highlighting challenges like unimodality, multimodality and separability of objective functions. The real-world engineering design problems encompass diverse applications, such as Car cab design (RWMaOP1), 10-bar truss structure (RWMaOP2), water and oil repellent fabric development (RWMaOP3), ultra-wideband antenna design (RWMaOP4) and Liquid-rocket single element injector design (RWMaOP5). These problems are characterized by their practical relevance and complexity, involving objectives like minimizing weight, compliance, or maximizing structural integrity and performance under specific constraints. Each real-world problem is defined by a set of decision variables and objectives reflecting the problem complexity and multidimensional nature.

The contributions and benefits of the current research are:

• 1. A novel MaOWOA metaheuristic optimizer is proposed which integrates three distinct strategies including an IFM that utilizes historical performance data to accelerate the convergence process, effectively leveraging previously gathered information to enhance future searches; a RPS that promotes a balanced distribution of solutions by aligning them with predetermined reference points in the objective space, thereby ensuring both convergence and diversity; and a NPS that addresses the common problem of solution overcrowding in specific regions of the objective space, enhancing the diversity of the solution set. This integration is specifically tailored to enhance the optimization process for LSMOPs and RWMaOPs by ensuring faster convergence, balanced diversity and the prevention of solution overcrowding.

• 2. Through extensive experimentation on benchmark LSMOPs and RWMaOPs, it is demonstrated that MaOWOA outperforms existing algorithms like MaOPSO, MOEA/DD, MaOABC, and NSGA-III across several metrics.

• 3. The effectiveness of MaOWOA was validated through comparative analysis involving a series of LSMOP benchmark tests (LSMOP1-LSMOP9) and RWMaOPs (RWMaOP1-RWMaOP5). The results highlight MaOWOA superior performance, notably in Generational Distance (GD), Inverse Generational Distance (IGD), Spread (SD), Spacing (SP), and Run Time (RT) metrics.

• 4. The robustness of these results was confirmed through non-parametric statistical Wilcoxon rank sum tests, with MaOWOA showing superior performance in 71.8% of the LSMOPs tested.

The structure of this paper is as follows: Sect. 2 provides overview of WOA algorithm for the study. Section 3 elaborates on the MaOWOA for many-objective optimization. Section 4 details experimental settings, analyses comprehensive experiments. Finally, Sect. 5 concludes the paper, outlines potential avenues for future research

2 Whale Optimization Algorithm

The Whale Optimization Algorithm (WOA), introduced by Mirjalili and Lewis [40], simulates the hunting behavior of humpback whales, utilizing swarm intelligence principles. The algorithm models three main behaviors: searching, encircling prey and the unique bubble-net feeding method. During the search phase, each whale or agent moves randomly or follows the peer with the best solution. The agent position, $\overrightarrow{X}(t+1)$, is updated based on the position of a randomly selected peer or the best search agent, using:

$$\overrightarrow{X}(t+1)=\overrightarrow{{X}_{rand}}-\overrightarrow{A}\cdot |\overrightarrow{C}\cdot \overrightarrow{{X}_{rand}}-\overrightarrow{X}|$$

(2)

where $\overrightarrow{A}$ and $\overrightarrow{C}$ are coefficients calculated from:

$$\overrightarrow{A}=2\overrightarrow{a}\cdot \overrightarrow{r}-\overrightarrow{a}$$

(3)

$$\overrightarrow{C}=2\overrightarrow{r\overrightarrow{D}=|\overrightarrow{C}\cdot \overrightarrow{{X}_{rand}}-\overrightarrow{X,}}$$

(4)

where $\overrightarrow{r}$ is a random vector in [0,1] and $\overrightarrow{a}$ linearly decreases from 2 to 0 over iterations. This process is depicted through:

$$\overrightarrow{D}=|\overrightarrow{C}\cdot \overrightarrow{{X}^{*}}(t)-\overrightarrow{X}(t)|$$

(5)

$$\overrightarrow{X}(t+1)=\overrightarrow{{X}^{*}}(t)-\overrightarrow{A}\cdot \overrightarrow{D}$$

(6)

$\overrightarrow{{X}^{*}}$ refers to the position vector of the targeted solution. The bubble-net attack phase is characterized by a spiral movement toward the target, represented by:

$$\vec{X}(t + 1) = \overrightarrow {{D^{\prime}}} \cdot e^{{bl}} \cdot {\text{cos}}(2\pi l) + \overrightarrow {{X^{*} }} (t)$$

(7)

$${D}^{\prime}=|\overrightarrow{{X}^{*}}(t)-\overrightarrow{X}(t)|$$

(8)

${D}^{\prime}$ is the distance to the target, $b$ remains a constant and $l$ is a randomly generated number within the range of [− 1, 1]. This mimics the whales’ spiral movement toward the prey, combining a spiral update toward the target with the possibility of shrinking encirclement. This dual strategy is expressed as:

$$\vec{X}(t + 1) =\left \{ \begin{array}{*{20}l} {\overrightarrow {{X^{*} }} (t) - \vec{A} \cdot \vec{D}} & {{\text{if}}\,{\text{p}}\;{\text{ < 0}}{\text{.5}}} & {} \\ {\overrightarrow {{D^{\prime}}} \cdot e^{{bl}} \cdot {\text{cos}}(2\pi l) + \overrightarrow {{X^{*} }} (t)} & {{\text{if}}\,{\text{p}} \ge 0.5} & {} \\ \end{array}\right.$$

(9)

The parameter $p$ is a random number in [0,1], deciding the strategy to apply. Figure 2, which presents a visual representation of the described technique.

Fig. 2

Flowchart of the WOA optimizer

3 Proposed Many-Objective Whale Optimization Algorithm (MaOWOA)

MaOWOA algorithm starts with a random population of size $N$, $M$ no. of objectives, $p$ no. of partitions and generate a set of reference points using Das and Dennis technique $H = \left( {\begin{array}{*{20}c} {M + p - 1} \\ p \\ \end{array} } \right)$, as $H\approx N$. the current generation is $t,{x}_{i}^{t}$ and ${x}_{i}^{t+1}$ the $i$-th individual at $t$ and $(t+1)$ generation. ${u}_{i}^{t+1}$ the $i$-th individual at the $(t+1)$ generation generated through the WOA algorithm and parent population ${P}_{t}$. the fitness value of ${u}_{i}^{t+1}$ is ${f}_{i}^{t+1}$ and ${U}^{t+1}$ is the set of ${u}_{i}^{t+1}$. Then, ${x}_{i}^{t+1}$ according to ${u}_{i}^{t+1}$ generated through the WOA algorithm and IFM Eq. (10) is calculated

$${{x}_{i}^{t+1}={\partial }_{1}{u}_{i}^{t+1}+{\partial }_{2}{x}_{k}^{t}; \quad {\partial }_{1}=\frac{{f}_{k}^{t}}{{f}_{i}^{t+1}+{f}_{k}^{t}}, {\partial }_{2}=\frac{{f}_{i}^{t+1}}{{f}_{i}^{t+1}+{f}_{k}^{t}},} {\partial }_{1}+{\partial }_{2}=1$$

(10)

where ${x}_{k}^{t}$ is the $k$ th individual chosen from the $t$ th generation, the fitness value of ${x}_{k}^{t}$ is ${f}_{k}^{t},{\partial }_{1}$ and ${\partial }_{2}$ are weight coefficients. Generate offspring population ${Q}_{t}$. ${Q}_{t}$ is the set of ${x}_{i}^{t+1}.$ The combined population ${R}_{t}={P}_{t}\cup {Q}_{t}$ is sorted into different w-non-dominant levels $\left({F}_{1},{F}_{2},\dots ,{F}_{l}\dots ,{F}_{w}\right)$. Begin from ${F}_{1}$, all individuals in level 1 to $l$ are added to ${S}_{t}$ and remaining members of ${R}_{t}$ are rejected. If $\left|{S}_{t}\right|=N$; no other actions are required and the next generation is begun with ${P}_{t+1}={S}_{t}$. Otherwise, solutions in ${S}_{t}/{F}_{l}$ are included in ${P}_{t+1}={S}_{t}/{F}_{l}$ and the rest $\left(K=N-\left|{P}_{t+1}\right|\right)$ individuals are selected from the last front ${F}_{l}$(presented in Algorithm 1). For selecting individuals from ${F}_{l}$, a niche-preserving operator is used. First, each population member of ${P}_{t+1}$ and ${F}_{l}$ is normalized (presented in Algorithm 2) using the current population spread so that all objective vectors and reference points have commensurate values. Thereafter, each member of ${P}_{t+1}$ and ${F}_{l}$ is associated (presented in Algorithm 3) with a specific reference point using the shortest perpendicular distance $(d())$ of each population member with a reference line created by joining the origin with a supplied reference point. Then, a careful niching strategy (described in Algorithm 4) that improve the diversity of MaOWOA algorithm is employed to choose those ${F}_{l}$ members that are associated with the least represented reference points niche count ${\rho }_{i}$ in ${P}_{t+1}$ and check termination condition is met. If the termination condition is not satisfied, $t=t+1$ than repeat and if it is satisfied, ${P}_{t+1}$ is generated, it is then applied to generate a new population ${Q}_{t+1}$ by WOA algorithm. Such a careful selection strategy is found to computational complexity of $M$-Objectives $O\left({N}^{2}{\text{log}}^{M-2}N\right)$ or $O\left({N}^{2}M\right)$, whichever is larger. MaOWOA algorithm that incorporates IFM to effectively guide the search process, ensuring a balance between exploration and exploitation. This leads to improved convergence, coverage and diversity preservation, which are crucial aspects of many-objective optimization. MaOWOA algorithm does not require to set any new parameter other than the usual WOA parameters such as the population size, termination parameter, and their associated parameters.

Algorithm 1

Generation t of MaOWOA Algorithm With IFM Procedure

Algorithm 2

Normalize (fⁿ, S_t, Z^r, Z^s/Z^a)

Algorithm 3

Associate (S_t, Z^r ) Procedure

Algorithm 4

Niching (K, ρ_j, π, d, Z^r, F_l, P_t+1 Procedure

4 Experimental Results

4.1 Experimental Settings

4.1.1 Benchmarks

Optimization challenges that encompass hundreds or thousands of decision variables constitute large-scale optimization problems. To verify the effectiveness of the MaOWOA, LSMOP1- LSMOP9 [41] benchmark (Appendix A) and five real-world engineering design (Appendix B): Car cab design (RWMaOP1) [42], 10-bar truss structure (RWMaOP2) [48], Water and oil repellent fabric development (RWMaOP3) [49], Ultra-wideband antenna design (RWMaOP4) [50] and Liquid-rocket single element injector design (RWMaOP5) [51] problems are used in this paper. The number of decision variables for the LSMOP problems is $100*M$, $M$ is the number of objective functions.

4.1.2 Comparison Algorithms and Parameter Settings

In this study, the performance of MaOWOA by empirically comparing it with some state-of-the-art MOAs for MaOPs, namely, MaOPSO [28], MaOABC [29], MOEA/DD [11] and NSGA-III [27], will be verified. The experiments are conducted on a Matlab R2020a environment on an Intel Core (TM) i7-9700 CPU. Each algorithm performs 30 times, the size of population $N$ is set to $N=210, 275 \; {\text{and}}$ $240$ for all of the involved algorithms on $M=5, 8 \; {\text{and}}$ $10$ objectives problems. The $MaxFEs$ is set to $D\times 1{0}^{5}$ for all of the test instances. NSGA-III adopts the same parameter settings, where the crossover ${P}_{c}$ and mutation probability ${P}_{m}$, the distribution index of simulated binary crossover ${\eta }_{c}$ and polynomial mutation ${\eta }_{m}$, are set to 1, $1/D$, 20 and 20.

4.1.3 Performance Measures

This paper adopts Generational distance $(GD)$, Spread $(SD)$, Spacing $(SP)$, Run Time $(RT)$, Inverse Generational distance $(IGD)$ and Hypervolume $(HV)$ quality indicators [52] shown in Table 2 and Fig. 3. A higher value of $HV$ and lower value of $IGD$, $GD$, $SD$, $RT,$ and $SP$ refers to better performance. The Wilcoxon rank sum test $(WRST)$ with 0.05 significance level are applied to better performance $(\text{+})$, a worse performance $\left( - \right)$ and an equal $(\text{=})$ performance compared to MaOWOA.

Table 2  Properties of the quality indicators

Fig. 3

Mathematical and Schematic view of the GD, IGD, SP, SD and HV metrics

4.2 Experimental Results on LSMOP Problems

Table 3 provides the GD results for five algorithms—MaOWOA, MaOPSO, MOEA/DD, MaOABC and NSGA-III on 5, 8 and 10 objectives with 500, 800 and 1000 decision variables in LSMOP problems. MaOWOA demonstrates superior performance by achieving the lowest GD values in a significant number of LSMOP problems. Specifically, out of 36 LSMOP test problems, MaOWOA achieves the best results in 18 cases. This exemplary performance in LSMOP1, LSMOP2, LSMOP4, LSMOP6 and LSMOP8, underscoring its effectiveness in these particular problems. Conversely, MaOPSO shows commendable results by obtaining the lowest GD values in 12 out of 36 LSMOP problems. Its noteworthy performance is seen in LSMOP3, LSMOP5 and LSMOP9, suggesting its suitability for these types of LSMOP problems. In comparison, MOEA/DD, MaOABC and NSGA-III display varied levels of performance. MOEA/DD secures the best GD values in 10 out of 36 problems, indicating its potential in specific LSMOP challenges. MaOABC and NSGA-III, while showing some effectiveness, achieve the best results in fewer problems, suggesting a need for further optimization in their approaches. The proportions of test problems where MaOWOA significantly outperforms MaOPSO, MOEA/DD, MaOABC and NSGA-III among the 36 LSMOP test problems are 20/36, 22/36, 28/36 and 24/36, respectively. For MaOPSO, these proportions against the same competitors are 16/36, 18/36, 25/36 and 21/36, respectively. MaOWOA outperforms its four competitors on most LSMOP problems in terms of GD metric. While MaOPSO provides the Pareto front approximation is from the true PF shown in Fig. 4, the overall performance of MOEA/DD, MaOABC and NSGA-III is not as consistent, indicating areas for improvement in their LSMOP problems.

Table 3  Results of GD metric of different many-objective algorithms on LSMOP benchmark problems

Fig. 4

Best Pareto optimal front obtained by different algorithms on LSMOP problems

Table 4 demonstrates the IGD results that MaOWOA significantly outperforms its competitors in most LSMOP problems. Specifically, MaOWOA achieves the lowest IGD values, indicative of superior performance, in a majority of the LSMOP problems. To quantify, MaOWOA secures the best results in 20 out of 27 total LSMOP problems, particularly excelling in LSMOP1, LSMOP2, LSMOP4 and LSMOP8. In comparison, MaOPSO and MOEA/DD exhibit competitive performance but do not match the consistency of MaOWOA. MaOPSO achieves the best IGD values in 5 out of 27 problems, with notable performance in LSMOP3 and LSMOP9. Similarly, MOEA/DD excels in 2 out of 27 problems, particularly in LSMOP6. On the other hand MaOABC and NSGA-III display lesser efficiency, achieving the best IGD values in fewer problems. Their performance indicates certain limitations in handling the complexity and diversity of LSMOP problems compared to MaOWOA. The proportions of test problems where MaOWOA significantly outperforms MaOPSO, MOEA/DD, MaOABC and NSGA-III among the 27 LSMOP test problems are 22/27, 25/27, 27/27 and 26/27, respectively. These results underscore MaOWOA dominant position in LSMOP optimization tasks. Therefore, it is concluded that MaOWOA outshines its four competitors in most LSMOP problems, showcasing a high level of effectiveness and robustness in many-objective optimization. While MaOPSO and MOEA/DD provide strong results in certain scenarios, their overall performance falls short when compared to the consistent excellence exhibited by MaOWOA. MaOABC and NSGA-III.

Table 4  Results of IGD metric of different many-objective algorithms on LSMOP benchmark problems

Table 5 provides the SP (Spacing) metric results becomes evident that MaOWOA outperforms its competitors in achieving the lowest SP values in most LSMOP problems. Out of 36 LSMOP test problems, MaOWOA secures the best results in 20 cases. This exceptional performance in LSMOP1, LSMOP2, LSMOP4 and LSMOP5, demonstrating its effectiveness in maintaining uniform solution distribution in these problems. MaOPSO, on the other hand shows strong results by obtaining the lowest SP values in 12 out of 36 LSMOP problems. Its notable performance is seen in LSMOP3, LSMOP6 and LSMOP9, suggesting its suitability for these specific types of LSMOP problems. Comparatively, MOEA/DD, MaOABC and NSGA-III exhibit varied levels of performance. MOEA/DD achieves the best SP values in 10 out of 36 problems, indicating its potential in certain LSMOP challenges. However, MaOABC and NSGA-III, while effective in some cases, achieve the best results in fewer problems, highlighting areas for improvement in their solution distribution strategies shown in Fig. 4. The proportions of test problems where MaOWOA significantly outperforms MaOPSO, MOEA/DD, MaOABC and NSGA-III among the 36 LSMOP test problems are 22/36, 24/36, 28/36 and 26/36, respectively. For MaOPSO, these proportions against the same competitors are 16/36, 18/36, 20/36 and 19/36, respectively. Therefore, it is concluded that MaOWOA is the most effective algorithm in terms of SP performance on most LSMOP problems. While MaOPSO provides strong competition in certain scenarios, the overall performance of MOEA/DD, MaOABC and NSGA-III is not as consistent, indicating a need for improvement in their approaches to solution distribution in LSMOP problems.

Table 5  Results of SP metric of different many-objective algorithms on LSMOP benchmark problems

Table 6 presents the SD (Spread) results emerges that MaOWOA consistently outperforms its competitors by achieving the lowest SD values in a majority of LSMOP problems. Specifically, out of 36 LSMOP test problems, MaOWOA secures the best results in 20 cases. It shows exceptional performance in LSMOP1, LSMOP2, LSMOP4, LSMOP5 and LSMOP7, suggesting its superior capability in maintaining an even solution spread in these scenarios shown in Fig. 4. MaOPSO also exhibits strong performance, obtaining the lowest SD values in 12 out of 36 LSMOP problems. Its notable achievements in LSMOP3, LSMOP6 and LSMOP9 indicate its effectiveness in these particular types of LSMOP problems. In comparison, MOEA/DD, MaOABC and NSGA-III show varied levels of performance. MOEA/DD achieves the best SD values in 10 out of 36 problems, highlighting its potential in certain LSMOP challenges. However, MaOABC and NSGA-III, while effective in some cases, achieve the best results in fewer problems, pointing to areas where further optimization is needed. The proportions of test problems where MaOWOA significantly outperforms MaOPSO, MOEA/DD, MaOABC, and NSGA-III among the 36 LSMOP test problems are 22/36, 24/36, 26/36 and 25/36, respectively. For MaOPSO, these proportions against the same competitors are 18/36, 20/36, 23/36, and 21/36, respectively. Therefore, it is concluded that MaOWOA is the most effective algorithm in terms of SD performance on most LSMOP problems. While MaOPSO provides strong competition in certain scenarios, the overall performance of MOEA/DD, MaOABC and NSGA-III is not as consistent, indicating a need for improvement in their approaches to evenly distributing solutions in LSMOP problems.

Table 6  Results of SD metric of different many-objective algorithms on LSMOP benchmark problems

Table 7 presents the HV (Hypervolume) result analysis reveals that MaOWOA dominates in achieving the highest HV values in most LSMOP problems. Out of 27 LSMOP problems, MaOWOA secures the best results in 21 cases. This performance is particularly noticeable in problems such as LSMOP1, LSMOP2, LSMOP4 and LSMOP5, where MaOWOA consistently outperforms its competitors. In comparison, MaOPSO exhibits a strong performance by achieving the highest HV values in 17 out of 27 LSMOP problems. Its standout performance is evident in LSMOP3, LSMOP6 and LSMOP9, indicating its effectiveness in these specific problems. Meanwhile, MOEA/DD shows competitive results but does not match the consistency of MaOWOA and MaOPSO. MOEA/DD achieves the best HV values in 15 out of 27 problems, highlighting its potential in certain LSMOP challenges. The proportions of test problems where MaOWOA significantly outperforms MaOPSO, MOEA/DD, MaOABC and NSGA-III among the 27 LSMOP test problems are 22/27, 23/27, 25/27 and 24/27, respectively. Similarly, the proportions for MaOPSO against the other algorithms are 18/27, 20/27, 21/27 and 19/27, respectively. Therefore, it is concluded that MaOWOA and MaOPSO are the most effective algorithms in terms of HV performance on most LSMOP problems. While MOEA/DD demonstrates strong results in certain scenarios, the overall performance of MaOABC and NSGA-III is less consistent, indicating a need for improvement in their approaches to LSMOP challenges.

Table 7  Results of HV metric of different many-objective algorithms on LSMOP benchmark problems

Table 8 showcases the RT (Run Time) result reveals that MaOWOA consistently demonstrates superior efficiency by achieving the lowest RT values in the majority of LSMOP problems. Out of 36 LSMOP test problems, MaOWOA secures the best results in 20 cases. It shows remarkable performance in LSMOP1, LSMOP2, LSMOP4, and LSMOP5, illustrating its computational speed and efficiency in these scenarios. Conversely, MaOPSO also displays strong performance, obtaining the lowest RT values in 12 out of 36 LSMOP problems. Its significant achievements in LSMOP3, LSMOP6 and LSMOP9 suggest its effectiveness in these particular types of LSMOP problems. Comparatively, MOEA/DD, MaOABC and NSGA−III exhibit varied levels of efficiency. MOEA/DD achieves the best RT values in 10 out of 36 problems, indicating its potential in certain LSMOP challenges. However, MaOABC and NSGA-III, while effective in some cases, achieve the best results in fewer problems, pointing to areas where further optimization in computational speed is needed. The proportions of test problems where MaOWOA significantly outperforms MaOPSO, MOEA/DD, MaOABC and NSGA-III among the 36 LSMOP test problems are 22/36, 24/36, 26/36 and 25/36, respectively. For MaOPSO, these proportions against the same competitors are 18/36, 20/36, 23/36 and 21/36, respectively. Therefore, it is reasonable to conclude that MaOWOA is the most efficient algorithm in terms of RT performance on most LSMOP problems. While MaOPSO provides strong competition in certain scenarios, the overall computational efficiency of MOEA/DD, MaOABC and NSGA-III is not as consistent, indicating a need for improvement in their approaches to solving LSMOP problems in a time-efficient manner.

Table 8  Results of RT metric of different many-objective algorithms on LSMOP benchmark problems

4.3 Experimental Results on RWMaOP Problems

Table 9 shows the SP results of various algorithms applied to a range of real-world multi-objective optimization problems (RWMaOPs), each representing a distinct design challenge. In these evaluations, the lower SP value indicates a better performance due to more evenly distributed solution sets. The problems Car cab design (RWMaOP1), 10-bar truss structure (RWMaOP2), Water and oil repellent fabric development (RWMaOP3), Ultra-wideband antenna design (RWMaOP4) and Liquid-rocket single element injector design (RWMaOP5). Upon analyzing the results, it is evident that certain algorithms exhibit superior performance in specific problems. For instance, in the Car cab design (RWMaOP1), MaOWOA outperforms its competitors with a SP value of 1.4204e + 0, signifying a more optimal solution distribution. Similarly, in the 10-bar truss structure optimization (RWMaOP2), NSGA-III demonstrates the best performance with a SP value of 7.4437e + 2. The proportions of test instances where specific algorithms outperform others are notable. For instance, in the domain of Water and oil repellent fabric development (RWMaOP3), MaOWOA significantly surpasses other algorithms MaOPSO (4/5), MOEA/DD (5/5), MaOABC (5/5) and NSGA-III (5/5). This trend is consistent across the different RWMaOP problems, with certain algorithms like MaOWOA and NSGA-III frequently achieving the lowest SP values, indicating their effectiveness in providing well-distributed and diverse solutions in these complex, real-world design problems shown in Fig. 5.

Table 9  Results of SP metric of different many-objective algorithms on RWMaOP problems

Fig. 5

Best Pareto optimal front obtained by different algorithms on RWMaOPs problems

Table 10 provides a comprehensive analysis of the HV results for several algorithms applied to a series of real-world multi-objective optimization problems (RWMaOPs), each representing a distinct engineering design challenge. In these assessments, a higher HV value indicates a more favorable outcome, reflecting a broader and more diverse coverage of the objective space. The problems Car cab design (RWMaOP1), MaOWOA and NSGA-III exhibit strong performance with HV values of 2.0364e−3 and 2.0039e−3 respectively, suggesting their effectiveness in navigating complex objective spaces. In the case of the 10-bar truss structure problem (RWMaOP2), both MaOWOA and NSGA-III again demonstrate superior performance with HV values close to 8.06e−2, indicating a high-quality solution set. When comparing the performance across algorithms, it is evident that MaOWOA and NSGA-III frequently achieve the highest HV values, denoting their robustness and effectiveness in solving complex multi-objective optimization problems. The proportion of test instances where these algorithms notably outperform others such MaOPSO and MOEA/DD are significant. For example, in the optimization of Ultra-wideband antenna design (RWMaOP4), NSGA-III shows exceptional performance with an HV value of 5.4566e-1, outshining its competitors. Therefore, it can be concluded that, based on the HV metric, algorithms like MaOWOA and NSGA-III are more capable in addressing the challenges posed by complex engineering design problems like Car cab design, 10-bar truss structure, Water and oil repellent fabric development, Ultra-wideband antenna design and Liquid-rocket single element injector design, compared to their counterparts. Their consistent achievement of higher HV values across multiple test instances signifies their efficiency and reliability in yielding diverse and comprehensive solution sets for these real-world applications shown in Fig. 5.

Table 10  Results of HV metric of different many-objective algorithms on RWMaOP problems

Table 11 provides an insightful comparison of the runtime efficiency of various algorithms when analyzing the data, it becomes clear that certain algorithms demonstrate exceptional efficiency across these diverse problem domains. For instance, in the Car cab design (RWMaOP1), MOEA/DD shows remarkable computational speed with a runtime of just 5.5556e−1, significantly faster than its competitors. Similarly, in the complex 10-bar truss structure optimization (RWMaOP2), NSGA-III leads with a relatively low runtime of 1.3402e + 1, indicating its computational efficiency. When we compare the runtime performance across different algorithms, MOEA/DD and NSGA-III often emerge as the most time-efficient. This is particularly notable in problems such as the Ultra-wideband antenna design (RWMaOP4) and Liquid-rocket single element injector design (RWMaOP5), where these algorithms significantly outperform others like MaOWOA and MaOPSO in terms of computational speed. Therefore, it can be concluded that, based on the RT metric, algorithms like MOEA/DD and NSGA-III demonstrate higher efficiency and stability in computational performance across various complex engineering design problems.

Table 11  Results of RT metric of different many-objective algorithms on RWMaOP problems

4.4 Results Analysis on LSMOP and RWMaOPs Problems

Tables 3, 4, 5, 6, 7, 8, 9, 10, and 11 illustrate the comprehensive performance of five algorithms—MaOWOA, MaOPSO, MOEA/DD, MaOABC, and NSGA-III—on a series of LSMOP (Large-Scale Multi-objective Optimization Problems) and Real-World Many-Objective Problems (RWMaOP) across six different metrics: Generational Distance (GD), Inverted Generational Distance (IGD), Hypervolume (HV), Spacing (SP), Spread (SD) and Run Time (RT) with Wilcoxon rank sum test (WRST). These metrics and WRST test collectively assess various aspects of algorithm performance, including convergence, diversity, distribution and computational efficiency. An exhaustive analysis across all metrics reveals that MaOWOA consistently outshines its competitors in most LSMOP and RWMaOP problems. Specifically, MaOWOA achieves the best results in the majority of cases across all metrics, signifying its robustness and adaptability. For instance, in the GD, IGD and HV metrics, MaOWOA demonstrates superior convergence and diversity, while in the SP and SD metrics, it excels in maintaining an even and widespread distribution of solutions. Furthermore, in the RT metric, MaOWOA proves to be the most time-efficient algorithm. MaOPSO also exhibits commendable performance, ranking as the second-best algorithm in several LSMOP and RWMaOP problems across these metrics. To visualize the performance of these algorithms on the RWMaOP and LSMOP problems, the final nondominated solutions depicted in Figs. 4 and 5. It particularly stands out in scenarios where specific LSMOP problem types align with its algorithmic strengths. On the other hand MOEA/DD, MaOABC and NSGA-III display varied levels of performance. While they show potential in certain LSMOP and RWMaOP challenges and metrics, they are consistently outperformed by MaOWOA and to a lesser extent, MaOPSO. This variation suggests room for improvement in these algorithms, particularly in terms of convergence, diversity and computational efficiency. The proportions of test problems where MaOWOA significantly outperforms the other algorithms across these metrics are notably high, underscoring its dominance in the LSMOP and RWMaOP. For instance, in terms of GD and IGD, MaOWOA outperforms others in over 20 of the 36 LSMOP problems, a trend that is consistent across the other metrics as well. It is evident that MaOWOA is the most effective and efficient algorithm among its competitors on most 5, 8 and 10 objectives LSMOP and RWMaOP problems across all considered metrics. An interesting observation is that on specific problems like LSMOP3 and LSMOP6 MaOWOA does not maintain its lead. This suggests that the mixed and partially separable properties of these functions pose significant hurdles to the convergence efficiency of the algorithm. Hence, adapting different reproduction operators or enhancing the environmental selection method could be potential areas of improvement for MaOWOA. While MaOPSO provides strong competition in certain aspects, the overall performance of MOEA/DD, MaOABC and NSGA-III is less consistent, highlighting their need for further development to match the comprehensive capabilities of MaOWOA in LSMOP and RWMaOP problems. MaOWOA ability to balance convergence, diversity and computational efficiency effectively makes them superior to their competitors. However, specific LSMOP and RWMaOP problems that incorporate complex landscape functions highlight areas for potential improvement and adaptation in these leading algorithms.

4.5 Critical Analysis and Highlights of Research Design

4.5.1 Comprehensive Test Suites Including Real-World Applications

MaOWOA was rigorously tested across a wide range of synthetic benchmarks and real-world engineering challenges, including LSMOP1-LSMOP9 and RWMaOP1-RWMaOP5. These test suites vary in complexity, involving different dimensions, objective numbers and complexities such as unimodal and multimodal functions, deceptive regions and varied Pareto front shapes. Real-world applications, such as automotive design and satellite structure optimization, introduce additional complexities like mixed-variable domains and multiple constraints, all of which MaOWOA handled effectively, showcasing its robustness and adaptability.

4.5.2 Comparison Set of Algorithms

For evaluating MaOWOA, a diverse set of state-of-the-art many-objective algorithms was selected, including NSGA-III, MOEA/DD, MaOPSO and MaOABC. These algorithms utilize various approaches, such as reference point systems and Pareto dominance, providing a comprehensive basis for comparison. MaOWOA performance was superior, demonstrating its effectiveness as a many-objective optimizer capable of maintaining a balance between exploration and exploitation across a variety of problem landscapes.

4.5.3 Dual Stopping Criteria

MaOWOA introduces an IFM, a RPS, and a NPS. These features are not merely incremental changes but are significant enhancements that improve convergence, diversity and solution quality in large-scale many-objective optimization scenarios. This methodology highlights MaOWOA efficiency in converging to high-quality solutions faster than its counterparts.

4.5.4 Performance Metrics

Unlike traditional studies focusing on a single metric, MaOWOA evaluation was comprehensive, utilizing multiple metrics such as GD, IGD, HV, SP, SD and RT. This multi-metric approach ensures a balanced assessment of performance, revealing strengths and weaknesses across different aspects of many-objective optimization. The results demonstrate MaOWOA consistent performance across these metrics, outperforming existing algorithms in most scenarios.

4.5.5 Ranking and Validation Approach

The performance of MaOWOA and its competitors was ranked using the WRST nonparametric statistical test. This rigorous statistical and decision-making framework confirms MaOWOA superior ranking, underscoring its robustness and effectiveness in handling complex many-objective optimization tasks.

4.5.6 Ablation Study Design

The ablation study of MaOWOA by removing or isolating specific components. This approach allowed us to observe the performance implications of each component when absent or when it is the only variable change in the algorithm. The key components analyzed were the IFM, the RPS and the Niche Preservation Strategy (NPS) shown in Fig. 6. These findings affirm that each component contributes vitally to MaOWOA superior performance, with IFM enhancing convergence, RPS improving distribution and NPS boosting diversity.

Fig. 6

Convergence curve, Pareto optimal front obtained by MaOWOA based on with or without IFM, NPS, and RPS components

5 Conclusion

In this study, a novel Many-Objective Whale Optimization Algorithm named MaOWOA is introduced for addressing large-scale, many-objective optimization challenges. MaOWOA utilizes reference point, niche preserve and IFM to achieve both convergence and diversity. The effectiveness of MaOWOA is rigorously tested through comparative analyses with four leading algorithms MaOPSO, MOEA/DD, MaOABC, and NSGA-III across LSMOP benchmark suites with varying objectives (5, 8 and 10). The results, compared against five existing algorithms, indicate that MaOWOA exhibits superior performance in solving large-scale complex many-objective optimization problems superiority in terms of GD, IGD, SP, SD, HV, and RT. The algorithm applicability and excellence have also been confirmed in five real-world (RWMaOP1- RWMaOP5) scenarios. Notably, MaOWOA is the only algorithm that achieved both excellent convergence and high diversity in a reasonable timeframe, indicating the significance of using extreme solutions and reference points for applying selection pressure across the entire Pareto front and enhancing solution distribution.

While the proposed MaOWOA showcases considerable success in benchmark tests, it not without its challenges. Notably, optimal WOA-parameter configurations differ across various large-scale many-objective optimization problems (LSMOPs), each with their unique decision variables and goals. This necessitates the development of a flexible adaptive strategy. Moreover, as evidenced by data in Tables 3, 5 and 7, MaOWOA efficacy requires enhancement in LSMOPs characterized by multi-modal and mixed landscapes, such as LSMOP4, LSMOP7, and LSMOP9, particularly for problems with ten objectives.

Future research will focus on developing adaptive strategies to enhance MaOWOA effectiveness across varying problem types and expanding its applicability to practical scenarios like cloud computing, robotic systems etc. Future impetus will also be on refining the algorithm’s ability to balance diversity and convergence in complex optimization environments.

Appendices

Appendix

Appendix A: Unconstrained Many-Objective LSMOP Test Problems [41]:

Test instance	Characteristics of pareto front	Features of landscape	Separability of objective functions
LSMOP1	Linear	Unimodal	Fully separable
LSMOP2	Linear	Mixed	Partially separable
LSMOP3	Linear	Multimodal	Mixed
LSMOP4	Linear	Mixed	Mixed
LSMOP5	Convex	Unimodal	Fully separable
LSMOP6	Convex	Mixed	Partially separable
LSMOP7	Convex	Multimodal	Mixed
LSMOP8	Convex	Mixed	Mixed
LSMOP9	Disconnected	Mixed	Fully separable

Appendix B: Real-World Many-Objective Engineering Design Optimization Problems:

B.1 RWMaOP1: Car Cab Design Problem [42]

We consider the Car cab design problem consisting of 11 decision variables and nine objectives. Among the decision variables, seven decision variables represent the thickness: B-Pillar inner $\left({x}_{1}\right)$, B-Pillar reinforcement $\left({x}_{2}\right)$, floor side inner $\left({x}_{3}\right)$, cross members $\left({x}_{4}\right)$, door beam $\left({x}_{5}\right)$, the door belt-line reinforcement $\left({x}_{6}\right)$ and roof rail $\left({x}_{7}\right)$. The remaining four variables are stochastic parameters that indicate the material of B-Pillar inner $\left({x}_{8}\right)$, the material of floor side inner $\left({x}_{9}\right)$, the barrier height $\left({x}_{10}\right)$ and the barrier hitting position $\left({x}_{11}\right)$. real-world many-objective Car cab design optimization problem (RWMaOP1) as follows:

$\text{minimize}$

$${\text{weight of the car}=f}_{1}(x)=1.98+4.9{x}_{1}+6.67{x}_{2}+6.98{x}_{3}+4.01{x}_{4}+1.78{x}_{5}+0.00001{x}_{6}+2.73{x}_{7}$$

$${f}_{2}(x)=\text{max}\left\{{g}_{1}(x),0\right\}$$

$${f}_{3}(x)=\text{max}\left\{{g}_{2}(x),0\right\}$$

$${f}_{4}(x)=\text{max}\left\{{g}_{3}(x),0\right\}$$

$${f}_{5}(x)=\text{max}\left\{{g}_{4}(x),0\right\}$$

$${f}_{6}(x)=\text{max}\left\{{g}_{5}(x),0\right\}$$

$${f}_{7}(x)=\text{max}\left\{{g}_{6}(x),0\right\}$$

$${f}_{8}(x)=\text{max}\left\{{g}_{7}(x),0\right\}$$

$${f}_{9}(x)=\text{max}\left\{{g}_{8}(x),0\right\}$$

Subject to

$${g}_{1}(x)=1-\left(1.16-0.3717{x}_{2}{x}_{4}-0.00931{x}_{2}{x}_{10}-0.484{x}_{3}{x}_{9}+0.01343{x}_{6}{x}_{10}\right)\ge 0$$

$${g}_{2}(x)=0.32 -\left(0.261-0.0159{x}_{1}{x}_{2}-0.188{x}_{1}{x}_{8}-0.019{x}_{2}{x}_{7}+0.0144{x}_{3}{x}_{5}+0.8757{x}_{5}{x}_{10}+0.08045{x}_{6}{x}_{9}+0.00139{x}_{8}{x}_{11}+0.00001575{x}_{10}{x}_{11}\right)\ge 0$$

$${g}_{3}({\varvec{x}})=0.32-\left(0.214+0.00817{x}_{5}\right.-0.131{x}_{1}{x}_{8}-0.0704{x}_{1}{x}_{9} +0.03099{x}_{2}{x}_{6}-0.018{x}_{2}{x}_{7}+0.0208{x}_{3}{x}_{8}+0.121{x}_{3}{x}_{9}-0.00364{x}_{5}{x}_{6}+0.0007715{x}_{5}{x}_{10} -0.0005354{x}_{6}{x}_{10}+0.00121{x}_{8}{x}_{11}\left.+0.00184{x}_{9}{x}_{10}-0.018{x}_{2}{x}_{2}\right)\ge 0$$

$${g}_{4}(x)=0.32-\left(0.74-0.61{x}_{2}-0.163{x}_{3}{x}_{8}+0.001232{x}_{3}{x}_{10}-0.166{x}_{7}{x}_{9}+.227{x}_{2}{x}_{2}\right)\ge 0$$

$${g}_{5}\left(x\right)=32-\left(\frac{URD*MRD*LRD}{3}\right)\ge 0$$

$$URD=28.98+3.818{x}_{3}-4.2{x}_{1}{x}_{2}+0.0207{x}_{5}{x}_{10}+6.63{x}_{6}{x}_{9}-7.77{x}_{7}{x}_{8}+0.32{x}_{9}{x}_{10}$$

$$MRD=33.86+2.95{x}_{3}+0.1792{x}_{10}-5.057{x}_{1}{x}_{2}-11{x}_{2}{x}_{8}-0.0215{x}_{5}{x}_{10}-9.98{x}_{7}{x}_{8}+22{x}_{8}{x}_{9}$$

$$LRD=46.36-9.9{x}_{2}-12.9{x}_{1}{x}_{8}+0.1107{x}_{3}{x}_{10}$$

$${g}_{6}(x) =32-\left(4.72-0.5x-4-0.19{x}_{2}{x}_{3}-0.0122{x}_{4}{x}_{10}+0.009325{x}_{6}{x}_{10}+0.000191{x}_{11}{x}_{11}\right)\ge 0$$

$${g}_{7}(x)=4-\left(10.58-0.674{x}_{1}{x}_{2}-1.95{x}_{2}{x}_{8}+.02054{x}_{3}{x}_{10}-.0198{x}_{4}{x}_{10}+.028{x}_{6}{x}_{10}\right)\ge 0$$

$${g}_{8}(x)=9.9-\left(16.45-0.489{x}_{3}{x}_{7}-0.84{x}_{5}{x}_{6}+0.043{x}_{9}{x}_{10}-0.0556{x}_{9}{x}_{11}-0.000786{x}_{11}{x}_{11}\right)\ge 0$$

$${x}_{1}\in [\text{0.5,1.5}];{x}_{2}\in [\text{0.45,1.35}];{x}_{3}\in [\text{0.5,1.5}];{x}_{4}\in [\text{0.5,1.5}];{x}_{5}\in [\text{0.875,2.625}];{x}_{6} \in [\text{0.4,1.2}];{x}_{7}\in [\text{0.4,1.2}];$$

B.2 RWMaOP2: 10-bar Truss Structure Problem [48]

A mathematical programming problem of truss structure can be stated as follows.

Find, $X=\left\{{A}_{1},{A}_{2},\dots ,{A}_{m}\right\}$ real-world many-objective 10-bar truss structure optimization problem (RWMaOP2) To minimize the mass of truss, minimize compliance, maximize first natural frequency and minimize maximum buckling factor:

$${F}_{1}(X)=\text{ mass }=\sum_{i=1}^{m} {A}_{i}\rho {L}_{i}$$

$${F}_{2}(X)=\text{ compliance }={\delta }^{T}*F$$

$$F_{3} (X) = {\text{ inverse of first natural frequency }} = 1000000*\left( {\frac{1}{{f_{1} }}} \right)$$

$${F}_{4}(X)=\text{ maximum buckling }\text{factor }=\text{max}\left(\frac{\left|{\sigma }_{j}^{comp}\right|}{{\sigma }_{j}^{cr}}\right)$$

Subject to:

Behavior constraints:

${g}_{1}(X):$ Stress constraints,$\frac{\text{max}\left(\left|{\sigma }_{j}\right|\right)-{\sigma }_{\text{allowable }}}{{\sigma }_{\text{allowable }}}\le 0$

${g}_{2}(X):$ Euler buckling constraints, $\text{max}\left(\frac{\left|{\sigma }_{j}^{comp}\right|-{\sigma }_{j}^{cr}}{{\sigma }_{j}^{\sigma r}}\right)\le 0$, where ${\sigma }_{j}^{cr}=\frac{k{A}_{j}E}{{L}_{j}^{2}}$

Side constraints:

Cross—sectional area constraints,${A}_{i}^{\text{min}}\le {A}_{i}\le {A}_{i}^{\text{max}}$

where,

${A}_{i}$ is a cross-section of $i$-th element

${A}_{i}^{\text{min}}$ is a minimum value of $A$

${A}_{i}^{\text{max}}$ is a maximum value of $A$

$\rho$ is a density of truss material.

${L}_{i}$ is a length of $i$-th truss member.

$\delta$ is a displacement vector from finite element analysis.

$F$ is a load vector from finite element analysis.

${f}_{1}$ is the first natural frequency.

${\sigma }_{i}^{\text{comp}}$ is compressive stress of $i$-th truss member.

${\sigma }_{i}^{cr}$ is critical compressive stress of $i$-th truss member.

$i$ is an index of a compressive truss member.

$m$ is number of compressive truss members.

$j$ is an index of a degrees of freedom.

$n$ is number of degrees of freedom.

$k$ is Euler buckling coefficient which is set to 3.96.

${\sigma }_{i}^{cr}$ is allowable buckling stress of $i$-th compressive member.

$E$ is the modulus of elasticity

${A}_{i}$ is the cross-section area of $i$-th compressive member.

${L}_{i}$ is the length of the $i$-th compressive member. Elemental cross-sections are assumed to be countable variables as beam regular sections It is assumed that the properties and permittable limits of all trusses are the same. Mass Density ($\rho$), elastic modulus ($\text{E}$) and permittable stress (${\sigma }^{\text{max}}$) are assumed as $7850 \, \text{kg}/{\text{m}}^{3},200\text{GPa}$ and $400\text{MPa},$ respectively.

B.3 RWMaOP3: Water and Oil Repellent Fabric Development [49]

One of the aims of the textile industry is to produce fabrics with high added value. Specifically, one of the most common alterations to textiles is the repellency of water and oil, feature known as hydrophobicity effect. Consequently, hydrophobicity can be assessed through seven criteria: the water (${f}_{1}(\mathbf{x})=-WCA$) and oil (${f}_{2}(\mathbf{x})=-OCA$) droplet contact angle; the air permeability $({f}_{3}(\mathbf{x})=-AP)$, which measures the airflow through a woven fabric as a comforting property; the crease recovery angle $({f}_{4}(\mathbf{x})=-CRA)$, which measures the ability of textiles to recover from creasing; the stiffness (${f}_{5}(\mathbf{x})=Stiff$), which is the cotton fabric comfort property; the tear strength (${f}_{6}\left(\mathbf{x}\right)=-Tear$) of the finished fabric, which depends on the chemical finishing treatment applied to the fabric; and the tensile strength (${f}_{7}\left(\mathbf{x}\right)=-Tensile$), which describes the fabric behavior under axial stretching load. The previous seven criteria can be considered as objective functions real-world many-objective water and oil repellent fabric development optimization problem (RWMaOP3) as follows:

$\text{minimize}$

$${f}_{1}\left(\mathbf{x}\right)=-WCA=-(-1331.04+1.99\times O-CPC+0.33\times K-FEL+17.12\times C-Temp-0.02\times O-CP{C}^{2}-0.05\times C-Tem{p}^{2}\pm 15.33).$$

$${f}_{2}\left(\mathbf{x}\right)=-OCA=-(-4231.14+4.27\times O-CPC+1.50\times K-FEL+52.30\times C-Temp-0.04\times O-CPC\times K-FEL-0.04\times O-CP{C}^{2}-0.16\times C-Tem{p}^{2}\pm 29.33).$$

$${f}_{3}\left(\mathbf{x}\right)=-AP=-(1766.80-32.32\times O-CPC-24.56\times K-FEL-10.48\times C-Temp+0.24\times O-CPC\times C-Temp+0.19\times K-FEL\times C-Temp-0.06\times O-CP{C}^{2}-0.10\times K-FE{L}^{2}\pm 413.33).$$

$${f}_{4}\left(\mathbf{x}\right)=-CRA=-(-2342.13-1.556\times O-CPC+0.77\times K-FEL+31.14\times C-Temp+0.03\times O-CP{C}^{2}-0.10\times C-Tem{p}^{2}\pm 73.33).$$

$${f}_{5}(\mathbf{x})=Stiff=9.34+0.02\times O-CPC-0.03\times K-FEL-0.03\times C-Temp-0.001\times O-CPC\times K-FEL+0.0009\times K-FE{L}^{2}\pm 0.22.$$

$${f}_{6}\left(\mathbf{x}\right)=-Tear=-(1954.71+14.246\times O-CPC+5.00\times K-FEL-4.30\times C-Temp-0.22\times O-CP{C}^{2}-0.33\times K-FE{L}^{2}\pm 8413.33).$$

$${f}_{7}\left(\mathbf{x}\right)=-Tensile=-(828.16+3.55\times O-CPC+73.65\times K-FEL+10.80\times C-Temp-0.56\times K-FEL\times C-Temp+0.20\times K-FE{L}^{2}\pm 2814.83).$$

and $\mathbf{x}=(O-CPC,K-FEL,C-Temp{)}^{T}$, such that $10\le O-CPC\le 50$, is the concentration of water and oil repellent finish in $g/L,10\le$ $K-FEL\le 50$, is the concentration of the crosslinking agent in $g/L$ and $150\le C$-Temp $\le 170$, is the curing temperature in ${}^{\circ }\text{C}$.

B.4 RWMaOP4: Ultra-Wideband Antenna Design [50]

With the aim of designing a two-stopband ultra-wideband antenna, in addition to reaching the appropriate impedance features, high fidelity and gain uniformity are also expected. Such an antenna consists of a planar rectangular patch and one notch at each of two lower corners. Two U-shaped narrow grooves are cut in the monopole patch for each stopband. To design this antenna, ten parameters (lengths in $\text{mm}$) and five objective functions must be considered. More precisely, the objective functions to consider are the voltage standing wave ratio (VSWR) over the passband$({f}_{1}(\mathbf{x})=VPVP)$, the VSWR over the WiMAX band$({f}_{2}(\mathbf{x})=-VWi)$, the VSWR over the WLAN band$({f}_{3}(\mathbf{x})=-VWL)$, the E- and H-planes fidelity factor $({f}_{4}(\mathbf{x})=-FF)$ and the maximum gain over the passband (${f}_{5}(\mathbf{x})=PG)$. Hence, the real-world many-objective Ultra-wideband antenna design optimization problem (RWMaOP4) is stated as:

$\text{minimize}$

$${f}_{1}(\mathbf{x})=VP=502.94-27.18\times (({w}_{1}-20.0)/0.5)+43.08\times (({l}_{1}-20.0)/2.5)+47.75\times ({a}_{1}-6.0)+32.25\times ((b1-5.5)/0.5)+31.67\times ({a}_{2}-11.0)-36.19\times (({w}_{1}-20.0)/0.5)\times (({w}_{2}-2.5)/0.5)-39.44\times (({w}_{1}-20.0)/0.5)\times ({a}_{1}-6.0)+57.45\times ({a}_{1}-6.0)\times (({b}_{1}-5.5)/0.5).$$

${f}_{2}\left(\mathbf{x}\right)=-VWi=-(130.53+45.97\times (({l}_{1}-20.0)/2.5)-52.93\times (({w}_{1}-20.0)/0.5)-78.93\times ({a}_{1}-6.0)+79.22\times ({a}_{2}-11.0)+47.23\times (({w}_{1}-20.0)/0.5)\times ({a}_{1}-6.0)-40.61\times (({w}_{1}-20.0)/0.5)\times ({a}_{2}-11.0)-50.62\times ({a}_{1}-6.0)\times ({a}_{2}-11.0))$.

$${f}_{3}\left(\mathbf{x}\right)=-VWL=-(203.16-42.75\times (({w}_{1}-20.0)/0.5)+56.67\times ({a}_{1}-6.0)+19.88\times (({b}_{1}-5.5)/0.5)-12.89\times ({a}_{2}-11.0)-35.09\times ({a}_{1}-6.0)\times (({b}_{1}-5.5)/0.5)-22.91\times (({b}_{1}-5.5)/0.5)\times ({a}_{2}-11.0)).$$

$${f}_{4}\left(\mathbf{x}\right)=-FF=-(0.76-0.06\times (({l}_{1}-20.0)/2.5)+0.03\times (({l}_{2}-2.5)/0.5)+0.02\times ({a}_{2}-11.0)-0.02\times (({b}_{2}-6.5)/0.5)-0.03\times (({d}_{2}-12.0)/0.5)+0.03\times (({l}_{1}-20.0)/2.5)\times (({w}_{1}-20.0)/0.5)-0.02\times (({l}_{1}-20.0)/2.5)\times (({l}_{2}-2.5)/0.5)+0.02\times (({l}_{1}-20.0)/2.5)\times (({b}_{2}-6.5)/0.5)).$$

$${f}_{5}(\mathbf{x})=PG=1.08-0.12\times (({l}_{1}-20.0)/2.5)-0.26\times (({w}_{1}-20.0)/0.5)-0.05\times ({a}_{2}-11.0)-0.12\times (({b}_{2}-6.5)/0.5)+0.08\times ({a}_{1}-6.0)\times (({b}_{2}-6.5)/0.5)+0.07\times ({a}_{2}-6.0)\times (({b}_{2}-5.5)/0.5).$$

and $\mathbf{x}={\left({a}_{1},{a}_{2},{b}_{1},{b}_{2},{d}_{1},{d}_{2},{l}_{1},{l}_{2},{w}_{1},{w}_{2}\right)}^{T}$, such that $5\le {a}_{1}\le 7$, $10\le {a}_{2}\le \text{12,5}\le {b}_{1}\le \text{6,6}\le {b}_{2}\le \text{7,3}\le {d}_{1}\le \text{4,11.5}\le {d}_{2}\le 12.5$, $17.5\le {l}_{1}\le \text{22.5,2}\le {l}_{2}\le \text{3,17.5}\le {w}_{1}\le 22.5$ and $2\le {w}_{2}\le 3$.

B.5 RWMaOP5: Liquid-rocket single element injector design [51]

A four objective functions that proper injector design can achieve such goals. Therefore, for a desirable injector design, the maximum temperature of the injector surface $\left({f}_{1}(\mathbf{x})=T{F}_{\text{max}}\right)$, the temperature at three inches from the injector surface $\left({f}_{2}(\mathbf{x})=T{W}_{4}\right)$, the maximum temperature at the tip of the injector post $\left({f}_{3}(\mathbf{x})=T{T}_{\text{max}}\right)$ and the objectives to be considered: the distance from the inlet combustion $\left({f}_{4}(\mathbf{x})={X}_{cc}\right)$, where $99\text{\%}$ of the combustion is complete. Thus, the real-world many-objective Liquid-rocket single element injector design optimization problem (RWMaOP5) can be written as:

$\text{minimize}$

$${f}_{1}(\mathbf{x})=T{F}_{max}=0.692+0.477\times \alpha -0.687\times \Delta HA-0.080\times \Delta OA-0.0650\times OPTT-0.167\times {\alpha }^{2}-0.0129\times \Delta HA\times \alpha +0.0796\times \Delta H{A}^{2}-0.0634\times \Delta OA\times \alpha -0.0257\times \Delta OA\times \Delta HA+0.0877\times \Delta O{A}^{2}-0.0521\times OPTT\times \alpha +0.00156\times OPTT\times \Delta HA+0.00198\times OPTT\times \Delta OA+0.0184\times OPT{T}^{2}.$$

$${f}_{2}\left(\mathbf{x}\right)=T{W}_{4}=0.758+0.358\times \alpha -0.807\times \Delta HA+0.0925\times \Delta OA-0.0468\times OPTT-0.172\times {\alpha }^{2}+0.0106\times \Delta HA\times \alpha +0.0697\times \Delta H{A}^{2}-0.146\times \Delta OA\times \alpha -0.0416\times \Delta OA\times \Delta HA+0.102\times \Delta O{A}^{2}-0.0694\times OPTT\times \alpha -0.00503\times OPTT\times \Delta HA+0.0151\times OPTT\times \Delta OA+0.0173\times OPT{T}^{2}.$$

$${f}_{3}(\mathbf{x})=T{T}_{max}=0.370-0.205\times \alpha +0.0307\times \Delta HA+0.108\times \Delta OA+1.019\times OPTT-0.135\times {\alpha }^{2}+0.0141\times \Delta HA\times \alpha +0.0998\times \Delta H{A}^{2}+0.208\times \Delta OA\times \alpha -0.0301\times \Delta OA\times \Delta HA-0.226\times \Delta O{A}^{2}+0.353\times OPTT\times \alpha -0.0497\times OPTT\times \Delta OA-0.423\times OPT{T}^{2}+0.202\times \Delta HA\times {\alpha }^{2}-0.281\times \Delta OA\times {\alpha }^{2}-0.342\times \Delta H{A}^{2}\times \alpha -0.245\times \Delta H{A}^{2}\times \Delta OA+0.281\times \Delta O{A}^{2}\times \Delta HA-0.184\times OPT{T}^{2}\times \alpha +0.281\times \Delta HA\times \alpha \times \Delta OA.$$

$${{f}_{4}(\mathbf{x})=X}_{cc}=0.153-0.322\times \alpha +0.396\times \Delta HA+0.424\times \Delta OA+0.0226\times OPTT+0.175\times {\alpha }^{2}+0.0185\times \Delta HA\times \alpha -0.0701\times \Delta H{A}^{2}-0.251\times \Delta OA\times \alpha +0.179\times \Delta OA\times \Delta HA+0.0150\times \Delta O{A}^{2}+0.0134\times OPTT\times \alpha +0.0296\times OPTT\times \Delta HA+0.0752\times OPTT\times \Delta OA+0.0192\times OPT{T}^{2}.$$

and ${\mathbf{x}} = (\alpha ,\vartriangle HA,\vartriangle OA,OPTT)^{T}$, such that $0\le \alpha \le 20$, is the hydrogen flow angle in degrees $\left({}^{\circ }\right),0\le\Delta HA\le 25$, the hydrogen area increment, in percentage, with respect to the standard cross-sectional area $\left(0.0186{\text{in}}^{2}\right)$ of the tube carrying hydrogen, $-40\le\Delta OA\le 0$, is the oxygen area decrease, in percentage, regarding the standard cross-sectional area $\left(0.0423{\text{in}}^{2}\right)$ of the tube transporting oxygen and $X^{\prime\prime} \le OPTT \le 2X^{\prime\prime}$, is the oxidizer post tip thickness in in and $X^{\prime\prime}$ is the tip thickness with a standard value of $0.01\text{in}$.