1 Introduction

Multi-objective optimization (MOO) serves as a multifaceted decision-making tool, focusing on the simultaneous optimization of problems with various objective functions [1,2,3]. As a cornerstone in fields ranging from economics to informatics to engineering. MOO aids in deriving optimal decisions by evaluating trade-offs between different objectives [4,5,6]. The significance of MOO in addressing real-world problems is substantial [7,8,9].

Addressing multi-objective issues generally yields a collection of compromise solutions, known as the Pareto optimal set [10]. Three core classifications utilizing stochastic optimization algorithms for handling these problems are a priori, a posteriori and interactive. In the a priori category, several objectives consolidate into a singular one [11], emphasizing the weight of each objective as perceived by decision-makers. Once combined, conventional single-objective algorithms can identify the optimal solution without alterations. Although computationally efficient, this method has limitations: it may require multiple algorithms runs to achieve the Pareto optimal set and can struggle with uniformly distributed solution sets and sensitivity to non-convex Pareto optimal fronts.

In contrast, the a posteriori approach maintains and simultaneously optimizes multi-objective problem (MOP) formulations [12]. This technique can derive a Pareto optimal solution set in a single run, facilitating post-optimization decision-making. Ensuring a broad diversity of solutions across all objectives is crucial, providing decision-makers with a comprehensive spectrum of choices. Scholarly works abound with algorithms developed from this approach can be found in literature [13,14,15].

The interactive approach evaluates and integrates decision-makers' preferences during the MOO process [16]. While maintaining the multi-objective setup, these methods intermittently halt optimization to seek input from decision-makers, avoiding non-viable search domains. However, the reliance on human input makes the interactive method more intricate and time-consuming than its counterparts.

David Schaffer introduced the concept of using evolutionary algorithms (EAs) for MOO in 1984 [17]. EAs, which mimic natural evolution, are randomized search and optimization methods compatible with MOPs due to their distinctive traits. For instance, they can yield a non-dominated set in one attempt and adeptly navigate vast and intricate search realms with minimal problem-specific demands. This compatibility led to the development of multi-objective evolutionary algorithms (MOEAs), which have seen a surge in research and applications across various domains over the last twenty years. MOEAs can be categorized into three primary types: Pareto-dominance-based, Decomposition-based and Indicator-based, with Pareto-based MOEAs emerging as a preferred strategy for effectively approximating the authentic Pareto front due to their intuitive mechanisms.

The Vector Evaluated Genetic Algorithms (VEGA) is often considered the first Pareto-based MOEA [18]. Evolving from the foundational Genetic Algorithm (GA), VEGA was adapted to tackle MOPs. It divides the population into subsets corresponding to the number of objective functions, with each subset focusing on a singular objective. However, VEGA often produces non-uniformly distributed non-dominated solutions across the Pareto front, particularly in areas of compromise. In contrast, the Non-Dominated Sorting Genetic Algorithm II (NSGA-II) is recognized as a favored MOEA in the literature [19]. Developed to address issues in its predecessor, NSGA, such as the absence of a sharing parameter, neglect of elitism and the substantial computational demands of non-dominated sorting, NSGA-II introduced a fast non-dominated sorting method, a diversity conservation technique and a crowded-comparison operator.

Other notable MOEAs include the Multi-objective Particle Swarm Optimization (MOPSO), introduced by Coello Coello & Lechuga [20], which uses Pareto dominance to steer particle flight direction and a mutation operator to enhance randomness and solution diversity. However, MOPSO's rapid convergence can sometimes lead to premature termination with an inaccurate Pareto front. The Multi-Objective Differential Evolution (MODE) [21] branched from the foundational DE algorithm and typically employs non-dominated sorting and rank selection on a combined group of parent and offspring populations.

Many algorithms rely heavily on the Pareto dominance philosophy, providing a practical toolkit for addressing MOPs. With numerous optimal solutions in the MOO realm, many algorithms use an archive (or repository) to store superior solutions, refining this archive throughout the optimization process. Recent years have seen the development of various novel and efficient Pareto-based MOEAs, each with unique mechanics, such as the multi-objective ant lion optimizer [22], MO equilibrium optimizer (MOEO) [23], MO slime mould algorithm [24], MO arithmetic optimization algorithm [25], non-dominated sorting ions motion algorithm [26], social cognitive optimization algorithm [27], multi-objective multi-verse optimization (MOMVO) [28], non-dominated sorting grey wolf optimizer [29], MO Gradient-Based Optimizer [30], MO plasma generation optimizer (MOPGO) [31], non-dominated sorting Harris hawks optimization [32], MO thermal exchange optimization [33], decomposition based multi-objective heat transfer search [34], Decomposition-Based Multi-Objective Symbiotic Organism Search (MOSOS/D) [35], MOGNDO Algorithm [36], Non-dominated sorting moth flame optimizer [37], Non-dominated sorting whale optimization algorithm [38] and Non-Dominated Sorting Dragonfly Algorithm [39]. However, the No-Free-Lunch theorem (NFL) [40] highlights that no single optimization technique can universally solve all MOPs, underscoring the need for continuous refinement of existing algorithms or the development of new ones.

Recently, Farshad Rezaei et al. introduced a metaheuristic technique: the Geometric Mean Optimizer (GMO) [41]. With strengths in both exploration and exploitation phases, the GMO harnesses potential solutions to create a search group, demonstrating efficacy across various engineering challenges [41] and emerging as a potent tool in the optimization toolkit.

No-Free-Lunch theorem (NFL) [40] posits that algorithms cannot be strictly classified as good or bad; rather, their suitability varies depending on the specific optimization problem at hand. It is challenging for a solitary algorithm to effectively address all facets of Multi-objective Optimization Problems (MOPs), including exploration, exploitation, convergence, coverage and computational efficiency, simultaneously. This reality indicates a continual opportunity for creating new meta-heuristic methods designed to tackle multi-objective optimization challenges effectively. In MOPs characterized by complex constraints tend to have intricate feasible zones, leading to a constrained Pareto Front (PF) rather than a true PF. This situation often traps algorithms in local optima, posing challenges for achieving satisfactory convergence and distribution. To address these issues, numerous MOPs have been developed. While these algorithms boast distinct features and benefits, they also exhibit limitations, particularly in scenarios involving narrow feasible spaces, multiple feasible zones and intricate distributions of these zones. Balancing convergence, diversity and feasibility remains a challenge for these algorithms. In response, this study introduces a Multi-Objective Geometric Mean Optimizer (MOGMO), designed for MOPs. MOGMO adapts the original GMO to serve the broader MOO ecosystem. The contributions of this paper include the development of a new multi-objective technique based on GMO, integrated with the memeplex structure of NSGA-II to address MOPs effectively. This integrated MOGMO with Information Feedback Mechanism (IFM) aims to efficiently and robustly uncover solutions in the multi-objective realm. The paper also verifies MOGMO's proficiency through various case studies, including unconstrained and constrained multi-objective benchmarks and complex engineering design challenges. The results are compared with those of esteemed MOO methods using various performance metrics and statistical tools. Analyses suggest that MOGMO is robust and versatile in addressing varied MOPs, consistently achieving Pareto optimal fronts marked by both convergence and diversity.

The structure of this paper is organized as follows: Sect. 2 offers foundational definitions relevant to GMO algorithm. Section 3 describes the proposed MOGMO algorithm. Section 4 is dedicated to the statistical evaluation of MOGMO against benchmark challenges and its application in multi-objective engineering design. Finally, Sect. 5 describes the conclusion and future research directions.

2 Geometric Mean Optimizer (GMO)

The Geometric Mean Optimizer (GMO) [41] represents an advanced meta-heuristic method that takes inspiration from the collective social behavior of multiple searching agents. Any optimization technique must define the most effective manner in which these agents collaborate. Initially, we delve into the GMO algorithm's inherent mathematical traits tailored for optimization tasks. Following this, an in-depth exploration of its problem-solving formulation is provided. Consider the representations \({X}_{i}=\left({x}_{i1},{x}_{i2},\dots ,{x}_{iD}\right)\) and \({V}_{i}=\left({v}_{i1},{v}_{i2},\dots ,{v}_{iD}\right)\) as the position and velocity of the \(i\)th agent, respectively. GMO can concurrently appraise both the efficiency associated fuzzy membership function (MF) values. This amplification process is synonymous with the product-based Larsen implication function, a prevalent technique in fuzzy logic. Conversely, the geometric mean of n membership degrees (MD) is represented by \(\sqrt[n]{{\mu }_{1}\times {\mu }_{2}\times \dots \times {\mu }_{n}}\). Therefore, multiplying various MDs i.e., \(\left({\mu }_{1}\times {\mu }_{2}\times \dots \times {\mu }_{n}\right)\), can be perceived as their geometric mean without factoring in the \(n\)th root, in which \({\mu }_{i}\) is the \(i\) th \({\text{MD}}\) and \(i=\mathrm{1,2},\dots ,n\). This version, termed the pseudo-geometric average calculated across the MF values of numerous variables, concurrently illustrates their average and likeness. Informed by the mathematical basis shared earlier, the GMO's architecture is further elucidated. Within GMO, a search agent's holistic fitness is determined by contrasting it with the fitness levels of its counterparts. Here, "counterparts" of a specific agent encompass the entire agent population excluding that specific agent. Each cycle identifies the most optimal position an agent has achieved until that point. Subsequently, for every contrasting top-performing agent relative to a specific one, the multiplication of the goal values, transmuted into fuzzy MFs, is ascertained. It is vital to note that in GMO's execution, the fuzzy membership functions should have a direct positive correlation with the fuzzified variables. For a minimization function, an agent is deemed more competent if the pseudo-geometric mean of the MFs, associated with its counterparts, is larger. This insinuates two simultaneous accomplishments for the agent in focus: first, the mean MF values of the counterparts are greater, signifying a lower MF value for the focused agent. Secondly, there is a heightened consistency among the counterparts' MF values, indicating a concentrated cluster and reduced diversity. As a result, the main agent exists in a relatively diverse area within the search space. This illuminates the agent's potential to possess a more beneficial status, merging both efficacy and variety, in comparison to another agent with a lower pseudo-geometric mean concerning its counterparts. The formulation used to determine MFs is elaborated in subsequent sections.

$$f(x)=\frac{1}{1+{e}^{a\left(x-c\right)}};a<0.$$
(1)

In the given equation Eq. (1), parameters a and c represent characteristics of the sigmoidal MF. The variables \(a\) and \(c\) in Eq. (1) are undetermined during every fuzzification effort, prompting the need for their calibration using a trial-and-error approach. However, this method is recognized to be imprecise and lengthy for parameter adjustments in fuzzy systems. A more proficient alternative would be to rely on other methods, like tying the parameters of the fuzzy membership functions in Eq. (1) to statistical measures. Building on this approach, Rezaei et al. (Rezaei et al. 2017) demonstrated that within a rising sigmoidal MF, \(c=\mu\) and \(a=\frac{-4}{\sigma \sqrt{e}}\); where \(\mu\) and \(\sigma\) denote the average and the spread of x values, respectively. Also, \(e\) represents Napier's constant. Replacing \(x\) with the value from the objective function for a top-performing search agent up to that point allows the determination of this agent's fuzzy MF value, as indicated in Eq. (2).

$${{\text{MF}}}_{j}^{t}=\frac{1}{1+{\text{exp}}\left[-\frac{4}{{\sigma }^{t}\sqrt{e}}\times \left({Z}_{\text{best }j}^{t}-{\mu }^{t}\right)\right]};j=\mathrm{1,2},\dots ,N,$$
(2)

where \({Z}_{\text{best. }j}^{t}\) signifies the objective value for the \(j\)th top-performing agent during the \(t\) th cycle. \({\mu }^{t}\) and \({\sigma }^{t}\) illustrate the average and spread for the objective values of all leading agents during that cycle, respectively, while \({{\text{MF}}}_{j}^{\mathrm{^{\prime}}}\) indicates the MF value for the \(j\) th top-performing agent. \(N\) remains the total population count. Moving forward, we introduce a unique metric termed the DFI as depicted:

$${{\text{DFI}}}_{i}^{t}={{\text{MF}}}_{1}^{t}\times \cdots \times {{\text{MF}}}_{i-1}^{t}\times {{\text{MF}}}_{i+1}^{t}\times \cdots \times {{\text{MF}}}_{N }^{t}=\prod_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{N} {{\text{MF}}}_{j}^{t}.$$
(3)

To ensure every top-performing agent collaboratively informs the creation of a single guiding global agent for each participant, we introduce a weighted average of all contrasting top-performing agents. These weights are represented by their associated DFI values. Equation (4) encapsulates this relationship.

$${Y}_{i}^{t}=\frac{\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{N} {{\text{DFl}}}_{j}^{t}\times {X}_{j}^{\text{best }}}{\sum_{j=1}^{N} {{\text{DFI}}}_{j}^{t}+\varepsilon },$$
(4)

where \({Y}_{i}^{t}\) is the position vector for the unique global guiding agent deduced for the \(i\) th agent during the \(t\) th cycle, while \({X}_{j}^{\text{best}}\) refers to the position vector for the best performance of the \(j\) th searching agent up to that point. \(DF{I}_{j}^{t}\) indicates the dual-fitness metric for the \(j\) th search agent during that cycle. Notably, a minuscule positive number, \(\varepsilon\), is integrated into the denominator of Eq. (4) to avert singularities. This inclusion is especially pertinent for more straightforward challenges, mainly those with optimal solutions centralized within their domains. However, for intricate challenges, especially when the optimal solution lies distant from the domain's center, \(\varepsilon\) becomes redundant. Absent any prior insights into the problem at hand, excluding ε from the denominator of Eq. (4) and subsequently from Eq. (5) is advised. To augment the search efficacy of the algorithm and reduce its computational load, focusing solely on the elite top-performing agents when deducing each guiding agent is recommended. To achieve this, all top-performing agents are ranked based on their DFI, from the highest to the lowest, with the top \(Nbest\) agents labeled as elite. An uncomplicated approach to determine \(Nbest\) is to reduce its value linearly across cycles. It should match the population count at the outset and 2 at the culmination. Fixing \(Nbest\) to 2 during the concluding cycle ensures that the elite agents perpetually modify their positions to preserve diversity. Therefore, when elitism is integrated into determining guide agents, Eq. (4) evolves into Eq. (5).

$${Y}_{i}^{t}=\frac{\sum_{j\in N\text{ best }j\ne i} DF{I}_{j}^{t}\times {X}_{j}^{\text{best }}}{\sum_{j\in Nbest} DF{I}_{j}^{t}+\varepsilon }.$$
(5)

In an attempt to boost the stochastic properties of \({Y}_{i}^{t}\), ensuring better conservation of guide agent diversity, these agents undergo mutation in GMO. This mutation is characterized by a Gaussian mutation approach. The mutation's mathematical representation is as shown:

$${Y}_{i,\text{ mut }}^{t}={Y}_{i}^{t}+w\times {\text{rand}}n\times \left(St{d}_{{\text{max}}}^{t}-St{d}^{t}\right),$$
(6)

within this representation, \(rand n\) signifies a random vector derived from a typical normal distribution. The \(w\) parameter attenuates the mutation step magnitude as iterations progress, which is derived from Eq. (9). The end product, \({Y}_{i,\text{ mut }}^{t}\), is the mutated \({Y}_{i}^{t}\) that directs the search agents. A notable observation is that this ensures the conservation of existing rich diversity among leading agents, which in turn fosters an overall diverse population in the search area. Conversely, a diminished standard deviation for a dimension prompts a larger mutation step, broadening the search area and amplifying agent diversity for that specific dimension. The refresh equations for each search agent are described by Eqs. (7) to (9):

$${V}_{i}^{t+1}=w\times {V}_{i}^{t}+\varphi \times \left({Y}_{i,\text{ nut }}^{t}-{X}_{i}^{t}\right),$$
(7)
$$\varphi =1+\left(2\times \text{ rand }-1\right)\times w,$$
(8)
$${X}_{i}^{t+1}={X}_{i}^{t}+{V}_{i}^{t+1};w=1-\frac{t}{{t}_{{\text{max}}}},$$
(9)

within these equations, \(w\) is an influential parameter, \(t\) denotes the present cycle and \({t}_{max}\) stands for the ultimate cycle count. \({V}_{i}^{t}\) signifies the velocity vector for the \(i\) th search agent during the \(t\) th cycle. \({V}_{i}^{t+1}\) represents the \(i\) th agent's velocity vector in the subsequent cycle, while \({X}_{i}^{t}\) shows the position vector for the \(i\) th agent at that cycle. Additionally, \(\varphi\) serves as a scaling vector, illustrating the trajectory of agent \(i\) towards its guide. The rand is a stochastic number from the range [0,1]. Evidently, the magnitude of the \(\varphi\) vector diminishes and changes through ranges like \([\mathrm{0,2}],[0.1\), \(1.9],[\mathrm{0.2,1.8}],\dots ,[\mathrm{0.8,1.2}],[\mathrm{0.9,1.1}]\) and so on, until it reaches \([\mathrm{1,1}]=\{1\}\), as iterations advance. The declining pattern adopted for the \(\varphi\) intervals boost GMO's exploration ability during the early cycles and accentuates exploitation towards the end, ensuring a harmonious exploration–exploitation shift.

3 Proposed Multi-objective Geometric Mean Optimizer (GMO) (MOGMO)

3.1 Basic Definitions of Multi-objective Optimization

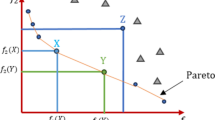
In multi-objective optimization tasks (MOPs), there is a simultaneous effort to minimize or maximize at least two clashing objective functions. While a single-objective optimization effort zeroes in on one optimal solution with the prime objective function value, MOO presents a spectrum of optimal outcomes known as Pareto optimal solutions. The majority of MOO techniques harness the idea of domination in their quest to manage diverse objectives and identify these Pareto solutions. An elaboration on the idea of domination and associated terminologies are illustrated in Fig. 1.

Fig. 1
figure 1

Multi-objective all definitions in search space of MO-Problem

Full size image

3.2 Multi-objective Geometric Mean Optimizer (GMO) (MOGMO)

MOGMO algorithm starts with a random population of size \(N\). the current generation is \(t, {x}_{i}^{t}\) and \({x}_{i}^{t+1}\) the \(i\) th individual at \(t\) and \((t+1)\) generation. \({u}_{i}^{t+1}\) the \(i\) th individual at the \((t+1)\) generation generated through the GMO algorithm and parent population\({P}_{t}\). the fitness value of \({u}_{i}^{t+1}\) is \({f}_{i}^{t+1}\) and \({U}^{t+1}\) is the set of\({u}_{i}^{t+1}\). Then, we can calculate \({x}_{i}^{t+1}\) according to \({u}_{i}^{t+1}\) generated through the GMO algorithm and Information Feedback Mechanism (IFM) Eq. (10)

$${{x}_{i}^{t+1}={\partial }_{1}{u}_{i}^{t+1}+{\partial }_{2}{x}_{k}^{t}; {\partial }_{1}=\frac{{f}_{k}^{t}}{{f}_{i}^{t+1}+{f}_{k}^{t}}, {\partial }_{2}=\frac{{f}_{i}^{t+1}}{{f}_{i}^{t+1}+{f}_{k}^{t}}}, {\partial }_{1}+{\partial }_{2}=1,$$
(10)

where \({x}_{k}^{t}\) is the \(k\) th individual we chose from the \(t\) th generation, the fitness value of \({x}_{k}^{t}\) is \({f}_{k}^{t},{\partial }_{1}\) and \({\partial }_{2}\) are weight coefficients. Generate offspring population \({Q}_{t}\). \({Q}_{t}\) is the set of \({x}_{i}^{t+1}.\) The combined population \({R}_{t}={P}_{t}\cup {Q}_{t}\) is sorted into different w-non-dominant levels \(\left({F}_{1},{F}_{2},\dots ,{F}_{l}\dots ,{F}_{w}\right)\). Beginning from \({F}_{1}\), all individuals in level 1 to \(l\) are added to \({S}_{t}={\bigcup }_{i=1}^{l} {F}_{i}\) and remaining members of \({R}_{t}\) are rejected, illustrated in Fig. 2. If \(\left|{S}_{t}\right|=N,\) no other actions are required and the next generation is begun with \({P}_{t+1}={S}_{t}\) directly. Otherwise, solutions in \({S}_{t}/{F}_{l}\) are included in \({P}_{t+1}\) and the remaining solutions \(N-{\sum }_{i=0}^{l-1} \left|{F}_{i}\right|\) are selected from \({F}_{l}\) according to the Crowding Distance (CD) mechanism, the way to select solutions is according to the CD of solutions in \({F}_{l}\). The larger the crowding distance, the higher the probability of selection and check termination condition is met. If the termination condition is not satisfied, \(t=t+1\) than repeat and if it is satisfied, \({P}_{t+1}\) is generated represent in Algorithm-1, it is then applied to generate a new population \({Q}_{t+1}\) by GMO algorithm. Such a careful selection strategy is found to computational complexity of \(M\)-Objectives \(O\left({N}^{2}M\right)\). MOGMO that incorporates proposed information feedback mechanism to effectively guide the search process, ensuring a balance between exploration and exploitation. This leads to improved convergence, coverage and diversity preservation, which are crucial aspects of multi-objective optimization. MOGMO algorithm does not require to set any new parameter other than the usual GMO parameters such as the population size, termination parameter and their associated parameters. The flowchart of MOGMO algorithm can be shown in Fig. 3.

Fig. 2
figure 2

The procedure of the NDS approach based on MOGMO algorithm

Full size image
Fig. 3
figure 3

Flowchart of MOGMO algorithm

Full size image
figure a

4 Results and Discussion

4.1 Algorithmic Comparison and Settings

To validate the results, MOGMO is weighed against NSGA-II widely acknowledged MOO methods. In addition, MOGMO is contrasted with the newer MOO algorithms: MOEO, MOSOS/D, MOMVO and MOPGO. Original papers recommended parameter settings were retained for this study.

4.2 Benchmark Settings and Parameters

This section utilizes thirty prominent multi-objective benchmark challenges, sourced from reputable academic works, to assess the efficacy of MOGMO. These challenges encompass objective functions with unique attributes and varying dimensions of design parameters. They are organized ZDT [42] (Appendix A), DTLZ [43] (Appendix B and Appendix C), Appendix D based on Constraint [44, 45] (CONSTR, TNK, SRN, BNH, OSY and KITA) and Appendix E based on real-world engineering design problems: Brushless DC wheel motor [46] (RWMOP1), Safety isolating transformer [47] (RWMOP2), Helical spring [45] (RWMOP3), Two-bar truss [45] (RWMOP4) and Welded beam [48] (RWMOP5). All mathematical models for these challenges can be found in Appendices A, B, C, D and E.

4.3 Evaluative Metrics

MOO fundamentally pursues two objectives: achieving solutions converging to the Pareto optimal front and ensuring diverse solutions within the Pareto set. Hence, a range of performance metrics is essential to accurately evaluate MOO algorithm outcomes. Within this work, 'PFtrue' represents the consistent Pareto optimal front as defined by functions constituting an MOP. On the other hand, 'PFob' denotes the Pareto optimal front derived from a specific MOO algorithm. In multi-objective optimization (MOO), the performance metrics [49] of algorithms in terms of faster convergence Generational Distance (GD), combined uniformity-convergence-coverage spread (SD), Hyper Volume (HV) and Inverted Generational Distance (IGD), Computational complexity (RT) and coverage spacing (SP) metrics shown in Fig. 4 to offer a comprehensive performance assessment. Comparative analysis employs four performance metrics: GD, IGD, SP, SD and HV. It is crucial to note that all performance metrics here are assessed in a normalized objective space. Optimal Pareto fronts are indicated by smaller values for GD, IGD, SP, SD and larger values for HV. Subsequent sections detail the metrics employed here. During benchmark optimization, every technique is independently executed thirty times per case, facilitating a statistical evaluation. “ + / − / ~ ” Wilcoxon signed-rank test (WSRT) was conducted at a significance level of 0.05 between the total amount of test problems on which the corresponding optimizers has a better performance, a worse performance and an equal performance of MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO w. r. t. MOGMO algorithm.

Fig. 4
figure 4

Mathematical and schematic view of the a GD, b IGD, c SP, d SD and e HV metrics

Full size image

4.4 Analysis and Observation

Simulations were conducted 30 times for each test issue on a system featuring: Windows 10 (64-bit), Intel i5 CPU, 8 GB RAM and MATLAB R2021a. This section delves into the results from distinct metrics and offers insights.

4.4.1 ZDT Benchmark Analysis

Tables 1, 2, 3, 4, 5, 6 provide the comprehensive statistical analysis using GD, IGD, SP, SD, HV and RT measurements for various algorithms like MOGMO, MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO. These are all tested against the ZDT suite. From the results in Table 2, it is evident that MOGMO outperforms the other algorithms, especially when we focus on the average and standard deviation for the IGD metric. A majority of the other algorithms could not achieve a near-optimal Pareto front. Their struggle is evident in their high IGD values. Notably, MOGMO leads in the SP and SD metrics and it also tops in the HV measurement. For visual clarity, Fig. 5 shows how MOGMO's results align with the true Pareto fronts for ZDT suites. The results depict a consistent alignment of MOGMO outputs with the true Pareto optimal fronts.

Table 1 Results of GD metric of different multi-objective algorithms on ZDT 2-objective benchmark
Full size table
Table 2 Results of IGD metric of different multi-objective algorithms on ZDT 2-objective benchmark
Full size table
Table 3 Results of SP metric of different multi-objective algorithms on ZDT 2-objective benchmark
Full size table
Table 4 Results of SD metric of different multi-objective algorithms on ZDT 2-objective benchmark
Full size table
Table 5 Results of HV metric of different multi-objective algorithms on ZDT 2-objective benchmark
Full size table
Table 6 Results of RT metric of different multi-objective algorithms on ZDT 2-objective benchmark
Full size table
Fig. 5
figure 5

Best Pareto optimal front obtained by the MOGMO algorithm on a ZDT1, b ZDT2, c ZDT3, d ZDT4, e ZDT5 and f ZDT6 problems

Full size image

4.4.2 DTLZ 2 and 3-Objective Benchmark Insights

Tables 7, 8, 9, 10, 11 and 12 dive into the performance metrics of each algorithm when tested on DTLZ1-DTLZ7 two and three objectives’ functions. MOGMO continues to shine, surpassing MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO, especially in DTLZ functions. Notably, MOMVO ranks after MOGMO in terms of performance. In general, MOGMO demonstrates better spread and distribution in Pareto optimal solutions compared to its counterparts. Using the HV metric to assess performance, MOGMO consistently ranks higher than its peers for the majority of functions. Figures 6 and 7 provide a visual representation for DTLZ1-DTLZ7 two and three objectives’ functions. The graphs solidify MOGMO ability to closely align with the true Pareto fronts.

Table 7 Results of GD metric of different multi-objective algorithms on DTLZ 2 and 3-objective benchmark
Full size table
Table 8 Results of IGD metric of different multi-objective algorithms on DTLZ 2 and 3-objective benchmark
Full size table
Table 9 Results of SP metric of different multi-objective algorithms on DTLZ 2 and 3-objective benchmark
Full size table
Table 10 Results of SD metric of different multi-objective algorithms on DTLZ 2 and 3-objective benchmark
Full size table
Table 11 Results of HV metric of different multi-objective algorithms on DTLZ 2 and 3-objective benchmark
Full size table
Table 12 Results of RT metric of different multi-objective algorithms on DTLZ 2 and 3-objective benchmark
Full size table
Fig. 6
figure 6

Best Pareto optimal front obtained by the MOGMO algorithm on DTLZ1-DTLZ7 problems with 2-objectives

Full size image
Fig. 7
figure 7

Best Pareto optimal front obtained by the MOGMO algorithm on DTLZ1-DTLZ7 problems with 3-objectives

Full size image

From Table 1, we observe that for the GD metric, MOGMO and MOSOS/D outperform other algorithms in most cases for ZDT1-ZDT6 problems, showing better convergence. MOGMO shows best results in 4 / 6 cases, whereas MOSOS/D and NSGA-II achieve 2 best results each. In Table 2, for the IGD metric, MOGMO again demonstrates superior performance in 3/6 cases, indicating better convergence and diversity. MOGMO, MOSOS/D and MOMVO each achieve the best results in some cases, with MOGMO leading. Table 3 shows the SP metric, where MOGMO stands out in 3/6 cases, indicating better divergence. MOGMO, MOSOS/D and MOPGO demonstrate competitive performance, but MOGMO leads in achieving the best results. As seen from Table 4 for the SD metric, MOGMO again leads by achieving the best performance in 3/6 cases. This suggests that MOGMO has a better spread of non-dominated solutions. Other algorithms like MOSOS/D and MOMVO also show good performance in some cases. In Table 5, considering the HV metric, MOGMO exhibits superior performance in 4/6 cases, indicating a better balance between convergence and diversity. MOSOS/D and NSGA-II also show competitive results in certain cases. Finally, Table 6 presents the RT metric, where MOGMO shows the best performance in 4/6 cases, indicating a faster running speed and minimal computational burden. Other algorithms like MOEO and MOSOS/D also perform well in certain instances. From Table 7, observing the GD metric, we can see that MOGMO, MOEO and MOSOS/D generally exhibit better convergence compared to other algorithms across most DTLZ problems. MOGMO particularly shows strong performance in DTLZ2 and DTLZ4 for both 2 and 3 objectives. In Table 8, analyzing the IGD metric, MOGMO and MOEO have superior performance in several instances, particularly in DTLZ1 and DTLZ2 for both 2 and 3 objectives. This indicates their better convergence and diversity in these scenarios. Looking at Table 9 for the SP metric, MOGMO, MOEO and MOSOS/D show competitive performances, with MOGMO excelling in DTLZ2 and DTLZ5 for both 2 and 3 objectives, suggesting better divergence capabilities. As seen in Table 10 for the SD metric, MOGMO consistently achieves strong performance across most DTLZ problems, indicating a better spread of non-dominated solutions. MOEO and MOSOS/D also show good results in specific instances like DTLZ2 and DTLZ3. In Table 11, examining the HV metric, MOGMO, MOEO and MOSOS/D again demonstrate superior performance in several instances, particularly in DTLZ2 and DTLZ4 for both 2 and 3 objectives. This suggests their effective balance between convergence and diversity. Finally, Table 12 presents the RT metric, where MOGMO and MOEO frequently exhibit better performance, indicating faster running speeds and lower computational burdens in scenarios like DTLZ1 and DTLZ2 for both 2 and 3 objectives. Overall, MOGMO appears to be the most consistent performer across different metrics for the ZDT 2-objective benchmark, MOGMO and MOEO appear to be the most consistent performers across different metrics for the DTLZ 2 and 3-objective benchmark demonstrating its effectiveness in various aspects such as convergence, diversity and computational efficiency.

4.4.3 Evaluation of Constraint Benchmark

Tables 13, 14, 15, 16, 17 and 18 present the performance data on GD, IGD, SP, SD, HV and RT metrics, as determined by the MOGMA for test operations including CONSTR, TNK, SRN, BNH, OSY and KITA. To manage constraints within MOGMO, a death penalty function is utilized. Other algorithms like MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO were also tested on these functions for a comparative view. Insights from Table 13 suggest that MOGMO consistently outperforms its counterparts, especially in the domain of constrained multi-objective scenarios. Table 14 also underscores the standout average and SD values for the IGD metric associated with MOGMO. Further, MOSGA achieves superior results in producing well-distributed Pareto optimal results. Moreover, the SP and SD indicators from Tables 15 and 16 signify MOGMO dominance over other methodologies. Regarding the HV metric in Table 17, MOGMO outcomes are more promising, pointing towards its enhanced convergence and stability. Amongst the algorithms considered, NSGA-II ranks just behind MOGMO in terms of IGD outcomes for the majority of test functions. However, the solutions derived from this algorithm exhibit subpar distribution characteristics, evident from its SP and SD metric values. Conversely, MOMVO lags in convergence. Figure 8 offers visual representations of the Pareto outcomes achieved by MOGMO across various test functions. Certain tests reveal unique Pareto optimal fronts; for instance, CONSTR possesses a combined concave and linear front. Moreover, while the KITA function showcases a continuous concave front, TNK's front is more erratic. The depicted results in Fig. 8 demonstrate MOGMO proficiency in aligning closely with true Pareto optimal outcomes, ensuring even distribution across all regions. This analysis underlines MOGMO adeptness at managing constraints and delivering high-convergence Pareto results.

Table 13 Results of GD metric of different multi-objective algorithms on constrained benchmark
Full size table
Table 14 Results of IGD metric of different multi-objective algorithms on constrained benchmark
Full size table
Table 15 Results of SP metric of different multi-objective algorithms on constrained benchmark
Full size table
Table 16 Results of SD metric of different multi-objective algorithms on constrained benchmark
Full size table
Table 17 Results of HV metric of different multi-objective algorithms on constrained benchmark
Full size table
Table 18 Results of RT metric of different multi-objective algorithms on constrained benchmark
Full size table
Fig. 8
figure 8

Best Pareto optimal front obtained by the MOGMO algorithm on constrained CONSTR, TANK, SRN, OSY, BIN and KITA

Full size image

4.4.4 Real-World Applications of MOGMO

While standard multi-objective test functions provide valuable insights, grappling with real-world optimization dilemmas often poses unique challenges. To test its real-world applicability, MOGMO is applied to five engineering design challenges, with their mathematical formulations found in Appendix E. Replicating earlier methods, MOGMO is run thirty times for every problem. The results are stacked against MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO, with all algorithms retaining consistent parameters. the six MOO algorithms are assessed using GD, IGD, SP, SD, HV and RT metrics. Tables 19, 20, 21, 22, 23 and 24 provide a comprehensive comparison, highlighting MOGMO knack for delivering a broader array of Pareto optimal solutions. This is further validated by MOGMO superior average and minimal deviation in SP, SD and HV metrics, establishing its edge in convergence and diversity. Further insights can be gleaned from Fig. 9, which exhibits the Pareto optimal front achieved by MOGMO. The outcomes underscore MOGMO efficiency, better in terms of convergence (GD, SP), divergence (IGD, HV), computational burden (RT) and solution distribution (SD) compared MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO algorithms for solving real world problems This underscores MOGMO supremacy in consistency and reliability over other MOO algorithms. Tables 6, 12, 18 and 24 delve into the mean CPU durations of all algorithms, showcasing that MOGMO computation speed trumps most others in 19 out of 25 test problems. In the remainder, MOGMO is a close second in computational speed.

Table 19 Results of GD metric of different multi-objective algorithms on engineering design problems
Full size table
Table 20 Results of IGD metric of different multi-objective algorithms on engineering design problems
Full size table
Table 21 Results of SP metric of different multi-objective algorithms on engineering design problems
Full size table
Table 22 Results of SD metric of different multi-objective algorithms on engineering design problems
Full size table
Table 23 Results of HV metric of different multi-objective algorithms on engineering design problems
Full size table
Table 24 Results of RT metric of different multi-objective algorithms on engineering design problems
Full size table
Fig. 9
figure 9

Best Pareto optimal front obtained by the MOGMO algorithm on real-world engineering problems: a RWMOP1 b RWMOP2 c RWMOP3 d RWMOP4 e RWMOP5

Full size image

The effectiveness of MOGMO has been assessed using 25 benchmark functions and five engineering problems oriented towards multiple objectives. In this assessment, MOGMO performance is juxtaposed with MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO, employing indicators like GD, IGD, SP, SD, HV and RT. Within this context, GD and IGD metrics evaluate the precision and convergence of the algorithm. Simultaneously, SP and SD metrics gauge the spread and distribution of the outcomes. Among the five metrics, HV stands out as a comprehensive measure, assessing an MOO method's convergence and diversity prowess. Analytical approaches like non-parametric statistical tests, robustness scrutiny and visual representations of Pareto optimal fronts showcase MOGMO outcomes. A perusal of the performance statistics highlights MOGMO capacity to deliver superior results relative to its counterparts. For all testing functions, the Pareto fronts generated by MOGMO splendidly align with genuine Pareto fronts, demonstrating considerable diversity. Non-parametric tests, including the Wilcoxon rank-sum tests, indicate MOGMO superior performance over MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO across most metrics. MOGMO balance between exploration and exploitation is commendable, stemming from the perturbation coefficient and strategies in the global and local stages. Its diversity, in terms of distribution and spread, is also noteworthy, originating from novel search group selections and Pareto archive updates. MOGMO utilizes tournament selection, favoring less-populated regions and selectively discards solutions from overcrowded regions when necessary, bolstering solution diversity throughout the optimization. Despite these strengths, MOGMO is not without its constraints. As it leans on Pareto dominance, MOGMO excels in solving MOPs with two or three conflicting objectives. However, with problems encompassing more than three objectives, MOGMO archive fills rapidly with non-dominated solutions, which might hamper its efficiency. As such, MOGMO is optimally geared for MOPs with two to three objectives.

From Tables 13 and 19, we can observe that MOGMO outperforms 7 out of 11 best results, whereas MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO achieves 0, 1, 0, 1 and 2 best results in terms of the GD values, respectively. Therefore, MOGMO has a better convergence for solving Constraint and real-world application. In Tables 14 and 20, IGD value compared to MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO, the proposed MOGMO is better in 9, 10, 10, 11 and 11 out of 11 cases. Therefore, MOGMO has a better convergence and diversity for solving Constraint and real-world application. In Tables 15 and 21, SP value compared to MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO, the proposed MOGMO worse in 0, 2, 0, 1 and 1 out of 11 cases. Therefore, MOGMO has a better divergence for solving Constraint and real-world application. As can be seen from Tables 16 and 22, MOGMO achieves the best performance in terms of SD values, having obtained 7 best results, followed by MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO that have obtained 1, 3, 0, 0 and 0 best results, respectively. Therefore, MOGMO has a better spread of non-dominated solutions on true PF for solving Constraint and real-world application. In Tables 17 and 23 on the HV values, when, respectively compared to MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO, the proposed MOGMO is better in 10, 10, 10, 11 and 11 out of 11. Therefore, MOGMO has a better balance between convergence and diversity for solving Constraint and real-world application. In Tables 18 and 24, RT value compared to MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO, the proposed MOGMO is better in 9, 9, 11, 11 and 11 out of 11 cases. Therefore, MOGMO has a faster running speed and minimum computational burden for solving Constraint and real-world application.

5 Conclusions

This study introduces the inaugural multi-objective adaptation of the GMO, termed MOGMO. The traditional workings of the GMO are evolved through the incorporation of two novel modules to shape MOGMO. To start, an elitist non-dominated sorting strategy is executed to identify non-dominated solutions, focusing on three pivotal processes: offspring creation and selection. The second module leverages the CD with IFM selection mechanism, ensuring the continuous enhancement of convergence and variety in non-dominated solutions throughout the optimization process.

MOGMO's efficiency is showcased through its application to twenty-five benchmark problems, both unconstrained and constrained. Metrics such as GD, IGD, SP, SD, HV and RT facilitate its performance evaluation. Statistical outcomes reveal that MOGMO yields higher quality solutions compared to the five esteemed MOEO, MOSOS/D, NSGA-II, MOMVO and MOPGO algorithms reviewed in this research. When measuring convergence using the GD, IGD metric, MOGMO consistently emerges on top. Moreover, in assessing diversity via the SP and SD metrics, MOGMO once again surpasses competing algorithms in the majority of cases. For the HV metric, MOGMO retains its superior stance. All Pareto optimal outcomes derived from MOGMO are closely aligned with genuine Pareto optimal solutions, demonstrating impressive diversity.

Furthermore, the research extends the application of MOGMO to five practical engineering challenges, confirming its versatility. Across all these scenarios, MOGMO consistently delivers superior solution quality when matched against alternative algorithms. This heightened convergence and variety of the yielded Pareto optimal outcomes can be credited to MOGMO 's robust exploitation and exploration capabilities. A thorough analysis validates that MOGMO efficiently tackles problems featuring two to three objectives with characteristics like convexity, non-convexity and discontinuity in their Pareto optimal fronts. It is recommended that MOGMO be further refined and adapted for real-world engineering challenges in forthcoming research. There is also potential in expanding MOGMO capabilities to address problems with a broader array of objectives. The MOGMO source code is available at: https://github.com/kanak02/MOGMO.