1 Introduction

Consensus decision-making is a procedure where a group of experts express their opinions on alternatives and strive to reach a consensus on the selection of the alternatives [1, 2]. Conventional studies on consensus decision-making generally operate on the assumption that experts do not have any influence on one another [3, 4]. Nevertheless, the advancement of information technology enables experts to connect, collaborate, and share knowledge in a more convenient manner, hence building trust relationships [5, 6]. Trust has emerged as a crucial factor in determining consensus decision-making, and there is a growing interest among scholars in studying trust-based consensus decision-making [7,8,9,10,11,12]. It has also been extensively applied to address practical issues such as selecting investment projects in complex and uncertain settings [6], deploying cellular base stations [13], making product design decisions [14], and choosing suitable sites for elderly care institutions [15]. Based on the extant research, this paper primarily explores the research issues related to trust-based consensus decision-making.

Currently, most research on trust-based consensus decision-making assumes that trust relationships contribute to achieving group consensus [16, 17]. Nevertheless, the veracity of this claim may be questionable, as a lack of trust among experts can impede the progress of reaching a consensus in decision-making [18]. For example, experts who have a lower degree of consensus must participate in discussions and negotiations with others to align their opinions with the group consensus [19]. When there is a low trust degree among experts, they may refuse to engage in discussions and negotiations with others [20], making it difficult to reach group consensus. Meanwhile, experts with lower trust degree may experience relational conflicts with others [21, 22], or even engage in non-cooperative behaviors [23, 24], such as dishonestly expressing their opinions or refusing to adjust their viewpoints [25], which decreases group consensus degree. It is evident that trust relationships are not entirely beneficial to consensus decision-making, and it is necessary to consider the negative effects of low trust degree of experts on hindering group consensus reaching. Trust improvement plays a crucial role in the consensus decision-making process by increasing experts’ trust degree in others, motivating them to actively engage in discussions and negotiations, and ultimately resulting in group consensus. Dong et al. [26] pointed out that trust improvement can facilitate group consensus reaching. However, their study specifically focuses on the development of new indirect trust relationships among experts who do not have initial trust. This essentially completes the trust network that is previously incomplete, and does not pertain to the trust improvement consensus model because of the low degree of trust among experts. Hence, given the low degree of trust among experts that obstructs group consensus reaching, this paper primarily explores the trust improvement consensus model.

Trust propagation is an effective tool to improve trust relationships among experts. This is because third-party experts can transmit information through trust propagation, which facilitates communication between the other two experts [13, 27]. However, current studies on trust propagation mostly concentrate on completing in incomplete trust relationships, while neglecting the potential of trust propagation in trust improvement [28,29,30]. Simultaneously, experts often have various trust propagation paths. The efficiency of trust propagation is significantly influenced by the trust degree and the quantity of intermediary experts. On the one hand, an excessive number of intermediary experts in the trust propagation process might result in inaccurate trust value evaluations [31, 32], and decreases the transmission efficiency [33]. On the other hand, higher trust degree with experts in propagation pathways might ensure the efficacy of information transfer [34, 35]. However, the above research does not concurrently take into account the influence of both trust degree and the number of intermediaries on the efficiency of trust propagation. Hence, it is imperative to explore an efficient approach for improving trust degree among experts through trust propagation.

In the consensus decision-making process based on trust improvement, the opinions provided by experts may not be completely reliable, which is related to their experience and level of knowledge. As the unreliability degree of opinions increases, the capacity of experts to accurately evaluate alternatives decreases [36]. According to Mondal et al. [37] and Xue et al. [38], experts may give unreliable opinions if they lack knowledge of the information that is used to make decisions, do not have the necessary experience, or are not interested in the topics involved in making decisions. Disregarding the unreliability degree of opinions may lead to irrational outcomes of consensus decision-making. As a result, they suggested implementing a consensus-based decision-making process that takes into account the reliability of expert opinions. However, with regard to unreliability degree of opinions, the existing research does not encompass the entire consensus decision-making process based on trust improvement [39,40,41,42,43]. In the consensus decision-making process based on trust improvement, experts need to consider unreliability degree of opinions to enhance trust in others and adjust their opinions to achieve group consensus. Neglecting unreliability degree of opinions may impact the outcomes of trust improvement consensus decision-making. On the one hand, neglecting unreliability degree of opinions diminishes the efficacy of trust improvement. The experts’ limited cognitive capacity can cause their evaluations of alternatives to be unreliable [44], which in turn reduces trust degree in those experts during the process of trust improvement. This is because experts typically have a greater degree of trust in individuals who possess a better level of knowledge [45]. Disregarding the unreliability degree of opinions can result in biases when assessing trust degree during the process of trust improvement. On the other hand, disregarding the unreliability degree of opinions may lead experts to trust and reliance on unreliable opinions, which undermines the logic and scientific nature of consensus decision-making process. The complexity of decision-making environments makes it challenging for experts to possess the time, knowledge, and information necessary to make accurate opinions [44, 46, 47]. If the inaccurate opinions provided by experts is not revised, these inaccurate opinions will be directly utilized in the final selecting process of alternatives, and there may even be a situation where certain highly trusted but unreliable opinions are excessively referenced during the opinion adjustment process. Consequently, this will inevitably lead to imprecise group consensus or subpar quality of consensus outcome. Hence, it is imperative to consider unreliability degree of opinions in the consensus decision-making based on trust improvement.

The experts’ higher level of hesitancy in assessing alternatives corresponds to a greater unreliability degree in their opinions. Nevertheless, the majority of current methods to measure the unreliability degree of opinions mostly based on the distance between expert and group opinions, or inconsistency in preferences [38, 42, 44]. Experts may be hesitant while evaluating alternatives due to restricted cognitive abilities or the intricate nature of decision-making context [48,49,50]. Experts displaying a greater degree of hesitation imply a significant amount of doubt in their judgment [51], which reduces the quality and scientific validity of decision-making information, leading to unreliable opinions from the experts. To explore the correlation between the hesitancy degree of experts and the unreliability degree of opinions, this study utilizes hesitant fuzzy sets to represent experts’ opinions. Hesitant fuzzy sets enable experts to express their opinions by hesitating between multiple membership degrees for a particular element, thus retaining as many evaluation opinions from the experts as possible [52, 53]. However, there is a limited amount of research available on measuring the unreliability degree of opinions by considering the hesitancy degree of experts in hesitant fuzzy sets. In addition, while several studies have proposed methods for quantifying the hesitancy degree of experts using hesitant fuzzy sets to represent experts’ hesitant evaluation information, there are still certain constraints. For instance, Li et al. [54] and Zhang et al. [55] proposed a method to quantify the hesitancy degree of experts through the number of membership degrees in a hesitant fuzzy set. A larger number of membership degrees indicates a higher hesitancy degree of experts for alternatives. However, they neglect to consider the impact of the level of membership degree discreteness on the hesitancy degree of experts. Lin et al. [56] introduced a method to measure the hesitancy degree in hesitant fuzzy elements. They considered both the number of membership degrees and the discreteness level of membership degree. However, they measured the discreteness degree of membership degree using variance, which resulted in a much smaller impact on the hesitancy degree in hesitant fuzzy elements compared to the number of membership degrees. Hence, there is a need to enhance the present methods for assessing the hesitancy degree and develop a method for quantifying the unreliability degree of opinions in judgments using this approach.

While scholars have explored consensus decision-making regarding trust relationships and unreliability degree of opinions, these studies still have the following limitations:

  1. (1)

    Existing research assumes trust relationships are entirely beneficial for consensus, but low trust degree among experts can decrease group consensus degree. Existing research overlooks the potential of trust propagation in trust improvement, and the influence of trust degree and intermediaries on the efficiency of trust propagation.

  2. (2)

    The process of trust improvement and opinion adjustment in consensus requires considering the unreliability degree of opinions, while neglecting it compromises decision outcome. Existing research does not involve.

  3. (3)

    There is limited research on measuring the unreliability degree of opinions based on the hesitancy degree of experts. Existing methods for measuring hesitancy degree of experts prioritize membership degree discreteness over the number of membership degrees.

Based on the aforementioned limitations, this paper aims to construct a trust improvement consensus model considering unreliability degree of opinions, and explores the impact of trust improvement on consensus decision-making process, as well as the influence of unreliability degree of opinions on trust improvement consensus. The main contributions of this paper are as follows:

  1. (1)

    A measurement method for unreliability degree of opinions is proposed based on hesitancy degree of experts. Specifically, an improved measurement method for hesitancy degree of experts addresses the issue that the influence of the discreteness of membership degree on hesitation is much smaller than the number of membership degrees.

  2. (2)

    A trust improvement method is proposed based on the measurement of unreliability degree of opinions. This method can enhance the trust degree of experts, promote group consensus, and ensure the accuracy of trust degree evaluation. Additionally, a score function for trust propagation path is introduced to select more efficient trust propagation paths, thus guaranteeing the efficiency of trust improvement.

  3. (3)

    A method for adjusting opinions among relevant experts is proposed based on unreliability degree of opinions and trust relationships between experts. This method can simultaneously increase individual consensus degree and reduce unreliability degree of opinions.

To illustrate the differences between this study and existing research more intuitively, Table 1 provides a comparison between the relevant literature and the proposed trust improvement consensus model in this paper.

Table 1 Comparison with existing research
Full size table

The rest of this paper is organized as follows: Sect. 2 introduces the relevant knowledge of hesitant fuzzy sets and trust propagation operator. Section 3 proposes a method for measuring unreliability degree of opinions. In Sect. 4, we present a trust improvement method considering unreliability degree of opinions. Section 5 constructs a trust improvement model including the method of opinions adjustment considering unreliability degree of opinions. Section 6 verifies the feasibility of the proposed model through a practical case study and simulation analysis. In Sect. 7, the effectiveness and advantages of the proposed model are validated through simulation and comparative analysis. Finally, Sect. 8 presents the conclusions of this paper.

2 Preliminaries

To measure unreliability degree of opinions and improve trust relationship among experts, it is necessary to define the concepts of hesitant fuzzy sets and trust propagation operator.

2.1 Hesitant Fuzzy Sets

In this paper, hesitant fuzzy sets are used to represent experts’ evaluation opinions. Due to the complexity of the decision-making environment [57], limited cognitive abilities of experts, or decision-making pressure [30], they may hesitate and provide multiple evaluation opinions when assessing alternatives. Hesitant fuzzy sets can extract imprecise and hesitant information [52].

Definition 1

[52]: Let \(X\) be a given non-empty set, then a hesitant fuzzy set on \(X\) is defined as:

$$A = \left\{ { < x,h_A \left( x \right) > |x \in X} \right\},$$
(1)

where \(h_A \left( x \right)\) is a set of several values in \(\left[ {0,1} \right]\), which represents the possible membership degrees of element \(x\) with respect to the \(A\), and \(h = h_A (x)\) is called a hesitant fuzzy element.

Definition 2

[56]: Let \(h = \left\{ {\gamma^i |i = 1,2,...,l_h } \right\}\) be a hesitant fuzzy element, then the hesitancy degree \(H\left( h \right)\) of \(h\) is defined as:

$$H(h) = \frac{1}{2}\left[ {\frac{1}{l_h }\sum_{i = 1}^{l_h } {\left[ {\gamma^i - \left( {\frac{1}{l_h }\sum_{i = 1}^{l_h } {\gamma^i } } \right)} \right]}^2 + \left( {1 - \frac{1}{l_h }} \right)} \right],$$
(2)

where \(l_h\) is the number of membership degrees in \(h\), \(\gamma^i\) is the \(i\) th membership degree in \(h\).

Definition 3

[52]: Let \(h\) be a hesitant fuzzy element, then the score function \(s\left( h \right)\) of \(h\) is defined as:

$$s\left( h \right) = \frac{1}{l_h }\sum_{i = 1}^{l_h } {\gamma^i } .$$
(3)

For \(h_1\) and \(h_2\), if \(s\left( {h_1 } \right) > s\left( {h_2 } \right)\), \(h_1\) is considered superior to \(h_2\), denoted as \(h_1 > h_2\); if \(s\left( {h_1 } \right) = s\left( {h_2 } \right)\), \(h_1\) and \(h_2\) are considered indistinguishable, denoted as \(h_1\) ~ \(h_2\).

2.2 Trust Propagation Operator

Based on the Einstein product operator, the trust degree of experts is calculated through the trust propagation process, aiming to improve the trust relationship among experts.

Definition 4

[58]: The trust propagation operator of the Einstein product is defined as:

$$E_\otimes \left( {x_1 ,...,x_n } \right) = \left( {\frac{{2\prod_{i = 1}^n {x_i } }}{{\prod_{i = 1}^n {\left( {2 - x_i } \right)} + \prod_{i = 1}^n {x_i } }}} \right),$$
(4)

where \(x_i\) represents the trust degree of the \(i\) th node on the trust propagation path.

3 Unreliability Degree of Opinions

The unreliability degree of opinions can ensure the effectiveness of improving trust relationships and achieve reasonable consensus decision-making results. In this paper, the unreliability degree of opinions is measured based on the hesitancy degree of experts, as experts may exhibit a certain level of hesitation due to limited cognitive abilities or the complexity of the decision-making environment [30, 57]. High hesitation of experts implies high uncertainty in their evaluations [51], which can lead to a decrease in the quality of decision-making information, resulting in unreliable opinions provided by experts. The higher the hesitancy degree of experts, the more unreliable their evaluation opinions on alternatives. Let \(E = \left\{ {e_1 ,e_2 ,...,e_k } \right\}\left( {k \ge 2} \right)\) be the set of experts. The set of alternatives is \(X = \left\{ {x_1 ,x_2 ,...,x_m } \right\}\left( {m \ge 2} \right)\), and the attribute set of the alternatives is denoted as \(A = \left\{ {a_1 ,a_2 ,...,a_n } \right\}\left( {n \ge 2} \right)\). The trust relationship matrix of the group is \(\Lambda = \left( {t_{ij} } \right)_{k \times k}\), where \(t_{ij}\) represents the trust degree of \(e_i\) to \(e_j\). The hesitant fuzzy decision matrix of \(e_i\) is denoted as \(S_i = \left( {s_i^{bf} } \right)_{m \times n}\), where \(s_i^{bf}\) represents the hesitant fuzzy element evaluation of \(e_i\) on \(x_b\) with respect to \(a_f\). \(s_i^{bfl_{(s_i^{bf} )} }\) represents the \(l_{(s_i^{bf} )}\) th membership degree in \(s_i^{bf}\), and \(p_{(s_i^{bf} )}\) represents the number of membership degrees in \(s_i^{bf}\), where \(s_i^{bfl_{(s_i^{bf} )} } \in \left[ {0,1} \right]\).

Definition 2 measures hesitancy degree of hesitant fuzzy elements based on the number of membership degrees and the degree of membership discreteness. However, this method uses variance to represent the degree of membership discreteness, which makes the influence of membership discreteness on the hesitancy degree of hesitant fuzzy elements much smaller than the number of membership degrees. In mathematical statistics, both variance and standard deviation can describe the discreteness of a dataset [59]. The variance is equal to the sum of the squares of the standard deviation. Since the standard deviation has a range of \(\left[ {0,1} \right]\), the square standard deviation will yield the variance of the smaller number. Consequently, hesitancy degree is not significantly impacted by the dispersion degree of membership using the variance metric. Therefore, in this paper, standard deviation is used to represent the degree of membership discreteness, and a parameter for membership discreteness is introduced. Meanwhile, in Sect. 7.3, the method of Definition 2 is compared with the improved method in this paper.

Definition 5:

Let \(\lambda\) be a parameter for membership discreteness, which is the standard deviation of the maximum and minimum values of \(s_i^{bfl_{(s_i^{bf} )} }\). The improved hesitancy degree \(HD_i^{bf}\) of \(s_i^{bf}\) is:

$$HD_i^{bf} = \frac{1}{2}\left[ {\frac{1}{\lambda }\sqrt {{\frac{1}{{p_{(s_i^{bf} )} }}\sum_{l_{(s_i^{bf} )} = 1}^{p_{(s_i^{bf} )} } {\left[ {s_i^{bfl_{(s_i^{bf} )} } - \left( {\frac{1}{{p_{(s_i^{bf} )} }}\sum_{l_{(s_i^{bf} )} = 1}^{p_{(s_i^{bf} )} } {s_i^{bfl_{(s_i^{bf} )} } } } \right)} \right]}^2 }} + \left( {1 - \frac{1}{{p_{(s_i^{bf} )} }}} \right)} \right],$$
(5)

where \(HD_i^{bf} \in \left[ {0,1} \right]\).

Definition 6:

The improved hesitancy degree \(HD_i\) of \(e_i\) is defined as:

$$HD_i = \frac{1}{2mn}\sum_{b = 1}^m {\sum_{f = 1}^n {\left[ {\frac{1}{\lambda }\sqrt {{\frac{1}{{p_{(s_i^{bf} )} }}\sum_{l_{(s_i^{bf} )} = 1}^{p_{(s_i^{bf} )} } {\left[ {s_i^{bfl_{(s_i^{bf} )} } - \left( {\frac{1}{{p_{(s_i^{bf} )} }}\sum_{l_{(s_i^{bf} )} = 1}^{p_{(s_i^{bf} )} } {s_i^{bfl_{(s_i^{bf} )} } } } \right)} \right]}^2 }} + \left( {1 - \frac{1}{{p_{(s_i^{bf} )} }}} \right)} \right]} } ,$$
(6)

where \(HD_i \in \left[ {0,1} \right]\).

Experts may be hesitant while evaluating alternatives due to restricted cognitive abilities or the intricate nature of decision-making context [48,49,50]. Experts with a greater degree of hesitation imply a significant amount of doubt in their judgment [51], which reduces the quality and scientific validity of decision-making information, and leads to unreliable opinions from the experts. Therefore, based on \(HD_i\), the unreliability degree of opinions \(NRD_i\) of \(e_i\) is proposed.

Definition 7:

The unreliability degree of opinions \(NRD_i\) of \(e_i\) is:

$$NRD_i = \left( {HD_i } \right)^2 ,$$
(7)

where \(NRD_i \in \left[ {0,1} \right]\).

Theorem 1:

\(HD_i\) increases with the increase of \(NRD_i\).

Proof

\(HD_i\) has a range of \(\left[ {0,1} \right]\). When \(x \in \left[ {0,1} \right]\), the range of function \(y = x^2\) is \(y \in \left[ {0,1} \right]\), and its derivative \(y^{\prime} = 2x\) is greater than 0 within \(x \in \left[ {0,1} \right]\), so \(y = x^2\) is monotonically increasing within \(x \in \left[ {0,1} \right]\). Therefore, it can be concluded that \(HD_i\) increases with the increase of \(NRD_i\)

Theorem 2:

The increment of \(NRD_i\) increases with the increase of \(HD_i\).

Proof

Since the second derivative \(y^{\prime\prime} = 2\) of \(y = x^2\) is always greater than 0, \(y = x^2\) is a convex function. Therefore, the increment of \(NRD_i\) increases with the increase of \(HD_i\).

4 Trust Improvement Method Considering Unreliability Degree of Opinions

In the process of consensus decision-making, low trust degree of experts toward others can trigger negative decision-making behaviors and hinder the group from reaching consensus [21]. Therefore, a trust degree threshold is set in this paper, and when the trust degree of experts towards others is lower than the trust degree threshold, their trust relationship needs to be improved. At the same time, considering unreliability degree of opinions can more accurately evaluate the trust of experts during the process of trust improvement.

According to [13] and [27], it is assumed that trust improvement among experts is caused by trust propagation paths, as the third-party experts can transmit information through trust propagation paths, facilitating communication between other pairs of experts and enhancing their trust degree. Moreover, the shorter the trust propagation path [31,32,33], and the higher the trust degree of experts [34, 35], the more efficient the trust propagation. This indicates that the efficiency of trust improvement is higher. Based on this, a score function for trust propagation path is constructed to identify the trust propagation path during trust improvement among experts.

Definition 8:

Let d be a trust propagation path from \(e_i\) to \(e_j\), \(\delta_d \left( {\delta_d \ge 3} \right)\) represents the number of experts on \(d\), \(t_{y\left( {y + 1} \right)}^d\) represents the trust degree of the \(y\) th expert on \(d\) towards the \(y + 1\) th expert, and \(y_d\) represents the number of experts on \(d\). The score function \(f\left( d \right)\) of \(d\) is defined as:

$$f\left( d \right) = \frac{1}{2}\left( {\frac{1}{\delta_d - 2} + \frac{{\sum_{y = 1}^{y_d - 1} {t_{y\left( {y + 1} \right)}^d } }}{\delta_d - 1}} \right),$$
(8)

where \(t_{y\left( {y + 1} \right)}^d \in \left[ {0,1} \right]\), \(f\left( d \right) \in \left[ {0,1} \right]\). For \(d_1\) and \(d_2\), if \(f\left( {d_1 } \right) > f\left( {d_2 } \right)\), \(d_1\) is considered superior to \(d_2\), denoted as \(d_1 > d_2\); if \(f\left( {d_1 } \right) = f\left( {d_2 } \right)\), \(d_1\) and \(d_2\) are considered indistinguishable, denoted as \(d_1\) ~ \(d_2\).

Based on \(f\left( d \right)\), trust propagation paths are identified to improve trust relationships among experts. If multiple trust propagation paths have the same \(f\left( d \right)\), one of them is randomly selected.

Ignoring unreliability degree of opinions in the trust improvement process can result in biases in the trust evaluations of experts towards others. Therefore, based on definition 4, a trust propagation operator considering the unreliability degree of opinions is proposed to calculate the trust degree increment of experts during the trust improvement process.

Definition 9:

Let \(NRD_{y + 1}^d\) be the unreliability degree of opinions of the \(y + 1\) th expert on \(d\), The trust propagation operator \(T_d\) considering unreliability degree of opinions is defined as:

$$T_d = \frac{{\prod_{y = 1}^{\delta_d - 1} {t_{y\left( {y + 1} \right)} \left( {1 - NRD_{y + 1}^d } \right)} }}{{1 + \prod_{y = 1}^{\delta_d - 1} {\left[ {1 - t_{y\left( {y + 1} \right)} \left( {1 - NRD_{y + 1}^d } \right)} \right]} }},$$
(9)

where \(T_d \in \left[ {0,1} \right]\).

Definition 10:

The trust degree \(t_{ij}^d\) of \(e_i\) to \(e_j\) after trust improvement based on \(d\) is calculated as:

$$t_{ij}^d = t_{ij} + \left( {1 - t_{ij} } \right)T_d ,$$
(10)

where \(t_{ij}^d \in \left[ {0,1} \right]\). Then, the trust relationship matrix is updated as \(\tilde{\Lambda }\) after trust improvement. The detailed trust improvement method considering unreliability degree of opinions is indicated in Algorithm 1.

Algorithm 1. Trust Improvement Method Considering Unreliability Degree of Opinions

Input: Initial trust relationship matrix \(\Lambda\), and trust degree threshold \(\overline{TD}\)

Step 1. Identify the experts whose trust relationships need to improve based on the latest trust relationship matrix and \(\overline{TD}\)

Step 2. Calculate \(HD_i\) based on the hesitant fuzzy decision matrix, then compute the \(NRD_i\)

Step 3. Identify the trust propagation path for the expert during the trust improvement process using the score function \(f\left( d \right)\)

Step 4. Calculate the trust degree of the experts after trust improvement using the identified trust propagation path and \(T_d\), and update the trust relationship matrix of experts as \(\tilde{\Lambda }\)

Step 5. Determine whether the trust degree of all experts in \(\tilde{\Lambda }\) reaches \(\overline{TD}\). If it reaches \(\overline{TD}\), the trust improvement process ends; otherwise, go back to Step 1

Output: Updated trust relationship matrix \(\tilde{\Lambda }\)

5 Trust Improvement Consensus Decision-Making

In consensus decision-making process, low trust by experts may result in detrimental decision-making behaviors that decrease group consensus degree. Meanwhile, it is important to note that experts’ opinions are not always reliable, and ignoring the unreliability degree of opinions may have an impact on the result of consensus decision-making. Therefore, this section will propose a trust improvement consensus decision-making process considering unreliability degree of opinions.

The trust improvement consensus decision-making process consists of the unreliability degree of opinions measurement process, trust improvement process, opinions adjustment process, and selection process.

5.1 Trust Improvement Consensus Framework

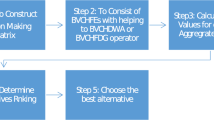
Based on the aforementioned works, a trust improvement consensus framework considering unreliability degree of opinions is constructed. The hesitancy degree of experts is calculated based on the hesitant fuzzy decision matrix of experts to measure the unreliability degree of opinions, then identify the experts whose trust degree is lower than the trust degree threshold. Using the score function for trust propagation paths, the trust relationships among experts are improved based on the consideration of unreliability degree of opinions. The experts who have not reached the individual consensus degree threshold or the unreliability degree of opinions threshold are identified, and their decision matrices are adjusted to facilitate the convergence of group opinions. Thus, a trust improvement consensus framework considering unreliability degree of opinions is constructed in Fig. 1.

Fig. 1
figure 1

Trust improvement consensus framework considering unreliability degree of opinions

Full size image

5.2 Trust Improvement Consensus Model

5.2.1 Trust Improvement Process

Given the trust degree threshold \(\overline{TD}\), when \(t_{ij}\) is lower than \(\overline{TD}\), \(e_i\) may exhibit negative decision-making behaviors. Algorithm 1 is used to improve the trust relationship between \(e_i\) and \(e_j\).

5.2.2 Experts Weight Allocation

If an expert is highly trusted by other experts and has a low unreliability degree of opinions, it indicates that the expert not only has a good reputation in the consensus decision-making process but also possesses abundant information resources [19, 44]. Therefore, the expert should be assigned a higher weight to play an important role in the consensus decision-making. Based on trust relationship matrix and unreliability degree of opinions, the weight \(\omega_j\) of \(e_j\) is determined as:

$$\omega_j = \frac{1}{2}\left( {\frac{{\sum_{i = 1}^{k\left( {i \ne j} \right)} {t_{ij} } }}{{\sum_{j = 1}^k {\sum_{i = 1}^{k\left( {i \ne j} \right)} {t_{ij} } } }} + \frac{1 - NRD_j }{{\sum_{j = 1}^k {\left( {1 - NRD_j } \right)} }}} \right).$$
(11)

According to Eq. (11), the set of expert weights \(\omega = \left\{ {\omega_1 ,\omega_2 ,...,\omega_k } \right\}^T\) is obtained, where \(\omega_j \in \left[ {0,1} \right]\), \(\sum_{j = 1}^k {\omega_j = 1}\).

5.2.3 Aggregation of Group Hesitant Fuzzy Decision Matrix

To facilitate the subsequent consensus degree measurement process and selection process, group decision matrix should be obtained. The hesitant fuzzy weighted average operator is used to aggregate individual hesitant fuzzy decision matrices into a group decision matrix. The hesitant fuzzy element \(s_G^{bf}\) of the group for \(x_b\) with respect to \(a_f\) is defined as [52]:

$$s_G^{bf} = HFWA\left( {s_1^{bf} ,s_2^{bf} ,...,s_k^{bf} } \right) = {\mathop \oplus \limits_{i = 1}^k} \left( {\omega_i s_i^{bf} } \right) = \bigcup\nolimits_{s_1^{bfl_{(s_1^{bf} )} } \in s_1^{bf} ,s_2^{bfl_{(s_2^{bf} )} } \in s_2^{bf} ,s_k^{bfl_{(s_k^{bf} )} } \in s_k^{bf} } {\left\{ {1 - \prod_{i = 1}^k {\left( {1 - s_i^{bfl_{(s_i^{bf} )} } } \right)^{\omega_i } } } \right\}} .$$
(12)

The group decision matrix is denoted as \(S_G^{bf} = \left( {s_G^{bf} } \right)_{m \times n}\).

5.2.4 Measurement of Individual Consensus Degree

After aggregating the group decision matrix, the individual consensus degree of experts is measured to determine if they have reached the individual consensus level. The number \(p_{(s_i^{bf} )}\) of membership degrees in \(s_i^{bf}\) of the individual decision matrix may be smaller than the number \(p_{(s_G^{bf} )}\) of evaluation values in \(s_G^{bf}\) of the group decision matrix, which makes it difficult to measure the individual consensus degree. Therefore, it is necessary to expand the expert individual hesitant fuzzy element [53]. Let \(\beta_{(s_i^{bf} )} = \max \left\{ {p_{(s_i^{bf} )} ,p_{(s_G^{bf} )} } \right\} = p_{(s_G^{bf} )}\), if \(p_{(s_i^{bf} )} < p_{(s_G^{bf} )}\), add the maximum value in \(s_i^{bf}\) to expand it to \(p_{(s_i^{bf} )} = \beta_{(s_i^{bf} )}\). Thus, the consensus degree \(CD_i^{bf}\) of \(s_i^{bf}\) in the decision matrix of \(e_i\) is obtained as:

$$CD_i = 1 - \frac{1}{mn}\sum_{b = 1}^m {\sum_{f = 1}^n {d\left( {s_i^{bf} ,s_G^{bf} } \right)} } = 1 - \frac{1}{mn}\sum_{b = 1}^m {\sum_{f = 1}^n {\frac{1}{{\beta_{(s_i^{bf} )} }}\sum_{\varepsilon = 1}^{\beta_{(s_i^{bf} )} } {\left| {s_i^{bf\varepsilon } - s_G^{bf\varepsilon } } \right|} } } .$$
(13)

Let the individual consensus degree threshold be \(\overline{CD}\). When \(CD_i\) is greater than or equal to \(\overline{CD}\), \(e_i\) has reached the individual consensus level. Conversely, when \(CD_i < \overline{CD}\), \(e_i\) has not reached the individual consensus level, he or she need to adjust opinions [60].

5.2.5 Opinions Adjustment Process Considering Unreliability Degree of Opinions

After measurement of individual consensus degree, experts should be judged whether they need to adjust opinions according to \(CD_i\) and \(NRD_i\). Let the threshold of unreliability degree of opinions is \(\overline{NRD}\), if \(CD_i\) is lower than \(\overline{CD}\), or \(NRD_i\) is greater than \(\overline{NRD}\), \(e_i\) needs to adjust opinions. In opinions adjustment process, \(e_i\) tends to refer to the opinions of their trusted experts. At the same time, referring to the opinions of experts with low unreliability is more conducive to obtaining reasonable consensus decision-making results.

Based on whether \(NRD_i\) is greater than \(\overline{NRD}\), experts are divided into subsets: the subset of unreliable opinions experts \(NRE = \left\{ {e_{\tau + 1} ,e_{\tau + 2} ,...,e_k } \right\}\), and the subset of reliable opinions experts \(RE = \left\{ {e_1 ,e_2 ,...,e_\tau } \right\}\), where \(e_v \in NRE\), \(e_u \in RE\), \(e_v ,e_u \in E\), \(NRE \cup RE = E\), \(NRE \cap RE = \emptyset\). Experts who need to adjust their opinions refer to the opinions of experts in \(RE\) based on the trust relationship matrix. Let expert \(e_{i^* }\) be the expert who needs to adjust their opinions, and the \(l_{(\tilde{s}_{i^* }^{bf} )}\) th membership degree \(\tilde{s}_{i^* }^{bfl_{(\tilde{s}_{i^* }^{bf} )} }\) of \(\tilde{s}_{i^* }^{bf}\) in their decision matrix after opinions adjustment is given by:

$$\tilde{s}_{i^* }^{bfl_{(\widetilde{S}_{i^* }^{bf} )} } = \frac{1}{2}\left( {s_{i^* }^{bfl_{(s_{i^* }^{bf} )} } + \sum_{u = 1}^{\tau \left( {u \ne i^* } \right)} {\left( {\frac{{t_{i^* u} }}{{\sum_{u = 1}^{\tau \left( {u \ne i^* } \right)} {t_{i^* u} } }}\sum_{l_{(s_u^{bf} )} = 1}^{p_{(s_u^{bf} )} } {\frac{{s_u^{bfl_{(s_u^{bf} )} } }}{{p_{(s_u^{bf} )} }}} } \right)} } \right).$$
(14)

The hesitant fuzzy decision matrix of \(e_{i^* }\) after opinions adjustment is denoted as \(\tilde{S}_{i^* } = \left( {\tilde{s}_{i^* }^{bf} } \right)_{m \times n}\). If \(RE\) is an empty set, \(e_{i^* }\) directly refers to the group decision matrix.

After adjusting their opinions, reconstruct the group decision matrix, then measure individual consensus degree and unreliability degree of opinions. If \(CD_{i^* }\) is greater than or equal to \(\overline{CD}\) and \(NRD_{i^* }\) is not greater than \(\overline{NRD}\), the selection process is entered. Otherwise, the expert opinions need to be adjusted again.

5.2.6 Selection Process Based on Hesitant Fuzzy Sets

Based on \(S_G\) and the hesitant fuzzy weighted average operator, the hesitant fuzzy element of each alternative is obtained [52]. Assuming equal weights for the attributes of the alternatives, \(s_G^b\) chosen by the group decision for \(x_b\) is given by:

$$s_G^b\,=\,HFWA\left( {s_G^{b1} ,s_G^{b2} ,...,s_G^{bn} } \right) = {\mathop \oplus \limits_{f = 1}^n} \left( {\frac{1}{n}s_G^{bf} } \right) = \bigcup\nolimits_{s_G^{bfl_{(s_G^{bf} )} } \in s_G^{bf} ,s_G^{bfl_{(s_G^{bf} )} } \in s_G^{bf} ,s_G^{bfl_{(s_G^{bf} )} } \in s_G^{bf} } {\left\{ {1 - \prod_{f = 1}^n {\left( {1 - s_G^{bfl_{(s_G^{bf} )} } } \right)^\frac{1}{n} } } \right\}} .$$
(15)

According to Definition 3, the score of each alternative is calculated, and the alternatives are ranked based on the scores to select the best alternative.

6 Application Example

Taking the selection of a cascade utilization scheme for power lithium-ion batteries in a certain region as an example, the feasibility of the proposed trust improvement consensus model is validated.

6.1 Problem Description

In recent years, with the rapid development of the global electric vehicle industry, an increasing number of people are choosing electric vehicles as a fashionable transportation. It is estimated that by 2030, the global total amount of power lithium-ion batteries recycling will reach 1500GWh [61]. Along with this comes the issue of power lithium-ion batteries recycling. One important approach to power lithium-ion batteries recycling is cascade utilization, which can effectively utilize the remaining performance of power lithium-ion batteries and reduce the cost of power lithium-ion batteries in other applications [62]. The selection of cascade utilization alternatives for power lithium-ion batteries not only needs to consider various factors such as battery performance [61, 63], economic factors, technical factors [64], environmental factors [62] and policy factors [64, 65], but also requires a focus on the opinions of relevant stakeholders (experts) [66]. Therefore, it can be seen as a consensus decision-making problem. The experts participating in the consensus decision-making process come from the local government (\(e_1\)), industry association (\(e_2\)), automobile manufacturer (\(e_3\)), power lithium-ion battery manufacturer (\(e_4\)), and cascade utilization enterprise (\(e_5\)), forming an expert set \(E = \left\{ {e_1 ,e_2 ,e_3 ,e_4 ,e_5 } \right\}\). The initial trust relationship matrix of group is \(\Lambda = \left( {t_{ij} } \right)_{5 \times 5}\). The proposed set of cascade utilization alternatives by the relevant department is \(X = \left\{ {x_1 ,x_2 ,x_3 ,x_4 } \right\}\). The evaluation of various alternatives by experts needs to consider battery health (\(a_1\)), technology (\(a_2\)), economy (\(a_3\)), policy (\(a_4\)) and environment (\(a_5\)), which constitute the attribute set \(A = \left\{ {a_1 ,a_2 ,a_3 ,a_4 ,a_5 } \right\}\). The trust degree threshold \(\overline{TD}\) is set to 0.5, the threshold of unreliability degree of opinions \(\overline{NRD}\) is set to 0.05, and the consensus degree threshold \(\overline{CD}\) is set to 0.85.

6.2 Consensus Decision-Making Process

The hesitant fuzzy decision matrices provided by experts are as follows:

$$\begin{gathered} S_1 = \left( {\begin{array}{*{20}c} {0.9} & {\left[ {0.2,0.3,0.4} \right]} & {\left[ {0.3,0.5} \right]} & {\left[ {0.4,0.6} \right]} & {\left[ {0.6,0.7} \right]} \\ {\left[ {0.6,0.7} \right]} & {\left[ {0.7,0.8} \right]} & {\left[ {0.4,0.5} \right]} & {\left[ {0.5,0.7} \right]} & {\left[ {0.4,0.6} \right]} \\ {0.9} & {\left[ {0.4,0.7} \right]} & {\left[ {0.6,0.7} \right]} & {\left[ {0.7,0.8} \right]} & {\left[ {0.7,0.8,0.9} \right]} \\ {\left[ {0.7,0.9} \right]} & {\left[ {0.4,0.5,0.6} \right]} & {0.9} & {0.8} & {0.3} \\ \end{array} } \right), \hfill \\ S_2 = \left( {\begin{array}{*{20}c} {\left[ {0.5,0.6} \right]} & {\left[ {0.5,0.6,0.7} \right]} & {0.9} & {\left[ {0.4,0.5} \right]} & {\left[ {0.7,0.8} \right]} \\ {\left[ {0.4,0.5,0.6} \right]} & {\left[ {0.6,0.7} \right]} & {\left[ {0.6,0.7} \right]} & {0.8} & {0.8} \\ {\left[ {0.4,0.6} \right]} & {0.4} & {0.6} & {\left[ {0.6,0.7,0.8} \right]} & {\left[ {0.4,0.5,0.6} \right]} \\ {\left[ {0.6,0.8} \right]} & {\left[ {0.6,0.8} \right]} & {0.8} & {0.8} & {0.7} \\ \end{array} } \right), \hfill \\ S_3 = \left( {\begin{array}{*{20}c} {\left[ {0.6,0.7} \right]} & {0.7} & {\left[ {0.6,0.7,0.8} \right]} & {\left[ {0.8,0.9} \right]} & {0.7} \\ {\left[ {0.5,0.6,0.7} \right]} & {\left[ {0.6,0.7} \right]} & {\left[ {0.8,0.9} \right]} & {\left[ {0.6,0.8} \right]} & {0.6} \\ {0.6} & {0.8} & {\left[ {0.7,0.8} \right]} & {\left[ {0.4,0.5} \right]} & {\left[ {0.4,0.5,0.6} \right]} \\ {\left[ {0.8,0.9} \right]} & {0.6} & {\left[ {0.7,0.8} \right]} & {\left[ {0.6,0.7,0.8} \right]} & {0.6} \\ \end{array} } \right), \hfill \\ S_4 = \left( {\begin{array}{*{20}c} {\left[ {0.6,0.7,0.8} \right]} & {\left[ {0.3,0.4,0.5} \right]} & {\left[ {0.3,0.6} \right]} & {\left[ {0.6,0.7} \right]} & {\left[ {0.8,0.9} \right]} \\ {0.8} & {0.6} & {0.6} & {0.8} & {\left[ {0.5,0.7} \right]} \\ {\left[ {0.5,0.7} \right]} & {\left[ {0.6,0.7,0.8} \right]} & {\left[ {0.8,0.9} \right]} & {\left[ {0.6,0.7} \right]} & {0.7} \\ {\left[ {0.3,0.4} \right]} & {\left[ {0.8,0.9} \right]} & {\left[ {0.5,0.6,0.7} \right]} & {0.1} & {\left[ {0.4,0.5,0.7} \right]} \\ \end{array} } \right), \hfill \\ S_5 = \left( {\begin{array}{*{20}c} {\left[ {0.7,0.8} \right]} & {0.7} & {\left[ {0.6,0.7,0.8} \right]} & {\left[ {0.3,0.4} \right]} & {\left[ {0.6,0.7} \right]} \\ {0.3} & {\left[ {0.8,0.9} \right]} & {\left[ {0.7,0.8} \right]} & {\left[ {0.5,0.7} \right]} & {\left[ {0.5,0.9} \right]} \\ {\left[ {0.6,0.7,0.8} \right]} & {\left[ {0.6,0.7} \right]} & {0.2} & {\left[ {0.5,0.6} \right]} & {0.5} \\ {0.2} & {0.7} & {0.4} & {\left[ {0.5,0.7} \right]} & {0.9} \\ \end{array} } \right). \hfill \\ \end{gathered}$$

Based on hesitant fuzzy decision matrices provided by experts, the hesitancy degree of the experts are calculated from Eq. (6) as \(HD_1 = 0.25\), \(HD_2 = 0.21\), \(HD_3 = 0.23\), \(HD_4 = 0.26\) and \(HD_5 = 0.20\). The unreliability degree of opinions \(NRD_1 = 0.07\), \(NRD_2 = 0.04\), \(NRD_3 = 0.05\), \(NRD_4 = 0.07\) and \(NRD_5 = 0.04\) are calculated according to Eq. (7). Based on \(\overline{NRD}\), the subset of unreliable opinions experts \(NRE = \left\{ {e_1 ,e_4 } \right\}\) and the subset of reliable opinions experts \(RE = \left\{ {e_2 ,e_3 ,e_5 } \right\}\) are determined.

The initial trust relationship matrix of group is:

$$\Lambda = \left( {\begin{array}{*{20}c} - & 0 & {0.70} & {0.20} & {0.50} \\ 0 & - & {0.70} & {0.80} & {0.30} \\ {0.30} & {0.50} & - & {0.80} & {0.60} \\ {0.90} & {0.90} & {0.60} & - & {0.50} \\ 0 & {0.60} & {0.60} & {0.70} & - \\ \end{array} } \right).$$

The initial trust relationships of group are shown in Fig. 2.

Fig. 2
figure 2

Initial trust relationships of group

Full size image

Obviously, \(t_{12}\), \(t_{14}\), \(t_{21}\), \(t_{25}\), \(t_{31}\) and \(t_{51}\) have not reached \(\overline{TD}\). Therefore, the involved experts need to undergo trust improvement according to Algorithm 1. The updated trust relationship matrix \(\tilde{\Lambda }\) of group is:

$$\tilde{\Lambda } = \left( {\begin{array}{*{20}c} - & {0.58} & {0.70} & {0.57} & {0.50} \\ {0.60} & - & {0.70} & {0.80} & {0.53} \\ {0.72} & {0.50} & - & {0.80} & {0.60} \\ {0.90} & {0.90} & {0.60} & - & {0.50} \\ {0.52} & {0.60} & {0.60} & {0.70} & - \\ \end{array} } \right).$$

The trust relationships of group after trust improvement are shown in Fig. 3.

Fig. 3
figure 3

Trust relationships of group after trust improvement

Full size image

The individual consensus degree of experts is measured to determine if they have reached the individual consensus level. The weights of each expert are calculated according to Eq. (11), resulting in \(\omega = \left\{ {0.23,0.18,0.19,0.24,0.16} \right\}^T\). Then, the group decision matrix \(S_G\) is aggregated according to Eq. (12):

$$S_G = \left( {\begin{array}{*{20}c} {\left[ {0.71,0.77,0.79} \right]} & {\left[ {0.50,0.55,0.60} \right]} & {\left[ {0.57,0.70,0.74} \right]} & {\left[ {0.55,0.68} \right]} & {\left[ {0.69,0.78} \right]} \\ {\left[ {0.58,0.64,0.67} \right]} & {\left[ {0.67,0.76} \right]} & {\left[ {0.69,0.74} \right]} & {\left[ {0.67,0.77} \right]} & {\left[ {0.58,0.74} \right]} \\ {\left[ {0.67,0.74,0.76} \right]} & {\left[ {0.59,0.68,0.71} \right]} & {\left[ {0.64,0.73} \right]} & {\left[ {0.58,0.69,0.71} \right]} & {\left[ {0.58,0.64,0.72} \right]} \\ {\left[ {0.58,0.76} \right]} & {\left[ {0.64,0.74,0.76} \right]} & {\left[ {0.73,0.76,0.78} \right]} & {\left[ {0.63,0.67,0.70} \right]} & {\left[ {0.62,0.64,0.68} \right]} \\ \end{array} } \right).$$

According to Eq. (13), the individual consensus degree of \(e_1 , e_5\) is measured, resulting in 0.85, 0.90, 0.90, 0.86, and 0.83, respectively. Based on \(\overline{CD} = 0.85\), it is determined that \(e_5\) has not reached the individual consensus level and needs to adjust his/her opinions. At the same time, \(e_1\) and \(e_4\) in \(NRE\) need to adjust their opinions.

According to Eq. (14), the adjusted decision matrices of the experts are:

$$\tilde{S}_1 = \left( {\begin{array}{*{20}c} {0.77} & {\left[ {0.43,0.48,0.53} \right]} & {\left[ {0.53,0.63} \right]} & {\left[ {0.49,0.59} \right]} & {\left[ {0.65,0.70} \right]} \\ {\left[ {0.56,0.61} \right]} & {\left[ {0.70,0.75} \right]} & {\left[ {0.58,0.63} \right]} & {\left[ {0.60,0.70} \right]} & {\left[ {0.55,0.65} \right]} \\ {0.75} & {\left[ {0.51,0.66} \right]} & {\left[ {0.57,0.62} \right]} & {\left[ {0.63,0.68} \right]} & {\left[ {0.60,0.65,0.70} \right]} \\ {\left[ {0.66,0.76} \right]} & {\left[ {0.53,0.58,0.63} \right]} & {0.78} & {0.75} & {0.51} \\ \end{array} } \right),$$
$$\tilde{S}_4 = \left( {\begin{array}{*{20}c} {\left[ {0.62,0.67,0.72} \right]} & {\left[ {0.48,0.53,0.58} \right]} & {\left[ {0.45,0.70} \right]} & {\left[ {0.57,0.62} \right]} & {\left[ {0.76,0.81} \right]} \\ {0.66} & {0.65} & {0.72} & {0.76} & {\left[ {0.61,0.71} \right]} \\ {\left[ {0.54,0.64} \right]} & {\left[ {0.59,0.64,0.69} \right]} & {\left[ {0.67,0.72} \right]} & {\left[ {0.57,0.62} \right]} & {0.60} \\ {\left[ {0.46,0.51} \right]} & {\left[ {0.74,0.79} \right]} & {\left[ {0.59,0.64,0.69} \right]} & {0.41} & {\left[ {0.56,0.61,0.71} \right]} \\ \end{array} } \right),$$
$$\tilde{S}_5 = \left( {\begin{array}{*{20}c} {\left[ {0.65,0.70} \right]} & {0.68} & {\left[ {0.70,0.75,0.80} \right]} & {\left[ {0.48,0.53} \right]} & {\left[ {0.66,0.71} \right]} \\ {0.45} & {\left[ {0.73,0.78} \right]} & {\left[ {0.73,0.78} \right]} & {\left[ {0.63,0.73} \right]} & {\left[ {0.60,0.80} \right]} \\ {\left[ {0.58,0.63,0.68} \right]} & {\left[ {0.60,0.65} \right]} & {0.44} & {\left[ {0.54,0.59} \right]} & {0.50} \\ {0.49} & {0.78} & {0.59} & {\left[ {0.63,0.73} \right]} & {0.78} \\ \end{array} } \right).$$

The group decision matrix after adjustment is:

$$\tilde{S}_G = \left( {\begin{array}{*{20}c} {\left[ {0.65,0.70,0.71} \right]} & {\left[ {0.56,0.60,0.64} \right]} & {\left[ {0.67,0.75,0.78} \right]} & {\left[ {0.58,0.68} \right]} & {\left[ {0.70,0.75} \right]} \\ {\left[ {0.53,0.58,0.62} \right]} & {\left[ {0.66,0.72} \right]} & {\left[ {0.71,0.76} \right]} & {\left[ {0.69,0.76} \right]} & {\left[ {0.64,0.72} \right]} \\ {\left[ {0.59,0.65,0.66} \right]} & {\left[ {0.60,0.65,0.67} \right]} & {\left[ {0.61,0.67} \right]} & {\left[ {0.56,0.63,0.66} \right]} & {\left[ {0.52,0.56,0.61} \right]} \\ {\left[ {0.52,0.74} \right]} & {\left[ {0.64,0.70,0.71} \right]} & {\left[ {0.71,0.74,0.75} \right]} & {\left[ {0.66,0.69,0.72} \right]} & {\left[ {0.63,0.64,0.66} \right]} \\ \end{array} } \right).$$

The individual consensus degree of \(e_1 , e_5\) are measured according to Eq. (13), resulting in 0.92, 0.91, 0.92, 0.93, and 0.93, respectively. Comparing them with the set consensus degree threshold of 0.85, all experts have reached the individual consensus level. In addition, according to Eq. (7), it is determined that the unreliability degree of opinions of \(e_1\) and \(e_4\) are \(NRD_1 = 0.05\) and \(NRD_4 = 0.05\), respectively, which are not greater than the threshold of unreliability degree of opinions 0.05. Therefore, they enter the selection process.

According to Eq. (3), the scores of the alternatives in the group decision matrix are calculated as \(s\left( {s_G^1 } \right) = 0.6836\), \(s\left( {s_G^2 } \right) = 0.6947\), \(s\left( {s_G^3 } \right) = 0.6211\) and \(s\left( {s_G^4 } \right) = 0.6930\). The alternatives are ranked with \(x_2 > x_4 > x_1 > x_3\), and \(x_2\) is selected as the best cascade utilization alternative for a certain region.

7 Simulation and Comparative Analysis

To verify the effectiveness and advantages of the proposed trust improvement consensus model, this section conducts an analysis of the effectiveness of trust improvement and the effectiveness of opinions adjustment methods. Additionally, the improved hesitancy degree measurement method is compared with existing research method, and the consensus models from existing research are compared with the proposed trust improvement consensus model.

7.1 Analysis of Trust Improvement Effectiveness

To verify that trust improvement can facilitate group consensus, 5 experts' opinions and trust degrees are randomly generated. The group consensus degree in the first round of the consensus process after trust improvement are shown in Fig. 4 for different trust degree thresholds.

Fig. 4
figure 4

Group consensus degree. Group consensus degree = Sum of \(CD_i\)/Number of experts

Full size image

As shown in Fig. 4, as the trust degree threshold increases, the group consensus degree in the first round of the consensus process after trust improvement also increases. Therefore, it can be concluded that trust improvement can facilitate group consensus, the higher the number of experts participating in trust improvement and the greater the degree of trust improvement, the higher the efficiency of achieving group consensus.

7.2 Analysis of Effectiveness of Opinions Adjustment Method

To verify that the proposed opinions adjustment method considering unreliability degree of opinions can lead to group consensus and reduce unreliability degree of opinions, 15 experts' opinions and trust degree are randomly generated. The evolution of opinions for the 15 experts is shown in Fig. 5, and the changes in unreliability degree of opinions are shown in Fig. 6.

Fig. 5
figure 5

Evolution of opinions

Full size image
Fig. 6
figure 6

Changes in unreliability degree of opinions

Full size image

As seen in Fig. 5, with the increase in consensus rounds, the opinions of the 15 experts converge to the circle area marked in red. Figure 6 shows that with the increase in consensus rounds, the unreliability degree of opinions of the 15 experts gradually decreases. Therefore, it can be concluded that the proposed opinions adjustment method considering unreliability degree of opinions can facilitate group consensus and reduce opinions unreliability.

7.3 Comparison with Existing Hesitancy Degree Measurement Method

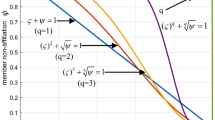
In [56], the influence of membership degree discreteness on the hesitancy degree of hesitant fuzzy elements is very small. Based on the measurement method in [56], this paper improves the measurement method to demonstrate the advantages of the improved hesitancy degree measurement method for hesitant fuzzy elements. The hesitancy degree of hesitant fuzzy element \(\left[ {a,0.9} \right]\) is measured using both the hesitancy degree measurement method in [56] and the improved method in this paper, as shown in Fig. 7.

Fig. 7
figure 7

Comparison of hesitancy degree measurement methods for hesitant fuzzy elements

Full size image

As shown in Fig. 7, when \(a = 0.1\) and \(a = 0.8\), the hesitancy degree measured by the method in [56] decreases from 0.33 to 0.25, with a decrease of only 0.08. The influence of membership degree discreteness on the hesitancy degree is very small. In contrast, the hesitancy degree measured by the improved method in this paper decreases from 0.65 to 0.30, with a decrease of 0.35, indicating a significant influence of membership degree discreteness on the hesitancy degree of hesitant fuzzy elements.

7.4 Comparison with Existing Research

To verify the advantages of the trust improvement consensus model considering unreliability degree of opinions, it is compared with existing research. The consensus models from existing research are applied to the case study in this paper and compared with the proposed trust improvement consensus model, as shown in Table 2.

Table 2 Quantitative comparison with existing research
Full size table

First, unlike the studies by Zhang et al. [18], Dong et al. [26], and Liu et al. [42], this paper proposes that trust relationships should be improved for all experts who have not reached the trust degree threshold. This results in a larger number of experts reaching the consensus degree threshold in the first round of the consensus process, with a higher degree of trust improvement. Additionally, this paper considers unreliability degree of opinions during the trust improvement process, which is different from the trust degree of experts after trust improvement in Dong et al. [26]. Therefore, the trust improvement method proposed in this paper can effectively facilitate group consensus, with a higher efficiency of trust improvement. Furthermore, unreliability degree of opinions can affect the degree of trust improvement.

Second, compared to the studies by Zhang et al. [18], Dong et al. [26] and Liu et al. [42], this paper achieves a higher group consensus degree and a greater reduction in unreliability degree of opinions after the first opinions adjustment. Thus, the proposed opinions adjustment method can effectively facilitate group consensus and reduce unreliability degree of opinions.

Finally, the studies by Zhang et al. [18] and Dong et al. [26], did not consider unreliability degree of opinions, resulting in different rankings of alternatives in the trust improvement consensus decision-making compared to the studies by Liu et al. [42] and this paper. Therefore, it can be seen that unreliability degree of opinions can affect the ranking of alternatives in trust improvement consensus decision-making.

8 Conclusions

To address the issue of low trust degree among experts hindering group consensus and unreliable opinions leading to unreasonable decision result, this paper constructs a trust improvement consensus model considering unreliability degree of opinions. First, the paper assumes that experts' evaluation opinions may be unreliable and proposes an improved unreliability degree of opinions measurement method. Second, considering unreliability degree of opinions, the paper proposes trust improvement method and opinion adjustment methods for relevant experts. Finally, the feasibility, effectiveness, and advantages of the proposed trust improvement consensus model are validated through a typical case study on the selection of cascade utilization alternatives for power lithium-ion batteries, as well as simulation and comparative analysis.

The main conclusions of this paper are as follows:

  1. (1)

    Trust improvement should be considered in the consensus decision-making process. Trust improvement can facilitate group consensus. Meanwhile, the score function of trust propagation path can enhance trust among experts more effectively.

  2. (2)

    The unreliability degree of opinions not only affects the degree of trust improvement but also affects the ranking of alternatives. By taking into account the unreliability degree of opinions throughout the process of adjusting opinions, it is possible to promote group consensus and decrease the unreliability degree of opinions.

  3. (3)

    Compared with the method of measuring the hesitancy degree of hesitant fuzzy elements in [56], the improved method in this paper exhibits a significant impact of the discreteness of membership degree on the hesitancy degree.

Although the trust improvement method proposed in this paper can facilitate group consensus, the cost of trust improvement is not considered. Future research can further explore trust improvement method taking into account cost. Meanwhile, this paper measure unreliability degree of opinions based on hesitant fuzzy sets. Future research can further explore the measurement methods for unreliability degree of opinions in complex and uncertain linguistic environments. Additionally, the paper assumes that experts are willing to undergo trust improvement, and further research is needed to explore trust improvement considering non-cooperative behavior of experts.