A Novel Distance Measure and CRADIS Method in Picture Fuzzy Environment

Abstract

Picture fuzzy set (PFS) is an extension of intuitionistic fuzzy set, providing a more realistic representation of information characterized by fuzziness, ambiguity, and inconsistency. Distance measure plays a crucial role in organizing diverse strategies for addressing multi-attribute decision-making (MADM) problems. In this paper, we provide a novel distance measure on the basis of Jensen–Shannon divergence in a picture fuzzy environment. This newly proposed PF distance measure not only satisfies the four properties of metric space, but also has good differentiation. Numerical example and pattern recognition are used to compare the proposed PF distance measure with some existing PF distance measures to illustrate that the new PF distance has effectiveness and superiority. Then, we develop a maximum deviation method in association with the proposed distance measure to evaluate the weight of the attribute with picture fuzzy information in the MADM problem. Subsequently, a new MADM method is proposed under picture fuzzy environment, which is on the basis of new PF distance measure and the compromise ranking of alternatives from distance to ideal solution (CRADIS) method. Finally, we furnish an illustrative example and perform a comparative analysis with various decision-making methods to confirm the validity and practicability of the improved MADM method.

1 Introduction

In actual daily life, numerous phenomena are found to have certain ambiguity or uncertainty. However, these fuzzy or uncertain phenomenon cannot be reasonably explained by the existing mathematical knowledge. In order to meet the practical needs, Zadeh [1] first proposed fuzzy theory (PF) in 1965, which was widely used in the field of MADM for resolving problems marked by fuzzy uncertainty [2,3,4,5]. Subsequently, in order to improve fuzzy theory, Atanassov [6] proposed intuitionistic fuzzy sets (IFS). Intuitionistic fuzzy set can deal with uncertainly information comprehensively, which has been successfully used in many different fields, including medical analysis [7,8,9], pattern recognition [10,11,12], cluster analysis [13,14,15,16,17], and decision-making problems [17,18,19]. However, intuitionistic fuzzy set still cannot solve all the uncertainties in reality. For example, with voting, some people support it, some oppose it, and some neither support nor oppose it, which is difficult for intuitionistic fuzzy theory to capture when solving these practical situations with mathematical models. To help deal with this type of problem, Cuong [20, 21] extended the intuitionistic fuzzy set to picture fuzzy set (PFS) and studied the basic algorithm and characteristics of PFS. Picture fuzzy sets can be adapted to situations requiring more answer types, such approval, neutral, against and abstention and cover far more decisions than intuitionistic fuzzy sets. Considering the advantages and practicability of picture fuzzy set theory, many scholars have begun to study picture fuzzy set theory [22,23,24,25,26,27,28,29,30,31] and have applied it to solve practical problems [32,33,34,35,36,37,38].

Distance measurement as a mathematical tool is significant in many practical application fields, all of which have attracted a great deal of interest from researchers in recent years. Up to now, numerous types of distance measures have been explored for Picture Fuzzy Sets (PFSs). For example, Guong [21] first proposed some distance measures for PFSs. Subsequently, Son [36] presented picture association measures and generalized picture fuzzy distance measures, which were used to clustering analysis. Son [26] demonstrated the applicability of the proposed work in clustering analysis by extending the fundamental distance measure in PFS to a new measure, which is called the generalised picture fuzzy distance measure. Dutta [32] presented distance measures for PFSs based on well-known distances like Euclidean and Hamming distances, initially applied to medical diagnosis. Singh et al. [33] developed multiple PF distance measures on the base of the geometric distance model, which were used to evaluate flood disaster risk in southern India. Khan et al. [39] defined a new two-parameter distance measure for PFSs, which was applied in pattern recognition and medical diagnosis. Later, Ganie and Singh [40] proposed an improved distance measure for PFSs that relied on direct operations and applied it to MADM problems. However, when we review the PF distance measures mentioned above, we note that some existing PF distance measures violate the triangle inequality, which is inconsistent with the distance measure in the metric space. Besides, some existing PF distance measures may not accurately reflect the judgement and may lead to unreasonable or sometimes even counterintuitive results. Accordingly, the distance measure for PFSs still needs to be improved to avoid the shortcomings of the above PF distance measures.

Picture fuzzy set theory can express more situations in real life and effectively reflect the fuzziness of subjective judgment. Because of the characteristics of picture fuzzy set, it is more suitable for the capture of inaccurate, uncertain and inconsistent information in MADM problems. Therefore, it is of utmost significance to analyse MADM problems in terms of picture fuzzy sets. In recent years, many researchers [41,42,43,44,45] have studied MADM method under the picture fuzzy environment. For example, the ARAS [46] method possesses broad applicability and accommodates the consideration of each alternative’s ratio to the ideal solution. Building on these advantages, Jovčić et al. [47] extended ARAS method to picture fuzzy environment, which effectively solves the problem of concept selection of goods distribution. MARCOS method represents a novel and efficient MADM approach, further adapted to the picture fuzzy environment by Simić et al. [48]. When determining the optimal solution, MARCOS method can consider not only ideal solution but also anti-ideal solution. Researchers firstly proposed Compromise ranking of alternatives from distance to ideal solution (CRADIS) method in [49], which integrates the strengths of MARCOS, ARAS, and TOPSIS methods, taking full advantage of these three methods to consider the optimal solution to MADM problems in a simpler and more comprehensive way. However, a comprehensive literature review revealed minimal utilization of the CRADIS method in picture fuzzy environment. Therefore, the CRADIS method will be extended to the picture fuzzy environment in this paper.

Now we will explore the key motivations behind our research. Firstly, we analyze the motivation for the new PF distance measure. When reviewing the current PF distance measures, we realize that some distance measures violate the triangle inequality, which is inconsistent with the properties of metric space (see Example 1), and others do not satisfy the axiomatic requirements (see Example 2). Besides, when calculating the difference between different PFSs with some existing PF distance measures, counterintuitive results can be produced. Some PF distance measures will provide unreasonable results in pattern recognition. Therefore, it is always desirable to have a new distance measure that meets metric space properties and reduces the number of counter-intuitive cases. Therefore, we attempt to develop a new distance measure which is on the basis of Jensen–Shannon divergence under picture fuzzy environments and illustrate its effectiveness and advantage compared to existing PF distance measures. Secondly, we give the motivation for building a new MADM method. PFNs can offer a more complete opportunity for decision-makers to be more independent, as it is possible to state the independent degrees for positive, negative and hesitant preferences. It is also possible to calculate the degree of refusal as the fourth element in the PFS. However, there is little in the MADM literature that considers the refusal degree in decision-making. Besides, it has been found that the CRADIS [49] approach is effective and brief in MADM problems, while it has never been applied in a picture fuzzy environment. Besides, the CRADIS method can apply different methods to compute the distance between the ideal point and the anti-ideal point, and other attribute weighting methods may be considered. Based on the above, we try to extend the CRADIS method to the fuzzy picture environment. We use the maximum deviation method in combination with the proposed distance measure to calculate the attribute weight and apply our proposed distance measure to calculate the deviation degree.

The main contributions of this study are listed below:

• 1. We define a new definition of distance measure under picture fuzzy environment.

• 2. We propose a novel distance measure on the basis of Jensen–Shannon divergence in the picture fuzzy environment.

• 3. We apply the maximizing deviation method on the basis of our proposed distance measure under picture fuzzy environment to obtain attribute weights.

• 4. We create a new picture fuzzy CRADIS decision-making system by combining the newly presented PF distance measure with the CRADIS approach.

The primary structure of this academic paper is illustrated below: Sect. 2 reviews the relevant theories. Section 3 lists some existing distances under picture fuzzy environment and defines a novel PF distance measure. Section 4 introduces a numerical example and two pattern recognition applications. Section 5 applies maximum deviation method combined with new PF distance to obtain attribute weight, and CRADIS method is generalised to picture fuzzy environment to solve MADM problem by a case study. Section 6 summarizes the study and discusses the related prospects to be explored.

2 Preliminaries

Some fundamental notions of picture fuzzy sets are reviewed in the following chapter.

Definition 1

[20] Assume X is an universal set. A picture fuzzy set $\Psi$ in X is expressed as: $\Psi =\{({{\tau }_{\kappa }},{{\xi }_{\Psi }}({{\tau }_{\kappa }}),{{\delta }_{\Psi }}({{\tau }_{\kappa }}),$${{\upsilon }_{\Psi }}({{\tau }_{\kappa }}))|{{\tau }_{\kappa }}\in X,\kappa =1,2,\ldots ,n\},$ where ${{\xi }_{\Psi }}:X\rightarrow [0,1],$ ${{\delta }_{\Psi }}:X\rightarrow [0,1]$ and ${{\upsilon }_{\Psi }}:X\rightarrow [0,1]$ characterize membership, neutral and non-membership functions. Here, ${{\xi }_{\Psi }}({{\tau }_{\kappa }})\in [0,1],$ ${{\delta }_{\Psi }}({{\tau }_{\kappa }})\in [0,1]$ and ${{\upsilon }_{\Psi }}({{\tau }_{\kappa }})\in [0,1]$ indicate the degree of membership, neutrality and non-membership with the condition $0\le {{\xi }_{\Psi }}({{\tau }_{\kappa }})+{{\delta }_{\Psi }}({{\tau }_{\kappa }})+{{\upsilon }_{\Psi }}({{\tau }_{\kappa }})\le 1$ for all ${{\tau }_{\kappa }}\in X$ in $\Psi .$ ${{\pi }_{\Psi }}({{\tau }_{\kappa }})$ $=1-\left( {{\xi }_{\Psi }}({{\tau }_{\kappa }})+{{\delta }_{\Psi }}({{\tau }_{\kappa }})+{{\upsilon }_{\Psi }}({{\tau }_{\kappa }}) \right) ,$ $\kappa =1,2,\ldots ,n$ represents the refusal degree in PFS $\Psi .$

Definition 2

[21] The operations of complement, inclusion, union and intersection are specified for any two PFSs ${{\Psi }_{1}}$ and ${{\Psi }_{2}}$ in X as follows:

• (1) ${{\left( \Psi \right) }^{C}}=\{({{\tau }_{\kappa }},{{\upsilon }_{\Psi }}({{\tau }_{\kappa }}),{{\delta }_{\Psi }}({{\tau }_{\kappa }}),{{\xi }_{\Psi }}({{\tau }_{\kappa }}))|{{\tau }_{\kappa }}\in X,\kappa =1,2,\ldots ,n\}$

• (2) ${{\Psi }_{1}}={{\Psi }_{2}},$ if and only if ${{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})={{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}),$ ${{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})={{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}),$ ${{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})={{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}),$ $\forall {{\tau }_{\kappa }}\in X.$

• (3) ${{\Psi }_{1}}\subseteq {{\Psi }_{2}},$ if and only if ${{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})\le {{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}),$ ${{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})\le {{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}),$ ${{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})\ge {{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}),$ $\forall {{\tau }_{\kappa }}\in X.$

• (4) ${{\Psi }_{1}}\cup {{\Psi }_{2}}=\left\{ \left\langle {{\tau }_{\kappa }},\max \left( {{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}) \right) ,\min \left( {{\delta }_{{{\Psi }_{1}}}}\right. \right. \right.$$\left. \left. \left. ({{\tau }_{\kappa }}),{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}) \right) , \right. \right. \left. \left. \min \left( {{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}) \right) \right\rangle \right.$$\left. |{{\tau }_{\kappa }}\in X \right\}$

• (5) ${{\Psi }_{1}}\cap {{\Psi }_{2}}=\left\{ \left\langle {{\tau }_{\kappa }},\min \left( {{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}) \right) ,\min \left( {{\delta }_{{{\Psi }_{1}}}}\right. \right. \right.$$\left. \left. \left. ({{\tau }_{\kappa }}),{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}) \right) , \right. \right.$ $\left. \left. \max \left( {{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}) \right) \right\rangle |{{\tau }_{\kappa }}\in X \right\} .$

Definition 3

[50] Let ${{\Psi }_{1}}=\left( {{\xi }_{{{\Psi }_{1}}}},{{\delta }_{{{\Psi }_{1}}}},{{\upsilon }_{{{\Psi }_{1}}}} \right)$ and ${{\Psi }_{2}}=\left( {{\xi }_{{{\Psi }_{2}}}},{{\delta }_{{{\Psi }_{2}}}},{{\upsilon }_{{{\Psi }_{2}}}} \right)$ be the two PFNs, then,

• (1) ${{\Psi }_{1}}\oplus {{\Psi }_{2}}=\left\langle 1-(1-{{\xi }_{{{\Psi }_{1}}}})(1-{{\xi }_{{{\Psi }_{2}}}}),{{\delta }_{{{\Psi }_{1}}}}{{\delta }_{{{\Psi }_{2}}}},\right.$$\left. ({{\upsilon }_{{{\Psi }_{1}}}}+{{\delta }_{{{\Psi }_{1}}}})({{\upsilon }_{{{\Psi }_{2}}}}+{{\delta }_{{{\Psi }_{2}}}})-{{\delta }_{{{\Psi }_{1}}}}{{\delta }_{{{\Psi }_{2}}}} \right\rangle .$

• (2) ${{\Psi }_{1}}\otimes {{\Psi }_{2}}=\left\langle \left( {{\xi }_{{{\Psi }_{1}}}}+{{\delta }_{{{\Psi }_{1}}}} \right) \left( {{\xi }_{{{\Psi }_{2}}}}+{{\delta }_{{{\Psi }_{2}}}} \right) -{{\delta }_{{{\Psi }_{1}}}}{{\delta }_{{{\Psi }_{2}}}},{{\delta }_{{{\Psi }_{1}}}}{{\delta }_{{{\Psi }_{2}}}},\right.$$\left. 1-(1-{{\upsilon }_{{{\Psi }_{1}}}})(1-{{\upsilon }_{{{\Psi }_{2}}}}) \right\rangle .$

• (3) $\lambda {{\Psi }_{1}}=\left\langle 1-{{(1-{{\xi }_{{{\Psi }_{1}}}})}^{\lambda }},\delta _{{{\Psi }_{1}}}^{\lambda },{{({{\upsilon }_{{{\Psi }_{1}}}}+{{\delta }_{{{\Psi }_{1}}}})}^{\lambda }}-\delta _{{{\Psi }_{1}}}^{\lambda } \right\rangle ,\lambda >0.$

• (4) ${{\Psi }_{1}}^{\lambda }=\left\langle {{({{\xi }_{{{\Psi }_{1}}}}+{{\delta }_{{{\Psi }_{1}}}})}^{\lambda }}-\delta _{{{\Psi }_{1}}}^{\lambda },\delta _{{{\Psi }_{1}}}^{\lambda },1-{{(1-{{\upsilon }_{{{\Psi }_{1}}}})}^{\lambda }} \right\rangle ,\lambda >0.$

In the previous references, there have been several definitions of distance measure in the picture fuzzy environment, but they have neglected to satisfy the triangle inequality. Therefore, we will define a new definition of distance measure, which is based on the definition of distance in Refs. [51, 52]. The new definition of the picture fuzzy distance measure is shown below:

Definition 4

Assume ${{\Psi }_{1}},$ ${{\Psi }_{2}},$ ${{\Psi }_{3}}$ are three PFSs on nonempty X. Then $(\text {PFS}(X), d)$ is a metric space, i.e. the following properties should true:

• (1) $d({{\Psi }_{1}},{{\Psi }_{2}})=0\Leftrightarrow {{\Psi }_{1}}={{\Psi }_{2}}.$

• (2) $d({{\Psi }_{1}},{{\Psi }_{2}})=d({{\Psi }_{2}},{{\Psi }_{1}}).$

• (3) $d({{\Psi }_{1}},{{\Psi }_{3}})\le d({{\Psi }_{1}},{{\Psi }_{2}})+d({{\Psi }_{2}},{{\Psi }_{3}}).$

• (4) $0\le d({{\Psi }_{1}},{{\Psi }_{2}})\le 1.$

Lemma 1

[51] Let the function $J(s,t): {{R}^{+}}\times {{R}^{+}}\rightarrow {{R}^{+}}$ be defined by

$$\begin{aligned} J\left( s,t \right) =s\log \frac{2s}{s+t}+t\log \frac{2t}{s+t} \end{aligned}$$

(1)

then, 

$$\begin{aligned} \sqrt{J(s,t)}\le \sqrt{J(s,u)}+\sqrt{J(u,t)}. \end{aligned}$$

(2)

3 The New Distance Under PFSs

3.1 The Existing PF Distance Measures

Distance measure is an effective tool for ranking different schemes in decision-making. In [20], Cuong et al. first defines the normalized distance for PFSs as follows:

$$\begin{aligned} {{d}_{{{C}_{1}}}}\left( {{\Psi }_{1}},{{\Psi }_{2}} \right)= & {} \frac{1}{n}\sum _{\kappa =1}^{n}{[|{{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})}-{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})|\nonumber \\{} & {} +|{{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})|\nonumber \\{} & {} +|{{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})|]. \end{aligned}$$

(3)

Singh defined the PF normalized Hamming distance [33]:

$$\begin{aligned} {{d}_{pnh}}\left( {{\Psi }_{1}},{{\Psi }_{2}} \right)= & {} \frac{1}{4n}\sum _{\kappa =1}^{n}{[|{{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})}-{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})|\nonumber \\{} & {} +|{{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})|+|{{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})\nonumber \\{} & {} -{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})|+|{{\pi }_{{{\Psi }_{1}}}} ({{\tau }_{\kappa }})-{{\pi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})|]. \end{aligned}$$

(4)

Subsequently, Dinh and Thao [53] defined several PF distance measures:

$$\begin{aligned} {{d}_{{{\textrm{DT}}_{2}}}}\left( {{\Psi }_{1}},{{\Psi }_{2}} \right)= & {} \frac{1}{n}\left\{ \sum _{\kappa =1}^{n}{[({{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})}-{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}){{)}^{2}}\right. \nonumber \\{} & {} +{{({{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))}^{2}} \nonumber \\{} & {} +({{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}){{\left. -{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}){{)}^{2}}] \right\} }^{\tfrac{1}{2}}} \end{aligned}$$

(5)

$$\begin{aligned} {{d}_{{\textrm{DT}}3}}\left( {{\Psi }_{1}},{{\Psi }_{2}} \right)= & {} \frac{1}{n}\sum _{\kappa =1}^{n}{max(|{{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})}-{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})|,\nonumber \\{} & {} |{{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})|,\nonumber \\{} & {} |{{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})|) \end{aligned}$$

(6)

$$\begin{aligned} {{d}_{{\textrm{DT}}4}}\left( {{\Psi }_{1}},{{\Psi }_{2}} \right)= & {} \frac{1}{n}\left[ \sum _{\kappa =1}^{n}{max(|{{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})}-{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}){{|}^{2}},\nonumber \right. \\{} & {} |{{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}){{|}^{2}}, \nonumber \\{} & {} {{\left. |{{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}){{|}^{2}}) \right] }^{\tfrac{1}{2}}}. \end{aligned}$$

(7)

Khan et al. [39] defined a bi-parametric PF distance measure:

$$\begin{aligned} {{d}_{\textrm{KKDK}}}({{\Psi }_{1}},{{\Psi }_{2}})= & {} \left[ \tfrac{1}{3n{{(t+1)}^{p}}}\sum _{\kappa =1}^{n}{(}|t({{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))\right. \nonumber \\{} & {} -({{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))\nonumber \\{} & {} -({{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})){{|}^{p}}+|t({{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})\nonumber \\{} & {} -{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))-({{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}) \nonumber \\{} & {} -{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))+({{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})){{|}^{p}}\nonumber \\{} & {} +|t({{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})) \nonumber \\{} & {} -({{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))\nonumber \\{} & {} \left. +({{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})){{|}^{p}})\right] ^{\tfrac{1}{p}} \end{aligned}$$

(8)

where $r=3, 4,\ldots$ and $q=1,2,3,\ldots$ denote the degree of the uncertainty and ${{l}_{p}}$ norm, severally.

Based on direct operations, Ganie and Singh [40] defined a PF distance measure:

$$\begin{aligned} {{d}_{\textrm{GS}}}({{\Psi }_{1}},{{\Psi }_{2}})= & {} 1- \frac{1}{4n}\sum _{\kappa =1}^{n}\left[ 3\sqrt{{{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}){{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})} \right. \nonumber \\{} & {} +3\sqrt{{{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}){{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})}+3\sqrt{{{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}){{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})}\nonumber \\{} & {} +\sqrt{{{\pi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}){{\pi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})} \nonumber \\{} & {} +\sqrt{(1-{{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}))\times (1-{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})-{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))} \nonumber \\{} & {} +\sqrt{(1-{{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}))\times (1-{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})-{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))} \nonumber \\{} & {} \left. +\sqrt{(1-{{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})-{{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}))\times (1-{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})-{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))}\right] . \nonumber \\ \end{aligned}$$

(9)

The axiomatic requirements of Definition 4 should be satisfied by the existing PF distance measures listed above. Unfortunately, there are some PF distance measures that do not satisfy some of the conditions of Definition 4. Some examples of violations are shown below:

Example 1

Consider E,  F,  and G to be three PFSs in the discourse universe $U=\left\{ \tau \right\} ,$ where $E=\left\{ \langle \tau ,0.0,0.0,0.5\rangle \right\} ,$ $F=\left\{ \langle \tau ,0.5,0.0,0.0\rangle \right\} ,$ $G=\left\{ \langle \tau ,0.6,0.2,0.0\rangle \right\} .$ We calculate d(E, F),  d(E, G)and d(F, G) using the distance measure (14) ${{d}_{\textrm{GS}}},$ and the results are as follows:

${{d}_{\textrm{GS}}}(E,F)=0.3964,$ ${{d}_{\textrm{GS}}}(E,G)=0.5392,$ ${{d}_{\textrm{GS}}}(F,G)=0.0957.$ Then, ${{d}_{\textrm{GS}}}\left( E,F \right) +{{d}_{\textrm{GS}}}\left( F,G \right) =0.4921.$ Therefore, ${{d}_{\textrm{GS}}}\left( E,F \right) +{{d}_{\textrm{GS}}}\left( F,G \right) <{{d}_{\textrm{GS}}}\left( E,G \right) .$ Obviously, ${{d}_{\textrm{GS}}}$ does not satisfy triangle inequality of Definition 4, which violates the axiomatic requirement of distance measure.

Example 2

Consider E and F be two PFSs in the discourse universe $U=\left\{ \tau \right\} ,$ where $E=\left\{ \left\langle \tau ,0.5,0.0,0.5 \right\rangle \right\} ,$ $F=\left\{ \left\langle \tau ,0.0,1.0,0.0 \right\rangle \right\} .$ Using the PF distance measure ${{d}_{{{\textrm{DT}}_{2}}}},$ we will calculate the distance between E and F. The distance result is ${{d}_{{{\textrm{DT}}_{2}}}}(E,F)=1.2247>1.$ Obviously, this result does not satisfy condition (P1) of Definition 4, which violates the axiomatic requirement of distance measure.

Therefore, we believe that it is necessary to further explore the distance measures between PFSs. In the next part, a novel PF distance measure will be introduced to overcome the deficiencies of existing PF distance measures.

3.2 The New PF Distance Measure

In this part, we will present a novel PFSs distance measure on the basis of the Jensen–Shannon divergence.

Let $M=\{({{m}_{1}},{{m}_{2}},\ldots ,{{m}_{n}})|\sum _{k=1}^{n}{{{m}_{k}}}=1\}$ and $N=\{({{n}_{1}},{{n}_{2}},\ldots ,{{n}_{n}})|\sum _{k=1}^{n}{{{n}_{k}}}=1\}$ are two probability distributions of the discrete random of variable U, then Jensen–Shannon divergence between M and N is described as [51]:

$$\begin{aligned} \text {JS}(M,N)= & {} \frac{1}{2}\left[ \sum _{k=1}^{n}{{m}_{k}}\ log \left( \frac{2{{m}_{k}}}{{{m}_{k}}+{{n}_{k}}}\right) \nonumber \right. \\{} & {} \left. +\sum _{i=1}^{n}{{n}_{k}}\log \left( \frac{2{{n}_{k}}}{{{m}_{k}}+{{n}_{k}}}\right) \right] . \end{aligned}$$

(10)

We are not the first one to use Jensen–Shannon divergence to construct distance measure in different environment [51, 52]. On the basis of the Jensen–Shannon divergence, this paper establishes a new distance measure for PFSs.

Let ${{\Psi }_{1}}=\{({{\tau }_{\kappa }},{{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}))|{{\tau }_{\kappa }}\in X,\kappa =1,2,\ldots ,n\}$ and ${{\Psi }_{2}}=\{({{\tau }_{\kappa }},{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}),{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}),{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))|{{\tau }_{\kappa }}\in X,\kappa =1,2,\ldots ,n\}$ are two PFSs of a variable $U=\{\tau \},$ where ${{\pi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})=1-({{\xi }_{_{{{\Psi }_{1}}}}}({{\tau }_{\kappa }})+{{\delta }_{_{{{\Psi }_{1}}}}}({{\tau }_{\kappa }})+{{\upsilon }_{_{{{\Psi }_{1}}}}}({{\tau }_{\kappa }}))$ and ${{\pi }_{_{{{\Psi }_{2}}}}}({{\tau }_{\kappa }})=1-({{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})+{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})+{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))$ are respectively the hesitancy degrees of ${{\Psi }_{1}}$ and ${{\Psi }_{2}}$ for PFSs. Then, the Jensen–Shannon divergence between PFSs ${{\Psi }_{1}}$ and ${{\Psi }_{2}}$ is defined as follows:

$$\begin{aligned} \text {JS}\left( {{\Psi }_{1}},{{\Psi }_{2}} \right)= & {} \frac{1}{2n}\sum _{\kappa =1}^{n}\left[ {{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})\log \frac{2{{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})}{{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})\right. \nonumber \\{} & {} +{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})+{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})\log \frac{2{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})}{{{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})+{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})}\nonumber \\{} & {} +{{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})\log \frac{2{{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})}{{{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})+{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})}\nonumber \\{} & {} +{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})\log \frac{2{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})}{{{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})+{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})} \nonumber \\{} & {} +{{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})\log \frac{2{{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})}{{{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})+{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})}\nonumber \\{} & {} +{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})\log \frac{2{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})}{{{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})+{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})} \nonumber \\{} & {} +{{\pi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})\log \frac{2{{\pi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})}{{{\pi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})+{{\pi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})}\nonumber \\{} & {} \left. \left. +{{\pi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})\log \frac{2{{\pi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})}{{{\pi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})+{{\pi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})}\right) \right] . \end{aligned}$$

(11)

A new distance measure between two PFSs ${{\Psi }_{1}}$ and ${{\Psi }_{2}}$ can be defined as follows:

$$\begin{aligned} d=\sqrt{{\text {JS}_{\textrm{PFS}}}\left( {{\Psi }_{1}},{{\Psi }_{2}} \right) }. \end{aligned}$$

(12)

Lemma 2

Suppose X is a discourse universe,  then the distance measure $d=\sqrt{{\text {JS}_{\textrm{PFS}}}\left( {{\Psi }_{1}},{{\Psi }_{2}} \right) }$ between two PFSs ${{\Psi }_{1}}$ and ${{\Psi }_{2}}$ is a metric.

Proof

• (1) $d({{\Psi }_{1}},{{\Psi }_{2}})=0\Leftrightarrow {{\Psi }_{1}}={{\Psi }_{2}}.$

  If two PFSs ${{\Psi }_{1}}={{\Psi }_{2}}$ in X,  we can get $d({{\Psi }_{1}},{{\Psi }_{2}})=0.$

  Then, when $d({{\Psi }_{1}},{{\Psi }_{2}})=0,$ we can derive that:

  $$\begin{aligned} {{\xi }_{{{\Psi }_{1}}}}(\tau )= & {} {{\xi }_{{{\Psi }_{2}}}}(\tau ),{{\delta }_{{{\Psi }_{1}}}}(\tau )={{\delta }_{{{\Psi }_{2}}}}(\tau ),{{\upsilon }_{{{\Psi }_{1}}}}(\tau )\\= & {} {{\upsilon }_{{{\Psi }_{2}}}}(\tau ),{{\pi }_{{{\Psi }_{1}}}}(\tau )={{\pi }_{{{\Psi }_{2}}}}(\tau ). \end{aligned}$$

  Thus, we can conclude that:

  $$\begin{aligned} {{\Psi }_{1}}={{\Psi }_{2}} \end{aligned}$$

• (2) $d({{\Psi }_{1}},{{\Psi }_{2}})=d({{\Psi }_{2}},{{\Psi }_{1}}).$

  Obviously, we can get:$d({{\Psi }_{1}},{{\Psi }_{2}})=d({{\Psi }_{2}},{{\Psi }_{1}}).$

• (3) $d({{\Psi }_{1}},{{\Psi }_{3}})\le d({{\Psi }_{1}},{{\Psi }_{2}})+d({{\Psi }_{2}},{{\Psi }_{3}}).$

We set up:

$$\begin{aligned} {{d}_{\text {JS}}}({{\Psi }_{1}},{{\Psi }_{2}}) =\sqrt{J({{\xi }_{{{\Psi }_{1}}}}(\tau ),{{\xi }_{{{\Psi }_{2}}}}(\tau ))+J({{\delta }_{{{\Psi }_{1}}}}(\tau ),{{\delta }_{{{\Psi }_{2}}}}(\tau ))+J({{\upsilon }_{{{\Psi }_{1}}}}(\tau ),{{\upsilon }_{{{\Psi }_{2}}}}(\tau ))+J({{\upsilon }_{{{\Psi }_{1}}}}(\tau ),{{\upsilon }_{{{\Psi }_{2}}}}(\tau ))} \end{aligned}$$

According to Lemma 1, we can get

$$\begin{aligned} \sqrt{J({{\xi }_{{{\Psi }_{1}}}}(\tau ),{{\xi }_{{{\Psi }_{2}}}}(\tau ))}\le & {} \sqrt{J({{\xi }_{{{\Psi }_{1}}}}(\tau ),{{\xi }_{{{\Psi }_{3}}}}(\tau ))}\\{} & {} +\sqrt{J({{\xi }_{{{\Psi }_{3}}}}(\tau ),{{\xi }_{{{\Psi }_{2}}}}(\tau ))}\\ \sqrt{J({{\delta }_{{{\Psi }_{1}}}}(\tau ),{{\delta }_{{{\Psi }_{2}}}}(\tau ))}\le & {} \sqrt{J({{\delta }_{{{\Psi }_{1}}}}(\tau ),{{\delta }_{{{\Psi }_{3}}}}(\tau ))}\\{} & {} +\sqrt{J({{\delta }_{{{\Psi }_{3}}}}(\tau ),{{\delta }_{{{\Psi }_{2}}}}(\tau ))}\\ \sqrt{J({{\upsilon }_{{{\Psi }_{1}}}}(\tau ),{{\upsilon }_{{{\Psi }_{2}}}}(\tau ))}\le & {} \sqrt{J({{\upsilon }_{{{\Psi }_{1}}}}(\tau ),{{\upsilon }_{{{\Psi }_{3}}}}(\tau ))}\\{} & {} +\sqrt{J({{\upsilon }_{{{\Psi }_{3}}}}(\tau ),{{\upsilon }_{{{\Psi }_{2}}}}(\tau ))}\\ \sqrt{J({{\pi }_{{{\Psi }_{1}}}}(\tau ),{{\pi }_{{{\Psi }_{2}}}}(\tau ))}\le & {} \sqrt{J({{\pi }_{{{\Psi }_{1}}}}(\tau ),{{\pi }_{{{\Psi }_{3}}}}(\tau ))}\\{} & {} +\sqrt{J({{\pi }_{{{\Psi }_{3}}}}(\tau ),{{\pi }_{{{\Psi }_{2}}}}(\tau ))}. \end{aligned}$$

Thus, we have

$$\begin{aligned} d({{\Psi }_{1}},{{\Psi }_{2}})\le & {} \left\{ \frac{1}{2n} \right. \sum _{\kappa =1}^{n}\left[ \left( \sqrt{J({{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\xi }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}))}\right. \right. \\{} & {} \left. +\sqrt{J({{\xi }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}),{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))}\right) ^{2} \\{} & {} +\left( \sqrt{J({{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\delta }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}))}\right. \\{} & {} \left. +\sqrt{J({{\delta }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}),{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))}\right) ^{2} \\{} & {} +\left( \sqrt{J({{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\upsilon }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}))}\right. \\{} & {} \left. +\sqrt{J({{\upsilon }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}),{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))}\right) ^{2} \\{} & {} +\left( \sqrt{J({{\pi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\pi }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}))}\right. \\{} & {} \left. \left. \left. +\sqrt{J({{\pi }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}),{{\pi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))}\right) ^{2}\right] \right\} ^{\frac{1}{2}}. \end{aligned}$$

According to Minkowski inequality:

$$\begin{aligned} {{\left( \sum _{k=1}^{n}{{{\left( {{x}_{k}}+{{y}_{k}} \right) }^{2}}} \right) }^{\frac{1}{2}}}\le {{\left( \sum _{k=1}^{n}{{{x}_{k}}^{2}} \right) }^{\frac{1}{2}}}+{{\left( \sum _{k=1}^{n}{{{y}_{k}}^{2}} \right) }^{\frac{1}{2}}}, \end{aligned}$$

we can derive the following formula:

$$\begin{aligned}{} & {} d({{\Psi }_{1}},{{\Psi }_{2}})\\{} & {} \quad \le \left\{ \frac{1}{2n} \right. \sum _{\kappa =1}^{n}\left\{ \left[ J({{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\xi }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}))\right. \right. \\{} & {} \qquad +J({{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\delta }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}) \\{} & {} \qquad \left. +J({{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\upsilon }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}))+J({{\pi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\pi }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }})) \right] ^{\frac{1}{2}} \\{} & {} \qquad +\left[ J({{\xi }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}),{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))+J({{\delta }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}),{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})) \right. \\{} & {} \qquad \left. \left. \left. +J({{\upsilon }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}),{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))+J({{\pi }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}),{{\pi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})) \right] ^{\tfrac{1}{2}} \right\} ^{2} \right\} ^{\tfrac{1}{2}} \\{} & {} \quad \le \left[ \frac{1}{2n} \right. \sum _{\kappa =1}^{n}\left( J({{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\xi }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}))\right. \\{} & {} \qquad +J({{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\delta }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}))+J({{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}), \\{} & {} \qquad \left. \left. {{\upsilon }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}))+J({{\pi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }}),{{\pi }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }})) \right) \right] ^{\frac{1}{2}} \\{} & {} \qquad +\left[ \frac{1}{2n} \right. \sum _{\kappa =1}^{n}{\left( J({{\xi }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}),{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})){{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})) \right. } \\{} & {} \qquad +J({{\delta }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}),\left. \left. +J({{\upsilon }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}),{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))\right. \right. \\{} & {} \qquad \left. \left. +J({{\pi }_{{{\Psi }_{3}}}}({{\tau }_{\kappa }}),{{\pi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }})) \right) \right] ^{\frac{1}{2}} \\{} & {} \quad =d({{\Psi }_{1}},{{\Psi }_{3}})+d({{\Psi }_{3}},{{\Psi }_{2}}). \end{aligned}$$

Thus, it is proven that the property of triangle inequality for d is satisfied, which is

$$\begin{aligned} d({{\Psi }_{1}},{{\Psi }_{3}})+d({{\Psi }_{3}},{{\Psi }_{2}})\ge d({{\Psi }_{1}},{{\Psi }_{2}}). \end{aligned}$$

• (4) $0\le d({{\Psi }_{1}},{{\Psi }_{2}})\le 1.$

$$\begin{aligned}{} & {} {{\xi }_{{{\Psi }_{1}}}}(\tau )\log \frac{2{{\xi }_{{{\Psi }_{1}}}}(\tau )}{{{\xi }_{{{\Psi }_{1}}}}(\tau )+{{\xi }_{{{\Psi }_{2}}}}(\tau )}+{{\xi }_{{{\Psi }_{2}}}}(\tau )\log \frac{2{{\xi }_{{{\Psi }_{2}}}}(\tau )}{{{\xi }_{{{\Psi }_{1}}}}(\tau )+{{\xi }_{{{\Psi }_{2}}}}(\tau )}\\{} & {} \quad \ge {{\xi }_{{{\Psi }_{1}}}}(\tau )\left( 1-\frac{{{\xi }_{{{\Psi }_{1}}}}(\tau )+{{\xi }_{{{\Psi }_{2}}}}(\tau )}{2{{\xi }_{{{\Psi }_{1}}}}(\tau )}\right) \\{} & {} \qquad +{{\xi }_{{{\Psi }_{2}}}}(\tau )\left( 1-\frac{{{\xi }_{{{\Psi }_{1}}}}(\tau )+{{\xi }_{{{\Psi }_{2}}}}(\tau )}{2{{\xi }_{{{\Psi }_{2}}}}(\tau )}\right) =0. \end{aligned}$$

Analogously, we can get:

$$\begin{aligned}{} & {} {{\delta }_{{{\Psi }_{1}}}}(\tau )\log \frac{2{{\delta }_{{{\Psi }_{1}}}}(\tau )}{{{\delta }_{{{\Psi }_{1}}}}(\tau )+{{\delta }_{{{\Psi }_{2}}}}(\tau )}\\{} & {} \qquad +{{\delta }_{{{\Psi }_{2}}}}(\tau )\log \frac{2{{\delta }_{{{\Psi }_{2}}}}(\tau )}{{{\delta }_{{{\Psi }_{1}}}}(\tau ) +{{\delta }_{{{\Psi }_{2}}}}(\tau )}\ge 0\\{} & {} {{\upsilon }_{{{\Psi }_{1}}}}(\tau )\log \frac{2{{\upsilon }_{{{\Psi }_{1}}}}(\tau )}{{{\upsilon }_{{{\Psi }_{1}}}}(\tau )+{{\upsilon }_{{{\Psi }_{2}}}}(\tau )}\\{} & {} \qquad +{{\upsilon }_{{{\Psi }_{2}}}}(\tau )\log \frac{2{{\upsilon }_{{{\Psi }_{2}}}}(\tau )}{{{\upsilon }_{{{\Psi }_{1}}}}(\tau )+{{\upsilon }_{{{\Psi }_{2}}}}(\tau )}\ge 0\\{} & {} {{\pi }_{{{\Psi }_{1}}}}(\tau )\log \frac{2{{\pi }_{{{\Psi }_{1}}}}(\tau )}{{{\pi }_{{{\Psi }_{1}}}}(\tau )+{{\pi }_{{{\Psi }_{2}}}}(\tau )}\\{} & {} \qquad +{{\pi }_{{{\Psi }_{2}}}}(\tau )\log \frac{2{{\pi }_{{{\Psi }_{2}}}}(\tau )}{{{\pi }_{{{\Psi }_{1}}}}(\tau )+{{\pi }_{{{\Psi }_{2}}}}(\tau )}\ge 0. \end{aligned}$$

Therefore, we can derive that

$$\begin{aligned}{} & {} d({{\Psi }_{1}},{{\Psi }_{2}})\ge 0. \\{} & {} {{\xi }_{{{\Psi }_{1}}}}(\tau )\log \frac{2{{\xi }_{{{\Psi }_{1}}}}(\tau )}{{{\xi }_{{{\Psi }_{1}}}}(\tau )+{{\xi }_{{{\Psi }_{2}}}}(\tau )}\\{} & {} \qquad +{{\xi }_{{{\Psi }_{2}}}}(\tau )\log \frac{2{{\xi }_{{{\Psi }_{2}}}}(\tau )}{{{\xi }_{{{\Psi }_{1}}}}(\tau )+{{\xi }_{{{\Psi }_{2}}}}(\tau )}\\{} & {} \quad =({{\xi }_{{{\Psi }_{1}}}}(\tau )+{{\xi }_{{{\Psi }_{2}}}}(\tau ))\log 2\\{} & {} \qquad +{{\xi }_{{{\Psi }_{1}}}}(\tau )\log \frac{{{\xi }_{{{\Psi }_{1}}}}(\tau )}{{{\xi }_{{{\Psi }_{1}}}}(\tau )+{{\xi }_{{{\Psi }_{2}}}}(\tau )}\\{} & {} \qquad +{{\xi }_{{{\Psi }_{2}}}}(\tau )\log \frac{{{\xi }_{{{\Psi }_{2}}}}(\tau )}{{{\xi }_{{{\Psi }_{1}}}}(\tau ) +{{\xi }_{{{\Psi }_{2}}}}(\tau )}\\{} & {} \quad \le ({{\xi }_{{{\Psi }_{1}}}}(\tau )+{{\xi }_{{{\Psi }_{2}}}}(\tau ))\log 2 \end{aligned}$$

Obviously, we can obtain:

$$\begin{aligned} d({{\Psi }_{1}},{{\Psi }_{2}})\le & {} \left\{ \frac{1}{2n} \right. \sum _{\kappa =1}^{n}\left[ ({{\xi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})+{{\xi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))\log 2\right. \\{} & {} +({{\delta }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})+{{\delta }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))\log 2\\{} & {} +({{\upsilon }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})+{{\upsilon }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))\log 2\\{} & {} \left. \left. +({{\pi }_{{{\Psi }_{1}}}}({{\tau }_{\kappa }})+{{\pi }_{{{\Psi }_{2}}}}({{\tau }_{\kappa }}))\log 2 \right] \right\} ^{\tfrac{1}{2}} \\= & {} {{\left( \frac{1}{2n}\cdot 2n\cdot \log 2 \right) }^{\tfrac{1}{2}}}\\= & {} {{\left( \log 2 \right) }^{\tfrac{1}{2}}}\\= & {} 1. \end{aligned}$$

Therefore, we prove that

$$\begin{aligned} 0\le d({{\Psi }_{1}},{{\Psi }_{2}})\le 1. \end{aligned}$$

$\square$

4 Experiments and Analysis

In this section, numerical example and pattern recognition are used to demonstrate the reasonability and superiority of our proposed distance measure over the existing PF distance measures.

4.1 Numerical Comparison

Example 3

We give a numerical cases based on [54] to compute the distance between samples using the existing distance measures and the distance measures proposed in this paper. Considering the following three PFSs in the universe of discourse $X=\left\{ \tau \right\} ,$ where $E=\left( 0.1,0.4,0.0 \right) ,$ $F=\left( 0.1,0.0,0.3 \right) ,$ $G=\left( 0.1,0.0,0.0 \right) .$ Obviously, PFS E is closer G than to F. So we can conclude that the distance between E and G is smaller than that between E and F,  which is $d\left( E,G \right) <d\left( E,F \right) .$ We use some existing distance measures to compute the distance between E and G and that between E and F. However, we get ${{d}_{{{\textrm{DT}}_{3}}}}\left( E,G \right) ={{d}_{{{\textrm{DT}}_{3}}}}\left( E,F \right) =0.4,$ ${{d}_{{{\textrm{DT}}_{4}}}}\left( E,G \right) ={{d}_{{{\textrm{DT}}_{4}}}}\left( E,F \right) =0.16,$ which are unreasonable and counterintuitive. Fortunately, PF distance measure defined by us gives a reasonable result, which is $d\left( E,G \right) =0.2698<d\left( E,F \right) =0.3261.$ The above data analysis shows that the distance measure proposed by us is more effective.

4.2 Pattern Recognition Application

Pattern recognition is one of the basic methods used in fuzzy decision making. Its main content is to know several known patterns and one unknown pattern, then determine which known pattern should be assigned to the unknown pattern. In this process, the distance measures (2)–(14) and our proposed PF distance measure are respectively applied to pattern recognition. The availability and superiority of the distance measure proposed by us are verified by the results of recognition.

Example 4

let us consider three known PF patterns ${{E}_{1}},$ ${{E}_{2}},$ ${{E}_{3}}$ and an unknown PF pattern F in $X=\left\{ {{\tau }_{1}},{{\tau }_{2}},{{\tau }_{3}},{{\tau }_{4}},{{\tau }_{5}} \right\}$ as:

$$\begin{aligned} {{E}_{1}}= & {} \left\{ (0.2,0.5,0.1),(0.1,0.2,0.5),\right. \\{} & {} (0.7,0.1,0.1),(0.4,0.3,0.2),\\{} & {} \left. (0.3,0.3,0.3) \right\} \\ {{E}_{2}}= & {} \left\{ (0.4,0.0,0.3),(0.7,0.2,0.0),\right. \\{} & {} (0.4,0.3,0.1),(0.2,0.3,0.5),\\{} & {} \left. (0.1,0.6,0.1) \right\} \\ {{E}_{3}}= & {} \left\{ (0.3,0.2,0.4),(0.2,0.3,0.5),\right. \\{} & {} (0.1,0.3,0.4),(0.1,0.3,0.4),\\{} & {} \left. (0.3,0.5,0.1) \right\} \\ F= & {} \left\{ (0.4,0.2,0.3),(0.7,0.0,0.1),\right. \\{} & {} (0.6,0.2,0.1),(0.2,0.4,0.3),\\{} & {} \left. (0.2,0.4,0.2) \right\} \end{aligned}$$

Table 1 shows the values calculated between the known pattern ${{E}_{\kappa }},$ $\kappa =1,2,3$ and the unknown pattern F by different PF distance measures. We have bolded counterintuitive date, which helps us analyze the data more intuitively.

Table 1 The results obtained from different PF distance measures in pattern recognition

From Table 1, we can easily see that all existing PF distance measures ${{d}_{{{C}_{1}}}},$ ${{d}_{{{C}_{2}}}},$ ${{d}_{{{\textrm{DT}}_{1}}}},$ ${{d}_{{{\textrm{DT}}_{2}}}},$ ${{d}_{{{\textrm{DT}}_{3}}}},$ ${{d}_{{{\textrm{DT}}_{4}}}},$ ${{d}_{pnh}},$ ${{d}_{pne}},$ ${{d}_{pnhh}},$ ${{d}_{pneh}},$ ${{d}_{\textrm{KKDK}}},$ ${{d}_{\textrm{GS}}},$ and the PF distance measure ${{d}_{\text {JS}}}$ recognize the unknown pattern F as known pattern ${{E}_{2}},$ which indicates that the PF distance measure we propose can maintain its consistency with the existing measures in picture fuzzy environment.

Example 5

Let us consider three known PF patterns ${{E}_{1}},$ ${{E}_{2}},$ ${{E}_{3}}$ and an unknown PF pattern F in $X=\{{{\tau }_{1}},{{\tau }_{2}},{{\tau }_{3}},{{\tau }_{4}}\}$ as:

$$\begin{aligned} {{E}_{1}}= & {} \left\{ (0.6,0.0,0.2),(0.8,0.0,0.2),\right. \\{} & {} \left. (0.5,0.0,0.2),(0.6,0.0,0.4) \right\} \\ {{E}_{2}}= & {} \left\{ (0.5,0.0,0.3),(0.6,0.0,0.3),\right. \\{} & {} \left. \text { (}0.7,0.0,0.0),(0.6,0.0,0.4) \right\} \\ {{E}_{3}}= & {} \left\{ (0.4,0.0,0.2),(0.7,0.0,0.3),\right. \\{} & {} \left. (0.5,0.0,0.2),(0.6,0.0,0.3) \right\} \\ F= & {} \left\{ (0.5,0.0,0.2),(0.7,0.0,0.2),\right. \\{} & {} \left. (0.6,0.0,0.1),(0.6,0.0,0.4) \right\} . \end{aligned}$$

Table 2 shows the values calculated between the known pattern ${{E}_{\kappa }},$ $\kappa =1,2,3$ and the unknown pattern F by different PF distance measures.

Table 2 The results obtained from different PF distance measures in pattern recognition

From Table 2, we can see that PF distance measures ${{d}_{{{\textrm{DT}}_{1}}}},$ ${{d}_{{{\textrm{DT}}_{2}}}},$ ${{d}_{{{\textrm{DT}}_{3}}}},$ ${{d}_{{{\textrm{DT}}_{4}}}},$ ${{d}_{pnh}},$ ${{d}_{pne}},$ ${{d}_{pnhh}},$ ${{d}_{pneh}}$ cannot identify which known patterns ${{E}_{k}},$ $\kappa =1,2,3$ the unknown pattern F belongs to. But the remaining 5 PF distance measures ${{d}_{{{C}_{1}}}},$ ${{d}_{{{C}_{2}}}},$ ${{d}_{\textrm{KKDK}}},$ ${{d}_{\textrm{GS}}},$ ${{d}_{\text {JS}}},$ including the PF distance measure proposed by us, can identify which known pattern ${{E}_{\kappa }},$ $\kappa =1,2,3$ the unknown pattern B belongs to.

Through the comparative analysis of the five examples, we can clearly draw the following advantages of the PF distance measure we proposed:

• 1. The PF distance measure proposed by us is not only neat and simple in form, but also satisfies the axiomatic requirements of distance measure.

• 2. Our proposed distance measure can not only differentiate, but also provide clearer and more rational data for some very similar but different PFSs.

• 3. In pattern recognition, the distance measure we define can produce the same identification result as the existing distance measure. This indicates that our proposed distance measure has consistency and rationality.

• 4. In pattern recognition, for some cases, the existing distance measures cannot identify the research object, but the distance measure proposed by us can identify which category the research object belongs to.

5 The CRADIS Method Distance-Based Under Picture Fuzzy Environment

In this section, the CRADIS [49] method is improved and extended to solve the picture fuzzy MADM problem. In this innovative MADM, PFNs will offer a more complete opportunity for decision-makers to be more independent, as it is possible to state the independent degrees for positive, negative and hesitant preferences. It is also possible to calculate the degree of refusal as the fourth element in the PFS. In particular, there is little in the MADM literature that considers the refusal degree in decision-making. In addition, the weighting process based on the proposed distance measure is aggregated with the method in the case that the attribute weights are not defined in the initial problem. The CRADIS method attempts to take advantage of the strengths of the methods used while minimising the weaknesses of those methods. There is now increasingly less scope for developing new methods, and the development of the CRADIS method is a new way of doing this, providing new ideas for creating new MADMs. MADM can be represented as follows: H is the alternatives, which is expressed as $H=\left\{ {{H}_{1}},{{H}_{2}},\ldots ,{{H}_{m}} \right\} .$ C is the attributes, which is regarded as $C=\left\{ {{C}_{1}},{{C}_{2}},\ldots ,{{C}_{n}} \right\} .$ W is the weight of the attribute, which is denoted as $W=\left\{ {{\omega }_{1}},{{\omega }_{2}},\ldots ,{{\omega }_{n}} \right\} .$

5.1 Numerical Comparison

To determine the deviation of alternatives relative to the ideal solution and the anti-ideal solution, the CRADIS method [49] is implemented. The above approach makes use of ideal solutions, which capture the ideal solution’s best qualities across all attributes. The stages of the MARCOS (Measurement of Alternatives and Ranking according to Compromise Solut), ARAS (Additive Ratio Assessment) and TOPSIS methodologies are combined in this method. It should be highlighted that the CRADIS approach may only be used when the attribute information is provided as clear numbers and the decision-maker directly specifies the attribute weight. The departure from the ideal and the anti-ideal positions are also not measured in terms of distance. The processes that comprise the traditional CRADIS approach are described as follows:

Step 1: Developing a decision matrix. A grouping of “n” criteria and “m” options are defined in decision matrix of multi-criteria models:

$$\begin{aligned} A=\left[ \begin{matrix} {{z}_{11}} &{} {{z}_{12}} &{} \cdots &{} {{z}_{1n}} \\ {{z}_{21}} &{} {{z}_{22}} &{} \ldots &{} {{z}_{2n}} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {{z}_{m1}} &{} {{z}_{m2}} &{} \ldots &{} {{z}_{mn}} \\ \end{matrix} \right] . \end{aligned}$$

(13)

Step 2: The decision matrix is normalized. The following formulas are used as the basis for normalization:

$$\begin{aligned} {{n}_{ij}}= & {} \frac{{{z}_{ij}}}{{{z}_{j\max }}} \end{aligned}$$

(14)

$$\begin{aligned} {{n}_{ij}}= & {} \frac{{{z}_{j\min }}}{{{z}_{ij}}}. \end{aligned}$$

(15)

Step 3: Decision-making matrices are aggravated. The normalized decision matrix’s value is multiplied by the corresponding weights, according to the following expression, to produce the aggravated decision matrix:

$$\begin{aligned} {{v}_{ij}}={{n}_{ij}}{{\omega }_{j}}. \end{aligned}$$

(16)

Step 4: The ideal and anti-ideal solution are identified. The biggest value ${{v}_{ij}}$ in the aggravated decision matrix is utilized to figure out the ideal solution, while the smallest value ${{v}_{ij}}$ in the aggravated decision matrix is utilized to figure out the anti-ideal solution.

$$\begin{aligned} {{t}_{i}}= & {} \max {{v}_{ij}} \end{aligned}$$

(17)

$$\begin{aligned} {{t}_{ai}}= & {} \min {{v}_{ij}}. \end{aligned}$$

(18)

Step 5: Deviations from ideal and anti-ideal solutions are calculated.

$$\begin{aligned} {{d}^{+}}= & {} {{t}_{i}}-{{v}_{ij}} \end{aligned}$$

(19)

$$\begin{aligned} {{d}^{-}}= & {} {{v}_{ij}}-{{t}_{ai}}. \end{aligned}$$

(20)

Step 6: Determining the degrees of deviation of every option from the ideal and undesirable solutions.

$$\begin{aligned} s_{i}^{+}= & {} \sum _{j=1}^{n}{{{d}^{+}}} \end{aligned}$$

(21)

$$\begin{aligned} s_{i}^{-}= & {} \sum _{j=1}^{n}{{{d}^{-}}}. \end{aligned}$$

(22)

Step 7: Computation of each alternative’s utility function in respect to its deviations from the ideal options.

$$\begin{aligned} K_{i}^{+}= & {} \frac{s_{0}^{+}}{s_{i}^{+}} \end{aligned}$$

(23)

$$\begin{aligned} K_{i}^{-}= & {} \frac{s_{i}^{-}}{s_{0}^{-}} \end{aligned}$$

(24)

where $s_{0}^{-}$ is the best option that is the furthest away from anti-ideal solution and $s_{0}^{+}$ is the best option that is the closest to the ideal solution.

Step 8: Ranking possible options. Finding the average departure of the options from the degree of value yields the final ranking.

$$\begin{aligned} {{Q}_{i}}=\frac{K_{i}^{+}+K_{i}^{-}}{2}. \end{aligned}$$

(25)

The option with the highest value is the ideal choice ${{Q}_{i}}.$

5.2 Determine the Evaluation Attribute Weights

For this part, we obtain the evaluation attribute weights with the maximum deviation method [55] based on our proposed PF distance measure under picture fuzzy environment.

Step 1: Compute the distance between alternative ${{H}_{i}}$ and other alternative ${{H}_{\kappa }}$ $\left( \kappa =1,2,\ldots ,m,\kappa \ne i \right)$ under the attribute ${{c}_{j}}$ by the following expression:

$$\begin{aligned} {{D}_{ij}}=\sum _{l=1}^{m}{d({{r}_{ij}},{{r}_{lj}}}),\quad i=1,2,\ldots ,m;\ j=1,2,\ldots ,n \end{aligned}$$

where

$$\begin{aligned} d({{r}_{ij}},{{r}_{lj}})= & {} \left\{ \frac{1}{2m} \right. \sum _{l=1}^{m}\left[ {{\xi }_{ij}}\log \frac{2{{\xi }_{ij}}}{{{\xi }_{ij}}+{{\xi }_{lj}}}\right. \\{} & {} +{{\xi }_{lj}}\log \frac{2{{\xi }_{lj}}}{{{\xi }_{ij}}+{{\xi }_{lj}}}+{{\delta }_{ij}}\log \frac{2{{\delta }_{ij}}}{{{\delta }_{ij}}+{{\delta }_{lj}}}\\{} & {} +{{\delta }_{lj}}\log \frac{2{{\delta }_{lj}}}{{{\delta }_{ij}}+{{\delta }_{lj}}} +{{\upsilon }_{ij}}\log \frac{2{{\upsilon }_{ij}}}{{{\upsilon }_{ij}}}\\ {}{} & {} {+{{\upsilon }_{lj}}}+{{\upsilon }_{lj}}\log \frac{2{{\upsilon }_{lj}}}{{{\upsilon }_{ij}}+{{\upsilon }_{lj}}}+{{\pi }_{ij}}\log \frac{2{{\pi }_{ij}}}{{{\pi }_{ij}}+{{\pi }_{lj}}}\\{} & {} \left. \left. +{{\pi }_{lj}}\log \frac{2{{\pi }_{lj}}}{{{\pi }_{ij}}+{{\pi }_{lj}}} \right] \right\} ^{\tfrac{1}{2}}. \end{aligned}$$

Step 2: Use the following expression to calculate the overall unweighted distance of each alternative for the attribute ${{c}_{j}}$:

$$\begin{aligned} {{D}_{j}}=\sum _{i=1}^{m}{{{D}_{ij}}=\sum _{i=1}^{m}{\sum _{l=1}^{m}{d\left( {{r}_{ij}},{{r}_{lj}} \right) }}}. \end{aligned}$$

Step 3: Compute the combined weighted distance of every attribute.

$$\begin{aligned}{} & {} {{D}_{j}}\left( \omega \right) =\sum _{i=1}^{m}{{{D}_{ij}}\left( \omega \right) =\sum _{i=1}^{m}{\sum _{l=1}^{m}{d\left( {{r}_{ij}},{{r}_{lj}} \right) }}}{{\omega }_{j}},\\{} & {} \quad j=1,2,\ldots ,n, \end{aligned}$$

where ${{\omega }_{j}}$ means the attribute weight of ${{c}_{j}}.$

Step 4: To get the weights with picture fuzzy information, design a nonlinear programming model.

$$\begin{aligned} (M-2):\left\{ \begin{array}{l} \max D(\omega )=\sum _{j=1}^{n}\sum _{i=1}^{m}{{D}_{ij}}\left( \omega \right) \\ \qquad =\sum _{j=1}^{n}{\sum _{i=1}^{m}{\sum _{l=1}^{m}{d({{r}_{ij}},{{r}_{lj}}){{\omega }_{j}}}}} \\ \text {s.t.}\ \sum _{j=1}^{n}{\omega _{j}^{2}=1,{{\omega }_{j}}\ge 0,j=1,2,\ldots ,n.} \\ \end{array} \right. \end{aligned}$$

Step 5: We construct the Lagrange function as follows to resolve this model:

$$\begin{aligned} L\left( \omega ,\lambda \right) =\sum _{j=1}^{n}{\sum _{i=1}^{m}{\sum _{l=1}^{m}{d({{r}_{ij}},{{r}_{lj}}){{\omega }_{j}}}}}+\frac{\lambda }{2}\left( \sum _{j=1}^{n}{\omega _{j}^{2}-1} \right) \end{aligned}$$

(26)

where $\lambda$ is the Lagrange multiplier.

Step 6: Differentiating Eq. (31) with regard to ${{\omega }_{j}}( j=1,2,\ldots ,n )$ and $\lambda ,$ the following formulas are obtained:

$$\begin{aligned} \frac{\partial L}{\partial {{\omega }_{j}}}= & {} \sum _{i=1}^{m}{\sum _{l=1}^{m}{d({{r}_{ij}},{{r}_{lj}})+\lambda {{\omega }_{j}}}}=0 \end{aligned}$$

(27)

$$\begin{aligned} \frac{\partial L}{\partial \lambda }= & {} \frac{1}{2}\left( \sum _{j=1}^{n}{\omega _{j}^{2}-1} \right) =0. \end{aligned}$$

(28)

And then, according to Eq. (32), we get

$$\begin{aligned} {{\omega }_{j}}=\frac{-\sum _{i=1}^{m}{\sum _{l=1}^{m}{d({{r}_{ij}},{{r}_{lj}})}}}{\lambda }. \end{aligned}$$

(29)

Substituting Eq. (34) into Eq. (33), we get

$$\begin{aligned} \lambda =-\sqrt{{{\sum _{j=1}^{n}{\left( \sum _{i=1}^{m}{\sum _{l=1}^{m}{d({{r}_{ij}},{{r}_{lj}})}} \right) }}^{2}}}. \end{aligned}$$

(30)

Combining Eqs. (34) and (35), we get the following statement for the attribute weights:

$$\begin{aligned} {{\omega }_{j}}=\frac{\sum _{i=1}^{m}{\sum _{l=1}^{m} {d({{r}_{ij}},{{r}_{lj}})}}}{\sqrt{{{\sum _{j=1}^{n}{\left( \sum _{i=1}^{m}{\sum _{l=1}^{m}{d({{r}_{ij}},{{r}_{lj}})}} \right) }}^{2}}}}. \end{aligned}$$

When ${{\omega }_{j}}\left( j=1,2,\ldots ,n \right)$ is normalized, we obtain

$$\begin{aligned} {{\omega }_{j}}=\frac{\sum _{i=1}^{m}{\sum _{l=1}^{m}{d({{r}_{ij}}, {{r}_{lj}})}}}{\sum _{j=1}^{n}{\sum _{i=1}^{m}{\sum _{l=1}^{m}{d({{r}_{ij}},{{r}_{lj}})}}}}. \end{aligned}$$

5.3 The Extended CRADIS Method Under Picture Fuzzy Environment

The CRADIS method is simple and flexible in application, combining the advantages of MARCOS, TOPSIS and ARAS methods. In Ref. [49], we understand that the CRADIS method can apply all types of normalization, and that it allows the algorithm to be modified so that other methods can be applied to calculate the deviation. In addition, by studying the literature, we find that the CRADIS method is not widely used. Therefore, we consider extending the CRADIS method to picture fuzzy environment to solve more complex and practical MADM problems and utilizing the PF distance measure proposed by us to determine the deviation. The following are the detailed procedure for the CRADIS method combined with distance measure (17) in the picture fuzzy environment.

Step 1: Generate the initial decision matrices $B={{({{b}_{ij}})}_{m\times n}}.$

Suppose that a classical multi-criteria decision problem involves “m” alternatives and “n” attributes. A group of experts are invited to provide judgements to attain the rank of the “m” alternatives in regard to “n” attributes. Then, construct the picture fuzzy evaluation matrix as follows:

$$\begin{aligned} B={{({{b}_{ij}})}_{m\times n}}=\left( \begin{matrix} {{b}_{11}} &{} {{b}_{12}} &{} \ldots &{} {{b}_{1n}} \\ {{b}_{21}} &{} {{b}_{22}} &{} \ldots &{} {{b}_{2n}} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {{b}_{m1}} &{} {{b}_{m2}} &{} \ldots &{} {{b}_{mn}} \\ \end{matrix} \right) \end{aligned}$$

(31)

where ${{b}_{ij}}=\left( {{\xi }_{ij}},{{\delta }_{ij}},{{\upsilon }_{ij}} \right) .$

Step 2: Construct the normalised decision matrix for PFSs.

The cost type and benefit type are the two groups into which attributes in MADC problems are split. The cost attributes need to be transformed into benefit attributes according to Definition (4). The normalised picture fuzzy decision matrix $D={{d}_{ij}}{{)}_{m\times n}}$ is as below:

$$\begin{aligned} D= & {} \left( d_{ij} \right) _{m\times n}\nonumber \\= & {} \left\{ \begin{array}{l} {{b}_{ij}}=\left( {{\xi }_{ij}},{{\delta }_{ij}},{{\upsilon }_{ij}} \right) ,{{C}_{j}}\text { is a benefit attribute}; \\ {{b}_{ij}}^{C}=\left( {{\upsilon }_{ij}},{{\delta }_{ij}},{{\xi }_{ij}} \right) ,{{C}_{j}}\text { is a cost attribute}. \\ \end{array} \right. \end{aligned}$$

(32)

Step 3: Build the picture fuzzy weighted decision matrix $T={{({{t}_{ij}})}_{m\times n}}$ according to the following expression:

$$\begin{aligned} {{t}_{ij}}= & {} {{d}_{ij}}{{\omega }_{j}}=\left( 1-{{(1-{{\xi }_{{{d}_{ij}}}})}^{{{\omega }_{j}}}},{{\delta }_{{{d}_{ij}}}}^{{{\omega }_{j}}},\nonumber \right. \\{} & {} \left. \quad {{({{\delta }_{{{d}_{ij}}}}+{{\upsilon }_{{{d}_{ij}}}})}^{{{\omega }_{j}}}}-{{\delta }_{{{d}_{ij}}}}^{{{\omega }_{j}}} \right) \end{aligned}$$

(33)

where ${{d}_{ij}}$ is the component of normalized decision matrix D,  and ${{\omega }_{j}}$ is the attribute weight ${{C}_{j}}.$

Step 4: Determine the ideal and anti-ideal solution.

• (1) Ideal alternative ${{A}_{0}}=\left\{ {{t}_{01}},{{t}_{02}},\ldots ,{{t}_{0n}} \right\}$:

  $$\begin{aligned} {{t}_{0j}}= & {} \left( {{\xi }_{{{t}_{0j}}}},{{\delta }_{{{t}_{0j}}}},{{\upsilon }_{{{t}_{0j}}}} \right) \nonumber \\= & {} \left( \underset{i=1,\ldots ,m}{\mathop {\max {{\xi }_{{{t}_{ij}}}}}},\underset{i=1,\ldots ,m}{\mathop {\min {{\delta }_{{{t}_{ij}}}}}},\underset{i=1,\ldots ,m}{\mathop {\min {{\upsilon }_{{{t}_{ij}}}}}}\, \right) j=1,2,\ldots ,n.\nonumber \\ \end{aligned}$$

  (34)

• (2) Anti-ideal alternative ${{A}_{m+1}}=\left\{ {{t}_{m+11}},\ldots ,{{t}_{m+1n}} \right\}$:

  $$\begin{aligned} {{t}_{m+1j}}= & {} \left( {{\xi }_{{{t}_{m+1j}}}},{{\delta }_{{{t}_{m+1j}}}},{{\upsilon }_{{{t}_{m+1j}}}} \right) \nonumber \\= & {} \left( \underset{i=1,\ldots ,m}{\mathop {\min {{\xi }_{{{t}_{ij}}}}}},\underset{i=1,\ldots ,m}{\mathop {\min {{\delta }_{{{t}_{ij}}}}}},\underset{i=1,\ldots ,m}{\mathop {\max {{\upsilon }_{{{t}_{ij}}}}}}\, \right) j=1,2,\ldots ,n.\nonumber \\ \end{aligned}$$

  (35)

Step 5: Deviations are obtained using PF distance (17).

$$\begin{aligned} {{d}^{+}}= & {} D\left( {{t}_{ij}},{{t}_{0j}} \right) \nonumber \\= & {} \left[ \frac{1}{2} \right. \left( {{\xi }_{ij}}\frac{2{{\xi }_{ij}}}{{{\xi }_{ij}}+{{\xi }_{0j}}}+{{\xi }_{0j}}\frac{2{{\xi }_{0j}}}{{{\xi }_{ij}}+{{\xi }_{0j}}} \right. \nonumber \\{} & {} +{{\delta }_{ij}}\frac{2{{\delta }_{ij}}}{{{\delta }_{ij}}+{{\delta }_{0j}}}+{{\delta }_{0j}}\frac{2{{\delta }_{0j}}}{{{\delta }_{ij}}+{{\delta }_{0j}}} \nonumber \\{} & {} +{{\upsilon }_{ij}}\frac{2{{\upsilon }_{ij}}}{{{\upsilon }_{ij}}+{{\upsilon }_{0j}}}+{{\upsilon }_{0j}}\frac{2{{\upsilon }_{0j}}}{{{\upsilon }_{ij}}+{{\upsilon }_{0j}}} \nonumber \\{} & {} {{\left. \left. +{{\pi }_{ij}}\frac{2{{\pi }_{ij}}}{{{\pi }_{ij}}+{{\pi }_{0j}}}+{{\pi }_{0j}}\frac{2{{\pi }_{0j}}}{{{\pi }_{ij}}+{{\pi }_{0j}}} \right) \right] }^{\frac{1}{2}}} \end{aligned}$$

(36)

$$\begin{aligned} i=1,2,\ldots ,m;j=1,2,\ldots ,n. \end{aligned}$$

$$\begin{aligned} {{d}^{-}}= & {} D\left( {{t}_{ij}},{{t}_{m+1j}} \right) \nonumber \\= & {} \left[ \frac{1}{2} \right. \left( {{\xi }_{ij}}\frac{2{{\xi }_{ij}}}{{{\xi }_{ij}}+{{\xi }_{m+1j}}}+{{\xi }_{m+1j}}\frac{2{{\xi }_{m+1j}}}{{{\xi }_{ij}}+{{\xi }_{m+1j}}} \right. \nonumber \\{} & {} +{{\delta }_{ij}}\frac{2{{\delta }_{ij}}}{{{\delta }_{ij}}+{{\delta }_{m+1j}}}+{{\delta }_{m+1j}}\frac{2{{\delta }_{m+1j}}}{{{\delta }_{ij}}+{{\delta }_{m+1j}}}\nonumber \\{} & {} +{{\upsilon }_{ij}}\frac{2{{\upsilon }_{ij}}}{{{\upsilon }_{ij}}+{{\upsilon }_{m+1j}}}+{{\upsilon }_{m+1j}}\frac{2{{\upsilon }_{m+1j}}}{{{\upsilon }_{ij}}+{{\upsilon }_{m+1j}}}\nonumber \\{} & {} \quad {{\left. \left. +{{\pi }_{ij}}\frac{2{{\pi }_{ij}}}{{{\pi }_{ij}}+{{\pi }_{m+1j}}}+{{\pi }_{m+1j}}\frac{2{{\pi }_{m+1j}}}{{{\pi }_{ij}}+{{\pi }_{m+1j}}} \right) \right] }^{\frac{1}{2}}}\nonumber \\ \end{aligned}$$

(37)

$$\begin{aligned} i=1,2,\ldots ,m;j=1,2,\ldots ,n. \end{aligned}$$

The following steps are the same as steps (23)–(27) in the classical CRADIS method.

The option with the highest value is the ideal choice ${{Q}_{i}}.$

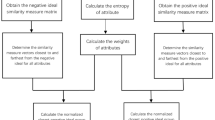
In order to present the steps of improved PFS-CRADIS method in a brief and clear manner, we make a flow chart which is presented in Fig. 1.

Fig. 1

Flow chart of the CRADIS method under picture fuzzy environment based on the proposed PFS distance measure

Example 6

In order to demonstrate the usefulness of the extended CRADIS method under picture fuzzy environment, we adapt the data in [56] to gain the preferred order of the options. It is supposed that there are six candidates ${{H}_{i}}\left( i=1,2,\ldots ,5 \right)$ to choose. The decision-maker considers these six alternatives according to four attributes, resource consumption $\left( {{C}_{1}} \right) ,$ carbon emission $\left( {{C}_{2}} \right) ,$ green production $\left( {{C}_{3}} \right) ,$ and the green technology $\left( {{C}_{4}} \right) .$ According to literature [56], we know ${{C}_{1}}$ and ${{C}_{2}}$ are cost, and ${{C}_{3}}$ and ${{C}_{4}}$ are benefit attributes. The weight of all attributes is unknown. Table 3 shows the decision matrix $B={{\left( {{b}_{ij}} \right) }_{6\times 4}}.$

5.4 The Process of Decision Making

Step 1: Depending on experts’ understanding of these attributes, the initial decision matrix is constructed, displayed in Table 3.

Table 3 The initial decision matrix in Example 6

Step 2: The decision matrix is normalised using Eq. (37) and is shown in Table 4.

Table 4 The normalized decision matrix in Example 6

Step 3: The maximum deviation method applied in 5.2 is used to calculate the attribute weight, which is ${{\omega }_{1}}=0.2706,$ ${{\omega }_{2}}=0.3442,$ ${{\omega }_{3}}=0.1846,$ ${{\omega }_{4}}=0.2006.$

Step 4: The picture fuzzy weighted decision matrix $T={{({{t}_{ij}})}_{6\times 4}}$ is determined using (33), which is presented in Table 5.

Table 5 The weighted picture fuzzy decision matrix

Step 5: The ideal solution and the anti-ideal solution are to be determined by means of equation, which are presented in Table 6.

Table 6 The ideal and anti-ideal solution

Step 6: The distance is calculated, which are based on Eqs. (36) and (37). Table 7 shows the results.

Table 7 The deviations from the ideal and the anti-ideal solutions

Step 7: Compute the distance sum of the attributes corresponding to each alternative using Eqs. (23) and (24). Table 8 shows the results.

Step 8: Calculate the deviation of each alternative from the best option according to formula (28) and (29), and the results are presented in Table 8.

Step 9: The alternatives are sorted depending on the results calculated in formula (30). The results are sorted from largest to smallest:

$$\begin{aligned} {{H}_{1}}>{{H}_{2}}>{{H}_{4}}>{{H}_{6}}>{{H}_{5}}>{{H}_{3}}. \end{aligned}$$

According to the above decision result, alternative ${{H}_{1}}$ is the optimal alternative, which is the same as the selection result in [56], indicating that the method we extended is effective.

Table 8 Results of PF CRADIS method

Table 9 The weight of the attributes which are based on several distance measures

Table 10 The alternative rankings based on several distance measures

5.5 Comparative Analysis

To illustrate the consistency and validity of our extended picture fuzzy CRADIS method, we make a comparative analysis from two perspectives. For the first comparison, the order of the alternatives is based on different distance measures. For the second comparison, several multi-attribute decision methods are used to determine the ranking order of alternatives.

With respect to the distance-based comparison, the weight sets will be calculated combined with the maximum deviation method. Table 9 shows the attribute weights based on different distance measures. Table 10 gives the rankings of the alternatives. In the determination of attribute weights, we make use of several existing distance measures: Eqs. (4), (5), (6), (8) and (9). Finally, we use the improved PFS-CRADIS method to separately determine the order of the alternatives in Example 6, the results of which are shown in Table 10.

By analyzing the results in the Table 9 , it is clear that there are few differences in each attribute weight sets. In all four groups, the weights corresponding to C1, C2, C3 and C4 maintain their order, and C1 has the largest weight value. Table 10 presents a comparison of the alternative rankings obtained with the distance-based weights identified in Table 9. Looking at Table 10, while the other four alternatives maintain their rankings in all five applications, the rankings for the alternative pair are slightly different. Another significant finding is that the same ranking as the proposed PF distance measure (Eq. (12)) is obtained by four applications using existing distance measures in the reference literature. In summary, the rankings of the alternatives are consistent during the process, in spite of differences in the distance measures and associated attribute weights.

The second comparison method aims to compare the ranking order determined by different multi-attribute decision methods. In this process, we need to use six existing methods: PFS-ARAS method [56], PFS-MARCOS method [48], PFS-WASPAS method [57], PFS-VIKOR method [56], PFS-EDAS method [58] and PFS-COPRAS method [59]. The MADM problem in example 6 is solved by using the above six decision methods, and the results of the decisions are summarised in Table 11.

It is manifest from the findings of Table 11 that the order of options determined by PFS-ARAS method, PFS-MARCOS method and PFS-WASPAS method are exactly the same as that of improved PFS-CRADIS method. The ranking of alternatives determined by PFS-VIKOR, PFS-EDAS and PFS-COPRAS methods does not exactly match that of the improved PFS-CRADIS method. With regard to the best alternative ${{H}_{1}}$ obtained by the PF-CRADIS method, it is ranked in second place by two methods, PF-EDAS and PF-COPRAS, which are also more advanced. Furthermore, the best alternative and the worst option determined by the PFS-ARAS method, the PFS-MARCOS method, the PFS-VIKOR method and the PFS-WASPAS method are consistent with the improved PFS-CRADIS method, which are ${{H}_{1}}$ and ${{H}_{3}}$ respectively. By comparing the results of the sorting in Table 11, the efficiency of the decision making method we have proposed can be illustrated.

In the above two comparative analyses, we have found that the use of different distance measures for determining attribute weights and deviations in the PFS-CRADIS method does not significantly affect the selection of the optimal alternative. In addition to this, multiple MADM calculations are applied, which in turn rank the alternatives in Example 6. The results of the research experiments conclude that the PFS-CRADIS method can obtain the same optimal alternatives as most MADMs. The above analyses can show that our proposed PFS-CRADIS method is effective and consistent.

Table 11 Ranking order of the different methods with Example 6

6 Conclusion

In this research, we have developed a novel PF distance measure based on Jensen–Shannon divergence. Our presented PF distance measure not only satisfies the properties of metric space but also defeats the counterintuitive case, as shown by our proof and examples. In order to solve problems involving pattern recognition and numerical example, the proposed and existing PF distance measure are applied. The experimental results demonstrate the superiority of our proposed PF distance measure in terms of its benefits. Besides, we combine the novel PF distance measure proposed by us and the maximum deviation approach to obtain the attribute weight in picture fuzzy environment. Meanwhile, in MADM problems, we extend CRADIS method to picture fuzzy environment and apply our proposed PF distance measure to it to calculate the deviation degree, which is effective and practical. In the future, we can explore more deeply based on our above article:

• 1. In other fuzzy environments, other distance measures satisfying axiomatic requirements can be proposed based on Jensen–Shannon divergence.

• 2. With respect to the superiority and effectivity of new PF distance metric, it is feasible to apply it to medical diagnosis and cluster analysis.

• 3. Extend the application of the CRADIS method to more fuzzy environments, such as interval-valued picture fuzzy sets and spherical fuzzy sets.