1 Introduction

Evolutionary computation (EC) and swarm intelligence (SI) have achieved tremendous success in the research field [1,2,3] and industrial design [4,5,6] thanks to their superior characteristics such as robustness, flexibility, efficiency, and applicability. However, as a kind of stochastic optimization technique, an enormous number of fitness evaluation times (FEs) are necessary to find acceptable solutions, which severely limits the scalability of these methodologies in computationally expensive optimization problems (EOPs). Therefore, many researchers attempt to combine these algorithms with mathematical methods to further accelerate the convergence of optimization. A common approach is to adopt the surrogate model and the infill sampling criterion to predict potential solutions, and then combine them with conventional evolutionary algorithms (EA) to improve search efficiency. An optimization framework like this that combines the two belongs to the surrogate-assisted evolutionary algorithm (SAEA) [7,8,9].

Up to now, many effective SAEAs have been reported: Dong et al. [10] extended the surrogate-assisted approach to the popular and powerful grey wolf optimization (SAGWO). The radial basis function (RBF) is employed to assist the meta-heuristic exploration and fitness landscape knowledge mining. Nishihara et al. [11] noticed that not only the model settings but also the training data chosen will influence the estimation performance and designed an adaption scheme for training data selection, which includes four criteria: All Data, Current Population, Recent Data, and Neighbor. These schemes collaborate with differential evolution (DE) for computationally expensive optimization problems. Wang et al. [12] proposed a global and local surrogate-assisted DE (GL-SADE) to solve high-dimensional EOPs. The global RBF model is trained with all samples to approximate the tendency of the whole fitness landscape, and the local Kriging model trained with the local population prefers to select solutions with well-performed prediction and great uncertainty, which can prevent the search direction from getting trapped into local optima. The unique reward search strategy in GL-SADE encourages the re-utilization of the Kriging model when the solution found by the local Kriging model is the best so far. Cai et al. [13] introduced the surrogate-assisted technique to multi-objective EOPs. Two strategies are proposed to balance the global and local search for multi-objective optimization: (1) Maximum angle-distance sequential sampling based improved surrogate-based multi-objective local search method. (2) Diversity-enhanced expected improvement matrix infill criterion-based pre-screening strategy. In addition, many SAEAs have been employed to deal with real-world applications: Wang et al. [14] proposed a committee-based active learning surrogate-assisted particle swarm optimization (CAL-SAPSO) for an airfoil design problem, where the best and most uncertain solutions found by the surrogate ensemble technique are evaluated using the expensive objective function, and the local surrogate model is built around the best solution obtained so far. Xiang et al. [15] proposed a clustering-based surrogate-assisted multi-objective evolutionary algorithm termed AR-MOEA+SA for the shelter location planning problem. The RBF is adopted to approximately calculate the evacuation distance under the uncertainty of road networks and the clustering strategy is cooperated to estimate the position of communities. Wakjira et al. [16] proposed a data-driven approach to determine the load and flexural capacities of reinforced concrete beams strengthened with fabric-reinforced cementitious matrix composites in flexure. Seven efficient surrogate models including kernel ridge regression, K-nearest neighbors, support vector regression, classification and regression trees, random forest, gradient boosted trees, and extreme gradient boosting are involved to estimate the best predictive model for this problem.

The introduction of surrogate-assisted techniques has promoted the development of the EC community rapidly and endowed the optimizers with a stronger ability to tackle more complex optimization problems at the cost of computational resources. However, No Free Lunch Theory [17] states that any pair of black-box optimization algorithms have identical averaging performance on all possible problems, and if an algorithm performs well on a specific category of problems, then, it must degenerate on the remaining problems, which is the only way for all algorithms to have the same performance on average across all functions. Thus, many researchers try to develop a generic optimization framework, which can dynamically modify the structure of the algorithm to adapt to the characteristics of certain problems.

Hyper-heuristics framework provides a potential opportunity to realize that. From the perspective of the hyper-heuristic algorithm (HHA), an optimization algorithm can be regarded as a combination of search strategies (e.g. the genetic algorithm (GA) repeats the crossover and mutation operators and particle swarm optimization (PSO) iterates the velocity and location update.), and this sequence of heuristics can also be optimized. As an “off-the-peg” technique rather than “made-to-measure” meta-heuristics [18], HHA is a high-level automatic methodology that manipulates a set of low-level heuristics (LLHs) to search for acceptable solutions [19]. Meanwhile, many HHAs have been reported to deal with combinatorial optimization problems [20,21,22,23] whilst only a few have dealt with continuous problems [24]. Therefore, the motivation of this research is to develop a hyper-heuristic algorithm for continuous optimization problems.

In this paper, we regard the surrogate-assisted estimation as a novel search operator and propose a novel surrogate ensemble-assisted hyper-heuristic algorithm (SEA-HHA) for continuous and computational EOPs. In the low-level component of SEA-HHA, we design four search strategy archives as the low-level heuristics (LLHs): The exploration strategy archive, exploitation strategy archive, surrogate-assisted estimation archive, and mutation strategy archive, each archive contains several search strategies. In the high-level component design, we apply a probabilistic random selection function to construct the optimization sequence dynamically. Specifically, the main contributions of this paper can be summarized as follows.

  1. (1)

    Four flexible and easy-implemented search strategy archives are designed as the LLHs, while the high-level component acts as the “brain” of SEA-HHA which randomly constructs the optimization sequence based on the pre-defined probabilities. This high-level component design is expected to enhance the diversity of the selected search strategies and avoid premature.

  2. (2)

    In the surrogate-assisted estimation archive, we provide three kinds of data selection fashions: All Data, Recent Data, and Neighbor, which corresponds to the global and local concepts. The selected data are randomly separated into the training dataset and testing dataset, and the most accurate model constructed by polynomial regression (PR), support vector regression (SVR), and Gaussian process regression (GPR) is chosen for solution estimation, which is hoped to estimate high-quality solutions and accelerate the convergence of optimization.

  3. (3)

    We implement a set of experiments on CEC2013 benchmark functions [25] and three real-world engineering optimization problems to evaluate our proposal. Four meta-heuristics algorithms and two surrogate-assisted optimization methods are applied as comparative algorithms. Numerical experiments show that our proposed SEA-HHA is competitive with these popular and state-of-the-art optimization techniques.

The remainder of this paper is organized as follows: Sect. 2 introduces the related works. Section 3 provides a detailed introduction to our proposal. Section 4 covers the numerical experiments and statistical results. Section 5 analyzes our proposal and lists some open topics. Finally, Sect. 6 concludes this paper.

2 Related Works

2.1 Hyper-Heuristic Algorithm (HHA)

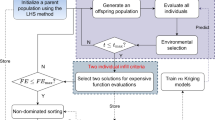
Motivated by solving classes of problems rather than one problem, the appearance of HHA can be traced to the early 1960s [26]. As an advanced methodology, HHA takes the sequence of strategies as the optimization object based on the knowledge, which can be described as “Heuristics to choose heuristics” [19]. Here, a typical structure of the HHA is shown in Fig. 1.

Fig. 1
figure 1

Representative architecture of the HHA [27, 28]. LLHs i: the \(i\textrm{th}\) low-level heuristics

Full size image

A classic HHA contains two constituents: the low-level component and the high-level component. The low-level component includes problem representation, the objective function(s), initial solutions, and a set of low-level heuristics (LLHs). The high-level component dominates the LLHs and constructs the sequence of heuristics. The move acceptance principle judges whether the generated offspring are accepted or rejected. Feedback is utilized as the reward to dynamically adjust the LLHs selection module. Here, we briefly review some works of literature on HHA approaches: Zhao et al. [29] proposed a cooperative multi-stage hyper-heuristic (CMS-HH) algorithm for combinatorial optimization, the GA is introduced to perturb the initial solution while an online learning mechanism based on the multi-armed bandits and relay hybridization technology is adopted to improve the quality of solutions. Qin et al. [30] developed a reinforcement learning-based hyper-heuristic algorithm to solve a practical heterogeneous vehicle routing problem. The policy-based reinforcement learning is a high-level selection strategy while several meta-heuristics with different characteristics are employed as low-level heuristics. Zhang et al. [31] proposed a hyper-heuristic algorithm for time-dependent green location routing problems with time windows, the Tabu search is adopted as the high-level selection module, and the greedy scheme is taken as the acceptance criterion. Most research focuses on combinatorial optimization problems.

2.2 Surrogate Models

In the usage of the surrogate-assisted technique, we concentrate on the performance indicators of the surrogate model, such as the robustness, computational complexity, flexibility, approximation ability, and so on. Polynomial regression (PR), support vector regression (SVR), and Gaussian process regression (GPR) are the three most popular and well-studied surrogate models, and the SAEAs can benefit from their easy implementation and excellent regression ability while the computational budget is affordable. Therefore, we adopt these three surrogate models to construct the surrogate-assisted estimation archive, and the detailed introduction is as follows.

2.2.1 Polynomial Regression (PR)

PR technique is an efficient and well-known model to solve the regression task, and the relationship between independent decision variables \(X=\{x_1, x_2,..., x_n\}\) and the dependent variables \(Y=\{y_1, y_2,..., y_n\}\) is described as an \(n^{th}\) polynomial in X [32]:

$$\begin{aligned} \begin{aligned} E_i(y \vert X_i) = w_1X_i + w_2X_i^2 + w_3X_i^3 + \cdots + w_nX_i^n + b_i. \end{aligned} \nonumber \\ \end{aligned}$$
(1)

From the matrix computation form, Eq. (1) can be rewritten to

$$\begin{aligned} \begin{aligned} \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_n \\ \end{bmatrix} = \begin{bmatrix} 1 &{}\quad x_1 &{}\quad x^2_1 &{}\quad \cdots &{}\quad x^m_1 \\ 1 &{}\quad x_2 &{}\quad x^2_2 &{}\quad \cdots &{}\quad x^m_2 \\ 1 &{}\quad x_3 &{}\quad x^2_3 &{}\quad \cdots &{}\quad x^m_3 \\ \vdots &{}\quad \vdots &{} \vdots &{} \ddots &{}\quad \vdots \\ 1 &{}\quad x_n &{}\quad x^2_n &{}\quad \cdots &{}\quad x^m_n \\ \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \\ w_3 \\ \vdots \\ w_n \\ \end{bmatrix} + \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ \vdots \\ b_n \\ \end{bmatrix}. \end{aligned} \end{aligned}$$
(2)

And this estimation can be approximated by least squares analysis [33]:

$$\begin{aligned} \begin{aligned} \min \sum _{i=1}^n\left( Y_i - E_i\left( y \vert X_i\right) \right) ^2, \end{aligned} \end{aligned}$$
(3)

where \(X_i\) is the \(i\textrm{th}\) sample, \(Y_i\) is the true solution of \(x_i\), and \(E_i(y \vert X_i)\) is the predicted solution of \(X_i\) by PR model.

2.2.2 Support Vector Regression (SVR)

SVR is a non-parametric machine learning technique that was first identified by Vladimir et al. in 1992 [34], which attempts to find a flat hyperplane that is within the tolerance margin (\(\varepsilon \)). Here, Fig. 2 demonstrates the SVR model in a regression task.

Fig. 2
figure 2

Demonstration of SVR

Full size image

Mathematically, the optimization of SVR can be expressed in Eq. (4):

$$\begin{aligned} \begin{aligned} \min _{w, b} \frac{1}{2} \Vert w \Vert ^2 + C\sum ^m_{i=1}l_{\varepsilon }\left( E_i\left( y \vert X_i\right) , Y_i\right) \end{aligned} \end{aligned}$$
(4)

where \(E_i(y \vert X_i)\) has similar structure to Eq. (1), C is a constant for regularization. \(l_{\varepsilon }(E_i(y \vert X_i), Y_i)\) is a \(\varepsilon \)-insensitive loss function that

$$\begin{aligned} \begin{aligned} l_{\varepsilon }\left( E_i\left( y \vert X_i\right) , Y_i\right) = {\left\{ \begin{array}{ll} 0, \ if \ \left| E_i\left( y \vert X_i\right) -Y_i \right| < \varepsilon \\ \left| E_i\left( y \vert X_i\right) -Y_i \right| - \varepsilon , \ \textrm{otherwise}. \\ \end{array}\right. } \end{aligned} \end{aligned}$$
(5)

More details can be found in [35].

2.2.3 Gaussian Process Regression (GPR)

A GP is a collection of random variables, any finite set of which have a joint Gaussian distribution and is completely specified by its mean function m(x) and the covariance function \(k(x, x')\):

$$\begin{aligned} \begin{aligned} f(x) \sim \mathcal {GPR}\left( m(x),k\left( x,x'\right) \right) . \end{aligned} \end{aligned}$$
(6)

In the regression problem, the prior distribution of output y can be denoted as

$$\begin{aligned} \begin{aligned} y \sim N\left( 0,k\left( x,x'\right) +\sigma ^2_nI_n\right) , \end{aligned} \end{aligned}$$
(7)

where \(N(\cdot )\) is the normal distribution. \(\sigma ^2_n\) denotes the noise term. Assuming the distribution of testing dataset \(x'\) and training dataset x are identical, then, the prediction \(y'\) would follow a joint prior distribution with the training output y as [36]:

$$\begin{aligned} \begin{aligned} \left[\frac{y}{y'} \right]\sim N\left( 0, \begin{bmatrix}k(x,x)+\sigma ^2_nI_n &{} k\left( x,x'\right) \\ k\left( x,x'\right) ^T &{} k\left( x',x'\right) \end{bmatrix}\right) , \end{aligned} \end{aligned}$$
(8)

where \(k(x,x), k(x,x')\) and \(k(x',x')\) represent the covariance matrices among inputs from the training dataset, the training and testing dataset, as well as the testing dataset.

Fig. 3
figure 3

Main architecture of SEA-HHA, the flowchart is similar to most EAs, and our proposal focuses on the search strategy determination part

Full size image

To guarantee the performance of the GPR, some hyper-parameters \(\theta \) in the covariance function require to be optimized with n samples in the training process. One efficient optimization solution is to minimize the negative log marginal likelihood \(L(\theta )\) as [37]:

$$\begin{aligned} \begin{aligned} L(\theta )&= \frac{1}{2}\log \left[ \det \lambda (\theta )+\frac{1}{2}y^T\lambda ^{-1}(\theta )y+\frac{n}{2}\log (2\pi )\right] \\ \lambda (\theta )&= k(\theta )+\sigma ^2_nI_n. \end{aligned} \end{aligned}$$
(9)

After the hyper-parameters optimization of the GPR, the prediction \(y'\) can be obtained at data set \(x'\) through calculating the corresponding conditional distribution \(p(y'\vert x',x,y)\) as

$$\begin{aligned} \begin{aligned} p\left( y'\vert x',x,y\right)&\sim N\left( y' \vert \bar{y}', \textrm{cov}\left( y'\right) \right) \\ \bar{y}'&=k\left( x,x'\right) ^T\left[ k(x,x)+\sigma ^2_nI_n\right] ^{-1}y \\ \textrm{cov}\left( y'\right)&=k\left( x',x'\right) -k\left( x,x'\right) ^T \\ {}&\quad \left[ k(x,x)+\sigma ^2_nI_n\right] ^{-1} k\left( x,x'\right) , \end{aligned} \end{aligned}$$
(10)

where \(\bar{y}'\) stands for values of prediction. \(\textrm{cov}(y')\) denotes a variance matrix to reflect the uncertainty range of these predictions. More details of the GPR model can be found in [38].

3 Our Proposal: SEA-HHA

The overall optimization framework of the proposed SEA-HHA can be summarized in Fig. 3. Specifically, in the low-level component of SEA-HHA, we design four generation archives containing the various LLHs: Exploration strategy archive, exploitation strategy archive, surrogate-assisted estimation archive, and mutation strategy archive. Besides, each archive has one or more search strategies, and different strategies in the same archive have an unbias probability to be chosen. In the high-level component of SEA-HHA, a stochastic selection function based on pre-defined probabilities is employed as the decision function to determine the optimization sequence dynamically.

3.1 Exploration Strategy Archive

The differential-based search strategy is first proposed in DE [39] and has been adopted in many bio-inspired EAs to describe the foraging behaviors of natural organism [40,41,42,43]. In this paper, we also use the basic form of the differential-based search strategy in the exploration strategy archive and provide three different ways to select the base individual:

$$\begin{aligned} \begin{aligned} X_{i+1} = X_{base} + F \cdot \left( X_{r2} - X_{r3}\right) \end{aligned} \end{aligned}$$
(11)

where \(X_{base}\) is randomly selected from \(\{X_i, X_{best}, X_{r1}\}\) with equal probability. \(X_i\) is the \(i\textrm{th}\) individual, \(X_{best}\) represents the best solution in the current population, and \(X_{r1}, X_{r2}\) and \(X_{r3}\) are mutually different solutions which randomly sampled from the current population. F is a scaling vector and each element is randomly sampled from \([-0.8, 0.8]\) [44].

The pseudocode of the exploration operation is shown in Algorithm 1.

Algorithm 1
figure a

Exploration operation

Full size image

3.2 Exploitation Strategy Archive

Rather than using the complex mechanism and parameters to realize the exploitation operation, we only adopt two parameters to determine the exploitation search strategy: the search direction D and the exploitation radius R. In addition, these operators can be described in Eq. (12):

$$\begin{aligned} \begin{aligned} X_{i+1} = X_{base} + D \cdot R \end{aligned} \end{aligned}$$
(12)

\(X_{base}\) is randomly selected from \(\{X_i, X_{best}, X_{r1}\}\) as well. D is a random vector and R is a constant. Once these two parameters are specified, the location of \(X_{i+1}\) can be identified. In our experiment settings, each element in D is uniformly sampled from \([-1, 1]\) and \(R=2\) as suggested in [45].

The pseudocode of the exploitation operation is shown in Algorithm 2.

Algorithm 2
figure b

Exploitation operation

Full size image

3.3 Surrogate-Assisted Estimation Archive

We regard surrogate-assisted estimation as a kind of search strategy to generate high-quality solutions, and the basic process is as follows. We first choose the dataset selection fashion among \(All \ Data, Recent \ Data,\) and Neighbor randomly, then, the dataset is randomly divided into the training dataset and the validation dataset with the proportion of \(80\%\) and \(20\%\) respectively. Three kinds of models described in Sect. 2.2 are employed to construct the approximation model, and we use an extra DE to estimate the best solution in the surrogate model which has the highest accuracy on the validation dataset. This estimated solution will be evaluated by the real objective function and participate in the optimization as an offspring individual. Next, we will introduce the selection training dataset and the surrogate model selection principles in detail.

Inspired by the SADE-ATDSC [11], three different strategies for selecting training datasets are applied in the archive: \(All \ Data, Recent \ Data,\) and Neighbor. \(All \ Data\) utilizes all solutions from optimization beginning to approximate the overview of the fitness landscape. \(Recent \ Data\) represents the recent k generated solutions which are selected as the dataset to describe the regularity of solution movements in the optimization. And Neighbor denotes the nearest-k solutions of \(X_{best}\) determined by the Manhattan distance, which can depict the characteristics of the fitness landscape near the current best solution. In our experimental setting, the k is set to 100, and a general demonstration of dataset selection is shown in Fig. 4.

Fig. 4
figure 4

Demonstration of dataset selection criteria, blue points are solutions in the \(1\textrm{st}\) generation, green points are solutions in the \(2\textrm{nd}\) generation, the red star represents the current best solution, and the selected dataset scale k is five in this example. The grey boundary point represents the selected data for model construction. a The original distribution of solutions. b \(All \ Data\) principle. c \(Recent \ Data\) principle. d Neighbor principle

Full size image

A subsequent problem is which model can approximate the fitness landscape better with these selected solutions. As we mentioned before, the selected dataset is randomly separated into two parts: The training dataset with the 80% proportion of the original data and the validation dataset with the remaining 20% proportion. Then, three kinds of models are constructed based on the training dataset, and the model that has the lowest mean squared error (MSE) loss on the validation dataset is considered the most accurate in this regression task. The calculation of MSE is in Eq. (13):

$$\begin{aligned} \begin{aligned} \textrm{MSE} = \frac{1}{n}\sum ^n_{i=1} \left( E\left( y\vert x_i\right) - y_i\right) ^2, \end{aligned} \end{aligned}$$
(13)

where n is the size of the dataset, \(E(y\vert x_i)\) is the expectation of the model given the solution \(x_i\), and \(y_i\) is the real fitness value of \(x_i\), and the well-performed solution in the surrogate model is considered as a high-quality solution on the real fitness landscape and will be evaluated by the real objective function and participate in the optimization process.

The pseudocode of the surrogate-assisted estimation strategy is shown in Algorithm 3.

Algorithm 3
figure c

Surrogate-assisted estimation

Full size image

3.4 Mutation Strategy Archive

The mutation strategy archive only contains one strategy that

$$\begin{aligned} \begin{aligned} X_{i+1} = X_{lb} + r \cdot \left( X_{ub} - X_{lb}\right) \end{aligned} \end{aligned}$$
(14)

r is a uniform random value from [0, 1]. \(X_{lb}\) and \(X_{ub}\) are the lower and upper bound of search space respectively. Simply, we randomly generate a new solution in the search space to endow an ability to SEA-HHA to get rid of the local optimum.

In summary, the involved search operators are summarized in Table 1, and the pseudocode of SEA-HHA is shown in Algorithm 4.

Table 1 Low-level heuristics (LLHs) in SEA-HHA
Full size table
Algorithm 4
figure d

SEA-HHA

Full size image

Algorithm 4 line 7 means to determine a specific search strategy from our designed four archives, and line 8 applies this sampled strategy to generate the offspring. Different from most EAs in which the search strategy is applied to the whole population, the object of the search strategy in our proposed SEA-HHA is applied to the individual. Each individual in the population has a high opportunity to generate offspring individual with various strategies, which is expected to enhance the diversity of the population and prevent premature convergence.

Table 2 Summary of the CEC2013 suite: Uni. unimodal function, Multi. multimodal function, Comp. composition function
Full size table
Table 3 Compared optimization techniques and their parameter configuration
Full size table
Fig. 5
figure 5

Convergence graphs of 5-D representative functions in the CEC2013 suite

Full size image

4 Numerical Experiments

We implement a set of experiments to evaluate the performance of our proposed SEA-HHA. Section 4.1 introduces the experiment settings, and Sect. 4.2 shows the experimental results.

4.1 Experiment Settings

4.1.1 Experiment Environment

The proposed SEA-HHA is programmed with Python 3.11 and implemented in Hokkaido University’s high-performance intercloud supercomputer equipped with a CentOS operating system, Intel Xeon Gold 6148 CPU, and 384GB RAM.

4.1.2 Benchmark Functions

We evaluate the performance of SEA-HHA on the 5-D, 10-D, and 30-D of 28 CEC2013 benchmark functions and three complex engineering problems, and the detailed features of the CEC2013 suite are listed in Table 2.

In addition, three famous engineering optimization problems include Cantilever Beam Design [46], Tension/Compression Spring Design [47], and Pressure Vessel Design [48].

Cantilever Beam Design: This problem is a structural engineering optimization problem that is related to the weight optimization of a cantilever beam with a square cross section. Equation (15) shows the mathematical model of this problem:

$$\begin{aligned} \begin{aligned}&\textrm{minimize} \\&f(X) = 0.0624\left( x_1 + x_2 + x_3 + x_4 + x_5\right) \\&\mathrm{subject \ to} \\&g(X) = \frac{61}{x^3_1} + \frac{37}{x^3_2} + \frac{19}{x^3_3} + \frac{7}{x^3_4} + \frac{1}{x^3_5} - 1 \le 0 \\&\textrm{where} \\&0.01 \le x_i\le 100, i=1,2,...,5 \end{aligned} \end{aligned}$$
(15)
Fig. 6
figure 6

Convergence graphs of 30-D representative functions in the CEC2013 suite

Full size image

Tension/Compression Spring Design: The objective of this problem is to minimize the weight of a tension/compression spring under the constraints of minimum deflection, shear stress, surge frequency, and outside diameter limitation. The formulation is presented in Eq. (16):

$$\begin{aligned} \begin{aligned}&\textrm{minimize} \\&f(X) = (x_3+2)x_2x^2_1 \\&\mathrm{subject \ to} \\&g_1(X) = 1-\frac{x^3_2x_3}{71785x^4_1} \le 0 \\&g_2(X) = \frac{4x^2_2-x_1x_2}{12566(x_2x^3_1-x^4_1)} + \frac{1}{5108x^2_1} - 1 \le 0 \\&g_3(X) = 1 - \frac{140.45x_1}{x^2_2x_3} \le 0 \\&g_4(X) = \frac{x_1 + x_2}{1.5} - 1 \le 0 \\&\textrm{where} \\&0.05 \le x_1 \le 2 \\&0.25 \le x_2 \le 1.3 \\&2 \le x_3 \le 15 \end{aligned} \end{aligned}$$
(16)

Pressure Vessel Design: This problem attempts to minimize the cost of the pressure vessel including the cost of forming, material, and welding. And this optimization problem can be expressed in Eq. (17):

$$\begin{aligned}&\textrm{minimize}\nonumber \\&f(X) = 0.6224x_1x_3x_4 + 1.7781x_2x^2_3 + 3.1661x^2_1x_4 \nonumber \\&\qquad \qquad + 19.84x^2_1x_3 \nonumber \\&\mathrm{subject \ to} \nonumber \\&g_1(X) = -x_1 + 0.0193x_3 \le 0 \nonumber \\&g_2(X) = -x_2 + 0.00954x_3 \le 0 \nonumber \\&g_3(X) = -\pi x^2_3x_4 - \frac{4}{3}\pi x^3_3 +1296000 \le 0 \nonumber \\&g_4(X) = x_4 - 240 \le 0\nonumber \\&\textrm{where} \nonumber \\&0 \le x_1 \le 99 \nonumber \\&0 \le x_2 \le 99 \nonumber \\&10 \le x_3 \le 200 \nonumber \\&10 \le x_4 \le 200 \end{aligned}$$
(17)

More detailed explanations and visual demonstrations of these engineering optimization problems can be found in [49].

4.1.3 Compared Methods and Parameters

We compare our proposal SEA-HHA with four EAs and two SAEAs, which are listed in Table 3. The selected probability for each search strategy archive in SEA-HHA plays an important role in guiding the optimization sequence construction. However, the determination of these parameters is also a difficult task. In this research, we fix the exploration probability, exploitation probability, surrogate-assisted estimation probability, and mutation probability with 0.33, 0.33, 0.33, and 0.01 respectively, which are also corresponding to the intuition of optimization algorithm design.

For all compared algorithms, the population size is 100, the maximum FEs by the real objective function in both the CEC2013 suite and engineering optimization problems are 1000, the sample size of the random search for promising solutions in surrogate models is 1000, which follows the recommend parameter setting in [11], and the independent trial run for each method is 30.

4.2 Experimental Results

This section shows the experimental and statistical results among seven compared optimization methods on CEC2013 benchmark functions and engineering optimization problems. Here, we collect the optimal fitness values in 30 trial runs of each optimization algorithm, and the Friedman test is applied to determine the significance. If significance exists, the Mann–Whitney U test is used to estimate the p value of every pair of algorithms, and the Holm multiple comparison test [57] corrects the p value obtained from the Mann–Whitney U test and further identifies the statistical significance.

\(+\), \(\approx \), and − are applied to represent that our proposed SEA-HHA is significantly better, with no significance, and significantly worse with the compared method, and the best fitness value is in bold. In addition, the convergence curve of representative functions (i.e., unimodal functions: \(f_2\) and \(f_4\); multimodal functions: \(f_6\), \(f_9\), \(f_{11}\), \(f_{12}\), \(f_{13}\), \(f_{14}\), and \(f_{15}\); composite functions: \(f_{25}\), \(f_{26}\), and \(f_{28}\)) of in 5-D and 30-D are provided in Figs. 5 and 6.

4.2.1 Optimization on CEC2013 Suite

Tables 4, 5, and 6 provide the experimental and statistical results on CEC2013 benchmark functions. The mean and standard deviation (std) are calculated at the end of the optimization within 30 trial runs.

4.2.2 Optimization on Engineering Optimization Problems

The original SEA-HHA cannot solve the constrained optimization problems while the real-world engineering problems presented in Sect. 4.1.2 contain constraints. Therefore, we need to introduce a constraint-handling technique to SEA-HHA. Coello et al. [58] summarized the various penalty functions including static, dynamic, simulated annealing, adaptive, and death penalty. As one of the simplest methods, the death penalty assigns an enormous fitness value to the individual which violates the constraint in the minimization optimization. For the sake of simplicity, we equip the SEA-HHA and all compared algorithms with a death penalty function to deal with constrained optimization problems. Tables 7 and 8 show the comparative results on the Cantilever Beam Design problem, Tables 9 and 10 show the optimization results on the Tension/Compression Spring Design problem, and Tables 11 and 12 show the results on the Pressure Vessel Design problem.

Table 4 Experimental and statistical results on 5-D CEC2013 Suite
Full size table
Table 5 Experimental and statistical results on 10-D CEC2013 Suite
Full size table
Table 6 Experimental and statistical results on 30-D CEC2013 Suite
Full size table
Table 7 Optimization results on the Cantilever Beam Design problem
Full size table

5 Discussion

5.1 Computational Complexity Analysis of SEA-HHA

In this section, we analyze the computational complexity of SEA-HHA. Supposing the population size is N, the dimension of the problem is D, the maximum iteration is T, and the computational complexity for surrogate-assisted estimation is C. For the sake of simplicity, we analyze each process independently.

  • population initialization: \(O(N\cdot D)\).

  • exploitative search operator: \(O(N\cdot D)\).

  • explorative search operator: \(O(N\cdot D)\).

  • surrogate-assisted estimation: O(C).

  • mutation search operator: \(O(N\cdot D)\).

  • selection operator: O(N).

Table 8 Optimum found by optimization techniques on the Cantilever Beam Design problem
Full size table

Therefore, the total computational complexity of SEA-HHA can be summarized by Eq. (18):

$$\begin{aligned} \begin{aligned}&O(N\cdot D) + T \cdot \left( O(\max (N\cdot D, C)) + O(N)\right) \\&\quad := O(T\cdot \max (N\cdot D, C)). \end{aligned} \end{aligned}$$
(18)

In numerical experiments, the real CPU time of C is larger than \(N\cdot D\) since the surrogate-assisted estimation involves the construction of the mathematical model and the sampling process based on the model.

5.2 Performance Analysis of Optimization on CEC2013

From the overview performance on CEC2013 benchmark functions among seven optimization techniques, our proposed SEA-HHA is competitive with these advanced algorithms, and we will analyze the performance of SEA-HHA from two perspectives: exploitation ability and exploration ability.

5.2.1 Exploitation Ability of SEA-HHA

In the CEC2013 suite, functions \(f_1\) through \(f_5\) are unimodal so that they are allowed to evaluate the exploitation ability of optimization algorithms. It’s worth noting that in \(f_1\), SHEALED outperforms our proposed SEA-HHA across three scales, which proves the efficiency and effectiveness of SHEALED in addressing such optimization problems. However, excluding \(f_1\), SEA-HHA consistently matches or even outperforms SHEALED, and the superior exploitation ability of SEA-HHA can be observed from these functions. When compared to other optimization algorithms on unimodal functions, our proposal outperforms them in most scenarios. Thus, experimental and statistical results provide adequate support for the excellent exploitation capacity of SEA-HHA.

However, the deterioration of SEA-HHA on \(f_4\) can be observed in Tables 4, 5, 6 and Figs. 5, 6, and this degeneration can be explained by the No Free Lunch Theory [17]. No Free Lunch Theory states that all stochastic optimization algorithms have identical average performance on all possible problems, and if an algorithm is well-performed on a category of the problem, it must compensate for the rest problems. Therefore, we can reasonably infer that the designed LLHs in SEA-HHA may not be good at dealing with this specific problem. Furthermore, as the dimension of the problem increases, the deterioration has been amplified, and we speculate that one reason is due to the curse of dimensionality [59]. As the dimension of the problem increases, the search space will increase exponentially, and the presence of this phenomenon can degenerate the accuracy of the surrogate model rapidly and further affect the quality of estimated solutions.

5.2.2 Exploration Ability of SEA-HHA

Considering that functions \(f_6\) through \(f_{20}\) are multimodal, and \(f_{21}\) through \(f_{28}\) are composition functions, these functions exhibit complex fitness landscapes and many local optima. Thus, they are allowed to evaluate the exploration capacity of optimization techniques. Through the experimental and statistical results in Tables 4, 5, and 6, the superior performance of SEA-HHA can be observed, and we owe this excellent performance to the diverse search strategy and effective surrogate-assisted estimation.

However, we also notice that slight degeneration exists in some benchmark functions such as \(f_{17}\), \(f_{18}\), and \(f_{21}\). These types of degeneration happen when the dimension of the problem increases, and we reasonably believe that this degeneration is also caused by the curse of dimensionality, which further affects the quality of solutions estimated by the approximation model, and how to overcome this issue will be considered in our future research.

5.3 Performance Analysis of Optimization on Three Engineering Problems

These engineering optimization problems contain multiple constraints and complex fitness landscapes, the optimization performance on these problems can reflect the ability of the algorithm to deal with the real-world tasks. Besides, this research focuses on solving EOPs, and only 1000 FEs are assigned for each task optimization, which is a severe challenge for optimization techniques.

Statistical results in Tables 7, 9, and 11 show that SEA-HHA at least is not inferior to any optimization method for any problem and can outperform in some problems (e.g. compared with DSIDE, aRBF-NFO, and SHEALED in Cantilever Beam Design). Another advantage of SEA-HHA is that the optimization process is stable even under the FEs limitation. In the Tension/Compression Spring Design problem, SEA-HHA can find a feasible solution in any independent trial run while SFO, SCSO, and aRBF-NFO can not at least once. In the Pressure Vessel Design, the worst solution found by SEA-HHA is apparently better than the compared methods and the standard deviation is also small. These experimental results reveal the excellent exploration and exploitation abilities of SEA-HHA in engineering optimization problems, which has great potential to deal with real-world applications.

Table 9 Optimization results on the Tension/Compression Spring Design problem. If more than 1 of 30 trial runs does not find a feasible solution, the worst, mean, and std cannot be calculated and we manually fill them with Nan. Statistical analysis is also meaningless
Full size table

5.4 Potential and Future Topics

Through the above analyses, we have known that our proposed SEA-HHA has broad prospects for dealing with EOPs. However, as a new optimization technique, there are still many aspects for further improvement. Here, we list some open topics.

5.4.1 More Powerful and Efficient Operators

Three exploration and exploitation strategies and one mutation strategy are employed as our basic search strategy archive. Without complex parameter tuning, our designed search strategies are the most common and easy-implemented. Meanwhile, Cruz et al. [24] summarizes ten search operations from well-known meta-heuristics such as Random Sample, Random Walk, Firefly Dynamic, Gravitational Search, and so on, which can also be absorbed into our proposed SEA-HHA to strengthen the diversity of the search strategy.

5.4.2 Dealing with High-Dimensional and Large-Scale EOPs

We implement the optimization experiments of SEA-HHA on relatively low-dimensional problems and have achieved satisfactory performance. However, we also observed the deterioration of SEA-HHA as the dimension of the problem increases, and how to alleviate the negative effect of the curse of dimensionality is a challenging topic. Inspired by the divide-and-conquer, cooperative coevolution (CC) [60] framework is a mature approach to solving high-dimensional and large-scale optimization problems, which divides the original problems into several sub-components and optimizes them separately. The remaining problem is how to decompose the original problems properly. To the best of our knowledge, merged differential grouping (MDG) [61] is the lightest decomposition method that only consumes 6.41e3 for CEC2013 large-scale benchmark functions on average with high accuracy. Therefore, the collaboration of MDG and our proposed optimizer SEA-HHA is promising to deal with high-dimensional and large-scale EOPs.

Table 10 Optimum found by optimization techniques on the Tension/Compression Spring Design problem
Full size table
Table 11 Optimization results on the Pressure Vessel Design problem
Full size table
Table 12 Optimum found by optimization techniques on the Pressure Vessel Design problem
Full size table

5.4.3 Determining the Optimization Sequence More Intelligently

As our first attempt to introduce the surrogate-assisted technique to the hyper-heuristic algorithm, we simply determine the sequence of heuristics by probabilistic selection function with pre-defined probabilities in this paper. Actually, many effective methodologies can contribute to the optimization sequence construction, such as Genetic Algorithm (GA) [62, 63], Reinforcement Learning techniques [28, 64], improvement-based choice function [65, 66], and so on. In our future research, we want to design a more flexible and intelligent method to determine the construction of the optimization sequence. A primary idea is to evaluate the generated solutions of different archives by the surrogate model and dynamically adjust the selected probability, which can fully utilize the surrogate model and is computationally cheap for EOPs.

6 Conclusion

In this paper, we propose a novel surrogate ensemble-assisted hyper-heuristic algorithm (SEA-HHA) to solve EOPs. In the high-level component design, the random selection function based on the pre-defined probabilities is adopted to dominate the LLHs. In the low-level component, we design four search strategy archives as LLHs: exploration strategy archive, exploitation strategy archive, surrogate-assisted estimation archive, and mutation strategy archive, each search strategy is easy-implemented. Besides, in the surrogate-assisted estimation archive, three different data selection principles are applied for model construction: \(All \ Data\), \(Recent \ Data\), and Neighbor, which correspond to the global and local concepts, and the most accurate model constructed by PR, SVR, and GPR is utilized to estimate the promising solutions.

In the numerical experiments, we compare our proposed SEA-HHA with six advanced optimization techniques on the CEC2013 benchmark functions and three popular engineering optimization problems. Experimental and statistical results show that SEA-HHA has broad prospects for solving EOPs.

At the end of this paper, we list some open topics to further develop the SEA-HHA. In the future, we will focus on combining the learning-based methods to determine the optimization sequence more intelligently and extend SEA-HHA to solve high-dimensional EOPs.