Introduction

In real-world applications, some optimization problems [7, 10, 17] are not able to be given in explicit mathematical models, which are called the black-box problems. Furthermore, some of them are time-consuming to evaluate the performance of a design, i.e., the time to evaluate the fitness or the objective function is very expensive. Evolutionary algorithms (EAs), such as genetic algorithms (GA) [8], differential evolution (DE) [5, 33], and particle swarm optimization (PSO) [20], have been shown good performances for solving optimization problems, especially for those discontinuous and non-differential problems. However, a large number of fitness evaluations are required by EAs to locate the optimal solution, which, thus, limits the applications of EAs on the optimization of computationally expensive problems [18]. Surrogate models, which are normally computationally cheaper than the exact expensive objective evaluation, are often adopted to assist the evolutionary algorithms, called surrogate-assisted evolutionary algorithms (SAEAs), for solving expensive optimization problems [16, 18]. The commonly utilized surrogate models include Gaussian process model (GP) [4, 19], radial basis function(RBF) [12, 13], artificial neural network (ANN) [14], support vector machine (SVM) [3, 32], and polynomial regression (PR) [11, 38].

Generally, surrogate-assisted evolutionary algorithms can be classified into online and offline methods according to whether any new solution will be evaluated using the real expensive objective function in the optimization [18, 29, 40]. In the offline SAEAs, no new solution will be evaluated using the exact objective function and added to the archive for updating the surrogate models. Wang et al. [40] proposed to build a number of surrogate models using different subsets of data, and then at each generation some of them will be selected to approximate the fitness of each individual in the current population. Li et al. [24] proposed to train a group of surrogates using all evaluated data and some generated data around them to approximate the expensive problem. Recently, Wang et al. [15] proposed an offline data-driven evolutionary optimization based on tri-training for expensive problems. On the contrary, the online surrogate-assisted evolutionary algorithms allow some solutions to be selected for exact fitness evaluation, which will be used to update the surrogate models. Many online surrogate-assisted evolutionary algorithms have been proposed [1], which can be classified into three categories according to what the surrogate model is used for, i.e., the global model-assisted EAs, the local model-assisted EAs, and the surrogate ensemble-assisted EAs. The global surrogate models are generally trained on the overall fitness landscape and used for assisting the global search. Tian et al. [37] proposed to train a global GP model and a multi-objective infill criterion focusing on the approximated value and the approximation uncertainty is used to select solutions on the first and last fronts to be evaluated using the exact objective function. Yu et al. [43] also proposed to train a global RBF model and the optimal solution of the model is searched by SL-PSO, which will be evaluated using the exact objective function. Recently, Li et al. [23] proposed to train a global RBF model, the optimal solution of which will be searched by both teaching-learning-based optimization (TLBO) and PSO. However, constructing accurate global surrogate models is less likely due to the curse of dimensionality. Therefore, local models are proposed to capture the local details of the fitness landscape. Ong et al. [28] proposed an evolutionary algorithm with a sequential quadratic programming solver in the spirit of Lamarckian learning, in which computationally cheap surrogate models are used in the local search. Sun et al. [36] proposed a new fitness estimation strategy based on the evolutionary dynamics of particle swarm optimization for solving computationally expensive problems. However, the key drawback of the local surrogate models is that they cannot assist the algorithm in escaping from the local optimum. A number of surrogate ensembles have been proposed, which are expected to take advantage of the global and local surrogate models. Generally, in the surrogate ensemble assisted evolutionary algorithms, a global surrogate model is used to smooth out the local optima to speed up the search for the optimal solution and a local model is utilized to assist in exploiting the local region to locate at the optimal solution accurately. Sun et al. [34] proposed a cooperative swarm optimization method for high-dimensional expensive problems, in which a global RBF surrogate model is used to assist SL-PSO to explore the decision space and the fitness estimation strategy is utilized as a local surrogate model to assist each individual of PSO to exploit a local region. In [44], Yu et al. utilized PSO assisted by an RBF surrogate model to explore the decision space, in which each solution will learn from its own experiences and the best position found by a local RBF model assisted social learning particle swarm optimization.

Surrogate ensembles have been paid more attention than a single surrogate model due to their better performances for finding a good solution of expensive problem [1]. However, model management, especially the infill criterion, plays a crucial role to get a good solution for computationally expensive problems. Liao [25] regarded two surrogate models, one is global and the other is local, as two tasks and utilized the multi-tasking optimization technique to search for the optimal solutions of these two tasks, which will be evaluated using the exact objective function. In [39], Wang et al. proposed to alternately optimize a global ensemble model and a local ensemble model, in which the individuals having the maximum uncertainty and minimum mean predicted value in the global search, and the individual with a minimum predicted function value by the local surrogate model will be selected to be evaluated using the exact objective function. Li et al. [22] utilized two kinds of surrogate ensemble, in which one is the ensemble of two RBF models with different kernel functions, and the other is the ensemble of RBF and PR models. The LCB function is adopted as the infill criterion of the two RBF ensembles, and in the RBF and PR ensemble, the solutions with minimum approximated value, and the best diversity, respectively, will be selected for exact objective evaluation. Recently, Ren et al. [31] proposed a bi-stage surrogate-assisted hybrid algorithm, in which a number of global searches will be conducted in the first stage for exploring the whole decision space, and the solution with the maximum uncertainty in the last generation of each global search will be evaluated using the exact objective function. In the second stage, the local search is conducted as a supplement to the global search to exploit the local region around the best solution found so far and the solution with the minimum approximated value will be evaluated using the exact objective function. From the literature review, we can see that an efficient infill criterion will significantly affect the performance of the optimization method.

In this paper, a global search and a local search are conducted in sequence at each generation of the optimization, and different infill criteria are utilized in two searches for choosing informative solutions to be evaluated using the exact fitness function. The algorithms for global and local searches can be either the same or different. Thus, we call the method multiple infill criteria assisted hybrid evolutionary algorithm, denoted as MIC-assisted HEA. The main contributions of this paper can be summarized as follows.

  1. 1.

    A new method is proposed to measure the approximation uncertainty of the RBF surrogate model. For any solution, the information of samples, including their positions in the decision space and the fitness values in the objective space, of the neighborhood of this solution will be utilized simultaneously to measure its approximation uncertainty.

  2. 2.

    A global search and a local search, assisted by RBF surrogate models trained using different sets of samples, are conducted in sequence in each generation.

  3. 3.

    The proposed approximation uncertainty is adopted to be the infill criterion to select a solution from the final population of the global search to be evaluated using the exact expensive objective function. It is expected to reduce the approximation error in the subspace where the optimal solution may be located. While in the local search, the solution with the best approximated fitness value found so far will be selected for exact fitness evaluation to improve the opportunity to find the real optimal solution.

The remainder of this paper is organized as follows. The next section briefly introduces the radial basis function network, differential evolution algorithm, and social learning particle swarm optimization algorithm. Details of the proposed MIC-assisted HEA are described in the subsequent section. Next, parameter settings and the analysis on the experimental results are given. Finally, the conclusion of this paper and the future work are summarized.

Preliminaries

Radial basis function network

Gaussian process [30] (also known as Kriging [4] or DACE [21]) is popular to be used as a model in the surrogate-assisted evolutionary algorithms because it can provide both the approximated value and the uncertainty of the approximation. However, GP is impeded to be widely applied due to the expensive cost to optimize the hyperparameters of GP, especially the dimension of decision space of the problem is high. Furthermore, a large number of training samples are required to train an accurate GP model for high-dimensional problems, which is impossible for expensive optimization problems. Contrary to GP, the radial basis function network (RBF) is insensitive to the number of decision variables [41]. Therefore, in this paper, the RBF is adopted to train both the global model and the local one for medium-dimension expensive problems. The RBF [13] model is a feedforward neural network only containing three layers, i.e., an input layer, a hidden layer and an output layer. The hidden layer consists of \(N_h\) neurons and each of them has an active function \(\varphi (\Vert {\mathbf {x}}-{\mathbf {x}}_p\Vert )\) that can be a Gaussian kernel, a thin plate spline, a multiquadrics, an inverse multiquadrics, a cubic kernel, etc. In this paper, the simple cubic kernel function is adopted to be utilized in the RBF model. Equation (1) gives the basic function form of an RBF model,

$$\begin{aligned} {\hat{f}}({\mathbf {x}}) = \sum _{p=1}^{N_h}\omega _p\varphi (\Vert {\mathbf {x}}-{\mathbf {x}}_p\Vert ) + \omega _0, \end{aligned}$$
(1)

where \({\mathbf {x}}_p\) is the center of pth hidden node, and \(\omega _p\) is the pth weight of the pth neuron in the hidden layer. Given an input \({\mathbf {x}}=\{x_1,x_2,...,x_n\}\), n is the number of decision variables, its output \({\hat{f}}({\mathbf {x}})\) is the sum of the weighted sum of \(N_h\) basis functions and the bias item \(\omega _0\). Generally, \(\omega _0\) is set to be zero or the mean of all data used to train the model.

Differential evolution algorithm

Differential evolution (DE) [33] is an evolutionary algorithm proposed by Storn and Price in the 1990s. The basic idea behind DE is a new scheme for generating trial parameter vectors. In one of the simplest forms of DE, an initial population with N individuals will be generated and evaluated using the objective function at first. Then an intermediate solution \({\mathbf {x}}^u_i\) will be generated for individual i by adding the weighted difference vector between two randomly selected parent individuals to a third parent individual, i.e.,

$$\begin{aligned} {\mathbf {x}}_{i}^{u}(t+1) = {\mathbf {x}}_{r1}(t)+F\times ({\mathbf {x}}_{r2}(t)-{\mathbf {x}}_{r3}(t)), \end{aligned}$$
(2)

where \({\mathbf {x}}_{r1}(t)\), \({\mathbf {x}}_{r2}(t)\), and \({\mathbf {x}}_{r3}(t)\) are three solutions selected randomly from the parent population, r1, r2 and r3 are three random number, \(r_1 \ne r_2 \ne r_3 \ne i\). \(F\in [0,2]\) is a control parameter that scaling the difference vector \(({\mathbf {x}}_{r2}(t)-{\mathbf {x}}_{r3}(t))\). Next, a crossover operation comes into play to generate a new solution according to Eq. (3).

$$\begin{aligned} \begin{aligned} {\mathbf {x}}^v_{i,j}(t+1)= \left\{ \begin{array}{ll} {\mathbf {x}}^u_{i,j}(t+1), &{} \quad \mathrm{rand}\le \mathrm{CR}|j=j_r\\ {\mathbf {x}}_{i,j}(t), &{}\quad \mathrm{otherwise}, \end{array} \right. \end{aligned} \end{aligned}$$
(3)

where CR is the probability of crossover, \(j = \{1,2,...,n\}\), n is the decision dimension, \(j_r\) is a random number of \(\{1,2,...,n\}\) and \(rand\in [0,1]\). Finally, the objective values of solutions \({\mathbf {x}}^v_i(t+1)\) and \({\mathbf {x}}_i(t)\) will be compared and the one with better fitness value will be kept to the next generation. Equation (4) gives the selection operation.

$$\begin{aligned} \begin{aligned} {\mathbf {x}}_{i}(t+1)= \left\{ \begin{array}{ll} {\mathbf {x}}^v_{i}(t+1), &{}\quad f({\mathbf {x}}^v_i(t+1)) < f({\mathbf {x}}_i(t))\\ {\mathbf {x}}_{i}(t), &{}\quad \mathrm{otherwise} \end{array} \right. \end{aligned} \end{aligned}$$
(4)

Social learning particle swarm optimization

The social learning particle swarm optimization (SL-PSO) was proposed by Cheng and Jin [2], which can get good balance between the exploration and exploitation due to its learning strategy as is given in the following:

$$\begin{aligned} v_{i,j}(t+1)&= r_1\times v_{i,j}(t)+r_2\times (x_{k,j}(t)-x_{i,j}(t))\nonumber \\&\quad + r_3\times \varepsilon \times ({\bar{x}}_j(t)-x_{i,j}(t)) \end{aligned}$$
(5)
$$\begin{aligned} x_{i,j}(t+1)&=x_{i,j}(t)+v_{i,j}(t+1). \end{aligned}$$
(6)

In Eqs. (5) and (6), \(v_{i,j}(t+1)\) and \(x_{i,j}(t+1)\) are the velocity and position of individual i on j-dimension at (\(t+1\))th generation, respectively. k represents an individual who has better fitness value at tth generation than individual i, and \({\bar{x}}_j(t)\) is the average position on jth dimension of the population at tth generation. \(r_1\), \(r_2\) and \(r_3\) are three random numbers generated from 0 to 1, respectively, and \(\varepsilon \) is the social influence factor determining the influence degree of the average position on the velocity of the individual in the next generation.

The proposed MIC-assisted HEA

Overall framework

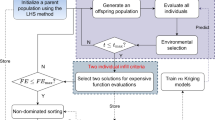
Using multiple surrogate models has been shown better performance than using a single one to assist evolutionary algorithms for expensive optimization problems [31, 39]. Thus, in this paper, we also adopt to use multiple models to assist the evolutionary algorithm. The global and local searches are conducted in sequence at each generation to search for the optimal solutions of two surrogate models, respectively. Figure 1 shows the general flowchart of the proposed MIC-assisted HEA. From Fig. 1, we can see that a number of solutions will be generated using Latin hypervolume sampling technique and evaluated using the exact objective function. All of these evaluated solutions will be saved to an archive DB. In the global search, a global surrogate model is trained using all solutions having been evaluated using the exact objective function. It is used to assist the DE algorithm to speed up locating close at the optimal solution on one hand, and on the other hand, to improve the exploration capability by evaluating the solution with the maximum approximation uncertainty in the final population of the search. While in the local search, a local surrogate model is trained using a set of data in the archive that have best fitness values. It is used to assist the algorithm to search for the optimal solution of the model. The optimal solution of the local search will be evaluated using the exact expensive objective function, which will be expected to improve the exploitation capability to find the optimal solution of the expensive optimization problem. Note that the final population of the global search will be the initial population of the following local and the global searches of the next round, respectively. In the following, we will give a detailed description of the global and local searches, respectively.

Fig. 1
figure 1

The general flowchart of the proposed MIC-assisted HEA

Full size image

The global search

Generally, the approximation error of the global surrogate model can give a potential positive impact to smooth out the local optima [26]. Thus, it can assist to speeding up the search to locate the region where a good optimal solution may stay. So in our proposed MIC-assisted HEA, a global surrogate model is trained using all data having been evaluated using the exact objective function, and used to assist the DE algorithm in exploring the decision space to find an informative population with potential good fitness values. To decrease the approximation error in the space where the informative population is located, the solution with the maximum approximation uncertainty will be selected for exact objective evaluation. However, different to the Gaussian process model, the RBF surrogate models are not able to provide the uncertainty of the approximation. Thus, in this paper, we propose a new method to measure the approximation uncertainty for each solution i, in which both the positional relationships in the decision space between solution i and its neighbors in the archive DB and the fitness variation of its neighbors in the archive are considered. Equation (7) gives the explicitly formula to calculate the approximation uncertainty of solution i.

$$\begin{aligned} \mathrm{us}_i(t) = \sum _{k=1}^{N_n}\left( -\frac{\cos \theta _{k}^{i}(t)}{d_{k}^{i}(t)} \times \sqrt{(f_{k}^{i}(t)-{\bar{f}}(t))^2}\right) , \end{aligned}$$
(7)

where \(\mathrm{us}_i(t)\) represents the approximation uncertainty of solution i at generation t, \(N_n\) is the number of closest neighbors in the archive DB of solution i. \(\theta _k^{i}(t)\) and \(d_k^{i}(t)\) represent the angle and Euclidean distance, respectively, between solution i and its kth neighbor in the archive DB at generation t of the global search. Note that all solutions are ensured to be located at the first quadrant so that the cosine value of any angle between two solutions is kept positive and monotonous. Thus, we transform the coordinate by transforming its origin to the lower bound of the problem before calculating the cosine value of each angle. That is, any position \({\mathbf {x}}_i\) in the original coordinate will be transformed to \({\mathbf {x}}_i-{\mathbf {L}}\), where \({\mathbf {L}}\) is the lower bound of the decision space. After that, the cosine value of the angle between two solutions can be calculated. On the other hand, to ensure that the contribution of each decision variable for the distance calculation is the same, in our method, each solution will be normalized as follows before calculating the distance: \({\mathbf {x}}_i = \frac{{\mathbf {x}}_i - {\mathbf {L}}}{{\mathbf {U}} - {\mathbf {L}}}\), where \({\mathbf {U}}\) is the upper bound of the problem. \(f_k^{i}(t)\) is the fitness value of kth neighbor of solution i in the archive DB and \({\bar{f}}(t)\) is the mean value of all fitness values of solutions in the archive DB at t-th generation. From Eq. (7), we can see that the larger \(\theta _k^{i}\) (the smaller \(\cos \theta _k^{i}\)) and \(d_{k}^{i}\) are, the smaller \(\frac{\cos \theta _k^{i}}{d_{k}^{i}}\) is, indicating that individual i is far from its kth neighbor in the archive DB in the decision space, thus the accuracy of the approximation is not able to be ensured. Furthermore, the ruggedness of the fitness landscape will also affect the approximation accuracy. Thus, in our proposed method, we propose to use the differences between the fitness values of the neighbors and the mean fitness value of all data in the archive DB, i.e., \(\sqrt{(f_{k}^{i}(t)-{\bar{f}}(t))^2)}, k=1,2,\ldots , N_n\), to roughly measure the ruggedness of the fitness landscape. Clearly, the larger the difference is, the more irregular the fitness landscape is, resulting in the difficulty of training a good surrogate model, which will affect the approximation accuracy. So in our proposed method, the ruggedness of the fitness landscape and the distance to the neighbor samples in the decision space are considered simultaneously to measure the approximation uncertainty. From Eq. (7), we can see that if a solution is far from its neighbors in the decision space and the fitness landscape is rugged in the objective space, then the approximated value will be highly uncertain. Thus, the solution with the maximum value of us will be selected for exact objective evaluation to prevent searching for the optimal solution in a wrong direction and improve the exploration capability of the proposed method.

Table 1 The function features and global optimal positions of seven problems
Full size table

The local search

Local surrogate models are normally used to assist the evolutionary algorithms to exploit the local region to improve the quality of the best solution found so far. In our proposed MIC-assisted HEA, we sort the solutions in the archive in ascending order, and a number of top solutions are used to train a local surrogate model. At the beginning of the proposed method, few solutions concentrate on a region. Therefore, the local search assisted by the local model also has the exploration capability to a certain extend. As the number of solutions in the archive increases, many solutions will locate close to the best solution found so far. Thus, the local search assisted by the local surrogate model will exploit the region where the best solution found so far is located.

The local search is used to exploit a sub-space of the decision space to find a solution with a better fitness value than the best solution found so far. Thus, the optimal solution of the local search is adopted to be evaluated using the exact objective function and used to update the best solution found so far. Note that all solutions that have been evaluated using the exact expensive fitness function at each generation will be saved to the archive.

Experimental studies

To verify the performance of the proposed MIC-assisted HEA, a number of experimental studies are conducted on seven benchmark problems with 10, 20, 30 and 50 decision variables and on a real-world application. The characteristics of the seven test problems are given in Table 1.

Table 2 The statistical results (median and standard deviation) obtained by the proposed MIC-assisted HEA and GM-assisted HEA on F1–F7 problems with 10, 20, 30 and 50 decision variables
Full size table

Parameter settings

In the proposed MIC-assisted HEA, \(2 \times n\) solutions will be generated using the Latin hypercube sampling (LHS) [42] method at first and will be saved to an archive DB after being evaluated using the exact objective function. Any algorithm can be utilized for global and local searches, respectively. In our method, the DE is adopted to the algorithm for searching for the optimal solution of the global surrogate model as the DE algorithms have good capability to escape from the local optima, and the SL-PSO algorithm is used as the local search algorithm because it has good performance to balance the exploration and exploitation capability. The population sizes of both algorithms are set to 50, the scale factor F and the crossover probability CR of DE are set to 0.5 [33] and 0.3 [27], respectively. The social influence factor of SL-PSO is set to 0 to speed up the convergence speed. The maximum number of iterations of both global and local searches are set to 20. All data are used to train a global model, and the \(2 \times n\) best data in the archive DB are used to train a local model. \(N_n=10\) data that are closest to each solution i in the global search are used to measure the approximation uncertainty of the solution i. The terminal condition is that the maximum number of objective evaluations, which are set to \(11 \times n\) for problems with 10, 20 and 30 decision variables and 1000 for those with 50 decision variables, respectively, is met. All comparison algorithms are run independently 20 times, and the Wilcoxon’s rank-sum test [42] with the significance level of 5\(\%\) is utilized to show whether the proposed algorithm MIC-assisted HEA is significantly different from other algorithms on the results, where ‘−’, ‘\(+\)’, and ‘\(=\)’ represent that the proposed MIC-assisted HEA is significantly worse than, better than, and approximated to the compared algorithms, respectively.

The performance analysis of local search

To investigate the contribution of the local search in MIC-assisted HEA, we compare the results to a MIC-assisted HEA variant, denoted as GM-assisted HEA, which has a global search only. Table 2 gives the statistical results obtained by MIC-assisted HEA and GM-assisted HEA on F1–F7 problems with 10, 20, 30 and 50 decision variables. From Table 2, we can see that compared to GM-assisted HEA, our proposed MIC-assisted HEA can obtain better results on 19/28 problems, and only loses to win GM-assisted EA on 1/28 problems, which shows that the local search can actually assist in improving the performance to find a better solution in a limited computational budget. To better show the contribution of the surrogate-assisted local search, Fig. 2 plots the convergence curves of the proposed MIC-assisted HEA and GM-assisted HEA on F1–F7 functions with 50 decision variables, from which we can see that MIC-assisted HEA can converge much faster than GM-assisted HEA on most of the test problems. The GM-assisted HEA method gets more quickly convergence speed than MIC-assisted HEA on F5 (Rastrigin problem). The reason we analyze is that the Rastrigin problem is a multimodal problem and has a large number of local minimums, while the approximation error of a global surrogate model has a potential benefit to smooth the local optima, thus being able to assist in searching for a good solution, especially for problems with a large number of local optima [35]. However, in our proposed MIC-assisted HEA method, two evaluations shall be spent at each generation. Therefore it means that the times of the global search will be cut down, resulting in poor performance for solving this problem. However, generally, the local search plays an important role in the proposed MIC-assisted HEA.

Fig. 2
figure 2

The convergence profiles obtained by the proposed MIC-assisted HEA and GM-assisted HEA on 50-dimension F1–F7 test problems

Full size image

Comparison to other recently proposed algorithms

To evaluate the performance of our proposed MIC-assisted HEA, we further compare the results on seven benchmark problems obtained by MIC-assisted HEA to those obtained by algorithms recently proposed for computationally expensive problems (including GORS-SSLPSO [43], CAL-SAPSO [39], SHPSO [44], MGP-SLPSO [37], BiS-SAHA [31] and DDEA-SE [40]). Among all comparison algorithms, CAL-SAPSO and DDEA-SE are proposed for low-dimensional expensive problems and others are presented for high-dimensional ones. Furthermore, DDEA-SE is an offline data-driven method and all others are online approaches. As SHPSO and MGP-SLPSO are specially proposed for high-dimensional problems, in our experiments, they are only used to compare MIC-assisted HEA on 50-dimensional problems.

Experimental results on low-dimensional problems

Table 3 gives the statistical results obtained by the proposed MIC-assisted HEA and other four algorithms, including GORS-SSLPSO, CAL-SAPSO, BiS-SAHA and DDEA-SE, on 10-, 20-, and 30-dimensional F1–F7 problems. From Table 3, we can see that MIC-assisted HEA performs significantly better on these problems than other algorithms. Specifically, MIC-assisted HEA gets better results than GORS-SSLPSO, CAL-SAPSO, BiS-SAHA, DDEA-SE on 14/21, 16/21, 13/21 and 20/21 problems, respectively.

Figure 3 plots the convergence profiles of the compared algorithms on 10-, 20- and 30-dimensional F1–F7 problems. From Fig. 3, we can see that MIC-assisted HEA shows good performance of the convergence speed on most of these problems. However, the proposed MIC-assisted HEA method is not able to get better results than others on F5 and F6 problems. The reason we analyze is that the Rastrigin problem (F5) has a large number of local optima, and the shifted rotated Rastrigin problem (F6) has very complicated multi-modal characteristics. Thus the search on the global surrogate model may mislead to an error global optimal solution, and the newly added solution for training the global surrogate model, which is the optimal solution found by the local search and evaluated using the exact objective function, may not contribute to improving the quality of the global model.

Experimental results on medium-dimensional problems

Table 4 summarizes the statistical results obtained by MIC-assisted HEA and other five algorithms, including SHPSO, GORS-SSLPSO, MGP-SLPSO, BiS-SAHA, and DDEA-SE, on 50-dimensional F1–F7 problems. From Table 4, we can see that compared to other algorithms, the proposed MIC-assisted HEA method can also obtain better results than other algorithms. To be specific, MIC-assisted HEA outperforms SHPSO, GORS-SSLPSO, MGP-SLPSO, BiS-SAHA, and DDEA-SE on 6, 6, 5, 5, and 7 out of 7 benchmark problems, which shows that our proposed method is also efficient for solving medium-dimensional expensive problems.

Experimental results on a real-world application

The choice of the appropriate waveform is significantly important in designing a radar system that uses pulse compression. To evaluate the performance of the proposed MIC-assisted HEA, we apply all comparison methods in the spread spectrum radar Polly phase code design, which is a min–max nonlinear non-convex optimization problem with many local optima. The mathematical model is given as follows:

$$\begin{aligned} \min ~f({\mathbf {x}})&= \max \{\phi _1({\mathbf {x}}),...,\phi _{2m}({\mathbf {x}})\}, ~m=2n-1 \end{aligned}$$
(8)
$$\begin{aligned} \phi _{2i-1}({\mathbf {x}})&=\sum _{j=i}^n \cos \left( \sum _{k=|2i-j-1|+1}^jx_k\right) ,\quad i = \{1,2,,n\} \end{aligned}$$
(9)
$$\begin{aligned} \phi _{2i}({\mathbf {x}})&=0.5+\sum _{j=i+1}^n \cos \left( \sum _{k=|2i-j|+1}^jx_k\right) ,\nonumber \\&\quad i = \{1,2,,n-1\} \end{aligned}$$
(10)
$$\begin{aligned} \phi _{m+i}({\mathbf {x}})&=-\phi _i(x),i = \{1,2,...,m\}, \end{aligned}$$
(11)

where \({\mathbf {x}}=(x_1,x_2,...,x_n), x_j\in [0,2\pi ]\) is the decision vector with n variables. More details of this problem can be referred to [6, 9].

Tables 5 and 6 give the best, worst, median, mean results and the standard deviation obtained by MIC-assisted HEA and other six methods on the spread spectrum radar Polly phase code design problem with 30 and 50 decision variables, respectively. All comparison algorithms are conducted 20 independently runs. The maximum number of objective evaluations is set to 11\(\times n\) and 1000 for 30- and 50-dimensional spread spectrum radar Polly phase code design problem, respectively. From Tables 5 and 6, we can see that the proposed MIC-assisted HEA can outperform other algorithms for the spread spectrum radar Polly phase code design problem, indicating further the good performance of MIC-assisted HEA for solving the expensive problems in a limited computational budget.

Table 3 The statistical results (median and standard variance) obtained by the proposed MIC-assisted HEA and other four algorithms on F1–F7 problems with 10, 20, and 30 decision variables, in which the best results are highlighted
Full size table
Table 4 The statistical results (median and standard variance) obtained by the proposed MIC-assisted HEA and other five algorithms on F1–F7 problems with 50 decision variables, in which the best results are highlighted
Full size table
Table 5 The results obtained by the proposed MIC-assisted HEA and other four algorithms, GORS-SSLPSO, CAL-SAPSO, BiS-SAHA, and DDEA-SE on the spread spectrum radar Polly phase code design problem with 30 decision variables, in which the best results are highlighted
Full size table
Table 6 The statistical results obtained by the proposed MIC-assisted HEA and other five algorithms, SHPSO, MGP-SLPSO, BiS-SAHA, GORS-SSLPSO and DDEA-SE on the spread spectrum radar Polly phase code design problem with 50 decision variables, in which the best results are highlighted
Full size table
Fig. 3
figure 3

The convergence profiles obtained by the proposed MIC-assisted HEA and other four algorithms on F1–F7 problems with 10, 20 and 30 decision variables

Full size image

Conclusion

A multiple infill criterion-assisted hybrid evolutionary algorithm is proposed for computationally expensive problems, in which a surrogate-assisted global search and a surrogate-assisted local search are conducted in sequence at each generation. The surrogate-assisted global search is used to provide a potential good population, in which a solution with the maximum approximation uncertainty measured by the proposed method in this paper, will be selected for exact objective evaluation to improve the exploration capability of the method. In the surrogate-assisted local search, the best solution found by the algorithm will be evaluated using the real objective function to improve the quality of the best solution found so far as much as possible. The experimental results on seven benchmark problems with 10, 20, 30 and 50 dimensions and a real-world application with 30 and 50 decision variables show that our proposed method is efficient for solving low- and medium-dimensional expensive problems. However, the method is not good for solving high-dimensional problems. The reason we analyze is that most solutions selected for exact objective evaluation may not play an important role in improving the quality of the best solution found so far. Therefore, in the future, we will consider to reduce the fitness evaluations at each generation as much as possible to save the number of evaluations so that more generations can be run in a limited computational budget.