Navigating Uncertainty in Weapon System-of-Systems Planning: A Hybrid Multiobjective Network-Based Optimization and Fuzzy Set Approach

Abstract

The evaluation of the capability of network-based systems of systems has replaced the simple method that considers return on investment, becoming a new paradigm for planning national defence capabilities. However, the dual uncertainty of the key system attributes of scenes and weapons has brought great challenges for decision-making. Based on this, we developed a multiobjective optimization model with multiple stages and scenarios under uncertainty to determine plans. In this study, we consider planning risk and planning cost as the two objectives. To solve this problem, we propose a hybrid solution for a network-based optimization method integrated with fuzzy set theory. The network-based optimization method combines the NSGA-II-DE and complex network theory. We use the characteristics of the network to evaluate the capabilities of the WSoS, and the NSGA-II-DE is used to generate a development plan and finally output a set of Pareto optimal solutions. We use fuzzy sets to determine the fuzzy membership of each plan on the Pareto front and determine a satisfactory solution. Finally, we conduct simulation experiments to verify the rationality of the methods proposed in this article. The results can provide a set of efficient solutions for military planners, helping generate a variety of planning solutions and trade-offs according to their preferences.

Graphical Abstract

1 Introduction

A weapon system of systems (WSoS) is a higher-level weapon system that integrates a variety of weapon systems that are interrelated in function and complementary in performance [1]. The architecture design, planning and deployment, and operation application of the WSoS can determine the success of a war and have received the attention of relevant decision-makers and researchers in the national defence field.

The development planning of the WSoS as a key link can support the scientific design and reasonable control of the construction direction, development path, key issues, time process and resource allocation of the WSoS. However, for countries, this is a challenging strategic analysis work because it often involves various aspects, such as mission tasks, capability requirements, weapon effectiveness, and economic benefits, and the quality of the planning solution will directly affect the national security capabilities of a country.

As early as 1998, the U.S. military tried to apply a development roadmap to the technical planning of the U.S. Navy. In recent years, focusing on the construction of weapons and equipment systems, the U.S. military successively formulated the “NASA Technology Roadmaps”, “Unmanned Systems Integrated Roadmap”, “Army Unified Network Plan”, etc. Judging by the implementation effect, U.S. military planning has undoubtedly played a positive role in promoting the construction of WSoS and the improvement of operational capabilities.

However, with the evolution of modern warfare in the direction of networking, informatization, and intelligence, greater challenges have arisen for the planning and construction of WSoS. Specifically, first, informatization wars accelerate the application of a large number of distributed platforms, sensors, and weapons, and the network effects of the weapon system are prominent; namely, simple weapons can also emerge through interactive collaboration [2]. The construction of the WSoS emphasizes the interconnection and interoperability between weapons. Second, the proposal of new operational concepts and the introduction of disruptive technology make the future battlefield more difficult to predict, and the construction of the WSoS will face deeper uncertainty. To cope with uncertainty in planning the equipment system, the U.S. Department of Defense proposed capability-based planning (CBP) [3], which focuses on capacity development rather than direct measures to cope with various possible future scenarios to prevent WSoS planning from falling into a bottleneck. Currently, CBP methods have penetrated into the design and planning of WSoS [4,5,6,7,8,9,10]. However, in the current process of WSoS development planning under CBP, the complex interactive relationships between weapons and many uncertainties are usually ignored.

Therefore, it is necessary for us to conduct further research on the planning and construction of the WSoS from the two perspectives of the network characteristics of the weapon system and the uncertainty of weapon construction based on the CBP. The topic under discussion in this paper is essentially a system-of-systems development and planning problem under uncertainty.

In this study, first, we analyse the input factors in the problem, and the interval number and stochastic number are used to characterize the uncertain factors. Second, we model the WSoS network and evaluate its capabilities. Then, based on the analysis of the uncertain factors, we introduce interval-number and opportunity constraints and build a multiobjective optimization model for development planning based on whether the capabilities of the WSoS match the requirements of the scene. Finally, the NSGA-II-DE algorithm is used to solve the constructed model, and the compromise solution considering the decision-maker’s preferences is obtained from the Pareto optimal solutions combined with fuzzy set theory. Through the above steps, the previous qualitative decision-making process based on expert experience is transformed into quantitative decision-making based on the multiobjective optimization model in the field of operations research, which improves the efficiency and scientificity of scheme formulation.

The remainder of this paper is organized as follows: Sect. 2 reviews related literature on network modelling in WSoS and planning methods under uncertainty; Sect. 3 describes the problem of planning WSoS and modelling the related factors; Sect. 4 describes the modelling process for the capability assessment model based on network theory and the planning model based on multiobjective optimization; Sect. 5 presents the specific method of solving the proposed model; and Sect. 6 illustrates the proposed method with an example. Finally, Sect. 7 discusses the main conclusions and suggests future research.

2 Literature Review

2.1 Network Modelling in WSoS

Objective description and modelling are basic steps in planning and evaluating a WSoS. The key is that the method of modelling description adopted must not only reflect the typical characteristics of weapon systems at the macro level but also describe their complex interactive relationships.

With the development of network science, complex network theory is considered to be an effective theoretical method for researching the modelling of complex weapon systems. Cares first used complex network theory to model a network formed by combat weapons. The weapon nodes were abstracted as sensor, decider, influencer, and target nodes to build a connection relationship between different nodes, forming a model of the information [11]. Based on the model proposed by Cares, Deller et al. summarized 18 interaction relationships between the weapons of the enemy and us [12]. Tan Y. et al. studied the WSoS based on the theory of complex networks and proposed the operation loop to regard sensors, deciders, influencers, and targets as a loop and define a series of indicators of the architecture resistance, capacity, and efficiency of WSoS [13]. Based on the operation loop, Wan et al. and Shang et al. applied the method to WSoS planning problems under confrontation conditions and built a threatened optimization model [14, 15]. Jichao Li et al. proposed a modelling method for the timing operation loop and proposed a combat capability contribution index to measure the degree of contribution of the weapons participating in an operation [16]. In addition, Domerçant & Mavris designed an architecture resource-based collaborative network evaluation tool (ARCNET) that abstracts a WSoS as a weighted network and represents the interoperability level and collaboration of each side to measure the collaboration effect between weapons on the success rate of combat tasks [17]. Li M. proposed the method of capability generation-oriented weapon network portfolio optimization [10].

With the deepening of study, scholars have found that the general complex network model cannot accurately reflect the diversity of the middle nodes and connectivity of the weapon system, so the methods of the heterogeneous network [18,19,20,21], multilayer network [22], and super network [23] have been proposed. The nodes and edges of heterogeneous networks can contain much information. Zhao D. applied a heterogeneous network to assess the contribution rate of an operational system of systems and calculated the efficiency value of the system of systems through meta-paths [18]. Chen et al. applied a heterogeneous network to link forecasting [19] and network disintegration [20]. Liu Peng et al. added a function chain model-building method to the idea of heterogeneous networks [21]. Multilayer networks focus on the physical significance of weapons. Xia B. et al. introduced multilayer networks into killing network modelling and extracted four types of network structures: reconnaissance networks, communication networks, charged networks, and strike networks, in weapon systems; then, they measured the redundancy, agility, and risk of the system based on network characteristics [22]. Super networks are used to describe cognitive attributes and information attributes in the real world. Zhao et al. applied this idea to construct an architecture design scheme for generating a WSoS [23].

It can be concluded through literature analysis that network modelling of WSoS is mostly focused on analysing and evaluating the operational system, and only [14, 15] applications for WSoS planning problems. At the same time, a WSoS can be classified in two ways. One is as a directed network based on the command and control relationship, and the other is as an undirected network based on communication relationships. Compared with the two types of modelling methods, they can represent some characteristics of the WSoS somewhat better. A directed weapon network built according to command and control can more clearly describe the interaction relationship between the operational units of the two sides. However, it also emphasizes the assumption regarding the capability of the WSoS to be generated that the operational links must be closed, which is a typical threat-based planning idea that is currently inconsistent with CBP thinking. Therefore, we conduct WSoS undirected network modelling based on the structure of the weapon information network. This network modelling method can analyse the impact of interaction and cooperation between weapon nodes on the generation of the capabilities of the WSoS, which is in line with current CBP construction ideas.

2.2 WSoS Planning Under Uncertainty

Uncertainty is a focus of research on the selection of weapon projects because decision-makers do not seem to fully predict future situations before planning. According to Fang’s research [24], the field can be divided into the five levels shown in Table 1. The degree of uncertainty increases in order of level, from low to high.

Table 1 Uncertainty classification

In the first level of uncertainty, the future scene can be described by a model while the input parameters are disturbed. The sensitivity analysis can usually be used to cope with this kind of uncertainty. The secondary uncertainty measures the future scene by introducing a probability distribution. The common analysis method is probability theory. The basic idea is to assume that a certain type of element in the planning of the WSoS meets a certain probability distribution. For example, a beta distribution is used to predict the completion time of military opponent weapon development projects [14, 15]. A truncated normal distribution is used to describe changes in the efficiency of weapons in different planning periods [25].

Because actual planning lacks sufficient probability distribution information, the traditional method of addressing uncertainty through probability is not suitable for a changing external environment. Therefore, the interval analysis method tends to be adopted for the three levels of uncertainty. For example, an interval modelling method was proposed for addressing capability needs, and the evolution of the capability requirements at different stages was analysed by drawing approximate scene trees [8]. For the problem of weapon combination planning under a vague environment, fuzzy numbers have been used to represent the uncertainty of resources during the planning process [26].

Fourth-level uncertainty emphasizes richer future predictions. For this kind of uncertainty, interval number modelling is usually combined with robust optimization or multiattribute decision-making methods. The idea of using interval numbers to characterize the uncertainty of capacity demand in various scenarios in the process of weapon system planning was proposed by Xia B., who introduced the two indicators of complete robustness and overall robustness and established a robust optimization model [9]. Li R. et al. directly used the weapon capability interval number and capability demand interval number as model inputs to construct a robust optimization model and used the Bertsimas-Sim method to transform the robust optimization model into a definite form [27]. Li R. et al. also analysed the situation in which the capability provided by a weapon decreases during the system planning process and designed a robust optimization model based on a dynamic transfer equation [28]. Dou et al. used interval number theory to extend the VIKOR method to the EVIKOR method and proposed sorting weapon systems with a heavy-duty constraint linear planning method [29]. Li et al. proposed a combination of weapons in a hesitant and fuzzy environment and introduced the hesitant and fuzzy indicators and attribute values to describe the weapon system; hesitation was used to measure the uncertainty of the relevant data information of the weapon systems [30].

For the WSoS planning problem under uncertain conditions, most scholars directly establish a multiobjective optimization model or a multicriteria decision-making model in the form of interval numbers, and few scholars combine this model with equipment system network modelling. Based on this, after establishing the WSoS network model, we develop a multiobjective optimization model with risk and economy as the evaluation criteria and use interval number modelling to represent uncertainty. Finally, we construct a network-based optimization model under uncertainty. It provides new ideas and methods for WSoS planning and construction-based CBP.

3 Description of the Problem

This section describes two essential aspects of our work: quantitatively describing, abstracting and transforming the proposed problem into a multiobjective constraint optimization problem and analysing and modelling the relevant elements of the problem.

3.1 Problem Analysis

WSoS planning is a typical multistage decision problem. Combined with the idea of CBP, WSoS planning follows the pattern of “typical scene analysis—capability requirement analysis—system capability assessment—preferred weapon system”. The goal is to select the appropriate weapon from among the weapons to be developed and arrange the development time to meet the capability requirements in various typical scenarios in different future planning periods.

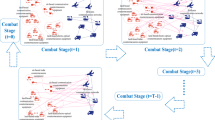
Assuming the planning period is $T$, $y \in \left[0,T\right]$ indicates year $y$ in the planning period. The planning period can be divided into $L$ stages according to the planning phases every 5 years. That is, $T=5\times L$, $l\in [1,L]$ indicates plan $L$, and ${B}_{l}$ represents the national defence budget at stage $l$. Combined with the analysis of weapon system planning issues, the key to rationally arranging the construction and planning of WSoS lies in the description and analysis of the three elements involved in the planning process: typical scenarios, capability requirements, and weapon systems. According to the characteristics and correlation of these three elements, we can extract a three-layer structure, including the scene layer, capability layer and system-of-systems layer, as shown in Fig. 1.

Fig. 1

Planning involves factors and multilayer mapping relationships

In summary, the problems studied in this paper can be transformed into a class of capability-centred, multistage, multiscenario weapon network optimization problems. As the planning stage progresses, changes will occur in the typical scenarios and the capability requirements will evolve. Decision-makers need to coordinate and cope with the uncertainties in the process of WSoS planning based on the existing weapon network and the capability of the system of systems. Under certain national defence budget conditions, decision-makers select an appropriate weapon from among the weapons to be developed and arrange the development time reasonably, and they combine the weapon with existing equipment to form a new weapon network to meet the capability requirements of different scenarios of future national defence planning as well as possible.

3.2 Analysis and Modelling of the Input Elements

Considering the uncertainty of element information, the three-layer elements involved in the problem can be modelled from the perspectives of certainty and uncertainty.

• (1) Certainty Factor

The scenario layer mainly includes typical scenarios for WSoS planning, and it summarizes the feasible state set for future national defence planning. A typical scenario is essentially an operational concept, which is the result of a demand argument and can be expressed by ${S}_{k}$. ${S}_{k}\in \{{S}_{k}|{S}_{k}\in {\varvec{S}},k\in \left[1,K\right]\}$ represents scene $k$ in the typical scene set ${\varvec{S}}$. A typical scenario has three attributes: capability requirements ${R}_{k}$, planning time ${st}_{k}$, and scenario importance ${sp}_{k}$. According to the planning time ${st}_{k}$ of a typical scenario, it can be divided into different planning stages, and the typical scenarios in different stages have a time sequence relationship with each other.

The capability layer mainly includes various capabilities related to WSoS planning. Type $j$ of capability in capability set ${\varvec{C}}$ can be represented as ${C}_{j}$, ${C}_{j}\in \{{C}_{j}|{C}_{j}\in {\varvec{C}},j\in [1,J]\}$. Capability ${C}_{j}$ is upwardly related to the capability requirements of a typical scenario ${R}_{jk}$, ${R}_{jk}\in {R}_{k}$, representing the requirement of capability $j$ in scene $k$. It also correlates in a downward direction with the capability attribute of each type of weapon, ${C}_{ij}$. ${C}_{ij}\in \{{C}_{ij}|{C}_{ij}\in {C}_{j},i\in [1,I]\}$ means that weapon ${w}_{i}$ has a capability of type $j$. Based on the idea of CBP, capability requirements and weapon capabilities can be expressed quantitatively as numbers between 0 and 1. When the value is equal to 0, the scene does not need this capability or the weapon does not have this capability. When the value is between 0 and 1, this can be considered a probability. For example, a reconnaissance and surveillance capability of 0.3 can be defined as a 30% probability of finding a target. Capability has the attribute of importance ${cp}_{j}$. However, there is no interactive relationship within the capability layer, and the capabilities are independent of each other.

The system-of-systems layer mainly includes various types of weapons in the WSoS. The collection of weapons can be represented by ${{\varvec{W}}}_{{\varvec{I}}}$, where ${w}_{i}\in \{{w}_{i}|{w}_{i}\in {{\varvec{W}}}_{{\varvec{I}}},i\in [1,I]\}$ indicates weapon $i$ in the weapon collection. According to the planned start time $y=0$, the WSoS can be divided into developed weapons and undeveloped weapons according to whether construction has been completed. The first $M$ elements in weapon set ${{\varvec{W}}}_{{\varvec{I}}}$ are developed weapons, and the set is represented by ${{\varvec{W}}}_{{\varvec{M}}}$. The last $N$ elements in ${{\varvec{W}}}_{{\varvec{I}}}$ are weapons to be developed, represented by ${{\varvec{W}}}_{{\varvec{N}}}$. Obviously, ${{\varvec{W}}}_{{\varvec{I}}}={{\varvec{W}}}_{{\varvec{M}}}\cup {{\varvec{W}}}_{{\varvec{N}}}$ and $I=M+N$. All types of weapons have four attributes: capability ${C}_{ij}$, development time ${wt}_{i}$, development cost ${wc}_{i}$ and interoperability level $IOL$. In information warfare, various types of weapons are related to each other based on information communication to form a weapon network and provide system-level capabilities through mutual cooperation [10]. The weapon network can be represented by a complex network $G$, and the specific modelling process will be described in the next section.

• (2) Uncertainty Factors

Since WSoS planning is long-term strategic planning, it usually faces uncertainty in the planning process. Uncertainty can be reflected on both the demand side and the supply side.

On the demand side, the operational styles of current and future wars are ever-changing; there are many operational elements, the battlefield environment is difficult to estimate, and WSoS planning faces multiple scenarios. At the same time, for each scenario, planning is limited by the understanding of the enemy’s operational level. For example, decision-makers cannot accurately obtain the deployment time of the enemy’s weapons, which will lead to uncertainty regarding the capability requirements in each scenario.

On the supply side, there are also uncertainties in the development and installation of weapons. This uncertainty is related to the fact that the technology, manpower and other resources required in the weapon development process cannot be obtained quickly, and uncertainty regarding the weapon itself can be subdivided into capability uncertainty, development period uncertainty and development cost uncertainty. Here, we fix the development period of weapons and discuss the uncertainty of capability and development cost under this condition. This can also reflect the uncertainty on the supply side to a certain extent, and it can be more convenient for modelling. After the development period is fixed, the uncertainty of weapon capability can be taken to mean that the capability of the weapon to be developed may change within the specified development time, and the uncertainty of development cost can be taken to mean that the possible cost of developing the weapon within the specified development time is uncertain.

In fact, regarding the uncertainty of capability requirements and the uncertainty of weapon capabilities, the uncertain elements have a large number of possible discrete or continuous values, which are difficult to enumerate. To solve this problem, an internalized form can be constructed to represent these two types of uncertain elements, represented by ${\widehat{R}}_{jk}$ and ${\widehat{C}}_{ij}$, respectively. ${\widehat{R}}_{jk}=[{\widehat{R}}_{jk}^{\mathrm{min}},{\widehat{R}}_{jk}^{\mathrm{max}}]$ and ${\widehat{C}}_{ij}=[{\widehat{C}}_{ij}^{\mathrm{min}},{\widehat{C}}_{ij}^{\mathrm{max}}]$. For the uncertainty of cost, most studies still define it as a random number that satisfies a certain distribution [31], and here it is defined as a normal distribution; that is, ${\widehat{wc}}_{n}\sim ({c}_{n},{\sigma }_{n}^{2})$.

3.3 Analysis and Modelling of Decision Variables

The WSoS development planning problem aims to select the appropriate weapons from the weapon set to be developed and reasonably arrange the planning time of the selected equipment. Therefore, the decision variables involved in the problem can be mainly divided into weapon selection variables and planning time variables.

• (1) Weapon selection variable

The weapon selection variable can be represented by ${x}_{n}$, ${x}_{n}$={0,1}. ${x}_{n}=1$ means that weapon ${w}_{n}$ is selected to be developed, and ${x}_{n}=0$ means that weapon ${w}_{n}$ is not selected to be developed.

• (2) Planning time variable

In this paper, ${t}_{n}$, ${t}_{n}\in [0,T]$, is used to represent the start time of developing equipment ${w}_{n}$, and ${t}_{n}=0$ means that weapon ${w}_{n}$ is developed in the 0th year of the planning period. At the same time, we use ${wt}_{n}$, ${wt}_{n}\in (0,T]$, to indicate the time required for the development of weapon ${w}_{n}$. When ${wt}_{n}$ = 0, it is usually considered to indicate purchasing the weapon, which can provide corresponding capabilities immediately, but weapon purchasing is not the object of this paper, so it is assumed that ${wt}_{n}>0$.

4 Model Construction

In Sect. 2, we described and analysed the problem of WSoS development planning in detail, so this section mainly constructs the solution model of the problem as follows. First, we introduce the concept of a collaborative network and analyse and evaluate the capability of the WSoS through the network. After obtaining the capabilities of the WSoS, we decompose the matching degree between the system-of-systems capabilities and the scenario capability requirements according to the two objectives, the minimum planning risk and minimum planning cost, and build a multiobjective optimization model for the development planning of WSoS.

4.1 WSoS Capability Assessment Model Based on Network Theory

• (1) Cooperative Network Modelling of a WSoS

As mentioned in Sect. 2, a WSoS in information warfare can be represented as a weapon network $G=(V,E)$. $V$ is a collection of weapon nodes; each node represents a certain weapon in the WSoS, and nodes are distinguished according to their capabilities. $E$ is a collection of relationships between nodes in the weapon network, which can be understood as collaborative relationships. ${e}_{ab}\in E$ means that there is an edge between weapon node $a$ and weapon node $b$, and $({v}_{a},{v}_{b})\in V$ means that weapon $a$ and weapon $b$ can interact and cooperate. An edge also has an interoperability level, which is mainly used to measure the amount of information exchanged. Usually, the information flow interaction between weapons is bidirectional, so the weapon network constructed in this paper is a weighted undirected network. The network structure can be stored in the adjacency matrix $A$, and the edge attributes can be stored in the interoperability level matrix $IOL$.

The WSoS planning process is dynamic, and we can regard it as a combination of different time-sliced weapon networks during the planning period. Generally, the weapon before improvement is called the basic weapon. There are two weapons development strategies: the first is to develop entirely new equipment and create new connections with basic weapons, and the other is to improve basic weapons. The basic weapon and the improved weapon have a replacement relationship, but this relationship does not affect the structure of the weapon network.

For convenience of illustration, we use ${G}_{y}$ to represent the weapon network formed in year $y$ of planning period $T$, ${G}_{y}=({V}_{y},{E}_{y})$. When $y=0$, the weapon network ${G}_{0}=({V}_{0},{E}_{0})$ is in the initial stage, as shown in Fig. 2a; at this time, the nodes in the weapon network are all developed weapons, ${V}_{0}=\{{v}_{m}|{w}_{m}\in {{\varvec{W}}}_{{\varvec{M}}}\}$. When $y=T$, it represents the weapon network after the end of the planning period, as shown in Fig. 2d. When $y={st}_{k}$, weapon network ${G}_{{st}_{k}}=({V}_{{st}_{k}},{E}_{{st}_{k}})$ is formed in the year when typical scenario $k$ applies, as Fig. 2c shows. The node set in ${V}_{{st}_{k}}$ includes the new weapon sets, improved sets and basic sets. The calculation process is shown in the following formula.

Fig. 2

Schematic diagram of weapon network evolution

$${V}_{{st}_{k}}^{n}={\{v}_{n}|0<{x}_{n}\times \left({t}_{n}+{wt}_{n}\right)\le {st}_{k},{w}_{n}\in {{\varvec{W}}}_{{\varvec{N}}}\}$$

(1)

$${V}_{{st}_{k}}^{m}=\{{v}_{m}|{v}_{m}\in {V}_{0},\eta ({v}_{m})\notin {V}_{{st}_{k}}^{m}\}$$

(2)

$${V}_{{st}_{k}}={V}_{{st}_{k}}^{m}\cup {V}_{{st}_{k}}^{n}$$

(3)

Here, set (1) represents the new weapon sets and the improved weapon sets before the planning time of scenario $k$. ${x}_{n}=\{\mathrm{0,1}\}$ indicates whether weapon ${w}_{n}$ is chosen to be developed, ${t}_{n}\in [0,T]$ is the start time of developing weapon ${w}_{n}$, and ${wt}_{n}$ is the time required to develop weapon ${w}_{n}$. Set (2) represents the weapon node set in the initial stage. Considering the two strategies of weapon development, the improved weapons should be removed from the basic weapons. $\eta$ represents the mapping relationship between the basic weapon and improved weapon; $\forall {v}_{m}\in {V}_{0}$, $\exists \eta ({v}_{m})\in {V}_{{st}_{k}}^{n}$ means that ${w}_{m}$ from the basic weapon set has been improved. Then, ${V}_{{st}_{k}}$ can be expressed as the union of the initial-stage node set and the new development weapon node set, as shown in set (3).

• (2) Capability Assessment Model of the WSoS

Based on the network modelling of the WSoS, we can analyse the capability generation mechanism of the WSoS under certainty. In the information age, weapons with the same capabilities can enhance collaboration and the corresponding capability through information sharing. For example, manned and unmanned aerial vehicles both have reconnaissance and surveillance capabilities, and the two types of weapons can share current reconnaissance and surveillance information through information communication and work together to complete tasks. The communication relationship between weapons may be direct or indirect. For example, manned and unmanned aerial vehicles can achieve interaction and cooperation by directly building a communication link, or they can cooperate by building a communication link with satellites. In this case, the interaction and cooperation between weapons with the same capability will have a positive impact on the capability of the system of systems, which is also called an emergent effect in the WSoS. Assuming that the ways in which weapons provide capabilities are independent of each other, according to the proposed formula for calculating the probability of parallel events [21], in a typical scenario $k$, the system-of-systems capabilities formed by the cooperation of weapons with the same capability $j$ can be calculated as follows in Eq. (4).

$$\begin{array}{c}{\mathbb{C}}_{jk}^{*}=1-\prod_{i\in \left\{i|{v}_{i}\in {V}_{{st}_{k}},{w}_{i}\in {{\varvec{W}}}_{{\varvec{I}}}\right\}}\left(1-{C}_{ij}\right)\end{array}$$

(4)

Equation (4) shows the emergent effect of weapon system capability in a nonlinear form. We can explain the calculation logic of the above formula through a simple example. Assuming that the weapon system includes fighter jets and UAVs with reconnaissance and surveillance capabilities, that there is a communication and cooperation relationship between them, and that the capability values are 0.6 and 0.3, respectively, the capability of the WSoS is 1 − (1–0.6) × (1–0.3), which is 0.82. It can be seen that collaboration effectively improves the capability of any single weapon.

However, the network construction of weapons will not have only a positive impact. As the complexity of the weapon network increases, it will have a negative impact on the capability of the WSoS. The complexity of the network is manifested in the scale of the number of network nodes and the scale of information exchange. With the introduction of new weapons, the number of communication links in the weapon system and the amount of information exchange may increase, which will cause the information exchange load to increase and the efficiency of information exchange to decrease, which will affect the capability of the WSoS. In this regard, Li gives a method of determining the information network structure effect [10], as shown in Eq. (5).

$$\begin{array}{c}0\le {\beta }_{{G}_{{st}_{k}}}=\frac{{\lambda }_{\mathrm{max}}\left({IOL}_{{G}_{{st}_{k}}}\right)}{{IOL}_{\mathrm{max}}\times Num\left({G}_{{st}_{k}}\right)}\times \left(1-\frac{1}{\sqrt{Num\left({G}_{{st}_{k}}\right)}}\right)\le 1\end{array}$$

(5)

Here, ${\lambda }_{\mathrm{max}}$ is the largest eigenvalue of the weapon network interoperability level matrix ${IOL}_{G}$, and ${IOL}_{\mathrm{max}}$ is the highest level on the interoperability scale. $\frac{1}{Num({G}_{{st}_{k}})}\times (1-\frac{1}{\sqrt{Num({G}_{{st}_{k}})}})$ represents the correction factor considering the size of the network. Without this parameter, the same connection density will yield the same results for small and large networks, which is obviously not practical. Therefore, the method of calculating the capability of a weapon system under complexity conditions is as shown in Eq. (6).

$$\begin{array}{c}{\mathbb{C}}_{jk}={\mathbb{C}}_{jk}^{*}\times \left(1-{\beta }_{{G}_{{st}_{k}}}\right)\end{array}$$

(6)

Considering the uncertainty of weapon capability, when the weapon capability changes from a certain value to a number of intervals, that is, ${\widehat{C}}_{ij}=[{\widehat{C}}_{ij}^{\mathrm{min}},{\widehat{C}}_{ij}^{\mathrm{max}}]$, according to the interval calculation method [32], the capability of the WSoS will change from a certain value ${\mathbb{C}}_{jk}$ to an interval number ${\widehat{\mathbb{C}}}_{jk}$. The value of ${\widehat{\mathbb{C}}}_{jk}$ satisfies Eq. (7).

$$\begin{array}{l}\left\{\begin{array}{l}{\widehat{\mathbb{C}}}_{jk}={[\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}},{\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}]\\ {\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}= \left(1-\prod_{i\in \left\{{i|v}_{i}\in {V}_{{st}_{k}},{w}_{i}\in {{\varvec{W}}}_{{\varvec{I}}}\right\}}\left(1-{\widehat{C}}_{ij}^{\mathrm{min}}\right) \right)\times (1-{\beta }_{{G}_{{st}_{k}}})\\ {\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}= \left(1-\prod_{i\in \left\{{i|v}_{i}\in {V}_{{st}_{k}},{w}_{i}\in {{\varvec{W}}}_{{\varvec{I}}}\right\}}\left(1-{\widehat{C}}_{ij}^{\mathrm{max}}\right) \right)\times (1-{\beta }_{{G}_{{st}_{k}}})\end{array}\right.\end{array}$$

(7)

4.2 Multiobjective Optimization Model for WSoS Planning

• 1) Objective function

(1) Minimize planning risk: the primary goal of WSoS planning is to meet the capability requirements of various future typical scenarios as well as possible. Considering the uncertainty of the capability requirements of the scenario and the capability of the WSoS, we can analyse the effect of the planning scheme from the perspective of planning risk. The less well the capability requirements are met, the greater the planning risk is, and the worse the WSoS planning effect is. The planning risk can be obtained by calculating the capability risk of each scenario, and the scenario capability risk can be understood as the probability that the capability requirement of a typical scenario is not met [27]. Suppose ${\widetilde{R}}_{jk}\in {\widehat{R}}_{jk}$ and ${\widetilde{\mathbb{C}}}_{jk}\in {\widehat{\mathbb{C}}}_{jk}$; then, the risk of capability $j$ in scenario $k$ can be defined as ${CR}_{jk}=P({\widetilde{\mathbb{C}}}_{jk}\le {\widetilde{R}}_{jk})$.

Since capability requirements ${\widehat{R}}_{jk}$ and WSoS capabilities ${\widehat{\mathbb{C}}}_{jk}$ are both represented by interval numbers, there are six types of relationships, as shown in Fig. 3. According to reference [33], the method of calculating scenario capability risk ${CR}_{jk}$ can be summarized as the following piecewise Eq. (8); these six piecewise functions correspond to Fig. 3a–f.

Fig. 3

Relationships of two types of interval numbers

$${CR}_{jk}=P\left({\widetilde{\mathbb{C}}}_{jk}\le {\widetilde{R}}_{jk}\right)=\left\{ \begin{array}{*{20}{l}}1, & {\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}\le {\widehat{R}}_{jk}^{min}\\ \frac{{\widehat{R}}_{jk}^{\mathrm{max}}-{\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}}{{\widehat{R}}_{jk}^{\mathrm{max}}-{\widehat{R}}_{jk}^{\mathrm{min}}}+\frac{{\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}-{\widehat{R}}_{jk}^{\mathrm{min}}}{{\widehat{R}}_{jk}^{\mathrm{max}}-{\widehat{R}}_{jk}^{\mathrm{min}}}\times \frac{{\widehat{R}}_{jk}^{\mathrm{min}}-{\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}}{{\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}-{\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}}+\frac{1}{2}\times \frac{{\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}-{\widehat{R}}_{jk}^{\mathrm{min}}}{{\widehat{R}}_{jk}^{\mathrm{max}}-{\widehat{R}}_{jk}^{\mathrm{min}}}\times \frac{{\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}-{\widehat{R}}_{jk}^{\mathrm{min}}}{{\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}-{\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}}, & {\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}\le {\widehat{R}}_{jk}^{\mathrm{min}} < {\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}\le {\widehat{R}}_{jk}^{\mathrm{max}}\\ \frac{{\widehat{R}}_{jk}^{\mathrm{max}}-{\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}}{{\widehat{R}}_{jk}^{\mathrm{max}}-{\widehat{R}}_{jk}^{\mathrm{min}}}+\frac{1}{2}\times \frac{{\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}-{\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}}{{\widehat{R}}_{jk}^{\mathrm{max}}-{\widehat{R}}_{jk}^{\mathrm{min}}}, & {\widehat{R}}_{jk}^{\mathrm{min}}< {\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}< {\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}\le {\widehat{R}}_{jk}^{max}\\ \frac{1}{2}\times \frac{{\widehat{R}}_{jk}^{\mathrm{max}}-{\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}}{{\widehat{R}}_{jk}^{\mathrm{max}}-{\widehat{R}}_{jk}^{\mathrm{min}}}\times \frac{{\widehat{R}}_{jk}^{\mathrm{max}}-{\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}}{{\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}-{\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}}, & {\widehat{R}}_{jk}^{\mathrm{min}}< {\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}\le {\widehat{R}}_{jk}^{\mathrm{max}}< {\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}\\ \frac{{\widehat{R}}_{jk}^{\mathrm{min}}-{\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}}{{\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}-{\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}}+\frac{1}{2}\times \frac{{\widehat{R}}_{jk}^{\mathrm{max}}-{\widehat{R}}_{jk}^{\mathrm{min}}}{{\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}-{\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}}, & {\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}\le {\widehat{R}}_{jk}^{\mathrm{min}}< {\widehat{\mathbb{C}}}_{jk}^{\mathrm{max}}\le {\widehat{R}}_{jk}^{\mathrm{max}}\\ 0, & {\widehat{R}}_{jk}^{\mathrm{max}}< {\widehat{\mathbb{C}}}_{jk}^{\mathrm{min}}\end{array} \right.$$

(8)

Of course, the capability requirements and capabilities of a WSoS are not always given in the form of interval numbers. For example, the capability of a weapon that has been used in the initial stage has a definite value. When the capability requirement or capability of the WSoS degenerates to a definite value, the method of calculating the scenario capability risk can be summarized as the following piecewise Eq. (9–11).

$$\begin{array}{l}P\left({\mathbb{C}}_{jk}\le {\widetilde{R}}_{jk}\right)=\left\{\begin{array}{l}0,{\mathbb{C}}_{jk}>{\widehat{R}}_{jk}^{\mathrm{max}}\\ \frac{{\widehat{R}}_{jk}^{\mathrm{max}}-{\mathbb{C}}_{jk}}{{\widehat{R}}_{jk}^{\mathrm{max}}-{\widehat{R}}_{jk}^{\mathrm{min}}},{\widehat{R}}_{jk}^{\mathrm{min}}<{\mathbb{C}}_{jk}\le {\widehat{R}}_{jk}^{\mathrm{max}}\\ 1,{\mathbb{C}}_{jk}\le {\widehat{R}}_{jk}^{\mathrm{min}}\end{array}\right. \end{array}$$

(9)

$$ P\left({\mathbb{C}}_{jk}\le {\widetilde{R}}_{jk}\right)=\left\{ \begin{array}{ll}0, &{\mathbb{C}}_{jk} >{\widehat{R}}_{jk}^{\mathrm{max}}\\ \frac{{\widehat{R}}_{jk}^{\mathrm{max}}-{\mathbb{C}}_{jk}}{{\widehat{R}}_{jk}^{\mathrm{max}}-{\widehat{R}}_{jk}^{\mathrm{min}}}, &{\widehat{R}}_{jk}^{\mathrm{min}} < {\mathbb{C}}_{jk}\le {\widehat{R}}_{jk}^{\mathrm{max}}\\ 1, & {\mathbb{C}}_{jk}\le {\widehat{R}}_{jk}^{\mathrm{min}}\end{array}\right. $$

(10)

$$\begin{array}{l}P\left({\mathbb{C}}_{jk}\le {R}_{jk}\right)=\left\{\begin{array}{cc}0,& {\mathbb{C}}_{jk}>{R}_{jk}\\ 1,& {\mathbb{C}}_{jk}\le {R}_{jk}\end{array}\right. \end{array}$$

(11)

Equation (9) represents the calculation of scenario capability risk when the system-of-systems capability degenerates to a definite value, Eq. (10) represents the calculation when the requirements of scenario capability degenerate to a definite value, and Eq. (11) represents the calculation when both the system-of-systems capability and capability requirements degenerate to definite values.

Based on the above analysis, the planning risk can be calculated as the weighted sum of scenario capability risks, as shown in Eq. (12).

$$\begin{array}{l}min{F}_{1}=\mathrm{min}\left(\sum\limits_{k=1}^{K}{sw}_{k}\sum\limits_{j=1}^{J}{cw}_{j}\times {CR}_{jk}\right) \end{array}$$

(12)

where ${sw}_{k}$ and ${cw}_{k}$ are the weights of the scene and the capability, respectively, which are obtained by normalizing the importance of scene ${sp}_{k}$ and the importance of capability ${cp}_{j}$. The relevant calculations are shown in Eqs. (13)–(14).

$$\begin{array}{l}{sw}_{k}=\frac{{sp}_{k}}{{\sum }_{k=1}^{K}{sp}_{k}} \end{array}$$

(13)

$$\begin{array}{l}{cw}_{j}=\frac{{cp}_{j}}{{\sum }_{j=1}^{J}{cp}_{j}} \end{array}$$

(14)

(2) Minimize planning cost: in considering planning risks, economics is another factor that needs to be considered. Intuitively, with the introduction of new weapons, the capability of a weapon system will increase, and the planning risk of the weapon system will decrease, but at the same time, the planning cost of the WSoS will increase. If only planning risk is taken as the goal, capacity redundancy may arise while pursuing the minimization of planning risk. Capacity redundancy can be understood as the part of the capability of the WSoS that completely exceeds the capability requirement. As shown in Fig. 3f, when the system capability completely exceeds the capability requirement, the planning risk will become zero. At this time, decision-makers need to consider the economics of the planning scheme.

By introducing the minimum planning cost as a target, which can guide the selection of a more economical plan from among planning schemes with the same planning risk, capacity redundancy in pursuing planning risk minimization can be avoided as much as possible. At the same time, analysis from the two perspectives of risk and economy can provide more diversified WSoS planning solutions. Considering that the development cost of the weapon to be developed satisfies a normal distribution, the planning cost of the WSoS can be obtained from the expected cost. Assuming that the development of each weapon is independent of the others, the calculation of the planning cost is as shown in Eq. (15).

$$\begin{array}{l}min{F}_{2}=\mathrm{min}\left(E\left(\widehat{c}\right)\right)=\mathrm{min}\left(\sum\limits_{n=1}^{N}w{c}_{n}{\times x}_{n}\right) \end{array}$$

(15)

• 2) Constraints

(1) Budget constraint: in the planning of the WSoS, the funding for national defence is not obtained at one time but in stages, generally taking 5 years as a stage. Therefore, while minimizing the planning cost is the goal, the budget at different planning stages should also be considered. Thus, the budget should be used as a constraint to make the WSoS planning plan more realistic. Considering that the development cost of a weapon satisfies a normal distribution, the budget constraint can be expressed in the form of a chance constraint, as shown in the following inequality (16).

$$\begin{array}{l}P\left(\displaystyle\sum_{n\in {N}_{l}}{\widehat{c}}_{n}\times {x}_{n}\le {B}_{l}\right)\ge {\alpha }_{l} \end{array}$$

(16)

In Formula (16), ${N}_{l}=\{n|5\times (l-1)\le {t}_{n}<5\times l,{x}_{n}=1,{w}_{n}\in {{\varvec{W}}}_{{\varvec{N}}}\}$, and ${\alpha }_{l}$ indicates the confidence level given in advance by the decision-maker and expresses the attitude of the decision-maker towards risk. A larger ${\alpha }_{l}$ means that the decision-maker wants the planning scheme to strictly meet the budget conditions of stage $l$, and the whole constraint indicates the probability of exceeding the budget of stage $l$ under the condition of uncertain development cost. Assuming that the development of each weapon is independent of the others, the abovementioned nonlinear constraints can be transformed into definite constraints by using the reconstruction method proposed [34], as shown in the following inequality (17).

$$\begin{array}{l}\sum\limits_{n\in {N}_{l}}{c}_{n}\times {x}_{n}+{\Phi }^{-1}\left({\alpha }_{l}\right)\sqrt{\sum_{n\in {N}_{l}}{\sigma }_{n}^{2}\times {x}_{n}^{2}}\le {B}_{l} \end{array}$$

(17)

(2) Connectivity constraint: the WSoS is an interconnected and interoperable whole, and any weapon independent of the WSoS cannot provide the capabilities it possesses. For example, if a weapon with reconnaissance and surveillance capabilities is independent of the WSoS and cannot transmit the obtained reconnaissance and surveillance information to other weapons, then the development of such a weapon will be meaningless. Therefore, connectivity constraints can be introduced to ensure that a connected weapon network can be formed before the planning time of each scenario. The connectivity constraints are shown in the following equation.

$$\begin{array}{l}{\lambda }_{\mathrm{fidler}}\left(L\left({G}_{{st}_{k}}\right)\right)>0\end{array}$$

(18)

In inequality (18), the left side is the second smallest eigenvalue of the Laplacian matrix used to calculate the weapon network ${G}_{{st}_{k}}$, also known as the Fiedler eigenvalue. If and only if the weapon network is a connected graph, the Fiedler eigenvalue is greater than 0; that is, there is at least one path between weapon nodes in the weapon network, and no node is independent of the network.

(3) Total period constraint: to ensure that the weapon to be developed can support the capability requirements, the weapon should be developed within the planning period. If a certain type of weapon cannot complete development, it can be regarded as a planning redundancy, and the capabilities of the weapon will not be able to support the capability requirements of any scenario. The development period constraints are shown in inequality (19), where ${t}_{n}$ is the start time of developing weapon ${w}_{n}$ and ${wt}_{n}$ is the time required to develop weapon ${w}_{n}$.

$$\begin{array}{l}\mathrm{max}\left({x}_{n}\times \left({t}_{n}+{wt}_{n}\right)\right)\le T\end{array}$$

(19)

5 Model Solution

This section uses the designed algorithm to solve the model established in Sect. 3, which includes two main steps: obtain the nondominated solutions in the Pareto front through NSGA-II-DE and use fuzzy set theory to obtain a nondominated compromise solution that the decision-makers are satisfied with.

5.1 Multiobjective Optimization Algorithm: NSGA-II-DE

In complex WSoS planning problems, the number of feasible planning schemes will increase exponentially with the increase in decision variables, so these problems are typical NP-hard problems, and it is impossible to obtain a feasible solution within a limited time using the traditional integer programming algorithm. Therefore, we can apply an intelligent optimization algorithm to such problems to obtain a satisfactory solution within a certain period of time. In Sect. 4.2, we construct a WSoS planning model based on multiobjective optimization. It can be seen from the two objective functions that planning new weapons may reduce the planning risk, but it will increase the planning cost, and there is a certain degree of mutual exclusion between the two objectives. Therefore, it is necessary to introduce a multiobjective optimization algorithm to solve the problem.

NSGA-II is a multiobjective optimization algorithm that has been widely used in recent years and can effectively retain elite solutions among offspring [35, 36]. DE is a good genetic operator that can maintain the diversity of the population [37]. Therefore, by combining the two, the advantages of both can be preserved, and a more satisfactory nondominated solution can be obtained. The detailed flow of the algorithm is shown below.

Step 1: definition of the algorithm parameters. The parameters include the number of iterations $Gen$, the size of the population $Pop$, the probability of crossing $Pc$, and the probability of mutation $Pm$.

Step 2: structure and calculation of the adaptation function and punishment function. There are two goals in setting the adaptation function: minimizing the planning risk and minimizing the planning cost. Each individual’s violation of the constraints is then calculated according to the constraint conditions, and individuals are punished.

Step 3: initialization of the population group. An initial population with a size of $Pop$ is generated according to the chromosome coding rules. As shown in Fig. 4 below, the chromosome coding form can be divided into selection coding and time coding according to the decision variables. The selection coding has a binary form, indicating whether a certain weapon is chosen. The time coding is in decimal form, indicating the time of beginning the development of the weapon.

Fig. 4

Encoding rules

Step 4: mutation and crossover. Randomly generate a subpopulation with the size $Pop$, combined with the DE/rand/1/bin operator in DE to guide the subpopulation to obtain a mutated population. Later, the initial population is mixed with the mutated population, and a binomial distribution operator is used for the crossover operation to obtain a temporary population. At this time, the whole population scale is 2Pop.

Step 5: evaluation of the temporary population. Perform nondominant sorting and crowding distance sorting for the temporary population, and obtain the top $Pop$ members of the population from the sorting results as the parent generation of the next evolution.

Step 6: evolution and iteration. Check whether the number of iterations has reached $Gen$ to determine whether the algorithm should be stopped. If so, the population of the step 5 output is the final result. If not, a new iteration will start from step 4.

5.2 Selecting the Compromise Solution: The Theory of Fuzzy Sets

The multiobjective optimization model is solved by the NSGA-II-DE and yields a set of nondominant solutions, also known as Pareto optimal solutions. To obtain the final WSoS plan, decision-makers need to concentrate on the Pareto front to select a satisfactory solution as the final result. This solution is also called a compromise solution. According to the practice of reference [38], this article adopts a weighted fuzzy membership method to select the compromise solution. The calculation steps of this method are shown below.

Step 1: calculate the maximum and minimum values of all nondominated solutions corresponding to the two objectives in the Pareto front, which are $({F}_{1}^{\mathrm{max}},{F}_{1}^{\mathrm{min}})$ and $({F}_{2}^{\mathrm{max}},{F}_{2}^{\mathrm{min}})$, respectively.

Step 2: using the fuzzy membership function, calculate the fuzzy membership values ${u}_{p1}$ and ${u}_{p2}$ corresponding to the two objective functions of each nondominated solution in the Pareto solution set. $({F}_{p1},{F}_{p2})$ represents the value of the planning risk and planning cost objective function of the $p$th nondominated solution among the Pareto solutions.

$$\begin{array}{l}{u}_{p1}=\frac{{F}_{1}^{\mathrm{max}}-{F}_{p1}}{{F}_{1}^{\mathrm{max}}-{F}_{1}^{\mathrm{min}}} \end{array}$$

(20)

$$\begin{array}{l}{u}_{p2}=\frac{{F}_{2}^{\mathrm{max}}-{F}_{p2}}{{F}_{2}^{\mathrm{max}}-{F}_{2}^{\mathrm{min}}} \end{array}$$

(21)

Step 3: according to the decision-makers’ preferences for planning risks and planning costs, obtain the corresponding weights. After the fuzzy membership degrees and weights of the two objectives are determined, the weighted sum of the fuzzy membership degrees ${u}_{p}$ can be calculated as a comprehensive evaluation index for each nondominated solution, as shown in Eq. (22). Here, ${fw}_{1}$ and ${fw}_{2}$ represent the preference weights of planning risk and planning cost, respectively.

$$\begin{array}{l}{u}_{p}={fw}_{1}\times \frac{{u}_{p1}}{{\sum }_{p=1}^{Pop}{u}_{p1}}+{fw}_{2}\times \frac{{u}_{p2}}{{\sum }_{p=1}^{Pop}{u}_{p2}} \end{array}$$

(22)

Step 4: sort the comprehensive evaluation indices and select a nondominated solution corresponding to the maximum value of ${u}_{p}$. This is also the compromise solution, which can be used as the planning scheme of the WSoS.

The whole process of model solution in this section is shown in Fig. 5.

Fig. 5

Process of model solution

6 Case Study

To verify the feasibility and rationality of the method proposed in this paper, in this section, we illustrate the proposed method with an example of unmanned WSoS planning. Considering that data related to weapons are difficult to obtain, the data used in this paper are all simulated and generated based on the U.S. Army’s unmanned system to simulate the characteristics of actual data as well as possible.

6.1 Case Description

With the further development of science and technology, the concept of unmanned operation based on informatization and intelligence has become mainstream in the world today, and unmanned weapons will be the main force in future warfare. Therefore, the planning and development of unmanned weapons will become an important direction for the construction of WSoS in all countries. Assume that a defence acquisition department is developing a plan for the development of unmanned WSoS between FY2020 and FY2035. After experts analyse the relevant requirements of the development plan of the unmanned WSoS, the defence acquisition department can summarize six typical scenarios and five key capabilities for future unmanned WSoS planning, as shown in Table 2 and Table 3. From Table 2, we can see that the application scenarios of the unmanned WSoS are gradually evolving from partial intelligence to global multidimensional intelligence, and the demand for various capabilities is increasing; of course, the uncertainty is also increasing. Table 4 summarizes the attribute information of related weapons in unmanned WSoS. The unmanned WSoS includes ten types of weapons that were developed in the initial stage and twenty types of weapons to be developed. Among the weapons to be developed, the last five types, weapons w25 to w29, are the improved weapons w0 to w4, respectively. The unmanned weapon network structure generated by the IOL matrix is shown in Fig. 6. The communication relationships and interoperability levels of the weapons are stored on the edges. In addition, assuming that every 5 years is a planning stage, the budgets of the three planning stages are 1000, 1200, and 1400 in sequence, and the confidence level ${\alpha }_{l}$ of each stage in the budget constraint is uniformly 0.9.

Table 2 Scene data input

Table 3 Capability priority

Table 4 Weapon capability value

Fig. 6

Unmanned weapon network structure

6.2 Analysis of Results

• 1) Multiobjective Optimization Results

We input the above example information into the multiobjective optimization model proposed in this paper and set the iteration number $Gen$ to 100, the population size $Pop$ to 400, the crossover probability $Pc$ to 0.9, and the mutation probability $Pm$ to 0.3.

First, we repeated thirty experiments on NSGA-II, NSGA-II-DE and NSGA-III to verify the effectiveness of the DE operator. The Pareto front of the results is shown in Fig. 7. It can be seen from the figure that the DE operator can find more high-risk and low-cost solutions, and the other solutions also perform well.

Fig. 7

Pareto fronts of NSGA-II, NSGA-II-DE and NSGA-III

Further analysis is shown in Table 5. Among the methods, NSGA-II-DE has the largest mean and the smallest variance and max–min of Hv, which shows that the convergence and diversity of the algorithm are better and it performs stably. In addition, we found that the mean spacing in NSGA-II is smaller, which shows that the solution set found by the algorithm is uniform, although the uniformity is not very stable. NSGA-III is not as good as the other algorithms in all indicators and the Pareto front, which may be because the algorithm is more suitable for high-dimensional problems. Overall, NSGA-II-DE has better global search ability and more stable performance on the problems proposed in this paper, so we choose this algorithm for solving.

Table 5 Comparison of the indices of NSGA-II, NSGA-II-DE and NSGA-III

Thus, the results of Pareto front random selection through NSGA-II-DE are shown in Fig. 8. It can be seen intuitively that when no equipment is developed, the risk in the planning period will reach 0.81. With the development of new equipment, the planning cost increases, and the planning risk decreases. After obtaining the Pareto front, we use a fuzzy set to choose a compromise solution. The weights of the planning risk and planning cost in the compromise solution selection method are 0.8 and 0.2, respectively.

• 2) Analysis of Compromise Solutions

Fig. 8

Pareto front and compromise solutions

Development planning for the unmanned WSoS represented by the compromise solution is shown in Fig. 9. Accordingly, we finally selected ten types of weapons to be developed from the set of 20 and drew up a roadmap for the development of unmanned weapons at each stage. In the first 5-year plan, unmanned weapons mainly play the role of reconnaissance in the WSoS. Therefore, when planning weapons, we chose weapons such as USV-5, UAV-3A and UAV-5A, which can quickly and stably provide reconnaissance capability. We also selected UAV-7 and UUV-5 to provide certain defence and logistical support capabilities and ensure the completeness of the capability spectrum of the WSoS. From FY2025 to FY2030, the scenarios faced by unmanned weapons will begin to evolve in the direction of air operations, and the demand for offensive and defensive capabilities will increase. To this end, we preplanned USV-4 with a long development period in the FY2020–FY2025 and developed UAV-6 in the FY2025–FY2030, both of which can provide higher firepower strike capability to meet the corresponding capability requirements. In addition to the above two types of weapons, at this stage, we plan to develop two other types of weapons, UAV-10 and UAV-4A, which will further improve the reconnaissance and surveillance capabilities, command and control capabilities, and fire strike capabilities of the WSoS, as well as UUV-4, planned in the FY2030–FY2035 to address more complex scenarios.

Fig. 9

Planning scheme of the unmanned WSoS

We can further analyse the rationality of the compromise solution selection method by changing the weight of the compromise solutions. Figure 10 below shows the scenario capability risk heatmap of three kinds of compromise solutions: that considering only the planning cost target (as shown in Fig. 10a), that considering only the planning risk target (as shown in Fig. 10c) and the compromise solution selected in Sect. 6.1 (as shown in Fig. 10b). When only planning costs are considered, that is, no new weapon is planned, only the WSoS in the initial stage is used, which can basically deal with typical short-term scenarios. When faced with the scenarios of the second stage and the third stage, there will be a greater risk regarding scenario capabilities. Considering only planning risks, it can be seen that all capability requirements are met well, and the capability risks of each scenario are significantly reduced. Comparing Fig. 10a and c, it can be seen that the compromise solution selected in Sect. 6.1 can also effectively meet all capability requirements and basically control the capability risk of each scenario to below 0.5. However, there is also a situation where the S5–C5 scene risk is high, but it is acceptable because the planning scheme represented by Fig. 10b saves nearly 600 units of funds compared with that in Fig. 10c, and this only increases the overall planning risk by 0.026 while ensuring that no scenario capability risk exceeds the warning line of 0.8.

Fig. 10

Compromise solution comparison

In addition to the abovementioned analysis from the perspective of WSoS capability, we can also carry out a corresponding analysis from the perspective of the structure of the WSoS. In evaluating weapon architecture, robustness is usually used as the evaluation criterion. In this regard, we can introduce the natural connectivity [39] to analyse the structural robustness of the WSoS represented by the compromise solution. As shown in Fig. 11, when the abilities of the equipment nodes are not different and the interoperability matrix is input, the structural robustness of the WSoS gradually rises during the planning period, indicating that the construction of the WSoS is in good condition.

Fig. 11

Robust evolution of the unmanned WSoS

We further distinguish between different nodes based on weapon capabilities and analyse the robustness of the subnetwork formed by unmanned weapons with the same capability. The result is shown in Fig. 12. In terms of the overall trend, with the development of new weapons, the robustness of different subnetworks gradually increases, especially for ${C}_{3}$, ${C}_{4}$ and ${C}_{5}$, and breakthroughs in similar weapons, from zero-cooperation to multicooperation weapons, are achieved. The subnetwork robustness is greatly improved. However, the development of new weapons may also lead to a decrease in the robustness of the subnetwork. As shown in Fig. 12, the subnetwork composed of reconnaissance and surveillance weapons has a downwards trend in the third 5-year plan, which is due to the introduction of UAV-10 and UAV-4A in the third planning period. They only have a single communication and coordination relationship with the installed weapons for reconnaissance and surveillance, which reduces the proportion of closed paths in the subnetwork, resulting in a decrease in the robustness of the subnetwork.

• 3) Sensitivity Analysis

Fig. 12

Robust evolution of the sub-unmanned weapon system

To further analyse the impact of uncertainty on the planning scheme, this section introduces sensitivity analysis to analyse the impact of changes in scenario capability requirements, the capability level of the WSoS, and development costs on the Pareto front. The results are shown in Fig. 13. In Fig. 13a, the Pareto front moves outward with the increase in the maximum number of scenario capability demand intervals, which is consistent with the actual situation. When the uncertainty of scenario capability requirements increases and the maximum value of the interval increases, decision-makers will increase investment in WSoS planning to meet the scenario capability requirements as well as possible. Similar results can be obtained by adjusting the maximum value of the interval number of the capability level of the WSoS, as shown in Fig. 13b. However, comparing the moving distance of the Pareto front in Fig. 13a, it can be seen that the impact of changes in the capability level of the WSoS on the Pareto front is less than that of the change in scene capability requirements. This is due to the influence of the weapon combination effect. By choosing different weapon components and equipment combinations, the negative impact caused by the value change of the capability level interval of the WSoS is alleviated. In addition, as shown in Fig. 13c, adjusting the variance of the development costs will only affect the upper half of the Pareto front. For the second half of the Pareto front, fewer weapons are selected, and they generally do not exceed the stage budget constraints, so the second half of the Pareto front tends to overlap. However, since the method used in this paper is not an exact solution method, it is impossible to determine the mutation point, and only the approximate change trend of the frontier can be analysed.

Fig. 13

Sensitivity analysis

7 Conclusion

In this paper, under the guidance of capability-based planning, we address the generation and trade-off problem of WSoS development and planning under the double uncertainty of the scene and the key weapon system attributes using a multiobjective network-based optimization method combined with fuzzy set theory as a hybrid solution approach. Network-based optimization is the integration of a complex network and the NSGA-II-DE model. We apply the proposed problem and model to a simulation scenario based on the U.S. unmanned system integrated roadmap. This results in a valuable paradigm for relevant decision-makers in the field of national defence to determine weapon development and planning under various conditions.

Of course, the method proposed in this paper still has certain limitations mainly in the following four respects:

In this paper, network modelling of the weapon system is carried out based on the weighted undirected information network, which does not distinguish differences in information flow between various types of weapons. In actual weapon system network analysis, the information flow between different types of weapon nodes has different characteristics, and the weapon network presents typical heterogeneity.

Second, the diversity of capability aggregation methods should be considered. To highlight the emergence effect of the WSoS, this paper presents a capability aggregation method based on the concept of interaction and collaboration. For different capabilities, the aggregation method is not unique, and capabilities can be aggregated in a linear or nonlinear manner.

Third, there is the initial planning and replanning problem. As the planning period evolves, uncertain information will become certain information. At the same time, new planning scenarios may emerge. Under such conditions, the effect of the preplanned scheme may become worse, and the initial plan may need to be adjusted to a certain extent according to the updated information.

Finally, regarding solving the model, NSGA-II has too many parameters, and any parameter change may lead to changes in the results. In addition, when faced with large-scale problems, the calculation may take a long time. For fuzzy set theory, the setting of expert preferences in this paper is subjective.

Thus, there are still many possible extensions for further research:

• Heterogeneous networks can be used to evaluate the capability of WSoS

• Using a variety of capability aggregation strategies for different weapon systems.

• Replanning problem under the initial condition change.

• Using reinforcement learning to solve the WSoS development planning problem.

• Pruning and adaptive parameter adjustment to deal with more large-scale problems.

• Incorporating related methods in the field of group decision-making to reduce the subjectivity of weight setting.