1 Introduction

As data accumulation and storage become easier and more processing methods are developed, studies related to deep learning that require a significant amount of computational power are being actively conducted. Deep learning models are used in various fields, such as for visual processing technology that generates useful information by analyzing images, natural language processing technology that understands and analyzes human language, and speech processing technology that synthesizes or converts human speech. Deep learning outperforms many existing techniques and continues to be developed. The superior performance of deep-learning models is possible because data-processing speeds driven by GPUs have advanced rapidly. However, achieving high-quality performance of deep learning leads to an inherent problem where the number of weights of the model (i.e., the model size) increases. Because of this problem, the required memory increases with the model size, and the training time becomes longer. In addition, it may be difficult to deploy and apply a trained model on a real-time basis because the speed deteriorates as the amount of calculations increase. For example, the YOLOv4 model, which is known to be the fastest among object-detection techniques, achieved about 65 FPS (frame per second) in MS COCO data; however, this was only possible when using an expensive GPU (Tesla V100).

Many approaches have been proposed to select an optimal or sub-optimal ensemble of traditional ML classifiers [1,2,3,4]. Recently, due to the inherent model-size issues in deep learning, network compression techniques have emerged as a new and challenging area to alleviate the problem of rapidly increasing memory and computational requirements. In particular, deploying deep neural networks (DNNs) to devices requiring real-time processing is a very promising research subject. Model compression aims to save memory, reduce the storage size of the model, and reduce computational requirements while taking full advantage of pretrained models. In the past few years, various model compression techniques have been in development, taking into account the tradeoff between the degree of compression and the accuracy.

According to [5], research into model compression in DNNs can be classified into four major categories: compact-model methods, tensor decomposition, data quantization, and network sparsification. A compact-model technique aims to create a smaller model itself that achieves acceptable performance among several candidates. Different from compact-model methods, the three other categories compress a DNN model by modifying the existing model in training sessions rather than creating a new model. Tensor decomposition decomposes an existing matrix (or tensor in general) into a matrix with smaller dimensionality. Data quantization is a method of compressing a DNN model by reducing the bit-width of data. Lastly, network sparsification simplifies the computational graph used for training a DNN model. Each of these four categories can be combined for better performance. Sharing a similar spirit to accomplish DNN model compression, each category has different characteristics in terms of the accuracy preservation degree, compression degree, structural information, and utilization method.

In particular, weight pruning in network sparsification aims to obtain sparse weights by removing edges from a deep-learning network graph. A prior work [6] solves a non-convex minimization problem using the alternating direction method of multipliers (ADMM) to maintain performance while sparsing weights based on existing CNN models, effectively pruning the weight of the model. This method has some advantages over other methods; for example, it has a higher compression ratio and can quickly reach a convergence rate by setting removal ratios. However, since model compression is generally used for large models, the method is practically limited in that it has to set removal ratios for each layer to [6] perform layer-wise pruning. For example, YOLOv4 has about 100 convolution layers, and it takes a substantial amount of time to experiment with the removal ratio of each layer. Obviously, the situation worsens for larger models because various hyperparameters (optimizer, learning rate, epoch, etc.) are used to find the optimal model and several tuning hyperparameters are used to prune weights by ADMM.

Our research aims to solve the above mentioned problems. Specifically, our approach formulates an optimization problem by applying ADMM to the entire layer instead of using layer-by-layer pruning. When structurally pruning a large network model with layer-by-layer and filter-by-filter pruning ratios, for example, it is difficult to find optimal parameters through a relatively small number of experiments. In fact, this issue often becomes a reality because a great number of experiments need to be conducted to find appropriate removal ratios when applying this technique to a large-size, real-life DNN model. Our method is able to easily grasp trends in the pruning degrees for the layers in a DNN model (e.g., different pruning ratios for the layers close to the input, those close to the output, and those for the intermediate layers). As a result, the application of our method can provide a base policy for pruning ratios in the layers of a DNN model. According to the findings in [6], the layers in charge of feature extraction, which are usually located near the input in tasks dealing with images, must be pruned at a small removal ratio. Our method prunes a DNN model without structural removal ratios, and our experiments show that it effectively prunes a deep layered model with a global removal ratio.

The structure of this paper is as follows. In Sect. 2, we briefly provide related studies on weight pruning and preliminaries of ADMM. Section 3 contains a detailed description of our proposed model. Section 4 compares the proposed model with a few selected pruning models through experiments, showing that the proposed model has a higher compression ratio. This section also shows the proposed weight pruning technique applied to YOLOv4, demonstrating the model’s effectiveness for a large and practical model. Section 5 concludes the paper by suggesting future research directions.

2 Background

2.1 Related Works

Among the categories of neural network model compression, network sparsification reduces the number of computations required and the size of the model by pruning unnecessary information. Pruning can be divided into weight pruning and neuron pruning. Weight pruning is a method of reducing the number of edges in a computational graph (to prune relatively insignificant or redundant weights), and neuron pruning is a method of reducing the number of nodes (to prune unnecessary nodes). In addition, pruning methods also can be divided in various ways according to the sparse structure: element-wise, vector-wise, and block-wise [7]. An element-wise method, also called unstructured pruning, evaluates the contribution of each weight element to the entire network. Removing insignificant connections without assumptions on the network structures, this method achieves gains in both the model flexibility and the predictive power. On the other hand, vector-wise and block-wise methods reveal compact network structures effectively by eliminating parameter groups instead of individual weights. Vector-wise methods [8, 9] estimate the importance of column vectors in the weight matrix and then prune a fixed set of groups by their priority. Similarly, block-wise methods [10, 11] divide the weight matrix into subblocks and consider each of the subblocks as a basic pruning unit. Unfortunately, these structured sparsity methods often fail to escalate the model accuracy due to the excessive loss of information. Our proposed model corresponds to ADMM-based weight pruning with an element-wise sparse method.

Most of the element-wise pruning methods in network sparsification are performed based on heuristic search. A heuristic-based method does not guarantee that it can effectively maintain the performance, so large performance decreases may occur. Therefore, in recent years, studies that perform pruning through optimization rather than heuristic methods have been preferred. Optimization-based methods can find less important or redundant information more effectively than heuristic-based methods, and they can also obtain higher performance. The proposed method adopts an optimization-based method to perform pruning while maintaining the existing performance.

Indeed, weight pruning was inspired by [12] and has been studied extensively. This work uses a method called optimal brain damage (OBD), which reduces the size of the model by removing information with small saliency of the second derivative of the objective function related to the weight. The optimal brain surgeon (OBS) method [13] incorporated weight pruning, which was a new technology that complemented the disadvantages of [12]. Since these two studies, weight pruning using various other methods has also been proposed. The study in [14] prunes the weights through the sensitivity of each layer based on the genetic algorithm, and then performs fine tuning on the pruned model based on the knowledge distillation framework. Another study [15] attempts effective weight pruning by solving the L0-norm constrained optimization problem through relaxant probabilistic projection (RPP) and L0-norm constrained gradient descent (LGD).

The algorithm proposed in this paper performs weight pruning based on optimization in an element-wise sparse structure that eliminates structural settings. Accordingly, we compare our method with other weight pruning methods performed on an element-wise structure in this experiment. Deep compression [16] attempts model compression using three stage pipelines consisting of pruning, trained quantization, and Huffman coding. In the weight pruning step, small weights are heuristically pruned and retrained, and model capacity is reduced by 9 to 13 times. Netpruning [17] eliminates redundant connections through three steps. The first step is to train the importance of connections. The second step removes unnecessary connections, and the third step finally retrains the network. Synthesizing DNN in the seed architecture, NeST [18] removes connections that are considered unnecessary through magnitude values to avoid duplication. To verify the effectiveness of the proposed global pruning, we further compare it with other structured pruning methods. Filter pruning proposed by Li et al. [19] removed filters with low weight magnitudes to reduce the redundancy in CNNs. NISP [20] measured the importance of filters based on their corresponding reconstruction errors in the next layer. HRank [21] mathematically proved that filters with lower ranks are less important to accuracy. CNN-FCF [22] presented an effective CNN compression approach which performs filter selection and filter learning jointly in a unified optimization scheme. DCP [23] proposed an iterative greedy algorithm to solve the channel selection problem considering both reconstruction error and discriminative power.

ADMM [24], an effective method for solving optimization problems, is widely used because of its parallel computing abilities. ADMM, which shows good performance, is often adopted for composite optimization problems, while gradient descent methods are mainly used for simple optimization problems. Noticeably, the optimization problem of the weight pruning method used in this study cannot be solved by gradient descent because differentiation is impossible and non-convex functions are included. Therefore, when using ADMM, we divided the original problem into two sub-optimization problems: one can be solved with gradient descent, and the other can be solved analytically. The study in [6] performs ADMM by constructing an optimization problem for each layer in weight pruning. Specifically, this method adds a cardinality function to the constraint of the optimization problem, and then performs pruning by setting a removal ratio for each layer. StructADMM [25] prunes weights for various structure types, such as filter-wise, shape-wise, and channel-wise sparsity, and similarly constructs an optimization problem and solves it through ADMM. We configure our method similarly to other ADMM-based methods. However, when comparing it with other methods while adopting a global removal ratio, we achieve effective sparsity without loss of performance in a short time.

2.2 Preliminary: ADMM

ADMM is a popular technique used for solving convex optimization problems in machine learning and deep leaning, making possible a large-scale optimization [26]. Recent works also demonstrate that under certain conditions, the ADMM is guaranteed to converge for non-convex problems [27]. Specifically, the ADMM can separate the variables and decompose the problem into two subproblems. We notice that the loss function associated with a constraint in this study includes a non-convex cardinality function to induce the sparsity of the weights.

Basically, the loss function of DNN consists of a basic loss \(f_0(x)\) and a regularizer h(x). ADMM separates the variable, x, in problem (1) and transforms it into problem (2). After that, we induce the augmented Lagrangian in (3):

$$\begin{aligned}{} & \quad \min _{x} f_0(x)+h(x), \end{aligned}$$
(1)
$$\begin{aligned}{} & \quad \min _{x,z} \quad f_0(x)+h(x) \quad \text {s.t.} \quad x-z=0, \end{aligned}$$
(2)
$$\begin{aligned}{} L_\rho (x,z,\nu ) & =f_0(x)+h(z)+\frac{\rho }{2}\Vert x-z\Vert ^2_2+\nu ^T(x-z). \end{aligned}$$
(3)

In (3), we update the primal variables x and z and the Lagrangian multiplier \(\nu\) while performing ADMM iterations, as shown in (4), (5), and (6):

$$\begin{aligned} x^{(k+1)}& = \underset{x}{\arg \min } \, L_\rho (x,z^{(k)},\nu ^{(k)}), \end{aligned}$$
(4)
$$\begin{aligned} z^{(k+1)}& = \underset{z}{\arg \min } \, L_\rho (x^{(k+1)},z,\nu ^{(k)}), \end{aligned}$$
(5)
$$\begin{aligned} \nu ^{(k+1)}& = \nu ^{(k)}+\rho (x^{(k+1)}-z^{(k+1)}). \end{aligned}$$
(6)

If \(\nu\) is transformed into \(\mu =\frac{1}{\rho }\nu\), \(\frac{\rho }{2}\Vert x-z\Vert ^2_2+\nu ^T(x-z)\) can be transformed into \(\frac{\rho }{2}\Vert x-z+\mu \Vert ^2_2-\frac{\rho }{2}\Vert \mu \Vert ^2_2\). As a result, (4), (5), and (6) can be changed to (7), (8), and (9):

$$\begin{aligned} x^{(k+1)}& = \underset{x}{\arg \min } \, f_0(x)+\frac{\rho }{2}\Vert x-z^{(k)}+\mu ^{(k)}\Vert ^2_2, \end{aligned}$$
(7)
$$\begin{aligned} z^{(k+1)}& = \underset{z}{\arg \min } \, h(z)+\frac{\rho }{2}\Vert x^{(k+1)}-z+\mu ^{(k)}\Vert ^2_2, \end{aligned}$$
(8)
$$\begin{aligned} \mu ^{(k+1)}& = \mu ^{(k)}+x^{(k+1)}-z^{(k+1)}. \end{aligned}$$
(9)

Finally, the optimal x can be obtained by sequentially solving the Eqs. (7), (8), and (9).

3 Global Weight Pruning

To solve the shortcomings of the technique described in [6], the proposed algorithm in this paper performs weight pruning with a global removal ratio, denoted by global weight pruning, rather than layer-wise removal ratios. Although it prunes a network without structural information, it runs sufficiently fast, even when applied to a large model. In addition, layers closer to the network input need to be pruned less than other layers to maintain input diversity and maintain performance. Our experiments show that the proposed model can automatically prune the first layer less.

Fig. 1
figure 1

Steps of the proposed method

Full size image

3.1 Steps of the Proposed Method

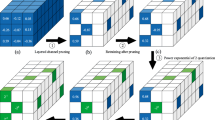
The proposed method proceeds in four steps, as shown in Fig. 1. First, we train a DNN model to find the weight that increases the model accuracy, similar to the training of a general deep-learning model. In the ADMM step, we decompose the global weight pruning problem into two subproblems and solve them iteratively, which is the essence of the proposed method. The resulting solutions force the value of unnecessary weights to converge towards zero. In the next pruning step, we keep the weights with the large magnitudes and set the rest to zero. Finally, we fine-tune the remaining non-zero weights to recover the inference accuracy.

3.2 Formulation of the Proposed Model

In this section, we describe the proposed model in detail mathematically. The first step involves a general DNN training step, and we assume that weights, \(\boldsymbol {W}\), of the pretrained model exist. The pretrained model possibly includes all machine-learning tasks through (original) loss functions, such as classification, regression, object detection, and segmentation.

For the second ADMM step, we first set the original loss function with an additional regularization term and follow the sequence described in Sect. 2.2:

$$\begin{aligned} Loss(\boldsymbol {W})=origin\_loss+\lambda \sum _{i=1}^{l}\Vert W_i\Vert ^2_2, \end{aligned}$$
(10)

where \(\boldsymbol {W}=\{W_1,\ldots ,W_l\}\) is the set of vectorized multi-dimensional tensor weights for layer i and \(W_i\) corresponds to the vector \(W_i \in {\mathbb {R}}^{d_i}\) of the \(d_i \in {\mathbb {R}}\) dimension. The vectorization of tensor weights can be a concatenation of the row vectors in the weight matrix between two layers, and the total number of layers is l. The first term can be thought of as the cross entropy loss in the case of classification, the mean-squared error in the case of regression, and some specific loss function adopted by each algorithm. For example, the loss function of the YOLOv4 object-detection model is a combination of the coordinates of a bounding box, the confidence of whether an object is included or not, and the class information of an object. The second term pertains to regularization with the Frobenius norm by default. It is easily differentiable and represents the squared energy.

To perform weight pruning, we introduce the cardinality function as a constraint in Eq. (10). Here, cardinality means the number of non-zero elements. To control the number of pruned weights in the network, we constrain the number of non-zero elements in the entire network to be less than a global parameter, n. The formulation is as follows:

$$\begin{aligned} \begin{aligned} \min _{\boldsymbol {W}} \quad&Loss(\boldsymbol {W})\\ \text {s.t.} \quad&cardinality(\boldsymbol {W})<\sum _{i}^{l}n_i=n,\\ \end{aligned} \end{aligned}$$
(11)

where the number of elements that have not been removed for all layers is n. As a tuning parameter, n is specified in advance by the user; for small n, the network will be highly sparse. One needs to set n carefully to avoid either too sparse or too dense networks in the results. Inherently, the number of elements that have not been removed for layer i is \(n_i\), which automatically emerges during pruning. Equation (10) can be easily solved with gradient descent, but the non-convex cardinality function in Eq. (11) means the gradient descent technique cannot guarantee the optimal solution. Thus, we modify the equation to use ADMM, which can be applied to non-convex optimization problems as follows:

$$\begin{aligned} \begin{aligned} \min _{\boldsymbol {W}} \quad&Loss(\boldsymbol {W})+h(\boldsymbol {W}),\\ \end{aligned} \end{aligned}$$
(12)

where \(h(\boldsymbol {W})\) is an indicator function for the cardinality constraint as follows:

$$\begin{aligned} h(\boldsymbol {W}) = {\left\{ \begin{array}{ll} 0, &{} cardinality(\boldsymbol {W})<n\\ \infty , &{} cardinality(\boldsymbol {W})\ge n. \end{array}\right. } \end{aligned}$$
(13)

We separate the variable from Eq. (12) and modify it as shown in Eq. (14):

$$\begin{aligned} \begin{aligned} \min _{\boldsymbol {W}} \quad&Loss(\boldsymbol {W})+h(\boldsymbol {Z})\\ \text {s.t.} \quad&\boldsymbol {W}=\boldsymbol {Z.}\\ \end{aligned} \end{aligned}$$
(14)

Next, the augmented Lagrangian of Eq. (14) is written as follows:

$$\begin{aligned} L_\rho (\boldsymbol {W},\boldsymbol {Z})& = Loss(\boldsymbol {W})+h(\boldsymbol {Z})\nonumber \\{} & +\frac{\rho }{2}\Vert \boldsymbol {W}-\boldsymbol {Z}+\boldsymbol {\mu }\Vert ^2_F-\frac{\rho }{2}\Vert \boldsymbol {\mu }\Vert ^2_F, \end{aligned}$$
(15)

where \(\rho\) is a penalty parameter indicating the step size. The scaled Lagrangian \(\boldsymbol {\mu }=\frac{\boldsymbol {\nu }}{\rho }\) is a variable expressed to simplify the equation with the original Lagrangian multiplier \(\boldsymbol {\nu }\). Finally, the ADMM equation is rewritten and \(\boldsymbol {W}\), \(\boldsymbol {Z}\), and \(\boldsymbol {\mu }\) are updated for iteration k:

$$\begin{aligned} \boldsymbol {W}^{(k+1)}& = \underset{\boldsymbol {W}}{\arg \min } \, Loss(\boldsymbol {W})+\frac{\rho }{2}\Vert \boldsymbol {W}-\boldsymbol {Z}^{(k)}+\boldsymbol {\mu }^{(k)}\Vert ^2_F, \end{aligned}$$
(16)
$$\begin{aligned} \boldsymbol {Z}^{(k+1)}& = \underset{\boldsymbol {Z}}{\arg \min } \, h(\boldsymbol {Z})+\frac{\rho }{2}\Vert \boldsymbol {W}^{(k+1)}-\boldsymbol {Z}+\boldsymbol {\mu }^{(k)}\Vert ^2_F, \end{aligned}$$
(17)
$$\begin{aligned} \boldsymbol {\mu }^{(k+1)}& = \boldsymbol {\mu }^{(k)}+\boldsymbol {W}^{(k+1)}-\boldsymbol {Z}^{(k+1)}. \end{aligned}$$
(18)

In the above equations, we obtain \(\boldsymbol {W}\) through Eq. (16) and then find \(\boldsymbol {Z}\) through Eq. (17). After that, \(\boldsymbol {\mu }\) can be obtained simply by gradient ascent through Eq. (18).

The first term of Eq. (16) uses the loss function, which can be differentiated from the pretrained model. The second term can also be differentiated. In general, it can be solved easily by gradient descent as in Eq. (19):

$$\begin{aligned} W_i^{(k+1)}= W_i^{(k)}-\alpha (\frac{\partial Loss(\boldsymbol {W}^{(k)})}{\partial W_i^{(k)}}+\rho (W_i^{(k)}-Z_i^{(k)}+\mu _i^{(k)})). \end{aligned}$$
(19)

Instead of inner iterations generated by gradient descent, depending on the form of \(Loss(\cdot )\), one can obtain a closed form solution for updating \(W_i^{(k+1)}\). Equation (17) cannot be solved through gradient descent, so we solve it using projection, similar to the approach used in [6]:

$$\begin{aligned} \begin{aligned} \boldsymbol {Z}^{(k+1)}&= \underset{\boldsymbol {Z}}{\arg \min } \, h(\boldsymbol {Z})+\sum _{i=1}^{l} \frac{\rho }{2}\Vert W_i^{(k+1)}-Z_i+\mu _i^{(k)}\Vert ^2_2 \\&= \underset{\boldsymbol {Z} \in \boldsymbol {C}}{\arg \min } \, \sum _{i=1}^{l} \frac{\rho }{2}\Vert W_i^{(k+1)}-Z_i+\mu _i^{(k)}\Vert ^2_2, \\&= Proj_{\boldsymbol {C}}(\boldsymbol {W}^{(k+1)}+\boldsymbol {\mu }^{(k)}) \end{aligned} \end{aligned}$$
(20)

where \(\boldsymbol {C}=\{ \boldsymbol {Z} \mid cardinality(\boldsymbol {Z}) < n \}\). Notice that \(\boldsymbol {C}\) is non-convex, and the projection operator \(Proj_{\boldsymbol {C}}(\cdot )\) is not unique. To make the number of non-zero elements in \(\boldsymbol {W}^{(k+1)}+\boldsymbol {\mu }^{(k)}\) less than the number specified by the user (n), we shrink the elements in \(\boldsymbol {W}^{(k+1)}+\boldsymbol {\mu }^{(k)}\) zero except for the first \(n-1\) elements in descending order by absolute value. In addition, we use the initial value \(\boldsymbol {W}^{(0)}\) as the trained weight, the initial value \(\boldsymbol {Z}^{(0)}\) as \(Proj_{\boldsymbol {C}}(\boldsymbol {W}^{(0)})\), and \(\boldsymbol {\mu }^{(0)}\) as a matrix with all zero elements. Being a good optimization technique in many applications, ADMM might undergo a great number of iterations to converge to a final solution when handling non-convex problems. To alleviate the computational burden, we mask the zero weights, and then retrain the DNN with the remaining non-zero weights while freezing the masked ones to 0. Noticeably, the retraining step allows fast convergence to a desired solution from the good initial point with only a few parameters to be fine-tuned. In this way, we can restore the accuracy of the pruned network such that it may achieve performance better than or at least comparable with the pretrained model.

The proposed global weight pruning automatically seeks a sparse set of weights without specifying layer-by-layer removal ratio. Algorithm 1 describes the overall process of our proposed method which consists of four steps: pretraining, ADMM iterations, pruning, and retraining. Algorithm 1 takes data as the input and then returns the pruned weight. The initial value settings of \(\boldsymbol {W}\),\(\boldsymbol {Z}\), and \(\boldsymbol {\mu }\) used in the ADMM step correspond to lines 4–6. The ADMM step corresponding to Eqs. 16, 17, and 18 proceeds in lines 7–13, and a sparse matrix can be obtained by performing pruning on \(\boldsymbol {W}\) in line 14. After that, it freezes the zero weight and finally performs retraining to obtain a final model with sparsity and comparable performance (lines 15–18). Algorithm 2 describes a function that performs projection, setting all elements equal to zero except for the first \(n-1\) largest elements. The Flatten and Reshape functions flatten, or vectorize, the input \(\boldsymbol {X}\) into a 1D sequence and recover the size of flatten_X back to the original input size, respectively. The \(Top\_n\) function takes a vector as an input and returns the n-th value with a large value, which corresponds to the threshold of line 6. The projection ends with the process of setting weights smaller than the calculated threshold to zero (lines 7–9).

figure a
figure b

4 Experiments

We conducted experiments with neural networks of various sizes and three known models: LeNet-5, Resnet-56, and YOLOv4. In Sect. 4.1, we observe the effect of the previous-layer weight and the removal ratio for each layer by training the proposed model by gradually increasing layers. In Sect. 4.2, we compare our model with existing element-wise weight pruning models. In Sect. 4.3, we conduct experiments with various weight pruning models, such as filter-wise and channel-wise methods. Finally, Sect. 4.4 provides a real-life application to YOLOv4, which is a large object-detection model that actually needs weight pruning. The experiments are run on TensorFlow 2 using one NVIDIA RTX 3090 GPU and two RTX 6000. For the sake of simplicity, we denote the proposed pruning methods as global pruning.

4.1 Convolution Neural Networks with Various Layers

Table 1 Removal ratio for each layer according to the number of layers
Full size table

In this experiment, we construct convolution neural network models by increasing the number of layers from two to ten to see if layers close to the input are relatively important among all the layers of the model. The experiment is conducted on MNIST data. We also investigate whether the removal ratios and performance of pruned models evolve according to the number of layers. Each layer, except the final fully connected (dense) layer, consists of a convolutional layer with filter configuration (3, 3, 64) and batch normalization. We increased the number of layers accordingly, applying weight pruning to examine the evolution of weight removal ratios for the layers. For simplicity, we denote the models as cnn-model k, where k is the total number of layers. In Table 1, we observe a pattern where the weights of the layers close to the input are not removed as much compared to those of the other layers. Specifically, the removal ratios of the first convolutional layer (CONV1) change from 76.74% for CNN-model 2 to 89.06% for CNN-model 6. For the following convolutional layers (CONV2 to CONV10), the minimum (90.59%) and the maximum (98.34%) removal ratios are greater than all of the removal ratios of the first convolutional layer (CONV1). In addition, the removal ratios for the dense layers range from 86.25% to 89.69%, which are not much different from those of CNN-model 2 to CNN-model 10. We also notice that the accuracy of the pruned model is comparable with that of the original model.

4.2 LeNet-5

Table 2 Removal ratio comparisons using different weight pruning models on LeNet-5
Full size table
Table 3 Weight pruning results on LeNet-5
Full size table
Fig. 2
figure 2

Weight distributions on LeNet-5

Full size image

LeNet-5 is an image classification model that uses 28 by 28 images as an input, and it has a structure consisting of two convolutional layers and two dense layers. The experiment is conducted on MNIST data.

Before weight pruning, when the comparison models use LeNet-5, they all show the same performance. The experiment revealed the optimal parameters of the proposed model to be \(\lambda =0.01\) and \(\rho =0.004\). Table 2 compares the proposed model (global pruning) with element-wise weight pruning models, showing not only that the highest removal ratio is achieved by the proposed model but also that the highest accuracy, being greater than that of the initial model, is obtained by our model. We performed the proposed global pruning on the pretrained baseline model, producing 99.43% Top-1 accuracy, which is slightly higher than that of previous works [6, 16,17,18]. It is known that CNNs provide impressive performance on many visual tasks, yet their architectures are usually over-parameterized. Therefore, we aim to compress the pretrained models while preserving the discriminative ability.

In addition, Table 3 shows the removal ratio of each layer for the optimal model. In the convolutional layer responsible for feature extraction, it is interesting to observe that the layer close to the input has a low removal ratio, indicating the input variables initially possess valuable information. This result is consistent with findings of the previous experiment, where the layers are gradually added.

After convergence, we visualize the weight distribution for each layer to confirm the change in the weight distribution for LeNet-5. In Fig. 2, the left column shows the distribution from the initial model, the middle column shows that from the model of the ADMM steps, and the right column shows that from the model of the retraining steps. Since 98.8% of the weights are removed, it is clear that a large number of weights are close to zero in the model of the ADMM steps. The retraining steps further shrink the weights to zero. Given the highly compressed model, it is worthwhile mentioning that the accuracy of the final pruned model exceeds that of the initial model. This shows the ability of the proposed model to effectively compress deep layered networks without sacrificing performance.

4.3 ResNet-56

Table 4 Removal ratio comparisons using different weight pruning models on ResNet-56
Full size table

In this experiment, we apply weight pruning to ResNet-56 [28] using the CIFAR-10 dataset consisting of 10 classes and 32 by 32 images. ResNet, based on VGGNet [29] stacking of 3 by 3 convolutional layers, uses a residual block to solve the problem of improper training when the number of layers of the model increases. The ResNet model used in the experiment consists of a total of 56 layers, the number of parameters is 0.85 M, and the accuracy is 93.07%.

For the ResNet-56 model, we compared the experimental results of our weight pruning with existing filter or channel pruning methods [19,20,21,22,23]. Table 4 reports the accuracy and removal ratio of different models before and after pruning. Each model shows the accuracy of the base model and the accuracy after pruning, and NISP [20] shows the difference in accuracy between the pruned model and the base model. We conducted an experiment to remove 10% to 90% of the total weight for the Resnet-56 model. After weight pruning, 10% to 40% removal ratio further increased accuracy. From 50% to 90%, the accuracy decreased by 0.09%, 0.34%, 0.43%, 1.11%, and 2.29%, respectively, in comparison with that of the base ResNet-56 model.

All weight pruning models achieved a removal ratio of less than 50% while maintaining accuracy performance. The results show that our proposed model maintains the accuracy performance sufficiently, even at a removal ratio of 50%. For example, when the removal ratio of HRank is 68.10%, the accuracy is 90.72%. In this case, the performance preservation is 97.2% (90.72/93.26). In contrast, the proposed method produces a performance preservation of 99.5% (92.64/93.07) when the removal ratio is 70%, which surpasses HRank. When comparing it with CNN-FCF, similar results are observed; global pruning achieves better performance preservation, even when the removal ratio is larger.

Fig. 3
figure 3

Weight distributions on LeNet-5

Full size image

In addition, Fig. 3 shows the weight removal ratio for each layer for the Resnet-56 model when the removal ratio is set to 50%. As in the previous experiment, the removal ratio of the frontmost layer is the lowest at 11.57%. In addition, the removal ratio tends to increase as it approaches the last layer.

4.4 Real-Life Application

Fig. 4
figure 4

Application workflow

Full size image

Among deep learning tasks with images and video frames, object detection and object tracking are very popular. Research in these areas is being actively conducted. To show the practicality of this study, we apply weight pruning to YOLOv4 [30], using the COCO dataset and combining Deepsort [31], which is an object tracking model. In short, YOLO is a popular object-detection algorithm, possessing similar performance to Fast R-CNN [32], which has shown high performance in the object-detection field. It has recently achieved tremendous speed improvement. While Fast R-CNN has a speed performance of 0.5 FPS, YOLO has a speed performance of 45 FPS, enabling real-time object detection. YOLO is constantly evolving. The fourth version, YOLOv4, uses a variety of the latest deep learning techniques to improve performance.

The aim is to compress video by removing unnecessary (i.e., no movement) states from CCTV video data utilizing YOLOv4 and Deepsort. To determine the unnecessary state of a certain object, the object tracking model (Deepsort) uses object information detected by YOLOv4. Afterwards, it goes through video compression by removing the state of no movement from the identified movement information. The entire workflow is depicted in Fig. 4.

Fig. 5
figure 5

Weight distributions on YOLOv4 are shown. The first column indicates the distribution of the 10th layer located in the beginning part, the second column is the distribution of the 50th layer located in the middle part, and the third column is the distribution of the 100th layer located in the last part

Full size image

As mentioned, YOLO is faster than other object-detection models, making real-time object detection possible. However, when used on a device with low computing power, such as a mobile device, real-time detection is hardly possible due to the large amount of computation required. In the case of YOLOv4, approximately 100 convolution layers exist, and many experiments are needed to structurally set the layer-by-layer removal ratios. Therefore, when using such a large model for an object-detection task, it is appropriate to apply our model.

The experimental results are as follows. We find that a removal ratio of 20%, as a result of weight pruning on YOLOv4, keep the mAP (mean average precision) of the base model similar. mAP is measurement of object-detection performance, and it describes the average of the area below the graph plotted through precision and recall for each class. Figure 5 shows the weight distribution of the representative layers located at the beginning (conv2d_10), middle (conv2d_50), and end (conv2d_100). The first row shows the weight distribution from the base YOLOv4, and the second row shows that from the pruned model. In the conv2d_10 layer, 164 of 8192 weights, which is 2%, become zero. In the conv2d_50 layer, 55493 of 589824 weights, which is 9.4%, become zero. In the conv2d_100 layer, 239034 of 1179648 weights, which is 20.2%, become zero. Therefore, the conv2d_10 layer has a small ratio of zeros, while the remaining layers have a larger ratio of weights to zero.

5 Conclusions

In this study, we propose an ADMM-based element-wise weight pruning method that sets only the removal ratio of the entire layer during the training process. Weight pruning using traditional ADMM-based optimization methods requires structurally setting a large number of removal ratios, such as by using a layer-wise, filter-wise, or channel-wise method. Therefore, in large models that actually require weight pruning, it is difficult to find the optimal removal ratio and the training times can be very large. We prune the weights simply by using one removal ratio, making only a small variation to the existing ADMM model. This achieves similar performance to ADMM-based models but with less training time.

In the model with convolution neural networks with various layers, we show that the layer closest to the input achieves a smaller removal ratio. This means that if we remove many of those layers, we will lose important information. The LeNet-5 experiment achieves higher removal ratios than element-wise based methods. In the Resnet-56 experiment, which is compared with various weight pruning methods (e.g., filter and channel-wise methods), a removal ratio of 50% is achieved. The higher the removal ratio, the lower the accuracy, which can be selected at the user’s discretion. In addition, the proposed model is also applied to a project that used YOLOv4, which is a very large model. This shows that our proposed technique can be applied to a large model to provide sufficient weight pruning. However, as a limitation, the ADMM optimization method does not guarantee optimum in non-convex problems. However, we note that this limitation is universal for objective functions in deep learning. In addition, though we attempted to verify the improved speed through our model compression, admittedly we were unable to observe speed improvement it due to the limitations of software and hardware. In the future, we envision verifying it when a comparison experiment on speed is possible with software support.

In future research, it is necessary to develop a model that can achieve a higher compression ratio while reducing the number of experiments by changing the \(\rho\) value, which is a very sensitive parameter in our model, to learnable parameter.