1 Introduction

Control charts have been used extensively in a variety of areas like manufacturing processes [1,2,3], goods and services providing companies [4], health care enterprises [5], nuclear engineering [6, 7], Software industry [8, 9], education [10], analytical laboratories [11, 12], etc. since its inception floated by Walter A. Shewhart during 1920s. The Statistical Process Control (SPC) experts are struggling hard to devise a robust control chart technique for the efficient monitoring of the process but in vain to launch a universal control chart methodology. Several modifications by SPC researchers have been proposed by mixing and combining the design structures of monitoring techniques. The multiple dependent state (MDS) sampling technique combined with a fixed deferred state sampling scheme for the correct decision of lot sentencing was promoted by Wortham and Baker [13]. The MDS sampling in combination with the double control limits can be used for the efficient monitoring of the production process [14]. The combination of exponentially distributed quality characteristics with the MDS has been shown as an efficient monitoring technique for the mean of the production process [15]. Further literature on proposed approaches for quick detection of unusual changes can be consulted [16,17,18,19,20].

The fuzzy approach is very common in the control chart literature due to its efficient capability of handling vague data [21]. Ambiguous and unclear data are well represented by the fuzzy logic which provides a systemic base by using algorithms of defuzzification methods [21]. The fuzzy approach provides the perfect means of dealing with human subjectivity by modeling uncertainty which is neither stochastic nor random. The fuzzy control charts are inevitable to deal with uncertain, vague, incomplete or data collected on human subjectivity. Several procedures have been proposed to develop fuzzy control charts since the inception of fuzzy set theory by Zadeh [22]. Fuzzy set theory can be used to develop the control chart for quality assurance of the industrial product when the observations are collected from linguistic terms [23]. A methodology for developing a quantitative control chart for nonprecise observations was given by Gülbay and Kahraman [24]. A hybrid fuzzy adaptive control chart was developed to enhance the performance of the Shewhart control chart using fuzzified sensitivity criteria by Zarandi et al. [25]. The X-bar chart using the fuzzy theorem for non-crispy data using the triangular fuzzy membership function was developed by Panthong and Pongpullponsak [26]. An attribute sampling plan under the multiple dependent state sampling for the fuzzy environment was designed by Afshari and Sadeghpour Gildeh [27]. Control charts under fuzzy theory for the univariate case and multivariate case were developed by Fernández [28]. Fuzzy logic is the special case of neutrosophic logic.

Neutrosophic statistics has attracted the attention of several SPC experts during the last few years due to its nice properties of analyzing the vague, incomplete, imprecise, unclear and uncrispy data from numerous practical, real-world and everyday circumstances. Neutrosophic logic was introduced by Smarandache [29]. The engineering rock mass using the joint roughness coefficient under the neutrosophic statistics for scale effect and anisotropy environment were analyzed by Chen et al. [30]. Sampling plan under the neutrosophic process loss consideration was developed by Aslam [31]. Sampling plans using regression estimators for the neutrosophic statistics through the neutrosophic optimization solution were presented by Aslam and AL-Marshadi [32]. Control charts for failure-censored reliability tests under the neutrosophic environment were presented by Aslam et al. [33]. Dispersion control charts using the neutrosophic statistical interval method were presented by Aslam et al. [34]. A control chart based upon gamma-distributed quality characteristic under the neutrosophic statistics was developed by Aslam et al.[35]. Shewhart S-control chart for process variability monitoring using the neutrosophic statistics was presented by Khan et al. [36]. A robust single-valued neutrosophic soft aggregation operator in multi-criteria decision-making was developed by Jana and Pal [37]. Trapezoidal neutrosophic aggregation operators and their application to the multi-attribute decision-making process are given by Jana et al. [38]. Multi-criteria decision making approach based on SVTrN Dombi aggregation functions proposed by Jana et al. [39]. Multi-criteria decision making process based on some single-valued neutrosophic Dombi power aggregation operators was developed by Jana and Pal [40]. Multiple-attribute decision making problems based on SVTNH methods were studied by Jana et al. [41]. More literature on neutrosophic statistics are suggested as [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58].

The performance of the newly developed chart can be evaluated by estimating the average run lengths (ARL) which is defined as the average number of samples falling in-control limits until it indicates the out-of-control process [59]. The existing classical or neutrosophic exponentially weighted moving average charts are not accomplished to capture the extraordinary changes vulnerable to the manufacturing processes. The EWMA chart under neutrosophic statistics using single sampling was developed by Aslam et al. [60]. By exploring the literature and according to the best of our knowledge, there is no work on EWMA chart under neutrosophic statistics using MDS sampling. The present control chart has been using the symmetry property of the Gaussian distribution for the uncertain environment. We will design the proposed control chart and compare the efficiency with the existing chart. We expect that the proposed chart will be efficient than the existing chart in detecting the shift earlier. The rest of the paper is organized as follows: the methodology of the proposed chart is given in Sect. 2. Control chart based on multiple dependent state sampling is given in Sect. 3. The simulation study for proposed neutrosophic control chart is addressed in Sect. 4. A comparison of the proposed chart has been given in Sect. 5. In Sect. 6, the application of the proposed methodology is discussed. Conclusion and recommendations have been stated in Sect. 7.

2 Methodology of the Proposed Chart

This section deals with proposing the NEWMA statistics. The neutrosophic random variable (NRV) is denoted as \(Y_{jN} \, \in \,\left[ {Y_{L} ,Y_{U} } \right];\;j = 1,2, \ldots ,n_{N}\), where \(n_{N}\) is the neutrosophic sample size (NSS). Assume that the neutrosophic sample mean (NSM) and sample variance are defined as \(\overline{Y}_{N} \, \in \,\left[ {\frac{{\mathop \sum \nolimits_{j = 1}^{{n_{L} }} Y_{j} }}{{n_{L} }},\frac{{\mathop \sum \nolimits_{j = 1}^{{n_{U} }} Y_{j} }}{{n_{U} }}} \right]\); \( \overline{Y}_{N} \, \in \,\left[ {\overline{Y}_{L} ,\overline{Y}_{U} } \right]\) and \( S_{N}^{2} \, = \,\mathop \sum \nolimits_{j = 1}^{{n_{N} }} \left( {Y_{N} \, - \,\overline{Y}_{N} } \right)^{2} /\left( {n_{N} \, - \,1} \right)\); \(S_{N}^{2} \, \in \,\left[ {S_{L}^{2} ,S_{L}^{2} } \right]\). According to Smarandache [29] and Aslam [31], the NSM comes from the neutrosophic normal distribution (NND) with a neutrosophic population mean and variance are respectively \(\mu_{N}\) and \(\sigma_{N}^{2} /n_{N}\), where \(\mu_{N} \, = \,\mathop \sum \nolimits_{j = 1}^{{N_{N} }} Y_{N} /N_{N}\); \(\mu_{N} \, \in \,\left[ {\mu_{L} ,\mu_{U} } \right]\) and \(\sigma_{N}^{2} \, = \,\mathop \sum \nolimits_{j = 1}^{{n_{N} }} \left( {Y_{N} - \mu_{N} } \right)^{2} /(N_{N} - 1)\); \(\sigma_{N}^{2} \, \in \,\left[ {\sigma_{L}^{2} ,\sigma_{U}^{2} } \right]\). Using foresaid acquaintance the NEWMA statistics is given below:

$$ {\text{EWMA}}_{N,j} \, = \,\lambda_{N} \overline{Y}_{N} \, + \,\left( {1\, - \,\lambda_{N} } \right)\;{\text{EWMA}}_{N,j - 1} ;\,{\text{EWMA}}_{N,j} \, \in \,\left[ {{\text{EWMA}}_{L,j} ,{\text{EWMA}}_{U,j} } \right] $$
(1)

where \(\lambda_{N}\) is neutrosophic smoothing constant, \(\lambda_{N} \, \in \,\left[ {\lambda_{L} ,\lambda_{U} } \right]\) and the range of \(\lambda_{N}\) is \( \left[ {0,0} \right]\, \le \,\lambda_{N} \, \le \,\left[ {1,1} \right]\). Note here that \(\overline{X}_{N} \, \in \,\left\{ {\overline{X}_{L} ,\overline{X}_{U} } \right\}\) are assumed to be independent random variables with neutrosophic variance \(\sigma_{N}^{2} /n_{N}\); \(\sigma_{N}^{2} /n_{N} \, \in \,\left[ {\sigma_{L}^{2} /n_{N} ,\sigma_{L}^{2} /n_{N} } \right]\) and known neutrosophic population variance, as shown in [61]. Montgomery [62] suggested that the smoothing constant should ranges from 0.05 to 0.25. The \({\text{EWMA}}_{N,j}\) comes from the NND with neutrosophic mean as \(\mu_{N} \, \in \,\left[ {\mu_{L} ,\mu_{U} } \right]\) and neutrosophic standard deviation as \(\frac{{\sigma_{N} }}{{\sqrt {n_{N} } }}\sqrt {\frac{{\lambda_{N} }}{{2 - \lambda_{N} }}}\).

3 The Proposed NEWMA X-Bar Control Chart Based on Multiple Dependent State Sampling

The NEWMA X-bar control chart using the MDS sampling plan under the NS is outlined in the below steps:

  1. 1.

    Drawn an NRV of size \(n_{N} \, \in \,\left[ {n_{L} ,n_{U} } \right]\) and determine \({\text{EWMA}}_{N,j}\) statistics given in Eq. (1).

  2. 2.

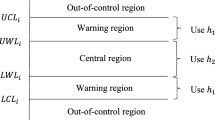
    Assert the process is stated as in-control when \({\text{LCL2}}_{N} \, \le \,{\text{EWMA}}_{N,i} \, \le \,{\text{UCL}}2_{N}\). Admit the process as out-of-control when \({\text{EWMA}}_{N,j} \, \ge \,{\text{UCL}}1_{N}\) or \({\text{EWMA}}_{N,j} \, \le \,{\text{LCL}}1_{N}\). If not move to step 3. Note here that \({\text{LCL}}1_{N} \, \in \,\left[ {{\text{LCL}}1_{L} ,{\text{LCL}}1_{U} } \right]\) and \({\text{UCL}}1_{N} \, \in \,\left[ {{\text{UCL}}1_{L} ,{\text{UCL}}1_{U} } \right]\) are outer neutrosophic limits; \({\text{LCL}}2_{N} \, \in \,\left[ {{\text{LCL}}2_{L} ,{\text{LCL}}2_{U} } \right]\) and \({\text{UCL}}2_{N} \, \in \,\left[ {{\text{UCL}}2_{L} ,{\text{UCL}}2_{U} } \right]\) are the inner neutrosophic limits respectively.

  3. 3.

    Pronounce the process is said to be in-control if \(m_{N}\) preceding subgroups have been affirming the process to be in-control.

Thus the proposed neutrosophic control limits are given below:

$$ {\text{LCL}}1_{N} \, = \,\mu_{N} \, - \,k1_{N} \frac{{\sigma_{N} }}{{\sqrt {n_{N} } }}\sqrt {\frac{{\lambda_{N} }}{{2 - \lambda_{N} }}} {; }\,{\text{LCL}}1_{N} \, \in \,\left[ {{\text{LCL}}1_{L} ,{\text{LCL}}1_{U} } \right];\;k1_{N} \, \in \,\left[ {k1_{L,} ,k1_{U} } \right] $$
(2)
$$ {\text{UCL}}1_{N} \, = \,\mu_{N} \, + \,k1_{N} \frac{{\sigma_{N} }}{{\sqrt {n_{N} } }}\sqrt {\frac{{\lambda_{N} }}{{2 - \lambda_{N} }}} ;\,{\text{UCL}}1_{N} \in \left[ {UCL1_{L} ,UCL1_{U} } \right];\,k1_{N} \in \left[ {k1_{L} ,k1_{U} } \right];\,\mu_{{\text{N}}} \in \left[ {\mu_{{{\text{L}},}} ,\mu_{{\text{U}}} } \right] $$
(3)
$$ \begin{gathered} {\text{LCL2}}_{N} \, = \,\mu_{N} - k2_{N} \frac{{\sigma_{N} }}{{\sqrt {n_{N} } }}\sqrt {\frac{{\lambda_{N} }}{{2 - \lambda_{N} }}} ;\,{\text{LCL2}}_{N} \, \in \,\left[ {{\text{LCL2}}_{L} ,{\text{LCL2}}_{U} } \right];\,k2_{N} \, \in \,\left[ {k2_{L,} ,k2_{U} } \right],\, \hfill \\ \mu_{{\text{N}}} \in \left[ {\mu_{{{\text{L}},}} ,\mu_{{\text{U}}} } \right] \hfill \\ \end{gathered} $$
(4)
$$ {\text{UCL2}}_{N} \, = \,\mu_{N} \, + \,k2_{N} \frac{{\sigma_{N} }}{{\sqrt {n_{N} } }}\sqrt {\frac{{\lambda_{N} }}{{2 - \lambda_{N} }}} ;\,{\text{UCL}}2_{N} \, \in \,\left[ {UCL2_{L} ,UCL2_{U} \left\{ {\left\{ {} \right\}} \right\}} \right];\,k2_{N} \, \in \,\left[ {k2_{L} ,k2_{U} } \right], \, \mu_{N} \, \in \,\left[ {\mu_{L} ,\mu_{U} } \right] $$
(5)

Where \(k1_{N} \in \left[ {k1_{L} ,k1_{U} } \right]\) and \(k2_{N} \in \left[ {k2_{L,} ,k2_{U} } \right]\) are the neutrosophic control limits coefficients. The developed control chart becomes an existing NS control chart proposed by [60] when \(k1_{N} = k2_{N} = k_{N}\), \(m_{N} = 1\) and developed control chart becomes a chart developed by [52] when \(\lambda_{N} \, \in \,\left\{ {1,1} \right\}\). When \(k1_{N} = k2_{N} = k_{N} = k\), \(m_{N} = m = 1\) the developed control chart becomes the classical Shewhart chart. Let \(\mu_{0N} \, \in \,\left[ {\mu_{0L} ,\mu_{0U} } \right]\) is a target mean value for the process. The probability of the process under the NS is an in-control state for the proposed control chart is given below:

$$ P_{inN}^{0} \, = \,P\left( {{\text{LCL2}}_{N} \, \le \,{\text{EWMA}}_{N,j} \, \le \,{\text{UCL2}}_{N} |\mu_{0N} } \right)\, + \,\left\{ {\begin{array}{*{20}c} {P\left( {{\text{LCL}}1_{N} \, \le \,{\text{EWMA}}_{N,j} \, \le \,{\text{LCL2}}_{N} |\mu_{0N} } \right) + } \\ {P\left( {{\text{UCL}}2_{N} \, \le \,{\text{EWMA}}_{N,j} \, \le \,{\text{UCL}}1_{N} |\mu_{0N} } \right)} \\ \end{array} } \right\}\left\{ {P\left( {{\text{LCL2}}_{N} \, \le \,{\text{EWMA}}_{N,j} \, \le \,{\text{UCL2}}_{N} |\mu_{0N} } \right)} \right\}^{{m_{N} }} $$
(6)

The neutrosophic average run length (NARL) for the developed control chart is as follows:

$$ {\text{ARL}}_{0N} \, = \,\frac{1}{{1\, - \,P_{inN}^{0} }} ;\,{\text{ARL}}_{0N} \, \in \,\left[ {{\text{ARL}}_{0L} ,{\text{ARL}}_{0U} } \right] $$
(7)

The neutrosophic probability of an in-control state when the process has shifted from \(\mu_{0N}\) to a new target at \(\mu_{1N} \, = \,\mu_{0N} \, + \,\delta \sigma_{N}\); \(\mu_{1N} \, \in \,\left[ {\mu_{1L} ,\mu_{1U} } \right]\), where \(\delta\) is the shift constant is as follows:

$$ P_{inN}^{1} \, = \,P\left( {{\text{LCL2}}_{N} \, \le \,{\text{EWMA}}_{N,j} \, \le \,{\text{UCL}}2_{N} {|}\mu_{1N} } \right)\, + \,\left\{ {\begin{array}{*{20}c} {P\left( {LCL1_{N} \le EWMA_{N,j} \le LCL2_{N} {|}\mu_{1N} } \right) + } \\ {P\left( {UCL2_{N} \le EWMA_{N,j} \le UCL1_{N} {|}\mu_{1N} } \right)} \\ \end{array} } \right\}\left\{ {P\left( {{\text{LCL}}2_{N} \, \le \,{\text{EWMA}}_{Nj} \, \le \,{\text{UCL2}}_{N} {|}\mu_{1N} } \right)} \right\}^{{m_{N} }} $$
(8)

The NARL at \(\mu_{1N} \, \in \,\left[ {\mu_{1L} ,\mu_{1U} } \right]\) is given below:

$$ {\text{ARL}}_{1N} \, = \,\frac{1}{{1 - P_{inN}^{1} }};\,{\text{ARL}}_{1N} \, \in \,\left[ {{\text{ARL}}_{1L} ,{\text{ARL}}_{1U} } \right] $$
(9)

4 The Simulation Study for Proposed Neutrosophic Control Chart

The neutrosophic average run length (NARL) and the neutrosophic standard deviation of run length (NSDRL) are usually used to investigate the accomplishment of the control charts. The neutrosophic Monte Carlo simulation is used to estimate neutrosophic control limits constants \(k1_{N} \, \in \,\left[ {k1_{L} ,k1_{U} } \right]\) and \(k2_{N} \, \in \,\left[ {k2_{L,} ,k2_{U} } \right]\) and hence, \({\text{ARL}}_{0N} \, \in \,\left[ {{\text{ARL}}_{0L} ,{\text{ARL}}_{0U} } \right]\). To compute the in-control state neutrosophic control limits constants \(k1_{N} \in \left[ {k1_{L} ,k1_{U} } \right]\) and \(k2_{N} \in \left[ {k2_{L,} ,k2_{U} } \right]\) generate a neutrosophic random sample of size \(n_{N} \, \in \,\left[ {n_{L} ,n_{U} } \right]\) from standard normal distribution. Compute the chart statistics \({\text{EWMA}}_{N,j}\), determine the in-control average run length \({\text{ARL}}_{0N} \, \in \,\left[ {{\text{ARL}}_{0L} ,{\text{ARL}}_{0U} } \right]\) and chart constants \(k1_{N}\) and \(k2_{N} \). The chart constants are determined such that \(ARL_{0N} \approx r_{0N}\), here \(r_{0N}\) could be planned value of \({\text{ARL}}_{0N} \, \in \,\left[ {{\text{ARL}}_{0L} ,{\text{ARL}}_{0U} } \right]\). To obtain \({\text{ARL}}_{0N} \, \in \,\left[ {{\text{ARL}}_{0L} ,{\text{ARL}}_{0U} } \right]\) and chart constants \(k1_{N}\) and \(k2_{N}\) we have performed 10,000 simulation runs. Once after obtaining the chart constants, \({\text{ARL}}_{0N} \, \in \,\left\{ {{\text{ARL}}_{0L} ,{\text{ARL}}_{0U} } \right\}\) and NSDRL value based on 10,000 simulation runs, we need to study the out-of-control performance of the proposed control chart.

To obtain the out-of-control average run length \({\text{ARL}}_{1N} \, \in \,\left\{ {{\text{ARL}}_{1L} ,{\text{ARL}}_{1U} } \right\}\), shifted the process from \(\mu_{0N}\) to a new target at \(\mu_{1N} \, = \,\mu_{0N} \, + \,\delta \sigma_{N}\); \(\mu_{1N} \, \in \,\left[ {\mu_{1L} ,\mu_{1U} } \right]\), where \(\delta\) is the shift constant. Using the chart constants obtained from the in-control process, now generate random numbers of size \(n_{N}\) from normal distribution with mean \(\mu_{1N}\) and variance \(\sigma_{N}^{2}\) and obtain \({\text{ARL}}_{1N} \, \in \,\left\{ {{\text{ARL}}_{1L} ,{\text{ARL}}_{1U} } \right\}\) for various shift values of \(\delta\). Repeat the entire procedure for 10,000 iterations and compute the \({\text{ARL}}_{1N} \, \in \,\left\{ {{\text{ARL}}_{1L} ,{\text{ARL}}_{1U} } \right\}\) values and NSDARL values. The results are displayed in Tables 1, 2, 3 and 4 for various shift values of \(\delta\), \(n_{N}\), \(m_{N}\), \(\lambda_{N}\) and \(ARL_{0N}\). The values of NARL when \(n_{N} = \left[ {3,5} \right];m_{N} = \left[ {2,4} \right];\lambda_{N} = \left[ {0.08,0.12} \right]\) are displayed in Table 1. The values of NARL when \(n_{N} = \left[ {3,5} \right];m_{N} = \left[ {2,4} \right] {\text{and}} \lambda_{N} = \left[ {0.18,0.22} \right]\) are given in Table 2. The values of NARL when \(n_{N} = \left[ {3,5} \right]; m_{N} = \left[ {2,4} \right];\lambda_{N} = \left[ {0.28,0.32} \right]\) are depicted in Table 3. The values of NARL when \(n_{N} \, \in \,\left[ {5,7} \right]\), \(n_{N} \, \in \,\left[ {8,10} \right]\), \(m_{N} = \left[ {2,4} \right] \) and \(\lambda_{N} \, \in \,\left[ {0.08,0.12} \right]\) are shown in Table 4. The importance of the proposed control chart can found in Tables 1, 2, 3 and 4, the results show that the NARL and NSDRL are increased when \(\lambda_{N} \, \in \,\left[ {\lambda_{L} ,\lambda_{U} } \right]\) values increase. It is significant to note that as shift parameter increases then there is a decreasing tendency in NARL and NSDRL values. Furthermore, from Table 4 it is interesting to note that the indeterminacy interval in NARL and NSDRL are decreases as \(n_{N} \, \in \,\left[ {n_{L} ,n_{U} } \right]\) increases from \(n_{N} \, \in\) [5, 7] to \(n_{N} \, \in \,\) [8, 10]. Hence we conclude that the indeterminacy interval in NARL and NSDRL are decreased as NSS increases.

Table 1 NARL and NSDRL values of under MDS sampling when \(n_{N} = \left[ {3,5} \right];m_{N} = \left[ {2,4} \right];\;\lambda_{N} = \left[ {0.08,0.12} \right]\)
Full size table
Table 2 The values of NARL and NSDRL under MDS sampling when \(n_{N} \, = \,\left[ {3,5} \right];\,m_{N} \, = \,\left[ {2,4} \right];\,\lambda_{N} \, = \,\left[ {0.18,0.22} \right]\)
Full size table
Table 3 The values of NARL and NSDRL under MDS sampling when \(n_{N} \, = \,\left[ {3,5} \right];\, m_{N} \, = \,\left[ {2,4} \right];\,\lambda_{N} \, = \,\left[ {0.28,0.32} \right]\)
Full size table
Table 4 The values of NARL and NSDRL under MDS sampling when \(r_{0}\) = 370
Full size table

5 Comparison Study of the Proposed Chart

Literature on control charts show that a proposed chart is considered efficient if the ARL and the standard deviation of ARL values are smaller than the counterpart chart under the same parametric settings. Thus the proposed chart has been compared with the [60] chart which had been developed for the process monitoring under the neutrosophic EWMA statistics. Table 5 has been given for the comparison of the proposed MDS sampling with the [60] using the same parametric settings of \(n\, = \,\left[ {3,\,5} \right];\;{\uplambda }\, = \,\left[ {0.08,\,0.12} \right]\) for \({\text{ARL}}_{0} = \left\{ {300{\text{ and }}370} \right\}\). From Table 5 it can be observed that the proposed chart has smaller values of ARL and SDARL for different values process shift. For instance, the small shift of 0.05 is detected in [210.81, 197.3] samples when \({\text{ARL}}_{0} = \left\{ {300} \right\}\) when the proposed chart is used while the same amount of shift is detected using [220.34, 202.5] samples when the existing chart is used. Further a small shift of 0.50 is detected in [3.01, 5.02] samples when the existing chart is used when \({\text{ARL}}_{0} = \left\{ {300} \right\}\) while the same amount of shift is detected using [220.34, 202.5] samples when the existing chart is used. In addition when \({\text{ARL}}_{0} = \left\{ {370} \right\}\) the small shift of 0.05 is detected in [254.12, 235.41] samples when the proposed chart is used while the same amount of shift is detected using [270.32, 248.92] samples when the existing chart is used. Further a small shift of 0.50 is detected in [3.01, 5.03] samples when the existing chart is used while the same amount of shift is detected using [12.24, 8.19] samples when the existing chart is used. The same pattern can be seen for all values of shift. So it can be claimed that the proposed chart is comparatively efficient in the quick detection of smaller shifts in the production process.

Table 5 Comparison of the proposed chart with the existing chart
Full size table

A simulation study of the proposed chart has also been carried out to detect the working of the proposed methodology. Table 6 has been produced for the data from the NND in which neutrosophic mean values, \(\overline{X}_{N} \, \in \,\left\{ {\overline{X}_{L} , \overline{X}_{U} } \right\}\) and the neutrosophic EWMA, EWMAN statistic have been calculated. The first 20 observations have been generated for the in-control process while the next 20 observations have been generated for the out-of-control process with a shift of \(d = 0.25\). Now we suppose that in our process the \(n_{N} \in \left[ {5,7} \right]\), \({\text{ARL}}_{0N} \, \in \,\left[ {370, 370} \right]\) and \(\lambda_{N} \in \left[ {0.08, 0.12} \right]\). From Table 4 the calculated NARL is \({\text{ARL}}_{1N} \, \in \,\left[ {6.67, \,9.64} \right]\) which indicates that the process will be declared as out-of-control in-between the seventh and tenth sample of the process having these parametric settings. The out-of-control process after the seventh and tenth has also been shown in Fig. 1 of the proposed chart simulation study with the chart coefficients \(k1 = \left[ {2.70613,2.98759} \right]\) and \(k2 = \left[ {2.49637,2.53893} \right]\) and the two pairs of control limits as \({\text{LCL}}1_{N} \, = \,\left[ {73.9995,73.99968} \right], \,{\text{LCL}}2_{N} \, = \,\left[ {73.99958,73.99971} \right]\), \( {\text{UCL}}2_{N} \, = \,\left[ {74.00029, 74.00044} \right] \) and \({\text{UCL}}1_{N} \, = \,\left[ {74.00032,\,74.00052} \right]\) For the purpose of comparative study, Fig. 1 has been generated with the same process settings having applied on the existing chart presented by [60] which shows that the process is in-control and unable to detect this shift. On observing Fig. 1 it can be concluded that the proposed chart is comparatively efficient in quick detection of the out-of-control process for any small shift being faced by the production process. To study robustness, we have conducted a comparative study with existing studies and also various parametric combinations. From simulation and comparative study the proposed methodology shows the robustness and validation in the field of statistical process control.

Table 6 The simulated EWMA neutrosophic data
Full size table
Fig. 1
figure 1

The proposed chart for simulated data (left) and existing chart proposed by [60] for the simulated data (right)

Full size image

6 Application of the Proposed Chart in Monitoring Road Accidents and Injuries

6.1 Application 1 (Monitoring Road Accidents)

In this section the practical application of the proposed chart has been given. The proposed methodology has been developed for the quick monitoring of the neutrosophic EWMA statistic using the MDS sampling. As stated above the proposed chart is quite effective, efficient and flexible to monitor the process for the neutrosophic statistics. Therefore the practical application has been given using the data related to road accident from Saudi Arabia for daily basis of the year. The aim of this application is to monitor the road accidents on the various days of the week. For ready reference data is shown in Table 7 along with the neutrosophic EWMA statistics of the reference data are calculated. The calculated limits are given using \(n_{N} = \left[ {5,7} \right], \mu_{N} = \left[ {502.62,485.23} \right]\) and \(\sigma_{N} = \left[ {79.92,83.24} \right]\). The control chart coefficients are calculated as \(k1 = \left[ {3.05698,3.10119} \right]\) and \(k2 = \left[ {2.4442,2.51186} \right]\). Thus the two pairs of limits are calculated as \({\text{LCL}}1_{N} \, = \,\left[ {477.97,480.31} \right]\), \({\text{LCL}}2_{N} \, = \,\left[ {482.65,484.64} \right]\), \({\text{UCL}}2_{N} \, = \,\left[ {520.45,522.58} \right]\) and \({\text{UCL}}1_{N} \, = \,\left[ {524.92.88,527.27} \right]\). Figure 2 has been given for the proposed chart methodology and Fig. 3 has been given for the existing chart proposed by [60]. It can be observed that the proposed chart provide the narrow limits as compared to the existing chart.

Table 7 Real example \(n_{N}\) = [5, 7] and \(\lambda_{N} = \left[ {0.08,0.12} \right]\)
Full size table
Fig. 2
figure 2

The proposed chart for monitoring road accidents

Full size image
Fig. 3
figure 3

The existing chart for monitoring road accidents by [60]

Full size image

6.2 Application 2 (Monitoring Road Injuries)

Furthermore, one more real-life application for the developed control chart is illustrated in this sub-section. The accident data of indeterminate nature different age groups of people in various months of the year is described in Table 8. The coefficients of control limits are \(k1 = \left[ {2.70613,2.98759} \right]\) and \(k2 = \left[ {2.49637,2.52893} \right]\) using \(n_{N} = \left[ {3,5} \right]\), \(\mu_{N} = \left[ {55.39,49.42} \right]\) and \(\sigma_{N} = \left[ {38.39,27.94} \right]\). The following two pairs of control limits are calculated \({\text{LCL}}1_{N} \, = \,\left[ {39.98,43.14} \right],\,{\text{LCL}}2_{N} \, = \,\left[ {41.43,44.09} \right]\), \({\text{UCL}}2_{N} \, = \,\left[ {57.40,66.68} \right]\) and \({\text{UCL}}1_{N} \, = \,\left[ {58.84,67.63} \right]\) and given in Fig. 4. Figure 4 has been given for the proposed chart methodology and Fig. 5 has been given for the existing chart proposed by [60]. Here again, it can be observed that the proposed chart provides narrow limits as compared to the existing chart.

Table 8 Real example \(n_{N}\) =  [3,5] and \(\lambda_{N} = [0.08,0.12\)]
Full size table
Fig. 4
figure 4

The proposed chart for monitoring road injuries

Full size image
Fig. 5
figure 5

The existing chart for monitoring road injuries by [60]

Full size image

7 Concluding Remarks

In this paper, neutrosophic multiple dependent state sampling control chart for the neutrosophic EWMA statistic has been presented. The coefficients of the proposed chart have been determined using the neutrosophic statistical interval method for different process settings. The average run lengths and the standard deviation of the average run lengths have been determined using the Monte Carlo simulation. The comparison of the proposed chart with the existing chart has been discussed. It has been concluded that the proposed chart is the comparatively efficient chart for monitoring the vague, incomplete, unclear and non-crispy quality characteristics. The limitation of our study is the production process should follow the normal distribution. The proposed new X-bar control chart for multiple dependent state sampling using neutrosophic exponentially weighted moving average statistics could be applied to chemical, packing and electronic industries. Future study is suggested for the non-normal processes on chemical, packing and electronic industries employed using the proposed methodology.