1 Introduction

The application of a control chart is a mandatory tool for any production process or any goods and services provider agency for maintaining its repute in the market as well as the profit maximization. The idea of a control chart was floated by American Physicist Walter A. Shewhart during 1920s. According to the Shewhart notion of control chart, any interested quality characteristic can be observed, judged, evaluated, examined and classified to fall in the zones of in-control for usual changes and out-of-control for unusual changes [1]. The X-bar chart is the most powerful tool for the quality control department to determine the unusual fluctuations during the production process. Usually, the X-bar control chart operates using three control limits namely lower control limit, upper control limit and central control limit. A statistic is plotted on the control chart and the process is declared out-of-control if the plotting statistic lies outside the control limits. The quick detection of the out-of-control process is the crucial need of any production process not only to avoid losses of scrape and burden of rework but also for improving the quality of the product. Normally situation of out-of-control arises when the quality of raw material is compromised, irresponsible attitude of attendants, fluctuations in environmental and weather conditions, etc. A bulk of literature on monitoring techniques is available since the inception of the notion of the control chart technique but only the most recent methodologies are reviewed here. Bakir [2] presented the control chart for monitoring the common and special causes of variation for workers in the management department. Calzada and Scariano [3] presented the monitoring scheme for the joint monitoring of the mean and the variance of the interested quality characteristics. MacNaughton and Coomans [4] proposed the composite control chart for the overall monitoring using the software with the complete algorithm. Nazir, Schoonhoven [5] presented a robust dispersion chart for the efficient monitoring of the variations. Goedhart, da Silva [6] developed adjusted control charts for the classical Shewhart chart using the analytical method under normality.

A multiple deferred/dependent state (MDS) sampling scheme was initially developed by [7] for the attribute acceptance sampling plans in which the fate of the submitted lot has three categories; accept the lot, reject the lot or conditionally accept or reject the lot depending on the fate of previously submitted lots. During the last two decades, MDS sampling has attracted the attention of several researchers of variable control chart for its quick detection ability. [8] studied the attribute control chart using the MDS sampling. Due to the efficient working of the MDS sampling, several modifications have been introduced by the quality control researchers. A control chart using modified MDS sampling for the exponentially distributed characteristic has been presented by [9]. The generalized multiple dependent state (GMDS) sampling scheme is used by adding an additional parameter for the decision of any sample based upon the fixed number of the selected samples and the number of samples falling within control limits, see Bhattacharya and Aslam [10] presented an efficient sampling plan using GMDS sampling for the measurement errors. A variable sampling plan using the GMDS sampling has been developed for the one-sided process capability index by [11]. The GMDS sampling plan has been developed for the exponential new Pareto distributed mean life assurance by [12].

Average run length (ARL), is a very commonly used technique to evaluate the performance of the proposed chart, which is defined as the average number of samples before the process indicates an out-of-control situation [1]. The notion of ARL calculation for evaluating the performance of the control chart was introduced by [13]. Numerical integration for calculating the ARL in the control charts has been presented by [14]. Usually, two types of ARLs are calculated i.e., in-control ARL denoted by \(AR{L}_{0}\) is calculated using the formula \(1/\alpha\) where \(\alpha\) is the probability of type-I error, a pre-defined value of 200, 300 or 370 and out-of-control ARL denoted by \({\mathrm{ARL}}_{1}\) is calculated using the formula \(1/\left(1-\beta \right)\) where \(\beta\) is the probability of type-II error. As a rule of thumb \({\mathrm{ARL}}_{0}\) must be higher for the in-control process whereas the \({\mathrm{ARL}}_{1}\) must be the least value for any efficient monitoring scheme [1]. Also, the ARL value for zero shift is known as in-control ARL. More detail on ARL can be found in [15, 16].

Several classical control charts have been developed for the normal, crispy, clear, complete and determined data of the interested quality characteristics. There are many situations in which the data are imprecise, soggy, vague, incomplete, inadequate or uncertain for which the traditional control charts may lead to erroneous conclusions. The neutrosophic logic introduced by [17] is based upon the percentage of indeterminacy which is the extension of the fuzzy logic. For more information on fuzzy, the readers are referred to Abu Arqub, Singh [18] and Abu Arqub, Singh [19]. Further [20] introduced the neutrosophic statistics using the neutrosophic logic treating the imprecise, soggy, vague, incomplete, inadequate or uncertain observations. There are many situations when the available data are consisted of ranges instead of exact values then the collected data cannot be analyzed using classical statistics. Classical statistics is unable to analyze and interpret the data having neutrosophic numbers or data having observations in intervals. Neutrosophic statistics is used as an alternative to deal with the data in indeterminacy intervals or expressed in neutrosophic numbers, see [21]. Albassam, Khan [22] developed the technique to test the normality of the data for the indeterminate intervals. Abu Arqub, Abo-Hammour [23] studied a continuous genetic algorithm for solving singular two-point boundary value problems. Arqub and Abo-Hammour [24] suggested a continuous genetic algorithm for the numerical solution of systems of second-order boundary values.

Aslam [25] presented an efficient monitoring scheme for variance using the neutrosophic interval method. Aslam, Bantan [26] introduced an attribute control chart for neutrosophic statistics. During the last few years, the neutrosophic statistics have attracted the attention of several researchers including [20, 27] and [28]. Aslam and Khan [29] proposed the X-bar control chart using the single sampling scheme using neutrosophic statistics. Aslam et al. [30] proposed the X-bar control chart using MDS under neutrosophic statistics. Aslam [31] worked on the X-bar control chart using the repetitive sampling scheme. Khan and Aslam [32] presented the X-bar control chart using the multiple dependent state repetitive sampling scheme. By exploring the literature and according to the best of the authors’ knowledge, there is no work on the control chart GMDS using neutrosophic statistics. As the prime objective, as mentioned earlier, the approach of a control chart is utilized for the efficient monitoring of the production process to avoid the burden of scrap and rework of the wanton production line. The quick the message is conveyed to the production and technical staff the fewer the defective items will be produced. In this article, the situation of quick monitoring for the neutrosophic data/ observation has been stated and a new technique is introduced to serve this purpose Therefore, we developed a variable control chart using neutrosophic statistics under the GMDS sampling technique.

2 Methodology of the Proposed Neutrosophic Statistics Chart

In this section, the methodology of the GMDS sampling control chart under the neutrosophic statistics has been elaborated. Suppose the interested quality characteristic (x) with mean \(\mu\) and standard deviation \(\sigma\) of the normal distribution are given then the procedure of the GMDS sampling repetitive sampling (GMDSRS) scheme under neutrosophic statistics is stated as follows

Step 1: Choose randomly a sample of size

$$n_{N} = n_{L} + n_{U} I_{nN} ;\quad I_{nN} \in \left[ {I_{nL} ,I_{nU} } \right]$$
(1)

and find

$$\overline{X}_{N} = \overline{X}_{L} + \overline{X}_{U} I_{{\overline{X}N}} ;\quad I_{{\overline{X}N}} \in \left[ {I_{{\overline{X}L}} ,I_{{\overline{X}U}} } \right]$$
(2)

where \({n}_{N}\) is a sample size of neutrosophic data, \({n}_{L}\) lower sample size and \({n}_{U}\) upper sample size, \({\overline{X} }_{N}\) is the mean of neutrosophic data.

Step 2: Declare the process in-control \({\mathrm{LCL}}_{2N}\le {\overline{X} }_{N}\le {\mathrm{UCL}}_{2N}\) and out-of-control if \({\overline{X} }_{N}\ge {\mathrm{UCL}}_{1N}\) or \({\overline{X} }_{N}\le {\mathrm{UCL}}_{1N}\).

where \({\mathrm{LCL}}_{2N}\le {\overline{X} }_{N}\le {\mathrm{UCL}}_{2N}\) are the inner upper and lower control limits and \({\overline{X} }_{N}\ge {\mathrm{UCL}}_{1N}\) and \({\overline{X} }_{N}\le {\mathrm{LCL}}_{1N}\) are the outer upper and lower control limits.

Step 3: The process is supposed to be in-control if at least \(k\) out of \(m\) preceding sample’s mean fall inside \({\mathrm{LCL}}_{2N}\le {\overline{X} }_{N}\le {\mathrm{UCL}}_{2N}\), where \(m\) and \(k\) are any positive integers such that \(m\ge k\) Otherwise, the process is stated to be out-of-control.

Following [30], the four neutrosophic control limits are constructed as

$${\text{LCL}}_{1N} = m_{N} - k_{1N} \frac{{\sigma_{N} }}{{\sqrt {n_{N} } }};\mu_{N} \in \left[ {\mu_{L} ,\mu_{U} } \right];\sigma_{N} \in \left[ {\sigma_{L} ,\sigma_{U} } \right];m_{N} \in \left[ {m_{L} ,m_{U} } \right]$$
(3)
$${\text{UCL}}_{1N} = m_{N} + k_{1N} \frac{{\sigma_{N} }}{{\sqrt {n_{N} } }};\mu_{N} \in \left[ {\mu_{L} ,\mu_{U} } \right];\sigma_{N} \in \left[ {\sigma_{L} ,\sigma_{U} } \right];m_{N} \in \left[ {m_{L} ,m_{U} } \right]$$
(4)
$${\text{LCL}}_{2N} = m_{N} - k_{2N} \frac{{\sigma_{N} }}{{\sqrt {n_{N} } }};\mu_{N} \in \left[ {\mu_{L} ,\mu_{U} } \right];\sigma_{N} \in \left[ {\sigma_{L} ,\sigma_{U} } \right];m_{N} \in \left[ {m_{L} ,m_{U} } \right]$$
(5)
$${\text{UCL}}_{2N} = m_{N} + k_{2N} \frac{{\sigma_{N} }}{{\sqrt {n_{N} } }};\mu_{N} \in \left[ {\mu_{L} ,\mu_{U} } \right];\sigma_{N} \in \left[ {\sigma_{L} ,\sigma_{U} } \right];m_{N} \in \left[ {m_{L} ,m_{U} } \right]$$
(6)

where \({k}_{1N}\epsilon \left[{k}_{1L},{k}_{1U}\right]\) and \({k}_{2N}\epsilon \left[{k}_{2L},{k}_{2U}\right]\) are neutrosophic control limits coefficients.

Assume that the quality control personnel are unclear about earlier subgroups \({i}_{N}={i}_{L}+{i}_{U}{I}_{iN};{I}_{iN}\epsilon \left[{I}_{iL},{I}_{iU}\right]\) and sample size \({n}_{N}={n}_{L}+{n}_{U}{I}_{nN};{I}_{nN}\epsilon \left[{I}_{nL},{I}_{nU}\right]\). The functioning state of the process is based upon the above-mentioned four control limits (Eqs. 3–6). The suggested chart is the generalization of the chart using the MDS sampling scheme under neutrosophic statistics. Further, suppose that \({{\mu }_{N}\epsilon \left[{\mu }_{L},{\mu }_{U}\right]=m}_{N}\epsilon \left[{m}_{L},{m}_{U}\right]\) be the targeted neutrosophic average. Then the probability that the process is in-control under GMDS is defined as

$${P}_{in,N}^{0}={P}_{a,N}+{P}_{s,N}\left[\sum_{J={k}_{N}}^{{m}_{N}}\frac{{m}_{N}!}{j!\left({m}_{N}-j\right)!}{P}_{a,N}^{J}{\left(1-{P}_{in,N}^{0}\right)}^{{m}_{N}-J}\right]$$
(7)
$${P}_{a,N}=\left(2{\Phi }_{N}\left({\mathrm{k}2}_{\mathrm{N}}\right)-1\right)$$
(8)

where \(P_{s,N} = P\left( {LCL_{1N} < \overline{X}_{N} < LCL_{2N} } \right) + P\left( {UCL_{2N} < \overline{X}_{N} < UCL_{1N} } \right) = 2\left\{ {\Phi_{N} \left( {k1_{N} } \right) - \Phi_{N} \left( {k2_{N} } \right)} \right\}\)

Therefore, the formula for in-control ARL is defined as

$${\mathrm{ARL}}_{0,N}=\frac{1}{1-{{\varvec{P}}}_{{\varvec{i}}{\varvec{n}},{\varvec{N}}}^{0}}$$
(9)

Let the process has shift to a new neutrosophic mean \({\mu }_{1N}={m}_{N}+c{\sigma }_{N}\), where \(c\) is a shift constant. Then for the shifted process, the formula for the out-of-control process under GMDS is defined as

$${P}_{in,N}^{1}={P}_{a1,N}+{P}_{s1,N}\left[\sum_{J={k}_{N}}^{{m}_{N}}\frac{{m}_{N}!}{j!\left({m}_{N}-j\right)!}{P}_{a1,N}^{J}{\left(1-{P}_{a1,N}\right)}^{{m}_{N}-J}\right]$$
(10)
$${P}_{a1,N}=P\left({\Phi }_{N}\left({k}_{2N}-c\sqrt{{n}_{N}}\right)+\Phi \left({k}_{2N}+c\sqrt{{n}_{N}}\right)-1\right)$$
(11)

and

$${P}_{s1,N}={\Phi }_{N}\left({k}_{1N}+c\sqrt{{n}_{N}}\right)-{\Phi }_{N}\left({k}_{2N}+c\sqrt{{n}_{N}}\right)+{\Phi }_{N}\left({k}_{1N}-c\sqrt{{n}_{N}}\right)-{\Phi }_{N}\left({k}_{2N}-c\sqrt{{n}_{N}}\right)$$
(12)

; \(i_{N} \in \left[ {i_{L} ,i_{U} } \right],\quad n_{N} \in \left[ {n_{L} ,n_{U} } \right]\)

Then the expression for ARL for the shifted process using GMDS under neutrosophic statistic is defined as

$${\mathrm{ARL}}_{1,N}=\frac{1}{1-{P}_{in,N}^{1}}$$
(13)

3 Results and Discussion

Using the above-mentioned methodology, the control chart coefficients, ARL of the in-control and out-of-control processes have been computed and given in this section. The ARL which is the mean of the run-length distribution is defined as the average number of samples before the process shows an out-of-control situation based upon type-I errors (\(\alpha\)) [1, 33]. When the process is running under an in-control situation the values of ARL are denoted by \({\mathrm{ARL}}_{o}\) and usually considered to be the larger values as the shift is set to zero [34, 35]. The performance of any proposed chart is evaluated by calculating the ARL values of the shifted process and is denoted by \({\mathrm{ARL}}_{1}\) based upon the type-II error (\(\beta\)). The smaller values of \({\mathrm{ARL}}_{1}\) are considered as the better chart for any industrial process, so that the corrective action may be taken quickly to avoid the non-conforming items [36]. Let \({r}_{0N}\) be the specified value of ARL for the in-control process. The influencing parameters are \({k}_{1N}\) and \({k}_{2N}\) which are non-negative integers, \({m}_{N}\) is the neutrosophic number with the condition that \(m\ge k\) and \({I}_{N}\) is the group number representing the contribution of multiple dependent scheme. The control chart coefficients and the values are ARLs are found using the following simulation procedure.

Step 1: Specify the value of \({r}_{0N}\) and determine the values of \({k}_{1N}\epsilon \left[{k}_{1L},{k}_{1U}\right]\) and \({k}_{2N}\epsilon \left[{k}_{2L},{k}_{2U}\right]\) such that \({ARL}_{0,N}\ge {r}_{0N}\).

Step 2: Specify the values of \(c\) and determine the values of \({\mathrm{ARL}}_{1,N}\)

Tables 1, 2, 3, 4, have been generated for \({n}_{L}=5, 10, 20\) and \(30\) with \({\mathrm{ARL}}_{0,N}=200.\) Note here that we assumed the indeterminacy in sample selection. In Tables 1, 2, 3, 4, the determinate value of sample size \({n}_{L}\) is mentioned. We determined the values of \({K}_{1N}\), \({K}_{2N}\) and ARL using various values of \({I}_{N}\) and a wide range of shift levels \(c=\) 0, 0.01, 0.02, 0.05, 0.08, 0.10, 0.20, 0.30, 0.40, 0.50, 0.60, 0.70, 0.80, 0.90, 0.95 and 1.00. It should be noted here that when the process is in-control that is when \(c\) = 0 the value of \({\mathrm{ARL}}_{0,N}\) is approximately equal to 200, which can be observed from Tables 1, 2, 3, 4. For instance in Table 1, when \({I}_{N}=0.2\) the \({\mathrm{ARL}}_{1,N}\epsilon\)[200.03,205.26], \({I}_{N}=0.4\) the \({\mathrm{ARL}}_{1,N}\epsilon\)[200.04,206.88], \({I}_{N}=0.6\) the \({\mathrm{ARL}}_{1,N}\epsilon\)[200.01,205.74], \({I}_{N}=0.8\) the \({\mathrm{ARL}}_{1,N}\epsilon\)[200.07,207.04] and when \({I}_{N}=1.0\) the \({\mathrm{ARL}}_{1,N}\epsilon\)[200.2,205.64]. The values of ARL of the shifted process \({\mathrm{ARL}}_{1,N}\) rapidly decrease as the \(c\), the shift levels going to increase from 0.01 to 1.00. For instance, from Table 2, when \({I}_{N}=0.5\) and \(c\) = 0.01 then \({\mathrm{ARL}}_{1,N}=\) [199.13,199.84], \(c\) = 0.02 then \({\mathrm{ARL}}_{1,N}\epsilon\) [196.57,196], \(c\) = 0.40 then \({\mathrm{ARL}}_{1,N}\epsilon\) [16.25,9.62] and for \(c\) = 1.0 \({\mathrm{ARL}}_{1,N}=\) [1.57,1.17]. These results show the validity of the developed technique. According to the definition of ARL of the shifted process, its smaller values convey quickly the process deterioration. Thus, if a shift of 0.02 amount creeps into the production process it is signaled after 196 samples, a shift of 0.40 amount is signaled after only 16 samples and a shift of amount 1.00 is detected as early as after only 1.57 samples. This shows that the developed methodology is very much effective in lessening the burden of defective items and ultimately leads to maximizing the profits and good repute to the firm. It can also be observed that as the value of \({n}_{L}\) increases from 5 to 30 then the \({\mathrm{ARL}}_{1,N}\) significantly decreases. For instance, in Table 1, when \({I}_{N}=0.4\) and \(c\) = 0.10 then \({\mathrm{ARL}}_{1,N}\) \(\epsilon\) [163.66, 157.2], in Table 2 for the same parameters \({\mathrm{ARL}}_{1,N}\) \(\epsilon\) [137.61, 126.2], in Table 3 for the same parameters \({\mathrm{ARL}}_{1}\) \(\epsilon\) [103.08, 85.06] and in Table 4 this range is [81.12, 63.9] which clearly indicate that larger values of \({I}_{N}\) are beneficial for early detection of out-of-control process.

Table 1 The average run length \({\mathrm{ARL}}_{1}\) values under neutrosophic statistics for \({n}_{L}=5\)
Full size table
Table 2 The average run length \({\mathrm{ARL}}_{1}\) values under neutrosophic statistics for \({n}_{L}=10\)
Full size table
Table 3 The average run length \({\mathrm{ARL}}_{1}\) values under neutrosophic statistics for \({n}_{L}=20\)
Full size table
Table 4 The average run length \({\mathrm{ARL}}_{1}\) values under neutrosophic statistics for \({n}_{L}=30\)
Full size table

Aslam and Khan [29] proposed the X-bar control chart using the single sampling scheme using neutrosophic statistics. Aslam et al. [30] proposed the X-bar control chart using MDS under neutrosophic statistics.

4 Monitoring Using Simulated Data

In this section, the advantages of the proposed control chart have been described on the basis of simulated data generated under the proposed methodology. We will compare the efficiency of the proposed study with those [29] and [30]. Simulation is used to describe the model of a real world situation/ process to be executed in the computer for monitoring key parameters of the selected system or process. The purpose is to gain insight into the working of the system under the random variation. To examine the competence of the proposed chart under the GMDS sampling, the data is simulated using specified control chart parameters.

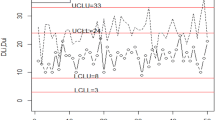
Through simulation, the first 20 observations are generated from an in-control process considering \({\mathrm{ARL}}_{0,N}\) = 200 with \({n}_{L}=5\) and \({I}_{N}=0.40\) from the normal distribution with mean zero and unit variance. The next 20 observations are generated from the shifted process with a shift of 0.50 in mean, then the \({\mathrm{ARL}}_{1,N}\) is [21.91, 14.82] when \({I}_{N}\) is 0.4 from Table 1. The proposed control is shown in Fig. 1. The control chart proposed by [30] is shown in Fig. 2 and the control chart proposed by [29] is shown in Fig. 3. Figure 1 shows that a shift of 0.50 is detected after the 33rd observation from the generated sample data having an interval [0.3175, 1.4171]. This shows the detecting ability of the proposed chart when the process mean is hit by a shift of 0.50. Figures 2 and 3 do not detect the shift in the process (Table 5).

Fig. 1
figure 1

The proposed control chart for simulated data

Full size image
Fig. 2
figure 2

The control chart proposed by [30] for the simulated data

Full size image
Fig. 3
figure 3

The control chart proposed by [29] for simulated data

Full size image
Table 5 Simulation data under \({\mathrm{ARL}}_{0}\)= 200 with \({n}_{L}=5\) and \({I}_{N}=0.40\)
Full size table

5 Fertilizer Monitoring Using Real Data

For the practical application of the proposed chart, an example from the fertilizer industry has been included in the paper. To achieve this objective data on fertilizer production has been included in this article. The fertilizer production data collected after every 10 min of a gap in an agriculture form in Malaysia [[37]] have been used to construct the control chart. Table 6 has been generated for 20 observations at six different time intervals with mean values. The four control limits are for the fertilizer production data calculated as:

Table 6 Real data of 20 samples of fertilizer production, taken from [37]
Full size table

\({LCL}_{1}=\left[15.59, 15.61\right]\),

LCL2 = [15.65, 15.70],

UCL2 = [16.58, 16.47],

UCL1 = [16.64, 16.58].

The statistics computed from fertilizer production data have been plotted on the control limits. The proposed control is shown in Fig. 4. The control chart proposed by [30] is shown in Fig. 5 and the control chart proposed by [29] is shown in Fig. 6. Figures 4, 5, 6 shows that some points are out of control for the fertilizer data. Figure 4 provided a narrow indeterminacy interval in control limits than the control limits in Figs. 5 and 6.

Fig. 4
figure 4

The proposed control for the real data

Full size image
Fig. 5
figure 5

The proposed control proposed by [30] for the real data

Full size image
Fig. 6
figure 6

The control chart proposed by [29] for real data

Full size image

6 Concluding Remarks

In this article, an efficient control chart using the generalized MDS sampling for neutrosophic statistics has been presented. The control chart coefficients have been computed for different sample sizes. The ARL values of the shifted process have been calculated which shows that the proposed chart is an efficient monitoring chart for quickly detecting different process shifts. The simulation study of the proposed chart has also been made for evaluating its quick detecting ability. A real-world example of fertilizer data has been included to evaluate the efficient detecting ability of the proposed chart. The proposed chart will explicitly reduce the amount of scrap and rework items in any manufacturing unit. It has been observed that the proposed chart is a valuable addition to the toolkit of the quality control experts. The proposed study using multivariate/complex analysis can be extended as future research.