Fuzzy Transforms for Hesitant, Soft or Intuitionistic Fuzzy Sets

Abstract

Classical F-transform for lattice-valued fuzzy sets can be defined using monadic relation in Zadeh’s monad or, equivalently, as a special semimodule homomorphism. In this paper, we use an analogical approach and by choosing suitable monads and semimodule homomorphisms, we define F-transform for hesitant, intuitionistic or fuzzy soft sets. We prove that these F-transforms naturally extend classical lattice-valued F-transform for lattice-valued fuzzy sets.

1 Introduction

Fuzzy transform (F-transform, shortly) represents a method in fuzzy set theory, which is used in many applications in signal and image processing [11, 13, 15], signal compressions [45, 51], numerical solutions of ordinary and partial differential equations [27, 52, 54], data analysis [14, 16, 46] and many other applications. This concept was introduced for the first time in [44] both for classically defined [0, 1]-valued fuzzy sets and L-valued fuzzy sets, where L is a complete residuated lattice. The F-transform method represents a special transformation map based on a system of fuzzy sets defined on a given universe, which is called a fuzzy partition. In general, any variant of a fuzzy partition then represents a pair $(X,{{\mathscr {A}}})$, where X is a set and ${{\mathscr {A}}}=\{A_i:i\in I\}$ is a set of fuzzy sets in X. Based on a fuzzy partition $(X,{{\mathscr {A}}})$, the F-transform is then a special map $[0,1]^X\rightarrow [0,1]^I$ transforming fuzzy sets from a set X to fuzzy sets in the index set I of a fuzzy partition ${\mathscr {A}}$. This procedure makes it possible to significantly reduce the work with the original fuzzy sets, especially in those areas, such as methods for image processing, where the original set X is huge, while the index set I from the fuzzy partition can be significantly smaller.

Fuzzy sets, both classical and with values in lattices, are not the only tool that allows us to work with uncertainty, both theoretically and with a number of practical applications. Currently, there is a whole range of theories and theoretical structures which are based on principles of fuzzy set theory but create their own tools and methods for solving theoretical and practical problems. These theories undoubtedly include the theory of intuitionistic fuzzy sets, the theory of fuzzy soft sets and the theory of hesitant fuzzy sets. The common feature of these three theories is, among other things, a large number of current publications dealing with theoretical properties and application possibilities of these theories. For a basic overview of these theories and their applications, see, e.g., [1, 4, 6, 29, 57, 60] for intuitionistic fuzzy sets, [2, 20, 31,32,33,34, 37, 42] for fuzzy soft sets and [50, 55, 56, 59] for hesitant fuzzy sets.

In our previous paper [39], we tried to unify some of methods used in all these theories. For this purpose, we used a special tool from the theory of categories, namely the theory of monads (see, e.g., [35, 38, 47, 48]), which allows to unify not only various types of relations but also transformation operators defined by these relations. In the present paper, we use these results concerning monads from [39] and we focus on the F-transform method and its possible modifications in these structures. For such F-transform variants, we will require that their definitions are based on the same principles as the F-transforms for classical L-fuzzy sets, where L is a complete residuated lattice. It is clear that there are several equivalent definitions of the F-transform which can be used (see, e.g., [38, 40]). For our purposes, we choose two seemingly different principles which can be used to define the F-transform for L-fuzzy sets. These two principles are based on the following methods which are equivalent for L-fuzzy sets:

• (I) The definition of the F-transform as a complete semimodule homomorphism for appropriate semiring ${\mathscr {R}}$ and ${\mathscr {R}}$-semimodules,

• (II) The definition of the F-transform as a mapping defined by a special monadic relation in the monad based on the power set structure Z(X).

These two methods of defining F-transforms then represent general possibilities how the definition of the F-transform can be extended to other fuzzy type structures. In the paper, we apply these two methods of defining F-transforms to fuzzy soft sets, hesitant fuzzy sets and intuitionistic fuzzy sets and we prove that F-transforms for these fuzzy type structures can be equivalently defined as extensions of special monadic relations or complete semimodule homomorphisms, respectively.

These results are a contribution to the unification of methods and theories of various fuzzy type structures. This unification makes it possible not only to use the same methods and tools in different types of these structures, but also brings the possibility to use hitherto unused tools and methods in various fuzzy type structures.

This paper is structured as follows: Sect. 2 presents some basic structures and methods we use in this work, including basic definitions of monads, semirings and semimodule homomorphisms. Section 3 describes basic ideas how to use monads and semimodule homomorphisms for a construction of the F-transform in some categories, or how the F-transform can be defined by general semimodule homomorphisms. Section 4 presents new theoretical results concerning equivalent constructions of the F-transform methods in hesitant, intuitionistic or fuzzy soft sets. In Sect. 5, we present a possible application of F-transform for these fuzzy type structures, namely we introduce a general fuzzy type inference mechanism based on IF–THEN fuzzy type rules as an application of fuzzy type F-transform for hesitant, intuitionistic or fuzzy soft sets. In Sect. 6 we present a matrix calculation of the F-transform for these fuzzy type structures.

2 Materials and Methods

This section introduces structures we use in lattice-valued fuzzy theory and some methods we use in fuzzy transform constructions.

The basic membership structure of fuzzy sets in the paper is a complete residuated lattice (see, e.g., [43]), i.e. a structure ${{\mathscr {L}}}=(L,\wedge ,\vee ,\otimes ,\rightarrow ,0_L,1_L)$ such that $(L,\wedge ,\vee )$ is a complete lattice, $(L,\otimes ,1_L)$ is a commutative monoid with operation $\otimes$ isotone in both arguments and $\rightarrow$ is a binary operation which is residuated with respect to $\otimes$. Recall that a negation of an element a in ${\mathscr {L}}$ is defined by $\lnot a=a\rightarrow 0_L$.

Although intuitionistic fuzzy sets are currently defined for much more general membership value structures, to simplify the technical side of this paper, we will use the classical membership value structure based on a complete MV-algebra with classically defined involutive negation. For an overview of current lattices used in the theory of intuitionistic fuzzy sets, see [7].

Hence, in the case of intuitionistic fuzzy sets we use a special example of a residuated lattice ${{\mathscr {L}}}$, namely, an MV-algebra [10], i.e., a structure $\mathcal{L}=(L,\oplus ,\otimes ,\lnot ,0_L,1_L)$ satisfying the following axioms:

• (i) $(L,\otimes ,1_L)$ is a commutative monoid,

• (ii) $(L,\oplus ,0_L)$ is a commutative monoid,

• (iii) $\lnot \lnot x=x$, $\lnot 0_L=1_L$,

• (iv) $x\oplus 1_L=1_L$, $x\oplus 0_L=x$, $x\otimes 0_L=0_L$,

• (v) $x\oplus \lnot x=1_L, x\otimes \lnot x=0_L$,

• (vi) $\lnot (x\oplus y)=\lnot x\otimes \lnot y$, $\lnot (x\otimes y)=\lnot x\oplus \lnot y$,

• (vii) $\lnot (\lnot x\oplus y)\oplus y=\lnot (\lnot y\oplus x)\oplus x$,

for all $x,y\in X$.

If we put

$$\begin{aligned} x\vee y& =(x\oplus \lnot y)\otimes y,\quad x\wedge y=(x\otimes \lnot y)\oplus y,\\x\rightarrow y& =\lnot x\oplus y, \end{aligned}$$

then $(L,\wedge ,\vee ,\otimes ,\rightarrow ,0_L,1_L)$ is a residuated lattice. MV-algebra is called a complete, if that lattice is a complete lattice. A standard example of an MV-algebra is the Lukasiewicz algebra ${{\mathscr {L}}}_{L}=([0,1], \oplus ,\otimes ,\lnot ,0,1)$, where

$$\begin{aligned} x\otimes y &=0\vee (x+y-1),\quad \lnot x=1-x,\\ x\oplus y &=1\wedge (x+y). \end{aligned}$$

If ${\mathscr {L}}$ is a complete residuated lattice, an ${\mathscr {L}}$-fuzzy set in a crisp set X is a map $f:X\rightarrow L$. The set of all $\mathcal L$-fuzzy sets in X is denoted by Z(X).

We recall a basic definition of a F-transform for ${\mathscr {L}}$-fuzzy sets defined by a fuzzy partition.

Definition 1

[44]

• 1. A set ${{\mathscr {A}}}=\{A_y:\in Y\}\subseteq Z(X)$ is called an ${\mathscr {L}}$-fuzzy partition of a set X.

• 2. A mapping $F_{X,{{\mathscr {A}}}}:Z(X)\rightarrow Z(Y)$ is called the F-transform based on ${\mathscr {A}}$, if for $s\in Z(X),y\in Y$, $F_{X,{{\mathscr {A}}}}(s)(y)=\bigvee _{x\in X}s(x)\otimes A_y(x)$.

Remark 1

The notion of the fuzzy partition for lattice-valued fuzzy sets can be defined in various ways. The above definition is based on the original definition of this term given in the [45]. An overview of possible definitions of fuzzy partitions was presented in [41].

2.1 Monads in Categories

For basic information about the category theory, see [23, 30]. As we mentioned in the introduction, the main tool from the category theory we will use is the monad in a category. Due to the type of fuzzy structures that we will use, we will focus only on monads in the category $\mathbf{Set}$, consisting of sets as objects and mappings as morphisms. We use the following version of the monad in the category $\mathbf{Set}$, which is called the monad in a clone form.

Definition 2

[39] A structure $\mathbf{T}=(T,\lozenge ,\eta )$ is called a monad (in clone form) in the category $\mathbf{Set}$, if

• 1. $T:\text {obj}(\mathbf{Set})\rightarrow \text {obj}(\mathbf{Set})$ is mapping between objects of $\mathbf{Set}$,

• 2. For morphisms $f:X\rightarrow T(Y)$ and $g:Y\rightarrow T(Z)$ there exists their composition $g\lozenge f:X\rightarrow T(Z)$, (called the Kleisli composition) which is associative,

• 3. $\eta$ is a system of morphisms $\eta _X:X\rightarrow T(X)$, for any object X of $\mathbf{Set}$,

• 4. For any morphism $f:X\rightarrow T(Y)$, $\eta _Y\lozenge f=f$ holds,

• 5. $\lozenge$ is compatible with composition of morphisms, i.e., for morphisms $f:X\rightarrow Y$, $g:Y\rightarrow T(Z)$, we have $g\lozenge (\eta _Y . f)=g . f$.

Let us consider the following classical example of a monadic theory.

Example 1

[49] Let ${{\mathscr {L}}}$ be a complete residuated lattice. The monad ${\mathbf{Z}}=({Z},\boxplus ,{\chi })$ is defined by

• 1. ${Z}:\mathbf{Set}\rightarrow \mathbf{Set}$ is an object function defined by ${Z}(X)=L^X$,

• 2. For each $X\in \mathbf{Set}$, ${\chi }^X:X\rightarrow Z(X)$ is the characteristic map of elements from X, i.e., for $x,y\in X$, $\chi ^X(x)(y)=\chi ^X_{\{x\}}(y)$,

• 3. For each $f:X\rightarrow Z(Y)$ and $g:Y\rightarrow Z(V)$ in $\mathbf{Set}$, $g\boxplus f:X\rightarrow Z(V)$ is defined by

  $$\begin{aligned} (g\boxplus f)(x)(z)=\bigvee _{y\in Y}f(x)(y)\otimes g(y)(z). \end{aligned}$$

$\square$

With the help of the monadic theory in a category, we can now recall the concept of a monadic relation. This construction was first explicitly mentioned in the paper of Manes [36] and has recently proven to be a universal construction of relations for many fuzzy type structures (e.g., see [38]). We use the following form of a monadic relation in the category $\mathbf{Set}$.

Definition 3

[36] Let $\mathbf{T}=(T,\lozenge ,\eta )$ be a monad in the category $\mathbf{Set}$.

• 1. A $\mathbf{T}$-relation R from an object X to an object Y in $\mathbf{Set}$, in symbol $R:X\rightsquigarrow Y$, is a morphism $R:X\rightarrow T(Y)$ in the category $\mathbf{Set}$.

• 2. If $R:X\rightsquigarrow Y$ and $S:Y\rightsquigarrow Z$ are $\mathbf{T}$-relations, their composition is a $\mathbf{T}$-relation $S\lozenge R:X\rightsquigarrow Z$.

In fuzzy mathematics and its applications, various types of approximation and transformation operators are very often used, which convert fuzzy objects defined over the basic structure X to fuzzy objects over the other structure Y. Many of these transformation operators are special examples of a general transformation operator defined by $\mathbf{T}$-relations as it is defined in the following definition.

Definition 4

[38] Let $\mathbf{T}=(T,\lozenge ,\xi )$ be a monad in the category $\mathbf{Set}$ and let $R:X\rightsquigarrow Y$ be a $\mathbf{T}$-relation from X to Y. Then a R-transformation of objects from T(X) is the morphism

$$\begin{aligned} R\lozenge 1_{T(X)}: T(X)\rightarrow T(Y). \end{aligned}$$

2.2 Semirings and Semimodules

Another tool that we will use for the construction of F-transforms for general fuzzy type structures is based on the theory of semirings and semimodules. The semiring appears for the first time in [8] and this notion was elaborated in [21]. For more information about semimodules and their applications see, e.g., [22, 58].

Definition 5

[8] A semiring ${{\mathscr {R}}}=(R,+,\times ,0_R,1_R)$ is an algebraic structure with the following properties:

• (i) $(R,+,0_R)$ is a commutative monoid,

• (ii) $(R,\times ,1_R)$ is a monoid,

• (iii) $x\times (y+z)=x\times y+x\times z$ holds for all $x,y,z\in R$,

• (iv) $0_R\times x=x\times 0_R=0_R$ holds for all $x\in R$.

A semiring is called commutative, if $(R,\times ,1_R)$ is a commutative monoid. A semiring is called complete, if the sum $+_R$ is defined for arbitrary set $X\subseteq R$ of elements. In that case this sum is denoted by $\sum _{x\in X}^{{\mathscr {R}}}$. An important example of a semiring which seem to be very useful for the F-transform theory was published in the paper of Di Nola and Gerla [18].

Example 2

• (1) Let ${\mathscr {L}}$ be a residuates lattice. Then, the reduct $\mathcal{L}^{\vee }=(L,\vee ,\otimes ,0_L,1_L)$ is a commutative semiring.

• (2) Let ${\mathscr {L}}$ be a MV-algebra. Then, the reduct $\mathcal{L}^{\wedge }=(L,\wedge ,\oplus ,1_L,0_L)$ is a commutative semiring.

$\square$

The notion of a semimodule over a semiring is taken from [21]. We use the commutative version of this notion only.

Definition 6

[21] Let ${{\mathscr {R}}}=(R,+,\times ,0_R,1_R)$ be a commutative semiring. An ${{\mathscr {R}}}$-semimodule is a commutative monoid $\mathcal{M}=(M,\oplus _M,0_M)$ for which the external multiplication $R\times M\rightarrow M$, denoted by r.m, is defined and which, for all $r,r'\in R$ and $m,m'\in M$, satisfies the following equations:

• (i) $(r\times r').m=r.(r'.m)$,

• (ii) $r.(m\oplus _M m')=r.m\oplus _M r.m'$,

• (iii) $(r+r').m=r.m\oplus _M r'.m$,

• (iv) $1_R.m=m$, $0_R.m=r.0_M=0_M$.

In the paper [17] the following examples of semimodules were presented.

Example 3

[17] (1) Let $X\ne \emptyset$, ${{\mathscr {L}}}$ be a residuated lattice and let ${{\mathscr {L}}}^{\vee }=(L,\vee ,\otimes ,0_L,1_L)$ be its semiring reduct. For all $f,g\in M=L^X$ define

$$\begin{aligned} (f\oplus _M g)(x)&= {} f(x)\vee g(x),\\ p.f(x)& = {} p\otimes f(x),\\ 0_M\in M,\quad 0_M(x)& = {} 0_L,\quad x\in X, p\in L. \end{aligned}$$

Then ${{\mathscr {L}}}^X=(M,\oplus _M,0_M)$ is an $\mathcal{L}^{\vee }$-semimodule.

(2) Let $X\ne \emptyset$, ${{\mathscr {L}}}$ be a MV-algebra and let ${{\mathscr {L}}}^{\wedge }=(L,\wedge ,\oplus ,1_L,0_L)$ be its semiring reduct. For all $f,g\in M=L^X$ define

$$\begin{aligned} (f\oplus _M g)(x)& = {} f(x)\wedge g(x),\\ p.f(x)& = {} p\oplus f(x),\\ 0_M\in M,\quad 0_M(x)& = {} 1_L,\quad x\in X,p\in L. \end{aligned}$$

Then, ${{\mathscr {L}}}^X=(M,\oplus _M,0_M)$ is an $\mathcal{L}^{\wedge }$-semimodule. $\square$

Definition 7

Let ${{\mathscr {R}}}=(R,+,\times ,0_R,1_R)$ be a semiring and $\mathcal{M}=(M,\oplus _M,0_M)$ and ${{\mathscr {N}}}=(N,\oplus _N,0_N)$ be $\mathcal{R}$-semimodules. Then, $G:{{\mathscr {M}}}\rightarrow {{\mathscr {N}}}$ is an $\mathcal{R}$-homomorphism from ${{\mathscr {M}}}$ to ${\mathscr {N}}$, if $G:M\rightarrow N$ is a mapping such that the following conditions hold:

• (i) $G(m\oplus _Mm')=G(m)\oplus _NG(n')$, for all $m,m'\in M$,

• (ii) $G(r\times m)=r\times G(m)$, for all $m\in M,r\in R$.

If a ${{\mathscr {R}}}$-semimodule ${{\mathscr {M}}}=(M,+_M,0_M)$ is such that for any subset $N\subseteq M$, there exists the sum of elements $x\in N$, then ${{\mathscr {M}}}$ is called a complete $\mathcal{R}$-semimodule. A sum of elements $x\in N$ is denoted by $\bigoplus _{x\in N}^{{\mathscr {M}}}x$. If ${{\mathscr {M}}}$ and ${{\mathscr {P}}}$ are complete ${{\mathscr {R}}}$-semimodules, then a ${\mathscr {R}}$-homomorphism $G:{{\mathscr {M}}}\rightarrow {{\mathscr {P}}}$ is called complete, if

$$\begin{aligned} \forall N\subseteq M,\quad G(\bigoplus _{x\in N}^\mathcal{M}x)=\bigoplus _{x\in N}^{{\mathscr {P}}}G(x). \end{aligned}$$

3 F-transform for Fuzzy Type Structures: Basic Ideas

As we mentioned in Introduction, the F-transform for fuzzy type structures can be based on methods (I) and (II). We describe basic ideas how it can be done in a general case. Concrete applications of these methods for fuzzy soft sets, hesitant fuzzy sets and intuitionistic fuzzy sets will be presented in the next section. For all these concrete applications, we prove that both methods (I) and (II) are equivalent.

3.1 F-transform Defined by a Monad

The idea how to use monads for a construction of the F-transform for some fuzzy type structures is based on the following equivalent formulation of the standard F-transform for ${\mathscr {L}}$-valued fuzzy sets, which was proven in [38]:

Let $\mathbf{Z}=({Z},\boxplus ,{\chi })$ be the monad in a category $\mathbf{Set}$ from Example 1 and let ${{\mathscr {A}}}=\{A_i:i\in |{{\mathscr {A}}}|\}$ be a $\mathcal L$-fuzzy partition of a set X. We can define a $\mathbf{Z}$-relation $Z_{{\mathscr {A}}}:X\rightsquigarrow |{{\mathscr {A}}}|$, such that

$$\begin{aligned} x\in X, i\in |{{\mathscr {A}}}|,\quad Z_{{\mathscr {A}}}(x)(i)=A_i(x). \end{aligned}$$

Then, it can be easily proven that for the F-transform $F_{X,{{\mathscr {A}}}}:Z(X)\rightarrow Z(|\mathcal{A}|)$, it holds

$$\begin{aligned} F_{X,{{\mathscr {A}}}}=Z_{{\mathscr {A}}}\boxplus 1_{Z(X)}. \end{aligned}$$

This equivalent formulation can be now used to define a more general form of the F-transform for various fuzzy type structures. To realize this construction for a given fuzzy type structure, in the category $\mathbf{Set}$ we need a monad $\mathbf{T}=(T,\eta ,\lozenge )$, which is based on power set objects of this fuzzy type structure. Moreover, to be able to use a general construction of the F-transform, we need to realize the following steps:

• 1. For an arbitrary object $X\in \mathbf{K}$, we need to define a subset ${{\mathscr {A}}}=\{q_i:i\in |{{\mathscr {A}}}|\}\subseteq T (X)$, called a $\mathbf{T}$-partition of X. For a $\mathbf{T}$-partition ${\mathscr {A}}$, by $|{{\mathscr {A}}}|$ we denote the index set of ${\mathscr {A}}$.

• 2. For a $\mathbf{T}$-partition ${{\mathscr {A}}}$ of X we need to define a $\mathbf{T}$-relation $T_{{\mathscr {A}} }:X\rightsquigarrow |{{\mathscr {A}}}|$ with some appropriate properties.

Then, the F-transform in the category $\mathbf{Set}$ based on a $\mathbf{T}$-partition ${{\mathscr {A}}}$ of an object X can be defined as a morphism

$$\begin{aligned} T_{{\mathscr {A}}}\lozenge 1_{T(X)}:T(X)\rightarrow T(|{{\mathscr {A}}}|). \end{aligned}$$

(1)

Morphisms defined in (1) by steps 1.–2., will be called F-transforms of a fuzzy type structure defined by the monad $\mathbf{T}$. It should be noted that this procedure is not intended for very general categories and monads, although it can be formally implemented for them as well. The goal of this procedure is to create meaningful variants of F-transforms for various fuzzy type objects, which would be analogous to the F-transform for classical ${\mathscr {L}}$-fuzzy sets. This means that we cannot describe a universal procedure how, for example, to choose a concrete definition of a $\mathbf{T}$-partition ${\mathscr {A}}$ or a $\mathbf{T}$-relation $T_{{\mathscr {A}}}$, which will always depend on the choice of a particular fuzzy type structure.

On the other hand, if a fuzzy type structure is an extension of ${\mathscr {L}}$-fuzzy sets, it is natural to assume that the F-transform of this fuzzy type structure in the category $\mathbf{Set}$ based on a $\mathbf{T}$-partition ${\mathscr {A}}$ is an extension of the standard F-transform of ${\mathscr {L}}$-fuzzy sets. To verify it, we can use the following definition.

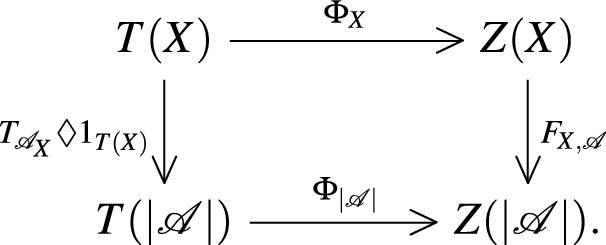
Definition 8

Let $\mathbf{T}=(T,\lozenge ,\eta )$ be a monad in a category $\mathbf{Set}$. Then the standard F-transform of ${\mathscr {L}}$-fuzzy sets is called to be a special case of the F-transform defined by the monad $\mathbf{T}$, if

• 1. For each set $X\in \mathbf{Set}$ and each ${\mathscr {L}}$-fuzzy partition ${{\mathscr {A}}}$ in X, there exists a $\mathbf{T}$-partition ${{\mathscr {A}}}_X\subseteq T(X)$ of X such that $|{{\mathscr {A}}}_X|=|\mathcal{A}|$,

• 2. There exists a natural transformation

  $$\begin{aligned} \Phi :T\rightarrow Z, \end{aligned}$$

  where for a morphism $f:X\rightarrow Y$, $T(f):T(X)\rightarrow T(Y)$ is defined by $T(f)=\eta _Y.f\lozenge 1_{T(X)}$.

• 3. For each object $X\in \mathbf{Set}$, the following diagram commutes:

  

3.2 F-transform Defined as a Semimodule Homomorphism

The idea how the F-transform of classical ${\mathscr {L}}$-fuzzy sets can be defined by semimodule homomorphisms was presented in [40]. Roughly speaking, the F-transforms of ${\mathscr {L}}$-fuzzy sets from Z(X) can be identified with complete ${{\mathscr {L}}}^{\vee }$-semimodule homomorphisms $G:{{\mathscr {L}}}^X\rightarrow {{\mathscr {L}}}^Y$ between $\mathcal{L}^{\vee }$-semimodules from Example 3(1). Hence, the F-transform of ${\mathscr {L}}$-fuzzy sets from Z(X) is a mapping $G:Z(X)\rightarrow Z(Y)$, such that for arbitrary set $\{f_i:i\in I\}\subseteq Z(X)$ and arbitrary $\alpha \in L,f\in Z(X)$, we have

$$\begin{aligned} G\left(\bigoplus ^{{{\mathscr {L}}}^X}_{i\in I}f_i\right)=\bigoplus ^{{{\mathscr {L}}}^Y}_{i\in I}G(f_i),\\ G(\alpha \otimes f)=\alpha \otimes G(f), \end{aligned}$$

where we use notations from Definition 7 and Example 3. To be able to use this procedure with another fuzzy type structure, we must first define a new semiring ${\mathscr {R}}$ and a new ${\mathscr {R}}$-semimodules corresponding this fuzzy type structure, which would be the basis for a new ${{\mathscr {R}}}$-semimodule homomorphisms. This ${\mathscr {R}}$-semimodule homomorphism can then be defined as the F-transform of this fuzzy type structure.

4 F-transforms for Soft, Hesitant and Intuitionistic ${\mathscr {L}}$-Fuzzy Sets

We will show how to use both methods mentioned in the previous section to define the F-transforms operators for the given fuzzy type structure. For this purpose, we will mainly use the monads for these fuzzy type structures, the existence of which was proven in [38] and which will allow us to define the F-transform using the method given in Sect. 3.1. For each of the mentioned fuzzy type structures and its monad $\mathbf{T}$, we define a $\mathbf{T}$-partition ${{\mathscr {A}}}$ and, in accordance with the method presented in Sect. 3.2, for each of these fuzzy type structures, we define a new example of a semiring ${\mathscr {R}}$ and an ${\mathscr {R}}$-semimodule $\mathcal{M}$. Using these two types of constructions, we prove that both generate the same F-transform morphisms.

Finally, we prove that this F-transform is a generalization of the standard F-transform for ${\mathscr {L}}$-fuzzy sets.

4.1 F-transform for Hesitant ${\mathscr {L}}$-Fuzzy Sets

We recall the definition of hesitant ${\mathscr {L}}$-fuzzy sets, which was presented in [56]. In this section ${\mathscr {L}}$ is a complete residuated lattice.

Definition 9

[56] A hesitant ${{\mathscr {L}}}$-fuzzy set in a set X is a mapping $h:X\rightarrow 2^L$, i.e., for $x\in X$, $h(x)\subseteq L$.

In this part we deal with the construction of the hesitant F-transform (i.e., F-transform for hesitant ${\mathscr {L}}$-fuzzy sets) using a monad and semimodule homomorphisms. For this purpose, we use the monad defined by the power set structure of all hesitant $\mathcal L$-fuzzy sets in a set X, the existence of which was proven in the [39] and which is presented in the following definition.

Definition 10

[39] The monad $\mathbf{H}=(H,\diamond ,\sigma )$ in the category $\mathbf{Set}$ is defined by

• 1. The object function $H:obj(\mathbf{Set})\rightarrow obj(\mathbf{Set})$ is defined by $H(X)=\{h|h:X\rightarrow 2^L\}$.

• 2. If $f:X\rightarrow H(Y)$ and $g:Y\rightarrow H(Z)$ are $\mathbf{Set}$-morphisms, for arbitrary $x\in X,z\in Z$ we set

  $$\begin{aligned}&g\diamond f:X\rightarrow H(Z), \end{aligned}$$

  (2)
  $$\begin{aligned}&g\diamond f(x)(z)=\bigcup _{y\in Y}f(x)(y)\otimes g(y)(z)\subseteq L, \end{aligned}$$

  (3)

  where for $A,B\subseteq L$, $A\otimes B=\{\alpha \otimes \beta |\alpha \in A,\beta \in B\}$ and $A\otimes \emptyset =\emptyset$.

• 3. For $X\in \mathbf{Set}$, $\sigma _X:X\rightarrow H(X)$ is defined by

  $$\begin{aligned} x,z\in X,\quad \sigma _X(x)(z)={\left\{ \begin{array}{ll}\{1_L\},&{} x=z\\ \emptyset , &{} x\ne z\end{array}\right. }. \end{aligned}$$

According to Sect. 3.1, for a definition of the hesitant F-transform defined by this monad we need to define $\mathbf{H}$-partitions (which are also called hesitant partitions of a set X) for a monad $\mathbf{H}$.

Definition 11

A subset ${{\mathscr {A}}}=\{h_y:y\in Y\}\subseteq H(X)$ is a called a $\mathbf{H}$-partition of X.

According to Sect. 3.2, let us consider the following propositions, introducing new semiring ${\mathscr {R}}$ and a complete ${\mathscr {R}}$-semimodule ${\mathscr {M}}$. In what follows, by $\otimes$ we understand a multiplication from a residuated lattice ${\mathscr {L}}$.

Proposition 1

Let ${\mathscr {L}}$ be a complete residuated lattice and let $\mathcal{R}=(R,+,\times ,0_R,1_R)$ be a structure such that

• 1. $R=2^L=\{A:A\subseteq L\}$,

• 2. $A,B\in R, \quad A+B:=A\cup B$,

• 3. $A,B\in R, \quad A\times B:=A\otimes B=\{a\otimes b:a\in A,b\in B\}, \quad A\times \emptyset =\emptyset$,

• 4. $0_R=\emptyset , 1_R=\{1_L\}$.

Then, ${\mathscr {R}}$ is a semiring.

The proof is straightforward and it will be omitted.

Proposition 2

Let $X\in \mathbf{Set}$ and let the structure $\mathcal{H}(X)=(H(X),\oplus _H,0_H)$ be defined by

• 1. Let ${\mathscr {R}}$ be the semiring from Proposition 1 and let the external multiplication $.:R\times H(X)\rightarrow H(X)$ be defined for arbitrary $A\in R,h\in H(X),x\in X$ by

  $$\begin{aligned} A.h(x):=A\otimes h(x)=\{\alpha \otimes \beta :\alpha \in A,\beta \in h(x)\}, \end{aligned}$$

• 2. $h,g\in H(X),\quad (h\oplus _H g)(x):=h(x)\cup g(x)$,

• 3. $0_H\in H(X)$ is such that $0_H(x)=\emptyset$ for all $x\in X$.

Then, ${{\mathscr {H}}}(X)$ is a complete ${{\mathscr {R}}}$-semimodule. The sum of elements $\{h_i:i\in I\}$ in ${{\mathscr {H}}}(X)$ will be denoted by $\bigoplus _{i\in I}^{H(X)}h_i$.

The proof represents only a simple calculations and it will be omitted.

To define a variant of the F-transform for hesitant fuzzy sets we need the following lemma which enables to describe elements from an ${\mathscr {R}}$-semimodule ${{\mathscr {H}}}(X)$ in a uniform way.

Lemma 1

Let $X\in \mathbf{Set}$.

• 1. The set $\{\sigma _X(x):x\in X\}$ is a ${{\mathscr {R}}}$-base of ${{\mathscr {H}}}(X)$.

• 2. For an arbitrary element h in the ${\mathscr {R}}$-semimodule ${{\mathscr {H}}}(X)$, we have

  $$\begin{aligned} h={\bigoplus _{x\in X}^{H(X)}}h(x).\sigma _X(x). \end{aligned}$$

Proof

In fact, for $z\in X$, we have

$$\begin{aligned} \left( \bigoplus _{x\in X}^{H(X)}h(x).\sigma _X(x)\right) (z)& = {} \bigcup _{x\in X}h(x)\otimes \sigma _X(x)(z)\\& = {} h(z)\otimes \{1_L\}=h(z). \end{aligned}$$

$\square$

The following theorem describes equivalent definitions of the F-transform for hesitant ${\mathscr {L}}$-fuzzy sets.

Theorem 1

Let $X,Y\in \mathbf{Set}$ and let $G:H(X)\rightarrow H(Y)$ be a mapping. Then, the following statements are equivalent.

• (1) There exists a $\mathbf{H}$-partition ${{\mathscr {A}}}=\{p_y:y\in Y\}$ such that

  $$\begin{aligned} h\in H(X),y\in Y,\quad G(h)(y)=\bigcup _{x\in X}h(x)\otimes p_y(x). \end{aligned}$$

  (4)

• (2) For the monad $\mathbf{H}$, there exists a $\mathbf{H}$-relation $S:X\rightsquigarrow Y$ such that

  $$\begin{aligned} G=S\diamond 1_{H(X)}:H(X)\rightarrow H(Y). \end{aligned}$$

  (5)

• (3) $G:{{\mathscr {H}}}(X)\rightarrow {{\mathscr {H}}}(Y)$ is a complete ${{\mathscr {R}}}$-semimodule homomorphism,

Proof

(1)$\Rightarrow$(2). Let ${{\mathscr {A}}}=\{p_y:y\in Y\}$ be a $\mathbf{H}$-partition such that (4) holds. Let $S:X\rightarrow H(Y)$ be defined by

$$\begin{aligned} x\in X,y\in Y,\quad S(x)(y)=p_y(x). \end{aligned}$$

Then, $S:X\rightsquigarrow Y$ is a $\mathbf{H}$-relation and according to (2) and (3) from Definition 10, we have

$$\begin{aligned} S\diamond 1_{H(X)}(h)(y)& = {} \bigcup _{x\in X}1_{H(X)}(h)(x)\otimes S(x)(y)\\& = {} \bigcup _{x\in X}h(x)\otimes S(x)(y)\\& = {} \bigcup _{x\in X}h(x)\otimes p_y(x)=G(h)(y). \end{aligned}$$

(2)$\Rightarrow$(3). Let $S:X\rightsquigarrow Y$ be a $\mathbf{H}$-relation which satisfies (5). We prove that G is a complete ${\mathscr {R}}$-semimodule homomorphisms ${{\mathscr {H}}}(X)\rightarrow {{\mathscr {H}}}(Y)$. In fact, let $\{h_i:i\in I\}\subseteq H(X)$. Then for $y\in Y$, we have

$$\begin{aligned} G\left( \bigoplus _{i\in I}^{H(X)}h_i\right) (y)& = {} (S\diamond 1_{H(X)})\left( \bigoplus _{i\in I}^{H(X)}h_i\right) (y)\\& = {} \bigcup _{x\in X}1_{H(X)}\left( \bigoplus _{i\in I}^{H(X)}h_i\right) (x)\otimes S(x)(y)\\& = {} \bigcup _{x\in X}\left( \bigcup _{i\in I}h_i(x)\right) \otimes S(x)(y)\\& = {} \bigcup _{i\in I}\left( \bigcup _{x\in X}h_i(x)\otimes S(x)(y)\right) \\& = {} \bigoplus _{i\in I}^{H(Y)}(S\diamond 1_{H(X)})(h_i)(y)=\bigoplus _{i\in I}^{H(Y)}G(h_i)(y). \end{aligned}$$

Further, for $A\in {{\mathscr {R}}}, h\in H(X)$, we have

$$\begin{aligned}&G(A.h)(y)=(S\diamond 1_{H(X)})(A.h)(y)\\&\quad =\bigcup _{x\in X}1_{H(X)}(A.h)(x)\otimes S(x)(y)\\&\quad = \bigcup _{x\in X}A\otimes h(x)\otimes S(x)(y)=A\otimes \bigcup _{x\in X}h(x)\otimes S(x)(y)\\&\quad =A\otimes (S\diamond 1_{H(X)})(h)(y)= A\otimes G(h)(y)=A.G(h)(y). \end{aligned}$$

Therefore, G is a ${\mathscr {R}}$-semimodule homomorphism with the required property.

(3)$\Rightarrow$ (1). Let $G:{{\mathscr {H}}}(X)\rightarrow {{\mathscr {H}}}(Y)$ be a $\mathcal R$-semimodule homomorphism. For $x\in X,y\in Y$ we define $p_y\in H(X), y\in Y,$ such that

$$\begin{aligned} p_y(x)=G(\sigma _X(x)(y)). \end{aligned}$$

Hence, ${{\mathscr {A}}}=\{p_y:y\in Y\}$ is a $\mathbf{H}$-partition of X. Let $h\in H(X),y\in Y$. According to Lemma 1, we obtain

$$\begin{aligned} G(h)(y)& = {} G(\bigoplus _{x\in X}^{H(X)}h(x).\sigma _X(x))(y)\\ {}& = {} \bigoplus _{x\in X}^{H(Y)}G(h(x).\sigma _X(x))(y)\\& = {} \bigoplus _{x\in X}^{H(Y)}h(x).G(\sigma _X(x))(y)=\bigcup _{x\in X}h(x)\otimes p_y(x). \end{aligned}$$

Therefore, G satisfies the equality (4). $\square$

Remark 2

The mapping $G:H(X)\rightarrow H(Y)$ from (4) will be called the hesitant F-transform based on a hesitant partition ${{\mathscr {A}}}$ and it will be denoted by $H_{X,{{\mathscr {A}}}}$.

We show that the classical F-transform of ${\mathscr {L}}$-fuzzy sets is a special case of the hesitant F-transform. For this, we use Definition 8.

Proposition 3

The standard F-transform of ${\mathscr {L}}$-fuzzy sets is a special case of the hesitant F-transform.

Proof

Let ${{\mathscr {A}}}=\{A_i:i\in |{{\mathscr {A}}}|\}$ be a fuzzy partition of a set X. Let ${{\mathscr {A}}}_H=\{h_i: i \in |\mathcal{A}|\}\subseteq H(X)$ be such that $h_i(x)=\{A_i(x)\}$. Then, $\mathcal{A}_H$ is a $\mathbf{H}$-partition of X, $|{{\mathscr {A}}}_{H}|=|{{\mathscr {A}}}|$ and we can consider hesitant F-transform $H_{X,{{\mathscr {A}}}_H}$. Let us consider a Z-morphism $\Phi _X:H(X)\rightarrow Z(X)$, such that for $h\in H(X),x\in X$, $\Phi _X(h)(x)=\bigvee _{\{\alpha \in h(x)\}}\alpha$. It is clear that $\Phi =\{\Phi _X:X\in \mathbf{Set}\}:H\rightarrow Z$ is a natural transformation between hesitant ${\mathscr {L}}$-fuzzy sets power set functor and classical ${\mathscr {L}}$-fuzzy sets power set functor. It can be proven easily (and the proof will be omitted) that the following diagram commutes. From this diagram, it follows that $F_{X,{{\mathscr {A}}}}$ is a special case of the hesitant F-transform.

$\square$

4.2 F-transform for Intuitionistic ${\mathscr {L}}$-Fuzzy Sets

As we mentioned in Sect. 2, for simplicity in this section, we suppose that ${\mathscr {L}}$ is a complete MV-algebra. We recall the definition of intuitionistic ${\mathscr {L}}$-fuzzy sets, which was presented in [5] in a modified but equivalent form.

Definition 12

[5] An intuitionistic ${{\mathscr {L}}}$-fuzzy set in a set X is a pair (u, v) of ${{\mathscr {L}}}$-fuzzy sets on X, such that $\lnot u\ge v$.

In this section, we deal with the construction of the intuitionistic F-transform (i.e., F-transform for intuitionistic ${\mathscr {L}}$-fuzzy sets) using a monad and semimodule homomorphisms. For this purpose, we use the monad defined by the power set structure of all intuitionistic ${\mathscr {L}}$-fuzzy sets in a set X, the existence of which was proven in the [39] and which is defined in the following definition.

Definition 13

[39] Let ${\mathscr {L}}$ be a complete MV-algebra. The monad $\mathbf{J}=(J,\boxtimes ,\varrho )$ in the category $\mathbf{Set}$ is defined by

• 1. $J:\text {obj}(\mathbf{Set})\rightarrow \text {obj}(\mathbf{Set})$ is a mapping defined by

  $$\begin{aligned} J(X)=\{(u,v)|u,v\in L^X, (\forall x\in X)\lnot u(x)\ge v(x)\}. \end{aligned}$$

• 2. If $f:X\rightarrow J(Y)$ and $g:Y\rightarrow J(Z)$ are $\mathbf{Set}$-morphisms, $g\boxtimes f:X\rightarrow J(Z)$ is defined by

  $$\begin{aligned} x\in X,\quad g\boxtimes f(x)=((g\boxtimes f)^x,(g\boxtimes f)_x)\in J(Z), \end{aligned}$$

  (6)

  where for $z\in Z$,

  $$\begin{aligned} (g\boxtimes f)^x(z)& = {} \bigvee _{y\in Y}f^x(y)\otimes g^y(z), \end{aligned}$$

  (7)
  $$\begin{aligned} (g\boxtimes f)_x(z)& = {} \bigwedge _{y\in Y}f_x(y)\oplus g_y(z), \end{aligned}$$

  (8)

  where for arbitrary mapping $f:X\rightarrow J(Y)$, $f(x)=(f^x,f_x)\in J(Y)$.

• 3. For $X\in \mathbf{Set}$, $\varrho _X:X\rightarrow J(X)$ is defined by

  $$\begin{aligned} x\in X,\quad \varrho _X(x)=(\chi ^X_{\{x\}},\lnot \chi ^X_{\{x\}}). \end{aligned}$$

  (9)

According to Sect. 3.1, for a definition of the intuitionistic F-transform defined by this monad, we need to define $\mathbf{J}$-partitions (which are also called intuitionistic partitions of a set X) for a monad $\mathbf{J}$. We use the following notation:

$$\begin{aligned} (u,v)\in J(X),x\in X,\quad (u,v)(x):=(u(x),v(x))\in L^2. \end{aligned}$$

Definition 14

A subset ${{\mathscr {A}}}=\{(u_y,v_y):y\in Y\}\subseteq J(X)$ is called a $\mathbf{J}$-partition of X.

Now, analogously to hesitant ${\mathscr {L}}$-fuzzy sets, we introduce a new semiring ${\mathscr {R}}$ and a complete ${\mathscr {R}}$-semimodule, which will be used to define intuitionistic F-transform according to the method from Sect. 3.2.

Proposition 4

Let ${{\mathscr {L}}}$ be a complete MV-algebra and let $\mathcal{R}=(R,+,\times ,0_R,1_R)$ be defined by

• 1. $R=\{(\alpha ,\beta )\in L^2:\lnot \alpha \ge \beta \}$,

• 2. $(\alpha ,\beta )+(\alpha _1,\beta _1):=(\alpha \vee \alpha _1,\beta \wedge \beta _1)$,

• 3. $(\alpha ,\beta )\times (\alpha _1,\beta _1):=(\alpha \otimes \alpha _1,\beta \oplus \beta _1)$,

• 4. $0_R=(0_L,1_L),\quad 1_R=(1_L,0_L)$.

Then, ${\mathscr {R}}$ is a semiring.

Proof

It is only a simple calculation, where we use a distributivity between $\otimes$ and $\vee$ and between $\oplus$ and $\wedge$, which hold in any MV-algebra. $\square$

Proposition 5

Let $X\in \mathbf{Set}$ and let ${\mathscr {R}}$ be the semiring from Proposition 4. Let the structure ${{\mathscr {J}}}(X)=(J(X),\oplus _J,0_J)$ be defined by

• 1. The external multiplication $.:{R}\times J(X)\rightarrow J(X)$ is defined for arbitrary $(\alpha ,\beta )\in R,(u,v)\in J(X)$ by

  $$\begin{aligned} (\alpha ,\beta ).(u,v)=(\alpha \otimes u,\beta \oplus v). \end{aligned}$$

• 2. For $(u,v),(u_1,v_1)\in J(X)$, $(u,v)\oplus _J(u_1,v_1):=(u\vee u_1, v\wedge v_1)$,

• 3. $0_J=(\underline{0}_L,\underline{1}_L)$, where ${\underline{\alpha }}\in L^X$ is such that ${\underline{\alpha }}(x)=\alpha$, for all $x\in X$.

Then, ${{\mathscr {J}}}(X)$ is a complete ${\mathscr {R}}$-semimodule.

Proof

First, we prove that the above definitions are correct. For example, we have

$$\begin{aligned} \lnot (\beta \oplus v)=\lnot \beta \otimes \lnot v\ge \alpha \otimes u, \end{aligned}$$

and it follows $(\alpha ,\beta ).(u,v)\in J(X)$. Analogously we prove the correctness of other definitions. $\square$

Analogously to hesitant fuzzy sets, to define a variant of F-transforms for intuitionistic fuzzy sets we need the following lemma which enables to describe elements from an ${\mathscr {R}}$-semimodule ${{\mathscr {J}}}(X)$ in a uniform way.

Lemma 2

Let $X\in \mathbf{Set}$.

• 1. The set $\{\rho _X(x):x\in X\}$ is a ${{\mathscr {R}}}$-base of ${{\mathscr {J}}}(X)$.

• 2. For arbitrary $(u,v)\in J(X)$ we have

  $$\begin{aligned} (u,v)=\bigoplus _{x\in X}^{J(X)}(u,v)(x).\varrho _X(x). \end{aligned}$$

Proof

For $z\in X$, we have

$$\begin{aligned} & \left(\bigoplus _{x\in X}^{J(X)}(u,v)(x).\varrho _X(x)\right)(z)\\ & \quad= \bigoplus _{x\in X}^{J(X)}(u(x)\otimes \chi ^X_{\{x\}},v(x)\oplus \lnot \chi ^X_{\{x\}})(z)\\ & \quad = \left(\bigvee _{x\in X}u(x)\otimes \chi ^X_{\{x\}},\bigwedge _{x\in X}v(x)\oplus \lnot \chi ^X_{\{x\}}\right)(z)& = {} (u(z),v(z)). \end{aligned}$$

$\square$

The following theorem describes three equivalent definitions of the intuitionistic F-transform.

Theorem 2

Let $X,Y\in \mathbf{Set}$ and let $G:J(X)\rightarrow J(Y)$ be a mapping. Then the following statements are equivalent.

• (1) There exists a $\mathbf{J}$-partition ${{\mathscr {A}}}=\{(s_y,t_y):y\in Y\}$ such that for arbitrary $(u,v)\in J(X),y\in Y$,

  $$\begin{aligned} G(u,v)(y)=\left(\bigvee _{x\in X}u(x)\otimes s_y(x),\bigwedge _{x\in X}v(x)\oplus t_y(x)\right). \end{aligned}$$

  (10)

• (2) For the monad $\mathbf{J}$, there exists a $\mathbf{J}$-relation $S:X\rightsquigarrow Y$ such that

  $$\begin{aligned} G=S\boxtimes 1_{J(X)}:J(X)\rightarrow J(Y). \end{aligned}$$

  (11)

• (3) $G:{{\mathscr {J}}}(X)\rightarrow {{\mathscr {J}}}(Y)$ is a complete ${{\mathscr {R}}}$-semimodule homomorphism

Proof

(1)$\Rightarrow$(2). Let ${{\mathscr {A}}}=\{(s_y,t_y):y\in Y\}$ be a $\mathbf{J}$-partition such that (10) holds. Let $S:X\rightarrow J(Y)$ be defined by

$$\begin{aligned} x\in X,\quad S(x)=({\overline{s}}_x,{\overline{t}}_x)\in J(Y),\\ y\in Y,\quad {\overline{s}}_x(y):=s_y(x),{\overline{t}}_x(y)=t_y(x). \end{aligned}$$

Then, $S:X\rightsquigarrow Y$ is a $\mathbf{J}$-relation and according to (6)–(9) from Definition 13, we have

$$\begin{aligned}&S\boxtimes 1_{J(X)}(u,v)(y)\\&\quad =((S\boxtimes 1_{J(X)})^{(u,v)}(y),(S\boxtimes 1_{J(X)})_{(u.v)})(y)\\&\quad = \left(\bigvee _{x\in X}1_{J(X)}^{(u,v)}(u,v)(x)\otimes S^x(y),\right.\\&\qquad \left.\bigwedge _{x\in X}1_{J(X),(u,v)}(u,v)(x)\oplus S_x(y)\right)\\&\quad = \left(\bigvee _{x\in X}u(x)\otimes {\overline{s}}_x(y),\bigwedge _{x\in X}v(x)\oplus {\overline{t}}_x(y)\right)\\&\quad =\left(\bigvee _{x\in X}u(x)\otimes s_y(x),\bigwedge _{x\in X}v(x)\oplus t_y(x)\right)= G(u,v)(y). \end{aligned}$$

Therefore, (11) holds.

(2)$\Rightarrow$(3). Let $S:X\rightsquigarrow Y$ be a $\mathbf{J}$-relation which satisfies (11). We prove that G is a complete ${\mathscr {R}}$-semimodule homomorphisms ${{\mathscr {J}}}(X)\rightarrow {{\mathscr {J}}}(Y)$. In fact, let $\{(u_i,v_i):i\in I\}\subseteq J(X)$. Then for $y\in Y$, we have

$$\begin{aligned}&G\left(\bigoplus _{i\in I}^{J(X)}(u_i,v_i)\right)(y)=(S\boxtimes 1_{J(X)})\left(\bigoplus _{i\in I}^{J(X)}(u_i,v_i)\right)(y)\\&\quad =(S\boxtimes 1_{J(X)})\left(\bigvee _{i\in I}u_i,\bigwedge _{i\in I}v_i\right)(y)\\&\quad = \left(\bigvee _{x\in X}\left(\bigvee _{i\in I}u_i\right)(x)\otimes S(x)(y),\bigwedge _{x\in X}\left(\bigwedge _{i\in I}v_i\right)(y)\oplus S(x)(y)\right)\\&\quad =\left(\bigvee _{i\in I}\left(\bigvee _{x\in X}u_i\right)(x)\otimes S(x)(y),\bigwedge _{i\in I}\left(\bigwedge _{x\in X}v_i\right)(y)\oplus S(x)(y)\right)\\&\quad = \bigoplus _{i\in I}^{J(X)}(S\boxtimes 1_{J(Y)})(u_i,v_i)(y) =\bigoplus _{i\in I}^{J(Y)}G(u_i,v_i)(y). \end{aligned}$$

Further, for $(\alpha ,\beta )\in {{\mathscr {R}}}, (u,v)\in J(X)$, we have

$$\begin{aligned}&G((\alpha ,\beta ).(u,v))(y)=(S\boxtimes 1_{J(X)})((\alpha ,\beta ).(u,v))(y)\\&\quad = (S\boxtimes 1_{J(X)})\left(\alpha \otimes \bigvee _{x\in X}u(x)\otimes S(x)(y),\right.\\&\qquad \left.\beta \oplus \bigwedge _{x\in X}v(x)\oplus S(x)(y)\right)\\&\quad =(\alpha ,\beta ).(S\boxtimes 1_{J(X)})(u,v)(y)=(\alpha ,\beta ).G(u,v)(y). \end{aligned}$$

Therefore, G is a ${\mathscr {R}}$-semimodule homomorphism with the required property.

(3)$\Rightarrow$ (1). Let $G:{{\mathscr {J}}}(X)\rightarrow {{\mathscr {J}}}(Y)$ be a $\mathcal R$-semimodule homomorphism. For $x\in X,y\in Y$ we define $({\overline{s}}_x,{\overline{t}}_x)\in J(Y)$ such that

$$\begin{aligned} ({\overline{s}}_x,{\overline{t}}_x)(y):=G(\varrho _X(x))(y), \end{aligned}$$

and we defined $(s_y,t_y)\in J(X)$, such that

$$\begin{aligned} x\in X,y\in Y,\quad s_y(x):={\overline{s}}_x(y),\quad t_y(x):=\overline{t}_x(y). \end{aligned}$$

Then, ${{\mathscr {A}}}=\{(s_y,t_y):y\in Y\}$ is a $\mathbf{J}$-partition of X. Let $(u,v)\in J(X),y\in Y$. According to Lemma 2, we obtain

$$\begin{aligned} G(u,v)(y)& = {} G\left(\bigoplus _{x\in X}^{J(X)}(u,v)(x).\varrho _X(x)\right)(y)\\&=\bigoplus _{x\in X}^{J(Y)}G((u,v)(x).\varrho _X(x))(y)\\&=\bigoplus _{x\in X}^{J(Y)}(u,v)(x).G(\varrho _X(x))(y)\\& =\bigoplus _{x\in X}^{J(Y)}(u,v)(x).({\overline{s}}_x,{\overline{t}}_x)(y)\\&= \bigoplus _{x\in X}^{J(Y)}(u(x)\otimes {\overline{s}}_x(y),v(x)\oplus {\overline{t}}_x(y))\\& =\left(\bigvee _{x\in X}u(x)\otimes s_y(x),\bigwedge _{x\in X}v(x)\oplus t_y(x)\right). \end{aligned}$$

Therefore, G satisfies the equality (10). $\square$

Remark 3

A mapping $G:J(X)\rightarrow J(Y)$ from (10) will be called the intuitionistic F-transform based on a intuitionistic partition ${{\mathscr {A}}}$ and it will be denoted by $J_{X,{{\mathscr {A}}}}$. $\square$

Analogously to hesitant ${\mathscr {L}}$-fuzzy sets, it holds that the F-transform of classical fuzzy sets is a special case of the intuitionistic F-transform according to Definition 8.

Proposition 6

The standard F-transform of ${\mathscr {L}}$-fuzzy sets is a special case of the intuitionistic F-transform.

Proof

Let ${{\mathscr {A}}}=\{A_i:i\in |{{\mathscr {A}}}|\}$ be a fuzzy partition of a set X. Let ${{\mathscr {A}}}_J=\{(A_i,\lnot A_i):i\in |\mathcal{A}|\}\subseteq J(X)$. Then, ${{\mathscr {A}}}_J$ is a $\mathbf{J}$-partition of X and we can consider the intuitionistic F-transform $J_{X,\mathcal{A}_J}$. According to Definition 8, we need to define a natural transformation $\Phi :J\rightarrow Z$. For $X\in \mathbf{Set}$ and $(s,t)\in J(X)$, we set $\Phi _X(s,t)=s$. According to [39]; Theorem 3, for a $\mathbf{Set}$-morphism $f:X\rightarrow Y$ and $(s,t)\in J(X),y\in Y$, we have $f^{\rightarrow }_J(s,t)(y)=(\bigvee _{x,f(x)=y}s(x),\bigwedge _{x, f(x)=y}t(x))$ and it follows that the diagram

commutes. Hence, $\Phi$ is a natural transformation. Using Theorem 2, it follows immediately that the following diagram commutes:

Hence, the standard F-transform is a special case of the intuitionistic F-transform. $\square$

4.3 F-transform for ${\mathscr {L}}$-Fuzzy Soft Sets

In this section, ${\mathscr {L}}$ be a complete residuated lattice. The notion of fuzzy soft sets was introduce in [31] and we recall a lattice variant of this notion.

Definition 15

[31] Let K be a fixed set of criteria and $X\in \mathbf{Set}$. A pair (E, s) is called an ${{\mathscr {L}}}$-fuzzy soft set in a X, if $\emptyset \ne E\subseteq K$ and $s:E\rightarrow L^X$. By T(X), we denote the set of all ${\mathscr {L}}$-fuzzy soft sets in X.

For simplicity of notations, in the rest of the paper, we use the fixed set of criteria K. For general constructions of fuzzy soft sets monads with various criteria sets see [39].

In this section, we show how F-transforms can be defined for $\mathcal L$-fuzzy soft sets by the monad or semimodule homomorphisms.

In what follows, K is the fixed set of criteria and we use the following notation. If $f:X\rightarrow T(Y)$ is a map, for $x\in X$ we denote

$$\begin{aligned} f(x)=(K^f_x,f_x)\in T(Y), K^f_x\subseteq K, f_x:K^f_x\rightarrow L^Y. \end{aligned}$$

(12)

For $(E,s)\in T(X)$ and $e\in E,x\in X$ we set $(E,s)(e)(x):=s(e)(x)$.

To construct a monad $\mathbf{T}$ for fuzzy soft sets, we use the monad $\widetilde{\mathbf{T}}$, which was defined in [39]. For this monad, however, we limit ourselves to the case where the set of criteria of fuzzy soft sets is the constant set $\mathbf{K}$. In this case, the reduced monad $\mathbf{T}$ will be defined in the category $\mathbf{Set}$ as follows.

Definition 16

[39] The monad $\mathbf{T}=(T,\vartriangle ,\tau )$ in the category $\mathbf{Set}$ is defined by

• 1. $T:obj(\mathbf{Set})\rightarrow obj(\mathbf{Set})$ is a mapping defined by $T(X)=\{(E,s):\star \in E\subseteq K, s:E\rightarrow L^X\}\in \mathbf{Set}$,

• 2. If $f:X\rightarrow T(Y)$ and $g:Y\rightarrow T(Z)$ are morphisms in $\mathbf{Set}$, using the notation (12), the Kleisli composition $\vartriangle$ is defined by

  $$\begin{aligned}&g\vartriangle f:X\rightarrow T(Z),\nonumber \\&\quad (g\vartriangle f)(x)=(K^{g\vartriangle f}_x, (g \vartriangle f)_x), \end{aligned}$$

  (13)
  $$\begin{aligned}&K^{g \vartriangle f}_x=K^f_x\cap \bigcup _{y\in Y} K^g_y,\end{aligned}$$

  (14)
  $$\begin{aligned} &(g\vartriangle f)_x(k)(z)\nonumber \\&\quad = \bigvee _{\{y|k\in K^g_y\}}f_x(k)(y)\otimes g_y(k)(z), \end{aligned}$$

  (15)

  for arbitrary $k\in K^{g\vartriangle f}_x,z\in Z$.

• 2. For $X\in \mathbf{Set}$, the $\mathbf{Set}$-morphism $\tau _X:X\rightarrow T(X)$ is defined by $\tau _X(x)=(K,\eta _{x}^X)$, where $\eta _x^X:K\rightarrow L^X$ is defined by $\eta _x^X(k)(z)={\left\{ \begin{array}{ll} 1_L,&{} x=z, \\ 0_L, &{} x\ne z.\end{array}\right. }$

According to Sect. 3.1, for a definition of the fuzzy soft F-transform we need to define $\mathbf{T}$-partitions (which are also called soft partitions) of a set X.

The notions of a $\mathbf{T}$-partition of a set X are defined by

Definition 17

A subset ${{\mathscr {A}}}=\{(K,p_y):y\in Y\}\subseteq T(X)$ is called a $\mathbf{T}$-partition of X.

Now, analogously to hesitant or intuitionistic ${\mathscr {L}}$-fuzzy sets we introduce a new semiring ${\mathscr {R}}$ and a complete $\mathcal R$-semimodule, which will be used to define soft F-transforms according to the method from Sect. 3.2. These structures are presented in the following propositions.

Proposition 7

Let K be the fixed set of criteria and let $\mathcal{R}(K)=(R(K),+,\times ,0_R,1_R)$ be defined by

• 1. $R=L^K$,

• 2. $\varphi ,\psi \in R(K),\quad \varphi +\psi =\varphi \vee \psi$, where $\vee$ is defined point-wise from ${\mathscr {L}}$,

• 3. $\varphi ,\psi \in R(K),\quad \varphi \times \psi =\varphi \otimes \psi$, where $\otimes$ is defied point-wise from a residuated lattice ${\mathscr {L}}$,

• 4. $0_{R(K)}={\underline{0}}_L, 1_{R(K)}={\underline{1}}_L$, where ${\underline{\alpha }}(k)=\alpha$ for arbitrary $k\in K$, $\alpha \in L$.

Then ${{\mathscr {R}}}(K)$ is a semiring.

The proof is straightforward and will be omitted.

Proposition 8

Let ${{\mathscr {R}}}(K)$ be the semiring from Proposition 7. Let $X\in \mathbf{Set}$ and let the structure ${{\mathscr {T}}}(X)=(T(X),\oplus _T,0_T)$ be defined by

• 1. The external multiplication $.:{R}(K)\times {T}(X)\rightarrow T(X)$ is defined for arbitrary $\psi \in R(K),(E,s)\in T(X)$ by

  $$\begin{aligned} & \psi .(E,s)={\left\{ \begin{array}{ll}(E,\psi *s), &{}\psi \ne 0_{R(K)}\\ (K,{\underline{0}}), &{} \psi =0_{R(K)}\end{array}\right. },\\ & e\in E,x\in X,\quad (\psi *s)(e)(x)=\psi (e)\otimes s(e)(x), \end{aligned}$$

• 2. $(E,s),(F,t)\in T(X),\quad (E,s)\oplus _T (F,t)=(E\cap F,s\vee t)$,

• 3. $0_T=(K,{\underline{0}})$,

where ${\underline{0}}(e)(x)=0_L$ for arbitrary $e\in K,x\in X$. Then, ${{\mathscr {T}}}(X)$ is a complete ${{\mathscr {R}}}(K)$-semimodule.

Proof

For $\psi ,\sigma \in R(K)$, $\{\psi _i:i\in I\}\subseteq R(K)$ and $\{(E_j,s_j):j\in J\}\subseteq T(X)$, we have

$$\begin{aligned}&\left(\bigoplus _{i\in I}^{R(K)}\psi _i\right).(E,s)=\left(E,\left(\bigvee _{i\in I}\psi _i\right)*s\right)\\&\quad =\left(E,\bigvee _{i\in I}\psi _i*s\right)=\bigoplus _{i\in I}^{{{\mathscr {T}}}(X)}\psi _i.(E,s), \\&\qquad \psi .(\sigma .(E,s))=\psi .(E,\sigma *s)\\&\quad =(E,\psi *\sigma *s)=(E,(\psi \times \sigma )*s)\\&\quad = (\psi \times \sigma ).(E,s),\\&\qquad \psi .\left(\bigoplus _{j\in J}^{{{\mathscr {T}}}(X)}(E_j,s_j)\right)=\psi . \left(\bigcap _{j\in J}E_j,\bigvee _{j\in J}s_j\right)\\&\quad =\left(\bigcap _{j\in J}E_j,\psi *\bigvee _{j\in J}s_j\right)\\&\quad = \left(\bigcap _{j\in J}E_j,\bigvee _{j\in J}\psi *s_j\right)=\bigoplus _{j\in J}^{{{\mathscr {T}}}(X)}(E_j,\psi *s_j)\\&\quad =\bigoplus _{j\in J}^{{{\mathscr {T}}}(X)}\psi .(E_j,s_j),\\&\qquad 1_{R(K)}.(E,s)=(E,{\underline{1}}_L*s)=(E,s),\\&\qquad 0_{R(K)}.(E,s)=(K,{\underline{0}})=0_T=\psi .(K,{\underline{0}})=\psi .0_T. \end{aligned}$$

Therefore, ${{\mathscr {T}}}(X)$ satisfies axioms of a complete $\mathcal{R}(K)$-semimodule. $\square$

Analogously to hesitant or intuitionistic fuzzy sets, to define a variant of the F-transform for ${\mathscr {L}}$-fuzzy soft sets, we need the following lemma which enables to describe elements from an $\mathcal{R}(K)$-semimodule ${{\mathscr {T}}}(X)$ in a uniform way. Recall that for $E\subseteq K$, by $\chi ^E_{\{e\}}$ we denote the characteristic mapping $E\rightarrow L$ such that for $e'\in E$, $\chi ^E_{\{e\}}(e')={\left\{ \begin{array}{ll}1_L, &{} e=e'\\ 0_L,&{} e\ne e'.\end{array}\right. }$

Lemma 3

• 1. The set $\{(K,\eta _x^X):x\in X\}$ is a ${{\mathscr {R}}}(X)$-base of ${{\mathscr {T}}}(X)$.

• 2. For arbitrary $(E,s)\in T(X)$, we have

  $$\begin{aligned} (E,s)=\bigoplus _{e\in K,x\in X}^{{{\mathscr {T}}}(X)}((E,s)(e)(x)\otimes \chi ^E_{\{e\}}).(K,\eta _x^X), \end{aligned}$$

Proof

Let $a\in E,z\in X$. Because $(E,s)(e)(x)\otimes \chi _{\{e\}}^X=s(e)(x)\otimes \chi _{\{e\}}^E\in {{\mathscr {R}}}(E)$, it follows that

$$\begin{aligned}&\left(\bigoplus _{e\in K,x\in X}^{{{\mathscr {T}}}(X)}((E,s)(e)(x)\otimes \chi ^E_{\{e\}}).(K,\eta _x^X)\right)(a)(z)\\&\quad = \bigoplus _{e\in K,x\in X}^{{{\mathscr {T}}}(X)}(K,(s(e)(x)\otimes \chi ^E_{\{e\}})*\eta _x^X)(a)(z)\\&\quad = \bigvee _{e\in E,x\in X}(s(e)(x)\otimes \chi ^E_{\{e\}}\otimes \eta _x^X)(a)(z)=s(a)(z)\\&\quad =(E,s)(a)(z). \end{aligned}$$

$\square$

The following theorem describes three equivalent definitions of the soft F-transform for ${\mathscr {L}}$-fuzzy soft sets.

Theorem 3

Let $X,Y\in \mathbf{Set}$ and let $G:T(X)\rightarrow T(Y)$ be a mapping. Then, the following statements are equivalent.

• (1) There exists a $\mathbf{T}$-partition ${{\mathscr {A}}}=\{(K,p_y):y\in Y\}$ of X such that for all $(E,s)\in T(X)$,

  $$\begin{aligned}&G(E,s)=(E,{\overline{s}})\in T(Y), \end{aligned}$$

  (16)
  $$\begin{aligned}&\forall e\in E,y\in Y,\quad {\overline{s}}(e)(y)=\bigvee _{x\in X}s(e)(x)\otimes p_y(e)(x), \end{aligned}$$

  (17)

• (2) For the monad $\mathbf{T}$, there exists a $\mathbf{T}$-relation $S:X\rightarrow T(Y)$ such that

  $$\begin{aligned} G=S\vartriangle 1_{T(X)}:T(X)\rightarrow T(Y),. \end{aligned}$$

  (18)

• (3) $G:{{\mathscr {T}}}(X)\rightarrow {{\mathscr {T}}}(Y)$ is a complete ${{\mathscr {R}}}(K)$-semimodule homomorphism

Proof

(1)$\Rightarrow$(2): Let ${{\mathscr {A}}}=\{(K,p_y):y\in Y\}$ be a soft partition of X. We define a $\mathbf{T}$-relation $S:X\rightarrow T(Y)$ such that

$$\begin{aligned}&x\in X,\quad S(x)=(K,q_x)\in T(Y),\\&y\in Y,e\in K,\quad q_x(e)(y)=p_y(e)(x). \end{aligned}$$

According to (13),(14) and (15) from Definition 16, for $(E,s)\in T(X)$ we obtain

$$\begin{aligned}&(S\vartriangle 1_{T(X,K)})(E,s)\\&\quad =(K^{S\vartriangle 1_{T(X,K)}}_{(E,s)},(S\vartriangle 1_{T(X,K)})_{(E,s)})\in T(Y),\\&\quad K^{S\vartriangle 1_{T(X)}}_{(E,s)}=E\cap \bigcup _{x\in X}K=E,\\&\quad \forall e\in E,y\in Y,\quad (S\vartriangle 1_{T(X)})_{(E,s)}(e)(y)\\&\quad =\bigvee _{x\in X}1_{T(X),(E,s)}(e)(x)\otimes S(x)(e)(y)\\&\quad = \bigvee _{x\in X}(E,s)(e)(x)\otimes p_y(e)(x)=G(E,s)(e)(y), \end{aligned}$$

and the equality (18) holds.

(2)$\Rightarrow$(3): Let the condition (18) holds for the monad $\mathbf{T}$. We prove that $G=S\vartriangle 1_{T(X)}:{{\mathscr {T}}}(X)\rightarrow \mathcal{T}(Y)$ is a ${{\mathscr {R}}}(K)$-semimodule homomorphism. Let $\{(E_i,s_i):i\in I\}\subseteq T(X)$. For simplicity, if $(E,s)\in T(X)$, instead of $(S\vartriangle 1_{T(X)})_{(E,s)}$ which is used in (13), we simply write ${\overline{s}}$. Therefore,

$$\begin{aligned} (E,\overline{s}):=(S\vartriangle 1_{T(X)})(E,s). \end{aligned}$$

For $e\in \bigcap _{i\in I}E_i$ and $y\in Y$, according to (13–15), analogously as in the previous implication, we obtain

$$\begin{aligned}&G\left(\bigoplus _{i\in I}^{{{\mathscr {T}}}(X)}(E_i,s_i)\right)(e)(y)=G\left(\bigcap _{i\in I}E_i,\bigvee _{i\in I}s_i\right)(e)(y)\\&\quad = (S\vartriangle 1_{T(X)})\left(\bigcap _{i\in I}E_i,\bigvee _{i\in I}s_i\right)(e)(y)=\left(\bigcap _{i\in I}E_i,{\overline{s}}\right)(e)(y)\\&\quad = \bigvee _{x\in X}\left(\bigcap _{i\in I}E_i,\bigvee _{i\in I}s_i\right)(e)(x)\otimes S(x)(e)(y)\\&\quad = \bigvee _{x\in X}\bigvee _{i\in I}s_i(e)(x)\otimes S(x)(e)(y)\\&\quad =\bigvee _{i\in i}\bigvee _{x\in X}s_i(e)(x)\otimes S(x)(e)(y). \end{aligned}$$

On the other hand, we have

$$\begin{aligned}&\left(\bigoplus _{i\in I}^{{{\mathscr {T}}}(Y)}G(E_i,s_i)\right)(e)(y)\\&\quad = \left(\bigoplus _{i\in I}^{{{\mathscr {T}}}(Y)}(S\vartriangle 1_{T(X)}\right)(E_i,s_i))(e)(y)\\&\quad = \left(\bigoplus _{i\in I}^{{{\mathscr {T}}}(Y)}(E_i,{\overline{s}}_i)\right)(e)(y)\\&\quad =\left(\bigcap _{i\in I}E_i,\bigvee _{i\in I}{\overline{s}}_i\right)(e)(y)=\bigvee _{i\in I}{\overline{s}}_i(e)(y)\\&\quad = \bigvee _{i\in I}\bigvee _{x\in X}s_i(e)(x)\otimes S(x)(e)(y). \end{aligned}$$

Further, for $\psi \in R(K), (E,s)\in T(X)$ and for $e\in E,y\in Y$, we have

$$\begin{aligned}&G(\psi .(E,s))(e)(y)=G(E,\psi *s)(e)(y)\\&\quad =(E,\overline{\psi *s})(e)(y)=\overline{\psi *s}(e)(y)\\&\quad = \bigvee _{x\in X}(\psi *s)(e)(x)\otimes S(x)(e)(y)\\&\quad =\bigvee _{x\in X}\psi (e)\otimes s(e)(x)\otimes S(x)(e)(y)\\&\quad = \psi (e)\otimes \bigvee _{x\in X}s(e)(x)\otimes S(x)(e)(y)=\psi *{\overline{s}}(e)(y)\\&\quad =(\psi . G(E,s))(e)(y). \end{aligned}$$

Therefore, G is a complete ${{\mathscr {R}}}(K)$-semimodule homomorphism.

(3)$\Rightarrow$(1): Let $G:{{\mathscr {T}}}(X)\rightarrow {{\mathscr {T}}}(Y)$ be a complete ${{\mathscr {R}}}(K)$-semimodule homomorphism. For $y\in Y$ we define a function $p_y:K\rightarrow L^X$ such that

$$\begin{aligned} e\in K,x\in X, \quad p_y(e)(x)=G(K,\eta _x^X)(e)(y)\in L. \end{aligned}$$

Let ${{\mathscr {A}}}=\{(K,p_y):y\in Y\}\subseteq T(X)$. Therefore, ${\mathscr {A}}$ is a soft partition of (X, K).

Let $(E,s)\in T(X)$. According to Lemma 3, for $a\in E,y\in Y$ we have

$$\begin{aligned}G(E,s)(a)(y)& =G\left(\bigvee _{e\in E,x\in X}(E,s)(e)(x)\otimes \chi ^E_{\{e\}}\right).(K,\eta _x^X))(a)(y)\\&= \bigvee _{e\in E,x\in X}s(e)(x)\otimes \chi ^E_{\{e\}}(a)\otimes G(K,\eta _x^X)(a)(y)\\&=\bigvee _{x\in X}s(a)(x)\otimes p_y(a)(x). \end{aligned}$$

Therefore, conditions (16), (17) hold for G. $\square$

Remark 4

A mapping $G:T(X)\rightarrow T(Y)$ defined in (20), (21) will be called the soft F-transform of X based on a soft partition ${{\mathscr {A}}}$ and it will be denoted by $T_{X,{{\mathscr {A}}}}$.

Analogously to hesitant or intuitionistic ${\mathscr {L}}$-fuzzy sets, it holds that F-transform of classical fuzzy sets is a special case of soft F-transform.

Proposition 9

The standard F-transform of ${\mathscr {L}}$-fuzzy sets is a special case of the soft F-transform.

Proof

According to Definition 6, we set

(1) For a fuzzy partition ${{\mathscr {A}}}=\{s_y:y\in Y\}$ of a set X, we consider a $\mathbf{T}$-partition ${{\mathscr {A}}}_X\subseteq \mathbf{T}(X)$, such that ${{\mathscr {A}}}_X=\{(K,t_y):y\in Y\}$, where $t_y(k)(x)=s_y(x)$ for arbitrary $x\in X$.

(3) We define a natural transformation $\Phi :\mathbf{T}\rightarrow Z$ such that for $X\in \mathbf{Set}$, $\Phi _X:T(X)\rightarrow Z(X)$ is such that for $(E,t)\in T(X)$, $\Phi _X(E,t)(x)=\bigvee _{k\in K}t(k)(x)$. We show that $\Phi$ is a natural transformation, i.e., we prove that the diagram commutes:

for arbitrary morphism $f:X\rightarrow Y$. According to [39]; Theorem 1, identities (7)–(9), for arbitrary $(E,s)\in T(X),y\in Y$ we have

$$\begin{aligned}&Z(f).\Phi _X(E,s)(y)=\bigvee _{x,f(x)=y}\Phi _X(E,s)(x)\\&\quad = \bigvee _{x,f(x)=y}\bigvee _{k\in K}s(k)(x)=\bigvee _{k\in K}T(f)(E,s)(k)(x)\\&\quad = \Phi _Y.T(f)(E,s)(y) \end{aligned}$$

and $\Phi$ is a natural transformation.

(4) Then, the following diagram commutes:

For $(E,s)\in T(X),y\in Y$, we obtain

$$\begin{aligned}&\Phi _{|{{\mathscr {A}}}|}.{T}_{X,{{\mathscr {A}}}_X}(E,s)(y)=\Phi _{|{{\mathscr {A}}}|}(S\vartriangle 1_{T(X)})(E,s)(y)\\&\quad = \bigvee _{k\in K}S\vartriangle 1_{T(X)}(E,s)(k)(y)=\bigvee _{k\in K}\bigvee _{x\in X}s(k)(x)\otimes S(x)(k)(y)\\&\quad = \bigvee _{k\in K}\bigvee _{x\in X}s(k)(x)\otimes s_u(x)\\&\quad = F_{X,{{\mathscr {A}}}}(\Phi _X(E,s))(y)=F_{X,{{\mathscr {A}}}}.\Phi _X(E,s)(y). \end{aligned}$$

and the diagram commutes. Therefore, $F_{X,{{\mathscr {A}}}}$ is a special case of ${T}_{X,{{\mathscr {A}}}_X}$.

$\square$

5 IF–THEN Rules: Possible Application of Generalized F-transform

One of the key advantages of fuzzy mathematics is its ability to model real-world phenomena that are inaccurate and vague. Due to their complexity and vagueness, an exact description of the behavior of these systems cannot be realized in most cases using the tools of the classical mathematics. On the other hand, in many cases, the behavior of these systems can be expressed by a verbal description expressing their causality. A typical example of such a description are IF–THEN rules, expressing the output response of a system if a value is entered at the input of this system. The advantage of these linguistic models is, among other things, that they make it possible to describe input values using linguistic expressions representing values of input quantities.

A typical example of structures of this type are the so-called fuzzy systems. In general, a fuzzy system is any system whose variables (or, at least, some of them) range over states that are fuzzy numbers rather than real numbers. These fuzzy numbers may represent linguistic terms such as very small, medium and so on, as interpreted in a particular context. If they do, the variables are called linguistic variables. In a linguistic variable, linguistic terms representing approximate values of a base variable, relevant to a particular application, are expressed by fuzzy sets in sets of input or output values. A typical example of the IF–THEN rules can be described as

$$\begin{aligned} R: \mathrm{IF } X =\text {high}\quad \mathrm{THEN }\quad Y = \text {very}\_\text {low}. \end{aligned}$$

If at the input of a system described by the IF–THEN rule $R:\text { IF } X=A\text { THEN }Y=B$ the input variable has the linguistic value $X = A'$, where $A'$ is some linguistic expression or directly fuzzy set in the input set X, then using the so-called fuzzy inference mechanism, it is possible to determine the output value as a fuzzy set $B'$ in Y. Hence, the fuzzy inference is a mapping $Z(X)\rightarrow Z(Y)$ that transforms the input fuzzy sets in X to the output fuzzy sets in Y according the rule R. IF–THEN rules and the fuzzy inference mechanism are typically used in fuzzy decision systems or fuzzy expert systems, or fuzzy control systems. For illustrative references of this applications see [3, 24, 25, 28, 53].

IF–THEN rules have so far been used mainly for classic fuzzy sets. The use of this method for applications using fuzzy soft sets, intuitionistic fuzzy sets or hesitant fuzzy sets was more or less based on ad hoc modifications of existing methods for classical fuzzy sets. For illustration of these modifications see [9, 19, 26].

In this section, we show how using fuzzy transform the fuzzy inference mechanisms for these structures can be defined, which allow to create, e.g., fuzzy type expert systems, fuzzy control systems or fuzzy type decision systems, whose values of input and output variables are fuzzy soft sets, hesitant fuzzy sets or fuzzy soft sets. In this way, the application potential of these fuzzy type structures is extended.

Let us consider any of hesitant, intuitionistic or fuzzy soft type structures and let $\mathbf{Q}=(Q,\lozenge ,\eta ),\mathcal{R}=(R,+,\times ,0_R,1_R)$ and ${{\mathscr {Q}}}(X)=(Q(X),\oplus _X,0_X)$ be the monad, semiring and ${{\mathscr {R}}}$-semimodule, respectively, corresponding to this structure and defined in previous sections. It follows from the construction of these structures that any element $s\in Q(X)$ is a mapping $s:X\rightarrow {{\mathscr {R}}}$.

For simplicity, we assume that the fuzzy system we deal with has only one input variable X and one output variable Y. For description of input and output values we use fuzzy type elements of a given type, i.e., input or output element could be hesitant fuzzy sets or intuitionistic fuzzy sets of fuzzy soft sets. In that case, the i-th IF–THEN rule $S_i$ has the following form:

$$\begin{aligned} S_i:\quad \mathrm{IF }X=s_i\quad { \mathrm THEN }\quad Y=t_i, \end{aligned}$$

where $s_i\in Q(X)$ and $t_i\in Q(Y)$. Instead of fuzzy type structures $s_i$ and $t_i$, we can alternatively use linguistic values describing, e.g., a size. In that case, we must interpret these linguistic values as fuzzy type objects in the respective universe of variables X and Y. Using these rules $S_i,\quad i\in I$, we can define a monadic relation

$$\begin{aligned} S:X\rightarrow Q(Y), \end{aligned}$$

such that for arbitrary $x\in X,y\in Y$,

$$\begin{aligned} S(x)(y)=\sum _{i\in I}^{{\mathscr {R}}}s_i(x)\times _R t_i(y). \end{aligned}$$

According to any of Theorem 1–3, this monadic relation defines the mapping

$$\begin{aligned} S^{\rightarrow }=S\lozenge 1_{Q(X)}:Q(X)\rightarrow Q(Y), \end{aligned}$$

which represents the fuzzy type inference mechanism transforming input values $X=s\in Q(X)$ to output values $Y=t\in Q(Y)$ according to rules $S_i,i\in I$. Using results from Lemmas 1–3 , the fuzzy type inference mechanism $S^{\rightarrow }$ can be simplified according to the following proposition.

Proposition 10

Let $\mathbf{Q},{{\mathscr {R}}},{{\mathscr {Q}}}(X)$ and the IF–THEN rules $S_i$ be defined as above. Then the fuzzy type inference mechanism defined by these fuzzy type rules $S_i$ is such that for arbitrary $s\in Q(X)$, $y\in Y$,

$$\begin{aligned} S^{\rightarrow }(s)(y)=\sum _{x\in X}^{{\mathscr {R}}}p_y(x)\times _R s(x), \end{aligned}$$

where $p_y\in Q(X)$ are elements of the $\mathbf{Q}$-partition $\{p_y:y\in Y\}$ defined by

$$\begin{aligned} x\in X,\quad p_y(x)=\sum _{i\in I}^{{\mathscr {R}}}s_i(x)\times _R t_i(y)=S(x)(y). \end{aligned}$$

Therefore, the fuzzy type inference mechanisms $R^{\rightarrow }$ defined by fuzzy type rules $R_i$ is a fuzzy type transform defined by a $\mathbf{Q}$-partition.

Example 4

Let ${{\mathscr {L}}}$ be the Lukasiewicz algebra and let us consider the intuitionistic fuzzy type inference mechanism with input variable $X=\{1,2,3,4,5,6,7,8,9,10\}$ and output variable $Y=\{1,2,3,4,5,6\}$ defined by the following intuitionistic fuzzy type IF–THEN rules:

$$\begin{aligned} S_1: \mathrm{IF } X =\text {Very}\_\text {big}\quad \mathrm{THEN }\quad Y = \text {Small},\\ S_2: \mathrm{IF } X =\text {Medium}\quad \mathrm{THEN }\quad Y = \text {Big}. \end{aligned}$$

The linguistic values Very_big, Small, Medium,Big are interpreted in sets X, Y, respectively, as ${\mathscr {L}}$-valued intuitionistic fuzzy sets from J(X) defined by the following tables:

• Intuitionistic fuzzy sets in X:

  X	Very_big	Medium
  1	(0,1)	(0.1,0.8)
  2	(0,0.9)	(0.2,0.7)
  3	(0.1,0.7)	(0.4,0.4)
  4	(0.3,0.6)	(0.8,0.1
  5	(0.4,0.4)	(1,0)
  6	(0.4,0.4)	(0.9,0.1)
  7	(0.6,0.3)	(0.6,0.3)
  8	(0.8,0.1)	(0.4,0.5)
  9	(0.9,0)	(0.1,0.9)
  10	(1,0)	(0,1)

• Intuitionistic fuzzy sets in Y:

  Y	Small	Big
  1	(1,0)	(0,1)
  2	(0.7,0.2)	(0.3,0.6)
  3	(0.3,0.6)	(0.5,0.4)
  4	(0.1,0.6)	(0.8,0.1)
  5	(0,0.9)	(0.9,0)
  6	(0,1)	(1,0)

Let us consider the input value described as the intuitionistic fuzzy sets $(u,v)\in J(X)$ defined by the following table.

X	(u, v)
1	(0,0.7)
2	(0.2,0.6)
3	(0.5,0.3)
4	(0.8,0.2)
5	(1,0)
6	(0.9,0.1)
7	(0.5,0.4)
8	(0.2,0.7)
9	(0.1,0.8)
10	(1,0)

We want to determine the response of our system described by these IF–THEN rules. This reaction is the intuitionistic fuzzy set $S^{\rightarrow }(u, v)$ in the set Y. Using definitions of the semiring ${\mathscr {R}}$ and the ${\mathscr {R}}$-semimodule ${{\mathscr {J}}}(X)$ from Propositions 4 and 5 , the output value $S^{\rightarrow }(u,v)$ is the intuitionistic fuzzy set in Y is defined by Proposition 10 with operations from ${{\mathscr {R}}}$, i.e., for $y_k\in Y$ we obtain

$$\begin{aligned} S^{\rightarrow }(u,v)(y_k)=\sum _{i=1,\dots ,10}^\mathcal{R}[\text {Very\_big}(x_i)\times _R \text {Small}(y_k) +_R\\ \text {Medium}(x_i)\times _R \text {Big}(y_k)]\times _R(u,v)(x_i). \end{aligned}$$

If we denote values of corresponding intuitionistic fuzzy sets by

$$\begin{aligned} \text {Very\_big}(x_i)=(\alpha _i,\beta _i),\quad \text {Medium}(x_i)=(\gamma _i,\delta _i),\\ \text {Small}(y_k)=(\omega _k,\tau _k),\quad \text {Big}(y_k)=(\rho _k,\sigma _k), \end{aligned}$$

for $y_3\in Y$ we obtain

$$\begin{aligned}S^{\rightarrow }(u,v)(y_3)&=\sum _i^{{\mathscr {R}}}((\alpha _i\otimes \omega _3)\vee (\gamma _i\oplus \rho _3),(\beta _i\oplus \tau _3)\wedge (\delta _i\oplus \sigma _3))\times _R (u(x_i),v(x_i))\\& = \left(\bigvee _{i=1}^{10}((\alpha _i\otimes \omega _3)\vee (\gamma _i\otimes \rho _3))\otimes u(x_i),\right.\\&\quad \left.\bigwedge _{i=1}^{10}((\beta _i\oplus \delta _3)\wedge (\delta _i\oplus \sigma _3))\oplus v(x_i)\right)=(0.5,0.3). \end{aligned}$$

Hence, the output value $y_3$ corresponds to the reaction of the system on the input value (u, v) with the intuitionistic membership value (0.5, 0.3).

6 Matrix Calculations of F-transforms $H_{X,{{\mathscr {A}}}},J_{X,{{\mathscr {A}}}}$ and $T_{X,{{\mathscr {A}}}}$

In this section, we show how we can calculate the F-transform of these generalized fuzzy sets using matrices in semirings and semimodules. Let us consider any of hesitant, intuitionistic or fuzzy soft type structures and let $\mathbf{Q}=(Q,\lozenge ,\eta ),\mathcal{R}=(R,+,\times ,0_R,1_R)$ and ${{\mathscr {Q}}}(X)=(Q(X),\oplus _X,0_X)$ be the same monad, semiring and ${{\mathscr {R}}}$-semimodule that were mentioned in previous sections.

Let ${{\mathscr {A}}}=\{s_y:y\in Y\}$ be a $\mathbf{Q}$-partition of X and let $F_{X,{{\mathscr {A}}}}:{{\mathscr {Q}}}(X)\rightarrow {{\mathscr {Q}}}(Y)$ be the F-transform defined by a $\mathbf{Q}$-partition ${{\mathscr {A}}}$ according to the part (1) of corresponding Theorems 1,2 or 3. According to Lemmas 1–3, the set $B_X=\{\eta _X(x)\in Q(X):x\in X\}$ is a base of the ${\mathscr {R}}$-semimodule ${{\mathscr {Q}}}(X)$. Hence, for arbitrary object $f\in Q(X)$ there exist coefficients $f_x\in {{\mathscr {R}}}$ such that

$$\begin{aligned} f=\bigoplus _{x\in X}^{{{\mathscr {Q}}}(X)}f_x.\eta _X(x), \end{aligned}$$

where . is the external multiplication in ${{\mathscr {Q}}}(X)$. Using the ${\mathscr {R}}$-matrix notation, we can write

$$\begin{aligned} f=\Vert f_x\Vert _x\star \mathbf{B}_X=\mathbf{f}\star \mathbf{B}_X, \end{aligned}$$

where $\mathbf{B}_X$ it the matrix of the base $B_X$ of the type $|X|\times 1$, with elements from ${\mathscr {R}}$, $\mathbf{f}$ is a matrix of the type $1\times |X|$ and the external multiplication of the $\mathcal{R}$-matrix $\mathbf{A}=\Vert A_{xy}\Vert _{xy}$ and ${{\mathscr {Q}}}(X)$-matrix $\mathbf{B}=\Vert B_x\Vert _x$ of the type $|X|\times |Y|$ and $1\times |X|$, respectively, is defined by

$$\begin{aligned}&\mathbf{B}\star \mathbf{A}=\mathbf{C}=\Vert C_y\Vert _{y\in Y},\\&C_y=\bigoplus _{x\in X}^{{{\mathscr {Q}}}(X)}B_x.A_{xy}, \end{aligned}$$

where the operation $\oplus$ and external multiplication “.” are defined in ${{\mathscr {Q}}}(X)$.

It is easy to see that for arbitrary $x\in X,y\in Y$, $F_{X,\mathcal{A}}(\eta _X(x))(y)=s_y(x)$. Let us define the ${{\mathscr {R}}}$-matrix $\mathbf{M}$ of the type $|X|\times |Y|$ by

$$\begin{aligned} \mathbf{M}=\Vert \lambda _{xy}\Vert _{x,y},\quad \lambda _{xy}=s_y(x). \end{aligned}$$

Therefore, for $f\in Q(X)$, the F-transform $F_{X,{{\mathscr {A}}}}(f)$ can be calculated by

$$\begin{aligned}F_{X,{{\mathscr {A}}}}(f)& =\mathbf{f}\star (\mathbf{M}\star \mathbf{B_Y})\\&= (\mathbf{f}\times \mathbf{M})\star \mathbf{B_Y}. \end{aligned}$$

The matrix $\mathbf{M}$ can be called the matrix of the $\mathbf{Q}$-partition ${{\mathscr {A}}}$ and $\times$ is the matrix multiplication defined by operations from ${{\mathscr {R}}}$, i.e.,

$$\begin{aligned} \mathbf{f}\times \mathbf{M}=\Vert \sum _{x\in X}^{{\mathscr {R}}}(f_x\times \lambda _{xy})\Vert _y. \end{aligned}$$

On the other hand, for arbitrary ${\mathscr {R}}$-matrix $\mathbf{M}=\Vert \lambda _{xy}\Vert$ of the type $|X|\times |Y|$, $\mathbf{M}$ is the matrix of a $\mathbf{Q}$-partition ${{\mathscr {A}}}=\{p_y:y\in Y\}$ of X, where $p_y(x)=\lambda _{xy}$ for arbitrary $y\in Y$.

Let us consider the following illustrative example.

Example 5

Let ${\mathscr {L}}$ be the Lukasiewicz algebra and let us consider the F-transform for hesitant fuzzy sets. Let ${{\mathscr {R}}}$ and $\mathcal{H}(X)$ be from Propositions 1 and 2 , respectively, where $X=\{1,2,3,4\}$. Let $Y=\{1,2\}$ and let us consider the ${{\mathscr {R}}}$-matrix of the type $4\times 2$

$$\begin{aligned} \mathbf{M}=\Vert \lambda _{xy}\Vert _{x,y}= \begin{bmatrix} \{1,0.9\} &{} \{0.6\} \\ \{1,0.7\} &{} \{0.5,0.4\} \\ \{0.3\} &{} \{1\}\\ \{0.5\} &{} \{1,0.9\}\\ \end{bmatrix}. \end{aligned}$$

The matrix $\mathbf{M}$ defines a $\mathbf{H}$-partition $\mathcal{A}=\{h_1,h_2\}\subseteq H(X)$, such that $h_1(x)=\lambda _{x,1}$ and $h_2(x)=\lambda _{x,2}$ for arbitrary $x\in X$. Let $h=\mathbf{h}\star \mathbf{B_X}\in H(X)$ be defined, e.g., by the ${{\mathscr {R}}}$-matrix

$$\begin{aligned} \mathbf{h}=\Vert h(x)\Vert _x= \Vert \{0.3\},\{0.4\},\{0.9\},\{0.9,0.8\}\Vert . \end{aligned}$$

Then the hesitant F-transform of h can be calculated by

$$\begin{aligned}H_{X,{{\mathscr {A}}}}(h)& =(\mathbf{h}\times _R \mathbf{M})\star \mathbf{B_Y}\\&= \left \Vert \sum _{x\in X}^{{\mathscr {R}}}h(x)\otimes \lambda _{xy}\right\Vert _y=\left\Vert \bigcup _{x\in X}^{{\mathscr {R}}}h(x)\otimes \lambda _{xy}\right \Vert _y\\& = \left(\begin{bmatrix} \{0.3\}&\{0.4\}&\{0.9\}&\{0.9,0.8\} \end{bmatrix} \right.\\&\quad \left.\times _R \begin{bmatrix} \{1,0.9\} &{} \{0.6\} \\ \{1,0.7\} &{} \{0.5,0.4\} \\ \{0.3\} &{} \{1\}\\ \{0.5\} &{} \{1,0.9\}\\ \end{bmatrix}\right)\\&\quad \star \begin{bmatrix} \sigma _Y(y_1)\\ \sigma _Y(y_2) \end{bmatrix}\\&= \begin{bmatrix} \{0.1,0.2,0.3,0.4\},\{0,0.8,0.9,0.7\} \end{bmatrix}\\&\quad \star \begin{bmatrix} \sigma _Y(y_1)\\ \sigma _Y(y_2) \end{bmatrix} \end{aligned}$$

$\square$

In the next example, we show that the analogy of Zadeh’s extension principle for hesitant, intuitionistic of fuzzy soft sets can be calculated using F-transform from Theorems 1,2,3. For illustration, we show how the Zadeh’s extension can be calculated for fuzzy soft sets only.

Example 6

Let ${\mathscr {L}}$ be the Lukasiewicz algebra. Let $f:X\rightarrow Y$ be a mapping and. Let K be a fixed set of criteria and let us consider the semiring ${{\mathscr {R}}}(K)$ and the ${{\mathscr {R}}}(K)$-semimodule $\mathcal{T}(X)$ of ${\mathscr {L}}$-fuzzy soft sets from Propositions 7 and 8. Let the ${{\mathscr {R}}}(K)$-matrix $\mathbf{M}=\Vert \lambda _{xy}\Vert _{x,y}$ of the type $|X|\times |Y|$ be defined by

$$\begin{aligned} \lambda _{xy}={\left\{ \begin{array}{ll} 1_{R(K)}&{} f(x)=y,\\ 0_{R(K)} &{}f(x)\ne y.\end{array}\right. }. \end{aligned}$$

Matrix $\mathbf{M}$ represents a $\mathbf{T}$-partition ${{\mathscr {A}}}$ of X and the F-transform $T_{X,{{\mathscr {A}}}}$ is the Zadeh’s extension $f^{\rightarrow }$ of a mapping f, i.e.,

$$\begin{aligned}f^{\rightarrow }& =T_{X,{{\mathscr {A}}}}:T(X)\rightarrow T(Y),\\&\quad (E,s)\in T(X),\quad f^{\rightarrow }(E,s)=(\mathbf{(E,s)}\times _{{{\mathscr {R}}}(K)}{} \mathbf{M})\star \mathbf{B_Y}\\& = \left\Vert \sum _{x\in X}^{{{\mathscr {T}}}(X)}(\lambda _{xy}\times _{{{\mathscr {R}}}(K)}(E,s)(e)(x))\right\Vert _{e\in K,y\in Y}\star \mathbf{B_Y}\\& = \left\Vert \bigvee _{x\in X}\lambda _{xy}(e)\otimes (E,s)(e)(x)\right\Vert _{e\in K,y\in Y}\star \mathbf{B_Y}\\& =\left\Vert \bigvee _{x\in X,f(x)=y}(E,s)(e)(x)\right \Vert _{e\in K,y\in Y}\star \mathbf{B_Y}. \end{aligned}$$

$\square$

7 Conclusions

The issue of lattice-valued F-transform of lattice-valued fuzzy sets appears to be an important tool not only for the theory of fuzzy sets but above all as a method with a wide range of applications. On the other hand, there are many generalizations of classical fuzzy sets that are used in many applications. It is, therefore, natural to deal with the problem of connecting these two approaches and to deal with the F-transform method applied to these generalizations of fuzzy sets. In this paper, we dealt with this issue for hesitant, intuitionistic and fuzzy soft sets, which have an important position in terms of applications. To introduce the concept of F-transform in these structures, we used three different methods, which for classical fuzzy sets lead to an equivalent definition of the F-transform, and we have generalized these methods for any of these structures. These methods are based on the general definition of a fuzzy partition, the definition of F-transform using a monad, and the definition of F-transform as a special semiring homomorphism.

The advantage of this procedure is, among other things, that it allows the application to other fuzzy structures based on classical fuzzy sets, such as various combinations of the three structures.

To further extend the F-transform method for various fuzzy type structures, it will be necessary to deal with, among other things, the issue of upper and lower variants of F-transform for these structures and especially the issue of inverse lattice-valued F-transform, which forms a direct link to applications.

Just as the lattice-valued F-transform is important for researching the theory of this method, the integral F-transform method for [0, 1]-valued fuzzy sets is important for practical applications. It would be therefore appropriate to deal with this variant of F-transform for these generalizations of fuzzy sets.