Distances Between Immersed Graphs: Metric Properties

Abstract

Graphs in metric spaces appear in a wide range of data sets, and there is a large body of work focused on comparing, matching, or analyzing collections of graphs in different ambient spaces. In this survey, we provide an overview of a diverse collection of distance measures that can be defined on the set of finite graphs immersed (and in some cases, embedded) in a metric space. For each of the distance measures, we recall their definitions and investigate which of the properties of a metric they satisfy. Furthermore we compare the distance measures based on these properties and discuss their computational complexity.

1 Introduction

In this survey, we provide a methodical overview of a collection of distance measures aimed at comparing graphs immersed and embedded in an ambient metric space, such as Euclidean space. Data in this form arises in a wide range of areas, including GIS, trajectory analysis, protein alignment, plant morphology, and commodity networks such as electrical grids. Intuitively comparing two networks might require a mapping or correspondence between the networks. For example, if one has a ground truth of a road network and a simplification or reconstruction of the same network, one may wish to measure the error of the latter. In this case, a mapping between the two networks would identify the parts of the ground truth that are successfully reconstructed/simplified and would enable one to study the local error of the reconstruction. In another example, two embedded graphs could serve as representations of a geographic network (e.g., rivers) in two different years, and mappings between them allow one to measure where and how much the networks have changed. On the other hand, many networks are not isomorphic, nor is one necessarily interested in true subgraph isomorphism.

Given the prevalence of immersed and embedded graphs, as well as the wide range of potential domain questions, we need mathematical foundations for comparing and measuring the resemblance of such structures. Moreover, such data is often collected from a noisy and error-prone process, leading to a need for a wide variety of distances that are robust to different types of issues in the data. Such measures are useful in machine learning and statistical approaches, where an understanding of the mathematical structure of the options gives stronger guarantees and theoretical analyses.

More formally, in this paper, we consider the set $\mathcal {G}_{M}$ of finite graphs immersed in a topological metric space $(M,\delta )$ and the set $\widetilde{\mathcal {G}}_{M}$ of finite graphs embedded in M. The most common setting is when we compare planar graphs immersed or embedded in Euclidean space, so that $M=\mathbb {R}^2$ and $\delta$ is the Euclidean distance $d_2$. We note that immersions (where edges are allowed to cross) and embeddings (where the image in the space M may not have crossings) are both of interest; for example, a road network is often considered to be embedded, but, in fact, given overpasses and bridges, in $M=\mathbb {R}^2$ an immersion is the correct representation. Our core question is the following: given $G_1, G_2 \in \mathcal {G}_{M}$ (or $\in \widetilde{\mathcal {G}}_{M}$), how can we measure the distance between $G_1$ and $G_2$? Moreover, what metric properties does a given distance satisfy?

Goal. The goal of this survey is to enumerate and to understand various metric properties of $\mathcal {G}_{M}$ and $\widetilde{\mathcal {G}}_{M}$ under different graph distance measures. We note that different distance measures capture different aspects of the given graphs, and we conjecture that a formal study of the mathematical properties strengthens our understanding of these tradeoffs. For example, some prioritize global similarity, while others focus on local matching; some are theoretically sound but difficult to compute. After briefly summarizing relevant definitions and background in Section 2, we discuss distances between immersed graphs in Section 3. Finally, we conclude in Section 4 by mentioning several natural open problems and possible future work in this area.

2 Preliminaries

We are motivated by the study of the spaces of graphs embedded in Euclidean space induced by different distances. In this work, we consider a more general setting: spaces of graphs immersed in a metric space $(M, \delta )$. (In fact, we consider spaces of pseudographs, allowing self-loops and multiple edges between pairs of vertices.) We begin by briefly defining some of the key concepts used in the remainder of this paper, but refer the reader to a topology text for full definitions [17, 24].

2.1 Distances and Metrics

A number of key properties are considered desirable for comparisons between sets. Here, we focus on the properties most relevant for graph comparison; see for example [9, 10] for more thorough surveys and discussion of distances in a range of more general settings. We note that there are additional studies of the geometry of graph spaces, e.g., [20].

Definition 1

(Key Properties of Dissimilarity Functions) Let $\mathbb {X}$ be a set. Consider a function $d :\mathbb {X} \times \mathbb {X} \rightarrow \overline{\mathbb {R}}_{\ge 0}$, where $\overline{\mathbb {R}}_{\ge 0}$ denotes the non-negative extended real line, i.e., $\overline{\mathbb {R}}_{\ge 0}:= \mathbb {R}_{\ge 0} \cup \infty$. We define the following properties:

• 1. Finiteness: for all $x,y \in \mathbb {X}$, $d(x,y) < \infty$.

• 2. Identity: for all $x \in \mathbb {X}$, $d(x,x)=0$.

• 3. Symmetry: for all $x,y \in \mathbb {X}$, $d(x,y) = d(y,x)$.

• 4. Separability: for all $x,y \in \mathbb {X}$, $d(x,y) = 0$ implies $x=y$.

• 5. Subadditivity (Triangle Ineq.): for all $x,y,z \in \mathbb {X}$, $d(x,y) \le d(x,z) + d(z,y)$.

We say that d is a distance metric (or simply a metric) if it satisfies all five properties. However, less strict notions of dissimilarity can be defined. We say that d is a pseudo-metric if it satisfies finiteness, identity, symmetry, and subadditivity, but not necessarily separability.¹

We say that d is a semi-metric if it satisfies finiteness, identity, symmetry, and separability, but not necessarily subadditivity. We say that d is a quasi-metric if it satisfies finiteness, identity, separability, and subadditivity, but not necessarily symmetry; see Table 1. If we do not know which, if any, of these properties d satisfies, then we simply refer to d as a distance.

Table 1 Types of distances

When we know that certain properties are not satisfied, we can add certain adjectives. We refer to distance functions that allow infinite distances as extended distances.

We say that d is asymmetric or directed² if it does not satisfy symmetry (and may or may not satisfy identity, separability, and subadditivity). For example, an extended directed quasi-metric is a distance that satisfies identity, separability, and subadditivity, but does not satisfy finiteness and symmetry.

Remark 1

(Distances Between Sets) Let $\mathbb {X}$ be a set and let $d :\mathbb {X} \times \mathbb {X} \rightarrow \overline{\mathbb {R}}_{\ge 0}$ be a distance. Let $A,B \subseteq \mathbb {X}$. Then, we define $d(A,B) := \displaystyle \inf _{(x,y) \in A \times B} d(x,y)$.

Remark 2

(Metrizing Distances) If d is not a metric, we can often metrize it. For example, if d is asymmetric, then we can symmetrize it to define a symmetric distance $D :\mathbb {X} \times \mathbb {X} \rightarrow \overline{\mathbb {R}}_{\ge 0}$, where $D(x,y) =\max \{d(x,y), d(y,x) \}$. Note that: if d satisfies separability, then D is also separable. Likewise, finiteness, identity, and subadditivity of D follow from finiteness, identity, and subaditivity of d, respectively. Throughout this paper, this is how we symmetrize asymmetric distances, but we note that there are other options as well.

As a more complicated example, if d is a pseudo-metric, we can make it separable by defining equivalence classes. For each $x \in \mathbb {X}$, we define its equivalence class, denoted [x], as the set of points $[x] := \{ y \in \mathbb {X}\mid d(x,y) = 0\}$ and let $\mathbb {Y}$ be the set of all equivalence classes. Then, we define $D :\mathbb {Y} \times \mathbb {Y} \rightarrow \overline{\mathbb {R}}_{\ge 0}$ by $D([x],[y]) =\displaystyle \max _{x'\in [x]} \max _{y'\in [y]} d(x',y')$.

2.2 Correspondences and Matchings

Let $(M,\delta )$ be a metric space, and $A,B \subset M$. One way to define the distance between A and B is to “line up” the points in the two sets and to use the distance $\delta$ to measure “how well” the two sets are aligned. For this, we define correspondences and matchings.

A correspondence $\tau$ between A and B is simply a subset of $A \times B$. Often, it is convenient to think of $\tau$ both as a subset and as a function that can take subsets of A to subsets of B and vice versa. Specifically, for $A' \subseteq A$, we define $\tau (A'):= \{ b \in B ~|~ \exists a \in A' \text { s.t.\ } (a,b) \in \tau \}$, and define $\tau ^{-1}(B')$ similarly to be $\{ a \in A ~|~ (a,b) \in \tau \}$. We call $\tau$ a matching if each element of $A \sqcup B$ appears in $\tau$ at most once. We call $\tau$ a perfect matching if $\tau$ induces a bijection between the two sets, $b :A \rightarrow B$ with $b(a)=\tau (\{a\})$.

2.3 Open Balls and the Metric Topology

Let $\mathbb {X}$ be a set and $d :\mathbb {X} \times \mathbb {X} \rightarrow \overline{\mathbb {R}}_{\ge 0}$ a distance. For each $r \ge 0$ and $x \in \mathbb {X}$, we define the open ball of radius r centered at x by taking all points in $\mathbb {X}$ whose distance to x is less than r:

$$\begin{aligned} \mathbb {B}_{d}(x,r) := \{ y \in \mathbb {X}~|~ d(x,y) < r \}. \end{aligned}$$

In the case that d is a metric, this is called a metric ball; if d is a pseudo-metric, it is a pseudo-metric ball, and so on. The closure of an open ball is a closed ball and can be written: $\overline{\mathbb {B}}_{d}(x,r) = \{ y \in \mathbb {X}~|~ d(x,y) \le r \}$.

We can use the set of all open balls in $\mathbb {X}$ under the distance d in order to define a topology on $\mathbb {X}$. This is called the open ball topology in general, and denoted $(\mathbb {X},d)$. If d is a metric, the resulting topological space is called a metric space. If d is a pseudo-metric, then it is a pseudo-metric space, and so on. We say that $(\mathbb {X},d)$ is a metric measure space if there exists a Borel measure $\mu$ on $(\mathbb {X},d)$ such that all open balls have positive measure (i.e., for all $x \in \mathbb {X}$ and $r>0$, $\mu (\mathbb {B}_{d}(x,r)) > 0$); see [16, Ch. $3\frac{1}{2}$] for more details on metric measure spaces.

At times, we may find it convenient to assume that a topological space is compact. We say that a topological space T is compact if every open cover has a finite subcover. On compact sets, minimum and maximum are defined:

Lemma 1

(Minimum and Maximum Over a Compact Space) If T is a compact topological space and $f :T \rightarrow \mathbb {R}$ is a continuous function, then $\sup f$ and $\inf f$ are attained by elements in T.

See, e.g., [27, Corollary 13.18] for a proof. In particular, the previous lemma allows us to write $\max f = \sup f$ and $\min f = \inf f$.

2.4 The Space of Paths

Let $\mathbb {X}$ be a set and $d :\mathbb {X} \times \mathbb {X} \rightarrow \overline{\mathbb {R}}_{\ge 0}$ be a distance function. Using the open ball topology in $\mathbb {X}$ and the subspace topology³ on the unit interval $I=[0,1] \subset \mathbb {R}$, a path in $\mathbb {X}$ is a continuous map $\gamma :I \rightarrow \mathbb {X}$, and we shall refer to $\gamma$ as a path from $\gamma (0)$ to $\gamma (1)$. If $\mathbb {X}$ is a metric space, then the length of $\gamma$ can be defined, and we call $\gamma$ rectifiable if its length is finite; see [26] for the formal definition of path lengths. A path is a geodesic if it is locally shortest, that is, if no local perturbation of $\gamma$ results in a shorter path.

A reparameterization $\varphi$ of the unit interval I is a continuous, non-decreasing, and bijective map $\varphi :I \rightarrow I$. Thus, we may also call $\varphi$ an orientation-preserving homeomorphism on I (here, the homeomorphism is orientation-preserving since $\phi (0)=0$ and $\phi (1)=1$). Thus, two paths $\gamma _1, \gamma _2 :I \rightarrow \mathbb {X}$ are equivalent, up to orientation-preserving homeomorphism, if there exist two reparameterizations $\varphi _1$ and $\varphi _2$ such that $\gamma _1 \circ \varphi _1 = \gamma _2 \circ \varphi _2$. (Note: we can always force one of the reparameterizations to be the identity map). For $a,b \in \mathbb {X}$, we use ${{\,\textrm{Paths}\,}}_{\mathbb {X}}(a,b)$ to denote the collection of all paths from a to b in $\mathbb {X}$, up to reparameterization. Then, for $A,B \subseteq \mathbb {X}$, we define

$$\begin{aligned} {{\,\textrm{Paths}\,}}_{\mathbb {X}}(A,B) := \bigcup _{(a,b) \in A \times B} {{\,\textrm{Paths}\,}}_{\mathbb {X}}(a,b). \end{aligned}$$

Let $(M, \delta )$ be a metric space, and let $\Pi :={{\,\textrm{Paths}\,}}_{M}(M,M)$. If we topologize $\Pi$ with the compact-open topology, then $\Pi$ is compact (and, by Lemma 1, we can take minima and maxima over $\Pi$).

2.4.1 The Hausdorff Distance (General Form)

Fig. 1

Two curves $\gamma _1$ and $\gamma _2$ with small Hausdorff distance, as each point on one curve is quite near some point on the other. However, these two curves have large Fréchet distance, realized by the gray leash connecting $\gamma _1(1)$ to $\gamma _0(1)$

Let $(M,\delta )$ be a metric space and let $2^{M}$ denote the collection of all subsets of M. Then, the directed Hausdorff distance $\overrightarrow{\delta }_H :2^{M} \times 2^{M} \rightarrow \overline{\mathbb {R}}_{\ge 0}$ in $(M,\delta )$ is defined by

$$\begin{aligned} \overrightarrow{\delta }_H(A,B) := \sup _{a \in A} \delta \left( a,B\right) = \sup _{a \in A} \inf _{b \in B} \delta \left( a,b\right) , \end{aligned}$$

(1)

where the supremum over an empty set is defined to be zero and the infimum over an empty set is defined to be $\infty$.⁴ See Fig. 1 We symmetrize this distance by taking the maximum (as in Remark 2) in order to obtain the Hausdorff distance $\delta _H :2^{M} \times 2^{M} \rightarrow \overline{\mathbb {R}}_{\ge 0}$, which is defined by

$$\begin{aligned} \delta _H(A,B) := \max \{ \overrightarrow{\delta }_H(A,B),\overrightarrow{\delta }_H(B,A) \}. \end{aligned}$$

The directed Hausdorff distance is not a metric, as it does not satisfy finiteness, symmetry, nor separability (e.g., consider $M=\mathbb {R}$, $A=\{0\}$ and $B=\mathbb {Z}$ and observe that $\overrightarrow{\delta }_H(A,B)=\infty$ and $\overrightarrow{\delta }_H(B,A)=0$). However, when restricted to the set of non-empty compact subspaces of M, the directed Hausdorff distance and the Hausdorff distance both satisfy finiteness.

Lemma 2

(The Hausdorff Distances) Let $(M,\delta )$ be a metric space. The directed Hausdorff distance on M satisfies identity and subadditivity, but not finiteness, symmetry, and separability (i.e., it is an extended directed pseudo-metric), and the Hausdorff distance is an extended metric on M.

Let $\mathbb {Y}\subset 2^{M}$ be a collection of non-empty, compact subspaces of M. Then, the directed Hausdorff distance when restricted to $\mathbb {Y}$ satisfies finiteness, identity, and subadditivity, but neither symmetry nor separability (i.e., it is a directed psuedo-metric on $\mathbb {Y}$), and the Hausdorff distance is a metric when restricted to $\mathbb {Y}$.

The proof of this lemma follows from the metric properties of $\delta$; see [19] for details. For a detailed study of the Hausdorff distance, see [22].

2.4.2 Fréchet Distance Between Paths

Fig. 2

Two curves $\gamma _0$ and $\gamma _1$, with the corresponding points on the curves shown connected in light grey. The Fréchet distance asks for the correspondence which minimizes the longest grey connection, shown here as a thicker line

We define the Fréchet distance $\delta _{F} :\Pi \times \Pi \rightarrow \overline{\mathbb {R}}_{\ge 0}$ by

$$\begin{aligned} \delta _{F}(\gamma _1,\gamma _2)=\inf _\varphi \max _{t\in [0,1]} \delta \left( \gamma _1(t),\gamma _2\big (\varphi \left( t\right) \big )\right) , \end{aligned}$$

where $\varphi$ ranges over all reparameterizations of I; see Fig. 2. The Fréchet distance is sometimes called the dog-walking distance, with the following intuition: if a woman is walking on one path, and her dog is walking on the other, find the shortest possible leash length that allows them to walk on their curves from start to end. In a sense, the Fréchet distance is really a continuous perfect matching between the curves, where the cost of the matching is the worst case distance between points that are paired under the correspondence.

Similarly, the weak Fréchet distance $\delta _{wF} :\Pi \times \Pi \rightarrow \overline{\mathbb {R}}_{\ge 0}$ is defined using the same formula, but where $\phi$ is allowed to range over all continuous surjections (as opposed to bijections) such that $\phi (0)=0$ and $\phi (1)=1$. In other words, these maps do not need to be monotonic and are allowed to decrease.

While introduced originally by Fréchet in his thesis as one of the first examples of a metric [14], this distance was first investigated from a computational perspective by Alt and Godau [4], who also established the following lemma.

Lemma 3

(The Fréchet Metrics) Let $(M,\delta )$ be a metric space, and let $\Pi ={{\,\textrm{Paths}\,}}_{M}(M,M)$. Both the Fréchet distance $\delta _{F}$ and the weak Fréchet distance $\delta _{wF}$ are metrics on M.

2.5 Immersions and Embeddings into Metric Spaces

Let $(M,\delta )$ be a metric space and $G=(V,E)$ be an abstract graph, which we view as a stratified one-dimensional simplicial complex. We restrict our attention to nontrivial graphs, so that each graph must contain at least one vertex. In this setting, note that when we write $x\in G$, the point x can either be a vertex in $V_G$ or a point interior to an edge in $E_G$. We topologize G using the quotient space topology, where each (closed) edge is homeomorphic to the unit interval $I=[0,1]$ in $\mathbb {R}^1$, and we topologize M using the open ball topology.

An immersion of G into M is a continuous map $\phi :G \rightarrow M$ such that for each point $x \in G$ and for all small enough open neighborhoods $n_x$ of x in G, the map $\phi$ restricted to $n_x$ (denoted $\phi |_{n_x}$) is a homeomorphism onto its image.⁵ We call the pair $(G,\phi )$ an immersed graph in M. We say that $(G,\phi )$ is ${\textbf {rectifiable}}$ if V and E are finite sets, and, for every edge $e \in E_G$, the length of $\phi (e)$ is finite. To simplify notation, we sometimes use G in place of the pair $(G,\phi )$.

Given two graphs $(G_1,\phi _{1})$ and $(G_2,\phi _{2})$ immersed in M, we say that they are equivalent up to homeomorphism, which we denote $(G_1,\phi _{1}) \cong (G_2,\phi _{2})$, if there exists a homeomorphism $\displaystyle \alpha :G_1 \rightarrow G_2$ such that the following diagram commutes:

In other words, for all $x \in G$, $\phi _{1}(x) = (\phi _{2} \circ \alpha )(x)$. The set of all rectifiable immersions of nontrivial graphs (up to homeomorphism) into M is denoted $\mathcal {G}_{M}$.

An immersion of G is said to be an ${\textbf {embedding}}$ if G is homeomorphic onto the image $\phi (G)$. In other words, immersions allow edge crossings and embeddings do not; see Fig. 3 and [12, 21, 23]. The set of all rectifiable embeddings of nontrivial graphs (up to homeomorphism) into M is denoted $\widetilde{\mathcal {G}}_{M}$.

Fig. 3

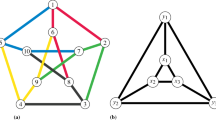
Two graphs with the same image in $(M,\delta )$. In (a), a graph with two vertices and one edge is immersed in M. Note that the edge self-intersects. In (b), a graph with three vertices and three edges is embedded in M with the same image as the graph in (a). In the embedding, the graph and its image in M are homeomorphic

3 Comparisons on Immersed Graphs

Given a metric space $(M, \delta )$, we consider the collection $\mathcal {G}_{M}$ of finite graphs immersed in this metric space. Each $(G,\phi ) \in \mathcal {G}_{M}$ is a graph $G=(V,E)$, where V is the vertex set and E is the edge set, together with an immersion $\phi :G \rightarrow M$. In this section, we investigate the metric properties of different distance functions on $\mathcal {G}_{M}$.

By default, we work on immersed graphs, where edges may cross each other. As every embedding is an immersion, the metric properties hold automatically when restricted to embedded graphs. However, when not all metric properties hold for immersed graphs, some additional properties may hold for embedded graphs that do not hold for the immersed graphs. We explicitly discuss this restriction and why it holds in the relevant sections.

3.1 Hausdorff Distances

In Sect. 2.4.1, we introduced the directed and undirected Hausdorff distances in the general setting, $\overrightarrow{\delta _H}$ and $\delta _H$, respectively. We now consider $\overrightarrow{\delta _H}$ restricted to $\mathcal {G}_{M}$. We call this restriction the directed Hausdorff distance between immersed graphs $\overrightarrow{d_H} :\mathcal {G}_{M} \times \mathcal {G}_{M} \rightarrow \overline{\mathbb {R}}_{\ge 0}$ and define it by

$$\begin{aligned} \overrightarrow{d_H}\left( G_1,G_2 \right) = \overrightarrow{\delta _H} \left( \phi _{1}(G_1),\phi _{2}(G_2) \right) , \end{aligned}$$

and the (undirected) Hausdorff distance $d_H :\mathcal {G}_{M} \times \mathcal {G}_{M} \rightarrow \overline{\mathbb {R}}_{\ge 0}$ is

$$\begin{aligned} d_H\left( G_1,G_2 \right)&= \delta _H(\phi _{1}(G_1),\phi _{2}(G_2))\\&= \max \{ \overrightarrow{d_H}\left( G_1,G_2 \right) , \overrightarrow{d_H}\left( G_2, G_1 \right) \}. \end{aligned}$$

Since each graph in $\mathcal {G}_{M}$ is a compact subset of M, by Lemma 1, we know that the Hausdorff distance between two graphs in $\mathcal {G}_{M}$ is realized by points in the graphs (and hence the $\inf$ and $\sup$ of Equation (1) are actually $\min$ and $\max$).

Theorem 1

(Metric Properties of Hausdorff Distances Between Immersed Graphs) Let $(M,\delta )$ be a metric space. The following statements hold:

• 1. The directed Hausdorff distance $\overrightarrow{d_H}$ on $\mathcal {G}_{M}$ satisfies finiteness, identity, and subadditivity, but not symmetry and separability (i.e., it is a directed pseudo-metric).

• 2. The Hausdorff distance $d_H$ on $\mathcal {G}_{M}$ satisfies finiteness, identity, symmetry, and subadditivity, but does not satisfy separability (i.e., the Hausdorff distance on immersed graphs is a pseudo-metric).

• 3. The Hausdorff distance $d_H$ restricted to embedded graphs in $\widetilde{\mathcal {G}}_{M}$ is a metric.

Proof

First, note that Statement 3 follows from Lemma 2 and the fact that each $G \in \widetilde{\mathcal {G}}_{M}$ is a compact subspace of M. Now, for Statements 1 and 1, $\overrightarrow{d_H}$ and $d_H$ on $\mathcal {G}_{M}$ also satisfy nonnegativity, identity, and subadditivity. Neither $\overrightarrow{d_H}$ nor $d_H$ satisfy separability, for two different immersed graphs may have the same image (e.g., a single edge mapped to a line segment and a Y-shaped graph mapped onto the same line segment; see Fig. 3), where two different graphs are mapped to the same subset of $\mathbb {R}^2$.

By construction, just as in the general case, $\overrightarrow{d_H}$ is asymmetric and $d_H$ is symmetric; for instance, if the immersion of $G_1$ is a true subset of the immersion of $G_2$, then $\overrightarrow{d_H}(G_1,G_2) = 0 > \overrightarrow{d_H}(G_2,G_1)$.

3.2 Fréchet Distance

The Fréchet distance is a metric originally defined on paths in $\mathbb {R}^n$ (see Sect. 2.4.2), but it can also be defined for more general objects, such as oriented manifolds. Let $A,B\subseteq \mathbb {R}^d$ be two oriented manifolds and let $f:A\rightarrow M$ and $g:B\rightarrow M$ be two immersions.⁶ Then the Fréchet distance between A and B is given by

$$\begin{aligned} \inf _\alpha \max _{t\in A}\,\delta \left( f(t),g(\alpha (t))\right) , \end{aligned}$$

where $\alpha :A\rightarrow B$ ranges over all orientation-preserving homeomorphisms. In fact, this definition can be generalized to any two homeomorphic spaces, such as graphs. However, care must be taken to either define an appropriate notion of orientation, or define the distance without requiring the homeomorphisms to be orientation-preserving.

Fig. 4

Graphs with large Fréchet but small Hausdorff distance

Here, the Fréchet distance between immersed graphs $d_{F} :\mathcal {G}_{M} \times \mathcal {G}_{M} \rightarrow \overline{\mathbb {R}}_{\ge 0}$ can be defined by restricting our attention to the Fréchet distance between paths, and avoiding any mention of orientation-preserving homeomorphims. In particular, for $(G_1,\phi _{1}),(G_2,\phi _{2}) \in \mathcal {G}_{M}$, the Fréchet distance is defined as

$$\begin{aligned} d_{F}(G_1,G_2 ) = \min _{\alpha } \max _{e\in E_{1}} \delta _{F}(\phi _{1}(e),\phi _{2}(\alpha (e))) \end{aligned}$$

if $G_1,G_2$ are homeomorphic, and $\infty$ if they are not.⁷ Here, $\alpha$ ranges over all edge mappings corresponding to the isomorphisms of $G_1$ and $G_2$, see [5], and we assume the graphs have no degree two vertices. The latter can be assumed since we consider graphs in $\mathcal {G}_{M}$ equivalent up to homeomorphism. Note that we are abusing notation slightly here and viewing $\phi _G(e)$ as a parameterized curve, rather than just an immersion of an edge; since the Fréchet distance considers all reparameterizations of the curve regardless, any parameterization of the image of the edge is sufficient. Since graphs are compared using an isomorphism, the Fréchet distance can be arbitrarily larger than the Hausdorff distance, see Fig 4.

Theorem 2

(Metric Properties of Fréchet Distance Between Immersed Graphs) The Fréchet distance $d_{F}$ is a metric.

Proof

It is well-known that the Fréchet distance is a pseudo-metric: Identity and symmetry follow directly from the definition.

Separability is also fulfilled: consider two graphs $(G_1,\phi _{1}), (G_2,\phi _{2})$ with Fréchet distance 0. These graphs must be isomorphic if their distance is 0, and hence $G_1$ is the same as $G_2$.

For completeness, we provide a proof that the subadditivity is satisfied: Consider three graphs $(G_1,\phi _{1}), (G_2,\phi _{2}) (G_3,\phi _{3}) \in \mathcal {G}_{M}$. Then

$$\begin{aligned}&d_{F}(G_1,G_2) + d_{F}(G_2,G_3)\\&= \min _{\alpha _1:G_1\rightarrow G_2}\max _{e_1\in E_1}d_{F}(\phi _{1}(e_1),\phi _{2}(\alpha _1(e_1)))\\&\quad \quad + \min _{\alpha _2:G_2\rightarrow G_3}\max _{e_2\in E_2}d_{F}(\phi _{2}(e_2),\phi _{3}(\alpha _2(e_2)))\\&\ge \min _{\alpha _1:G_1\rightarrow G_2}\min _{\alpha _2:G_2\rightarrow G_3} \bigl (\max _{e_1\in E_1}d_{F}(\phi _{1}(e_1),\phi _{2}(\alpha _1(e_1)))\\&\quad \quad + \max _{e_2\in \alpha _1(e_1)}d_{F}(\phi _{2}(e_2),\phi _{3}(\alpha _2(e_2))) \bigr )\\&\ge \min _{\alpha _1:G_1\rightarrow G_2}\min _{\alpha _2:G_2\rightarrow G_3} \max _{e_1\in E_1}d_{F}(\phi _{1}(e_1),\alpha _2(\phi _{2}(\alpha _1(e_1))))\\&= \min _{\alpha :G_1\rightarrow G_3}\max _{e_1\in E_1}d_{F}(\phi _{1}(e_1),\phi _{3}(\alpha (e_1)))\ = \ d_{F}(G_1,G_3) \end{aligned}$$

The first inequality follows simply by combining the two terms, and the second inequality follows from the triangle inequality that is fulfilled by $d_{F}$ for curves (which in turn follows from it being fulfilled by $\delta _{F}$).

Note that if $G_1$ and $G_2$ are simple graphs, each isomorphism has a unique edge mapping. Hence computing this distance is at least as hard as determining graph isomorphism. For trees [5], it can be computed in polynomial time and for graphs of bounded tree width [7] it is fixed-parameter tractable. For planar embedded graphs, it is desirable that isomorphisms are “orientation-preserving” in the sense that they preserve orderings of edges around each vertex. This property can be used to enumerate all such planar orientation-preserving isomorphisms, and thus compute the distance for embedded graphs in polynomial time [13].

3.3 Path-Based Distance

The path-based distance was originally presented in [1]. This distance uses the Fréchet distance between paths in graphs (see Sect. 2.4.2) to define a distance between graphs.

Let $(M,\delta )$ be a metric space. For each $(G,\phi ) \in \mathcal {G}_{M}$, let $\Pi _G$ denote the set of all paths in G up to reparameterization; that is, $\Pi _G={{\,\textrm{Paths}\,}}_{G}(G,G)$. See Sect. 2.4. The directed path-based distance $\overrightarrow{d_{path}}:\mathcal {G}_{M} \times \mathcal {G}_{M} \rightarrow \mathbb {R}_{\ge 0}$ is the directed Hausdorff distance between $(G_1,\phi _{1})$ and $(G_2,\phi _{2})$:

$$\begin{aligned} \overrightarrow{d_{path}}(G_1,G_2)=\max _{{P}\in \Pi _{1}}\min _{{Q}\in \Pi _{2}}\delta _{F}(\phi _{1}({P}),\phi _{2}({Q})). \end{aligned}$$

As noted in Remark 2, we can symmetrize this asymmetric distance in order to define the path-based distance $d_{path} :\mathcal {G}_{M} \times \mathcal {G}_{M} \rightarrow \overline{\mathbb {R}}_{\ge 0}$ as the Hausdorff distance between path sets $\Pi _{1}$ and $\Pi _{2}$. Specifically,

$$\begin{aligned} d_{path}(G_1,G_2) = \max \left\{ \overrightarrow{d_{path}}(G_1,G_2),\overrightarrow{d_{path}}(G_2,G_1)\right\} . \end{aligned}$$

Due to compactness of $\Pi _{1}$ and $\Pi _{2}$ and by Lemma 1, we can always find paths where this distance is realized. In other words, if $\overrightarrow{d_{path}}(G_1,G_2)=\varepsilon$, then there exist paths ${P}_1 \in \Pi _{1}$ and ${P}_2 \in \Pi _{2}$ such that the Fréchet distance between ${P}_1$ and ${P}_2$ is $\varepsilon$. See Fig. 5 for an example; note that the two graphs shown have infinite Fréchet distance, as they are not homeomorphic.

Theorem 3

(Metric Properties of Path-Based Distances) The directed path-based distance satisfies finiteness, identity, and subadditivity, but not separability nor symmetry. The path-based distance is a metric.

Fig. 5

Two graphs, $G_1$ and $G_2$, shown separately for ease of visibility. When they are embedded to be overlapping (so that the outer four vertices are in the same location in the plane), these graphs have small path based distance: each edge in $G_1$ will can map to two edges in $G_2$, and the path based distance will be less than the radius of $G_2$’s inner loop

Proof

For each $(G,\phi ) \in \mathcal {G}_{M}$, define the set of paths $\Pi _G={{\,\textrm{Paths}\,}}_{G}(G,G)$ and the set of immersed paths $\phi _G(\Pi _G):= \{ \phi _G \circ f \mid f \in \Pi _G \}$. Since $\phi _G$ is an immersion and $\Pi _G$ is compact, we know that $\phi _G(\Pi _G)$ is also compact. Hence, the theorem follows from setting $\mathbb {Y}= \left\{ \phi _G(\Pi _G) \mid {(G,\phi _G) \in \mathcal {G}_{M}} \right\}$ in Lemma 2, where $\mathbb {Y}$ is a collection of compact subspaces of ${{\,\textrm{Paths}\,}}_{M}(M,M)$.

The exact complexity of the path-based distance is still an open and potentially challenging question, as the measure depends up Fréchet mappings between curves in the graph, of which there could be exponentially many to consider. However, in the paper that introduces it [1], the authors present a polynomial time approximation algorithm which is based on the maximum Fréchet distance and demonstrate its efficacy on real-world map datasets.

3.4 Traversal Distance

The traversal distance, introduced by Alt et al. in [3], for a pair of immersed graphs $(G_1, \phi _{1}),(G_2, \phi _{2}) \in \mathcal {G}_{M}$ is defined as follows. Let $f:[0,1]\rightarrow G_1$ be a continuous and surjective function, called a (full) traversal of $G_1$, and let ${g} :[0,1]\rightarrow G_2$ be a continuous—but not necessarily surjective—function, called a partial traversal of $G_2$. We compare functions f and g by their $L_{\infty }$ norm, $\displaystyle \max _{t\in [0,1]} \delta \left( f(t),{g}(t)\right)$. Taking the infimum over all possible f and g, we arrive at the traversal distance $\overrightarrow{d_{T}} :\mathcal {G}_{M} \times \mathcal {G}_{M} \rightarrow \overline{\mathbb {R}}_{\ge 0}$. Formally, the traversal distance from $(G_1, \phi _{1})$ to $(G_2, \phi _{2})$ is defined by

$$\begin{aligned} \overrightarrow{d_{T}}\left( G_1,G_2\right) =\displaystyle \inf _{f,{g}}\max _{t\in [0,1]} \delta \left( f(t),{g}(t)\right) , \end{aligned}$$

where f ranges over all full traversals of $G_1$ and g ranges over all partial traversals of $G_2$. Noticing that reparametrizations of each traversal f and each partial traversal g are included in that infimum, we observe the following equivalence:

$$\begin{aligned} \overrightarrow{d_{T}}\left( G_1,G_2\right) =\displaystyle \inf _{f,{g}}\delta _{F}(f,{g}). \end{aligned}$$

Compared to the Fréchet distance, the traversal distance can also be applied to non-homeomorphic graphs. On homeomorphic graphs, the Fréchet distance is an upper bound for the traversal distance, as the Fréchet correspondence yields a candidate traversal to consider. However, the traversal distance can be arbitrarily smaller than the Fréchet distance, see Fig. 6.

Fig. 6

Homeomorphic graphs with small traversal but large Fréchet and path-based distances

We take the symmetric version of the traversal distance by maximizing the two directed distances. In other words, we define $d_{T} :\mathcal {G}_{M} \times \mathcal {G}_{M} \rightarrow \overline{\mathbb {R}}_{\ge 0}$ by

$$\begin{aligned} d_{T}\left( G_1,G_2\right) = \max \{ \overrightarrow{d_{T}}\left( G_1,G_2\right) ,\overrightarrow{d_{T}}\left( G_2,G_1\right) \}. \end{aligned}$$

Theorem 4

(Metric Properties of Traversal Distance) The directed traversal distance $\overrightarrow{d_{T}}$ satisfies finiteness and identity but does not satisfy symmetry, separability, and subadditivity.

The symmetric traversal distance $d_{T}$ satisfies finitesness, identity, and symmetry, but it does not satisfy separability nor subadditivity.

Proof

Since the distance between f and g is finite and since the traversal distance is taking the infimum over all possible traversals f and partial traversals g, we know that $\overrightarrow{d_{T}}$ is finite. When $(G_1, \phi _{1}) = (G_2, \phi _{2})$, taking the same traversal yields a traversal distance of zero. Hence, the traversal distance satisfies the identity property. Since any proper subgraph has distance zero to its supergraph, but not vice versa, we also have that it is not symmetric.

Fig. 7

Example showing that the traversal distance violates both separability and subadditivity. Assume that the four vertices of these graphs are the same, i.e., $G_1$ and $G_3$ are subgraphs of $G_2$. Since $G_1$ is a subgraph of $G_2$, the traversal distance from $G_1$ to $G_2$ is zero. To compute $\overrightarrow{d_{T}}\left( G_1,G_3\right)$, conside the traversal of $G_1$ that starts at the bottom left, goes up to the next vertex, right to the third vertex, and finally down to the last vertex. The best partial traversal of $G_3$ would be one that goes up and down one of the vertical edges

To see that the traversal distance does not fulfill separability and subadditivity, consider the following graphs: $G_2$ is comprised of four vertices and four edges forming an axis-aligned rectangle in $\mathbb {R}^2$, $G_1$ is the subgraph of $G_2$ obtained by removing the bottom edge, and $G_3$ is the subgraph of $G_2$ obtained by removing the top edge. See Fig. 7. Then, $\overrightarrow{d_{T}}\left( G_1,G_2\right) =0$, but $(G_1, \phi _{1})$ and $(G_2, \phi _{2})$ are not equivalent (up to homeomorphism). Thus, separability is not satisfied. In addition, we have $\overrightarrow{d_{T}}\left( G_2,G_3\right) =w/2$ and $\overrightarrow{d_{T}}\left( G_1,G_3\right) =w$. Since $w > w/2 + 0$, subadditivity is not satisfied.

Since $\overrightarrow{d_{T}}$ satisfies finiteness and symmetry and identity, so does the symmetrized version $d_{T}$. By construction, $d_{T}$ is also symmetric. The two graphs of Fig. 3 have distance zero, which means that $d_{T}$ does not satisfy separability. However, for $d_{T}$, subadditivity does not hold. For this, consider again the graphs in Fig. 7. We have $d_{T}\left( G_1,G_3\right) =w$. If we add small outward left and right spikes (say, they are length $\epsilon$ with $\epsilon < \frac{w}{2}$) on all graphs at height h/2 (calling the resulting graphs $G_1^*$, $G_2^*$, and $G_3^*$, respectively), then we have $d_{T}\left( G_1,G_2\right) =d_{T}\left( G_2,G_3\right) =w/2$ and $d_{T}\left( G_1^*,G_3^*\right) =w+\epsilon$. Hence, subadditivity does not hold.

Since a (partial) traversal is also a path in the graph, the traversal distance is related to the path-based distance. Both take the Fréchet distance from a traversal/path in $(G_1, \phi _{1})$ to a closest partial traversal/path in $(G_2, \phi _{2})$. However, the traversal distance minimizes over all traversals, whereas the path-based distance maximizes over all paths. Hence, the traversal distance is a lower bound to the path-based distance, i.e.,

$$\begin{aligned} d_{T}\left( G_2,G_1\right) \le \overrightarrow{d_{path}}(G_2,G_1). \end{aligned}$$

Fig. 8 gives an example where the path-based distance is strictly larger than the traversal distance.

Fig. 8

The path p highlighted red in $(G_1, \phi _{1})$ has large distance to any path in $(G_2, \phi _{2})$, but the traversal distance from $(G_1, \phi _{1})$ to $(G_2, \phi _{2})$ is small

3.5 Strong and Weak Graph Distance

The strong and weak graph distances were first introduced in [2], with the goal of combining topology and geometry. They are based on the strong/normal and weak Fréchet distance between graphs.

Let $(G_1,\phi _{1}), (G_2,\phi _{2})\in \mathcal {G}_{M}$. A graph mapping $s:G_1\rightarrow G_2$ is a continuous map. An alternative characterization of a graph mapping for planar embedded graphs is as follows: each vertex $v\in V_{1}$ is sent to a point $s(u) \in G_2$, and each edge $\{u,v\}\in E_{1}$ is sent to a path⁸ from s(u) to s(v) in $G_2$. Note that s(u) can be a vertex or any point internal to an edge.

Letting s range over all graph mappings from $G_1$ to $G_2$, the directed strong graph distance $\overrightarrow{d_{S}} :\mathcal {G}_{M} \times \mathcal {G}_{M} \rightarrow \overline{\mathbb {R}}_{\ge 0}$ between $G_1$ and $G_2$ is given by

$$\begin{aligned} \overrightarrow{d_{S}}(G_1,G_2) =\inf _{s:G_1\rightarrow G_2}\max _{e\in E_{1}}\delta _{F}(\phi _{1}(e),\phi _{2}(s(e))), \end{aligned}$$

and the directed weak graph distance $\overrightarrow{d_{W}} :\mathcal {G}_{M} \times \mathcal {G}_{M} \rightarrow \overline{\mathbb {R}}_{\ge 0}$ is given by

$$\begin{aligned} \overrightarrow{d_{W}}(G_1,G_2)=\inf _{s:G_1\rightarrow G_2}\max _{e\in E_{1}}\delta _{wF}(\phi _{1}(e),(\phi _{2}(s(e)). \end{aligned}$$

Note that these distances are not symmetric. However, we may define their undirected versions by taking the maximum of the directed distances, i.e.,

$$\begin{aligned} d_{S}(G_1,G_2)=\max \{\overrightarrow{d_{S}}(G_1,G_2),\overrightarrow{d_{S}}(G_2,G_1)\} \end{aligned}$$

and

$$\begin{aligned} d_{W}(G_1,G_2)=\max \{\overrightarrow{d_{W}}(G_1,G_2),\overrightarrow{d_{W}}(G_2,G_1)\}. \end{aligned}$$

In [2] it was shown that these distances are metrics for planar embedded graphs and pseudo-metrics for non-planar graphs. However, for immersed graphs, separability also holds for graphs when defining graph mappings as continuous maps between the (abstract) graphs. Hence we obtain:

Theorem 5

(Metric Properties of Strong and Weak Graph Distances) The directed strong and weak graph distances ($\overrightarrow{d_{S}}$ and $\overrightarrow{d_{W}}$) satisfy finiteness, identity, separability, and subadditivity, but not symmetry (i.e., they are quasi-metrics). The undirected strong and weak graph distances ($d_{S}$ and $d_{W}$, respectively) are metrics.

Furthermore, in [2] the authors point out that

$$\begin{aligned} d_T(G_1,G_2)\le \overrightarrow{d_{W}}(G_1,G_2) \le \overrightarrow{d_{S}}(G_1,G_2), \end{aligned}$$

which connects this distance to the traversal distance discussed in Sect. 3.4. See also Fig. 9.

Fig. 9

Graph $G_2$ has strictly larger (strong or weak) graph distance than traversal distance to $G_1$. And graph $G_2$ has strictly larger strong than weak graph distance to $G_3$

Both the strong and weak graph distances are NP-hard to decide for general graphs. However, for trees we can compute them in cubic time for the strong graph distance and quadratic time for the weak graph distance. For planar embedded graphs under a geometric assumption (which requires cycles to have a nice shape), the weak distance can be computed in quadratic time, but the strong distance remains NP-hard. An open question is whether a “stronger/symmetric” version of the graph distance, which requires the same graph mapping for both directions, would be equivalent to a generalization of the contour tree distance; see Sect. 3.6 for a discussion of that distance.

3.6 Contour Tree Distance

In [6], motivated by computing the Fréchet distance between two surfaces, the “contour tree distance” is defined between the contour trees of two surfaces. We naturally extend this distance to a distance on the subset of $\mathcal {G}_{M}$ consisting of connected (immersed) graphs; let $\mathcal {C}_M$ denote this space. The contour tree distance $d_C :\mathcal {C}_M \times \mathcal {C}_M \rightarrow \mathbb {R}$ is defined to be

$$\begin{aligned} d_C(G_1,G_2) = \inf _{\tau } \sup _{(x,y)\in \tau } \delta (\phi _{1}(x),\phi _{2}(y)), \end{aligned}$$

where $\tau$ ranges over the set of all correspondences between $(G_1, \phi _1)$ and $(G_2,\phi _2)$ such that:

• 1. $\tau$ is a connected subset of $G_1 \times G_2$.

• 2. For each $x \in G_1$, $\tau \cap ( \{x\} \times G_2 )$ is a non-empty, connected subset of $G_2$.

• 3. For each $y \in G_2$, $\tau \cap ( G_1 \times \{y\} )$ is a non-empty, connected subset of $G_1$.

The connectedness of the correspondence $\tau$ requires the graphs to be connected, too. This is the reason that we are restricting our attention to $\mathcal {C}_M$ as opposed to $\mathcal {G}_{M}$.

The contour tree distance resembles the Fréchet distance in that it establishes a correspondence between portions of the graphs. However, unlike standard Fréchet distance, the contour tree distance allows a comparison of non-homeomorphic graphs using $G_1 \times G_2$, in a manner similar to the Fréchet distance. It allows for “stretching" a region of the graph, as any vertex in one can correspond to a connected subregion in the other. See Fig. 10 for an illustration.

Fig. 10

Two graphs with small contour tree distance showing corresponding parts of the graphs

Theorem 6

($d_C$ is a Metric) On the space $\mathcal {C}_M$ of connected graphs, $d_C$ is a metric.

Proof

The distance fulfills identity via the trivial correspondence, and symmetry because the same correspondence works for $G_1 \times G_2$ and $G_2 \times G_1$.

For separability, assume that $d_C(G_1,G_2)=0$. Then either a correspondence $\tau$ exists such that $d(\phi (x),\phi (y))=0$ for all $(x,y)\in \tau$ or there is a limit of correspondences such that $d(\phi (x),\phi (y))< \varepsilon$ for arbitrary small $\varepsilon$ and $(x,y)\in \tau$. In both cases it follows that $G_1$ and $G_2$ have the same immersion.

To see that it also satisfies subadditivity, we concatenate the correspondences and use subadditivity in $(M,\delta )$.

The contour tree distance is NP-complete to compute, even for trees [6]. It seems that the contour tree distance can be considered as a symmetric version of the strong graph distance; see Sect. 3.5. Both align portions of the graphs, but where the strong graph distance uses two separate mappings between the two graphs, the contour tree distance uses symmetric correspondences.

3.7 Local Persistent Homology Distance

The next distance we investigate is the local persistent homology (LPH) distance, originally presented in [1] as a metric on plane graphs. To define this distance, we compare the graphs at a local level using persistent homology (see, e.g., [11]). Briefly, persistent homology is a multiscale version of the fundamental topological notion of homology, which measures the “features" in a space (i. e. connected components, holes, and higher-dimensional voids).

More formally: given a nested sequence of topological spaces (called a filtration), persistent homology tracks the appearance (“births”) and disappearance (”deaths”) of topological features within the filtration. The results are then encoded in a persistence diagram as pairs of (birth, death) points in the first quadrant of the plane. A standard distance between persistence diagrams is as follows: given persistence diagrams $D_1$ and $D_2$, their bottleneck distance $d_b$ is defined to be

$$\begin{aligned} \displaystyle d_b(D_1,D_2):=\inf _{f:D_1\rightarrow D_2} \sup _{x\in D_1} ||x-f(x)|| \end{aligned}$$

where f ranges over all bijections between $D_1$ and $D_2$.

The local persistent homology distance compares graphs at a local level and requires the following additional preliminary definition. Let $\mathbb {Y}\subseteq \mathbb {X}$ a set. We define an $\varepsilon$-thickening of Y, denoted $\mathbb {Y}^{\varepsilon }$, to be

$$\begin{aligned} \mathbb {Y}^{\varepsilon }&:= \bigcup _{x \in \mathbb {Y}} \mathbb {B}_{d}(x,\varepsilon )\\&= \{ x \in \mathbb {X}\mid d(\mathbb {Y},x) \le \varepsilon \}. \end{aligned}$$

When $\mathbb {X}$ is a real vector space, $\mathbb {Y}^{\varepsilon }$ is referred to as the Minkowski sum of $\mathbb {Y}$ with a closed ball of radius $\varepsilon$ in $(\mathbb {X}, d)$.

Fig. 11

A picture of a geometric graph embedded in $\mathbb {R}^2$, shown in the leftmost box, along with $\varepsilon$-thickenings for increasing values of $\varepsilon$. The graph contains 3 loops: two that are entirely in red graph, as well as one “relative" loop which is formed by the leftmost partial cycle of the graph along with its boundary. The birth and death times of each are indicated below the filtration; each such pair will form a point in the persistence diagram, with longer lifetime loops appearing further from the diagonal that has slope 1

Let $(G,\phi _G) \in \mathcal {G}_{M}$. Then $G^{\varepsilon }$ is the $\varepsilon$-thickening of G in $(M,\delta )$. We define the function $\delta _G :M \rightarrow \mathbb {R}$ as the distance function to the set $\phi _G(G)$; namely, for all $x \in M$, we define $\delta _G(x):=\displaystyle \min _{y\in \phi _G(G)}\delta \left( x,y\right)$. Equivalently, $\delta _G(x)$ is the smallest non-negative $\epsilon$ such that x is in the $\epsilon$-thickening $G^{\epsilon }$. Let U be a closed subset of M, and let $\partial {U}$ denote the boundary of U. We consider the distance function restricted to the quotient space $U_*:={U} / \partial U$; that is, we define $\delta _{G,U} :U_* \rightarrow \mathbb {R}$ by

$$\begin{aligned} \delta _{G,U} ([x]) = {\left\{ \begin{array}{ll} \delta _G(x), &{} [x] \ne \partial U \\ \displaystyle \min _{y \in \partial U} \delta _G(y), &{} [x] = \partial U. \end{array}\right. } \end{aligned}$$

See Fig. 11 for an example.

Given graphs $(G_1,\phi _{1})$ and $(G_2,\phi _{2})$ in $\mathcal {G}_{M}$, let $D_{1}$ and $D_{2}$ be the persistence diagrams of $\delta _{G_1,U}$ and $\delta _{G_2,U}$, respectively. A local distance signature between $G_1$ and $G_2$ is the assignment of a distance to the neighborhood U; in our case, we assign the bottleneck distance between $D_{1}$ and $D_{2}$ to the set U, and denote it $B_{U}(G_1,G_2)$. The local distance signature is valuable in its own right and can be used in heatmaps to visualize the locations of large differences between the two graphs, as shown in Fig. 12.

We use the construction described above to define an overall distance between the two graphs.

Fig. 12

Comparison of two constructed road networks $G_1$ in color and $G_2$ in gray. The color-coded network visualizes the heatmap of the local distance signature for $x\in G_1$. Figure rights: ©2014 Ahmed, Fasy, and Wenk. First appeared in [1]

Let $\mathcal {B}$ denote the set of all metric balls in $(M, \delta )$; that is,

$$\begin{aligned} \mathcal {B} = \{ \mathbb {B}_{\delta }(x,r) \mid x \in M, r \in \mathbb {R}_{\ge 0} \}. \end{aligned}$$

As a set, $\mathcal {B}$ is equivalent to the product $M \times \mathbb {R}_{\ge 0}$. And so, we use the product topology on $M \times \mathbb {R}_{\ge 0}$ to define a topology on $\mathcal {B}$.

We call $\omega :\mathcal {B} \rightarrow \mathbb {R}_{\ge 0}$ a weight function if it: (i) vanishes for large enough balls (i.e., there is an $R \in \mathbb {R}$ such that $\omega (\mathbb {B}_{\delta }(x,r))=0$ for all $r > R$), (ii) has a finite integral ($\displaystyle \int _{U \in \mathcal {B}} \omega (U) \, dU < \infty$), and (iii) is continuous. The local persistent homology distance with respect to the weight function $\omega$ is the function $d_{LH}:\mathcal {G}_{M}\times \mathcal {G}_{M} \rightarrow \mathbb {R}$ defined by

$$\begin{aligned} d_{LH}(G_1,G_2) = \int _{U \in \mathcal {B}} \omega (U) B_{U}(G_1,G_2) \, dU. \end{aligned}$$

(2)

If M is a metric measure space, this integral is well-defined. In particular, we can expand it to a double integral as follows:

$$\begin{aligned} d_{LH}(G_1,G_2) = \int _{r=0}^{\infty } \int _{x \in M} \omega (U) B_{U}(G_1,G_2) \, dx \, dr, \end{aligned}$$

(3)

where $U=\mathbb {B}_{\delta }(x,r)$. Moreover, as we see in the next theorem, this distance is a pseudo-metric:

Theorem 7

(Metric Properties of $d_{LH}$) For a given metric measure space M and weight function $\omega$, the local homology distance $d_{LH}$ satisfies finiteness, identity, symmetry, and subadditivity but does not satisfy separability (i.e., it is a pseudo-metric). The LPH distance restricted to comparing embedded graphs is a metric.

Proof

Let $\omega :\mathcal {B} \rightarrow \mathbb {R}_{\ge 0}$ be the weight function defining $d_{LH}$.

We prove that $d_{LH}$ satisfies nonnegativity, finiteness, identity, symmetry, and subadditivity.

Nonnegativity. Let $G_1,G_2 \in \mathcal {G}_{M}$. The distance $d_{LH}$ is defined in Equation (2) using an integral over $\mathcal {U}$ with integrand $\omega (U) B_{U}(G_1,G_2)$. Since $\omega$ is a weight function, we know that $\omega$ is nonnegative. As $B_{U}(G_1,G_2)$ is the bottleneck distance between two persistence diagrams, we know this term is also nonnegative. Thus, $d_{LH}(G_1,G_2)$, being the integral of the product of two nonnegative functions, is nonnegative.

Finiteness. Let $X \subset M$ be the support of $\omega$. Since $\omega$ is a weight function, we know that there exists an R such that $\omega$ vanishes on all $U=\mathbb {B}_{\delta }(x,r) \in \mathcal {B}$ satisfying $R \le r$, i.e., we have $\omega (U)=0$. On the other hand, for all balls $U =\mathbb {B}_{\delta }(x,r) \in \mathcal {B}$ such that $r \le R$, we know that $B_{U}(G_1,G_2) \le 2R$ (since thickening by 2R or more results in the empty topological space). Then, letting $c=\displaystyle \int _{U \in \mathcal {B}} \omega (U) \, dU$ and $\mathcal {B}'$ denote the support of $\omega$, we bound the expression of Equation (2):

$$\begin{aligned} d_{LH}(G_1,G_2) \le \int _{U \in \mathcal {B}'} \omega (U) R \, dU + \int _{U \in \mathcal {B} \setminus \mathcal {B}'} 0 \cdot B_{U}(G_1,G_2) \, dU = cR + 0 < \infty . \end{aligned}$$

Identity. If $G_1=G_2 \in \mathcal {G}_{M}$, then $B_{U}(G_1,G_2) = 0$ for all U, and so $d_{LH}(G_1,G_2) = 0$.

Symmetry. The symmetry of $d_{LH}$ follows immediately from the symmetry of the bottleneck distance between persistence diagrams.

Subadditivity. Subadditivity follows, again, from the subadditivity of the bottleneck distance between persistence diagrams.

Inseparability. Let $(G_1,\phi _{1})$ be the immersion of the graph with two vertices and one edge from Fig. 3(a) and let $G_2$ be the graph with three vertices and three edges from Fig. 3(b). Note that $G_1$ and $G_2$ are not homeomorphic, yet have the same image in M. Then, for all metric balls U in $(M,\delta )$, we have $B_U(G_1,G_2)=0$. Thus, $d_{LH}$ is not separable.

Remark 3

(Variants of the LPH Distance) When restricted to the setting where M is compact, then $d_{LH}$ also satisfies separability if $\omega$ is nonvanishing on small enough balls. This was observed in [1] for M a compact subspace of $\mathbb {R}^n$.

The definition of the LPH distance given in Equation (2) integrates the bottleneck distance over the space of all metric balls $\mathcal {B}$. We can aggregate over $\mathcal {B}$ in other ways, such as using the $L_p$-norm $\displaystyle \left( \int _{U \in \mathcal {B}} \omega (U) B_U(G_1,G_2)^p \, dU \right) ^ {1/p}$ in place of the bottleneck distance. We can also replace the bottleneck distance $B_U$ with the Wasserstein metric or erosion distance between persistence diagrams. Changing the distance in these ways, the same metric properties hold. In addition, there are many different descriptors that one could consider in place of the persistence diagram, such as the Euler characteristic curve of $\delta _{G,U}$ or a simpler descriptor such as the number of connected components in $G \cap U$. However, if we use a weaker invariant, we may lose additional metric properties.

3.8 Graph Edit Distances

We next consider graph edit distances, which take a completely different and more combinatorial view when comparing graphs. Introduced in the 1980s, edit distances for general graphs are a well-studied way to compare graphs [25]. Given associated weights or costs for graph operations (e.g., vertices or edges to be inserted or deleted), the edit distance is the infimum of the sum of edit costs over all sequences of edit operations needed to transform one graph into the other. Edit distances are drastically different than other notions covered so far, in that they do not minimize some maximum correspondence, but rather sum all costs, leading to much larger distances. We give a brief overview of two versions of geometric edit distances and their metric properties here, as studied in [8]; see[15] for a survey of the many variants and heuristics on broader classes of graphs.

A natural notion of edit distance for geometric graphs, which to the best of our knowledge was first discussed in [8], allows deleting and inserting vertices and edges for some cost related to the distance in the ambient space M, as well as moving vertices for cost propotional to the distance moved in M and change in edge lengths. More formally, the cost is then defined for each edit operation as follows:

• 1. Edge Deletion and Insertion. The cost of removing or inserting an edge is the length of the edge.

• 2. Vertex Deletion and Insertion. The cost of inserting or deleting an isolated vertex is 1. The cost of inserting a vertex in the middle of an edge to create two edges is free, as is the reverse operation. Otherwise, the cost of deleting a vertex is 1, plus the cost of deleting all incident edges.

• 3. Vertex Moving. The cost of moving a vertex is the distance that the vertex is moved, plus the sum of the changes in edge lengths of all incident edges.

The graph edit distance $d_{edit} :\mathcal {G}_{M} \times \mathcal {G}_{M} \rightarrow \overline{\mathbb {R}}_{\ge 0}$ is defined by

$$\begin{aligned} d_{edit}(G_1,G_2) = \inf _{\tau } \sum _{\tau _i \in \tau } c(\tau _i), \end{aligned}$$

(4)

where $\tau$ ranges over all finite sequences of edit operations that start at $G_1$ and end at $G_2$ and $c(\tau _i)$ denotes the cost of the edit operation $\tau _i$.

In Fig. 13a, we see two graphs, $G_1$ and $G_2$, which each have two vertices and a single edge. The edit sequence between them is moving the right vertex first (shown as a grey double arrow), for a cost of $\delta$ to move the vertex itself plus the difference in length between the blue edge and the grey diagonal; the next edit move will shift the left vertex up, which again costs $\delta$ plus the difference in length between the diagonal and the red upper edge. This simple example already demonstrates the distinction of the edit distance and previous distances introduced in this survey, as the Fréchet, Hausdorff, and the path-based distance are all equal to $\delta$ on these graphs, while the edit distance must always be $\ge 2\delta$, given that each vertex must move $\delta$.

Fig. 13

Two examples of edit sequences between graphs $G_1$ and $G_2$. Both the edit distance and the geometric graph distance are $\ge 2 \delta$, which Fréchet, Hausdorff, and path-based distances are all equal to $\delta$ on this example

We note that variations of edit distance could be examined, particularly with regards to different costs for vertex insertion or deletion costs; however, we begin with this definition as it is the one proposed and studied in the literature [8]. We begin by exploring metric proerties of graph edit distance, before discussing some of its limitations. The following properties hold for this distance:⁹

Theorem 8

(Metric Properties of Graph Edit Distance) The graph edit distance $d_{edit}$ is a semi-metric that satisfies sub-additivity.

Proof

To see that $d_{edit}$ is finite, consider the following weighted graph $\mathbb {G}=(\mathcal {G}_{M},\mathcal {E},\omega )$, where the vertex sets are all immersed graphs. A pair of immersed graphs $\left( (G_1,\phi _1),(G_2,\phi _2) \right)$ corresponds to an edge in $\mathcal {E}$ if and only if they are connected through a single edit operation. The weight of the edge, $\omega \left( (G_1,\phi _1),(G_2,\phi _2) \right)$, is the cost of that edit. Then, $d_{edit}((G_1,\phi _1),(G_2,\phi _2))$ is the length of the shortest path from $(G_1,\phi _1)$ to $(G_2,\phi _2)$ in $\mathbb {G}$. Since any graph is connected to the empty graph by a finite sequence of edit operations by removing all edges then removing all vertices, we know that the edit distance between two graphs is finite.

Identity follows because an empty sequence of edits transforms a graph to itself. Separability follows because, given $(G_1,\phi _1) \not \cong (G_2,\phi _2) \in \mathcal {G}_{M}$, we know that there must be some edit operation of positive cost to convert $(G_1,\phi _1)$ to $(G_2,\phi _2)$.

To prove symmetry, consider a fixed finite sequence $\tau$ in Equation (4). Let $-\tau$ denote the reverse sequence. Since any finite sequence of edits can be reversed to transform one graph to another, we know that $-\tau$ is one of the sequences considered by the infimum when defining $d_{edit}(G_2,G_1)$. Moreover, since costs of edit operations is symmetric, the cost of $\tau$ is the same as the cost of $-\tau$. Hence, we obtain:

$$\begin{aligned} d_{edit}(G_1,G_2) = \inf _{\tau } \sum _{\tau _i \in \tau } c(\tau _i) = \inf _{-\tau } \sum _{-\tau _i \in \tau } c(\tau _i) = d_{edit}(G_2,G_1). \end{aligned}$$

Sub-additivity follows a similar argument.

However, one major limitation, especially when considering algorithms to calculate this distance, is that the edit distance may never be attained by a finite sequence of edit operations. For instance, consider again our simple example of two graphs consisting of single straight edges, shown in Fig. 13. As pointed out by [8], an optimal edit sequence would be to alternate moving the vertices by an infinitesimal amount so as to minimize the change in edge length incurred; see Fig. 13b. Taking the limit as that infinitesmal amount decreases to zero, we get that the edit distance is exactly $2 \delta$, but that value can never be realized by any finite sequence of edits.

In order to get around this issue, [8] introduces an edit-like distance, which they call the geometric graph distance, that makes a few notable changes to the edit distance above. Rather than charging a unit for a vertex addition or deletion, vertex additions and deletions are free. Also, they introduce two fixed parameters—an edge weight and a vertex weight—which factor multiplicatively into the relevant edit operations.¹⁰ To avoid pathological examples of infinite edit sequences as discussed above, instead of charging costs for individual moves, they instead look at the total change in length at the end of all edits. They then observe that edits can be required to be done in the following order:

• 1. Edge Deletion Phase. The cost of removing an edge is the length of the edge times the edge weight.

• 2. Vertex Deletion Phase. Deleting an isolated vertex is free. Non-isolated vertices may not be deleted.

• 3. Vertex Moving Phase. The cost of moving a vertex is the distance that the vertex is moved times the vertex weight, plus for all incident edges the change in edge lengths times the edge weight.

• 4. Vertex Insertions Phase. The cost of adding vertices is free. In contrast to the edit distance defined above, adding a vertex in the middle of an edge is not an allowable edit operation. (However, it can be attained by removing the edge in the Edge Deletion phase, then adding a vertex in this phase, and adding the two edges in the next phase).

• 5. Edge Insertion Phase. The cost of inserting an edge is the length of the edge times the edge weight.

Then, the geometric graph distance $d_{ggd} :\mathcal {G}_{M} \times \mathcal {G}_{M} \rightarrow \overline{\mathbb {R}}_{\ge 0}$ is defined by

$$\begin{aligned} d_{ggd}(G_1,G_2) = \inf _{\kappa } \sum _{\kappa _i \in \kappa } c(\kappa _i), \end{aligned}$$

where $\kappa$ ranges over all finite sequences of edit operations that start at $G_1$ and end at $G_2$ and preserve the phases described above. As proven in [8], this distance is a metric:

Theorem 9

(Metric Properties of Geometric Graph Distance) The geometric graph distance $d_{ggd}$ is a metric on the set of geometric graphs without isolated vertices for positive edge and vertex weight.

However, as also shown in [8] the geometric graph distance is NP-complete to compute when considering non-planar graphs or choosing the edge weight much larger than the vertex weight. It is unknown if the problem remains NP-hard for planar graphs, or if the original edit distance formulation is also NP-hard.

4 Conclusion

In this paper, we survey commonly used distance measures on graphs immersed or embedded in a metric space. We also explored the metric properties induced on this space of graphs. For this, we studied the immersed graphs up to homeomorphism. If we did not consider graphs up to homeomorphism, then none of these distances would satisfy the separability property, since adding a vertex in the middle of an edge would result in a combinatorially different, yet homeomorphic, graph that has the same collection of immersions. In circumstances where the combinatorics are important, the proofs above can be adapted for studying immersions up to graph isomorphism instead of up to homeomorphism, in which case separability would no longer hold.

Many future areas of study remain in this area, so we conclude by mentioning one or two particularly natural questions. First, we are unsure if any of these metrics are equivalent to each other, where by “equivalent" we mean bounded within constant factors of each other. Another natural research path is to explore topological equivalences of the spaces of graphs as well as other topological properties of these spaces, such as stability under certain types of perturbations. Finally, while we have briefly mentioned computational complexity of a few of these where results exist, the exact complexity or hardness of most remains open.