1 Introduction

The study of instability phenomena remains essential to solve the problems posed by the control and control of industrial processes, and it is also essential when it comes to explaining the mechanisms and properties of these processes. In this sense, many works have focused on the phenomena of instability, let us quote those of Chandrasekhar, Drazin [1, 2].

Hydrodynamic instabilities are in fact the reflection of the competition between the various phenomena of opposite tendencies occurring in the moving fluid. In In the case of the centrifugal instabilities that interest us, here the forces in question mainly relate to viscosity and inertia. To understand these phenomena of instability and transition to turbulence, fluid mechanics is particularly interested in relatively simple systems, such as the Taylor–Couette system, which is the subject of our study, rotating spheres, rotating cones, rotating discs, etc.. This field continues to arouse the interest of researchers despite the considerable number of theoretical, experimental and numerical works that have been submitted to it. consecrated.

The Taylor–Couette flow system has received a lot attention of several research since the initial work of Taylor [3] and is still relevant today. This flow present between two coaxial cylinders in motion, can lose its hydrodynamic stability to generate toroidal vortices. In the case of lower angular velocities, basic flow is axisymmetric and invariant under vertical translation. It is appear that at specific value, the flow become unstable and a pattern of counter-rotating toroidal rollers appears which extend all around the cylinder; the flow always remains axisymmetric, but this time the vertical translational symmetry disappears, it is broken. By further increasing the angular velocity, this structured flow can in turn become unstable and transit towards turbulence.

Donnelly initiated investigating on unsteady Taylor–Couette flows through experiments [4] where the effect of a periodic modulation added to the angular velocity of the interior cylinder has been processed. The pioneering experiments of Donnelly [4] have given rise to numerous theoretical studies carried out mainly by Hall [5] as well as by Riley and Lawrence [6]. Hall found that the instability triggering threshold, in the case of small air gap, decreased slightly compared to Riley and Lawrence used a Galerkin expansion with time-dependent coefficients to solve the linear equations regulating the disturbance motion, and they then used Floquet theory to assess the stability of the system. Their findings support Hall's research, which indicates that modulation has an instability impact. Carmi and Tustaniwskyj [7] asserted that the theoretical treatments were not able to achieve a suitable level of agreement with the trials in the high amplitude modulation region and low frequency. The question that arose: does the low frequency modulation produce a stabilizing or destabilizing effect. This last statement has been confirmed by the results of Kuhlmann et al. [8] who observed the destabilizing effect by a numerical simulation using finite differences on the complete Navier–Stokes equations. The numerical results show that the time-modulated coils exhibit a subharmonic response. Barenghi and Jones have shown [9], using the amplitude model developed by Hall [5], that the presence of experimental imperfections can substantially alter the dynamics below a critical frequency.

The special case of periodic base flows in Taylor–Couette geometry, the angular velocity component was set to nill, which considered in the work of Riley [6] and Carmi [7] respectively in the case where the external cylinder is at rest and the case where the two cylinders have rotational speeds modulated either in phase or in phase shift. The stability of this flow was then theoretically and experimentally studied by Aouidef et al. [10,11,12] in the case where both the interior and exterior cylinders oscillate with angular velocities of \({\Omega }_{0}\mathrm{cos}\left({\omega }_{1}^{*}{t}^{*}\right)\) and \({\Omega }_{0}\mathrm{cos}\left({\omega }_{2}^{*}{t}^{*}\right)\), respectively, and ″ is the amplitude ratio of the two cylinders. Three possibilities were taken into consideration: the exterior cylinder at rest (Ɛ = 0), the two cylinders oscillating in phase (Ɛ = 1), and the two cylinders oscillating in phase opposition (Ɛ = − 1). Their findings demonstrate that the flow stabilizes at low and high frequencies, while destabilization is greatest at middle frequencies. The theoretical and numerical results are in good agreement in the high frequency limit while a disagreement between these two types of results was observed in the low frequency limit. This disagreement is due to numerical predictions. \({\Omega }_{0}\mathrm{cos}\left({\omega }_{1}^{*}{t}^{*}\right)\) and \({\Omega }_{0}\mathrm{cos}\left({\omega }_{2}^{*}{t}^{*}\right)\)

In the present work, we are interested in the instability of the Taylor Couette flow within a Newtonian fluid, in the case of a quasi-periodic modulation with two incommensurable frequencies \({\omega }_{1}\) and \({\omega }_{2}\). The two cylinders, interior and exterior, oscillate respectively with angular velocities \({\Omega }_{0}\mathrm{cos}\left({\omega }_{1}^{*}{t}^{*}\right)\) and \({\Omega }_{0}\mathrm{cos}\left({\omega }_{2}^{*}{t}^{*}\right)\). An interest is devoted to the effects of the frequency ratio \(\omega =\frac{{\omega }_{2}}{{\omega }_{1}}\) on the marginal stability curves, in particular on the curves of the critical parameters, Taylor number and wave number. Also this study allows to show that the modulation with two frequencies makes it possible to control the instability of the pulsating flow by adjusting the frequencies \({\omega }_{1}\) and \({\omega }_{2}\). This work is a continuation of works which were interested in the modulation, with two incommensurable frequencies, in thermal convection and in Faraday instability [13].

For the vortex stability problem, a spectral collocation method appears more attractive since a computational algorithm based on that method does not require major modifications from case to case and at the same time the computations are accurate and efficient. Therefore, a spectral collocation formulation of the linearized equations of motion for a steady, 3-dimensional, constant density fluid flow has been developed. The formulation is described in the subsequent sections. Although the spectral collocation technique has been applied to the Orr–Sommerfeld equation (Herbert [14], Spalart [15]), there appears to be no previous application of the method to the type of problems discussed in this paper. A Chebyshev collocation matrix algorithm has been constructed for both spatial and temporal stability calculations. In the present method, the derivatives of the eigenfunctions are evaluated in the physical space at the collocation points. Through numerous test cases which examined annular flow (including the narrow gap limit of plane Poiseuille flow), cylindrical Poiseuille flow, rotating pipe flow, and a trailing line vortex, we have shown that the developed algorithm produces accurate global eigenvalues for each case without requiring any substantial changes in the computer code.

A future goal of this research will be to perform stability analyses of the similarity solutions for porous rotating pipe flow obtained by Donaldson and Sullivan [16]. Their computed profiles which are exact solutions to the 3-dimensional equations of motion have shown many of the flow features which are of interest in the study of unconfined trailing line vortices. For example, their solutions range from those which can be characterized as a single cell vortex to multiple cell vortices. In addition, experimental measurements have documented the existance of many of these flows (see Adams and Gilmore [17], Leuchter and Solignac [18], and Graham and Newman [19]). However, this study has been concerned primarily with validation of the spectral collocation method and to that end, the algorithm has been studied for some classical velocity profiles for which some stability results are available.

In the next, we present the mathematical formulation of the approached problem. First, we determine the Taylor–Couette pulsating flow in quasiperiodic regime considering that the air gap, \(d\), is very small compared to the radius, \({R}_{1}\), of the inner cylinder. The stability study will concern this basic solution. Then, we proceed to an adimensionalization by introducingadimensional variables allowing to simplify the treatment of the equations governing the problem studied. Finally, we adopt the linear stability theory for the determination of the disturbance equations resulting from the superposition of the basic flow and that of the disturbance.

2 Description of the problem

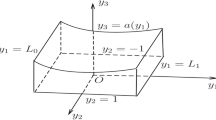
We are interested in this study of a pulsed and axisymmetric flow of an incompressible Newtonian fluid between two coaxial cylinders of respective rays \({R}_{1}\) and \({R}_{2}\) turning around their axis with angular speeds 1 and 2 defined by \({\Omega }_{1}={\Omega }_{0}\mathrm{cos}\left({\omega }_{1}^{*}{t}^{*}\right)\), \({\Omega }_{2}={\Omega }_{0}\mathrm{cos}\left({\omega }_{2}^{*}{t}^{*}\right)\) (Fig. 1). Where \({\Omega }_{0}\) is the amplitude, \({\upomega }_{1}^{*}\) and \({\upomega }_{2}^{*}\) are the pulsation frequencies considered immeasurable.

Fig. 1
figure 1

Diagram of the Taylor–Couette system

Full size image

The conservation equations of mass and quantity of motion are written in the form:

$$\nabla .{\mathbf{V}}^{\boldsymbol{*}}=0$$
(1)
$$\rho \frac{d{{\varvec{V}}}^{\boldsymbol{*}}}{d{t}^{*}}=\rho \left(\frac{\partial {{\varvec{V}}}^{\boldsymbol{*}}}{\partial {t}^{*}}+{{\varvec{V}}}^{\boldsymbol{*}}.\nabla .{\mathbf{V}}^{\boldsymbol{*}}\right)=-\nabla {P}^{*}+\mu\Delta {\mathbf{V}}^{\boldsymbol{*}}$$
(2)

where:

\(\rho\) the volumetric density of the fluid, \({\mathbf{V}}^{\boldsymbol{*}}=\left(\begin{array}{ccc}{u}^{\boldsymbol{*}}& {v}^{\boldsymbol{*}}& {w}^{\boldsymbol{*}}\end{array}\right)\) the velocity field, μ the dynamic viscosity of the fluid and \({P}^{*}\) is the pressure.

In the system of cylindrical coordinates, these equations are written:

$$\frac{1}{r}\frac{\partial (r{u}^{\boldsymbol{*}})}{\partial r}+\frac{1}{r}\frac{\partial {v}^{\boldsymbol{*}}}{\partial {\theta }^{*}}+\frac{\partial {w}^{\boldsymbol{*}}}{\partial {z}^{*}}=0$$
(3)
$$\left\{\begin{array}{l}\rho \left(\frac{\partial {u}^{\boldsymbol{*}}}{\partial {t}^{*}}+{u}^{\boldsymbol{*}}\frac{\partial {u}^{\boldsymbol{*}}}{\partial r}+\frac{{v}^{\boldsymbol{*}}}{r}\frac{\partial {u}^{\boldsymbol{*}}}{\partial {\theta }^{*}}-\frac{{{v}^{\boldsymbol{*}}}^{2}}{r}+{w}^{\boldsymbol{*}}\frac{\partial {u}^{\boldsymbol{*}}}{\partial {z}^{*}}\right)=-\frac{\partial {P}^{*}}{\partial r}+\mu \left(\frac{\partial }{\partial r}\left(\frac{1}{r}\frac{\partial }{\partial r}\left(r{u}^{\boldsymbol{*}}\right)\right)+\frac{1}{{r}^{2}}\frac{{\partial }^{2}{u}^{\boldsymbol{*}}}{\partial {{\theta }^{*}}^{2}}-\frac{2}{{r}^{2}}\frac{\partial {{\varvec{v}}}^{\boldsymbol{*}}}{\partial {\theta }^{*}}+\frac{{\partial }^{2}{u}^{\boldsymbol{*}}}{\partial {{z}^{*}}^{2}}\right)\\ \rho \left(\frac{\partial {{\varvec{v}}}^{\boldsymbol{*}}}{\partial {t}^{*}}+{u}^{\boldsymbol{*}}\frac{\partial {{\varvec{v}}}^{\boldsymbol{*}}}{\partial r}+\frac{{v}^{\boldsymbol{*}}}{r}\frac{\partial {{\varvec{v}}}^{\boldsymbol{*}}}{\partial {\theta }^{*}}+\frac{{v}^{\boldsymbol{*}}{u}^{\boldsymbol{*}}}{r}+{w}^{\boldsymbol{*}}\frac{\partial {v}^{\boldsymbol{*}}}{\partial {z}^{*}}\right)=-\frac{1}{r}\frac{\partial {P}^{*}}{\partial {\theta }^{*}}+\mu \left(\frac{\partial }{\partial r}\left(\frac{1}{r}\frac{\partial }{\partial r}\left(r{{\varvec{v}}}^{\boldsymbol{*}}\right)\right)+\frac{1}{{r}^{2}}\frac{{\partial }^{2}{v}^{\boldsymbol{*}}}{\partial {{\theta }^{*}}^{2}}-\frac{2}{{r}^{2}}\frac{\partial {u}^{\boldsymbol{*}}}{\partial {\theta }^{*}}+\frac{{\partial }^{2}{v}^{\boldsymbol{*}}}{\partial {{z}^{*}}^{2}}\right)\\ \rho \left(\frac{\partial {w}^{\boldsymbol{*}}}{\partial {t}^{*}}+{u}^{\boldsymbol{*}}\frac{\partial {w}^{\boldsymbol{*}}}{\partial r}+\frac{{v}^{\boldsymbol{*}}}{r}\frac{\partial {w}^{\boldsymbol{*}}}{\partial {\theta }^{*}}+{w}^{\boldsymbol{*}}\frac{\partial {w}^{\boldsymbol{*}}}{\partial {z}^{*}}\right)=-\frac{\partial {P}^{*}}{\partial {z}^{*}}+\mu \left(\frac{\partial }{\partial r}\left(\frac{1}{r}\frac{\partial }{\partial r}\left(r{w}^{\boldsymbol{*}}\right)\right)+\frac{1}{{r}^{2}}\frac{{\partial }^{2}{v}^{\boldsymbol{*}}}{\partial {{\theta }^{*}}^{2}}+\frac{1}{{r}^{2}}\frac{{\partial }^{2}{w}^{\boldsymbol{*}}}{\partial {{\theta }^{*}}^{2}}+\frac{{\partial }^{2}{w}^{\boldsymbol{*}}}{\partial {{z}^{*}}^{2}}\right)\end{array}\right.$$
(4)

3 Basic flow

Given the nature of the boundary conditions imposed on both cylinders, the flow is azimuthal and considered axisymmetrical. The velocity field is therefore given by:

$${V}_{B}^{*}=\left(\begin{array}{ccc}0& {v}_{B}^{*}\left(r , {t}^{*}\right)& 0\end{array}\right)$$

The system (4) is reduced to the following system:

$$\left\{\begin{array}{l}\rho \frac{{v}_{B}^{*}}{r}=-\frac{\partial {P}_{B}^{*}}{\partial r}\\ \rho \frac{\partial {v}_{B}^{*}}{\partial {t}^{*}}=\mu \frac{\partial }{\partial r}\left(\frac{1}{r}\frac{\partial }{\partial r}\left(r{v}_{B}^{*}\right)\right)\\ 0=-\frac{\partial {P}_{B}^{*}}{\partial {z}^{*}}\end{array}\right.$$
(5)

Also, for axisymmetric flow, the continuity equation is reduced to:

$$\frac{1}{r}\frac{\partial (r{u}^{\boldsymbol{*}})}{\partial r}+\frac{\partial {w}^{\boldsymbol{*}}}{\partial {z}^{*}}$$
(6)

The system (5) is associated with the following boundary conditions:

$$\left\{\begin{array}{l}{v}_{B}^{*}\left({R}_{1} , {t}^{*}\right)={\Omega }_{0}\mathrm{cos}\left({\upomega }_{1}^{*}{t}^{*}\right)\\ {v}_{B}^{*}\left({R}_{2} , {t}^{*}\right)={\Omega }_{0}\mathrm{cos}\left({\upomega }_{2}^{*}{t}^{*}\right)\end{array}\right.$$
(7)

4 Adimensional analysis

We introduce dimensionless variables:

\(x=\frac{r-{R}_{1}}{d}\), \(t = \frac{{t^{*} }}{{{{d^{2} } \mathord{\left/ {\vphantom {{d^{2} } v}} \right. \kern-0pt} v}}}\), \({v}^{B}=\frac{{v}_{B}^{*}}{{R}_{1}{\omega }_{0}}\), \({P}_{B}=\frac{{P}_{B}^{*}}{\rho {R}_{1}d{\Omega }_{0}^{2}}\), \(\omega_{i} = \frac{{\omega_{i}^{*} }}{{{\nu \mathord{\left/ {\vphantom {\nu {d^{2} }}} \right. \kern-0pt} {d^{2} }}}}\), \(z=\frac{{z}^{*}}{d}\), avec \(d={R}_{2}-{R}_{1}\).

We consider the approximation of low air gap, the terms of order \(\frac{d}{{R}_{1}}\) become negligible. In this case, we arrive at:

$${{v}_{B}}^{2}=\frac{\partial {P}_{B}}{\partial x}$$
(8)
$$\frac{\partial {v}_{B}}{\partial t}=\frac{{\partial }^{2}{v}_{B}}{\partial {x}^{2}}$$
(9)
$$0=-\frac{\partial {P}_{B}}{\partial z}$$
(10)

with the following boundary conditions:

$$\left\{\begin{array}{l}{v}_{B}\left(0 ,t\right)=\mathrm{cos}\left({\upomega }_{1}t\right)\\ {v}_{B}\left(1 ,t\right)=\mathrm{cos}\left({\upomega }_{1}t\right)\end{array}\right.$$
(11)

Solving Eqs. (8)–(10) with conditions (11) allows to write the basic speed in the following form (calculation details are in Annex A):

$${v}_{B}\left(x ,t\right)={F}_{1}\left(x\right)\mathrm{cos}\left({\upomega }_{1}t\right)+{F}_{2}\left(x\right)\mathrm{sin}\left({\upomega }_{1}t\right)+{G}_{1}\left(x\right)\mathrm{cos}\left({\upomega }_{2}t\right)+{G}_{2}\left(x\right)\mathrm{sin}\left({\upomega }_{2}t\right)$$
(12)

Expressions of \({F}_{1}\left(x\right)\), \({F}_{2}\left(x\right)\), F2(x), \({G}_{1}\left(x\right)\) and \({G}_{2}\left(x\right)\) are given by:

$${F}_{1}\left(x\right)=\frac{\mathrm{cos}\left({\gamma }_{1}x\right)\mathrm{cosh}\left({\gamma }_{1}\left(2-x\right)\right)-\mathrm{cosh}\left({\gamma }_{1}x\right)\mathrm{cos}\left({\gamma }_{1}\left(2-x\right)\right)}{\mathrm{cosh}\left(2{\gamma }_{1}\right)-2\mathrm{cos}\left(2{\gamma }_{1}\right)}$$
$${F}_{2}\left(x\right)=\frac{\mathrm{sin}\left({\gamma }_{1}x\right)\mathrm{sinh}\left({\gamma }_{1}\left(2-x\right)\right)-\mathrm{sinh}\left({\gamma }_{1}x\right)\mathrm{sin}\left({\gamma }_{1}\left(2-x\right)\right)}{\mathrm{cosh}\left(2{\gamma }_{1}\right)-2\mathrm{cos}\left(2{\gamma }_{1}\right)}$$
$${G}_{1}\left(x\right)=\frac{\mathrm{cos}\left({\gamma }_{2}\left(1-x\right)\right)\mathrm{cosh}\left({\gamma }_{2}\left(1+x\right)\right)-\mathrm{cosh}\left({\gamma }_{2}\left(1-x\right)\right)\mathrm{cos}\left({\gamma }_{2}\left(1+x\right)\right)}{\mathrm{cosh}\left(2{\gamma }_{2}\right)-2\mathrm{cos}\left(2{\gamma }_{2}\right)}$$
$${G}_{2}\left(x\right)=\frac{\mathrm{sin}\left({\gamma }_{2}\left(1-x\right)\right)\mathrm{sinh}\left({\gamma }_{2}\left(1+x\right)\right)-\mathrm{sinh}\left({\gamma }_{2}\left(1-x\right)\right)\mathrm{sin}\left({\gamma }_{2}\left(1+x\right)\right)}{\mathrm{cosh}\left(2{\gamma }_{2}\right)-2\mathrm{cos}\left(2{\gamma }_{2}\right)}$$

where \({\gamma }_{1}=\sqrt{\frac{{\omega }_{1}}{2}}\) and \({\gamma }_{2}=\sqrt{\frac{{\omega }_{2}}{2}}\).

In case, where \({\omega }_{1}={\omega }_{2}=\sigma\) we checked that the basic solution corresponds to that of Aouidef et al. [10]:

$${v}_{B}\left(x ,t\right)={V}_{1}\left(x\right)\mathrm{cos}\left(\upsigma t\right)+{V}_{2}\left(x\right)\mathrm{sin}\left(\upsigma t\right)$$
(13)

where:

$${V}_{1}\left(x\right)=\frac{\mathrm{cos}\left(\gamma x\right)\mathrm{cosh}\left(\gamma \left(1-x\right)\right)+\mathrm{cosh}\left(\gamma x\right)\mathrm{cos}\left(\gamma \left(1-x\right)\right)}{\mathrm{cosh}\left(\gamma \right)+\mathrm{cos}\left(\gamma \right)}$$
$${V}_{2}\left(x\right)=\frac{\mathrm{sin}\left(\gamma x\right)\mathrm{sinh}\left(\gamma \left(1-x\right)\right)+\mathrm{sinh}\left(\gamma \left(1-x\right)\right)\mathrm{sin}\left(\gamma x\right)}{\mathrm{cosh}\left(\gamma \right)+\mathrm{cos}\left(\gamma \right)}$$

5 Linear stability analysis

In the analysis of the linear stability, we assume infinitesimal perturbations, in which the velocity and pressure state take the following dimensionless form:

$${\varvec{V}}=\left(\begin{array}{ccc}0& {v}_{B}\left(x ,t\right)& 0\end{array}\right)+\left(\begin{array}{ccc}{u}^{\prime}\left(x,y,t\right)& {v}^{\prime}\left(x,y,t\right)& {w}^{\prime}\left(x,y,t\right)\end{array}\right)$$
(14)
$$P={P}_{B}+{p}^{\prime}$$
(15)

After inserting the Eqs. (14, 15) in the Eq. (3) and in the system (4), we end up with the following dimensionless equations (calculation details are in Annex B):

$$\frac{\partial {u}^{\prime}}{\partial x}+\frac{\partial {v}^{\prime}}{\partial y}=0$$
(16)
$$\left({\Delta }_{2}-\frac{\partial }{\partial t}\right){u}^{\prime}+2{{T}_{a}}^{2}{v}^{\prime}{v}_{B}={{T}_{a}}^{2}\frac{\partial {p}^{\prime}}{\partial x}$$
(17)
$$\left({\Delta }_{2}-\frac{\partial }{\partial t}\right){v}^{\prime}={u}^{\prime}\frac{\partial {v}_{B}}{\partial x}$$
(18)
$$\left({\Delta }_{2}-\frac{\partial }{\partial t}\right){w}^{\prime}={{T}_{a}}^{2}\frac{\partial {p}^{\prime}}{\partial z}$$
(19)

where: \({\Delta }_{2}=\frac{{\partial }^{2}}{\partial {x}^{2}}+\frac{{\partial }^{2}}{\partial {y}^{2}}\)

\(T_{a} = \frac{{R_{1} \Omega_{0} d}}{\upsilon }\sqrt {\frac{d}{{R_{1} }}}\) this factor is the Taylor number, which represents the ratio between centrifugal forces and viscous forces. The boundary conditions are:

$${u}^{\prime}={v}^{\prime}={w}^{\prime}=0 \quad \mathrm{at } \; x=\mathrm{0,1}$$
(20)

6 Analysis in normal modes

We are looking for solutions in normal modes:

$$\left(\begin{array}{ccc}{u}^{\prime}\left(x,t\right)& {v}^{\prime}\left(x,t\right)& \begin{array}{cc}{w}^{\prime}\left(x,t\right)& {p}^{\prime}\left(x,t\right)\end{array}\end{array}\right)=\left(\begin{array}{ccc}\widehat{u}\left(x,t\right)& \widehat{v}\left(x,t\right)& \begin{array}{cc}\widehat{w}\left(x,t\right)& {p}^{\prime}\left(x,t\right)\end{array}\end{array}\right)\mathrm{exp}(ikz)$$
(21)

where \(k\) is the wave number.

By inserting the expressions (21) in the equations of motion (16)–(19) we obtain:

$$\frac{\partial \widehat{u}}{\partial x}+ik\widehat{w}=0$$
(22)
$$\left(M-\frac{\partial }{\partial t}\right)\widehat{u}+2{{T}_{a}}^{2}{v}_{B}\widehat{v}={{T}_{a}}^{2}\frac{\partial \widehat{p}}{\partial x}$$
(23)
$$\left(M-\frac{\partial }{\partial t}\right)\widehat{v}=\widehat{u}\frac{\partial {v}_{B}}{\partial x}$$
(24)
$$\left(M-\frac{\partial }{\partial t}\right)\widehat{w}={{T}_{a}}^{2}\frac{\partial \widehat{p}}{\partial z}$$
(25)

where \(M=\frac{{\partial }^{2}}{\partial {x}^{2}}-{k}^{2}\)

The expression for b from the continuity Eq. (26) is inserted into Eq. (25) to obtain:

$$\frac{1}{k}\left(M-\frac{\partial }{\partial t}\right)\frac{\partial \widehat{u}}{\partial x}=\frac{\partial \widehat{p}}{\partial z}$$
(26)

Finally, the perturbed equations reduce to:

$$\left\{\begin{array}{l}\left(M-\frac{\partial }{\partial t}\right)M\widehat{u}=2{k}^{2}{{T}_{a}}^{2}{v}_{B}\widehat{v}\\ \left(M-\frac{\partial }{\partial t}\right)\widehat{v}=\widehat{u}\frac{\partial {v}_{B}}{\partial x}\end{array}\right.$$
(27)

The boundary conditions are:

$$\widehat{u}=\widehat{v}=\frac{\partial \widehat{u}}{\partial x}=0 \quad \mathrm{at} \; x=\mathrm{0,1}$$
(28)

We include the variation of variable \({\text{T}} = \omega_{1} t\) The basic velocity becomes:

$$v_{B} \left( {x ,{\text{T}}} \right) = F_{1} \left( x \right)\cos \left( {\text{T}} \right) + F_{2} \left( x \right)\sin \left( {\text{T}} \right) + G_{1} \left( x \right)\cos \left( {\omega {\text{T}}} \right) + G_{2} \left( x \right)\sin \left( {\omega {\text{T}}} \right)$$
(29)

where \(\omega =\frac{{\omega }_{1}}{{\omega }_{2}}\). Then, we use an approximation which consists in making an irrational number \(\omega\), into a rational number in the form \(\omega =\frac{p}{q}\), where p and q are prime integers, on Matlab the "rat" function allows to obtain p and q. For example, \(\sqrt{2}=\frac{1393}{985}\), \(\sqrt{3}=\frac{1351}{780}\) and \(\sqrt{37}=\frac{882}{145}\).

We introduce another change of variable \({\text{T}} = 2q{\text{T}}^{\prime }\), basic speed becomes of period \(\pi\):

$$v_{B} \left( {x ,{\text{T}}^{\prime } } \right) = F_{1} \left( x \right)\cos \left( {2q{\text{T}}^{\prime } } \right) + F_{2} \left( x \right)\sin \left( {2q{\text{T}}^{\prime } } \right) + G_{1} \left( x \right)\cos \left( {2p{\text{T}}^{\prime } } \right) + G_{2} \left( x \right)\sin \left( {2p{\text{T}}^{\prime } } \right)$$
(30)

In this case, we arrive at the following final system:

$$\left\{ {\begin{array}{*{20}c} {\left( {M - \frac{{{\upomega }_{1} }}{2q}\frac{\partial }{{\partial {\text{T}}^{\prime } }}} \right)M\hat{u} = 2k^{2} T_{a}^{2} v_{B} \hat{v}} \\ {\left( {M - \frac{{{\upomega }_{1} }}{2q}\frac{\partial }{{\partial {\text{T}}^{\prime } }}} \right)\hat{v} = \hat{u}\frac{{\partial v_{B} }}{\partial x}} \\ \end{array} } \right.$$
(31)

We considered, in this part, the mathematical formulation of the linear stability of the pulsating flow established in quasi-periodic mode in geometry by Taylor Couette. This formulation was accompanied by an adimensionalization of the conservation equations used. The linear problem has been reduced to the system (31) with the conditions (28). To solve this system, we will present, in the following chapter, the numerical method allowing to finalize the study of stability.

7 Méthodes spectrales de collocation de Chebychev

Chebyshev spectral collocation methods [20] are focused on the decomposition of the elements of a vector space on the basis of the Lagrange function Lj(x). Thus, we have:

$$\left(\begin{array}{cc}\widehat{u}\left(x,t\right)& \widehat{v}\left(x,t\right)\end{array}\right)\approx \sum_{j=1}^{i=N}\left(\begin{array}{cc}\widehat{{u}_{j}}\left(x,t\right)& \widehat{{v}_{j}}\left(x,t\right)\end{array}\right){L}_{j}\left(x\right)$$
(32)

\(\widehat{{u}_{j}}\left(x,t\right)\) and \(\widehat{{v}_{j}}\left(x,t\right)\) sont les amplitudes dépendant du temps et \({L}_{j}\left(x\right)\) sont les fonctions de base de Lagrange définis comme suit:

$${L}_{j}\left(x\right)=\prod_{\begin{array}{l}i\ne j\\ i=1\end{array}}^{i=N}\left(\frac{x-{x}_{i}}{{x}_{j}-{x}_{i}}\right) j=1\dots .N$$
(33)

The amplitudes \(\widehat{{u}_{j}}\left(x,t\right)\) and \(\widehat{{v}_{j}}\left(x,t\right)\) exactly satisfy the solutions \(\widehat{u}\left(x,t\right)\) and \(\widehat{v}\left(x,t\right)\) at N collocation points \({x}_{i}\) such that:

$${L}_{j}\left(x\right)={\delta }_{ij}$$
(34)

where \({\delta }_{ij}\) is the Kronecker symbol.

Thus, the Tchebychev polynomial of order N, denoted \({T}_{N}\) is defined by:

$${T}_{N}\left(x\right)=\mathrm{cos}\left(N{\mathrm{cos}}^{-1}\left(x\right)\right)$$
(35)

This polynomial admits exactly \(N\) extrema. The last are named the Chebychev–Gauss–Lobatto collocation points defined in the interval \([-1, 1]\) and are given as follows:

$${x}_{i}=\mathrm{cos}\left(\frac{\pi \left(i-1\right)}{N-1}\right) I=1\dots .N$$
(36)

The Tchebyshev interpolation polynomial of Lagrange is then defined for the case of the Tchabyshev-Gauss–Lobatto collocation points as follow:

$${L}_{j}\left(x\right)=\frac{{\left(-1\right)}^{j}\left({x}^{2}-1\right){T}_{N}^{\prime}\left(x\right)}{{c}_{j}{\left(N-1\right)}^{2}\left(x-{x}_{i}\right)}$$
(37)

where \({c}_{1}={c}_{N}=2\) et \({c}_{2}=\dots ={c}_{N-1}=1\).

The derivatives of order \(n\) of the functions \(\widehat{u}\left(x,t\right)\) and \(\widehat{v}\left(x,t\right)\) with respect to x, evaluated in N collocation points are expressed in terms of derived matrices \({D}_{ij}^{n}\) of the same order of size n ∗ n, whose indices i and j denote their rows and columns respectively:

$$\frac{{\partial }^{n}\widehat{u}\left({x}_{i},t\right)}{\partial {x}^{n}}=\sum_{j=1}^{N}\widehat{{u}_{j}}\left(t\right){L}_{j}^{n}\left({x}_{i}\right)=\sum_{i=1}^{N}\widehat{{u}_{j}}\left(t\right){D}_{ij}^{n}$$
(38)
$$\frac{{\partial }^{n}\widehat{v}\left({x}_{i},t\right)}{\partial {x}^{n}}=\sum_{j=1}^{N}\widehat{{v}_{j}}\left(t\right){L}_{j}^{n}\left({x}_{i}\right)=\sum_{i=1}^{N}\widehat{{v}_{j}}\left(t\right){D}_{ij}^{n}$$
(39)

The components of the matrices \({D}_{ij}^{n}\) are the derivatives of order \(n\) of the basis functions (Lagrange polynomials) taken at each of the collocation points. The first-order derivative matrix \({D}_{ij}^{\left(1\right)}\) calculated at the points at the Chebyshev–Gauss–Lobatto collocation points is written explicitly in this form:

$${D}_{ij}^{\left(1\right)}=\left\{\begin{array}{l}\frac{{c}_{j{\left(-1\right)}^{i+j}}}{{c}_{j}\left({x}_{i}-{x}_{j}\right)} i\ne j\\ -\frac{{x}_{i}}{2\left(1-{x}^{2}\right)} i=j\ne 1,N\\ \begin{array}{l}\frac{2{\left(N-1\right)}^{2}+1}{6} i=j=1\\ -\frac{2{\left(N-1\right)}^{2}+1}{6}\end{array}\end{array}\right.$$
(40)

The derivatives of order \(p > 1\) of this matrix are obtained by raising the matrix \({D}^{\left(1\right)}\) to the power \(p\), i.e.:

$${D}^{\left(p\right)}={\left({D}^{\left(1\right)}\right)}^{p}$$
(41)

In order for us to apply Chebyshev spectral collocation method whose collocation points are defined in the interval \([-1, 1]\), we make the following modification of variable:

$$X=2x-1$$
(42)

where \(X\) is now the new spatial variable of the problem defined in the interval [− 1, 1]. Taking into account the change of spatial variable (42), the n-th derivatives with respect to \(x\) are expressed as a function of that with respect to \(X\) in the following form:

$$\frac{{\partial }^{n}}{\partial {x}^{n}}={2}^{n}\frac{{\partial }^{n}}{\partial {X}^{n}}$$
(43)

8 Résolution spatiale

By introducing the change of variable (42, 43) on the system (31) and the conditions (28), we get:

$$\left(4\frac{{\partial }^{2}}{\partial {X}^{2}}-{k}^{2}\right)\frac{{\upomega }_{1}}{2q}\frac{\partial \widehat{u}}{\partial {\mathrm{T}}^{\prime}}=\left(16\frac{{\partial }^{16}}{\partial {X}^{16}}-8{k}^{2}\frac{{\partial }^{2}}{\partial {X}^{2}}+{k}^{4}\right)\widehat{u}-2{k}^{2}{{T}_{a}}^{2}{v}_{B}\widehat{v}$$
(44)
$$\frac{{\upomega }_{1}}{2q}\frac{\partial \widehat{v}}{\partial {\mathrm{T}}^{\prime}}=\left(4\frac{{\partial }^{2}}{\partial {X}^{2}}-{k}^{2}\right)\widehat{v}-\widehat{u}\frac{\partial {v}_{B}}{\partial X}$$
(45)
$$\widehat{u}=\widehat{v}=\frac{\partial \widehat{u}}{\partial X}=0 \, \mathrm{en} \, x=\pm 1$$
(46)

Spatial discretization leads us to a time-dependent matrix system of \(2N\) unknowns. These are defined as follows:

$$\left(\widehat{{u}_{1}}\left({\mathrm{T}}^{\prime}\right), \widehat{{u}_{2}}\left({\mathrm{T}}^{\prime}\right),\dots .,\widehat{{u}_{N}}\left({{\mathrm{T}}^{\prime}}\right),\widehat{{v}_{1}}\left({\mathrm{T}}^{\prime}\right),\widehat{{v}_{2}}\left({\mathrm{T}}^{\prime}\right),\dots .,\widehat{{v}_{N}}\left({{\mathrm{T}}^{\prime}}\right)\right)$$
(47)

The system (32) with the six conditions discretized is expressed as follows:

$$\frac{{\upomega }_{1}}{2q}\left(-4{D}_{ij}^{\left(2\right)}+{k}^{2}{I}_{ij},{0}_{ij}\right)\left(\begin{array}{l}\frac{\partial \widehat{{u}_{j}}}{\partial {\mathrm{T}}^{\prime}}\\ \frac{\partial \widehat{{v}_{j}}}{\partial {\mathrm{T}}^{\prime}}\end{array}\right)=\left(-16{D}_{ij}^{\left(4\right)}+8{k}^{2}{D}_{ij}^{\left(2\right)}-{k}^{2}{I}_{ij}+4{D}_{ij}^{\left(2\right)}\right)\left(\begin{array}{l}\widehat{{u}_{j}}\\ \widehat{{v}_{j}}\end{array}\right)$$
(48)
$$\frac{{\upomega }_{1}}{2q}\left({0}_{ij} ,{I}_{ij} \right)\left(\begin{array}{l}\frac{\partial \widehat{{u}_{j}}}{\partial {\mathrm{T}}^{\prime}}\\ \frac{\partial \widehat{{v}_{j}}}{\partial {\mathrm{T}}^{\prime}}\end{array}\right)=$$
(49)
$$\left(\begin{array}{cc}{I}_{1j}& {0}_{1j}\end{array}\right)\left(\begin{array}{l}\widehat{{u}_{i}}\\ \widehat{{v}_{j}}\end{array}\right)=0$$
(50)
$$\left(\begin{array}{cc}{I}_{Nj}& {0}_{Nj}\end{array}\right)\left(\begin{array}{l}\widehat{{u}_{i}}\\ \widehat{{v}_{j}}\end{array}\right)=0$$
(51)
$$\left(\begin{array}{cc}{0}_{1j}& {I}_{1j}\end{array}\right)\left(\begin{array}{l}\widehat{{u}_{i}}\\ \widehat{{v}_{j}}\end{array}\right)=0$$
(52)
$$\left( {\begin{array}{*{20}c} {0_{Nj} } & {I_{Nj} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\widehat{{u_{i} }}} \\ {\widehat{{v_{j} }}} \\ \end{array} } \right) = 0$$
(53)
$$\left(\begin{array}{cc}{D}_{ij}^{\left(1\right)}& {0}_{1j}\end{array}\right)\left(\begin{array}{l}\widehat{{u}_{i}}\\ \widehat{{v}_{j}}\end{array}\right)=0$$
(54)
$$\left(\begin{array}{cc}{D}_{Nj}^{\left(1\right)}& {0}_{Nj}\end{array}\right)\left(\begin{array}{l}\widehat{{u}_{i}}\\ \widehat{{v}_{j}}\end{array}\right)=0$$
(55)

These Eqs. (48–55) constitute a time-dependent matrix system defined in the following formulation:

$${\varvec{B}}\frac{\partial \varphi }{\partial {\mathrm{T}}^{\prime}}=\left({{\varvec{A}}}_{0}+{{\varvec{C}}}_{1}\mathrm{cos}\left(2q{\mathrm{T}}^{\prime}\right)+{{\varvec{S}}}_{1}\mathrm{sin}\left(2q{\mathrm{T}}^{\prime}\right)+{{\varvec{C}}}_{2}\mathrm{cos}\left(2q{\mathrm{T}}^{\prime}\right)+{{\varvec{S}}}_{2}\mathrm{sin}\left(2q{\mathrm{T}}^{\prime}\right)\right)\varphi$$
(56)

with \({{\varvec{A}}}_{0}\), \({{\varvec{C}}}_{1}\), \({{\varvec{S}}}_{1}\), \({{\varvec{C}}}_{2}\) and \({{\varvec{S}}}_{2}\) are matrices of order \(2N\) and \({\varvec{B}}\) is a singular matrix. And\(\varphi =\left\{\begin{array}{l}\widehat{{u}_{i}}\\ \widehat{{v}_{j}}\end{array}\right\}\).

9 Résolution temporelle

According to Floquet's theory, the fundamental matrix solution of (36) has the following form:

$${\varvec{\phi}}\left({\mathrm{T}}^{\prime}\right)={\varvec{P}}{\left({\mathrm{T}}^{\prime}\right)}^{{{\varvec{Q}}}_{{\mathrm{T}}^{\prime}}}$$
(57)

where \({\varvec{P}}\left( {{\text{T}}^{\prime } } \right)\) is a periodic matrix of period π and the propre values of the matrix \({\varvec{Q}}\) are the Floquet exponents\({u}_{j}\). We set as an initial condition:

$${\varvec{\phi}}\left(0\right)={\varvec{I}}$$
(58)

By integrating Eq. (57) over a period, we obtain the condition:

$${\varvec{\phi}}\left(\pi \right)={e}^{\pi {\varvec{Q}}}$$
(59)

The propre values \({\lambda }_{j}\) of \({\varvec{\phi}}\left(\pi \right)\) are linked to the Floquet exponents by the relation:

$${u}_{j}=\frac{1}{\pi }\mathrm{ln}({\lambda }_{j})$$
(60)

The system (56) is integrated using the Runge–Kutta method of the fourth order with the initial condition (58). Finally, we have a relationship between the frequency \({\gamma }_{1}\), the frequency ratio \(\omega\), the Taylor number, \({T}_{a}\) and the wave number, \(k\). This relation is written formally in the form:

$$R\left({T}_{a};k;{\upgamma }_{1};\upomega \right)=0$$
(61)

10 Results and discussion

10.1 Convergence analysis

In order to evaluate the convergence of the numerical method at given frequencies \({\omega }_{1}\), we analyze the prediction of the critical Taylor number \({T}_{a}\) as a function of \(N\). We place ourselves in the case where \(k = 2\), \(\omega = \sqrt{37}\) and \({\gamma }_{1}=4\). In Table 1, we report the values of the critical Taylor number \({T}_{a}\) obtained for \(N\) varying from 8 to 14. We note that from \(N = 11\), the Taylor number \({T}_{a}\) no longer presents any perceptible variations.

Table 1 Taylor number \({T}_{a}\) and wave \(k\) for different numbers of collocation points \(N\) and for \({\gamma }_{1}=4\)
Full size table

10.2 Validation of the method in the periodic case

Figure 2 represents the curves stability in the periodic case \(\omega = 1\) studied in [10] corresponding to the evolution of the Taylor number \({T}_{a}\), under different number N of the wave number, \(k\), for different values of \(\gamma =\frac{\sigma }{2}\). We can deduce the three cases of stable flow (\({T}_{a} < {T}_{ac}\)), marginal (\({T}_{a} = {T}_{ac}\)) and unstable (\({T}_{a} > {T}_{ac}\)). The critical parameters corresponding to the minimum of the marginal stability curve defining the instability threshold are defined in the following table (Table 2).

Fig. 2
figure 2

Marginal stability curves for \(\omega = 1\)

Full size image
Table 2 Critical Taylor \({T}_{ac}\) and critical wave \({k}_{c}\) numbers for different values of frequency
Full size table

Figures 3 and 4 represent respectively the evolution of the critical Taylor number and the critical wave number, for\(\omega = 1\), depending on the frequency parameter \(\gamma\). The results obtained are in close accordance with those found by Aouidef et al. [10]. We thus note that the basic solution is stable for low and high frequencies and for an intermediate frequency the flow is potentially unstable. Also the wave number is constant for low frequencies \(\gamma\) and increases with when this parameter takes values greater than \(\gamma =4\)

Fig. 3
figure 3

Variation of the critical Taylor number as a function of frequency for \(\omega = 1\)

Full size image
Fig. 4
figure 4

The variation of the critical wave number at different frequency for \(\omega = 1\)

Full size image

10.3 Result and discussion in the quasi-periodic case

The determination of the control parameter, Taylor number, therefore passes through the determination of the marginal stability curve, \({T}_{a}\) as a function of \(k\). In this context, we analyze the evolution of the critical parameters, namely, the critical Taylor number and the critical wave number, as a function of the frequency ratio.

Figures 5, 6 and 7, obtained respectively for \({\gamma }_{1}=2.4\) and \(10\), present the marginal stability curves corresponding to the evolution of the Taylor number \({T}_{a}\) as a function of the wave number k for given frequency ratios (\(\omega = \frac{1}{{\sqrt {37} }}\), \(\omega = \frac{1}{\sqrt 2 }\), \(\omega =\sqrt{3}\) and \(\omega =\sqrt{37}\)).

Fig. 5
figure 5

Marginal stability curve for \({\gamma }_{1}=2\)

Full size image
Fig. 6
figure 6

Marginal stability curve for \({\gamma }_{1}=4\)

Full size image
Fig. 7
figure 7

Marginal stability curve for \({\gamma }_{1}=10\)

Full size image

Numerical calculations show that below \(\frac{1}{{\sqrt {37} }}\) and above \(\sqrt{37}\) the curves obtained coincide with those corresponding to these two values. Thus if there is an effect of the frequency ratio, it is in the interval \(\left[ {\frac{1}{{\sqrt {37} }},\sqrt {37} } \right]\). The critical Taylor number and the critical wave number corresponding to the minimum of the marginal stability curve for \({\gamma }_{1}=2.4\) and \(10\) defining the instability threshold are presented for different values of the frequency ratio in the following tables (Tables 3, 4).

Table 3 Critical Taylor number for different frequency ratios
Full size table
Table 4 Critical wave number for different frequency ratios
Full size table

We find that the instability threshold decreases considerably when the frequency ratio varies from \(\omega = \frac{1}{{\sqrt {37} }}\) to \(\omega =\sqrt{37}\). Thus the frequency ratio can have a stabilizing or destabilizing effect with respect to the periodic case, \(\omega =1\).

The results on the effect of the frequency ratio are summarized in Figs. 8 and 9. In Fig. 8, we present the evolution of the critical Taylor number as a function of \({\gamma }_{1}\) for different values of \(\omega\). In the low frequency limit, when \({\gamma }_{1}<1\), the critical Taylor number decreases in the three considered cases \(\omega = \frac{1}{{\sqrt {37} }}\), \(\omega =\sqrt{3}\) and \(\omega =\sqrt{37}\)) and for intermediate frequencies, the flow remains potentially unstable for an intermediate frequency\({\gamma }_{p}\), this frequency remains constant with respect to \(\omega\), (Table 5) with the exception of that obtained by Aouidef et al. [10] the critical Taylor number increases with the decrease in \(\omega\) on the other hand, the critical wave umber decreases. From the values in Table 5, the frequency ratio has a stabilizing or destabilizing effect compared to the situation of Aouide et al. [10]. This evolution begins to increase for large frequency values. We find that for \({\gamma }_{1}\) given, the critical Taylor number decreases as the frequency ratio increases.

Fig. 8
figure 8

The variation of the critical Taylor number as a function of the frequency parameter for different frequency ratios

Full size image
Fig. 9
figure 9

The variation of the critical wave number as a function of the frequency parameter for different frequency ratios

Full size image
Table 5 Critical wave number for different frequency ratios
Full size table

With regard to the critical wave number, we represent in Fig. 9 its evolution under different frequency number \({\gamma }_{1}\) for different values of the frequency ratio. It remains constant for low frequencies and it starts to increase from \({\gamma }_{1}=3\). We also note that for a fixed value of the frequency \({\gamma }_{1}\), the critical wave number, \({k}_{c}\), increases when \(\omega\) decreases.

In this part, we solved the system obtained in the first chapter numerically. We used the Floquet theory and the Runge–Kutta method to study the influence of the frequency ratio on the centrifugal instabilities of the base flow in terms of the critical Taylor number and the critical wave number. The effect of the frequency ratio was well observed in the interval \(\left[ {\frac{1}{{\sqrt {37} }},\sqrt {37} } \right]\).

figure a

11 General conclusion

In this work, we are interested in hydrodynamic instabilities within pulsating flow in a Taylor–Couette system. The aim of this study is to show the impact of two-frequency modulation through the frequency ratio on the critical instability threshold.

First, we determined the basic solution, in quasiperiodic regime, which corresponds to a flow dependent on space and time. The linear perturbation of this basic solution leads to a system whose parameters are: the Taylor number, the wave number, the frequency ratio and the frequency of the interior cylinder.

The linear system obtained was solved by the spectral methods of Chebyshev which we combined with the theory of Floquet and the method of Runge–Kutta. The impact of the frequency ratio on the critical threshold of instability, in terms of Taylor number and wavenumber, was observed. We have shown that the modulation with two frequencies has a stabilizing or destabilizing effect compared to the periodic case, where the two frequencies are equal. As a perspective, it would be interesting to validate our results using the fluent simulation code to address the centrifugal instabilities of pulsating flow in quasiperiodic regime for viscoelastic fluids.