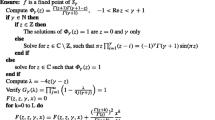Certain results associated with mixed integral equations and their comparison via numerical methods

Abstract

In this article, we consider existence and unique of solutions of linear mixed integral equations of third, second and first kinds. Then, we use the collection method to discuss numerical solutions by employing Chebyshev and Legendre polynomials. To support our results, we use Mable 18 to compute errors in all existing cases.

1 Introduction

Several problems of mathematical physics, theory of elasticity, viscodynamic fluids and mixed problems of mechanics start in a form of linear mixed integral equation with different kinds. For example, in the displacement problem in the theory of elasticity, see Abdou et al. [1, 2], in contact problems, see Georgiadis [3] and Popov [4], in the thermomechanics, see Chirita et al. [5],in thermoelastic models, see Chirita [6], in quantum mechanics, see Rehab and Sheikh [7, 8], and in thermoelasticity for an elastic plate weakened by curvilinear holes, see Abdou et al. [9]. Such equations occur as reformulations of integral mathematical problems in the linear or nonlinear form, see He [10] and Abdou and Youssef [11]. Therefore, the authors have interested in studying different methods to solve the linear and nonlinear integral equations in analytic and numerical forms. In [12], Mirzaee and Samadyar used orthonormal Bernstein collocation method to solve a mixed Volterra–Fredholm integral equation in two- dimensional. In [13], Abdou et al. the orthogonal polynomial method with the aid of Chebyshev polynomial to discuss the solution of the quadratic integral equation. While Al-Bugami in [14], used the orthogonal polynomial method to discuss the solution of Hammerstein integral equation. More information for different numerical methods can be found in Gu [15, 16], Elzaki, and Alamri [17], Abdou and El-Kojok [18], Alhazmi [19], and Basseem and Alalyani [20].

Consider the following integral equation of the third kind,

$$ \mu \left( x \right)\varphi \left( {x,t} \right) = f\left( {x,t} \right) + \lambda \mathop \int \limits_{0}^{1} k\left( {x,y} \right)\varphi \left( {y,t} \right)dy + \lambda \mathop \int \limits_{0}^{t} \mathop \int \limits_{0}^{1} k\left( {x,y} \right)F\left( {t,\tau } \right)\varphi \left( {y,\tau } \right)dyd\tau.$$

(1)

The mixed integral Eq. (1) is investigated from the semi-symmetric contact problem of Hertz type of two rigid surfaces $\left( {G_{i} ,\nu_{i}\,,\,i = 1,2} \right)$ having two elastic materials occupying the domain $[0,1]$. If the upper surface is impressed into the lower surface by a variable force $p\left( t \right)$, whose eccentricity of application $e\left( t \right)$ and a moment $M\left( t \right)$ that case rigid displacements $\gamma \left( t \right)$ and $\beta \left( t \right)$ respectively, through the time interval $0 \le t \le T < 1$ and $\gamma \left( t \right), \, \beta \left( t \right) \in C\left[ {0,T} \right]$. In the absence of body forces, and when the frictional forces in the domain of contact between the two surfaces are so small in which it can be neglected. The unknown function $\varphi \left( {x;t} \right)$ represents the unknown normal stresses between the two surfaces through the time $t$, $t \in \left[ {0,T} \right]$. The positive continuous function $F\left( {t,\tau } \right) \in C\left( {\left[ {0,T} \right] \times \left[ {0,T} \right]} \right)$ represents the resistance force of the lower material against the total pressure and moment. Here $\lambda$ is the coefficients bed of the compressible materials that depend on its geometry and its physical properties $\theta_{i} = \frac{{1 - \mu_{i}^{2} }}{{\pi E_{i} }}, \, i = 1,2$ where $\mu_{i} ,\nu_{i}$ are called the poison’s coefficients and $E_{i}$ are the coefficients of Young. The mixed linear integral Eq. (1) has a Fredholm integral term in position, in the space ${L}_{2}[\mathrm{0,1}]$, with continuous k(x, y). While, the second term of Volterra is considered in time in the class $C[0,T],T<1,$ with the continuous kernel $F(t,\tau ).$ The known function $\varphi_{n}$ is called the free term. While, the unknown function $\varphi (x, t)$ is called the potential function which can be obtained in the space $L_{2} (0,1) \times C[0,T].$ $\lambda$ being a constant of many physical meaning. While, $\mu (x)$ defines the kind of the integral equation. For the third kind, $\mu (x)$ is variable, the second kind, $\mu (x)=constant\ne 0.$ Finally, the first kind $\mu (x)=0.$

In the remainder part of this paper especially in Sect. 2, the existence of a unique solution of mixed linear integral Eq. (1), under certain conditions is considered. In Sect. 3, when Picard method fails, we use Banach fixed point thermo to prove the existence of a unique solution of mixed linear integral equation of the first kind. In Sect. 4, Collocation method using Chebyshev and Legendre Polynomials is conceded to discuss numerically Eq. (1). In Sect. 5, some examples are considered to discuss the numerical results for the three different kind of the mixed integral equation.

2 The existence and uniqueness solution

In order to guarantee the existence of a unique solution of mixed linear integral Eq. (1), we assume the following conditions:

• (i) The kernel of the Fredholm integral term satisfies the continuous condition:

  $\left[ {\mathop \int \nolimits_{0}^{1} \mathop \int \nolimits_{0}^{1} k^{2} \left( {x,y} \right)dxdy} \right]^{\frac{1}{2}} = c < 1 ,$ c is constant, $n = 1.$

• (ii) The continuous kernel of Volterra $F(t,\tau ) \in C[0,T],0 \le t \le \tau < T$ satisfies the condition $\left| {F(t,\tau )} \right| \le M,\forall t,\tau \in [0,T],M$ is a constant. Also, we have$\left|\mu (x)\right|={\mu }_{1}$.

• (iii) The given function $f\,(x,t)$ with its partial derivatives with respect to $x,t$ are continuous in $L_{2} [0,1] \times C[0,T]$ and its norm can be defined as:

  $$ \left\| {f\left( {x,t} \right)} \right\|_{{L_{2} \times C\left[ {0,T} \right]}} = \mathop {max}\limits_{{0 \le t \le T}} \mathop \int \limits_{0}^{t} \left[ {\mathop \int \limits_{0}^{1} f^{2} \left( {x,t} \right)dx} \right]^{{1/2}} d\tau = H, H\,\text{is \,as\, constant} $$

Theorem 1

The solution of Eq. (1) exists and has a unique form in the space $L_{2} (0.1) \times C[0,T]$

Under the condition

$$\left|\lambda \right|<\frac{{\mu }_{1}}{(c+MT)}$$

Proof:

To prove existence of a unique solution of (1), under the conditions (i–iii), we use the successive approximation method. For this, we pick up any real continuous function $\varphi_{0} (x;t)$ and assume $f(x,t) = \varphi_{0} (x,t) \in L_{2} [a,b] \times C[0,T].$

Then, from Eq. (1) we can construct sequences of solution ${{\{\boldsymbol{\varphi }}_{{\varvec{n}}}\left({\varvec{x}},{\varvec{t}}\right)\}}_{{\varvec{n}}=0}^{\boldsymbol{\infty }}.$ And then we pick two functions $\varphi_{n} (x,\,\,t),\,\,\,\,\varphi_{n - 1} (x,\,\,t)$.

For simplicity of manipulation, it is convenient to introduce

$$ \psi_{n} \left( {x,t} \right) = \left[ {\varphi_{n} \left( {x,t} \right) - \varphi_{n - 1} \left( {x,t} \right)} \right];\, \psi_{0} \left( {x;t} \right) = f\left( {x;t} \right) , $$

(2)

to construct the following

$$ \varphi_{n} \left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{n} \psi_{i} \left( {x,t} \right). $$

(3)

Hence, we have

$$ \mu \left( x \right)\psi_{n} \left( {x,t} \right) = \lambda \mathop \int \limits_{0}^{1} k\left( {x,y} \right)\psi_{n - 1} \left( {y,t} \right)dy + \lambda \mathop \int \limits_{0}^{t} \mathop \int \limits_{0}^{1} k\left( {x,y} \right)F\left( {t,\tau } \right)\psi_{n - 1} \left( {y,\tau } \right)dyd\tau . $$

(4)

Applying the norm properties for all terms, then after assuming $\frac{\lambda }{{\mu }_{1}}=\widetilde{A},$ we obtain

$$ \left\| {\psi_{n} \left( {x,t} \right)} \right\| = \left| {\tilde{A}} \right|\left\| {\mathop \int \limits_{0}^{1} k\left( {x,y} \right)\psi_{n - 1} \left( {y,t} \right)dy} \right\| + \left| {\tilde{A}} \right|\left\| {\mathop \int \limits_{0}^{t} \mathop \int \limits_{0}^{1} k\left( {x,y} \right)F\left( {t,\tau } \right)\psi_{n - 1} \left( {y,\tau } \right)dyd\tau } \right\|. $$

(5)

When, $n=1$, we have

$$ \left\| {\left\| {\psi_{1} \left( {x,t} \right)} \right\| \le \left| {\tilde{A}} \right|} \right\|\left\| {\mathop \int \limits_{0}^{1} k\left( {x,y} \right)\psi_{0} \left( {y,t} \right)dy} \right\| + \left| {\tilde{A}} \right|\left\| {\mathop \int \limits_{0}^{t} \mathop \int \limits_{0}^{1} k\left( {x,y} \right)F\left( {t,\tau } \right)\psi_{0} \left( {y,\tau } \right)dyd\tau } \right\| $$

(6)

By applying the Cauchy–Schwarz inequality and using the conditions (i) and (ii), and using ${\psi }_{0}(x,t)=f(x,t),\Vert f\Vert =H,$ we get

$$ \left\| {\psi_{1} \left( {x,t} \right)} \right\| \le \left| {\tilde{A}} \right|{\text{ H }}\left( {c + MT} \right). $$

(7)

By induction, we obtain

$$ \left\| {\psi_{n} \left( {x,t} \right)} \right\| \le H\left| {\tilde{A}} \right|^{n} ({\text{c + MT}})^{n} {. } $$

(8)

Finally, we have

$$ \left\| {\psi_{n} \left( {x,t} \right)} \right\| \le \alpha^{n} {\text{ H; }}\alpha = \left| {\tilde{A}} \right|\left( {\text{c + MT}} \right). $$

(9)

The result of (9), leads us to say that the formula (3) has a convergent solution. Therefore, the solution is stable. So, let ${\varvec{n}} \to \infty$, to obtain

$$ \mathop {lim}\limits_{n \to \infty } \varphi_{n} \left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{\infty } \psi_{i} \left( {x,t} \right) = \varphi \left( {x,t} \right). $$

(10)

The infinite series of (10) is convergent, and $\varphi \left(x,t\right)$ represents the convergent solution of (1). Also, each of ${\psi }_{i}$ is continuous, therefore $\varphi \left(x,t\right)$ is also continuous.

To show that $\mu \, = \,1,\,\,\,t = 0.01,\,\,\,\lambda = 0.01$ is a unique solution, we assume that $\mu \,{ = 1,}\,\,\,\,\,\,\,{{ t = 0}}{.1, }\,\,\,\,$ is a continuous solution of (1), then we write

$$ \left[ {\varphi \left( {x,t} \right) - \tilde{\varphi }\left( {x,t} \right)} \right] = \left| {\tilde{A}} \right|\left\| {\mathop \int \limits_{0}^{1} k\left( {\left| {x,y} \right|} \right)\left[ {\varphi \left( {y,t} \right) - \tilde{\varphi }\left( {y,t} \right)} \right]dy} \right\| + \left| {\tilde{A}} \right|\left\| {\mathop \int \limits_{0}^{t} \mathop \int \limits_{0}^{1} k\left( {x,y} \right)F\left( {t,\tau } \right)\left[ {\varphi \left( {y,\tau } \right) - \tilde{\varphi }\left( {y,\tau } \right)} \right]dyd\tau } \right\|{\text{~,}}\left( {\frac{\lambda }{{\mu _{1} }} = \tilde{A}} \right). $$

(11)

Rewriting (11) and using conditions (i), (ii), we can arrive at the relation:

$$\left(1-\alpha \right)\Vert \phi (x,t)-\widetilde{\phi }(x,t)\Vert \le \text{0.}$$

Since $\alpha <1 ,$ the inequality is true only if $\mu \, = \,1,\,\,\,t = 0.99,\,\,\,\lambda = 0.01$. This leads to the uniqueness of the solution of (1).

Note. The Picard method always fail to prove the existence and uniqueness of a solution of the homogeneous integral Eq. (1) (f(x, t) = 0) or the first kind of the same equation ($\mu \,$ = 0). For this, the existence and uniqueness solution can be obtained by proving the continuity and normality of the integral operator.

3 The normality and continuity of the integral operator

To discuss the normality and continuity of (1), we rewrite it in the integral operator form as following:

$$W\phi =KF\phi +K\phi $$

(12)

where

$$ KF\phi = \lambda \mathop \int \limits_{0}^{t} \mathop \int \limits_{0}^{1} k\left( {\left| {x - y} \right|} \right){\text{ F}}\left( {{\mathrm{t,}}\tau } \right)\phi \left( {{\text{y,}}\tau } \right){\mathrm{dy}}d\tau . $$

(13)

$$ K\phi = \lambda \mathop \int \limits_{0}^{1} k\left( {\left| {x - y} \right|} \right)\phi \left( {\text{y,t }} \right){\mathrm{dy}}{.} $$

(14)

Hence,

$$ \mu \left( x \right)\varphi = f + W\varphi . $$

(15)

Using the conditions (i–iii), after applying Cauchy–Schwarz inequality, we get,

$$ \left\| {W\phi } \right\| \le \left| {\tilde{A}} \right|c\left\| \phi \right\| + \left| {\frac{\lambda }{\mu }} \right|MT\left\| \phi \right\| = \left| {\tilde{A}} \right|\left( {c + MT} \right)\left\| \phi \right\|. $$

(16)

Therefore, we have.

$$ \left\| {W\phi \left( {x,t} \right)} \right\| \le \alpha \left\| {\phi \left( {x,t} \right)} \right\|\,,\,\alpha = \left| {\frac{\lambda }{{\mu_{1} }}} \right|\left( {c + MT} \right) < {1} $$

(17)

Hence, the integral operator is bounded.

For continuity, we assume the two potential functions are $\varphi_{1} \,\,\left( {\,x,t\,} \right),\,\varphi_{2} \,\,\left( {\,x,t\,} \right)$. Hence, we have.

$$ W\left( {\phi_{1} - \phi_{2} } \right) \le \alpha { }\phi_{1} - \phi_{2}\,,\,\alpha\,=\,\left| {\tilde{A}} \right|\left[ {c + MT} \right]{ < 1, }\,\left( {\alpha {\text{ is constant}}} \right). $$

This result leads us to the continuity of the operator $\overline{W}$ since, $\, \alpha \,\, < \,\,\,1$. Hence $\overline{W}$ is a Contraction operator.

4 Collocation method using Chebyshev and Legendre polynomials

4.1 Chebyshev polynomials

4.1.1 Chebyshev polynomials

Chebyshev polynomials are applied to approximate the solution of (1). For this, let the unknown function $\varphi \,\left( {x,\,t} \right)$ and the known function $f\,\left( {x,\,t} \right)$ take the series form of Chebyshev polynomials.

$$ \varphi \left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{N} \mathop \sum \limits_{j = 0}^{M} C_{i,j} T_{i} \left( x \right)T_{j} \left( t \right);f\left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{N} \mathop \sum \limits_{j = 0}^{M} f_{i,j} T_{i} \left( x \right)T_{j} \left( t \right). $$

(18)

Here, ${C}_{i,j}$ are unknown constants, while ${f}_{i,j}$ are known constants can be determined from the orthogonal relation of Chebyshev polynomials.

Using Eq. (18) in Eq. (1), we follow

$$ \mu (x)\sum _{{i = 0}}^{N} \sum _{{j = 0}}^{M} C_{{i,j}} T_{i} \left( x \right)T_{j} \left( t \right) = \sum _{{i = 0}}^{N} \sum _{{j = 0}}^{M} f_{{i,j}} T_{i} \left( x \right)T_{j} \left( t \right) + \lambda \smallint _{0}^{1} k\left( {x,y} \right)\sum _{{i = 0}}^{N} \sum _{{j = 0}}^{M} C_{{i,j}} T_{i} \left( y \right)T_{j} \left( t \right)dy + \lambda \smallint _{0}^{1} \smallint _{0}^{t} F(t,\tau )k\left( {x,y} \right)\sum _{{i = 0}}^{N} \sum _{{j = 0}}^{M} C_{{i,j}} T_{i} \left( y \right)T_{j} \left( \tau \right)dyd\tau . $$

(19)

Applying the collocation method, the Residual error $R_{M,N} (x,t)$ is given by

$$ R_{{M,N}} (x,t) = \mu (x)\sum _{{i = 0}}^{N} \sum _{{j = 0}}^{M} C_{{i,j}} T_{i} \left( x \right)T_{j} \left( t \right) - \lambda \int _{0}^{1} k\left( {x,y} \right)\sum _{{i = 0}}^{N} \sum _{{j = 0}}^{M} C_{{i,j}} T_{i} \left( y \right)T_{j} \left( t \right)dy - \lambda \int _{0}^{1} \int _{0}^{t} F\left( {t,\tau } \right)k\left( {x,y} \right)\sum _{{i = 0}}^{N} \sum _{{j = 0}}^{M} C_{{i,j}} T_{i} \left( y \right)T_{j} \left( \tau \right)dyd\tau - \sum _{{i = 0}}^{N} \sum _{{j = 0}}^{M} f_{{i,j}} T_{i} \left( x \right)T_{j} \left( t \right), $$

(20)

where ${R}_{M,N}(x,t)$ are the error of the order $\left(M,N\right)$ and vanishes at m points of position and n points of time, depending on the principal of collection method. Hence, we let ${R}_{m,n}(x,t)=0$

$$t={t}_{0}, x={x}_{0},\, {\text{then}}\,{ S}_{\mathrm{0,0}}=R\left({x}_{0},{t}_{0}\right),\,\text{put}\, x={x}_{0},t={t}_{1},\, \text{we\, get}\,{ S}_{\mathrm{0,1}}=R\left({x}_{0},{t}_{1}\right),{S}_{n,m}=R\left({x}_{n},{t}_{m}\right).$$

(21)

This algebraic system can be solved for us to obtain ${C}_{i,j}$ and substitutes in Eq. 20 to get the solution.

4.2 Legendre polynomials

To represent the solution of (1) in the Legendre polynomial form of the first order, we assume

$$ \varphi \left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{N} \mathop \sum \limits_{j = 0}^{M} C_{i,j} P_{i} \left( x \right)P_{j} \left( t \right);{ }f\left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{N} \mathop \sum \limits_{j = 0}^{M} f_{i,j} P_{i} \left( x \right)P_{j} \left( t \right). $$

(22)

Using (22) in (1), we follow

$$ \mu (x)\sum _{{i = 0}}^{N} \sum _{{j = 0}}^{M} C_{{i,j}} P_{i} \left( x \right)P_{j} \left( t \right) = \sum _{{i = 0}}^{N} \sum _{{j = 0}}^{M} f_{{i,j}} P_{i} \left( x \right)P_{j} \left( t \right) + \lambda \int _{0}^{1} k\left( {x,y} \right)\sum _{{i = 0}}^{N} \sum _{{j = 0}}^{M} C_{{i,j}} P_{i} \left( y \right)P_{j} \left( t \right) + \lambda \int _{0}^{t} \int _{0}^{1} F\left( {t,\tau } \right)k\left( {x,y} \right)\sum _{{i = 0}}^{N} \sum _{{j = 0}}^{M} C_{{i,j}} P_{i} \left( y \right)P_{j} \left( \tau \right)dyd\tau . $$

(23)

Applying the collocation method, we make it a zero equation, which is called the residual error ${R}_{M,N}\left(x,t\right),$ where

$$ R_{M,N} \left( {x,t} \right) = \mu \left( x \right)\mathop \sum \limits_{i = 0}^{N} \mathop \sum \limits_{j = 0}^{M} C_{i,j} P_{i} \left( x \right)P_{j} \left( t \right) - \mathop \sum \limits_{i = 0}^{N} \mathop \sum \limits_{j = 0}^{M} f_{i,j} P_{i} \left( x \right)P_{j} \left( t \right) - \lambda \mathop \int \limits_{0}^{1} k\left( {x,y} \right)\mathop \sum \limits_{i = 0}^{N} \mathop \sum \limits_{j = 0}^{M} C_{i,j} P_{i} \left( y \right)P_{j} \left( t \right) - \lambda \mathop \int \limits_{0}^{t} \mathop \int \limits_{0}^{1} F\left( {t,\tau } \right)k\left( {x,y} \right)\mathop \sum \limits_{i = 0}^{N} \mathop \sum \limits_{j = 0}^{M} C_{i,j} P_{i} \left( y \right)P_{j} \left( \tau \right)dyd\tau $$

Where, ${R}_{M,N}(x,t)$ are the error of order$\left(M\times N\right)$, which vanishes at $\left(m,n\right)$ where $m,n$ are the points w. r. t position and time, respectively, i.e., ${R}_{m,n}(x,t)=0$.

Let, $x={x}_{i}=a+ih, t={t}_{j}=0+jh\,, i=\mathrm{0,1},2,...m,\, j=\mathrm{0,1},2,...n,$

$$ {\text{at}}\, 0 \le x_{0} \le x_{1} \le x_{2} \le ... \le x_{m} = 1;\, 0 \le t_{0} \le t_{1} \le t_{2}\, \le\, ... \le t_{n} = T. $$

Hence, we assume

$$ t = t_{0} ,x = x_{0} ,\,{\text{then}}\,S_{0,0} = R\left( {x_{0} ,t_{0} } \right)\,{\text{put}}\,{ }x = x_{0} ,t = t_{{1{ }}} ,{\text{we}}\,{\mathrm{get}}\,S_{0,1} = R\left( {x_{0} ,t_{1} } \right),S_{n,m} = R\left( {x_{n} ,t_{m} } \right). $$

This algebraic system can be solved to obtain C_i,j and substitute in Eq. (22) to get the solution.

5 Applications

Example 1

Assume in Eq. (1) $F\left(t,\tau \right)= \text{ t} \tau , \mathrm{ k}\left(x,y\right)= x+y, \{exact solution \phi \left(x,t\right)={t}^{2}{x}^{2}\}.$

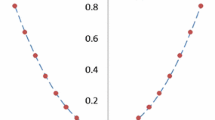
Case (1): For the third kind equation, consider ${\varvec{\mu}}\text{= x, t = }\mathrm{0.1, }{\varvec{\lambda}}=0.01$. and the comparison between the errors results in Chebyshev and Legendre polynomials methods is listed in Table 1. The relationship the relationship between exact solution, numerical and error solution using Chebyshev and Legendre polynomials methods for third kind is shown in Fig. 1. with respect to Case (1).

Table 1 Shows the comparison between the errors results in Chebyshev and Legendre polynomials methods

Fig. 1

Describe the relationship between exact solution, numerical and error solution using Chebyshev and Legendre polynomials methods for third kind

Case (2): For the third kind equations we consider $\mu = \mathrm{ x} \text{, t}\mathrm{ = 0.01 , }\lambda =0.01$ and the comparison between the errors results in Chebyshev and Legendre polynomials methods are displayed in Table 2. In addition, Fig. 2 describes the relationship between exact and numerical solution using Chebyshev and Legendre polynomials methods for third kind according to case 2.

Table 2 The comparison results between Chebyshev and Legendre polynomials methods

Fig. 2

Describes the relationship between exact and numerical solution using Chebyshev and Legendre polynomials methods for third kind

Example 2

Case (3): For the second kind equation consider ${\varvec{\mu}}\text{= 1, t = 0.01, }{\varvec{\lambda}}=0.5$ where the comparison between the errors results in Chebyshev and Legendre polynomials methods are demonstrated in Table 3 and Fig. 3 displays the behaviour of the curve for exact solution and numerical solution for both Chebyshev and Legendre polynomials in accordance with case (3).

Table 3 The errors result between the two method Chebyshev and Legendre

Fig. 3

The behaviour of the curve for exact solution and numerical solution for both Chebyshev and Legendre polynomials

Case (4): For the second kind equation assume $\mu = \text{ 1} \mathrm{, t}\text{ = 0.1, }\lambda =0.5$ where the results are depicted in Table 4. In addition, Fig. 4 shows the behaviour the exact solution and numerical solution in Chebyshev and Legendre polynomials for second kind in accordance with case (4).

Table 4 The comparison between errors results in Chebyshev and Legendre Polynomials

Fig. 4

This diagram shows, the behaviour the exact solution and numerical solution in Chebyshev and Legendre polynomials for second kind

Case (5): For the first kind assume${\varvec{\mu}}\text{= 0, t = 0.1}, {\varvec{\lambda}}=0.01$. The results are shown in Table 5. Furthermore, Fig. 5 diplays The relationship between exact solution, numerical and error solution using Chebyshev and Legendre polynomials methods for first kind depending in case (5).

Table 5 Shows, the comparison between the errors results in Chebyshev and Legendre Polynomials

Fig. 5

The relationship between exact solution, numerical and error solution using Chebyshev and Legendre polynomials methods for first kind

Case (6): For the first kind equation $\, \mu \,{ = 0,}\,\,\,\,\,\,\,{\text{ t = 0}}{.01, }\,\,\,\,\,\,\,\lambda \,{ = }\,0.01$.

The results are demonstrated in Table 6 besides Fig. 6

Table 6 Shows, the comparison between the errors results in Chebyshev and Legendre polynomials

Fig. 6

Describes the relationship between exact solution and numerical solution using Chebyshev and Legendre polynomials methods for first kind

describes the relationship between exact solution and numerical solution using Chebyshev and Legendre polynomials methods for first kind depending on Case (6).

6 Conclusion

In the present paper, we consider the three kinds of the mixed linear integral equation with continuous kernels. In general, we discussed the existence and uniqueness solution of the mixed integral equation of the third kind. And then, we established the second kind as special case from the integral equations. To prove the existence and uniqueness solution of the mixed integral equation of the first kind, we use Banach fixed point theorem, where the Picard method fails. We obtain a numerical solution of the MLIE using Chebyshev method and Legendre method, while, the functions of the integral equations are represented in the form of Chebyshev and Legendre rules. The error in each example is computed.

• In Table 1 At $\mu = x,\,\,\,\,\,\,t = 0.1,\,\,\,\,\,\& \,\,\lambda = 0.01$, the error in Chebyshev is decreasing in period $0.1\le x\le 0.2$ and increasing in $0.3\le x\le 1$, while, in Legendre, the take the same behave of the error.

• In Table 2 At $\mu =x,t=0.01,\& \lambda =0.01$, the error in Chebyshev is decreased in period $0.1\le x\le 0.9$, and increasing in $0.9\le x\le 1$ while, in Legendre has the same behave of the error.

• In Table 3 At$\mu =1 ,t=0.01,\& \lambda =0.01$, the error in Chebyshev stability is decreased in period$0\le x\le 1$, while, in Legendret, the error is stable decreasing in the period$0\le x\le 1$.

• In Table 4 At $\mu =1, t=0.1, \lambda =0.5$ the error in Chebyshev is a stability of decreasing in the period $0\le x\le 1$, while, in Legendre, the error stable decreasing in period $0\le x\le 1$.

• In Table 5 At $\mu =0, t=0.1,\& \lambda =0.01$, the error in Chebyshev is decreasing in the interval of $0.1\le x\le 0.6$ and increasing in the interval of $0.7\le x\le 1$.

• In Table 6 At $\mu =0, t=0.01,\& \lambda =0.01$, the error in Chebyshev is stable decreasing in the period $0\le x\le 1$, while, in Legendre, the error is also stable decreasing in the period $0\le x\le 1$.