1 Introduction

In the Sixth Assessment Report (AR6) of the Intergovernmental Panel on Climate Change (IPCC), the Working Group I (WGI) assessed an increase in global surface temperature of 1.09 °C (0.95 to 1.20 at 90% interval) in 2011–2020 above 1850–1900 [1, 2]. This increase in global surface temperature since previous report is given due to further warming since 2003–2012 (+ 0.19 0.16 to 0.22] °C). These fast modifications in the climate patterns demand investigations on available datasets in order to detect trends and changes in the hydroclimatological systems. Apart from the global and local models, regional models at the watershed level can be developed to access the degree of these water regime changes as the effect of modifications occurring far distant from where they are felt. With the increasing availability and quality of spatial data and the popularization of methods and techniques for data processing and analysis, the management of water resources is going through a moment of a paradigm shift in terms of how to evaluate the territory. Traditional climatological studies focus on time trends of certain periods, based mostly on point-based observations such as rain gauge stations and networks. [3] listed several non-climatic factors that have been affecting long-term climatological time series and making these data not representative over time, including changes in station environment and locations, observing practices, instruments, methods used to calculate statistics, among others. The collected data are usually processed checking for consistency and fill gaps and later analyzed using time series analysis and trend detection methods to verify punctual patterns in hydrological series. However, with the establishment of satellite-based monitoring of water cycle variables since the late 90's/early 00's, the available products can be used to accesses not only time trends but also spatial clusters, indicating spatial trends over the same periods. Analyzing patterns in the hydrological cycle components based on scarce punctual data no longer seems to be representative in the face of data obtained by remote sensors in continuous time and space.

In general, spatial variability is controlled by several properties and variables working over different spatial scales in the natural landscape, which imposes precipitation a highly dynamic behavior over large river basins. The Integrated Multi-satellitE Retrievals for GPM (IMERG) algorithm produces the latest generation of satellite precipitation estimates and has been widely used since its release in 2014 [4]. Starting with the Tropical Rainfall Measuring Mission (TRMM) launched in 1997 and advancing to Global Precipitation Measurement (GPM) core observatory launched in 2014, the IMERG algorithm was designed to intercalibrate, merge, and interpolate available satellite microwave precipitation estimates, together with microwave-calibrated infrared satellite estimates, precipitation gauge analyses, and potentially other precipitation estimators at fine time and space scales for the TRMM and GPM eras over the entire globe [5]. In fact, there is a number of early IMERG satellite-based precipitation products available to the general public like PERSIANN (Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks) [6], HE (Hydro-Estimator) [7], CMORPH (Climate Prediction Center Morphing Method) [8], TMPA (Tropical Rainfall Measuring Mission Multi-satellite Precipitation Analysis) [9], CoSch (Combined Scheme) [10], among others. This timeline denotes the fast evolution of the remote sensing precipitation products in the past decades. Despite its limitations, IMERG evolution in the last years have been revealing an exciting way for current and future applications [4, 11]. The confidence in IMERG products quality and accuracy allows its gradual incorporation into routine analysis for water resources management and watershed planning purposes.

Boosted by climate change, explore the precipitation dynamism over spatial and temporal scales can provide useful insights to planners, landscape modelers and water boards and local users about current and future water scenarios based on precipitation. Nowadays, series longer than 20 years of data are available for spatial and temporal analysis, as in the case of precipitation data, allowing to access information about spatial patterns and temporal trends. However, the treatment of these data and its transformation in reliable information is still an important point [12]. Exploratory spatial data analysis (ESDA) is defined by [13] as “a set of techniques to describe and visualize spatial distributions, identify atypical locations (spatial outliers), describe patterns of spatial association (spatial clusters), and suggest different spatial regimes and other forms of spatial instability or spatial non-stationarity”. There is a variety of spatial statistics techniques developed in the context of ESDA [14, 15]. Global spatial statistics express the spatial autocorrelation present in the target variable across the data set and local spatial statistics decompose the spatial autocorrelation to each of the component areas [16]. Local statistics can reveal from where the contributions to global spatial autocorrelation came in terms of geographical space, and address questions about the spatial dependence and clusters near specific locations [14].

Since the water resources management in Brazil has the watershed as a management unit, and they are usually large areas in extension, it is important to detect areas with spatial clusters of higher and lower values, in addition to anomalous values, instead of treating their subdivisions as homogeneous areas. Apart from its strength in revealing complex spatial phenomena, ESDA still has not become prevalent in hydrological studies but received more attention in recent years [17,18,19,20,21,22], even not considering the temporal dimension. In addition to ESDA, trends, homogeneity, and possible change point detection diagnosis in the time series can be incorporated in the exploratory spatial and temporal data analysis (ESTDA) approach, going beyond the static data and better revealing the spatial and temporal dynamics of various geographic events and phenomena [15]. The search for spatial and temporal patterns of precipitation based on the use of spatial autocorrelation metrics has been reported in studies like [15, 23,24,25,26,27,29]. This becomes even more important in tropical regions where precipitation is the main input of the hydrological cycle and its values are taken as the basis for various economic activities, social development, and environmental protection. In this perspective, remotely sensed data can indicate spatial and temporal changes of hydrological key parameters like precipitation.

The aim of this study was to verify spatial and temporal precipitation patterns in watersheds integrating spatial and temporal statistics within a framework of remotely sensed data analysis. The study is illustrated with a case study in the Paranapanema River Basin, Brazil, between 2000 and 2021, a period in which the region faced a severe water crisis due to precipitation shortage.

2 Study area — Paranapanema River Basin

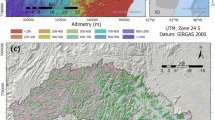
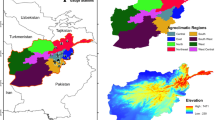
The Paranapanema River Basin (PPRB) is an important agricultural region and hydropower hub of southeastern Brazil. Since 2018, the Brazilian Water and Sanitation National Agency (ANA) implemented a crisis room to help the watershed committee to deal with the water scarcity frame that was becoming critical. The PPRB is located in the southeastern part of Brazil between the states of São Paulo (SP) and Paraná (PR), with 106,562.18 km2 centred at latitude 23° 27’ South and longitude 50° 18’ West (Fig. 1). PPRB has 247 municipalities (212 with urban centers in the basin) with 51% of the territory in PR and 49% in SP, with an estimative population of 4,680,725 inhabitants [30].

Fig. 1
figure 1

Location of the PPRB and its HPU (detail) in the Brazilian territory divided by states

Full size image

Following Köppen-Geiger's climate classification, PPRB is inside two climate zone according to [31], Tropical (A) and Subtropical (C), with four climate types: Cfa (central portion) and Cfb (south part and southeastern border), Aw and Am (western part). The mean precipitation of PPRB is 1450 mm, with higher values of up to 1800 mm in the central-south portion and lower values of down to 1300 mm in the east and northwest parts [32]. A more extensive physical description of PPRB is presented in [33].

The PPRB is divided into 22 watersheds or hydrological planning units (HPU): Alto Tibagi, Médio-Alto Tibagi, Baixo Tibagi, Alto Cinzas, Baixo Cinzas, Itararé Norte Pioneiro, Itararé Alto Paranapanema, Taquari, Alto Paranapanema M.D., Alto Paranapanema M.E., Pardo, Pari/Novo, Turvo, Capivara, Vermelho/Capim, Pirapó, Baixo Paranapanema M.E., Baixo Paranapanema M.D., Pirapozinho, Laranja Doce, Tributários Rio Paraná, and Santo Anastácio. These units were designed for water management purposes and selected for this study as the final diagnosis scale.

3 Dataset

Accumulated precipitation rates were recovered for the PPRB region from Nasa's Earth data repository using the Giovanni (Geospatial Interactive Online Visualization ANd aNalysis Infrastructure) web-based application (https://giovanni.gsfc.nasa.gov/) developed by the Goddard Earth Sciences Data and Information Services Center (GES DISC). The product analyzed was the GPM (Global Precipitation Mapping) IMERG (Integrated Multi-satellitE Retrievals for GPM) Final Precipitation Level 3 (GPM_3IMERGDF) in 0.1° × 0.1° (roughly 10 × 10 km) resolution [5]. The total precipitation accumulated in 21 hydrological years was organized in hydrological years, from September 22, 2000, until September 21, 2021, resulting in the spatial coverage presented in Fig. 2. The data derived from the half-hourly GPM_3IMERGHHL estimate daily accumulated precipitation, accumulated later for yearly intervals.

Fig. 2
figure 2

Spatial coverage of GPM/IMERG data at PPRB represented by the center of each image pixel

Full size image

4 Exploratory spatial and temporal data analysis

The present study proposes a methodology to verify possible spatial and temporal patterns of precipitation data obtained by satellite-based on four questions, as described in the flowchart of Fig. 3. For spatial patterns investigation, we have two questions. Are there any significant hot/cold spots of values in the region? Are there any significant outliers in the region? For temporal patterns investigation, we have other two questions. Are there any significant trends in the time series? Are there any significant change points in the time series?

Fig. 3
figure 3

Exploratory spatial and temporal data analysis for precipitation data obtained by satellite

Full size image

If any of these questions have the answer yes, it would already demand future investigations to identify the causes and reasons for the detected process. Thus, the statistical tests used in this ESTDA methodology, and the criteria adopted to determine their significance, are described below.

4.1 Spatial clustering analysis and outliers detection

Spatial clusters can be identified in various disciplines, from point process data or areal data, trying to verify if the locations of observed data are spatially clustered or simply random or if similar observations tend to be closer together. These kinds of analyses can be described as spatial clustering analysis techniques. Getis–Ord Gi* [34, 35] and Local Moran's I [13] are examples of local spatial statistics used to measure or test for spatial association in some variable of interest surrounding a specific location. Getis-Ord Gi* identifies statistically significant spatial clusters of high and low values while Local Moran's I identifies statistically significant spatial clusters of features with high or low values and spatial outliers.

4.1.1 The Getis-Ord G i * local statistic

The Getis-Ord Gi* local statistic identifies areas where high or low values cluster in space. To test whether a particular location i and its surroundings regions have higher than average values on a variable (x) of interest, the Gi* local statistic is given by Eq. 1:

$${G}_{i}^{*}=\frac{\sum_{j=1}^{n}{w}_{i,j}{x}_{j}-\overline{X }\sum_{j=1}^{n}{w}_{i,j}}{S\sqrt{\frac{\left[n\sum_{j=1}^{n}{w}_{i,j}^{2}-({\sum_{j=1}^{n}{w}_{i,j})}^{2}\right]}{n-1}}}$$
(1)

where xj is the attribute value for feature j, wi,j is the spatial weight between feature i and j, n is equal to the total number of features, and \(\overline{X }\) and \(S\) are given by Eqs. 2 and 3 respectively:

$$\overline{X }=\frac{\sum_{j=1}^{n}{x}_{j}}{n}$$
(2)
$$S=\sqrt{\frac{\sum_{j=1}^{n}{x}_{j}^{2}}{n}-({\overline{X })}^{2}}$$
(3)

As explained by [36], the numerator of Eq. 1 represents, for region i, the difference between the weighted value of x in the neighborhood of i and the value that would be expected if the neighborhood was average in its x characteristics. In other words, the Gi* statistic is a Z-score with respective p-values, indicating if a given point is statistically clustered compared to a neighboring point across study domain. Z-scores indicate the degree of variability expressed in terms of a number of standard deviations an observation is away from the mean [36]. Gi* is positive if the sum of values within a neighborhood is high in relation to the global average and negative if the sum of values within a neighborhood is small in relation to the global average. The magnitude and significance of the Z-score indicated the intensity of the clustering processes. Large positive z-scores indicate more intense high values clusters (hot spot) while small negative Z-scores indicate more intense low values clusters (cold spot). In this study, Z-score significance is measured by its p-values with a False Discovery Rate (FDR) correction that potentially reduces the critical p-value thresholds.

4.1.2 Local Moran’s Ii statistic

The Local Moran's Ii statistic of spatial association [13] is given by Eq. 4:

$${I}_{i}=\frac{{x}_{i}-\overline{X}}{{S }_{i}^{2}} \sum_{j=1,j\ne 1}^{n}{w}_{i,j} ({x}_{j}-\overline{X })$$
(4)

where xi is the attribute value for feature i, \(\overline{X }\) is the corresponding attribute mean, wi,j is the spatial weight between feature i and j, and \({S}_{i}^{2}\) is given by Eq. 5:

$${S}_{i}^{2}=\frac{\sum_{j=1,j\ne 1}^{n}{({x}_{j}-\overline{X })}^{2}}{n-1}$$
(5)

with n as the total number of features.

Local Moran's Ii calculation removes a value from its neighborhood, and checks if the neighborhood is significantly different from the study area. Then, it is checked if each value is significantly different from its neighborhood, finding possible outliers within clusters (for example points with significantly low values in hot spot neighborhoods or significantly high values in a cold spot neighborhood). A positive Ii value is an indicator that a feature has neighboring features with similarly values and is considered part of a cluster. On the other hand, a negative I value is an indicator that a feature has neighboring features with dissimilar values, being considered an outlier. The Ii index can only be interpreted within the context of its associated Z-score or p-value because is a relative measure. For cluster or outlier detection, the feature p-value must be small enough to be considered statistically significant.

Getis-Ord Gi* and Local Moran’s Ii statistics handle locations and observed values of spatial data, and both statistics are calculated for each feature (point or polygon). When applying Gi* or Ii statistics, the observation locations are treated as fixed, while the associated values are considered random variables. [13] explains that Gi* statistic is a slightly different Local Indicators of Spatial Association (LISA) when compared to Ii statistic because Gi* individual components are not related to a global statistic of spatial association. If this requirement is not needed for the identification of significant local spatial clusters using Gi* statistic, it is an important component of Ii statistic, which allows a diagnostic of local instability in measurements of global spatial association in terms of presence of outliers. Once the Gi* statistic can not identify outliers, it can be used in conjunction with the Ii statistic to understand spatial patterns more fully.

In this study, the default neighborhood search threshold for spatial Gi and Ii statistics calculation was 11,072.6250 m, using Euclidean distance as distance method. Values of Z-score and its p-values were used to verify the hot/cold spots at each HPU in order to detect possible areas with recurrent high or low precipitation values during the 21 years of observed period, individually. All spatial statistics calculations were performed using ArcGIS 10.3 in its Spatial Statistics toolbox.

4.2 Temporal trends analysis

4.2.1 Mann–Kendall test

Mann–Kendall (MK) test is a non-parametric trend test proposed by [37] whose test statistic distribution was derived by [38]. Many authors observe the wide use of the MK test for trend detection in hydrological and meteorological time series [39,40,41,42,43,44]. [39] describe the MK test as an exploratory tool to identify and quantify locations where changes are significant and its magnitude. The MK test does not require normality in the data, having low sensitivity to abrupt breaks given by inhomogeneous time series [45]. The World Meteorological Organization (WMO) has been widely recommending this test by for public application [46]. The MK test statistic is calculated as follow:

$$S=\sum_{k=1}^{n-1}\sum_{j=k+1}^{n}sgn({x}_{j}-{x}_{k})$$
(6)

\(with\)

$$sgn\left( {x_{j} - x_{i} } \right) = \left\{ \begin{gathered} 1x_{i} < x_{j} \hfill \\ 0x_{i} = x_{j} \hfill \\ - 1x_{i} > x_{j} \hfill \\ \end{gathered} \right.$$
(7)

The mean of S is approximately normally distributed with µ = 0. The variance including a ties correction term is:

$${\sigma }^{2}=\left\{n\left(n-1\right)\left(2n+5\right)-\sum_{j=1}^{p}({t}_{j}-1)(2{t}_{j}+5)\right\}/18$$
(8)

where p is the number of the tied groups in the data set and tj is the number of data points in the j-th tied group.

If the sample size n is greater than 10, the standard normal test statistic Zs is calculated as follows:

$$Z_{s} = \left\{ \begin{gathered} \frac{{S - 1}}{{\surd Var(S)}},ifS > 0 \hfill \\ 0,ifS = 0 \hfill \\ \frac{{S + 1}}{{\surd Var(S)}},ifS < 0 \hfill \\ \end{gathered} \right.$$
(9)

Negative Zs values denote decreasing trends while positive values denote increasing trends. For trend detection, [42] highlights the importance of the significance level that indicates the strength of the trend and the magnitude of the slope that indicates the direction of the trend.

4.2.2 Sen's slope

The magnitude of the trend in time series and its statistical significance detected by the MK test are estimated by Sen's estimator [47], computing both the slope (linear rate of change) and the confidence levels. In this procedure, a set of linear slopes dk is calculated:

$${d}_{k}=\frac{{x}_{j}-{x}_{i}}{j-i}$$
(10)

for (1 ≤ i < j ≤ n), where d is the slope, x denotes the variable, n is the number of data, and i, j are indices. Sen's slope is then calculated as the median from all slopes:

$${b}_{sen}=median \,({d}_{k})$$
(11)

4.3 Homogeneity tests and change point detection

The homogeneity and change point detection tests were be used to assess possible periods where significant change in the characteristics of the time series occurred. Standard normal homogeneity, Pettitt’s, Buishand range and von Neumann ratio are examples of tests designed for homogeneity check and change point detection in climatological time series [3, 45, 48, 49].

4.3.1 Standard normal homogeneity test (SHNT)

As described by [50], a model for a normal random variate with a single shift (change point) can be described as:

$${x}_{i}=\left\{\begin{array}{c}\mu +{\epsilon }_{i}, \\ \mu +\Delta {+\epsilon }_{i}\end{array} \begin{array}{c}i=1,\dots ,m \\ i=m+1,\dots ,n\end{array}\right.$$
(12)

with ϵ ≈ N(0, σ). For no change is considered the null hypothesis (∆ = 0), tested against the alternative (∆ ≠ 0) for change. The SNHT test is calculated as follows:

$$T_{k} = kz_{i}^{2} + \left( {n + k} \right)z_{2}^{2} \,\,(1 \le k ; n)$$
(13)

where:

$${z}_{1}=\frac{1}{k}{\sum }_{i=1}^{k}\frac{{x}_{i}-\overline{x}}{\sigma } {z }_{2}=\frac{1}{n-k}{\sum }_{i=k+1}^{n}\frac{{x}_{i}-\overline{x}}{\sigma }$$
(14)

The critical value is \(T=max{ T}_{k}\). The critical values of the SHNT test based on p-values are presented by [51].

4.3.2 Pettit’s test

The test was calculated as given by [52], performing a non-parametric test after [53] in order to test possible shifts in the central tendency of the time series. The null hypothesis (no change) is tested against the alternative hypothesis (change), where the ranks r1,…,rn of the Xi,…,Xn are used for the statistic:

$${U}_{k}=2\sum_{i=1}^{k}{r}_{i}-k\left(n+1\right)\, k=1,\dots ,n$$
(15)

The test statistic is the maximum of the absolute value of the vector:

$$\widehat{U}=max\left|{U}_{k}\right|$$
(16)

The probable change-point K is located where \(\widehat{U}\) has its maximum. The approximate probability for a two-sided test is calculated according to:

$$p=2{exp}^{-6{K}^{2}/({T}^{3}-{T}^{2})}$$
(17)

4.3.3 Buishand test

As in the SHNT test, a single shift (change point) is proposed (Eq. 12). In the Buishand range test [54], the rescaled adjusted partial sums are calculated as:

$${S}_{k}=\sum_{i=1}^{k}\left({x}_{i}-\widehat{x}\right) \,\,(1\le i\le n)$$
(18)

The test statistic is calculated as:

$${R}_{b}=(max{ S}_{k}-\mathrm{min}{S}_{k})/\sigma$$
(19)

The critical values of the Buishand range test based on p-values are presented by [54].

4.3.4 Bartels test

[55] proposed a rank version of von Neumann's ratio test [56] where the null hypothesis of randomness is tested against the alternative hypothesis. In this function, the ranks r1,…,rn of the Xi,…,Xn are used for the statistic:

$$T=\frac{{\sum }_{i=1}^{n}({{r}_{i}-{r}_{i+1})}^{2}}{{\sum }_{i=1}^{n}({{r}_{i}-\overline{r })}^{2}}$$
(20)

The p-values are calculated for sample sizes in the range of (10 ≤ n < 100) with the non-standard beta distribution for the range 0 ≤ x ≤ 4 with parameters:

$$a=b=\frac{5n(n+1){(n-1)}^{2}}{2(n-2)(5{n}^{2}-2n-9)}-\frac{1}{2}$$
(21)

For sample sizes n ≥ 100 a normal approximation with N(2, 20/(5n + 7)) is used for p-value calculation.

Observing the advantages and disadvantages of these tests, it is important to use not only one selected method, avoiding a wrong test decision. In this study, we adopted a classification for homogeneity assessment based on [45, 49 and 57]. The classification follows the number of tests rejecting the hypothesis of no change from a number of four tests, distinguishing three classes:

  • Class 1 (NCP—no change point): the series are considered homogeneous if none or one tests reject the null hypothesis at the 5% significance level.

  • Class 2 (DS—doubtful series): if two tests reject the null hypothesis at the 5% significance level.

  • Class 3 (CP—change point): the series are considered inhomogeneous if three or four tests reject the null hypothesis at the 5% significance level.

The statistical tests for trends, homogeneity, and change point detection were calculated using the R package ‘trend’ [58]. The tests were performed on the entire PPRB region, as well as for each HPU, in order to detect possible regional and/or local insights about the temporal behavior of precipitation in the region. For these calculations, the point data was interpolated using the inverse distance weighted method with a 0.05° grid tolerance and power 2 and then annual values were calculated with zonal function, both available at ArcGIS 10.3 in its Spatial Analyst toolbox. The study period from 2000 until 2021 was analyzed in a yearly frequency, based on the hydrological year, resulting in an n = 21.

5 Results

5.1 Spatial analysis

Integrating both spatial statistics Gi and Ii, we first investigate UPHs with significant hot and cold spots in the PPRB, spatial autocorrelation, and the presence of outliers. Table 1 presents the Getis-Ord Gi* statistics by year for the whole PPRB. Only the 2002 and 2016 hydrological years presented random precipitation patterns. The given Z-scores for 2002 and 2016 indicated the pattern does not appear to be significantly different than random. In the other hydrological years, we had eleven periods with significant low values clusters and eight periods with significantly high values clusters. There is a less than 1% likelihood that this high/low-clustered pattern could be the result of random chance for nineteen periods. Figure 4 presents examples of hydrological years with low and high values clusters, as well as random patterns. For the Gi* statistics, positive values indicate spatial clusters of high values, meanwhile negative values a spatial cluster of low values.

Table 1 General Gi statistics for precipitation in the PPRB from 2000 to 2020's hydrological years
Full size table
Fig. 4
figure 4

Examples of hydrological years with significant high and low clusters and random patterns

Full size image

Nevertheless, as shown in Fig. 4, the presence of significant hot/cold spots in the region over the years does not mean that these high/low-clustered patterns were widespread in the whole PPRB. Even the periods with random patterns over the basin presented significant hot/cold spots when analyzing the patterns per HPU. The determination of where these clusters are located by HPU is key for water management practices considering the size of the basin. Table 2 presents the results of Getis-Ord statistics in terms of Z-scores and their significance per HPU. Significant hot spots with clusters of high values of precipitation were more concentrated in the southern part of the PPRB, highlighting HPUs Alto Tibagi and Médio-Alto Tibagi. In these HPUs there was a persistence of hot spots, mostly in the first half of the analyzed period (2000 – 2010). In the second half of the analyzed period (2011–2020) the hot spots were more present in the Alto Tibagi HPU. As presented in [33], these HPUs are located under Cfb subtropical oceanic climate, so it is expected a different precipitation regime due to its proximity to the Atlantic Ocean and Antarctic air fronts.

Table 2 Gi* statistics for precipitation per HPU in the PPRB from 2000 to 2020's hydrological years
Full size table

In other regions and HPUs of the PPRB, the presence of hot/cold spots is not as persistent. In the western region, clusters of low values were initially detected, which proved to be erratic over the years, alternating moments of clusters of low and high values, with emphasis on the HPUs Santo Anastácio, Tributários Rio Paraná, Laranja Doce, Pirapozinho, Baixo Paranapanema M.D., all located in the Pontal do Paranapanema region. Giving as an example the Tributários Rio Paraná HPU, this region presented hot spots of precipitation from 2014 to 2020, after several years of alternating moments of low and high values.

Local Moran's statistics and their significance are presented in Table 3. For Ii statistics, positive values indicate spatial clusters of similar values (either high or low), meanwhile negative values are a spatial cluster of dissimilar values (high values surrounded by low values, or vice-versa). These statistics showed only clusters with similar values (positive), denoting no outliers in the dataset and confirmed significant spatial autocorrelation mostly in the Alto Tibagi and Médio-Alto Tibagi HPUs (in the southern part of PPRB) and in some HPUs of the western part of PPRB. The spatial autocorrelation can vary from one period to another, but confirms some patterns verified by Getis-Ord statistics. From the insights given by Gi* and Ii statistics as measures of local spatial clusters, pointing out spatial patterns, it is possible to suggest explanations or hypotheses. For example, why some regions have more precipitation than others or establish correlations between precipitation inputs and economic development, environmental protection and conservation, and social awareness against extreme events, among others precipitation related effects. In addition, the indication of spurious observations can point to data quality problems [13]. The years in which the general G values presented in Table 1 were higher (2006, 2015, 2017, and 2019) were the years in which the highest significant values of Ii were observed in several HPUs, such as Pari/Novo in 2006, Alto Paranapanema M.D., Pardo, Pirapó, Baixo Paranapanema M.D., Turvo and Tributários Rio Paraná in 2015, Turvo and Pirapó in 2017 and Pirapó and Tributários Rio Paraná in 2019. All these HPUs are concentrated in the western part (outlet) of the PPRB and stand out HPU Pirapó with a recurrence of lower values grouped in its limits in 2015, 2017, and 2019.

Table 3 Local Moran's Ii statistics for precipitation per HPU in the PPRB from 2000 to 2020’s hydrological years
Full size table

5.2 Time series analysis

The temporal analysis can verify if significant trends and changes in the precipitation regime were observed in the PPRB. Autocorrelation and partial autocorrelation functions of the precipitation time series per HPU did not present significant values, allowing the application of Mann–Kendall test without any further corrections for autocorrelation.

Table 4 presents the results of the trends test and change point detection tests. The negative S values at the Mann–Kendall tests indicates a downward trend over time, while positive S values indicates an upward trend over time. An S value close to zero indicates an almost equal number of positive and negative differences. The significance of these trends is verified with the Mann-Kendal Z and its p-values. Significant trends were denoted when the p-value of the Mann–Kendall test were statistically significant. HPUs Alto Paranapanema M.E. and Itararé Norte Pioneiro presented significant negative trends at a 5% significance level and Alto Cinzas at a 10% significance level. The magnitude of these trends was verified using Sen's slope test. The Sen's slope estimator calculated decreases of annual precipitation at HPUs Alto Paranapanema M.E., Itararé Norte Pioneiro and Alto Cinzas of − 20.20, − 14.43 and − 11.66 mm, respectively. During the 21 years period of analysis, these HPUs presented an annual precipitation mean of 1545.89, 1525.89 and 1519.23 mm, respectively. If in terms of total volume, the decreases are not so significant, in terms of geographic location these trends trigger special concerns since these HPUs are in the heads of the PPRB and contribute substantially to the basin discharge. Also, [33] verified important land use changes in these HPUs, with the consolidation of cash crops like soybeans in the region from 1990 to 2020 using MapBiomas Collection 7.0 (https://mapbiomas.org/). Most of these crops advance into pasture areas, increasing water consumption and evapotranspiration. Further changes in the water cycle components should be investigated in detail.

Table 4 Trend tests for annual precipitation in the HPUs of the PPRB between the hydrological years 2000 and 2020
Full size table

After verifying the trend, we focus on changes in the precipitation regime over the period using SNHT, Pettit's, Buishand and Bartels tests. All HPU were classified in one of the three categories proposed for homogeneity in the series, with eight HPUs at Class 1, eight HPUs at Class 2 and 6 HPUs at Class 3.

When analyzing the homogeneity of the series of each HPU regarding the significance of the tests, eight HPUs are classified as Class 1, eight as Class 2 and six as Class 3. If we analyze the entire PPRB, we can also classify it as Class 3. The HPUs Médio-Alto Tibagi, Alto Paranapanema M.E., Alto Paranapanema M.D., Baixo Cinzas, Pari/Novo and Capivara had three significant tests for change point. In the Médio-Alto Tibagi, this change was verified in 20125 and 2017, in the Alto Paranapanema M.E. between 2012 and 2016, in the Alto Paranapanema M.D. between 2012 and 2017, Baixo Cinzas in 2017, Pari/Novo between 2016 and 2017 and Capivara between 2015 and 2017. Considering the entire PPRB, the change was verified between 2015 and 2017. Coincidentally, from 2017 onwards, the PPRB began to suffer from a severe water crisis that culminated in the installation of the ANA’s crisis room in 2018, which lasted until December 2022 when it was transformed into a situation room by the agency. The average precipitation data per HPU for each hydrological year studied are presented in Appendix 1. Between 2014 and 2020 there were significant reductions in precipitated volumes over the PPRB. The mean precipitation in the studied period for the PPRB was 1523.46 (± 189.25) mm. Based on the precipitation of 1686.77 mm in 2014, except for 2015 which was the year with the highest precipitation volumes in the entire analyzed period, all subsequent years had reductions of at least 10% in 2017 and a maximum of 32% in 2020. If we take as a basis the 2088.72 mm precipitated in 2015, the reductions in 2017 would be 27% and in 2020 they would reach 45%. These results represent a major challenge for the management of water resources in the region in terms of water use planning, water grants and charging, demanding additional studies about the conditions of each HPU. Conflicts over water use are already frequent in the Alto Paranapanema region, for example, where the energy, tourism and irrigated agriculture sectors have been competing for the right to use water.

6 Discussions

These analyses presented alternatives for better natural resources management through Earth Observation data and methods. Studies on the spatial and temporal variability of precipitation patterns have been the target of researchers in different parts of the world such as Iran [18, 20, 22, 25], Serbia [17, 24], Turkey [23], India [29], China [26], Great Britain [28], France [19], but it has also gained visibility in regional [27] and global studies [21].

Despite this, studies at the watershed scale are limited, despite being indispensable for efficient water management and planning. A discussion presented by [59] almost two decades ago about the non-use of uncertainty analysis (error measures, probabilities, confidence intervals, statistical methods in general) by hydrologists seems still current with regard to spatial statistics. For [60], the level of mathematical knowledge necessary to understand stochastic theories is far beyond most hydrologists have. For [61], regulations made with simple numbers and the uncertainty associated with them (such as probabilities of exceeding certain thresholds) is not something regulators can really deal with. [62] comment that problems in the interpretation of data originated by misusing predictive tools contribute to a lack of consensus on the need for strategic actions in water management. [63] believes in an exaggerated importance given to statistical tests, particularly in adopting significance levels, saying that it is not about applying statistical methods without the necessary rigor, but about understanding the limitations of methods and data and then adapting them to models capable of providing applicable results.

If the water research community want to advance in their role in the management of this increasingly scarce resource that is water more effectively, it is time for professionals in the area to start becoming familiar with these methods from the first years of undergraduate courses and that special attention be given to postgraduate education of geosciences and geotechnologies with emphasis on stochastic approaches. Also, a geoethical perspective incorporated in the profile of the new geoscientists can help to elucidate the use of geothecnologies and statistical methods and dismiss conflicts originated from competing claims for water resources. [64] proposed an open-minded (geo)ethical roadmap for data analytics applications, focusing on groundwater governance. Following this approach, [65] presented what happened in the PPRB western part with the expansion of sugarcane crops without a geoethical thinking, encouraging researchers to include it in their reasearchs to anticipate issues, create scenarios, and guide the decision-making processes, enhancing water governance. With the enormous range of satellite data increasingly available over time, it is necessary to disseminate and train in techniques such as those presented in this article, which, although not new, can become powerful exploratory tools when combined within the scope of ESTDA. This methodology can be extended to data observed by satellites on evapotranspiration, soil moisture, gravimetric fields, among other components of the hydrological cycle subject to changes in their patterns in space and time.

7 Conclusions

From the precipitation IMERG/GPM data, we verified significant spatial clusters in nineteen of the twenty-one years analyzed, denoting a strong presence of precipitation spatial pattens in the PPRB. Several spots of high and low values were detected over the 21 hydrological years analyzed from 2000 to 2021. However, recurrent hot and cold spots were verified only in few HPU. The first ten years of analysis showed more persistent patterns with spatial clusters of high values of precipitation were in the eastern part of PPRB and with spatial clusters of low values in the central-western part of PPRB. These patterns were more erratic from 2011 to 2020. Apart the significant spatial clusters, no outliers were detected in the dataset. Alto Paranapanema M.E., Itararé Norte Pioneiro and Alto Cinzas HPUs presented significant decreases in precipitation and Médio-Alto Tibagi, Alto Paranapanema M.E., Alto Paranapanema M.D., Baixo Cinzas, Pari/Novo and Capivara presented significant change points in the precipitation series from 2012 to 2017. The PPRB presented modifications in the precipitation regime, with a significant change points around 2015—2017. This method can be applied to other satellite-based datasets, revealing spatial and temporal patterns over water cycle components and supporting an informative water management.