A quantum convolutional neural network on NISQ devices

Abstract

Quantum machine learning is one of the most promising applications of quantum computing in the noisy intermediate-scale quantum (NISQ) era. We propose a quantum convolutional neural network(QCNN) inspired by convolutional neural networks (CNN), which greatly reduces the computing complexity compared with its classical counterparts, with O((log₂M)⁶) basic gates and O(m²+e) variational parameters, where M is the input data size, m is the filter mask size, and e is the number of parameters in a Hamiltonian. Our model is robust to certain noise for image recognition tasks and the parameters are independent on the input sizes, making it friendly to near-term quantum devices. We demonstrate QCNN with two explicit examples. First, QCNN is applied to image processing, and numerical simulation of three types of spatial filtering, image smoothing, sharpening, and edge detection is performed. Secondly, we demonstrate QCNN in recognizing image, namely, the recognition of handwritten numbers. Compared with previous work, this machine learning model can provide implementable quantum circuits that accurately corresponds to a specific classical convolutional kernel. It provides an efficient avenue to transform CNN to QCNN directly and opens up the prospect of exploiting quantum power to process information in the era of big data.

1 Introduction

Machine learning has fundamentally transformed the way people think and behave. Convolutional neural network (CNN) is an important machine learning model which has the advantage of utilizing the correlation information of data, with many interesting applications ranging from image recognition to precision medicine.

Quantum information processing (QIP) [1, 2], which exploits quantum-mechanical phenomena such as quantum superpositions and quantum entanglement, allows one to overcome the limitations of classical computation and reaches higher computational speed for certain problems [3–5]. Quantum machine learning, as an interdisciplinary study between machine learning and quantum information, has undergone a flurry of developments in recent years [6–15]. Machine learning algorithm consists of three components: representation, evaluation and optimization, and the quantum version [16–20] usually concentrates on realizing the evaluation part, the fundamental construct in deep learning [21].

A CNN generally consists of three layers, convolution layers, pooling layers, and fully connected layers. The convolution layer calculates new pixel values $x_{{ij}}^{(\ell)}$ from a linear combination of the neighborhood pixels in the preceding map with the specific weights, $x_{i,j}^{(\ell)} = \sum _{a,b=1}^{m} w_{a,b} x_{i+a-2,j+b-2}^{(\ell -1)}$, where the weights w_a,b form a m×m matrix named as a convolution kernel or a filter mask. Pooling layer reduces feature map size, e.g., by taking the average value from four contiguous pixels, and is often followed by application of a nonlinear (activation) function. The fully connected layer computes the final output by a linear combination of all remaining pixels with specific weights determined by parameters in a fully connected layer. The weights in the filter mask and fully connected layer are optimized by training on large datasets.

In this article, we demonstrate the basic framework of a quantum convolutional neural network (QCNN) by sequentially realizing convolution layers, pooling layers, and fully connected layers. Firstly, we implement convolution layers based on linear combination of unitary operators (LCU) [22–24]. Secondly, we abandon some qubits in the quantum circuit to simulate the effect of the classical pooling layer. Finally, the fully connected layer is realized by measuring the expectation value of a parametrized Hamiltonian and then a nonlinear (activation) function to post-process the expectation value. We perform numerical demonstrations with two examples to show the validity of our algorithm. Finally, the computing complexity and trainability of our QCNN model are discussed followed by a summary.

2 Results

2.1 Framework of quantum neural networks

2.1.1 Quantum convolution layer

The first step for performing quantum convolution layer is to encode the image data into a quantum system. In this work, we encode the pixel positions in the computational basis states and the pixel values in the probability amplitudes, forming a pure quantum state (Fig. 1). Given a 2D image F=(F_i,j)_M×L, where F_i,j represents the pixel value at position (i,j) with $i = 1,\dots, M$ and $j = 1,\dots,L$. F is transformed as a vector $\vec {f}$ with ML elements by putting the first column of F into the first M elements of $\vec {f}$, the second column the next M elements, etc. That is,

$$\begin{array}{@{}rcl@{}} \vec{f}=(F_{1,1},F_{2,1},\dots,F_{M,1},F_{1,2},\dots,F_{i,j},\dots,F_{M,L})^{T}. \end{array} $$

(1)

Fig. 1

Comparison of classical convolution processing and quantum convolution processing. F and G are the input and output image data, respectively. On the classical computer, a M×M image can be represented as a matrix and encoded with at least 2ⁿ bits [ n=⌈log2(M²)⌉]. The classical image transformation through the convolution layer is performed by matrix computation F∗W, which leads to $x_{i,j}^{(\ell)} = \sum _{a,b=1}^{m} w_{a,b} x_{i+a-2,j+b-2}^{(\ell -1)}$. The same image can be represented as a quantum state and encoded in at least n qubits on a quantum computer. The quantum image transformation is realized by the unitary evolution U on a specific quantum state

Accordingly, the image data $\vec {f}$ can be mapped onto a pure quantum state $\phantom {\dot {i}\!}| f \rangle = \sum _{k=0}^{2^{n}-1} c_{k} | k \rangle$ with n=⌈log2(ML)⌉ qubits, where the computational basis |k〉 encodes the position (i,j) of each pixel, and the coefficient c_k encodes the pixel value, i.e., $c_{k} = F_{i,j}/\left (\sum {F_{i,j}^{2}}\right)^{1/2}$ for k<ML and c_k=0 for k≥ML. Here, $\left (\sum {F_{i,j}^{2}}\right)^{1/2}$ is a constant factor to normalizing the quantum state.

Without loss of generality, we focus on the input image with M=L=2ⁿ pixels. The convolution layer transforms an input image F=(F_i,j)_M×M into an output image G=(G_i,j)_M×M by a specific filter mask W. In the quantum context, this linear transformation, corresponding to a specific spatial filter operation, can be represented as |g〉=U|f〉 with the input image state |f〉 and the output image state |g〉. For simplicity, we take a 3×3 filter mask as an example

$$ W=\left[\begin{array}{ccc} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\\ w_{31} & w_{32} & w_{33}\\ \end{array}\right]. $$

(2)

The generalization to arbitrary m×m filter mask is straightforward. Convolution operation will transform the input image F=(F_i,j)_M×M into the output image as G=(G_i,j)_M×M with the pixel $G_{i,j} = \sum _{u,v =1}^{3} w_{{uv}} F_{i+u-2,j+v-2}$ (2≤i,j≤M−1). The corresponding quantum evolution U|f〉 can be performed as follows. We represent input image F=(F_i,j)_M×M as an initial state

$$\begin{array}{@{}rcl@{}} | f \rangle = \sum_{k=0}^{M^{2}-1} c_{k} | k \rangle, \end{array} $$

(3)

where $c_{k} = F_{i,j}/\left (\sum {F_{i,j}^{2}}\right)^{1/2}$. The M²×M² linear filtering operator U can be defined as [25]:

$$ U=\left[\begin{array}{cccccc} E & & & & & \\ V_{1} & V_{2} & V_{3} & & & \\ & \ddots & \ddots & \ddots & &\\ & & \ddots & \ddots &\ddots &\\ & & & V_{1} & V_{2} & V_{3}\\ & & & & & E \\ \end{array}\right], $$

(4)

where E is an M dimensional identity matrix, and V₁,V₂,V₃ are M×M matrices defined by

$$\begin{aligned} V_{1}&=\left(\begin{array}{ccccc} 0 & & & & \\ w_{11} & w_{21} & w_{31} & & \\ & \ddots & \ddots & \ddots & \\ & & w_{11} &w_{21} & w_{31}\\ & & & & 0 \\ \end{array} \right)_{M\times M} \end{aligned} $$

$$ \begin{aligned} V_{2}&=\left(\begin{array}{ccccc} 1 & & & & \\ w_{12} & w_{22} & w_{32} & & \\ & \ddots & \ddots & \ddots& \\ & & w_{12} &w_{22} & w_{32}\\ & & & & 1 \\ \end{array} \right)_{M\times M}\\ V_{3}&=\left(\begin{array}{ccccc} 0 & & & & \\ w_{13} & w_{23} & w_{33} & & \\ & \ddots & \ddots & \ddots & \\ & & w_{13} &w_{23} & w_{33}\\ & & & & 0 \\ \end{array} \right)_{M\times M}. \end{aligned} $$

(5)

Generally speaking, the linear filtering operator U is non-unitary that can not be performed directly. Actually, we can embed U in a bigger system with an ancillary system and decompose it into a linear combination of four unitary operators [26]. U=U₁+U₂+U₃+U₄, where $U_{1}=(U+U^{\dagger })/2 +i \sqrt {I-(U+U^{\dagger })^{2}/4}, U_{2}=(U+U^{\dagger })/2 -i \sqrt {I-(U+U^{\dagger })^{2}/4}, U_{3}=(U-U^{\dagger })/2i +i \sqrt {I+(U-U^{\dagger })^{2}/4}$and $U_{4}=(U-U^{\dagger })/2i -i \sqrt {I+(U-U^{\dagger })^{2}/4}$. However, the basic gates consumed to perform U_i scale exponentially in the dimensions of quantum systems, making the quantum advantage diminishing. In [25], the efficient decomposition or the gate complexity of U is an open question. However, the gate complexity is the fundamental standard for measuring algorithm efficiency. Therefore, we present a new approach to construct the filter operator to reduce the gate complexity. For convenience, we change the elements of the first row, the last row, the first column, and the last column in the matrix V₁,V₂, and V₃, which is allowable in imagining processing, to the following form

$$ \begin{aligned} V^{\prime}_{1}&=\left(\begin{array}{ccccc} w_{21} & w_{31} & & & w_{11} \\ w_{11} & w_{21} & w_{31} & & \\ & \ddots & \ddots & \ddots & \\ & & w_{11} &w_{21} & w_{31}\\ w_{31} & & & w_{11} & w_{21} \\ \end{array} \right)_{M\times M}\\ V^{\prime}_{2}&=\left(\begin{array}{ccccc} w_{22} & w_{32} & & & w_{12} \\ w_{12} & w_{22} & w_{32} & & \\ & \ddots & \ddots & \ddots& \\ & & w_{12} &w_{22} & w_{32}\\ w_{32} & & & w_{12} & w_{22} \\ \end{array} \right)_{M\times M}\\ V^{\prime}_{3}&=\left(\begin{array}{ccccc} w_{23} & w_{33} & & & w_{13} \\ w_{13} & w_{23} & w_{33} & & \\ & \ddots & \ddots & \ddots & \\ & & w_{13} &w_{23} & w_{33}\\ w_{33} & & & w_{13} & w_{23} \\ \end{array} \right)_{M\times M}. \end{aligned} $$

(6)

Defining the adjusted linear filtering operator U^′ as

$$ U^{\prime} = \left[\begin{array}{cccccc} V^{\prime}_{2} & V^{\prime}_{3} & & & & V^{\prime}_{1} \\ V^{\prime}_{1} & V^{\prime}_{2} & V^{\prime}_{3} & & & \\ & \ddots & \ddots & \ddots & &\\ & & \ddots & \ddots &\ddots &\\ & & & V^{\prime}_{1} & V^{\prime}_{2} & V^{\prime}_{3}\\ V^{\prime}_{3} & & & & V^{\prime}_{1} & V^{\prime}_{2} \\ \end{array}\right], $$

(7)

Next, we decompose $V^{\prime }_{\mu }(\mu =1,2,3)$ into three unitary matrices without normalization, $V^{\prime }_{\mu }=V^{\prime }_{1 \mu }+V^{\prime }_{2 \mu }+V^{\prime }_{3 \mu }$, where

$$ \begin{aligned} V^{\prime}_{1 \mu}&=\left(\begin{array}{ccccc} & & & & w_{1\mu} \\ w_{1\mu} & & & & \\ \ddots & \ddots & \ddots & &\\ & & w_{1\mu} & & \\ & & & w_{1\mu} & \\ \end{array}\right)_{M\times M}\\ V^{\prime}_{2 \mu}&=\left(\begin{array}{ccccc} w_{2\mu} & & & & \\ & w_{2\mu} & & & \\ & \ddots & \ddots &\ddots & \\ & & &w_{2\mu} & \\ & & & & w_{2\mu} \\ \end{array}\right)_{M\times M}\\ V^{\prime}_{3\mu}&=\left(\begin{array}{ccccc} & w_{3\mu} & & & \\ & & w_{3\mu} & & \\ & &\ddots \ddots & \ddots & \\ & & & & w_{3\mu}\\ w_{3\mu} & & & & \\ \end{array}\right)_{M\times M}. \end{aligned} $$

(8)

Thus, the linear filtering operator U^′ can be expressed as

$$\begin{array}{@{}rcl@{}} U^{\prime}=\sum_{\mu=1}^{3} \sum_{v=1}^{3}\left(V^{\prime}_{\mu\mu}/w_{\mu\mu}\right)\otimes V^{\prime}_{v\mu}. \end{array} $$

(9)

which can be simplified to

$$\begin{array}{@{}rcl@{}} U^{\prime}=\sum_{k=1}^{9}\beta_{k} Q_{k}, \end{array} $$

(10)

where $Q_{k}=\left (V^{\prime }_{\mu \mu }/w_{\mu \mu }\right)\otimes V^{\prime }_{v\mu }/w_{v\mu }$ is unitary, and β_k is a relabelling of the indices.

Now, we can perform U^′ through the linear combination of unitary operators Q_k. The number of unitary operators is equal to the size of filter mask. The quantum circuit to realize U^′ is shown in Fig. 2. The work register |f〉 and four ancillary qubits |0000〉_a are entangled together to form a bigger system.

Fig. 2

Quantum circuit for realizing the QCNN. |f〉 denotes the initial state of work system after encoded the image data, and the ancillary system is a four qubits system in the |0000〉_a state. The squares represent unitary operations and the circles represent the state of the controlling system. Unitary operations Q₁,Q₂,⋯,Q₉, are activated only when the auxiliary system is in state |0000〉,|0001〉⋯,|1000〉 respectively

Firstly, we prepare the initial state |f〉 using amplitude encoding method or quantum random access memory (qRAM). Then, performing unitary matrix S on the ancillary registers to transform |0000〉_a into a specific superposition state |ψ〉_a

$$\begin{array}{@{}rcl@{}} S|0000\rangle_{a}=|\psi\rangle_{a}= \sum_{v=1}^{9}\beta_{k}/N|k\rangle \end{array} $$

(11)

where $N_{c}=\sqrt {\sum _{k=1}^{9}\beta _{k}^{2}}$ and S satisfies

$$ S_{k,1} = \left\{\begin{array}{ll} \beta_{k}/N_{c} &\text{if}\ k\leq 9\\ 0 & \text{if}\ k > 9. \end{array}\right. $$

(12)

S is a parameter matrix corresponding to a specific filter mask that realizes a specific task.

Then, we implement a series of ancillary system controlled operations Q_k⊗|k〉〈k| on the work system |f〉 to realize LCU. Nextly, Hadamard gates H^T=H^⊗4 are acted to uncompute the ancillary registers |ψ〉_a. The state is transformed to

$$\begin{array}{@{}rcl@{}} | g^{\prime} \rangle= \sum_{i=1}^{16}\frac{1}{N_{c}}|i\rangle \sum_{k=1}^{9} H^{T}_{(ik)}S_{(k1)} Q_{k}| f \rangle, \end{array} $$

(13)

where $H^{T}_{(ik)}$ is the ith row and kth column in matrix H^T and S_(k1) is kth row and the first column in matrix S. The first term equals to

$$\begin{array}{@{}rcl@{}} \frac{1}{N_{c}}|0\rangle \sum_{k=1}^{9} \beta_{k} Q_{k}| f \rangle, \end{array} $$

(14)

which corresponds to the filter mask W. The ith term equals to filter mask $W^{i}(i=2,3,\dots,16)$, where

$$ W^{i}= \left[\begin{array}{ccc} H^{T}_{i1}w_{11} & H^{T}_{i4}w_{12} & H^{T}_{i7}w_{13}\\ H^{T}_{i2}w_{21} & H^{T}_{i5}w_{22} & H^{T}_{i8}w_{23}\\ H^{T}_{i3}w_{31} & H^{T}_{i6}w_{32} & H^{T}_{i9}w_{33}\\ \end{array}\right]. $$

(15)

Totally, 16 filter masks are realized, corresponding to ancilla qubits in 16 different state $| i \rangle (i=1,2,\dots,16)$. Therefore, the whole effect of evolution on state |f〉 without considering the ancilla qubits, is the linear combination of the effects of 16 filter masks.

If we only need one filter mask W, measuring the ancillary register and conditioned on seeing |0000〉. We have the state $\frac {1}{N_{c}}|0000\rangle U^{\prime }| f \rangle$, which is proportional to our expected result state |g〉. The probability of detecting the ancillary state |0000〉 is $P_{s}= \parallel \sum _{k=1}^{9}\beta _{k} Q_{k} | f \rangle \parallel ^{2}/{N_{c}^{2}}$.

After obtaining the final result $\frac {1}{N_{c}}U^{\prime }|f\rangle$, we can multiply the constant factor N_c to compute |g^′〉=U^′|f〉. In conclusion, the filter operator U^′ can be decomposed into a linear combination of nine unitary operators in the case that the general filter mask is W. Only four qubits or a nine energy level ancillary system is consumed to realize the general filter operator U^′, which is independent on the dimensions of image size.

The final stage of our method is to extract useful information from the processed results |g^′〉. Clearly, the image state |g〉 is different from |g^′〉. However, not all elements in |f〉 are evaluated, the elements corresponding to the four edges of original image remain unchanged. One is only interested in the pixel values which are evaluated by W in |f〉. These pixel values in |g^′〉 are as same as that in |g〉 (see details in Appendix C). So, we can obtain the information of G=(G_i,j)_M×M (2≤i,j≤M−1) by evaluating the |f〉 under operator U^′ instead of U.

2.1.2 Quantum pooling layer

The function of pooling layer after the convolutional layer is to reduce the spatial size of the representation so as to reduce the amount of parameters. We adopt average pooling which calculates the average value for each patch on the feature map as pooling layers in our model. Consider a 2∗2 pixel pooling operation applied with a stride of 2 pixels. It can be directly realized by ignoring the last qubit and the mth qubit in quantum context. The input image $| g^{\prime } \rangle =(g_{1},g_{2},g_{3},g_{4},\dots,\dots,g_{M^{2}})^{T}$ after this operation can be expressed as the output image

$$ \begin{aligned} | p \rangle=& \left(\sqrt{g_{1}^{2}+g_{2}^{2}+g_{M+1}^{2}+g_{M+2}^{2}},\sqrt{g_{3}^{2}+g_{4}^{2}+g_{M+3}^{2}+g_{M+4}^{2}},\dots,\right.\\ &\left.\sqrt{g_{M^{2}-M-1}^{2}+g_{M^{2}-M}^{2}+g_{M^{2}-1}^{2}+g_{M}^{2}}{\vphantom{\sqrt{g_{1}^{2}+g_{2}^{2}+g_{M+1}^{2}+g_{M+2}^{2}}}}\right)^{T}. \end{aligned} $$

(16)

2.1.3 Quantum fully connected layer

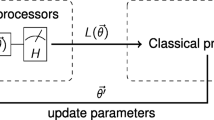
Fully connected layers compile the data extracted by previous layers to form the final output; it usually appears at the end of the convolutional neural networks. We define a parametrized Hamiltonian up to a seconder order correlation as the quantum fully connected layer. This Hamiltonian consists of identity operators I and Pauli operators σ_z,

$$\begin{array}{*{20}l} \mathcal{H}=h^{0}I+\sum_{i}h^{i}\sigma_{z}^{i}+\sum_{i,j}h^{ij}\sigma_{z}^{i}\sigma_{z}^{j} \end{array} $$

(17)

where h⁰,hⁱ,h^ij are the parameters, and Roman indices i,j denote the qubit on which the operator acts, i.e., $\sigma ^{i}_{z}$ means Pauli matrix σ_z acting on a qubit at site i. We measure the expectation value of the parametrized Hamiltonian $f(p)=\langle {p}| \mathcal {H} | p \rangle$. As shown in [27], the local cost function f(p) is more trainable than global cost function. f(p) is the final output of the whole quantum neural network. Then, we add an active function to nonlinearly map f(p) to R(f(p)).

The parameters in Hamiltonian matrix $\mathcal {H}$ are updated by gradient descent method, i.e., are calculated by $\frac {\partial f(p)}{\partial h^{i}} =\left \langle {p}| \sigma _{z}^{i} | p \right \rangle$ and $\frac {\partial f(p)}{\partial h^{ij}} =\left \langle {p}| \sigma _{z}^{i}\sigma _{z}^{j} | p \right \rangle$. We rewrite the cost function as

$$ \begin{aligned} f(p)&=Tr\left(\!\frac{1}{N_{c}^{2}}\!\sum_{i=1}^{16}|i\rangle\!\sum_{k=1}^{9} \!H^{T}_{(ik)}S_{(k1)} Q_{k}| f \rangle\langle {f}|\sum_{i'=1}^{16}\langle i'|\sum_{k^{\prime}=1}^{9} \!H^{T}_{(i'k^{\prime})}S_{(k^{\prime}1)} Q_{k^{\prime}}^{\dagger}\!\mathcal{H}\!\right)\\ &=Tr\left(\frac{1}{N_{c}^{2}}\sum_{i=1}^{16}\sum_{k=1}^{9} H^{T}_{(ik)}S_{(k1)} Q_{k}\rho_{i} \sum_{k^{\prime}=1}^{9} H^{T}_{(ik^{\prime})}S_{(k^{\prime}1)} Q_{k^{\prime}}^{\dagger}\mathcal{H}\right), \end{aligned} $$

(18)

here ρ_i=|f〉|i〉〈i|〈f|. From Eq.(18), the cost function partial derivative with respect to w_k is

$$\begin{aligned} \frac{\partial f(p)}{\partial w_{k}} =\frac{1}{N_{c}^{2}}Tr\left(\sum_{i=1}^{16}\sum_{k^{\prime}=1}^{9} H^{T}_{(ik)}H^{T}_{(ik^{\prime})}S_{(k^{\prime}1)} \left(Q_{k^{\prime}}^{\dagger} \mathcal{H}Q_{k}+Q_{k}^{\dagger} \mathcal{H}Q_{k^{\prime}}\right)\rho_{i}\right). \end{aligned} $$

Therefore, the parameters can be updated by measuring the expectation values of specific operators.

Now, we have constructed the framework of quantum neural networks. We demonstrate the performance of our method in image processing and handwritten number recognition in the next section.

2.2 Numerical simulations

2.2.1 Image processing: edge detection, image smoothing, and sharpening

In addition to constructing QCNN, the quantum convolutional layer can also be used to spatial filtering which is a technique for image processing [25, 28–30], such as image smoothing, sharpening, edge detection, and edge enhancement. To show the quantum convolutional layer can handle various image processing tasks, we demonstrate three types of image processing, edge detection, image smoothing, and sharpening with fixed filter mask W_de,W_sm and W_sh respectively

$$ \begin{aligned} W_{{de}}&=\left(\begin{array}{ccc} -1 & -1 & -1\\ -1 & 8 & -1\\ -1 & -1 & -1\\ \end{array}\right), W_{{sm}}=\frac{1}{13}\left(\begin{array}{ccc} 1 & 1 & 1\\ 1 & 5 & 1\\ 1 & 1 & 1\\ \end{array}\right),\\ W_{{sh}}&=\frac{1}{16}\left(\begin{array}{ccc} -2 & -2 & -2\\ -2 & 32 & -2\\ -2 & -2 & -2\\ \end{array}\right). \end{aligned} $$

(19)

In a spatial image processing task, we only need one specific filter mask. Therefore, after performing the above quantum convolutional layer mentioned, we measure the ancillary register. If we obtain |0〉, our algorithm succeeds and the spatial filtering task is completed. The numerical simulation proves that the output images transformed by a classical and quantum convolutional layer are exactly the same, as shown in Fig. 3.

Fig. 3

Three types of image processing, edge detection, image smoothing, and sharpening, are implemented on an image by classical method and quantum method respectively

2.2.2 Handwritten number recognition

Here, we demonstrate a type of image recognition task on a real-world dataset, called MNIST, a handwritten character dataset. In this case, we simulate a complete quantum convolutional neural network model, including a convolutional layer, a pooling layer, and a full-connected layer, as shown in Fig. 2. We consider the two-class image recognition task(recognizing handwritten characters ^′1^′ and ^′8^′) and ten-class image recognition task(recognizing handwritten characters ^′0^′- ^′9^′). Meanwhile, considering the noise on NISQ quantum system, we respectively simulate two circumstances that are the quantum gate Q_k is a perfect gate or a gate with certain noise. The noise is simulated by randomly acting a single qubit Pauli gate in [I,X,Y,Z] with a probability of 0.01 on the quantum circuit after an operation implemented. In detail, the handwritten character image of MNIST has 28×28 pixels. For convenience, we expand 0 at the edge of the initial image until 32×32 pixels. Thus, the work register of QCNN consists of 10 qubits, and the ancillary register needs 4 qubits. The convolutional layer is characterized by 9 learnable parameters in matrix W that is the same for QCNN and CNN. In QCNN, by abandoning the 4-th and 9-th qubit of the work register, we perform the pooling layer on quantum circuit. In CNN, we perform average pooling layer directly. Through measuring the expected values of different Hamiltonians on the remaining work qubits, we can obtain the measurement values. After putting them in an activation function, we get the final classification result. In CNN, we perform a two-layer fully connected neural network and an activation function. In the two-classification problem, the QCNN’s parametrized Hamiltonian has 37 learnable parameters, and the CNN’s fully-connected layer has 256 learnable parameters. The classification result that is close to 0 are classified as handwritten character ^′1^′, and the result that is close to 1 are classified as handwritten character ^′8^′. In the ten-classification problem, the parametrized Hamiltonian has 10×37 learnable parameters and the CNN’s fully-connected layer has 10×256 learnable parameters. The result is a 10-dimension vector. The classification results are classified as the index of the max element of the vector. Details of parameters, accuracy, and gate complexity are listed in Table 1.

Table 1 The important parameters of models

For the 2 class classification problem, the training set and test set have a total of 5000 images and 2100 images, respectively. For the 10 class classification problem, the training set and test set have a total of 60000 images and 10000 images, respectively. Because in a training process, 100 images are randomly chosen in one epoch, and 50 epochs in total, the accuracy of the training set and the test set will fluctuate. So, we repeatedly execute noisy QCNN, noise-free, and CNN 100 times, under the same construction. In this way, we obtain the average accuracy and the field of accuracy, as shown in Fig. 4. We can conclude that from the numerical simulation result, QCNN and CNN provide similar performance. QCNN involves fewer parameters and has a smaller fluctuation range.

Fig. 4

The performance of QCNN based on MNIST. The blue, red, and green curves denote the average accuracy of the noisy QCNN, noise-free QCNN, and CNN, respectively. The shadow areas of the corresponding color denote the accuracy fluctuation range in the 100 times simulation results. The insets are the typical images from MNIST set. a, b The curves representing the result from the training set and the test set for the 2 class classification problem respectively. c, d The result from the training set and the test set for the 10 class classification problem respectively

3 Algorithm complexity and trainability analysis

We analyze the computing resources in gate complexity and qubit consumption. (1) Gate complexity. At the convolutional layer stage, we could prepare an initial state in O(poly(log₂(M²)) steps. In the case of preparing a particular input |f〉, we employ the amplitude encoding method in [31–33]. It was shown that if the amplitude c_k and $P_{k}=\sum _{k} |c_{k}|^{2}$ can be efficiently calculated by a classical algorithm, constructing the log₂(M²)-qubit X state takes O(poly(log₂(M²)) steps. Alternatively, we can resort to quantum random access memory [34–36]. Quantum random access memory (qRAM) is an efficient method to do state preparation, whose complexity is O(log₂(M²)) after the quantum memory cell established. Moreover, the controlled operations Q_k can be decomposed into O((log₂M)⁶) basic gates (see details in Appendix A). In summary, our algorithm uses O((log₂M)⁶) basic steps to realize the filter progress in the convolutional layer. For CNN, the complexity of implementing a classical convolutional layer is O(M²). Thus, this algorithm achieves an exponential speedup over classical algorithms in gate complexity. The measurement complexity in fully connected layers is O(e), where e is the number of parameters in the Hamiltonian.

(2) Memory consumption. The ancillary qubits in the whole algorithm are O(log₂(m²)), where m is the dimension of the filter mask, and the work qubits are O(log₂(M²)). Thus, the total qubits resource needed is O(log₂(m²)+O(log₂(M²).

According to [27, 37–39], we can analyze the trainability of the parameters in our QCNN model by studying the scaling of the variance

$$ Var\left[\frac{\partial f(p)}{\partial w}\right]=\left\langle \left(\frac{\partial f(p)}{\partial w}\right)_{S}^{2}\right\rangle-\left\langle\frac{\partial f(p)}{\partial w}\right\rangle_{S}^{2}, $$

(20)

where the expectation value 〈⋯ 〉 is taken over the parameters in S [39, 40]. The cost will exhibit a barren plateau in the case the variance is exponentially small, and hence leads to the circuit untrainable. In contrast, large variances (polynomial small) indicate the absence of barren plateaus and that the trainability of the parameters can be guaranteed.

The variance in our model is (see details in Appendix C)

$$\begin{array}{@{}rcl@{}} Var\left[\frac{\partial f(p)}{\partial w}\right]&=&\left\langle \left(\frac{\partial f(p)}{\partial w}\right)_{S}^{2}\right\rangle-\left\langle\frac{\partial f(p)}{\partial w}\right\rangle_{S}^{2}\\ &=&\frac{1}{N_{c}^{4}}\!\left(\frac{1}{17}\left(2\alpha_{0}^{2}+\!\sum_{i}\alpha_{i}^{2}+\!\sum_{{ij}}\alpha_{{ij}}^{2}\right)\!-\alpha_{0}^{2}\right) \end{array} $$

(21)

If $\frac {\left (2\alpha _{0}^{2}+\sum _{i}\alpha _{i}^{2}+\sum _{{ij}}\alpha _{{ij}}^{2}\right)-\alpha _{0}^{2}}{N_{c}^{4}} \in O(poly(log(n))$, then Var$\left [\frac {\partial f(p)}{\partial w}\right ] \propto O(1/poly(log(n)).$ This assumption is reasonable and easy to be satisfied, because parameters $N_{c}^{4}$ in a convolutional kernel which is usually a 3×3 or 5×5 matrix are independent on input image size. This implies that the cost function landscape does not present a barren plateau,and hence that this QCNN architecture is trainable under a convolutional kernel.

4 Discussion

In summary, we designed a quantum neural network which provides exponential speed-ups over their classical counterparts in gate complexity. With fewer parameters, our model achieves similar performance compared with classical algorithm in handwritten number recognition tasks. Therefore, this algorithm has significant advantages over the classical algorithms for large data. We present two interesting and practical applications, image processing and handwritten number recognition, to demonstrate the validity of our method. The mapping relations between a specific classical convolutional kernel to a quantum circuit is given that provides a bridge between QCNN to CNN. We analyze the trainability and the existence of barren plateaus in our QCNN model. It is a general algorithm and can be implemented on any programmable quantum computer, such as superconducting, trapped ions, and photonic quantum computer. In the big data era, this algorithm has great potential to outperform its classical counterpart, and works as an efficient solution.

5 Appendix A: Adjusted operator U ^′ can provide enough information to remap the output imagine

Proof.- The different elements of image matrix after implementing operator U^′ compared with U are in the edges of image matrix. We prove that the evolution under operator U^′ can provide enough information to remap the output image. The different elements between U^′ and U are included in

$$ \begin{aligned} U^{\prime}_{k,n}\! \neq\ \! U_{k,n} \! \left\{\begin{array}{l} (1\leq k \leq M; 1\leq n \leq 2M, M^{2}-M\leq n \leq M^{2})\\ (M^{2}-\! M\! \leq k \! \leq M^{2}; 1\! \leq n \! \leq M,M^{2}\! -\! 3M\! \leq n \! \leq M^{2}\! -\! M)\\ (k=sM+1; n=1+(s-1)M,2+(s-1)M,sM,sM\\+1,sM+2,(s+1)M,(s+1)M+1,(s+1)M+2,(s+2)M)\\ (k=(s+1)M;n=\!1,sM-1,sM,sM+1,(s+1)M\!-2,\\(s+1)M-1,(s+\!1)M+1,(s+2)M-2,(s+2)M\!-1) \end{array}\right. \end{aligned} $$

(22)

where 1≤s≤M−2.

After performing U^′ and U on quantum state |f〉 respectively, the difference exits in the elements $| g^{\prime }_{k} \rangle \neq | g_{k} \rangle (k=1,2,\cdots,M,sM+1,(s+1)M,M^{2}-M+1,\cdots,M^{2})$, where 1≤s≤M−2. Since |g^′〉 can be remapped to G^′,U^′ will give the output image $G^{\prime }=(G^{\prime }_{i,j})_{M \times M}$. The elements in U^′ which is different from U only affect the pixel i,j∉2,⋯,M−1. Thus, only and if only i,j∉2,⋯,M−1, the matrix elements satisfy $G_{i,j} \neq G^{\prime }_{i,j}$. Namely, the output imagine $G^{\prime }_{i,j}=G_{i,j}$(2≤i,j≤M−1).

6 Appendix B: Decomposing operator Q into basic gates

Considering the nine operators Q₁,Q₂,⋯,Q₉ consist of filter operator U^′. Q_k is the tensor product of two of the following three operators

$$ \begin{aligned} E_{1 }&=\left(\begin{array}{cccccc} & & & & 1 \\ 1 & & & & \\ \ddots & \ddots & \ddots & &\\ & & 1 & & \\ & & & 1 & \\ \end{array}\right)_{M\times M} E_{2 }&=\left(\begin{array}{cccccc} 1 & & & & \\ & 1 & & & \\ & \ddots & \ddots &\ddots & \\ & & &1 & \\ & & & & 1 \\ \end{array}\right)_{M\times M}\\ E_{3}&=\left(\begin{array}{cccccc} & 1 & & & \\ & & 1 & & \\ & &\ddots \ddots & \ddots & \\ & & & & 1\\ 1 & & & & \\ \end{array}\right)_{M\times M}. \end{aligned} $$

(23)

E₂ is a M×M identity matrix not need to be further decomposed. For convenient, consider a n-qubits operator E₁ with dimension M×M, where n=log₂(M²). It can be expressed by the combination of O(n³) CNOT gates and Pauli X gates as shown in Fig. 5. Consequently, E₃ can be decomposed into the inverse of combinations of basic gate as shown in Fig. 5, because of the fact $E_{3}=E_{1}^{\dagger }$. Thus, Q_k can be implemented by no more than O(n⁶) basic gates. Totally, the controlled Q_k operation can be implemented by no more than O(n⁶)=O((log₂M)⁶)(ignoring constant number).

Fig. 5

Decomposition of operator E₁ in the form of basic gates

7 Appendix C: Trainable analysis of the QCNN model

Firstly, we recall the definition of a t-design. Consider a finite set S={S_y}_y∈Y contains |Y| number d-dimensional unitaries S_y. And P_t,t(S) is a polynomial function with degree at most t in the matrix elements of S and at most of degree t in those of S^†. Then, we say that this finite set is a t-design if

$$ \frac{1}{|Y|}\sum_{y\in Y} P_{t,t}(S_{y})=\int d\mu(S) P_{t,t}(S), $$

(24)

where the integral is over U(d) with respect to the Haar distribution. In our QCNN model, S forms a 2-design and for any function F(S), and for any unitary matrix A

$$\begin{array}{*{20}l} \int F(AS)d\mu(S)=&\int F(S) d\mu(S). \end{array} $$

(25)

The average of the partial derivative of the cost function is

$$\begin{aligned} \left\langle\!\frac{\partial f(p)}{\partial w_{k}}\!\right\rangle_{S}=\frac{1}{N_{c}^{2}}Tr\!\left(\sum_{k^{\prime}=1}^{9} \!H^{T}_{(ik)}H^{T}_{(ik^{\prime})}S_{(k^{\prime}1)}\! \left(Q_{k^{\prime}}^{\dagger} \mathcal{H}Q_{k}+Q_{k}^{\dagger} \mathcal{H}Q_{k^{\prime}}\right)\!\right)\!Tr(| f \rangle\langle {f}|) \end{aligned} $$

and Tr(|f〉〈f|)=1. Consider the fact that $\mathcal {H}$ maintains the property that being constructed by Pauli product matrices under the transformation of Q_k,i.e., $\phantom {\dot {i}\!}\sum _{k^{\prime }=1}^{9} H^{T}_{(ik)}H^{T}_{(ik^{\prime })}S_{(k^{\prime }1)} (Q_{k^{\prime }}^{\dagger } \mathcal {H}Q_{k}+Q_{k}^{\dagger } \mathcal {H}Q_{k})=\mathcal {H}^{new}$, where $\mathcal {H}^{new}=\alpha _{0}I+\sum _{i}\alpha _{i}\sigma _{z}^{i}+\sum _{i,j}(\alpha _{{ij}})\sigma _{z}^{i}\sigma _{z}^{j}$. Then, we have $Tr(\mathcal {H}^{new})=\alpha _{0}$, and

$$\left\langle\frac{\partial f(p)}{\partial w_{k}}\right\rangle=\frac{\alpha_{0}}{N_{c}^{4}}. $$

The expectation value of the squares of gradients is

$$ \begin{aligned} \left\langle \left(\frac{\partial f(p)}{\partial w}\right)^{2}\right\rangle_{S} =&\int d\mu(S)\frac{1}{N_{c}^{4}}Tr\left(\sum_{i=1}^{16}\sum_{k^{\prime}=1}^{9} H^{T}_{(ik)}H^{T}_{(ik^{\prime})}S_{(k^{\prime}1)} \left({\vphantom{\sum_{k^{\prime}=1}^{9}}}Q_{k^{\prime}}^{\dagger} \mathcal{H}Q_{k}\right.\right.\\&\left.\left.+Q_{k}^{\dagger} \mathcal{H}Q_{k^{\prime}}{\vphantom{\sum_{k^{\prime}=1}^{9}}}\right)\rho_{i}\right)^{2}\\ =&\frac{1}{N_{c}^{4}}\frac{1}{16^{2}-1}\left(Tr(\mathcal{H}^{new})Tr(| f \rangle\langle {f}|)Tr(\mathcal{H}^{new})Tr(| f \rangle\langle {f}|) \right.\\&\left.+Tr((\mathcal{H}^{new})^{2})Tr(| f \rangle\langle {f}|)\right)\\ &- \frac{1}{N_{c}^{4}}\frac{1}{16(16^{2}-1)}\left(Tr((\mathcal{H}^{new})^{2})Tr(| f \rangle\langle {f}|)Tr(| f \rangle\langle {f}|) \right.\\&\left.+ Tr(\mathcal{H}^{new})Tr(\mathcal{H}^{new})Tr(| f \rangle\langle {f}|)\right)\\ =&\frac{1}{N_{c}^{4}}\left(\frac{1}{16^{2}-1}(\alpha_{0}^{2}+Tr((\mathcal{H}^{new})^{2}))-\frac{1}{16(16^{2}-1)}\right.\\&\left.(\alpha_{0}^{2}+Tr((\mathcal{H}^{new})^{2})){\vphantom{\frac{1}{16^{2}-1}}}\right)\\ =&\frac{1}{N_{c}^{4}}\left(\frac{1}{17}(2\alpha_{0}^{2}+\sum_{i}\alpha_{i}^{2}+\sum_{{ij}}\alpha_{{ij}}^{2})\right) \end{aligned} $$

Therefore, the variance is

$$\begin{array}{@{}rcl@{}} Var[\frac{\partial f(p)}{\partial w}]&=&\left\langle \left(\frac{\partial f(p)}{\partial w}\right)_{S}^{2}\right\rangle-\left\langle\frac{\partial f(p)}{\partial w}\right\rangle_{S}^{2}\\ &=&\frac{1}{N_{c}^{4}}\left(\frac{1}{17}(2\alpha_{0}^{2}+\sum_{i}\alpha_{i}^{2}+\sum_{{ij}}\alpha_{{ij}}^{2})-\alpha_{0}^{2}\right) \end{array} $$

(26)