1 Introduction

Nuclei are bound states of protons and neutrons via the strong interaction. The fundamental theory of the strong interaction is quantum chromodynamics (QCD). In QCD, gluons are massless due to gauge symmetry; up (u) quarks are as light as mu=3−4 MeV and down (d) quarks are heavier than u-quarks, i.e., mu/md∼0.5 (see Ref. [1] for a recent review of quark masses from the lattice-QCD). The strange (s) quark mass is comparable to the typical QCD energy scale, that is, ms=80−90 MeV of the same order as ΛQCD=100−200 MeV. Since charm (c) and bottom (b) quarks are much heavier than ΛQCD, they would make only small contributions to bulk thermodynamics and they serve as external probes. Here, we focus on two puzzling QCD features for the nucleons which are composed of Nc valence quarks (where Nc=3 is the number of colors in QCD) and have a mass, mN≃940 MeV∼NcΛQCD. The first question is how can almost massless particles form a bound state with a positive binding energy? The second question is how can the nucleons become so extremely massive out of almost massless particles? The former question on the existence of bound states is referred to as confinement and the latter on the origin of the mass is via spontaneous chiral symmetry breaking.

The key to resolve these puzzles lies in QCD vacuum structure. The vacuum in quantum field theory is not empty in general but is full of quantum fluctuations dictated by fundamental interactions. Thus, the QCD vacuum is regarded as a “medium” in analogy to condensed matter physics. Just like spin systems for example, the QCD vacuum structure may be either an ordered/disordered state according to external environments such as the temperature T, the baryon density ρB (or the baryon chemical potential μB), the magnetic field B, and the vorticity ω, etc. The idea of using the relativistic nucleus-nucleus collisions or heavy-ion collisions is to shake the QCD vacuum with high energy density to observe new states of matter out of quarks and gluons and to seek for traces of phase transitions associated with confinement and/or chiral symmetry breaking (see Ref. [2] for historical backgrounds).

The saturation density around the center of heavy nuclei is ρ0≃0.16 nucleons/fm3 corresponding to the energy density ε0≃0.15 GeV/fm3. At the initial stage of the heavy-ion collisions, the energy density can reach hundreds times larger than the saturation density depending on the collision energy per nucleon, \(\sqrt {s_{NN}}\). The thermodynamic relation between the energy density ε and the temperature T (i.e., the Stefan-Boltzmann law) converts ε=0.8−1.0 GeV/fm3 to T=150−160 MeV which is comparable to LQCD, above which a quark-gluon plasma (QGP) is realized. In the history of the Universe such high-T matter should have existed shortly (on the order of μs) after the Big Bang. In this sense, the QGP physics can be regarded as an emulation of the Big Bang in the laboratory on the Earth, which may well be called the Little Bang.

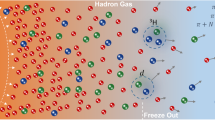
Now that we have learnt intriguing properties of the QGP in the regime at high T and low μB, a next direction of the relativistic heavy-ion collision physics is expanding toward the regime at high baryon density. The phase structures could have much richer contents in these high-density regions, see Refs. [3–5] for reviews on the QCD phase diagrams. We have already known that symmetric nuclear matter has a first-order phase transition at μB≈923 MeV, that is, the nucleon mass minus the binding energy ∼16 MeV. Then, a terminal point of the first-order phase boundary, namely, a critical point of liquid-gas phase transition in nuclear matter exists around T=(10−20) MeV (see Ref. [6] for a comprehensive review including experimental signatures). The question is what new state of matter is anticipated for nuclear matter at higher baryon density. The central core of a neutron star could exhibit the most baryon-rich and equilibrated state of matter in the Universe, where the density could be as large as ∼5ρ0 or even higher. The baryon density may become even larger in transient processes such as neutron star mergers. Analogously, by adjusting the collision energy in the heavy-ion collisions, the baryon density could transiently increase up to several times of ρ0 according to numerical simulations [7]. Such a femtometer-scale explosion of baryon rich matter can be called the femto-nova. This concept is illustrated in Fig. 1.

Fig. 1
figure 1

Schematic illustration of a femto-nova as a femtometer-scale explosion of baryon-rich matter in relativistic heavy-ion collisions

Full size image

Historically, studies with heavy-ion collisions started from low energy and we had to wait for high-energy colliders, the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC), to arrive at a definitive conclusion on the QGP formation. As for the low-energy regions, unfortunately, only little is known in theory about the phase structures in low-T and high- μB (or high- ρB) regions. There are some speculations on the ground state structures in such regimes which will be partially reviewed in this article. The most important landmark is the QCD critical point. In the same way as the critical point of the nuclear liquid-gas phase transition, deconfined QCD matter may have a first-order phase boundary and the QCD critical point appears at the terminal point of the first-order line. Its exact location is not well constrained yet, and the experimental efforts to discover the QCD critical point are still continuing.

This article is organized as follows. We will first describe the phase diagram, the QCD critical point, and properties of baryon-rich matter including strangeness degrees of freedom. We will then proceed to the current status of experimental data on these topics. After this, we will return to theory to cover speculations and challenges to be clarified in the future. Finally, we discuss the future directions of ongoing experimental projects as well as future experimental facilities.

2 Current status—theory

2.1 Theoretical background for the QCD phase diagram

It has been established that hadronic matter continuously changes into the QGP with increasing temperature T as long as μB is sufficiently smaller than T. Although this continuous change of matter takes place around T=(156.5±1.5) MeV according to the lattice-QCD simulations [8], there is no strict phase transition. In the QCD community this transitional but still continuous change of matter is commonly referred to as a crossover.

If masses of u and d quarks are zero and other quarks are massive, such 2-flavor QCD, matter would go through a second-order phase transition for which various derivatives of thermodynamic quantities diverge with critical exponents belonging to the O(4) universality class (or a first-order transition if the axial anomaly is restored, see Ref. [9]). Physical values of mu and md are much smaller than ΛQCD, and it is conceivable to observe some remnants of the second-order phase transition. Indeed, in the lattice-QCD simulation [10], it has been numerically confirmed that the magnetic scaling follows consistently with the O(4) universality class, from which the “pseudo-critical” temperature, Tpc, can be deduced.

The pseudo-critical temperature should be a function of the density. Generally, Tpc(μB) is a decreasing function with increasing μB due to the Pauli blocking of quarks in phase space. Because of the notorious sign problem in the Monte-Carlo algorithm, expectation values of observables cannot be computed and the first-principles lattice-QCD simulation cannot access a region with a substantial value of baryon density, and so there is no reliable theoretical prediction for Tpc(μB) at μB much larger than T.

Instead, a phenomenologically determined boundary on the μB-T plane is known, called the line of the chemical freeze-out, which has been identified from a hybrid approach of theory and experiment. The chemical freeze-out literally means that inelastic reactions stop and chemical compositions are fixed there. In QCD matter hadrons interact and particle species can change like chemical reactions. In heavy-ion collision the physical system is expanding and the temperature rapidly drops down. Therefore, the average inter-particle distance would increase as the temperature gets lowered. In particular, around Tpc, the entropy density significantly falls down, and correspondingly the degrees of freedom in thermal excitations decrease [11]. Since the average inter-particle distance becomes large, the interaction among hadrons is considered to be diminished. In this way, the observed particle yields keep the footprint of the hot and dense hadronic matter when the interaction was turned off at a temperature Tch, that is presumably close to the temperature when the matter underwent a crossover at Tpc. As observed experimentally, relative abundances of hadrons obey the thermal distribution at common T and μB, so that the thermal fit can fix T and μB, or a line of chemical freeze-out, T=Tch(μB) [12]. We note that the charge chemical potential μQ is fixed from the proton/neutron ratio and the strangeness chemical potential μS is fixed from the strangeness free condition. With various center-of-mass colliding energies, we can change accessible μB to sample Tch(μB) from the thermal fit [13, 14], see Fig. 2. Generally speaking, collisions at smaller \(\sqrt {s_{NN}}\) have larger baryon stopping, leading to larger values of μB (and smaller values of T) [15]. Thus, the line of chemical freeze-out on the μB-T plane should be regarded as an experimentally determined QCD phase diagram under the assumption that Tch stays close to Tpc, which has been verified by the lattice-QCD simulations for μB≲0.3 GeV [8], as also displayed in Fig. 2. This underlies the idea of the beam energy scan (BES) program at RHIC. The thermal description is applicable for not only particle abundances but also thermodynamic quantities such as pressure and entropy density.

Fig. 2
figure 2

Chemical freeze-out temperature Tch(μB) from the top 5% central Au+Au collisions at RHIC. Open-circles represent the parameters extracted from hadron yields [13], while the filled-squares are extracted from net-proton higher moments (up to third order) [14]. Representing the smooth crossover region is the lattice-QCD results shown by the green band. The empirical thermal fit results to global hadron yield data are shown as yellow line [15]. The coverage of the RHIC BES program, the STAR fixed target program (FXT), and future (FAIR, JPARC-HI, and NICA) experimental facilities are also indicated at the top of the figure. The liquid-gas transition region that features a second order critical point is shown by the red-circle, and a first-order transition line is shown by the black dashed line, which connects the critical point to the ground state of nuclear matter

Full size image

We note that the thermal models often assume the grand canonical ensemble (GCE) that is equivalent to the canonical ensemble (CE) in the thermodynamic (infinite volume) limit but is not so when the system size becomes small in the heavy-ion collision. We will discuss which of the GCE and the CE better fits the experimental data later.

2.2 Observables for the QCD critical point

It is known from the theoretical analysis that the QCD crossover has a general tendency to become closer to a first-order transition at larger μB (see discussions in a review [16]). It is thus a natural anticipation that the QCD crossover may turn to a first order phase transition in a high-density regime. If this is the case, as suggested by some effective model studies, there must be a “critical” value of μB above which a first-order phase transition occurs and below which only a crossover is found. This separating point is the QCD critical point and critical fluctuations associated with the second-order phase transition should be expected at this point. Its exact location is still under dispute, and the lattice-QCD results [17] disfavors the existence of the QCD critical point for μB/T≲2.

Interestingly, the QCD critical point emerges with nonzero physical quark masses, so that it belongs to not the O(4) but the Z(2) universality class. Moreover, the dynamical universality class has been also identified as the model H (dynamics of the liquid-gas critical point of a fluid) [18] (see a review [19] for detailed classification). The dynamical critical exponents are important inputs for simulations including the critical slowing down effects [20].

For experimental signatures, we can in principle seek for enhanced fluctuations coupled to the critical modes. Since the critical modes appear in a mixed scalar (i.e., chiral condensate) and vector (i.e., baryon density) channel at the QCD critical point [21], the baryon number fluctuations are sensitive to the criticality. Let us denote the baryon number fluctuation by δN=N−〈N〉 where N is the number of net baryons at each collision event and 〈⋯ 〉 stands for the ensemble average taken over collision events. At the critical point, generally, the correlation length ξ diverges, and it was pointed out in Ref. [22] that the non-Gaussian fluctuations behave as

$$ \langle (\delta N)^{k} \rangle_{c} \;\sim\; \xi^{k(5-\eta)/2 - 3} \,. $$
(1)

Here, the subscript c represents a part of the correlation function corresponding to the connected diagrams (to extract non-Gaussian fluctuations) and η is the anomalous dimension (which is usually η≪1). Higher-order fluctuations are more sensitive to the criticality, but they need more statistics, in particular, to construct connected contributions. Now, the third order (k=3) and the fourth order (k=4), normalized by the k=2 fluctuation (variance), \(\sigma _{B}^{2}=\langle (\delta N)^{2}\rangle \), in Eq. (1) are common measures for the QCD critical point search; namely,

$$ S_{B} = \frac{\langle (\delta N)^{3}\rangle}{\sigma_{B}^{3}},\qquad \kappa_{B} = \frac{\langle (\delta N)^{4} \rangle_{c}}{\sigma^{4}} = \frac{\langle (\delta N)^{4}\rangle}{\sigma_{B}^{4}} - 3\,. $$
(2)

SB and κB are called the skewness and the kurtosis with respect to the baryon number, and characterize how skewed and how sharp the distribution of δN appears, respectively. It is noted that, in the QCD-physics context, κB (or the fourth-order cumulant) was first considered in the lattice-QCD simulation to diagnose whether quarks are confined or deconfined [23].

This idea can be easily generalized to other observables coupled to the critical modes. Because observables in the heavy-ion collisions are integrated quantities over the whole dynamical evolution, we should look at fluctuations of conserved charges; otherwise, critical enhancement would be wiped off through the dynamical evolution. There are three representative candidates available in the heavy-ion collisions, i.e., the baryon number (B), the electric charge (Q), and the strangeness (S). In thermodynamics those fluctuations are defined by the derivatives of the pressure with respect to the chemical potentials corresponding to conserved charges, i.e., [24]

$$ \chi_{q}^{(n)} = \frac{\partial^{n} [ p(T,\mu_{\mathrm{B}},\mu_{Q},\mu_{S})/T^{4}]} {\partial(\mu_{q} / T)^{n}}, $$
(3)

where q=B, Q, S. In terms of these fluctuations the skewness and the kurtosis are represented as \(S_{q} \sigma _{q} = \chi _{q}^{(3)}/\chi _{q}^{(2)}\) and \(\kappa _{q} \sigma _{q}^{2} = \chi _{q}^{(4)}/\chi _{q}^{(2)}\), respectively. Susceptibilities in mixed channels can also be defined in a similar fashion.

The baseline to be compared for the critical enhancement is estimated by an approximation of non-interacting and dilute hadronic gasses described by the Boltzmann distribution. Then, in this Boltzmann gas approximation, the chemical potential dependence is factored out, yielding,

$$ S_{q} \sigma_{q} \simeq \tanh(\mu_{q}/T),\qquad \kappa_{q} \sigma_{q}^{2} \simeq 1\,. $$
(4)

Since only the net charge is conserved, calculated as a difference between the particle and the anti-particle contributions, the above estimate is often referred to as the baseline by the Skellam distribution that is the probability distribution of two statistically independent variables. It is also possible to apply the Hadron Resonance Gas (HRG) model to estimate the baselines, and then, Sqσq and \(\kappa _{q}\sigma _{q}^{2}\) are generally suppressed by quantum statistical effects, that reflects deviations of the Bose and the Fermi distribution functions from the Boltzmann distribution. The major strategy for the QCD critical point search is to measure Sq and κq at various \(\sqrt {s_{NN}}\) and look for enhancement as compared to the baseline (4).

2.3 Baryon-rich matter, an approximate triple point, and strangeness

From the HRG model estimate, the baryon number density along the chemical freeze-out line is maximized around T≃150 MeV and μB≃400 MeV between \(\sqrt {s_{NN}}=3-19.6\text {\,GeV}\). This has been experimentally confirmed through the K+/π+ ratio peaked around \(\sqrt {s_{NN}}\simeq 8\text {\,GeV}\). It is intuitively easy to understand that K+/π+ is sensitive to the baryon density, while K−/π− is not. In the heavy-ion collisions, the time scale is much shorter than the weak interaction, so the net strangeness should be vanishing. This means that the net chemical potential coupled to s quarks must be zero. Since s quarks have S=−1 and B=1/3, the strangeness free condition leads to

$$ \mu_{S} \;\simeq\; \frac{1}{3} \mu_{\mathrm{B}}, $$
(5)

which means that the dense baryonic matter should contain strange baryons or hyperons that must be canceled by mesons involving \(\bar {s}\) quarks such as K+. Therefore, K+ is enhanced at high density, while K− is not.

In this sense, the point that is reached around \(\sqrt {s_{NN}}\simeq 8\text {\,GeV}\) plays a special role to tell us about a regime transition: at smaller μB≲400 MeV where physics is dominated by mesonic degrees of freedom, and at larger \(\mu _{\mathrm {B}}\gtrsim 400\text {\,MeV}\) where baryon’s are dominate. Roughly speaking, the QGP transition is understood from the Hagedorn transition with the exponentially rising meson-mass spectrum, while the transition at the dense region arises from the Hagedorn transition with the baryon-mass spectrum, and two Hagedorn transition lines cross just around \(\sqrt {s_{NN}}\simeq 8\text {\,GeV}\). In this way, the most baryonic point around \(\sqrt {s_{NN}}\simeq 8\text {\,GeV}\) could be regarded as a QCD triple point approximately facing baryon-less deconfined matter, baryon-rich deconfined matter, and confined hadronic matter [25].

From the correlations between baryon number and strangeness, the QCD triple point can be a landmark for the realization of the most strangeness matter that contains hyperons. In particular, the interactions between nucleons (N) and hyperons (Y), i.e., Y-N and Y-Y interactions are important parameters for the structure of neutron stars. The most strangeness matter would provide us with chances to constrain those interactions.

Before closing the theory status section, let us mention that the polarization measurements of Λ and \(\bar {\Lambda }\) have signified the formation of matter with huge vorticity, and interestingly the polarization increases as \(\sqrt {s_{NN}}\) decreases. The theory is still being developed (we cannot fully cover the literature, and see Refs. [26, 27] for reviews) and we will briefly discuss this issue next in the experimental section.

3 Current status—experiment

3.1 QCD critical point search

The latest experimental results on the QCD critical point search are shown in Fig. 3. The left panel (1) and the right panel (2) show the measurements of Spσp and \(\kappa _{p}\sigma _{p}^{2}\) (where p stands for the proton) for the net-proton number distribution in Au+Au collisions at various \(\sqrt {s_{NN}}\). We note that N in Eq. (2) is the baryon number (that is a conserved charge), but neutrons are not electrically charged, and the proton number is used experimentally as a proxy for the baryon number. Results of Sp and κp are shown for both central (0−5%, small impact parameter) and peripheral (70−80%, large impact parameter) collisions. Also shown are the expectations from the HRG model and a transport based model called Ultra relativistic Quantum Molecular Dynamics (UrQMD), calculations for central Au+Au collisions without including critical fluctuations.

Fig. 3
figure 3

Experimental results [28] of \(\sqrt {s_{NN}}\) dependence of the net-proton Spσp (left) and \(\kappa _{p}\sigma _{p}^{2}\) (right) from 70–80% peripheral (open squares) and 0–5% central (filled circles) Au+Au collisions. In the figures the subscript, p, is omitted. Projected statistical uncertainty for the second phase of the RHIC BES program is shown by the green-band. The STAR experiments fixed-target program extends the center of the mass collision energy down to 3 GeV. Results of calculations are shown as black and gold bands for the HRG model and transport model (UrQMD), respectively. The solid red and the dashed blue line in plot (2) is a schematic representation of the expectation from a QCD-based model calculation in the presence of a critical point

Full size image

The following conclusions can be drawn: (a) as we go from lower order moments (Spσp) to higher order moments (\(\kappa _{p}\sigma _{p}^{2}\)), deviations between central and peripheral collisions for the measured values increase. (b) Central \(\kappa _{p}\sigma _{p}^{2}\) data show a non-monotonic variation with collision energy at a significance of ∼3σ [28]. (c) Experimental data show deviation from heavy-ion collision models without a critical point. Although a non-monotonic variation of the experimental data with collision energy looks promising from the point of view of the QCD critical point search, a more robust conclusion can be derived when the uncertainties get reduced and significance above 5σ is reached. The goal of the second phase of the BES program (BES-II) at RHIC and the fixed target (FXT) programs designed to have high precision measurements in the energy range of \(\sqrt {s_{NN}}= 3-19.6\text {\,GeV}\).

The data presented in Fig. 3 provides the most relevant measurements over the widest range in μB (20−450 MeV) to date for the critical point search and for comparison with the baryon number susceptibilities computed from QCD to understand the various features of the QCD phase structure. The deviations of \(\kappa _{p}\sigma _{p}^{2}\) below the baseline, shown in Eq. (4), are qualitatively consistent with theoretical considerations including a critical point [29]. However, the conclusions on the experimental confirmation of the QCD critical point might be made only after improving the precision of the measurements at lower collision energies and by comparing the QCD calculations with critical point behavior which includes the dynamics associated with heavy-ion collisions. See Ref. [30] for the latest report.

3.2 High baryon density matter

Figure 4a in the upper panel shows the energy dependence of K/ π particle yield ratio. The results are from AGS [31–33], SPS [34, 35], and RHIC [13]. These ratios reflect the strangeness content relative to entropy of the system formed in heavy-ion collisions. The thermal model calculation is shown as yellow band for K+/ π+ and green band for K−/ π−. The dot-dashed line represents the net-baryon density at the chemical freeze-out as a function of collision energy, calculated from the thermal model [36].

Fig. 4
figure 4

a Particle yield ratios of kaons to pions as a function of \(\sqrt {s_{NN}}\). Thermal fits are also shown as bands in the plot. The dot dashed line represents the net-baryon density at the chemical freeze-out. K+/π+ (circles) trace the baryon density at the chemical freeze-out well, while K−/π− (triangles) increase smoothly as a function of \(\sqrt {s_{NN}}\). b Particle yield ratios of ϕ-meson to kaon (ϕ/K−) as a function of \(\sqrt {s_{NN}}\). At energy below 8 GeV, the GCE fit no longer works, and the strangeness CE takes over

Full size image

The following observations can be made. (a) The collision energy dependence of both the ratios is fairly well described by a thermal model calculation. (b) A peak position in energy dependence of K+/ π+ is observed and has been suggested to be a signature of a change in degrees of freedom (baryon to meson [37] or hadrons to QGP [38]) while going from lower to higher energies. (c) The calculated net baryon density exhibits a maximum value as the collision energy is scanned, with a value of about three-fourth of the normal nuclear saturation density (i.e., ρ0≃0.16 nucleons/fm3). The collision energy where the maximum net-baryon density occurs is very close to the peak position of the K+/ π+ ratio. This way of representating the results of experimental measurements and theory calculations serve to demonstrate clearly that the freeze-out density and K+/ π+ ratio could be related. (d) The K−/ π− ratio seems unaffected by the changes in the net-baryon density with collision energy and shows a smooth increasing trend.

Through these measurements we have the knowledge of regions in collision energy where the maximal net-baryon density is reached. This is an important aspect in the context of planning of experiments that seek to explore compressed baryonic matter.

3.3 Tests of thermal model—GCE vs. CE

Relativistic statistical thermodynamics has been applied to systems ranging from cosmology to heavy-ion collisions in the laboratory. The cosmological applications usually deal with systems having large volumes and matter or radiation; hence, the GCE is a suitable description, as we slightly mentioned in the theory section of this paper. For heavy-ion collisions, the situation is complicated due to the femtometer-scale nature of the systems. Often one assumes (approximate) local thermal equilibrium for such processes. Further, such thermal models based on the GCE employ chemical potentials to account for conservation of quantum numbers on average. These GCE models have been able to explain the particle production successfully for a wide range of collision energies [12]. However, conservation laws do impose restriction on particle production if the available phase space is reduced. Hence, the relativistic statistical thermodynamics provides two choices for the formalisms: a GCE and a CE approaches [39]. In the thermodynamic (large volume) limit, the GCE and the CE formalisms are equivalent, but it is an interesting question to ask where and when the transition from a GCE picture to a CE one occurs for finite volume systems produced in collisions in man made collisions, where the collision energy spans from a few GeV to a few TeV (three orders in magnitude).

Figure 4b in the lower panel shows the energy dependence of ϕ/ K− yield ratio. For most collision energies, the ratio remains constant. Similar to the K−/ π− ratio, the ϕ/ K− ratios seem not to be affected by the net-baryon density. Below the collision energy where the freeze-out net-baryon density peaks [shown by the dot-dashed line in Fig. 4a] the ϕ/ K− ratio starts to increase. Thermal model calculations, adopting the GCE, which has been quite successful in accounting for the observed yields of the hadrons in heavy-ion collisions, explains the measurements up to collision energy of 5 GeV. Then, the GCE model values decrease, while the increase in ϕ/ K− at lower energies is explained by using a thermal model within the CE framework for strangeness. Note that a control parameter, rsc, is introduced for strangeness CE results in Fig. 4b. The physical meaning of rsc is a typical spatial size of \(s\bar {s}\) correlations. For smaller rsc, pairs of s and \(\bar {s}\) stick together and the strangeness free condition is satisfied locally, which suppresses the yield of K− and thus enhances ϕ/K−. This makes a quantitative difference from the GCE results. For a given volume of the whole system, rsc determines how close to the GCE/CE situation the strangeness sector in the system should be. Since the rsc reflects the intrinsic properties of matter, the shifting from the GCE to the CE in strangeness signals a considerable change of the medium properties. Future measurements of ϕ/ K− at lower collision energies can be used as an observable to estimate the volume in which the open strangeness is produced (reflected by the value of rsc).

3.4 Lifetime of hypernuclei

Hypernuclei are bound states of nucleons and hyperons; hence, they are natural hyperon-nucleon correlated systems [40]. They can be used as an experimental probe to study the hyperon-nucleon (Y-N) interaction. Studying hypernuclei properties is one of the best ways to investigate the strengths of Y-N interactions. Theoretically, the lifetime of a hypernucleus depends on the strength of the Y-N interactions. Therefore, a precise determination of the lifetime of hypernuclei provides direct information on the Y-N interaction strength. The high energy heavy-ion collisions at RHIC and LHC create favorable conditions to produce hypernuclei in significant quantities. At the moment, the experiments have measured the production of the lightest hypernuclei, i.e., the hypertriton, Λ3H, which is a bound state of a proton, a neutron and a Λ.

Figure 5 shows a compilation of the measurement of the hypertriton lifetime from various experiments and theory calculations [41, 42]. The lifetime of the (anti-) hypertriton is determined by reconstructing the mesonic decay channels. A statistical combination of all the experimental results yields a global average lifetime of \(206_{-13}^{+15}\) picoseconds. The lifetime is about 22% shorter than the lifetime of a free Λ of 263.2 ±2.0 picoseconds, indicating a possibility of a reasonable hyperon-nucleon interaction in the hypernucleus system. Most calculations predict the hypertriton lifetime to be in the range of 213−256 picoseconds. The Y-N interaction is of fundamental interest, for it controls the onset of strange degrees of freedom in high density nuclear matter, such as matter in the neutron star. The lifetime measurements of hypernuclei thus provides a crucial input for models attempting to understand physics of the neutron star. One should be aware of discrepancies in the measured lifetime of Λ3H from RHIC and LHC. High statistics data are called for in order to resolve these discrepancies.

Fig. 5
figure 5

Collection of the hypertriton lifetime measurements from different experiments [41, 42]. The vertical lines and boxes are the statistical and the systematic uncertainties, respectively. The orange band represents the average of the lifetime values and the lines at the edge correspond to 1 σ uncertainty. The dot-dashed lines are four theoretical predictions

Full size image

3.5 Polarization and spin alignment

Recently, it was realized that the initial condition of the QGP in relativistic heavy-ion collisions is subjected to two extraordinary parameters. The angular momentum and the magnetic field. The angular momentum of the order of \(10^{7}\hbar \) is theorized to be imparted to the system through the torque generated when two nuclei collide at non-zero impact parameter with center-of-mass energies per nucleon of a few 100 GeV [43]. This leads to a thermal vorticity of the order of 1021 per second for QCD matter formed in the collisions [44]. Furthermore, when the two nuclei collide in the LHC, an extremely strong magnetic field of the order of 1015 T is generated by the spectator protons, which pass by the collision zone without breaking apart in inelastic collisions. The effect of the angular momentum (which is a conserved quantity) is expected to be felt throughout the evolution of the system. In contrast to that, the magnetic field is transient in nature and stays for a short time of the order of ∼0.1 fm/c unless the electric conductivity is large (but this is disfavored, see discussions in Ref. [45]). Just to give an idea of the magnitude of these values, the highest angular momentum measured for nuclei (near the Yrast line) is \(\sim 70\hbar \) and the strongest magnetic field we have managed to produce in the laboratory is ∼103 T using the electromagnetic flux compression technique. Getting experimental signatures of these phenomena is not easy due to the femtoscopic nature of the system (both in space and time) formed in the heavy-ion collisions. Nevertheless, the experiments at RHIC and LHC have been able to address this challenging problem.

It is known that the spin-orbit LS coupling causes the fine structure in atomic physics and the shell structure in nuclear physics, and is a key ingredient in the field of spintronics in materials sciences. The LS coupling is also expected to affect the development of the rotating QGP created in collisions of nuclei at high energies. The extremely large initial value of the orbital angular momentum is expected to lead to the polarization of quark spin along the direction of the angular momentum of the plasma’s rotation due to the LS coupling [46]. This should in turn cause the spins of vector (spin = 1) mesons (K∗0 and ϕ) to align [47] and hyperons like Λ baryons to be polarized [44]. Both hyperon polarization and the spin alignment can be studied by measuring the angular distribution of the decay products of Λ and vector mesons. The hyperon polarization is found to increase with decreases in heavy-ion collision energy. The thermal vorticity values thus show that the QGP formed in the collisions, along with exhibiting the emergent properties of relativistic fluid, is also the most vortical fluid found in nature [44]. Meanwhile, the observed spin alignment of vector mesons (with J=1) was quantified by obtaining the probability of finding a vector meson in a Jz=0 state along the z direction that is the direction of the orbital angular momentum of the rotating QGP. The momentum dependence of these probability values indicated polarization of quarks in the presence of large initial angular momentum in heavy-ion collisions and a subsequent hadronization by the process of recombination [47].

4 Future directions—theory

There remain many theoretical challenges in understanding the physics of dense baryonic/quark matter with magnetic field and rotation. Below we present brief summaries on some of these issues.

4.1 QCD phase structures and quark matter at high baryon density

Theoretically, it is highly nontrivial how quarks can melt from hadrons in cold and dense matter. Unlike hot QCD even an approximate measure for quark deconfinement is still unknown or such an order parameter simply may not exist.

The QCD critical point is a landmark on the QCD phase diagram; the next intriguing question is where we can find quark matter. One might naively think that the asymptotic freedom with a large quark chemical potential, μq≫ΛQCD, makes quarks unbound from hadrons, but this is not necessarily true. When μq is large, quarks form a Fermi sphere, and the typical energy scale of quarks near the Fermi surface is ∼μq. However, gluons can still carry soft momenta, mediating confining forces. Therefore, excitations on top of the Fermi surface are still confined, while the Fermi sphere itself is dominated by quarks, and this refined picture of a dense baryonic state is called quarkyonic matter [48].

One can develop a more precise definition of quarkyonic matter by deforming the fundamental theory; in reality Nc=3 where Nc is the number of colors, and one can significantly simplify theoretical treatments by taking the Nc→∞ limit. In this special limit, the ground state could have an inhomogeneous crystalline shape [49] (see also a review [4] for comprehensive studies of inhomogeneous phases). In reality, mesonic fluctuations would destroy inhomogeneity, but some remnant correlations can still remain. Those remnants of enhanced spatial correlations would increase the density fluctuation. For experimental detections to discriminate it from bubble formation associated with a first-order transition beyond the QCD critical point, more theoretical work is needed.

4.2 Neutron star phenomenology

We specifically pick two problems here in neutron star phenomenology. One is a question of whether quark matter is found in cores of the neutron star, which is a continued subject from the above problem of the phase diagram, and the other is what is called the hyperon puzzle.

It is an experimental fact that massive neutron stars whose masses are greater than 2M⊙ exist, where M⊙ represents the solar mass. This observations is strong enough to constrain the stiffness of the equation of state (EoS) and a strong first-order phase transition has already been excluded. Thus, even if quark matter existed in cores of the neutron star, it is likely that there is only a smooth crossover or a weak first-order transition from nuclear to quark matter.

Matter created in heavy-ion collision is regarded better as hot and dense baryonic matter. Since the physical observables are sensitive to the EoS, the global analysis of experimental data would quantify the most likely regions of EoS parameters. Such a program of global Bayesian analysis has already been successful at large \(\sqrt {s_{NN}}\) where the experimentally inferred EoS is found to be consistent with the lattice-QCD results [50]. The same machinery could in principle constrain the EoS of hot and dense baryonic matter. One of the most interesting EoS parameters is the speed of sound \(c_{s}^{2}\), which hints the presence of quark matter as discussed in Ref. [51]. We also mention that the global analysis of the flow measurements could constrain the viscosities of dense matter (apart from leptonic contributions), which should be useful for considerations of the r-mode evolutions of neutron stars [52]. See, for example, Ref. [53] for a theoretical estimate of viscosities of dense nuclear matter.

Let us now turn into the hyperon puzzle that has twofold manifestations. If the baryon density reaches several times ρ0, inside the neutron star to balance the gravitational force, it is energetically more favorable to activate the strangeness degrees of freedom. One problem is that the introduction of strangeness generally softens the EoS and it would become more difficult to support the neutron stars with a mass \(\gtrsim 2M_{\odot }\). Another problem is that once hyperons are favored, the direct Urca process would shorten the time scale of the neutron star cooling, which would make the neutron star too cold. Thus, the threshold of the neutron star mass to open the direct Urca process is an important parameter, and this is dictated by the Y-N and Y-Y interactions as well as three-body forces involving hyperons.

Theoretically speaking, the most promising approach is the first-principles calculation of the baryon interactions including nontrivial strangeness from lattice-QCD simulations [54]. In the HAL QCD method, the Nambu-Bethe-Salpeter wave functions are computed on the lattice, from which the potential is extracted; see Ref. [55] for a review on the HAL QCD method including hyperon results. For example, pΞ− correlation has been theoretically predicted to have attractive interaction [56]; this is an interesting system since Ξ−∼dss is a multi-strange baryon, and the experimental signature is reported [57]. Also, the correlations of ΩΩ and NΩ have also been estimated in Ref. [58] based on the lattice-QCD determined potential. For more comprehensive discussions to quantify the potential from the correlations in heavy-ion collisions, see a recent review [59].

4.3 Dibaryons and diquarks

ΩΩ is an interesting candidate for one of possible dibaryons [60] are six-quark objects. There is a long history of the dibaryon hunting (see Ref. [61] for a review); the idea is traced back to the conjecture on the H-dibaryon [62]. One might think that the deuteron is also a six-quark bound state, but what is special about the H-dibaryon is that diquark correlation plays an essential role. From the one-gluon exchange interaction, the color-triplet diquarks are favored and the low-energy reduction leads to the Breit interaction involving the color and the spin degrees of freedom. It is an established notion that the energetically most favored channel is the spin-singlet and the flavor-triplet, and diquarks in this channel are called “good diquarks,” while the second stable diquarks, i.e., “bad diquark,” are found in the spin-triplet and the flavor-sextet channel. The structure of the H-dibaryon is considered to be dominated by three good diquarks, i.e., H∼(ud)(ds)(su).

It is still challenging to find a direct signature of the strong diquark correlation. From the theoretical point of view, the difficulty lies in the fact that diquarks are not gauge invariant. Nevertheless, the density-density correlation in baryon wave-functions could quantify the diquark correlation in a gauge-invariant way [63]. Interestingly, the diquark correlations would be more prominent at higher baryon density. Actually, it is a solid theoretical prediction that QCD matter at asymptotically high density should be a color superconductor in which the diquarks form condensates. If there is no sharp transition separating baryonic matter from color-superconducting quark matter, as is conjectured in the quark-hadron continuity scenario, one can expect some remnants of the diquark correlations in density regions accessible by the heavy-ion collision. The interesting question is whether diquarks are treated as active thermal degrees of freedom, participating in the thermal model in dense matter; see Ref. [64] for a model with colored thermal excitations like diquarks. Since the lattice-QCD calculation is not functional at finite density, the test can be made only in comparison to experimental data.

4.4 Femto-nova rotating with magnetic fields

One of the profound features of matter created in the heavy-ion collisions is that non-central collisions are accompanied by vorticity and magnetic fields as illustrated in Fig. 1. Such a hot, dense, and rotating object exposed under the magnetic field can be thought of as an emulator of a proto-neutron star after a supernova, and we may well call this heavy-ion system the femto-nova.

The femto-nova investigations have a lot of research potentials. Relativistic rotation and magnetic fields would change the properties of matter, or even the phase diagram should be affected [65]. In numerical simulations of the supernovae and the neutron-star-mergers, effects of rotation and magnetic fields have not been taken into account yet. Thus, the heavy-ion collision experiments can constrain uncertainties in the interplay of rotation and magnetic field in strongly interacting matter. In particular, relativistic formulations of spin- and magneto-hydrodynamics are still in the process of developments.

From the point of view of the topological effects, rotation and magnetic fields are of paramount importance. Once the density (finite μB), the rotation (finite angular velocity ω), and the magnetic field B are coupled together, the QCD theory tells us that the chiral separation effect (CSE) and the chiral vortical effect (CVE) should appear (see Ref. [66] for a review):

$$ \boldsymbol{J}_{5} = \sigma_{s} \boldsymbol{B},\qquad \boldsymbol{J}_{5} = \sigma_{v} \boldsymbol{\omega}, $$
(6)

where σs∝μB if the particle masses are negligible. The coefficient σv has two components; one is ∝T2 and the other \(\propto \mu _{\mathrm {B}}^{2}\). Here, J5 is the axial current, and its physical meaning is the spin expectation value of matter. Therefore, the left equation in Eq. (6) physically represents the spin polarization, and what is nontrivial in relativistic systems is that the spin and the momentum of massless fermions are tightly correlated with a certain handedness. Therefore, global spin polarization results from the CSE leading to the chirality separation associated with a chirality flow along the polarization.

The second equation, i.e., the CVE, looks like a counterpart of the CSE with B replaced by ω, but physical interpretations are rather nontrivial. In this context, the physical meaning of the CVE is the relativistic realization of the Barnett effect (see Ref. [67] for a review by Barnett himself); a mechanical rotation yields nonzero magnetization [68]. One might then wonder if the chiral anomaly mechanism could be an independent origin from the conventional LS coupling. Actually, in the nonrelativistic Barnett effect, the magnetization is inversely proportional to the gyromagnetic ratio, and so, it is proportional to the mass; this has motivated the nuclear Barnett effect experiment [69]. The CVE is more prominent, however, for massless fermions, and their mass dependences look competing. The theoretical framework is not yet complete to incorporate all those effects consistently for arbitrary masses of fermions. Establishing a firm bridge between nonrelativistic and relativistic (as seen in the heavy-ion collision) Barnett effects is a challenging subject in theory.

5 Future directions—experiment

5.1 More on the QCD critical point

As discussed above, the search for the QCD critical point has been led by the RHIC BES program, where the collision energy has been dialed down from 200 GeV (see Fig. 3). It spans a μB-range from 20 to 400 MeV of the phase diagram. The fluctuations near the QCD critical point are predicted to make \(\kappa _{B}\sigma _{B}^{2}\) swing below its baseline value (=1.0) as the critical point is approached, then going well above, with both the dip and the rise being significant for head-on nuclear collisions [29]. The data show a substantial drop and intriguing hints of a rise for the lowest energy collisions, although the uncertainties at present are too large to draw definitive conclusions, see panel (2) of Fig. 3. The ongoing phase-II of the BES program and the fixed target program at RHIC aim to gather high statistics data to look for this important landmark in the QCD phase diagram. The lattice-QCD calculations suggest that the QCD critical point, if exists, lies in the region of \(\mu _{\mathrm {B}}/T\gtrsim 2\) [17]. Thus, the role of the upcoming high baryon density experiments as listed below becomes important in the critical point search program. Not only do they extend the search to high μB regions (≈750 MeV) of the phase diagram, they also provide a reverse approach of studying the critical point observable by dialing up the beam energy. This approach is complimentary to the current searches and the observable studied from both directions of collision energy (i.e., from both above and below the QCD critical point) is expected to meet at a common point. This would be a complete test of the theoretical prediction of non-monotonic variation of \(\kappa _{B}\sigma _{B}^{2}\) with collision energies.

5.2 Light hypernuclei production

Figure 6 shows the yields of light-nuclei and (multi-)hypernuclei at mid-rapidity, from thermal (HRG) model calculations, shown as a function of colliding energy. All of the data points are from Refs. [70, 71] (see also Ref. [72] for a theoretical analysis). As one can see in the figure, all of the light hypernuclei yields peak around the range of 3−8 GeV that is fully covered by both the STAR fixed target (FXT) program [73] (hatched region) and the future CBM experiment at FAIR [74].

Fig. 6
figure 6

Heavy nuclei (dashed lines) and (multi-)hypernuclei (symbols) yields calculated in the HRG model [70, 71] for central heavy-ion collisions at mid-rapidity as a function of center-of-mass energy. Also shown for comparison are the yields of Λ hyperon from the same model. The collision energy region of fixed target program in STAR is indicated as a yellow band. Model results from Ref. [71]

Full size image

Data of K+ over pion ratios show a peak at the center-of-mass energy of 8 GeV implying that the baryon density at chemical freeze-out reaches maximum around this colliding energy; see Fig. 4 top panel. Due to the relatively low production threshold, the production of the Λ hyperon becomes abundant. The coalescence process [75] combines these advantages and leads to the copious production of the hypernuclei in this energy region. The strangeness degrees of freedom are therefore introduced into the dense nuclear matter. The cross sections for hypernuclei production in high energy nuclear collisions are much higher than that in either elementary collisions or in Kaon-induced interactions, thus making heavy-ion collision as a hypernuclei factory (HNF). HNFs offer a new opportunity for studying fundamental interactions of hyperon-nucleon (Y-N), hyperon-hyperon (Y-Y) within the many-body baryonic system, and the spectroscopy of nuclear structure with strangeness [76].

In addition, these nuclear collisions could provide the means to study the inner dynamics of compact stars in the laboratory. We should note that most of the studies on hypernuclei so far utilized a “light system” with electron or pion or Kaon beams. In such cases, the hypernuclei were produced in the vacuum. Data on hyperon production in nuclear collisions is scarce [77]. Measurements of hypernuclei collectivity in the truly heavy-ion, Au+Au, collisions, for example, allow us to extract information on the transport properties (crucial for neutron star stability, see Ref. [53]) as well as the Y-N interaction driven EoS, with the strangeness degrees of freedom, in the hot and dense environment where the baryon density could be very high. Simulations for neutron star inner properties crucially depend on the EoS; see Ref. [78] for the effect of Y-Y interactions and also Ref. [79] for the hyperon effects including the possibility of quark mixture. Furthermore, an additional benefit of the unique high baryon density environment is the enhanced production of multi- Λ hypernuclei as already suggested in Fig. 6.

The future fixed target experiments, aimed for high baryon density matter, will collect data in heavy-ion collisions around 2−8 GeV, which is within ideal energy range serving as the HNF, see Fig. 6. Hence, these future experiments could make tremendous contributions towards measuring the yields of hypernuclei and their life-time. This would then provide valuable inputs to understanding the hyperon-nucleon (Y-N) interactions in heavy-ion collisions and the inner dynamics of the compact stars.

5.3 Fluid vorticity of high baryon density matter

Experiments at RHIC and LHC have observed that the polarization of hyperons and vector mesons have a distinct energy dependence. Their values increase with decrease in collision energy. The physics reasons attributed for the observed energy dependence are twofold. First, the baryon stopping is enhanced and shear flow patterns in the beam direction emerge; second, the shorter lifetime of the fluid phase thereby allows perseverance of the initial vorticity in the system and keeps it from getting diluted [80]. The possibility of high interaction rate experiments in high baryon density matter at the upcoming facilities opens up a unique opportunity to study relativistic effects of the spin, the orbital angular momentum, and the magnetic field in QCD matter. This will guide theoretical developments in the field of relativistic spin- and magneto-hydrodynamics.

5.4 Future experimental facilities for high baryon density matter

The upcoming facilities for studying high baryon density matter includes (a) the Nuclotron-based Ion Collider fAcility (NICA) at the Joint Institute for Nuclear Research (JINR), Dubna, Russia, (b) the Compressed Baryonic Matter (CBM) at Facility for Antiproton and Ion Research (FAIR), Darmstadt, Germany, (c) the Japan Proton Accelerator Research Complex (J-PARC), Ibaraki, Japan, and (d) the CSR External-target Experiment (CEE) at High Intensity heavy-ion Accelerator Facility (HIAF) [81], Huizhou, China. The interaction rates of these upcoming experiments compared to existing and other future facilities are shown in Fig. 7. Note that all the new facilities will focus on the energy region where the baryon density is high. Below, we discuss briefly the salient features of these four experiments.

Fig. 7
figure 7

Interaction rates (in Hz) for high-energy nuclear collision facilities. Collider mode: the second phase RHIC beam energy scan (BES-II) [73] for \(7.7\text {\,GeV} <\sqrt {s_{NN}} <19.6 \text {\,GeV}\) (filled-red-circles) and NICA (filled-red-squares) [82]. Fixed target mode: STAR fixed target (FXT) program for \(3.0\text {\,GeV}<\sqrt {s_{NN}}< 7.2 \text {\,GeV}\) (filled-black-circles), FAIR (CBM, SIS) [74], HADES [83], J-PARC [84], and HIAF [85]. Also shown for reference are the expected collision rates of ALICE at LHC [86] and sPHENIX at RHIC [87]

Full size image

5.4.1 NICA#x24ZZZ;acircleZZZJINR

At this new accelerator complex that is under construction, the plan is to provide accelerated particle beams both in collider (Multi Purpose Detector) and fixed target (Baryonic Matter at Nuclotron) modes [82]. The center of mass collision energies will be in the range of \(\sqrt {s_{NN}}= 4-11\text {\,GeV}\). The dominant physics goals are dominantly to explore the QCD phase diagram through measurements of particle yields, collective flow, femtoscopy, etc. In addition, NICA will also study polarization of hyperons and investigate hyperon-nucleon (Y-N) interactions through hypernuclei production. As seen in Fig. 7, NICA connects the high-energy collider experiments with the FXT experiments nicely.

5.4.2 CBM#x24ZZZ;acircleZZZFAIR

This facility currently under construction will offer the opportunity to study nuclear collisions at extreme interaction rates. It will initially comprise of the SIS100 ring will provide center of mass energy for gold beams of \(\sqrt {s_{NN}} = 2.7 - 4.9 \text {\,GeV}\) and μB>500 MeV. The CBM detector at FAIR has been designed as a multi-purpose device that will be capable of measuring hadrons, electrons, and muons in heavy-ion collisions over the above beam energy range at interaction rates up to 10 MHz for selected observables. The physics goals include studying the phase structure of the QCD phase diagram (i.e., the order of the transition, the QCD critical point, and chiral symmetry), the possible modification of properties of hadrons in dense baryonic matter, and the EoS at high density, which is expected to be relevant to the core of neutron stars through measurements of hypernuclei and heavy multi-strange objects.

5.4.3 JPARC-HI#x24ZZZ;acircleZZZKEK/JAEA

The idea of this facility has been under discussion for quite a few years and the planned J-PARC-HI will provide heavy-ion beams up to uranium for center-of-mass energies of 2−6.2 GeV. This corresponds to exploring the QCD phase diagram in very high baryon densities [84]. The J-PARC-HI experiment will carry out important measurements including dileptons in order to understand QCD transitions, in-medium modifications of ρ,ω, and ϕ mesons decaying into dileptons, and rare particles such as multi-strangeness hadrons, exotic hadrons, and hypernuclei utilizing its high rates capability. According to the plan, the J-PARC-HI would be the experiment with the highest beam rate capability, up to 100MHz, which would allow measurement of rare processes with unprecedented precision in heavy ion collisions.

5.4.4 CEE#x24ZZZ;acircleZZZHIAF

HIAF’s is under construction and it is expected to be in operation in 2025. The machine is designed to deliver bright ion beams of protons and heavy nuclei such as uranium with the center-of-mass energy up to 10 GeV and 4 GeV, respectively. A superconducting dipole magnet spectrometer experiment (CEE) [88] is also under construction. In many respects, this is a simple hadron spectrometer with the main physics focused on the measurements of proton, light nuclei including hypernuclear production and the correlation functions for understanding the QCD phase structure. In addition, meson ratios of pions will be measured with high precision in order to extract the EoS parameters at the high baryon density region.

Future new experiments are all designed with high rates, large acceptance, and state-of-the-art particle identification, at the center of mass energy region where baryon density is high, i.e., 500 MeV<μB<800 MeV, see Fig. 7.

6 Conclusions

We reviewed what we have understood so far and what we are trying to understand in the future using relativistic heavy-ion collisions. There are three important physics targets:

  • Scanning the QCD phase diagram and seeking for the QCD critical point.

  • Constraining the Y-N and Y-Y interactions and the EoS in dense baryonic matter including strangeness degrees of freedom.

  • Exploring the effects of large angular momentum and strong magnetic fields.

For (1), the “criticality” is essential to detect the critical point, and the extraction of the EoS as (2) requires global analysis including the “collectivity,” and the physics of (3) exhibits topologically nontrivial effects once nonzero “chirality” is involved. These three Cs abbreviate the future directions of the heavy-ion collision physics.

The first-principles calculations from the lattice-QCD simulation have shown tremendous progresses with the cutting-edge computing technologies also toward the high-density region. Now understanding the QCD phase structure requires experimental data together with theoretical approaches. The QCD critical point is a landmark, and the next question is what awaits beyond it. If a first-order phase transition is reached, the spinodal decomposition and the nucleation processes would lead to characteristic patterns of baryon fluctuations.

In the heavy-ion collisions of center-of-mass energy below 15 GeV, one of the important features is that the baryon density is high enough to be above the threshold for strangeness production. An interesting observation is the transitional behavior from the grand canonical to the canonical ensembles in the strangeness sector with different collision energies. Also, with abundant strangeness, N-N, Y-N, and Y-Y interactions can be investigated not only in the vacuum but in an environment with a surrounding baryonic mean field. Under such a situation, measurements of baryon correlations and collectivity involving multi-strange hadrons such as ϕ-meson, Λ,Ξ, and Ω-baryons, and hypernuclei would provide us with the information on the EoS relevant to the neutron star structures and simulations of the supernovae and the neutron star mergers. Although it is not covered in this article, as long as the penetrating observables are concerned, dilepton mass distributions for example give us information on the initial thermal properties for matter created during heavy-ion collision (see a recent review [89]).

The unique property of matter during the heavy-ion collision is the presence of rotation (or the angular momentum) and the external magnetic fields. Such extreme environments at high baryon density, with rapid rotation, and strong magnetic fields can be found not only in heavy-ion collisions but also in astrophysical phenomena. Therefore, revealing those effects in the controlled laboratory experiments could create connerstones for understanding the nature of visible matter, through the femto-nova, in the Universe.