Abstract
This study provides a holistic and quantitative overview of over 800 mathematical methods (e.g., financial and risk models, statistical tests, statistics and advanced algorithms) taken out of sampled scientific literature on quantitative modelling, particularly, from financial and risk modelling by applying a bibliometric approach from 2008 to 2019 and a citation network analysis. This is done to elaborate on the influence in the field after the Financial Crisis 2008. We present a content analysis of journals, main topics, applied data sets and frontiers within quantitative modelling and highlight details about quantitative features such as implemented models, algorithms and aggregated model-family combinations. Moreover, we describe explications and ties to empirical stylised facts (e.g., asymmetry or nonlinearity). Finally, we discuss insights such as our main finding, namely, the non-existence of a “single-best”-approach as well as the future prospects.
Similar content being viewed by others
Introduction
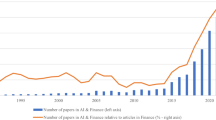
Whether it be professionally managed investment funds, corporate pension plans or single privately owned assets, during economic buoyancies, and primarily during recessions, the financial system and its stability wields an enormous influence on our modern-day societies (Aguilar-Rivera et al. 2015; Gong and Xu 2018). Starting from the “dot-com bubble”, the terroristic attacks of September 11, 2001, the Great Financial Crisis of 2008, the European sovereign crisis to the outbreak of the COVID-19 virus in the year 2020 and the Ukrainian war in 2022, turmoil, irrational panic and breakdowns of financial markets influence the public confidence and the stability of the financial system as a whole and necessitate governmental interventions (Beltratti and Stulz 2019; McKibbin and Fernando 2020). All private persons, investment corporations or other market actors taking an active part in financial market activities must face the demanding task of foreseeing the future risks to and the developments of their investments. Anticipating the progress of financial instruments and attempting to pinpoint the next financial crises are actively pursued aspirations of many practitioners and academics (Lo Duca and Peltonen 2013; Poon and Granger 2003). In the world of academia, the importance of quantitative modelling, especially the task of volatility modelling since the 1990s, continues to surge and has been dominant for several decades (Poon and Granger 2003; Aguilar-Rivera et al. 2015). Actors who intend to find and explore financial market patterns, corporate pension funds and single private persons surely differ from traditionally assumed rational actors (taken out of neoclassical and modern finance) in terms of risk tolerance, assimilation of market information, institutional constraints and heterogeneous beliefs (Andrada-Félix et al. 2016). This, therefore, leads to heterogeneity and irrationality within financial markets as well as to differences concerning investment horizons (Ramiah et al. 2015). The aforementioned suppositions can possibly be explained by new technological developments, empirically depicted stylised facts and newly found conventions (for example, the Fractal Market Hypothesis [FMH]) but not with traditional approaches (Chakrabarty et al. 2015; Aguilar-Rivera et al. 2015).
Among the empirical evidence of stylised facts in financial time-series, volatility dynamics (e.g., Adams et al. 2017), nonlinearity (e.g., Alexandridis et al., 2017), asymmetry (e.g., Aguilar-Rivera et al., 2015), long memory (e.g., Shi and Ho, 2015), multifractal and trending characteristics, among other anomalies, can be found (Berghorn 2015; Daniel and Moskowitz 2016). Contrastingly, traditional approaches such as the Efficient Market Hypothesis (EMH), which fails to explain irrational behaviour, the Capital Asset Pricing Model (CAPM) and other long-held beliefs and conceptions have been severely critiqued and challenged in the light of these opposing findings and panic-induced crashes such as the COVID-19 crash in 2020 (Narayan and Smyth 2015; Ramiah et al. 2015; McKibbin and Fernando 2020). Since new crises possess the capability to exhibit essential risks for the global economy, the venture towards an improved financial and risk modelling understanding is not only an obligation but is of great relevance not only for academics but also for the entire financial industry, whole countries and even non-participating individuals influenced by such events (Herrera and Schipp 2013; Poon and Granger 2003). Triggered by the above-mentioned incidents, crises-induced severities between theoretical rationales and practical applications occur frequently in terms of (econometric) financial and risk modelling (Linnenluecke et al. 2017). Consequently, the determination of the true data generating process (DGP) of financial time-series, with respect to stylised facts and other innovations, is advantageous for financial market actors (Beltratti and Stulz 2019; Charfeddine 2014). Therefore, researchers react to these implications by further extending and creating new mathematical models and methods through the application of artificial intelligence, big data analytics, machine learning concepts, signal processing and various other technical conceptions, which may occur solely as well as in combination with each other to cope with the above mentioned critics (Alexandridis et al. 2017; Berghorn 2015; Duan et al. 2019). Notwithstanding, many properties and stated stylised facts are still not fully explainable; neither does the research community agree upon the exploited approaches or given explanations of the latter perspicacity, which still leaves many open gaps and potentials (Berghorn 2015; Daniel and Moskowitz 2016; Poon and Granger 2003). Our review builds upon the former research findings of Poon and Granger (2003), who analysed 93 different volatility-modelling papers. Other past literature reviews deduct sophisticated overviews regarding metaheuristics of portfolio optimisation (e.g., Doering et al., 2019), term structured predictabilities of stock prices (e.g., Amini et al. 2013), price predictability (e.g., Narayan and Smyth 2015) as well as about most influential publications (e.g., Linnenlücke et al. 2017), which unveiled respective insights but left the aforementioned gap centred around the current development of financial and risk modelling itself open. Additionally, almost two decades (filled with turmoil and crisis on financial markets) have passed since then, leading to a significant gap after the Financial Crisis.
Thus, we intend to close the stated gap and contribute to this ongoing process threefold:
First, we will apply a bibliometric analysis paired with a snowball-sampling approach to present an inductive content analysis, highlighting information about journals, main research topics and frontiers of scientific research following the Hart-framework (Hart 1998). Moreover, we will display a full citation network analysis, outlining the most relevant publications, defining relevant measures and showing the interconnectivities and gaps within the existing research. Second, we will elucidate the stylised facts and properties applied in the sampled literature and their interconnections. Finally, we will provide a quantitative overview of the applied data sets and mathematical methods (e.g., models, tests, statistics and algorithms). We will then present a rationale to indicate the interconnection and respective numbers of model families in the form of a combination matrix. Furthermore, we will provide an in-depth qualitative description of important models and applications alongside practical implications and challenges. We will conclude by discussing results and limitations of the paper, the current status quo and future prospects of the field.
Bibliometric analysis and snowball sampling
Methodology
We execute a bibliometric analysis with three main steps: First, we apply a bibliometric analysis to identify relevant publications and conduct a subsequent snowball sampling procedure by performing an inductive content analysis (Biernacki and Waldorf 1981; Duriau et al. 2007). Second, we explore the definitions and methods of financial and risk modelling, illustrating empirical insights and identify the most influential publications. Third, we implement a citation network analysis. Following Kitchenham and Brereton (2013), we conduct a literature search in two major databases (i.e., “Science Direct” and “Emerald”), looking for the keywords and keyword combinations shown in Table 1. The resulting literature needs to comply with the following conditions: written in English; published after 2008 and before the end of 2019 (to represent the development since the Financial Crisis until the end of 2019 accordingly) and being blind peer-reviewed. The keywords focus on financial and risk modelling as well as specified terms from the relevant fields (e.g., “volatility modelling”, “momentum”, “trends”). Thus, we query the keywords as stated or in any combination with each other to gather all the relevant, non-duplicate results. The data set resulting purely from keywords consists of 15,566 papers. To secure the quality and validity of the gathered literature, we apply Harzing’s journal ranking listFootnote 1 to select the relevant journals (Harzing 2019). After removing duplicates, filtering the stored data executing this framework results in a list of literature further analysed by this paper, which initially sums up to 2012 papers.
Further, following Kitchenham and Brereton (2013), the analysis requires sorting all papers of the sampled literature into categories. Reading of the abstracts of all the selected papers leads to a categorisation. The eight resulting categories stem from the content and origin of the papers represented in the sampled literature. We define the categories as Economical (EC), Green Management (GM), Behavioral Finance (BF), Financial Modelling (FM), Supply Chain (SC), Risk Modelling (RM), Health Management (HM) and Non-Relevant (NR). Important (in-scope) areas of research consist of the categories EC, BF, FM and RM, while we label the others as out of scope. Moreover, in the style of Linnenluecke et al. (2017), displaying research trends based on influential publication content categories, we can determine that the mentioned categories yield an additional meaning, namely, the representation of research streams. Hence, we can interpret the categories (excluding NR) as research streams and will conduct a detailed analysis on the single research trends in the streams FM and RM matching the research question. Please note that there exist many other fields in parallel, not regarded within this study, which propose sufficient insights into financial and risk modelling such as taken out of nonlinear dynamics, computer science or econophysics, which are not elucidated within this study due its stricter scope and methods.
Nevertheless, please refer to Vogl (2022) for an in-depth literature review about financial modelling in econophysics and nonlinear dynamics, to Bustos and Pomares-Quimbaya (2020) for a market movement forecasting overview, to Goodell et al. (2022) for emotions on markets and to Kumbure et al. (2022) for a state-of-the-art review for computer science and machine learning approaches on financial markets. Regarding the FM and RM research stream results in initially 684 publications. We rate the previously denoted literature deploying a framework described in Briner and Deyner (2012), which ranks a paper in accordance with four qualitative criteria, namely Contribution, Theory, Methodology and Data Analysis (Briner and Deyner 2012). For each criterion, it is possible to grade the content of a paper from low (zero) to high (three) or “not applicable” (Briner and Deyner 2012). Thus, we only analyse papers in detail, which results in a Deyner Rating equal to or greater than two on average over all criteria. After the initial round of search and selection, we obtain a sample of 114 papers. Additionally, these 114 papers act as input for a snowball-sampling procedure (Biernacki and Waldorf 1981). We finish the snowball sampling with 4263 additional papers and select again following the criteria described above and update the results. We end up with 487 publications after applying the Harzing’s journal ranking list, which results in an addition of 18 sufficiently Deyner-rated publications. A summary is contained in Table 2. The categories FM and RM represent a share of 32.12% of all in-scope papers, from which we rate 15.10% valid enough for further analysis with regard to the referred Deyner ratings. The category FM counts 85 and RM 47 publications in the sampled literature.
Descriptive results
Publication activity
Subsequently, we analyse the dispersion of the number of analysed papers over the last decade by investigating the development of the number of peer-reviewed journal publications per year across all areas of research as given in Table 3. Further, we calculate a linear regression analysis stating \(publications\left( {age} \right) = 15.2879\,\, - \,\,0.6469 \,\,age\), with age (age = 2020-year) as independent and the number of publications per year as dependent variable. The results indicate a positive correlation of 0.5541 between the number of papers and age. Nevertheless, the slope coefficient is not significant \(\left( {p > 0.05} \right)\). Therefore, we assume that the number of papers selected in this specific sample is not significantly age dependent. Further, we will conduct the insights of the “Ortega hypothesis” stated by Cole and Cole (1972). The hypothesis claims that only a small percentage of authors are responsible for scientific progress in a given field (Cole and Cole 1972). In total, 307 authors contributed the 132 papers in our sample. While 287 are single authorships, 19 authorships consist of two respective publications each and only one author is represented with three papers. Regarding the high number of single authors, the count of multiple submissive authors is not conclusive enough to reject the Null-hypothesis.
Impact of the financial crisis and discourse in the literature
To determine whether the cause of the sample publications leads back to the Financial Crisis and if there exists an ongoing discourse and fragmentation inside the research community, we have defined two sentiment indicators as shown in Table 4, which we will deploy in a binary form. The indication of which of the binary outcomes should be chosen is determined by analysing, whether the authors state the origin of their paper to be associated with the Financial Crisis (this is mainly the cause) or not. Otherwise, we analyse the introductory parts, the periods of deployed data as well as the concluding parts of the papers on statements stating the corresponding information about the crisis indication. In terms of the fragmentation of the research community indicator, we also analyse the introductory and concluding parts. In addition, we also interpret the connotations and indications of the data analysis parts, the general alignment and the discussion parts of the respective publications carefully. In the scope of the crisis indicator, we conclude that the Financial Crisis caused the creation of a vast majority (84.84%) of our sample papers. Furthermore, we see a clear fragmentation of the research community with 71.21%, which displays the ongoing discourse about the enigmas of the Financial Crisis and its influence on research, society and the daily reality of financial markets.
Content analysis
Methodology of the content analysis
We extract relevant informationFootnote 2 from the selected publications deploying the Hart framework as displayed in Hart (1998). Thus, we examine the models implemented in the research papers and focus on the boundaries and frontiers of research, analysed data and quantitative findings. The analysis of the papers is focused on its main research questions, the boundaries of research and whether or not the research community has a common ground of understanding. In addition, the major focus is on the mathematical model composition implemented, the applied data sets and stylised facts over the past ten years of research. The criteria are summed up in the appendix.
Underlying theories and methodological approaches
We analyse the main topics first and examine the abstracts, the research questions and the introductory parts of each paper to evaluate the main topics or questions that each of the papers are willing to answer.
Afterwards, we execute tag marks, indicating main topics, questions themselves or some given reasoning within the latter. In Table 5, we show the aggregated main topic tags in descending order, which will partly be described in the following sections. Moreover, we include two representative papers from our sampled literature for each tag to provide further reference. The highest aggregated main topic counts referring to tag occurrences belong to the three topics “forecast time-series”, “volatility modelling” and “dynamics” of time-series.
Volatility dynamics
Assuming the (financial time-series) volatility to be constant, the corresponding interval of confidence can be described as a function of its sample standard deviation. Thus, the conditional variance will be implied by the volatility (Bhar and Hamori 2005). If certain sudden or unexpected events, called shocks, such as breakdowns, affect the financial series, the underlying volatility will no longer be constant (Bhar and Hamori 2005; Amado and Teräsvirta 2014). Volatility can multiplicatively be decomposed into a conditional and an unconditional part, where only the unconditional part faces changes over time, called dynamics (Bhar and Hamori 2005; Amado and Teräsvirta 2014).
Nonlinearity
The empirical modelling of time-series mostly assumes the underlying dynamics to be linear (Pesaran and Potter 1992). This is due to the ability of the estimated models to express the dynamics in terms of their impulse response functions, which is, in fact, directly relatable to linear models (Pesaran and Potter 1992). Temporal aggregation across equities, commodities and the behaviour of actors as well as differing investment horizons (e.g., noise trader speculations) can cause nonlinearity in time-series dynamics (Narayan and Smyth 2015; Righi and Ceretta 2013).
Asymmetry and persistence
Volatility dynamics tend to increase drastically with negative news impacts and decline with positive ones, resulting in asymmetric effects or simple asymmetry (Sener et al. 2012). Therefore, the decomposition of the innovations of the time-series volatility process into negative and positive shocks will each follow distinct processes (Palandri 2015). The resulting upward volatility is more persistent in nature, based on its own past evolution. The persistent part of the downward volatility resembles the upward volatility, paired with a fast mean-reverting component, displaying decaying patterns of impacts to the downward volatility, which results in lesser predictability (Palandri 2015; Bodnar and Hautsch 2016). Since these separations evolve differently, they lead to heteroscedasticity, left-skewed financial time-series returns, fat-tails and a respective departure from Gaussianity, thus, leading to asymmetric characteristics (Zhu and Galbraith 2011; Scharth and Medeiros 2009). Persistence in volatility is not constant over time and seen as indicator of the presence of nonlinearities (Zhu and Galbraith 2011).
Structural breaks and volatility clusters
Sudden changes in the parameters of a given forecasting model are commonly referred to as structural breaks (Hansen 2001). Due to crisis or shock-indicated increases of the permanent component of the conditional variance, structural breaks can be tracked (Wang et al. 2016). Market movements that are sufficiently large to cause structural breaks lead to spurious correlation dynamics, while volatility persistence can be reduced when accounting for structural breaks (Wang et al. 2016). These movements display the tendency to occur at the same time, or in (time-varying volatility) clusters, leading volatility to remain at higher levels during market distress and vice versa respectively (Charfeddine 2014; Mandelbrot 1977; Boubaker and Raza 2017).
Long memory (long-range dependence) and shocks
The non-constant unconditional (time-series) variance displays long-range dependence or long memory property due to deterministic shifts and changes over time (Klein and Walther 2017; Zhu and Galbraith 2011). Long memory can be described for a time-series whose autocorrelation functions (ACFs) are significantly different from zero, even for large lags, while the effects of the volatility shocks slowly decay and approach zero at the same time, implying that shocks bear long-lasting effects on volatility. Additionally, ACFs’ spectral densities reveal divergence to infinity as the respective frequencies approach zero (Charfeddine 2014; Shi and Ho 2015). Long memory or long-range dependence effects do not only co-exist, yet, are labelled synonymous with the occurrence of nonlinearity in options, exchange rate and stock market data. Thus, it is possible to conduct forecasts based on historical financial time-series data sets, which outlines a complete contradiction to the EMH (Shi and Ho 2015; Charfeddine 2014; Kilic 2011).
Regime switches and structural shifts
Structural breaks or shifts (easily to be confused with long memory effects) between different regimes affect the statistical properties of volatility, as financial markets often face sudden changes in behaviour (Ang and Timmermann 2012; Ma et al. 2017). We further specify the terms “regime” and “change” to facilitate sufficient differentiation and understanding. The timely dimension of the persistence of a change is generally referred to as regime, while change is defined and induced as a shock, altered macroeconomic behaviour, business cycle, or a different period in regulation, money market decisions or general politics, among others (Ang and Timmermann 2012; Shi and Ho 2015). Furthermore, a regime exhibits different formations such as recurrence (e.g., crisis or economic drawbacks), uniqueness (e.g., structural breaks), and persistence (e.g., effects or shocks lasting over several periods) as well as jumps, which we regard as a special case, as jumps are left after the next period terminates (Ang and Timmermann 2012). The regime-switching process is able to display structural shifts in the volatility. For respective control for regime switches, a differentiation between long memory and regime switches is possible (Shi and Ho 2015).
In addition, the inclusion of information measures within the respective regime-switching coefficients through smooth transition co-integration provides the ability to comply with nonlinearities as well as market frictions or shocks (Narayan and Smyth 2015). Since the stated long-run effects of shocks vanish, once we account for structural changes, it is advisable to apply non-normal innovation distributions to cohere with the effects of long memory and regime switches (Charfeddine 2014; Shi and Ho 2015).
Spill-over and contagion
Financial distress or shocks in general are not tied and contained in one financial market and rather tend to spread through the financial system (as aggregate of financial markets), as drastically seen in the COVID-19 crash in 2020 or the Ukrainian war in 2022, indicating connected or integrated markets. Integration as an extreme realisation of interdependence is the basis of effect transmissions between these respective financial markets. Thus, the channels of effect transmissions play a crucial role in the market linkage (Ioan et al. 2013; McKibbin and Fernando 2020). If no measurable increase in correlation between two respective linked financial markets is detected in the aftermath of a shock, these markets are interdependent or integrated (Ioan et al. 2013). Regarding the interdependence of financial markets, the effects of contagion and spill-overs mostly occur (Righi and Ceretta 2013; Ioan et al. 2013). To separate and differentiate those two effects, it is required to analyse the speed of the diffusion of financial distress (Ioan et al. 2013). Therefore, we take the propagation (continuance) of a shock between integrated markets into account, where the interdependence speeds up the respective effect transmissions, the latter itself not being the cause (Ioan et al. 2013). If the propagation of a shock is gradual, we refer to the effect of spill-overs, while, in straight contrast, we only consider contagion if no prior interdependence between respective financial markets is present, before accounting for a shock (Ioan et al. 2013). Prior research finds that contagion is described as a strong and sudden change in observed cross-market synchronisation, which is due to changes in fundamental macroeconomic rationales and variables, combined with a rapid increase in co-movements after a respective shock. Contagion is measured by return correlations, but it may be influenced by conditional heteroscedasticity of the return time-series (Righi and Ceretta 2013; Jung and Maderitsch 2014).
(Multi-)fractality, scaling and trending
Market actors differ in terms of expectations and investment horizons, thus, enforcing heterogeneity on financial markets. Theories such as the FMH assume that actors undertake similar decisions on different investment time horizons, resulting in turmoil and high volatility if actors change their respective time preferences (Celeste et al. 2019). Stylised facts and properties (e.g., excess kurtosis, fat tails, volatility clustering and long memory) appear as well in these dynamic interactions at heterogeneous investment horizons of market actors, which we may analyse with fractal properties, also called self-similarity with non-integer dimensions (e.g., Hausdorff–Besicovitch dimension) (Chakrabarty et al. 2015; Celeste et al. 2019).
Fractality is often synonymously notated with the term “scaling”; thus, to describe fractal dynamics, we state that each scale illustrates similar but not identical patterns, resulting in scale-invariant or self-similar data sets (Celeste et al. 2019). Since we regard the financial markets as a whole, several scales confront us at once, which results in multifractal (multi-scaling) properties of financial time-series. These scales are measurable with the Hurst exponentFootnote 3 (Celeste et al. 2019). Since actors, interact on different investment horizons, now labelled as scales, the assimilation of respective price adjustments reflects new information successively, constituting trending effects (e.g., the existence of measurable market trends) (Daniel and Moskowitz 2016; Berghorn 2015). Apart from this, trending is often regarded synonymously with persistency in financial time-series data (Berghorn 2015; Boubaker and Raza 2017; Chakrabarty et al. 2015).
Momentum and momentum crashes
Momentum strategies state that betting on past returns may predict the cross-sections of future time-series returns by being implementable in buying past winners and short-selling past losers (Daniel and Moskowitz 2016; Berghorn 2015). Nevertheless, partly foreseeable momentum crashes in high volatility, panic-induced regimes, which are contemporaneous with market rebounds, may occur (Daniel and Moskowitz 2016). Following a wavelet decomposition scheme, it is possible to show via experiment that, on average, the size, drift, segment and volatility of a trend is scaling (resulting in fractal patterns) and follows a respective power law, stating the momentum effect, which holds that descriptive outperformance is measurable via the momentum exponent (Berghorn 2015). Moreover, trends in real-world data are ubiquitous, yielding neither any price independency nor any reproducibility via classical random walk (with drift) processes. This fact is a contradiction of the traditional (neoclassical) assumptions since the exploitation of excess returns is not possible under the EMH (Celeste et al. 2019; Berghorn 2015).
Multi-resolution analysis and neural networks
Multi-resolution analysis, sometimes called wavelet multi-resolution analysis (MRA), can be applied to recover timely fluctuations across differing scales by decomposing level prices into orthogonal components at different resolutions (Chakrabarty et al. 2015; Khalfaoui et al. 2015). MRA can be applied to isolate high-frequency noise from given time-series, refered to as an explanation of changes in trading activities at different frequency levels as well as being utilised for investment heterogeneity in general (Chakrabarty et al. 2015). Even if appropriate for superior forecasting attempts, MRA faces the drawback of being shift invariant, which means a reduction of availability of data points over long horizons, thereby resulting in high-scale information losses. Nevertheless, MRA dependencies are appropriate for identifying higher co-movements at low frequencies and higher spill-overs at higher frequencies (de Souza e Silva and Legey 2010; Chakrabarty et al. 2015).
Speaking of extracting valuable information from financial time-series, neural networks (NNs) can extract applicable information from complex, nonlinear and mostly noisy data sets and solve insufficiently defined problems via parallel compositions. Artificial neural networks (ANNs) synonymously with NNs as computational structures show characteristics such as efficiency, robustness and adaptability in terms of classification, decision support or financial analysis problems (Tkac and Verner 2016). ANNs further analyse patterns in given data sets by iteratively adjusting the underlying synaptic weights according to a respective learning algorithm. Nevertheless, optimisation procedures such as genetic algorithms (GAs) demand sufficient data sets, present in historical financial market data collections (Tkac and Verner 2016; Duan et al. 2019).
Mathematical methods
We present the mathematical methods given in the sampled literature as displayed in Tables 6 and 7, which build strongly on the main topics and described stylised facts and properties.
In the following, we discuss the mathematical methods by stating didactic rationales between the tags through respective groupings. Eventually, we will investigate potentially featured models in more detail in “Interconnections between models and blind spots of research”.
Stochastic processes
The first group of Table 6, namely, stochastic processes, contains stationary processes, Markov processes and autoregressive models, among others. First, we will define stochastic processes, since they are not mutually exclusive. A stochastic process can be seen as a random element in a given function space, which increments, are the differences between two index values, or respective points in time (Gusak et al. 2010; Lamperti 1977). Classifications of stochastic processes depend mainly on their underlying mathematical properties, including, e.g., random walks, Markov processes, Gaussian processes or Lévy processes, among others (Lawler and Limic 2010; Lifshits 2012). The unconditional joint probability distribution of a stationary stochastic process is time invariant under shifts, meaning parameters of moments do not change over time, which is the underlying assumption of neoclassical approaches (Lamperti 1977; Gagniuc 2017). Unit roots or deterministic trends present in a time-series are called trend-in-mean and cause violations of stationarity. Especially, shocks are persistent and are non-mean-reverting if regarding unit roots (Rahman and Saadi 2008). Constancy over time indicates the absence of memory in the data series, which will lead to problems, namely the loss of information while trying to extract exactly this relevant information of a time-series, once transforming non-stationary series into stationary ones, as commonly practised (López de Prado 2018; Chkili et al. 2014). Other important stochastic processes are the discrete Markov chain and the continuous Markov process, yielding the Markov-property, which states, that the next value of the process depends on the current value, but is conditionally independent of previous values of the process (Asmussen 2003; Ross 1996). Examples for Markov processes are the Brownian motion (BM) (or Wiener process) and the Poisson process, while discrete Markov chains are represented via random walks, among others (Serfozo 2009; Rozanov 2012). Markov switching (MS) models depend on the respective model specifications, e.g., hidden Markov Models (HMM) for nonlinearity or Markov switching multifractal volatility (MSM) models for fractality (Wang et al. 2016; Shi and Ho 2015). In general, time-varying transition probabilities are applied for MS models, enabling them to switch between different regimes (de Souza e Silva and Legey 2010; Gagniuc 2017). If a given time-series faces correlations with itself at different points in time by a specified function of decay, we speak of autocorrelation or serial-correlation, present for instance in unit roots, trend-stationary processes or autoregressive processes (Doob 1990; Mackevičius 2016). The autoregressive model (AR), which is applied as a stochastic difference equation to describe time-varying processes, can be mentioned as highest counted representative in our sample. Further, the AR(1) model is seen as a discrete time adaptation of the continuous Ornstein–Uhlenbeck (OU) process, as well as an expression of a two-state Markov chain (Cordis and Kirby 2014; Gagniuc 2017).
The generalisation of the AR model is called vector autoregressive model (VAR) and can capture linear interdependencies between respective variables (Parzen 2015; Zhou et al. 2011). Another autoregressive model is the Moving-Average (MA) model, which is assumed stationary and mostly applied to univariate time-series data, since the specified output variable depends linearly on its own and the respective error terms past (Bhar and Hamori 2005; Karlin and Taylor 2012). Together with the AR model, the MA model is a key component of the autoregressive-moving average (ARMA) model, which provides a parsimonious two polynomial description of a stationary stochastic process (Sun et al. 2015; Rahman and Saadi 2008). When the data indicates non-stationarity properties, the generalisation of ARMA, namely, the autoregressive integrated Moving-Average (ARIMA) model can be applied (Serfozo 2009; Maia and de Carvalho 2011). We label the innovations of a stochastic process as a function of previous periods of the occurring error term, which implicates a non-constant error term variance (Brooks 2014; Shreve 2004). When the variance of the error term follows an AR model, we can model time-series exhibiting time-varying volatility and volatility clusters by applying the autoregressive conditional heteroscedasticity (ARCH) model (Brooks 2014; Engle 1982). Moreover, when regarding the value development in ARCH models, the volatility is assumed to be completely deterministic in nature, contrasting the family of stochastic volatility (SV) models (Brooks 2014). In SV models, the variance of a stochastic process is assumed to be time-varying like in ARCH specifications, but further seen as randomly distributed. Therefore, it can be seen as a non-deterministic stochastic process in itself, which is previously described as representative Markov process realisation and builds on a BM (or Wiener) process as a basic model (Takahashi et al. 2016; Gagniuc 2017). The SV, in contrast to an ARCH model, is appropriately modelled via the generalised autoregressive conditional heteroscedasticity (GARCH) model if the variance of the error term follows an ARMA model specification (Engle 1982; Bollerslev 1986). If a unit root is present in the GARCH process, it is possible to apply an integrated GARCH (IGARCH) model (Tsay 2010).
Regime switching and smooth transition models
The most commonly applied model in terms of regime switches are MS models (Chang et al. 2017). Examples for extensions are MS-VAR models and specified threshold models. The latter apply time-varying transitions in the MS or respective autoregressive fractionally integrated moving average (ARFIMA) model structures (Ma et al. 2017; Piger 2007). As we regard MS models as well as ARFIMA specifications, the distribution of respective innovations is assumed to be normal. Nevertheless, regimes of financial time-series are not normal, but leptokurtic distributed, therefore, normality also should not be assumed inside the respective regimes, leading to estimators’ loss of efficiency and consistency in MS models (Shi and Ho 2015). Threshold ARFIMA (TARFIMA) models can cope with the regime-switching volatility dynamics (Ma et al. 2017). In more detail, examining the DGP of a volatility series under the assumption of persistent volatility shocks leads to further extensions in the models.
Examples for those extensions are the regime-switching ARCH (SWARCH) model, which assumes an ARCH(q)-process within the MS-model, an MS-GARCH realisation, whose parameters fluctuate between low and high volatility regimes, or alternatively an adaptive GARCH (A-GARCH), which respects structural changes in the conditional variance with intercept switches between regimes as dictated by the smooth flexible functional form of Gallant 1984 (Charfeddine 2014; Chang et al. 2017). If the regime is left after one period, jump model specifications can be calculated (Aït-Sahalia et al. 2015).
Nonlinear models
In the volatility of a financial time-series, or realised volatility (RV), highly persistent dynamics, which tend to be nonlinear in nature, are observable (Ma et al. 2017). Modelling nonlinear and persistent dynamics in RV can enhance forecasting performance (Alexandridis et al. 2017). Introducing thresholds and smooth transition probabilities into AR processes result in nonlinear TAR and STAR models that are able to cope with above mentioned dynamic features (Guidolin et al. 2009; Lin et al. 2012). Additionally, HMM models, which are the simplest dynamic Bayesian network realisations, can be applied to examine nonlinear time-series properties. The term “hidden” indicates provided information about sequences of states, whilst the state itself is not directly observable, even if the state transition parameters are perfectly known (Baum and Petrie 1966; de Souza e Silva and Legey 2010). Different models for respective nonlinearities are the nonlinear asymmetric GARCH (NGARCH) as well as the smooth transition ARCH (STARCH) and smooth transition GARCH (STGARCH), which provide possibilities to deal with nonlinear volatility dynamics and asymmetric features (Zhu and Galbraith 2011).
Asymmetric models
The volatility dynamic process can be distinguished in distinct processes, depending on the positivity or negativity of news impacts leading to asymmetry within the volatility realisation (Palandri 2015; Sener et al. 2012). Especially, the behaviour of noise traders can cause anomalies, due to investor’s sentiments, which can be captured by applying a SWARCH, or an asymmetric version of the exponential GARCH (EGARCH) model with no parameter restrictions (Ramiah et al. 2015; Wang et al. 2016). Regarding the conditional variance, it is seen as favourable to incorporate thicker tails and asymmetries, which can be specified in the indicator function of the Glosten-Jagannathan-Runkle GARCH (GJR-GARCH) model (Wang et al. 2016; Palandri, 2015). Since the autoregressive dynamics of volatility display persistency, time-varying characteristics as well as asymmetries, a flexible classification of Markov chains, labelled as discrete stochastic autoregressive volatility (DSARV) models, is able to accommodate stated features properly (Cordis and Kirby 2014). Additionally, regarding time-varying asymmetric response changes in volatility across different regimes, allows for non-zero thresholds, which can be applied in nonlinear as well as asymmetric models (Kilic 2011; Amado and Teräsvirta 2014).
Structural break models
Structural changes or regime switches are indicated by inherent structural breaks, which results in sudden asymmetric changes within respective regression parameters (Mumtaz et al. 2017; Hansen 2001). Building structural break models or break point models (BPMs) require to determine the points in time at which the break occurs, called break-dates or break-points (Bekiros and Marcellino 2013; Choi et al. 2010). To test for structural breaks, the Chow-test or cumulative sum (CUSUM) test is applicable, among others, such as Lagrange multiplier (LM) test variations (Bekiros and Marcellino 2013; Conrad et al. 2011).
Long memory and fractional integration models
In contrast to short memory, long memory or long-range dependence is seen parallel to self-similar processes (e.g., fractal processes), since their decay functions follow a given power law and not an exponential realisation (Malamud and Turcotte 1999; Samorodnitsky 2007). Since persistency indicates nonlinearity, smooth transitions, should be included within respective models (Kilic 2011; Lin et al. 2012). Additionally, to cope with the non-exponential power laws of long-range dependence, it is suitable to apply fractional integrated models, which allow for non-integer values in their respective differencing parameters, resulting in slower rates of decay (Granger and Joyeux 1980; Hosking 1981). Only dealing with long memory like in fractional integrated GARCH (FIGARCH) models, leads to hyperbolic decays in the ACFs, mainly caused by structural breaks. Regarding structural breaks by allowing the intercept of the FIGARCH to follow a slowly time-varying flexible function, leads to loss of efficiency, if no structural breaks occur in the respective period (Amado and Teräsvirta 2014; Charfeddine 2014). The FIGARCH can be generalised by allowing the intercept to deterministically alter its values, being possibly extended by using an adaptive form (A-FIGARCH) to cope with structural breaks (Amado and Teräsvirta 2014; Charfeddine 2014). To account for long memory and nonlinear dynamics in the conditional variance at the same time, a smooth transition fractional integrated GARCH (ST-FIGARCH) can be applied, which also generalises the FIGARCH by allowing for smooth transition probability specifications (Chkili et al. 2014; Choi et al. 2010). Extending asymmetric power formulations of variance with fractional integration leads to sufficient results, as seen in FIAPARCH models (Shi and Ho 2015; Conrad et al. 2011). FIAPARCH models increase conditional variance specifications flexibility by allowing for the distinct processes of positive and negative news impacts. If implementing controls for long memory and regime switches, a distinction should be possible, as seen in ARFIMA or MS specifications (Scharth and Medeiros 2009; Shi and Ho 2015). Further, extensions of given models are possible, e.g., ARFIMA-FIGARCH models, which perform better out of sample, or by applying ARIMA-GARCH, ARFIMA-GARCH, ARFIMA-IGARCH among the before-mentioned ARFIMA-FIGARCH model to cope with extreme events, which origin of long memory behaviour of time-series (Charfeddine 2014; Chkili et al. 2014). In addition, there exists no formal test, which can differentiate between true or spurious long memory in literature until the end of the year 2019.
Nevertheless, one may test for structural breaks and long memory by applying iterated cumulative sum of squares (ICSS) algorithms, rescaled range (R/S) statistics Gaussian semi-parametric methods (GSP), detrended fluctuation analysis (DFA) or two-step feasible exact local Whittle (2FELW) methods, among others (Chalamandaris and Tsekrekos 2011; Charfeddine 2014; Liu 2015). As indicated, long-range dependence follows non-exponential power laws, facing similarities to self-similar or fractal processes (Samorodnitsky 2007).
(Multi-)fractals momentum and trend models
Self-similarity is a characteristic property of fractals resulting in scale invariance (an exact form of self-similarity) (Mandelbrot 1977, 1967). A fractal itself is a non-differentiable scaling subset of a Euclidean space, which fractal dimension exceeds the referring topological dimension (Mandelbrot 2004). Therefore, fractals show similar patterns at increasingly small scales, labelled self-similar. If the replication at each level is identical, the fractal is affine self-similar (Mandelbrot 1977). Self-affinity is defined as another characteristic of fractals, which means different scaling of realised values in each of the dimensional directions. Financial market movements reveal self-affine properties, which can be applied for via affine level transformations (Hallam and Olmo 2014; Hassan et al. 2011). Further, regarding characteristics of power laws (i.e., scaling laws) are scale invariance, well-defined means and finite variances. Additionally, power laws in natural processes, do not exhibit well-defined variances, indicating the existence of black swan events (e.g., on financial markets) (Müller et al. 1990; Glattfelder et al. 2011). It can be concluded that financial time-series exhibit scaling characteristics, following specified power laws, due to fractality and the resulting self-similarity property in the respective DGP (Mitzenmacher 2004; Etro and Stepanova 2018). Neoclassical (traditional) methods as well as GARCH class models are not able to reflect multi-scaling characteristics of financial time-series data (Ma et al. 2017; Ñíguez and Perote 2016). If we intend to capture fractal features in respective models, the heteroscedastic AR (HAR) model, which is a linear model with constant coefficients, is applicable. It can cope with long memory and multi-scaling behaviour of data series and, therefore, often executed when describing the RV dynamics of high frequency (as well as other) data sets (Ma et al. 2017; Andrada-Félix et al. 2016).
Another model type capable of respecting fractality is the before-mentioned MSM model, which corresponds to multi-scaling, long memory and structural breaks, since it applies parsimonious parametrisations, while allowing for hundreds of different regimes at different time levels in the respective volatility process (Charles and Darné 2017; Wang et al. 2016). The MSM assumes hierarchical as well as multiplicative structures of the heterogeneous volatility components, which contrasts neoclassical (or traditional) volatility models fundamentally (Charles and Darné 2017; Wang et al. 2016). To cope with the drawbacks of MSM, namely, to generate outliers and spurious long memory, the parameters can be treated more parsimoniously by applying heterogeneous rates of decay while assuming the underlying returns follow a Markov chain with multi-frequency SV (Gagniuc 2017; Wang et al. 2016). Regarding the return distributions of financial time-series, we cannot testify Gaussianity.
Once we introduce trade-time, which is determined to be dependent on subordinated transaction processes of actors, we are able to see nearly Gaussian distributions in the respective processes (Aldrich et al. 2016). If a Gaussian random walk is generated while applying trade-time, it is fully consistent with a fat-tailed, Lévy-stable distribution (Aldrich et al. 2016). Thus, trade-time returns, which are assumed unconditional exhibit fat tails as well as low-volatility clustering. Hence, it is possible to develop a time-changed variant of the BM process, allowing for non-Lévy directing processes, characterised by inter-trade durations, as displayed in the autoregressive conditional duration (ACD) model or the Markov switching multifractal duration (MSMD) model (Aldrich et al. 2016; Herrera and Schipp 2013). This opens ways towards momentum strategies, building on the persistence or trending of financial time-series (Ramiah et al. 2015; Berghorn 2015). These trends can be measured by applying wavelet decomposition schemes in combination with R/S statistics to measure the respective momentum and Hurst exponent (Celeste et al. 2019; Berghorn 2015). Additionally, it is possible to enhance the performance of momentum strategies by introducing percentile cut-offs, while following an Jegadeesh and Titman (JT-) momentum trading rule to identify respective trends (Mitra et al. 2017).Momentum can also be applied in dynamic factor models, which can be based on statistical arbitrage, while trading on different time horizons simultaneously. Stylised facts occur on different scales for financial time-series. Once we regard more than one time-series, but the aggregate, we analyse the financial market as a whole, which results in multi-dynamic or multi-fractal appearances (Hallam and Olmo 2014; Bekiros and Marcellino 2013).
Spill-over and contagion models
If we aim to present the transmissions between volatility on different markets, the HAR-ADL (autoregressive distributed lag) model can be applied to calculate the RV, whilst TVAR or MS models are additionally able to cope with turmoil regimes, indicating strong evidence for structural breaks in causality patterns and contagion (Jammazi and Aloui 2010; Jung and Maderitsch 2014). Moreover, to depict spill-over effects among different financial markets, MGARCH models, especially, the Baba, Engle, Kraft and Kroner specification (BEKK-GARCH, or simply BEKK model) of the MGARCH, which is applied to investigate international market linkages, are suitable (Khalfaoui et al. 2015). Further, bivariate GARCH models, also a bivariate BEKK-MGARCH, which simultaneously estimates moments on different markets, as well as combinations such as dynamic conditional correlation (DCC) with GJR-GARCH specifications (DCC-GJR-GARCH) are considerable (Khalfaoui et al. 2015; Adams et al. 2017). MGARCH models are attractive, since they impose correlation dynamics, resembling time-varying volatility (Adams et al. 2017). Now, if we take a closer look at the multi-scaling details, it is possible to decompose spill-over on moment’s effects (e.g., mean or variance) into numerous sub-spill-overs, which occur on different scales, due to heterogeneity on financial markets (Khalfaoui et al. 2015; Ang and Timmermann 2012).
Signal processing
Tending or scaling time-series yield two meanings, namely, (1) distributions of financial instruments behave differently at different frequencies and (2) financial markets reveal frequency properties as well as time properties, which hence are exploitable (Chakrabarty et al. 2015).
To enable those exploitations, signal analysis, which is taken from the field of applied physics, can be applied (Blackledget 2006). Signal analysis encompasses topics such as MRA, Fourier transformation (FT) and wavelets, among others. FT characterises the frequency composition of a given time signal while applying linear combinations of basic trigonometric sine and cosine functions on periodic (or stationary) functions (Chakrabarty et al. 2015). Nevertheless, extracting the frequency information with FT results in a complete loss of time information, since the basis-functions are not localised in time, as well as in the inability to detect spectral variations across time (Chakrabarty et al. 2015). If we still want to apply FT concepts on signals with properties such as for example long memory, fast fractional differencing, which is based upon fast FT (FFT) offers recommendable computational speedups. Additionally, FT does not cope well with non-stationary (or non-periodic) signals, since sinusoids basic functions in the transformation range to infinity and are not localised in time, which voids detection of frequency component variations across time (Chakrabarty et al. 2015). Application of constant time localised windows, which each will assumed to be stationary and, therefore, be analysable for spectral components with FT, is an often-used extension varyingly called Short-Time FT (STFT), Windowed FT (WFT), Local FT (LFT) or Gabor Transformation (Chakrabarty et al. 2015).
The wavelet multi-scale analysis or wavelet transformation (WT) was developed from synergies with FT, driven by its drawbacks as well as from harmonic analysis and coherent state formalism (Chakrabarty et al. 2015). To detect changes of frequency components across time, wavelets can be translated across time, since a wavelet basis is a flexible alternative for the Fourier basis. It is possible to capture frequency variations across time or time variations across frequency ranges when applying respective wavelet functions (Boubaker and Raza 2017). By considering dyadic regrouping of FT, wavelets can be seen as undulatory mathematical functions with constant shape, limited duration and time integral of zero (Chakrabarty et al. 2015; Jammazi and Aloui, 2010). To define this phenomenon in more detail, the analysis requires orthogonal bases obtained by dyadically dilating and translating a pair of wavelet functions, called mother and father wavelet (Boubaker and Raza 2017). Smooth and low-frequency components of a given signal are captured by the father wavelet, which is a scaling function with corresponding coarse scale coefficients, while details and high-frequency parts are described by the mother wavelet, whose coefficients are localised in time (i.e., prone to the Heisenberg uncertainty) (Boubaker and Raza 2017; de Souza e Silva and Legey, 2010). To analyse multi-scale coherence and phase properties in multiple time-series, which are non-stationary and time-varying, wavelet coherence models (e.g., maximum overlap discrete wavelet transforms [MODWT]) can be implemented, capturing covariation of both time- and frequency varying features (Boubaker and Raza 2017; Khalfaoui et al. 2015). Wavelet decomposition methods are able to cope with first and second-order non-stationarity, asymmetries, heterogeneity, structural breaks and nonlinearity, among others (Chakrabarty et al. 2015).
Possible extensions are the optimisation of time–frequency localisations by orthogonal wavelet basis functions, which are part of Hilbert spaces as well as the transition from continuous to discrete wavelets based on computer sub-band filters (Chakrabarty et al. 2015; Jammazi and Aloui 2010). The latter application of low- and high-pass filters via pyramid algorithms are part of formerly introduced MRA and decompose finite energy signals into dyadic frequency bands, which can be reassembled using inverse discrete wavelet transformations (Chakrabarty et al. 2015). Alternatively, the already mentioned MODWT can be used instead of discrete wavelet transforms (DWT), since it applies non-orthogonal transforms leading to non-dyadic length sample sizes, invariant translations and results in higher resolutions at coarser scales (Alexandridis et al. 2017; Khalfaoui et al. 2015). Locating MODWT into discrete Hilbert spaces results in MODHWT, allowing for multi-scale coherence and phase property investigations of non-stationary and time-varying signals (Khalfaoui et al., 2015).
Neural networks and machine learning algorithms
Examples of the application of NNs next to volatility analysis are predictions of financial market indices, bankruptcy, stock performance, macroeconomic indications, the rating of bonds and derivatives, among others (Aguilar-Rivera et al. 2015; Tkac and Verner 2016). NNs are able to deliver approximations of nonlinear processes, while setting no further beforehand assumptions about the DGP (Aguilar-Rivera et al. 2015; Tkac and Verner 2016). Most of the time backpropagation with gradient decent algorithms are deployed in same-labelled conventional backpropagation NNs. Other implementations are support vector machines (SVMs), fuzzy NNs and multi-layered NNs, which stand in contrast to more traditional logit models in terms of bankruptcy predictions as well as crisis, risk and fraud assessments (Tkac and Verner 2016). Furthermore, combining mathematical techniques and models with NNs delivers promising results (Tkac and Verner 2016). One example are volatility forecasts with wavelet neural networks (WNNs), where the activation function is represented via wavelet functions, called wavelons (Alexandridis et al. 2017). Others are the determination of shifts with genetic reinforcements, or hybrid NNs, instead of standard backpropagation approaches or SVMs (Aguilar-Rivera et al. 2015; Tkac and Verner 2016). Optimisations are applicable while deploying a type of algorithm taken out of computer science, namely evolutionary or genetic algorithms (GA) and genetic programming (GPs), representing white-box solutions (Aguilar-Rivera et al. 2015; Alexandridis et al. 2017).
Copula models
Nonlinearity, asymmetry, autocorrelations, heavy tails or other stylised features occur within time-series marginal and joint probability functions. Therefore, a new type of function, namely, a copula function, can be applied (Righi and Ceretta, 2013). Copula families determine the shape and magnitude of nonlinear serial- and cross-interdependence between returns and volatilities of financial instrument time-series, since they are functions that link a univariate marginal to its respective multivariate distributions (Righi and Ceretta 2013; Lira Salvatierra and Patton 2015).
It is mostly possible to map vectors of random variables into a vector with uniform margins, which can be split into the respective dependence, namely, the copula (Righi and Ceretta 2013; Lira Salvatierra and Patton 2015). Copulas do not need information about the marginal distribution; hence, it is possible to model an individual series, while the interdependence is displayed via the copula function. The copula returns the joint probability of respective events as a function of the marginal event probabilities building univariate behaviour of regarded variables (Righi and Ceretta 2013; Bodnar and Hautsch 2016). Copula functions can further be related to other dependence measures; for example, the absolute dependence by Kendall´s tau through conversions with according bivariate copulas (Righi and Ceretta 2013; Bodnar and Hautsch, 2016). To model volatility, the Joe copula, Clayton 180° rotated copula (survival), Gumbel copula, BB6-copula or the BB8-copula, among others, can be implemented (Righi and Ceretta 2013). If we map innovations of a non-negative dynamic process (e.g., volatility process) into the Gaussian domain, it is possible to apply a copula transformation, by assuming the innovations origin from a vector multiplicative error model (VMEM) (Righi and Ceretta 2013; Bodnar and Hautsch 2016). Trying to capture higher-order dependence structures can be implemented by decomposing the dynamics via Gaussian copulas (Righi and Ceretta 2013).
Extreme value models
To determine the potential loss and risk, which may occur during financial crises or other negative impacts, we can apply risk measures such as the expected shortfall (ES), Value-at-Risk (VaR), RiskMetrics, among others, or can alternatively apply the concept of extreme value theory (EVT) (Chiu and Chuang 2016; Sener et al. 2012). The ES is a coherent risk measure, which considers extreme negative returns in a given financial time-series (Zhu and Galbraith 2011). When we talk about the RiskMetrics model, we mean a parametrisation for volatilities of financial instrument return-series executing an exponentially weighted moving average (EWMA) for the conditional variance (Chiu and Chuang 2016). One of the most popular and widely spread risk-loss measure is the VaR method, which estimates the distribution function of a specified asset return-series, with a fully parametric setup for volatility dynamics under the assumption of conditional normality (Zhu and Galbraith 2011). In consideration of stylised facts and clustering of extreme events and crisis paired with serial-correlations, the underlying Gaussianity and ~ iid assumptions typically are violated, leading to massive misspecifications of the VaR as shown by financial institutions during market turbulences (Zhu and Galbraith 2011; Chiu and Chuang 2016). These volatility clusters, paired with before-mentioned effects, result in critical issues within practical implementations of VaR during turmoil, crises or other extreme events, which could lead to respective corporate insolvencies (Herrera and Schipp 2013). This is due to the unconditional DGP method of the VaR estimates, which focuses on the entirety of the predefined distribution and does not regard potential dynamics in the respective underlying volatility process (Sener et al. 2012).
To cope with those drawbacks, extensions of the VaR methods can be seen, such as the fractionally co-integrated VaR (CoVaR), which assumes the time between extreme events as a distinct stochastic process (Zhu and Galbraith 2011). Another, more common extension is the conditional VaR (CVaR) method, which when fractionally integrated (FCVaR) is the link in the literature to unit root co-integration tests (Chiu and Chuang 2016; Herrera and Schipp 2013). Applying asymmetric characteristics to CVaR methods result in more accurate calculations (Zhu and Galbraith 2011). Further, the highest return-to-risk performance under capital allocation penalisations can be attained by respecting for volatility dynamics in corresponding distributions, namely, by applying conditional autoregressive VaR (CaViaR) models (Chiu and Chuang 2016; Rodriguez et al. 2017). Along with the VaR specifications, it is possible to apply the EVT concept in combination with other models to determine extremes. Examples hereto include applications of EVT to the conditional return distribution through a two-stage method in combination with GARCH specifications for respective residuals, called GARCH-EVT (Rodriguez et al. 2017). EVT with residuals of ARMA-GARCH models, follow an EVT distribution, which is designed to model extreme movements with given excess loss over a given threshold. Once this threshold is reached, the excess loss distribution is displayed via a generalised Pareto distribution (GPD), while the VaR can be extracted via the peaks over threshold (POT) model (Chiu and Chuang, 2016; Rodriguez et al. 2017). If clusters in volatility are assumed, a self-exciting point process version of the POT method is applicable, called Hawkes POT (Rodriguez et al. 2017). Another method to capture respective clusters is the combination of ACD and POT (ACD-POT), which in contrast to GARCH-EVT is able to model the conditional intensity for inter-exceedance times, which is interpretable as volatility proxy (Chiu and Chuang 2016; Rodriguez et al. 2017).
Simulations, performance and other methods
If sufficient data is not present, or if we aim to model defaults or want to reduce future errors, simulations such as the Monte Carlo (MC) simulation or historical simulation are applicable (de Almeida et al. 2018; Fahling et al. 2018). MC simulation means generating respective return-series based on a stochastic differential equation, which reflects the asset dynamics. Hence, MC simulations can for example differentiate between pure ARFIMA and MS processes (Sener et al. 2012). Alternatively, MC simulations can be employed with maximum likelihood estimators for the inference modelling of SV in Markov Chain Monte Carlo (MCMC) models (Saloff-Coste 2004; Shi and Ho 2015). Another simulation method is the historical simulation, which actually is no simulation, since distributions of actual return-series are used to determine sampled quantile measures (Chiu and Chuang 2016; Sener et al. 2012). Both historical and MC simulation are non-parametric approaches, which aim to determine quantiles in tailed ends of specified distributions, assuming the exploitability of the past for near-future predictions (e.g., performance, bankruptcy or default probabilities, among others) (Chiu and Chuang 2016; Sener et al. 2012).
Assets and data sets
Table 8 provides an overview regarding asset classes, periods and frequencies and state asset classes and the corresponding data specifications, financial instruments or underlying financial instruments in case of derivatives sorted, descending by denoted frequency (from high to low). For each asset class, we count the according financial instruments for each frequency notation separately. This indicates that the same financial instrument can occur more than once in each asset class, but in a different frequency notation, respectively. The count defines how often the authors use a specific financial instrument time-series at a given frequency. In total, we identify 13 asset classes, 8 different frequency notations and a sum of 180 time-series. The most frequently analysed asset classes are stocks, commodities and exchange rates at a daily frequency. Sorted by total count per frequency, the daily-denoted financial instrument time-series of S&P500, Nikkei225, WTI-Oil, DIJA30 and FTSE100 (the last three facing equal counts) take dominant roles in the sample. In addition, authors regard daily denoted time-series of HSI, DAX30, Brent-Oil, USD/JPY, USD/EUR, CAC40 and USD/GBP as data sets worthy to analyse. Notwithstanding, we abstain from taking a particular position in the ongoing discourse of whether opportunity and volatility time-series should be recognised and acknowledged as distinct asset-class or not, but state them as such for didactic reasons. We do so because some authors mention VIX time-series as differently typed entities in comparison to other asset typesFootnote 4 (Basher and Sadorsky 2016; Fahling et al. 2018; Nohel and Todd 2015).
Models and research design
We analyse the complete context, data analysis and mathematical sections of the sampled literature and note every unique method (e.g., models, algorithms) occurrence per paper within a dictionary accordingly.Footnote 5 Table 9 shows an overview of the mathematical composition. We find a total of almost 850 unique techniques, models, tests and other mathematical constructs within the analysed papers. More than five authors account for only 80 composites each at the same time in our sample, which equals 9.42% of the total composition. This means, only in 80 cases, more than five authors apply the same mathematical method. In contrast, 634 findings occur only once in the sample, which corresponds to 74.68% of all findings. In total, we count 1905 non-unique models, tests and other mathematical method usages contained in the condensed list of literature. On average, we identify 14.3018 methods (with a standard deviation of 7.060) in total per research paper, from which six techniques or models are unique in comparison with the overall condensed list of literature. We notice that only a few authors apply the same set of mathematical methods at the same time, whilst the majority implements different methods. We differentiate these 849 mathematical procedures into six categories: “Models”, “Tests-Statistics and Estimators”, “Distributions”, “Ratios and Criterions”, “Algorithms, Processes and Mathematical Functions” and “Other Types”, which do not fit into the before mentioned categories. We find 387 models (45.58%), 155 algorithms, processes and functions (18.26%) as well as 136 tests, statistics and estimators (16.01%) as main categories of the 849 total unique composites. In the following, we present the highest-ranking findings in each category by further introducing the top 15 counted results (with example reference and explication) if they have at least a count of two.
First, we ascertain that neoclassical (traditional) models as well as basic variants such as GARCH, ARCH, AR, ARMA and VAR to be the highest-counted models as annotated in former sections and as displayed in Table 10. The analysis of the data sections of the referring papers indicate that authors tend to apply basic and accepted models as benchmark for potential enhancements, extensions or the creation of new models. In addition, several historical enhancements have been established as points of orientation as well, namely, EGARCH, FIGARCH, IGARCH ARFIMA, HAR and MCMCs among others, which can be interpreted as ongoing extension of respective models under consideration with regards to earlier mentioned stylised facts and properties.
In terms of statistical tests, statistics and estimators, we state the highest-counting method to be the maximum likelihood estimation (for distribution parameters). Regarding tests, accepted set ups such as Jarque–Bera (for normality), Augmented-Dickey-Fuller (for unit roots), Ljung-Box (for ACs), Diebold-Mariano (for forecast performance comparison), Kolmogorov-Smirnow (for distribution fits) and Phillips-Perron (for integration) tests take the highest place in the authors test choices as stated in Table 11. Additional tests are the Kwiatkowsi–Phillips–Schmidt–Shin (for trend stationarity), likelihood (for model comparison), model confidence set (also for model comparison), probability integral transformation (for uniformity) and the Wald (for variable significance) test.
The most frequently applied distribution is the Student´s t – Distribution executed to test for Gaussianity in a given set of data (see Table 12). We find other counts of distributions such as the Weibull (for failure rates over time), generalised Pareto (for decay densities), gamma (for maximum entropy probabilities), complementary cumulative distribution function (CCDF) (for tail exceedances), generalised error (for continuous symmetry) and the generalised extreme value (for EVT distribution) among others.
Regarding ratios and information criterions, the Bayesian information criterion, synonymous with the Schwarz information criterion (both deployed for model selection), the Akaike information criterion (for model quality determination) count highest as Table 13 displays. Furthermore, the authors apply the mean squared error, which measures average squared model errors. In addition, scholars seem to accept root mean square errors (for forecasting performance differences), quasi-maximum likelihood estimators (for distribution parameters) and mean absolute errors (for continuous variable differences) as vastly acceptable measures.
Additionally, the Sharpe ratio (for excess return), quasi-likelihood (for overdispersion) and the mean square forecast error (for prediction quality), among several others, must be mentioned.
Note, that the number of models fairly exceed those of distributions, tests and performance measures. Since the same test or performance measure as well as the same distribution is applicable for many model realisations and data sets at the same time, their respective total number is lower. Table 14 shows algorithms, processes and functions, which we cluster in three categories, namely, stochastic processes, signal analysis as well as other diverse functions. In terms of stochastic processes, we see the DGP as means to describe potential real data set mechanisms, random walks, BMs and ACs. Signal analysis represents different types of FTs, WTs and functions.
Table 15 shows framework calculation methods. Most of these belong into the domains of artificial intelligence (AI), into signal analysis or are split into other methods. The majority of AI concepts contain ANNs (or NNs) and backward propagation of variance, while MRA is part of signal analysis, respectively. Others (e.g., superior predictive ability, filtered historical simulation method and mixed data sampling) are frameworks for simulations or performance measures.
Interconnections between models and blind spots of research
We investigate interconnections of the category “Models”, while visualising interconnections by a heat map as displayed in Fig. 1. To gain deeper insights from 387 unique models, we firstly analyse them and form root- and junction model groups. Each group can be interpreted as particular model family, while a junction stems from its root.Footnote 6 This means, a junction model is the offspring of a root model. Thus, we label the latter proposition as model evolution. Additionally, we take stylised facts and properties into account, which the authors reference or seem important enough to explicitly model into their mathematical conceptions. Table 16 shows 13 root families, 14 junction families and four properties. For each root family, existing junctions are presented. The first root-junction tree displays AR models. HAR and VAR models are based upon AR models, which means that HAR and VAR are the junctions of the root AR. The next root are MA models, which in this case cross with the AR root to create combined junctions, namely ARMA, ARFIMA and ARIMA models. The same logic applies for CC and GARCH model roots and their respective junctions.Footnote 7 In addition, some roots as well as junctions may have been created to express specific properties or stylised facts accordingly. The properties, which are partly inherited in roots and junctions, are fractal characteristics, smooth transitions, regime switches and threshold functionalities. We deduce whether or not a selected single model belongs to one or more respective model families. If the model is part of several model families, we mark it accordingly. Further, we count the models, which belong to one model family only.
Symmetric combinatory matrix of model variations per model family, which combines all defined roots, junctions and properties with each other. The main diagonal itself represents the number of variations (saplings) occurring solely within each root or junction. Off the main diagonal counts show which root or junction- model families or properties are combined with each other and how often. Since it is symmetric, the counts above (or below) the main diagonal are redundant by conception
Therefore, one unique model count represents one variation of the respective root or junction model (labelled saplingFootnote 8) of the concurring model family.
We present their aggregated numbers, which we interpret as the number of variations in each respective model family. With this approach, we separate the variations in two aspects. First, the number of variations of the root-model within a model family itself and second, the number of variations of models, which originate from several model families. If a model belongs to more than one model family, each respective model family receives one variation count as result. We consider several models as junction, even if these models originally belong to a given root-model family also represented within the graphic. This is due to the fact that these respective junction models form families of their own. Therefore, we define such junction families as too important to cluster them as saplings into their original root-model family. To sum up, we see two kind of model families, namely root model and junction model families, which we interpret as daughter families of a given root model family. Variations (or saplings) of the latter two can additionally represent stated properties, which seem to be worth modelled into authors research as new model, respectively. We did not include all stylised facts and properties shown in this study since many root or junction models themselves can properly incorporate some of the stated features. We only include properties, which are explicitly modelled as model family variation, hence as a new model specification.
A combinatory matrix of model variations (or saplings) per model family is shown in Fig. 1 and combines all defined root and junction model families and presented properties with each other. The main diagonal itself represents the number of variations (saplings) occurring solely within each root or junction model family, respectively. There are models whose only purpose is to catch some of the announced properties, which we state in the matrix as well. Examples of such models are MSM, TGARCH, MRS-GARCH, ST-GARCH, 2S-ARFIMA or TSTRSM, among many others. The other values off the main diagonal represent the number of variations (cross-saplings), which occur in combinations of the model families. Figure 1 shows which root model families, junction model families or properties are combined and how often. The families with the highest number of saplings are the GARCH family with 26, the volatility family (e.g., RV, IV models) with 15, the Copula family with 10 and the AR family with 7 variations. We exclude the “others family” with 52 counts in this comparison since it represents unique models that do not belong to a superordinate family. The ones with the lowest amount are the threshold and regime-switching property-based families with zero and one sapling correspondingly, the MGARCH as well as the ARIMA daughter families and the GJR-GARCH family with one sapling each. As we continue with the cross-combinations between different model families, we identify four major, two weaker fields and some single occurrences of model family “pairings”. The field with the highest counts represents the combinations of BEKK-GARCH, Markov and volatility models with the stated properties, especially, the combinations of Markovian with regime-switching properties bear models with 23 saplings, which seem to be very promising in terms of combination numbers, followed by the combination of general volatility models with unrelated other models counting 12 variations.
The second field represents the same families, namely BEKK-GARCH, Markov and volatility models in combination with AR, HAR and VAR families. The pairing of volatility models with the HAR family leads with 12 respective saplings. The third field consists of AR, HAR and VAR families crossing the given properties. We find that HAR and other unrelated models count 12 variations. The fourth major field takes a combination of GARCH, EGARCH and FIGARCH families with ARMA, ARIMA and ARFIMA families, while the highest count of eight saplings belongs to the GARCH and ARMA constellations. The first of the two minor fields consist of the combination of GARCH, EGARCH, FIGARCH families with the respective properties, where the combination of GARCH models with regime-switching and threshold-based models are represented with eight and, respectively, six counted saplings. The second minor field shows the crossing of property bearing models with themselves, mainly resulting in eight counted saplings for fractal and regime-switching model combinations. Furthermore, we identify some single occurrences in the combination of BEKK-GARCH and Markov families counting seven respectively, in the combination of Markov and VEC as well as regime-switching models and ARFIMA models bearing five counted saplings each. Our approach allows us to identify some blind spots or “missing links”, i.e., combinations that are not sufficiently tested in prior research.
First, there are model families, with which we do not see any intersections with any other model family, such as copula, probit or logit, MA and ARIMA model families. Second, there exist clusters, which do not show combinations of certain model families at all. Examples are the combination of VEC, ACD and POT families with GJR-GARCH, AR, HAR, VAR, MA, ARMA, ARFIMA, ARIMA, CC, CCC, DCC and BEKK-GARCH models. To sum up, we find enhancements and variations in each model family itself respectively, as indicated by Poon and Granger (2003). Therefore, we confirm their expected course of action, stating that initially variations occur inside of root model families themselves as logical first step, especially, shortly after the occurrence of the Financial Crisis in 2008. Furthermore, we confirm combinations of model families as crossing of different model families as successive next step, yielding the highest number of saplings. As a third step, we recognise the combination of root and junction families with the properties of financial instrument time-series as well as the combination of model families with unrelated models not regarded so far. In addition, we either remark empty spots as mathematically not viable options, simply not researched model combinations or combinations, which may not be contained in our sample.
Frontiers, conclusions and avenues of research
We identify frontiers (or boundaries) by examining the research papers data sections, findings and parts of the conclusions. Further, we define frontiers as unresolved issues or open gaps, as research boundaries, which mirror questions and upcoming challenges and as technical limitations. In total, frontiers in our understanding should reflect the state-of-the-art of current research activities as well as the border towards technological capabilities. Thus, we group frontiers, displayed in Table 17, into three topics, namely, boundaries and limitations arising with modelling extensions itself, borders of understanding of the causes or origin of given properties (or certain effects) and the front occurring with technological enhancement or improvement of given methods or models.
Volatility modelling
Since financial markets are highly dynamic environments, a sufficient level of adaptability is required, which in terms of determining the true DGP of financial assets drive the border for existing econometric methods (Narayan and Smyth 2015; Ghandar et al. 2016). In the scientific literature the latter supposition is centred on econometric models or stochastic time-changes applied to explain the underlying dynamics, which have mostly been drawn out of the volatility directly. Further, determining the trading dynamics outside the first conditional moments, but also in conditional covariance and by inserting time-varying uncertainty measures, resulting in dynamic correlation structures, can be stated as future tasks of modelling attempts (Aldrich et al. 2016). Not only the correct specification of dynamics, but also of the full-featured variety of other stated stylised facts and properties, determine the frontiers in terms of understanding these stylised facts as well as in upcoming implementations of respective model implementations.
Predictive capabilities
Reviewing forecasting attempts with nonlinear specifications reveal high demands of computational power as well as the menace of overfitting, which is only solvable by optimisation of the nonlinear complex problematics (Ghandar et al. 2016). However, since financial market relationships are time-variant, optimisation for nonlinear dynamics results in increased complexity. This may lead to the processing of redundant information and non-optimal solutions. The possible solutions to complex tasks in dynamic environments are not fully examined yet (Narayan and Smyth 2015; Exterkate et al. 2016). The majority of research focuses on financial distress, bankruptcy, forecasting of financial time-series and decision supports with special attention to classifications (e.g., Tables 1 and 2 in Tkac and Verner, 2016), which are solvable via NNs or ML-algorithms due to availability of computational power (e.g., Tables 1 and 2 in Aguilar-Rivera et al. 2015) (Duan et al. 2019; López de Prado 2018). Until recent years, computational demands have been a major barrier, which concurrently lowers and simultaneously reveals new application possibilities to optimisations via new families of algorithms (e.g., CI, GA or evolutionary specifications in GP) (Cordis and Kirby 2014; Narayan and Smyth 2015).
Forecasting accuracy
The frontier until the end of 2019 can be seen in the combination or synthetisation across multiple econometric methods, which should not be extended piecewise, but integrated into panel-based frameworks, resulting in cross-validations of model performances in a standardised manner (Narayan and Smyth 2015; Doering et al. 2019). Speaking of optimisation, Ghandar et al. (2016) see the majority of current research focusing on the outperformance of neoclassical (traditional) or more common methods when applying new algorithms (e.g., CI), while the selection of optimal optimisation procedures for given model settings is concurrently underrepresented. After analysing our sample, we see these trends in our sample occurring in a similar manner, stating that the majority of authors aim towards performing better than a respective benchmark model, instead of seeking optimisation procedures for given model settings or specifications first. Nonetheless, implementing heuristics based on CI or AI methods, have the capability to achieve high-quality solutions, since CI algorithms can successfully be implemented for large numbers of nonlinear variables, potentially widen upper mentioned frontiers. This is due to the closeness of CI to evolutionary algorithms and AI (Ghandar et al. 2016; Duan et al. 2019). Therefore, optimisation algorithms can be seen as a mean to drive frontiers to the rear, since they are able to provide more realistic decision-making solutions in financial modelling (e.g., optimisation of implied volatility of option prices via prediction of random subset selection algorithms). Further, the availability of big financial data on a tick-by-tick basis reveals potentials towards a deeper understanding of stated properties, trading processes or the management and assimilation of financial asset risks (Cordis and Kirby 2014; Bodnar and Hautsch 2016).
Combination of research fields
Moreover, we do not only see frontiers in terms of technical capabilities, but also with regards to human behaviour, yielding the ongoing synergetic metamorphosis between econophysics and BF, providing new methodologies (e.g., GP, GA, qualitative research or neuro finance) (Chakrabarty et al. 2015; Linnenluecke et al. 2017). The combination of respective research fields and cross application of models and methods leads to a new variety of possible applications. For example, we state the combination of WNNs with GAs and a human behaviour factor (e.g., stress, irrational decision probabilities), which can be compared to benchmarks such as standardised NNs with radial basis functions and SVMs (Alexandridis et al. 2017; Chakrabarty et al. 2015). Regarding nonlinear dynamics in combination with irrational actors at different scales, may lead to chaotic behaviour, which can be tangled with Mackey–Glass equations in combination with GA-NNs, which has not been intensively researched yet (Alexandridis et al. 2017; Boubaker and Raza 2017).
In conclusion, we will now evaluate the findings and conclusions of the authors as stated in Table 18, which will reflect key points as well as stated fields of our study. The topic with the most counts is volatility dynamics. Time-varying volatility, meaning parameter evolution over time inside time-series paired with autoregressive features (Bekiros and Marcellino 2013). Asymmetric and, therefore, nonlinear features follow volatility dynamics in time-series. Since positive and negative news affects the latter data series differently, they lead to differing (or asymmetric) dynamics, hence, nonlinearity (Exterkate et al. 2016; Aloui and Mabrouk 2010). In addition, long memory (or long-range dependence), which yields the persistence of shocks and structural breaks within respective time-series belong to the corresponding conclusions. Further, regime switches or jumps as a special case, which mostly follow structural breaks, enhance nonlinearity and bear different dynamics (Choi et al. 2010; Shi and Ho 2015). Moreover, empirically confirmed stylised facts and features, are scaling, trending and fractal patterns, which are incorporated in momentum strategies to exploit such structural patterns (Berghorn 2015; Wang et al. 2016).
Irrational actors trade on different time-levels or scales, but also effects may spread throughout different (integrated) financial markets, yielding spill-over and contagion effects, which can be decomposed on different time-levels into sub-effects as well (Jung and Maderitsch 2014; Khalfaoui et al. 2015). In conclusion, researchers conclude neoclassical (traditional) models as insufficient in hindsight of stylised facts and properties (e.g., trending and scaling characteristics, momentum, see Berghorn, 2015), which are further examinable due to the upcoming availability of high frequency and financial big data as well as advanced AI and ML-algorithms. In addition, actors are challenged by this broad variety of effects which occurs at distinct interconnected markets at different time-levels simultaneously (e.g., Celeste et al. 2019), while traditionally relied upon thought-constructs such as the EMH are contradicted completely (Duan et al. 2019; Berghorn 2015).
Citation network analysis
Citation network
The structure of the analysis is as follows: First, we calculate metrics and other test parameters for the complete sample. Second, we plot the citation network deploying the “Force-Atlas2-algorithm” provided by the software package Gephi (Jacomy et al. 2014). Third, we modify the plot by implementing filters, size as well as colour manipulations, which represent given metrics (Cherven 2015). Lastly, we provide an interpretation.
To prepare the input data for Gephi, we include the sampled literature as “mother-nodes”, whilst deploying their respective references of papers as “daughter-nodes”.Footnote 9 Once uploaded, we calculate the HITS-metrics, randomised modularity, Eigenvector Centrality (EC) with 100 iterations and the average path length as displays in Table 19. In terms of HITS, we concur that not many research papers provide hyperlinks and are not dominant within the visible surface web, since the value tends to be zeroFootnote 10 (Kleinberg 1999). Regarding the EC, which represents the influence of a node within the network, we see a weak influence between the respective research papers. We state a diameter of two as well as an average path length of 1.015, which suggests that the nodes in the network tend to be closer together (Newman 2010). Modularity, which represents the weights of the edges, is very strong, with a value of 0.914 (Blondel et al. 2008). After the creation of in total 53 communities in terms of modularity, we apply three different node-size and colour manipulations and one filtration each. First, we change the node-sizes from small to large as well as their colour, regarding the “Betweenness Centrality (BC)”, which measures how often a node appears on the shortest paths between nodes in the network. Furthermore, we then apply a filter, which only shows nodes, which correspond to a degree greater than two. In our second attempt, we set the colours in terms of the authority measure, where red tones indicate significance and the sizes equal the EC of each node as displayed in Fig. 2. The aggregate of important publications as well as their measure values,Footnote 11 are shown in Table 20. In the final round of changes, we let the node-sizes remain at the EC and change the colours to display the communities, which remain after the degree-filter greater than two applies, as shown in Fig. 3. Following the modularity construction, we regard the five highest-scoring communities. Orange labelled nodes (community I) belong to the contents of “Predictability and Modelling”, pink labels (community III) reflect “Regimes and Shocks” and red nodes (community V) contain represent papers, which contribute to “Volatility and Asymmetries”, whilst green marked papers (community IV) originate from “Dynamics and Copulas”. Finally, blue-labelled nodes (community II) centre on “Oil and Stock Markets”. These major groups reflect the findings and are consistent with the contents presented in this paper so far. We present two respective example papers out of each community in Table 21
Citation network: version 2: Degree > 2, Size equal to significance in Eigenvector Centrality and colours representing major (Top 5) modularity communities (Orange; I: Predictability & Modelling, Pink; III: Regimes & Shocks, Red; V: Volatility & Asymmetries, Green; IV: Dynamics & Copulas, Blue; II: Oil & Stock Markets, Black-collections: centralisation of all other publications, which do not belong into the Top 5 communities)
Behaviour of bubbles, crashes and financial crises
An elaboration on the definition and modelling of bubbles, crashes and crises serves as bridging avenue between the topics and various scientific fields. It represents the connection between nonlinear dynamics, financial and risk modelling and proposes potential explications for the occurrence of said bubbles and crises. To begin, no agreed upon nor precisely noted definition of bubblesFootnote 12 is stated within the sampled academic literature of the citation network, while given presuppositions or attempts of definitions are inconclusive (Balcilar et al. 2016; Bhattacharya and Yu 2008). The first major insight to note is that a rise in a given asset price per se does not represent always a proper implication of irrationality or respective bubble formation (Balcilar et al. 2016). Second, the presupposition is agreed upon that the determination of bubbles are not possible in an ex-ante point of view (Balcilar et al. 2016; Kaizoji and Sornette 2008; Bhattacharya and Yu 2008; Gurkaynak 2008). Moreover, analysing existing literature dictates complicated as well as contradictory theories and tests about bubble formation and statements of their respective existence (Balcilar et al. 2016). Little consensus about the cause and effect relation in hindsight of bubbles exist, large crashes are deemed outliers and, thus, a specialised theoretical rationale as well as specific treatment of these events is required (Sornette 2003; Kaizoji and Sornette 2008).
Moreover, several types of bubbles are depicted within the literature, namely, (1) rational expectation bubbles, i.e. the appearance in presence of rational actors, who excerpt their will to gain large returns offered as remuneration of crash risk during bubbly periods within the markets, (2) credit fuelled bubbles and (3) irrational behaviour bubbles, among others (Hüsler et al. 2013; Balcilar et al. 2016). Bhattacharya and Yu (2008) display an early reasoning for bubble formation within the literature as follows: (1) existent limits to arbitrage, which are caused by respective noise traders, (2) existence of synchronisation risk, (3) existing constraints in term of short selling opportunities, (4) lack of closely given substitutes for herding, (5) existence of heterogeneous beliefs within the markets and (6) delegated investments and the existence of psychological biases. Previously depiction states the seemingly “outdatedness” of the EMH clearly (Kaizoji and Sornette 2008). Furthermore, two conditions in general have to be invoked to set deviations from fundamental asset values in motion, namely, a given level of irrationality and rational investors’ inability to drive back asset prices due to given limits in arbitrage (Kaizoji and Sornette 2008). A more financial analytical proposition in terms of bubble definition can be found in DeMarzo et al. (2008), stating the following points: (1) existence of asset market prices, which are higher than their discounted sums of expected cash flows, supposing the risk free rate as discount rate, (2) said cash flows yield non-negative correlations with aggregate risks and (3) a holding decision is made by risk-averse investors given the information proposed in (1) and (2).
The general opinion within the literature is to denote positive feedback effects and herding behaviour as key factors for bubble growth (Kaizoji and Sornette 2008). This is seen due to (1) synchronisation failures among rational traders, which destabilise the market systems, (2) noise traders, (3) agency costs and monetary incentives given to competing fund managers and (4) rational imitation effects in the presence of uncertainty in combination with social imitations (Kaizoji and Sornette, 2008).
As stated previously, stock market shocks are capable to yield adverse consequences with significant repercussions (Balcilar et al. 2016). Following Sornette (2003), stock market crashes are an inherent personification of extreme events, observed within the study of complex systems. Systemic stock market price shocks imply actual returns to investment and financial stability to be interwoven within a complex financial system (Balcilar et al. 2016). Thus, the pinpointing of a bubble (or crash) origin is more subtle as assumed within the literature so far, thence, is progressively constructed by the market as a whole, namely, as a self-organising process or systemic instability (Sornette 2003). Such a process indicates investment rewards and market catastrophes (i.e., bubbles and crashes) occur in irregularly frequented, generational cycles (Sornette 2003). Therefore, this is seen as the main mechanism leading to proposed positive feedback effects (i.e., self-reinforcement such as imitative behaviour and herding) assumed within the literature (Sornette 2003). The latter positive feedbacks provide an inherent implication for the development of speculative bubbles, which prepare the instability for a major market drawdown (or crash) (Sornette 2003). Elaborating on the nature of complex systems further, reveals that the complex structures are indeed fractal, leading to the presupposition that predictions of the detailed evolutionary paths of such a complex system is futile (i.e., void or not worth it) (Sornette 2003). Nonetheless, the latter premise does not exclude the possibility to predict evolutionary phases of the complex systems, which matter in the predictability of extreme events, which are representable, via bifurcation points (Sornette 2003). Further, crises are labelled as rarely occurring extreme events, albeit featuring extraordinary impact, thus, such events are completely undersampled, leading analytical theoretical rationales as well as “brute force” numerical algorithms to fail (Sornette 2003). The movement of asset prices is determined by the according market actors buying and selling activities, which may lead to deviations from a random walk in the stock market price trajectory (Sornette 2003). Negative feedback effects, therefore, tend to regulate growth within markets towards an equilibrium, while positive feedback effects asserts that the price increase of the recent past will lead to future price growth effects (Sornette 2003). According to Youssefmir et al. (1998), the latter positive feedback effects, when unchecked, tend to produce runaways until the deviation from denoted equilibrium is large enough to trigger otherly effects, which lead to ruptures and bubble bursts. According to Vogel and Werner (2015) most of the academic literatures’ models are based upon the presupposition that rationality will prevail and that markets are predominantly efficient, leading in general to insufficient models and a vast critique, namely the “you know one if you see one” ex-post detection approach.
Further, following Vogel and Werner (2015), states that the power of economic testing is weak due to the definition aspect, namely, inventive bubble notations such as rational, churning, collapsing, exploding, intrinsic, which reflects the “tenuous grasping at straws” in terms of bubble predictability. An overview of most common existing bubble models is proposed in Table 22, while a detailed review and summary is proposed by Sornette (2003).
Discussion and conclusions
In this paper, we answer the question, “What are the insights, cognitions and developments in financial and risk modelling in the information age and since the Financial Crisis of 2008, till the end of 2019?”. To oblige and answer the research question at hand, we construct a bibliometric content analysis in combination with a snowball sampling approach and a citation network analysis. Hence, we do so by rating the research papers applying the Deyner-rating to ensure high quality, before analysing them with the Hart framework. The main subjects of authors’ research are the topics of “financial forecasting”, “volatility modelling” and “financial time-series dynamics”.
Theoretical implications
Time-series (or volatility) dynamics are the non-constant unconditional variance changes over time, which react to news differently (Amado and Teräsvirta 2014). These different reactions can be presented as distinct processes, asymmetric characteristics, which lead the time-series (or volatility) dynamics to show (multivariate) nonlinearity (Righi and Ceretta 2013; Palandri 2015). In these multivariate dynamic volatility processes, downward volatility is less predictable (Bodnar and Hautsch 2016). Moreover, nonlinear volatility dynamics result in heteroscedasticity, left-skewed returns and a deviation from Gaussianity (Zhu and Galbraith 2011; Scharth and Medeiros 2009). Sudden changes in the unconditional variance of financial time-series are labelled as structural breaks, which occur due to persistency inducing shocks to the conditional variance (Ñíguez and Perote 2016).
Persistency mainly causes volatility clusters, which reflect the occurrence of certain events at the same time (Charfeddine 2014; Boubaker and Raza 2017). Deterministic shifts in the unconditional variance lead to long memory (or long-range dependence), which reveals non-exponential decays (non-exponential power laws) of the respective time-series ACFs (Klein and Walther 2017; Zhu and Galbraith 2011). Long memory may easily be confused with regime switches (or jumps as a special one-period case), since regimes display the timely dimension of persistency, which, in contrast, is caused by the aforementioned structural breaks. This problem is solvable with co-integrative or smooth transitive methods (Ang and Timmermann 2012; Ma et al. 2017). If we observe persistency on different time horizons at the same time, we identify fractal patterns, scaling and trending characteristics within respective time-series, which are exploitable through momentum-based strategies (Chakrabarty et al. 2015; Celeste et al. 2019). In the case of shock transfers between different markets, we can detect changes in transmission speed while respecting the effects of contagion for non-integrated markets and spill-overs for integrated markets (Ioan et al. 2013; Jung and Maderitsch 2014). When regarding spill-overs and contagion between different markets at different scales, we can determine the possibility of, for example, sub-spill-overs, as decomposition depends on the respective time-level (Khalfaoui et al. 2015). Therefore, we state that the aforementioned stylised facts and properties occur on different markets at different scales simultaneously, generating an extreme complex aggregate called financial market, which is susceptible to respective theoretical as well as practical rationales, implications and modelling suspects.
In our sample, the majority of applied models are stochastic processes, mainly Markov and autoregressive processes. While Markov chains are representable via random walks, Markov processes tend to occur in the form of BMs or Poisson processes (Parzen 2015). Autoregressive processes yield the vast majority of presented models, building on the AR model, which in the case of an AR(1) specification can be approximated via a two-step Markov chain (Florescu 2015; Gagniuc, 2017). In general, most stochastic processes can be approximated via each other. As we regard several time-series at once, the AR can be extended to the VAR model, while, in combination with MA models, it can build the basis for the ARMA model, which can again be enhanced to the ARIMA model with non-stationary data (Parzen 2015; Sun et al. 2015). Not only are the financial time-series assumed time-varying, but so are their respective error variances too, yielding ARCH models as long as this variance follows an AR process (Brooks 2014). In contrast to ARCH models, SV models assume the error variance realisations to be randomly distributed (Gagniuc 2017). If the error variance follows an ARMA process, the standard GARCH model, with a unit root in the IGARCH model, is applicable (Tsay 2010).
To deal with regime switches in MS models, combinations such as MS-VAR models or threshold specifications (e.g., TARFIMA) are suitable (Ma et al. 2017). Since the displayed regime switches are related to the persistency of respective shocks SWARCH (ARCH[q] in MS processes), MS-GARCH or AGARCH models are applicable (Charfeddine 2014; Chang et al. 2017).
We assume regimes and persistency dynamics to be different, which results in presented nonlinear characteristics; again, other models are appropriate, namely, TAR, STAR, NGARCH, ST-GARCH or STARCH models, among others (Lin et al. 2012; Chkili et al. 2014). Nevertheless, nonlinearity can also be caused by asymmetric features, which can additionally be respected by SWARCH models, asymmetric EGARCH or the GJR-GARCH inter alia (Wang et al. 2016). Models trying to combine the aforementioned properties are DSARV models, among others (Cordis and Kirby, 2014). Shock persistency leads to long memory effects, which standard GARCH models with a short memory cannot reflect properly, enforcing the necessity to apply fractional integration methods such as FIGARCH models. Such models yield a loss of efficiency if no structural breaks occur (Jammazi and Aloui 2010; McMillan & Ruiz, 2009). To be able to cope with those drawbacks as well as with nonlinearity, smoothing transitions, in combination with fractional integration, can be used in models such as A-FIGARCH, ST-FIGARCH or in MS environments with FIAPARCH or 2S-ARFIMA models (Chkili et al. 2014; Shi and Ho 2015). To deal with more properties, a variety of combinations are observable, such as ARIMA-GARCH, ARFIMA-GARCH and ARFIMA-FIGARCH. Furthermore, various tests and algorithms for verification are deployed in the sampled literature, such as ICSS algorithms or R/S statistics (Chkili et al. 2014; Liu 2015). Nevertheless, almost all of the aforementioned models are unable to display fractality (and multifractality) or respective scaling and trending characteristics properly on different scales or time-levels. The GARCH class cannot reflect multi-scaling or self-similarity properly and, thus, cannot describe financial time-series volatility properly (Hallam and Olmo 2014; Mandelbrot 2004).
Models that can outline multi-scaling as well as other properties are, for example, the HAR, MSM, or, if they apply different time definitions, the ACD or MSMD, among others (Aldrich et al. 2016; Charles and Darné 2017). In addition, trends can be modelled and exploited with momentum strategies, while betas are observed to be scale sensitive (Mitra et al. 2017; Focardi et al. 2016). If we analyse more than one market at once, the effects of contagion and spill-overs are seen, which can be represented by BEKK-GARCH models (Jung and Maderitsch 2014). Respecting multi-markets and multi-scaling effects simultaneously, the HAR-ADL or TVAR models are suitable (Jammazi and Aloui 2010; Bekiros and Marcellino 2013). Leaving stochastic processes, applications to measure risks, defaults or potential losses such as VaR and EVT are applicable. Extensions, also in combination with Monte Carlo simulations, are possible (e.g., CVaR, CaViaR, GARCH-EVT, POTs and ACD-POTs) (Chiu and Chuang 2016; Rodriguez et al. 2017).
Linkages
To sum up, we can confirm the future indications by Poon and Granger (2003), prospecting that models will first be combined within their respective families. We show this feature with our main diagonal of the combinatory matrix, stating respective root family models and their combinations.
Furthermore, Poon and Granger (2003) indicate for the future that models will be cross-combined with different model families, building new families, respectively. This can be demonstrated in the root-junction trees in the combination matrix and be confirmed as well. Moreover, among the vast variety of models (over 800 unique mathematical methods alone in this study), a lack of panel-based comparisons reveals another gap within the field of financial and risk modelling (Narayan and Smyth 2015). Since different performance and error measures (see Table 13) as well as diverging data sets (see Tables 8 and 9) exist, we do not find an overall comparison of explanatory power and forecasting performance unambiguously to be feasible and overall conclusive. In signal analysis, we state the result that time-series bear frequency as well as time information, which is first extracted implementing FT or STFT methods. Due to the loss of all time information by applying FT, MRA and further wavelet (e.g., MODWT, MODHWT or DWT) transformations can be applied to obtain respective time–frequency resolution information (Klein and Walther 2017; Alexandridis et al. 2017). In terms of computer science, we see a rise in the implementation of AI and ANN concepts, which is driven by the availability of higher computational power. We also see a development ranging from the standard backpropagation NN or SVM towards more sophisticated applications such as multi-layered NNs or combinations with signal theoretical concepts such as WNNs, resulting in high quality outcomes (Tkac and Verner, 2016; Alexandridis et al. 2017).These cross combinations of model families with respective properties or technological advances are also prospected for the future by Poon and Granger (2003) and can be confirmed for our sampled literature. Moreover, outstanding advances are the optimisation of respective procedures.
Further, we do not deduce a triangulation of methods, but an extension of application areas from one field of research to another. In conclusion, we see a major academic advance in the field of financial and risk modelling in terms of model extensions, model creation and the beginning of crossing with different fields.
Practical implications, limitations and future research
Turmoil in financial markets affects actors and may as well lead to corporate bankruptcies. Therefore, the proper ability to cope with financial market properties and implement well-defined and well-functioning models in practical systems is inevitable and of major importance to practitioners. Many academic solutions (e.g., the transformation of non-stationary into stationary time-series with the inherent loss of valuable memory information) cannot be implemented or applied to daily practical routines (Emrouznejad et al. 2016; López de Prado 2018). In addition, we confirm alluded crises-induced severities between theoretical rationales and practical applications. Examples of underlying problems refer to the definition of importance within the modelling approaches. Only one paper of our sample deemed it worthwhile to explicate the impulses of their research on the generation of respective excess returns (or alphas), while the creation of alphas for practitioners yields more essential prominence than for mathematical rigour, elegant constructions and rationales (Amini et al. 2013; López de Prado 2018).
Thus, we will discuss these limitations by further elucidating stated frontiers and barriers of current research attempts. One main frontier is the determination of the true DGP of time-series (Ghandar et al. 2016). When it comes to explaining the mentioned stylised facts and properties, researchers tend to apply new technical concepts (e.g., NNs) to create models, which outperform other models, rather than optimising existing procedures first. Additionally, optimisations in terms of nonlinear dynamics are computational demanding and not exhausted yet (Emrouznejad et al. 2016; Exterkate et al. 2016). One given boundary is the not yet fully accepted crossing of fields (e.g., with econophysics, BF) (Chakrabarty et al. 2015).
Moreover, we specify the potential limitations of our study, namely the number of 132 papers under review, the subjective aspect of the application of respective Deyner ratings as well as the categorisation in itself. Moreover, we exclude the research streams BF and EC, as well as other research fields such as nonlinear dynamics or econophysics which may reveal further information. In addition, we do not review other innovative approaches such as Islamic finance or alternative financial systems (Linnenluecke et al., 2017). Furthermore, we did not elaborate on the distinct difference between financial and risk model deployment on developed versus emerging markets. This is of importance, since our sample majorly (yet, not exclusively) has data sets under analysis originating from developed markets. Thus, we refer to Kearney (2012), Isik and Uygur (2021) as well as Nazlioglu et al. (2022) for further guidance. We do not elaborate on evolutionary algorithms (e.g., Darwinian algorithms, GP, GA), which can be seen as the current frontier in the emergence of finance and computer science (Aguilar-Rivera et al. 2015). We have not presented a timeline for the evolution of the sampled models and methods, which in addition to our combination matrix is expected to reveal further correlations and interconnections with the dates of the respective crisis. Thence, we did not elaborate on the distinct influence of the Basel regulations in the aftermath of the Financial Crises in 2008 on financial and risk modelling, in particular. In total, we need to state the unquestionable contribution of neoclassical (traditional) finance, but in view of the prevalent properties, stylised facts and results contradicting the doctrine, we cannot attribute EMH and other represents of traditional concepts, to be able to clarify the present financial markets anymore (Aguilar-Rivera et al. 2015; Berghorn 2015; Ramiah et al. 2015).
Therefore, we see an increase in theoretical research after the Financial Crisis in 2008 as well as an ongoing discourse and fragmentation of the research community in terms of providing valid answers to the cause and best practise of modelling of the stated properties as well as the essential functioning of the financial markets themselves. Authors implement many different approaches, models and latest technologies to provide progressive as well as valid views of financial markets. Simultaneously, we carefully note that only one paper of our sample elucidated the model performance in hindsight of the generation of maximised alpha returns, which are seen as favourable by practitioners (Amini et al. 2013; Aït-Sahalia et al. 2015).
This leads to the question, which trends and applications are feasible tools for practical implementations. From a practitioner’s point of view financial and risk modelling needs to comply with regulatory demands (e.g., Gong and Xu 2018), being technical implementable as well as fast executable (e.g., Duan and Dwivedi 2019), while still being able to create before mentioned alpha returns in a maximisation procedure (Amini et al. 2013). Thus, for instance, we see important trends in the application of intelligent algorithms in AI concepts in combination with combined modelling attempts (e.g., combinations of different model families with respective stylised facts and properties). Moreover, enormous potential losses in insufficiently explored crossed-fields and newly provided technological advances can be pointed out. We illustrate those topics as the current frontier of research. Nevertheless, we need to follow the conclusions of former papers, such as Narayan and Smyth (2015), Linnenluecke et al. (2017), Ghandar et al. (2016), as well as Doering et al. (2019), namely, that there is clear support for the combination of forecast models in the literature, but it is not obvious which scheme performs best. Overall, combinations perform better than single model implementations, despite the unclearness, which method is the best. For our sample and, henceforth, for our study, we also need to conclude, that there is no “single best” approach. Several questions remain to be answered such as the reasoning behind the slight superiority of nonlinear models. Therefore, we leave the question of the exact determination of the functioning of the underlying working mechanic of financial markets, the impacts of the stated stylised facts and properties (e.g., nonlinear dynamics) on portfolios or banking regulations and the future implementation, optimisation and comparable cross validation of financial and risk models to future research.
Data availability
The underlying data of this manuscript is available through “Science Direct” and “Emerald” access. The data details are described in “Bibliometric analysis and snowball sampling”. The data consists solely out of sampled papers, the remaining calculations and displays solely depend on the latter. There are no other data sets to declare.
Notes
Harzing’s journal ranking list consists of 12 different and independent journal rankings (e.g., Ejis2007, VHB-JQ3, UQ2011 and EJL2016). Our criteria are blind peer-review, more than two rankings in Harzing’s list and a rank that is not the lowest in more than 50% of all given rankings on average.
Please note that all citations of the sampled literature as well as all table references, are proposed in the supplementary material of this study.
Hurst exponent = 0.5 equals random walk (EMH valid), < 0.5 mean-reversion and > 0.5 persistence (Mackevičius, 2016).
Further information and literature review about VIX as asset can be found in Gonzales-Perez (2015).
We provide a complete model dictionary stating every single finding with its abbreviation and name in the supplementary material.
Root-Junction relationships can be seen similar to mother-daughter relationships, therefore as (1: n)-relations. One root (or mother) model can be the origin of one or more junction (or daughter) models.
CCC and DCC models offspring CC models, while EGARCH, FIGARCH, among others, originate from the standard GARCH model.
Each root model can have several junctions, while each of them can show manifold realisation counts (saplings) on their own. As an example, we can state AR as the root, HAR as the junction and within the AR-HAR relation, a sapling as a HARX (HAR with exogenous variables) or a TV-HAR (time-varying HAR) model, among others. Therefore, we label a root-junction-sapling realisation as, e.g., AR-HAR-HARX, since HARX is a variation of its junction HAR, which stems from the root, namely AR. If we regard ARX (AR with exogenous variables), we see a sapling of a root model only, where no junction is involved, resulting in a (1: m) relation.
This process uses pdf-files of the sample literature, extracts references and creates JSON-files, which we then convert into Gephi-readable-formats deploying self-written Python code.
Each parameter starts with the value of one and will be normalised into [0, 1], which can be interpreted as probabilities.
The Hub parameter has two representations, namely, 0.003688 in paper Scharth and Medeiros (2009), which yields a “Betweenness-Centrality” of 49.0 and Gupta and Wohar (2017) with 0.170282. The only other paper with a “Betweenness-Centrality” is Arroyo and Maté (2009) with a value of 29.0. Others yield zero-values.
Due to the inexistence of a proper definition, one may see bubbles, crashes or crises as either synonymous or may follow our suggestion of bubbles being smaller or equal to crashes, which are smaller or equal to crises in magnitude. Note that the latter suggestion is our opinion and not backed up by the literature. Mostly, extreme events are referred to as bubbles within the literature.
References
Adams Z, Füss R, Glück T (2017) Are correlations constant? Empirical and theoretical results on popular correlation models in finance. J Bank Finance 84:9–24
Agosto A, Cavaliere G, Kristensen D, Rahbek A (2016) Modeling corporate defaults: poisson autoregressions with exogenous covariates (PARX). J Emp Financ 38:640–663. https://doi.org/10.1016/j.jempfin.2016.02.007
Aguilar-Rivera R, Valenzuela-Rendón M, Rodríguez-Ortiz J (2015) Genetic algorithms and darwinian approaches in financial applications: a survey. Expert Syst Appl 42:7684–7697
Aït-Sahalia Y, Cacho-Diaz J, Laeven RJ (2015) Modeling financial contagion using mutually exciting jump processes. J Financ Econ 117:585–606
Aldrich EM, Heckenbach WE, Laughlin G (2016) A comound duration model for high-frequency asset returns. J Empirical Finance 39:105–128
Alexandridis AK, Kampouridis M, Cramer S (2017) A comparison of wavelet networks and genetic programming in the context of temperature derivatives. Int J Forecast 33:21–47
Aloui C, Mabrouk S (2010) Value-at-risk estimations of energy commodities via long-memory, asymmetry and fat-tailed GARCH models. Energy Policy 38:2326–2339
Amado C, Teräsvirta T (2014) Modelling changes in the unconditional variance of long stock return series. J Empir Financ 25:15–35
Amini S, Gebka B, Hudson R, Keasey K (2013) A review of the international literature on the short term predictability of stock prices conditional on large prior price changes: microstructure, behavioral and risk related explanations. Int Rev Financ Anal 26:1–17
Andrada-Félix J, Fernández-Rodríguez F, Fuertes A-M (2016) Combining nearest neighbor predictions and model-based predictions of realized variance: does it pay? Int J Forecast 32:695–715
Ang A, Timmermann A (2012) Regime changes and financial markets. Annu Rev Financ Econ 4:313–337
Asmussen S (2003) Applied probability and queues, vol 51. Springer Verlag, New York
Balcilar M, Gupta R, Jooste C, Wohar M (2016) Periodically collapsing bubbles in the South African stock market. Res Int Bus Financ 38:191–201
Barenblatt G (1996) Scaling, self-similarity, and intermediate asymptotics (Cambridge texts in applied mathematics). Cambridge University Press, Cambridge
Basher SA, Sadorsky P (2016) Hedging emerging market stock prices with oil, gold, VIX, and bonds: a comparison between DCC, ADCC and GO-GARCH. Energy Economics 54:235–247
Baum L, Petrie T (1966) Statistical inference for probabilistic functions of finite state markov chains. Ann Math Stat 37:1554–1563
Bekiros S, Marcellino M (2013) The multiscale causal dynamics of foreign exchange markets. J Int Money Financ 33:282–305
Beltratti A, Stulz RM (2019) Why is contagion asymmetric during the European sovereign crisis? J Int Money Finance 99:102081
Berghorn W (2015) Trend momentum. Quantitative Finance 15:261–284
Bhar R, Hamori S (2005) Empirical techniques in finance. Springer, Heidelberg
Bhattacharya U, Yu X (2008) The causes and consequenses of recent financial market bubbles: an introduction. Review Financial Studies 21(1):3–10
Biernacki P, Waldorf D (1981) Snowball sampling: Problems and techniques of chain referral sampling. Sociological Methods Res 10:141–163
Blackledget, J. M. (2006). Digital signal processing (2nd Edn): Mathematical and Computational Methods, Software Development and Applications. Woodhead Publishing Series in Electronic and Optical Materials
Blondel VD, Guillaume J-L, Lambiotte R, Lefebvre E (2008) Fast unfolding of communities in large networks. J Statistical Mech: Theory Exp 10:1000
Bodnar T, Hautsch N (2016) Dynamic conditional correlation mutiplicative error process. J Empir Financ 36:41–67
Bollerslev T (1986) Generalized autoregressive conditional heteroskedasticity. J Econometrics 31:307–327
Boubaker H, Raza SA (2017) A wavelet analysis of mean and volatility spill-overs between oil and BRICS stock markets. Energy Economics 64:105–117
Box GE (1970) Time-series analysis: forecasting and control. Holden Day, San Francisco
Briner RB, Deyner D (2012) Systematic review and evidence synthesis as a practice and scholarship tool. In: Rousseau DM (ed) The Oxford handbook of evidence-based management. Oxford Univ, Press, pp 112–129
Brockwell PJ, Dahlhaus R, Trindade AA (2005) Modified burg algorithms for multivariate subset autoregression. Stat Sin 15:197–213
Brooks C (2014) Introductory econometrics for finance. Cambridge University Press, Cambridge
Bustos O, Pomares-Quimbaya A (2020) Stock market movement forecast: a systematic review. Expert Syst Appl 156:113464
Celeste V, Corbet S, Gurdgiev C (2019) Fractal dynamics and wavelet analysis: Deep volatility and return properties of Bitcoin, Ethereum and Ripple. Quartely Rev Eco Finance 76:310–324
Chakrabarty A, De A, Gunasekaran A, Dubey R (2015) Investment horizon heterogeneity and wavelet: overview and further research directions. Physica A 429:45–61
Chalamandaris G, Tsekrekos AE (2011) How important is the term structure in implied volatility surface modeling? Evidence from foreign exchange options. J Int Money Financ 30:623–640
Chang C-L, McAleer M, Tansuchat R (2010) Analyzing and forecasting volatility spill-overs, asymmetries and hedging in major oil markets. Energy Econ 32:1445–1455. https://doi.org/10.1016/j.eneco.2010.04.014
Chang Y, Choi Y, Park JY (2017) A new approach to model regime switching. Journal of Econometrics 196:127–143
Charfeddine L (2014) True or spurious long memory in volatility: further evidence on the energy futures markets. Energy Policy 71–C:76–93
Charles A, Darné O (2017) Forecasting crude-oil market volatility: further evidence with jumps. Energy Economics 67–C:508–519
Cherven K (2015) Mastering Gephi Network Visualisation. Packt Publishing Ltd
Chiu Y-C, Chuang I-Y (2016) The performance of the switching forecast model of value-at-risk in the Asian stock markets. Finance Res Lett 18:43–51
Chkili W, Hammoudeh S, Nguyen DK (2014) Volatility forecasting and risk management for commodity markets in the presence of asymmetry and long memory. Energy Economics 41:1–18
Choi K, Yu W-C, Zivot E (2010) Long memory versus structural breaks in modeling and forecasting realized volatility. J Int Money Financ 29:857–875
Cole J, Cole S (1972) The ortega hypothesis: citation analysis suggests that only a few scientists contribute to scientific progress. Science (new York) 178:368–375
Conrad C, Karanasos M, Zeng N (2011) Multivariate fractionally integrated APARCH modeling of stock market volatility: a multi-country study. J Empir Financ 18:147–159
Cordis AS, Kirby C (2014) Discrete stochastic autoregressive volatility. J Bank Finance 43–C:160–178
Da Fonseca J, Zaatour R (2015) Clustering and mean reversion in a Hawkes microstructure model. J Future Market 35:813–838. https://doi.org/10.1002/fut.21676
Daniel K, Moskowitz TJ (2016) Momentum crashes. J Financ Econ 122:221–247
de Souza e Silva EG, Legey LF. (2010). Forecasting oil price trends using wavelets and hidden Markov models. Energy Economics, 32, 1507-1519
Dimpfl T, Peter FJ (2018) Analyzing volatility transmission using group transfer entropy. Energy Econ 75:368–376. https://doi.org/10.1016/j.eneco.2018.08.008
de Almeida D, Hotta LK, Ruiz E (2018) MGARCH models: trade-off between feasibility and flexibility. Int J Forecast 34:45–63
DeMarzo P, Kaniel R, Kremer I (2008) Relative wealth concerns and financial bubbles. Rev Financial Studies 21(1):19–50
Doering J, Kizys R, Juan AA, Polat O (2019) Metaheuristics for rich portfolio optimisation and risk management: current state and future trends. Operations Res Perspect 6:100–121
Doob JL (1990) Stochastic processes. Wiley, University of Virgina
Duan Y, Edwards JS, Dwivedi YK (2019) Artificial intelligence for decision making in the era of Big data—evolution, challenges and research agenda. Int J Inf Manage 48:63–71
Duriau VJ, Reger RK, Pfarrer MD (2007) A content analysis of the content analysis literature in organization studies: research themes, data sources, and methodological refinements. Organ Res Methods 10(1):5–34
Dzieliński M, Rieger MO, Talpsepp T (2018) Asymmetric attention and volatility asymmetry. J Emp Financ 45:59–67. https://doi.org/10.1016/j.jempfin.2017.09.010
Emrouznejad A, Rostami-Tabar B, Petridis K (2016) A novel ranking procedure for forecasting approaches using data envelopment analysis. Technol Forecast Soc Chang 111:235–243
Engle RF (1982) Autoregressive conditional heteroscedasticity with estimates of the variance of united kingdom inflation. Econometrica 50:987–1007
Etro F, Stepanova E (2018) Power-laws in art. Physica A 506:217–220
Exterkate P, Groenen PJ, Heij C, van Dijk D (2016) Nonlinear forecasting with many predictors using kernel ridge regression. Int J Forecast 32:736–753
Fahling EJ, Steurer T, Schädler T, Volz A (2018) Next level in risk management? Hedging and trading strategies of volatility derivatives using VIX futures. J Financ Risk Management 7:442–459
Family F, Vicsek T (1985) Scaling of the active zone in the Eden process on percolation networks and the ballistic deposition model. J Phys a: A Math General 18:L75
Florescu WE. (2015). Probability and stochastic processes. John Wiley & Sons Inc
Focardi SM, Fabozzi FJ, Mitov K (2016) A new approach to statisticasl arbitrage: Strategies based on dynamic factor models of prices and their performance. J Bank Finance 65:134–155
Gagniuc PA (2017) Markov chains: from theory to implementation and experimentation. John Wiley & Sons, USA, NJ
Garfield E (1979) Is citation analysis a legitimate evaluation tool? Scientometrics 1(4):359–375
Ghandar A, Michalewicz Z, Zurbruegg R (2016) The relationship between model complexity and forecasting performance for computer intelligence optimization in finance. Int J Forecasting 32:598–613
Glattfelder J, Dupuis A, Olsen R (2011) Patterns in high-frequency FX data: discovery of 12 empirical scaling laws. Quantitative Finance 11:599–614
Gong X, Lin B (2018) The incremental information content of investor fear gauge for volatility forecasting in the crude oil futures market. Energy Economics 74:370–386
Gonzales-Perez MT (2015) Model-free volatility indexes in the financial literature: A review. Int Rev Econ Financ 40:141–159
Goodell J, Kumar S, Rao P, Verma S. (2022) Emotions and stock market anomalies: a systematic review. J Behav Ex Finance, 100722
Granger C, Joyeux R (1980) An introduction to long-memory time-series models and fractional differencing. J Time-Series Analy 1:15–29
Guidolin M, Hyde S, McMillan D, Ono S (2009) Non-linear predictability in stock and bond returns: when and where is it exploitable? Int J Forecast 25:373–399
Gurkaynak R (2008) Econometric tests of asset price bubbles: taking stock. J Economic Surv 22(1):166–186
Gusak D, Kukush A, Kulik A, Mishura Y, Pilipenko A (2010) Theory of stochastic processes—with applications to financial mathematics and risk theory. Springer Science & Business Media, Berlin
Hallam M, Olmo J (2014) Forecasting daily return densities from intraday data: a multifractal approach. Int J Forecast 30:863–881
Hansen BE (2001) The new econometrics of structural change: dating breaks in US labor productivity. J Economic Perspect 15:117–128
Hart C (1998) Doing a literature review: releasing the social science research imagination. Sage Publications, London
Harzing A-W. (2019, Juni 3). https://harzing.com/. Retrieved from https://harzing.com/resources/journal-quality-list
Hassan MK, Hassan MZ, Pavel N (2011) Dynamic scaling, data-collapse and self-similarity in Barabási-Albert networks. Physica A 44:175101
Herrera R, Schipp B (2013) Value at risk forecasts by extreme value models in a conditional duration framework. J Empir Financ 23:33–47
Herrera R, Rodriguez A, Pino G (2017) Modeling and forecasting extreme commodity prices: a Markov-Switching based extreme value model. Energy Econ 63:129–143. https://doi.org/10.1016/j.eneco.2017.01.012
Hosking J (1981) Fractional differencing. Biometrika 68:165–176
Hüsler A, Sornette D, Hommes C (2013) Super-exponential bubbles in lab experiments: evidence for anchoring over-optimistic expectations on price. J Econ Behav Organ 92:304–316
Ioan T, Petria N, Deszi E (2013) An inquiry into contagion transmission and spill-over effects in stock markets. Ann Faculty Economics 1:472–482
Isik I, Uygur O (2021) Financial crises, bank efficiency and survival: theory, literature and emerging market evidence. Int Rev Econ Financ 76:952–987
Jacomy M, Venturini T, Heymann S, Bastian M (2014) ForceAltas 2, a continous graph layout algorithm for handy network visualisation designed for the Gephi software. Plos One 9(6):e98679
Jammazi R, Aloui C (2010) Wavelet decomposition and regime shifts: assessing the effects of crude oil shocks on stock market returns. Energy Policy 38:1415–1435
Janus P, Koopman S, Lucas A (2014) Long memory dynamics for multivariate dependence under heavy tails. J Emp Financ 29:187–206. https://doi.org/10.1016/j.jempfin.2014.09.007
Jung R, Maderitsch R (2014) Structural breaks in volatility spill-overs between international financial markets: contagion or mere interdependence? J Bank Finance 47:331–342
Kaizoji T, Sornette D. (2008) Market bubbles and crashes. ArXiv, 1–25
Karlin S, Taylor HE (2012) A first course in stochastic processes. Academic Press, Cambridge
Kearney C (2012) Emerging markets research: trends, issues and future directions. Emerg Mark Rev 13:159–183
Kendall DG (1984) Shape manifolds, procrustean metrics, and complex projective spaces. Bull Lond Math Soc 16:81–121
Khalfaoui R, Boutahar M, Boubaker H (2015) Analyzing volatility spill-overs and hedging between oil and stock markets: Evidence from wavelet analysis. Energy Economics 49–C:540–549
Kilic R (2011) Long memory and nonlinearity in conditional variances: a smooth transition FIGARCH model. J Empir Financ 18:368–378
Kitchenham B, Brereton P (2013) A systematic review of systematic review process research in software engineering. Inf Softw Technol 55:2049–2075
Klein T, Walther T (2017) Fast fractional differencing in modeling long memory of conditional variance for high-frequency data. Financ Res Lett 22:274–279
Kleinberg JM (1999) Authoritative sources in a hyperlinked environment. J ACM 46:604–632
Koliai L (2016) Extreme risk modeling: an EVT–pair-copulas approach for financial stress tests. J Bank Financ 70:1–22. https://doi.org/10.1016/j.jbankfin.2016.02.004
Kumbure M, Lohrmann C, Luuka P, Porras J (2022) Machine learning techniques and data for stock market forecasting: a literature review. Expert Syst Appl 197:116659
Lambiotte R, Delvenne J-C, Barahona M (2009) Laplacian dynamics and multiscale modular structure. Networks 1:76–90
Lamperti J (1977) Stochastic processes: a survey of the mathematical theory. Springer, University of Michigan
Lawler GF, Limic V (2010) Random walk: a modern introduction. Cambridge University Press, Cambridge
Lee K, Seo BK (2017) Marked Hawkes process modeling of price dynamics and volatility estimation. J Emp Financ 40:174–200. https://doi.org/10.1016/j.jempfin.2016.08.004
Leland W, Taqqu M, Willinger W, Wilson D (1994) On the self-similar nature of ethernet traffic (extended version). IEEE/ACM Trans Netw 2:1–15
Lifshits M (2012) Lectures on gaussian processes. Springer Science & Business Media, Berlin
Lin EM, Chen CW, Gerlach R (2012) Forecasting volatility with asymmetric smooth transition dynamic range models. Int J Forecast 28:384–390
Linnenluecke MK, Chen X, Ling X, Smith T, Zhu Y (2017) Research in finance: a review of influential publications and a research agenda. Pac Basin Financ J 43:188–199
Liu X (2015) Modeling time-varying skewness via decomposition for out-of-sample forecast. Int J Forecast 31:296–311
Lo Duca M, Peltonen TA (2013) Assessing systemic risk and predicting systemic events. J Bank Finance 37:2183–2195
Lönnbark C (2017) Long vs. short term asymmetry in volatility and the term structure of risk. Finance Res Lett 23–C:202–209
López de Prado M (2018) Advances in Financial Machine Learning. John Wiley & Sons Inc, Hoboken
Loterman G, Brown I, Martens D, Mues C, Baesens B (2012) Benchmarking regression algorithms for loss given default modeling. Int J Forecast 28:161–170. https://doi.org/10.1016/j.ijforecast.2011.01.006
Luca GD, Guégan D, Rivieccio G (2019) Assessing tail risk for nonlinear dependence of MSCI sector indices: a copula three-stage approach. Financ Res Lett 30:327–333. https://doi.org/10.1016/j.frl.2018.10.018
Ma F, Wahab M, Huang HD, Xu W (2017) Forecasting the realized volatility of the oil futures market: a regime switching approach. Energy Economics 67:136–145
Mackevičius V (2016) Stochastic models of financial mathematics. ISTE Press, Elsevier
Maia AL, de Carvalho FD (2011) Holt’s exponential smoothing and neural network models for forecasting interval-valued time-series. Int J Forecast 27:740–759
Malamud BD, Turcotte DL (1999) Self-affine time-series: we generation and analysis. Adv Geophys 40:1–90
Mandelbrot B (1967) How long is the coast of britain? Statistical self-similarity and fractional dimension. Science 165:636–638
Mandelbrot B (1977) The fractal geometry of nature. Freeman, USA
Mandelbrot B (2004) Fractals and chaos. Springer, New York
Mao X, Ruiz E, Veiga H (2017) Threshold stochastic volatility: properties and forecasting. Int J Forecast 33:1105–1123. https://doi.org/10.1016/j.ijforecast.2017.07.001
McKibbin WJ, Fernando R. (2020) The global macroeconomic impacts of COVID-19: seven scenarios. SSRN; CAMA Working Paper No. 19/2020, 1–45
McMillan DG, Ruiz I (2009) Volatility persistence, long memory and time-varying unconditional mean: evidence from 10 equity indices. Quarterly Rev Economics Finance 49:578–595
Mitra SK, Bawa J, Kannadhasan M, Goyal V, Chattopadhyay M (2017) Can profitability through momentum strategies be enhanced applying a range to standard deviation filter? Financ Res Lett 20:269–273
Mitzenmacher M (2004) A brief history of generative models for power law and lognormal distributions. Internet Math 1:226–251
Müller UA, Dacorogna M, Olsen RB, Pictet OV, Morgenegg C (1990) Statistical study of foreign exchange rates, empirical evidence of a price change scaling law, and intraday analysis. J Bank Finance 14:1189–1208
Mumtaz A, Gulfam H, Asad Z (2017) Detecting structural change with heteroskedasticity. Commun Statistics—Theory Methods 46:10446–10455
Narayan S, Smyth R (2015) The financial econometrics of price discovery and predictability. Int Rev Financ Anal 42:380–393
Nazliogliu S, Kucukkaplan I, Kilic E, Altuntas M (2022) Financial market integration of emerging markets: heavy tails, structural shifts, nonlinearity, and asymmetric persitence. Res Int Bus Financ 62:101742
Newman M (2010) Networks. Oxford University Press, Oxford
Ng J, Forbes CS, Martin GM, McCabe BPM (2013) Non-parametric estimation of forecast distributions in non-Gaussian, non-linear state space models. Int J Forecast 29:411–430. https://doi.org/10.1016/j.ijforecast.2012.10.005
Ñíguez T-M, Perote J (2016) Multivariate moments expansion density: Application of the dynamic equicorrelation model. J Bank Finance 72-S:216-S232
Nohel T, Todd SK. (2015) Chapter 14: Volatility as an asset class. The world scientific handbook of futures market, 437–464
Palandri A (2015) Do negative and positive equity returns share the same volatility dynamics? J Bank Finance 58:486–505
Parzen E (2015) Stochastic processes. Courier Dover Publications, Mineola
Pesaran M, Potter S (1992) Nonlinear dynamics and econometrics: an introduction. J Appl Economet 7:1–7
Piger J. (2007) Econometrics: models of regime changes. Complex systems in finance and econometrics
Poon S-H, Granger CW (2003) Forecasting volatility in financial markets: a review. J Economic Lit 41:478–539
Rahman A, Saadi S (2008) Random walk and breaking trend in financial series: an econometric critique of unit root tests. Rev Financial Economics 17:204–212
Ramiah V, Xu X, Moosa A (2015) Neoclassical finance, behavioural finance and noise traders: A review and assessment of the literature. Int Rev Financial Analy 41:89–100
Righi MB, Ceretta PS (2013) Estimating non-linear serial and cross-interdependence between financial assets. J Bank Finance 37:837–846
Risse M, Ohl L (2017) Using dynamic model averaging in state space representation with dynamic Occam’s window and applications to the stock and gold market. J Emp Financ 44:158–176. https://doi.org/10.1016/j.jempfin.2017.09.005
Rodriguez A, Pino G, Herrera R (2017) Modeling and forecasting extreme commodity prices: a markov-switching based extreme value model. Energy Economics 63:129–143
Rogers L, Williams D (2000) Diffusions, markov processes, and martingales. Cambridge University Press, Cambridge
Ross SM (1996) Stochastic processes. University of Michigan: Wiley series in probability and statistics: Probability and Statistics
Rozanov Y (2012) Markov Random Fields. Springer Science & Business Media, Berlin
Saloff-Coste L. (2004) Random walks on finite groups. Probability on discrete structures, pp 263–346
Salvatierra IDL, Patton AJ (2015) Dynamic copula models and high frequency data. J Empir Finance 30:120–135
Samorodnitsky G. (2007) Long range dependence. Foundations and trends in stochastic systems, 163–257
Scharth M, Medeiros MC (2009) Asymmetric effects and long memory in the volatility of Dow Jones stocks. Int J Forecast 25:304–327
Sener E, Baronyan S, Mengütürk LA (2012) Ranking the predictive performances of value-at-risk estimation methods. Int J Forecast 28:849–873
Serfozo R (2009) Basics of applied stochastic processes. Springer Science & Business Media, Berlin
Shi Y, Ho K-Y (2015) Long memory and regime switching: a simulation study on the Markov regime-switching ARFIMA model. J Bank Finance 61:189–204
Shreve ES (2004) Stochastic calculus for Finance II: continous-time models. Springer Science & Business Media, Berlin
Small H (1978) Co-citation context analysis and the structure of paradigms. J Doc 36:183–196
Sornette D (2003) Critical market crashes. Phys Rep 378:1–98
Sun EW, Chen Y-T, Yu M-T (2015) Generalized optimal wavelet decomposing algorithm for big financial data. Int J Prod Econ 165:194–214
Takahashi M, Watanabe T, Omori Y (2016) Volatility and quantile forecasts by realized stochastic volatility models with generalized hyperbolic distribution. Int J Forecast 32:437–457
Tkac M, Verner R (2016) Artificial neural networks in business: two decades of research. Appl Soft Comput 38:788–804
Tsay RS (2010) Analysis of financial time-series, 3rd edn. Wiley, Hoboken
Vicsek T, Family F (1984) Dynamic scaling for aggregation of clusters. Phys Rev Lett 52:1669–1672
Vogel H, Werner R (2015) An analytical review of volatility metrics for bubbles and crashes. Int Rev Financ Anal 38:15–28
Vogl M (2022) Controversy in financial chaos research and nonlinear dynamics: a short literature review. Chaos, Solitons Fractals 162:112444
Wang Y, Wu C, Yang L (2016) Forecasting crude oil market volatility: A Markov switching multifractal volatility approach. Int J Forecast 32:1–9
Xie H, Yu C (2019) Realized GARCH models: simpler is better. Finan Res Lett 33C
Xu J, Perron P (2014) Forecasting return volatility: level shifts with varying jump probability and mean reversion. Int J Forecast 30:449–463. https://doi.org/10.1016/j.ijforecast.2013.12.012
Youssefmir M, Huberman B, Hogg T (1998) Bubbles and market crashes. Comput Econ 12:97–114
Zhou X, Nakajima J, West M (2011) Bayesian forecasting and portfolio decisions using dynamic dependent sparse factor models. Int J Forecast 30:963–980
Zhu D, Galbraith JW (2011) Modeling and forecasting expected shortfall with the generalized asymmetric Student-t and asymmetric exponential power distributions. J Empir Financ 18:765–778
Acknowledgements
There are no further acknowledgments to be stated besides those given.
Funding
There are no sources of funding or funding interests to declare.
Author information
Authors and Affiliations
Contributions
Besides the stated single author no other person or author contributed to the creation of the manuscript. All steps have been conducted by the stated author. There are no other contributions to declare.
Corresponding author
Ethics declarations
Conflict of interest
There are no conflicts of interest to be declared for this manuscript.
Consent for publication
The author consents to the terms of publication in the SNBE Journal.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Vogl, M. Quantitative modelling frontiers: a literature review on the evolution in financial and risk modelling after the financial crisis (2008–2019). SN Bus Econ 2, 183 (2022). https://doi.org/10.1007/s43546-022-00359-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43546-022-00359-3
Keywords
- Literature review
- Financial modelling
- Risk modelling
- Financial markets
- Stylised facts
- Quantitative models