1 Introduction

Unlike traditional hardness measurement methods, since its first introduction in 1992 [1], Instrumented Indentation Test (IIT) has been developed to effectively measure the hardness of various soft and hard metals, ranging from bulk to films, and coated surfaces [2]. This capability is achieved by utilizing an indenter with a known geometry to incrementally indent the surface with high precision, down to sub-micrometer levels. Throughout the testing process, the machine continuously monitors the depth and normal force applied to the indenter’s tip as it interacts with the tested surface. The measurement outcome is represented by a curve showing the relationship between the normal force and the depth of the indenter’s tip during loading and unloading cycles. From this curve, the hardness on a classical scale and the elastic modulus of the material can be determined. With advancements in modern technology, IIT can now also measure the material’s viscoelasticity and creep properties in a single run [3]. Since these properties are measured in-situ, there is no longer a need to isolate the components from their working condition and evaluate the final imprints that the indenter leaves on its surface. Additionally, the method can be highly automated and enhanced with various evaluation protocols, leading to a diverse range of possibilities for further development of IIT techniques.

A part of this is the utilization of Neural Networks (NN) and Finite Element Method (FEM) to forecast the mechanical properties of materials based on IIT results, typically represented by Force–Displacement (F–D) curves. Conventionally, these \(F-D\) curves are used with empirical formulas to calculate the material properties [4]. However, challenges arise when dealing with the excessive work-hardening phenomenon, especially the pile-up or sink-in effects [5]. To overcome these limitations, researchers have adopted FEM while utilizing a specific material model, to simulate multiple IITs and collect corresponding \(F-D\) curves. These data points are then employed to train an NN and the trained NN is later used to predict material model parameters, a methodology termed as the “inverse approach" in [5]. By utilizing this inverse approach, it becomes possible to predict uniaxial tensile flow [6], nanomechanical properties [7], and residual stress [8].

In particular, in [6], NN is utilized to predict the tensile properties of six different types of steels, including lean duplex, dual-phase, ferritic-bainitic, transformation-induced plasticity, and austenitic stainless steel. A highlight is that the Taguchi orthogonal array method is employed to reduce the training data pairs for better prediction efficiency and accuracy (below 1%). Authors in [7] propose a combination of nanoindentation and NN to determine nanomechanical properties. First, a database of material properties is created, that includes yield strength-to-modulus ratio, coefficient for work-hardening, Poisson’s ratio, and indentation angle. This database is used to train the NN to predict these parameters by taking the F–D relation as input. The authors validate their approach on a diverse range of steel and aluminum materials. Another work attempts to predict the equibiaxial residual stresses and mechanical properties of an aluminum plate [8]. They compare the performance of the k-nearest neighbor (a supervised machine learning model) with the Kriging model and demonstrate that the former exhibits slightly better prediction accuracy for this particular task.

In traditional IIT, the tensile properties of a material are determined following the stress–strain approach, as described in [9]. It is important to emphasize that this technique is only applicable to metallic materials with spherical indenters. The process involves calculating the actual imprint area, considering the pile-up/sink-in effect, to derive the true stress (based on the contact force and contact area) and true strain (obtained from the contact angle). These values are then fitted into a chosen constitutive model to assess the material’s tensile properties. The key inputs for this approach are F and D. However, this traditional approach has certain limitations. First, it relies on empirical parameters obtained from physical tests, which necessitates extensive knowledge of material properties and leads to high testing costs. Consequently, it is suitable only for specific material groups. Second, it cannot be applied to “soft” materials with significant pile-up/sink-in effects, since it requires determining the actual contact area. To overcome these challenges, our study aims to determine the tensile properties of a typically soft material, specifically austenitic stainless steel SS304L, using the potential of NNs for data-driven modeling. By harnessing the benefits of the NN model, we can significantly reduce the expenses associated with physical tests and computational time.

The proper use of the indentation technique to measure the elasto-plastic properties of various materials is discussed in [10]. The important conclusion of the study is that there is a unique solution of the tensile stress–strain curve for some materials when using the force-indentation depth curve as input. Earlier, authors in [11] developed an inverse approach useful for various metallic materials based on the complete F–D curve (loading–unloading) from a spherical indentation. In our study, we focus only on the estimation of the plastic properties of SS304 steel. For such a case, only the monotonic part of the F–D curve is necessary. For viscoplastic materials, the indentation technique is also very beneficial in calibrating rate-dependent material models [12].

In summary, the main contributions of this work are the following:

(i):

Successful FEM modeling of IIT using Ansys Parametric Design Language (APDL). The model can be automated to simulate multiple IITs and to extract learning data for NN optimization.

(ii):

Establishing a general procedure for using NNs to estimate the parameters of austenitic steel SS304L from IIT measurements.

The rest of the paper is organized as follows. Aside from Sect. 1 which introduces the background for the study, Sect. 2 reports preliminary concepts to set forth a foundation for the technical tools that we use in this paper. Section 3 describes the general workflow and reports the primary results from IIT, tensile tests with Digital Image Correlation (DIC), and FEM modeling of IIT. Section 4 presents the results of NN training and testing along with discussions of the findings. Finally, the paper is concluded in Sect. 5.

2 Preliminary concepts

2.1 Digital image correlation

Falling under the category of Non-Destructive Testing (NDT) method, DIC is an optical, non-contact measurement that is widely utilized to capture displacement fields on the surfaces of structures under loading [13]. DIC captures and works with images in a numerical format represented as matrices of pixels. By tracking pixel positions before (reference state) and after applying a loading condition (strained state), it becomes possible to calculate in-situ displacement, enabling the determination of strain from which stress and other related results can be calculated. To conduct measurements, the surface of interest must exhibit a random visual pattern to facilitate the capture of reference images. These patterns can arise naturally from surface roughness or can be created artificially by painting a white background and adding arbitrary black dots (speckles) [14]. DIC offers a straightforward setup and can be applied to a wide range of solid materials, including metals, polymers, rocks, composites, and ceramics, regardless of their transparency [15]. It proves particularly useful in testing environments with extreme conditions, such as high corrosion, underwater, extreme strain, or temperature variations [14]. Compared to strain gauge measurements, DIC offers significant advantages as it enables full-field measurements without the need for intricate strain gauge installation and calibration. Instead of using physical strain gauges, the software generates virtual strain gauges on the areas of interest, allowing for the extraction of comprehensive full-field or localized strain results. The accuracy of DIC measurements depends on factors, such as the Field of View (FoV), the number of pixels, and their numerical range (gray-scale resolution) [16]. Larger numerical ranges lead to better differentiation of colors and lighting conditions, improving pixel tracking. By tracking pixel blocks, full-field 2D/3D deformation vector fields can be constructed. To achieve more precise DIC measurements, researchers have explored various software techniques for obtaining sub-pixel resolutions. However, these techniques require significant computational time and memory usage due to the analysis of images with much higher resolutions [17].

2.2 Constitutive model

A material model, known as the constitutive model, is an equation that establishes a relationship between the stress (applied force) and the corresponding strain (deformation) of a material or vice versa. In the context of IIT, where cyclic loading beyond the yield limit occurs, it is essential to understand the kinematic hardening phenomenon. Unlike isotropic hardening, for kinematic hardening, there is a reduction of yield stress in compressive loading after the first tensile loading, referred to as the Bauschinger effect, which is particularly useful to capture cyclic loading effect. Additionally, there is a combined hardening model that combines isotropic and kinematic hardening. For kinematic hardening models, Armstrong–Frederick (AF) model [18] and its extension, the Chaboche (CHAB) model [19] are widely used. They are deployed mainly in commercial Finite Element Method (FEM) codes to describe the cyclic elasto-plastic behavior of materials under low-cycle fatigue load or when studying the spring back effect [20]. The AF and CHAB models are employed to describe the strain-hardening behavior of materials or work-hardening, which refers to the increase in material strength under a constant load rate. The more load or stress a material withstands, the stronger it becomes, due to the formation and rearrangement of dislocations in its crystal lattice structure. Strain-hardening models attempt to predict changes in mechanical properties resulting from plastic deformation. To describe the non-linear behaviors of materials in cyclic and high-/low-cycle fatigue problems, choosing an appropriate constitutive model is therefore of utmost importance [21].

2.3 Neural networks

Machine Learning (ML) applications have seen remarkable growth in both industrial and scientific areas, spanning prediction, information retrieval, computer vision, semantic analysis, and natural language processing [22]. Over the past decades, the NN family (probably the most popular data-driven model today) has been extensively developed and applied to solve complex real-world problems. NNs provide an efficient alternative to solve problems that otherwise require substantial computing resources or remain unsolvable using only human expertise. Furthermore, NN stands apart from traditional calculation methods due to its diverse approaches, encompassing various NN models [23], enabling efficient handling of large and intricate data sets, leading to highly accurate and dependable results across several problems, such as time-series forecasting, sequential modeling, and chaotic dynamical system analysis [24]. The applications cover several fields, such as natural language processing [25], and environmental sciences and agriculture, manufacturing and education [23].

In the mechanical engineering field, the NN model has been also studied, mainly in situations involving numerical simulations and a database. It was employed to predict the seismic response and assess the performance of the Reinforced Concrete Moment-Resisting Frames [26]. In another study, it was an NN for identifying the damage stages of degraded low alloy steel with acoustic emission data [27]. In [28], the problem of plastic flow of S355 steel under high-temperature deformation was analyzed with NNs.

In this study, we use a specific subgroup of NNs named feedforward NNs. Formally, a feedforward NN is a parametric function [29], in which the parameters are adjusted to satisfactory solve a given problem. Feedforward NNs are simpler and easier to train in comparison to other NN methods [24]. In spite of their simplicity, they are powerful tools and have been used for solving many data-driven applications [23]. Specifically, in applications related to embedding systems and robotics, as well as other problems with real-time restrictions, low computational costsn and low amount of data. In other words, in situations where deep learning cannot be efficiently used, because it requires a large amount of data and computational resources. At the moment of using a feedforward NN for solving a specific task, an optimization problem appears. In the optimization that is necessary to define a suitable metric for evaluating the performance of the model, the performance evaluation is often referred to as the error/loss/fitness function, which assesses the accuracy of the model’s predictions [30]. The optimization process adjusts the model parameters. The most common algorithms are iterative based on the gradient information of the loss function. The procedure iterates modifying the parameters until a satisfactory error threshold is reached [23, 31].

Most problems requiring NNs do not have exact analytical solutions, but require approximate ones achieved through iterative optimization algorithms that minimize the loss function. Examples of such algorithms include gradient descent, stochastic gradient descent, and adaptive moment estimation [32]. One particular algorithm, Adam optimization [33], incorporates adaptive estimation of first-order and second-order moments through stochastic gradient descent. This approach is memory-efficient, invariant to diagonal rescaling of gradients, and particularly well suited for dealing with extensive data sets and numerous parameters [34]. A popular technique for the computation of gradients is propagation, which is used to calculate the loss value using any of the listed optimization algorithms. In our experiments, we apply the gradient descent-based approach for the optimizing the architecture of the network.

3 Materials and methods

3.1 Global overview of the proposed approach

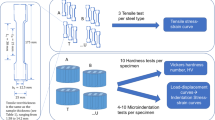
We propose in this study a methodology based on the NN approach, where a NN is employed to calibrate an appropriate plasticity model. According to the ISO/TR 29381 [35], the traditional evaluation method of IIT, representative stress and strain approach, requires first defining the true stress and strain with indentation parameters as input. Subsequently, the collected data are fitted to a constitutive equation from which the tensile properties can be obtained. This approach provides robust results with deterministic but rigid algorithm and requires numerical estimation of parameters, making it limited to a certain group of materials. On the other hand, the NN approach can determine time-dependent parameters with a relatively more flexible algorithm that can be applied to different material groups, because its input is \(F-D\) curves. The downside of such an approach is the requirement of specialized software and expertise to conduct FEA and NN training, whereas FEA is used to simulate the IIT and NN is used to encapsulate many FEA. A pipeline of the NN-based process is depicted in Fig. 1.

As can be observed in Fig. 1, the data collection stage follows the traditional approach. First, tensile tests are conducted on SS304L tensile specimens with DIC to measure the stress–strain curve, from which the true stress–true plastic strain curve is calculated. Next, a constitutive (material) model is fitted to this true stress–true plastic strain curve using the Least Square Method (LSM). Then, the fitted material model is utilized in FEM to simulate the plastic behavior of the material under IIT. The FEM model is carefully constructed to produce highly accurate results within a relatively short computational time, enabling automation for generating multiple F–D curves. The FEM model is calibrated with physical IIT by adding a compliance value. Then, multiple material parameter configurations from the fitted material model are created, which are then inputted into the calibrated FEM model to generate multiple F–D curves, replacing the need for multiple time-consuming and expensive physical IITs. The generated F–D curves are then used for NN training. Before training, the data are standardized to facilitate easier training tasks. Various configurations regarding its architecture are experimented with to find the optimal NN model for the task. The performance of the NN is evaluated with loss value over epochs and the errors between the training data and the predicted data. The objective of the paper is to establish and verify the workflow for the implementation of the NN approach.

The sample used for IIT is obtained by cutting a 10 mm-high cylinder from a cold-drawn SS304L bar. To meet the roughness requirement for the IIT test, one side of the sample’s circular surface is grinded as per the requirement for Brinell test outlined in ISO 6506 [36]. For surface roughness inspection, we use the Alicona Infinite Focus 5 G optical microscope from Alicona Imaging GmbH. From the sample bar, the tensile specimens are produced. The tensile test is conducted at room temperature using a hydraulic machine called LabControl 100 kN/1000 Nm, in accordance with the ISO 6892-1 standard. The test is performed at a constant position rate of 10 mm/min, and DIC is carried out with the MERCURY RT software.

The IIT is performed using the PIIS 3000 machine manufactured by UTM company [37]. This fully automatic and portable machine is specifically designed to test the mechanical properties, crack resistance, and residual weld stress of structural components in situ. The indenter utilized in the machine is made of carbide material with an elastic modulus (E) of 624 GPa at \(23\,^{\circ }\hbox {C}\). The machine complies with various standards, including B0950, B0951, ISO/TR 29381, KEPIC code MDF A370, and ASME Code case 2703. The measurement process begins when the contact force reaches 2 N, starting from a depth of 0 mm. Each step in the measurement process is kept relatively long to avoid any undesirable material behavior due to rapid loading or temperature fluctuations. Throughout the measurement, special care is taken to ensure that the machine is free of shock and vibration.

For automation of the IIT simulations, scripting is prepared in ANSYS Mechanical APDL 2019 R1. It can be used for various tasks such as geometry creation and FEM analysis with complex solver settings. Furthermore, the Python programming language, specifically version 3.11.0, is used to build the NN and visualize the data throughout the study. The main packages used include numpy (version 1.23.5), pandas (version 2.0.0), plotly (version 5.14.1), sklearn (version 0.0.post2), tensorflow (version 2.12.0), and matplotlib (version 3.7.1), among others. The tensorflow package is used to implement the FFNN. The construction of the FFNN is possible by prescribing the division of the data set for training and testing, the number of inputs/outputs/hidden layers (and associated nodes), the optimizer, the loss function, the number of epochs, and other parameters. This level of detailed configurations enables users to tailor the NN according to their specific requirements and experimental design.

Fig. 1
figure 1

Top–down workflow of the proposed approach

Full size image

The rest of this section is organized as follows. With regard to Fig. 1, IIT results are reported following the right branch (Subsection 3.2). Meanwhile, tensile tests with DIC and subsequent FEM are reported following the left branch (Sects. 3.3 and  3.4, respectively). Moreover, in Sect. 3.4, after calibration with IIT results, the FEM model is used to create a data set of multiple IITs, corresponding to the next two steps after the two branches are joined. Finally, the data set is used for training and testing of the NN following the last two steps in the workflow as presented in Sect. 4.

3.2 Instrumented Indentation Test

A ball indenter has several advantages for hardness testing. One key benefit is its ability to average out variations in hardness caused by surface irregularities due to the large contact area. Moreover, its shape ensures that the force is applied perpendicular to the tested surface, leading to consistent and reliable results throughout the testing process. However, for more accurate measurement with highly sensitive IIT, it is recommended to have an areal average roughness (Sa) of around 2 \(\upmu\)m. The specific area sampled for the hardness test is 1.614 mm \(\times\) 1.610 mm, resulting in a true area of 2.597 mm\(^2\), as presented in Fig. 2. Within this area, a total of 3 348 896 points were measured to illustrate the surface roughness.

Fig. 2
figure 2

Surface roughness before (left), and after applying the contour map (right)

Full size image

As can be seen in Fig. 2, the surface of the specimen bears marks from the cutting tool and scratches, likely due to storage with other specimens. The roughness analysis reveals a maximum roughness of 2.241 \(\upmu\)m and a minimum roughness of \(-\)1.539 \(\upmu\)m. The Sa value, indicating areal average roughness, is measured at 0.193 \(\upmu\)m, meeting the requirements for the subsequent IIT. It is crucial to ensure that the surface is even and devoid of any lubricants, dust, or oxide scale. Additionally, any surface alterations resulting from hot-working or cold-working must be avoided as they may introduce a layer of hardened material, which is unfavorable for the IIT unless the hardness of the hardened layer is the subject of the study itself. Moreover, when performing IIT on a machine component in-situ, it becomes essential to remove any painted, hardened, oxidized, or scratched outer layers while maintaining cleanliness and eliminating other foreign substances from the surface. The test setup and its results are presented in Fig. 3.

Fig. 3
figure 3

Setup for IIT of PIIS 3000 (left) and results on SS304L sample (right)

Full size image

Figure 3 shows that the hardness specimen’s bottom side is machined to have two perpendicular faces, facilitating secure clamping on the jig during testing. Since the testing machine remains fixed on its frame, multiple IIT measurements are conducted by moving the jig beneath the indentor. The hardness test is carried out along the diameter, and all the imprints can be observed. The positioning of the tests is done manually, ensuring a suitable distance between the test imprints while attempting to maintain a straight-line alignment. This distance is maintained to prevent any build-up or shrink-in effects around one test imprint from influencing the results of another. Slight variation of the distances among the indentations also helps to introduce the randomness into the F–D measurement. Besides, no visible deformation is observed on the back surface of the specimen, indicating that the specimen’s height of 10 mm is sufficient for the IIT, and the results are not affected by the specimen’s thickness. In this case, the thickness of the test piece meets the requirement of being at least eight times the depth of the indentation (150 \(\upmu\)m). The F–D curves are exported by the PIIS machine in.csv format. The imprints are numbered from left to right, following Fig. 3. Point 6 is at the middle of the measured line. The F–D curves of 11 points are plotted in Fig. 4.

Fig. 4
figure 4

F–D curve results: point 1 to point 6 (left), and point 6 to point 11 (right); point 6 is middle point

Full size image

As depicted in Fig. 4, the maximum force (interpreted as hardness) of the specimen is highest at the outer edges (point 1 and point 11) and gradually decreases toward the center. This variation in force indicates that the investigated specimen possesses harder outer layers, proving that it is inhomogeneous in nature. The difference in hardness arises due to the cold-drawn nature of the material, resulting in increased hardness in the outer layers. In fact, the tensile specimen used in this study has its outer layers machined out, leaving only the core with the weakest strength. Consequently, direct comparisons between the tensile test results and the IITs are only valid in the middle of the bar, where both tests can provide consistent data.

3.3 Digital Image Correlation measurement

The tensile specimens are manufactured using the turning method from the identical billet used for IIT. For tensile tests, DIC is used due to its availability and its non-contact nature, which eliminates the burden of mounting strain gauges on tensile samples. Moreover, compared to traditional tensile tests, non-contact tests with DIC are better, because the deformation/strain field can be visualized [38]. To perform DIC measurements, the samples need to be painted on a white background and sprayed with randomly colored black dots. For DIC setup, initially, the camera requires calibration with the appropriate software, and a virtual probe is created to capture longitudinal strain data. It is crucial to ensure that the position of the probe remains visible to the camera throughout the entire testing duration. This visibility enables the recording of both the initial length and the elongated length of the specimen. Figure 5 shows the test setup and highlights of the specimen during the testing process.

Fig. 5
figure 5

Setup for tensile test of SS304L specimen with DIC (left) and highlights of the test results (right four)

Full size image

As can be observed in Fig. 5, the specimen is intentionally gripped to ensure that the gauge section remains visible to the camera during testing. A flashlight is incorporated to provide adequate illumination for image capturing. Extra tapes are applied to the bottom grips to prevent redundant reflections that might interfere with the software’s recognition of the virtual probe. For this study, a total of five specimens are tested using a position rate of 10 mm/min, and their average results and standard deviation are calculated. Additionally, two additional samples are tested, one at 1 mm/min and the other at 100 mm/min. The software tracks the patterns in consecutive image frames, enabling the calculation of axial displacement and axial strain of the specimen. While a contour map can be exported for better visualization, the study opts to report the unprocessed snapshots of the DIC measurement, which suffices for their purposes.

The specimens exhibited a desirable failure mode, breaking in the middle. This outcome indicates that the specimens were properly machined with no defects near their shoulders. The presence of necking and considerable elongation suggests that the material is highly ductile. The initial virtual strain gauge is stretched and disappears after the specimen fractures. Additionally, breakages in the painted surface appear as horizontal cracks along the gauge length of the specimen. A close-up view of the fracture of the tensile specimen is presented, captured using the optical microscope Alicona InfiniteFocus 5 G. This detailed view further confirms the ductile nature of the material, which is attributed to the high chromium composition of SS304L. Remarkably, there is a substantial reduction in the cross-section of the specimen due to necking, indicating its highly ductile nature. An interesting observation is that the outer surface of the sample exhibits a staircase-like pattern inherited from the turning process. From the specimen’s failure mode and the shape of the necking, it can be inferred that the tool’s imprints have some influence on the tensile results. However, the extent of this effect is not the primary focus of this study. Indeed, we attempt to establish a framework that integrates FEM with NN and subsequently refines it with material inputs. Additionally, one crucial property that holds significance for this study is the material’s dependency on the strain rate, known as the strain rate sensitivity. To investigate this, the stress–strain curves of the material are plotted under three different strain rates, as depicted in Fig. 6.

In addition, it can be deduced that varying the strain rate has little impact on the yield limit of the material. However, it significantly reduces the ductility of the material. The mechanical properties obtained from these three tests are reported in Table 1. Properties include the Young’s modulus (E), yield strength (\(\sigma _{y}\)), ultimate strength (\(\sigma _{u}\)), ultimate strain (\(\varepsilon _{u}\)), and the ductility or strain at fracture (\(\varepsilon _{max}\)). Remarkably, the “N/A" marking in Table 1 indicates data that are missing from the tensile tests. For this study, the results obtained at a strain rate of 10 mm/min are selected, because it represents a commonly encountered condition for technical components made from this material in real-world IIT applications. This choice avoids the use of extreme test conditions, such as very slow (1 mm/min) or very fast (100 mm/min) strain rates. Tensile data acquired from tests conducted at different speeds can be utilized to establish a time-hardening model, such as the Perzyna model [39], which can be incorporated with the kinematic hardening model to better describe the plastic behavior of the material. For the verification of the methodology, a low strain rate is considered, while time-independent incremental plasticity can be applied with a sufficient accuracy.

Fig. 6
figure 6

Stress–strain curves of SS304L tensile specimen with three different testing speeds

Full size image
Table 1 Tensile properties of SS304L with three different testing speeds
Full size table

3.4 Finite element method

To simulate an IIT using FEM, it is essential to identify a constitutive model that accurately describes the plastic behavior of the material being tested. This involves calculating a number of data points from tensile test results to true stress (\(\sigma _\textrm{true}\)) and true plastic strain (\(\varepsilon _\textrm{pl}\)). These recalculated data points can then be fitted using the LSM to a chosen constitutive model, such as the AF model given by Eq. (1)

$$\begin{aligned} \sigma _\textrm{true}=\sigma _{y}+\frac{C}{\gamma }\left( 1-e^{-\gamma \varepsilon _{pl}}\right) . \end{aligned}$$
(1)

The AF model parameters fitted for the testing data are \(\sigma _{y}\) = 535 MPa, C = 1567 MPa, and \(\gamma\) = 2, using the tensile results obtained at a test speed of 10 mm/min. These fitted material parameters allow for the use of the constitutive model in FEM simulations. The material sample under IIT is represented by a deformable cube measuring 1 mm \(\times\) 1 mm on 2D plane, which is indented by a rigid 2D circle representing the ball indenter with a diameter of 1 mm. To reduce computational time, a 2D axisymmetric simulation approach is adopted. Details regarding the experiment with different constraints are elaborated in the subsequent paragraph. The simulation setup follows the methodology presented in [9], and the meshing strategy is based on [40]. The geometry is meshed using 2D linear elements (PLANE182), and the resulting mesh is illustrated in Fig. 7.

Fig. 7
figure 7

Mesh for IIT simulation in ANSYS APDL with meshing strategy, where sides a, b, c are assigned with numbers of nodes for automeshing (left) and the \(F-D\) curve result of 15 loading–unloading cycles (right)

Full size image

The meshed geometry depicted in Fig. 7 (left) undergoes an indentation process by a carbide ball indenter. Given that indenter is inspected prior to the test to meet the IIT requirement, and the measured objectives are the reaction force on the indenter’s head and its depth, its exact roundness is not the deciding factor for the simulation. The ball indenter is controlled by a pilot node located at the center. It also serves the purpose of collecting both the reaction force and depth data to construct the Force–Displacement (F–D) curve, which forms the backbone of the entire study. The contact type utilized for the simulation is Surface-to-Surface (CONTA172) between the rigid indentation ball geometry (TARGE169) and the deformable 2D cube (PLANE182). To handle the contact interactions, the augmented method is employed as the contact algorithm. To prevent any potential coincident node issues, the pilot node is assigned a high ID value (99999). This ensures that the pilot node does not overlap with any other node, particularly when the geometry is refined with a larger number of elements. Our initial simulations show that changing the coefficient of friction from 0.1 to 0.5 does not change the \(F-D\) curve results with regard to the growth of the curve and their peaks, supported by the findings in [41]. This can be explained by the fact that the F–D curve is collected from the pilot node of the rigid ball indenter. Thus, the interaction between the surfaces of the ball indenter and the sample is negligible. In this study, the friction coefficient is chosen to be a representative value of 0.1.

Regarding constraints, we first experiment with a 4 mm cube with a symmetric boundary condition on the left edge of the cube, that is, fixation along the Ox axis. The bottom edge is fixed in both the Ox and Oy axes, and the right edge is left free. A total of 15 loading–unloading cycles that reach the maximum depth 150 \(\upmu\)m are simulated to observe the stress field under the ball indenter. The result of the stress contour shows that almost 75% of the area surrounding the 1 mm\(^2\) area under the indenter is with a stress level of 0. Therefore, the cube is scaled down to 1 mm \(\times\) 1 mm with an addition fixation along the Ox axis on the right edge to simulate the rigid effect of the surrounding material. The \(F-D\) results of the two cases are equivalent, and thus, the 1 mm cube is chosen given that the FEM model consists of 2502 elements and the entire process takes approximately 480 s per simulation.

The reaction force of the indenter is plotted versus the depth of the indentation ball yielding the F–D curve in Fig. 7 (right). It should be noted that for the PIIS setup, the loading phase is depth-controlled (indents 10 \(\upmu\)m per step), and the unloading phase is force-controlled (retracts 50% of force per step). For simplification purposes, IIT simulation is depth-controlled with one cycle consisting of 10 \(\mu\)m loading and 5 \(\upmu\)m unloading. From the figure, it is evident that withdrawing the indenter by 5 \(\upmu\)m results in the almost complete retraction of the indenter head from contact with the specimen, force value approaching zero. In conventional approaches, the 15 peaks on the F–D curve are calculated to points on a true stress–true plastic strain curve using a number of empirical formulas for fitting and determining the material’s constitutive model. Figure 8 displays contour maps of the Von Mises Stress (VMS) value when the indenter is pressed 15 cycles to the depth of 150 \(\mu\)m and after complete withdrawal from the specimen. It should be noted that within the first few \(\upmu\)m, the elastic limit of the material has been exceeded and its behavior is completely plastic. The plasticity of the material then plays the crucial role in how it will react to repeated indenting load. Therefore, using the Young’s modulus collected from the tensile tests to setup is sufficient for the study.

Fig. 8
figure 8

VMS results before (left) and after IIT for 15 loading–unloading cycles (right)

Full size image

In Fig. 8, the distribution of VMS follows the Hertz contact theory [42]. Specifically, the maximum stress is observed below the contact surface, and the highest VMS value recorded in the region with the red contour is 1020 MPa. The plot in Fig. 8 (left) illustrates that the maximum VMS occurs when the indenter is at its deepest position, reaching 982 MPa. After the indenter retreats, the maximum VMS reduces to 667 MPa as depicted in Fig. 8 (right). The distribution of equivalent plastic strain is depicted in Fig. 9.

Fig. 9
figure 9

Equivalent plastic strain after IIT for 15 loading–unloading cycles

Full size image

Figure 9 illustrates the plastic strain distribution after all the elastic strain is completely released owing to the complete retraction of the indenter. The permanent deformation, represented by the imprint of the indenter, results from a significant amount of plastic deformation occurring in the material under the contact surface. The maximum equivalent plastic strain recorded in the simulation is 1.168. The majority of the region with permanent deformation exhibits equivalent plastic strain values ranging from 0.19 to 0.91.

In the traditional approach, obtaining the full information from loading–unloading cycles is crucial, so that each force peak is considered to back-calculate points on the true stress–true plastic strain curve. By selecting five peaks from five consecutive loading–unloading cycles in the F–D curve, one can calculate five true stress–true plastic strain points, following the procedure described in [9]. These points are then used to find an appropriate material model through curve fitting, leading to the calculation of corresponding material parameters.

With the NN approach, it is not necessary to obtain complete F–D curves with unloading portions (elastic releases) for curve fitting purposes. In addition, our initial simulations show that compared to the 15-cycle simulation, the one-cycle simulation significantly reduces computational time, approximately 4.3 times lower, while the highest point on the F–D curve and the final stress distribution in the sample remain the same. Therefore, simulating only one loading–unloading cycle is sufficient, which has been shown to be feasible as well in previous research [43]. Saving the computational time by reducing the number of loading–unloading cycles is particularly important, as future simulations will be automated to generate hundreds or even thousands of \(F-D\) curves. Generally, reducing the simulation size facilitates practical scalability in generating a large data set of F–D curves for further analysis.

NN approach involves collecting F–D curves directly from FEM simulations of a calibrated IIT model rather than performing many physical IITs. These simulated curves are then used to train an NN to predict the material properties. It should be noted that the loading–unloading cycles in these curves (both simulation and physical measurement) do not have linear relationships. This can be observed from the non-linear growth of theF–D curve between two peaks of the intermediate cycles. Including these trivial intermediate nonlinearities will complicate the analysis. Therefore, we decide to first simplify the 15-cycle simulation to one-cycle simulation to decrease the simulation time. As a step further, we record only two key points from these F–D curves, that is, point 0 (initial position) and the maximum force, instead of every data point to reduce the size of the NN training dataset. A line is then created from these two points, representing the linearized F–D curve, and it is adjusted with a fixed compliance to better match physical measurements. By adopting this approach, the focus is mainly on the slope of the F–Dcurve, rendering the unloading cycles negligible. The investigation of the effect of mesh size on the FEM results is listed in Table 2.

Table 2 Computation time for different element numbers of simulation for one loading–unloading cycle
Full size table

As reported in Table 2, the calculation time increases exponentially as we increase the number of nodes on the a, b, and c sides. It should be noted that refining the mesh results in a better contour map for stress/strain results and a smoother F–D curve. The maximum VMS stress values recorded in all three cases are roughly 982 MPa (difference of less than 1%) with relatively the same maximum reaction force on the F–D curve (neglectable difference of less than 0.5%). Indeed, the maximum reaction force on the indenter is more crucial than the VMS stress result. Thus, we have chosen the model with the least number of elements to minimize computational time, taking into account that the model has to be automated 1000 times later to create a data set for NN training. It should be noted that this decision was made, because the paper prioritized the establishment of a framework with an acceptable accuracy level given limited computational resources. To better simulate reality, a finer mesh and complete modeling of 15 loading–unloading cycles are recommended, which unavoidably requires higher computational power and increases computational time by many folds.

Remarkably, the simulated results are slightly lower than the experimental results obtained from the IIT measurements due to machine compliance. This discrepancy is evident from the difference between the two highest points of the simulated and experimental curves, as shown in Fig. 10.

Fig. 10
figure 10

Comparison of the \(F-D\) curves between the physical IIT (15 cycles), and the simulated IIT (one cycle)

Full size image

In Fig. 10, it is observed that the maximum force recorded in the experimental test is 1145 N, whereas the maximum force obtained from the simulation is 931 N. Consequently, the compliance value is calculated to be 214 N. It should be noted that there should be 15 compliance values corresponding to 15 loading–unloading cycles. However, for simplicity, only the compliance value at the maximum force is considered in this study. This is followed by the assumption that the path from 0 N to the maximum force is linear. The calculated compliance value will be added to all F–D results used in the ML model.

The simulation process is now ready for automation, where multiple material models are simulated to obtain the corresponding set of F–D curves. These F–D curves are then utilized for subsequent training of the NN. In particular, the fitted parameters of the AF model are varied within their chosen specific ranges (or domains): \(\sigma _{y}\) \(\in\) [400; 625] MPa with a step size of 25 MPa, C \(\in\) [500; 9500] MPa with a step size of 500 MPa, and \(\gamma\) \(\in\) [1; 10] with a step size of 1. As a result, by combining 10 values for each parameter \(\sigma _{y}\), C, and \(\gamma\), a total of 1000 configurations of different true stress-true plastic strain inputs are obtained, as illustrated in Fig. 11.

Fig. 11
figure 11

True stress–true plastic strain curves generated from 1000 configurations of AF model

Full size image

A unique combination of the three material parameters is referred to as a configuration. In total, there are 1000 configurations in Fig. 11 that correspond to 1000 true stress–true strain curves. From these, 1000 IIT simulations are conducted from which 1000 maximum force values are extracted. Recorded from the simulations, the minimum VMS is 434 MPa with given \(\sigma _{y}\) = 400 MPa, C = 500 MPa, and \(\gamma\) = 10. On the other hand, the maximum VMS is 2147 MPa with given \(\sigma _{y}\) = 625 MPa, C = 9500 MPa, and \(\gamma\) = 1. The material parameters are varied widely to capture the outliners of the austenitic stainless steel group, including hardened SS304L that can have ultimate strength greater than 2000 MPa [44]. The VMS level justifies the physical meaning of the chosen intervals. Therefore, we can progress with the simulated force values. Figure 12 illustrates the maximum reaction forces collected from 1000 simulations before and after adding compliance.

Fig. 12
figure 12

Simplified F–D curves (one cycle) simulated with 1000 configurations before (left) and after adding the machine compliance (right)

Full size image

The results obtained from Fig. 12 can be used for NN training. It is important to note that for the NN training, only the last point (maximum force) of each simulation is required, resulting in the need for only one value per simulation. It should be noted that in practical scenarios, the F–D curve obtained from the IIT measurement is not a straight line. To address this, a better approach involves calculating the compliance for all 15 peaks and adding those compliance values to every 10 \(\upmu\)m of depth. However, for automation purposes, in the FEM simulation, the F–D curve is simplified to indenting 150 \(\upmu\)m in one loading cycle, and the model is meshed with a relatively small number of elements. As a consequence, the peaks between 0 \(\upmu\)m and 150 \(\upmu\)m lack sufficient accuracy to be considered for the NN study.

4 Results

Following the gathering of 1000 distinct F–D curves, the maximum force values and their corresponding configurations of three parameters are extracted and combined for training and testing of a FFNN. The force values are designated as input, while the configurations of the three parameters serve as the output for the NN. Because the material parameters and the resulting force exhibit considerable variability, it becomes essential to normalize the data within narrow ranges, that is, [0, 1]. This normalization process ensures that the data are presented in small, uniform values, which proves to be more beneficial for effective training and testing of the NN, because the NN can learn without the need to consider the unit and meaning of the fed [45]. The original data set of 1000 samples is split into two subsets, that is, a training set (80% of the data, or 800 samples) and a testing set (20% of the data, or 200 samples). The splitting ratio of 80:20 is chosen following the classic procedure [46]. The training and testing sets are shuffled and then split from the original data set. Randomization is facilitated by the pseudorandom number generator (PRNG) [47]. The testing set is used to evaluate the performance of the trained NN for unseen data. The random state is fixed, so that consistent comparison of different NN architectures can be done. Figure 13 illustrates the normalized maximum force values acquired from 1000 simulations, with 80% of them after the splitting and randomization process.

Fig. 13
figure 13

Simulated force values from the original data set with 1000 samples (left), and training data set with 800 force values after splitting and randomization (right)

Full size image

In Fig. 13 (left), it is evident that the original set of force values appears to exhibit a certain level of structure. This structure arises, because the simulations are conducted with variations of material parameters in a sequential manner. However, after the process of splitting and randomization, the force values for training, shown in Fig. 13 (right), become nearly randomly distributed. This poses a challenge during the training and testing of the NN because of the need to identify a function that effectively fits the randomized data with LSM. The accuracy of the NN is significantly influenced by this fitting process. It should be noted that, in this study, the symbol “y" stands for the output. The testing data, comprising 20% of the total data set, is distinguished with the suffix “_test" and the predictions based on this testing data are denoted by the suffix “_te."

The three parameters and their corresponding forces from each simulation are extracted and then normalized. They are combined into a numpy matrix of 1000 rows and four columns (.npy file) to be utilized for training the FFNN. Each combination of three parameters and one force is called a sample. The FFNN is designed with one input (F) and three outputs (\(\sigma _{y}\), C, and \(\gamma\)). The activation function employed for all the nodes is the sigmoid function. Sigmoid is chosen, because it is a non-linear activation function that can fit well to the nature of IIT, the non-linear relationship between material parameters and its behavior in terms of F–D curves in plastic zone [48]. To achieve convergence, the number of training epochs is set to 200, ensuring that saturation is observed. The learning rate is established as 0.0011. Moreover, the training data is normalized within the range of [0, 1]. Different NN structures with different combinations of 1, 3, 5 hidden layers and 1, 5, 10 nodes per hidden layer are examined. The computation is conducted with AMD Ryzen 5 3500U core. The loss results are shown in Table 3.

Table 3 Comparison of loss values calculated with different NN structures
Full size table

As can be observed from Table 3, the most efficient configuration consists of one input layer, one hidden layer with five nodes, and three output layers, as it provides the best performance in terms of loss calculation and computational time. However, it is important to note that the loss results may exhibit slight variations due to several factors, including the evaluation procedure, numerical precision of the inputs and outputs, and the stochastic nature of the algorithm that is used as the optimizer (herein Adam). To ensure robustness, each simulation is run multiple times, and the average outcomes are reported. The NN with a single hidden layer consisting of five nodes is considered the most appropriate choice considering both the minimized loss value and the simplicity of the network structure. The material parameters \(\sigma _{y}\), C, and \(\gamma\) are in order denoted as \(p_1\), \(p_2\), and \(p_3\). We evaluate the performance of the FFNN with one input three outputs (combined model, loss value \(p\_all\)), and one input one output (single model, loss values \(p_1\)/\(p_2\)/\(p_3\)). The loss values obtained from training and testing (for combined model and single models) with the data set of 1000 samples are reported in Table 4.

Mathematically, when the number of inputs is greater than the number of outputs, it is preferable for the interpolation of the NN [49]. Therefore, it offers us a way to increase the size of the data set for better NN training, by utilization of a surrogate model to replace the FEM simulations. With this insight, the study proceeds to investigate a reversed structure of the current FFNN model. This reversed model has three inputs (\(p_1\)/\(p_2\)/\(p_3\)) and one output (F). Besides, other configurations regarding the hidden layer, the activation function, the optimizer, etc. are the same. The initial FFNN model, with one input and three outputs, is referred to as the “original model" going forward. The reversed model is trained with the data set of 1000 samples that delivers the loss value of 0.0011; see Fig. 14.

Fig. 14
figure 14

Performance of the reversed NN in force prediction: loss per epoch (left), and error between the real data and the prediction (right)

Full size image

In Fig. 14, it can be seen that there are some outlines that cannot be learned (or approximated by the fitting function). This is a common challenge in ML applications, where learning models often encounter difficulties with extreme values, as they tend to perform better with smooth and regular functions. Despite this limitation, the force values are generally predicted with a notably high level of accuracy, proving that the reversed model can be utilized as a substitute for the FEM simulation in APDL. This enables the generation of additional force predictions for a larger set of parameter configurations.

Subsequently, to increase the number of data, the material parameters are varied within the same domains with half of the original step size. This gives us 6859 configurations that can be input into the reversed model to predict corresponding 6859 forces. These newly predicted forces are coupled with the parameters and combined with the initial 1000 samples to create 7859 samples in total. The data set of 7859 samples is then used for training and testing of the original model, resulting in the loss values in Table 4, whose performance is compared with 1000 samples.

Table 4 Loss values calculated with combined model and single models for FFNN trained with 1000 and 7859 samples
Full size table

Together with Table 4, the performance of the NN working with 1000 samples and 7859 samples is compared in Fig. 15 (right column versus left column). With the increase in the amount of data, the structure of the original model is adjusted to include three hidden layers, each consisting of 10 nodes. Other NN configurations remain the same. As a result, the loss converges to a value of 0.0610. Compared to the original model, overall, the loss values are approximately 1% better except for \(p_2\). This is evident from the prediction being closer to the trend line of the test data in Fig. 15. This observation confirms that a higher number of training samples lead to improved predictions by the NN model. Furthermore, it should be noted that \(p_2\) (parameter C) is learned best. From the perspective of material properties, referred to Eq. (1), C defines the initial slope of the plastic curve from \(\sigma _{y}\). When the material is indented to the first few \(\mu\)m of depth, it surpasses the yield limit, and its behavior becomes completely plastic. Hence, it is reasonable to conclude that C has the most significant influence on the force values.

As evident from Fig. 15, the prediction error can be reduced when we increase the number of training samples and the influences of parameters can be studied. However, the parameter prediction still has high errors. To conclude, the study only investigates the regression in a simulated environment without the real data included in the physical objective function. Therefore, the data used to learn the mapping lack additional input information to identify that the parameter set for a particular force value is unique. It would be interesting to consider in the future the FEM Updating (FEMU) method, using gradient methods and evolutionary algorithm (EA) or genetic algorithms (GA), as a candidate for future improvement [12].

Fig. 15
figure 15

Performance of the NN in parameter prediction: Loss per epoch (first row), and error between the real data and the prediction (bottom three rows) for NN trained with 1000 samples (left column) and 7859 samples (right column)

Full size image

5 Conclusions and future works

In this paper, we present a methodical procedure based on NN that is potentially able to replace the complex analytical solution of IIT and expensive physical measurements. The results of both physical and numerical tests effectively showcase the advantage of the proposed approach. The methodology unfolds as follows: Initially, physical IIT and tensile tests are conducted on SS304L samples to be used for description of the material in FEM modeling. Although the cold-drawn SS304L has higher strength in the outer layers, by considering only the F–D result in the core of the IIT sample, the IIT test result is comparable with the tensile tests and both can be used. Besides, the strain-dependent plastic behavior of the material is revealed, which is beneficial for future employment of time-hardening material models.

Subsequently, an appropriate FEM model is employed to simulate IIT, and this simulation is fine-tuned to match real-world data from prior physical tests. The size of the FEM modeling is kept modest taking into account the fact that the simulation will be automated a thousand times to generate a large data set for subsequent NN training. Remarkably, the simplification of the full 15 loading–unloading cycles to one loading–unloading cycle is realized to keep the simulation time short. After obtaining the FEM model that has been calibrated with reality, by manipulating material parameters given to the model, diverse material property configurations can be simulated to produce corresponding F–D curves.

Finally, these curves are harnessed to train an FFNN capable of predicting constitutive model parameters based on any provided F–D curve. In the experimental evaluation, we considered several FFNN architectures. The best-predicted parameter is C indicating that it has the highest influence on the F–D curves. From the material point of view, it is a coherent result, because this parameter sets the initial slope of the plastic curve which describes the entire behavior of the material after a few \(\upmu\)m of indentation. We also evaluated and reported slight variations on the architectonic design of the NNs, which obtain a slightly better prediction for parameters \(\sigma _y\) and \(\gamma\), while C remains relatively the same.

We plan to simulate, in the future work, several loading–unloading cycles (e.g., 15 cycles) and incorporate the corresponding compliance. Furthermore, the FEM model can be prepared with a finer mesh and smaller steps for a more precise simulation. The simultaneous force/depth control following the real machine setup can be modeled. In addition, different constitutive models can be employed to describe the strain-hardening and/or time-hardening behaviors of the material. Regarding the NN tools, we plan to compare the achieved results of the feedforward architecture with other machine learning tools, such as kernel-based methods. Last but not least, the FEMU methods using gradient methods, EA, or GA based on physical objective function can be incorporated for future studies.