Numerical modeling of cyclic softening/hardening behavior of carbon steels from low- to high-cycle fatigue regime

Abstract

The aim of this study is to characterize the stress–strain behavior of three construction steels (SM490, SM570, and F18B) through both experimental and numerical investigations. The material performance was evaluated by conducting tests on round bar specimens subjected to monotonic, fatigue, and incremental step fully reversed loading conditions. The experimental campaign was conducted to provide valuable information on the mechanical performances of the steels and data for calibrating the material constants required for numerical analyses. The numerical simulations aimed to demonstrate the effectiveness of the proposed unconventional plasticity model, the Fatigue SS model (FSS), in describing the non-linear behavior of the materials under a broad range of loading conditions, including stress states below and beyond the macroscopic yield condition. This aspect is a significant advantage of the FSS model, as conventional elastoplastic theories fail to provide a phenomenological description of inelastic material deformation under stress states within the yield condition. The good agreement between the experimental and numerical results confirms the validity of the calibration of the material constants and the reliability of the computational approach.

1 Introduction

Steel is widely used in many industrial sectors, including naval, automotive, heavy machinery, and construction. Therefore, investigations on its mechanical properties represent a fundamental aspect of the correct design/maintenance of components and structures.

In particular, the durability of structures or components represents a crucial issue in terms of fatigue. According to several authors [1,2,3,4], fatigue should be regarded as the leading cause of material rupture in bridge metallic members among the different mechanisms that produce significant losses (e.g., corrosion, construction and supervision mistakes, accidental overload, impact). Examples of metal fatigue on structures are numerous, for instance, on the railway bridge analyzed by Deler and Unterweger [5] or the comprehensive investigation by Haghani et al. [6] that deals with more than 100 failure damage cases reported in steel and composite bridges. Fatigue of metals is an important issue not only for structures but also for vehicle components. One recent example is the axle rupture and subsequent derailment of trains 9T90 and 9T92 in Australia in 2019 [7]. The tragedy of the Viareggio disaster represents another case in 2009 [9], where fatigue failure played a significant role.

In the last decades, the progressive transition to renewable energies renovated the interest in fatigue failure of wind towers and turbines [8,9,10,11,12], both on land and offshore, investigating the optimal design of the blades as well as the main causes affecting the in-service life. Recently, Dong et al. [13] published an interesting paper discussing the necessity of considering the uncertainties in fatigue loads in the reliability assessment of ship and offshore structures.

Due to the importance of evaluating the remaining in-service life of many structures and components in various industrial sectors, a wide range of non-destructive evaluation (NDE) methods have been developed to detect fatigue failure. Several techniques have been developed to monitor crack growth [14,15,16], among others, aided by the use of artificial intelligence (AI) technologies for identifying surface defects [17, 18] and even for the prediction of crack growth [19]. On the other hand, fatigue life in metals is a process that incubates at an early stage of the in-service life due to localized plastic deformation associated with stress concentration and accumulated under repeated loading [20,21,22]. Crack initiation is a complex phenomenon influenced by several variables, including the material microstructure, and can occur at any stage during fatigue life. Although the crack growth can be monitored using various instruments, the process leading to crack formation cannot be monitored. Therefore, crack initiation life can be evaluated through different methods that can be classified into two groups: stress–strain approaches ([23,24,25], among others) and local approaches based on damage mechanics ([26,27,28], among others). The design of metallic components or structures often assumes an elastic behavior of the materials, and linear fracture mechanics frameworks such as S–N diagrams and stress intensity factor K are widely used to evaluate fatigue life in engineering practice. This approach can provide a reasonable estimation of material performance. However, it may not be appropriate in cases involving strong material non-linearities or non-linearities caused by previous loading history [29, 30]. Other approaches, such as the J-integral [31] or the cyclic J-integral [32] can consider the contribution of inelastic deformation to the generation and propagation of cracks; however, the influence of the local geometry at the crack tip depends on the choice of the integration contour surrounding the crack.

Recently, the authors developed a methodology [33, 34] based on finite-element analyses (FEA) for the evaluation of crack initiation and propagation using the unconventional plasticity model FSS [35]. The advantage of this approach lies in the constitutive model formulation, which can account for the smooth development of plastic strain even for stress states below the macroscopic yield stress. Phenomenological conventional plastic theories allow the generation of irreversible deformation only for stress states that lie on the yield surface during the material loading. Therefore, cyclic loading within the elastic domain produces a purely elastic response. On the contrary, the FSS model proved to catch a realistic non-linear description of the material behavior in cyclic mobility problems and low/high-cycle fatigue problems (e.g., [36, 37]). In addition, steel with suppressed fatigue crack propagation by cyclic softening has been developed [38]; however, the effects of microstructure and mechanical properties on fatigue crack propagation are complex and have not been quantified. The FSS model is expected to contribute to understanding the mechanism for suppressing fatigue crack propagation in future research. Employing a finite-element analysis (FEA) methodology to investigate the fatigue life of components/structures offers advantages such as reducing the costs of experimental campaigns, conducting geometrical parametric studies, and quick analysis. However, the accuracy of the results is highly dependent on the modeling characteristics, including mesh, element type, 2D or 3D analyses, boundary conditions, as well as material parameter characterization. Specifically, the latter requires a preliminary experimental campaign to obtain the mechanical response of the material and a thorough calibration of the constants and parameters used in the constitutive model. The paper aims to offer an experimental characterization of the stress–strain behavior of three different construction steels, named SM490, SM570 (according to the Japanese Industrial Standards (JIS) [39, 40]) and cyclic softening steel (F18B). SM490 steel has been widely adopted in bridges and civil structures due to its low cost, good machinability, and weldability. Moreover, its ductility represents an advantage for safety in seismic areas. Steel SM570 has been progressively used in recent years due to its higher yield strength, good corrosion, and wear resistance. F18B steel is an in-house steel, prepared to have a high cyclic softening rate to suppress fatigue crack propagation, characterized by a static strength equivalent to SM570. SM490 and SM570 are often used in welded structures, however, the present work does not consider welding effects (i.e., phase transformations, microstructural changes, heat affected and weld zone mechanical properties [41,42,43,44]).

The experiments were performed using quasi-static, monotonic and fully reversed loading conditions under a wide range of prescribed displacement conditions, allowing for material characterization under low and high loading cycles. The second objective of this study is to calibrate the material constants for the SM490, SM570, and F18B steels using the Fatigue SS model to provide a valuable database for future fatigue investigations on complex structures or components. The paper is organized as follows. Section 2 deals with the experimental campaign to characterize the stress–strain behavior of the three different steels, describing the equipment and the experimental conditions. Section 3 is dedicated to explaining the numerical approach adopted for the FEA. In detail, Sect. 3.1 highlights the main features of the FSS model, referring the reader to [35] for a detailed discussion of the theory. The following Sects. 3.3, 3.4, and 3.5 present the material calibration and the numerical modeling of the fatigue performances of SM490, SM570 and F18B steels. A discussion on the experimental results is also discussed in these subsections. Lastly, Sect. 4 reports the concluding remarks.

2 Experimental characterization

2.1 Material characterization

The present study used three different construction steels named SM490, SM570 and F18B. The chemical compositions of each test steel are shown in Table 1. Figure 1 shows the microstructures of the steels. As observable in Fig. 1, SM490 consists of ferrite and layered pearlite. SM570 displays single-phase bainite, while F18B contains bainite with dispersed ferrite particles.

Table 1 Chemical compositions of test steels (mass%)

Fig. 1

Microstructure of a SM490, b SM570 and c F18B steels

2.2 Mechanical tests conditions

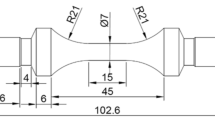
Monotonic tensile tests were carried out using the tensile test specimen shown in Fig. 2 to measure the 0.2% proof stress (YS), tensile strength (TS) and elongation at break (EL). The gauge length was 40 mm, and the tensile speed was 2 mm/min.

Fig. 2

Specimen geometry for monotonic tensile test

Cyclic softening properties were evaluated by incremental step tests using the test specimen shown in Fig. 3. In this test, the increasing/decreasing waveform block of strain shown in Fig. 4 was repeatedly loaded 20 times on the specimen. The test conditions are shown in Table 2. The cyclic softening rate R_CS was calculated using Eq. (1):

$$R_{CS} = \frac{{\sigma_{1} - \sigma_{20} }}{{\sigma_{1} }}$$

(1)

where σ₁ and σ₂₀ are the stresses at ε = 1.2% in the 1st and 20th blocks, respectively.

Fig. 3

Specimen geometry for incremental step test

Fig. 4

Strain waveform block for incremental step tests

Table 2 Conditions of incremental step tests

Uniaxial fatigue tests were conducted using the tensile test specimen shown in Fig. 5. In this test, tensile and compressive loads were applied under strain control until the specimens failed. The gauge length was 8 mm, and the strain speed was 0.3 to 0.8%/s.

Fig. 5

Specimen geometry for fatigue test

2.3 Experimental results

Table 3 presents the results of the monotonic tensile test and incremental step test. The SM490 steel exhibited a tensile strength exceeding 490 MPa, while the SM570 steel demonstrated a tensile strength 1.26 times higher than SM490. Both SM490 and SM570 steels showed slight cyclic softening with 1% and 6% RCS rates, respectively. F18B was inferior to SM570 in terms of 0.2% proof strength but had an equivalent tensile strength. Moreover, F18B showed a cyclic softening rate of 12.5%, approximately twice that of SM570. All three steels exhibited good elongation, with elongation at break exceeding 30%. Experimental results are reported in Sects.  3.3, 3.4, and 3.5.

Table 3 Mechanical properties of test steels

3 Numerical analyses

The constitutive equations of the FSS model have been implemented in a programming language for the numerical simulation of the materials’ behavior under fully reversed loading conditions. Section 3.1 provides a summary of the FSS model's main features, as well as modifications introduced to model an isotropic softening behavior for stress states beyond the macroscopic yield stress, updating the formulation presented in [37]. It should be pointed out that although previous works by the authors [36, 37, 39] employed a user subroutine for the commercial code Abaqus, the current FSS model implementation has been formulated for a single quadrature point code due to the large number of cycles and simple geometry of the specimens. The integration point is located at the center of the specimens and can represent a material point where stress conditions are close to a uniaxial stress state. The numerical simulations return the true stress and true strain values of stress and deformation.

3.1 The fatigue SS model

The stress–strain material response was evaluated by means of a phenomenological elastoplastic constitutive model named Fatigue SS [35]. The FSS model combines the features of an unconventional plasticity theory [45] with an isotropic scalar damage-like variable to describe the irreversible deformation accumulation in cyclic mobility problems. A detailed discussion of the numerical model is not the purpose of the present paper; the reader is referred to Tsutsumi and Fincato [35] for an in-depth discussion. Here, a brief description of the model’s features is given, focusing on a few modifications introduced in the present formulation that improved the material description compared to [35]. In detail, Box 1 contains a summary of the constitutive equations implemented in the single quadrature point code (see also Fig. 6).

Fig. 6

Sketch of the subloading and normal-yield surface

Experimental observations have led to the conclusion that fatigue can be explained by the accumulation of plastic strain caused by stress localizations around material defects and impurities [46,47,48]. In particular, irreversible deformations can occur locally even if the macroscopic load results in a nominal stress state within the elastic domain [49, 50]. While micro- or mesoscale approaches can accurately describe the aforementioned phenomenon [46, 47, 51], a macroscopic point of view requires an ad hoc formulation. The FSS is a phenomenological model that allows the generation of irreversible stretches for all stress states that satisfy the loading criterion, even below the macroscopic yield stress ${{\varvec{\upsigma}}}_{y}$. In particular, the subloading surface, Eq. (3)₁ is created within the conventional yield surface (renamed here normal-yield surface, Eq. (3)₂) utilizing a similarity transformation, whose center s moves in the stress space following the plastic flow. The subloading surface always passes through the current stress state ${{\varvec{\upsigma}}}$, acting as a loading surface, expanding or shrinking depending on the loading or unloading of the material. The similarity ratio R assumes values lower than unity for stress states within the conventional elastic domain and a maximum value of R = 1 for a fully plastic stress state (i.e., the subloading surface and the normal-yield surface coincide). The non-linear stress–strain response within the normal-yield surface depends on a material constant named u, which regulates the evolution of the similarity ratio R. Lower values of u enhance the generation of irreversible strain, while higher values recover the material response of conventional plasticity theories (see [45]).

In addition, the constitutive model is enriched by an additional scalar internal variable D (0 ≤ D ≤ 1), representing the accumulation of the damage inside the material to generate the opening of the hysteresis loops. The damage-like variable evolution in Eq. (7) depends on the cumulative plastic deformation and, vice versa, affects the generation of inelastic strain by affecting the evolution of the similarity center in Eq. (6)₂ and the similarity ratio in Eq. (8). However, it does not affect the elastic response of the material.

In detail, Eq. (8) has been modified compared to the formulation in [35] by adding an exponential parameter $\beta$ that allows modifying the material’s stress–strain response, as explained in the following subsections.

A second modification, compared to the formulation presented in [35], is the incorporation of an isotropic softening contribution in Eq. (5)₁, which is a function of two material parameters, h_1s, h_2s, and depends on a plastic work-like parameter, w. h_1s, h_2s regulate the magnitude of the softening contribution and its saturation rate, similarly to their hardening constants counterparts h_1h, h_2h. w depends on the accumulation of plastic strain, and at the same time, the magnitude of the Mises stress normalized by the initial yield stress affects its evolution. Therefore, if the value of the exponent $\mu$ is higher than unity, the softening term returns a relevant contribution for cyclic loading conditions beyond the macroscopic yield stress, while it is less significant for sub-yield states. It should be pointed out that the softening contribution in (5)₁ is considered only during cyclic loading conditions. The idea is to describe the cyclic hardening and softening behavior of metals not observable during monotonic tensile conditions [52]. Therefore, the softening term in Eq. (5)₁ was not considered in the numerical analyses reproducing the monotonic loading conditions. A memory surface concept, as presented in [53,54,55], would be a suitable method to incorporate this modeling approach.

Box 1 Summary of the FSS constitutive model

• Additive decomposition of the total strain rate D into elastic D^e and plastic D^p parts

  $${\mathbf{D}} = {\mathbf{D}}^{e} + {\mathbf{D}}^{p}$$

  (2)

• Subloading loading surface, normal-yield surface

  $$\begin{gathered} f({\overline{\mathbf{\sigma }}}) = \sqrt {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}} \left| {{\overline{\mathbf{\sigma }}}} \right| - RF;\quad f({\hat{\mathbf{\sigma }}}) = \sqrt {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}} \left| {{\hat{\mathbf{\sigma }}}} \right| - F \\ {\overline{\mathbf{\sigma }}} = {{\varvec{\upsigma}}} - \left( {1 - R} \right){\mathbf{s}} - R{{\varvec{\upalpha}}};\quad {\hat{\mathbf{\sigma }}} = {{\varvec{\upsigma}}} - {{\varvec{\upalpha}}} \\ \end{gathered}$$

  (3)

• Plastic flow rule ($\lambda$ plastic multiplier):

  $${\mathbf{D}}^{p} = \sqrt {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}} \lambda {\mathbf{N}};\quad {\mathbf{N}} = {{\frac{{\partial f({\overline{\mathbf{\sigma }}})}}{{\partial {\overline{\mathbf{\sigma }}}}}} \mathord{\left/ {\vphantom {{\frac{{\partial f({\overline{\mathbf{\sigma }}})}}{{\partial {\overline{\mathbf{\sigma }}}}}} {\left| {\frac{{\partial f({\overline{\mathbf{\sigma }}})}}{{\partial {\overline{\mathbf{\sigma }}}}}} \right|}}} \right. \kern-0pt} {\left| {\frac{{\partial f({\overline{\mathbf{\sigma }}})}}{{\partial {\overline{\mathbf{\sigma }}}}}} \right|}};\quad \left| {\mathbf{N}} \right| = \sqrt {{\mathbf{N}}:{\mathbf{N}}} = 1$$

  (4)

• Isotropic hardening law, modified with respect to [35], F₀ initial yield stress:

  $$\begin{gathered} F = F_{0} \left[ {1 + h_{1h} \left( {1 - \exp \left( { - h_{2h} H} \right)} \right) - h_{1s} \left( {1 - \exp \left( { - h_{2s} w} \right)} \right)} \right];\quad \\ H = \int_{0}^{T} \lambda dt;\quad w = \int_{0}^{T} {\lambda \left( {\frac{{\sqrt {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}} \left| {{\mathbf{\sigma }}} \right|}}{{F_{0} }}} \right)}^{\mu } dt;\quad t \in \left[ {0,T} \right] \\ \end{gathered}$$

  (5)

• Back stress and similarity center rates, 〈〉 Macauley’s brackets:

  $$\begin{gathered} \mathop \alpha \limits^{^\circ } = {\mathbf{a}}\left| {{\mathbf{D}}^{p} } \right| = a_{1} \left( {a_{2} {\mathbf{N}} - \alpha } \right)\left[ {1 + a_{3} \left( {1 - \frac{{\left\langle {R - R_{e} } \right\rangle }}{{1 - R_{e} }}} \right)} \right]\left| {{\mathbf{D}}^{p} } \right| \hfill \\ \mathop {\mathbf{s}}\limits^{^\circ } = \left[ {\left( {1 - D} \right)c\left\{ {\frac{{\overline{{\mathbf{\sigma }}} }}{R} - \left( {\frac{1}{\chi } - 1} \right)\widehat{{\mathbf{s}}}} \right\} + {\mathbf{a}} + \sqrt {\frac{2}{3}} \frac{{dF(H,w) }}{F}\widehat{{\mathbf{s}}}} \right]\left| {{\mathbf{D}}^{p} } \right|; \hfill \\ \end{gathered}$$

  (6)

• Damage evolution law:

  $$\begin{gathered} D\left( {H_{d} } \right) = \left( {1 - d_{2} } \right)\left[ {1 + \left( {{{d_{1} } \mathord{\left/ {\vphantom {{d_{1} } {H_{d} }}} \right. \kern-0pt} {H_{d} }}} \right)^{{d_{3} }} } \right]^{ - 1} ;\quad H_{d} = \int\limits_{0}^{T} {\lambda \overline{D}dt} \quad t \in [0,T] \\ \overline{D}\left( {\overline{R}} \right) = \left( {1 - k_{2} } \right)\left[ {1 + \left( {{{k_{1} } \mathord{\left/ {\vphantom {{k_{1} } {\overline{R}}}} \right. \kern-0pt} {\overline{R}}}} \right)^{{k_{3} }} } \right]^{ - 1} ;\quad \overline{R} = R - R_{e} \\ \end{gathered}$$

  (7)

• Similarity ratio R (loading process), modified with respect to [35]. R_e size of sub-yield elastic domain (see [35, 56]):

  $$\begin{gathered} R = \frac{2}{\pi }\left( {1 - R_{e} } \right)\cos^{ - 1} \left[ {\cos \left( {\frac{\pi }{2}\frac{{\left\langle {R_{0} - R_{e} } \right\rangle }}{{1 - R_{e} }}} \right)\exp \left( { - \frac{\pi }{2}u(1 - D^{\beta } )\frac{{H - H_{0} }}{{1 - R_{e} }}} \right)} \right] + R_{e} \\ H_{0} ,R_{0} \quad {\text{initial conditions}} \\ \end{gathered}$$

  (8)

• Similarity ratio R (elastic unloading process), ${\mathbf{b^{\prime}}}$ deviatoric part of the generic second order tensor ${\mathbf{b}}$:

  $$\begin{gathered} R = {{\left[ {tr\left( {{\mathbf{\tilde{\sigma }^{\prime}\hat{s}^{\prime}}}} \right) + \sqrt {tr^{2} \left( {{\mathbf{\tilde{\sigma }^{\prime}\hat{s}^{\prime}}}} \right) + \left( {\frac{2}{3}F^{2} - \left| {{\mathbf{\hat{s}^{\prime}}}} \right|^{2} } \right)\left| {{\mathbf{\tilde{\sigma }^{\prime}}}} \right|^{2} } } \right]} \mathord{\left/ {\vphantom {{\left[ {tr\left( {{\mathbf{\tilde{\sigma }^{\prime}\hat{s}^{\prime}}}} \right) + \sqrt {tr^{2} \left( {{\mathbf{\tilde{\sigma }^{\prime}\hat{s}^{\prime}}}} \right) + \left( {\frac{2}{3}F^{2} - \left| {{\mathbf{\hat{s}^{\prime}}}} \right|^{2} } \right)\left| {{\mathbf{\tilde{\sigma }^{\prime}}}} \right|^{2} } } \right]} {\left[ {\left( {\frac{2}{3}F^{2} - \left| {{\mathbf{\hat{s}^{\prime}}}} \right|^{2} } \right)} \right]}}} \right. \kern-0pt} {\left[ {\left( {\frac{2}{3}F^{2} - \left| {{\mathbf{\hat{s}^{\prime}}}} \right|^{2} } \right)} \right]}} \\ {\tilde{\mathbf{\sigma }}} = {{\varvec{\upsigma}}} - {\mathbf{s}};\quad {\hat{\mathbf{s}}} = {\mathbf{s}} - {{\varvec{\upalpha}}} \\ \end{gathered}$$

  (9)

A last aspect to discuss is the analogy between the variable H_d, already introduced in [35], and the variable w proposed in this work. They both represent work-like variables. However, while H_d depends directly on the similarity ratio R, which expresses a stress ratio observed from the center of the plastic potential and therefore does not account for material hardening, w was introduced to model isotropic softening behavior for stress states beyond the macroscopic yield stress. The normalization carried out in Eq. (5)₃ is obtained against the initial size of the normal-yield surface and, therefore, accounts for the material hardening. From a phenomenological point of view, the two variables are associated with different mechanisms: H_d is linked with a fatigue damage concept, used here to describe the progressive opening of the hysteresis loops in high-cycle fatigue, while w is more related to a ductile damage concept for low-cycle fatigue.

The numerical ability of the Fatigue SS model to describe the behavior of metallic materials under cyclic loading has been validated against experimental data [23, 34, 36, 37]. The results indicate the possibility of describing the progressive plastic accumulation through cycles in cyclic mobility problems (ultra-low, low, and even under high-cycle fatigue conditions). Lastly, it should be pointed out that phenomenological conventional plasticity models cannot describe the inelastic strain generation under cyclic loading conditions below the macroscopic yield stress since the material response is assumed to be purely elastic (see [57]).

3.2 Calibration of the fatigue SS material constants

The constitutive equations presented in Box 1 need the calibration of 22 material parameters. Compared to the formulation in [35], four additional constants should be defined: $h_{1s} ,h_{2s} ,\mu ,\beta$. Although the FSS involves a substantial number of parameters, it enables the characterization of material behavior across a broad spectrum of loading conditions, spanning from low- to high-cycle fatigue, in a phenomenological manner. Moreover, the model is capable of describing stress states below the macroscopic yield stress.

The constants in Tables 4, 5, and 6 were obtained by minimizing the differences between the stress–strain curves in the experiments and the numerical analyses. A summary of the material calibration process is offered in the following bullet points:

• Monotonic loading tests. The monotonic loading tests were functional to assess the elastic properties of the materials (i.e., Young’s modulus E, and Poisson’s ratio $\upsilon$, initial yield stress F₀, size of the elastic subdomain R_e), and to give a first tentative value to the hardening coefficients h_1h, h_2h, a₁, a₂, a₃. A refinement of the selected values for the isotropic and hardening constants was carried out in the fatigue (see Fig. 8) and cyclic loading under variable strain ranges (see Fig. 10) analyses. The parameter u was chosen to capture the gradual development of irreversible strain in the sub-yield domain. The red lines in Fig. 7 represent the Fatigue SS material description, while the blue lines (continuous and dashed) describe the experimental response. The numerical curves predict higher plastic deformations below the transition between the elastic and fully plastic domains, indicating that higher values of u should be selected. However, the blue curves were obtained adopting samples with different geometries compared with the ones used in the fatigue and cyclic loading analyses (see Fig. 2 and Fig. 3). The values of u were calibrated to reproduce the smoother transition obtained in the experiments of Sect. 2.

  • Fatigue test. The fatigue tests reported in Fig. 8 were used to refine the values of the material hardening parameters h_1h, h_2h, a₁, a₂, a₃ and to select the constants responsible for the material isotropic softening h_1s, h_2s, $\mu$. First, SM490 steel does not show softening behavior for stress states over the macroscopic yield stress state; therefore, softening was not considered in Eq. (5)₁ (i.e., h_1s, h_2s are null). In the SM570 and F18B steels cases, the exponent $\mu$ was selected to be greater than unity to reduce the effect of isotropic softening in sub-yield stress states. h_1s, h_2s were chosen to reproduce the total amount of softening, and the rate to achieve it, observed for the loading strain ranges that generated an over-yield stress response.

Table 4 Material parameters for SM490 steel

Table 5 Material parameters for SM570 steel

Table 6 Material parameters for F18B steel

Fig. 7

True stress–true strain and nominal stress–strain curves under monotonic tensile loading. a SM490, b SM570 and c F18B steels (obtained with the specimen in Fig. 2)

Fig. 8

Comparison between experiments and numerical analyses under fatigue loading for: a, b SM490; c, d SM570 and e, f F18B steels

Parameters k₁, k₂, k₃ in Eq. (7)₃ affect the damage evolution through the variable H_d. Higher values of k₁, k₂, and k₃ result in lower values of $\overline{D}$ and, therefore, a slower evolution of H_d, especially for cyclic loading in low-stress regimes.d₁, d₂, d₃ are responsible for the damage evolution. d₁ can be calibrated by observing if the damaging effect manifests at an early stage of the fatigue loading (lower values of d₁) or if it develops after a high number of cycles (higher values of d₁). d₂ can be calibrated to reproduce the total softening at the stabilization of the hysteresis loops. Finally, d₃ regulates the smooth effect of the damaged-induced softening. Higher values of d₃ correspond to a sudden drop in the stress state, while lower values display a gentler and progressive softening.

• Cyclic loading under variable strain ranges. This set of tests has been used to validate the parameters calibrated in the monotonic and fatigue analyses and define the variable $\beta$. As reported in Eq. (8) $\beta$ is an exponent affecting the damage in the evolution equation of the similarity center. This constant has been incorporated into the FSS model formulation to regulate the shape of the hysteresis loops. The sets of parameter, calibrated under the two loading conditions mentioned above, provide an appropriate material description. However, they result in an unrealistically stiffer response in the stress–strain curve during the initial loading blocks of the cyclic tests conducted under variable strain ranges (see Fig. 7e). The exponent $\beta$ was introduced to enhance ($0 < \beta \ll 1$) or reduce ($\beta > 1$) the damaging effect on the stress–strain curves at low D values. The greater the magnitude of the damage is, the weaker the effect of the exponent. If $\beta = 1$, the model returns the original R evolution equation of [35].

3.3 Monotonic loading

This subsection discusses the results and calibration of the monotonic tensile loading tests. Figure 7a, b, and c shows the experimental stress–strain curves in blue, with solid lines representing the nominal stress–strain results and dashed lines representing the true stress–strain ones obtained using Eq. (10). The continuous red lines depict the numerical outcome of the FSS model using the material parameters discussed in the previous subsection:

$$D_{true} = \ln \left( {1 + D_{{{\text{nominal}}}} } \right);\quad \sigma_{true} = \sigma_{{{\text{nominal}}}} \left( {1 + D_{{{\text{nominal}}}} } \right)$$

(10)

As shown by the overlap between the solid red and dashed blue lines, the numerical results are in good agreement with the experimental data. As mentioned in Sect. 3.2, the transition in stress between the sub-yield and fully plastic states is smoother in the numerical analyses due to the choice of relatively small values for the u coefficient. This is because the specimens used in the monotonic tensile tests have a different geometry compared to those used in the fatigue and cyclic loading tests under variable strain ranges, resulting in an abrupt transition between elastic and plastic domains.

SM490 steel shows an upper yield of approximately 361 MPa, followed by a marked stress plateau up to 2% axial strain. On the contrary, no upper yield is observed in SM570 and F18B steels, where hardening regions follow a negligible stress plateau. Among the three materials, SM570 steel is characterized by the highest yield stress (≈ 567 MPa), followed by F18B steel with a F₀ of ≈488 MPa and SM490 steel. Despite having lower yield stress, SM490 shows good ductility and the largest elongation, followed by SM570 and F18B, respectively. Specifically, F18B and SM570 exhibit comparable elongation before failure (i.e., approximately 31.1% and 32% engineering strain). With respect to material hardening, all three materials show good performances with a stress increase (i.e., ultimate tensile strength) of 48% for SM490, 34% for F18B, and 19% for SM570 compared to the initial yield stress. The different values of the yield stress between the experimental data in Table 3 and the ones adopted in the numerical simulations in Table 4, Table 5, and Table 6 are due to different yielding stresses observed between the specimens used in the monotonic and cyclic loading experiments. The parameters selected for the FSS guaranteed a better fit of the stress–strain material responses during cyclic loading conditions.

3.4 Fatigue tests

The numerical analyses on the fatigue performance were conducted considering constant strain amplitudes, reproducing the experimental procedure. Previous works of the authors verified the capability of the FSS to describe the material response under similar loading conditions [34, 35, 37]. Furthermore, recent research has highlighted the potential for extending the predictive capability of the FSS theory to more complex loading conditions [23].

Figure 8 presents the experimental and numerical results of the fatigue tests, including details of the stabilized hysteresis loops under different loading conditions. Solid circles of different colors, depending on the loading condition, represent the SM490 experimental results in Fig. 8a. As visible, the loading conditions $\Delta \varepsilon = 4.0$ and $\Delta \varepsilon = 2.0$ trigger a stress response beyond the macroscopic yield stress where the steel shows a monotonically increasing hardening trend prior to failure. However, the graph does not report the peak stresses before failure because the failure mechanism is associated with crack growth and coalescence, proper of a ductile damage framework. On the contrary, the remaining loading conditions, i.e., $\Delta \varepsilon = 0.36,\,\;0.30,\;\,0.2$, trigger a stress response in the neighborhood or below the normal-yield surface, where the material does not develop hardening due to the progressive increase of the damage, which appears dominant over the kinematic and isotropic hardening contributions. In the $\Delta \varepsilon = 0.36\;{\text{and}}\;0.30$ loading conditions, material softening appears to be evident within the first 100 cycles, indicating the significant susceptibility of SM490 to fatigue damage. The effect of the damage is more relevant for the strain range loading condition of $\Delta \varepsilon = 0.36$, inducing a stress softening of 21% compared to the peak stress registered at the first cycle, and it becomes less evident for the $\Delta \varepsilon = 0.30$ case (i.e., 16% compared to the peak stress registered at the first cycle). Finally, the $\Delta \varepsilon = 0.20$ loading case does not show relevant hardening nor softening responses, maintaining constant peak stresses throughout the test until one million cycles (test run out).

Figure 8c displays the fatigue test results for the SM570 steel. The second steel shows a negligible hardening response during cyclic loading under constant strain amplitude. In detail, the larger strain range loading conditions $\Delta \varepsilon = 4.0$ and $\Delta \varepsilon = 2.0$, result in a small hardening response during the first cycle, followed by significant softening starting within the first ten loading cycles. The $\Delta \varepsilon = 0.8$ loading case is characterized by a flat stress peak curve with a linear softening decrease after 100 cycles until failure. The softening is maximum for this loading condition, with a stress decrease of 13% compared to the peak stress registered in the first loading cycle. A second difference between SM490 and SM570 steels lies in the material response for stress peaks within the normal-yield condition, with the latter material less sensitive to fatigue damage. In SM490, a progressive opening of the hysteresis loops was observed within the first 100 cycles for the loading conditions $\Delta \varepsilon$ = 0.36 and 0.30, while SM570 showed constant peak stress curves for the $\Delta \varepsilon$ = 0.4 ad 0.38 strain ranges up to almost 5000 cycles, with a minor gentle softening trend afterwards until failure. The loading condition $\Delta \varepsilon = 0.3$ does induce any changes in stress peaks in SM570.

Finally, Fig. 8e shows the fatigue test results for F18B steel. The F18B steel displays similar features to SM490 and others to SM570. In particular, the material response for strain range loading conditions above the macroscopic yield stress, i.e., $\Delta \varepsilon = 4.0$ and $\Delta \varepsilon = 2.0$, shows a small hardening response within the first loading cycle followed by a significant softening with 11% and 12% stress reduction, respectively. Compared with SM570, the softening does not continue until failure, but it exhibits stabilized hysteresis loops with constant stress peaks. The $\Delta \varepsilon = 0.8$ loading condition, generating a stress response in the neighborhood of the normal-yield surface, is also characterized by higher stress softening with a decrease of 23% compared to the peak stress registered in the first loading cycle, similar to SM570 steel. However, in F18B steel, the softening has a more visible effect between the 10^th and 100^th cycles, generating a milder stress decrease afterwards. On the other hand, the remaining strain range loading conditions display a behavior closer to the SM490 steel. The $\Delta \varepsilon = 0.4\;{\text{and}}\;0.36$ loading cases return constant peak stresses up to 100 cycles, followed by stress softening, which becomes negligible around 30,000 cycles until failure. The material softening is delayed compared to SM490 but is more marked than SM570, making the F18B behave with intermediate properties compared with the other two metals.

From a modeling point of view, the material constants h_1s, h_2s were set to zero for SM490 due to the absence of isotropic softening under cyclic conditions that generate stress states below the macroscopic yield. However, isotropic softening was incorporated for SM570 and F18B to describe the material behavior. The exponent μ was chosen to be greater than unity to influence the $\Delta \varepsilon = 4.0$ and $\Delta \varepsilon = 2.0$ loading cases and less relevant for stress states in the neighborhood or within the normal-yield surface. h_1s is set to be higher for F18B compared to SM570 since the former return higher decreases of stress through cycles. Moreover, h_2s for F18B is almost double the value assigned to SM570 since the first steel showed an early stabilization of the hysteresis loops with a final stress plateau before failure.

The fatigue experiments on SM570 revealed an almost negligible softening under small strain range loading conditions; therefore, the value of k₁ was set to be the highest, i.e., 0.995, resulting in a slow evolution of the variable H_d (see Eq. (7)₂ and ₃). On the contrary, SM490 and F18B steels showed higher fatigue softening at low-stress states, particularly in the former, resulting in lower k₁, k₂, and k₃. Similarly, the parameter d₁ for SM570 steel was assigned a higher value than the other two metals because the fatigue damage in the $\Delta \varepsilon$ = 0.4 and 0.38 loading cases becomes relevant only after 5000 loading cycles, whereas for SM490 and F18B steels, it became relevant at a lower number of cycles.

Overall, the FSS model adopted in this work returned a good material description in all loading descriptions for the three metals. Minor discrepancies can be observed for loading conditions in the vicinity of the macroscopic yield stress, i.e., $\Delta \varepsilon = 0.36$ for SM490 and $\Delta \varepsilon = 0.8$ for the SM570 and F18B. In fact, in these cases, the material softening description in the FSS model is influenced by the hardening/softening laws in Eqs. (5) and (6)₁ together with the damage variable in Eq. (7), leading to inaccuracies. A better description could be achieved by formulating a unique constitutive law for material softening regulated by different mechanisms depending on the loading conditions. Nonetheless, the accuracy of the FSS model in the current development can be considered satisfactory in industrial design. Future work will aim to develop a better constitutive system of equations to address this issue. In addition, the FSS model underestimates the peak stresses under the larger strain range loading conditions. This aspect could be due to the loading rate used in the experiments, which might activate a dynamic response of the material that the rate-independent formulation of the constitutive equations cannot capture. Figure 8b, d and f reports the stabilized hysteresis loops under the larger loading conditions. The continuous solid lines represent the experimental results, while the dotted ones show the corresponding numerical curves. As can be seen, the FSS model can describe the final size of stabilized loops well, indicating the correct choice of the material constants reported in Tables 4, 5 and 6.

A small study was conducted to evaluate the sensitivity of the FSS theory to variations in the damage material parameters. As previously mentioned, the constitutive model requires the calibration of 22 constants. Given the mutual influence of each parameter on the others, conducting a detailed evaluation of the error induced by variations of the single constants is a challenging task that necessitates extensive study. On the other hand, the cyclic softening behavior is regulated by a damage-like variable, as reported in Eq. (7)₁, which depends on three parameters, namely d₁, d₂ and d₃. Figure 9 illustrates the model’s errors for SM490 steel under a fully reversed prescribed loading condition Δε = 0.3, obtained by a perturbation of ± 10% and ± 20% of the constants d₁, d₂ and d₃. The relative error (Err) is estimated using the formula in Eq. (11):

$$\frac{{\left| {\sigma_{{{\text{peak}},{\text{experiments}}}} - \sigma_{{{\text{peak}},{\text{FSS}}}} } \right|}}{{\sigma_{{{\text{peak}},{\text{experiments}}}} }} \times 100 = {\text{Err}}(\% )$$

(11)

Fig. 9

Influence of the damage parameters a d₁, b d₂ and c d₃ on the cyclic response of SM490 under the prescribed fully reversed cyclic loading condition Δε = 0.3

Further information on the role of these parameters can be found in [35]. It is important to note that the errors obtained in the very low cycle regime (i.e., 1–10 cycles) may be partially due to a possible upper yield sensitivity of the SM490 steel (see Fig. 7a).

The solid black markers report the solution obtained with the values in Table 4. The blue hollow square and circle markers indicate a negative perturbation of the parameters of – 10% and – 20%, respectively. The red hollow square and circle markers indicate a positive perturbation of the parameters of + 10% and + 20%. d₁ represents the value at which the damage-like variable D assumes half of its maximum contribution (see Eq. (7)₁ and [35]). This implies that the parameter plays a significant role in delineating the progression of cyclic softening, as opposed to influencing its ultimate saturation. Figure 9a shows the effects of the perturbation of the constant d₁, indicating that the maximum relative errors are obtained around 10⁴ cycles, when the cyclic softening is not saturated and tends to decrease close to saturation (i.e., 10⁵–3 × 10⁵ cycles).

The effects of perturbating the material constant d₂ are shown in Fig. 9b. d₂ regulates the maximum value of the damage-like variable and, therefore, affects the size of the stabilized hysteresis loops. As it can be seen, the errors generated by a perturbation of the constants become relevant for a high number of cycles (10⁵–3 × 10⁵) due to a lower/higher contribution of the cyclic softening. Finally, the effects of the perturbation of the exponent d₃ are shown in Fig. 9c. d₃ influences the rate of evolution of the damage-like variable. Lower values of d₃ induce a constant rate of evolution of D and a progressive cyclic softening, while high values of d₃ return a more sudden saturation of the hysteresis loops. In this case, the constant variation produces an effect even at a very low number of cycles (i.e., 1–10 cycles) with the negative perturbations characterized by higher errors. Vice versa, at a high-cycle regime, the positive perturbations induce higher errors. Overall, the model response obtained with the values reported in Table 4 displays the lowest relative errors.

3.5 Cyclic loading under variable amplitude strain ranges (incremental step tests)

This subsection compares the experimental and numerical results obtained under cyclic loading conditions with variable strain ranges (i.e., incremental step analyses) applying the same loading sequence depicted in Fig. 4, consisting of 20 repetitions of the illustrated block. The test aims to validate the material constants calibrated in the monotonic tensile and fatigue simulations. While the hysteresis loops shown in Fig. 8b, d and f represent the final stage of the material description when the stress–strain curves are stabilized, they do not fully explain the FFS model’s ability to describe the material performance evolution under cyclic loading. Figure 10a, b and c reports the numerical curves (solid blue lines) against the experimental ones (solid black curves). Overall, the numerical analyses seem in good agreement with the experiments displaying a good overlap between the results. A slight overestimation of the elastoplastic response can be observed in all the steels, where the experimental data seems to give gentler stress–strain curves during the loading and subsequent reloading. The current formulation of the FSS model adopts an exponential parameter to modify the similarity ratio evolution (see Eq. (8)) already discussed in Sect. 3.2. As shown in Fig. 10d, the effect of $\beta$ is quite relevant, especially for lower values of the damage variable D, resulting in gentler stress–strain curves if set lower than unity. Despite adopting the new coefficient $\beta$ a slight discrepancy between the numerical and experimental curves persists; however, the error committed by the FSS appears to be acceptable. One possible explanation for this phenomenon could be the neglect of the sample geometry in the numerical modeling, as the stress and strain variables are obtained at a quadrature point level and cannot consider the real sample geometry. Investigation on real sample geometries carried out by FEA could improve the material description, although this aspect goes beyond the current aim of the work. It should be pointed out that the calibration of the $\beta$ constants has been done in this last set of analyses and consequently introduced the necessity to slightly modify the previous set of variables since it affected the amount of inelastic deformation that cumulates through cycles.

Fig. 10

Comparison between experiments and numerical analyses for: a SM490, b SM570 and c F18B steels. d Effect of the β coefficient on the hysteresis loop shape during the first cyclic block, F18B steel

3.6 FFS model for abaqus/UMAT

Finally, the constitutive equations presented in Box 1 were implemented in Abaqus 2022 commercial software via the user-subroutine UMAT. The purpose was to assess the consistency of the numerical results obtained through a single quadrature point code with those obtained via finite-element analysis (FEA). The finite step integration for the subroutine was conducted using a fully implicit algorithm, as described in [35]. Further details on the formulation of the consistent tangent operator can be found in the referenced literature. In the FEA, a single cubic hexahedral element with reduced integration (i.e., C3D8R Abaqus element) was considered, isostatically constrained and subjected to fully reversed cyclic loading conditions. The cube dimensions were set to unity. The comparison of numerical results was limited to F18B steel, characterized by both isotropic hardening and isotropic softening, under cyclic loading conditions of Δε = 4.0%. While the authors also tested other loading conditions and different materials (i.e., SM490 and SM570), only the aforementioned case is reported for brevity. Figure 11a presents a comparison between the single quadrature point code results (i.e., blue triangle markers) and the user-subroutine (i.e., circle pink hollow markers) performance in the fatigue test. Figure 11b displays the stabilized hysteresis loops under the same loading conditions. As can be seen, the two different numerical algorithms yield highly similar results with minor discrepancies, which can be attributed to the adopted integration schemes (forward Euler for the single quadrature point code and backward Euler for the FE implementation) and the finite step discretization of the prescribed loading condition. The single quadrature point code allows for the imposition of a perfect uniaxial stress state under a prescribed strain loading condition (i.e., strain increment of ΔD = 0.0001%). In contrast, the boundary value problem was carried out by imposing a prescribed displacement increment equivalent to ΔD = 0.01%. Overall, the results obtained in the two numerical simulations are in good agreement, allowing for the use of the same sets of material parameters in Table 4, Table 5 and Table 6 in FEA.

Fig. 11

Comparison between experimental data, single quadrature point FFS code and FSS model implemented for Abaqus2022. a Fatigue loading condition Δε = 4.0%, b stabilized hysteresis loops under Δε = 4.0% fatigue loading condition

4 Concluding remarks

This work aimed to present an experimental and numerical characterization of the cyclic elastoplastic behavior of three construction steels. SM490 and SM570 steels are widely used in several industrial sectors; therefore, evaluating their performance in terms of low/high-cycle fatigue is instrumental for gaining a better understanding of the behavior of the materials and facilitating the design of future components and structures. F18B is a in-house steel designed to have static behavior similar to SM470 steel but with a higher cyclic softening rate for the suppression of crack propagation. Future research will concentrate on investigating crack propagation in F18B steel.

The work carried out in this paper can be summarized as follows:

• This study characterized the SM490, SM570, and F18B steels under various loading conditions, including monotonic, fatigue, and cyclic loading under variable loading amplitude. These experiments aimed to investigate the material response under a broad range of stress states, from below to beyond the macroscopic yield conditions, to provide a more or less complete description of their mechanical performance.

• The monotonic tensile tests revealed good ductile behavior of SM490, with the highest elongation upon failure, followed by SM570 and F18B steels. The material hardening followed the same trend. The highest yield stress was registered for SM570 steel, whereas the lowest was observed in SM490.

• The fatigue tests revealed varying behavior depending on the steel. For cyclic loading conditions beyond the macroscopic yield stress, SM570 and F18B displayed a marked softening behavior, while hardening was observed in SM490. For cyclic loading below the macroscopic yield stress, marked cyclic softening was observed at a lower number of cycles in SM490 and F18B steels, while less evident cyclic softening was visible for SM570 from ≈5000 cycles.

• This work introduced a modified version of the Fatigue SS model, previously developed by the authors, enhancing the material description to reproduce the experimental data. The novel formulation of the FSS includes the possibility of describing isotropic softening for stress states beyond the macroscopic yield stress linked to a ductile damage-like mechanism. Furthermore, the effect of damage on the shape of the stress–strain curves can be regulated by means of an exponent β affecting the evolution of the similarity ratio. The advantages of adopting the FSS model include adopting a unique set of material parameters to describe the inelastic stretching in the sub-yield or fully plastic stress state under a phenomenological approach.

• The FSS material constants were calibrated and validated, minimizing the difference between the numerical and experimental stress–strain curves. The parameters were calibrated in several steps, including the selection of elastic properties and tentative values for the hardening constants, followed by the refinement of the hardening parameters in the numerical simulations of the fatigue tests. The selection of the isotropic softening and damage coefficients was also performed in the fatigue analyses. Final refinement of all the hardening/softening and damage constants and the selection of the exponent β were carried out by reproducing the experimental results in the incremental step tests. The three sets of parameters reported in Tables 4, 5, and 6 will be used as a database for future investigations on fatigue behaviors involving the three selected metals.

• The characterization of the material softening and stabilized hysteresis loops under fatigue loading could be used to predict the crack initiation life in metallic components (e.g., [23, 33, 36]) or even to predict the total fatigue life (crack initiation life and subsequent crack propagation life) through a methodology recently developed by the authors [34].

Developing a reliable constitutive model is essential for improving the design of components in structural problems, reducing the costs of experiments, and allowing the exploration of innovative solutions. Numerical results can also help investigate design alternatives that require extensive time to be analyzed in experimental campaigns. Therefore, finite-element analyses adopting the FSS model could represent a valuable tool for evaluating and designing the service life of components or structures in several engineering applications.