1 Introduction

Continuous development of industry is associated with the search for new construction materials that combine high strength with good formability, as well as high strength-to-density ratio. These features can be obtained for steels with heterogeneous microstructures, in which hard constituents of bainite, martensite and retained austenite are dispersed in a soft ferrite matrix [1]. Exceptional properties of materials with heterogeneous microstructures are discussed in many publications. As far as steels are considered, recent papers on complex phase [2], pipeline [3], multiphase [4] and ferritic/martensitic steels [5] should be mentioned. On the other hand, sharp gradients of properties between phases in these materials cause tendency to the local fracture, which limits the stretch-forming processes [6]. Better local formability can be obtained for the multiphase microstructures with smoother gradients of their features, and such hypothesis was put forward in [7]. Advanced numerical models are needed to gain knowledge on the local heterogeneities of the microstructural features and resulting properties. A review of material models dedicated to plastic forming and heat treatment of metallic materials is presented in [8], with the emphasis on a competition between predictive capabilities of models and computing costs. The material models, which are used today, are divided into two groups: mean field and full field models. In the former, the microstructure is implicitly represented by closed form equations describing its average parameters. In the latter the microstructure is represented explicitly in a geometrical form using Representative Volume Element (RVE) [9] or Digital Materials Representation (DMR) concept [10]. This approach is classified as Integrative Computational Materials and Process Engineering (ICMPE), see [11] for details. Predictive capabilities of the full field models are much wider, but they involve much larger computing times. Therefore, despite their limited predictive capabilities, due to their low computing costs mean field models are still used in the design of materials processing.

In the present work, we concentrate on the upgrade of the mean field internal variable model, which is based on the stochastic solution of the equation describing evolution of the dislocation density. It was assumed in [12] that introduction of the stochastic variables in the model will allow to predict heterogeneity of the final microstructure, which is important in the design of multiphase materials. Brief review of the papers, which account for the random effects in plastic deformation and propose stochastic models describing contours of the dislocation propagation fronts, is presented in [13]. It was concluded that a stochastic approach to plastic deformation, presented in the reviewed publications, was generally based on the introduction of an explicit stochastic forcing term in the internal variable constitutive equations. The papers, which deal with application of the stochastic models to describe distributions of selected microstructural features, are rare and they usually consider problem of correlation between material microstructure and mechanical properties of products. Among the recent papers, authors of [14] used statistics for geometry description in homogenization methods and in [15] n-point statistics was applied to predict crack probability. In few papers random distribution of selected parameter is used as an input for the deterministic material model, e.g. [16] studies an influence of distribution of the austenite grain size prior to recrystallization on the recrystallization kinetics.

The objective of our research was to account for the random character of the recrystallization which occurs during deformation and after deformation at elevated temperatures and to transfer this randomness to equations describing evolution of dislocation populations. The original model developed in [12] used dislocation density as a single stochastic independent variable. Since that model incorporates random character of the phenomena, it may predict the distribution of output parameters instead of their average values. Publication [12] was focused on the mathematical basis of the model and on searching for optimal parameters of the numerical solution of the stochastic differential equation. Following this, the grain size was added as the second stochastic internal variable and upgraded model for deformation at elevated temperatures was proposed in [13]. Identification of the model constrained to the hot deformation is described in [13], as well. Description of the heterogeneous microstructure of metals and alloys using internal variables as independent ones and with the distribution functions of various features allowed building the mean field model with the prospective capability to predict gradients of microstructural features. This allowed understanding of the history of the process and, as a result, describing the micro features, which determine the material behaviour in the macro scale. In consequence, a link bridge between mean field and full field models was built.

The particular goals of the present work were twofold. The first was development and validation of the stochastic approach to modelling hot deformation of steel including both dynamic phenomena during deformation and static phenomena during interpass times. In comparison to [13], the model allows simulation of multistage hot forming processes and accounts for the material softening during interpass times. Performing an inverse solution for this approach using the objective function based on the distance between measured and calculated histograms was the second goal. The focus was on the static recrystallization experiments [17], which supplied measured grain size histograms in various times after the end of the deformation. The particular emphasis was on verification of the model for the experiments, which were not used in the identification procedure. Elaborated mean field model was implemented in the finite element (FE) code and results of its application to hot plate and strip rolling processes are presented in the paper, as well.

2 Model

The stochastic model of the softening phenomena occurring after hot deformation is an extension of the hot deformation model described in [13]. That model origins from Kocks–Estrin–Mecking (KEM) approach [18, 19] with the additional dynamic recrystallization term proposed in [20]. Thorough discussion of the deterministic model based on KEM is described in [21], including mathematical background, analysis of various approximations of the solution, as well as the proof of its convergence and stability. In [22] this deterministic model was extended by including static phenomena and simulations of industrial processes were performed. As it was discussed in [12], the deterministic model contains artificial critical time for dynamic recrystallization tcr, which is not a physical quantity and hence it cannot be measured. Therefore, for more realistic description of a random character of the recrystallization, the stochastic variable ξ(ti) was introduced, see [12] for details. After discretization in time, the evolution of the dislocation density is governed by the equation:

$$\rho (t_{i} ) = \rho \left( {t_{0} } \right)\left[ {1 - \xi \left( {t_{i} } \right)} \right] + \left\{ {\rho \left( {t_{i - 1} } \right) + \left[ {A_{1} \dot{\varepsilon } - A_{2} \rho \left( {t_{i - 1} } \right)\dot{\varepsilon }^{{1 - a_{7} }} } \right]\Delta t} \right\}\xi \left( {t_{i} } \right)$$
(1)

where: t—time, \(\dot{\varepsilon }\)–strain rate.

Coefficients A1 and A2 responsible for hardening and recovery are defined in Table 1, where: b—a module of the Burgers vector, Z—Zener Hollomon parameter, l—average free path for dislocations, T—temperature in K, R—universal gas constant, a1, a2, a3, a9, a10—coefficients. When dynamic recovery is considered, mobility of recovery is proportional to \(\dot{\varepsilon }^{{ - a_{7} }}\) as shown in [19], where a7 = 0.25 is reported. For mathematical reasons constant coefficient a2 is introduced in Table  3 and dependence of the dynamic recovery on the strain rate was moved to Eq. (1).

Table 1 Relationships describing coefficients in equation (1)
Full size table

In the present work, the model was extended by including interpass times and static phenomena into simulations. Softening phenomena occurring after the deformation include static recovery (SRV) and static recrystallization (SRX). Since the strain rate in the interpass time becomes zero, Eq. (1) was modified. The first term with A1 responsible for hardening was automatically removed. As far as the recovery is considered, the term with A2 in Eq. (1) was modified accounting for the difference between dynamic and static processes. The dislocation structure produced during deformation and interpass time at elevated temperatures is described by a statistical distribution of segments under varying driving forces and resistances to rearrangement. Thermal activation of the metastable positions leads to recovery, which is exhaustive when static, but occurs at a steady rate when dynamic [24]. Static and dynamic recovery follows the same laws, although at different rates, and they lead to similar dislocation structures. The modifications of the model were made with the above remarks in mind.

Since static recovery depends only on the temperature, the term \(\dot{\varepsilon }\)(1−a7) was removed and mobility of recovery coefficient a2 was substituted by a22, which was included in the vector of the design variables. The activation energy for self-diffusion a3 has not changed. In the case of the recrystallization, the same coefficients were used for the static and dynamic process [25]. The difference in the kinetics between SRX and DRX was automatically accounted for because the mobility of the grain boundary in equation (3) depends on the dislocation density.

The parameter ξ(ti) in equation (1) accounts for a random character of the recrystallization and its distribution is described by the conditions:

$$\begin{gathered} {\mathbf{P}}\left[ {\xi \left( {t_{i} } \right) = 0} \right] = \left\{ {\begin{array}{*{20}c} {p\left( {t_{i} } \right)\,\,\,\,if\,\,p\left( {t_{i} } \right) < 1} \\ {1\,\,\,\;\quad otherwise} \\ \end{array} } \right. \hfill \\ {\mathbf{P}}\left[ {\xi \left( {t_{i} } \right) = 1} \right] = 1 - {\mathbf{P}}\left[ {\xi \left( {t_{i} } \right) = 0} \right] \hfill \\ \end{gathered}$$
(2)

In Eq. (2) p(ti) is a function, which bounds together the probability that the material point recrystallizes in a current time step and present state of the material:

$$p\left( {t_{i} } \right) = a_{4} \rho \left( {t_{i - 1} } \right)^{{a_{6} }} \frac{{3\gamma \left( {t_{i} } \right)\tau }}{{D\left( {t_{i - 1} } \right)^{{a_{21} }} }}\exp \left( {\frac{{ - a_{5} }}{RT}} \right)\Delta t$$
(3)

where: D—grain size in μm, τ—energy per unit dislocation length, a4, a5, a6, a21 – coefficients.

In equation (3) coefficient γ represents a mobile fraction of the recrystallized grain boundary [20] and depends on (already known) distribution of ξ(ti-1) in the previous step:

$$\gamma \left( {t_{i} } \right) = 1 - \exp \left\{ { - {\mathbf{P}}\left[ {\xi \left( {t_{i - 1} } \right) = 0} \right] - q} \right\}^{{a_{8} }} \left\{ {1 - {\mathbf{P}}\left[ {\xi \left( {t_{i - 1} } \right) = 0} \right]} \right\}$$
(4)

where: a8 – coefficient, q—a small number representing a nucleus of a recrystallized grain, which is added to avoid zero value of γ(ti) in the case P[ξ(ti-1) = 0] = 0.

Several numerical tests of Eq. (1) were performed in [12] for a pure copper and for a DP steel. The influence of numerical parameters such as number of points, number of bins and number of steps was evaluated and the optimal values were defined as 20,000 points, which generate histograms with 10 bins. Number of steps is selected depending on the total time of the process assuming maximum time step of 0.05 s.

It was assumed in [12] that the grain size D in equation (3) is constant and is equal to the average grain size prior to deformation. However, in the real material the grain size changes during deformation due to competitive effects of growth and recrystallization [23]. Therefore, in publication [13] a natural extension of the model was proposed and the grain size D(ti) was introduced as the second stochastic variable. This variable is conditioning probability in (3).

As it has been mentioned [12], in real materials certain distributions of the dislocation density and the grain size in the microstructure exist. To reveal those distributions numerically, several trajectories of (1) were calculated, each time using randomly generated values of ρ(t0) and D(t0). These individual trajectories were then aggregated into histograms at consecutive time steps ti. Strictly speaking, we start with the grain size D(t0) ≡ D0 which is a random variable. Weibull distribution was assumed, which is described by the following probability density function:

$${\text{f}} \left( {D_{0} } \right) = \frac{k}{{\overline{D}_{0} }}\left( {\frac{{D_{0} }}{{\overline{D}_{0} }}} \right)^{k - 1} \exp \left[ { - \left( {\frac{{D_{0} }}{{\overline{D}_{0} }}} \right)^{k} } \right]$$
(5)

where: k, \(\overline{D}_{0}\)—the shape parameter and the scale parameter of the distribution, respectively. The shape parameter k = 10 was determined on the basis of measured grain size distributions shown in [13]. The scale parameter \(\overline{D}_{0}\) was established as the average grain size measured after preheating.

The changes of the grain size during deformation and during the interpass time were calculated based on the fundamental research of Sellars [23], who proposed modelling of the grain growth using the following equation:

$$D\left( {t_{i} } \right) = \left[ {D\left( {t_{i - 1} } \right)^{{a_{11} }} + a_{12} \exp \left( {\frac{{a_{13} }}{RT}} \right)\Delta t} \right]^{{\frac{1}{{a_{11} }}}}$$
(6)

where: Δt = ti—ti-1—time step, D(ti), D(ti+1) – grain size at the beginning and at the end of the time step, respectively, a11, a12, a13—coefficients.

When during the calculation the random parameter ξ(ti) = 0, the considered point recrystallizes and its new grain size D(ti) is drawn from the Gauss distribution:

$${\text{f}} \left[ {D\left( {t_{i} } \right)} \right] = \frac{1}{{\sqrt {2\pi \sigma^{2} } }}\exp \left\{ { - \frac{{\left[ {D\left( {t_{i} } \right) - \overline{D}\left( {t_{i} } \right)} \right]^{2} }}{{2\sigma^{2} }}} \right\}$$
(7)

where: \(\overline{D}\left( {t_{i} } \right)\)—the expected value of the grain size, σ—standard deviation, which is an optimization variable a16 in the model.

The expected value in equation (7) is either the dynamically recrystallized grain size (for \(\dot{\varepsilon }\) > 0) or the statically recrystallized grain size (for \(\dot{\varepsilon }\) = 0). It was shown in many experiments, e.g. [23], that dynamically recrystallized grain size depends only on the Zener–Hollomon parameter Z defined in Table 1:

$$\overline{D}\left( {t_{i} } \right) = a_{14} Z^{{ - a_{15} }}$$
(8)

where: a14, a15—coefficients.

When static recrystallization occurs, the expected value in equation (7) depends on the grain size prior to deformation and on the current dislocation density:

$$\overline{D}\left( {t_{i} } \right) = a_{17} \rho \left( {t_{i} } \right)^{{ - a_{18} }} D\left( {t_{0} } \right)^{{a_{19} }} \exp \left( {\frac{{a_{20} }}{RT}} \right)$$
(9)

where: a18, a19, a20, a21 – coefficients.

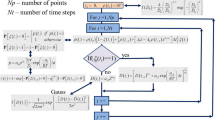
The flow of calculations in the model is presented in Fig. 1.

Fig. 1
figure 1

Flow chart of the stochastic model

Full size image

The whole model composed of Eqns. (1)—(9) contains 22 coefficients grouped in the vector a. Some of these coefficients have physical meaning: a3—activation energy for self-diffusion, a5—activation energy for recrystallization, a10—activation energy in the Zener–Hollomon parameter. a13—activation energy for the grain growth. Other were introduced for technical reasons. Application of the model to real materials and processing methods requires identification of the model coefficients. The identification was performed using inverse approach, which is described in the next Chapter.

3 Inverse analysis

3.1 Inverse algorithm

The problem of coefficients identification in material models is well known and widely discussed in the scientific literature as an inverse problem [26, 27]. The algorithm for the stochastic inverse problem is described in detail in [22]; we repeat it briefly below for the readers convenience. Since our model is stochastic, there is no analytic solution for the inverse problem. Therefore, we reformulated the inverse problem as an optimization task with the coefficients in the model a becoming the state variables. The aim of the inverse analysis was finding the optimal values of coefficients a, which are determined by searching for a minimum of the following objective function:

$$\Phi ({\mathbf{a}}) = d\left( {y_{c} ({\mathbf{a}}),y_{m} } \right)$$
(10)

where: yc(a)—outputs calculated for the model coefficients a, ym—measurements in the experimental tests, d – metric in the output space Y.The optimization task defined for deterministic model by Eq. (10), was redefined in [12] for stochastic variable model and the following objective function was proposed:

$$\Phi ({\mathbf{a}}) = d\left( {H_{c} \left( {\mathbf{a}} \right),H_{m} } \right)$$
(11)

where: Hc(a)—histogram obtained by several calculations of y(a), Hm—measured histogram (from the experiment), d—a ranking function comparing two histograms.

The model solution is in the form of distribution of dislocation density and grain size (histograms). Therefore, it was necessary to compare the model outputs for particular sets of coefficients, taking into account that the random factor ξ(ti-1) in Eq. (1) and stochastic nature of D in equations (5)-(7) can lead to completely different single solutions for the same starting values of ρ0 and D0, see discussion in [12]. Different metrics d(Hc(a),Hm) were analysed in [12] and the Bhattacharyya distance measure [28] was selected as ensuring the fastest convergence in the optimization. Let us recall, that this measure is defined as:

$$d_{H} \left( {H_{1} ,H_{2} } \right) = - \log \sum\limits_{i = 1}^{n} {\sqrt {P_{1} \left( i \right)P_{2} \left( i \right)} }$$
(12)

where: n – number of points and

$$P_{k} \left( i \right) = \frac{{H_{k} \left( i \right)}}{{\mathop \sum \limits_{i = 1}^{n} H_{k} \left( i \right)}}$$
(13)

As we said before, for the identification task the objective function (11) should be minimized with respect to the model coefficients a. To be able to apply (12), the experimental data should include the information on distributions of the dislocation density and the grain size. Since measurement of dislocation density is difficult in practice, we decided to compare only average dislocation densities, which for observed processes were indirectly obtained from the measurements of loads, see [17]. The objective function (11) was reformulated as follows:

$$\Phi ({\mathbf{a}}) = \Phi_{\rho } ({\mathbf{a}}) + \Phi_{DDRX} ({\mathbf{a}}) + \Phi_{DSRX} ({\mathbf{a}})$$
(14)

where:

$$\Phi_{\rho } ({\mathbf{a}}) = w_{\rho } \sum\limits_{i = 1}^{Ntc} {d\left( {\rho_{ci} \left( {\mathbf{a}} \right),\rho_{mi} } \right)}$$
(15)
$$\Phi_{DDRX} ({\mathbf{a}}) = w_{D} \sum\limits_{i = 1}^{Ntc} {d_{H} \left( {H_{ci} \left( {\mathbf{a}} \right),H_{mi} } \right)}$$
(16)
$$\Phi_{DSRX} ({\mathbf{a}}) = w_{D} \sum\limits_{i = 1}^{Nti*Ntc} {d_{H} \left( {H_{ci} \left( {\mathbf{a}} \right),H_{mi} } \right)}$$
(17)

ρc(a)—expected average value of the dislocation density calculated for model coefficients a, ρm—average dislocation density determined from the compression tests [17], Hc(a)—distribution of the grain size calculated for the model using coefficients a, Hm—distribution of the grain size measured in the experiments, Ntc—number of compression tests, Nti—number of measurements of histograms during interpass times, wρ, wD—weighted coefficients.

In Eq. (15) d(ρci(a),ρmi) was defined as the mean square root error (MSRE) between measured and calculated average dislocation density in the i-th experiment:

$$d\left( {\rho_{ci} \left( {\mathbf{a}} \right),\rho_{mi} } \right) = \frac{1}{Ns}\sqrt {\sum\limits_{j = 1}^{Ns} {\left( {\frac{{\rho_{cij} \left( {\mathbf{a}} \right) - \rho_{mij} }}{{\rho_{mij} }}} \right)^{2} } }$$
(18)

where: Ns—number of sampling points for measurements of the average dislocation density in the i-th test.

Distance between histograms in Eqs. (16) and (17) is calculated from Eq. (12).

3.2 Sensitivity analysis

Identification of the model with 22 coefficients is time consuming and problems with the uniqueness of the solution can be encountered. To avoid these problems sensitivity analysis (SA) [29] was applied prior to the inverse analysis. The goal of the SA was to find the coefficients which influence the output most and to identify these coefficients in the first step of the IA. The effect of the change of the ith coefficient (Δai) on the solution (χi) at the time t is:

For the average dislocation density:

$$\chi_{i} ({\mathbf{a}}) = \frac{{a_{i} }}{{\Delta a_{i} }}\frac{{y_{c} \left( {a_{1} , \ldots ,a_{i - 1} ,a_{i} + \Delta a_{i} ,a_{i + 1} , \ldots ,a_{k} } \right) - y_{c} \left( {\mathbf{a}} \right)}}{{y_{c} \left( {\mathbf{a}} \right)}}$$
(19)

For the grain size histograms:

$$\chi_{i} ({\mathbf{a}}) = a_{i} \frac{{d_{H} \left( {H_{1} ,H_{2} } \right)}}{{\Delta a_{i} }}$$
(20)

where: Δai—small increment of the ith parameter, yc(a)—model output, H1—the basic histogram calculated for the coefficients a, H2—histogram obtained after small disturbance of the coefficient ai by Δai.

The metric (12) was used to calculate the distance between histograms H1 and H2 in equation (20). The SA determined the model parameters, which contribute the most to the model output and those, which are not significant [8]. The SA preceded identification of the model using inverse analysis and the SA results were used to design the best optimization strategy.

4 Experiment

The objective of the experiment was to supply data for identification and validation of the model. To enable evaluation of the generality of the model, three steels with different characteristics were considered:

Medium-carbon steel (C45) containing 0.48%C, 0.58%Mn, 0.23%Si, 0.12%Cr and 0.16%Ni. The prospective applications are mainly in the forging, but plate rolling application are common, as well. Due to easiness of the microstructure analysis, this material was used mainly for identification and verification of the model. Details and results of the experiments are described in [22, 30].

Steel S355J2, which is an unalloyed, low carbon welded structural steel. The prospective applications in plate rolling were considered. Details and results of the experiments are described in [17]. As previously, due to easiness of the microstructure analysis this material was used for identification and verification of the model.

Dual Phase steel (DP600) containing 0.11%C, 1.95%Mn, 0.98%Si, 0.2%Mo and 0.18%Ti. This material was used for simulation of the hot strip rolling process. Details and results of the experiments are described in [31].

All the experiments were performed on the thermomechanical simulator Gleeble 3800 in the IMŻ Gliwice using cylindrical samples with dimensions ϕ10 × 12 mm. Briefly, the deformation experiments were performed under controlled parameters, including temperature, strain, strain rate and time following deformation. The deformed samples were water cooled to capture the austenite microstructure state during and after dynamic, metadynamic, and static recrystallization, as well as grain growth following recrystallization. Detailed description of these tests is given in earlier publications and only a brief information about the conditions of the tests is given below.

Steel C45 [22, 30]. The samples were preheated at 1275 °C, 1200 °C and 1100 °C for 10 s and cooled to the deformation temperature with the rate of 5 °C/s. These preheating temperatures gave an average grain size equal 102 μm, 94 μm and 77 μm, respectively. Three deformation temperatures (1275 °C, 1200 °C and 1100 °C) and two strain rates (0.1 s−1 and 1 s−1) were applied. The total strain was 1 in all hot deformation tests. The second set of experiments composed smaller strains (0.1–0.4) followed by holding at the deformation temperature for different times. The holding time was approximately equal to the static recrystallization time calculated by the conventional model.

Steel S355J2 [17]. Two preheating temperatures, 1200 °C and 1100 °C, were applied. The average grain size was 35.5 μm and 22.2 μm for these temperatures, respectively. Four deformation temperatures (1200 °C, 1100 °C, 1000 °C, and 900 °C,) and three strain rates (0.1 s−1, 1 s−1 and 10 s−1) were applied. The total strain in these tests was 1. The second set of experiments composed smaller strains (0.1–0.4) followed by holding at the deformation temperature for different times. The holding time was approximately equal to the static recrystallization time calculated by the conventional model.

Steel DP600 [31]. The samples were preheated at 1200 °C for 10 s and cooled to the deformation temperature with the rate of 5 °C/s. Three deformation temperatures (1200 °C, 1100 °C and 1000 °C) and three strain rates (0.1 s−1 1 s−1 and 5 s−1) were applied. Two sets of the tests were performed. The first set supplied data for identification of the model for hot deformation including dynamic recrystallization. The total strain in these tests was 0.9 and the samples were quenched right after the deformation.

After each test the polished sections of the samples were etched to reveal the austenite grains boundaries. Next, the austenite grain size was measured for the population of 200–300 grains and histograms were generated. Examples of the obtained microstructures for the steel S355J2 are shown in Fig. 2. It is seen that dynamic recrystallization occurred during the deformation at all strain rates. The recrystallized grain size was strain rate sensitive and was equal to (equivalent diameter): 24 μm at strain rate 0.1 s−1, 21 μm at strain rate 1 s−1 and 18 μm at strain rate 10 s−1. The measured histograms of the grain size were used as an input for the identification and validation of the model.

Fig. 2
figure 2

Micrographs of the steel S355J2 after deformation to total strain 0.9 at 1000 °C after preheating temperature 1200 °C with the strain rate 0.1 s−1 (a), 1 s−1 (b) and 10 s−1 (c). The samples were water cooled following the deformation

Full size image

5 Results

5.1 Sensitivity analysis

The sensitivity analysis was preceded by primary identification of the model. Coefficients a were determined by optimization of the objective function (14) using Nelder–Mead method and these coefficients were used to generate the target histogram H1 and the histogram H2 for the disturbed coefficient ai. An increment of each coefficient Δai was 0.1 ai. The histograms H1 and H2 were used to determine the sensitivity with respect to the coefficients a according to equation (20). To improve the robustness of the results, the simulation for each histogram H1 and H2 was repeated 5 times and the resulting histograms were averaged.

Sensitivity analysis for the hot deformation model was performed in [13] and it is not repeated here. In the present work, the model was extended by including static recrystallization and coefficients a11, a12, a13, a17, a18, a19 and a20 were added, the sensitivity of the grain size histograms with respect to these coefficients only is presented below. Sensitivity factors were calculated using equation (20) for the three investigated steels but the differences between the steels were small.

Sensitivity analysis was performed for the practical range of the deformation parameters and for different times after deformation. The general conclusion was that sensitivity of the histograms with respect to the coefficients responsible for the static recrystallization is small, comparing to those observed in [13] for hot forming. Only selected examples of the calculated SA factors are presented in Fig. 3. Results of all calculations allowed to conclude that sensitivity factors were larger for process conditions, which accelerate static recrystallization, namely for higher temperatures of deformation, for larger strains and for larger strain rates. As could be expected, the sensitivity of the dislocation density histograms was larger for the short time after the deformation and it decreased for longer times. In general, the coefficients a11 and a13 in the grain growth equation and coefficients a19 in the equation describing recrystallized grain size have the strongest influence on the output histograms.

Fig. 3
figure 3

Local sensitivity of the histograms of the dislocation density (dark blue) and the grain size (yellow) with respect to the coefficients a for the strain rate  = 1 s−1 and two times after deformation. Remaining process parameters: strain ε = 0.2 and temperature of the deformation Td = 900 °C (a); ε = 0.2 and Td = 1000 °C (b); ε = 0.4 and Td = 1000 °C (c)

Full size image

The SA performed in [13] and in the present work allowed drawing conclusions, which were considered in the final identification of the model. The coefficients a1 (in the hardening term), a5 (activation energy for the recrystallization) and a7 (describes strain rate dependence of the recovery) have the strongest influence on the function ΦD(a). The coefficients a2 (in the hardening term), a4, a5, a8 (coefficients in recrystallization term) and a10 (activation energy in the Zener-Hollomon parameter) have the strongest influence on the function Φρ(a). Finally, the coefficients a11 and a13 in the grain growth equation and coefficients a19 in the equation describing recrystallized grain size have the strongest influence on the grain size histograms. The optimization was performed first only for coefficients with noticeable influence on the objective function. In the final optimization all 22 coefficients were the state variables. This approach allowed for a decrease of the computing costs.

5.2 Identification of the model

Following assumptions described in the Chapter 3, the identification of the model was performed by searching for the minimum of the objective function (14). Parameters of the tests, which were used in the identification procedure for the steel C45 and S355J2, are given in Table 2. In the case of the steel DP600 all the tests listed in Chapter 4C [31] were used. Optimal coefficients a are given in Table 3 for the steel C45 and in Table 4 for the steel DP600. The optimal coefficients for the steel S355J2 are given in publication [17].

Table 2 Parameters of the tests, which were used in the identification of the model
Full size table
Table 3 Optimal coefficients in the stochastic model (1) for the steel C45
Full size table
Table 4 Optimal coefficients in the stochastic model (1) for the steel DP600
Full size table

Evaluation of the accuracy of the inverse analysis in the hot forming part for the steel S355J2 is presented in [17]. The Bhattacharyya distance between measured and calculated histograms of the grain size after deformation and after different holding times was compared for all the tests and good accuracy was obtained. Therefore, only some results for the static recrystallization for the steel C45 are presented below. Figure 4 shows the histograms of the grain size for the samples held for the different times th after the deformation. The Bhattacharyya distance, which is given in the left bottom corner of the plot, is very low in all test. It means that the model predicts well changes of the grain size during static softening of the material after hot deformation.

Fig. 4
figure 4

Examples of the comparison of the grain size histograms obtained from the measurements and calculated by the stochastic model (1) with the optimal coefficients for the steel C45. The preheating temperature 1200 °C (average grain size 94 μm), the deformation temperature 1100 °C, the strain rate 10 s−1, the strain 0.2 and holding times after deformation th = 0 s (a), 1 s (b), 2 s (c), 5 s (d), 10 s (e) and 30 s (f)

Full size image

The accuracy of the predictions of the average dislocation density was evaluated, as well, and the selected results for the steel C45 are shown in Fig. 5. The effect of the preheating temperature was small, therefor the results for Tp = 1200 °C (grain size 94 μm) only are presented. These results show that, beyond the grain size histograms, the model predicts well an average parameters of the deformation process.

Fig. 5
figure 5

Comparison of the average dislocation density measured in the experiments (full symbols) and calculated using the model with the optimal coefficients (open symbols with lines), steel C45, strain rate 0.1 s−1 (a) and 1 s−1 (b), preheating temperature 1200 °C

Full size image

5.3 Validation of the model

Validation of the model was performed for the two steels for the tests, which were not used in the identification procedure (Table 5). All the results for the steel S355J2 are given in [17]. The results for the steel C45 are shown in [13] (hot deformation) and in Fig. 6 (static recrystallization). The values of the Bhattacharyya distance were slightly higher than those in Fig. 4, but reasonably good agreement between measured and calculated histograms was obtained for all the tests. Similarly good results of the validation of the model were obtained in [17] for the steel S355J2. Several more experimental tests (e.g. for different preheating temperatures) were used in the validation of the model and it should be emphasized that the Bhattacharyya distance between measured and calculated histograms for the grain size has not exceeded 0.05 in any of the tests. This is a good accuracy for the metallurgical processes. All these results confirmed models capability to simulate grain size changes during both hot deformation and static recrystallization. Since less data were available for the steel DP600, validation of the model for this steel was not performed.

Table 5 Parameters of the tests, which were used in the validation of the model
Full size table
Fig. 6
figure 6

Examples of the comparison of the grain size histograms obtained from the measurements and calculated by the stochastic model (1) with the optimal coefficients for the steel C45. The preheating temperature 1100 °C (average grain size 77 μm), the deformation temperature 1100 °C (a, b, c) and 1000 °C (d, e, f), the strain rate 0.1 s−1, the strain 0.2 and holding times after deformation th = 0 s (a), 1 s (b), 2 s (c), 5 s (d), 10 s (e) and 30 s (f)

Full size image

5.4 Numerical tests of the model

The stochastic model (1) with optimal coefficients a was implemented in the finite element (FE) program and this model was solved in Gauss points of the FE mesh. The FE model is based on the rigid-plastic thermo-mechanical finite element approach proposed in [32]. Description of the algorithm and the program, which was used in the present work, is given in [33]. To evaluate the capabilities of the FE + stochastic material model, typical uniaxial compression test was considered first. The second set of simulations was performed for industrial hot plate and strip rolling processes, see next Chapter.

In the uniaxial compression test a cylindrical sample measuring ϕ12 × 10 mm made of the steel C45 was compressed with the height reduction to 4.5 mm (homogeneous strain ε = ln(h1/h2) = 0.9, where: h1,h2—height of the sample before and after the compression, respectively). The die velocity was changing during the test to maintain constant nominal strain rate in the sample. Selected results of simulation for the preheating temperature of 1100 °C, the nominal strain rate of 1 s−1 and the nominal deformation temperature of 1000 °C are presented in Fig. 7. Distribution of the strain and the temperature at the cross section is shown in this figure. Due to two axes of symmetry only a quarter of the cross section is displayed. The average austenite grain size prior to deformation was 77 μm and the friction coefficient between the die and the sample was 0.15. Inhomogeneity of strains and temperature caused by the effects of friction and deformation heating is seen in Fig. 7. The local strains and temperatures differ from the nominal ones. The stochastic model was solved at each Gauss point of the FE mesh and the results for the points A and B (Fig. 7a) are presented in Fig. 8. These results show that full dynamic recrystallization was obtained for the point B while some non-recrystallized grains remained in the point A.

Fig. 7
figure 7

Calculated distributions of the strain (a) and the temperature (b) after uniaxial compression

Full size image
Fig. 8
figure 8

Calculated histograms of the dislocation density (a) and grain size (b) in the points A and B in Fig. 7a, steel C45

Full size image

6 Results: simulation of hot rolling processes

6.1 Plate rolling

Modern hot plate rolling mills use metallurgical precision to manufacture quality plates characterised by high strength and toughness at alloying levels that keep costs down and preserve weldability. The typical mill is composed of the roughing and finishing stands, accelerated cooling and levelling. Design of optimal process technology requires modelling of thermal, mechanical and metallurgical phenomena during the whole process. The FE + stochastic material model developed in the present paper was applied to simulate hot rolling of thick plates made of the steel S355J2. The whole process was simulated, however, since only finishing passes influence microstructure after rolling, the results for the finishing stand only are presented. The entry thickness was 57 mm, the entry temperature was 990 °C and the average entry grain size was 64 μm. Rolling in 6 passes was considered with the following pass schedule [34]: 57 → 46.6 → 36.5 → 27.5 → 21.7 → 17.9 → 15.2 mm. The interpass times were 7.7, 8.7, 10.2, 11.9 and 13.6 after passes 1–5, respectively. The average end of rolling temperature was 950 °C.

FE simulations were performed first to evaluate heterogeneity of strains and temperatures in the roll gap. The results for the last pass are shown in Fig. 9. Due to horizontal axis of symmetry only the top half of the roll gap is presented. Large roll radius resulted in uniform strains through the plate thickness. Slight increase of the temperature caused by the deformation heating is observed in the centre of the plate and the temperature close to the surface is lower due to the heat transfer to the roll. Since the layer with low temperature is thin, the results of calculations of the dislocation density and grain size in the centre of the plate only are presented below.

Fig. 9
figure 9

Distribution of the strain (a) and temperature (b) in the roll gap

Full size image

Stochastic model was solved along the whole production line accounting for the current temperatures and strain rates in the centre of the plate. Calculated histograms of the dislocation density and the grain size at various stages of the conventional process are shown in Fig. 10. The model predicts full recrystallization in all interpass times. The grain size decreases in the first two passes and it remains at the approximately stable level during remaining passes. After the last pass the recrystallization is fast and after 2 s over 80% of the material has recrystallized.

Fig. 10
figure 10

Calculated histograms of the dislocation density (a) and the grain size (b) in the centre of the plate at the entry to passes 2–6, at the exit from the pass 6 and 2 s after the exit

Full size image

Controlled plate rolling, which has been used for about half of the century, was considered next. The major purpose of this process is to refine grain structure. The deformation in the non-recrystallization region but above Ae3 is one of the methods of the controlled plate rolling, see review in [35]. In this process additional fast cooling is applied before the last 2–3 passes. Results of simulations of controlled plate rolling (passes 5 and 6 only with reductions 0.175 and 0.15, respectively) are shown in Fig. 11. The results for the passes 1–4 were identical to those in Fig. 10. The end of rolling temperature was 840 °C. It is seen that at the beginning of phase transformations (temperature Ae3) only 15% of the austenite has recrystallized.

Fig. 11
figure 11

Calculated histograms of the dislocation density (a) and the grain size (b) in the centre of the plate at the entry to passes 5 and 6, at the exit from the pass 6, 2 s after the exit from the pass 6 and at the temperature Ae3

Full size image

6.2 Strip rolling

Hot strip rolling is commonly used to produce strips, which can be either directly used to manufacture final product or can be subject to further cold rolling process. Prediction of the microstructure evolution during this process is essential for the design of the rolling technology. The stochastic material model implemented in the FE code was used in simulations. The rolling sequence of the DP600 steel strip with the finishing pass schedule 66 → 40.6 → 19.1 → 9.4 → 5.43 → 3.58 → 2.9 mm was considered, see [22] for details. The entry temperature was 1010 °C and the rolling velocity in the last stand was 9.5 m/s. The innovative route for the DP steel strip, which was also considered, assumed additional decrease of the entry temperature by 50 °C and ultra-fast cooling (UFC) after stands 4 and 5 [36]. Calculated time temperature profiles in the last three stands for the standard rolling (Variant 1) and for the innovative route (Variant 2) are shown in Fig. 12. The time in this figure is counted from the exit of the slab from the furnace. Due to the homogeneity of strains through the strip thickness, only the point located in the centre of the strip was considered. Calculated average dislocation density for the innovative schedule (Variant 2) is presented in [22]. This schedule led to end of rolling below the recrystallization temperature. In the present work distributions of the dislocation density and the grain size for the two rolling routes were calculated and compared in Fig. 13.

Fig. 12
figure 12

Calculated time temperature profile in the two locations in the strip for the investigated hot strip rolling process; solid lines with filled symbols for the variant 1 and dashed lines with open symbols for the variant 2

Full size image
Fig. 13
figure 13

Calculated distributions of the dislocation density (a, c) and the grain size (b, d) for the variant 1 (a, b) and for the variant 2 (c, d)

Full size image

Presented results agree qualitatively with our knowledge regarding hot plate and strip rolling. It is seen that in the conventional processes the recrystallization was completed in the centre of the strip during the whole process. In consequence, the material was recrystallized at the beginning of transformations during cooling and only grain size distribution should be accounted for in the phase transformation model.

In the controlled rolling deformation in lower temperatures in the last two passes was considered. The model predicted that for the plates (slower cooling) about 85% of the austenite has not recrystallized. In the case of strips (faster cooling) this fraction was below 10%. Calculated distributions of the dislocation density and the grain size can be used as an input for simulations of phase transformations.

7 Conclusions

In the present paper, we extended the mean field stochastic model described in [13] by including static recrystallization during interpass times. In consequence, simulation of multistage forming processes became possible. Although this approach still can be classified as mean field model, it supplies additional information about distribution of the grain size, which cannot be obtained from classical microstructure evolution models. The model reproduced the results similar to those obtained from deterministic mean field models but a richer description of the material in the form of histograms of the microstructural parameters was obtained.

The inverse solution using the objective function based on the histograms of the grain size was performed and coefficients in the model were determined. Extensive experiments, in which microstructure was analysed in different times after the deformation, supplied additional data for identification of the static recrystallization part in the model.

The following conclusions were drawn on the basis of the performed research

Sensitivity analysis has shown that the coefficients a3 (activation energy for self-diffusion), a6 (coefficient, which controls influence of the dislocation density on the recrystallization) and a10 (activation energy in the Zener-Hollomon parameter) have the strongest influence on the distribution of the dislocation density while coefficients a10, a14 and a15 (the last two control the grain size after the recrystallization) have the strongest influence on the distribution of the grain size. The sensitivities of the grains size histograms with respect to the coefficients responsible for the static recrystallization a17—a20 is smaller comparing to those describing the hot deformation part. In general, the coefficients a11, a13 (activation energy for grain growth), a17 and a19 have the strongest influence on the distribution of the grain size after static recrystallization. The effect of these coefficients was larger for larger strains and higher temperatures

Identification problem was solved by optimization of the objective function composed of MSRE between measured and calculated average dislocation density and Bhattacharyya distance between measured and calculated histograms for the grain size. The static recrystallization data were included in the objective function (14). In consequence, the model proved to be accurate for both hot deformation and interpass times.

Case studies confirmed capabilities of the model to predict distribution of microstructural parameters for various technological variants of hot rolling.

The developed model can be used to design metal deformation processes, which give required distribution of selected microstructural parameter.

Calculated histograms of the dislocation density and the grain size can be used as input data for simulation of phase transformations. This problem will be a scope of our future work.