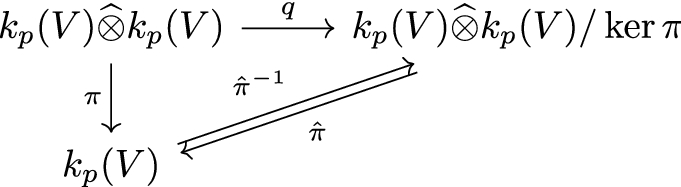Topological amenability and Köthe co-echelon algebras

Abstract

We introduce a notion of a topologically flat locally convex module, which extends the notion of a flat Banach module and which is well adapted to the nonmetrizable setting (and especially to the setting of DF-modules). Using this notion, we introduce topologically amenable locally convex algebras and we show that a complete barrelled DF-algebra is topologically amenable if and only if it is Johnson amenable, extending thereby Helemskii–Sheinberg’s criterion for Banach algebras. As an application, we completely characterize topologically amenable Köthe co-echelon algebras.

1 Introduction

The paper is devoted to the study of amenability properties in the framework of DF-algebras. These are algebras with jointly continuous multiplication whose underlying topological vector spaces are DF-spaces. The category of DF-spaces contains spaces of distributions, e.g. tempered distributions or distributions with compact support. More generally, duals of Fréchet spaces belong to this category. In particular, the duals of Köthe echelon spaces are DF-spaces. These are the so-called Köthe co-echelon spaces and this class of objects will be of particular importance for us.

The general study of amenable DF-algebras meets two major difficulties which come from the facts that the category of DF-spaces does not respect subspaces and that there is no Open Mapping Theorem available. This implies that the two well-known approaches to amenability (namely, Johnson’s approach based on derivations [10] and Helemskii–Sheinberg’s approach based on flat modules [6]) which are equivalent in the category of Banach (or Fréchet) algebras are potentially inequivalent in the DF-algebra framework (however, we have no explicit counterexample so far). The main aim of this paper is to modify the notion of a flat module in such a way that the above-mentioned problem disappears. The resulting notion of a topologically flat module is equivalent to that of a flat module in the case of Banach (or Fréchet) modules, but, in our view, is better adapted to the nonmetrizable setting. We define topologically amenable algebras in terms of topologically flat modules, and we show that topological amenability for complete barrelled DF-algebras is equivalent to amenability in Johnson’s sense. We also obtain a topological amenability criterion for Köthe co-echelon algebras, complementing thereby recent results of the second author [23, 24]. Note that such algebras need not be complete, so that our definition of topological amenability is made in terms of the completion (see Definition 3.21).

The theory of amenable Banach algebras essentially starts with the famous result of Johnson [10, Theorem 2.5] who proved that the convolution algebra $L^1(G)$ is amenable if and only if the locally compact group G is amenable. Since then, amenable Banach algebras became an inseparable part of functional analysis and operator algebra theory (see [28] for a recent and detailed account). A few years after the publication of Johnson’s memoir, Helemskii and Sheinberg [6] observed that the notion of an amenable algebra perfectly fits into the general “Banach homological algebra” developed earlier by Helemskii [5] (and, independently, by Kiehl and Verdier [11] and by Taylor [31]). Namely, Helemskii and Sheinberg proved that a Banach algebra A is amenable in Johnson’s sense if and only if the unitization of A is a flat Banach A-bimodule. This result was extended by the first author [20, Corollary 3.5] to the setting of Fréchet algebras. In the present article, we continue this investigation and study amenability properties of DF-algebras, with a special emphasis on Köthe co-echelon algebras.

The paper is organized as follows. The next section is Notation and Preliminaries, and it contains basic definitions, facts and notation that is used in the sequel. In Sect. 3, we introduce and study topologically flat locally convex modules and topologically amenable locally convex algebras. The main results here are Theorem 3.12, which characterizes topologically flat DF-modules in terms of the ${{\,\mathrm{Ext}\,}}$ functor, and Theorem 3.18, which shows that, for complete barrelled DF-algebras, the topological amenability in our sense is equivalent to the Johnson amenability. In Sect. 4, we characterize topologically amenable Köthe co-echelon algebras $k_p(V)$ in terms of the corresponding weight sets V (Theorems 4.5 and 4.6). Finally, in Sect. 5 we give some concrete examples of topologically amenable (and non-amenable) co-echelon algebras. In particular, we construct a topologically amenable co-echelon algebra of order $\infty$ which, in a sense, cannot be reduced to a direct sum of $\ell _\infty$ with a contractible co-echelon algebra.

General references are: [17] for functional analysis, [4, 15] for Banach and topological algebra theory, and [7] for the homology theory of topological algebras.

2 Notation and preliminaries

We start by recalling some basic definitions and introducing some notation that will be used in the sequel. By a locally convex algebra, we mean a locally convex space (lcs) over $\mathbb C$ equipped with a separately continuous associative multiplication. In general, locally convex algebras are not assumed to have an identity. Given a locally convex algebra A, we denote by $A_+$ the unconditional unitization of A, and we denote by $A^{{{\,\mathrm{op}\,}}}$ the opposite algebra, i.e., the lcs A with multiplication $a\cdot b:=ba$. In what follows, when using the word “algebra” with an adjective that describes a linear topological property (such as “complete”, “Fréchet”, “Banach”, etc.), we mean that the underlying lcs of the algebra in question has the specified property. The same applies to locally convex modules (see below).

Given a locally convex algebra A, a left locally convex A-module is an lcs X together with a left A-module structure such that the action $A\times X\rightarrow X$ is separately continuous. Right locally convex modules and locally convex bimodules are defined similarly. At some point, we will be using a concrete locally convex bimodule $A\otimes \mathbb C$ which is the lcs A itself with trivial right module action and multiplication as the left module action.

The completed projective tensor product of lcs's E and F will be denoted by $E\mathop {\widehat{\otimes }}F$, and the completion of E will be denoted by $\widetilde{E}$ or by $E^\sim$. A complete locally convex algebra with jointly continuous multiplication is called a $\mathop {\widehat{\otimes }}$ -algebra. If A is a $\mathop {\widehat{\otimes }}$-algebra, then the assignment $a\otimes b\mapsto ab$ gives rise to the so-called product map $\pi _A:A\mathop {\widehat{\otimes }}A\rightarrow A$. We will simply write $\pi$ whenever it is clear to which algebra the product map is referred to. If A is a $\mathop {\widehat{\otimes }}$-algebra, then a left locally convex A-module X is a left A-$\mathop {\widehat{\otimes }}$-module if X is complete and if the action of A on X is jointly continuous. Right $\mathop {\widehat{\otimes }}$-modules and $\mathop {\widehat{\otimes }}$-bimodules are defined similarly. The category of left A-$\mathop {\widehat{\otimes }}$-modules (respectively, of right A-$\mathop {\widehat{\otimes }}$-modules, of A–B-$\mathop {\widehat{\otimes }}$-bimodules) will be denoted by $A\text{-}\!\mathop {\mathsf {mod}}$ (respectively, $\mathop {\mathsf {mod}}\!\text{-}A$, $A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}B$). Note that A-$\mathop {\widehat{\otimes }}$-bimodules are nothing but left unital $A^e$-$\mathop {\widehat{\otimes }}$-modules, where $A^e:=A_+\mathop {\widehat{\otimes }}A_+^{{{\,\mathrm{op}\,}}}$ is the enveloping algebra of A (see [7, §II.5.2]). If $X\in \mathop {\mathsf {mod}}\!\text{-}A$ and $Y\in A\text{-}\!\mathop {\mathsf {mod}}$, then the A-module projective tensor product of X and Y is defined as

$$\begin{aligned} X\mathop {\widehat{\otimes }}_{A} Y:=(X\mathop {\widehat{\otimes }}Y/N)^\sim , \end{aligned}$$

where

$$\begin{aligned} N:=\overline{{{\,\mathrm{span}\,}}}\bigl \{x\cdot a\otimes y-x\otimes a\cdot y : a\in A,\, x\in X,\, y\in Y\bigr \} \subset X\mathop {\widehat{\otimes }}Y. \end{aligned}$$

If X and Y are two lcs's, then L(X, Y) stands for the vector space of continuous linear operators from X to Y. We equip L(X, Y) with the topology of uniform convergence on bounded sets. As usual, we let $X'=L(X,\mathbb C)$. If A is a locally convex algebra and X, Y are left locally convex A-modules, then $_AL(X,Y)$ denotes the vector space of continuous linear A-module maps, i.e., operators $T\in L(X,Y)$ satisfying $T(a\cdot x)=a\cdot Tx$ for all $a\in A$, $x\in X$. In the case of right A-modules, resp. A–B-bimodules, the vector spaces $L_A(X,Y)$ and $_AL_B(X,Y)$ are defined analogously.

Suppose that A, B, C are locally convex algebras, X is a locally convex B–C-bimodule, and Y is a locally convex A–C-bimodule. Then, $L_C(X,Y)$ has a natural A–B-bimodule structure given by

$$\begin{aligned} (a\cdot T)(x)=a\cdot T(x),\quad (T\cdot b)(x)=T(b\cdot x) \qquad (a\in A,\; b\in B,\; T\in L_C(X,Y)). \end{aligned}$$

If the actions of A on Y and of B on X are hypocontinuous with respect to the families of bounded subsets of Y and X, respectively, then $L_C(X,Y)$ is easily seen to be a locally convex A–B-bimodule (cf. [31, Section 3]). In particular, this condition is satisfied provided that the actions are jointly continuous. In particular, for each $\mathop {\widehat{\otimes }}$-algebra A and each left (respectively, right) A-$\mathop {\widehat{\otimes }}$-module X the dual space $X'$ is a right (respectively, left) locally convex A-module. Note, however, that the action of A on $X'$ need not be jointly continuous.

Let $\mathsf {CLCS}$ denote the category of complete lcs's and continuous linear maps. Suppose that $\mathsf {C}\subset \mathsf {CLCS}$ is a full additive subcategory. We write $\mathsf {alg}(\mathsf {C})$ for the category of all $\mathop {\widehat{\otimes }}$-algebras whose underlying spaces are objects of $\mathsf {C}$. If A is a $\mathop {\widehat{\otimes }}$-algebra, then we denote by $A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$ the full subcategory of $A\text{-}\!\mathop {\mathsf {mod}}$ consisting of those modules whose underlying spaces are objects of $\mathsf {C}$. The symbols $\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$ and $A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}B(\mathsf {C})$ are understood in a similar way.

Following [22] (cf. also [7]), we say that $\mathsf {C}$ is admissible if the following holds:

• (C1) if $E\in \mathsf {C}$ and F is a locally convex space isomorphic to E, then $F\in \mathsf {C}$;

• (C2) if $E\in \mathsf {C}$ and $E_0\subset E$ is a complemented vector subspace, then $E_0\in \mathsf {C}$;

• (C3) if $E,F\in \mathsf {C}$, then $E\mathop {\widehat{\otimes }}F\in \mathsf {C}$.

Most of the categories of complete lcs's used in functional analysis are admissible. In this paper, the concrete admissible subcategories we are mostly interested in are $\mathsf {CLCS}$ itself, the category $\mathsf {Ban}$ of Banach spaces, the category $\mathsf {Fr}$ of Fréchet spaces, and the category $\mathsf {CBDF}$ of complete barrelled (DF)-spaces. The admissibility of $\mathsf {Ban}$ and $\mathsf {Fr}$ is well known. As for $\mathsf {CBDF}$, property $(\mathsf {C}2)$ follows from the fact that the classes of barrelled spaces and of (DF)-spaces are stable under taking quotients modulo closed subspaces [12, 27.1.(4) and 29.5.(1)], while property $(\mathsf {C}3)$ follows from [13, 41.4.(7) and 41.4.(8)].

Let A be a $\mathop {\widehat{\otimes }}$-algebra, and let $\mathsf {C}$ be an admissible subcategory of $\mathsf {CLCS}$. A sequence

$$\begin{aligned} 0 \rightarrow X \xrightarrow {i} Y \xrightarrow {p} Z \rightarrow 0 \end{aligned}$$

(1)

in $A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$ is admissible if it is split exact in $\mathsf {CLCS}$, i.e., if it has a contracting homotopy consisting of continuous linear maps. Geometrically, this means that i is topologically injective (i.e., a homeomorphism onto its range), p is open (i.e., a quotient map), $i(X)=\ker p$, and i(X) is a complemented subspace of Y. We say that a morphism $i:X\rightarrow Y$ (respectively, $p:Y\rightarrow Z$) in $A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$ is an admissible monomorphism (respectively, an admissible epimorphism) if it fits into an admissible sequence (1).

It is easy to show that $A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$ together with the class of all admissible sequences is an exact category in Quillen’s sense [26]. Therefore, most of the main notions and constructions of homological algebra (projective objects, projective resolutions, derived functors, etc.) make sense in $A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$. For details, we refer to [7]. An important property of $A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$ is that, if $A\in \mathsf {alg}(\mathsf {C})$, then $A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$ has enough projectives. As a consequence, each covariant functor $F:A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})\rightarrow \mathsf {Vect}$ (where $\mathsf {Vect}$ is the category of vector spaces) has left derived functors $\mathrm L_n F$, and each contravariant functor $F:A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})\rightarrow \mathsf {Vect}$ has right derived functors $\mathrm R^n F$ ($n\ge 0$). In particular, for each left locally convex A-module Y the functor ${{\,\mathrm{Ext}\,}}^n_A(-,Y)$ is defined to be the nth right derived functor of ${_A}L(-,Y):A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})\rightarrow \mathsf {Vect}$. We would like to stress that, in contrast to [7], we do not require Y to be an object of $A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$. In particular, we may let $Y=Z'$ for some $Z\in \mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$. This special case will be essential in our characterization of topologically flat modules (see Theorem 3.12). In fact, this is the only reason why we have to consider general locally convex modules rather than $\mathop {\widehat{\otimes }}$-modules only.

Note that the above facts on $A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$ have obvious analogs for the categories $\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$ and $A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}B(\mathsf {C})$. For details, see [7].

Let us now recall some basic facts on strictly exact sequences of locally convex spaces. Suppose that $\mathsf {C}$ is an additive category. Following [30], we say that a short sequence (1) in $\mathsf {C}$ is strictly exact if i is a kernel of p and p is a cokernel of i.

Example 2.1

If $\mathsf {C}=\mathsf {Vect}$, then (1) is strictly exact iff it is exact in the usual sense.

Example 2.2

If $\mathsf {C}=\mathsf {CLCS}$, then (1) is strictly exact iff i is topologically injective, $i(X)=\ker p$, p is an open map of Y onto p(Y), and p(Y) is dense in Z. This follows from [25, Proposition 4.1.8]. Essentially, this means that X can be identified with a closed subspace of Y, and Z is the completion of Y/X.

Example 2.3

If $\mathsf {C}=\mathsf {Fr}$ or $\mathsf {C}=\mathsf {Ban}$, then (1) is strictly exact in $\mathsf {C}$ iff it is strictly exact in $\mathsf {CLCS}$ iff it is exact (or, equivalently, strictly exact) in $\mathsf {Vect}$. This is essentially a combination of Example 2.2 with the Open Mapping Theorem. See also [33, Chapter 2].

The following result is a special case of V. P. Palamodov’s theorem [18, Proposition 4.2] (see also [33, Theorem 2.2.2]). Given a set S, let $\ell _\infty (S)$ denote the Banach space of bounded $\mathbb C$-valued functions on S.

Theorem 2.4

(Palamodov) A short sequence (1) in $\mathsf {CLCS}$ is strictly exact if and only if, for each set S, the sequence

$$\begin{aligned} 0 \rightarrow L(Z,\ell _\infty (S))\rightarrow L(Y,\ell _\infty (S)) \rightarrow L(X,\ell _\infty (S)) \rightarrow 0 \end{aligned}$$

is exact in $\mathsf {Vect}$.

We end this section with a definition and a collection of basic facts concerning Köthe co-echelon spaces and algebras. Let I be a countable set, and let $V:=(v_n)_{n\in {\mathbb {N}}}$ be a sequence of weights $v_n:I\rightarrow (0,\infty ]$ such that

$$\begin{aligned} \forall \,i\in I\quad \exists \,n\in {\mathbb {N}}\quad v_n(i)<\infty ,\qquad\qquad\mathrm{(W1)}\\ \forall \,n\in {\mathbb {N}}\quad \forall i\in I\quad v_{n+1}(i)\le v_n(i).\qquad\qquad\mathrm{(W2)} \end{aligned}$$

For $1\le p<\infty$, we define the Köthe co-echelon space of order p as

$$\begin{aligned} k_p(I,V):=\Big \{x=(x_i)\in \mathbb C^I:\sum _{i\in I}|x_i|^pv_n(i)^p<\infty \text { for some }n\in {\mathbb {N}}\Big \}, \end{aligned}$$

and we also let

$$\begin{aligned} k_{\infty }(I,V):=\Big \{x=(x_i)\in \mathbb C^I:\sup _{i\in I}|x_i|v_n(i)<\infty \text { for some }n\in {\mathbb {N}}\Big \},\\ k_0(I,V):=\Big \{x=(x_i)\in \mathbb C^I:\lim _{i\rightarrow \infty }|x_i|v_n(i)=0\text { for some }n\in {\mathbb {N}}\Big \}. \end{aligned}$$

We often write $k_p(V)$ for $k_p(I,V)$ when the index set I is clear from the context. In most examples, we actually have $I={\mathbb {N}}$ (see Examples 2.5–2.8), but sometimes it is more convenient to let $I={\mathbb {N}}\times {\mathbb {N}}$ (see Example 5.6).

The above definition is a bit unusual since we allow $v_n(i)=\infty$ for some $n\in {\mathbb {N}}$ and $i\in I$. However, this less restrictive approach does not affect our proofs and allows us to consider in particular the space $\varphi :=\mathbb C^{({\mathbb {N}})}$ of finitely supported sequences (see Example 2.5 below). The space $k_p(I,V)$ is canonically endowed with the inductive limit topology of the system $(\ell _p(I,v_n))_{n\in {\mathbb {N}}}$ (for $p\ge 1$) or $(c_0(I,v_n))_{n\in {\mathbb {N}}}$ (for $p=0$), where $\ell _p(I,v_n)$ and $c_0(I,v_n)$ are the weighted Banach spaces of scalar sequences equipped with their canonical norms. Clearly, if $v_n(i)=\infty$, then $x\in \ell _p(I,v_n)$ implies that $x_i=0$. Thus, we usually write

$$\begin{aligned} k_p(I,V)={{\,\mathrm{ind}\,}}_n\ell _p(I,v_n)\quad (1\le p\le \infty ),\qquad k_0(I,V)={{\,\mathrm{ind}\,}}_nc_0(I,v_n). \end{aligned}$$

Since Köthe co-echelon spaces are countable inductive limits of Banach spaces, they are barrelled DF-spaces (see [9, 12.4, Theorem 8]). By [1, Theorem 2.3], $k_p(V)$ is complete for all $1\le p\le \infty$. On the other hand, $k_0(V)$ is not always complete, see [12, §31.6] or [1, Theorem 3.7 and Examples 3.11, 4.11.2, 4.11.3].

In many concrete cases (see examples below), Köthe co-echelon spaces are algebras with respect to the coordinatewise multiplication of sequences. A systematic study of such algebras was initiated in [3]. Recall from [3, Proposition 2.1] that $k_p(V)$ is an algebra if and only if

$$\begin{aligned} \forall \,n\in {\mathbb {N}}\quad \exists \,m\in {\mathbb {N}}\quad v_m/v_n^2\in \ell _{\infty }\qquad\qquad\mathrm{(W3)} \end{aligned}$$

(we let $\infty /\infty =1$ for convenience). Moreover, if (W3) holds, then the multiplication on $k_p(V)$ is automatically jointly continuous [loc. cit.]. From now on, when we write something like “let $k_p(V)$ be a Köthe co-echelon algebra”, we tacitly assume that V is a sequence of weights satisfying conditions (W1)–(W3), and that $k_p(V)$ is considered as a locally convex algebra under the coordinatewise multiplication.

Example 2.5

For each $n\in {\mathbb {N}}$, define $v_n:{\mathbb {N}}\rightarrow (0,\infty ]$ by $v_n(j)=1$ for $j\le n$, and $v_n(j)=\infty$ for $j>n$. Conditions (W1)–(W3) are clearly satisfied, and $k_p(V)$ is nothing but the algebra $\varphi$ of finite sequences equipped with the strongest locally convex topology.

Example 2.6

Let $R\in [0,+\infty )$, and let $\alpha =(\alpha _i)_{i\in {\mathbb {N}}}$ be a sequence of positive numbers increasing to infinity. Consider the dual power series spaces¹

$$\begin{aligned} D\Lambda _R^p(\alpha )=\Bigl \{ x=(x_j)\in \mathbb C^{\mathbb {N}}: \sum _j |x_j|^p r^{\alpha _j p}<\infty \;\text {for some}\; r>R\Bigr \} \end{aligned}$$

(where $1\le p<\infty )$, and

$$\begin{aligned} D\Lambda _R^\infty (\alpha )=\Bigl \{ x=(x_j)\in \mathbb C^{\mathbb {N}}: \sup _j |x_j| r^{\alpha _j}<\infty \;\text {for some}\; r>R\Bigr \}. \end{aligned}$$

If $(r_n)$ is a fixed sequence of positive numbers strictly decreasing to R, then we clearly have $D\Lambda _R^p(\alpha )=k_p(V)$, where $v_n(j)=r_n^{\alpha _j}$ for all $n,j\in {\mathbb {N}}$. We could also consider the space $D\Lambda _R^0(\alpha )=k_0(V)$ with V as above, but the condition that $\alpha _j\rightarrow \infty$ easily implies that $D\Lambda _R^0(\alpha )=D\Lambda _R^\infty (\alpha )$.

An elementary computation shows that $D\Lambda _R^p(\alpha )$ satisfies (W3) if and only if for each $r>R$, there exists $\rho >R$ such that $\rho \le r^2$. Equivalently, this means that if $r>R$, then $r^2>R$. If $R\ge 1$ or $R=0$, then this condition is clearly satisfied, so $D\Lambda _R^p(\alpha )$ is a Köthe co-echelon algebra in this case. If $0<R<1$, then the above condition fails (take any $r\in (R,\sqrt{R}]$).

Example 2.7

Letting $\alpha _j=\log j$ in Example 2.6, we see that $D\Lambda _0^p(\alpha )$ is nothing but the algebra $s'$ of sequences of polynomial growth.

Example 2.8

If $\alpha _j=j$, then $D\Lambda _R^p(\alpha )$ is topologically isomorphic to the space of germs of holomorphic functions on the closed disc $\overline{\mathbb D}_R=\{ z\in \mathbb C: |z| \le R\}$. If $R\ge 1$ or $R=0$, then the multiplication on $D\Lambda _R^p(\alpha )$ corresponds to the “componentwise” multiplication of the Taylor expansions of holomorphic functions (the Hadamard multiplication, cf. [27]). The resulting locally convex algebra will be denoted by $\mathscr {H}(\overline{\mathbb D}_R)$.

Given $p\in [1,\infty ]$ and a sequence $V=(v_n)$ of weights satisfying (W1)–(W3), we say that V is eventually in $\ell _p$ if $v_n\in \ell _p(I)$ for some $n\in {\mathbb {N}}$. Because of (W2), this means precisely that there exists $n\in {\mathbb {N}}$ such that $v_k\in \ell _p(I)$ for all $k\ge n$. If V is eventually in $\ell _\infty$, then we say that V is eventually bounded. By [3, Proposition 2.5], if $1\le p<\infty$, then

$$\begin{aligned} V \text { is eventually in } \ell _p &\iff V \text { is eventually in } \ell _1 \iff k_p(V)\text{ is unital }\\ &\iff V \text { is eventually bounded, and } k_p(V)\text { is nuclear. } \end{aligned}$$

In fact, if the above conditions are satisfied, then we have $k_p(V)=k_q(V)$ for all $p,q\in [1,\infty ]\cup \{ 0\}$ (see [2, Proposition 15]).

A comprehensive study of Köthe co-echelon spaces may be found in [1]. Köthe co-echelon algebras appear as a main object of investigation in [3, 23, 24].

3 Topological flatness and topological amenability

Let $\mathsf {C}$ be an admissible subcategory of $\mathsf {CLCS}$, and let $A\in \mathsf {alg}(\mathsf {C})$.

Definition 3.1

We say that a module $X\in A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$ is topologically flat (relative to $\mathsf {C}$) if for each short admissible sequence

$$\begin{aligned} 0 \rightarrow Y_1\rightarrow Y_2 \rightarrow Y_3 \rightarrow 0 \end{aligned}$$

(2)

in $\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$, the sequence

$$\begin{aligned} 0 \rightarrow Y_1\mathop {\widehat{\otimes }}_{A} X \rightarrow Y_2\mathop {\widehat{\otimes }}_{A} X \rightarrow Y_3\mathop {\widehat{\otimes }}_{A} X \rightarrow 0 \end{aligned}$$

(3)

is strictly exact in $\mathsf {CLCS}$. A right module in $\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$ (respectively, a bimodule in $A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$) is topologically flat if it is topologically flat as a left module over $A^{{{\,\mathrm{op}\,}}}$ (respectively, over $A^e$).

Remark 3.2

According to [7], a module $X\in A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$ is flat (relative to $\mathsf {C}$) if for each short admissible sequence (2) in $\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$ the sequence (3) is exact in $\mathsf {Vect}$. If $\mathsf {C}\subset \mathsf {Fr}$, then flatness and topological flatness are equivalent (see Example 2.3). We conjecture that, in the general case, neither topological flatness implies flatness, nor vice versa. However, we do not have concrete counterexamples at the moment.

Example 3.3

Each projective module $P\in A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$ is topologically flat. Indeed, if P is free, i.e., if P is isomorphic to $A_+\mathop {\widehat{\otimes }}E$ for some $E\in \mathsf {C}$, then (3) is isomorphic to the sequence

$$\begin{aligned} 0 \rightarrow Y_1\mathop {\widehat{\otimes }}E \rightarrow Y_2\mathop {\widehat{\otimes }}E \rightarrow Y_3\mathop {\widehat{\otimes }}E \rightarrow 0, \end{aligned}$$

which is split exact and is a fortiori strictly exact in $\mathsf {CLCS}$. Since each projective module is a retract of a free module [7, III.1.27], the result follows.

Proposition 3.4

A module $X\in A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$ is topologically flat if and only if for each admissible monomorphism $Y\rightarrow Z$ in $\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$ the induced map $Y\mathop {\widehat{\otimes }}_{A} X\rightarrow Z\mathop {\widehat{\otimes }}_{A} X$ is topologically injective.

Proof

This is immediate from Definition 3.1 and from the fact that the functor $(-)\mathop {\widehat{\otimes }}_{A} X:\mathop {\mathsf {mod}}\!\text{-}A\rightarrow \mathsf {CLCS}$ preserves cokernels [21, Proposition 3.3]. $\square$

Remark 3.5

For $\mathsf {C}=\mathsf {Ban}$, Proposition 3.4 is well known (cf. [8, Theorem VII.1.42]). For $\mathsf {C}=\mathsf {Fr}$, this fact was observed in [20].

The following “adjoint associativity” (or “exponential law”) for locally convex spaces is a kind of folklore. Since we have not found an exact reference, we give a proof here for the convenience of the reader.

Proposition 3.6

Let X, Y, Z be locally convex spaces. Suppose that Z is complete. There is a natural linear map

$$\begin{aligned} L(X\mathop {\widehat{\otimes }}Y,Z)\rightarrow L(X,L(Y,Z)), \qquad f\mapsto (x\mapsto (y\mapsto f(x\otimes y))). \end{aligned}$$

(4)

The above map is a vector space isomorphism in either of the following cases:

• (i) X and Y are Fréchet spaces;

• (ii) X and Y are DF-spaces, and Y is barrelled.

Proof

By the universal property of the projective tensor product (see, e.g., [13, 41.3.(1)]), $L(X\mathop {\widehat{\otimes }}Y,Z)$ is naturally identified with the space of jointly continuous bilinear maps from $X\times Y$ to Z. On the other hand, each $\varphi \in L(X,L(Y,Z))$ determines a separately continuous bilinear map $\varPhi :X\times Y\rightarrow Z$ via $\varPhi (x,y)=\varphi (x)(y)$ ($x\in X$, $y\in Y$). Moreover, the rule $\varphi \mapsto \varPhi$ determines a vector space isomorphism between L(X, L(Y, Z)) and the space of those separately continuous bilinear maps $X\times Y\rightarrow Z$ which are $\mathscr {B}_Y$-hypocontinuous, where $\mathscr {B}_Y$ is the family of all bounded subsets of Y [13, 40.1.(3)]. This implies that (4) indeed takes $L(X\mathop {\widehat{\otimes }}Y,Z)$ to L(X, L(Y, Z)), is always injective, and is surjective if and only if each separately continuous, $\mathscr {B}_Y$-hypocontinuous bilinear map from $X\times Y$ to Z is jointly continuous. In case (i), this condition is clearly satisfied because the separate continuity and the joint continuity are equivalent for maps $X\times Y\rightarrow Z$ (see, e.g., [13, 40.2.(1)]). Assume now that (ii) holds, and let $\varPhi :X\times Y\rightarrow Z$ be a separately continuous, $\mathscr {B}_Y$-hypocontinuous bilinear map. Since Y is barrelled, $\varPhi$ is also $\mathscr {B}_X$-hypocontinuous by [13, 40.2.(3)]. Finally, since X and Y are DF-spaces, and since $\varPhi$ is $(\mathscr {B}_X,\mathscr {B}_Y)$-hypocontinuous, we conclude that $\varPhi$ is jointly continuous [13, 40.2.(10)]. In view of the above remarks, this completes the proof. $\square$

Corollary 3.7

Let X, Y be either Fréchet spaces or barrelled DF-spaces. Then, there exist natural vector space isomorphisms

$$\begin{aligned} (X\mathop {\widehat{\otimes }}Y)'\cong L(X,Y') \cong L(Y,X'). \end{aligned}$$

The following is a natural extension of [7, II.5.22] to the locally convex setting.

Proposition 3.8

Let A, B, C be $\mathop {\widehat{\otimes }}$-algebras, and let $X\in A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}B$, $Y\in B\text{-}\!\mathop {\mathsf {mod}}\!\text{-}C$, and $Z\in A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}C$. There is a natural linear map

$$\begin{aligned} {_A}L_C(X\mathop {\widehat{\otimes }}_{B} Y,Z)\rightarrow {_A}L_B(X,L_C(Y,Z)), \quad f\mapsto (x\mapsto (y\mapsto f(x\otimes y))). \end{aligned}$$

(5)

The above map is a vector space isomorphism if either of the conditions (i), (ii) of Proposition 3.6 are satisfied.

Proof

By the universal property of $\mathop {\widehat{\otimes }}_{B}$ [7, II.4.2], ${_A}L_C(X\mathop {\widehat{\otimes }}_{B} Y,Z)$ is naturally identified with the space of those jointly continuous bilinear maps from $X\times Y$ to Z which are (1) B-balanced, (2) A-linear in the first variable, and (3) C-linear in the second variable. A routine calculation shows that a jointly continuous bilinear map $X\times Y\rightarrow Z$ has the above three properties if and only if the respective linear map $X\rightarrow L(Y,Z)$ takes X to $L_C(Y,Z)$ and is an A–B-bimodule morphism. The rest follows from Proposition 3.6. $\square$

Corollary 3.9

Let B be a $\mathop {\widehat{\otimes }}$-algebra, $X\in \mathop {\mathsf {mod}}\!\text{-}B$, and $Y\in B\text{-}\!\mathop {\mathsf {mod}}$. If X and Y are either Fréchet spaces or barrelled DF-spaces, then there exist natural vector space isomorphisms

$$\begin{aligned} (X\mathop {\widehat{\otimes }}_{B} Y)'\cong L_B(X,Y')\cong {_B}L(Y,X'). \end{aligned}$$

Corollary 3.10

Let $\mathsf {C}\in \{\mathsf {Fr},\mathsf {CBDF}\}$, let A be a $\mathop {\widehat{\otimes }}$-algebra, and let $X\in \mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$, $Y\in A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$, $Z\in \mathsf {C}$. Then, there exists a natural vector space isomorphism

$$\begin{aligned} L(X\mathop {\widehat{\otimes }}_{A} Y,Z')\cong L_A(Z\mathop {\widehat{\otimes }}X,Y'). \end{aligned}$$

Proof

This follows from Corollaries 3.7, 3.9, the commutativity of $\mathop {\widehat{\otimes }}$, and the associativity of $\mathop{\widehat\otimes}_A$, since we have

$$\begin{aligned} L(X\mathop {\widehat{\otimes }}_{A} Y,Z') \cong ((X\mathop {\widehat{\otimes }}_{A} Y)\mathop {\widehat{\otimes }}Z)' \cong ((Z\mathop {\widehat{\otimes }}X)\mathop {\widehat{\otimes }}_{A}Y)' \cong L_A(Z\mathop {\widehat{\otimes }}X,Y'). \end{aligned}$$

$\square$

The following result was proved in [20, Proposition 3.3] for $\mathsf {C}=\mathsf {Fr}$. We now give a shorter proof which holds both for $\mathsf {C}=\mathsf {Fr}$ and $\mathsf {C}=\mathsf {CBDF}$.

Proposition 3.11

Let $\mathsf {C}\in \{\mathsf {Fr},\mathsf {CBDF}\}$, and let $A\in \mathsf {alg}(\mathsf {C})$. Then for all $X\in A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$, $Y\in \mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$, $n\in \mathbb Z_+$, there is a natural vector space isomorphism ${{\,\mathrm{Ext}\,}}^n_A(X,Y')\cong {{\,\mathrm{Ext}\,}}^n_A(Y,X')$.

Proof

Let $P_\bullet \rightarrow A_+$ be a projective resolution of $A_+$ in $A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$. Then $P_\bullet \mathop {\widehat{\otimes }}_{A} X\rightarrow X$ is a projective resolution of X in $A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$, and $Y\mathop {\widehat{\otimes }}_{A} P_\bullet \rightarrow Y$ is a projective resolution of Y in $\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$. Applying Corollary 3.9 twice, we obtain natural vector space isomorphisms

$$\begin{aligned} \mathrm{Ext}^n_A(X,Y') &=H^n({_A}L\bigl (P_\bullet \mathop {\widehat{\otimes }}_{A} X,Y')\bigr ) \cong H^n\bigl ((Y\mathop {\widehat{\otimes }}_{A} P_\bullet \mathop {\widehat{\otimes }}_{A} X)'\bigr )\\ &\cong H^n\bigl (L_A(Y\mathop {\widehat{\otimes }}_{A} P_\bullet ,X')\bigr ) =\mathrm{Ext}^n_A(Y,X'). \end{aligned}$$

$\square$

Our next theorem generalizes [20, Proposition 3.4].

Theorem 3.12

Let $\mathsf {C}\in \{\mathsf {Fr},\mathsf {CBDF}\}$, and let $A\in \mathsf {alg}(\mathsf {C})$. The following properties of $X\in A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$ are equivalent:

• (i) X is topologically flat;

• (ii) ${{\,\mathrm{Ext}\,}}_A^1(Y,X')=0\quad \forall \,\,Y\in \mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$;

• (iii) ${{\,\mathrm{Ext}\,}}_A^1(X,Y')=0\quad \forall \,\,Y\in \mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$;

• (iv) ${{\,\mathrm{Ext}\,}}_A^n(Y,X')=0\quad \forall \,\,Y\in \mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C}),\quad \forall \,\,n\in {\mathbb {N}}$;

• (v) ${{\,\mathrm{Ext}\,}}_A^n(X,Y')=0\quad \forall \,\,Y\in \mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C}),\quad \forall \,\,n\in {\mathbb {N}}$;

• (vi) the functor $L_A(-,X'):\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})\rightarrow \mathsf {Vect}$ takes short admissible sequences to exact sequences.

Proof

$\mathrm {(ii)\Leftrightarrow (iii)}$, $\mathrm {(iv)\Leftrightarrow (v)}$: these are special cases of Proposition 3.11.

$\mathrm {(ii)\Leftrightarrow (iv)\Leftrightarrow (vi)}$: these are special cases of [7, III.3.7].

$\mathrm {(i)\Rightarrow (vi)}$. By assumption, for each short admissible sequence (2) in $\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$ the sequence (3) is strictly exact in $\mathsf {CLCS}$. By Palamodov’s Theorem 2.4, the dual sequence

$$\begin{aligned} 0 \rightarrow (Y_3\mathop {\widehat{\otimes }}_{A} X)' \rightarrow (Y_2\mathop {\widehat{\otimes }}_{A} X)' \rightarrow (Y_1\mathop {\widehat{\otimes }}_{A} X)' \rightarrow 0 \end{aligned}$$

(6)

is exact in $\mathsf {Vect}$. Corollary 3.9 implies that (6) is isomorphic to

$$\begin{aligned} 0 \rightarrow L_A(Y_3,X') \rightarrow L_A(Y_2,X')\rightarrow L_A(Y_1,X') \rightarrow 0. \end{aligned}$$

(7)

This yields (vi).

$\mathrm {(vi)\Rightarrow (i)}$. We want to show that for each short admissible sequence (2) in $\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$ the sequence (3) is strictly exact in $\mathsf {CLCS}$. By Palamodov’s Theorem 2.4, this means precisely that for each set S the sequence

$$\begin{aligned} 0 \rightarrow L(Y_3\mathop {\widehat{\otimes }}_{A} X,\ell _\infty (S)) \rightarrow L(Y_2\mathop {\widehat{\otimes }}_{A} X,\ell _\infty (S)) \rightarrow L(Y_1\mathop {\widehat{\otimes }}_{A} X,\ell _\infty (S)) \rightarrow 0 \end{aligned}$$

(8)

is exact in $\mathsf {Vect}$. Taking into account the isomorphism $\ell _\infty (S)\cong (\ell _1(S))'$ and applying Corollary 3.10, we see that (8) is isomorphic to

$$ 0 \rightarrow L_A(\ell _1(S)\mathop {\widehat{\otimes }}Y_3,X') \rightarrow L_A(\ell _1(S)\mathop {\widehat{\otimes }}Y_2,X')\rightarrow L_A(\ell _1(S)\mathop {\widehat{\otimes }}Y_1,X') \rightarrow 0.$$

(9)

Since $\ell _1(S)\mathop {\widehat{\otimes }}Y_\bullet$ is admissible in $\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$, we see that (9) is exact in $\mathsf {Vect}$ by (vi). In view of the above remarks, this completes the proof. $\square$

The next proposition shows that a flat Banach module over a Banach algebra remains topologically flat if we consider it as an object of the bigger category of Fréchet modules or of complete barrelled DF-modules.

Proposition 3.13

Let A be a Banach algebra and let X be a left Banach A-module. The following conditions are equivalent:

• (i) X is flat (or, equivalently, topologically flat) relative to $\mathsf {Ban}$;

• (ii) X is flat (or, equivalently, topologically flat) relative to $\mathsf {Fr}$;

• (iii) X is topologically flat relative to $\mathsf {CBDF}$.

Proof

Clearly, each of the conditions (ii) and (iii) implies (i). Conversely, let $\mathsf {C}$ denote either of the categories $\mathsf {Fr}$ or $\mathsf {CBDF}$, and suppose that (i) holds. By [7, VII.1.14], condition (i) means precisely that $X'$ is injective in $\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {Ban})$. Using [7, III.1.31], we see that $X'$ is a retract of $L(A_+,X')$ in $\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {Ban})$. Hence, for each short admissible sequence $Y_\bullet$ in $\mathop {\mathsf {mod}}\!\text{-}A$, the sequence $L_A(Y_\bullet ,X')$ is a retract of $L_A(Y_\bullet ,L(A_+,X'))$. On the other hand, [31, Proposition 3.2] implies that

$$\begin{aligned} L_A(Y_\bullet ,L(A_+,X')) \cong L(Y_\bullet ,X'). \end{aligned}$$

Hence, $L_A(Y_\bullet ,X')$ is a retract of $L(Y_\bullet ,X')$, which is clearly exact in $\mathsf {Vect}$. Therefore, $L_A(Y_\bullet ,X')$ is exact in $\mathsf {Vect}$. Applying Theorem 2.4, we conclude that X is topologically flat in $A\text{-}\!\mathop {\mathsf {mod}}(\mathsf {C})$.

Remark 3.14

The equivalence of (i) and (ii) in Proposition 3.13 was proved in [21, Proposition 4.11].

We now turn to topological amenability, using Helemskii–Sheinberg’s approach [6] as a motivation. Let $\mathsf {C}$ be an admissible subcategory of $\mathsf {CLCS}$, and let $A\in \mathsf {alg}(\mathsf {C})$.

Definition 3.15

We say that A is topologically amenable (relative to $\mathsf {C}$) if $A_+$ is topologically flat in $A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$.

Remark 3.16

According to [7], A is amenable if $A_+$ is flat in $A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$. As in Remark 3.2, we would like to stress that amenability and topological amenability are formally different in the general case, but they are equivalent if $\mathsf {C}\subset \mathsf {Fr}$.

Example 3.17

Recall from [8, Chap. VII] (see also [7, Postscript]) that A is contractible if $A_+$ is projective in $A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$. Since projective modules are topologically flat (see Example 3.3), we conclude that each contractible algebra is topologically amenable.

Recall that the amenability of a Banach algebra can be rephrased in the language of derivations. Our next result gives a similar characterization in the categories $\mathsf {Fr}$ and $\mathsf {CBDF}$. For Fréchet algebras, this was proved in [20, Corollary 3.5].

Theorem 3.18

Let $\mathsf {C}\in \{\mathsf {Fr},\mathsf {CBDF}\}$, and let $A\in \mathsf {alg}(\mathsf {C})$. Then A is topologically amenable relative to $\mathsf {C}$ if and only if for each $X\in A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$ every continuous derivation $A\rightarrow X'$ is inner.

Proof

It is a standard fact (see, e.g., [7, Chap. I, Subsection 2.1]) that every continuous derivation $A\rightarrow X'$ is inner if and only if $\mathscr {H}^1(A,X')=0$, where $\mathscr {H}^1(A,X')$ is the 1st continuous Hochschild cohomology group of A with coefficients in $X'$. By [7, III.4.9], we have a vector space isomorphism $\mathscr {H}^1(A,X')\cong {{\,\mathrm{Ext}\,}}^1_{A^e}(A_+,X')$. Now the result follows from Theorem 3.12. $\square$

In the $\mathsf {CBDF}$ category, it is also possible to relate topological amenability to amenability.

Corollary 3.19

Let A be a complete barrelled DF-algebra which is amenable relative to $\mathsf {CBDF}$. Then A is topologically amenable relative to $\mathsf {CBDF}$.

Proof

By [23, Theorem 4.4], for each $X\in A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {CBDF})$ every continuous derivation $A\rightarrow X'$ is inner. Now the result follows from Theorem 3.18. $\square$

If A is a Banach algebra, then the above notions coincide.

Proposition 3.20

Let $\mathsf {C}\in \{\mathsf {Fr},\mathsf {CBDF}\}$, and let A be a Banach algebra. Then A is topologically amenable relative to $\mathsf {C}$ if and only if A is amenable relative to $\mathsf {Ban}$.

Proof

This follows immediately from Proposition 3.13. $\square$

Since the algebras $k_0(V)$ that appear in the next section are not necessarily complete, we adopt the following definition of topological amenability for non-complete algebras.

Definition 3.21

Let $\mathsf {C}\in \{\mathsf {Fr},\mathsf {CBDF}\}$, and let A be a locally convex algebra with jointly continuous multiplication such that $\widetilde{A}\in \mathsf {alg}(\mathsf {C})$ (where $\widetilde{A}$ is the completion of A). We say that A is topologically amenable relative to $\mathsf {C}$ if $\widetilde{A}$ is topologically amenable relative to $\mathsf {C}$.

Given A as above, let $A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$ denote the category of locally convex A-bimodules X such that the left and right actions of A on X are jointly continuous and such that the underlying space of X is an object of $\mathsf {C}$. Clearly, we have an isomorphism of categories $A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})\cong \widetilde{A}\text{-}\!\mathop {\mathsf {mod}}\!\text{-}\widetilde{A}(\mathsf {C})$.

Using the above definition, we can easily extend Theorem 3.18 to non-complete algebras.

Theorem 3.22

Let $\mathsf {C}\in \{\mathsf {Fr},\mathsf {CBDF}\}$, and let A be a locally convex algebra with jointly continuous multiplication such that $\widetilde{A}\in \mathsf {alg}(\mathsf {C})$. Then, A is topologically amenable relative to $\mathsf {C}$ if and only if for each $X\in A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})$ every continuous derivation $A\rightarrow X'$ is inner.

Proof

Given $X\in A\text{-}\!\mathop {\mathsf {mod}}\!\text{-}A(\mathsf {C})\cong \widetilde{A}\text{-}\!\mathop {\mathsf {mod}}\!\text{-}\widetilde{A}(\mathsf {C})$, observe that $X'$ is complete (see, e.g., [12, 28.5.(1)]). Hence each continuous derivation $A\rightarrow X'$ uniquely extends to a continuous linear map $\widetilde{A}\rightarrow X'$, which is easily seen to be a derivation. Thus, we have a 1–1 correspondence between the continuous derivations $A\rightarrow X'$ and $\widetilde{A}\rightarrow X'$, which obviously takes the inner derivations onto the inner derivations. Now the result follows from Theorem 3.18 applied to $\widetilde{A}$. $\square$

We end this section with another consequence of topological amenability. The proof is similar to that of [4, Proposition 2.8.64], therefore we omit it.

Proposition 3.23

Let $\mathsf {C}\in \{\mathsf {Fr},\mathsf {CBDF}\}$, and let A and B be locally convex algebras with jointly continuous multiplication such that $\widetilde{A},\widetilde{B}\in \mathsf {alg}(\mathsf {C})$. Suppose that $\theta :A\rightarrow B$ is a continuous homomorphism with dense range. If A is topologically amenable relative to $\mathsf {C}$, then so is B.

4 Topological amenability for co-echelon algebras

We are now going to investigate topological amenability in the framework of Köthe co-echelon algebras. Throughout this section, amenability and topological amenability are considered relative to the category $\mathsf {CBDF}$ of complete barrelled DF-spaces.

The following result is a restatement of [7, Lemma 0.5.1] adapted to DF-spaces. The proof is essentially the same.

Lemma 4.1

Let X and Y be DF-spaces such that X is complete and Y is quasi-barrelled, and let $u:X\rightarrow Y$ be a continuous linear injection. If u has dense range and its adjoint $u':Y'\rightarrow X'$ is surjective, then u is a topological isomorphism between X and Y.

Proof

By assumption, $u':Y'\rightarrow X'$ is a continuous linear bijection between Fréchet spaces, thus it is a topological isomorphism by the Open Mapping Theorem [17, Theorem 24.30]. Therefore, $u''$ is a topological isomorphism as well. We have

$$\begin{aligned} \iota _Y\circ u=u''\circ \iota _X, \end{aligned}$$

(10)

where $\iota _X:X\hookrightarrow X''$ and $\iota _Y:Y\hookrightarrow Y''$ are the canonical inclusions. Since Y is quasi-barrelled, it follows from [9, 11.2, Proposition 2] that $\iota _Y$ is a topological embedding. Since $u''$ is a topological isomorphism, we conclude from (10) that $\iota _X$ is continuous, or, equivalently, a topological embedding [loc. cit.]. Hence, $u''$ induces a topological isomorphism $u:X\rightarrow {{\,\mathrm{im}\,}}u$. Since X is complete, ${{\,\mathrm{im}\,}}u$ is complete as well, so ${{\,\mathrm{im}\,}}u$ is closed in Y. Therefore, u is a topological isomorphism of X onto ${{\,\mathrm{im}\,}}u=\overline{{{\,\mathrm{im}\,}}u}=Y$. $\square$

Before proceeding to the characterization results, we list some properties of topologically amenable Köthe co-echelon algebras of finite order.

Lemma 4.2

Let $1\le p<\infty$, and let $k_p(V)$ be a Köthe co-echelon algebra. Then the kernel of the multiplication map $\pi :k_p(V)\mathop {\widehat{\otimes }}k_p(V)\rightarrow k_p(V)$ is a complemented subspace of $k_p(V)\mathop {\widehat{\otimes }}k_p(V)$. As a consequence, the quotient $k_p(V)\mathop {\widehat{\otimes }}k_p(V)/\ker \pi$ is complete.

Proof

To begin with, let us show that the family $(e_i\otimes e_j)_{i,j\in {\mathbb {N}}}$ is a Schauder basis in $k_p(V)\mathop {\widehat{\otimes }}k_p(V)$ with respect to the square ordering of ${\mathbb {N}}\times {\mathbb {N}}$ (see [29, Section 4.3]). Indeed, we have $k_p(V)\mathop {\widehat{\otimes }}k_p(V)={{\,\mathrm{ind}\,}}_n \ell _p(v_n)\mathop {\widehat{\otimes }}\ell _p(v_n)$ by [16, Theorem 7]. Hence if $u\in k_p(V)\mathop {\widehat{\otimes }}k_p(V)$ then $u\in \ell _p(v_n)\mathop {\widehat{\otimes }}\ell _p(v_n)$ for some $n\in {\mathbb {N}}$. Since $(e_j)_{j\in {\mathbb {N}}}$ is a Schauder basis in $\ell _p(v_n)$, it follows from [29, Proposition 4.25] that $(e_i\otimes e_j)_{i,j\in {\mathbb {N}}}$ is a Schauder basis in $\ell _p(v_n)\mathop {\widehat{\otimes }}\ell _p(v_n)$ with respect to the square ordering. Therefore, $u=\sum _{i,j=1}^{\infty }u_{ij}e_i\otimes e_j$ in $\ell _p(v_n)\mathop {\widehat{\otimes }}\ell _p(v_n)$, hence also in $k_p(V)\mathop {\widehat{\otimes }}k_p(V)$. Consequently, $(e_i\otimes e_j)_{i,j\in {\mathbb {N}}}$ is a basis in $k_p(V)\mathop {\widehat{\otimes }}k_p(V)$. Since the coefficient functionals $e_i^*:x\mapsto x_i$ on $k_p(V)$ are obviously continuous, so are the functionals $e_i^*\otimes e_j^*$ on $k_p(V)\mathop {\widehat{\otimes }}k_p(V)$. Thus, $(e_i\otimes e_j)_{i,j\in {\mathbb {N}}}$ is a Schauder basis.

Given $u=\sum _{i,j} u_{ij} e_i\otimes e_j\in k_p(V)\mathop {\widehat{\otimes }}k_p(V)$, we clearly have $\pi (u)=\sum _i u_{ii} e_i$. Hence,

$$\begin{aligned} \ker \pi =\overline{{{\,\mathrm{span}\,}}}\{ e_i\otimes e_j : i\ne j\}. \end{aligned}$$

Therefore, to complete the proof, it suffices to construct a continuous linear projection P on $k_p(V)\mathop {\widehat{\otimes }}k_p(V)$ such that $P(e_i\otimes e_j)=\delta _{ij} e_i\otimes e_j$ for all i, j, where $\delta _{ij}$ is the Kronecker delta.

Given $n\in {\mathbb {N}}$, let $\ell _p^0(v_n)$ denote the subspace of $\ell _p(v_n)$ consisting of finitely supported sequences. Consider the bilinear map

$$\begin{aligned} B_n:\ell _p^0(v_n)\times \ell _p^0(v_n)\rightarrow \ell _p(v_n)\mathop {\widehat{\otimes }}\ell _p(v_n),\qquad B_n(x,y)=\sum _{j=1}^\infty x_j y_j e_j\otimes e_j. \end{aligned}$$

We claim that $B_n$ is bounded. Indeed, using [29, Lemma 2.22], we obtain

$$\begin{aligned} \sum _jx_jy_je_j\otimes e_j=\int _0^1\Big (\sum _jr_j(t)x_je_j\Big )\otimes \Big (\sum _jr_j(t)y_je_j\Big )dt, \end{aligned}$$

where $(r_j)$ are the Rademacher functions on [0, 1]. Hence

$$\begin{aligned} \Vert B_n(x,y)\Vert _{\ell _p(v_n)\mathop {\widehat{\otimes }}\ell _p(v_n)}&\le \sup _{0\le t\le 1}\Big \Vert \sum _jr_j(t)x_je_j\Big \Vert _{\ell _p(v_n)}\Big \Vert \sum _jr_j(t)y_je_j\Big \Vert _{\ell _p(v_n)} \\&=\Vert x\Vert _{\ell _p(v_n)}\Vert y\Vert _{\ell _p(v_n)}. \end{aligned}$$

Therefore $B_n$ is bounded. Extending $B_n$ by continuity to $\ell _p(v_n)\times \ell _p(v_n)$ and then linearizing, we obtain a bounded linear operator $P_n$ on $\ell _p(v_n)\mathop {\widehat{\otimes }}\ell _p(v_n)$. Finally, letting $P={{\,\mathrm{ind}\,}}_n P_n$, we obtain a continuous linear operator P on $k_p(V)\mathop {\widehat{\otimes }}k_p(V)$ with the required properties. In view of the above remarks, this completes the proof. $\square$

Remark 4.3

Recall that the quotient of a complete DF-space modulo a closed subspace is not necessarily complete (see, e.g., [12, 31.6]). Therefore the completeness of $k_p(V)\mathop {\widehat{\otimes }}k_p(V)/\ker \pi$ in Lemma 4.2 is not automatic.

Proposition 4.4

Let $1\le p<\infty$ and let $k_p(V)$ be a Köthe co-echelon algebra. Suppose that $k_p(V)$ is topologically amenable. Then:

• (i) V is eventually bounded;

• (ii) the product map $\pi :k_p(V)\widehat{\otimes }k_p(V)\rightarrow k_p(V)$ is open, and there is a commutative diagram

  

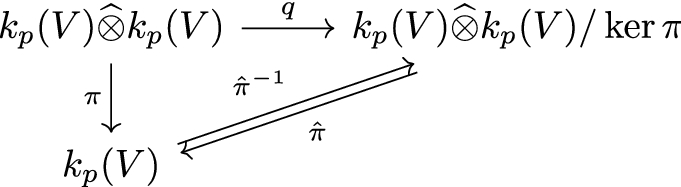
  where q is the quotient map. Moreover,

  $$\begin{aligned} \hat{\pi }^{-1}(a)=\sum _{j=1}^{\infty }a_je_j\otimes e_j+\ker \pi \qquad (a\in k_p(V)); \end{aligned}$$

  (11)

• (iii) $k_p(V)$ is nuclear.

Proof

(i) Suppose towards a contradiction that all the weights $v_n$ are unbounded. This implies that there is a sequence $j_l\nearrow \infty$ such that $v_k(j_l)\ge 1$ for all $l\in {\mathbb {N}}$ and all $k\le l$. Define a dense range homomorphism

$$\begin{aligned} \theta :k_p(V)\rightarrow \ell _p,\quad \theta (a):=(a_{j_l})_{l\in {\mathbb {N}}}, \end{aligned}$$

where we consider $\ell _p$ with the coordinate-wise multiplication. For every $k\in {\mathbb {N}}$ we get

$$\begin{aligned} \Vert \theta (a)\Vert _{\ell _p}^p=\sum _{l\le k}|a_{j_l}|^p+\sum _{l>k}|a_{j_l}|^p\le C_k\Vert a\Vert _{k,p}^p \end{aligned}$$

with $C_k:=\max \{1/v_k(j_l)^p:\,l\le k\}+1$. Consequently, $\theta$ indeed takes $k_p(V)$ to $\ell _p$ and is continuous. Since $k_p(V)$ is topologically amenable, it follows from Propositions 3.20 and 3.23 that the Banach algebra $\ell _p$ is amenable. This leads to a contradiction since $\ell _p$ is known to be non-amenable (see, e.g., [4, Example 4.1.42(iii)]). Therefore V is eventually bounded.

(ii) To prove that $\pi$ is open, it suffices to show that $\hat{\pi }$ is a topological isomorphism. Taking into account Lemma 4.2, we see that $\hat{\pi }$ acts between complete barrelled DF-spaces and, clearly, has dense range. By Lemma 4.1, the proof will be complete if we show that $\hat{\pi }'$ is surjective. Towards this goal, take $\psi \in (k_p(V)\mathop {\widehat{\otimes }}k_p(V)/\ker \pi )'$ and let $\psi _0=\psi \circ q$. Since $\psi _0$ vanishes on $\ker \pi$, we have

$$\begin{aligned} \psi _0(a\otimes b)=\sum _{j=1}^{\infty }a_jb_j\psi _0(e_j\otimes e_j)\qquad (a,b\in k_p(V)). \end{aligned}$$

(12)

Define now a linear map

$$\begin{aligned} \delta :k_p(V)\rightarrow (k_p(V)\otimes \mathbb C)',\qquad \langle b,\delta (a)\rangle :=\psi _0(a\otimes b). \end{aligned}$$

In other words, $\delta$ is the image of $\psi _0$ under (4) (where $X=Y=k_p(V)$ and $Z=\mathbb C$). Hence $\delta$ is continuous. Using (12), we see that

$$\begin{aligned} \langle c,\delta (ab)\rangle =\langle ab\otimes c,\psi _0\rangle =\langle a\otimes bc,\psi _0\rangle =\langle c,\delta (a)\cdot b\rangle \qquad (a,b,c\in k_p(V)). \end{aligned}$$

Since the left action of $k_p(V)$ on $(k_p(V)\otimes \mathbb C)'$ is trivial, we conclude that $\delta$ is a derivation. By Theorem 3.18, there is $\phi \in (k_p(V))'$ such that

$$\begin{aligned} \delta (a)=\phi \cdot a \qquad (a\in k_p(V)). \end{aligned}$$

Hence for all $a,b\in k_p(V)$, we have

$$\begin{aligned} \langle a\otimes b+\ker \pi ,\hat{\pi }'(\phi )\rangle &=\langle ab,\phi \rangle =\langle b,\phi \cdot a\rangle \\ &=\langle b,\delta (a)\rangle =\langle a\otimes b,\psi _0\rangle =\langle a\otimes b+\ker \pi ,\psi \rangle , \end{aligned}$$

that is, $\hat{\pi }'(\phi )=\psi$. Therefore, the map $\hat{\pi }'$ is surjective. In view of the above remarks, this implies that $\pi$ is open. To prove (11), observe that for every $j\in {\mathbb {N}}$ we have

$$\begin{aligned} \hat{\pi }^{-1}(e_j)=\hat{\pi }^{-1}\circ \hat{\pi }(e_j\otimes e_j+\ker \pi )=e_j\otimes e_j+\ker \pi . \end{aligned}$$

Since $(e_j)_{j\in {\mathbb {N}}}$ is a Schauder basis in $k_p(V)$, this implies (11).

(iii) To get the nuclearity of $k_p(V)$ we repeat exactly the proof of [23, Theorem 5.1]. We can indeed do so, since $\hat{\pi }^{-1}$ is a topological isomorphism not only in the case of amenability (which was the assumption in [23]) but also under the weaker assumption of topological amenability. $\square$

Theorem 4.5

Let $1\le p<\infty$, and let $k_p(V)$ be a Köthe co-echelon algebra. TFAE:

• (i) $k_p(V)$ is topologically amenable;

• (ii) $k_p(V)$ is amenable;

• (iii) $k_p(V)$ is contractible;

• (iv) $k_p(V)$ is unital;

• (v) V is eventually in $\ell _1$;

• (vi) V is eventually bounded, and $k_p(V)$ is nuclear.

Proof

$\mathrm {(ii)\Leftrightarrow (iii)\Leftrightarrow (iv)}$: see [23, Theorem 5.1].

$\mathrm {(iv)\Leftrightarrow (v)\Leftrightarrow (vi)}$: see [3, Proposition 2.5].

$\mathrm {(ii)\Rightarrow (i)}$ follows from Corollary 3.19.

$\mathrm {(i)\Rightarrow (vi)}$ follows from Proposition 4.4. $\square$

It turns out that the cases of Köthe co-echelon algebras of order zero and infinity can be treated simultaneously.

Theorem 4.6

Let $p\in \{0,\infty \}$, and let $k_p(V)$ be a Köthe co-echelon algebra. TFAE:

• (i) $k_0(V)$ is topologically amenable;

• (ii) $k_{\infty }(V)$ is topologically amenable;

• (iii) V is eventually bounded.

Proof

$\mathrm {(ii)\Rightarrow (iii)}$. If $k_{\infty }(V)$ is topologically amenable then we can follow the proof of Proposition 4.4 to show that V is eventually bounded. Indeed, suppose towards a contradiction that all the weights $v_n$ are unbounded. This implies that there is a sequence $j_l\nearrow \infty$ such that $v_k(j_l)\ge 2^l$ for all $l\in {\mathbb {N}}$ and all $k\le l$. Define a dense range homomorphism

$$\begin{aligned} \theta :k_\infty (V)\rightarrow \ell _1,\quad \theta (a):=(a_{j_l})_{l\in {\mathbb {N}}}, \end{aligned}$$

where we consider $\ell _1$ with the coordinate-wise multiplication. For every $k\in {\mathbb {N}}$ we get

$$\begin{aligned} \Vert \theta (a)\Vert _{\ell _1}=\sum _{l\le k}|a_{j_l}|+\sum _{l>k}|a_{j_l}|\le C_k\Vert a\Vert _{k,\infty } \end{aligned}$$

with $C_k:=\sum _{l\le k} (1/v_k(j_l))+1$. Consequently, $\theta$ indeed takes $k_\infty (V)$ to $\ell _1$ and is continuous. Since $k_\infty (V)$ is topologically amenable, it follows from Propositions 3.20 and 3.23 that the Banach algebra $\ell _1$ is amenable. This leads to a contradiction since $\ell _1$ is known to be non-amenable (see, e.g., [4, Example 4.1.42(iii)]). Therefore, V is eventually bounded.

$\mathrm {(iii)\Rightarrow (ii)}$. Without loss of generality, we may assume that $v_1\in V$ is bounded. We then have $\ell _\infty \subset \ell _\infty (v_1)$, and the inclusion is clearly bounded. Composing with the inclusion of $\ell _\infty (v_1)$ into $k_\infty (V)$, we obtain a continuous homomorphism

$$\begin{aligned} \theta :\ell _{\infty }\rightarrow k_{\infty }(V),\quad \theta (a):=a. \end{aligned}$$

(13)

We claim that $\theta$ has dense range. To this end, let $a\in k_{\infty }(V){\setminus }\{ 0\}$, i.e., $0<\Vert a\Vert _{n,\infty }<\infty$ for some $n\in {\mathbb {N}}$. Using (W3), find $m\in {\mathbb {N}}$ and $C>0$ such that

$$\begin{aligned} \forall \,j\in {\mathbb {N}}\quad v_m(j)\le C v_n(j)^2. \end{aligned}$$

Fix $\varepsilon >0$ and denote $J_1:=\{j\in {\mathbb {N}}:\,v_n(j)\ge \frac{\varepsilon }{2C\Vert a\Vert _{n,\infty }}\}$ and $J_2:={\mathbb {N}}{\setminus } J_1$. Define a scalar sequence $b^{\varepsilon }=(b_j)_j$ as

$$\begin{aligned}b_j:={\left\{ \begin{array}{ll} a_j,\,\,j\in J_1 \\ 0,\,\,\,j\in J_2. \end{array}\right. } \end{aligned}$$

For each $j\in J_1$, we have

$$\begin{aligned} |b_j|\le \frac{2C}{\varepsilon }\Vert a\Vert _{n,\infty }|a_j|v_n(j)\le \frac{2C}{\varepsilon }\Vert a\Vert _{n,\infty }^2. \end{aligned}$$

Consequently, $b^{\varepsilon }\in \ell _{\infty }$ with $\Vert b^{\varepsilon }\Vert _{\ell _{\infty }}\le \frac{2C}{\varepsilon }\Vert a\Vert _{n,\infty }^2$. If $J_2$ is empty, we conclude that $a=b^\varepsilon$ is in the range of $\theta$. Otherwise, observe that

$$\begin{aligned} \Vert a-b^{\varepsilon }\Vert _{m,\infty }=\sup _{j\in J_2}|a_j|v_m(j). \end{aligned}$$

For any $j\in J_2$ we get

$$\begin{aligned} |a_j|v_m(j)\le C|a_j|v_n(j)^2&\le C\Vert a\Vert _{n,\infty }v_n(j) \\&<C\Vert a\Vert _{n,\infty }\frac{\varepsilon }{2C\Vert a\Vert _{n,\infty }}=\frac{\varepsilon }{2}<\varepsilon . \end{aligned}$$

Thus, $\Vert a-b^{\varepsilon }\Vert _{m,\infty }<\varepsilon$. This implies that for a sequence $\varepsilon _k\searrow 0$ we get another sequence $b^k:=b^{\varepsilon _k}\in \ell _{\infty }$ such that

$$\begin{aligned} \lim _{k\rightarrow \infty }b^k=a\quad \text {in}\,\,\ell _{\infty }(v_m). \end{aligned}$$

But the topology of $\ell _{\infty }(v_m)$ is stronger than that of $k_{\infty }(V)$, thus

$$\begin{aligned} \lim _{k\rightarrow \infty }b^k=a\quad \text {in}\,\,k_{\infty }(V). \end{aligned}$$

Consequently, the homomorphism (13) has dense range. Since $\ell _\infty$ is amenable by [10, Lemma 7.10] (see also [4, Theorem 5.6.2], [7, Theorem VII.2.42]), the topological amenability of $k_\infty (V)$ now follows from Propositions 3.20 and 3.23.

$\mathrm {(i)\Leftrightarrow (iii)}$. This part is even easier since $(e_j)_{j\in {\mathbb {N}}}$ is a common Schauder basis for both $c_0$ and $k_0(V)$, thus the density of the range of $\theta$ in (13) is immediate. $\square$

5 Examples

Let us now give some concrete examples which illustrate Theorems 4.5 and 4.6.

Example 5.1

Applying Theorem 4.5, we see that the algebra $\varphi$ of finite sequences (see Example 2.5) is not topologically amenable.

Example 5.2

Consider the dual power series space $D\Lambda _R^p(\alpha )$, where $1\le p\le \infty$ and $R\in \{ 0\}\cup [1,+\infty )$ (see Example 2.6). If $R\ge 1$, then the respective weights $(r^{\alpha _j})_{j\in {\mathbb {N}}}$ are clearly unbounded for all $r>R$, so $D\Lambda _R^p(\alpha )$ is not topologically amenable in this case (see Theorems 4.5 and 4.6). On the other hand, $(r^{\alpha _j})_{j\in {\mathbb {N}}}$ is bounded for each $0<r\le 1$, and so $D\Lambda _0^\infty (\alpha )$ is topologically amenable by Theorem 4.6.

In fact, more is true. Indeed, all dual power series spaces $D\Lambda _R^p(\alpha )$ are Schwartz spaces by [1, Theorem 4.9]. Also, it is clear that $D\Lambda _0^\infty (\alpha )$ is unital. Now [24, Theorem 12] implies that $D\Lambda _0^\infty (\alpha )$ is contractible.

Finally, if $p<\infty$, then $D\Lambda _0^p(\alpha )$ is topologically amenable iff it is contractible iff $\sum _j r^{\alpha _j}<\infty$ for some $r>0$ (see Theorem 4.5).

Example 5.3

The algebra $s'$ of sequences of polynomial growth is contractible. This follows from [32, Proposition 7.3] and is explicitly mentioned in [19, Example 3.1], [14, Example 6.6]. Since $s'=D\Lambda _0^p(\alpha )$, where $\alpha _j=\log j$ (see Example 2.7), we see that the contractibility of $s'$ is also a special case of Example 5.2.

Example 5.4

As another special case of Example 5.2, we see that the Hadamard algebra $\mathscr {H}(\overline{\mathbb D}_R)$ of germs of holomorphic functions on the disc $\overline{\mathbb D}_R$ (see Example 2.8) is not topologically amenable for $R\ge 1$. On the other hand, letting $R=0$, we see that the Hadamard algebra $\mathscr {H}_0$ of holomorphic germs at zero is contractible.

The reader may have noticed that for all the algebras mentioned in Examples 5.1–5.4 topological amenability is equivalent to contractibility. On the other hand, there are two obvious examples of topologically amenable co-echelon algebras that are not contractible—namely, $c_0$ and $\ell _\infty$. To construct more examples of the same kind, let us first observe that the direct sum of two co-echelon algebras of the same order is also a co-echelon algebra. More exactly, if $V=(v_n)_{n\in {\mathbb {N}}}$ and $W=(w_n)_{n\in {\mathbb {N}}}$ are sequences of weights on index sets I and J, respectively, then we have $k_p(I,V)\mathop {\oplus } k_p(J,W)\cong k_p(I\sqcup J,U)$, where the sequence $U=(u_n)_{n\in {\mathbb {N}}}$ of weights on $I\sqcup J$ is given by $u_n(i)=v_n(i)$ if $i\in I$, and $u_n(j)=w_n(j)$ if $j\in J$. Conversely, each partition $I=S\sqcup T$ induces a direct sum decomposition $k_p(I,V)\cong k_p(S,V_S)\mathop {\oplus } k_p(T,V_T)$, where $V_S$ and $V_T$ consist of the restrictions to S and T of weights from V.

Example 5.5

Let $A_1=c_0\mathop {\oplus } D\Lambda _0^\infty (\alpha )$ and $A_2=\ell _\infty \mathop {\oplus } D\Lambda _0^\infty (\alpha )$. In view of the above discussion, $A_1$ and $A_2$ are co-echelon algebras of order 0 and $\infty$, respectively. By Theorem 4.6, $A_1$ and $A_2$ are topologically amenable. On the other hand, $A_1$ and $A_2$ are not Montel spaces, so they are not contractible by [24, Theorems 12 and 13] (moreover, $A_1$ is not unital, which already implies that it is not contractible).

Of course, the above example is degenerate in a sense. Our next goal is to construct a “genuine” example of a co-echelon algebra of order $\infty$ which is topologically amenable and unital, but is not contractible. By “genuine”, we mean that the algebra we are going to construct is not reduced to a direct sum of $\ell _\infty$ with a contractible algebra of the form $k_\infty (V)$ in the sense explained before Example 5.5.

Example 5.6

We fix a sequence $(c_j)_{j\in {\mathbb {N}}}$ of positive numbers such that $c_j\le 1$ for all j, and such that $c_j\rightarrow 0$ as $j\rightarrow \infty$. For each $n\in {\mathbb {N}}$ define a weight $v_n$ on ${\mathbb {N}}^2$ by

$$\begin{aligned} v_n(i,j)= {\left\{ \begin{array}{ll} c_j^n, &{} i<n,\\ 1, &{} i\ge n. \end{array}\right. } \end{aligned}$$

(14)

Clearly, the sequence $V=(v_n)_{n\in {\mathbb {N}}}$ satisfies (W1) and (W2). Furthermore, we have $v_{2n}\le v_n^2$ for all $n\in {\mathbb {N}}$, whence V satisfies (W3). Thus $k_p({\mathbb {N}}^2,V)$ is a Köthe co-echelon algebra for all p. Since V is eventually bounded, we see that $k_0({\mathbb {N}}^2,V)$ and $k_\infty ({\mathbb {N}}^2,V)$ are topologically amenable (see Theorem 4.6). Moreover, $k_\infty ({\mathbb {N}}^2,V)$ is clearly unital.

For each $i\in {\mathbb {N}}$, let $L_i=\{ (i,j) : j\in {\mathbb {N}}\}\subset {\mathbb {N}}^2$.

Lemma 5.7

If $S\subset {\mathbb {N}}^2$, then $k_\infty (S,V_S)$ is a Banach space if and only if $S\cap L_n$ is finite for all $n\in {\mathbb {N}}$.

Proof

We will use the well-known fact that an (LB)-space $E={{\,\mathrm{ind}\,}}_n E_n$ (where $E_n$ are Banach spaces, and $E_n\rightarrow E_{n+1}$ are bounded linear injections) is a Banach space if and only if the sequence $(E_n)$ stabilizes in the sense that there exists $N\in {\mathbb {N}}$ such that $E_n\rightarrow E_{n+1}$ is a topological isomorphism for all $n\ge N$ (this follows, for example, from [12, 19.5.(4)]).

If $S\cap L_n$ is finite for all $n\in {\mathbb {N}}$, then so is $S_n=\bigcup _{k\le n} (S\cap L_k)$. We clearly have $v_n=v_{n+1}=1$ outside $S_n$. Letting

$$\begin{aligned} C_n=\max _{(i,j)\in S_n} \frac{v_n(i,j)}{v_{n+1}(i,j)}, \end{aligned}$$

we obtain $v_n\le C_n v_{n+1}$ everywhere on S. This readily implies that the map $\ell _\infty (S,v_n)\rightarrow \ell _\infty (S,v_{n+1})$ is a topological isomorphism. Hence $k_\infty (S,V_S)$ is a Banach space.

Conversely, suppose that $S\cap L_k$ is infinite for some k. Since for each $n\ge k+1$ we have $v_n(k,j)=c_j^n$, and since $c_j\rightarrow 0$ as $j\rightarrow \infty$, we see that there is no $C>0$ such that $v_n\le C v_{n+1}$ on $S\cap L_k$. Therefore, $\ell _\infty (S,v_n)\rightarrow \ell _\infty (S,v_{n+1})$ is not a topological isomorphism, and so $k_\infty (S,V_S)$ is not a Banach space. $\square$

Lemma 5.8

There is no decomposition ${\mathbb {N}}^2=S\sqcup T$ such that $k_\infty (S,V_S)$ is a Banach space and such that $k_\infty (T,V_T)$ is a Montel space.

Proof

Suppose that $S\subset {\mathbb {N}}^2$ is a subset such that $k_\infty (S,V_S)$ is a Banach space, and let $T={\mathbb {N}}^2{\setminus } S$. By Lemma 5.7, for each $n\in {\mathbb {N}}$ there exists $j_n\in {\mathbb {N}}$ such that $(n,j_n)\in T$. We clearly have $v_m(n,j_n)=1$ for all $n\ge m$. Letting $R=\{ (n,j_n) : n\in {\mathbb {N}}\}$, we conclude that

$$\begin{aligned} \inf _{(i,j)\in R}\frac{v_m(i,j)}{v_1(i,j)} =\inf _{n\in {\mathbb {N}}} \frac{v_m(n,j_n)}{v_1(n,j_n)} >0 \qquad (m\in {\mathbb {N}}). \end{aligned}$$

The existence of an infinite set $R\subset T$ with the above property means precisely that $k_\infty (T,V_T)$ is not Montel [1, Theorem 4.7]. $\square$

Essentially the same argument applies to $k_0({\mathbb {N}}^2,V)$. However, more is true.

Lemma 5.9

Let V be the weight sequence on ${\mathbb {N}}^2$ given by (14). Then $k_0({{\mathbb {N}}^2},V)$ is not complete, and the underlying lcs of $k_0({\mathbb {N}}^2,V)$ is not isomorphic to a direct sum of a normed space and a dense subspace of a reflexive space.

Proof

Recall from [1, Theorem 2.7] that, for each set I and each sequence $V=(v_n)_{n\in {\mathbb {N}}}$ of weights on I satisfying (W1) and (W2), the strong dual of $k_0(I,V)$ is topologically isomorphic to the Köthe echelon space

$$\begin{aligned} \lambda _1(I,A)=\Bigl \{ x=(x_i)\in \mathbb C^I : \Vert x\Vert _n=\sum _{i\in I} |x_i| a_n(i)<\infty \;\forall n\in {\mathbb {N}}\Bigr \}, \end{aligned}$$

where $a_n(i)=v_n(i)^{-1}$ and $A=(a_n)_{n\in {\mathbb {N}}}$ is the corresponding Köthe set.

Let now $I={\mathbb {N}}^2$, let V be given by (14), and let $E=k_0({\mathbb {N}}^2,V)$. Assume, towards a contradiction, that $E\cong E_0\mathop {\oplus } E_1$, where $E_0$ is a normed space and $E_1$ is a dense subspace of a reflexive space. Hence we have a topological isomorphism $E'\cong E'_0\mathop {\oplus } E'_1$. Moreover, $E'_0$ is a Banach space, and $E'_1$ is a reflexive Fréchet space (see, e.g., [12, 23.5.(5) and 29.3.(1)]). Now recall from [17, Corollary 25.14] that all reflexive Fréchet spaces are distinguished, i.e., their strong duals are barrelled. Clearly, each normed space is distinguished, and a direct sum of two distinguished spaces is distinguished. Therefore, $E'$ is distinguished.

On the other hand, it is easily seen that the Köthe set $A=(a_n)_{n\in {\mathbb {N}}}$ on ${\mathbb {N}}^2$, where $a_n(i,j)=v_n(i,j)^{-1}$, satisfies the conditions of [17, Corollary 27.18]. Hence $\lambda _1({\mathbb {N}}^2,A)$ is not distinguished. This is a contradiction since $E'\cong \lambda _1({\mathbb {N}}^2,A)$ (see above).

Applying now [1, Corollary 3.5 and Theorem 3.7], we conclude that $k_0({\mathbb {N}}^2,V)$ is not complete. $\square$

Proposition 5.10

Let V be the weight sequence on ${\mathbb {N}}^2$ given by (14). Then

• (i) $k_0({\mathbb {N}}^2,V)$ and $k_\infty ({\mathbb {N}}^2,V)$ are topologically amenable Köthe co-echelon algebras;

• (ii) $k_\infty ({\mathbb {N}}^2,V)$ is unital;

• (iii) $k_0({\mathbb {N}}^2,V)$ is not complete;

• (iv) there is no decomposition ${\mathbb {N}}^2=S\sqcup T$ such that $k_\infty (S,V_S)$ is a Banach algebra and such that $k_\infty (T,V_T)$ is a contractible algebra;

• (v) the underlying lcs of $k_0({\mathbb {N}}^2,V)$ is not isomorphic to a direct sum of a normed algebra and a contractible Köthe co-echelon algebra.

Proof

Properties (i) and (ii) are mentioned in Example 5.6, while (iii) is contained in Lemma 5.9. To prove (iv) and (v), observe that each contractible co-echelon algebra of order $p>0$ is a Montel space (for $p<\infty$ this follows from Theorem 4.5, while for $p=\infty$ this is [24, Theorem 12]). Also, if a co-echelon algebra of order 0 is contractible, then its completion is a Montel space [24, Theorem 13]. Now, (iv) and (v) follow from Lemmas 5.8 and 5.9, respectively. $\square$

We conjecture that (v) holds for $k_\infty ({\mathbb {N}}^2,V)$ as well.