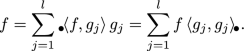Abstract
We demonstrate how to construct spectral triples for twisted group \(C^*\)-algebras of lattices in phase space of a second-countable locally compact abelian group using a class of weights appearing in time–frequency analysis. This yields a way of constructing quantum \(C^k\)-structures on Heisenberg modules, and we show how to obtain such structures using Gabor analysis and certain weighted analogues of Feichtinger’s algebra. We treat the standard spectral triple for noncommutative 2-tori as a special case, and as another example we define a spectral triple on noncommutative solenoids and a quantum \(C^k\)-structure on the associated Heisenberg modules.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The interplay between Gabor analysis and noncommutative geometry [8] has been explored earlier and has recently attracted some interest, see for example [2,3,4, 10, 11, 22, 23, 25, 28, 29]. Indeed, problems in Gabor analysis can often effectively be rephrased as operator algebraic questions. Moreover, Gabor analysis provides a way to generate projective modules over noncommutative tori [28]. Hence, results in Gabor analysis supply interesting examples of structures studied in operator algebra theory and noncommutative geometry. The main part of this paper focuses on the latter aspect.
We are interested in smooth structures on the level of projective modules over \(C^*\)-algebras, which we call quantum \(C^k\)-structures, or \(QC^k\)-structures. These are based on \(QC^k\)-structures on spectral triples for these \(C^*\)-algebras. Our focus is on Heisenberg modules over twisted group \(C^*\)-algebras of lattices in \(G\times \widehat{G}\) for a second-countable locally compact abelian group G.
In terms of Gabor analysis, the notion of \(QC^k\)-modules over noncommutative tori translates into better time-frequency localization of the window function generating the frame. It is common to refer to a Gabor frame generated by a Gaussian as better than one generated by e.g. a triangle function. Our results turn this observation into a rigorous statement and weighted analogues of Feichtinger’s algebra appear naturally in this context.
We discuss in detail the noncommutative 2-torus and noncommutative solenoids, introduced in [26, 27]. For the noncommutative 2-torus, we show that our approach yields an equal \(QC^k\)-structure as if using the standard spectral triple, and for the noncommutative solenoid, our construction provides a definition of smoothness which so far has not appeared in the literature. Note that the smooth structures introduced by Connes for noncommutative tori are also smooth in our sense but his approach does not allow one to identify structures with a fixed regularity like \(QC^k\)-structures.
In Sect. 2, we review relevant material on Hilbert \(C^*\)-modules and standard module frames with a focus on equivalence bimodules describing Morita equivalent \(C^*\)-algebras. Section 3 contains the basics on Gabor frames for lattices in \(G\times \widehat{G}\) for a second-countable locally compact abelian group G, and we define Feichtinger’s algebra \(M^1 (G)\), the prime example of a modulation space, and weighted variants \(M^1_v(G)\) for a natural class of weights on \(G\times \widehat{G}\). In this section, we also show how to obtain twisted group \(C^*\)-algebras and Heisenberg modules by ways of convolution algebras and modulation spaces. In Sect. 4, we make precise the meaning of quantum \(C^k\)-structures. Furthermore, this section contains the main results of the paper: (i) the construction of \(QC^k\)-structures on twisted group \(C^*\)-algebras of lattices in \(G\times \widehat{G}\), and (ii) a description of \(QC^k\)-structures on Heisenberg modules, and that these are just weighted Feichtinger algebras. At the end of the section, we treat the noncommutative 2-torus and the noncommutative solenoid in detail. We provide examples of projective modules that are \(QC^k\) but not \(QC^{k+1}\), and some that are smooth.
2 Preliminaries
This section is dedicated to reminding the reader about module frames and Morita equivalence. We assume basic knowledge about \(C^*\)-algebras, Banach \(*\)-algebras, and their modules.
In the sequel, we will let the \(C^*\)-algebra-valued inner product on a left Hilbert \(C^*\)-module be denoted by 
, and likewise the \(C^*\)-algebra-valued inner product on a right Hilbert \(C^*\)-module will be denoted by 
.
Module frames were introduced in [16]. However, for the purposes of this paper, it will suffice to look at finite module frames.
Definition 2.1
Let A be a \(C^*\)-algebra, let E be a left Hilbert A-module, and let \(( g_i)_{i=1}^l\) be a sequence in E. We say \(( g_i)_{i=1}^l\) is a module frame for E if there exist constants \(C,D > 0\) such that
as elements of A for all \(f \in E\). If \(C=D=1\) we say \(( g_i)_{i=1}^l\) is a Parseval module frame for E.
For a left Hilbert A-module E, we associate to any finite sequence \((g_i)_{i=1}^l \subset E\) the A-adjointable operator
This operator is called the frame operator of \((g_i)_{i=1}^l\). Note that the frame operator is a positive operator on E as 
for all \(f \in E\). The following is a special case of [1, Theorem 1.2] and might be useful to keep in mind.
Proposition 2.2
Let \((g_i)_{i=1}^l\) be a sequence in a left Hilbert A-module E. Then \((g_i)_{i=1}^l\) is a module frame for E if and only if \(\Theta _{(g_i)}:E \rightarrow E\) is invertible.
Definition 2.3
Let E be a left Hilbert A-module and let \(( g_i)_{i=1}^l \subset E\) be a frame. Denote by \(\Theta\) the frame operator of \(( g_i)_{i=1}^l\). We say \((\Theta ^{-1} g_i)_{i=1}^l\) is the canonical dual frame of \(( g_i)_{i=1}^l\), and we say \((\Theta ^{-1/2} g_i)_{i=1}^l\) is the canonical Parseval frame associated to \((g_i)_{i=1}^l\).
Given a frame \((g_i)_{i=1}^l\) for a left Hilbert A-module E, with frame operator \(\Theta\), we see that the canonical dual frame \((\Theta ^{-1} g_i)_{i=1}^l\) has the property that
for all \(f \in E\). Indeed, this follows by writing out \(f = \Theta ^{-1} \Theta f = \Theta \Theta ^{-1} f\). Any sequence \((h_i)_{i=1}^l\) such that
for all \(f \in E\) will be called a dual sequence of \(( g_i)_{i=1}^l\). Likewise, if we write out \(f = \Theta ^{-1/2} \Theta \Theta ^{-1/2} f\), we get that the canonical Parseval frame associated to \((g_i)_{i=1}^l\) has the property
for all \(f \in E\), and is a Parseval module frame as in (2.1).
The following result follows from [24, Proposition 3.9]. There it is assumed the \(C^*\)-algebra is unital, but we include a weakened version of the result so that it is clear that this assumption can be dropped.
Proposition 2.4
Let E be a Hilbert A-module and let \((g_i)_{i=1}^l\) and \((h_i)_{i=1}^l\) be sequences in E. If
for all \(f \in E\), then \((h_i)_{i=1}^l\) is a frame for E.
The modules of interest in this paper will be Morita equivalence bimodules. For a reference on Morita equivalence of \(C^*\)-algebras, we refer the reader to [34].
Definition 2.5
Let A and B be \(C^*\)-algebras. A Morita equivalence bimodule between A and B, or an A-B-equivalence bimodule, is a Hilbert A-B-bimodule E satisfying the following conditions:
-
i)
\(\overline{{{\,{{}_{\bullet }\langle }\,}}E,E\rangle }=A\) and \(\overline{\langle E , E {{\,{\rangle _{\bullet }}\,}}} = B\), where \({{\,{{}_{\bullet }\langle }\,}}E,E\rangle = {{\,\mathrm{span}\,}}_\mathbb {C}\{ {{\,{{}_{\bullet }\langle }\,}}f,g \rangle \mid f,g\in E\}\) and likewise for \(\langle E,E{{\,{\rangle _{\bullet }}\,}}\).
-
ii)
For all \(f,g \in E\), \(a \in A\) and \(b \in B\),
$$\begin{aligned} \langle a f, g{{\,{\rangle _{\bullet }}\,}}= \langle f, a^* g {{\,{\rangle _{\bullet }}\,}}\text { and }{{\,{{}_{\bullet }\langle }\,}}fb, g\rangle = {{\,{{}_{\bullet }\langle }\,}}f,gb^*\rangle . \end{aligned}$$ -
iii)
For all \(f,g,h \in E\),
$$\begin{aligned} {{\,{{}_{\bullet }\langle }\,}}f,g \rangle h = f\langle g,h {{\,{\rangle _{\bullet }}\,}}. \end{aligned}$$
Now let \(\mathcal {A}\subset A\) and \(\mathcal {B}\subset B\) be dense Banach \(*\)-subalgebras such that the enveloping \(C^*\)-algebra of \(\mathcal {A}\) is A, and the enveloping \(C^*\)-algebra of \(\mathcal {B}\) is B. Suppose further that there is a dense \(\mathcal {A}\)-\(\mathcal {B}\)-inner product submodule \(\mathcal {E}\subset E\) such that the conditions above hold with \(\mathcal {A},\mathcal {B},\mathcal {E}\) instead of A, B, E. In that case, we say \(\mathcal {E}\) is an \(\mathcal {A}\)-\(\mathcal {B}\)-pre-equivalence bimodule.
Module frames in Morita equivalence bimodules were extensively studied in [4]. We summarize the results we will need.
Proposition 2.6
Let E be an A-B-equivalence bimodule where B is unital, with an \(\mathcal {A}\)-\(\mathcal {B}\)-pre-equivalence bimodule \(\mathcal {E}\subset E\). Moreover, let \((g_i)_{i=1}^l\) be a sequence in E and let \(\Theta\) denote the frame operator of \((g_i)_{i=1}^l\). Then the following hold:
- i):
-
\((g_i)_{i=1}^l\) is a module frame for E as a Hilbert A-module if and only if
is invertible in B. - ii):
-
If \((g_i)_{i=1}^l\) is a module frame for E as an A-module, then the canonical dual is given by \((h_i)_{i=1}^l\), where
for all \(j=1, \ldots , l\), and the canonical Parseval frame associated to \((g_i)_{i=1}^l\) is given by \((h'_i)_{i=1}^l\), where
for all \(j =1, \ldots ,l\).
- iii):
-
Suppose \(\mathcal {B}\subset B\) is spectrally invariant with the same unit, and that \((g_i)_{i=1}^l\) is a module frame for E as an A-module with \(g_i \in \mathcal {E}\) for all \(i=1, \ldots , l\). Then \(\Theta ^{-1} g_i \in \mathcal {E}\) and \(\Theta ^{-1/2} g_i \in \mathcal {E}\) for all \(i=1,\ldots ,l\).
is invertible in B.
Proof
Statement i) is immediate by [4, Proposition 3.14]. Since the action of \(\Theta\) is implemented by right multiplication by 
by [4], it follows that \(\Theta ^{-1}\) is implemented by right multiplication by 
, and the action of \(\Theta ^{-1/2}\) is implemented by right multiplication by 
. Hence statement ii) follows as well. In statement iii) the fact that \(\Theta ^{-1} g_i \in \mathcal {E}\) for all \(i=1, \ldots ,l\) is immediate by [4, Proposition 3.15]. But then if 
by spectral invariance, so is 
. So it follows that \(\Theta ^{-1/2} g_i \in \mathcal {E}\) for all \(i=1,\ldots ,l\) also. \(\square\)
3 Gabor analysis on LCA groups, weighted Feichtinger algebras and twisted group \(C^{*}\)-algebras
Before discussing the mathematical objects of interest, we recall some central concepts from Gabor analysis on locally compact abelian (LCA) groups.
3.1 Gabor analysis on LCA groups and weighted Feichtinger algebras
Througout this section, we fix a second-countable LCA group G, and we will let \(\Lambda\) be a lattice in \(G \times \widehat{G}\), that is, \(\Lambda\) is a cocompact and discrete subgroup in \(G \times \widehat{G}\). Here \(\widehat{G}\) is the dual group of G. The group \(G \times \widehat{G}\) is sometimes called the time-frequency plane of G or the phase space of G. We will have to restrict to lattices \(\Lambda\) as we wish to make use of the localization procedure developed in [3] in a particular case. Namely, we need to be able to localize both the \(C^*\)-algebra \(C^* (\Lambda ,c)\) and a Heisenberg module, defined in (3.2) and (3.3). Further, the assumption that G is second-countable is imposed due to our proof of (4.6) relying on \(\Lambda\) being \(\sigma\)-compact.
Given G and \(\Lambda\) we will need to make some choices regarding the Haar measures and how they relate to one another. The convention we will use is the following: Given a second-countable LCA group G, we fix a Haar measure \(\mu _G\) on G and normalize the Haar measure \(\mu _{\widehat{G}}\) on \(\widehat{G}\) such that the Plancherel theorem holds. The lattice \(\Lambda\) will be equipped with the counting measure. On \((G \times \widehat{G})/\Lambda\) we put the Haar measure such that Weil’s formula holds, that is, such that for all \(f \in L^1 (G\times \widehat{G})\) we have
where \(\dot{\xi } = \xi + \Lambda\).
Definition 3.1
The size of \(\Lambda\), denoted \(s(\Lambda )\), is defined as
Remark 3.2
When \(\Lambda\) is a lattice it is in particular cocompact. Hence \((G \times \widehat{G})/\Lambda\) is compact, which implies \(s(\Lambda ) < \infty\).
For any point \(\xi = (x,\omega )\in G \times \widehat{G}\) we define the time-frequency shift \(\pi (\xi )\) by
where \(T_x\) is the time-shift operator given by
and \(M_\omega\) is the modulation operator, or the frequency-shift operator, given by
We define the Heisenberg 2-cocycle
for any two elements \(\xi _1 = (x_1 , \omega _1), \xi _2 = (x_2 , \omega _2)\in G \times \widehat{G}\). Moreover, we define the associated symplectic cocycle
for \(\xi _1 = (x_1 , \omega _1), \xi _2 = (x_2 , \omega _2)\in G \times \widehat{G}\). Make particular note of the fact that
The 2-cocycle and the symplectic cocycle are intimately related to time–frequency shifts. Indeed, routine calculations yield the following identities which may be helpful to keep in mind
Using the symplectic cocycle \(c_s\), we define the adjoint subgroup of \(\Lambda\), denoted \(\Lambda ^{\circ }\), by
It is then clear that \([\pi (\lambda ) , \pi (\chi )] = 0\) for all \(\lambda \in \Lambda\) and all \(\chi \in \Lambda ^{\circ }\). By [21, p. 234] we may identify \(\Lambda ^{\circ }\) with \(((G \times \widehat{G})/\Lambda )^{\widehat{}}\) and we pick the dual measure on \(\Lambda ^{\circ }\) corresponding to the measure on \((G \times \widehat{G})/\Lambda\) induced from the chosen measure on \(\Lambda\). That is, the measures are chosen so that the Plancherel theorem holds with respect to \(\Lambda ^{\circ }\) and \((G \times \widehat{G})/\Lambda\). Since \(\Lambda\) is a lattice, it is in particular cocompact, hence it follows that \(((G \times \widehat{G})/\Lambda )^{\widehat{}}\) is discrete, from which it follows that \(\Lambda ^{\circ }\) is discrete. But \((\Lambda ^{\circ })^\circ \cong \Lambda\) is discrete, from which the analogous argument implies \(\Lambda ^{\circ }\) is also cocompact. Hence \(\Lambda ^{\circ }\) is also a lattice, and we may rightfully call it the adjoint lattice of \(\Lambda\). Having picked the counting measure on \(\Lambda\), the induced measure on \(\Lambda ^{\circ }\) is the counting measure scaled with the constant \(s(\Lambda )^{-1}\) [22, equation (13)].
For any function \(g \in L^2 (G)\), we may define the short-time Fourier transform with respect to g. It is the operator
Using the short-time Fourier transform, we define the Feichtinger algebra \(M^1 (G)\) by
\(M^1 (G)\) becomes a Banach space when equipped with the norm
for some \(g \in M^1 (G)\setminus \{0\}\). Indeed it is known that any nonzero \(g \in M^1 (G)\) yields an equivalent norm on \(M^1 (G)\). We may of course do the same for \(\Lambda\). It is, however, known that when \(\Lambda\) is discrete, \(M^1 (\Lambda ) = \ell ^1 (\Lambda )\) with equivalent norms. For proofs of these statements, see for example [20, Proposition 4.10, Lemma 4.11, Theorem 4.12].
To describe smoothness, we will need dense subspaces of \(M^1 (\Lambda )\) and \(M^1 (G)\). To this end, we have the following definition.
Definition 3.3
Let \(\Delta\) be a second-countable LCA group. By a weight on \(\Delta\) we mean a function \(v: \Delta \rightarrow [0,\infty )\) satisfying the following conditions:
-
i)
\(v(\xi + \chi ) \le v(\xi ) v(\chi )\) for all \(\xi , \chi \in \Delta\) (submultiplicativity).
-
ii)
v has polynomial growth, i.e. there are \(D > 0\) and \(s >0\) such that \(v(\xi )\le D(1+d(\xi ,0))^s\) for all \(\xi \in \Delta\), where d is a translation-invariant metric generating the topology of \(\Delta\).
-
iii)
\(v(\xi ) = v(-\xi )\) for all \(\xi \in \Delta\) (radial symmetry).
Remark 3.4
If \(v(0) = 0\), then for any \(\xi \in \Delta\)
hence the weight v is identically zero. For this reason, we will assume in the rest of the article that \(v(0) \ne 0\). Note then that submultiplicativity of the weight v implies \(v(0)\ge 1\). Indeed, by the calculation
we obtain the desired relation by dividing by v(0) on both sides. But by radial symmetry we then have
for all \(\xi \in \Delta\). It follows that \(v(\xi )\ge 1\) for all \(\xi \in \Delta\).
Example
Let \(G = \mathbb {R}\) and consider the phase space \(G \times \widehat{G} \cong \mathbb {R} \times \widehat{\mathbb {R}} \cong \mathbb {R}^2\). For every \(s>0\), the function \(v_s (x,\omega ) = (1 + \vert x \vert ^2 + \vert \omega \vert ^2)^{s/2}\), \(x, \omega \in \mathbb {R}\), is a weight on \(\mathbb {R}^2\).
Some of the above assumptions in the definition of a weight are sometimes not present to get a more general version of weights, see for example [18]. In the interest of brevity, we adopt the definition of weight above.
Definition 3.5
Let \(\Delta\) be a second-countable LCA group and let v be a weight on \(\Delta\). We then define the weighted \(L^1\)-space \(L^1_v (\Delta )\) by
It is well known that \(L^1_v (\Delta )\) is a Banach space with the natural norm, that is, with the norm
for \(f \in L^1_v (\Delta )\).
We may then define the relevant subspaces of the Feichtinger algebra.
Definition 3.6
Let \(v: G \times \widehat{G}\rightarrow [0,\infty )\) be a weight. We then define the weighted Feichtinger algebra \(M^1_v (G)\) by
We do the same for \(\Lambda\) by restricting weights from \(G \times \widehat{G}\) to \(\Lambda \subset G \times \widehat{G}\).
We have the following result from [14, Theorem 4.1] which will be important to keep in mind when we define a Banach module action of \(\ell ^1_v (\Lambda ,c)\) (see (3.2)) on \(M^1_v (G)\) in (3.3).
Proposition 3.7
\(M^1_v (G)\) is a Banach space when equipped with the norm
for some \(g \in M^1_v (G)\setminus \{0\}\). Any \(g \in M^1_v (G)\setminus \{0\}\) yields an equivalent norm.
Note that for a weight v of polynomial growth on \(G \times \widehat{G}\) \(M^1_v (G)\) is dense in the Banach space \(M^1 (G)\), because the Schwartz–Bruhat space is dense in \(M^1(G)\) by [33] and by Osborne’s characterization of the Schwartz–Bruhat space [32].
In (4.4), we will link the \(QC^k\)-structure statements for Heisenberg modules of (4.3) with the study of Gabor frames. To this end we introduce the relevant concepts from Gabor analysis now.
Definition 3.8
A Gabor system \(\mathcal {G}( g; \Lambda )\) is a collection of time-frequency shifts of a function g of the form \(\{ \pi (\lambda )g \mid \lambda \in \Lambda \}\). We call it a Gabor frame for \(L^2 (G )\) if it is a frame for the Hilbert space \(L^2 (G)\), that is, if the following inequalities are satisfied for all \(f\in L^2 (G)\)
for some \(0<C \le D<\infty\). If \(C=D=1\), we call \(\mathcal {G}( g; \Lambda )\) a Parseval Gabor frame. If only the upper frame bound is satisfied, we say \(\mathcal {G}( g; \Lambda )\) is a Bessel system, and the function g is called a Bessel vector for \(\Lambda\).
Extending to the case where we have functions \(g_1 ,\ldots , g_l \in L^2 (G)\), we define a multi-window Gabor system by \(\mathcal {G} (g_1 , \ldots , g_l; \Lambda ) := \mathcal {G}(g_1 ; \Lambda ) \cup \cdots \cup \mathcal {G}(g_l ; \Lambda )\). We call it a multi-window Gabor frame for \(L^2 (G)\) if there exist constants \(0<C \le D<\infty\) such that
for all \(f\in L^2 (G)\). Again, if \(C=D=1\) we call \(\mathcal {G} ( g_1 , \ldots , g_l ; \Lambda )\) a Parseval multi-window Gabor frame. If only the upper frame bound is satisfied, we say \(\mathcal {G} ( g_1 , \ldots , g_l ; \Lambda )\) is a Bessel system, and the functions \(\{g_1, \ldots , g_l \}\) are called Bessel vectors for \(\Lambda\).
Intimately related to Bessel systems \(\mathcal {G}(g;\Lambda )\) are the coefficient mapping
and the synthesis mapping
A straightforward calculation shows that \(D_{g, \Lambda } = C_{g, \Lambda }^*\). These allow us to define the following operator.
Definition 3.9
For a Bessel system \(\mathcal {G}( g ; \Lambda )\), we define the Gabor frame operator \(S_{g, \Lambda }\) by
Likewise, given a multi-window Bessel system \(\mathcal {G} ( g_1 , \ldots , g_l ; \Lambda )\), we define the multi-window Gabor frame operator \(S_{g_1, \ldots , g_l , \Lambda }\) by
Note that boundedness of the (multi-window) Gabor frame operator is guaranteed by the upper norm bounds in (3.2) and (3.3). If \(\mathcal {G}(g_1, \ldots , g_l ; \Lambda )\) is a frame, the corresponding lower bound guarantees that the (multi-window) Gabor frame operator is invertible. Also, since \(S_{g, \Lambda } = C_{g, \Lambda }^* \circ C_{g, \Lambda }\), the Gabor frame operator is positive and thus the multi-window Gabor frame operator is positive, too. Hence for a Gabor frame \(\mathcal {G} (g; \Lambda )\) (resp. a multi-window Gabor frame \(\mathcal {G} (g_1 , \ldots g_l ; \Lambda )\)) the corresponding Gabor frame operator \(S_{g, \Lambda }\) (resp. multi-window Gabor frame operator \(S_{g_1, \ldots g_l , \Lambda }\)) is a bounded, positive, and invertible operator. Indeed, it is well known that the converse statement is also true.
3.2 Twisted group \(C^*\)-algebras
We proceed to introduce the relevant Banach \(*\)-algebras and \(C^*\)-algebras. As above we let G denote a second-countable LCA group and let \(\Lambda \subset G \times \widehat{G}\) be a lattice. Furthermore, v will be a weight on \(G \times \widehat{G}\), and c denotes the Heisenberg 2-cocycle. Indeed, in the rest of the paper, c will denote this 2-cocycle. We then wish to study the v-weighted c-twisted group algebra \(\ell ^1_v (\Lambda ,c)\). This is the space \(\ell ^1_v (\Lambda )\) equipped with c-twisted convolution
and c-twisted involution
for \(a,a_1,a_2 \in \ell ^1_v (\Lambda )\) and \(\lambda \in \Lambda\). The unweighted space, that is, with weight \(v=1\), will be denoted \(\ell ^1 (\Lambda ,c)\).
Remark 3.10
We will sometimes suppress the notation \(*_c\) and just write \(a_1 a_2\) instead of \(a_1 *_c a_2\).
The following result is well known.
Proposition 3.11
\(\ell ^1_v (\Lambda ,c)\) is a Banach \(*\)-algebra when equipped with the norm \(\Vert a \Vert _{\ell ^1_v (\Lambda ,c)} = \Vert a\cdot v\Vert _{\ell ^1 (\Lambda )}\).
We may do the same for \(\ell ^1_v (\Lambda ^{\circ })\) to make \(\ell ^1_v (\Lambda ^{\circ }, \overline{c})\). Note the conjugate cocycle.
The following result may be considered folklore, but proofs in special cases as well as allusions to a proof of the general case can be found in [12, 18, Lemma 5.1] and [17, Proposition 11.1.3]
Proposition 3.12
Let \(\Lambda\) be a (second-countable) discrete group, let v be a weight on \(\Lambda\) and let \(p \in [1,\infty )\). Then \(\ell ^1_v (\Lambda )\) acts continuously on \(\ell ^p_v (\Lambda )\) by convolution. That is, \(\ell ^1_v (\Lambda ) * \ell ^p_v (\Lambda ) \subset \ell ^p_v (\Lambda )\) and there exists a constant \(C >0\) such that
for \(a \in \ell ^1_v (\Lambda )\) and \(b \in \ell ^p_v (\Lambda )\).
There is a natural way of associating to \(\ell _v^1 (\Lambda ,c)\) a \(C^*\)-algebra. Indeed, we do the procedure for \(\ell ^1 (\Lambda ,c)\) to complete it to a \(C^*\)-algebra, and it will be clear that by density of \(\ell _v^1 (\Lambda ,c)\) in \(\ell ^1 (\Lambda ,c)\) we would obtain the same \(C^*\)-algebra if we were to do the same procedure with \(\ell _v^1 (\Lambda ,c)\). The procedure is as follows. We have a c-projective unitary representation of \(\Lambda\) on \(L^2 (G)\) via (3.1). This gives a nondegenerate c-projective \(*\)-representation of \(\ell ^1 (\Lambda )\), or equivalently, a nondegenerate \(*\)-representation of \(\ell ^1 (\Lambda ,c)\), on \(L^2 (G)\) by setting
for \(f \in L^2 (G)\) and \(a \in \ell ^1 (\Lambda )\). This representation is faithful [38]. We thus obtain a \(C^*\)-algebra by completing \(\ell ^1 (\Lambda ,c)\) in the norm \(\Vert a \Vert _{\mathbb {B}(L^2 (G))}\) for \(a \in \ell ^1 (\Lambda ,c)\). But \(\Lambda\) is an abelian group, hence \(\ell ^1 (\Lambda ,c)\) has a unique \(C^*\)-completion [2, Theorem 3.1]. So we may denote the (unique) \(C^*\)-completion of \(\ell ^1 (\Lambda ,c)\) by \(C^* (\Lambda ,c)\), and denote the norm by \(\Vert \cdot \Vert _{C^*}\). We refer to this \(C^*\)-algebra as the c-twisted group \(C^*\)-algebra of \(\Lambda\). Since \(\ell _v^1 (\Lambda ,c)\) is dense in \(\ell ^1 (\Lambda ,c)\) and \(\Vert \cdot \Vert _{\ell ^1_v} \ge \Vert \cdot \Vert _{\ell ^1} \ge \Vert \cdot \Vert _{C^*}\), we would obtain the same \(C^*\)-algebra by doing the procedure with \(\ell _v^1 (\Lambda ,c)\). We do the same procedure for \(\ell _v^1 (\Lambda ^{\circ },\overline{c})\) and obtain \(C^* (\Lambda ^{\circ }, \overline{c})\). The \(C^*\)-algebras \(C^* (\Lambda ,c)\) and \(C^* (\Lambda ^{\circ }, \overline{c})\) are closely related. Indeed, they are Morita equivalent, which we will discuss in (3.3), and will have use for in (4.3).
To show that weighted Feichtinger algebras are examples of \(QC^k\)-modules in (4.3), we will show how certain module frames implement said \(QC^k\)-structure. It will then be important that the module frames are suitably regular. To guarantee this, we need the following important result from [19]. We also refer to [2] for the result in the unweighted case written out explicitly for other LCA groups than just \(\mathbb {R}^d\).
Proposition 3.13
Let G be a second-countable LCA group and let \(\Lambda \subset G \times \widehat{G}\) be a lattice. Then \(\ell ^1 (\Lambda ,c)\) is spectrally invariant in \(C^* (\Lambda ,c)\). If, in addition, \(\Lambda\) is finitely generated and v is a weight on \(G \times \widehat{G}\), then \(\ell ^1_v (\Lambda ,c)\) is spectrally invariant in \(C^* (\Lambda ,c)\).
3.3 Weighted Feichtinger algebras as modules
To get the desired modules, we will need the following result, see [15, Proposition 5.1, Proposition 5.2]. The arguments for \(G=\mathbb {R}\) extend in a straightforward way to the general case.
Proposition 3.14
Let \(\Lambda \subset G \times \widehat{G}\) be a lattice and let v be a weight on \(G \times \widehat{G}\). Then the following hold:
- i):
-
Let \(\lambda \in \Lambda\) and \(f \in M_v^1 (G)\). Then \(\pi (\lambda )f \in M_v^1 (G)\) and
$$\begin{aligned} \Vert \pi (\lambda )f \Vert _{M^1_v} \le v(\lambda ) \Vert f\Vert _{M^1_v}. \end{aligned}$$ - ii):
-
If \(a \in \ell _v^1 (\Lambda )\) and \(f \in M_v^1 (G)\), then \(\sum _{ \lambda \in \Lambda } a(\lambda )\pi (\lambda )f \in M_v^1 (G)\) and
$$\begin{aligned} \Vert \sum _{ \lambda \in \Lambda } a(\lambda )\pi (\lambda )f \Vert _{M_v^1} \le C \Vert a \Vert _{\ell _v^1} \Vert f \Vert _{M_v^1} \end{aligned}$$for some \(C > 0\) independent of a and f.
- iii):
-
If \(f,g \in M_v^1 (G)\), then \((\left\langle f,\pi (\lambda )g\right\rangle )_{\lambda \in \Lambda } \in \ell _v^1 (\Lambda )\).
Since \(\ell ^1_v (\Lambda ,c)\) is a Banach \(*\)-algebra by (3.11), we may now give \(M_v^1 (G)\) a left Banach \(\ell _v^1 (\Lambda ,c)\)-module structure by defining
for \(a \in \ell _v^1 (\Lambda ,c)\) and \(f \in M_v^1 (G)\). We may turn \(M_v^1 (G)\) into an inner product module over \(\ell _v^1 (\Lambda ,c)\) by defining
for \(f,g \in M_v^1 (G)\). Here 
is the \(\ell _v^1 (\Lambda ,c)\)-valued inner product. That the module action is continuous, and that the module action and the inner product are well-defined follows from (3.14). We likewise get a right \(\ell _v^1 (\Lambda ^{\circ },\overline{c})\)-inner product module structure on \(M_v^1 (G)\) by setting
for \(f \in M_v^1 (G)\) and \(b \in \ell _v^1 (\Lambda ^{\circ }, \overline{c})\), and
for \(f,g \in M_v^1 (G)\). These are also well-defined by (3.14). Actually, with the above defined actions and inner products, \(M_v^1 (G)\) becomes a pre-equivalence bimodule between \(\ell _v^1 (\Lambda ,c)\) and \(\ell _v^1 (\Lambda ^{\circ },\overline{c})\). This verification was done for the Schwartz-Bruhat case in [38, Theorem 2.15] and for the Feichtinger algebra case in [28, Theorem 3.13]. We may complete \(M_v^1 (G)\) in the Hilbert \(C^*\)-module norm coming from \(C^* (\Lambda ,c)\) (or equivalently the norm from \(C^* (\Lambda ^{\circ },\overline{c})\)) to obtain a \(C^* (\Lambda ,c)\)-\(C^* (\Lambda ^{\circ },\overline{c})\)-equivalence bimodule, which we will denote by \(E_{G,\Lambda }\). Such modules are known in the literature as Heisenberg modules.
The \(C^*\)-algebra \(C^* (\Lambda ,c)\) has a very useful property which we will have great need for in (4.2). Indeed, through the standard GNS-construction using the canonical trace coming from the extension of
and the c-left regular representation we get that \(C^* (\Lambda ,c)\) embeds continuously into the Hilbert space \(\ell ^2 (\Lambda )\). Likewise \(C^* (\Lambda ^{\circ }, \overline{c})\) embeds continuously into the Hilbert space \(\ell ^2 (\Lambda ^{\circ })\). Furthermore, the Heisenberg module \(E_{G,\Lambda }\) can be continuously embedded in \(L^2 (G)\). This statement can be proved by ways of localization as in [3]. However, since we are working exclusively with lattices in phase space, we use a different and simpler proof.
Proposition 3.15
\(E_{G,\Lambda } \hookrightarrow L^2 (G)\) continuously.
Proof
A straightforward calculation will show that
for all \(g \in M^1 (G)\). Now let \((f_n)_n \subset M^1 (G)\) be a Cauchy sequence in \(E_{G,\Lambda }\)-norm. Then since \({{\,\mathrm{tr}\,}}\) is continuous, we have
We may then define a map \(\iota : E_{G,\Lambda } \rightarrow L^2 (G)\) as the continuous extension of the identity map on \(M^1 (G)\). Using that \(\iota (\overline{M^1 (G)})\subset \overline{\iota (M^1 (G))}\) it follows that \(E_{G,\Lambda }\subset L^2 (G)\). \(\square\)
Example 1
(The noncommutative 2-torus) We look at how we obtain the noncommutative 2-torus from the above constructions and how the weighted Feichtinger algebras \(M_v^1 (\mathbb {R})\) can be completed to Hilbert \(C^*\)-modules. For details, we refer the reader to [28] where this is done in depth for more general noncommutative 2d-tori, \(d \in \mathbb {N}\).
Let \((x, \omega )\in \mathbb {R}\times \widehat{\mathbb {R}} \cong \mathbb {R}^2\). On \(L^2 (\mathbb {R})\) the time shift operator \(T_x\) is then
and the modulation operator \(M_{\omega }\) is
for \(f \in L^2 (\mathbb {R})\). The time–frequency shift \(\pi (x,\omega )\) is then
for \(f \in L^2 (\mathbb {R})\). Moreover, the Heisenberg 2-cocycle is given by
Now let \(\Lambda \subset \mathbb {R}^2\) be a lattice and let v be a weight on \(\mathbb {R}^2\). As before we get a faithful representation of \(\ell _v^1 (\Lambda , c)\) on \(L^2 (\mathbb {R})\) by
for \(f \in L^2 (\mathbb {R})\) and \(a \in \ell _v^1 (\Lambda , c)\). Completing \(\ell _v^1 (\Lambda , c)\) in the induced operator norm we obtain a \(C^*\)-algebra \(C^* (\Lambda ,c)\), which is also known as the noncommutative 2-torus. The usual noncommutativity parameter \(\theta\) of e.g. [37] is determined by the lattice. In particular, \(\Lambda = L \mathbb {Z}^2\) for some \(L \in GL(\mathbb {R}^2)\), and then \(\theta = \det L\). By ways of (3.4) and (3.5) we complete \(M^1_v (\mathbb {R})\) to a Heisenberg module \(E_{\mathbb {R},\Lambda }\) over \(C^* (\Lambda ,c)\). We may indeed do the same for \(\ell ^1_v (\Lambda ^{\circ },\overline{c})\) and get a right Hilbert module structure by ways of (3.6) and (3.7). Then \(E_{\mathbb {R},\Lambda }\) becomes a \(C^* (\Lambda ,c)\)-\(C^* (\Lambda ^{\circ },\overline{c})\)-equivalence bimodule with \(M^1_v (\mathbb {R})\) as an \(\ell ^1_v (\Lambda ,c)\)-\(\ell ^1_v (\Lambda ^{\circ },\overline{c})\)-pre-equivalence bimodule.
4 \(QC^k\) and smooth quantum structures on twisted group algebras
4.1 Smoothness in noncommutative geometry
We dedicate this section to presenting a notion of smoothness used in noncommutative geometry. Given a \(C^*\)-algebra A, we fix a spectral triple \((\mathcal {A}, \mathcal {H}, D)\) for A, where \(\mathcal {A}\subset A\) is a dense \(*\)-subalgebra, \(\mathcal {H}\) is a Hilbert space and \(D: \mathcal {H} \rightarrow \mathcal {H}\) is a densely defined selfadjoint operator.
The concept of regular spectral triples was introduced by Connes in [9], but we adopt the terminology of quantum \(C^k\) spectral triples introduced in [6].
Definition 4.1
Let A be a \(C^*\)-algebra and let \((\mathcal {A}, \mathcal {H}, D)\) be a spectral triple for A. We say \((\mathcal {A}, \mathcal {H}, D)\) is quantum \(C^n\), or \(QC^n\), \(n \in \mathbb {N}\), if for all \(a \in \mathcal {A}\) both a and [D, a] are in the domain of \({{\,\mathrm{ad}\,}}^n(\vert D \vert )\). Here \({{\,\mathrm{ad}\,}}^j (|D|)(a)\) is the j times iterated commutator \([|D|,[|D|,\ldots ,[|D|,a]\ldots ]]\), \(j\in \mathbb {N}\). If \((\mathcal {A}, \mathcal {H}, D)\) is \(QC^n\) for all \(n \in \mathbb {N}\), we say it is \(QC^{\infty }\).
With this definition, we obtain a notion of smoothness on the \(C^*\)-algebra A. Namely, for any \(n \in \mathbb {N}\) it is by (4.1) natural to define
Indeed, given a spectral triple \((\mathcal {A}, \mathcal {H}, D)\) for a \(C^*\)-algebra A, saying \(\mathcal {A}\subset QA_n\) is equivalent to saying \((\mathcal {A}, \mathcal {H}, D)\) is \(QC^n\).
With a \(QC^n\)-structure on a \(C^*\)-algebra A we can, for any Hilbert A-module E, specify natural \(QC^n\)-submodules.
Definition 4.2
Let A be a \(C^*\)-algebra equipped with a \(QC^n\) spectral triple for some \(n \ge 1\), and let E be a left Hilbert A-module. Suppose there exists a uniformly norm bounded approximate unit \((e_m)_{m=1}^{\infty }\) for E, with
Here \(\Theta _{g,h}\) is the rank one module operator 
. We say that \((E, (e_m)_{m=1}^{\infty })\) is a \(QC^n\)-A-module if 
for all \(i,j \in \{1,\ldots ,m\}\) and all \(m \in \mathbb {N}\). If \((E, (e_m)_{m=1}^{\infty })\) is a \(QC^k\)-A-module for all \(k\in \mathbb {N}\), we say \((E, (e_m)_{m=1}^{\infty })\) is a \(QC^{\infty }\)-A-module.
The above definition has, to the authors’ knowledge, not appeared in the literature before, but is inspired by the definition of \(C^k\)-modules in [31].
4.2 Smooth structures on twisted group \(C^*\)-algebras
At last, we can make precise a \(QC^k\)-structure on twisted group \(C^*\)-algebras of lattices in phase space. To do this, we introduce the relevant spectral triples. We remind the reader that the LCA group G is assumed to be second-countable.
To construct spectral triples we shall want to consider the following.
Definition 4.3
Let v be a weight on \(G \times \widehat{G}\), let \(\Lambda \subset G \times \widehat{G}\) be a lattice, and let \(f: [0,\infty ) \rightarrow [0,\infty )\) be a function. We say f is spectral triple compatible for v with respect to \(\Lambda\) if the following conditions are satisfied:
-
i)
There is a constant \(C_{\mathrm {dif}}\in [0,\infty )\) such that
$$\begin{aligned} |(f\circ v) (\lambda +\mu ) - (f\circ v)(\lambda )| \le C_{\mathrm {dif}}(f\circ v)(\mu ) \end{aligned}$$for all \(\lambda , \mu \in \Lambda\).
-
ii)
There are constants \(C_{\mathrm {fin}},C_{\mathrm {gr}}\in (0,\infty )\) such that
$$\begin{aligned} (f\circ v)(\lambda ) \le C_{\mathrm {gr}}v(\lambda ) \end{aligned}$$for all \(\lambda \in \Lambda\), and
$$\begin{aligned} v(\lambda ) \le C_{\mathrm {fin}} (f\circ v)(\lambda ), \end{aligned}$$for all but finitely many \(\lambda \in \Lambda\).
-
iii)
For any real number \(M>0\), the set \(\{ \lambda \in \Lambda \mid (f\circ v)(\lambda )<M\}\) is finite.
Remark 4.4
Note that condition ii) of (4.3) implies that for any \(q \in [1,\infty ]\) there is a constant \(C_q \in [0,\infty )\), depending only on q, such that
for all \(a \in \ell ^q_{(f\circ v)}(\Lambda )\). Moreover, since f may have zeros, \(\ell ^q_{(f\circ v)}(\Lambda )\) is in general not a Banach space.
Remark 4.5
The subscripts \(\mathrm {dif}\) and \(\mathrm {gr}\) on the constants in (4.3) are chosen so that in subsequent calculations it will be easier to understand which properties of f are being invoked. The subscript \(\mathrm {dif}\) reflects that it expresses a bound on a difference and \(\mathrm {gr}\) reflects a growth condition. The constant \(C_{\mathrm {fin}}\) will not be repeatedly invoked, but is needed for a norm estimate in the proof of (4.6).
Even though in (3.3), we had very few restrictions on the weight v in terms of growth, condition iii) of (4.3) will generally require both v and f to “grow”. For example, if v is a constant weight, there can not exist any spectral triple compatible function f for v unless \(\Lambda\) is a finite group. Thus we note that for a general weight on \(\Lambda\), the collection of spectral triple compatible functions may be empty.
For a lattice \(\Lambda \subset G \times \widehat{G}\), a weight v on \(G \times \widehat{G}\), and a spectral triple compatible function f for v with respect to \(\Lambda\), we consider the (unbounded) selfadjoint operator D on \(\ell ^2 (\Lambda ) \oplus \ell ^2 (\Lambda )\) given by
We have the following result.
Theorem 4.6
Let v be a weight on \(G \times \widehat{G}\), let \(\Lambda\) be a lattice in \(G \times \widehat{G}\), let f be a spectral triple compatible function for v with respect to \(\Lambda\), and let D be defined by (4.2). Then \((\ell _{v^n}^1 (\Lambda ,c), \ell ^2 (\Lambda )\oplus \ell ^2 (\Lambda ), D)\) is an even spectral triple for \(C^*(\Lambda ,c)\) whenever \(n\ge 1\), and \(\ell _{v^n}^1 (\Lambda ,c) \subset QC^* (\Lambda ,c)_k\) for \(n\ge k+1\). In other words, if \(n\ge k+1\) then the spectral triple is quantum \(C^k\).
Proof
We begin by verifying that \((\ell _{v^n}^1 (\Lambda ,c), \ell ^2 (\Lambda )\oplus \ell ^2 (\Lambda ), D)\) is an even spectral triple for \(C^*(\Lambda ,c)\) when \(n\ge 1\). Note first that \({{\,\mathrm{Dom}\,}}(D)\) is given by
Throughout the proof, will do the calculations as if the action of \(\ell _{v^n}^1 (\Lambda ,c)\) on \(\ell ^2 (\Lambda )\) is by c-twisted convolution, denoted \(*_c\). This is technically only true on a dense subspace (for example \(\ell ^1_v (\Lambda )\subset \ell ^2 (\Lambda )\)), but the actual action is the continuous extension of c-twisted convolution. Due to the many conditions we need to check in this proof, we will not make an effort to specify that the elements of \(\ell ^2 (\Lambda )\) are such that the action of \(\ell ^1 (\Lambda ,c)\) on them is given by c-twisted convolution. Rather we will just assume this for simplicity, and it will be clear from the calculations that the results go through with the usual extension by density arguments.
To see that \(a \cdot {{\,\mathrm{Dom}\,}}(D) \subset {{\,\mathrm{Dom}\,}}(D)\) for all \(a \in \ell _{v^n}^1 (\Lambda ,c)\), let \((b,b')^T \in {{\,\mathrm{Dom}\,}}(D)\).
Due to the form of D it suffices to show \((f\circ v) \cdot (a *_c b)\in \ell ^2 (\Lambda )\). We have the following
where C is the constant obtained using (3.12). Note that \(\Vert b \Vert ^2_{\ell ^2_v (\Lambda )}\) is finite by the assumption of the existence of \(C_{\mathrm {fin}}\) in condition ii) of (4.3). By the calculation it then follows that \(a {{\,\mathrm{Dom}\,}}(D) \subset {{\,\mathrm{Dom}\,}}(D)\) for all \(a \in \ell _{v^n}^1 (\Lambda ,c)\).
To show that [D, a] extends to a bounded operator on \(\ell ^2 (\Lambda )\) for all \(a \in \ell ^1_{v^n}(\Lambda )\), note that for \((b , b')^T \in \ell ^2 (\Lambda )\oplus \ell ^2 (\Lambda )\) we have
Hence it suffices to show that there is \(K \ge 0\) such that \(\Vert (f\circ v)\cdot (a*_c b) - a *_c ((f\circ v)\cdot b)\Vert _{\ell ^2 (\Lambda )} \le K \Vert b\Vert _{\ell ^2 (\Lambda )}\) for all \(b \in \ell ^2 (\Lambda )\). Using (4.3) we then have
where we once again obtain the constant C using (3.12). It follows that [D, a] extends to a bounded operator on \(\ell ^2 (\Lambda )\).
Lastly, we need to verify that \((1+D^2)^{-1/2}\) extends to a compact operator on \(\ell ^2 (\Lambda )\). Since D is just a multiplication operator, we see that \((1+D^2)^{-1/2}\) is just the multiplication operator
We will find a sequence of finite rank operators converging to \((1+D^2)^{-1/2}\). For simplicity, we only look at one component, and denote by A the multiplication operator given by multiplication by \((1+(f\circ v)^{2})^{-1/2}\). As G is locally compact and second-countable, it is \(\sigma\)-compact, and so we deduce that \(\Lambda\) is also \(\sigma\)-compact. We may then find a nested sequence of finite sets \((F_n)\) with \(\cup _{n\in \mathbb {N}} F_n = \Lambda\). Denote by \(\delta _\lambda\), \(\lambda \in \Lambda\), the standard basis for \(\ell ^2 (\Lambda )\). We then define \(A_n\), \(n\in \mathbb {N}\), to be the multiplication operator given by
Then \(A_n\) is a finite-rank operator for all \(n \in \mathbb {N}\), and we claim that \(A_n\) converges to A in operator norm as \(n \rightarrow \infty\). For an operator defined by scalar multiplication on an orthonormal basis it is easy to prove that the operator norm is given by the supremum of the absolute value of the scalars. Using this, we get
which goes to 0 as \(n \rightarrow \infty\) by condition iii) of (4.3). We deduce that A is the operator norm limit of finite rank operators, hence a compact operator. As
we also deduce that \((1+D^2)^{-1/2}\) is a compact operator. This shows that \((\ell _{v^n}^1 (\Lambda ,c), \ell ^2 (\Lambda )\oplus \ell ^2 (\Lambda ), D)\) is a spectral triple for \(C^* (\Lambda ,c)\) whenever \(n \ge 1\). It is an even spectral triple since it is graded by
It remains to show that \((\ell _{v^n}^1 (\Lambda ,c), \ell ^2 (\Lambda )\oplus \ell ^2 (\Lambda ), D)\) is a \(QC^k\) spectral triple for \(n \ge k+1\). Note that
since D is just a multiplication operator and \((f\circ v) (\lambda ) \ge 0\) for all \(\lambda \in \Lambda\). We also note that we can write out the commutator quite explicitly. An easy induction argument will show that
We need only look at what happens in one component. Let \(b \in \ell ^2 (\Lambda )\) and \(a \in \ell ^1_{v^{n}} (\Lambda ,c)\). We have by slight abuse of notation
with the constant C obtained using (3.12). It follows that \(a \in \ell ^1_{v^{k}}(\Lambda )\) implies \(a \in {{\,\mathrm{Dom}\,}}({{\,\mathrm{ad}\,}}^k (|D|))\). In particular it holds for \(a \in \ell ^1_{v^n}(\Lambda ,c)\) as long as \(n \ge k\).
Along the same lines, we verify that \([D,a] \in {{\,\mathrm{Dom}\,}}({{\,\mathrm{ad}\,}}^k (|D|))\) for \(a \in \ell ^1_{v^n}(\Lambda ,c)\), \(n \ge k+1\). Ignoring the fact that D interchanges the two components, we have for \(b \in \ell ^2 (\Lambda )\) by slight abuse of notation
once again with constant C obtained from (3.12). We then see that \(\ell ^1_{v^{n}}(\Lambda ,c) \subset QC^*(\Lambda ,c)_k\) if \(n \ge k+1\), which finishes the proof. \(\square\)
Now let D be given by
Then \(D = |D|\), and the following is also true by more or less the same proof as above except for the grading.
Theorem 4.7
Let v be a weight on \(G \times \widehat{G}\), let \(\Lambda\) be a lattice in \(G \times \widehat{G}\), let f be a spectral triple compatible function for v with respect to \(\Lambda\), and let D be defined by (4.3). Then \((\ell _{v^n}^1 (\Lambda ,c), \ell ^2 (\Lambda )\oplus \ell ^2 (\Lambda ), D)\) is a spectral triple for \(C^*(\Lambda ,c)\) whenever \(n\ge 1\), and \(\ell _{v^n}^1 (\Lambda ,c) \subset QC^* (\Lambda ,c)_k\) for \(n\ge k+1\). In other words, if \(n\ge k+1\) then the spectral triple is quantum \(C^k\).
4.3 Modulation spaces as smooth modules
In (4.6), we saw how to obtain an even \(QC^k\) spectral triple \((\ell _{v^n}^1 (\Lambda ,c), \ell ^2 (\Lambda )\oplus \ell ^2 (\Lambda ), D)\) for \(C^* (\Lambda ,c)\) whenever \(n \ge k+1\). The goal of this section is to show how the Heisenberg module \(E_{G,\Lambda }\) of (3.3) can be equipped with a \(QC^k\)-structure for any \(k \in \mathbb {N}\). The proof follows the lines of [37, Proposition 2.1] and [38, Proposition 3.7].
Proposition 4.8
Let v be a weight on \(G \times \widehat{G}\), let \(\Lambda\) be a finitely generated lattice in \(G \times \widehat{G}\), let f be a spectral triple compatible function for v with respect to \(\Lambda\), and let \(C^*(\Lambda ,c)\) be given a \(QC^k\)-structure by ways of (4.6) or (4.7) for some \(k \in \mathbb {N}\). Then there is a uniformly norm bounded approximate unit \((e_m)_{m=1}^{\infty }\) of the form (4.1) such that \((E_{G,\Lambda }, (e_m)_{m=1}^{\infty })\) is a \(QC^k\)-module over \(C^* (\Lambda ,c)\).
Proof
We first fix \(k \in \mathbb {N}\). It suffices to prove that we can find a (uniformly norm bounded) approximate unit \((e_m)_{m=1}^{\infty }\) where
for which 
for all \(i,j \in \{1,\ldots , m\}\) and all \(m \in \mathbb {N}\), as determined by (4.6) or (4.7). Indeed, we will find a unit. Note first that \(E_{G,\Lambda }\) is a \(C^* (\Lambda ,c)\)-\(C^* (\Lambda ^{\circ }, \overline{c})\)-equivalence bimodule and both \(C^*\)-algebras are unital. Moreover, we know that \(M^1_{v^{k+1}}(G)\) is an \(\ell ^1_{v^{k+1}}(\Lambda ,c)\)-\(\ell ^1_{v^{k+1}}(\Lambda ^{\circ },\overline{c})\)-pre-equivalence bimodule. Now note that \(\ell ^1_{v^{k+1}}(\Lambda ^{\circ },\overline{c})\) is unital with the same unit as \(C^* (\Lambda ^{\circ }, \overline{c})\). Furthermore, \(\ell ^1_{v^{k+1}}(\Lambda ^{\circ },\overline{c})\) is spectrally invariant in \(C^* (\Lambda ^{\circ }, \overline{c})\) by (3.13). Hence we are in the situation of (2.6). Since \(M^1_{v^{k+1}}(G)\) is a pre-equivalence bimodule, we may find finitely many elements \(h_1, \ldots ,h_l, h'_1 , \ldots , h'_l \in M^1_{v^{k+1}}(G)\) such that 
is invertible. As \(\ell ^1_{v^{k+1}}(\Lambda ^{\circ },\overline{c})\) is spectrally invariant in \(C^* (\Lambda ^{\circ }, \overline{c})\), it follows that
If we then set 
we get
But then \((h_i)_{i=1}^l\) is a module frame for \(E_{G,\Lambda }\) by (2.4) with \(h_i \in M^1_{v^{k+1}}(G)\) for all \(i=1,\ldots ,l\). It then follows by (2.6) that there are \(g_1, \ldots , g_l \in M^1_{v^{k+1}}(G)\) such that 
For any \(f \in E_{G,\Lambda }\) we then have
which shows that \((g_i)_{i=1}^l\) has the desired property. Since 
for all \(i,j=1,\ldots ,l\), it follows that \((E_{G,\Lambda }, (g_i)_{i=1}^l)\) is a \(QC^k\)-module over \(C^* (\Lambda ,c)\). \(\square\)
Remark 4.9
Note that in (4.8) one can omit the assumption that \(\Lambda\) is finitely generated if we can guarantee that the \(g_i\)’s in the proof exist with \(g_i \in M^1_{v^{k+1}}(G)\) for all \(i=1,\ldots , l\). Indeed the only reason to include the qualifier that \(\Lambda\) is finitely generated is that we a priori do not know that such a generating sequence \((g_i)_{i=1}^l\) exists in the general case, and therefore want to use (3.13).
Even in the case of elementary groups as in [38], the above results are stronger than just being able to find tight module frames with elements in the Schwartz space. Indeed, in case \(G = \mathbb {R}^d\), \(d \in \mathbb {N}\), and \(\Lambda\) is a lattice in \(\mathbb {R}^d \times \widehat{\mathbb {R}^d}\cong \mathbb {R}^{2d}\), Parseval module frames with elements in Schwartz space \(\mathcal {S}(\mathbb {R}^d)\) would give the Heisenberg module a \(QC^{\infty }\)-structure. However, the Feichtinger algebra approach gives the possibility of finding Parseval module frames which give the Heisenberg module a \(QC^k\)-structure, which is not simultaneously a \(QC^{k+1}\)-structure. We give some examples for the noncommutative 2-torus in (4.5).
4.4 The link to Gabor analysis
The existence of sufficiently regular approximate identities from (4.2) is in the setting of Heisenberg modules a result about existence of multi-window Gabor frames with windows in suitably weighted Feichtinger algebras.
The following result is a special case of [3, Theorem 3.16].
Proposition 4.10
Let G be a second-countable LCA group, let \(\Lambda \subset G \times \widehat{G}\) be a lattice, and let \(g_1, \ldots , g_l\) be elements of the Heisenberg module \(E_{G,\Lambda }\). Then the following are equivalent:
- i):
-
The set \(\{ g_1, \ldots , g_l \}\) is a Parseval module frame for \(E_{G,\Lambda }\) as a left \(C^*(\Lambda ,c)\)-module. That is, for all \(f \in E_{G,\Lambda }\) we have
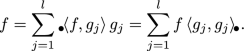
- ii):
-
The system
$$\begin{aligned} \mathcal {G}(g_1, \ldots , g_l ; \Lambda ) = \{ \pi (\lambda ) g_j : \lambda \in \Lambda , 1 \le j \le l \} \end{aligned}$$is a Parseval multi-window Gabor frame for \(L^2(G)\).
The following is then immediate by (4.8) and (4.10).
Theorem 4.11
Let v be a weight on \(G \times \widehat{G}\), let \(\Lambda\) be a lattice in \(G \times \widehat{G}\), let f be a spectral triple compatible function for v with respect to \(\Lambda\), and let \(C^*(\Lambda ,c)\) be given a \(QC^k\)-structure by ways of (4.6) or (4.7) for some \(k \in \mathbb {N}\). Then a Parseval multi-window Gabor frame \(\mathcal {G}(g_1, \ldots , g_l ; \Lambda )\) for \(L^2 (G)\) with \(g_j \in M^1_{v^{n}}(G)\), \(j=1,\ldots ,l\), \(n\ge k+1\), gives the Heisenberg module \(E_{G,\Lambda }\) the structure of a \(QC^k\)-module over \(C^* (\Lambda ,c)\).
4.5 Example: the noncommutative 2-torus
We refer the reader to [6] or [40] for details on this example. What follows will also build on (1).
On the noncommutative 2-torus, denoted \(C^* (\Lambda ,c)\) in this section, there are two canonical unbounded derivations denoted by \(\partial _1\) and \(\partial _2\). They are given by
for \((a(x,\omega ))_{(x,\omega )\in \Lambda } \in C^* (\Lambda ,c)\). These are only densely defined, but we see that \(\ell ^1_v(\Lambda ,c)\subset {{\,\mathrm{Dom}\,}}\partial _i\) for \(i=1,2\), where v is the weight \(v(x,\omega ) = (1+x^2 + \omega ^2)^{1/2}\). In the rest of this section v will denote this weight. We may then consider the spectral triple for the noncommutative 2-torus given by
where D is the unbounded operator given by
Lemma 4.12
The triple
defined above is a spectral triple for \(C^* (\Lambda ,c)\).
Proof
For \(a \in \ell ^1_v (\Lambda ,c)\) it follows by the Leibniz rule for \(\partial _i\), \(i=1,2\), that \(a \cdot {{\,\mathrm{Dom}\,}}(D) \subset {{\,\mathrm{Dom}\,}}(D)\). Moreover, a standard calculation will show that the commutator [D, a] extends to left multiplication by the matrix
which is a bounded operator. That \(a(1+D^2)^{-1/2}\) extends to a compact operator follows as in the proof of (4.6). \(\square\)
Remark 4.13
The spectral triple of (4.12) is also known as the canonical spectral triple for the noncommutative 2-torus. However, the \(*\)-subalgebra of \(C^* (\Lambda ,c)\) typically chosen is the one consisting of the Schwartz sequences.
D is a selfadjoint operator and \(D^2\) is the multiplication operator given by
We now let \((f\circ v)(\lambda ) = 2\pi (v(\lambda )^2 -1)^{1/2}\) for \(\lambda \in \Lambda\). Then one can verify that f is spectral triple compatible for v with respect to any lattice \(\Lambda \subset \mathbb {R}^2\), and we obtain
Hence
which we create by ways of (4.2) is related to the canonical spectral triple for the noncommutative 2-torus. By (4.7),
equips the noncommutative 2-torus with a \(QC^k\)-structure if \(n \ge k+1\). However,
also equips the noncommutative 2-torus with a \(QC^k\)-structure if \(n \ge k+1\). We saw that it defined a spectral triple in (4.12). That \(a \in \ell ^1_{v^{n}} (\Lambda ,c)\) is such that \(a \in {{\,\mathrm{Dom}\,}}({{\,\mathrm{ad}\,}}^k (|D|)\) for \(n \ge k+1\) follows exactly as in the proof of (4.6). If we realize that \(\partial _1 (a) + i \partial _2 (a) \in \ell ^1_{v^{n-1}} (\Lambda ,c)\) and \(- \partial _1 (a) + i\partial _2 (a) \in \ell ^1_{v^{n-1}} (\Lambda ,c)\), it also follows that \([D,a] \in {{\,\mathrm{Dom}\,}}({{\,\mathrm{ad}\,}}^k (|D|))\) for \(n \ge k+1\) by essentially the same argument as in the proof of (4.6), since we did that proof looking only at one component. Hence the twisted convolution algebra \(\ell ^1_{v^{n}} (\Lambda ,c)\) becomes a suitable \(*\)-subalgebra to give the noncommutative 2-torus a \(QC^k\)-structure for \(n \ge k+1\) both for the canonical spectral triple and for the spectral triple constructed by ways of (4.2).
By (4.4), we may then equip Heisenberg modules with \(QC^k\)-structures by finding suitably regular multi-window Gabor frames. We illustrate this with some examples. Note, however, that there are very few functions \(g \in L^2 (\mathbb {R})\) for which the set
is known.
Example
(\(QC^\infty\)-structures) Let \(\Lambda = \alpha \mathbb {Z}\times \beta \mathbb {Z}\) be a lattice in \(\mathbb {R}^2\) with \(\alpha ,\beta >0\) and \(\alpha \beta <1\). This yields a Heisenberg module \(E_{\mathbb {R},\Lambda }\) by the constructions above. A celebrated result in time–frequency analysis tells us that time–frequency shifts of the Gaussian \(g (t) = 2^{1/4} e^{-\pi t^{2}}\) determine a Gabor frame \(\mathcal {G}(g, \alpha \mathbb {Z}\times \beta \mathbb {Z})\) for \(L^2 (\mathbb {R})\) if and only if \(\alpha \beta <1\), see [30, 39]. If S then denotes the frame operator with respect to g, \(\mathcal {G}(S^{-1/2} g, \alpha \mathbb {Z}\times \beta \mathbb {Z})\) is a Parseval frame for \(L^2 (\mathbb {R})\). By (2.6) it follows that if \(g \in M^1_{v^{s}} (\mathbb {R})\), \(s\in [0,\infty )\), so is \(S^{-1/2} g\). But g is a Schwartz function, hence it is in \(\cap _{s\ge 0} M^1_{v^s} (\mathbb {R}) = \mathcal {S}(\mathbb {R})\) [17, Proposition 11.3.1], where \(\mathcal {S}(\mathbb {R})\) denotes the Schwartz functions on \(\mathbb {R}\). It follows that \(\{ S^{-1/2} g \}\) gives the Heisenberg module \(E_{\mathbb {R},\Lambda }\) a \(QC^{\infty }\)-structure for all \(\alpha \beta <1\).
Example
(\(QC^k\)-structure) Let g be a function in \(M^1_{v^{k+1}}(\mathbb {R})\). Then by [17, p. 120] \(\mathcal {G}(g;\Lambda )\) is a frame for \(L^2 (\mathbb {R})\) for some \(\Lambda = \alpha \mathbb {Z}\times \beta \mathbb {Z}\), as long as \(\alpha , \beta >0\) are small enough. Let S be the frame operator of g. Then as above it follows that \(S^{-1/2} g \in M^1_{v^{k+1}}(\mathbb {R})\) also. As in the previous example it follows that \(\{S^{-1/2}g\}\) then gives \(E_{\mathbb {R},\Lambda }\) a \(QC^k\)-structure.
For explicit examples of \(QC^k\)-structures on Heisenberg modules that are not simultaneously \(QC^{\infty }\)-structures one may use B-splines \(B_N\), see [7, Section A.8, Section 11.7]. It is known that \(\mathcal {G}(B_N, \Lambda )\) is a frame for \(L^2 (\mathbb {R})\) whenever \(\Lambda = \alpha \mathbb {Z}\times \beta \mathbb {Z}\subset \mathbb {R}^2\) is such that \(\alpha \in (0,N)\) and \(\beta \in (0,1/N]\) [7, Corollary 11.7.1]. Values of k for which a given \(B_N\) gives a Heisenberg module a \(QC^k\)-structure can be done via the Rihaczek distribution \(R(g,g)(x,\omega )=g(x)\overline{\widehat{g}}(\omega )e^{-2\pi ix\omega }\).
For the following example, note that if \(g \in L^2 (\mathbb {R})\) and \(\Lambda \subset \mathbb {R} \times \widehat{\mathbb {R}}\) is so that \(\mathcal {G}(g;\Lambda )\) is a frame for \(L^2 (\mathbb {R})\), then \(s(\Lambda ) \le 1\) [36]. For \(\Lambda = \alpha \mathbb {Z}\times \beta \mathbb {Z}\), \(\alpha ,\beta >0\), \(s(\Lambda ) = \alpha \beta\). However, even for \(s(\Lambda ) > 1\) we may construct Heisenberg modules. To obtain \(QC^k\)-structures on such Heisenberg modules \(E_{\mathbb {R},\Lambda }\), we need several generators.
Example
(Multiple generators) Suppose \(\mathcal {G}(g;\Lambda )\) is a Gabor system for \(L^2 (\mathbb {R})\) and suppose \(s(\Lambda )\in [l-1,l)\), for some integer \(l \ge 2\). Then there exist points \(z_1,...,z_l\) in \(\mathbb {R}^2\) and a lattice \(\Lambda _0\) such that \(\Lambda =z_1\Lambda _0\cup \cdots \cup z_n\Lambda _0\) with \(s(\Lambda _0)<1\), see the proof of [22, Corollary 5.6]. Hence if \(\mathcal {G}(g,\Lambda _0)\) is a Gabor frame, then \(\mathcal {G}(\pi (z_1)g,...,\pi (z_l)g;\Lambda )\) is a multi-window Gabor frame for \(L^2(\mathbb {R})\).
In particular, let g be the Gaussian and let \(\alpha \beta\) be in \([l-1,l)\) for some \(n\in \mathbb {N}\). Then there exist \(z_1,...,z_l\) in \(\mathbb {R}^2\) such that \(\mathcal {G}(\pi (z_1)g,...,\pi (z_l)g;\alpha \mathbb {Z}\times \beta \mathbb {Z})\) is a multi-window Gabor frame for \(L^2(\mathbb {R})\). Hence if S is the multi-window frame operator for \(\mathcal {G}(\pi (z_1)g,...,\pi (z_l)g;\alpha \mathbb {Z}\times \beta \mathbb {Z})\), then \(\{ S^{-1/2}g_1, \ldots ,S^{-1/2}g_n \}\) implements a \(QC^\infty\)-structure on \(E_{\mathbb {R},\Lambda }\).
4.6 Example: the noncommutative solenoid
Noncommutative solenoids have attracted some interest in the theory of operator algebras [26, 27] and time–frequency analysis [11]. Let us discuss how it fits into our framework. We denote the field of p-adic numbers by \(\mathbb {Q}_p\) and by \(\mathbb {Z}_p\) its closed unit ball, the p-adic integers. Recall that \(\mathbb {R}\times \mathbb {Q}_{p}\) is a self-dual locally compact group, see [35].
For any \(\alpha \in \mathbb {R}\setminus \{ 0 \}\) the mapping
embeds \(\mathbb {Z}[1/p]\) as a lattice into \(\mathbb {R}\times \mathbb {Q}_{p}\) and is self-dual, see e.g. [27]. Heisenberg modules over noncommutative solenoids have been linked with Gabor frames for lattices in \(\mathbb {R}\times \mathbb {Q}_{p}\) in [11]. Noncommutative solenoids are the twisted group \(C^*\)-algebra \(C^*(\Lambda , c)\) of \(\Lambda\),
see [26, 27]. Note that \(\Lambda\) is not finitely generated and hence \(C^*(\Lambda , c)\) is not generated by finitely many unitaries as is the case of the noncommutative 2-torus.
For every \(\omega = (\omega _{\infty },\omega _{p})\in \mathbb {R}\times \mathbb {Q}_{p}\) we define the modulation operator by
for \((t_{\infty },t_{p}) \in \mathbb {R}\times \mathbb {Q}_{p}\). A Gabor system generated by a function \(g\in L^{2}(\mathbb {R}\times \mathbb {Q}_{p})\) and the lattice
is thus of the form
Let us construct a spectral triple on noncommutative solenoids, which as far as we know has not been considered before in the literature. As Dirac operator, we take the one introduced in (4.2) to \(\mathbb {R}\times \mathbb {Q}_{p}\) for the lattice \(\Lambda =\{ (\alpha q, q, \beta r, r) : q,r \in \mathbb {Z}[1/p]\}\)
One of the results in [11, Corollary 3.3] allows us to construct \(QC^k\) structures on the Heisenberg module \(E_{\mathbb {R}\times \mathbb {Q}_{p},\Lambda }\).
For the construction of smooth structures, we consider the weighted Feichtinger algebras \(M^1_{v_s}(\mathbb {R}\times \mathbb {Q}_{p})\), where the weight \(v_s(x,\omega ,q,r)=(1+|x|^2+|\omega |^2+|q|^2+|r|^2)^{s/2}\) for \(s\ge 0\). It follows from, e.g., [13, Theorem 7], that the functions in \(M^1_{v_s}(\mathbb {R}\times \mathbb {Q}_{p})\) are exactly those of the form
for all \(j\in \mathbb {N}\) and such that \(\sum _{j\in \mathbb {N}} \Vert f^{(\mathbb {R})}_{j} \Vert _{M^1_{v_s}(\mathbb {R})} \, \Vert f^{(\mathbb {Q}_{p})}_{j} \Vert _{M^1_{v_s}(\mathbb {Q}_{p})} <\infty\). The norm on \(M^1_{v_s}(\mathbb {R}\times \mathbb {Q}_{p})\) is given by
where the functions f, \(\{f_{j}^{(\mathbb {R})}\}_{j\in \mathbb {N}}\) and \(\{ f_{j}^{(\mathbb {Q}_{p})}\}_{j\in \mathbb {N}}\) are related as in (4.4) and the infimum is taken over all possible representations of f as in (4.4).
Theorem 4.14
For any \(g^{(\mathbb {R})}\in {\mathbf{S}}_{0}(\mathbb {R})\) and \(\alpha ,\beta >0\) the following statements are equivalent:
- i):
-
The function \(g^{(\mathbb {R})}\) generates a Gabor frame for \(L^{2}(\mathbb {R})\) with respect to the lattice \(\alpha \mathbb {Z}\times \beta \mathbb {Z}\).
- ii):
-
For any prime number p the function \(g=g^{(\mathbb {R})}\otimes \mathbb {1}_{\mathbb {Z}_{p}}\) generates a Gabor frame for \(L^{2}(\mathbb {R}\times \mathbb {Q}_{p})\) with respect to the lattice
$$\begin{aligned} \Lambda = \psi _{\alpha }(\mathbb {Z}[1/p])\times \psi _{\beta }(\mathbb {Z}[1/p])= \{ (\alpha q, q, \beta r, r) : q,r \in \mathbb {Z}[1/p] \} \end{aligned}$$in \(\mathbb {R}\times \mathbb {Q}_{p}\times \widehat{\mathbb {R}}\times \widehat{\mathbb {Q}_{p}}\).
Even though the lattice \(\Lambda\) of (4.14) is not finitely generated, we can still use the developed machinery to describe \(QC^k\) structures on \(E_{\mathbb {R}\times \mathbb {Q}_{p},\Lambda }\), as alluded to in (4.9). Indeed, we have that \(\{\pi (q,r)\mathbb {1}_{\mathbb {Z}_{p}}\}_{q,r\in \mathbb {Z}[1/p]}\) is an orthonormal basis for \(L^2(\mathbb {Q}_{p})\) and if \(g^{(\mathbb {R})}\) is the Gaussian function, then \(g^{(\mathbb {R})}\otimes \mathbb {1}_{\mathbb {Z}_{p}}\) generates a Gabor frame for \(L^2(\mathbb {R}\times \mathbb {Q}_{p})\) if and only if \(\alpha \beta <1\). Since \(\mathbb {1}_{\mathbb {Z}_{p}}\) is in \(M^1_{v_k}(\mathbb {Q}_{p})\) for any \(k\ge 0\), then \(S^{-1/2}g^{(\mathbb {R})}\otimes \mathbb {1}_{\mathbb {Z}_{p}}\) generates a Parseval frame for \(L^2(\mathbb {R}\times \mathbb {Q}_{p})\) if and only if \(\alpha \beta <1\). By the explicit description of \(M^1_{v_k}(\mathbb {R}\times \mathbb {Q}_{p})\) given in (4.4), we have that there exists a \(QC^k\) structure on \(E_{\mathbb {R}\times \mathbb {Q}_{p},\Lambda }\) for any \(k\ge 0\). We could of course do similar constructions by for example choosing \(g^{(\mathbb {R})}\) to be some other function from the examples of (4.5).
Thus the results for the noncommutative 2-torus may also be used to obtain \(QC^k\)-structures for the Heisenberg modules over noncommutative solenoids. Hence we have \(QC^k\)-structures on the Heisenberg module \(E_{\mathbb {R}\times \mathbb {Q}_{p},\Lambda }\) which does not rely on any kind of derivations on the noncommutative solenoids and indicates the usefulness of modulation spaces in this context.
References
Arambašić, L., Bakić, D.: Frames and outer frames for Hilbert \(C^{\ast }\)-modules. Linear Multilinear Algebra 65(2), 381–431 (2017)
Austad, A.: Spectral invariance of \(\ast\)-representations of twisted convolution algebras with applications in Gabor analysis. arXiv:2002.02235v2 (2020)
Austad, A., Enstad, U.: Heisenberg modules as function spaces. J. Fourier Anal. Appl. 26(2), 24 (2020). https://doi.org/10.1007/s00041-020-09729-7
Austad, A., Jakobsen, M.S., Luef, F.: Gabor duality theory for Morita equivalent \(C^{\ast }\)-algebras. Int. J. Math. 31(10), 2050073 (2020)
Bédos, E., Omland, T.: On reduced twisted group \(C^{\ast }\)-algebras that are simple and/or have a unique trace. J. Noncommut. Geom. 12(3), 947–996 (2018)
Carey, A., Phillips, J., Rennie, A.: Spectral triples: examples and index theory. Noncommutative geometry and physics: renormalisation, motives, index theory, pp. 175–265 (2011)
Christensen, O.: An introduction to frames and Riesz bases, 2nd edn. Birkhäuser, Basel (2016)
Connes, A.: Noncommutative geometry. Academic Press Inc., San Diego (1994)
Connes, A.: Noncommutative geometry and reality. J. Math. Phys. 6(11), 6194–6231 (1995)
Enstad, U.: The Balian-Low theorem for locally compact abelian groups and vector bundles. J. Math. Pures Appl. 139, 143–176 (2020)
Enstad, U., Jakobsen, M.S., Luef, F.: Time-frequency analysis on the adeles over the rationals. (Analyse des temps-frequences sur lanneau des adeles des rationnels.). C. R. Math. Acad. Sci. Paris 357(2), 188–199 (2019)
Feichtinger, H.G.: Gewichtsfunktionen auf lokalkompakten Gruppen. Sitzber. d. österr. Akad. Wiss. 188, 451–471 (1979)
Feichtinger, H.G.: On a new Segal algebra. Monatsh. Math. 92, 269–289 (1981)
Feichtinger, H.G.: Modulation spaces on locally compact Abelian groups. Technical report, University of Vienna (1983)
Feichtinger, H.G., Gröchenig, K.: Banach spaces related to integrable group representations and their atomic decompositions. Int. J. Funct. Anal. 86(2), 307–340 (1989)
Frank, M., Larson, D.R.: Frames in Hilbert \({C}^*\)-modules and \({C}^*\)-algebras. J. Oper. Theory 48(2), 273–314 (2002)
Gröchenig, K.: Foundations of time-frequency analysis. Birkhäuser, Boston (2001)
Gröchenig, K.: Weight functions in time-frequency analysis. In. Rodino, L., et al. (eds.) Pseudodifferential operators: partial differential equations and time-frequency analysis, Fields Inst. Commun., vol. 52, pp. 343–366. Am. Math. Soc., Providence, RI (2007)
Gröchenig, K., Leinert, M.: Wiener’s lemma for twisted convolution and Gabor frames. J. Am. Math. Soc. 17, 1–18 (2004)
Jakobsen, M.S.: On a (no longer) new Segal algebra: a review of the Feichtinger algebra. J. Fourier Anal. Appl. 24(6), 1579–1660 (2018)
Jakobsen, M.S., Lemvig, J.: Density and duality theorems for regular Gabor frames. J. Funct. Anal. 270(1), 229–263 (2016)
Jakobsen, M.S., Luef, F.: Duality of Gabor frames and Heisenberg modules. J. Noncommut. Geom. (accepted). arXiv:1806.05616 [math.FA]
Jakobsen, M.S., Luef, F.: Sampling and periodization of generators of Heisenberg modules. Int. J. Math. 30(10), 1950051 (2019)
Jing, W.: Frames in Hilbert \(C^{\ast }\)-modules. ProQuest LLC, Ann Arbor, MI, 2006. Thesis (Ph.D.), University of Central Florida (2006)
Kreisel, M.: Gabor frames for quasicrystals, \({K}\)-theory, and twisted gap labeling. J. Funct. Anal. 270(3), 1001–1030 (2016)
Latremoliere, F., Packer, J.: Noncommutative solenoids and their projective modules. Commut. Noncommut. Harmon. Anal. Appl. 603, 35–53 (2013)
Latremoliere, F., Packer, J.: Explicit construction of equivalence bimodules between noncommutative solenoids. Contemp. Math. Am. Math. Soc. 650, 111–140 (2015)
Luef, F.: Projective modules over non-commutative tori are multi-window Gabor frames for modulation spaces. J. Funct. Anal. 257(6), 1921–1946 (2009)
Luef, F.: The Balian-Low theorem and noncommutative tori. Expos. Math. 36(2), 221–227 (2018)
Lyubarskii, Yu.: Frames in the Bargmann space of entire functions. In: Entire and subharmonic functions, Adv. Sov. Math., vol. 11, pp. 167–180. American Mathematical Society (AMS), Providence, RI (1992)
Mesland, B.: Unbounded bivariant K-theory and correspondences in noncommutative geometry. Journal für die reine und angewandte Mathematik Crelles J. 2014(691), 101–172 (2014)
Osborne, M.S.: On the Schwartz-Bruhat space and the Paley-Wiener theorem for locally compact Abelian groups. J. Funct. Anal. 19, 40–49 (1975)
Poguntke, D.: Gewisse Segalsche Algebren auf lokalkompakten Gruppen. Arch. Math. 33, 454–460 (1980)
Raeburn, I., Williams, D.P.: Morita equivalence and continuous-trace \(C^*\)-algebras. American Mathematical Society, Providence (1998)
Ramakrishnan, D., Valenza, R.J.: Fourier analysis on number fields. Springer, New York (1999)
Ramanathan, J., Steger, T.: Incompleteness of sparse coherent states. Appl. Comput. Harmon. Anal. 2(2), 148–153 (1995)
Rieffel, M.A.: C*-algebras associated with irrational rotations. Pac. J. Math. 93, 415–429 (1981)
Rieffel, M.A.: Projective modules over higher-dimensional noncommutative tori. Can. J. Math. 40(2), 257–338 (1988)
Seip, K.: Density theorems for sampling and interpolation in the Bargmann-Fock space. I. J. Reine Angew. Math. 429, 91–106 (1992)
Várilly, J.: An introduction to noncommutative geometry. EMS Series of Lectures in Mathematics. European Mathematical Society (EMS), Zürich (2006)
Acknowledgements
The authors would like to thank Adam Rennie for his comments on earlier drafts of this manuscript. The authors also wish to thank Eirik Skrettingland for help with the examples, and an anonymous referee for pointing out a crucial flaw in the proof of (4.6) in an earlier draft of this manuscript.
Funding
Open Access funding provided by NTNU Norwegian University of Science and Technology (incl St. Olavs Hospital - Trondheim University Hospital).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Yong Zhang.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Austad, A., Luef, F. Modulation spaces as a smooth structure in noncommutative geometry. Banach J. Math. Anal. 15, 35 (2021). https://doi.org/10.1007/s43037-020-00117-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43037-020-00117-3