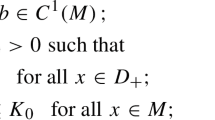Global functional calculus, lower/upper bounds and evolution equations on manifolds with boundary

Abstract

Given a smooth manifold M (with or without boundary), in this paper we establish a global functional calculus, without the standard assumption that the operators are classical pseudo-differential operators, and the Gårding inequality for global pseudo-differential operators associated with boundary value problems. The analysis that we follow is free of local coordinate systems. Applications of the Gårding inequality to the global solvability for a class of evolution problems are also considered.

1 Introduction

Let $M=\overline{\Omega }$ be a smooth manifold (with or without boundary). This work deals with the $L^2$-theory for the pseudo-differential calculus associated with a boundary-value problem $L_{\Omega },$ determined by a pseudo-differential operator L on $\Omega$ with discrete spectrum, having suitable boundary conditions, in the framework of the non-harmonic analysis developed by the last two authors in [21, 32, 33]. To be precise,

• we will formulate a (Dunford–Riesz) global functional calculus for the $(\rho ,\delta )$-Hörmander classes associated with $L_{\Omega }.$

• Once established, the functional calculus will be applied to the proof of a global Gårding inequality on M,  and in establishing the $L^2$-boundedness for the $(\rho ,\delta )$-class of order zero of this calculus. With the exception of the borderline case $\rho =\delta ,$ our $L^2$-boundedness result is an analogue of the Calderón–Vaillancourt theorem [14, 15].

• Finally, we will use the $L^2$-theory developed, applying it to the global solvability for a class of evolution problems on $\Omega ,$ associated with (possibly time-dependent) L-strongly elliptic pseudo-differential operators on M,  (which is the class of elliptic operators in the calculus determined by $L_\Omega$).

The discreteness of the spectrum of $L_{\Omega }$ becomes a natural setting to study eigenfunctions expansions of $L^2$-functions, or equivalently, in terms of its spectral decomposition and its associated Fourier analysis, is inspired by the harmonic analysis techniques for elliptic operators on closed manifolds (or even on manifolds with boundary, taking care of the required conditions such as the transmission property [12]), which serve as a predominant class of operators with discrete spectrum studied in spectral geometry, see [2,3,4,5,6,7,8,9].

Before presenting our contributions, we give a historical overview to the functional calculus on ${\mathbb {R}}^n,$ its localisation by Seeley in [50], and the classical Gårding type inequalities. In view of the standard conditions $1-\rho<\delta <\rho \leqslant 1$ for the $(\rho ,\delta )$-Hörmander class on compact manifolds [25], the main novelty of the present work is the validity of our results (complex functional calculus, $L^2$-boundedness, Gårding inequality, etc.) in the whole range $1\leqslant \delta <\rho \leqslant 1,$ for the $(\rho ,\delta )$-Hörmander classes in [21, 32, 33]. While the restriction $1-\rho<\delta <\rho \leqslant 1$ in Hörmander’s calculus implies that $\rho >1/2,$ we provide a global analysis for any $0\leqslant \delta <\rho \leqslant 1,$ for the pseudo-differential calculus developed in [21, 32, 33].

1.1 Historical overview

In their seminal work [26], Kohn and Nirenberg introduced a calculus of pseudo-differential operators for the classes $S^{m}_{1,0}({\mathbb {R}}^n\times {\mathbb {R}}^n),$¹ which was applied by Friedrichs and Lax in their classical work [22] to study boundary value problems of first order. The appearance of both works, [22, 26], in the same volume of Comm. Pure Appl. Math. shows an immediate profound impact of the Kohn–Nirenberg calculus of pseudo-differential operators in the development of the solvability theory of partial differential operators. Nevertheless, the pseudo-differential technique (which means, to solve problems in mathematics using microlocal methods), appeared before 1959 in the classical works of Mihlin, and in the theory of singular integrals developed by Calderón and Zygmund approximating inverses of elliptic operators, and in 1959 in Calderon’s proof of Cauchy uniqueness for a wide class of principal type operators, using a pseudo-differential factorisation to prove a Carleman estimates [19].

Generalising the Kohn–Nirenberg classes $S^m({\mathbb {R}}^n\times {\mathbb {R}}^n),$ L. Hörmander introduced in 1967, the classes $S^m_{\rho ,\delta }({\mathbb {R}}^n\times {\mathbb {R}}^n),$²$0\leqslant \delta <\rho \leqslant 1,$ motivated by construction of the parametrix P of the heat operator

$$\begin{aligned} \partial _t-\Delta _x, \end{aligned}$$

which has symbol $\sigma _P$ in the class $S^{-1}_{\frac{1}{2},\frac{1}{2}}({\mathbb {R}}^n\times {\mathbb {R}}^n).$ At the same time, in [50] Seeley, developed the asymptotic expansions for the symbols of the complex powers of elliptic operators. Therefore, Seeley tackled one of the fundamental problems of the functional calculus of pseudo-differential operators. This can be regarded as the first model for a functional calculus of pseudo-differential operators. The theory of pseudo-differential operators got a major breakthrough when they proved to be worthwhile in the proof of the seminal work of Atiyah and Singer on the index theory of elliptic operators on compact manifolds [7]. The ideas developed by Seeley for functional calculus [50] have been carried forward by several researchers. We cite [11, 13, 20, 27, 29,30,31, 39, 47, 48, 52, 53] to mention a very few of them. In particular, in [53], the author has investigated only the case of complex powers of differential operators, and in [11] the structure of the inverse of an elliptic operator, which is also considered as the second fundamental problem of the functional calculus, has been examined by using different techniques of Seeley. In [27], the formal theory of complex powers was developed by Kumano-go and Tsutsumi using similar methods to those in [50], and in [31] they developed functional calculus on connected unimodular Lie groups. On the other hand, the functional calculus for pseudo-differential operators on the manifolds with certain geometry (on the boundary or on the manifold itself) was studied in [20, 29, 30, 47, 48]. For example, Coriasco et al. [20] looked over the bounded imaginary powers of differential operators on manifolds with conical singularities, Schrohe [48] analysed the complex powers on noncompact manifolds and manifolds with fibered boundaries, and Loya [29] explored the manifolds with canonical singularity, where the author used the heat kernels techniques [30] in [29].

In 2014, the third author with Wirth [39] developed the global functional calculus for the elliptic pseudo-differential operators on compact Lie groups using the globally defined matrix symbols instead of representations in local coordinates, which is the version of the analysis well adopted to the operator theory on compact Lie groups. The global theory of symbols and their calculus was introduced and investigated in detail by the third author and Turunen in [34, 36]. Hörmander classes on compact Lie groups were investigated by Ruzhansky et al. [37] providing the characterisation of operators in Hörmander’s classes $S^m_{1,0}$ on the compact Lie group viewed as a manifold was given in terms of these matrix symbols, thus providing a link between local and global symbolic calculi. Matrix-valued symbols also proved to be important in the study of the $L^p$-multipliers problems on general compact Lie groups [38]. The functional calculus (complex powers of elliptic operators) has several important applications to index theory, evolution equations, $\zeta$-functions of an operator, Wodzicki-type (non-commutative) residues, and Gårding inequalities [35]. We refer to [13, 52] for several aspects of the functional calculus and extensive reviews of the above topics and to [18] for the functional calculus of subelliptic pseudo-differential operators on compact Lie groups.

1.2 Main results

In this paper, we work in the setting of the Fourier analysis arising from the spectral decomposition of a model operator $L_{\Omega }$ on a smooth manifold $\overline{\Omega }$ (with or without boundary) [32, 33].

1.2.1 The functional calculus for the non-harmonic analysis and its applications

To address the problem of the functional calculus from the view of Hörmander symbolic calculus developed by the last two authors [32] in this setting, we first introduce in Sect. 3 the concept of parameter dependent L-ellipticity with respect to a sector in the complex plane in the setting of nonharmonic analysis and examine its properties. In general, for the pseudo-differential operators on manifolds one puts some restrictions on the Hörmander symbol classes $S^m_{\rho , \delta }$ [53, Section 4]; usually one requires $1-\rho<\delta <\rho ,$ which in turn gives $\rho >\frac{1}{2}.$ It is worth noting that, in this paper, we allow $0\leqslant \delta <\rho \leqslant 1.$ This freedom on the condition on $\rho$ and $\delta$ enables us to handle some specific classes of operator, for example the resolvent of an L-elliptic symbol, or its complex powers which cannot be handled by the standard theory due the restriction $\rho >\frac{1}{2}.$ The following is our first, and main result. Here, we establish the complex-functional calculus for the Hörmander classes developed in [21, 32, 33]. All the preliminaries notions, assumptions, and notations to be used in our main results are presented in Sect. 2.

Theorem 1.1

Let $m>0,$ and let $0\leqslant \delta <\rho \leqslant 1.$ Let $a\in S^m_{\rho ,\delta }(M\times {\mathcal {I}})$ be a parameter L-elliptic symbol with respect to $\Lambda .$ Let us assume that F satisfies the estimate $|F(\lambda )|\leqslant C|\lambda |^s$ uniformly in $\lambda ,$ for some $s<0.$ Then the symbol of F(A),  $\sigma _{F(A)}\in S^{ms}_{\rho ,\delta }(M\times {\mathcal {I}})$ admits an asymptotic expansion of the form

$$\begin{aligned} \sigma _{F(A)}(x,\xi )\sim \sum _{N=0}^\infty \sigma _{{B}_{N}}(x,\xi ),\quad (x,\xi )\in M\times {\mathcal {I}}, \end{aligned}$$

where $\sigma _{{B}_{N}}(x,\xi )\in {S}^{ms-(\rho -\delta )N}_{\rho ,\delta }(M\times {\mathcal {I}})$ and

$$\begin{aligned} \sigma _{{B}_{0}}(x,\xi )=-\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }F(z)(a(x,\xi )-z)^{-1}{\textrm{d}}z\in {S}^{ms}_{\rho ,\delta }(M\times {\mathcal {I}}). \end{aligned}$$

Moreover, 

$$\begin{aligned} \sigma _{F(A)}(x,\xi )\equiv -\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }F(z)a^{-\#}(x,\xi ,\lambda ){\textrm{d}}z \text { mod } {S}^{-\infty }(M\times {\mathcal {I}}), \end{aligned}$$

where $a^{-\#}(x,\xi ,\lambda )$ is the symbol of the parametrix to $A-\lambda I,$ in Corollary 3.3.

After developing the global functional calculus for pseudo-differential operators in the nonharmonic analysis setting on manifolds, we present applications of functional calculus to the Gårding inequality, $L^2$-boundedness of pseudo-differential operators and global solvability of evolution problems of hyperbolic/parabolic type on compact manifolds. We will now discuss each application separately in detail.

First, we will establish a fundamental estimate first proved by Gårding [23] for differential operators. This inequality proved to be a powerful tool to study nonlinear equations. This was further improved and generalised by several researchers including Agmon [1], Smith [44] and Schechter [45, 46]. The proofs given in aforementioned papers, e.g. in [1] make use of the usual reduction of the problem to the constant coefficient case in a special domain and then apply Fourier transform techniques. The Gårding inequality for pseudo-differential operators on ${\mathbb {R}}^n$ is also now a well-known and important inequality with $0\leqslant \delta <\rho \leqslant 1$ and on manifolds with the restriction $1-\rho<\delta <\rho$ (see [54, Chapter 2]). The Gårding inequality for pseudo-differential operators on the Euclidean space or manifolds is proved using pseudo-differential calculus techniques [54]. For Lie groups, this was proved for the operators in the Hörmander class (1, 0) type using the results developed by Langlands [28] for the semigroups of Lie groups. The third author and Wirth [39] have obtained it for operators on compact Lie groups with matrix-valued symbols under the condition $0\leqslant \delta <\rho \leqslant 1,$ using the global functional calculus developed by them.

In this paper, we carry forward the ideas of [39] to establish the Gårding inequality for operators with the global Hörmander symbols [34] under the same condition $0\leqslant \delta <\rho \leqslant 1,$ using the global functional calculus developed for pseudo-differential operator in Sect. 4.

Theorem 1.2

For $0\leqslant \delta <\rho \leqslant 1,$ let $a(x,D):C^\infty _L(M)\rightarrow {\mathcal {D}}'_L(M)$ be an operator with symbol $a\in {S}^{m}_{\rho ,\delta }( M\times {\mathcal {I}}),$ $m\in {\mathbb {R}}.$ Let us assume that

$$\begin{aligned} A(x,\xi ):=\frac{1}{2}(a(x,\xi )+\overline{a(x,\xi )}),\,(x,\xi )\in M\times {\mathcal {I}},\quad a\in S^m_{\rho ,\delta }(M\times {\mathcal {I}}) \end{aligned}$$

satisfies

$$\begin{aligned} \vert \langle \xi \rangle ^mA(x,\xi )^{-1} \vert \leqslant C_{0}. \end{aligned}$$

Then,  there exist $C_{1},C_{2}>0,$ such that the lower bound

$$\begin{aligned} \text {Re}(a(x,D)u,u) \geqslant C_1\Vert u\Vert _{{\mathcal {H}}^{\frac{m}{2}}(M)}-C_2\Vert u\Vert _{L^2(M)}^2 \end{aligned}$$

holds true for every $u\in C^\infty _L(M).$

The second application of the functional calculus is to prove the $L^2$-boundedness of global operators associated with the symbol class $S^0_{\rho , \delta }(\overline{\Omega } \times {\mathcal {I}})$ with $0 \leqslant \delta <\rho \leqslant 1,$ which is presented in Sect. 5. With the exception of the borderline case $\rho =\delta ,$ the following result is, indeed, an analogue of the well-known Calderón–Vaillancourt theorem [14, 15].

Theorem 1.3

Let $a(x,D):C^\infty _L(M)\rightarrow {\mathcal {D}}'_L(M)$ be a pseudo-differential operator with symbol $a\in {S}^{0}_{\rho ,\delta }( M\times {\mathcal {I}})$ with $0 \leqslant \delta <\rho \leqslant 1.$ Then, a(x, D) extends to a bounded operator on $L^2({M}).$

In Sect. 6, we present an application of the Gårding inequality and, consequently, an application of the functional calculus to study the existence and uniqueness of the solution of the following Cauchy problem:

$$\begin{aligned} (\text {IVP}): {\left\{ \begin{array}{ll} \frac{\partial v}{\partial t}=K(t,x,D)v+f,&{}\\ v(0)=u_0, &{} \end{array}\right. } \end{aligned}$$

where the initial data $u_0\in L^2(M),$ $K(t):=K(t,x,D)$ with a symbol in $S^m_{\rho ,\delta }(M\times {\mathcal {I}}),$ $f\in L^2([0,T]\times M) \simeq L^2([0,T],L^2(M)),$ $m>0,$ and a suitable positivity condition is imposed on K.

1.2.2 The philosophy of the non-harmonic analysis and its state of the art with respect to the existing quantisation theories

We end the introduction with this short section explaining the philosophy of the non-harmonic analysis in [21, 32, 33], and also the motivations for considering global symbols in the setting of smooth manifolds. As both of the reviewers of this work have remarked, there are deep difficulties when considering a pseudo-differential calculus on manifolds with boundary. Indeed, an almost sharp condition is required (the Hörmander transmission property, see Boutet de Monvel [12]). However, there are specific situations where differential (or pseudo-differential) operators on compact or non-compact manifolds have discrete spectrum (e.g. any elliptic operator on a closed manifold, or the case of the harmonic oscillator on ${\mathbb {R}}^n$) and the Fourier analysis associated to them can provide a global notion of symbol. There are several Dirichlet type problems on domains of ${\mathbb {R}}^n$ with a discrete set of eigenvalues associated with differential operators (for example, the Laplacian), and in that case, it is not necessary to put on perspective the transmission property.

Before presenting the preliminaries and the proofs of our main results, we clarify our motivation to work with such a global notion of symbol and the origin of this notion. Indeed, the main tool of our work is the following quantisation formula (see Theorem 2.21):

$$\begin{aligned} Af(x)=\sum _{\xi \in {\mathcal I}} u_{\xi }(x)\sigma _{A}(x, \xi ) \widehat{f}(\xi ), \end{aligned}$$

(1.1)

and due to the extensive list of preliminaries for its understanding, we postpone its analysis in Sect. 2.

Fundamentally, as in the case of the torus, pseudo-differential operators are just transformations of the Fourier inversion formula when the discrete spectrum of an operator is available. For instance, on the torus ${\mathbb {T}}^n,$ the Fourier inversion formula is given by

$$\begin{aligned} f(x)=\sum _{\xi \in {\mathbb {Z}}^n}e_{\xi }(x)\widehat{f}(\xi ),\quad f\in L^1({\mathbb {T}}^n), \end{aligned}$$

and any pseudo-differential operator in the sense of Hörmander [25] has the form

$$\begin{aligned} Af(x)=\sum _{\xi \in {\mathbb {Z}}^n}e_{\xi }(x)\sigma _A(x,\xi )\widehat{f}(\xi ),\quad f\in L^1({\mathbb {T}}^n). \end{aligned}$$

(1.2)

Here, the Fourier coefficients $\widehat{f}(\xi )=\int _{{\mathbb {T}}^n}e_{-\xi }(x)f(x){\textrm{d}}x,\,\, \xi \in {\mathbb {Z}}^n$ are defined using the eigenfunctions $e_\xi (x)={\textrm{e}}^{i2\pi x\cdot \xi }$ of the Laplacian $\Delta _{{\mathbb {T}}^n}$ on ${\mathbb {T}}^n.$ Compare the similitude of (1.2) with (1.1), where the sequence of functions $u_{\xi }$ determines the eigenfunction system of $L_{\Omega }.$

In terms of the standard differences operators,

$$\begin{aligned} \Delta _\xi ^{\alpha }=\Delta _{\xi _1}^{\alpha _1}\cdots \Delta _{\xi _n}^{\alpha _n},\text { with } \Delta _{\xi _j} \mu =\mu (\cdot +e_j)-\mu ,\,\Delta ^{k}_{\xi _j}:=\Delta _{\xi _j}^{k-1}\Delta _{\xi _j}, \end{aligned}$$

it was proved in [34], with previous contributions by Vainikko and McLean, that a pseudo-differential operator A is in the $(\rho ,\delta )$-Hörmander class of order $m\in {\mathbb {R}},$ if the function $\sigma _A:{\mathbb {T}}^{n}\times {\mathbb {Z}}^n\rightarrow {\mathbb {C}}$ in (1.2) satisfies the following symbol inequality:

$$\begin{aligned} |\partial _{x}^\beta \Delta _\xi ^{\alpha }\sigma _A(x,\xi )|\leqslant C_{\alpha ,\beta }(1+|\xi |)^{m-\rho |\alpha |+\delta |\beta |}. \end{aligned}$$

Note that the aforementioned approach replaces the symbol $\sigma _{\text {Hor},A},$ which is a function on $T^{*}{\mathbb {T}}^n\cong {\mathbb {T}}^n\times {\mathbb {R}}^n,$ of A,  defined by local coordinates system and the Fourier analysis under changes of coordinates by a function $\sigma _A$ on ${\mathbb {T}}^{n}\times {\mathbb {Z}}^n,$ which, among other things, is a much simpler object. It is easy to show that

$$\begin{aligned} \forall (x,\xi )\in {\mathbb {T}}^n\times {\mathbb {Z}}^n,\quad \sigma _A(x,\xi )=e_{-\xi }(x)(Ae_{\xi })(x). \end{aligned}$$

The torus is a good prototype to extend the global quantisation to any compact Lie group G. In this case, the Fourier analysis is presented using unitary representation of the group G,  and the equivalence classes of such a unitary and irreducible representations are usually denoted by $\widehat{G},$ see [34] for more details. The group Fourier inversion formula on G is given by

$$\begin{aligned} f(x)=\sum _{[e_\xi ]\in \widehat{G}}\text {dim}(e_\xi )\text {Tr}[e_{\xi }(x)\widehat{f}(\xi )],\quad f\in L^1(G), \end{aligned}$$

and any pseudo-differential operator in the sense of Hörmander [25] has the form

$$\begin{aligned} Af(x)=\sum _{[e_\xi ]\in \widehat{G}}\text {dim}(e_\xi ) \text {Tr}[e_{\xi }(x)\sigma _A(x,e_\xi )\widehat{f}(e_\xi )],\quad f\in C^\infty (G). \end{aligned}$$

(1.3)

It is worth noting in (1.3) that the matrix-valued functions $e_{\xi }:G\rightarrow {\mathbb {C}}^{d_\xi \times d_\xi }$ have entries $e_{\xi }^{ij},$ which are eigenfunctions of the Laplacian $\Delta _{G}$ on G. We have used $\text {dim}(e_\xi )=d_\xi$ for the dimension of the representation space of $e_\xi ,$ that is, ${\mathbb {C}}^{d_\xi }.$ Therefore, by writing explicitly the trace $\text {Tr}[\cdot ]$ in (1.3), we obtain

$$\begin{aligned} Af(x)=\sum _{[e_\xi ]\in \widehat{G}}\sum _{1\leqslant i,j,k\leqslant \dim (e_\xi )}\text {dim}(e_\xi )e_{\xi }^{ij}(x)\sigma _A(x,e_\xi )^{jk} \widehat{f}(\xi )^{ki},\quad f\in C^\infty (G) \end{aligned}$$

(1.4)

in terms of the matrix entries of the Fourier coefficients $\widehat{f}(\xi )^{ki}=\int _{G}f(x)e_{\xi }^{ij}{\textrm{d}}x.$ Again, compare the similitude of (1.1) with (1.4) having in mind that the functions $e_{\xi }^{ij}$ are eigenfunctions of the Laplacian $\Delta _{G}$ and its corresponding eigenvalue $\lambda _{e_\xi }$ has geometric multiplicity equal to $\text {dim}(e_\xi )^2.$ Now, it is a relevant fact in the theory of pseudo-differential operators that the Hörmander classes on G can be again (as in the case of the torus, that is, $G={\mathbb {T}}^n,$ $\widehat{G}\cong {\mathbb {Z}}^n$) characterised in terms of a family of differences operators $\Delta _{e_\xi }^{\alpha }$ (that generalises the difference operators on ${\mathbb {Z}}^n,$ re-obtaining this class in the case of the torus) on $\widehat{G}.$ By utilising these difference operators on $\widehat{G},$ it was proved in [37] that a pseudo-differential operator A is in the $(\rho ,\delta )$-Hörmander class of order $m\in {\mathbb {R}}$ on G,  if its symbol $\sigma _A$ in (1.3) satisfies inequalities of the type

$$\begin{aligned} \Vert \partial _{x}^\beta \Delta _\xi ^{\alpha }\sigma _A(x,e_\xi ) \Vert _{\text {End}({\mathbb {C}}^{d_\xi })}\leqslant C_{\alpha ,\beta }(1+\lambda _{|\xi |})^{\frac{m-\rho |\alpha |+\delta |\beta |}{2}},\quad (x,[e_\xi ])\in G\times \widehat{G}. \end{aligned}$$

Again, the symbol identity

$$\begin{aligned} \forall (x,\xi )\in G\times \widehat{G},\quad \sigma _A(x,e_\xi )=e_{\xi }(x)^{-1}(Ae_{\xi })(x) \end{aligned}$$

(1.5)

remains valid.

The pseudo-differential calculus based on the quantisation formula (1.1) in [32, 33] and the further developments of these works make use of the symbol classes $S^m_{\rho ,\delta }(M\times {\mathcal {I}})$ (see Definition 2.20), defined by the functions a on the global phase space $M\times {\mathcal {I}}$ such that

$$\begin{aligned} \left| \Delta _{(x)}^\alpha D^{(\beta )}_{x} a(x,\xi ) \right| \leqslant C_{\alpha ,\beta } \ \langle \xi \rangle ^{m-\rho |\alpha |+\delta |\beta |}. \end{aligned}$$

By following the spirit of the symbol formulas in (1.5), we have assumed that the system of eigenfunctions $u_\xi$ in (1.1) satisfies the WZ-condition stated in Definition 2.1. The theory in [32, 33] is still a source of many open problems, among them, to remove the WZ-condition with partial results in [33] and its relation with the Boutet de Monvel calculus in the case of manifolds with boundary, with partial results in [16, Pages 135-139]. Examples satisfying the WZ-conditions are presented in Sect. 2. In particular, Example 2.2 for $h=(1,\ldots , 1)$ shows that the classes $S^m_{\rho ,\delta }(M\times {\mathcal {I}})$ recover the standard Hörmander classes on the torus.

Fig. 1

The construction of the pseudo-differential calculus for boundary value-problems according to the procedure e.g. by L. Boutet de Mounvel. In this case the Hörmander transmission property is required

In Fig. 1, we illustrate the different constructions of the pseudo-differential calculus on smooth manifolds. For manifolds without boundary (when $\partial M=\emptyset$), the construction by Hörmander of the principal symbol is done by local coordinate systems. In the case of manifolds with boundary $(\partial M\ne \emptyset ),$ the construction by Boutet de Monvel [12] was inspired by the abstract consideration of two copies of the manifold $M=M^{+}$ and $M\cong M^{-},$ with a suitable orientation of their boundaries and glued them by using the identification $\partial M^+\sim \partial M^-$ to get a new closed manifold $\dot{M}=M^{+}\cup M^{-}.$ Then, he used restriction and extension operators to recover an algebra of pseudo-differential operators on the original manifold M from the ones defined in the sense of Hörmander on $\dot{M}.$ In [32, 33], it was proposed to follow the Fourier analysis approach instead of the geometric construction as in the calculus by Boutet de Monvel, and then to consider transformations of the Fourier inversion formula as in the case of the torus ${\mathbb {T}}^n$ or $\text {SU}(2)\cong \mathbb {S}^3$ or even any arbitrary compact Lie group, where these techniques have shown to be useful and effective (see [34]). Then, the analysis of the quantisation formula (1.1) is the main goal of the theory developed in [21, 32, 33] and also in this work.

In contrast to the case of the torus as well as compact Lie groups, it is still an open problem to construct a model operator $L_\Omega$ in such a way that its Hörmander classes $S^m_{\rho ,\delta }(M\times {\mathcal {I}})$ could re-obtain a known pseudo-differential calculus, as the one by Boutet de Monvel. Indeed, the absence of symmetries in this case makes the understanding of the classes $S^m_{\rho ,\delta }(M\times {\mathcal {I}})$ much more difficult than that in the case of the torus or compact Lie groups and, consequently, it leaves several open research questions. Just to mention a few, one of the more recent developments on the subject was done in [24], where the author links the Fourier analysis on fundamental domains of ${\mathbb {R}}^{d},$ and the construction of a WZ-system with the Fuglede conjecture, which was outside of the perspective of the authors of this manuscript.

2 Preliminaries: global pseudo-differential calculus associated with boundary value problems

Let $M=\overline{\Omega }$ be a $C^\infty$-manifold with (possibly empty) boundary $\partial \Omega .$ Let us formulate some basics of the non-harmonic analysis and the pseudo-differential calculus developed by the third and the fourth author in [32] (see also [17, 21]):

• Consider a pseudo-differential operator $L:=L_{\Omega }$ of order m on a smooth manifold ${\Omega }$ (in the sense of Hörmander [25]) equipped with some boundary conditions (BC) defining a space of functions endowed with a complex structure of vector space. We assume that L equipped with these boundary conditions (BC) admits a closed extension on $L^2(\Omega ).$ We will also assume the condition (BC+), which states that the boundary conditions define a closed topological space.³

• The pseudo-differential operator ${L}_\Omega$ is assumed to have a discrete spectrum $\{\lambda _{\xi }\in {{\mathbb {C}}}: \, \xi \in {\mathcal I}\}$ on $L^{2}(\Omega ),$ and we order the eigenvalues with the occurring multiplicities in the ascending order: $|\lambda _{j}|\leqslant |\lambda _{k}| \quad \text { for } |j|\leqslant |k|.$⁴

• The eigenfunctions $u_\xi$ of L (associated with $\lambda _\xi$) and $v_\xi$ of ${L}^*$ are considered to be $L^2$-normalised. Also, they satisfy the condition of biorthogonality, i.e.

  $$\begin{aligned} (u_{\xi },v_{\eta })_{L^2}=\delta _{\xi ,\eta }, \end{aligned}$$

  where $\delta _{\xi ,\eta }$ is the Kronecker-Delta and $(\cdot , \cdot )_{L^{2}}$ is the usual $L^{2}$-inner product given by $(f, g)_{L^{2}}:=\int _{\Omega }f(x)\overline{g(x)}{\textrm{d}}x, f, g\in L^{2}(\Omega ).$

From [10], it follows that the system $\{u_{\xi }: \,\,\, \xi \in {\mathcal I}\}$ is a basis in $L^{2}(\Omega )$ if and only if the system $\{v_{\xi }: \,\,\, \xi \in {\mathcal I}\}$ is a basis in $L^{2}(\Omega ).$ So, from now, we assume the following:

• The system $\{u_{\xi }: \xi \in {\mathcal I}\}$ is a basis in $L^{2}(\Omega ),$ i.e. for every $f\in L^{2}(\Omega )$ there exists a unique series $\sum _{\xi \in {\mathcal I}} a_\xi u_\xi (x)$ that converges to f in $L^{2}(\Omega ).$

Let us define the following notation (L-Japanese bracket)

$$\begin{aligned} \langle \xi \rangle :=(1+|\lambda _{\xi }|^2)^{\frac{1}{2m}}, \end{aligned}$$

(2.1)

which will be used later in measuring the growth/decay of Fourier coefficients of the distributions in our context. Define the operator ${L}^{\circ }$ by setting its values on the basis $u_{\xi }$ by

$$\begin{aligned} {L}^{\circ } u_{\xi }:=\overline{\lambda _{\xi }} u_{\xi },\quad \text {for all } \xi \in {\mathcal I}; \end{aligned}$$

(2.2)

we can informally think of $\langle \xi \rangle ,$ $\xi \in {\mathcal {I}},$ as the eigenvalues of the positive (first order) pseudo-differential operator $(\textrm{I}+{L^\circ \, L})^{\frac{1}{2\,m}}.$

The following technical definition will be useful to single out the case when the eigenfunctions of both L and ${L}^{*}$ do not have zeros (WZ stands for ‘without zeros’):

Definition 2.1

The system $\{u_{\xi }: \,\,\, \xi \in {\mathcal I}\}$ is called a $\textrm{WZ}$-system if the functions $u_{\xi }(x), \, v_{\xi }(x)$ do not have zeros on the domain $\overline{\Omega }$ for all $\xi \in {\mathcal I},$ and if there exist $C>0$ and $N\geqslant 0$ such that

$$\begin{aligned} \inf _{x\in \Omega }|u_{\xi }(x)|\geqslant C\langle \xi \rangle ^{-N},\quad \inf _{x\in \Omega }|v_{\xi }(x)|\geqslant C\langle \xi \rangle ^{-N}, \end{aligned}$$

as $\langle \xi \rangle \rightarrow \infty .$ Here, WZ stands for ‘without zeros’.

One can find examples and a discussion of WZ-systems in [32, Section 2]. There are plenty of problems where this conditions holds, and a few of them are described below.

Example 2.2

For this example, we set $M=\overline{\Omega }$ with $\Omega :=(0,1)^n$ and $h>0 \text { i.e. } h=(h_1,\dots ,h_n)\in {\mathbb {R}}^{n}: h_j>0 \text{ for } \text{ every } j=1,\dots ,n.$ The operator $L_\Omega =:\textrm{O}_h^{(n)}$ on $\Omega$ is defined by the differential operator

$$\begin{aligned} \textrm{O}_h^{(n)}:=\sum _{j=1}^{n}\frac{\partial ^2}{\partial x_j^2}, \end{aligned}$$

together with the boundary conditions (BC):

$$\begin{aligned} h_{j} f(x)|_{x_{j}=0}=f(x)|_{x_{j}=1},\quad h_{j} \frac{\partial f}{\partial x_j}(x)|_{x_{j}=0}=\frac{\partial f}{\partial x_j}(x)|_{x_{j}=1}, \quad j=1,\ldots ,n, \end{aligned}$$

(2.3)

and the domain

$$\begin{aligned} \textrm{Dom}({\textrm{O}_h^{(n)}})=\{f\in L^{2}(\Omega ): \Delta f\in L^{2}(\Omega ): f \text { satisfies } (2,3) \}. \end{aligned}$$

To describe the corresponding biorthogonal system, we first note that since $b^0=1$ for all $b>0,$ we can define $0^0=1.$ In particular, we write

$$\begin{aligned} h^x=h_1^{x_1}\cdots h_n^{x_n}=\prod _{j=1}^{n}h_{j}^{x_{j}} \end{aligned}$$

for $x\in [0,1]^n.$ Then, with ${\mathcal I}={\mathbb {Z}}^{n},$ the system of eigenfunctions of the operator $L_h$ is

$$\begin{aligned} \{u_{\xi }(x)=h^{x}{\textrm{e}}^{2\pi i x\cdot \xi }, \xi \in {\mathbb {Z}}^{n}\}, \end{aligned}$$

and the conjugate system is

$$\begin{aligned} \{v_{\xi }(x)=h^{-x}{\textrm{e}}^{ 2\pi i x\cdot \xi }, \xi \in {\mathbb {Z}}^{n}\}, \end{aligned}$$

where $x\cdot \xi =x_{1}\xi _{1}+ \cdots + x_{n}\xi _{n}.$ Note that $u_{\xi }(x)=\otimes _{j=1}^{n}u_{\xi _{j}}(x_{j}),$ where $u_{\xi _{j}}(x_{j})=h_{j}^{x_{j}}{\textrm{e}}^{{ 2\pi i x_{j}\xi _{j} }}.$

It is easy to see that the system of eigenfunctions of the operator $L_\Omega =\textrm{O}_{h}^{(n)}$ is a Riesz basis in $L^{2}(\Omega ).$ These families also form WZ-systems

Example 2.3

We briefly give another example of a non-local boundary condition, see [32, Example 2.4] for details. We now consider $M=[0,1]$ and the operator $L_\Omega =-i\frac{{\textrm{d}}}{{\textrm{d}}x}$ on $\Omega =(0,1)$ with the domain

$$\begin{aligned} D({L_\Omega })=\left\{ f\in W_2^1[0,1]: af(0)+bf(1)+\int _{0}^1 f(x) q(x) {\textrm{d}}x=0\right\} , \end{aligned}$$

where $a\not =0,$ $b\not =0,$ and $q\in C^1[0,1].$ We assume that $a+b+\int _0^1 q(x) {\textrm{d}}x=1,$ so that the inverse ${L}_\Omega ^{-1}$ exists and is bounded. The operator $L_\Omega$ has a discrete spectrum and its eigenvalues can be enumerated so that

$$\begin{aligned} \lambda _{j}=-i\ln \left( -\frac{a}{b}\right) +2j\pi +\alpha _j, \quad j\in {\mathbb {Z}}, \end{aligned}$$

and for any $\epsilon >0$ we have $\sum _{j\in {\mathbb {Z}}} |\alpha _j|^{1+\epsilon }<\infty .$ If $m_j$ denotes the multiplicity of the eigenvalue $\lambda _j,$ then $m_j=1$ for sufficiently large |j|. The system of extended eigenfunctions

$$\begin{aligned} u_{jk}(x)=\frac{(ix)^k}{k!} {\textrm{e}}^{ i \lambda _j x }:\quad 0\leqslant k\leqslant m_j-1, j\in {\mathbb {Z}}, \end{aligned}$$

(2.4)

of the operator $L_\Omega$ is a Riesz basis in $L^{2}(0,1),$ and its biorthogonal system is given by

$$\begin{aligned} v_{jk}(x)=\lim _{\lambda \rightarrow \lambda _j} \frac{1}{k!} \frac{{\textrm{d}}^k}{{\textrm{d}}\lambda ^k} \left( \frac{(\lambda -\lambda _j)^{m_j}}{\Delta (\lambda )} (ib{\textrm{e}}^{i\lambda (1-x)}+i\int _x^1 {\textrm{e}}^{i\lambda (t-x)}q(t) {\textrm{d}}t) \right) , \end{aligned}$$

$0\leqslant k\leqslant m_j-1, j\in {\mathbb {Z}},$ where $\Delta (\lambda )=a+b {\textrm{e}}^{i\lambda }+\int _0^1 {\textrm{e}}^{i\lambda x} q(x) {\textrm{d}}x.$ It can be shown that eigenfunctions ${\textrm{e}}^{i\lambda _j x}$ satisfy

$$\begin{aligned} \sum _{j\in {\mathbb {Z}}} \Vert {\textrm{e}}^{i\lambda _j x}-{\textrm{e}}^{i 2\pi j x}\Vert ^2_{L^2(0,1)}<\infty . \end{aligned}$$

In particular, this implies modulo finitely many elements, and the system (2.4) is a WZ-system.

In the sequel, unless stated otherwise, whenever we use inverses $u_{\xi }^{-1}$ of the functions $u_{\xi },$ we will suppose that the system $\{u_{\xi }: \, \xi \in {\mathcal I}\}$ is a $\textrm{WZ}$-system. However, we will also try to mention explicitly when we make such an additional assumption.

2.1 Global distributions generated by the boundary value problem

Now, we will present the spaces of distributions generated by the boundary value problem ${L}_\Omega$ and by its adjoint ${L}_\Omega ^*$ and the related global Fourier analysis. We first define the space $C_{{L}}^{\infty }(\overline{\Omega })$ of test functions.

Definition 2.4

The space $C_{{L}}^{\infty }(\overline{\Omega }):=\textrm{Dom}({L}_\Omega ^{\infty })$ is called the space of test functions for ${L}_\Omega .$ Here, we define

$$\begin{aligned} \textrm{Dom}({L}_\Omega ^{\infty }):=\bigcap _{k=1}^{\infty }\textrm{Dom}({ L}_\Omega ^{k}), \end{aligned}$$

where $\textrm{Dom}({L}_\Omega ^{k}),$ or just $\textrm{Dom}({L}^{k})$ for simplicity, is the domain of the operator ${L}^{k},$ in turn defined as

$$\begin{aligned} \textrm{Dom}({L}^{k}):=\{f\in L^{2}(\Omega ): \,\,\, { L}^{j}f\in \textrm{Dom}({L}), \,\,\, j=0, \,1, \, 2, \ldots , k-1\}. \end{aligned}$$

The operators ${L}^{k},$ $k\in {{\mathbb {N}}},$ are endowed with the same boundary conditions (BC). The Fréchet topology of $C_{{L}}^{\infty }(\overline{\Omega })$ is given by the family of norms:

$$\begin{aligned} \Vert \varphi \Vert _{C^{k}_{{L}}}:=\max _{j\leqslant k} \Vert {L}^{j}\varphi \Vert _{L^2(\Omega )}, \quad k\in {{\mathbb {N}}}_0,\, \varphi \in C_{{L}}^{\infty }(\overline{\Omega }). \end{aligned}$$

(2.5)

Analogously, we introduce the space $C_{{ L^{*}}}^{\infty }(\overline{\Omega })$ corresponding to the adjoint operator ${L}_\Omega ^*$ by

$$\begin{aligned} C_{{L^{*}}}^{\infty }(\overline{\Omega }):= \textrm{Dom}(({L^{*}})^{\infty })=\bigcap _{k=1}^{\infty }\textrm{Dom}(({L^{*}})^{k}), \end{aligned}$$

where $\textrm{Dom}(({L^{*}})^{k})$ is the domain of the operator $({L^{*}})^{k},$

$$\begin{aligned} \textrm{Dom}(({L^{*}})^{k}):=\{f\in L^{2}(\Omega ): \,\,\, ({ L^{*}})^{j}f\in \textrm{Dom}({L^{*}}), \,\,\, j=0, \ldots , k-1\}, \end{aligned}$$

which satisfy the adjoint boundary conditions corresponding to the operator ${L}_\Omega ^*.$ The Fréchet topology of $C_{{L}^*}^{\infty }(\overline{\Omega })$ is given by the family of norms:

$$\begin{aligned} \Vert \psi \Vert _{C^{k}_{{L}^*}}:=\max _{j\leqslant k} \Vert ({L}^*)^{j}\psi \Vert _{L^2(\Omega )}, \quad k\in {{\mathbb {N}}}_0, \, \psi \in C_{{L}^*}^{\infty }(\overline{\Omega }). \end{aligned}$$

(2.6)

Remark 2.5

If ${L}_\Omega$ is self-adjoint, i.e. if ${L}_\Omega ^*={L}_\Omega$ with the equality of domains, then $C_{{L^{*}}}^{\infty }(\overline{\Omega })=C_{{L}}^{\infty }(\overline{\Omega }).$ On the other hand, since we have $u_\xi \in C^\infty _{{L}}(\overline{\Omega })$ and $v_\xi \in C^\infty _{{L}^*}(\overline{\Omega })$ for all $\xi \in {\mathcal I},$ we observe that the biorthogonality condition of the systems $\{u_\xi \}_{\xi \in {\mathcal {I}}},$ and $\{v_\xi \}_{\xi \in {\mathcal {I}}}$ implies that the spaces $C^\infty _{{L}}(\overline{\Omega })$ and $C^\infty _{{L}^*}(\overline{\Omega })$ are dense in $L^2(\Omega ).$

In general, for functions $f\in C_{{L}}^{\infty }(\overline{\Omega })$ and $g\in C_{{L}^*}^{\infty }(\overline{\Omega }),$ the $L^2$-duality makes sense in view of the formula

$$\begin{aligned} ({L}f, g)_{L^2(\Omega )}=(f,{L}^*g)_{L^2(\Omega )}. \end{aligned}$$

(2.7)

Therefore, in view of the formula (2.7), it makes sense to define the distributions ${\mathcal {D}}'_{{L}}(\Omega )$ as the space which is dual to $C_{{L}^*}^{\infty }(\overline{\Omega }).$ Note that the respective boundary conditions of ${L}_\Omega$ and ${L}_\Omega ^*$ are satisfied by the choice of f and g in the corresponding domains.

Definition 2.6

The space

$$\begin{aligned} {\mathcal {D}}'_{{ L}}(\Omega ):=\mathcal L(C_{{L}^*}^{\infty }(\overline{\Omega }), {{\mathbb {C}}}) \end{aligned}$$

of linear continuous functionals on $C_{{L}^*}^{\infty }(\overline{\Omega })$ is called the space of L-distributions.⁵ For $w\in {\mathcal {D}}'_{{L}}(\Omega )$ and $\varphi \in C_{{L}^*}^{\infty }(\overline{\Omega }),$ we shall write

$$\begin{aligned} w(\varphi )=\langle w, \varphi \rangle . \end{aligned}$$

Observe that, for any $\psi \in C_{{L}}^{\infty }(\overline{\Omega }),$

$$\begin{aligned} C_{{L}^*}^{\infty }(\overline{\Omega })\ni \varphi \mapsto \int _{\Omega }{\psi (x)} \, \varphi (x)\, {\textrm{d}}x \end{aligned}$$

is an L-distribution, which gives an embedding $\psi \in C_{{L}}^{\infty }(\overline{\Omega })\hookrightarrow {\mathcal {D}}'_{{ L}}(\Omega ).$ We note that the distributional notation formula (2.7) becomes

$$\begin{aligned} \langle {L}\psi , \varphi \rangle =\langle \psi ,\overline{{L}^* \overline{\varphi }}\rangle . \end{aligned}$$

(2.8)

With the topology on $C_{{L}}^{\infty }(\overline{\Omega })$ defined by (2.5), the space

$$\begin{aligned} {\mathcal {D}}'_{{L^{*}}}(\Omega ):=\mathcal L(C_{{L}}^{\infty }(\overline{\Omega }), {{\mathbb {C}}}) \end{aligned}$$

of linear continuous functionals on $C_{{L}}^{\infty }(\overline{\Omega })$ is called the space of ${L^{*}}$-distributions.

Proposition 2.7

A linear functional w on $C_{{L}^*}^{\infty }(\overline{\Omega })$ belongs to ${\mathcal {D}}'_{{ L}}(\Omega )$ if and only if there exists a constant $c>0$ and a number $k\in {{\mathbb {N}}}_0$ with the property

$$\begin{aligned} |w(\varphi )|\leqslant c \Vert \varphi \Vert _{C^{k}_{{L}^*}} \quad \text {for all } \, \varphi \in C_{{ L}^*}^{\infty }(\overline{\Omega }). \end{aligned}$$

The space ${\mathcal {D}}'_{{L}}(\Omega )$⁶ has many similarities with the usual spaces of distributions. For example, suppose that for a linear continuous operator $D:C_{{L}}^{\infty }(\overline{\Omega })\rightarrow C_{{L}}^{\infty }(\overline{\Omega }),$ its adjoint $D^*$ preserves the adjoint boundary conditions (domain) of ${L}_\Omega ^*$ and is continuous on the space $C_{{L}^*}^{\infty }(\overline{\Omega }),$ i.e. that the operator $D^*:C_{{L}^*}^{\infty }(\overline{\Omega })\rightarrow C_{{L}^*}^{\infty }(\overline{\Omega })$ is continuous. Then we can extend D to ${\mathcal {D}}'_{{L}}(\Omega )$ by

$$\begin{aligned} \langle Dw,{\varphi }\rangle := \langle w, \overline{D^* \overline{\varphi }}\rangle \quad (w\in {\mathcal {D}}'_{{L}}(\Omega ),\, \varphi \in C_{{ L}^*}^{\infty }(\overline{\Omega })). \end{aligned}$$

This extends (2.8) from L to other operators.

The following principle of uniform boundedness is based on the Banach–Steinhaus Theorem applied to the Fréchet space $C_{{ L}^*}^{\infty }(\overline{\Omega }).$

Lemma 2.8

Let $\{w_{j}\}_{j\in {{\mathbb {N}}}}$ be a sequence in ${\mathcal {D}}'_{{L}}(\Omega )$ with the property that for every $\varphi \in C_{{L}^*}^{\infty }(\overline{\Omega }),$ the sequence $\{w_{j}(\varphi )\}_{j\in {{\mathbb {N}}}}$ in ${{\mathbb {C}}}$ is bounded. Then there exist constants $c>0$ and $k\in {{\mathbb {N}}}_0$ such that

$$\begin{aligned} |w_{j}(\varphi )|\leqslant c \Vert \varphi \Vert _{C^{k}_{{L}^*}} \quad \text {for all } \, j\in {{\mathbb {N}}}, \,\, \varphi \in C_{{L}^*}^{\infty }(\overline{\Omega }). \end{aligned}$$

The lemma above leads to the following property of completeness of the space of L-distributions.

Theorem 2.9

Let $\{w_{j}\}_{j\in {{\mathbb {N}}}}$ be a sequence in ${\mathcal {D}}'_{{L}}(\Omega )$ with the property that for every $\varphi \in C_{{L}^*}^{\infty }(\overline{\Omega }),$ the sequence $\{w_{j}(\varphi )\}_{j\in {{\mathbb {N}}}}$ converges in ${{\mathbb {C}}}$ as $j\rightarrow \infty .$ Denote the limit by $w(\varphi ).$

• (i) Then $w:\varphi \mapsto w(\varphi )$ defines an L-distribution on $\Omega .$ Furthermore, 

  $$\begin{aligned} \lim _{j\rightarrow \infty }w_{j}=w \quad \hbox {in} \ {\mathcal {D}}'_{{L}}(\Omega ). \end{aligned}$$

• (ii) If $\varphi _{j}\rightarrow \varphi$ in $\in C_{{ L}^*}^{\infty }(\overline{\Omega }),$ then

  $$\begin{aligned} \lim _{j\rightarrow \infty }w_{j}(\varphi _{j})=w(\varphi ) \quad \hbox {in}\ {{\mathbb {C}}}. \end{aligned}$$

Similarly to the previous case, we have analogues of Proposition 2.7 and Theorem 2.9 for ${L^{*}}$-distributions.

2.2 L-Fourier transform, L-convolution, Plancherel formula, Sobolev spaces and their Fourier images

Let us start by defining the L-Fourier transform introduced in [32], which is generated by the boundary value problem ${L}_\Omega$ and its main properties. Here, we record that:

      (BC+)         assume that, with ${L}_0$ denoting L or ${L}^*,$ if $f_j\in C_{{L}_0}^{\infty }(\overline{\Omega })$

               satisfies $f_j\rightarrow f$ in $C_{{L}_0}^{\infty }(\overline{\Omega }),$ then $f\in C_{{L}_0}^{\infty }(\overline{\Omega }).$

Let us denote by ${\mathcal {S}}({\mathcal I})$ the space of rapidly decaying functions $\varphi :{\mathcal I}\rightarrow {{\mathbb {C}}}.$⁷ In this space, the continuous linear functionals are of the form

$$\begin{aligned} \varphi \mapsto \langle u, \varphi \rangle :=\sum _{\xi \in {\mathcal I}}u(\xi )\varphi (\xi ), \end{aligned}$$

where the functions $u:{\mathcal I}\rightarrow {{\mathbb {C}}}$ grow at most polynomially at infinity, i.e. there exist constants $M<\infty$ and $C_{u, M}$ such that $|u(\xi )|\leqslant C_{u, M}\langle \xi \rangle ^{M}$ holds for all $\xi \in {\mathcal I}.$ Such distributions $u:{\mathcal I}\rightarrow {{\mathbb {C}}}$ form the space of distributions which we denote by ${\mathcal {S}}'({\mathcal I}).$ We now define the L-Fourier transform on $C_{{L}}^{\infty }(\overline{\Omega }).$

Definition 2.10

We define the L-Fourier transform

$$\begin{aligned} ({\mathcal {F}}_{{L}}f)(\xi )=(f\mapsto \widehat{f}): C_{{L}}^{\infty }(\overline{\Omega })\rightarrow {\mathcal {S}}({\mathcal I}) \end{aligned}$$

by

$$\begin{aligned} \widehat{f}(\xi ):=({\mathcal {F}}_{{L}}f)(\xi )=\int _{\Omega }f(x) \overline{v_{\xi }(x)}{\textrm{d}}x. \end{aligned}$$

(2.9)

Analogously, we define the ${L}^{*}$-Fourier transform

$$\begin{aligned} ({\mathcal {F}}_{{L}^{*}}f)(\xi )=(f\mapsto \widehat{f}_{*}): C_{{L}^{*}}^{\infty }(\overline{\Omega })\rightarrow {\mathcal {S}}({\mathcal I}) \end{aligned}$$

by

$$\begin{aligned} \widehat{f}_{*}(\xi ):=({\mathcal {F}}_{{ L}^{*}}f)(\xi )=\int _{\Omega }f(x)\overline{u_{\xi }(x)}{\textrm{d}}x. \end{aligned}$$

(2.10)

The expressions (2.9) and (2.10) are well defined. Moreover, we have:

Proposition 2.11

The L-Fourier transform ${\mathcal {F}}_{{L}}$ is a bijective homeomorphism from $C_{{ L}}^{\infty }(\overline{\Omega })$ to ${\mathcal {S}}({\mathcal I}).$ Its inverse

$$\begin{aligned} {\mathcal {F}}_{{L}}^{-1}: {\mathcal {S}}({\mathcal I}) \rightarrow C_{{L}}^{\infty }(\overline{\Omega }) \end{aligned}$$

is given by

$$\begin{aligned} ({\mathcal {F}}^{-1}_{{ L}}h)(x)=\sum _{\xi \in {\mathcal I}}h(\xi )u_{\xi }(x),\quad h\in {\mathcal {S}}({\mathcal I}), \end{aligned}$$

so that the Fourier inversion formula becomes

$$\begin{aligned} f(x)=\sum _{\xi \in {\mathcal I}}\widehat{f}(\xi )u_{\xi }(x) \quad \text {for all } f\in C_{{ L}}^{\infty }(\overline{\Omega }). \end{aligned}$$

Similarly, ${\mathcal {F}}_{{L}^{*}}:C_{{L}^{*}}^{\infty }(\overline{\Omega })\rightarrow {\mathcal {S}}({\mathcal I})$ is a bijective homeomorphism and its inverse

$$\begin{aligned} {\mathcal {F}}_{{L}^{*}}^{-1}: {\mathcal {S}}({\mathcal I})\rightarrow C_{{L}^{*}}^{\infty }(\overline{\Omega }) \end{aligned}$$

is given by

$$\begin{aligned} ({\mathcal {F}}^{-1}_{{ L}^{*}}h)(x):=\sum _{\xi \in {\mathcal I}}h(\xi )v_{\xi }(x), \quad h\in {\mathcal {S}}({\mathcal I}), \end{aligned}$$

so that the conjugate Fourier inversion formula becomes

$$\begin{aligned} f(x)=\sum _{\xi \in {\mathcal I}}\widehat{f}_{*}(\xi )v_{\xi }(x)\quad \text {for all } f\in C_{{ L^*}}^{\infty }(\overline{\Omega }). \end{aligned}$$

By dualising the inverse L-Fourier transform ${\mathcal {F}}_{{L}}^{-1}: {\mathcal {S}}({\mathcal I}) \rightarrow C_{{L}}^{\infty }(\overline{\Omega }),$ the L-Fourier transform extends uniquely to the mapping

$$\begin{aligned} {\mathcal {F}}_{{L}}: {\mathcal {D}}'_{{L}}(\Omega )\rightarrow {\mathcal {S}}'({\mathcal I}) \end{aligned}$$

by the formula

$$\begin{aligned} \langle {\mathcal {F}}_{{L}}w, \varphi \rangle := \langle w,\overline{{\mathcal {F}}_{{L}^*}^{-1}\overline{\varphi }}\rangle , \quad \text {with } w\in {\mathcal {D}}'_{{L}}(\Omega ),\, \varphi \in {\mathcal {S}}({\mathcal I}). \end{aligned}$$

(2.11)

It can be readily seen that if $w\in {\mathcal {D}}'_{{ L}}(\Omega ),$ then $\widehat{w}\in {\mathcal {S}}'({\mathcal I}).$ The reason for taking complex conjugates in (2.11) is that, if $w\in C_{{L}}^{\infty }(\overline{\Omega }),$ we have the equality

$$\begin{aligned}{} & {} \langle \widehat{w},\varphi \rangle = \sum _{\xi \in {\mathcal I}} \widehat{w}(\xi ) \varphi (\xi )= \sum _{\xi \in {\mathcal I}} \left( \int _\Omega w(x) \overline{v_\xi (x)}{\textrm{d}}x\right) \varphi (\xi )\\{} & {} \quad = \int _\Omega w(x) \overline{\left( \sum _{\xi \in {\mathcal I}} \overline{\varphi (\xi )} v_\xi (x)\right) } {\textrm{d}}x = \int _\Omega w(x) \overline{\left( {\mathcal {F}}_{{L}^*}^{-1} \overline{\varphi } \right) } {\textrm{d}}x =\langle w,\overline{{\mathcal {F}}_{{L}^*}^{-1}\overline{\varphi }}\rangle . \end{aligned}$$

Analogously, we have the mapping

$$\begin{aligned} {\mathcal {F}}_{{L}^*}: {\mathcal {D}}'_{{L}^*}(\Omega )\rightarrow {\mathcal {S}}'({\mathcal I}), \end{aligned}$$

defined by the formula

$$\begin{aligned} \langle {\mathcal {F}}_{{L}^*}w, \varphi \rangle := \langle w,\overline{{\mathcal {F}}_{{L}}^{-1}\overline{\varphi }}\rangle , \quad \text {with } w\in {\mathcal {D}}'_{{L}^*}(\Omega ),\, \varphi \in {\mathcal {S}}({\mathcal I}). \end{aligned}$$

It can be also seen that if $w\in {\mathcal {D}}'_{{ L}^*}(\Omega ),$ then $\widehat{w}\in {\mathcal {S}}'({\mathcal I}).$ The following statement follows from the work of Bari [10, Theorem 9]:

Lemma 2.12

There exist constants $K,m,M>0$ such that for every $f\in L^{2}(\Omega ),$ we have

$$\begin{aligned} m^2\Vert f\Vert _{L^{2}}^2 \leqslant \sum _{\xi \in {\mathcal I}} |\widehat{f}(\xi )|^2\leqslant M^2\Vert f\Vert _{L^{2}}^2 \leqslant \sum _{\xi \in {\mathcal I}} |\widehat{f}_*(\xi )|^2\leqslant K^2\Vert f\Vert _{L^{2}}^2. \end{aligned}$$

However, we note that the Plancherel identity can be also achieved in suitably defined $l^2$-spaces of Fourier coefficients, see Proposition 2.15.

Let us introduce a notion of the L-convolution, an analogue of the convolution adapted to the boundary problem ${L}_\Omega .$

Definition 2.13

(L-Convolution) For $f, g\in C_{{L}}^{\infty }(\overline{\Omega })$ define their L-convolution by

$$\begin{aligned} (f{\star _{L}}g)(x):=\sum _{\xi \in {\mathcal I}}\widehat{f}(\xi )\widehat{g}(\xi )u_{\xi }(x). \end{aligned}$$

(2.12)

By Proposition 2.11, it is well defined and we have $f{\star _{L}}g\in C_{{L}}^{\infty }(\overline{\Omega }).$⁸

Analogously to the L-convolution, we can introduce the ${L}^*$-convolution. Thus, for $f, g\in C_{{ L^{*}}}^{\infty }(\overline{\Omega }),$ we define the ${ L^{*}}$-convolution using the ${L}^*$-Fourier transform by

$$\begin{aligned} (f\widetilde{\star }_{L}g)(x):=\sum _{\xi \in {\mathcal I}}\widehat{f}_{*}(\xi )\widehat{g}_{*}(\xi )v_{\xi }(x). \end{aligned}$$

Its properties are similar to those of the L-convolution, so we may formulate only the latter. We would like to mention here that the L-convolution depends on the biorthonormal system, and therefore the symbol classes, considered later in this section, will also be depending on the chosen basis.

Proposition 2.14

For any $f, g\in C_{{ L}}^{\infty }(\overline{\Omega }),$ we have

$$\begin{aligned} \widehat{f{\star _{L}}g}=\widehat{f}\times \widehat{g},\quad \xi \in {\mathcal {I}}. \end{aligned}$$

The convolution is commutative and associative. If $g \in C_{{ L}}^{\infty }(\overline{\Omega }),$ then for all $f\in {\mathcal {D}}^\prime _{L}(\Omega ),$ we have

$$\begin{aligned} f{\star _{L}}g\in C_{{L}}^{\infty }(\overline{\Omega }). \end{aligned}$$

In addition, if $\Omega \subset {\mathbb {R}}^n$ is bounded, and $f,g\in L^{2}(\Omega ),$ then $f{\star _{L}}g\in L^{1}(\Omega )$ with

$$\begin{aligned} \Vert f{\star _{L}}g\Vert _{L^1}\leqslant C|\Omega |^{1/2} \Vert f\Vert _{L^2}\Vert g\Vert _{L^2}, \end{aligned}$$

where $|\Omega |\in (0,\infty ]$ is the volume of $\Omega ,$ with C independent of $f,g,\Omega .$

Let us denote by $l^{2}_{{L}}=l^2({L})$ the linear space of complex-valued functions a on ${\mathcal I}$ such that ${\mathcal {F}}^{-1}_{{L}}a\in L^{2}(\Omega ),$ i.e. if there exists $f\in L^{2}(\Omega )$ such that ${\mathcal {F}}_{{L}}f=a,$ then the space of sequences $l^{2}_{{L}}$ is a Hilbert space with the inner product

$$\begin{aligned} (a,\ b)_{l^{2}_{{ L}}}:=\sum _{\xi \in {\mathcal I}}a(\xi )\ \overline{({\mathcal {F}}_{{ L^{*}}}\circ {\mathcal {F}}^{-1}_{{L}}b)(\xi )} \end{aligned}$$

(2.13)

for arbitrary $a,\,b\in l^{2}_{{L}}.$ The norm of $l^{2}_{{L}}$ is then given by the formula

$$\begin{aligned} \Vert a\Vert _{l^{2}_{{L}}}=\left( \sum _{\xi \in {\mathcal I}}a(\xi )\ \overline{({\mathcal {F}}_{{L^{*}}}\circ {\mathcal {F}}^{-1}_{{ L}}a)(\xi )}\right) ^{1/2}, \quad \text {for all } \, a\in l^{2}_{{L}}. \end{aligned}$$

Analogously, we introduce the Hilbert space $l^{2}_{{L^{*}}}=l^{2}({L^{*}})$ as the space of functions a on ${\mathcal I}$ such that ${\mathcal {F}}^{-1}_{{L^{*}}}a\in L^{2}(\Omega ),$ with the inner product

$$\begin{aligned} (a,\ b)_{l^{2}_{{ L^{*}}}}:=\sum _{\xi \in {\mathcal I}}a(\xi )\ \overline{({\mathcal {F}}_{{L}}\circ {\mathcal {F}}^{-1}_{{L^{*}}}b)(\xi )} \end{aligned}$$

(2.14)

for arbitrary $a,\,b\in l^{2}_{{L^{*}}}.$ The norm of $l^{2}_{{L^{*}}}$ is given by the formula

$$\begin{aligned} \Vert a\Vert _{l^{2}_{{L^{*}}}}=\left( \sum _{\xi \in {\mathcal I}}a(\xi )\ \overline{({\mathcal {F}}_{{L}}\circ {\mathcal {F}}^{-1}_{{ L^{*}}}a)(\xi )}\right) ^{1/2} \end{aligned}$$

for all $a\in l^{2}_{{L^{*}}}.$ The spaces of sequences $l^{2}_{{L}}$ and $l^{2}_{{L^{*}}}$ are thus generated by biorthogonal systems $\{u_{\xi }\}_{\xi \in {\mathcal I}}$ and $\{v_{\xi }\}_{\xi \in {\mathcal I}}.$ The reason for their definition in the above forms becomes clear again in view of the following Plancherel identity:

Proposition 2.15

(Plancherel’s identity) If $f,\,g\in L^{2}(\Omega ),$ then $\widehat{f},\,\widehat{g}\in l^{2}_{{L}}, \,\,\, \widehat{f}_{*},\, \widehat{g}_{*}\in l^{2}_{\mathrm{L^{*}}},$ and the inner products (2.13), (2.14) take the form

$$\begin{aligned} (\widehat{f},\ \widehat{g})_{l^{2}_{{L}}}=\sum _{\xi \in {\mathcal I}}\widehat{f}(\xi )\ \overline{\widehat{g}_{*}(\xi )},\quad (\widehat{f}_{*},\ \widehat{g}_{*})_{l^{2}_{{ L^{*}}}}=\sum _{\xi \in {\mathcal I}}\widehat{f}_{*}(\xi )\ \overline{\widehat{g}(\xi )}. \end{aligned}$$

In particular,  we have

$$\begin{aligned} \overline{(\widehat{f},\ \widehat{g})_{l^{2}_{{L}}}}= (\widehat{g}_{*},\ \widehat{f}_{*})_{l^{2}_{{ L^{*}}}}. \end{aligned}$$

The Parseval identity takes the form:

$$\begin{aligned} (f,g)_{L^{2}}=(\widehat{f},\widehat{g})_{l^{2}_{{ L}}}=\sum _{\xi \in {\mathcal I}}\widehat{f}(\xi )\ \overline{\widehat{g}_{*}(\xi )}. \end{aligned}$$

Furthermore,  for any $f\in L^{2}(\Omega ),$ we have $\widehat{f}\in l^{2}_{{L}},$ $\widehat{f}_{*}\in l^{2}_{{ L^{*}}},$ and $\Vert f\Vert _{L^{2}}=\Vert \widehat{f}\Vert _{l^{2}_{{ L}}}=\Vert \widehat{f}_{*}\Vert _{l^{2}_{{L^{*}}}}.$

Now, we introduce Sobolev spaces generated by the operator ${L}_{\Omega }$:

Definition 2.16

(Sobolev spaces ${H}^{s}_{{L}}(\Omega )$) For $f\in {\mathcal {D}}'_{{L}}(\Omega )\cap {\mathcal {D}}'_{{L}^{*}}(\Omega )$ and $s\in {\mathbb {R}},$ we say that

$$\begin{aligned} f\in {H}^{s}_{{L}}(\Omega )\, {\text { if and only if }}\, \langle \xi \rangle ^{s}\widehat{f}(\xi )\in l^{2}_{{L}}. \end{aligned}$$

We define the norm on ${H}^{s}_{{L}}(\Omega )$ by

$$\begin{aligned} \Vert f\Vert _{{H}^{s}_{{ L}}(\Omega )}:=\left( \sum _{\xi \in {\mathcal I}} \langle \xi \rangle ^{2s}\widehat{f}(\xi )\overline{\widehat{f}_{*}(\xi )}\right) ^{1/2}. \end{aligned}$$

(2.15)

The Sobolev space ${H}^{s}_{{L}}(\Omega )$ is then the space of L-distributions f for which we have $\Vert f\Vert _{{H}^{s}_{{L}}(\Omega )}<\infty .$ Similarly, we can define the space ${H}^{s}_{{L^{*}}}(\Omega )$ by the condition

$$\begin{aligned} \Vert f\Vert _{{H}^{s}_{{L^{*}}}(\Omega )}:=\left( \sum _{\xi \in {\mathcal I}} \langle \xi \rangle ^{2s}\widehat{f}_{*}(\xi )\overline{\widehat{f}(\xi )}\right) ^{1/2}<\infty . \end{aligned}$$

(2.16)

We note that the expressions in (2.15) and (2.16) are well defined, since the sum

$$\begin{aligned} \sum _{\xi \in {\mathcal I}} \langle \xi \rangle ^{2s}\widehat{f}(\xi )\overline{\widehat{f}_{*}(\xi )}= (\langle \xi \rangle ^{s}\widehat{f}(\xi ),\langle \xi \rangle ^{s}\widehat{f}(\xi ))_{l^{2}_{L}}\geqslant 0 \end{aligned}$$

is real and non-negative. Consequently, since we can write the sum in (2.16) as the complex conjugate of that in (2.15), and with both being real, we see that the spaces ${H}^{s}_{{L}}(\Omega )$ and ${H}^{s}_{{L^{*}}}(\Omega )$ coincide as sets. Moreover, we have

Proposition 2.17

For every $s\in {\mathbb {R}},$ the Sobolev space ${H}^{s}_{{L}}(\Omega )$ is a Hilbert space with the inner product

$$\begin{aligned} (f,\ g)_{{H}^{s}_{{L}}(\Omega )}:=\sum _{\xi \in {\mathcal I}}\langle \xi \rangle ^{2s}\widehat{f}(\xi )\overline{\widehat{g}_{*}(\xi )}. \end{aligned}$$

Similarly,  the Sobolev space ${H}^{s}_{{L^{*}}}(\Omega )$ is a Hilbert space with the inner product

$$\begin{aligned} (f,\ g)_{{H}^{s}_{{L^{*}}}(\Omega )}:=\sum _{\xi \in {\mathcal I}}\langle \xi \rangle ^{2s}\widehat{f}_{*}(\xi )\overline{\widehat{g}(\xi )}. \end{aligned}$$

For every $s\in {\mathbb {R}},$ the Sobolev spaces ${H}^{s}_{{L}}(\Omega ),$ and ${H}^{s}_{{L}^*}(\Omega )$ are isometrically isomorphic.

2.3 L-Schwartz kernel theorem

This subsection is devoted to discuss the Schwartz kernel theorem in the space of distributions ${\mathcal {D}}'_{{L}}(\Omega ).$ In this analysis, we will need the following assumption which may be also regarded as the definition of the number $s_{0}.$ So, from now on we will make the following:

Assumption 2.18

Assume that the number $s_0\in {\mathbb {R}}$ is such that we have

$$\begin{aligned} \sum _{\xi \in {\mathcal I}} \langle \xi \rangle ^{-s_0}<\infty . \end{aligned}$$

Recalling the operator ${L}^{\circ }$ in (2.2), the assumption (2.18) is equivalent to assuming that the operator $(\textrm{I}+{L^\circ L})^{-\frac{s_0}{4m}}$ is Hilbert–Schmidt on $L^2(\Omega ).$

Indeed, recalling the definition of $\langle \xi \rangle$ in (2.1), namely that $\langle \xi \rangle$ are the eigenvalues of $(\textrm{I}+{L^\circ L})^{-\frac{s_0}{2m}},$ and that the operator $(\textrm{I}+{L^\circ L})^{-\frac{s_0}{4m}}$ is Hilbert–Schmidt on $L^2(\Omega )$ is equivalent to the condition that

$$\begin{aligned} \Vert (\textrm{I}+{L^\circ L})^{-\frac{s_0}{4m}}\Vert _\texttt{HS}^2\cong \sum _{\xi \in {\mathcal I}} \langle \xi \rangle ^{-s_0}<\infty . \end{aligned}$$

Remark 2.19

If L is elliptic, we may expect that we can take any $s_0>n:=\text {dim}(\Omega ),$ but this depends on the boundary conditions in general. The order $s_0$ will enter the regularity properties of the Schwartz kernels.

We will use the notation:

$$\begin{aligned} C^{\infty }_{{L}}(\overline{\Omega }\times \overline{\Omega }):= C^{\infty }_{{L}}(\overline{\Omega })\otimes C^{\infty }_{{L}}(\overline{\Omega }), \end{aligned}$$

and for the corresponding dual space we write ${\mathcal {D}}'_{{L}}(\Omega \times \Omega ):= \left( C^{\infty }_{{L}}(\overline{\Omega }\times \overline{\Omega })\right) ^\prime .$ By following [32], to any continuous linear operator $A:C^{\infty }_{{ L}}(\overline{\Omega })\rightarrow {\mathcal {D}}'_{{L}}(\Omega ),$ we can associate a kernel $K\in {\mathcal {D}}'_{{L}}(\Omega \times \Omega )$ such that

$$\begin{aligned} \langle Af,g\rangle =\int _{\Omega }\int _{\Omega }K(x,y)f(x)g(y){\textrm{d}}x{\textrm{d}}y, \end{aligned}$$

and, using the notion of the L-convolution, also a convolution kernel $k_{A}(x)\in {\mathcal {D}}'_{{L}}(\Omega ),$ such that

$$\begin{aligned} Af(x)=(k_{A}(x){\star _{L}}f)(x), \end{aligned}$$

provided that $\{u_{\xi }: \,\,\, \xi \in {\mathcal I}\}$ is a $\textrm{WZ}$-system in the sense of Definition 2.1. As usual, $K_{A}$ is called the Schwartz kernel of A. Note that, by using the Fourier series formula for $f\in C^{\infty }_{{L}}(\overline{\Omega }),$

$$\begin{aligned} f(y)=\sum _{\eta \in {\mathcal I}}\widehat{f}(\eta ) u_{\eta }(y), \end{aligned}$$

we can also write

$$\begin{aligned} Af(x)=\sum _{\eta \in {\mathcal I}}\widehat{f}(\eta ) \int _{\Omega }K_{A}(x,y)u_{\eta }(y){\textrm{d}}y, \end{aligned}$$

(2.17)

and the L-distribution $k_{A}\in {\mathcal {D}}'_{{L}}(\Omega \times \Omega )$ is determined by the formula

$$\begin{aligned} k_{A}(x,z):=k_A(x)(z):=\sum _{\eta \in {\mathcal I}}u_{\eta }^{-1}(x) \int _{\Omega }K_{A}(x,y)u_{\eta }(y){\textrm{d}}y \, u_{\eta }(z). \end{aligned}$$

(2.18)

Since for some $C>0$ and $N\geqslant 0,$ we have, by Definition 2.1,

$$\begin{aligned} \inf _{x\in \overline{\Omega }}|u_{\eta }(x)|\geqslant C\langle \eta \rangle ^{-N}, \end{aligned}$$

the series in (2.18) converges in the sense of L-distributions. Formula (2.18) means that the Fourier transform of $k_A$ in the second variable satisfies

$$\begin{aligned} \widehat{k}_{A} (x,\eta )u_{\eta }(x)= \int _{\Omega }K_{A}(x,y)u_{\eta }(y){\textrm{d}}y. \end{aligned}$$

Combining this and (2.17), we get

$$\begin{aligned} Af(x)=\sum _{\eta \in {\mathcal I}} \widehat{f}(\eta )\int _{\Omega }K_{A}(x,y)u_{\eta }(y){\textrm{d}}y =\sum _{\eta \in {\mathcal I}}\widehat{f}(\eta )\widehat{k}_{A}(x,\eta )u_{\eta }(x) =(f{\star _{L}}k_{A}(x))(x), \end{aligned}$$

where in the last equality we used the notion of the L-convolution in Definition 2.13.

2.4 L-Quantisation and full symbols

In this subsection, we describe the L-quantisation induced by the boundary value problem ${L}_\Omega .$ From now on, we will assume that the system of functions $\{u_{\xi }:\, \xi \in {\mathcal I}\}$ is a $\textrm{WZ}$-system in the sense of Definition 2.1. Later, we will make some remarks on what happens when this assumption is not satisfied.

Definition 2.20

(L-Symbols of operators on $\Omega )$ The L-symbol of a linear continuous operator

$$\begin{aligned} A:C^{\infty }_{{L}}(\overline{\Omega })\rightarrow {\mathcal {D}}'_{{L}}(\Omega ) \end{aligned}$$

at $x\in \Omega$ and $\xi \in {\mathcal I}$ is defined by

$$\begin{aligned} \sigma _{A}(x, \xi ):=\widehat{k_{A}(x)}(\xi )={\mathcal {F}}_{{L}}(k_{A}(x))(\xi ). \end{aligned}$$

Hence, we can also write

$$\begin{aligned} \sigma _{A}(x, \xi )=\int _{\Omega }k_{A}(x,y)\overline{v_{\xi }(y)}{\textrm{d}}y= \langle k_{A}(x),\overline{v_{\xi }}\rangle . \end{aligned}$$

By the L-Fourier inversion formula, the convolution kernel can be recovered from the symbol:

$$\begin{aligned} k_{A}(x, y)=\sum _{\xi \in {\mathcal I}}\sigma _{A}(x, \xi )u_{\xi }(y), \end{aligned}$$

all in the sense of L-distributions. We now show that an operator A can be represented by its symbol [32].

Theorem 2.21

(L-quantisation) Let $A:C^{\infty }_{{L}}(\overline{\Omega })\rightarrow C^{\infty }_{{L}}(\overline{\Omega })$ be a continuous linear operator with L-symbol $\sigma _{A}.$ Then,

$$\begin{aligned} Af(x)=\sum _{\xi \in {\mathcal I}} u_{\xi }(x)\sigma _{A}(x, \xi ) \widehat{f}(\xi ) \end{aligned}$$

for every $f\in C^{\infty }_{{L}}(\overline{\Omega })$ and $x\in \Omega .$ The L-symbol $\sigma _{A}$ satisfies

$$\begin{aligned} \sigma _{A}(x,\xi )=u_{\xi }(x)^{-1}(Au_{\xi })(x) \end{aligned}$$

for all $x\in \Omega$ and $\xi \in {\mathcal I}.$

Now, we collect several formulae for the symbol under the assumption that the biorthogonal system $u_\xi$ is a WZ-system⁹

Corollary 2.22

We have the following equivalent formulae for L-symbols : 

$$\begin{aligned} \mathrm{(i)}\quad \sigma _{A}(x, \xi )&=\int _{\Omega }k_{A}(x,y)\overline{v_{\xi }(y)}{\textrm{d}}y;\\ \mathrm{(ii)}\quad \sigma _{A}(x, \xi )&=u_{\xi }^{-1}(x)(Au_{\xi })(x);\\ \mathrm{(iii)}\quad \sigma _{A}(x,\xi )&=u_{\xi }^{-1}(x)\int _{\Omega } K_{A}(x,y)u_{\xi }(y){\textrm{d}}y;\\ \mathrm{(iv)}\quad \sigma _{A}(x,\xi )&=u_{\xi }^{-1}(x)\int _{\Omega } \int _{\Omega }F(x,y,z)k_{A}(x,y) u_{\xi }(z){\textrm{d}}y{\textrm{d}}z. \end{aligned}$$

Here and in the sequel, we write $u_{\xi }^{-1}(x)=u_{\xi }(x)^{-1}.$ Formula (iii) also implies

$$\begin{aligned} \mathrm{(v)}\quad K_A(x,y)= \sum _{\xi \in {\mathcal I}} u_\xi (x) \sigma _A(x,\xi ) \overline{v_\xi (y)}. \end{aligned}$$

Similarly, we can introduce an analogous notion of the ${L^{*}}$-quantisation.

Definition 2.23

$({L^{*}}$-Symbols of operators on $\Omega )$ The ${L^{*}}$-symbol of a linear continuous operator

$$\begin{aligned} A:C^{\infty }_{{ L^{*}}}(\overline{\Omega })\rightarrow {\mathcal {D}}'_{{L}^*}(\Omega ) \end{aligned}$$

at $x\in {\Omega }$ and $\xi \in {\mathcal I}$ is defined by

$$\begin{aligned} \tau _{A}(x, \xi ):={\mathcal {F}}_{{L^{*}}}(\widetilde{k}_{A}(x))(\xi ). \end{aligned}$$

We can also write

$$\begin{aligned} \tau _{A}(x, \xi )=\int _{\Omega }\widetilde{k}_{A}(x,y)\overline{u_{\xi }(y)}{\textrm{d}}y= \langle \widetilde{k}_{A}(x),\overline{u_{\xi }}\rangle . \end{aligned}$$

By the ${L^{*}}$-Fourier inversion formula, the convolution kernel can be regained from the symbol:

$$\begin{aligned} \widetilde{k}_{A}(x, y)=\sum _{\xi \in {\mathcal I}}\tau _{A}(x, \xi )v_{\xi }(y) \end{aligned}$$

in the sense of ${L^{*}}$-distributions. Analogously to the L-quantisation, we have:

Corollary 2.24

$({L^{*}}$-quantisation) Let $\tau _{A}$ be the ${L}^*$-symbol of a continuous linear operator $A:C^{\infty }_{{ L^{*}}}(\overline{\Omega })\rightarrow C^{\infty }_{{ L^{*}}}(\overline{\Omega }).$ Then,

$$\begin{aligned} Af(x)=\sum _{\xi \in {\mathcal I}} v_{\xi }(x) \tau _{A}(x, \xi ) \widehat{f}_{*}(\xi ) \end{aligned}$$

for every $f\in C^{\infty }_{{L^{*}}}(\overline{\Omega })$ and $x\in \Omega .$ For all $x\in \Omega$ and $\xi \in {\mathcal I},$ we have

$$\begin{aligned} \tau _{A}(x, \xi )=v_{\xi }(x)^{-1}(Av_{\xi })(x). \end{aligned}$$

We also have the following equivalent formulae for the ${L^{*}}$-symbol : 

$$\begin{aligned} \mathrm{(i)}\quad \tau _{A}(x, \xi )&=\int _{\Omega }\widetilde{k}_{A}(x,y)\overline{u_{\xi }(y)}{\textrm{d}}y;\\ \mathrm{(ii)}\quad \tau _{A}(x,\xi )&=v_{\xi }^{-1}(x)\int _{\Omega } \widetilde{K}_{A}(x,y)v_{\xi }(y){\textrm{d}}y. \end{aligned}$$

2.5 Difference operators and symbolic calculus

In this subsection, we discuss difference operators that will be instrumental in defining symbol classes for the symbolic calculus of operators.

Let $q_{j}\in C^{\infty }({\Omega }\times {\Omega }),$ $j=1,\ldots ,l,$ be a given family of smooth functions. We will call the collection of $q_j$’s L-strongly admissible if the following properties hold:

• For every $x\in \Omega ,$ the multiplication by $q_{j}(x,\cdot )$ is a continuous linear mapping on $C^{\infty }_{{L}}(\overline{\Omega }),$ for all $j=1,\ldots ,l$;

• $q_{j}(x,x)=0$ for all $j=1,\ldots ,l$;

• $\textrm{rank}(\nabla _{y}q_{1}(x,y), \ldots , \nabla _{y}q_{l}(x,y))|_{y=x}=n;$

• the diagonal in $\Omega \times \Omega$ is the only set when all of $q_j$’s vanish:

  $$\begin{aligned} \bigcap _{j=1}^l \left\{ (x,y)\in \Omega \times \Omega : \, q_j(x,y)=0\right\} =\{(x,x):\, x\in \Omega \}. \end{aligned}$$

We note that the first property above implies that for every $x\in \Omega ,$ the multiplication by $q_{j}(x,\cdot )$ is also well defined and extends to a continuous linear mapping on ${\mathcal {D}}'_{{L}}(\Omega ).$ Also, the last property above contains the second one but we chose to still give it explicitly for the clarity of the exposition.

The collection of $q_j$s with the above properties generalises the notion of a strongly admissible collection of functions for difference operators introduced in [37] in the context of compact Lie groups. We will use the multi-index notation

$$\begin{aligned} q^{\alpha }(x,y):=q^{\alpha _1}_{1}(x,y)\cdots q^{\alpha _l}_{l}(x,y). \end{aligned}$$

Analogously, the notion of an ${L}^{*}$-strongly admissible collection suitable for the conjugate problem is that of a family $\widetilde{q}_{j}\in C^{\infty }({\Omega }\times {\Omega }),$ $j=1,\ldots ,l,$ satisfying the properties:

• For every $x\in \Omega ,$ the multiplication by $\widetilde{q}_{j}(x,\cdot )$ is a continuous linear mapping on $C^{\infty }_{{L}^{*}}(\overline{\Omega }),$ for all $j=1,\ldots ,l$;

• $\widetilde{q}_{j}(x,x)=0$ for all $j=1,\ldots ,l$;

• $\textrm{rank}(\nabla _{y}\widetilde{q}_{1}(x,y), \ldots , \nabla _{y}\widetilde{q}_{l}(x,y))|_{y=x}=n;$

• the diagonal in $\Omega \times \Omega$ is the only set when all of $\widetilde{q}_j$s vanish:

  $$\begin{aligned} \bigcap _{j=1}^l \left\{ (x,y)\in \Omega \times \Omega : \, \widetilde{q}_j(x,y)=0\right\} =\{(x,x):\, x\in \Omega \}. \end{aligned}$$

We also write

$$\begin{aligned} \widetilde{q}^{\alpha }(x,y):=\widetilde{q}^{\alpha _1}_{1}(x,y)\cdots \widetilde{q}^{\alpha _l}_{l}(x,y). \end{aligned}$$

We now record the Taylor expansion formula with respect to a family of $q_j$s, which follows from expansions of functions g and $q^{\alpha }(e,\cdot )$ by the common Taylor series [32]:

Proposition 2.25

Any smooth function $g\in C^{\infty }({\Omega })$ can be approximated by Taylor polynomial-type expansions,  i.e. for $e\in \Omega ,$ we have

$$\begin{aligned}{} & {} g(x)=\sum _{|\alpha |< N}\frac{1}{\alpha !}D^{(\alpha )}_{x}g(x)|_{x=e}\, q^{\alpha }(e,x)+\sum _{|\alpha |= N}\frac{1}{\alpha !}q^{\alpha }(e,x)g_{N}(x)\\{} & {} \quad \sim \sum _{\alpha \geqslant 0}\frac{1}{\alpha !}D^{(\alpha )}_{x}g(x)|_{x=e}\, q^{\alpha }(e,x) \end{aligned}$$

in a neighbourhood of $e\in \Omega ,$ where $g_{N}\in C^{\infty }({\Omega })$ and $D^{(\alpha )}_{x}g(x)|_{x=e}$ can be found from the recurrent formulae :  $D^{(0,\ldots ,0)}_{x}:=I$ and for $\alpha \in {{\mathbb {N}}}_0^l,$

$$\begin{aligned} {\partial }^{\beta }_{x}g(x)|_{x=e}= \sum _{|\alpha |\leqslant |\beta |}\frac{1}{\alpha !} \left[ {\partial }^{\beta }_{x}q^{\alpha }(e,x)\right] \Big |_{x=e}D^{(\alpha )}_{x}g(x)|_{x=e}, \end{aligned}$$

where $\beta =(\beta _1, \ldots , \beta _n)$ and $\partial ^{\beta }_{x}=\frac{\partial ^{\beta _{1}}}{\partial x_{1}^{\beta _{1}}}\cdots \frac{\partial ^{\beta _{n}}}{\partial x_{n}^{\beta _{n}}}.$

Analogously, any function $g\in C^{\infty }({\Omega })$ can be approximated by Taylor polynomial-type expansions corresponding to the adjoint problem, i.e. we have

$$\begin{aligned}{} & {} g(x)=\sum _{|\alpha |< N}\frac{1}{\alpha !}\widetilde{D}^{(\alpha )}_{x}g(x)|_{x=e}\, \widetilde{q}^{\alpha }(e,x)+\sum _{|\alpha |= N}\frac{1}{\alpha !}\widetilde{q}^{\alpha }(e,x)g_{N}(x)\\{} & {} \quad \sim \sum _{\alpha \geqslant 0}\frac{1}{\alpha !}\widetilde{D}^{(\alpha )}_{x}g(x)|_{x=e}\, \widetilde{q}^{\alpha }(e,x) \end{aligned}$$

in a neighbourhood of $e\in \Omega ,$ where $g_{N}\in C^{\infty }({\Omega })$ and $\widetilde{D}^{(\alpha )}_{x}g(x)|_{x=e}$ are found from the recurrent formula: $\widetilde{D}^{(0,\ldots ,0)}:=I$ and for $\alpha \in {{\mathbb {N}}}_{0}^{l},$

$$\begin{aligned} \partial ^{\beta }_{x}g(x)|_{x=e}=\sum _{|\alpha |\leqslant |\beta |}\frac{1}{\alpha !} \left[ \partial ^{k}_{x}\widetilde{q}^{\alpha }(e,x)\right] \Big |_{x=e} \widetilde{D}^{(\alpha )}_{x}g(x)|_{x=e}, \end{aligned}$$

where $\beta =(\beta _1, \ldots , \beta _n),$ and $\partial ^{\beta }$ is defined as in Proposition 2.25.

It can be seen that operators $D^{(\alpha )}$ and $\widetilde{D}^{(\alpha )}$ are differential operators of order $|\alpha |.$ We now define difference operators acting on Fourier coefficients. Since the problem in general may lack any invariance or symmetry structure, the introduced difference operators will depend on a point x where they will be taken when applied to symbols.

Definition 2.26

For WZ-systems, we define difference operator $\Delta _{q,(x)}^{\alpha }$ acting on Fourier coefficients by any of the following equal expressions:

$$\begin{aligned} \Delta _{q,(x)}^{\alpha }\widehat{f}(\xi )&= u_{\xi }^{-1}(x) \int _{\Omega }\Big [\int _{\Omega }q^{\alpha }(x,y) F(x,y,z)f(z){\textrm{d}}z\Big ]u_{\xi }(y){\textrm{d}}y\\&= u_{\xi }^{-1}(x) \sum _{\eta \in {\mathcal I}}{\mathcal {F}}_{L} \Big (q^{\alpha }(x,\cdot )u_{\xi }(\cdot )\Big )(\eta )\widehat{f}(\eta )u_{\eta }(x)\\&= u_{\xi }^{-1}(x) \left( [q^{\alpha }(x,\cdot )u_{\xi }(\cdot )]{\star _{L}}f\right) (x). \end{aligned}$$

Analogously, we define the difference operator $\widetilde{\Delta }_{q,(x)}^{\alpha }$ acting on adjoint Fourier coefficients by

$$\begin{aligned} \widetilde{\Delta }_{\widetilde{q},(x)}^{\alpha }\widehat{f}_{*}(\xi ):= v_{\xi }^{-1}(x)\sum _{\eta \in {\mathcal I}}{\mathcal {F}}_{{L^{*}}} \Big (\widetilde{q}^{\alpha }(x,\cdot )v_{\xi }(\cdot )\Big )(\eta ) \widehat{f}_{*}(\eta )v_{\eta }(x). \end{aligned}$$

For simplicity, if there is no confusion, for a fixed collection of $q_j$’s, instead of $\Delta _{q,(x)}$ and $\widetilde{\Delta }_{\widetilde{q},(x)},$ we will often simply write $\Delta _{(x)}$ and $\widetilde{\Delta }_{(x)}.$

Remark 2.27

Applying difference operators to a symbol and using formulae from Sect. 2.4, we obtain

$$\begin{aligned} \Delta _{(x)}^{\alpha }a(x,\xi )&=u_{\xi }^{-1}(x)\sum _{\eta \in {\mathcal I}} {\mathcal {F}}_{L}\Big (q^{\alpha }(x,\cdot )u_{\xi }(\cdot )\Big ) (\eta )a(x,\eta )u_{\eta }(x)\nonumber \\&=u_{\xi }^{-1}(x)\sum _{\eta \in {\mathcal I}}{\mathcal {F}}_{L} \Big (q^{\alpha }(x,\cdot )u_{\xi }(\cdot )\Big )(\eta ) \int _{\Omega }K(x,y)u_{\eta }(y){\textrm{d}}y\nonumber \\&=u_{\xi }^{-1}(x)\int _{\Omega }K(x,y)\left[ \sum _{\eta \in {\mathcal I}} {\mathcal {F}}_{L}\Big (q^{\alpha }(x,\cdot )u_{\xi }(\cdot )\Big )(\eta ) u_{\eta }(y)\right] {\textrm{d}}y\nonumber \\&=u_{\xi }^{-1}(x)\int _{\Omega }q^{\alpha }(x,y)K(x,y)u_{\xi }(y){\textrm{d}}y. \end{aligned}$$

(2.19)

In view of the first property of the strongly admissible collections, for each $x\in \Omega ,$ the multiplication by $q^{\alpha }(x,\cdot )$ is well defined on ${\mathcal {D}}'_{{L}}(\Omega ).$ Therefore, we can write (2.19) also in the distributional form

$$\begin{aligned} \Delta _{(x)}^{\alpha }a(x,\xi ) = u_{\xi }^{-1}(x)\, \langle q^{\alpha }(x,\cdot )K(x,\cdot ),u_{\xi }\rangle . \end{aligned}$$

Plugging the expression (v) from Corollary 2.22 for the kernel in terms of the symbol into (2.19), namely, using

$$\begin{aligned} K(x,y)= \sum _{\eta \in {\mathcal I}} u_\eta (x) a(x,\eta ) \overline{v_\eta (y)}, \end{aligned}$$

we record another useful form of (2.19) to be used later as

$$\begin{aligned}\nonumber \Delta _{(x)}^{\alpha }a(x,\xi )&= u_{\xi }^{-1}(x)\int _{\Omega }q^{\alpha }(x,y)\left[ \sum _{\eta \in {\mathcal I}} u_\eta (x) a(x,\eta ) \overline{v_\eta (y)} \right] u_{\xi }(y){\textrm{d}}y \\&= u_{\xi }^{-1}(x) \sum _{\eta \in {\mathcal I}}u_\eta (x) a(x,\eta ) \left[ \int _{\Omega }q^{\alpha }(x,y) \overline{v_\eta (y)} u_{\xi }(y){\textrm{d}}y\right] , \nonumber \end{aligned}$$

with the usual distributional interpretation of all the steps. In the sequel, we will also require the ${L^*}$-version of this formula, which we record now as

$$\begin{aligned} \widetilde{\Delta }_{(x)}^{\alpha }a(x,\xi )= v_{\xi }^{-1}(x) \sum _{\eta \in {\mathcal I}}v_\eta (x) a(x,\eta ) \left[ \int _{\Omega }\widetilde{q}^{\alpha }(x,y) \overline{u_\eta (y)} v_{\xi }(y){\textrm{d}}y\right] . \end{aligned}$$

Using such difference operators and derivatives $D^{(\alpha )}$ from Proposition 2.25, we can now define classes of symbols.

Definition 2.28

(Symbol class $S^m_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I}))$ Let $m\in {\mathbb {R}}$ and $0\leqslant \delta ,\rho \leqslant 1.$ The L-symbol class $S^m_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I})$ consists of those functions $a(x,\xi )$ which are smooth in x for all $\xi \in {\mathcal I},$ and which satisfy

$$\begin{aligned} \left| \Delta _{(x)}^\alpha D^{(\beta )}_{x} a(x,\xi ) \right| \leqslant C_{a\alpha \beta m} \ \langle \xi \rangle ^{m-\rho |\alpha |+\delta |\beta |} \end{aligned}$$

(2.20)

for all $x\in \overline{\Omega },$ for all $\alpha ,\beta \geqslant 0,$ and for all $\xi \in {\mathcal I}.$ Here, the operators $D^{(\beta )}_{x}$ are defined in Proposition 2.25. We will often denote them simply by $D^{(\beta )}.$

The class $S^m_{1,0}(\overline{\Omega }\times {\mathcal I})$ will be often denoted by writing simply $S^m(\overline{\Omega }\times {\mathcal I}).$ In (2.20), we assume that the inequality is satisfied for $x\in \Omega$ and it extends to the closure $\overline{\Omega }.$ Furthermore, we define

$$\begin{aligned} S^{\infty }_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I}):=\bigcup _{m\in {\mathbb {R}}}S^{m}_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I}) \end{aligned}$$

and

$$\begin{aligned} S^{-\infty }(\overline{\Omega }\times {\mathcal I}):=\bigcap _{m\in {\mathbb {R}}}S^{m}(\overline{\Omega }\times {\mathcal I}). \end{aligned}$$

When we have two L-strongly admissible collections, expressing one in terms of the other similarly to Proposition 2.25 and arguing similarly to [37], we can convince ourselves that for $\rho >\delta$ the definition of the symbol class does not depend on the choice of an L-strongly admissible collection.

Analogously, we define the ${L^{*}}$-symbol class $\widetilde{S}^m_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I})$ as the space of those functions $a(x,\xi )$ which are smooth in x for all $\xi \in {\mathcal I},$ and satisfy

$$\begin{aligned} \left| \widetilde{\Delta }_{(x)}^\alpha \widetilde{D}^{(\beta )} a(x,\xi ) \right| \leqslant C_{a\alpha \beta m} \ \langle \xi \rangle ^{m-\rho |\alpha |+\delta |\beta |} \end{aligned}$$

for all $x\in \overline{\Omega },$ for all $\alpha ,\beta \geqslant 0,$ and for all $\xi \in {\mathcal I}.$ Similarly, we can define classes $\widetilde{S}^{\infty }_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I})$ and $\widetilde{S}^{-\infty }(\overline{\Omega }\times {\mathcal I}).$

If $a\in S^m_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I}),$ it is convenient to denote by $a(X,D)= \textrm{Op}_L (a)$ the corresponding L-pseudo-differential operator defined by

$$\begin{aligned} \textrm{Op}_L(a)f(x)=a(X,D)f(x):=\sum _{\xi \in {\mathcal I}} u_{\xi }(x)\ a(x,\xi )\widehat{f}(\xi ). \end{aligned}$$

(2.21)

The set of operators $\textrm{Op}_L (a)$ of the form (2.21) with $a\in S^m_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I})$ will be denoted by $\textrm{Op}_L (S^m_{\rho ,\delta } (\overline{\Omega }\times {\mathcal I})),$ or by $\Psi ^m_{\rho ,\delta } (\overline{\Omega }\times {\mathcal I}).$ If an operator A satisfies $A\in \mathrm{Op_L}(S^m_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I})),$ we denote its L-symbol by $\sigma _{A}=\sigma _{A}(x, \xi ), \,\, x\in \overline{\Omega }, \, \xi \in {\mathcal I}.$

Remark 2.29

(Topology on $S^{m}_{\rho , \delta }(\overline{\Omega }\times {\mathcal I})$ ($\widetilde{S}^{m}_{\rho , \delta }(\overline{\Omega }\times {\mathcal I})$)). The set $S^{m}_{\rho , \delta }(\overline{\Omega }\times {\mathcal I})$ ($\widetilde{S}^{m}_{\rho , \delta }(\overline{\Omega }\times {\mathcal I})$) of symbols has a natural topology. Let us consider the functions $p_{\alpha \beta }^{l}: S^{m}_{\rho , \delta }(\overline{\Omega }\times {\mathcal I})\rightarrow {\mathbb {R}}$ ($\widetilde{p}_{\alpha \beta }^{l}: \widetilde{S}^{m}_{\rho , \delta }(\overline{\Omega }\times {\mathcal I})\rightarrow {\mathbb {R}}$) defined by

$$\begin{aligned}{} & {} p_{\alpha \beta }^{l}(\sigma ):=\textrm{sup}\left[ {\left| \Delta _{(x)}^{\alpha }D^{(\beta )}\sigma (x, \xi )\right| }{\langle \xi \rangle ^{-l+\rho |\alpha |-\delta |\beta |}}:\,\, (x, \xi )\in \overline{\Omega }\times {\mathcal I}\right] \\{} & {} \left( \widetilde{p}_{\alpha \beta }^{l}(\sigma ):=\textrm{sup}\left[ {\left| \widetilde{\Delta }_{(x)}^{\alpha }\widetilde{D}^{(\beta )}\sigma (x, \xi )\right| }{\langle \xi \rangle ^{-l+\rho |\alpha |-\delta |\beta |}}:\,\, (x, \xi )\in \overline{\Omega }\times {\mathcal I}\right] \right) . \end{aligned}$$

Now, $\{p_{\alpha \beta }^{l}\}$ ($\{\widetilde{p}_{\alpha \beta }^{l}\}$) is a countable family of seminorms, and they define a Fréchet topology on $S^{m}_{\rho , \delta }(\overline{\Omega }\times {\mathcal I})$ ($\widetilde{S}^{m}_{\rho , \delta }(\overline{\Omega }\times {\mathbb {Z}})$).

The next theorem is a prelude to asymptotic expansions, which are the main tools in the symbolic analysis of L-pseudo-differential operators.

Theorem 2.30

(Asymptotic sums of symbols) Let $(m_{j})_{j=0}^{\infty }\subset {\mathbb {R}}$ be a sequence such that $m_{j}>m_{j+1},$ and $m_{j}\rightarrow -\infty$ as $j\rightarrow \infty ,$ and $\sigma _{j}\in S^{m_{j}}_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I})$ for all $j\in {\mathcal I}.$ Then there exists an L-symbol $\sigma \in S^{m_{0}}_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I})$ such that for all $N\in {\mathcal I},$

$$\begin{aligned} \sigma {\mathop {\sim }\limits ^{m_{N},\rho ,\delta }}\sum _{j=0}^{N-1}\sigma _{j}. \end{aligned}$$

We will now look at the formulae in [32] for the symbol of the adjoint operator and for the composition of pseudo-differential operators, which establish the pseudo-differential calculus for boundary value problems from the non-harmonic point of view.

Theorem 2.31

(Adjoint operators) Let $0\leqslant \delta <\rho \leqslant 1.$ Let $A\in \textrm{Op}_L (S^m_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I})).$ Assume that the conjugate symbol class $\widetilde{S}^{m}_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I})$ is defined with strongly admissible functions $\widetilde{q}_{j}(x,y):=\overline{q_{j}(x,y)},$ which are ${L}^{*}$-strongly admissible. Then the adjoint of A satisfies $A^{*}\in \textrm{Op}_{L^*}(\widetilde{S}^{m}_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I})),$ with its ${L}^*$-symbol $\tau _{A^*}\in \widetilde{S}^{m}_{\rho ,\delta }(\overline{\Omega }\times {\mathcal I})$ having the asymptotic expansion

$$\begin{aligned} \tau _{A^*}(x,\xi ) \sim \sum _\alpha \frac{1}{\alpha !} \widetilde{\Delta }_x^\alpha D_x^{(\alpha )}\overline{\sigma _A(x,\xi )}. \end{aligned}$$

We now formulate the composition formula given [32].

Theorem 2.32

Let $m_{1}, m_{2}\in {\mathbb {R}}$ and $\rho >\delta \geqslant 0.$ Let $A, B:C_{{L}}^{\infty }(\overline{\Omega })\rightarrow C_{{ L}}^{\infty }(\overline{\Omega })$ be continuous and linear, and assume that their L-symbols satisfy

$$\begin{aligned} |\Delta _{(x)}^{\alpha }\sigma _{A}(x,\xi )|&\leqslant C_{\alpha }\langle \xi \rangle ^{m_{1}-\rho |\alpha |},\\ |D^{(\beta )}\sigma _{B}(x,\xi )|&\leqslant C_{\beta }\langle \xi \rangle ^{m_{2}+\delta |\beta |}, \end{aligned}$$

for all $\alpha ,\beta \geqslant 0,$ uniformly in $x\in \overline{\Omega }$ and $\xi \in {\mathcal I}.$ Then,

$$\begin{aligned} \sigma _{AB}(x,\xi )\sim \sum _{\alpha \geqslant 0} \frac{1}{\alpha !}(\Delta _{(x)}^{\alpha }\sigma _{A}(x,\xi ))D^{(\alpha )}\sigma _{B}(x,\xi ), \end{aligned}$$

where the asymptotic expansion means that for every $N\in {{\mathbb {N}}},$ we have

$$\begin{aligned} |\sigma _{AB}(x,\xi )-\sum _{|\alpha |<N}\frac{1}{\alpha !} (\Delta _{(x)}^{\alpha }\sigma _{A}(x,\xi ))D^{(\alpha )}\sigma _{B}(x,\xi )|\leqslant C_{N}\langle \xi \rangle ^{m_{1}+m_{2}-(\rho -\delta )N}. \end{aligned}$$

2.6 Construction of parametrices

Now, we will present a technical result about the existence of parametrices for L-elliptic operators in the global pseudo-differential calculus from [32]. We denote ${S}^{-\infty }(M\times {\mathcal {I}})=\cap _{m\in {\mathbb {R}}}{S}^{m}_{\rho ,\delta }(M\times {\mathcal {I}})=\cap _{m\in {\mathbb {R}}}{S}^{m}_{1,0}(M\times {\mathcal {I}}).$

Proposition 2.33

Let $m\in {\mathbb {R}},$ and let $0\leqslant \delta <\rho \leqslant 1.$ Let $a=a(x,\xi )\in {S}^{m}_{\rho ,\delta }(M\times {\mathcal {I}}).$ Assume also that $a(x,\xi )$ is invertible for every $(x,\xi )\in M\times {\mathcal {I}}$ and satisfies

$$\begin{aligned} \sup _{(x,\xi )\in M\times {\mathcal {I}}} \vert \langle \xi \rangle ^ma(x,\xi )^{-1}\vert <\infty . \end{aligned}$$

Then,  there exists $B\in {S}^{-m}_{\rho ,\delta }(M\times {\mathcal {I}}),$ such that $AB-I,BA-I\in {S}^{-\infty }(M\times {\mathcal {I}}).$ Moreover,  the symbol of B satisfies the following asymptotic expansion:

$$\begin{aligned} \widehat{B}(x,\xi )\sim \sum _{N=0}^\infty \widehat{B}_{N}(x,\xi ),\quad (x,\xi )\in M\times {\mathcal {I}}, \end{aligned}$$

where $\widehat{B}_{N}(x,\xi )\in {S}^{-m-(\rho -\delta )N}_{\rho ,\delta }(M\times {\mathcal {I}})$ obeys the inductive formula:

$$\begin{aligned} \widehat{B}_{N}(x,\xi )=-a(x,\xi )^{-1}\left( \sum _{k=0}^{N-1}\sum _{|\gamma |=N-k}(\Delta _{(x)}^{\gamma } a(x,\xi ))(D_{x}^{(\gamma )}\widehat{B}_{k}(x,\xi ))\right) ,\quad N\geqslant 1, \end{aligned}$$

with $\widehat{B}_{0}(x,\xi )=a(x,\xi )^{-1}.$

3 Parameter L-ellipticity

We start our contributions to the pseudo-differential calculus in the context of non-harmonic analysis developed by the last two authors in [32], by developing the functional calculus for Hörmander classes $\text {Op}(S^{m}_{\rho ,\delta }(M\times {\mathcal {I}})).$ For this, we need a more wide notion of ellipticity, which we introduce as follows.

Definition 3.1

Let $m>0,$ and let $0\leqslant \delta <\rho \leqslant 1.$ Let $m>0,$ and let $0\leqslant \delta <\rho \leqslant 1.$ Let $\Lambda$ be a sector in the complex plane ${\mathbb {C}}.$ Let $a=a(x,\xi )\in {S}^{m}_{\rho ,\delta }(M\times {\mathcal {I}}).$ Assume also that $R_{\lambda }(x,\xi )^{-1}:=a(x,\xi )-\lambda \ne 0$ for every $(x,\xi )\in M\times {\mathcal {I}},$ and $\lambda \in \Lambda .$ We say that a is parameter L-elliptic with respect to $\Lambda ,$ if

$$\begin{aligned} \sup _{\lambda \in \Lambda }\sup _{(x,\xi )\in M\times {\mathcal {I}}}\vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^{m}R_{\lambda }(x,\xi )\vert <\infty . \end{aligned}$$

The following theorem classifies the resolvent $R_{\lambda }(x,\xi )$ of a parameter L-elliptic symbol a.

Theorem 3.2

Let $m>0,$ and let $0\leqslant \delta <\rho \leqslant 1.$ If a is parameter L-elliptic with respect to $\Lambda ,$ the following estimate

$$\begin{aligned} \sup _{\lambda \in \Lambda }\sup _{(x,\xi )\in M\times {\mathcal {I}}}\vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^{m(k+1)}\langle \xi \rangle ^{\rho |\alpha |-\delta |\beta |}\partial _{\lambda }^kD_{x}^{(\beta )} \Delta _{(x)}^{\alpha }R_{\lambda }(x,\xi )\vert <\infty \end{aligned}$$

holds true for all $\alpha ,\beta \in {\mathbb {N}}_0^n$ and $k\in {\mathbb {N}}_0.$

Proof

We will split the proof in the cases $|\lambda |\leqslant 1,$ and $|\lambda |> 1,$ where $\lambda \in \Lambda .$ It is possible, however, that one of these two cases could be trivial in the sense that $\Lambda _{1}:=\{\lambda \in \Lambda :|\lambda |\leqslant 1\}$ or $\Lambda _{1}^{c}:=\{\lambda \in \Lambda :|\lambda |> 1\}$ could be an empty set. In such a case, the proof is self-contained in the situation that we will consider where we assume that $\Lambda _{1}$ and $\Lambda _{1}^c$ are not trivial sets. For $|\lambda |\leqslant 1,$ observe that

$$\begin{aligned}&\vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^{m(k+1)}\langle \xi \rangle ^{\rho |\alpha |-\delta |\beta |}\partial _{\lambda }^kD_{x}^{(\beta )} \Delta _{(x)}^{\alpha }R_{\lambda }(x,\xi )\vert \\&\quad =\vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^{m(k+1)} \langle \xi \rangle ^{-m(k+1)}\langle \xi \rangle ^{m(k+1)+\rho |\alpha | -\delta |\beta |}\partial _{\lambda }^kD_{x}^{(\beta )}\Delta _{(x)}^{\alpha } R_{\lambda }(x,\xi )\vert \\&\quad \leqslant \vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^{m(k+1)} \langle \xi \rangle ^{-m(k+1)}\vert \\&\qquad \times \vert \langle \xi \rangle ^{m(k+1)+\rho |\alpha |- \delta |\beta |}\partial _{\lambda }^kD_{x}^{(\beta )} \Delta _{(x)}^{\alpha }R_{\lambda }(x,\xi )\vert . \end{aligned}$$

We note that

$$\begin{aligned}&\vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^{m(k+1)}\langle \xi \rangle ^{-m(k+1)}\vert \\&\quad = \vert (|\lambda |^{\frac{1}{m}}\langle \xi \rangle ^{-1}+1)^{m(k+1)} \vert = \vert |\lambda |^{\frac{1}{m}}\langle \xi \rangle ^{-1}+1\vert ^{m(k+1)}\\&\quad \leqslant \sup _{|\lambda |\in [0,1]}\vert (|\lambda |^{\frac{1}{m}}\langle \xi \rangle ^{-1}+1)^{m(k+1)}\vert =O(1). \end{aligned}$$

On the other hand, we can prove that

$$\begin{aligned} \vert \langle \xi \rangle ^{m(k+1)+\rho |\alpha |-\delta |\beta |} \partial _{\lambda }^kD_{x}^{(\beta )}\Delta _{(x)}^{\alpha }R_{\lambda }(x,\xi )\vert =O(1). \end{aligned}$$

For $k=1,$ $\partial _{\lambda }R_{\lambda }(x,\xi )= R_{\lambda }(x,\xi )^{2}.$ This can be deduced from the Leibniz rule; indeed,

$$\begin{aligned} 0=\partial _{\lambda }(R_{\lambda }(x,\xi )(a(x,\xi )-\lambda )) =(\partial _{\lambda }R_{\lambda }(x,\xi )) (a(x,\xi )-\lambda )+ R_{\lambda }(x,\xi )(-1) \end{aligned}$$

implies that

$$\begin{aligned} -\partial _{\lambda }(R_{\lambda }(x,\xi ))(a(x,\xi )-\lambda )=- R_{\lambda }(x,\xi ). \end{aligned}$$

Because $(a(x,\xi )-\lambda )=R_{\lambda }(x,\xi )^{-1},$ the identity for the first derivative of $R_\lambda ,$ $\partial _{\lambda }R_{\lambda }$ follows. So, from the chain rule, we obtain that the term of higher-order expanding the derivative $\partial _{\lambda }^kR_{\lambda }$ is a multiple of $R_{\lambda }^{k+1}.$ So, $R_{\lambda }\in S^{-m}_{\rho ,\delta }(M\times {\mathcal {I}}).$ The global pseudo-differential calculus implies that $R_{\lambda }^{k+1}\in S^{-m(k+1)}_{\rho ,\delta }(M\times {\mathcal {I}}).$ This fact and the compactness of $\Lambda _1\subset {\mathbb {C}}$ provide us the uniform estimate

$$\begin{aligned} \sup _{\lambda \in \Lambda _1}\sup _{(x,\xi )\in M\times {\mathcal {I}}}\vert \langle \xi \rangle ^{m(k+1)+\rho |\alpha |-\delta |\beta |} \partial _{\lambda }^kD_{x}^{(\beta )}\Delta _{(x)}^{\alpha }R_{\lambda }(x,\xi )\vert <\infty . \end{aligned}$$

Now, we will analyse the situation for $\lambda \in \Lambda _1^c.$ We will use induction over k to prove that

$$\begin{aligned} \sup _{\lambda \in \Lambda _1^c}\sup _{(x,\xi )\in M\times {\mathcal {I}}}\vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^{m(k+1)}\langle \xi \rangle ^{\rho |\alpha |-\delta |\beta |}\partial _{\lambda }^kD_{x}^{(\beta )} \Delta _{(x)}^{\alpha }R_{\lambda }(x,\xi )\vert <\infty . \end{aligned}$$

For $k=0,$ notice that

$$\begin{aligned}&\vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^{m(k+1)}\langle \xi \rangle ^{\rho |\alpha |-\delta |\beta |}\partial _{\lambda }^kD_{x}^{(\beta )} \Delta _{(x)}^{\alpha }R_{\lambda }(x,\xi )\vert \\&\quad =\vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^{m}\langle \xi \rangle ^{\rho |\alpha |-\delta |\beta |}D_{x}^{(\beta )}\Delta _{(x)}^{\alpha } (a(x,\xi )-\lambda )^{-1}\vert , \end{aligned}$$

and denoting $\theta =\frac{1}{|\lambda |},$ $\omega =\frac{\lambda }{|\lambda |},$ we have

$$\begin{aligned}&\vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^{m(k+1)}\langle \xi \rangle ^{\rho |\alpha |-\delta |\beta |}\partial _{\lambda }^kD_{x}^{(\beta )} \Delta _{(x)}^{\alpha }R_{\lambda }(x,\xi )\vert \\&\quad =\vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle ^{m})| \lambda |^{-1}\langle \xi \rangle ^{\rho |\alpha |-\delta |\beta |} D_{x}^{(\beta )}\Delta _{(x)}^{\alpha }(\theta \times a(x,\xi )-\omega )^{-1}\vert \\&\quad =\vert (1+|\lambda |^{-\frac{1}{m}}\langle \xi \rangle )^{m}\langle \xi \rangle ^{\rho |\alpha |-\delta |\beta |}D_{x}^{(\beta )}\Delta _{(x)}^{\alpha } (\theta \times a(x,\xi )-\omega )^{-1}\vert \\&\quad =\vert (1+\theta ^{\frac{1}{m}}\langle \xi \rangle )^{m} \langle \xi \rangle ^{\rho |\alpha |-\delta |\beta |}D_{x}^{(\beta )} \Delta _{(x)}^{\alpha }(\theta \times a(x,\xi )-\omega )^{-1}\vert \\&\quad =\vert (1+\theta ^{\frac{1}{m}}\langle \xi \rangle )^{m}\langle \xi \rangle ^{-m}\langle \xi \rangle ^{m+\rho |\alpha |-\delta |\beta |} D_{x}^{(\beta )}\Delta _{(x)}^{\alpha }(\theta \times a(x,\xi )-\omega )^{-1}\vert \\&\quad \leqslant \vert (1+\theta ^{\frac{1}{m}}\langle \xi \rangle )^{m}\langle \xi \rangle ^{-m}\vert \vert \langle \xi \rangle ^{m+\rho |\alpha |-\delta |\beta |}D_{x}^{(\beta )}\Delta _{(x)}^{\alpha }(\theta \times a(x,\xi )-\omega )^{-1}\vert . \end{aligned}$$

Observe that $(1+\theta ^{\frac{1}{m}}\langle \xi \rangle )^{m}\langle \xi \rangle ^{-m} \in S^{0}_{\rho ,\delta }(M\times {\mathcal {I}}),$ is uniformly bounded in $\theta \in [0,1].$ Similarly, observe that

$$\begin{aligned} \sup _{\theta \in [0,1]} \vert \langle \xi \rangle ^{m+\rho |\alpha |-\delta |\beta |}D_{x}^{(\beta )}\Delta _{(x)}^{\alpha }(\theta \times a(x,\xi )-\omega )^{-1}\vert <\infty . \end{aligned}$$

Indeed, $(\theta \times a(x,\xi )-\omega )^{-1}\in S^{-m}_{\rho ,\delta }(M\times {\mathcal {I}}),$ with $\theta \in [0,1]$ and $\omega$ being an element of the complex circle. The case $k\geqslant 1$ for $\lambda \in \Lambda _1^c$ can be proved in an analogous way. $\square$

Combining Proposition 2.33 and Theorem 3.2 we obtain the following corollaries.

Corollary 3.3

Let $m>0,$ and let $0\leqslant \delta <\rho \leqslant 1.$ Let a be a parameter L-elliptic symbol with respect to $\Lambda .$ Then there exists a parameter-dependent parametrix of $A-\lambda I,$ with symbol $a^{-\#}(x,\xi ,\lambda )$ satisfying the estimates

$$\begin{aligned} \sup _{\lambda \in \Lambda }\sup _{(x,\xi )\in M\times {\mathcal {I}}}\vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^{m(k+1)}\langle \xi \rangle ^{\rho |\alpha |-\delta |\beta |}\partial _{\lambda }^kD_{x}^{(\beta )} \Delta _{(x)}^{\alpha }a^{-\#}(x,\xi ,\lambda )\vert <\infty , \end{aligned}$$

for all $\alpha ,\beta \in {\mathbb {N}}_0^n$ and $k\in {\mathbb {N}}_0.$

Corollary 3.4

Let $m>0,$ and let $a\in S^m_{\rho ,\delta }(M\times {\mathcal {I}})$ where $0\leqslant \delta <\rho \leqslant 1.$ Let us assume that $\Lambda$ is a subset of the $L^2$-resolvent set of A,  $\text {Resolv}(A):={\mathbb {C}}{\setminus } \text {Spec}(A).$ Then $A-\lambda I$ is invertible on ${\mathcal {D}}'_L(M)$ and the symbol of the resolvent operator ${\mathcal {R}}_{\lambda }:=(A-\lambda I)^{-1},$ $\widehat{{\mathcal {R}}}_{\lambda }(x,\xi )$ belongs to $S^{-m}_{\rho ,\delta }(M\times {\mathcal {I}}).$

4 Global functional calculus

In this section, we develop the global functional calculus for the classes $S^{m}_{\rho ,\delta }(M\times {\mathcal {I}}).$ The global pseudo-differential calculus will be applied to obtain a global Gårding inequality.

4.1 Symbols defined by functions of pseudo-differential operators

Let $a\in S^m_{\rho ,\delta }(M\times {\mathcal {I}})$ be a parameter L-elliptic symbol of order $m>0$ with respect to the sector $\Lambda \subset {\mathbb {C}}.$ For $A=\text {Op}(a),$ let us define the operator F(A) by the (Dunford–Riesz) complex functional calculus

$$\begin{aligned} F(A)=-\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }F(z)(A-zI)^{-1}{\textrm{d}}z, \end{aligned}$$

(4.1)

where

(CI):

$\Lambda _{\varepsilon }:=\Lambda \cup \{z:|z|\leqslant \varepsilon \},$ $\varepsilon >0,$ and $\Gamma =\partial \Lambda _\varepsilon \subset \text {Resolv}(A)$ is a positively oriented curve in the complex plane ${\mathbb {C}}.$

(CII):

F is a holomorphic function in ${\mathbb {C}}{\setminus } \Lambda _{\varepsilon },$ and continuous on its closure.

(CIII):

We will assume decay of F along $\partial \Lambda _\varepsilon$ in order that the operator (4.1) will be densely defined on $C^\infty _L(M)$ in the strong sense of the topology on $L^2(M).$

Now, we will compute the global symbols for operators defined by this complex functional calculus. So, we will assume the $\text {WZ}$ condition.

Lemma 4.1

Let $a\in S^m_{\rho ,\delta }(M\times {\mathcal {I}})$ be a parameter L-elliptic symbol of order $m>0$ with respect to the sector $\Lambda \subset {\mathbb {C}}.$ Let $F(A):C^\infty _L(M)\rightarrow {\mathcal {D}}'_L(M)$ be the operator defined by the analytical functional calculus as in (4.1). Under the assumptions $\text {(CI)},$ $\text {(CII)},$ and $\text {(CIII)},$ the global symbol of F(A),  $\sigma _{F(A)}(x,\xi )$ is given by : 

$$\begin{aligned} \sigma _{F(A)}(x,\xi )=-\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }F(z)\widehat{{\mathcal {R}}}_z(x,\xi ){\textrm{d}}z, \end{aligned}$$

where ${\mathcal {R}}_z=(A-zI)^{-1}$ denotes the resolvent of A,  and $\widehat{{\mathcal {R}}}_z(x,\xi )\in S^{-m}_{\rho ,\delta }(M\times {\mathcal {I}})$ its symbol.

Proof

From Corollary 3.4, we have that $\widehat{{\mathcal {R}}}_z(x,\xi )\in S^{-m}_{\rho ,\delta }(M\times {\mathcal {I}}).$ Now, observe that

$$\begin{aligned} \sigma _{F(A)}(x,\xi )=u_\xi (x)^{-1}F(A)u_\xi (x)=-\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }F(z)u_\xi (x)^{-1}(A-zI)^{-1}u_\xi (x){\textrm{d}}z. \end{aligned}$$

We finish the proof by observing that $\widehat{{\mathcal {R}}}_z(x,\xi )=u_\xi (x)^{-1}(A-zI)^{-1}u_\xi (x),$ for every $z\in \text {Resolv}(A).$ $\square$

Assumption (CIII) will be clarified in the following theorem where we show that the global pseudo-differential calculus is stable under the action of the complex functional calculus.

Theorem 4.2

Let $m>0,$ and let $0\leqslant \delta <\rho \leqslant 1.$ Let $a\in S^m_{\rho ,\delta }(M\times {\mathcal {I}})$ be a parameter L-elliptic symbol with respect to $\Lambda .$ Let us assume that F satisfies the estimate $|F(\lambda )|\leqslant C|\lambda |^s$ uniformly in $\lambda ,$ for some $s<0.$ Then the symbol of F(A),  $\sigma _{F(A)}\in S^{ms}_{\rho ,\delta }(M\times {\mathcal {I}})$ admits an asymptotic expansion of the form

$$\begin{aligned} \sigma _{F(A)}(x,\xi )\sim \sum _{N=0}^\infty \sigma _{{B}_{N}}(x,\xi ),\quad (x,\xi )\in M\times {\mathcal {I}}, \end{aligned}$$

(4.2)

where $\sigma _{{B}_{N}}(x,\xi )\in {S}^{ms-(\rho -\delta )N}_{\rho ,\delta }(M\times {\mathcal {I}})$ and

$$\begin{aligned} \sigma _{{B}_{0}}(x,\xi )=-\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }F(z)(a(x,\xi )-z)^{-1}{\textrm{d}}z\in {S}^{ms}_{\rho ,\delta }(M\times {\mathcal {I}}). \end{aligned}$$

Moreover, 

$$\begin{aligned} \sigma _{F(A)}(x,\xi )\equiv -\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }F(z)a^{-\#}(x,\xi ,\lambda ){\textrm{d}}z \text { mod } {S}^{-\infty }(M\times {\mathcal {I}}), \end{aligned}$$

where $a^{-\#}(x,\xi ,\lambda )$ is the symbol of the parametrix to $A-\lambda I,$ in Corollary 3.3.

Proof

First, we need to prove that the condition $|F(\lambda )|\leqslant C|\lambda |^s$ uniformly in $\lambda ,$ for some $s<0,$ is enough to guarantee that

$$\begin{aligned} \sigma _{{B}_{0}}(x,\xi ):=-\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }F(z)(a(x,\xi )-z)^{-1}{\textrm{d}}z \end{aligned}$$

is a well-defined global symbol. From Theorem 3.2, we deduce that $(a(x,\xi )-z)^{-1}$ satisfies the estimate

$$\begin{aligned} \vert (|z|^{\frac{1}{m}}+\langle \xi \rangle )^{m(k+1)}\langle \xi \rangle ^{\rho |\alpha |-\delta |\beta |}\partial _{z}^kD_{x}^{(\beta )} \Delta _{(x)}^{\alpha }(a(x,\xi )-z)^{-1}\vert <\infty . \end{aligned}$$

Observe that

$$\begin{aligned}&\vert (a(x,\xi )-z)^{-1}\vert \\&\quad =\vert (|z|^{\frac{1}{m}}+\langle \xi \rangle )^{-m}(|z|^{\frac{1}{m}}+ \langle \xi \rangle )^{m}(a(x,\xi )-z)^{-1}\vert \\&\quad \lesssim (|z|^{\frac{1}{m}}+\langle \xi \rangle )^{-m}\\&\quad \leqslant |z|^{-1}, \end{aligned}$$

and the condition $s<0$ implies that

$$\begin{aligned} \left| \frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }F(z)(a(x,\xi )-z)^{-1}{\textrm{d}}z\right| \lesssim \oint _{\partial \Lambda _\varepsilon }|z|^{-1+s}|{\textrm{d}}z|<\infty , \end{aligned}$$

uniformly in $(x,\xi )\in M\times {\mathcal {I}}.$ To check that $\sigma _{B_0}\in {S}^{ms}_{\rho ,\delta }(M\times {\mathcal {I}}),$ let us analyse the cases $-1<s<0$ and $s\leqslant -1$ separately:

Case 1: Let us analyse first the situation of $-1<s<0.$ We observe that

$$\begin{aligned}&\vert \langle \xi \rangle ^{-ms+\rho |\alpha |-\delta |\beta |}D_{x}^{(\beta )} \Delta _{(x)}^{\alpha }\sigma _{B_0}(x,\xi )\vert \\&\quad \leqslant \frac{C}{2\pi }\oint _{\partial \Lambda _\varepsilon } |z|^{s}\vert \langle \xi \rangle ^{-ms+\rho |\alpha |-\delta |\beta |}D_{x}^{(\beta )} \Delta _{(x)}^{\alpha }(a(x,\xi )-z)^{-1}\vert |{\textrm{d}}z|. \end{aligned}$$

Now, we will estimate the operator norm inside of the integral. Indeed, the identity

$$\begin{aligned}&\vert \langle \xi \rangle ^{-ms+\rho |\alpha |-\delta |\beta |}D_{x}^{(\beta )} \Delta _{(x)}^{\alpha }(a(x,\xi )-z)^{-1}\vert \\&\quad =\vert (|z|^{\frac{1}{m}}+\langle \xi \rangle )^{-m}(|z|^{\frac{1}{m}}+\langle \xi \rangle )^{m}\langle \xi \rangle ^{-ms+\rho |\alpha |-\delta |\beta |}D_{x}^{(\beta )} \Delta _{(x)}^{\alpha }(a(x,\xi )-z)^{-1}\vert \end{aligned}$$

implies that

$$\begin{aligned}&\vert \langle \xi \rangle ^{-ms+\rho |\alpha |-\delta |\beta |}D_{x}^{(\beta )} \Delta _{(x)}^{\alpha }(a(x,\xi )-z)^{-1}\vert \lesssim \vert (|z|^{\frac{1}{m}}+\langle \xi \rangle )^{-m}\langle \xi \rangle ^{-ms}\vert , \end{aligned}$$

where we have used that

$$\begin{aligned} \sup _{z\in \partial \Lambda _\varepsilon } \sup _{(x,\xi )} \vert (|z|^{\frac{1}{m}}+\langle \xi \rangle )^{m}\langle \xi \rangle ^{\rho |\alpha |-\delta |\beta |}D_{x}^{(\beta )} \Delta _{(x)}^{\alpha }(a(x,\xi )-z)^{-1}\vert <\infty . \end{aligned}$$

Consequently, by using that $s<0,$ we deduce

$$\begin{aligned}&\frac{C}{2\pi }\oint _{\partial \Lambda _\varepsilon } |z|^{s}\vert \langle \xi \rangle ^{ms+\rho |\alpha |-\delta |\beta |}D_{x}^{(\beta )} \Delta _{(x)}^{\alpha }(a(x,\xi )-z)^{-1}\vert |{\textrm{d}}z|\\&\quad \lesssim \frac{C}{2\pi }\oint _{\partial \Lambda _\varepsilon } |z|^{s}\vert (|z|^{\frac{1}{m}}+\langle \xi \rangle )^{-m} \langle \xi \rangle ^{-ms}\vert |{\textrm{d}}z| . \end{aligned}$$

To study the convergence of the last contour integral, we only need to check the convergence of $\int _{1}^{\infty }r^s(r^{\frac{1}{m}}+\varkappa )^{-m}\varkappa ^{-ms}{\textrm{d}}r,$ where $\varkappa >1$ is a parameter. The change of variable $r=\varkappa ^{m}t$ implies that

$$\begin{aligned} \int _{1}^{\infty }r^s(r^{\frac{1}{m}}+\varkappa )^{-m}\varkappa ^{-ms}{\textrm{d}}r&= \int _{\varkappa ^{-m}}^{\infty }\varkappa ^{ms}t^s(\varkappa t^{\frac{1}{m}}+ \varkappa )^{-m}\varkappa ^{-ms}\varkappa ^m{\textrm{d}}t\\&=\int _{\varkappa ^{-m}}^{\infty }t^s(t^{\frac{1}{m}}+1)^{-m}{\textrm{d}}t\lesssim \int _{\varkappa ^{-m}}^{1}t^s{\textrm{d}}t+\int _{1}^{\infty }t^{-1+s}<\infty . \end{aligned}$$

Indeed, for $t\rightarrow \infty ,$ $t^s(t^{\frac{1}{m}}+1)^{-m}\lesssim t^{-1+s},$ and we conclude the estimate because $\int _{1}^{\infty } t^{-1+s'}{\textrm{d}}t<\infty ,$ for all $s'<0.$ On the other hand, the condition $-1<s<0$ implies that

$$\begin{aligned} \int _{\varkappa ^{-m}}^{1}t^s{\textrm{d}}t=\frac{1}{1+s}-\frac{\varkappa ^{-m(1+s)}}{1+s}= O(1). \end{aligned}$$

Case 2. In the case where $s\leqslant -1,$ we can find an analytic function $\tilde{G}(z)$ such that it is a holomorphic function in ${\mathbb {C}}{\setminus } \Lambda _{\varepsilon },$ and continuous on its closure and additionally satisfying that $F(\lambda )=\tilde{G}(\lambda )^{1+[-s]}.$¹⁰ In this case, $\tilde{G}(A),$ defined by the complex functional calculus

$$\begin{aligned} \tilde{G}(A)=-\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }\tilde{G}(z)(A-zI)^{-1}{\textrm{d}}z, \end{aligned}$$

has symbol belonging to ${S}^{\frac{sm}{1+[-s]}}_{\rho ,\delta }(M\times {\mathcal {I}}),$ this in view of Case 1, because $\tilde{G}$ satisfies the estimate $|\tilde{G}(\lambda )|\leqslant C|\lambda |^{\frac{s}{1+[-s]}},$ with $-1<\frac{s}{1+[-s]}<0.$ By observing that

$$\begin{aligned} \sigma _{F(A)}(x,\xi )&=-\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }F(z)\widehat{{\mathcal {R}}}_z(x,\xi ){\textrm{d}}z=-\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }\tilde{G}(z)^{1+[-s]}\widehat{{\mathcal {R}}}_z(x,\xi ){\textrm{d}}z\\&=\sigma _{\tilde{G}(A)^{1+[-s]}}(x,\xi ), \end{aligned}$$

and computing the symbol $\sigma _{\tilde{G}(A)^{1+[-s]}}(x,\xi )$ by iterating $1+[-s]$-times the asymptotic formula for the composition in the global pseudo-differential calculus, we can see that the term with higher order in such expansion is $\sigma _{\tilde{G}(A)}(x,\xi )^{1+[-s]}\in {S}^{ms}_{\rho ,\delta }(M\times {\mathcal {I}}).$ Consequently, we have proved that $\sigma _{F(A)}(x,\xi )\in {S}^{ms}_{\rho ,\delta }(M\times {\mathcal {I}}).$ This completes the proof for the first part of the theorem. For the second part of the proof, let us denote by $a^{-\#}(x,\xi ,\lambda )$ the symbol of the parametrix to $A-\lambda I,$ in Corollary 3.3. Let $P_{\lambda }=\text {Op}(a^{-\#}(\cdot ,\cdot ,\lambda )).$ Because $\lambda \in \text {Resolv}(A)$ for $\lambda \in \partial \Lambda _\varepsilon ,$ $(A-\lambda )^{-1}-P_{\lambda }$ is a smoothing operator. Consequently, from Lemma 4.1, we deduce that

$$\begin{aligned}&\sigma _{F(A)}(x,\xi )\\&\quad =-\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }F(z) \widehat{{\mathcal {R}}}_z(x,\xi ){\textrm{d}}z\\&\quad =-\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }F(z) a^{-\#}(x,\xi ,z){\textrm{d}}z-\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }F(z)(\widehat{{\mathcal {R}}}_z(x,\xi )-a^{-\#}(x,\xi ,z)){\textrm{d}}z\\&\quad \equiv -\frac{1}{2\pi i}\oint _{\partial \Lambda _\varepsilon }F(z)a^{-\#}(x,\xi ,z){\textrm{d}}z \text { mod } {S}^{-\infty }(M\times {\mathcal {I}}). \end{aligned}$$

The asymptotic expansion (4.2) came from the construction of the parametrix in the global pseudo-differential calculus (see Proposition 2.33). $\square$

4.2 Gårding inequality

In this subsection, we prove the Gårding inequality for the global pseudo-differential calculus. To do so, we need some preliminaries.

Proposition 4.3

Let $0\leqslant \delta <\rho \leqslant 1.$ Let $a\in S^m_{\rho ,\delta }(M\times {\mathcal {I}})$ be an L-elliptic global symbol where $m\geqslant 0$ and let us assume that $a>0.$ Then, a is parameter elliptic with respect to ${\mathbb {R}}_{-}:=\{z=x+i0:x<0\}\subset {\mathbb {C}}.$ Furthermore, for any number $s\in {\mathbb {C}},$

$$\begin{aligned} \widehat{B}(x,\xi )\equiv a(x,\xi )^s:=\exp (s\log (a(x,\xi ))),\quad (x,\xi )\in M\times {\mathcal {I}} \end{aligned}$$

defines a symbol $\widehat{B}(x,\xi )\in S^{m\times \text {Re}(s)}_{\rho ,\delta }(M\times {\mathcal {I}}).$

Proof

From the estimates,

$$\begin{aligned} \sup _{(x,\xi )}\vert \langle \xi \rangle ^{-m} a(x,\xi ) \vert<\infty ,\quad \sup _{(x,\xi )}\vert \langle \xi \rangle ^{m}a(x,\xi )^{-1} \vert <\infty , \end{aligned}$$

we deduce that

$$\begin{aligned} \langle \xi \rangle ^{-m}|a(x,\xi )|\subset [c,C], \end{aligned}$$

where $c,C>0$ are positive real numbers. Now, for every $\lambda \in {\mathbb {R}}_{-},$ we have

$$\begin{aligned}&\vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^m (a(x,\xi )-\lambda )^{-1}\vert \\&\quad \asymp \vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^m (\langle \xi \rangle ^m-\lambda )^{-1}(\langle \xi \rangle ^m-\lambda )(a(x,\xi )-\lambda )^{-1}\vert \\&\quad \lesssim \vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^m (\langle \xi \rangle ^m-\lambda )^{-1}\vert \vert (\langle \xi \rangle ^m-\lambda )(a(x,\xi ) -\lambda )^{-1}\vert \\&\quad \lesssim \vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^m (\langle \xi \rangle ^m-\lambda )^{-1}\vert . \end{aligned}$$

By fixing again $\lambda \in {\mathbb {R}}_{-},$ we observe that from the compactness of [0, 1/2] we deduce that

$$\begin{aligned} \sup _{0\leqslant |\lambda |\leqslant 1/2}\vert (|\lambda |^{\frac{1}{m}}+\langle \xi \rangle )^m (\langle \xi \rangle ^m-\lambda )^{-1}\vert&\asymp \sup _{0 \leqslant |\lambda |\leqslant 1/2}\vert \langle \xi \rangle ^m (\langle \xi \rangle ^m-\lambda )^{-1}\vert \\&\asymp \sup _{0\leqslant |\lambda |\leqslant 1/2}\vert \langle \xi \rangle ^m (\langle \xi \rangle ^m-\lambda )^{-1}\vert \\&\asymp \sup _{0\leqslant |\lambda |\leqslant 1/2}\vert (1-\lambda \langle \xi \rangle ^{-m})^{-1}\vert \\&\lesssim 1. \end{aligned}$$

On the other hand,

$$\begin{aligned}&\sup _{|\lambda |\geqslant 1/2}\vert (|\lambda |^{\frac{1}{m}}+ \langle \xi \rangle )^m (\langle \xi \rangle ^m-\lambda )^{-1}\vert \\&\quad =\sup _{|\lambda |\geqslant 1/2}\vert (|\lambda |^{\frac{1}{m}} \langle \xi \rangle ^{-1}+1)^m (1-\langle \xi \rangle ^{-m}\lambda )^{-1}\vert \\&\quad =\sup _{|\lambda |\geqslant 1/2}\vert (\langle \xi \rangle ^{-1} +|\lambda |^{-\frac{1}{m}})^m |\lambda |(1-\langle \xi \rangle ^{-m}\lambda )^{-1}\vert \\&\quad \lesssim \sup _{|\lambda |\geqslant 1/2}\vert \langle \xi \rangle ^{-m} | \lambda |(-\lambda )^{-1}\langle \xi \rangle ^m\vert \\&\quad =1. \end{aligned}$$

So, we have proved that a is parameter elliptic with respect to ${\mathbb {R}}_{-}.$ To prove that $\widehat{B}(x,\xi )\in S^{m\times \text {Re}(s)}_{\rho ,\delta }(M\times {\mathcal {I}}),$ we observe that for $\text {Re}(s)<0,$ Theorem 4.2 can be applied. If $\text {Re}(s)\geqslant 0,$ then there exists $k\in {\mathbb {N}}$ such that $\text {Re}(s)-k<0.$ Consequently, from the spectral calculus of matrices, we deduce that $a(x,\xi )^{\text {Re}(s)-k}\in S^{m\times (\text {Re}(s)-k)}_{\rho ,\delta }(M\times {\mathcal {I}}).$ So, from the global pseudo-differential calculus, we conclude that

$$\begin{aligned} a(x,\xi )^{s}=a(x,\xi )^{s-k}a(x,\xi )^{k}\in S^{m\times \text {Re}(s)}_{\rho ,\delta }(M\times {\mathcal {I}}). \end{aligned}$$

Thus, the proof is complete. $\square$

Corollary 4.4

Let $0\leqslant \delta ,\rho \leqslant 1.$ Let $a\in S^m_{\rho ,\delta }(M\times {\mathcal {I}}),$ be an L-elliptic symbol where $m\geqslant 0$ and let us assume that $a>0.$ Then, $\widehat{B}(x,\xi )\equiv a(x,\xi )^\frac{1}{2}:=\exp (\frac{1}{2}\log (a(x,\xi )))\in S^{\frac{m}{2}}_{\rho ,\delta }(M\times {\mathcal {I}}).$

Now, we prove the following lower bound.

Theorem 4.5

(Gårding inequality) For $0\leqslant \delta <\rho \leqslant 1,$ let $a(x,D):C^\infty _L(M)\rightarrow {\mathcal {D}}'_L(M)$ be an operator with symbol $a\in {S}^{m}_{\rho ,\delta }( M\times {\mathcal {I}}),$ $m\in {\mathbb {R}}.$ Let us assume that

$$\begin{aligned} A(x,\xi ):=\frac{1}{2}(a(x,\xi )+\overline{a(x,\xi )}),\,(x,\xi )\in M\times {\mathcal {I}},\quad a\in S^m_{\rho ,\delta }(M\times {\mathcal {I}}) \end{aligned}$$

satisfies

$$\begin{aligned} \vert \langle \xi \rangle ^mA(x,\xi )^{-1} \vert \leqslant C_{0}. \end{aligned}$$

Then,  there exist $C_{1},C_{2}>0,$ such that the lower bound

$$\begin{aligned} \text {Re}(a(x,D)u,u) \geqslant C_1\Vert u\Vert _{{\mathcal {H}}^{\frac{m}{2}}(M)}-C_2\Vert u\Vert _{L^2(M)}^2 \end{aligned}$$

holds true for every $u\in C^\infty _L(M).$

Proof

In view of that,

$$\begin{aligned} A(x,\xi ):=\frac{1}{2}(a(x,\xi )+\overline{a(x,\xi )}),\,(x,\xi )\in M\times {\mathcal {I}},\,\,a\in S^m_{\rho ,\delta }(M\times {\mathcal {I}}) \end{aligned}$$

satisfies

$$\begin{aligned} \vert \langle \xi \rangle ^mA(x,\xi )^{-1} \vert \leqslant C_{0}, \end{aligned}$$

and we get

$$\begin{aligned} \langle \xi \rangle ^{-m}A(x,\xi )\geqslant {1}/{C_0}. \end{aligned}$$

This implies that

$$\begin{aligned} A(x,\xi )\geqslant \frac{1}{C_0}\langle \xi \rangle ^m, \end{aligned}$$

and for $C_1\in (0, \frac{1}{C_0})$ we have that

$$\begin{aligned} A(x,\xi )-C_{1} \langle \xi \rangle ^m\geqslant \left( \frac{1}{C_0}-C_1\right) \langle \xi \rangle ^m>0. \end{aligned}$$

If $0\leqslant \delta <\rho \leqslant 1,$ from Corollary 4.4, we have

$$\begin{aligned} q(x,\xi ):=(A(x,\xi )-C_{1} \langle \xi \rangle ^m)^{\frac{1}{2}}\in S^{\frac{m}{2}}_{\rho ,\delta }(M\times {\mathcal {I}}). \end{aligned}$$

From the symbolic calculus, we obtain

$$\begin{aligned} q(x,D)q(x,D)^{*}= A(x,D)-C_{1}\text {Op}( \langle \xi \rangle ^m)+r(x,D),\quad r(x,\xi )\in S^{m-(\rho -\delta )}_{\rho ,\delta }(M\times {\mathcal {I}}). \end{aligned}$$

Now, let us assume that $u\in C^\infty _L(M).$ Denoting ${\mathcal {M}}_{s}:=(1+L^{\circ }L)^{\frac{s}{2\text {ord}(L)}}=\text {Op}(\langle \xi \rangle ^s),$ $s\in {\mathbb {R}},$ we have

$$\begin{aligned} \text {Re}(a(x,D)u,u)&=\frac{1}{2}((a(x,D)+\text {Op}(a^*))u,u)=(A(x,D)u,u)\\&=C_{1}({\mathcal {M}}_{m}u,u)+(q(x,D)q(x,D)^{*}u,u)+(r(x,D)u,u)\\&=C_{1}({\mathcal {M}}_{m}u,u)+(q(x,D)^{*}u,q(x,D)^*u)-(r(x,D)u,u)\\&\geqslant C_{1}\Vert u\Vert _{{\mathcal {H}}^{\frac{m}{2}}(M)}-(r(x,D)u,u)\\&= C_{1}\Vert u\Vert _{{\mathcal {H}}^{\frac{m}{2}}(M)}-({\mathcal {M}}_{- \frac{m-(\rho -\delta )}{2}}r(x,D)u,{\mathcal {M}}_{\frac{m-(\rho -\delta )}{2}}u). \end{aligned}$$

Observe that

$$\begin{aligned} ({\mathcal {M}}_{-\frac{m-(\rho -\delta )}{2}}r(x,D)u, {\mathcal {M}}_{\frac{m-(\rho -\delta )}{2}}u)&\leqslant \Vert {\mathcal {M}}_{-\frac{m-(\rho -\delta )}{2}}r(x,D)u \Vert _{L^2(M)}\Vert u\Vert _{{\mathcal {H}}^{\frac{m-(\rho -\delta )}{2}}(M)}\\&= \Vert r(x,D)u \Vert _{{\mathcal {H}}^{-\frac{m-(\rho -\delta )}{2}}(M)} \Vert u\Vert _{{\mathcal {H}}^{\frac{m-(\rho -\delta )}{2}}(M)}\\&\leqslant C_1\Vert u \Vert _{{\mathcal {H}}^{\frac{m-(\rho -\delta )}{2}}(M)}\Vert u\Vert _{{\mathcal {H}}^{\frac{m-(\rho -\delta )}{2}}(M)}, \end{aligned}$$

where in the last line we have used the Sobolev boundedness of r(x, D) from ${\mathcal {H}}^{\frac{m-(\rho -\delta )}{2}}(M)$ into ${\mathcal {H}}^{-\frac{m-(\rho -\delta )}{2}}(M).$ Consequently, we deduce the lower bound

$$\begin{aligned} \text {Re}(a(x,D)u,u) \geqslant C_{1}\Vert u\Vert _{{\mathcal {H}}^{\frac{m}{2}}(M)}-C\Vert u\Vert _{{\mathcal {H}}^{\frac{m-(\rho -\delta )}{2}}(M)}^2. \end{aligned}$$

If we assume for a moment that for every $\varepsilon >0,$ there exists $C_{\varepsilon }>0,$ such that

$$\begin{aligned} \Vert u\Vert _{{L}^{2}_{\frac{m-(\rho -\delta )}{2}}(M)}^2\leqslant \varepsilon \Vert u\Vert _{{\mathcal {H}}^{\frac{m}{2}}(M)}^2+C_{\varepsilon }\Vert u \Vert _{L^2(M)}^2, \end{aligned}$$

(4.3)

for $0<\varepsilon <C_{1}$ we have

$$\begin{aligned} \text {Re}(a(x,D)u,u) \geqslant (C_{1}-\varepsilon )\Vert u\Vert ^2_{{\mathcal {H}}^{\frac{m}{2}}(M)}-C_{\varepsilon }\Vert u\Vert _{L^2(M)}^2. \end{aligned}$$

So, with the exception of the proof of (4.3) in view of the analysis above, for the proof of Theorem 4.5 we only need to prove (4.3). However, we will deduce it from the following more general lemma. $\square$

Lemma 4.6

Let us assume that $s\geqslant t\geqslant 0$ or that $s,t<0.$ Then,  for every $\varepsilon >0,$ there exists $C_\varepsilon >0$ such that

$$\begin{aligned} \Vert u\Vert _{{L}^{2,L}_{t}(M)}^2\leqslant \varepsilon \Vert u\Vert _{{L}^{2,L}_{s}(M)}^2+C_{\varepsilon }\Vert u \Vert _{L^2(M)}^2 \end{aligned}$$

(4.4)

holds true for every $u\in C^\infty _L(M).$

Proof

Let $\varepsilon >0.$ Then, there exists $C_{\varepsilon }>0$ such that

$$\begin{aligned} \langle \xi \rangle ^{2t}-\varepsilon \langle \xi \rangle ^{2s}\leqslant C_{\varepsilon }, \end{aligned}$$

uniformly in $\xi \in {\mathcal {I}}.$ Then, (4.4) follows from the Plancherel theorem. Indeed,

$$\begin{aligned} \Vert u\Vert _{{L}^{2,L}_{t}(M)}^2&=\sum _{\xi \in {\mathcal {I}}} \langle \xi \rangle ^{2t}|\widehat{u}(\xi )|^{2} \leqslant \sum _{\xi \in {\mathcal {I}}} (\varepsilon \langle \xi \rangle ^{2s}+C_\varepsilon )|\widehat{u}(\xi )|^{2} \\&= \varepsilon \Vert u\Vert _{{L}^{2,L}_{s}(M)}^2+C_{\varepsilon }\Vert u \Vert _{L^2(M)}^2, \end{aligned}$$

completing the proof. $\square$

Corollary 4.7

Let $a(x,D):C^\infty _L(M)\rightarrow {\mathcal {D}}'_L(M)$ be an operator with symbol $a\in {S}^{m}_{\rho ,\delta }( M\times {\mathcal {I}}),$ $m\in {\mathbb {R}}.$ Let us assume that

$$\begin{aligned} a(x,\xi )\geqslant 0,\quad (x,\xi )\in M\times {\mathcal {I}}, \end{aligned}$$

satisfies

$$\begin{aligned} \vert \langle \xi \rangle ^ma(x,\xi )^{-1} \vert \leqslant C_{0}. \end{aligned}$$

Then,  there exist $C_{1},C_{2}>0,$ such that the lower bound

$$\begin{aligned} \text {Re}(a(x,D)u,u) \geqslant C_1\Vert u\Vert _{{\mathcal {H}}^{\frac{m}{2}}(M)}-C_2\Vert u\Vert _{L^2(M)}^2 \end{aligned}$$

holds true for every $u\in C^\infty _L(M).$

5 $L^2$-estimates for pseudo-differential operators

In this section, we prove the following analogue of the Calderón–Vaillancourt theorem, see [14, 15].

Theorem 5.1

Let $a(x,D):C^\infty _L(M)\rightarrow {\mathcal {D}}'_L(M)$ be a pseudo-differential operator with symbol $a\in {S}^{0}_{\rho ,\delta }( M\times {\mathcal {I}})$ with $0 \leqslant \delta <\rho \leqslant 1.$ Then a(x, D) extends to a bounded operator on $L^2({M}).$

Proof

Assume first that $a(x,\xi )\in {S}^{-m_0}_{\rho ',\delta '}(M\times {\mathcal {I}}),$ where $m_0>0.$ The kernel of $a(x,D)=\text {Op}(a),$ $K_{a}(x,y),$ belongs to $L^\infty (M\times M)$ for $m_0$ large enough. Indeed, by using

$$\begin{aligned} K_{a}(x,y)=\sum _{\xi \in {\mathcal {I}}}u_{\xi }(x)\overline{v_{\xi }(y)}a(x,\xi ), \end{aligned}$$

let us identify for which $m_0,$ a(x, D) is Hilbert–Schmidt. Since, a(x, D) is Hilbert–Schmidt if and only if $K_a\in L^{2}(M\times M).$ By simple calculations, we obtain

$$\begin{aligned} \Vert K_a(x,y) \Vert _{L^2(M\times M)}&\leqslant \sum _{\xi \in {\mathcal {I}}}\sup _{x\in M}|a(x,\xi )| \Vert u_{\xi }(x) v_{\xi }(y)\Vert _{L^{2}(M\times M)}\\&\lesssim \sum _{\xi \in {\mathcal {I}}}\langle \xi \rangle ^{-m_0} \Vert u_{\xi }\Vert _{L^{2}(M)}\Vert {v_{\xi }}\Vert _{L^{2}(M)}\\&= \sum _{\xi \in {\mathcal {I}}}\langle \xi \rangle ^{-m_0}. \end{aligned}$$

Thus, for $m_0\geqslant s_{0},$ a(x, D) is Hilbert–Schmidt on $L^2(M)$ and, consequently, a bounded operator on $L^2(M).$

Next by induction, we prove that a(x, D) is $L^2$-bounded if $p(x,\xi )\in {S}^{-m_0,{\mathcal {L}}}_{\rho ',\delta '}(M\times {\mathcal {I}}),$ for $m_0< m\leqslant -(\rho '-\delta ').$ To do so, for $u\in C^{\infty }(M)$ we form

$$\begin{aligned} \Vert a(x,D)u \Vert ^2_{L^2(M)}&=( a(x,D)u, a(x,D)u)_{L^2(M)}\\&=( a^{*}(x,D)a(x,D)u, u)_{L^2(M)}\\&=( b(x,D)u,u )_{L^2(M)} , \end{aligned}$$

where $b(x,D)=a^{*}(x,D)a(x,D)$ has a symbol in ${S}^{2m,{\mathcal {L}}}_{\rho ',\delta '}(M\times {\mathcal {I}}),$ for $0\leqslant \delta '<\rho '\leqslant 1.$ From the induction hypothesis, the continuity of a(x, D) for all $a\in S^{2\,m,{\mathcal {L}}}_{\rho ',\delta '}$ follows successively for $m\leqslant -\frac{m_0}{2},-\frac{m_0}{4},\ldots , -\frac{m_0}{2^{\ell _0}},\ldots ,$ $\ell _0\in {\mathbb {N}},$ and hence for $m\leqslant -\frac{m_0}{2^{\ell _0}},$ where $\frac{m_0}{2^{\ell _0}}<\rho '-\delta ',$ after a finite number of steps.

Assume that $a(x,\xi )\in S^{0,{\mathcal {L}}}_{\rho ',\delta '}(M\times {\mathcal {I}}),$ and choose

$$\begin{aligned} M>2\sup _{(x,\xi )} \vert a(x,\xi ) \vert ^{2}, \end{aligned}$$

then $c(x,\xi )=(M-a(x,\xi )a(x,\xi )^* )^{1/2}\in S^{0,{\mathcal {L}}}_{\rho ',\delta '}(M\times {\mathcal {I}}).$ Now, we have

$$\begin{aligned} c(x,D)^{*}c(x,D)=M-a^{*}(x,D)a(x,D)+r(x,D), \end{aligned}$$

where $r\in {S}^{-(\rho '-\delta ')}_{{\rho ',\delta '}}(M\times {\mathcal {I}}).$ Hence, $\Vert a(x,D) \Vert _{{\mathscr {B}}(L^2)}\leqslant M+\Vert r(x,D)\Vert _{{\mathscr {B}}(L^2)}.$ $\square$

Remark 5.2

For the $L^{p}$-$L^q$-boundedness of pseudo-differential operators in the setting of non-harmonic analysis, we refer the reader to [17].

6 Global solvability for evolution problems

In this section, we apply the Gårding inequality to some problems of PDEs, the global solvability of parabolic and hyperbolic type of problems associated with the non-harmonic pseudo-differential calculus. More precisely, we study the existence and uniqueness of the solution of the Cauchy problem:

$$\begin{aligned} (\text {IVP}): {\left\{ \begin{array}{ll}\frac{\partial v}{\partial t}=K(t,x,D)v+f ,&{}\\ v(0)=u_0, &{} \end{array}\right. } \end{aligned}$$

(6.1)

where the initial data $u_0\in L^2(M),$ $K(t):=K(t,x,D)$ with a symbol in $S^m_{\rho ,\delta }(M\times {\mathcal {I}}),$ $f\in L^2([0,T]\times M) \simeq L^2([0,T],L^2(M)),$ $m>0,$ and a suitable positivity condition is imposed on K.

We say that the problem (6.1) has a solution if there exists $v\in {\mathscr {D}}'((0,T)\times M)$ which satisfies the equation in (6.1) with the initial condition $v(0)=u_0\in L^2(M)$ such that $v\in C^1([0,T],L^2(M))\bigcap C([0,T],{\mathcal {H}}^{m,L}(M)).$

In what follows, we assume that¹¹

$$\begin{aligned} \text {Re}(K(t)):=\frac{1}{2}(K(t)+K(t)^*),\quad 0\leqslant t\leqslant T, \end{aligned}$$

is L-elliptic. Under such assumption, we prove the existence and uniqueness of the solution $v\in C^1([0,T],L^2(M))\bigcap C([0,T],{\mathcal {H}}^{m,L}(M)).$ We start with the following energy estimate.

Theorem 6.1

Let $K(t)=K(t,x,D),$ $0\leqslant \delta <\rho \leqslant 1,$ be a pseudo-differential operator of order $m>0$ with a symbol in $S^m_{\rho ,\delta }(M\times {\mathcal {I}}).$ Assume that $\text {Re}(K(t))$ is an L-elliptic operator,  for every $t\in [0,T]$ with $T>0.$ If

$$\begin{aligned} v\in C^1([0,T], L^2(M) ) \bigcap C([0,T],{\mathcal {H}}^{m,L}(M)) \end{aligned}$$

is a solution of the problem (6.1), then there exist $C, C'(T)>0$ such that

$$\begin{aligned} \Vert v(t)\Vert _{L^2(M)}\leqslant C \Vert u_0\Vert ^2_{L^2(M)}+C'(T)\int _{0}^T \Vert (\partial _{t}-K(\tau ))v(\tau ) \Vert ^2_{L^2(M)}{\textrm{d}}\tau \end{aligned}$$

holds for every $0\leqslant t\leqslant T.$

Moreover,  we also have the estimate

$$\begin{aligned} \Vert v(t)\Vert _{L^2(M)}\leqslant C \Vert u_0\Vert ^2_{L^2(M)} + C'(T) \int _{0}^T \Vert (\partial _{t}-K(\tau )^{*})v(\tau ) \Vert ^2_{L^2(M)}{\textrm{d}}\tau . \end{aligned}$$

Proof

Let $v\in C^1([0,T], L^2(M) ) \cap C([0,T],{\mathcal {H}}^{m,L}(M)).$ Let us start by observing that $v\in C([0,T],{\mathcal {H}}^{\frac{m}{2},L}(M))$ because of the embedding ${\mathcal {H}}^{m,L}\hookrightarrow {\mathcal {H}}^{\frac{m}{2},L}.$ This fact will be useful later because we will use the Gårding inequality applied to the operator $\text {Re}(K(t)).$ So, $v\in \text {Dom}(\partial _{\tau }-K(\tau ))$ for every $0\leqslant \tau \leqslant T.$ In view of the embedding ${\mathcal {H}}^{m,L}\hookrightarrow L^2(M),$ we also have that $v\in C([0,T], L^2(M) ).$ Let us define $f(\tau ):=Q(\tau )v(\tau ),$ $Q(\tau ):=(\partial _{\tau }-K(\tau )),$ for every $0\leqslant \tau \leqslant T.$ Observe that

$$\begin{aligned} \frac{{\textrm{d}}}{{\textrm{d}}t}\Vert v(t)\Vert ^2_{L^2(M)}&= \frac{{\textrm{d}}}{{\textrm{d}}t}\left( v(t),v(t)\right) _{L^2(M)}\\&=\left( \frac{d v(t)}{{\textrm{d}}t},v(t)\right) _{L^2(M)}+\left( v(t),\frac{d v(t)}{{\textrm{d}}t}\right) _{L^2(M)}\\&=\left( K(t)v(t)+f(t),v(t)\right) _{L^2(M)}+\left( v(t),K(t)v(t)+f(t)\right) _{L^2(M)}\\&=\left( (K(t)+K(t)^{*})v(t),v(t)\right) _{L^2(M)}+2\text {Re}(f(t), v(t))_{L^2(M)}\\&=\text {Re}(K(t)v(t),v(t))_{L^2(M)}+2\text {Re}(f(t), v(t))_{L^2(M)}. \end{aligned}$$

Now, from the Gårding inequality,

$$\begin{aligned} \text {Re}(-K(t)v(t),v(t)) \geqslant C_1\Vert v(t)\Vert _{{\mathcal {H}}^{\frac{m}{2},L}(M)}-C_2\Vert v(t)\Vert _{L^2(M)}^2, \end{aligned}$$

and from the parallelogram law, we have

$$\begin{aligned} 2\text {Re}(f(t), v(t))_{L^2(M)}&\leqslant 2\text {Re}(f(t), v(t))_{L^2(M)}+ \Vert f(t)\Vert _{L^2(M)}^2+\vert v(t)\vert _{L^2(M)}^2 \\&= \Vert f(t)+v(t)\Vert ^2\leqslant \Vert f(t)+v(t)\Vert ^2+\Vert f(t)-v(t)\Vert ^2 \\&= 2\Vert f(t)\Vert ^2_{L^2(M)}+2\Vert v(t)\Vert ^2_{L^2(M)}. \end{aligned}$$

Thus, we obtain

$$\begin{aligned}&\frac{{\textrm{d}}}{{\textrm{d}}t}\Vert v(t)\Vert ^2_{L^2(M)}\\&\quad \leqslant 2\left( C_2\Vert v(t)\Vert _{L^2(M)}^2-C_1\Vert v(t)\Vert _{{\mathcal {H}}^{\frac{m}{2},L}(M)}\right) +2\Vert f(t)\Vert ^2_{L^2(M)}+2\Vert v(t)\Vert ^2_{L^2(M)}. \end{aligned}$$

So, we have proved that

$$\begin{aligned} \frac{{\textrm{d}}}{{\textrm{d}}t}\Vert v(t)\Vert ^2_{L^2(M)}\lesssim \Vert f(t)\Vert ^2_{L^2(M)}+\Vert v(t)\Vert ^2_{L^2(M)}. \end{aligned}$$

By using Gronwall’s Lemma, we obtain the energy estimate

$$\begin{aligned} \Vert v(t)\Vert ^2_{L^2(M)}\leqslant C\Vert u_0\Vert _{L^2(M)}^2+C'(T)\int _{0}^T \Vert f(\tau ) \Vert _{L^2(M)}^2{\textrm{d}}\tau , \end{aligned}$$

(6.2)

for every $0\leqslant t\leqslant T,$ and $T>0.$ To finish the proof, we can change the calculations above with $v(T-\cdot )$ instead of $v(\cdot ),$ $f(T-\cdot )$ instead of $f(\cdot )$ and $Q^{*}=-\partial _{t}-K(t)^{*}$ (or equivalently, $Q=\partial _{t}-K(t)$) instead of $Q^{*}=-\partial _{t}+K(t)^{*}$ (or equivalently, $Q=\partial _{t}-K(t)$) using that $\text {Re}(K(T-t)^*)=\text {Re}(K(T-t))$ to deduce that

$$\begin{aligned}&\Vert v(T-t) \Vert ^2_{L^2(M)}\\&\quad \leqslant C\Vert u_0\Vert ^2_{L^2(M)}+C'(T)\int _{0}^{T} \Vert (-\partial _{t}+K(T-t)^{*})v(T-\tau ) \Vert ^2_{L^2(M)}{\textrm{d}}\tau \\&\quad = C\Vert u_0\Vert ^2_{L^2(M)}+C'(T)\int _{0}^T \Vert (-\partial _{t}-K(t)^{*})v(s) \Vert ^2_{L^2(M)}{\textrm{d}}s. \end{aligned}$$

So, we conclude the proof. $\square$

Theorem 6.2

Let $K(t)=K(t,x,D)\in S^m_{\rho ,\delta }(M\times {\mathcal {I}}),$ $0\leqslant \delta <\rho \leqslant 1,$ be a pseudo-differential operator of order $m>0,$ and let us assume that $\text {Re}(K(t))$ is L-elliptic,  for every $t\in [0,T]$ with $T>0.$ Let $f\in L^2(M).$ Then there exists a unique solution $v\in C^1([0,T], L^2(M) ) \bigcap C([0,T],{\mathcal {H}}^{m,L}(M))$ of the problem (6.1). Moreover,  v satisfies the energy estimate

$$\begin{aligned} \Vert v(t)\Vert ^2_{L^2(M)}\leqslant \left( C\Vert u_0 \Vert ^2_{L^2(M)}+C'\Vert f \Vert ^2_{L^2([0,T],L^2(M))} \right) , \end{aligned}$$

for every $0\leqslant t\leqslant T.$

Proof

The energy estimate (6.2) and the classical Picard iteration theorem imply the existence result. Now, to show the uniqueness of v,  let us assume that $u\in C^1([0,T], L^2(M) ) \bigcap C([0,T],{\mathcal {H}}^{m,L}(M))$ is also a solution of the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t}=K(t,x,D)u+f,&{} u\in {\mathscr {D}}'((0,T)\times M),\\ u(0)=u_0.&{} \end{array}\right. } \end{aligned}$$

Then, $\omega :=v-u\in C^1([0,T], L^2(M) ) \bigcap C([0,T],{\mathcal {H}}^{m,L}(M))$ solves the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial \omega }{\partial t}=K(t,x,D)\omega ,&{} \omega \in {\mathscr {D}}'((0,T)\times M),\\ \omega (0)=0.&{} \end{array}\right. } \end{aligned}$$

From Theorem 6.1 it follows that $\Vert \omega (t)\Vert _{L^2(M)}=0,$ for all $0\leqslant t\leqslant T.$ Hence, from the continuity in t of the functions we have that $v(t,x)=u(t,x)$ for all $t\in [0,T]$ and a.e. $x\in M.$ $\square$