Abstract
In this paper a convergence analysis of a Galerkin boundary element method for resonance problems arising from the time harmonic Maxwell’s equations is presented. The cavity resonance problem with perfect conducting boundary conditions and the scattering resonance problem for impenetrable and penetrable scatterers are treated. The considered boundary integral formulations of the resonance problems are eigenvalue problems for holomorphic Fredholm operator-valued functions, where the occurring operators satisfy a so-called generalized Gårding’s inequality. The convergence of a conforming Galerkin approximation of this kind of eigenvalue problems is in general only guaranteed if the approximation spaces fulfill special requirements. We use recent abstract results for the convergence of the Galerkin approximation of this kind of eigenvalue problems in order to show that two classical boundary element spaces for Maxwell’s equations, the Raviart–Thomas and the Brezzi–Douglas–Marini boundary element spaces, satisfy these requirements. Numerical examples are presented, which confirm the theoretical results.
Similar content being viewed by others
1 Introduction
The numerical solution of electromagnetic resonance problems is an important task in different fields of engineering and technology. In this paper we consider for a given bounded, simply connected Lipschitz domain \(\varOmega ^{\mathrm {i}}\subset {\mathbb {R}}^3\) the cavity resonance problem and the scattering resonance problem for an impenetrable and a penetrable scatterer arising from the time harmonic Maxwell’s equations with a time variation of the form \(e^{-i\omega t}\). It is assumed that the exterior domain \(\varOmega ^{\mathrm {e}}\,{:}{=}\,{\mathbb {R}}^3\setminus {\overline{\varOmega ^{\mathrm {i}}}}\) is connected.
The cavity resonance problem, usually referred to as interior resonance problem, is given as follows: Find \(\kappa \in {\mathbb {C}}\) and \(\mathbf{E}^{\mathrm {i}}\in \mathbf{H}(\mathbf {curl};\varOmega ^{\mathrm {i}})\), \(\mathbf{E}^{\mathrm {i}}\ne 0\), such that
where \(\kappa =\omega \sqrt{\varepsilon \mu }\) is the wavenumber, \(\omega \) is the angular frequency, \(\varepsilon \) is the electric permittivity, \(\mu \) is the magnetic permeability, and \(\mathbf {n}\) is the unit normal vector field on the boundary \(\varGamma \) pointing into the exterior domain \(\varOmega ^{\mathrm {e}}\). For the cavity resonance problem and the resonance problem for the impenetrable scatterer we assume throughout this paper that \(\varepsilon >0\) and \(\mu >0\) are constant. This assumption implies that the resonances of the interior resonance problem (1) are real [27, Thm. 4.18] and non-zero.
The scattering resonance problem for the impenetrable scatterer, which is usually referred to as exterior resonance problem, is formulated in \(\varOmega ^{\mathrm {e}}\) and is given as follows: Find \(\kappa \in {\mathbb {C}}\) and \(\mathbf{E}^{\mathrm {e}}\in \mathbf{H}_{\text {loc}}(\mathbf {curl};\varOmega ^{\mathrm {e}})\), \(\mathbf{E}^{\mathrm {e}}\ne 0\), such that:
As radiation condition in (2d) we impose that each Cartesian component of \(\mathbf{E}^{\mathrm {e}}\) has outside of any ball \(B_{r_0}\,{:}{=}\,\{x:\Vert \mathbf {x}\Vert <r_0\}\) which contains \(\varOmega ^{\mathrm {i}}\) an expansion in terms of the spherical Hankel functions of the first kind \(h^{(1)}_n\) of the form
for \(r=\Vert \mathbf {x}\Vert > r_0\) and \(j\in \{1,2,3\}\), where \(Y_n^m\) are the spherical harmonics. If \(\kappa \) is such that \(0\le \arg \kappa < \pi \), then the radiation condition (3) for a solution \(\mathbf{E}\in \mathbf{H}_{\text {loc}}(\mathbf {curl};\varOmega ^{\mathrm {e}})\) of Maxwell’s equations in \(\varOmega ^{\mathrm {e}}\) is equivalent to that the Cartesian components of \(\mathbf{E}\) satisfy the Sommerfeld radiation condition [11, Thm. 2.15]. The latter condition is again for \(0\le \arg \kappa < \pi \) equivalent to that \(\mathbf{E}\) satisfies the Silver–Müller radiation condition [11, Thm. 6.8]. The Silver–Müller radiation condition is usually imposed for scattering problems for wavenumbers \(\kappa \) with \(0\le \arg \kappa <\pi \). But it is well known that for wavenumbers with negative imaginary part the Silver–Müller radiation condition does not correctly characterize outgoing waves, see e. g., [28, Sect. 1]. Since the resonances of the exterior resonance problem (2a) have negative imaginary part, instead of the Silver–Müller radiation condition the radiation condition (3) is used.
The definition of the scattering resonance problem for the penetrable scatterer will be given in Sect. 5. For this kind of resonance problem we will allow complex and frequency-dependent permittivities and permeabilities. Such configurations occur for example in the field of plasmonics or in the context of metamaterials.
Boundary integral formulations and boundary element methods have been considered for different kinds of electromagnetic resonance problems. Examples are the interior resonance problem [13, 37], the interior transmission eigenvalue problem [12, 22] or the resonance problem for the penetrable scatterer [24, 26, 35], to mention just a few. A rigorous convergence analysis of the boundary element approximations of such kind of resonance problems has not been provided so far.
The presented numerical analysis in this paper is based on the classical theory of the regular approximation of eigenvalue problems for holomorphic Fredholm operator-valued functions [17, 18]. This theory has already been applied to boundary integral formulations of acoustic resonance problems [33] and to coupled FEM-BEM formulations of vibro-acoustic resonance problems [20]. For these cases sufficient conditions for the convergence of conforming Galerkin approximations follow from the fact that the occurring operators satisfy a standard Gårding’s inequality. For electromagnetic resonance problems the occurring boundary integral operators satisfy only a generalized Gårding’s inequality. In such a case additional properties of the approximation spaces are required in order to guarantee convergence. In [15, 16] sufficient conditions for the convergence of a conforming Galerkin approximation for such kind of eigenvalue problems are derived in an abstract setting. In this paper we show that these conditions are satisfied for the Galerkin approximation of the proposed boundary integral formulations of the considered electromagnetic resonance problems when classical boundary elements of Raviart–Thomas or Brezzi–Douglas–Marini type are used.
The rest of the paper is organized as follows: in the next section we introduce the boundary integral formulation for the interior and exterior resonance problem and collect the basic properties of the occurring boundary integral operators. In Sect. 3 we provide abstract convergence results for the Galerkin approximation of eigenvalue problems for holomorphic Fredholm operator-valued functions, where we assume that the occurring operators satisfy a generalized Gårding’s inequality. We specify for this case sufficient conditions such that the classical convergence results are valid. The abstract results of Sect. 3 are then applied in Sect. 4 to a Galerkin approximation of the boundary integral formulation of the interior and exterior resonance problem. In Sect. 5 a boundary integral formulation for the scattering resonance problem for a penetrable scatterer is analyzed and sufficient conditions on the material parameter are given such that convergence of boundary element methods are guaranteed. Numerical examples are presented in Sect. 6, which confirm the theoretical results.
2 Boundary integral formulation of the interior and exterior resonance problem
In this section we introduce and analyze the boundary integral formulation for the interior and exterior resonance problem (1) and (2a). The main references for the definitions and properties of the occurring boundary integral operators are [8, 9]. Note that the notations in the present paper only partially coincides with the notations in [8, 9].
2.1 Trace spaces
In this subsection we summarize the properties of the trace spaces which we need for the analysis of the boundary integral formulations of the resonance problems. For a detailed presentation of the trace spaces related to Maxwell’s equations for Lipschitz domains we refer to [7].
Let \(\varOmega \) be a Lipschitz domain. We denote by \(H^s(\varOmega )\), \(s\in \mathbb {R}\), and by \(H^t(\partial \varOmega )\), \(t\in [-1,1]\), the standard Sobolev spaces of scalar functions on the domain \(\varOmega \) and its boundary \(\partial \varOmega \), cf. [25]. The vector-valued counterparts \({\mathbf{H}}^s(\varOmega )\,{:}{=}\,\left( H^s(\varOmega )\right) ^3\) and \({\mathbf{H}}^t(\partial \varOmega )\,{:}{=}\,\left( H^t(\partial \varOmega )\right) ^3\) are written in bold letters. Throughout the paper we use bold letters for vector-valued functions. Further, we define
where \({\mathbf{L}}^2_\text {loc}(\varOmega )\,{:}{=}\,{\mathbf{H}}^0_\text {loc}(\varOmega )\).
In the following let us consider the domains \(\varOmega ^{\mathrm {i}}\) and \(\varOmega ^{\mathrm {e}}=\mathbb {R}^3\setminus {\overline{\varOmega ^{\mathrm {i}}}} \) as introduced in Sect. 1. For smooth functions \(\mathbf{E}^{\mathrm {i/e}}\in \{\mathbf{E}_{\vert \overline{\varOmega ^{\mathrm {i/e}}}}:\mathbf{E}\in (C^\infty _0(\mathbb {R}^3))^3\} \) we define the interior/exterior tangential trace operators \(\gamma _\tau ^{\mathrm {i/e}}\) and \(\pi _{\tau }^{\mathrm {i/e}}\) by
The operators \(\gamma _\tau ^{\mathrm {i/e}}\) and \(\pi _\tau ^{\mathrm {i/e}}\) can be extended for \(s\in (0,1)\) to continuous operators
where \({\mathbf{V}}_{\gamma }^s\) and \({\mathbf{V}}_{\pi }^s\) are endowed with the norms
The dual space of \({\mathbf{V}}_{\gamma }^s\) and \({\mathbf{V}}_{\pi }^s\), \(s\in (0,1)\), are denoted by \({\mathbf{V}}_{\gamma }^{-s}\) and \({\mathbf{V}}_\pi ^{-s}\), respectively. For \(s=0\) we set \({\mathbf{V}}_\gamma ^0={\mathbf{V}}_\pi ^0\,{:}{=}\,{\mathbf {L}}^2_\tau (\varGamma )\,{:}{=}\,\{\mathbf{u}\in {\mathbf {L}}^2(\varGamma ):\mathbf{u}\cdot \mathbf {n}=0\}\), where \({\mathbf {L}}^2_\tau (\varGamma )\) acts as pivot space for \({\mathbf{V}}_\gamma ^{-s}\) and \({\mathbf{V}}_{\gamma }^s\) as well as for \({\mathbf{V}}_\pi ^{-s}\) and \({\mathbf{V}}_{\pi }^s\). Finally, we define the space
endowed with the graph norm \(\Vert \mathbf{u}\Vert ^2_{ \mathbf {H}^{-1/2}(\mathrm {div}_\varGamma ,\varGamma )}\,{:}{=}\,\Vert \mathbf{u}\Vert ^2_{{\mathbf{V}}_\pi ^{-\frac{1}{2}}} +\Vert \mathrm {div}_\varGamma \mathbf{u}\Vert ^2_{{ H}^{-\frac{1}{2}}(\varGamma )}\). The space \( \mathbf {H}^{-1/2}(\mathrm {div}_\varGamma ,\varGamma )\) is a Hilbert space and the tangential trace operators \(\gamma _{\tau }^{\mathrm {i}}\) and \(\gamma _{\tau }^{\mathrm {e}}\) can be extended such that
are continuous, surjective and possess a continuous right inverse [7, Thm. 4.1]. In the sequel we will use the shorthand notation
The antisymmetric pairing
can be extended to \(\mathbf {V}\) such that \(\mathbf {V}\) becomes its own dual [9, Thm. 3.3], i.e., there exists a linear and isometric isomorphism \({J}_\times :\mathbf {V}\rightarrow \mathbf {V}^\prime \) such that
The operator \({J}_\times :\mathbf {V}\rightarrow \mathbf {V}^\prime \) is the extension of the mapping \( {\tilde{J}}_\times :{\mathbf {L}}^2_\tau (\varGamma )\rightarrow {\mathbf {L}}^2_\tau (\varGamma )\) defined by \( {\tilde{J}}_\times (\mathbf{u})\,{:}{=}\, \mathbf{u}\times \mathbf {n}\), see [9, Thm. 3.3]. Since \(\mathbf {V}\) is a Hilbert space we can identify the pairing \(\langle \cdot ,{\overline{\cdot }} \rangle _{\tau }\) with the inner product \(( \cdot ,\cdot )_{\mathbf {V}}\) by
where \({J}_\mathbf {V}:( \mathbf {H}^{-1/2}(\mathrm {div}_\varGamma ,\varGamma ))^\prime \rightarrow \mathbf {H}^{-1/2}(\mathrm {div}_\varGamma ,\varGamma )\) is a linear, isometric isomorphism.
As additional traces we introduce the traces \(\gamma ^{\mathrm {i/e}}_{\mathrm {N}}\,{:}{=}\,\gamma ^{\mathrm {i/e}}_{\tau }\circ \mathbf {curl}\). The mappings \(\gamma ^{\mathrm {i}}_{\mathrm {N}}: \mathbf{H}(\mathbf {curl}^2;\varOmega ^{\mathrm {i}})\mapsto \mathbf {V}\) and \(\gamma ^{\mathrm {e}}_{\mathrm {N}}:\mathbf{H}_{\text {loc}}(\mathbf {curl}^2;\varOmega ^{\mathrm {e}})\mapsto \mathbf {V}\) are linear and continuous [8], where
2.2 Derivation and analysis of the boundary integral formulation
The boundary integral formulation of the resonance problems (1) and (2a) is based on the Stratton–Chu representation formula for the solution of Maxwell’s equations. For exterior problems this formula is in the literature only considered for wavenumbers with non-negative imaginary part and together with the Silver–Müller radiation condition; see, e.g., [8, Sect. 4], [21, Thm. 5.49], [29, Sect. 5.5]. For wavenumbers with negative imaginary part the Stratton–Chu representation formula is also valid if instead of the Silver–Müller radiation condition the radiation condition (3) is imposed. This can be shown in the same way as it is done for positive wavenumbers in [8, Sect. 4, p. 95–97] by considering the Cartesian components of the solution of Maxwell’s equations, which have to satisfy the scalar Helmholtz equation. The representation formula for outgoing solutions of the scalar Helmholtz equation is also valid for wavenumbers with negative imaginary part [34, Appendix, Cor. 6.5] and therefore the Stratton–Chu representation formula is also valid for wavenumbers with negative imaginary part for exterior problems. We consider the Stratton–Chu representation formula in following compact form as in [8, Sect. 4]: any solution \(\mathbf{E}\) of Maxwell’s equations in \(\varOmega ^{\mathrm {i}}\cup \varOmega ^{\mathrm {e}}\) with wavenumber \(\kappa \in \mathbb {C}\setminus \{0\}\) which satisfies the radiation condition (3) is given by
where
is the Maxwell single layer potential and where
is the Maxwell double layer potential. Here, \(\Psi _\mathbf{{A}}(\kappa )\) and \( \Psi _{V}(\kappa )\) are the vectorial and scalar single layer potentials related to the Helmholtz equation, which have the integral representations
with \(E_\kappa (\mathbf {x})=\exp (i\kappa \Vert \mathbf {x}\Vert )/ 4\pi \Vert \mathbf {x}\Vert \).
Let \((\kappa ^{\mathrm {i}},\mathbf{E}^{\mathrm {i}})\) be an eigenpair of (1) and let us extend \(\mathbf{E}^{\mathrm {i}}\) in \(\varOmega ^{\mathrm {e}}\) by zero, then the Stratton–Chu representation formula (5) gives
If \((\kappa ^{\mathrm {e}},\mathbf{E}^{\mathrm {e}})\) is an eigenpair of (2a) and if we extend \(\mathbf{E}^{\mathrm {e}}\) by zero in \(\varOmega ^{\mathrm {i}}\), then we have
We consider a boundary integral formulation of the eigenvalue problems (1) and (2a) in terms of the single layer boundary integral operator \({\mathsf {S}}(\kappa )\) which is defined by
The operator \({\mathsf {S}}(\kappa ):\mathbf {V}\rightarrow \mathbf {V}\) is linear and continuous [8, Cor. 2] and it holds \({\mathsf {S}}(\kappa )=\gamma ^{\mathrm {i}}_{\tau }{\Psi }_{\mathrm {SL}}(\kappa ) = \gamma ^{\mathrm {e}}_{\tau }{\Psi }_{\mathrm {SL}}(\kappa ) \) [8, Thm. 7]. Further, we have the following representation [8, Eq. (31)]
Here \(V(\kappa )\) is the single layer operator of the Helmholtz equation and the pairing \(\langle \cdot ,\cdot \rangle _{\mp \frac{1}{2}}\) denotes the duality pairing of \(H^{-\frac{1}{2}}(\varGamma )\) and \(H^{\frac{1}{2}}(\varGamma )\). By applying the tangential trace to (6) and (7) we see that \((\kappa ^{\mathrm {i}},\mathbf{E}^{\mathrm {i}})\) and \((\kappa ^{\mathrm {e}},\mathbf{E}^{\mathrm {e}})\) satisfy the following boundary integral equation
As boundary integral formulation of the eigenvalue problems (1) and (2a) we consider the following eigenvalue problem: Find \(\kappa \in {\mathbb {C}}\setminus \{0\}\) and \(\mathbf{u}\in \mathbf {V}\setminus \{0\}\) such that:
Note that this eigenvalue problem is nonlinear with respect to the eigenvalue parameter \(\kappa \). The eigenvalue problem (10) is referred to as eigenvalue problem for the operator-valued function \({{\mathsf S}}:\mathbb {C}\setminus \{0\}\rightarrow {\mathcal B}(\mathbf {V},\mathbf {V})\). Here \({\mathcal B}(\mathbf {V},\mathbf {V})\) denotes the space of linear and bounded operators mapping from \(\mathbf {V}\) into \(\mathbf {V}\). The equivalence of the eigenvalue problem (10) with the interior and exterior resonance problem (1) and (2a) is specified next.
Proposition 1
The following assertions hold true :
-
(i)
Suppose that \((\kappa ,\mathbf{E})\) is an resonance pair either of the interior resonance problem (1) or of the exterior resonance problem (2a). Then \((\kappa ,\gamma ^{\mathrm {i/e}}_{\mathrm N }\mathbf{E})\) is an eigenpair of the eigenvalue problem (10).
-
(ii)
Let \((\kappa ,\mathbf{u})\) be an eigenpair of the eigenvalue problem (10). If \(\kappa \) is real, then it is a resonance of the interior resonance problem (1) and \(\left( {\Psi }_{\mathrm {SL}}(\kappa )\mathbf{u}\right) _{\vert \varOmega ^{\mathrm {i}}}\) is a corresponding resonance function. Otherwise, \(\kappa \) is a resonance of the exterior resonance problem (2a) and \(\left( {\Psi }_{\mathrm {SL}}(\kappa )\mathbf{u}\right) _{\vert \varOmega ^{\mathrm {e}}}\) is a corresponding resonance function.
Proof
The assertion (i) has been already shown, see (9). Suppose now that \((\kappa ,\mathbf{u})\) is an eigenpair of (10). We define \(\mathbf{E}={\Psi }_{\mathrm {SL}}(\kappa )\mathbf{u}\) in \(\varOmega ^{\mathrm {i}}\cup \varOmega ^{\mathrm {e}}\). Then \(\gamma ^{\mathrm {i}}_{\tau }\mathbf{E}=\gamma ^{\mathrm {e}}_{\tau }\mathbf{E}= {\mathsf {S}}(\kappa )\mathbf{u}=0.\) It remains to show that \(\mathbf{E}_{\vert \varOmega ^{\mathrm {i}}}\ne 0\) if \(\kappa \in \mathbb {R}\), and \(\mathbf{E}_{\vert \varOmega ^{\mathrm {e}}}\ne 0\) if \(\kappa \in \mathbb {C}\setminus \mathbb {R}\).
First we consider the case that \(\kappa \in \mathbb {R}\). Then \(\mathbf{E}_{\vert \varOmega ^{\mathrm {e}}}=0\) because of the unique solvability of the related exterior boundary value problem [21, Cor. 5.63]. From this we get \(\gamma ^{\mathrm {e}}_{\mathrm {N}}\mathbf{E}= 0\) and the jump relation \(\gamma ^{\mathrm {e}}_{\mathrm {N}}{\Psi }_{\mathrm {SL}}(\kappa ) \mathbf{u}- \gamma ^{\mathrm {i}}_{N}{\Psi }_{\mathrm {SL}}(\kappa ) \mathbf{u}=-\mathbf{u}\) [8, Thm. 7] implies \(\mathbf{E}_{\vert \varOmega ^{\mathrm {i}}}\ne 0\).
Suppose now that \(\kappa \) is non-real. Then \(\mathbf{E}_{\vert \varOmega ^{\mathrm {i}}}=0\) because otherwise \((\kappa , \mathbf{E}_{\vert \varOmega ^{\mathrm {i}}})\) would be an interior resonance pair which is not possible since all interior resonances are real [27, Thm. 4.18]. From the jump relation of the single layer potential we get \(\gamma ^{\mathrm {e}}_{\mathrm {N}}\mathbf{E}=\mathbf{u}\). Hence we have \(\mathbf{E}_{\vert \varOmega ^{\mathrm {e}}}\ne 0\). \(\square \)
For the analysis of the eigenvalue problem (10) and its Galerkin approximation it is essential that the single layer boundary integral operator \({\mathsf {S}}(\kappa )\) satisfies a generalized Gårding’s inequality in \(\mathbf {V}\) for all wavenumbers \(\kappa \in \mathbb {C}\setminus \{0\}\). This property is based on the direct sum decomposition
where \({\mathcal X}\) and \({\mathcal N}\) are closed subspaces of \(\mathbf {V}\) with \({\mathcal X}\subset {V}^{-\frac{1}{2}}_\pi \) \({\mathcal N}=(\ker \mathrm {div}_\varGamma )\cap \;\mathbf {V}\) [9, Thm. 3.4]. We denote by \({\mathsf {R}}\) and \({\mathsf {Z}}\) the associated continuous projectors onto \({\mathcal X}\) and \({\mathcal N}\), respectively. An equivalent norm in \(\mathbf {V}\) is given by
see [9, Thm. 3.4]. Further, we define the operator

which is by construction an isomorphism.
Lemma 1
Let \(\kappa \in \mathbb {C}\setminus \{0\}\). There exist a compact operator \({\mathsf {C} }(\kappa ):\mathbf {V}\rightarrow \mathbf {V},\) an isomorphism \({\mathsf T }(\kappa ):\mathbf {V}\rightarrow \mathbf {V}\) and an \(\alpha (\kappa )>0\) such that the following generalized Gårding’s inequality is satisfied
where

\(\beta (\kappa )\,{:}{=}\,{{\,\mathrm{sgn}\,}}({{\,\mathrm{Re}\,}}(\kappa ))\) for \({{\,\mathrm{Re}\,}}(\kappa )\ne 0,\) and \(\beta (\kappa )\,{:}{=}\,-{{\,\mathrm{sgn}\,}}({{\,\mathrm{Im}\,}}(\kappa ))i\) for \({{\,\mathrm{Re}\,}}(\kappa )= 0\).
Proof
The assertion has been proven for positive wavenumbers e.g. in [6, Thm. 5], [8, Lem. 10], [9, Thm. 5.4]. Using the same arguments as in [6, 8, 9] an extension to \(\kappa \in \mathbb {C}\setminus \{0\}\) is straightforward. We want to mention that the assertion follows also from Prop. 3 below when setting \({\mathfrak {u}}=(0,\mathbf{u})\) in (49). \(\square \)
Next, we show that the mapping \({\mathsf {S}}:\mathbb {C}\setminus \{0\}\rightarrow {\mathcal B}(\mathbf {V},\mathbf {V})\), \( \kappa \mapsto {\mathsf {S}}(\kappa )\), is holomorphic, i.e., the derivative \(\frac{\text {d}}{\text {d} \kappa } {\mathsf {S}}(\kappa _0)\,{:}{=}\,\lim _{\kappa \rightarrow \kappa _0} \frac{1}{\kappa -\kappa _0} \left( {\mathsf {S}}(\kappa ) - {\mathsf {S}}(\kappa _0)\right) \) exists as operator in \({\mathcal {B}}(\mathbf {V},\mathbf {V})\) for each \(\kappa _0 \in \mathbb {C}\setminus \{0\}\).
Lemma 2
The mapping \({{\mathsf {S}} }:\mathbb {C}\setminus \{0\}\rightarrow {\mathcal B}(\mathbf {V},\mathbf {V}),\) \(\kappa \mapsto {{\mathsf {S}} }(\kappa ),\) is holomorphic.
Proof
It is sufficient to show that the mapping
is holomorphic as mapping from \(\mathbb {C}\setminus \{0\}\) into \(\mathbb {C}\) for all \(\mathbf{u},\mathbf{r}\) of a dense subspace of \(\mathbf {V}\), see Theorem III.3.12 in [19] and the remark following it. Let us choose \( \gamma ^{\mathrm {i}}_{\tau }(( C^\infty _0(\mathbb {R}^3))^3)\) as dense subspace of \(\mathbf {V}\). Then we can use the following integral representation of the pairing \(\langle \cdot ,\cdot \rangle _{\tau }\) and of the boundary integral operator \({\mathsf {S}}(\kappa )\) [8, Eq. 32]:
Hence, it is sufficient to show that both terms on the right hand side in (15) are holomorphic in \(\kappa \) on \(\mathbb {C}\setminus \{0\}\). We give a proof for the first term only, since the second term can be treated analogously. We divide the proof in two steps.
Step 1: Consider for a fixed \(\kappa \in \mathbb {C}\) the series expansion of the kernel
We show that the order of integration and summation can be interchanged by using Lebesgue’s dominated convergence theorem. Let
Obviously \(\sum _{n=0}^Nf_n(\kappa ,\mathbf {x},\mathbf {y})\) converges pointwise almost everywhere on \(\varGamma \times \varGamma \) to the kernel on the left hand side in (16) as \(N\rightarrow \infty \). Further, for \(R\,{:}{=}\,\max _{\mathbf {x},\mathbf {y}\in \varGamma }\Vert \mathbf {x}-\mathbf {y}\Vert \) we have
Since \(g(\kappa ,\mathbf {x},\mathbf {y})\) is integrable on \(\varGamma \times \varGamma \) the order of integration and summation in (16) may be interchanged.
Step 2: Define for \(\kappa \in B_K(0)\), \(K>0\),
We have
where V(0) is the single layer boundary integral operator of the Laplace equation, see [32, Sect. 6.2]. Obviously, \(\sum _{n=0}^\infty M_n\) is convergent. Hence, by the Weierstrass M-test it follows that the series \(\sum _{n=0}^\infty h_n(\kappa )\) converges absolutely and uniformly on \(B_K(0)\) to a limit function \(h(\kappa )\). Since \(\sum _{n=0}^N h_n(\kappa )\) is a polynomial in \(\kappa \) and therefore holomorphic in \(\kappa \) the uniform convergence of \(\sum _{n=0}^N h_n(\kappa )\) implies that the limit function \(h(\kappa )\) is holomorphic on \(B_K(0)\). From the first part of the proof we get
which shows that the first term on the right hand side in (15) defines a holomorphic function on \(\mathbb {C}\). Analogously, the holomorphy of the second term can be shown. \(\square \)
3 Galerkin approximation of eigenvalue problems for holomorphic Fredholm operator-valued functions
In this section we provide abstract convergence results for the Galerkin approximation of eigenvalue problems for holomorphic Fredholm operator-valued functions where we assume that the occurring operators satisfy a generalized Gårding’s inequality. We specify for this case sufficient conditions such that the classical convergence results for the approximation of eigenvalue problems for holomorphic Fredholm operator-valued functions as given in [17, 18] can be applied. Our analysis is based on results on the approximation of non-coercive operators [4] and on recent results on the regular approximation of operators which satisfy a generalized Gårding’s inequality [15, 16].
The results of this section build the abstract framework which we will utilize in order to show the convergence of the boundary element method for the approximation of the interior and exterior resonance problem as well as of the resonance problem for the penetrable scatterer.
3.1 Assumptions on the eigenvalue problem
Let V be a Hilbert space and suppose that V is equipped with a conjugation, i. e., with a continuous, unary operation \(v\mapsto {\overline{v}}\) satisfying
for all \(u,v\in V\) and \(\alpha \in \mathbb {C}\). We denote by \((\cdot ,\cdot )_V\) the inner product in V and consider in addition a bilinear form \(\langle \cdot ,\cdot \rangle _V:V\times V\rightarrow \mathbb {C}\) with the property
where \(J\in {\mathcal B}(V,V)\) is a given isomorphism. Further, we assume that there exists a direct sum decomposition \(V=X\oplus N\) which is stable, i. e., there exists a constant \(c>0\) such that for all \(v^X\in X\) and \(v^N\in N\) the inequality
is satisfied. We define the operator \(\varTheta :V\rightarrow V\) by
Note that \(\varTheta \) is an isomorphism and that \(\varTheta \in {\mathcal {B}}(V,V)\) since the decomposition \(V=X\oplus N\) is stable.
Let \(\varLambda \subset \mathbb {C}\) be an open and connected subset of \(\mathbb {C}\) and \(S:\varLambda \rightarrow {\mathcal {B}}(V,V)\) be a holomorphic operator-valued function. We assume that \(S(\lambda )\) satisfies a generalized Gårding’s inequality for all \(\lambda \in \varLambda \) of the following kind: there exist a compact operator \(C(\lambda )\in {\mathcal B}(V,V)\) and an \(\alpha (\lambda )>0\) such that
where \(T(\lambda )=\beta (\lambda ) I\) or \(T(\lambda )=\beta (\lambda )\varTheta \) with \(\beta (\lambda )\ne 0\). Since \(T(\lambda )\) is an isomorphism and \(\varTheta \in {\mathcal {B}}(V,V)\) this implies that \(T(\lambda )^*JS(\lambda )\) as well as that \(S(\lambda )\) is a Fredholm operator of index zero [25, Thm. 2.33]. We want to mention that we do not require that the operator-valued functions \(C(\cdot )\) and \(T(\cdot )\) are holomorphic in \(\varLambda \).
We consider the eigenvalue problem for the operator-valued function \(S(\cdot )\) of the form: find eigenvalues \(\lambda \in \varLambda \) and corresponding eigenelements \(u\in V\setminus \{0\}\) such that
If \((\lambda ,u)\) satisfy (21), then we say that \((\lambda ,u)\) is an eigenpair of the operator-valued function \(S(\cdot )\).
3.2 Notations and properties of eigenvalue problems for holomorphic Fredholm operator-valued functions
We briefly summarize basic results of the theory of eigenvalue problems for holomorphic Fredholm operator-valued functions [14, 23]. The set
is called the resolvent set of \(S(\cdot )\). In the following we will assume that the resolvent set of \(S(\cdot )\) is not empty. The complement of the resolvent set \(\rho (S(\cdot ))\) in \(\varLambda \) is called the spectrum \(\sigma (S(\cdot ))\). The spectrum \(\sigma (S(\cdot ))\) has no accumulation points inside of \(\varLambda \) [14, Cor. XI 8.4]. The dimension of the null space \(\ker S(\lambda )\) of an eigenvalue \(\lambda \) is called the geometric multiplicity of \(\lambda \). An ordered collection of elements \(u_0, u_1,\ldots ,u_{m-1}\) in X is called a Jordan chain of \((\lambda ,u_0)\), if \((\lambda ,u_0)\) is an eigenpair and if
is satisfied, where \(S^{(j)}\) denotes the jth derivative. The length of any Jordan chain of an eigenvalue is finite [23, Lem. A.8.3]. Elements of any Jordan chain of an eigenvalue \(\lambda \) are called generalized eigenelements of \(\lambda \). The closed linear hull of all generalized eigenelements of an eigenvalue \(\lambda \) is called generalized eigenspace of \(\lambda \) and is denoted by \(G(S(\cdot ),\lambda )\). The dimension of the generalized eigenspace \(G(S(\cdot ),\lambda )\) is finite [23, Prop. A.8.4] and it is referred to as algebraic multiplicity of \(\lambda \).
3.3 Galerkin approximation
For the approximation of the eigenvalue problem (21) we consider a conforming Galerkin approximation. Let \(\left( V_h\right) _{h}\) be a sequence of finite-dimensional subspaces of V and let \( P_h: V \rightarrow V_h\) be the orthogonal projection of V onto \(V_h\). As usual we assume that
The Galerkin approximation of the eigenvalue problem (21) reads as: find eigenpairs \((\lambda _h,u_{h}) \in \varLambda \times V_h\setminus \{0\}\) such that
For the convergence analysis it is convenient to consider instead of the variational formulation (23) the equivalent operator formulation
Further, we will also consider the eigenvalue problem for the operator-valued function \(JS(\cdot )\), which is equivalent to the eigenvalue problem for \(S(\cdot )\), i. e., \((\lambda ,u)\) is an eigenpair of the eigenvalue problem for \( JS(\cdot )\) if and only if it is an eigenpair of the eigenvalue problem for \( S(\cdot )\).
3.3.1 Regular convergence
In order to apply the convergence theory of [17, 18] to the Galerkin eigenvalue problem (24) it is necessary to show that the sequence \((P_hJS(\lambda )P_h)_h\) converges regularly to \(JS(\lambda )\) as \(h\rightarrow 0\) for all \(\lambda \in \varLambda \). For the definition of the regular convergence we need the definition of a compact sequence first.
Definition 3.1
A sequence \((v_h)_{h}\), \(v_h\in V\), is compact in V, if every subsequence \((v_{h^\prime })_{h^\prime }\) of \((v_h)_{h}\) has a convergent subsequence \((v_{h^{\prime \prime }})_{h^{\prime \prime }}\) in V.
Definition 3.2
Let \(B\in {\mathcal B}(V,V)\) and suppose that \((V_h)_h\) satisfies (22). The sequence \((P_h B P_h)_{h}\) converges regularly to B, if for any bounded sequence \((v_h)_h\), \(v_h\in V_h\), the compactness of \(( P_h B P_hv_h)_h\) implies already the compactness of \((v_h)_h\).
If the operator B is a compact perturbation of a coercive operator, then the sequence \((P_h B P_h)_h\) converges regularly to B [36, Sect. 2: Prop. 5]. For the case that B satisfies only a generalized Gårding’s inequality the regular convergence of \((P_h B P_h)_h\) to B is in general not guaranteed. Sufficient conditions for that case are specified in the next lemma.
Lemma 3
([15, Lem. 3.15], [16, Thm. 1.8]) Let \(B\in {\mathcal B}(V,V)\) and assume that there exit a compact operator \(C\in {\mathcal B}(V,V),\) an isomorphism \(T\in {\mathcal B}(V,V),\) and an \(\alpha >0\) such that
Further, suppose that \(\left( V_h\right) _{h}\) satisfies (22). If there exists a sequence \((T_h)_h,\) \(T_h\in {\mathcal B}(V_h,V_h)\) such that
then \((P_h B P_h)_h\) converges regularly to B.
Sufficient conditions for the existence of a sequence of discrete operators \((T_h)_h\) such that (26) is satisfied will be provided next for the case of a stable splitting \(V=X\oplus N\) and \(T=\varTheta \), where \(\varTheta \) is defined by (19). First we need to define the gap \(\delta _V(U,W)\) of two subspaces U and W of V:
We say that the sequence \((V_h)_h\) satisfies a gap property with respect to the splitting \(V=X\oplus N\) if the following condition is satisfied:
- (GAP):
-
There exist sequences \((X_h)_h\) and \((N_h)_h\) satisfying the following properties:
-
(i)
\(X_h\text { and }N_h \text{ are } \text{ subspaces } \text{ of } V_h \text { such that } V_h=X_h\oplus N_h\text { for all }h\),
-
(ii)
\( \delta _h\,{:}{=}\,\max \{\delta _V(X_h,X),\delta _V(N_h,N)\}\rightarrow 0\quad \text {as }h\rightarrow 0\).
This condition is a usual condition for Galerkin boundary element methods for Maxwell’s equation, see e g. [4, 5, 8,9,10]. We will discuss this in detail in Sect. 4 below.
Lemma 4
Let \(V=X\oplus N\) be a stable splitting and suppose that \((V_h)_h\) satisfy (22) and the property (GAP). Then we have :
-
(a)
For any continuous projector \(Q:V\rightarrow X\) which is onto in X, there exists a constant \(c>0\) such that for sufficiently small h we have
$$\begin{aligned} \Vert v_h-Qv_h\Vert _V\le c \delta _h \Vert v_h\Vert _V\quad \text {for all }v_h\in V_h. \end{aligned}$$ -
(b)
The splitting \(V_h=X_h\oplus N_h\) is uniformly stable for all \(h<h_1\) for some \(h_1>0,\) i.e., there exists a constant \(c>0\) such that for all \(h<h_1\) it holds
$$\begin{aligned} \left( \Vert v^{X_h}_h\Vert _V+\Vert v^{N_h}_h\Vert _V\right) \le c\Vert v^{X_h}_h+v^{N_h}_h\Vert _V\quad \text {for all } v^{X_h}_h\in X_h, v^{N_h}_h\in N_h. \end{aligned}$$
Proof
For assertion (a) we refer to [4, Lem. 3.1] and for assertion (b) to [4, Thm. 3.2]. \(\square \)
Proposition 2
Let \(V=X\oplus N\) be a stable splitting and \(\varTheta \) be defined by (19). Suppose that \((V_h)_h\) satisfy (22) and the property (GAP). Then there exists a sequence \((\varTheta _h)_h,\) \(\varTheta _h\in {\mathcal B}(V_h,V_h),\) such that
Proof
Since \(V=X\oplus N\) is a stable splitting there exists a continuous projection \(R:V\rightarrow V\) with range X and kernel N. By definition of \(\varTheta \) we have \(\varTheta v = v^{X}- v^{N}\) for \(v\in V\), where \(v^X\in X\), \(v^N\in N\) such that \(v=v^X+v^N\). This implies that we can write \(\varTheta = R-Z\), where \(Z\,{:}{=}\,I-R\).
From the decomposition \(V_h=X_h\oplus N_h\) and the fact that \(V_h\) is finite-dimensional it follows that there exists a continuous projection \(R_h:V_h\rightarrow V_h\) with range \(X_h\) and kernel \(N_h\). We will show that
satisfies (27). The proof for that will be done in two steps.
(i) First we show that there exists a constant \(c>0\) such that for sufficiently small h
holds for all \(v_h\in V_h\), where \(\delta _h\) is defined as in (GAP)(ii). Let \(v_h\in V_h\) and consider the decomposition \(v_h=v_h^{X_h}+v_h^{N_h}\), where \(v_h^{X_h}\in X_h\) and \(v_h^{N_h}\in N_h\). Using Lemma 4(a) we get
By Lemma 4(b) the decomposition \(V_h=X_h\oplus N_h\) is uniformly stable for sufficiently small h and therefore inequality (29) follows.
(ii) Since \(Z=(I-R)\) and \(Z_h=(I-R_h)\) we get from (29) also
Hence, we have
from which (27) follows. \(\square \)
Corollary 1
Let \(V=X\oplus N\) be a stable splitting and \(\lambda \in \varLambda \). Assume that \(S(\lambda )\in {\mathcal B}(V,V)\) fulfills a generalized Gårding’s inequality of the form as in (20). Further, suppose that \((V_h)_h\) satisfy (22) and the property (GAP). Then \((P_h JS(\lambda )P_h)_h\) converges regularly to \(JS(\lambda )\).
Proof
Since \(S(\lambda )\in {\mathcal B}(V,V)\) fulfills a generalized Gårding’s inequality of the form as in (20), there exist a compact operator \(C(\lambda )\in {\mathcal B}(V,V)\) and an \(\alpha (\lambda )>0\) such that
where \(T(\lambda )=\beta (\lambda ) I\) or \(T(\lambda )=\beta (\lambda )\varTheta \) with \(\beta (\lambda )\ne 0\). From \(\langle \cdot ,{\overline{\cdot }}\rangle _V=(J\cdot ,\cdot )_V\) it follows that \(JS(\lambda )\) satisfies a generalized inequality of the form as in (25), i. e. ,
By Lemma 3 it is sufficient to show that there exists a sequence \(\left( T_h(\lambda )\right) _h\), \(T_h(\lambda )\in {\mathcal B}(V_h,V_h)\), such that
For \(T(\lambda )=\beta (\lambda )I\), obviously (31) holds for \(T_h(\lambda )=\beta (\lambda )I\). If \(T(\lambda )=\beta (\lambda )\varTheta \), then (31) follows form Proposition 2 for \(T_h(\lambda )=\beta (\lambda )\varTheta _h\). \(\square \)
3.3.2 Asymptotic convergence results
In the next theorem we summarize main convergence results for the Galerkin approximation of the eigenvalue problem \(S(\lambda )u=0\) as given in (21). For additional convergence results we refer to [15,16,17,18].
Theorem 1
Let \(V=X\oplus N\) be a stable splitting and let \(S:\varLambda \rightarrow {\mathcal {B}}(V,V)\) be a holomorphic operator-valued function. Assume that \(S(\lambda )\) fulfills a generalized Gårding’s inequality of the form as in (20) for all \(\lambda \in \varLambda \). Further, suppose that \((V_h)_h\) satisfy (22) and the property (GAP). Then the following holds true :
-
(i)
(Completeness of the spectrum of the Galerkin eigenvalue problem) For each eigenvalue \(\lambda \in \varLambda \) of the operator-valued function \(S(\cdot )\) there exists a sequence \((\lambda _h)_{h}\) of eigenvalues of the Galerkin eigenvalue problem (23) such that
$$\begin{aligned} \lambda _h\rightarrow \lambda \quad \text {as }h\rightarrow 0. \end{aligned}$$ -
(ii)
(Non-pollution of the spectrum of the Galerkin eigenvalue problem) Let \(K\subset \varLambda \) be a compact and connected set such that \(\partial K\) is a simple rectifiable curve. Suppose that there is no eigenvalue of \(S(\cdot )\) in K. Then there exists an \(h_0>0\) such that for all \(h\le h_0\) the Galerkin eigenvalue problem (23) has no eigenvalues in K.
-
(iii)
Let \(D\subset \varLambda \) be a compact and connected set such that \(\partial D\) is a simple rectifiable curve. Suppose that \(\lambda \in {\mathring{D}}\) is the only eigenvalue of \(S(\cdot )\) in D. Then there exist an \(h_0>0\) and a constant \(c>0\) such that for all \(h\le h_0\) we have :
-
(a)
For all eigenvalues \(\lambda _h\) of the Galerkin eigenvalue problem (23) in D
$$\begin{aligned} \vert \lambda -\lambda _h\vert \le c\delta _V(G(S(\cdot ),\lambda ),V_h)^{1/\ell }\delta _{V}(G(S^*(\cdot ),{\overline{\lambda }}),V_h)^{1/\ell } \end{aligned}$$(32)holds, where \(S^*(\cdot )\,{:}{=}\,(S({\overline{\cdot }}))^*\) and \(\ell \) is the maximal length of a Jordan chain corresponding to \(\lambda \).
-
(b)
Let
$$\begin{aligned} {\overline{\lambda }}_h\,{:}{=}\,\frac{1}{\dim G(S(\cdot ),\lambda ) } \sum _{\lambda _h\in \sigma (P_hJS(\cdot ) P_h)\cap D}\lambda _h\dim G(P_h JS(\cdot )P_h,\lambda _h) \end{aligned}$$be the weighted mean of all eigenvalues of the Galerkin eigenvalue problem (23) in D. Then it holds
$$\begin{aligned} \vert \lambda -{\overline{\lambda }}_h\vert \le c\delta _V\left( G(S(\cdot ),\lambda ),V_h\right) \delta _{V}\left( G(S^*(\cdot ),{\overline{\lambda }}),V_h\right) . \end{aligned}$$(33) -
(c)
If \((\lambda _h,u_h)\) is an eigenpair of (23) with \(\lambda _h\in D\) and \(\Vert u_h\Vert _{V}=1,\) then
$$\begin{aligned} \inf _{u\in \ker (S(\lambda ))}\Vert u-u_h\Vert _{V} \le c \left( \vert \lambda _h-\lambda \vert + \delta _V(\ker (S(\lambda ),V_h)\right) . \end{aligned}$$
-
(a)
Proof
By Corollary 1 the sequence \((P_hJS(\lambda )P_h)_h\) provides a regular approximation of the operator \(JS(\lambda )\) for all \(\lambda \in \varLambda \). Further, the Galerkin scheme is a discrete approximation scheme in the sense of [17], see, e.g. [15, Lem. 3.6], [16, Lem. 2.6]. The assertions (i) to (iii)(b) follow then from the abstract results in [17, 18]. For assertion (i) and (ii) we refer to [17, Thm. 2], and for (iii)(a) and (iii)(b) to [18, Thm. 2,Thm. 3].
The error estimate in (iii)(c) follows from [15, Lem. 3.17], [16, Lem. 2.6]. \(\square \)
4 Galerkin approximation of the interior and exterior resonance problem
In this section we apply the abstract convergence results of Theorem 1 to the Galerkin approximation of the eigenvalue problem
Lemma 1 shows that \({\mathsf {S}}(\kappa )\) satisfies for all \(\kappa \in \mathbb {C}\setminus \{0\}\) a generalized Gårding’s inequality of the form
where  or \( {{\mathsf T}}(\kappa )=\beta (\kappa ){\mathsf I}\) with \(\beta (\kappa )\ne 0\). The operator
or \( {{\mathsf T}}(\kappa )=\beta (\kappa ){\mathsf I}\) with \(\beta (\kappa )\ne 0\). The operator  is defined by
is defined by  , see (13), where \({\mathsf {R}}\) and \({\mathsf {Z}}\) are projections associated to the splitting \(\mathbf {V}={\mathcal X}\oplus {\mathcal N}\) as given in (11). Further, (4) shows that \(\langle \cdot ,{\overline{\cdot }}\rangle _\tau =({{\mathsf J}}\cdot ,\cdot )_\mathbf {V}\) holds, where \({{\mathsf J}}\,{:}{=}\,{J}_\mathbf {V}{J}_{\times }\) is an isometric isomorphism. Since \({\mathsf {S}}(\cdot )\) is in \(\mathbb {C}\setminus \{0\}\) in addition holomorphic, \({\mathsf {S}}(\cdot )\) satisfies the assumption of Theorem 1. It remains to provide adequate ansatz spaces for the Galerkin approximation of the eigenvalue problem for \({\mathsf {S}}(\cdot )\).
, see (13), where \({\mathsf {R}}\) and \({\mathsf {Z}}\) are projections associated to the splitting \(\mathbf {V}={\mathcal X}\oplus {\mathcal N}\) as given in (11). Further, (4) shows that \(\langle \cdot ,{\overline{\cdot }}\rangle _\tau =({{\mathsf J}}\cdot ,\cdot )_\mathbf {V}\) holds, where \({{\mathsf J}}\,{:}{=}\,{J}_\mathbf {V}{J}_{\times }\) is an isometric isomorphism. Since \({\mathsf {S}}(\cdot )\) is in \(\mathbb {C}\setminus \{0\}\) in addition holomorphic, \({\mathsf {S}}(\cdot )\) satisfies the assumption of Theorem 1. It remains to provide adequate ansatz spaces for the Galerkin approximation of the eigenvalue problem for \({\mathsf {S}}(\cdot )\).
In what follows, we make the additional assumption that \(\varOmega ^{\mathrm {i}}\) is a polyhedron, possibly curvilinear. Let \(({\mathcal T}_h)_h\) be a sequence of regular triangulations of the boundary \(\varGamma \) with mesh size h. We denote by \({\mathbf{RT}}_{k}({\mathcal T}_h)\) the space generated by Raviart–Thomas elements of order k on \({\mathcal T}_h\) and by \(\mathbf{BMD}_{k}({\mathcal T}_h) \) the space generated by Brezzi–Douglas–Marini elements of order k on \({\mathcal T}_h\), where we refer to [5, 8] for their definition. We adopt the convention of [5, 8] that \(k = 0\) means lowest order Raviart–Thomas or Brezzi–Douglas–Marini finite elements.
In the sequel \({\mathbf{V}}_{h}^k\) denotes either \({\mathbf{RT}}_{k}({\mathcal T}_h)\) or \(\mathbf{BMD}_{k}({\mathcal T}_h) \). We consider the following Galerkin eigenvalue problem: Find \((\kappa _h,\mathbf{u}_h)\in \mathbb {C}\setminus \{0\}\times {\mathbf{V}}_{h}^k\setminus \{0\}\) such that:
In the next theorem we summarize the approximation properties of \({\mathbf{V}}_{h}^k\) which we need for the convergence analysis of the Galerkin eigenvalue problem (34).
Theorem 2
The following assertions hold true :
-
(i)
For any \(\mathbf{u}\in \mathbf {V}\) it holds
$$\begin{aligned} \inf _{\mathbf{u}_h\in {\mathbf{V}}_{h}^k} \Vert \mathbf{u}_h - \mathbf{u}\Vert _V\rightarrow 0\quad \text {as } h\rightarrow 0. \end{aligned}$$ -
(ii)
\(({\mathbf{V}}_{h}^k)_h\) satisfies the property (GAP) with respect to the splitting \(\mathbf {V}={{\mathcal X}}\oplus {{\mathcal N}}\).
-
(iii)
For \(-\frac{1}{2}\le s\le k+1\) it holds
$$\begin{aligned} \inf _{\mathbf{u}_h\in {\mathbf{V}}_{h}^k} \Vert \mathbf{u}-\mathbf{u}_h\Vert _{\mathbf {V}}\le C h^{s+\frac{1}{2}}\Vert \mathbf{u}\Vert _{\mathbf {H}^s(\mathrm {div}_\varGamma ,\varGamma )} \qquad \forall \mathbf{u}\in {\mathbf {H}}^s(\mathrm {div}_\varGamma ,\varGamma ), \end{aligned}$$(35)where we refer to [8, Sect. 2.2] for the definition of \({\mathbf {H}}^s(\mathrm {div}_\varGamma ,\varGamma )\) for \(s>-\tfrac{1}{2}\).
Proof
For assertion (i) and (iii) we refer to [8, Sect. 8]. Assertion (ii) is shown in [9, Thm. 4.2]. \(\square \)
From the last theorem and the properties of \({\mathsf {S}}(\cdot )\) it follows that we can apply the convergence results of Theorem 1 to the Galerkin eigenvalue problem (34).
For the specification of the error estimates we consider the adjoint eigenvalue problem for \({\mathsf {S}}(\cdot )\) with respect to the pairing \(\langle \cdot ,{\overline{\cdot }}\rangle _\tau \). Let us first define the so-called adjoint function \({\mathsf {S}}^*(\kappa )\,{:}{=}\,({\mathsf {S}}({\overline{\kappa }}))^*\). The adjoint eigenvalue problem for \({\mathsf {S}}(\cdot )\) is then given by
Note that the Fredholm alternative implies that \(\kappa \) is an eigenvalue of \({\mathsf {S}}(\cdot )\) if and only if \( {\overline{\kappa }}\) is an eigenvalue of \({\mathsf {S}}^*(\cdot )\).
Lemma 5
The following holds true :
-
(i)
\(({{\mathsf {S}} }({\kappa }))^*=-{{\mathsf {S}} }(-{\overline{\kappa }}),\) i.e., \({{\mathsf {S}} }^*({\kappa })=-{{\mathsf {S}} }(-{\kappa }).\)
-
(ii)
\(\kappa \) is an eigenvalue of \({{\mathsf {S}} }(\cdot )\) if and only if \(-{\overline{\kappa }}\) is an eigenvalue of \({{\mathsf {S}} }(\cdot )\).
-
(iii)
\((\kappa ,\mathbf{u})\) is an eigenpair of \({{\mathsf {S}} }(\cdot )\) if and only if \(({\overline{\kappa }},{\overline{\mathbf{u}}})\) is an eigenpair of \({{\mathsf {S}} }^*(\cdot )\).
-
(iv)
The ordered collection \(\mathbf{u}_0,\mathbf{u}_1\ldots ,\mathbf{u}_m\) is a Jordan chain corresponding to \(\kappa \) for \({{\mathsf {S}} }(\cdot )\) if and only if \({\overline{\mathbf{u}}}_0,-{\overline{\mathbf{u}}}_1,{\overline{\mathbf{u}}}_2\ldots ,(-1)^m\overline{\mathbf{u}}_m\) is a Jordan chain corresponding to \({\overline{\kappa }}\) for \({{\mathsf {S}} }^*(\cdot ),\) i.e., the following relation between the generalized eigenspaces holds \(\overline{G({{\mathsf {S}} }(\cdot ),\kappa )} = G({{\mathsf {S}} }^*(\cdot ),{\overline{\kappa }}).\)
Proof
In the proof of the assertions we employ the identity:
(i) It is sufficient to show that
holds for all \(\mathbf{u},\mathbf{r}\in \gamma ^{\mathrm {i}}_{\tau }({\mathbf{C}}_0^\infty (\mathbb {R}^3))\). Let \(\mathbf{u},\mathbf{r}\in \gamma ^{\mathrm {i}}_{\tau }({\mathbf{C}}_0^\infty (\mathbb {R}^3))\), then we can use the integral representation for the pairings in (38) and get with (37):
From the anti-symmetry of the pairing, the assertion follows.
(ii) The Fredholm alternative implies that \(\kappa \) is an eigenvalue of \({\mathsf {S}}(\cdot )\) if and only if \(({\mathsf {S}}(\kappa ))^*\mathbf {t}=0\) for some \(\mathbf {t}\in \mathbf {V}\setminus \{0\}\). The latter is by the result in (i) equivalent to \({\mathsf {S}}(-{\overline{\kappa }})\mathbf {t}=0\).
(iii) Because of (37) we have \(\overline{{\mathsf {S}}(\kappa )\mathbf{r}}={\mathsf {S}}(-{\overline{\kappa }}){\overline{\mathbf{r}}}\). If \((\kappa ,\mathbf{u})\) is an eigenpair of \({\mathsf {S}}(\cdot )\), then we get by i)
(iv) Again, integral representations of the pairing \(\langle \cdot ,\cdot \rangle _{\tau }\) and of the functions \({\mathsf {S}}(\cdot )\) and \({\mathsf {S}}^*\) show that \({\mathsf {S}}^{*(j)}(\kappa )=(-1)^{j+1}({\mathsf {S}}^{(j)}(-\kappa ))\) and \(\overline{({\mathsf {S}}^{(j)}(-\kappa ))\mathbf{r}}={\mathsf {S}}^{(j)}(-{\overline{\kappa }})\overline{ \mathbf{r}}\). From this, the assertion follows directly from the definition of the generalized eigenelements. \(\square \)
In the next theorem we specify the convergence order of the eigenvalues and eigenfunctions of the Galerkin eigenvalue problem (34).
Theorem 3
Let \(D\subset \mathbb {C}\setminus \{0\}\) be a compact and connected set with a simple rectifiable boundary \(\partial D\). Suppose that \(\kappa \in {\mathring{D}}\) is the only eigenvalue of \({{\mathsf {S}} }(\cdot )\) in D and that the generalized eigenspace \(G({{\mathsf {S}} }(\cdot ),\kappa )\subset {\mathbf{H}}^{s}({{\,\mathrm{div}\,}}_\varGamma ,\varGamma )\) for some \(s\in [-\frac{1}{2}, k+1]\). Then there exist an \(h_0>0\) and a constant \(c>0\) such that for all \(h<h_0\) we have :
-
(i)
For all eigenvalues \(\kappa _h\) of the Galerkin eigenvalue problem (34) in D
$$\begin{aligned} \vert \kappa -\kappa _h\vert \le c h^{(2s+1)/m} \end{aligned}$$(39)holds, where m is the maximal length of a Jordan chain corresponding to \(\kappa \).
-
(ii)
If \((\kappa _h,\mathbf{u}_h)\) is an eigenpair of (34) with \(\kappa _h\in D\) and \(\Vert \mathbf{u}_h\Vert _{\mathbf {V}}=1,\) then
$$\begin{aligned} \inf _{\mathbf{u}\in \ker ({{\mathsf {S}} }(\kappa ))}\Vert \mathbf{u}-\mathbf{u}_h\Vert _{\mathbf {V}} \le c \left( \vert \kappa -\kappa _h \vert + h^{(s+1/2)/m} \right) . \end{aligned}$$
Proof
As pointed out above the Galerkin eigenvalue problem satisfies the assumptions of Theorem 1. The error estimates follow then from the approximation property (35) of \({\mathbf{V}}_{h}^k\) and the fact that \(\overline{G({\mathsf {S}}(\cdot ),\kappa )} = G({\mathsf {S}}^*(\cdot ),{\overline{\kappa }})\), see Lemma 5(iv). \(\square \)
5 Scattering resonance problem for a penetrable scatterer
In this section we consider the scattering resonance problem for a penetrable scatterer. We now allow that the permittivity and the permeability are complex and frequency dependent. We assume that the frequency dependence is holomorphic in an open set \(\varLambda \subset \mathbb {C}\). Such configurations occur for example in the field of plasmonics or in the context of metamaterials.
The scattering resonance problem for the penetrable scatterer reads as follows: Find \(\omega \in \varLambda \) and \((0,0)\ne (\mathbf{E}_1,\mathbf{E}_2)\in {\mathbf {H}}(\mathbf {curl};\varOmega ^{\mathrm {i}})\times {\mathbf {H}}_{\text {loc}}(\mathbf {curl};\varOmega ^{\mathrm {e}})\) such that
In the following we will often suppress the dependence of \(\omega \) on \(\varepsilon _\ell (\omega )\) and on \(\mu _\ell (\omega )\), \(\ell =1,2\).
The interior and exterior Calderón identities are used for deriving a boundary integral formulation of the scattering resonance problem (40). A function \(\mathbf {U}_1\in {\mathbf {H}}(\mathbf {curl};\varOmega ^{\mathrm {i}})\) is a solution of the Maxwell’s equations in \(\varOmega ^{\mathrm {i}}\) with wavenumber \(\omega \sqrt{\varepsilon _1\mu _1}\) if and only if it satisfies the interior Calderón identity [8, Thm. 8]
where
We define for \(\ell =1,2\) the block operator
A function \(\mathbf {U}_2\in \mathbf{H}_{\text {loc}}(\mathbf {curl};\varOmega ^{\mathrm {e}})\) is an outgoing solution of Maxwell’s equations in \(\varOmega ^{\mathrm {e}}\) with wavenumber \(\omega \sqrt{\varepsilon _2\mu _2}\) if and only if it satisfies the exterior Calderón identity [8, Thm. 8]
We obtain the following boundary integral formulation of the scattering resonance problem (40) by using the interior and exterior Calderón identity and by setting \((\mathbf{w},\mathbf{u})\,{:}{=}\,(\gamma ^{\mathrm {i}}_{\tau }\mathbf{E}_1, \mu _1^{-1}\gamma _N^{\mathrm {i} }\mathbf{E}_1)= (\gamma ^{\mathrm {e}}_{\tau }\mathbf{E}_2, \mu _2^{-1}\gamma _N^{\mathrm {e} }\mathbf{E}_2)\):
Note that the eigenvalue problems (40) and (43) are not equivalent. If in the eigenvalue problem (40) \(\varepsilon _1\) is interchanged with \(\varepsilon _2\) and \(\mu _1\) with \(\mu _2\), then one also obtains (43) as corresponding boundary integral formulation. However, the equivalence of (40) and (43) is guaranteed if for (43) a constraint is imposed, as shown next.
Theorem 4
The following assertions hold true :
-
(i)
Suppose that \((\omega , \mathbf{E}_1,\mathbf{E}_2)\) is a solution of the scattering resonance problem (40). Then \((\kappa ,\gamma ^{\mathrm {i/e}}_{\mathrm N }\mathbf {E})\) is a solution of the eigenvalue problem (43) and satisfies \(( \tfrac{1}{2}{\mathcal I}-{{\mathcal B}}_1(\omega ))(\gamma ^{\mathrm {i}}_{\tau }\mathbf{E}_1, \mu _1^{-1}\gamma _N^{\mathrm {i} }\mathbf{E}_1)^\top =0\).
-
(ii)
Conversely, suppose that \((\omega , \mathbf{w}, \mathbf{u})\) is a solution of the eigenvalue problem (43) satisfying
 . Define $$\begin{aligned} \mathbf{E}_1\,{:}{=}\, {\Psi }_{\mathrm {SL}}(\kappa _1)\mu _1\mathbf{u}+{\Psi }_{\mathrm {DL}}(\kappa _1)\mathbf{w}\text { and } \mathbf{E}_2\,{:}{=}\, -{\Psi }_{\mathrm {SL}}(\kappa _2)\mu _2\mathbf{u}-{\Psi }_{\mathrm {DL}}(\kappa _2)\mathbf{w}, \end{aligned}$$
. Define $$\begin{aligned} \mathbf{E}_1\,{:}{=}\, {\Psi }_{\mathrm {SL}}(\kappa _1)\mu _1\mathbf{u}+{\Psi }_{\mathrm {DL}}(\kappa _1)\mathbf{w}\text { and } \mathbf{E}_2\,{:}{=}\, -{\Psi }_{\mathrm {SL}}(\kappa _2)\mu _2\mathbf{u}-{\Psi }_{\mathrm {DL}}(\kappa _2)\mathbf{w}, \end{aligned}$$where \(\kappa _\ell \,{:}{=}\,\omega \sqrt{\varepsilon _\ell \mu _\ell },\) \(\ell =1,2\). Then \((\omega , \mathbf{E}_1, \mathbf{E}_2)\) is a solution of the resonance problem (40) and \((\mathbf{w},\mathbf{u})=(\gamma ^{\mathrm {i}}_{\tau }\mathbf{E}_1, \mu _1^{-1}\gamma _N^{\mathrm {i} }\mathbf{E}_1)\).
Proof
(i) We have already shown that if \((\omega , \mathbf{E}_1,\mathbf{E}_2)\) is a solution of the resonance problem (40) that then \((\omega ,\gamma ^{\mathrm {i}}_{\tau }\mathbf{E}_1, \mu _1^{-1}\gamma _N^{\mathrm {i} }\mathbf{E}_1)\) is a solution of (43). The interior Calderón identity (41) implies that \(\left( \tfrac{1}{2}{\mathcal I}-{{\mathcal B}}_1(\omega )\right) (\gamma ^{\mathrm {i}}_{\tau }\mathbf{E}_1, \mu _1^{-1}\gamma _N^{\mathrm {i} }\mathbf{E}_1)^\top =0\).
(ii) Assume now that \((\omega ,\mathbf{w},\mathbf{u})\), \(\mathbf{w},\mathbf{u}\in \mathbf {V}\setminus \{0\}\), satisfies the eigenvalue problem (43) and that the equation  holds. We first show that
holds. We first show that
satisfy the resonance problem (40), where \(\kappa _\ell \,{:}{=}\,\omega _\ell \sqrt{\varepsilon _\ell \mu _\ell }\), \(\ell =1,2\). By construction \(\mathbf{E}_1\) is a solution of the Maxwell’s equations in \(\varOmega ^{\mathrm {i}}\) and \(\mathbf{E}_2\) is an outgoing solution of the Maxwell’s equations in \(\varOmega ^{\mathrm {e}}\). Applying the trace operators to \(\mathbf{E}_1\) and \(\mathbf{E}_2\) yields
Subtracting the second equation from the first equation in (44) and using that \((\mathbf{w}, \mathbf{u})\) satisfies the eigenvalue problem (43) gives
Hence, \(\mathbf{E}_1\) and \(\mathbf{E}_2\) satisfy the transmission conditions of the eigenvalue problem (43). From the assumption  and the first equation in (44), we finally get
and the first equation in (44), we finally get
\(\square \)
For the analysis of the eigenvalue problem (43) we consider the following antisymmetric pairing on the product space \(\mathbf {V}^2\times \mathbf {V}^2\rightarrow \mathbb {C}\):
In the next lemma we collect results on boundary integral operators which we need in order to prove that \({{\mathcal B}}_1(\omega )+{{\mathcal B}}_2(\omega )\) satisfies a generalized Gårding’s inequality.
Lemma 6
Let \(\kappa \in \mathbb {C},\) and \({\mathsf A }(\kappa )\) be as defined in (8) and \({\mathsf M }(\kappa )\) defined by (42). Further, let V(0) be the single layer boundary integral operator of the Laplace equation. Then we have :
-
(a)
The bilinear forms
$$\begin{aligned}&\langle {\mathsf M }(\kappa )\cdot ,\cdot \rangle _{\tau }:{{\mathcal X}}\times {{\mathcal X}}\rightarrow \mathbb {C}\quad \text {and}\quad \langle {\mathsf M }(\kappa )\cdot ,\cdot \rangle _{\tau }: {{\mathcal N}}\times {{\mathcal N}}\rightarrow \mathbb {C}, \end{aligned}$$(45)$$\begin{aligned}&\langle {\mathsf {A} }(\kappa )\cdot ,\cdot \rangle _{\tau }:{{\mathcal X}}\times {\mathbf{V}}_\pi ^{-1/2}\rightarrow \mathbb {C}\quad \text {and}\quad \langle {\mathsf {A} }(\kappa )\cdot ,\cdot \rangle _{\tau }: {\mathbf{V}}_\pi ^{-1/2}\times {{\mathcal X}}\rightarrow \mathbb {C}, \end{aligned}$$(46)are compact.
-
(b)
There exists a constant \(c>0\) such that
$$\begin{aligned} \langle {\overline{\mathbf{u}}},{\mathsf A }(0)\mathbf{u}\rangle _\tau&\ge c\Vert \mathbf{u}\Vert _{ {\mathbf{V}}_\pi ^{-1/2}}^2\qquad \text {for all }\mathbf{u}\in {{\mathcal N}}, \end{aligned}$$(47)$$\begin{aligned} \langle {\overline{v}},V(0)v\rangle _{-\frac{1}{ 2},\frac{1}{2}}&\ge c\Vert v\Vert _{ H^{-1/2}(\varGamma )}^2\qquad \text {for all }v\in H^{-1/2}(\varGamma ). \end{aligned}$$(48)
Proof
For assertion (a) we refer to [8, Lem. 9] and for assertion (b) to [8, Lem. 8]. \(\square \)
Proposition 3
Let \(\omega \in \mathbb {C}\setminus \{0\}\) and \(\kappa _\ell =\omega \sqrt{\mu _\ell (\omega )\varepsilon _\ell (\omega )}\ne 0\) for \(\ell =1,2\). Then there exist a compact operator \({{\mathcal C}}_\ell (\omega ):\mathbf {V}^2\rightarrow \mathbf {V}^2,\) an isomorphism \({{\mathcal T}}_\ell (\omega ):\mathbf {V}^2\rightarrow \mathbf {V}^2,\) and an \(\alpha _\ell (\omega )>0\) such that for all \({\mathfrak {u}}\in \mathbf {V}^2\) it holds
where

\(\beta _\ell (\omega )\,{:}{=}\,{{\,\mathrm{sgn}\,}}({{\,\mathrm{Re}\,}}(\kappa _\ell ))\) if \({{\,\mathrm{Re}\,}}(\kappa _\ell )\ne 0,\) and \(\beta _\ell (\omega )\,{:}{=}\,-{{\,\mathrm{sgn}\,}}({{\,\mathrm{Im}\,}}(\kappa _\ell ))i\) if \({{\,\mathrm{Re}\,}}(\kappa _\ell )= 0.\)
Proof
A proof for positive wavenumbers \(\kappa \) is given in [9, Thm. 3.12] and [8, Thm. 9]. We adapt this proof for complex wavenumbers. In what follows, we will suppress the index \(\ell \), and for the occurring block operators the dependence on the frequency \(\omega \).
Consider the scaling
where
Since for any \({{\mathcal K}}:\mathbf {V}^2\rightarrow \mathbf {V}^2\) and for any \({\mathfrak {u}}\in \mathbf {V}^2\) it holds
where \({{\mathcal R}}\,{:}{=}\,\text {diag}({{\mathsf U}},{{\mathsf U}})\), \({\widetilde{{{\mathcal D}}}}\,{:}{=}\,\text {diag}(\overline{\mu \kappa ^{-1}}{\mathsf I}, {\mathsf I})\), \({{\mathcal C}}\,{:}{=}\,{{\mathcal D}}^{-1}{{\mathcal K}}{{\mathcal D}}\) and \({{\mathcal T}}\,{:}{=}\,{\widetilde{{{\mathcal D}}}}{{\mathcal R}}{{\mathcal D}}\), we will first determine an adequate compact perturbation \({{\mathcal K}}\) of \({{\mathcal A}}\).
Let us define the operator \({\hat{{\mathsf {S}}}}(\kappa ):\mathbf {V}\rightarrow \mathbf {V}\) by
where we refer to (8) for the definition of \({\mathsf A}(\kappa )\) and \(V(\kappa )\). Since \({\mathsf {M}}(\kappa )-{\mathsf {M}}(0)\) and \(\kappa {\mathsf {S}}(\kappa )-{\hat{{\mathsf {S}}}}(\kappa )\) are compact operators in \(\mathbf {V}\) [9, p. 472] the operator
is a compact perturbation of \({{\mathcal A}}\) in \(\mathbf {V}^2\). Let \({\mathfrak {u}}\in \mathbf {V}^2\) and \({{\mathcal D}}{\mathfrak {u}}{=}{:} {\mathfrak {v}}{=}{:}({\mathfrak {v}}_1,{\mathfrak {v}}_2)^\top \). Decompose \({\mathfrak {v}}_1={\mathfrak {v}}_1^{{{\mathcal X}}} +{\mathfrak {v}}_1^{{{\mathcal N}}}\) and \({\mathfrak {v}}_2={\mathfrak {v}}_2^{{{\mathcal X}}} +{\mathfrak {v}}_2^{{{\mathcal N}}}\) according to the splitting \(\mathbf {V}={{\mathcal X}}\oplus {{\mathcal N}}\) as given in (11), where \({\mathfrak {v}}_1^{{{\mathcal X}}}, {\mathfrak {v}}_2^{{{\mathcal X}}}\in {{\mathcal X}}\) and \({\mathfrak {v}}_1^{{{\mathcal N}}},{\mathfrak {v}}_2^{{{\mathcal N}}}\in {{\mathcal N}}\).
First we consider the case that \({{\,\mathrm{Re}\,}}(\kappa )\ne 0\). Then,  and
and
where we have used that \( \langle {\hat{{\mathsf {S}}}}(\kappa )\mathbf{u},\mathbf{r} \rangle _{\tau }=\kappa \langle {\mathsf A}(0)\mathbf{u},\mathbf{r} \rangle _{\tau } \) if \(\mathbf{u}\in {{\mathcal N}}\) or if \(\mathbf{r}\in {{\mathcal N}}\). From the compactness properties of \({\mathsf A}(0)\) and \({\mathsf {M}}(0)\), see (46) and (45), it follows that there exists a compact operator \({\hat{{{\mathcal K}}}}:\mathbf {V}^2\rightarrow \mathbf {V}^2\) such that
The symmetry of \({\mathsf {M}}(0)\) implies
Combining (52) and (53) gives using the ellipticity properties of V(0) and \({\mathsf A}(0)\) from Lemma 6(b)
Hence, we get with \({\mathfrak {v}}={{\mathcal D}}{\mathfrak {u}}=({\mathfrak {u}}_1^{{{\mathcal X}}}+{\mathfrak {u}}_1^{{{\mathcal N}}}, \mu \kappa ^{-1}({\mathfrak {u}}_2^{{{\mathcal X}}}+{\mathfrak {u}}_2^{{{\mathcal N}}}))^\top \), \({\mathfrak {u}}_j^{{{\mathcal X}}}\in {{\mathcal X}}\), \({\mathfrak {u}}_j^{{{\mathcal N}}}\in {{\mathcal N}}\), \(j=1,2\),
Since \({{\mathcal A}}_0\) is a compact perturbation of \({{\mathcal A}}\), the identities (51) and (54) imply that there exists a compact operator \({{\mathcal C}}:\mathbf {V}^2\rightarrow \mathbf {V}^2\) and a constant \({\widetilde{\alpha }}>0\) such that for \(\beta ={{\,\mathrm{sgn}\,}}({{\,\mathrm{Re}\,}}(\kappa ))\) it holds
The ellipticity properties of V(0) and \({\mathsf A}(0)\) from Lemma 6(b) together with the norm equivalence (12) yields the inequality (49) for \({{\,\mathrm{Re}\,}}(\kappa )\ne 0\).
It remains to consider the case \({{\,\mathrm{Re}\,}}(\kappa )= 0\). Again, the compactness properties of \({\mathsf A}(0)\) and \({\mathsf {M}}(0)\), see (46) and (45), imply that there exists a compact operator \({\widetilde{{{\mathcal K}}}}:\mathbf {V}^2\rightarrow \mathbf {V}^2\) such that
From
we get
For \(\beta =-{{\,\mathrm{sgn}\,}}({{\,\mathrm{Im}\,}}(\kappa ))i\), we have \(\kappa ^{-1}{\overline{\beta }}=\vert \kappa ^{-1}\vert \) and \(\kappa {\overline{\beta }}=-\vert \kappa \vert \) because \({{\,\mathrm{Re}\,}}(\kappa )=0\). Using the ellipticity properties of V(0) and \({\mathsf A}(0)\) from Lemma 6(b) this implies
Inequality (49) follows now with the same arguments as for \({{\,\mathrm{Re}\,}}(\kappa )\ne 0\). \(\square \)
Theorem 5
Let \(\omega \in \mathbb {C}\setminus \{0\}\) and \(\kappa _\ell =\omega \sqrt{\mu _\ell (\omega )\varepsilon _\ell (\omega )}\ne 0\) for \(\ell =1,2\). Suppose that
if \({{\,\mathrm{Re}\,}}(\kappa _1)\ne 0\) and \({{\,\mathrm{Re}\,}}(\kappa _2)\ne 0\) and if \({{\,\mathrm{Re}\,}}(\kappa _1)= {{\,\mathrm{Re}\,}}(\kappa _2)= 0,\) and that
if \({{\,\mathrm{Re}\,}}(\kappa _j)\ne 0\) and \({{\,\mathrm{Re}\,}}(\kappa _k)=0\) for \(j\ne k\). Then there exist a compact operator \({{\mathcal C}}(\omega ):\mathbf {V}^2\rightarrow \mathbf {V}^2,\) an isomorphism \({{\mathcal T}}(\omega ):\mathbf {V}^2\rightarrow \mathbf {V}^2,\) and an \(\alpha (\omega )>0\) such that for all \({\mathfrak {u}}\in \mathbf {V}^2\) it holds
Proof
Proposition 3 shows that for \(\ell =1,2\) there exist compact operators \({{\mathcal C}}_\ell (\omega ):\mathbf {V}^2\rightarrow \mathbf {V}^2\), isomorphisms \(\beta _\ell (\omega ){{\mathcal T}}_\ell (\omega ):\mathbf {V}^2\rightarrow \mathbf {V}^2\) and \(\alpha _\ell (\omega )>0\) such that
Choosing \({{\mathcal C}}(\omega )={{\mathcal C}}_1(\omega )+{{\mathcal C}}_2(\omega )\) and \({{\mathcal T}}(\omega )=\beta _1(\omega ){{\mathcal T}}_1(\omega )+\beta _2(\omega ){{\mathcal T}}_2(\omega )\) yields inequality (57). It remains to show that
is an isomorphism from \(\mathbf {V}^2\) to \(\mathbf {V}^2\), which holds if the diagonal blocks are isomorphisms from \(\mathbf {V}\) to \(\mathbf {V}\). This will be shown for the upper block of \({{\mathcal T}}(\omega )\) and the case that both \({{\,\mathrm{Re}\,}}(\kappa _1)\ne 0\) and \({{\,\mathrm{Re}\,}}(\kappa _2)\ne 0\). The other cases can be treated similarly.
Assume that \({{\,\mathrm{Re}\,}}(\kappa _1)\ne 0\) and
\({{\,\mathrm{Re}\,}}(\kappa _2)\ne 0\). Then,
\(\beta _\ell (\omega )={{\,\mathrm{sgn}\,}}({{\,\mathrm{Re}\,}}(\kappa _\ell )) \) and
 , and the upper block of
\({{\mathcal T}}(\omega )\) in (58) reads as
, and the upper block of
\({{\mathcal T}}(\omega )\) in (58) reads as

From \(\mu _1\sqrt{\mu _2\varepsilon _2}\ne \pm \mu _2\sqrt{\mu _1\varepsilon _1}\) it follows that \(\mu _1(\sqrt{\mu _1\varepsilon _1})^{-1}\ne \pm \mu _2(\sqrt{\mu _2\varepsilon _2})^{-1}\) and
This shows that the upper block of
\({{\mathcal T}}(\omega )\) is an isomorphism, since
 is an isomorphism.
\(\square \)
is an isomorphism.
\(\square \)
The assumptions on the material parameters \(\varepsilon _\ell \) and \(\mu _\ell \) in (55) and (56) of Theorem 5 are satisfied for example if the scatterer and background medium are dielectrics but also for typical configurations of scattering problems in plasmonics.
5.1 Galerkin approximation
For the Galerkin approximation of the eigenvalue problem (43) we use \({\mathbf{V}}_{h}^k\times {\mathbf{V}}_{h}^k\) as ansatz space, where again \({\mathbf{V}}_{h}^k\) denotes either \({\mathbf{RT}}_{k}({\mathcal T}_h)\) or \(\mathbf{BMD}_{k}({\mathcal T}_h) \), see Sect. 4. We assume that \(\varLambda \subset \mathbb {C}\setminus \{0\}\) is an open set such that \(\sqrt{\mu _\ell (\omega )\varepsilon _j(\omega )}\), \(\ell \in \{1,2\}\), are holomorphic on \(\varLambda \) and that the assumptions in (55) and (56) of Theorem 5 are satisfied. The Galerkin eigenvalue problem reads as follows: Find \(\omega _h\in \varLambda \) and \({\mathfrak {u}}_h\in {\mathbf{V}}_{h}^k\times {\mathbf{V}}_{h}^k\), \({\mathfrak {u}}_h\ne 0\), such that
We use the abstract results of Sect. 3 in order to show the convergence of the eigenvalues and eigenfunctions of the Galerkin eigenvalue problem (59). Define
where
 for
\({{\,\mathrm{Re}\,}}(\kappa _\ell )\ne 0\) and
\({{\mathsf U}}_\ell ^h(\omega )\,{:}{=}\,{\mathsf I}\) for
\({{\,\mathrm{Re}\,}}(\kappa _\ell )=0\). Here,
for
\({{\,\mathrm{Re}\,}}(\kappa _\ell )\ne 0\) and
\({{\mathsf U}}_\ell ^h(\omega )\,{:}{=}\,{\mathsf I}\) for
\({{\,\mathrm{Re}\,}}(\kappa _\ell )=0\). Here,
 is defined by (28). Then
\({{\mathcal T}}_h(\omega )\in {\mathcal B}({\mathbf{V}}_{h}^k\times {\mathbf{V}}_{h}^k,{\mathbf{V}}_{h}^k\times {\mathbf{V}}_{h}^k) \) and
is defined by (28). Then
\({{\mathcal T}}_h(\omega )\in {\mathcal B}({\mathbf{V}}_{h}^k\times {\mathbf{V}}_{h}^k,{\mathbf{V}}_{h}^k\times {\mathbf{V}}_{h}^k) \) and
Further, let \({P_h}:\mathbf {V}\rightarrow {\mathbf{V}}_{h}^k\) be the orthogonal projection of \(\mathbf {V}\) onto \({\mathbf{V}}_h\), and define
Then, from Corollary 1 it follows that the sequence \(\left( {\mathcal P}_h{\mathcal J}({{\mathcal B}}_1(\omega )+{{\mathcal B}}_2(\omega )){\mathcal P}_h\right) _h\) converges regularly to \({\mathcal J}({{\mathcal B}}_1(\omega )+{{\mathcal B}}_2(\omega ))\) for all \(\omega \in \varLambda \). As a consequence, we can apply the convergence results of Theorem 1 to the eigenvalues and eigenfunctions of the Galerkin eigenvalue problem (59).
6 Numerical examples
In this section we report on results from some numerical experiments for the approximation of the eigenvalues of the boundary integral formulations of the interior and exterior resonance problem (1) and (2a), and of the scattering resonance problem for the penetrable scatterer (40). In all experiments Raviart–Thomas elements of lowest order \(k=0\) are used. For the computations of the boundary element matrices the open-source library BEM++ [31] is employed.
The Galerkin approximations of the eigenvalue problems for \({\mathsf {S}}(\cdot )\) and for \({{\mathcal B}}_1(\cdot )+{{\mathcal B}}_2(\cdot )\) result in holomorphic matrix eigenvalue problems in \(\mathbb {C}\setminus \{0\}\) and in \(\varLambda \), respectively. The related matrix-valued functions are denoted by \({\mathsf {S}}_h(\cdot )\) and \({{\mathcal B}}_{1,h}(\cdot )+{{\mathcal B}}_{2,h}(\cdot )\). For the numerical solution of the matrix eigenvalue problems we use the contour integral method as given in [2]. For other variants of the contour integral method we refer to [1, 38]. The contour integral method is a reliable method for the approximation of all eigenvalues which lie inside of a given contour in the complex plane, and for the approximation of the corresponding eigenvectors. The method is based on the contour integration of the resolvent, \(({\mathsf {S}}_h(\cdot ))^{-1}\) and \(({{\mathcal B}}_{1,h}(\cdot )+{{\mathcal B}}_{2,h}(\cdot ))^{-1}\) in our case, and utilizes that the eigenvalues of eigenvalue problems for holomorphic matrix-valued functions are poles of the resolvent. By contour integration of the resolvent applied to some randomly chosen set of test vectors a reduction of the holomorphic eigenvalue problem to an equivalent linear eigenvalue problem is possible such that the eigenvalues of the linear eigenvalue problem coincide with the eigenvalues of the nonlinear eigenvalue problem inside the contour.
The main computational cost of the numerical implementation of the contour integral method consists in the approximation of the contour integral of the resolvent. In our numerical experiments we use for that the composite trapezoidal rule as suggested in [2]. In general, with such an approximation of the contour integral an exponential convergence order for the approximation of the eigenvalues with respect to number of quadrature nodes is achieved [2]. The composite trapezoidal rule requires in each quadrature node \(\xi _j\), \(j=1,\ldots ,N\), the application of \(({\mathsf {S}}_h(\xi _j))^{-1}\) and \(({{\mathcal B}}_{1,h}(\xi _j)+{{\mathcal B}}_{2,h}(\xi _j))^{-1}\), respectively, to some randomly chosen set of test vectors, for which in our numerical experiments an LU decomposition is utilized.
Remark 6.1
For the analysis of the contour integral method it is usually assumed that the underlying matrix-valued function of the eigenvalue problem is holomorphic inside the contour. However, the contour integral method is also suitable for eigenvalue problems where the underlying function has isolated singularities in the case of that the resolvent has a holomorphic continuation in the neighborhood of the singularities. The reason for that is that the contour integral method operates on the resolvent of the eigenvalue problem and approximates the poles of the resolvent. Our numerical experiments indicates that there is a holomorphic continuation of \(({\mathsf {S}}_h(\cdot ))^{-1}\) as well as of \(({{\mathcal B}}_{1,h}(\cdot )+{{\mathcal B}}_{2,h}(\cdot ))^{-1}\) in the neighborhood of 0, see Figs. 1, 2 and 3, respectively. The conjecture is that this property holds in general if the material parameters are holomorphic in the neighborhood of 0.
6.1 Interior and exterior resonance problem
In the first numerical examples we consider the Galerkin approximation (34) of the boundary integral formulation (10) of the interior and exterior resonance problem (1) and (2a). The unit cube and the unit ball are chosen for \(\varOmega ^{\mathrm {i}}\). In all examples in this subsection we take \(\varepsilon =\mu =1.0\).
6.1.1 Interior resonance problem for the unit cube
For the unit cube only the interior resonances are known analytically. Therefore we restrict ourselves to the approximation of the resonances of the interior problem. The interior resonances have the form \(\kappa ={\pi {k}}\), where \(k=\sqrt{k_1^2+k_2^2+k_3^2}\) with \(k_1,k_2, k_3\in \mathbb {N}_0\) and \(k_1k_2+k_2k_3+k_3k_1>0\) [3, Sect. 6]. For the contour integral method we choose as contour the ellipse \(\varphi (t)=c+a\cos (t)+i b \sin (t)\), \(t\in [0,2\pi ]\), with \(c=5.0\), \(a=5.1\) and \(b=0.5\). There are seven distinct eigenvalues within this ellipse which have a total algebraic multiplicity of 32. The number of quadrature nodes for the approximation of the contour integral is 25. In Table 1 the errors of the approximations of the two smallest resonances and of the largest resonance for discretizations with mesh sizes \(h=\sqrt{2}2^{-j}\), \(j=2,\ldots ,5\), are given.
We observe that the experimental orders of convergence (eoc) match the theoretical predicted cubic asymptotic convergence order, see (39). Further, for the specified mesh sizes all exact resonances are approximated with the right multiplicities and no spurious resonances occur within the ellipse. A plot of the computed resonances for the mesh with mesh size \(h=\sqrt{2}2^{-4}\) is given in Fig. 1. The experiments also confirm the mentioned conjecture that the resolvent \({\mathsf {S}}_h(\cdot )^{-1}\) can be holomorphically extended to \(\kappa =0\). We want to mention that for coarser discretizations with 18 and 72 degrees of freedom, which corresponds to the mesh sizes \(h=\sqrt{2}\) and \(h=\sqrt{2}2^{-1}\), only the two smallest resonances are approximated well and that for these discretizations the cubic convergence order is no longer observable.
6.1.2 Interior and exterior resonance problem for the unit ball
The interior and exterior resonances of the unit ball can be represented as zeros using the spherical Bessel and Hankel functions [29]. We denote by \(j_n\) the spherical Bessel functions of the first kind and as before by \(h_n^{(1)}\) the spherical Hankel functions of the first kind. The set of the interior resonances is given by
and that of the exterior resonances by
As contour for the contour integral method the ellipse \(\varphi (t)=c+a\cos (t)+i b \sin (t)\), \(t\in [0,2\pi ]\), is chosen with \(c=5.0\), \(a=5.3\) and \(b=1.0\). There are 23 distinct eigenvalues within this ellipse having a total algebraic multiplicity of 157. For the approximation of the contour integral 100 quadrature nodes are taken. In Table 2 the errors of the smallest and the largest interior and exterior resonance in modulus inside the ellipse are given.
The experimental convergence order is in contrast to the cube of one order reduced since the sphere is approximated by flat triangles. Again, all exact resonances are approximated with the right multiplicities and no spurious resonances occur. In Fig. 2 the computed resonances by the contour integral method for the mesh with mesh size \(h=0.082\) are plotted.
6.2 Scattering resonance problem for a penetrable scatterer
In this subsection we consider the Galerkin approximation of the boundary integral formulation (43) of the scattering resonance problem for the penetrable scatterer (40). The domains \(\varOmega ^{\mathrm {i}}\) for the numerical examples are again the unit cube and the unit ball. As approximation space we choose \(\mathbf {V}_h^0\times \mathbf {V}_h^0 ={\mathbf{RT}_0({{\mathcal T}}_h)}\times {\mathbf{RT}_0({\mathcal T}_h)}\).
6.2.1 Unit cube
For this example the material parameters are set to \(\varepsilon _1= 4.0\) and \(\varepsilon _2= \mu _1=\mu _2=1.0\). The exact resonances of the resonance problem for a penetrable cube are not known. As reference resonances the computed resonances of a very fine mesh with mesh size \(h=0.03125\) are taken. As contour for the contour integral method we chose the ellipse \(\varphi (t)=c+a\cos (t)+i b\sin (t)\), \(t\in [0,2\pi ]\), with \(c=2.5\), \(a=2.7\) and \(b=0.5\). For the approximation of the contour integral 20 quadrature nodes are used. The numerical experiments suggest a cubic asymptotic convergence order, see Table 3, which is in accordance with the theoretical results.
The computed approximations of the resonances by the contour integral method inside the ellipse for \(h=0.177\) are plotted in Fig. 3. The numerical experiments indicate that the resolvent \((\mathcal B_{1,h}(\cdot )+\mathcal B_{2,h}(\cdot ))^{-1}\) can be holomorphically extended to \(\omega =0\).
6.2.2 Unit ball
In the last example we consider a plasmonic resonance problem for a golden nano-sphere with diameter \(d=100\)nm embedded in a host medium with refractive index of 1.5 [35]. A Drude model for the permittivity of gold is taken of the form [30]
with \(\varepsilon _0\) being the vacuum permittivity, \(\omega _p=1.26\times 10^{16}\,\)s\(^{-1}\) and \(\gamma =1.41\times 10^{14}\,\)s\(^{-1}\). The other material parameter are chosen as \(\varepsilon _2=1.5\varepsilon _0\), \(\mu _1=\mu _2=\mu _0\), where \(\mu _0\) is the vacuum permeability.
The exact resonances of the scattering resonance problem for a penetrable scatterer for a ball with radius R can be determined by the Mie series method [35, Supplemental material, Sect. 3]. A number \(\omega \in \mathbb {C}\) is a resonance if it satisfies either
or
for some \(n\in \mathbb {N}\), where \(\kappa _\ell =\omega \sqrt{\varepsilon _\ell (\omega )\mu _\ell (\omega )}\), \(\ell =1,2\).
In plasmonics those scattering resonances are of interest which are close to the frequency range of light which corresponds to \([1.7,3.1]\hslash ^{-1}\), where \(\hslash \) is the reduced Planck constant in eV s given by \(\hslash =6.58211957\)e−16. For the contour integral method as contour an ellipse is chosen with \(\varphi (t)=\hslash ^{-1}\left[ c+a\cos (t)+i b \sin (t)\right] \), \(t\in [0,2\pi ]\), with \(c=2.5\), \(a=1.4\) and \(b=0.75\). The number of quadrature nodes for the approximation of the contour integral is 20. Three distinct resonances with total algebraic multiplicity of 15 lie inside the ellipse, which are solutions of Eq. (61) for \(n=1,2,3\).
The principal square root, with the branch cut along the non-positive real axis, applied to the permittivity \(\varepsilon _1(\omega )\) defined in (60) is non-continuous along the contour. Instead we take the square root with the branch cut \(\{z=r(\cos (\phi _0)+i\sin (\phi _0)):r\ge 0\}\), \(\phi _0 = 1.9\pi \), which guarantees that \(\sqrt{\varepsilon _1(\omega )\mu _1}\) is continuous along the contour and inside of it. In Table 4 the relative error and the experimental order of convergence for the approximation of the resonances inside the contour are given. The convergence order is compared to the cube of one order reduced as expected since the sphere is approximated by flat triangles.
Again, all eigenvalues inside the ellipse are approximated with the right multiplicity and no spurious eigenvalues occur. In Fig. 4 the computed resonances by the contour integral method for the mesh with mesh size \(h=7.67\) are plotted.
7 Conclusions
In this paper we have analyzed the Galerkin approximation of boundary integral formulations for three different types of electromagnetic resonance problems. We have considered the single layer boundary integral formulation for the interior and exterior resonance problem with perfect conducting boundary conditions and a first kind boundary integral formulation of the resonance problem for the penetrable scatterer. These boundary integral formulations are eigenvalue problems for holomorphic Fredholm operator-valued functions. For the numerical approximation of these eigenvalue problems a Galerkin approximation with Raviart–Thomas and Brezzi–Douglas–Marini type elements are considered. The extension of recent results [15, 16] on the regular approximations of operators satisfying a generalized Gårding’s inequality enables us to apply the classical convergence theory on the approximation of eigenvalue problems for holomorphic Fredholm operator-valued functions to the proposed boundary element approximations. Numerical examples confirm the theoretical convergence results and show that the asymptotic convergence behavior appears on rather coarse meshes.
References
Asakura, J., Sakurai, T., Tadano, H., Ikegami, T., Kimura, K.: A numerical method for nonlinear eigenvalue problems using contour integrals. JSIAM Lett. 1, 52–55 (2009)
Beyn, W.J.: An integral method for solving nonlinear eigenvalue problems. Linear Algebra Appl. 436(10), 3839–3863 (2012)
Bramble, J.H., Kolev, T.V., Pasciak, J.E.: The approximation of the Maxwell eigenvalue problem using a least-squares method. Math. Comp. 74(252), 1575–1598 (2005)
Buffa, A.: Remarks on the discretization of some noncoercive operator with applications to heterogeneous Maxwell equations. SIAM J. Numer. Anal. 43(1), 1–18 (2005)
Buffa, A., Christiansen, S.H.: The electric field integral equation on Lipschitz screens: definitions and numerical approximation. Numer. Math. 94(2), 229–267 (2003)
Buffa, A., Costabel, M., Schwab, C.: Boundary element methods for Maxwell’s equations on non-smooth domains. Numer. Math. 92(4), 679–710 (2002)
Buffa, A., Costabel, M., Sheen, D.: On traces for \({\mathbf{H}}({\mathbf{curl}},\varOmega )\) in Lipschitz domains. J. Math. Anal. Appl. 276(2), 845–867 (2002)
Buffa, A., Hiptmair, R.: Galerkin boundary element methods for electromagnetic scattering. In: Topics in computational wave propagation, Lect. Notes Comput. Sci. Eng., vol. 31, pp. 83–124. Springer, Berlin (2003)
Buffa, A., Hiptmair, R., von Petersdorff, T., Schwab, C.: Boundary element methods for Maxwell transmission problems in Lipschitz domains. Numer. Math. 95(3), 459–485 (2003)
Christiansen, S.H.: Discrete Fredholm properties and convergence estimates for the electric field integral equation. Math. Comp. 73(245), 143–167 (2004)
Colton, D., Kress, R.: Inverse acoustic and electromagnetic scattering theory, Applied Mathematical Sciences, vol. 93, third edn. Springer, New York (2013)
Cossonnière, A.: Valeurs propres de transmission et leur utilisation dans l’identification d’inclusions à partir de mesures électromagnétiques. Phd thesis, INSA Toulouse (2011)
Durán, M., Nédélec, J.C., Ossandón, S.: An efficient Galerkin BEM to compute high acoustic eigenfrequencies. J. Vib. Acoust. 131(3), (31001)1–9 (2009)
Gohberg, I., Goldberg, S., Kaashoek, M.A.: Classes of Linear Operators, vol. I. Birkhäuser Verlag, Basel (1990)
Halla, M.: Analysis of radial complex scaling methods for scalar resonance problems in open systems. Ph.d. thesis, TU Vienna (2019)
Halla, M.: Galerkin approximation of holomorphic eigenvalue problems: weak T-coercivity and T-compatibility. arXiv e-prints arXiv:1908.05029 (2019)
Karma, O.: Approximation in eigenvalue problems for holomorphic Fredholm operator functions. I. Numer. Funct. Anal. Optim. 17(3–4), 365–387 (1996)
Karma, O.: Approximation in eigenvalue problems for holomorphic Fredholm operator functions. II. (Convergence rate). Numer. Funct. Anal. Optim. 17(3–4), 389–408 (1996)
Kato, T.: Perturbation Theory for Linear Operators. Classics in Mathematics. Springer-Verlag, Berlin (1995)
Kimeswenger, A., Steinbach, O., Unger, G.: Coupled finite and boundary element methods for fluid-solid interaction eigenvalue problems. SIAM J. Numer. Anal. 52(5), 2400–2414 (2014)
Kirsch, A., Hettlich, F.: The mathematical theory of time-harmonic Maxwell’s equations, Applied Mathematical Sciences, vol. 190. Springer, Cham (2015)
Kleefeld, A.: Numerical methods for acoustic and electromagnetic scattering: Transmission boundary-value problems, interior transmission eigenvalues, and the factorization method. Habilitation thesis, BTU Cottbus-Senftenberg (2015)
Kozlov, V., Maz\(^{\prime }\)ya, V.: Differential Equations with Operator Coefficients with Applications to Boundary Value Problems for Partial Differential Equations. Springer Monographs in Mathematics. Springer-Verlag, Berlin (1999)
Maäkitalo, J., Kauranen, M., Suuriniemi, S.: Modes and resonances of plasmonic scatterers. Phys. Rev. B 89, 165429 (2014)
McLean, W.: Strongly Elliptic Systems and Boundary Integral Equations. Cambridge University Press, Cambridge (2000)
Misawa, R., Niino, K., Nishimura, N.: Boundary integral equations for calculating complex eigenvalues of transmission problems. SIAM J. Appl. Math. 77(2), 770–788 (2017)
Monk, P.: Finite element methods for Maxwell’s equations. Oxford University Press, New York (2003)
Nannen, L., Hohage, T., Schädle, A., Schöberl, J.: Exact sequences of high order Hardy space infinite elements for exterior Maxwell problems. SIAM J. Sci. Comput. 35(2), A1024–A1048 (2013)
Nédélec, J.C.: Acoustic and electromagnetic equations. Springer-Verlag, New York (2001)
Sauvan, C., Hugonin, J.P., Maksymov, I.S., Lalanne, P.: Theory of the spontaneous optical emission of nanosize photonic and plasmon resonators. Phys. Rev. Lett. 110, 237401 (2013)
Śmigaj, W., Arridge, S., Betcke, T., Phillips, J., Schweiger, J.: Solving Boundary Integral Problems with BEM++. ACM Trans. Math. Softw. 41(6), 1–40 (2015)
Steinbach, O.: Numerical Approximation Methods for Elliptic Boundary Value Problems. Finite and Boundary Elements. Springer, New York (2008)
Steinbach, O., Unger, G.: Convergence analysis of a Galerkin boundary element method for the Dirichlet Laplacian eigenvalue problem. SIAM J. Numer. Anal. 50, 710–728 (2012)
Steinbach, O., Unger, G.: Combined boundary integral equations for acoustic scattering-resonance problems. Math. Methods Appl. Sci. 40(5), 1516–1530 (2017)
Unger, G., Trügler, A., Hohenester, U.: Novel modal approximation scheme for plasmonic transmission problems. Phys. Rev. Lett. 121, 246802 (2018)
Vainikko, G.: Approximative methods for nonlinear equations (two approaches to the convergence problem). Nonlinear Anal. 2(6), 647–687 (1978)
Wieners, C., Xin, J.: Boundary element approximation for Maxwell’s eigenvalue problem. Math. Methods Appl. Sci. 36(18), 2524–2539 (2013)
Yokota, S., Sakurai, T.: A projection method for nonlinear eigenvalue problems using contour integrals. JSIAM Lett. 5, 41–44 (2013)
Funding
Open access funding provided by Graz University of Technology.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is part of the topical collection “Waves 2019 – invited papers” edited by Manfred Kaltenbacher and Markus Melenk.
The author acknowledges support from the Austrian Science Fund (FWF): P31264.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Unger, G. Convergence analysis of a Galerkin boundary element method for electromagnetic resonance problems. Partial Differ. Equ. Appl. 2, 39 (2021). https://doi.org/10.1007/s42985-020-00049-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42985-020-00049-5


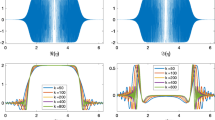


 . Define
. Define 


