Abstract
Tewari et al. (Parametric characterization of multimodal distributions with non-Gaussian modes, pp 286–292, 2011) introduced Gaussian mixture copula models (GMCM) for clustering problems which do not assume normality of the mixture components as Gaussian mixture models (GMM) do. In this paper, we propose Student t mixture copula models (SMCM) as an extension of GMCMs. GMCMs require weak assumptions, yielding a flexible fit and a powerful cluster tool. Our SMCM extension offers, in a natural way, even more flexibility than the GMCM approach. We discuss estimation issues and compare Expectation-Maximization (EM)-based with numerical simplex optimization methods. We illustrate the SMCM as a tool for image segmentation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Data clustering is a major domain of unsupervised learning which means that we do not observe an outcome or response variable. The aim of clustering is to segment the data into groups or “clusters” which are nearby in some sense. One approach is to group the data via the famous non-parametric k-means algorithm. Roughly said, k-means partitions the data into k clusters by minimizing the sum of the squared Euclidean distance from each point to its cluster center. Often k-means is used as a first-step or to determine the appropriate number of clusters. For more information on k-means and clustering in general, see, e.g., [1, 11].
The focus in this paper, however, lies on probabilistic methods for clustering. The basic idea is to fit a multimodal mixture probability distribution to the data. The clustering then works by assigning the mixture component with the highest probability proportion to each data point. Gaussian mixture models (GMMs), where the mixture components are multivariate normal distributed, are certainly the most frequent widely used as a mixture distribution model for clustering in the literature. For example, Carson et al. [6] and Permuter et al. [17] applied GMMs for clustering in image segmentation, Chen et al. [7] and Torres-Carrasquillo et al. [24] for language and accent identification, or Yeung et al. [28] for biostatistical clustering. Aggarwal [1] and Friedman [11] gave a detailed introduction into probabilistic model-based clustering. Berkhin [3] surveys several clustering algorithms including mixture models. Steinley and Brusco [22] investigated empirical properties of mixture models for clustering in several simulation studies.
The determination of the number of clusters is delicate issue. However, the literature offers several approaches, see [1, 3, 11] and their references therein. In this paper, we assume the number of clusters to be known and fixed and refer to the extensions in the literature for unknown cluster numbers.
The underlying normality assumption of the mixture components may not be reasonable for many applications, which motivated Tewari et al. [23] to introduce Gaussian mixture copula models (GMCMs) instead. Here, the normality assumption of the mixture components is dropped (in fact there is no distributional assumption for these) with only assumptions on the dependence structure of the data. Bilgrau et al. [4] implemented the R package GMCM which allows the easy application of the GMC model. The GMCM has also been applied in various context. For instance, Tewari et al. [23] and Bilgrau et al. [4] used it for image segmentation, Wang et al. [27] and Yu et al. [29] for wind energy predictions, or Samudra et al. [20] for surgery scheduling. Rajan and Bhattacharya [19] extended the GMCM approach to also handle mixed data (continuous and discrete) and Kasa et al. [13] improved it for high-dimensional data.
In this paper, we discuss the extension of GMCMs to Student t mixture copula models (SMCMs). We, therefore, combine the GMCM approach of [23] as a generalization of GMMs and Student t mixture models (SMMs) of [9] (they applied the SMM to image compression). The difference between GMM and SMM is the distribution for the mixture components. Both models can be learned with an appropriate version of the Expectation-Maximization (EM) algorithm [8]. The extension is to model the dependence structure via copulas rather than to model the observed data. Thus, GMCMs are capable of modeling multimodality (in contrast to, e.g., Gaussian copulas) and a dependence structure (in contrast to GMMs). The SMCM additionally allows for heavy tails of the mixture components in the dependence structure.
The remainder of this paper is organized as follows. The next section gives a brief technical introduction to general copula models and mixture distributions and proposes the SMCM. The third section discusses the estimation algorithms used to learn SMCMs. The fourth section applies the proposed SMCM to test datasets and the task of image segmentation and compares it with the GMCM. The last section concludes.
Student Mixture Copulas
First, we introduce some general background on copulas, see [16] for more details. We call \(C:[0,1]^d\rightarrow [0,1]\) a d-dimensional copula if it is a joint distribution function of a d-dimensional random vector on \([0,1]^d\) with marginals that are distributed uniformly on [0, 1].
Sklar’s theorem [21] states that the relationship between a multivariate cumulative distribution function \(F(z_1,\ldots ,z_d;\theta )=P[Z_1\le z_1,\ldots ,Z_d\le z_d]\) of random variables \(Z_1,\ldots ,Z_d\) can be expressed in terms of its marginal distribution functions \(F_j(z_j)=P[Z_j\le z_j]\) and a copula C. Here, \(\theta \) denotes the parameter vector to be estimated. Precisely, the statement is
If the copula function C and the marginal distribution functions \(F_j\) are differentiable, we can express the joint density in terms of the copula density c and the marginal densities \(f_j\):
where \(u_j=F_j(z_j;\theta )\). Hence, the copula density is given by
where \(z_j=F_j^{-1}(u_j;\theta )\), \(j=1,\ldots ,d\).
We proceed by introducing the class of finite mixture distributions. An m-component mixture distribution has a density function of the form
where \(\pi _k\ge 0\), for \(1\le k\le m\) and \(\sum _{k=1}^m\pi _k=1\). The multivariate density function g only depends on the parameter vector \(\theta _{k}\) of the k-th component. If we take g to be the density of a d-dimensional normal distribution we obtain the GMM and for the Student t distribution we obtain the SMM.
Joining the copula approach with mixture densities we obtain the SMCM (and analogously the GMCM). Let c be as in (3) with f as in (4). If g is the normal density, c is the copula density of the GMCM and if g is the Student t density, c is the copula density of the SMCM. More precisely, the SMCM has density function
with
and \(f_{\mathrm {sm},j}\) is its j-th marginal. Let \(g_{\mathrm {s}}(z_1,\ldots ,z_d;\theta _{k})\) denote the d-dimensional Student t density function with \(\theta _{k}=(\mu _k,\Sigma _k^{\mathrm {vec}},\nu _k)\) and \(\mu _k\) is the location parameter vector, \(\Sigma _k\) is a scaling matrix and \(\nu _k\) is the degree of freedom. The full parameter vector is \(\theta =(\pi _1,\ldots ,\pi _m,\mu _1,\ldots ,\mu _m,\Sigma _1^{\mathrm {vec}},\ldots ,\Sigma _m^{\mathrm {vec}}, \nu _1,\ldots ,\nu _m)\).
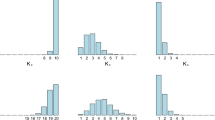
Assume we observe i.i.d. d-dimensional data \(\{x^{(i)}\}_{i=1}^n\) with \(x^{(i)}=(x_1^{(i)},\ldots ,x_d^{(i)})\). That is, a dependence structure is allowed along the d dimensions but not between the n vector-valued observations. Each \(x_j^{(i)}\) has marginal distribution function \(H_j(x)\) which is, for now, assumed to be known. Thus, \((u_1^{(i)},\ldots ,u_d^{(i)})=(H_1(x_1^{(i)}),\ldots ,H_d(x_d^{(i)}))\) where the \(u_j^{(i)}\) are distributed uniformly on (0, 1). This means that \((u_1^{(i)},\ldots ,u_d^{(i)})\) can be modeled by a copula C, where C is the copula function of, e.g., the GMCM or SMCM. The relation between \(u_j^{(i)}\), \(x_j^{(i)}\) and \(z_j^{(i)}\) can be described by \(u_j^{(i)}=F_j(z_j^{(i)})=H_j(x_j^{(i)})\) for any \(i=1,\ldots ,n\) and \(j=1,\ldots ,d\). The data thus have three different levels. \(\{x^{(i)}\}_{i=1}^n\) is the observed process, \(\{u^{(i)}\}_{i=1}^n\) is the copula process and \(\{z^{(i)}\}_{i=1}^n\) is the latent process. When the copula level is modeled with an SMCM (GMCM), the latent process follows the SMM (GMM). Figure 1 compares the observed data, the copula level and the latent level of an SMCM with a GMCM for \(n=10{,}000\). For this figure, we simulated \(\{u^{(i)}\}_{i=1}^n\) according to a 2-dimensional and 3-modal SMCM and a GMCM using the same set of parameters (except the degrees of freedom). To simulate the observed level, we set \(H_j^{-1}\equiv \Phi ^{-1}\) for any j, the standard normal quantile function. We see that on the observed level the clusters of the SMCM have more outliers than those of the GMCM. This transfers to the copula and the latent levels where the SMCM clusters have more fuzzy and overlapping boundaries than the GMCM clusters. This property may be more realistic in some scenarios.
c, f Show 2-dimensional and 3-modal simulated data of a GMM and an SMM with the same means and scaling matrices for \(n=10{,}000\). All degrees of freedom are equal to 4. b, e Show the corresponding copula levels of the GMCM and the SMCM. a, d Visualize the corresponding observed level by transforming the copula level with the inverse distribution function of the standard normal distribution
Estimation
In this section, we follow [23] and propose two maximum likelihood estimation algorithms for the parameters of an SMCM. We aim to learn an SMCM by maximizing the log-likelihood corresponding to the copula density. First, we discuss an Expectation-Maximization-based algorithm and second a Simplex approach. Both also work well for the GMCM. We also highlight the differences.
Consider n observed i.i.d. d-dimensional random vectors \(\{x^{(i)}\}_{i=1}^n\) with \(x^{(i)}=(x_1^{(i)},\ldots ,x_d^{(i)})\). We assume \(d<n\), extensions are discussed in the last section. We obtain the corresponding marginal distribution values \(u^{(i)}=(u_1^{(i)},\ldots ,u_d^{(i)})\) for \(i=1,\ldots ,n\) using \(H_j(x_j^{(i)})\) for any i and j. The log likelihood function is given by
Pseudo EM Algorithm
We propose a Pseudo Expectation-Maximization (PEM) algorithm to estimate the parameters of the SMCM. It is important to note that we cannot apply the EM algorithm as for mixtures of Student’s distributions. This is likewise the case for the GMCM where [23] discussed why the EM algorithm does not necessarily find the true maximum. The key point is that the inputs to an EM algorithm have to remain fixed which is indeed the case when we only consider an SMM or GMM. However, this is not the case for the SMCM (or GMCM). The problem is that, while the input \(\{u^{(i)}\}_{i=1}^n\) to an SMCM remains fixed, the inverse distribution values or pseudo observations \(z_j=F_j^{-1}(u_j|\theta )\) depend on the parameters. Since the parameter estimate is updated after each iteration in an EM algorithm the pseudo observations also change in every step. Thus, the assumption of fixed observations is violated.
Therefore, the PEM does not necessarily converge to a local optimum. Nevertheless, it can provide plausible starting values for simplex or gradient based methods as discussed below.
Another issue is that we only observe \((x_1^{(i)},\ldots ,x_d^{(i)})\) as data. The required \((u_1^{(i)},\ldots ,u_d^{(i)})=(H_1(x_1^{(i)}),\ldots ,H_d(x_d^{(i)}))\) depend on the distribution functions \(H_j\) of \(x_j^{(i)}\). In practice, \(H_j\) is unknown and has to be estimated. We follow [4, 23] and estimate \((u_1^{(i)},\ldots ,u_d^{(i)})\) non-parametrically using the empirical cumulative distribution function \(\hat{H}_j(x)=\frac{1}{n}\sum _{i=1}^n\mathbb {1}[x_j^{(i)}\le x]\) such that
To avoid infinities in the computations \(\hat{u}_j^{(i)}\) is rescaled with the factor \(\frac{n}{n+1}\).

Algorithm 1 outlines the PEM. Remarks on the notation: \(F_{\mathrm {sm},j}^{-1}\) denotes the j-th marginal distribution function and \(\psi \) denotes the digamma function. With the index t we denote the t-th step of the PEM. We stop the PEM algorithm after some convergence criterion \(d(\theta ^{(t+1)},\theta ^{(t)})\) is met. Possible choices for convergence criteria are the following:
-
1.
\(\max (\theta ^{(t+1)}-\theta ^{(t)})\)
-
2.
\(\ell \left( \theta ^{(t+1)}|\{\hat{u}^{(i)}\}_{i=1}^n\right) -\ell \left( \theta ^{(t)}|\{\hat{u}^{(i)}\}_{i=1}^n\right) \)
-
3.
\(\left| \ell \left( \theta ^{(t+1)}|\{\hat{u}^{(i)}\}_{i=1}^n\right) -\ell \left( \theta ^{(t)}|\{\hat{u}^{(i)}\}_{i=1}^n\right) \right| \)
Criterion 1 was used in [23] and criteria 2 and 3 were discussed in [4] for the GMCM. Bilgrau et al. [4] also discussed convergence criteria based on the likelihood for the hidden GMM. However, we stick with the third criterion because in our experimental results the effect of the stopping rule was minor. The reason for this is, which is more drastic compared to GMCM, that the log-likelihood of the SMCM attains a maximal value over the iterations rather early while the log-likelihood of the hidden SMM is still increasing. This suggests to use a rather high \(\varepsilon \) or to additionally employ a deterministic stopping rule after too many iterations.
Of course, this algorithm rarely computes the true maximum which is why we use it as a first guess in the following way. We choose different initial vectors \(\theta ^{(0)}\), for each we run the PEM algorithm and obtain an estimate \(\hat{\theta }\). Out of these, we choose the parameter vector with the highest log-likelihood (7). This parameter vector is then used in the numerical optimization outlined in the next subsection.
We discuss the computational complexity of the proposed PEM in Algorithm 1. The complexity of each E-Step is \(O(mnd^3)\) (the \(d^3\) is due to the matrix inversions \(\Sigma _k^{-1}\)). The complexity of each M-Step is \(O(mnd^2)\). Thus, the complexity of each EM-iteration is \(O(mnd^3)\). Given a deterministic additional stopping rule of the PEM after T iterations the overall complexity is \(O(Tmnd^3)\). This means the complexity is higher than the PEM of GMCMs with complexity \(O(Tmnd^2)\). In practice, if the dimensionality is not too high, the runtime is dominated by the k root searches in the M-Step.
Numerical Maximization
Since the PEM algorithm discussed above finds only a pseudo maximum, we cannot expect that the different seeds for the PEM will lead to a good estimator of \(\theta \). This motivates us to additionally apply a numerical optimization scheme like in [4, 23] for the GMCM. Tewari et al. [23] proposed a gradient descent-based algorithm and Bilgrau et al. [4] compared the Nelder and Mead [15], simulated annealing [2] and L-BFGS-B [5] optimization procedures. In their experiments, Bilgrau et al. [4] found that the Nelder–Mead procedure worked best in terms of runtime and numerical robustness and with similar clustering accuracy. We found the same for the Nelder–Mead approach. There are additional difficulties for the SMCM in the optimization compared with the GMCM because of the m additional parameters \(\nu _1,\ldots ,\nu _m\).
As in [4], we use the Cholesky decomposition for the scaling matrices \(\Sigma _k=A_kA_k^{\mathrm {T}}\) whose elements are vectorized so that the Nelder–Mead algorithm can maximize over identifiable parameters. Moreover, as [4] also noted, the GMCM (and the SMCM) are invariant to translations and scaling, meaning that only relative distances between the component modes can be inferred. Hence, we set \(\mu _1=0\) and \(\Sigma _1\) is scaled such that it has only 1’s on the diagonal. The remaining parameters are to be estimated via Nelder–Mead maximization.
Applications
Monte Carlo Experiments
We discuss some experimental evidence for GMCMs and SMCMs clustering. We simulate data according to GMCMs and SMCMs each with \(n=1000\), \(d=2\) and \(m=3\) for \(R=1000\) repetitions. The parameters \(\pi _k\), \(\mu _k\) and \(\Sigma _k\) are drawn randomly for each run. The degrees of freedom \(\nu _k\) for SMCM are fixed at the value 4 for all runs. Like in Fig. 1, we simulate the observed level using \(H_j^{-1}\equiv \Phi ^{-1}\) for any j. For each dataset we use the GMCM-PEM, SMCM-PEM (maximized over different initial values), and k-means (as a baseline) clustering algorithms. To save computational time, we omit to use an additional Nelder–Mead after the PEMs. We compare the clustering results with the ground truth using the Adjusted Rand Index (ARI) by [12] and the Adjusted Mutual Information (AMI) metric by [26].
Table 1 reports the mean ARIs and AMIs averaged over the R runs. The top panel shows the results for data simulated with an GMCM and the bottom panel for data of an SMCM. The three columns stand for the different clustering algorithms. We observe that, obviously, the correct specified model is suited best for clustering. The corresponding other mixture copula model clusters on average similarly well. However, the difference between SMCMs and GMCMs for SMCM data (ARI: 0.749 vs. 0.708) is larger than the corresponding for GMCM data (ARI: 0.786 vs. 0.803). For a given data set the results may, however, differ more substantially. Hence, in practice, it is advisory to check both models for a given dataset. The k-means performs worse in this experiment.
Benchmark Data
We test the SMCM clustering for some benchmark datasets given in the literature. First, we consider the artificial dataset from [23] which is 2-dimensional and 3-modal. Figure 2 shows the ground truth data and clustering results using the GMCM, the SMCM (both by applying a Nelder–Mead search after the PEM) and k-means. Figure 3 shows the copula level of the data using \(\hat{H}_j(x_j^{(i)})\). Table 2 presents the corresponding ARI and AMI statistics. Both GMCM and SMCM work very well.
Figure plot data of [23] and three clustering results where different colors and point symbols indicate cluster membership
Figure plot data of [23] and three clustering results transformed to the copula level where different colors and point symbols indicate cluster membership
We additionally test the clustering algorithms on several publicly available benchmark datasets. We consider the artificial datasets of [25] (except the trivial with only one cluster) which can be found on https://www.uni-marburg.de/fb12/arbeitsgruppen/datenbionik/data. Moreover, we consider the Iris flower data of [10] which can be found on https://archive.ics.uci.edu/ml/datasets/iris. Again, we compare GMCM, SMCM with k-means. We omit to plot the data and clusters here and refer to [25] for a visual inspection of the datasets (also cf. for the true number of clusters). Instead, Table 3 compares ARI and AMI metrics by comparing the clustering results with the ground truth. We observe that the clustering quality strongly depends on the given special case. The GMCM works best over all given examples meaning that it did not fail to provide a reasonable clustering. Of course, the artificial datasets are somewhat unrealistic but a good clustering algorithm should handle these well, too. As said, we advise to try different models and compare the clustering results.
Image Segmentation
In this section, we discuss the application of learning an SMCM to segment images. The SMCM might be useful in other settings where the data exhibits multimodality, heavy tails of the mixing components due to frequent outliers, and a non-trivial dependence structure. A visual inspection might be helpful to assess if these features are present in the data unless the dimensionality is not too high.
Image segmentation (which is also discussed in [4, 23]) is an important field of visual learning as it aims to simplify and extract patterns from pictures. For a deeper discussion on image segmentation, see [18]. We choose 20 images from the publicly available images of the Berkeley Segmentation Dataset and Benchmark [14]. The images have \(154,401=481\times 321\) pixels and we cluster the images in the RGB space meaning that each pixel can be represented as a 3-dimensional vector with values in \([0,1]^3\). As in [4], we segment the images into 10 colors. In this application, the pixels are the observed data \(\{x_j^{(i)}\}\). We use the empirical distribution function to estimate the copula level \(\{\hat{u}_j^{(i)}\}\).
We fit an SMCM to the copula levels of the images by running the PEM with 10 different initial configurations and choosing the pseudo maximum with the highest log-likelihood. We take this as initial value for the Nelder–Mead search. Given the SMCM, we assign the cluster k with the highest posterior probability to each pixel. We choose the segmented color to be the color at the cluster location estimate \(\hat{\mu }_k\), i.e., the color \((\hat{H}_1^{-1}(F_{\mathrm {sm},1}(\hat{\mu }_1;\hat{\theta }_1)),\hat{H}_2^{-1}(F_{\mathrm {sm},2}(\hat{\mu }_2;\hat{\theta }_2)), \hat{H}_3^{-1}(F_{\mathrm {sm},3}(\hat{\mu }_3;\hat{\theta }_3))\).
For comparison purposes, we proceed analogously for the GMCM. Furthermore, we cluster the pixel colors using k-means and assign the color of its cluster center to each pixel.
Figures 4 and 5 show the original images and the segmented pictures for 6 of the 20 images (others and code are upon request). For each figure, the top row shows the original image, the second row the GMCM segmentation, the second-to-bottom row the SMCM segmentation, and the bottom row the k-means segmentation. We observe that all three methods perform differently well for different regions in the pictures. Hence, there is no obvious first choice. However, the SMCM seems to capture more features in the pictures than the GMCM. For example, the wall in the background in Fig. 4, left column, or the hats of the soldiers in Fig. 5, left column, are less blurry. Another example is that the GMCM shows an odd boundary of the large rock in Fig. 5, middle column.
The GMCM and SMCM algorithms have a fairly long runtime compared with the k-means algorithm. While the PEM (even for different initial parameter choices) is decently fast for both GMCM and SMCM the Nelder–Mead search for a true maximum is time-consuming given the number of parameters. The k-means clustering is in contrast fast. Therefore, the copula-based methods have the drawback of a longer runtime for a comparable outcome. However, the estimates of the degree of freedom parameters are in the most cases between 1 and 10. This means that small \(\nu \)’s yield a higher likelihood which supports use of the SMCM. Otherwise high values of \(\nu \)’s would be estimated.
Conclusions and Discussion
We proposed a natural extension of GMCMs using mixtures of Student t distributions. The SMCM performed well in the application of image segmentation and in several experimental setups. However, the benefits are not striking compared with existing methods. Nevertheless, it has proven reasonable to use SMCMs in addition to GMCMs (and other clustering methods) because the goodness of clustering may vary fundamentally in some scenarios.
We discuss some further limitations of the approach. As for GMCMs, the SMCM-PEM cannot handle high-dimensional data. More specifically, the PEM does not run for \(d>n\). Note that the complexity for the SMCM-PEM is \(O(Tmnd^3)\) so a high dimension is more influential in terms of complexity than for GMCMs. [13] proposed an extension of the PEM for high-dimensional data for GMCM clustering. Their approach may be transferred to SMCMs so that high-dimensionality issues can be addressed.
Although Fig. 1 reveals that simulated data of GMCMs and SMCMs appear quite different the clustering results often are very similar. One interesting research direction may be the investigation of this phenomenon and the comparison of mixture copula models using other flexible distributions.
Change history
08 April 2021
Open access funding note missed in the original publication. Now, it has been added in the section Funding.
References
Aggarwal CC. Data mining: the textbook. Cham: Springer; 2015. http://digitale-objekte.hbz-nrw.de/storage2/2016/05/21/file_30/6765076.pdf.
Bélisle CJ. Convergence theorems for a class of simulated annealing algorithms on \({R}^d\). J Appl Probab. 1992;29(4):885–95.
Berkhin P. A survey of clustering data mining techniques. In: Grouping multidimensional data. Berlin: Springer; 2006. p. 25–71.
Bilgrau A, Eriksen P, Rasmussen J, Johnsen H, Dybkaer K, Bogsted M. GMCM: unsupervised clustering and meta-analysis using Gaussian mixture copula models. J Stat Softw. 2016;70(2):1–23.
Byrd RH, Lu P, Nocedal J, Zhu C. A limited memory algorithm for bound constrained optimization. SIAM J Sci Comput. 1995;16(5):1190–208.
Carson C, Belongie S, Greenspan H, Malik J. Blobworld: image segmentation using expectation-maximization and its application to image querying. IEEE Trans Pattern Anal Mach Intell. 2002;24(8):1026–38.
Chen T, Huang C, Chang E, Wang J. Automatic accent identification using Gaussian mixture models. In: IEEE Workshop on Automatic Speech Recognition and Understanding, 2001. ASRU ’01, p. 343–6. IEEE; 2001.
Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soci Ser B (Methodol) 1977;39(1):1–38. http://www.jstor.org/stable/2984875.
van Den Oord A, Schrauwen B. The Student-\(t\) mixture as a natural image patch prior with application to image compression. J Mach Learn Res. 2014;15:2061–86.
Fisher RA. The use of multiple measurements in taxonomic problems. Ann Eugen. 1936;7(2):179–88.
Friedman J. The elements of statistical learning : data mining, inference, and prediction. New York: Springer; 2009. https://doi.org/10.1007/b94608.
Hubert L, Arabie P. Comparing partitions. J Classif. 1985;2(1):193–218.
Kasa S, Bhattacharya S, Rajan V. Gaussian mixture copulas for high-dimensional clustering and dependency-based subtyping. Bioinformatics (Oxford, England). 2020;36(2):621–8.
Martin D, Fowlkes C, Tal D, Malik J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In: Proceedings Eighth IEEE International Conference on Computer Vision. ICCV 2001, vol. 2, p. 416–23. IEEE; 2001.
Nelder JA, Mead R. A simplex method for function minimization. Comput J. 1965;7(4):308–13.
Nelsen RB. An introduction to copulas, 2nd ed. New York: Springer; 2006. http://deposit.ddb.de/cgi-bin/dokserv?id=2665354&prov=M&dok_var=1&dok_ext=htm
Permuter H, Francos J, Jermyn I. Gaussian mixture models of texture and colour for image database retrieval. In: 2003 IEEE International Conference on Acoustics, Speech, and Signal Processing, 2003. Proceedings (ICASSP ’03), vol. 3, p. III–569. IEEE; 2003.
Pratt WK. Introduction to digital image processing. Boca Raton: CRC Press; 2013.
Rajan V, Bhattacharya S. Dependency clustering of mixed data with Gaussian mixture copulas. In: IJCAI, p. 1967–73. 2016.
Samudra M, Demeulemeester E, Cardoen B, Vansteenkiste N, Rademakers FE. Due time driven surgery scheduling. Healthca Manag Sci. 2017;20(3):326.
Sklar M. Fonctions de repartition an dimensions et leurs marges. Publ Inst Stat Univ Paris. 1959;8:229–31.
Steinley D, Brusco MJ. Evaluating mixture modeling for clustering: recommendations and cautions. Psychol Methods. 2011;16(1):63.
Tewari A, Giering MJ, Raghunathan A. Parametric characterization of multimodal distributions with non-Gaussian modes. In: 2011 IEEE 11th International Conference on Data Mining Workshops, p. 286–92. IEEE; 2011.
Torres-Carrasquillo PA, Singer E, Kohler MA, Greene RJ, Reynolds DA, Deller Jr JR. Approaches to language identification using Gaussian mixture models and shifted delta cepstral features. In: Seventh International Conference on Spoken Language Processing. 2002.
Ultsch, A.: Clustering with som: U\(\hat{~}\)* c. In: Proceedings of the workshop on self-organizing maps, 2005. 2005.
Vinh N, Epps J, Bailey J. Information theoretic measures for clusterings comparison: variants, properties, normalization and correction for chance. J Mach Learn Res. 2010;11:2837–54.
Wang Y, Infield DG, Stephen B, Galloway SJ. Copula-based model for wind turbine power curve outlier rejection. Wind Energy. 2014;17(11):1677–88.
Yeung KY, Fraley C, Murua A, Raftery AE, Ruzzo WL. Model-based clustering and data transformations for gene expression data. Bioinformatics. 2001;17(10):977–87.
Yu J, Chen K, Mori J, Rashid MM. A Gaussian mixture copula model based localized Gaussian process regression approach for long-term wind speed prediction. Energy. 2013;61:673–86. https://doi.org/10.1016/j.energy.2013.09.013.
Acknowledgements
Financial support of the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) via the Collaborative Research Center “Statistical modelling of nonlinear dynamic processes” (SFB 823, Teilprojekt A4) is gratefully acknowledged. I thank Christoph Hanck, Stephan Hetzenecker and Yannick Hoga for valuable comments and Ashutosh Tewari and Aäron van den Oord for graciously sharing their codes.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Massing, T. Clustering Using Student t Mixture Copulas. SN COMPUT. SCI. 2, 97 (2021). https://doi.org/10.1007/s42979-021-00503-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42979-021-00503-0