Secret Key Rate Adaption for Multicarrier Continuous-Variable Quantum Key Distribution

Abstract

A multicarrier continuous-variable quantum key distribution (CVQKD) protocol uses Gaussian subcarrier quantum continuous variables (CVs) for the transmission. Here, we define an iterative error-minimizing secret key adaption method for multicarrier CVQKD. The proposed method allows for the parties to reach a given target secret key rate with minimized error rate through the Gaussian sub-channels by a sub-channel adaption procedure. The adaption algorithm iteratively determines the optimal transmit conditions to achieve the target secret key rate and the minimal error rate over the sub-channels. The solution requires no complex calculations or computational tools, allowing for easy implementation for experimental scenarios.

Introduction

Continuous-variable quantum key distribution (CVQKD) represents an important practical manifestation of the fundamentals of quantum mechanics [1, 2, 4,5,6, 11,12,13,14,15,16,17, 19,20,21, 37, 49, 50, 58, 59]. CVQKD does not require single-photon sources and detectors and can be implemented in an experimental scenario by standard devices [29,30,31, 39, 43,44,45,46, 48, 57, 60]. In a CVQKD setting, the information is carried by a continuous-variable quantum state that is defined in the phase space via the position and momentum quadratures. In an experimental CVQKD scenario, the CV quantum states have a Gaussian random distribution, and the quantum channel between the sender (Alice) and receiver (Bob) is also Gaussian, because the presence of an eavesdropper (Eve) adds a white Gaussian noise into the transmission [3, 7,8,9,10, 25, 26, 35, 40,41,42, 51, 54, 61,62,63].

The relevant performance attributes of experimental CVQKD (i.e., secret key rates, transmission distances, tolerable excess noise, etc.) still require significant improvements [6, 11,12,13,14, 17, 49, 58, 59]. The multicarrier CVQKD has been recently introduced through the adaptive quadrature division modulation (AMQD) [15]. The multicarrier CVQKD scheme injects several additional degrees of freedom into the transmission, which are not available for a standard (single carrier) CVQKD setting [15, 17, 18, 20,21,22,23,24, 27,28,29,30,31, 64, 65]. These results also made possible to utilize several significant phenomena for CVQKD that are unavailable in a standard CVQKD protocol [16,17,18, 21,22,23, 28, 29]. The secret key rates of multicarrier CVQKD confirm the multimode bounds of [7] (see the results on fundamental rate-loss scaling in quantum optical communications in [7]). Further information on the bounds of private quantum communications can be found in [8].

Here, a secret key adaption method is defined for multicarrier CVQKD. The proposed secret key adaption successively utilizes private rate curves for the sub-channels. The curves also define an adaption region for each sub-channel. Particularly, the adaption region provides a base for the iterative, private rate increment method utilized by our secret key rate adaption algorithm. The iterative sub-channel selection procedure depends on the actual target private rate and the noise levels of the sub-channels. We demonstrate the results through the framework of AMQD and also extend the results to the multiple-access multicarrier CVQKD.

The novel contributions of our manuscript are as follows:

• 1. We define an iterative error-minimizing secret key adaption method for multicarrier CVQKD. The proposed secret key adaption algorithm iteratively determines the optimal transmit conditions at a given target secret key rate to realize minimal error transmission over the sub-channels.

• 2. The proposed method allows for the parties to reach a given target secret key rate with minimized error rate through the Gaussian sub-channels by a sub-channel adaption procedure.

• 3. At a given transmission rate of private classical information (private rate), the method determines and selects that sub-channel from the set of available sub-channels for the transmission of the quadratures which sub-channel provides a minimal error rate.

• 4. The scheme provably yields a minimized error rate transmission for all sub-channels while achieving the selected target secret key rate.

• 5. The solution requires no complex calculations or computational tools, allowing for easy implementation for experimental CVQKD scenarios.

This paper is organized as follows. In “Preliminaries”, preliminary findings are summarized. Section “Secret Key Rate Adaption with Minimized Error Rate” discusses the iterative secret key adaption scheme. Section “Secret Key Rate Adaption in Multiuser Multicarrier CVQKD” extends the results to a multiuser setting. In “Numerical Evidence”, a numerical evidence is proposed. Finally, Section “Conclusions” concludes the results. Supplemental material is included in the Appendix.

Preliminaries

The notations and basic terms of multicarrier CVQKD can be found in [15]. A brief summary is also included in Appendix 1.

Multiuser quadrature allocation (MQA)

In an MQA multiple access multicarrier CVQKD [20], a given user $U_{k} ,k=0,\ldots ,K-1$, where K is the number of total users, is characterized via m subcarriers, formulating an ${\mathcal {M}}_{U_{k} }$ logical channel of $U_{k}$,

$$\begin{aligned} {\mathcal {M}}_{U_{k} } =\left[ {\mathcal {N}}_{U_{k} ,0} ,\ldots ,{\mathcal {N}}_{U_{k} ,m-1} \right] ^\mathrm{T} , \end{aligned}$$

(1)

where ${\mathcal {N}}_{U_{k} ,i}$ is the ith sub-channel of ${\mathcal {M}}_{U_{k} }$. For a detailed description of MQA for multicarrier CVQKD, see [20].

Private Classical Rate Curves

The secret key adaption method utilizes $r+2$ rate curves for the sub-channels, defined via set

$$\begin{aligned} {\mathcal {S}}=\left\{ R_{\min } \left( {\mathcal {N}}_{i} \right) ,R\left( q\right) ,R_{\max } \left( {\mathcal {N}}_{i} \right) \right\} , q=0\ldots r-1. \end{aligned}$$

(2)

Specifically, for all sub-channels ${\mathcal {N}}_{i}$, $i=0,\ldots ,l-1$ a given rate curve is selected from ${\mathcal {S}}$ (2) according to the sub-channel conditions.

In particular, a $R\left( q\right)$ rate curve refers to the transmission rate of private classical information (private rate) over ${\mathcal {N}}_{i}$, with the relation

$$\begin{aligned} R_{\min } \left( {\mathcal {N}}_{i} \right)<R\left( 0\right) \cdots<R\left( r-1\right) <R_{\max } \left( {\mathcal {N}}_{i} \right) , \end{aligned}$$

(3)

where $R\left( q\right)$ is referred to as the target private rate at an $R\left( q-1\right)$ actual private rate in an iteration procedure.

Assuming a reverse reconciliation [6], a given target private rate $R\left( q\right)$ is defined as

$$\begin{aligned} \begin{aligned} R\left( q \right)&\le P\left( {{{\mathcal {N}}}_{i}} \right) \\&=\underset{n\rightarrow \infty }{\mathop {\lim }}\,\tfrac{1}{n}\underset{\forall {{p}_{i}},{{\rho }_{i}}}{\mathop {\max }}\,\left( {{\chi }_\mathrm{AB}}\left( {{{\mathcal {N}}}_{i}} \right) -{{\chi }_\mathrm{BE}}\left( {{{\mathcal {N}}}_{i}} \right) \right) , \end{aligned} \end{aligned}$$

(4)

where $P\left( {\mathcal {N}}_{i} \right)$ is the private classical capacity of ${\mathcal {N}}_{i}$ [2, 34], and $\chi _\mathrm{AB} \left( {\mathcal {N}}_{i} \right)$ and $\chi _\mathrm{BE} \left( {\mathcal {N}}_{i} \right)$ are the Holevo information of Alice (transmitter) and Bob (receiver), and Bob and Eve (eavesdropper), respectively.

Secret Key Rate Adaption with Minimized Error Rate

Theorem 1

A given target secret key rate $S^{\mathrm{*}} \left( {\mathcal {N}}\right) =\sum _{i=0}^{l-1}R_{i} \left( {\mathcal {N}}_{i} \right)$, where $R_{i} \left( {\mathcal {N}}_{i} \right)$ is the private rate of sub-channel ${\mathcal {N}}_{i}$, can be achieved over the l sub-channels such that the error rate of all sub-channels is minimized.

Proof

The proof focuses on a single sub-channel ${\mathcal {N}}_{i}$ for the private transmission of a single quadrature component $x_{i}$ (or $p_{i}$), which refers to a $x_{i} \in {{\mathcal {N}}}\left( 0,\sigma _{\omega }^{2} \right)$ position or a $p_{i} \in {{\mathcal {N}}}\left( 0,\sigma _{\omega }^{2} \right)$ momentum quadrature of the ith subcarrier, respectively.

Let

$$\begin{aligned} \nu _{i} \left( {\mathcal {N}}_{i} \right) ={\frac{\sigma _{{\mathcal {N}}_{i} }^{2} }{\left| F\left( T_{i} \left( {\mathcal {N}}_{i} \right) \right) \right| ^{2} }}, \end{aligned}$$

(5)

of the ith, $i=0,\ldots ,l-1$ sub-channel ${\mathcal {N}}_{i}$.

Let $R_{\min } \left( {\mathcal {N}}_{i} \right)$ and $R_{\max } \left( {\mathcal {N}}_{i} \right)$ be the minimal and maximal private classical information transmission rates selected for ${\mathcal {N}}_{i}$. The private rates are referring to the transmission of a given quadrature $x_{i}$.

These rate curves, $R\left( q\right) >R\left( q-1\right)$, allow us to reach a target secret key rate $S^{\mathrm{*}} \left( {\mathcal {N}}\right)$ over the sub-channels with a minimized error rate in a multicarrier CVQKD setting. Specifically, it requires a rigorously defined iterative condition on the selection of the sub-channels for each target rate $R\left( q\right)$.

From $R_{\min } \left( {\mathcal {N}}_{i} \right)$ and $R_{\max } \left( {\mathcal {N}}_{i} \right)$, an adaption region $\mathrm{A}$ can be characterized with r rate curves inside the region. Define r rate curves for the transmission of $x_{i}$ in the region of $\mathrm{A}$

$$\begin{aligned} \mathrm{A}=\left[ R_{\min } \left( {\mathcal {N}}_{i} \right) ,R_{\max } \left( {\mathcal {N}}_{i} \right) \right] , \end{aligned}$$

(6)

as

$$\begin{aligned} R\left( q\right) , q=0\ldots r-1, \end{aligned}$$

(7)

such that (3) holds.

Precisely, at a given private rate $R\left( {\mathcal {N}}_{i} \right)$, (5) is referred to as $\nu _{i} \left( R\left( {\mathcal {N}}_{i} \right) \right)$,

$$\begin{aligned} \nu _{i} \left( R\left( {\mathcal {N}}_{i} \right) \right) ={\frac{\sigma _{R\left( {\mathcal {N}}_{i} \right) }^{2} }{\left| F\left( T\left( R\left( {\mathcal {N}}_{i} \right) \right) \right) \right| ^{2} }} , \end{aligned}$$

(8)

where $\sigma _{R\left( {\mathcal {N}}_{i} \right) }^{2}$ is the noise variance of ${\mathcal {N}}_{i}$ at $R\left( {\mathcal {N}}_{i} \right)$, while $F\left( T\left( R\left( {\mathcal {N}}_{i} \right) \right) \right)$ is the transmittance coefficient of ${\mathcal {N}}_{i}$ at $R\left( {\mathcal {N}}_{i} \right)$. Note that in function of (8), after a scaling the rate curves of (7) are almost parallel to $R_{\min } \left( {\mathcal {N}}_{i} \right)$. By theory, at $R\left( {\mathcal {N}}_{i} \right) =0$ (8) is directly defined from $\sigma _{{\mathcal {N}}_{i} }^{2}$ is the noise variance and $T_{i} \left( {\mathcal {N}}_{i} \right)$ is the transmittance coefficient of ${\mathcal {N}}_{i}$, as given in (5).

In function of $\nu _{i} \left( R\left( {\mathcal {N}}_{i} \right) \right)$, the SNR of ${\mathcal {N}}_{i}$ at a given $R\left( {\mathcal {N}}_{i} \right)$ is expressed as [55]

$$\begin{aligned} \mathrm{SNR}\left( R\left( {\mathcal {N}}_{i} \right) \right) =10\log _{10} {\frac{1}{\nu _{i} \left( R\left( {\mathcal {N}}_{i} \right) \right) }} . \end{aligned}$$

(9)

To step forward, we have to focus on the behavior of parameter $\nu _{i} \left( \cdot \right)$ at an increased transmission rate.

Particularly, let $\mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{i} \right)$ be the current private rate and $R\left( {\mathcal {N}}_{i} \right)$ be the target private rate for a sub-channel ${\mathcal {N}}_{i}$, such that $\mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{i} \right)<R\left( {\mathcal {N}}_{i} \right) <\tilde{R}\left( {\mathcal {N}}_{i} \right)$. Then, let $\delta _{\nu _{i} } \left( R\left( {\mathcal {N}}_{i} \right) \right)$ identify the cumulative $\nu _{i} \left( R\left( {\mathcal {N}}_{i} \right) \right)$ parameter of ${\mathcal {N}}_{i}$ at an increased (target) private rate $R\left( {\mathcal {N}}_{i} \right)$, evaluated via the following iteration:

$$\begin{aligned} \delta _{\nu _{i} } \left( R\left( {\mathcal {N}}_{i} \right) \right) =\delta _{\nu _{i} } \left({R}_{{\kern-10pt}_\smile }\left( {\mathcal {N}}_{i} \right) \right) +\Delta _{\nu _{i} } \left( R\left( {\mathcal {N}}_{i} \right) ,\tilde{R}\left( {\mathcal {N}}_{i} \right) \right) , \end{aligned}$$

(10)

where $\Delta _{\nu _{i} }$ identifies the difference of $\nu _{i}$ at $R\left( {\mathcal {N}}_{i} \right)$ and $\tilde{R}\left( {\mathcal {N}}_{i} \right)$ as

$$\begin{aligned} \Delta _{\nu _{i} } =\nu _{i} \left( R\left( {\mathcal {N}}_{i} \right) \right) -\nu _{i} \left( \tilde{R}\left( {\mathcal {N}}_{i} \right) \right) , \end{aligned}$$

(11)

the iteration (10) at no transmission, $R\left( {\mathcal {N}}_{i} \right) =0$, identifies $\nu _{i} \left( {\mathcal {N}}_{i} \right)$ as

$$\begin{aligned} \delta _{\nu _{i} } \left( R\left( {\mathcal {N}}_{i} \right) =0\right) =\nu _{i} \left( {\mathcal {N}}_{i} \right) , \end{aligned}$$

(12)

while for any $R\left( {\mathcal {N}}_{i} \right)>\mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{i} \right) >0$,

$$\begin{aligned} \nu _{i} \left( R\left( {\mathcal {N}}_{i} \right) \right) <\nu _{i} \left( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{i} \right) \right) . \end{aligned}$$

(13)

To conclude, from (10) follows that a rate increment from $\mathop {R}\limits _{\smile }( {\mathcal {N}}_{i} )$ to $R\left( {\mathcal {N}}_{i} \right)$ also increases $\delta _{\nu _{i} } \left( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{i} \right) \right)$ by $\Delta _{\nu _{i} } \left( R\left( {\mathcal {N}}_{i} \right) ,\tilde{R}\left( {\mathcal {N}}_{i} \right) \right)$, thus for any $R\left( {\mathcal {N}}_{i} \right) >\mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{i} \right)$, the following relation holds [55]:

$$\begin{aligned} \delta _{\nu _{i} } \left( R\left( {\mathcal {N}}_{i} \right) \right) >\delta _{\nu _{i} } \left( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{i} \right) \right) . \end{aligned}$$

(14)

Let us then define r private transmission curves in the adaption region $\mathrm{A}$ of ${\mathcal {N}}_{i}$. The aim of the iterative secret key adaption scheme is to provide a rate increment in each step by selecting that sub-channel ${\mathcal {N}}_{i}$, for which (10) is minimal. Specifically, it is a convenient approach because this sub-channel provides the best condition for the transmission.

As we show, using this sub-channel, the increased rate $\tilde{R}$ can be achieved with a minimized error rate, but at the same time, it keeps the target secret key rate. Therefore, applying the sub-channel selection procedure with respect to the iterative condition of (10), a desired target secret key rate can be achieved such that the transmission is adapted to not just the sub-channel conditions, but also to yield a minimized error rate for all sub-channels.

Applying (10) for a $R_{\min } \left( {\mathcal {N}}_{i} \right)$ private rate is as follows. An $R_{\min } \left( {\mathcal {N}}_{i} \right)$ target private rate over ${\mathcal {N}}_{i}$, $\delta _{\nu _{i} } \left( R_{\min } \left( {\mathcal {N}}_{i} \right) \right)$ is yielded via $\nu _{i} \left( {\mathcal {N}}_{i} \right)$ and $\Delta _{\nu _{i} } \left( R_{\min } \left( {\mathcal {N}}_{i} \right) ,R\left( 0\right) \right)$ derived from $R\left( 0\right) \in \mathrm{A}$ as

$$\begin{aligned} \delta _{\nu _{i} } \left( R_{\min } \left( {\mathcal {N}}_{i} \right) \right) =\nu _{i} \left( {\mathcal {N}}_{i} \right) +\Delta _{\nu _{i} } \left( R_{\min } \left( {\mathcal {N}}_{i} \right) ,R\left( 0\right) \right) . \end{aligned}$$

(15)

Applying (10) to the r rate curves $R\left( q\right) \in \mathrm{A}$, $q=0\ldots r-2$ at a target rate $R\left( q\right)$ results in $\delta _{\nu _{i} } \left( R\left( q\right) \right)$ as

$$\begin{aligned} \delta _{\nu _{i} } \left( R\left( q\right) \right) =\delta _{\nu _{i} } \left( R\left( q-1\right) \right) +\Delta _{\nu _{i} } \left( R\left( q\right) ,R\left( q+1\right) \right) , \end{aligned}$$

(16)

Specifically, in each step for a given target $R\left( q\right)$, the method selects that ${\mathcal {N}}_{i}$, for which (36) is minimal, because that sub-channel provides the best conditions. Thus, the secret key adaption is an iterative process and depends on the $\delta _{\nu _{i} } \left( R\left( q-1\right) \right)$ parameter obtained at $R\left( q-1\right)$ and on $\Delta _{\nu _{i} } \left( R\left( q\right) ,R\left( q+1\right) \right)$.

In particular, for $q=0$, (16) yields

$$\begin{aligned} \begin{aligned} {{\delta }_{{{\nu }_{i}}}}\left( R\left( 0 \right) \right)&={{\delta }_{{{\nu }_{i}}}}\left( {{R}_{\min }}\left( {{{\mathcal {N}}}_{i}} \right) \right) +{{\Delta }_{{{\nu }_{i}}}}\left( R\left( 0 \right) ,R\left( 1 \right) \right) \\&={{\nu }_{i}}\left( {{{\mathcal {N}}}_{i}} \right) +{{\Delta }_{{{\nu }_{i}}}}\left( {{R}_{\min }}\left( {{{\mathcal {N}}}_{i}} \right) ,R\left( 0 \right) \right) \\&\quad +{{\Delta }_{{{\nu }_{i}}}}\left( R\left( 0 \right) ,R\left( 1 \right) \right) , \end{aligned} \end{aligned}$$

(17)

where $R\left( 1\right) \in \mathrm{A}$. While, for $q=r-1$, (10) results in

$$\begin{aligned} \begin{aligned}&{{\delta }_{{{\nu }_{i}}}}\left( R\left( r-1 \right) \right) \\&\quad = {{\delta }_{{{\nu }_{i}}}}\left( R\left( r-2 \right) \right) +{{\Delta }_{{{\nu }_{i}}}}\left( R\left( r-1 \right) ,{{R}_{\max }}\left( {{{\mathcal {N}}}_{i}} \right) \right) \\&\quad =\left(\vphantom{\sum \limits _{k=0}^{r-2}} {{\nu }_{i}}\left( {{{\mathcal {N}}}_{i}} \right) +{{\Delta }_{{{\nu }_{i}}}}\left( {{R}_{\min }}\left( {{{\mathcal {N}}}_{i}} \right) ,R\left( 0 \right) \right) \right. \\&\qquad \quad \left. +\sum \limits _{k=0}^{r-2}{{{\Delta }_{{{\nu }_{i}}}} \left( R\left( k \right) ,R\left( k+1 \right) \right) } \right) \\&\qquad\quad +{{\Delta }_{{{\nu }_{i}}}}\left( R\left( r-1 \right) ,{{R}_{\max }}\left( {{{\mathcal {N}}}_{i}} \right) \right) , \end{aligned} \end{aligned}$$

(18)

where $R\left( k\right) \in \mathrm{A}$, $k=0\ldots r-2$. For $R_{\max } \left( {\mathcal {N}}_{i} \right)$, by definition $\delta _{\nu _{i} } \left( R_{\max } \left( {\mathcal {N}}_{i} \right) \right) =+\infty$ [55].

The distribution of a sample set $\delta _{\nu _{i} } \left( R\left( q\right) \right)$ for m sub-channels, $i=0,\ldots ,m-1$, in a low-SNR CVQKD scenario is illustrated in Fig. 1a. The SNR in Fig. 1b is derived from the $\delta _{\nu _{i} } \left( R\left( q\right) \right)$ set of the m sub-channels as $\mathrm{SNR}\left( \nu _{i} \left( R\left( q\right) \right) \right) =10\log _{10} \left( {1/ \left( \nu _{i} \left( R\left( q\right) \right) \right) } \right)$.

Fig. 1

a The distribution of a low-SNR set $\delta _{\nu _{i} } \left( R\left( q\right) \right)$, $i=0,\ldots ,m-1$, for $m=1000$ sub-channels. b The SNR is derived from $\delta _{\nu _{i} } \left( R\left( q\right) \right)$ for all sub-channels

Next, we show that for an arbitrary target private rate $R\left( {\mathcal {N}}_{i} \right) >0$, the iterative condition on $\delta _{\nu _{i} } \left( R\left( {\mathcal {N}}_{i} \right) \right)$ (see (16)) provides a minimized error rate over the selected ${\mathcal {N}}_{i}$.

Let ${\mathcal {B}}$ be the bit error rate (BER), and let ${\mathcal {B}}\left( R\left( q\right) _{\delta _{\nu _{i} } \left( R\left( q-1\right) \right) } \right)$ refer to the bit error rate of ${\mathcal {N}}_{i}$ at target private rate $R\left( q\right)$, at an actual rate $R\left( q-1\right)$, and $\delta _{\nu _{i} } \left( R\left( q-1\right) \right)$. Then, at a given $R\left( q\right)$, selecting that ${\mathcal {N}}_{i}$, $i=0,\ldots ,l-1$ from the total l, for which $\delta _{\nu _{i} } \left( R\left( q-1\right) \right)$ is minimal, as

$$\begin{aligned} \xi \left( R\left( q-1\right) \right) =\mathop {\min }\limits _{\forall i} \delta _{\nu _{i} } \left( R\left( q-1\right) \right) \end{aligned}$$

(19)

yields a minimized bit error rate at a given $R\left( q\right)$ over the selected ${\mathcal {N}}_{i}$ as

$$\begin{aligned} {\mathcal {B}}\left( R\left( q\right) _{\xi \left( R\left( q-1\right) \right) } \right) ={\mathcal {B}}\left( R_{\min } \left( {\mathcal {N}}_{i} \right) _{\delta _{\nu _{i} } \left( R\left( q-1\right) \right) } \right) , \end{aligned}$$

(20)

where ${\mathcal {B}}\left( R_{\min } \left( {\mathcal {N}}_{i} \right) _{\delta _{\nu _{i} } \left( R\left( q-1\right) \right) } \right)$ is defined as

$$\begin{aligned} \begin{aligned}&{\mathcal {B}}\left( {{R}_{\min }}{{\left( {{\mathcal {N}}_{i}} \right) }_{{{\nu }_{i}}\left( {{\mathcal {N}}_{i}} \right) +\left( {{\Delta }_{{{\nu }_{i}}}}\left( {{R}_{\min }}\left( {{\mathcal {N}}_{i}} \right) ,R\left( 0 \right) \right) +\sum \limits _{k=0}^{q-1}{{{\Delta }_{{{\nu }_{i}}}}\left( R\left( k \right) ,R\left( k+1 \right) \right) } \right) }} \right) \\&\quad =\tfrac{1}{2}\text {erfc}\mathcal {F}\left( {{\nu }_{i}}\left( {{\mathcal {N}}_{i}} \right) +\left( {{\Delta }_{{{\nu }_{i}}}}\left( {{R}_{\min }}\left( {{\mathcal {N}}_{i}} \right) ,R\left( 0 \right) \right) +\cdots \right. \right. \\&\left. \left. \qquad +{{\Delta }_{{{\nu }_{i}}}}\left( R\left( q-1 \right) ,R\left( q \right) \right) \right) \right) , \end{aligned} \end{aligned}$$

(21)

where function ${\mathcal {F}}\left( \cdot \right)$ is evaluated as

$$\begin{aligned} \begin{aligned}&\mathcal {F}\left( {{\nu }_{i}}\left( {{\mathcal {N}}_{i}} \right) +\left( {{\Delta }_{{{\nu }_{i}}}}\left( {{R}_{\min }}\left( {{\mathcal {N}}_{i}} \right) ,R\left( 0 \right) \right) +\cdots +{{\Delta }_{{{\nu }_{i}}}}\left( R\left( q-1 \right) ,R\left( q \right) \right) \right) \right) \\&=\left( \sqrt{\begin{aligned}&\text {SNR}\left( {{\nu }_{i}}\left( {{\mathcal {N}}_{i}} \right) \right) -\left[ \text {SNR}\left( {{\nu }_{i}}\left( R\left( 0 \right) \right) \right) -\text {SNR}\left( {{\nu }_{i}}\left( {{R}_{\min }}\left( {{\mathcal {N}}_{i}} \right) \right) \right) \right] \\&-\left( \sum \limits _{k=0}^{q-1}{\left[ \text {SNR}\left( {{\nu }_{i}}\left( R\left( k+1 \right) \right) \right) -\text {SNR}\left( {{\nu }_{i}}\left( R\left( k \right) \right) \right) \right] } \right) \\ \end{aligned}} \right) , \\ \end{aligned} \end{aligned}$$

(22)

where $\mathrm{SNR}\left( \nu _{i} \left( R\left( x\right) \right) \right) =10\log _{10} \left( {1/ \left( \nu _{i} \left( R\left( x\right) \right) \right) } \right)$, while $\text {erfc}\left( \cdot \right)$ is the complementary error function

$$\begin{aligned} \text {erfc}\left( x\right) ={\frac{2}{\sqrt{\pi } }} \int \limits _{x}^{\infty }e^{-t^{2} } \mathrm{d}t. \end{aligned}$$

(23)

The aim of the error minimization procedure is to achieve (20) for all $R\left( \cdot \right)$ via the selection of that ${\mathcal {N}}_{i}$ for which $\delta _{\nu _{i} } \left( R\left( q-1\right) \right)$ is minimal.

Let $R\left( k+1\right) _{\delta _{\nu _{i} } \left( R\left( k\right) \right) }$ refer to a private rate $R\left( k+1\right)$ over at $\delta _{\nu _{i} } \left( R\left( k\right) \right)$ with respect to the transmission of a single quadrature component $x_{i}$ (or $p_{i}$).

First, we apply (19) to the minimal rate $R_{\min } \left( {\mathcal {N}}_{i} \right)$ by the selection of that ${\mathcal {N}}_{i}$, for which $\nu _{i} \left( {\mathcal {N}}_{i} \right)$ is minimal, thus

$$\begin{aligned} \xi \left( 0\right) =\mathop {\min }\limits _{\forall i} \delta _{\nu _{i} } \left( 0\right) =\mathop {\min }\limits _{\forall i} \nu _{i} , \end{aligned}$$

(24)

which yields

$$\begin{aligned} {\mathcal {B}}\left( R_{\min } \left( {\mathcal {N}}_{i} \right) _{\xi \left( 0\right) } \right) ={\mathcal {B}}\left( R_{\min } \left( {\mathcal {N}}_{i} \right) _{\nu _{i} \left( {\mathcal {N}}_{i} \right) } \right) . \end{aligned}$$

(25)

Similarly, at $R\left( 0\right)$, that sub-channel is selected for the $R\left( 0\right)$ rate transmission, for which $\delta _{\nu _{i} } \left( R_{\min } \left( {\mathcal {N}}_{i} \right) \right)$ is minimal.

In particular, due to the iterative determination of $\delta _{\nu _{i} } \left( R_{\min } \left( {\mathcal {N}}_{i} \right) \right)$, the corresponding ${\mathcal {B}}\left( R\left( 0\right) _{\xi \left( R_{\min } \left( {\mathcal {N}}_{i} \right) \right) } \right)$ is yielded as

$$\begin{aligned} {\mathcal {B}}\left( R\left( 0\right) _{\xi \left( R_{\min } \left( {\mathcal {N}}_{i} \right) \right) } \right) ={\mathcal {B}}\left( R_{\min } \left( {\mathcal {N}}_{i} \right) _{\nu _{i} \left( {\mathcal {N}}_{i} \right) +\Delta _{\nu _{i} } \left( R_{\min } \left( {\mathcal {N}}_{i} \right) ,R\left( 0\right) \right) } \right) . \end{aligned}$$

(26)

Precisely, for $R\left( q\right)$, $q=1\ldots r-1$, therefore, in each step, that sub-channel selected for the transmission, for which $\xi \left( R\left( q-1\right) \right)$ is minimal, ensures that the resulting ${\mathcal {B}}\left( R\left( q\right) _{\xi \left( R\left( q-1\right) \right) } \right)$ is evaluated as

$$\begin{aligned} \begin{aligned}&{\mathcal {B}}\left( R\left( q\right) _{\xi \left( R\left( q-1\right) \right) } \right) \\&\quad ={\mathcal {B}}\left( R_{\min } \left( {\mathcal {N}}_{i} \right) _{\delta _{\nu _{i} } \left( R\left( q-2\right) \right) + \Delta _{\nu _{i} } \left( R\left( q-1\right) ,R\left( q\right) \right) } \right) . \end{aligned} \end{aligned}$$

(27)

Putting the pieces together, the utilization of (27) for $q=1$ is as

$$\begin{aligned} \begin{aligned}&{\mathcal {B}}\left( R\left( 1\right) _{\xi \left( R\left( 0\right) \right) } \right) \\&\quad ={\mathcal {B}}\left( R_{\min } \left( {\mathcal {N}}_{i} \right) _{\delta _{\nu _{i} } \left( R_{\min } \left( {\mathcal {N}}_{i} \right) \right) +\Delta _{\nu _{i} } \left( R\left( 0\right) ,R\left( 1\right) \right) } \right) , \end{aligned} \end{aligned}$$

(28)

while for $q=r-1$,

$$\begin{aligned} \begin{aligned}&{\mathcal {B}}\left( R\left( r-1\right) _{\xi \left( R\left( r-2\right) \right) } \right) \\&\quad ={\mathcal {B}}\left( R_{\min } \left( {\mathcal {N}}_{i} \right) _{\delta _{\nu _{i} } \left( R\left( r-3\right) \right) +\Delta _{\nu _{i} } \left( R\left( r-2\right) ,R\left( r-1\right) \right) } \right) , \end{aligned} \end{aligned}$$

(29)

and, finally, for $R_{\max } \left( {\mathcal {N}}_{i} \right) _{\xi \left( R\left( r-1\right) \right) }$, the corresponding error rate is

$$\begin{aligned} \begin{aligned}&{\mathcal {B}}\left( R_{\max } \left( {\mathcal {N}}_{i} \right) _{\xi \left( R\left( r-1\right) \right) } \right) \\&\quad ={\mathcal {B}}\left( R_{\min } \left( {\mathcal {N}}_{i} \right) _{\delta _{\nu _{i} } \left( R\left( r-2\right) \right) + \Delta _{\nu _{i} } \left( R\left( r-1\right) ,R_{\max } \left( {\mathcal {N}}_{i} \right) \right) } \right) . \end{aligned} \end{aligned}$$

(30)

The ${\mathcal {B}}$ bit error rates at private rates, $R_{\min } \left( {\mathcal {N}}_{i} \right) ,R\left( 0\right) ,\ldots ,R_{\min } \left( r-1\right) ,R_{\max } \left( {\mathcal {N}}_{i} \right)$, for a given sub-channel ${\mathcal {N}}_{i}$ in function of $\nu _{i}$ (low-SNR scenario) are summarized in Fig. 2 for the range $\nu _{i} =\left[ 0.1,0.3\right]$ (Fig. 2a), and $\nu _{i} =\left[ 0.3,0.9\right]$ (Fig. 2b).

Fig. 2

The ${\mathcal {B}}$ bit error rates at $R_{\min } \left( {\mathcal {N}}_{i} \right) ,R\left( 0\right) ,\ldots ,R\left( r-1\right) ,R_{\max } \left( {\mathcal {N}}_{i} \right)$ in a low-SNR scenario for a given sub-channel ${\mathcal {N}}_{i}$ at a $\nu _{i} =\left[ 0.1,0.3\right]$ and b $\nu _{i} =\left[ 0.3,0.9\right]$

The iterative secret key adapting method with the error minimization is detailed in Algorithm 1.

The proof is concluded here. $\square$

The resulting ${{\mathcal {B}}}$ bit error rates of the secret key rate adapting method for a given sub-channel ${\mathcal {N}}_{i}$ in function of $\nu _{i}$ are summarized in Fig. 3. Parameter $\nu _{i}$ is scaled for the SNR with $5\; {\mathrm{dB}}$ steps in the range of $\left[ 15,-5\right]$ as $\nu _{i} \left( R_{i} \left( x\right) \right) =10^{-{{\mathrm{SNR}}\left( \nu _{i} \left( R\left( x\right) \right) \right) / 10} }.$

Fig. 3

The ${\mathcal {B}}$ bit error rate of secret key adapting for a sub-channel ${\mathcal {N}}_{i}$ in function of ${{\nu }_{i}}\left( {{R}_{i}}\left( x \right) \right) ={{10}^{-{\text {SNR}\left( {{\nu }_{i}}\left( R\left( x \right) \right) \right) }/{10}\;}}$. The adaption is made via r rate curves $R\left( q\right)$, $q=0\ldots r-1$, $R_{\min } \left( {\mathcal {N}}_{i} \right)<R\left( 0\right) \ldots<R\left( r-1\right) <R_{\max } \left( {\mathcal {N}}_{i} \right)$ in the $\mathrm{A=}\left[ R_{\min } \left( {\mathcal {N}}_{i} \right) ,R_{\max } \left( {\mathcal {N}}_{i} \right) \right]$ adaption region (shaded area)

Secret Key Rate Adaption in Multiuser Multicarrier CVQKD

This section extends the results for a multiuser multicarrier CVQKD [20] scenario.

Lemma 1

The secret key adaption can be extended to a $U_{k} ,k=0,\ldots , K-1$ multiuser setting, where K is the number of users, to achieve target secret key rate $S^{\mathrm{*}} \left( {\mathcal {M}}_{U_{k} } \right)$ with minimized error rate over the m sub-channels of ${\mathcal {M}}_{U_{k}}$ of $U_{k}$, for $\forall k$.

Proof

The proof focuses on a given logical channel ${\mathcal {M}}_{U_{k} } =\left[ {\mathcal {N}}_{U_{k} ,0} ,\ldots ,{\mathcal {N}}_{U_{k} ,m-1} \right] ^\mathrm{T}$ of a user $U_{k}$, where ${\mathcal {N}}_{U_{k} ,i}$, $i=0,\ldots ,m-1$ is the ith sub-channel.

Let K be the number of transmit users and select a given $U_{k} ,k=0,\ldots ,K-1$. Let $S^{\mathrm{*}} \left( {\mathcal {M}}_{U_{k} } \right)$ be the target secret key rate of users over ${\mathcal {M}}_{U_{k} }$, and let $R\left( {\mathcal {N}}_{U_{k} ,i} \right)$ be the private rate of ${\mathcal {N}}_{U_{k} ,i}$. The steps of the extension are summarized as follows.

Let

$$\begin{aligned} \nu _{i} \left( {\mathcal {N}}_{U_{k} ,i} \right) ={\frac{\sigma _{{\mathcal {N}}_{U_{k} ,i} }^{2} }{\left| F\left( T\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) \right| ^{2} }} , \end{aligned}$$

(31)

where $\sigma _{{\mathcal {N}}_{U_{k} ,i} }^{2}$ is the noise variance of ${\mathcal {N}}_{U_{k} ,i}$, while $T_{i} \left( {\mathcal {N}}_{U_{k} ,i} \right)$ is the transmittance coefficient of ${\mathcal {N}}_{U_{k} ,i}$. At a given rate curve $R\left( {\mathcal {N}}_{U_{k} ,i} \right) >0$,

$$\begin{aligned} \nu _{i} \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) ={\frac{\sigma _{R\left( {\mathcal {N}}_{U_{k} ,i} \right) }^{2} }{\left| F\left( T\left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) \right) \right| ^{2} }}, \end{aligned}$$

(32)

where $\sigma _{R\left( {\mathcal {N}}_{U_{k} ,i} \right) }^{2}$ is the noise variance at $R\left( {\mathcal {N}}_{U_{k} ,i} \right)$, while $T_{i} \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right)$ is the transmittance coefficient of ${\mathcal {N}}_{U_{k} ,i}$ at $R\left( {\mathcal {N}}_{U_{k} ,i} \right)$, respectively. Apply the secret key rate adaption method over the set ${\mathcal {M}}_{U_{k} }$ of m ${\mathcal {N}}_{U_{k} ,i}$, sub-channels of ${\mathcal {M}}_{U_{k} }$, until

$$\begin{aligned} S^{\mathrm{*}} \left( {\mathcal {M}}_{U_{k} } \right) \le \sum _{i=0}^{m-1}R\left( {\mathcal {N}}_{U_{k} ,i} \right) . \end{aligned}$$

(33)

Apply the steps for all transmit users $U_{k}$ for their ${\mathcal {M}}_{U_{k} }$ sets of m sub-channels. Therefore, one can utilize (27) at a given $R\left( {\mathcal {N}}_{U_{k} ,i} \right) =R_{i} \left( q\right)$, where $R_{i} \left( q\right)$ refers to the $R\left( q\right)$ curve of ${\mathcal {N}}_{U_{k} ,i}$, and from (12) follows $\delta _{\nu _{i} } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) =0\right) =\nu _{i} \left( {\mathcal {N}}_{U_{k} ,i} \right)$, which yields the error rate for ${\mathcal {N}}_{U_{k} ,i}$ of ${\mathcal {M}}_{U_{k} }$ as

$$\begin{aligned} \begin{aligned}&{\mathcal {B}}\left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) _{\xi \left( R\left( q-1\right) \right) } \right) \\&\quad ={\mathcal {B}}\left( R_{\min } \left( {\mathcal {N}}_{U_{k} ,i} \right) _{\nu _{i} \left( {\mathcal {N}}_{U_{k} ,i} \right) + \left( \Delta _{\nu _{i} } \left( R_{\min } \left( {\mathcal {N}}_{U_{k},i} \right) ,R_{i} \left( 0\right) \right) +\sum _{k=0}^{q-1} \Delta _{\nu _{i} } \left( R_{i} \left( k\right) ,R_{i} \left( k+1\right) \right) \right) } \right) . \end{aligned} \end{aligned}$$

(34)

$\square$

Variance Adaption for an Equalized Error Rate

In this section, we propose a modulation variance adaption method to achieve an equally minimized error rate for the sub-channels of a given user. The results can be extended to an arbitrary number of users.

Theorem 2

For all $U_{k}$, $k=0,\ldots ,K-1$, the error rate of the ${\mathcal {N}}_{U_{k} ,i}$, $i=0,\ldots ,m-1$ sub-channels of ${\mathcal {M}}_{U_{k}}$ of user $U_{k}$ can be equally minimized via a $\tilde{\sigma }_{\omega }^{2} =\sigma _{\omega }^{2} +\Delta _{\sigma _{\omega _{i} }^{2}}$ modulation variance correction, where $\Delta _{\sigma _{\omega _{i} }^{2} } >0$.

Proof

Let

$$\begin{aligned} \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{U_{k} ,i} \right) =R_{i} \left( q-1\right) ,q=0,\ldots ,r-1, \end{aligned}$$

(35)

and $R\left( {\mathcal {N}}_{U_{k} ,i} \right)$ be the target private rate,

$$\begin{aligned} R\left( {\mathcal {N}}_{U_{k} ,i} \right) =R_{i} \left( q\right) , \end{aligned}$$

(36)

where $R_{i} \left( q\right)$ refers to the $R\left( q\right)$ curve of ${\mathcal {N}}_{U_{k} ,i}$, with relation to $R_{i} \left( q-1\right) <R_{i} \left( q\right)$, and let us identify $R_{i} \left( -1\right) =R_{\min } \left( {\mathcal {N}}_{U_{k} ,i} \right)$ and $R_{i} \left( r\right) =R_{\max } \left( {\mathcal {N}}_{U_{k} ,i} \right)$.

Precisely, for a given $U_{k}$ at $R\left( {\mathcal {N}}_{U_{k} ,i} \right)$, the minimal $\delta _{\nu _{i} } ( \mathop {R}\limits _{\smile }( {\mathcal {N}}_{U_{k} ,i} ) )$ parameter for the ${\mathcal {N}}_{U_{k} ,i}$, $i=0,\ldots ,m-1$ sub-channels of the set ${\mathcal {M}}_{U_{k} }$is evaluated as

$$\begin{aligned} \xi _{U_{k} } =\mathop {\min }\limits _{\forall i\in {\mathcal {M}}_{U_{k} } } \delta _{\nu _{i} } \left( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) . \end{aligned}$$

(37)

Let $\sigma _{\omega }^{2}$ refer to the input modulation variance of the ith subcarrier of $U_{k}$. Specifically, using the expression of $\xi _{U_{k} }$ in (37), the $\sigma _{\omega }^{2}$ modulation variance of the ith subcarrier is corrected by $\Delta _{\sigma _{\omega _{i} }^{2} }$ as

$$\begin{aligned} \Delta _{\sigma _{\omega _{i} }^{2} } =\delta _{\nu _{i} } \left( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) -\xi _{U_{k} } , \end{aligned}$$

(38)

yielding a modulation variance increment

$$\begin{aligned} \tilde{\sigma }_{\omega }^{2} =\sigma _{\omega }^{2} +\Delta _{\sigma _{\omega _{i} }^{2} } \end{aligned}$$

(39)

for the input of ${\mathcal {N}}_{U_{k} ,i}$.

In particular, using (39), the $\varphi _{\delta _{\nu _{i} } } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right)$ resulting $\delta _{\nu _{i} }$ parameter for ${\mathcal {N}}_{U_{k} ,i}$ at a target rate $R\left( {\mathcal {N}}_{U_{k} ,i} \right)$ is, therefore,

$$\begin{aligned} \varphi _{\delta _{\nu _{i} } } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) =\delta _{\nu _{i} } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) -\xi _{U_{k} } , \end{aligned}$$

(40)

from which the $\Delta _{\mathrm{SNR}} \left( \varphi _{\delta _{\nu _{i} } } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) \right)$ SNR increment of ${\mathcal {N}}_{U_{k} ,i}$ at a given $R\left( {\mathcal {N}}_{U_{k} ,i} \right) =R\left( q\right)$ is as

$$\begin{aligned} \begin{aligned}&{{\Delta }_{\text {SNR}}}\left( {{\varphi }_{{{\delta }_{{{\nu }_{i}}}}}}\left( R\left( {{\mathcal {N}}_{{{U}_{k}},i}} \right) \right) \right) \\&\quad =10{{\log }_{10}}\tfrac{1}{{{\xi }_{{{U}_{k}}}}} -\mathcal {F}\left( {{\nu }_{i}}\left( {{\mathcal {N}}_{{{U}_{k}},i}} \right) +\left( {{\Delta }_{{{\nu }_{i}}}}\left( {{R}_{\min }}\left( {{\mathcal {N}}_{{{U}_{k}},i}} \right) ,R\left( 0 \right) \right) \right. \right. \\&\qquad \qquad \left. \left. +\ldots +{{\Delta }_{{{\nu }_{i}}}} \left( R\left( q \right) ,R\left( q+1 \right) \right) \right) \right) , \end{aligned} \end{aligned}$$

(41)

where ${\mathcal {F}}\left( \cdot \right)$ is specified in (22).

Therefore, the ${\mathcal {B}}( R\left( {\mathcal {N}}_{U_{k} ,i} \right) _{\xi _{U_{k} } } )$ error rate for all ${\mathcal {N}}_{U_{k} ,i}$ at an arbitrary $R\left( {\mathcal {N}}_{U_{k} ,i} \right) _{\delta _{\nu _{i} } \left( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) }$ is equally minimized by $\xi _{U_{k} }$ via (21) as

$$\begin{aligned} \begin{aligned}&\mathcal {B}\left( R{{\left( {{\mathcal {N}}_{{{U}_{k}},i}} \right) }_{{{\xi }_{{{U}_{k}}}}}} \right) =\underset{\forall i\in {{\mathcal {M}}_{{{U}_{k}}}}}{\mathop {\min }}\,\mathcal {B}\left( R{{\left( {{\mathcal {N}}_{{{U}_{k}},i}} \right) }_{{{\delta }_{{{\nu }_{i}}}}\left( \mathop {R}\limits _{\smile }\left( {{\mathcal {N}}_{{{U}_{k}},i}} \right) \right) }} \right) \\&=\mathcal {B}\left( {{R}_{\min }}{{\left( {{\mathcal {N}}_{{{U}_{k}},i}} \right) }_{{{\delta }_{{{\nu }_{i}}}}\left( \mathop {R}\limits _{\smile }\left( {{\mathcal {N}}_{{{U}_{k}},i}} \right) \right) }} \right) , i=0,\ldots ,m-1. \end{aligned} \end{aligned}$$

(42)

The formula of (42) proves the minimal error rate at arbitrary $S^{\mathrm{*}} \left( {\mathcal {M}}_{U_{k} } \right)$ over ${\mathcal {M}}_{U_{k} }$for all ${\mathcal {N}}_{U_{k} ,i}$ sub-channels of $U_{k}$.

Without loss of generality, the results can be extended for all K users to achieve minimized equalized error rate over all ${\mathcal {M}}_{U_{k} }$, $k=0,\ldots ,K-1$ logical channels.

In a single user setting, e.g., $K=1$, the method provides an equal, minimized error rate over the l sub-channels.

The proof is concluded here. $\square$

Numerical Evidence

This section proposes numerical evidence to demonstrate the results through a multiuser multicarrier CVQKD environment (AMQD-MQA [20]). The numerical evidence serves demonstration purposes.

Parameters

To demonstrate the results of Section 4.1, let $U_{k}$ be a given user with m sub-channels. The parameters of the numerical evidence are summarized as follows.

The single-carrier inputs of user $U_{k}$,

$$\begin{aligned} x_{U_{k} ,j} \in {\mathcal {N}}\left( 0,\sigma _{\omega _{0} }^{2} \right) , \end{aligned}$$

(43)

have a modulation variance of $\sigma _{\omega _{0} }^{2}$ and formulate a d-dimensional input vector $\mathbf {x}_{U_{k} }$.

The jth single carrier is dedicated to a single-carrier channel ${\mathcal {N}}_{U_{k} ,j}$. The single-carrier channel transmittance coefficient is depicted by $T\left( {\mathcal {N}}_{U_{k} ,j} \right)$, $j=0,\ldots ,d-1$, where d is the dimension of the input vector.

The single carriers are granulated into m subcarriers, where the ith subcarrier is

$$\begin{aligned} x_{U_{k} ,i} \in {\mathcal {N}}\left( 0,\sigma _{\omega }^{2} \right) , \end{aligned}$$

(44)

and has a modulation variance of $\sigma _{\omega }^{2}$.

The m sub-channels,

$$\begin{aligned} {\mathcal {N}}_{U_{k} ,i} , i=0,\ldots ,m-1, \end{aligned}$$

(45)

formulate the ${\mathcal {M}}_{U_{k} }$ logical channel of user $U_{k}$,

$$\begin{aligned} {\mathcal {M}}_{U_{k} } =\left[ {\mathcal {N}}_{U_{k} ,0} ,\ldots ,{\mathcal {N}}_{U_{k} ,m-1} \right] ^{T} . \end{aligned}$$

(46)

The $\Delta _{x_{i} } \in {\mathcal {N}}\left( 0,\sigma _{{\mathcal {N}}_{U_{k} ,i} }^{2} \right)$ noise of ${\mathcal {N}}_{U_{k} ,i}$ is added to the subcarriers, where $\sigma _{{\mathcal {N}}_{U_{k} ,i} }^{2}$ is the noise variance of ${\mathcal {N}}_{U_{k} ,i}$.

For a given sub-channel ${\mathcal {N}}_{U_{k} ,i}$ of $U_{k}$, parameters $\nu _{i} \left( {\mathcal {N}}_{U_{k} ,i} \right)$ and $\nu _{i} \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right)$ are evaluated via (31) and (32), such that the $T\left( {\mathcal {N}}_{U_{k} ,i} \right)$ sub-channel transmittance coefficients are estimated in a pre-communication phase via the subcarrier spreading technique [30].

The $\delta _{\nu _{i} } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right)$ of ${\mathcal {N}}_{U_{k} ,i}$ parameters are determined from $\nu _{i} \left( {\mathcal {N}}_{U_{k} ,i} \right)$ for all sub-channels via the iterative method of Theorem 2.

Modulation Variance Adaption

The analysis focuses on a low-SNR CVQKD scenario. An initial low-SNR set of $\delta _{\nu _{i} } ( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{U_{k} ,i} \right) )$, $i=0,\ldots ,m-1$ of user $U_{k}$ from a low-SNR scenario is illustrated in Fig. 4a. The minimum of the set is $\xi _{U_{k} } = \min \limits _{\forall i\in {\mathcal {M}}_{U_{k} } } \delta _{\nu _{i} } \left( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{U_{k} ,i} \right) \right)$, from which the modulation variance correction for ${\mathcal {N}}_{U_{k} ,i}$ is $\Delta _{\sigma _{\omega _{i} }^{2} } =\delta _{\nu _{i} } \left( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) -\xi _{U_{k} }$. The corresponding $\Delta _{\sigma _{\omega _{i} }^{2} }$ (see (38)), $i=0,\ldots ,m-1$ values determined from the $\delta _{\nu _{i} } ( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{U_{k} ,i} \right) )$ elements are depicted in Fig. 4b.

Fig. 4

An initial low-SNR set of $\delta _{\nu _{i} } ( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{U_{k} ,i} \right) )$ of user $U_{k}$, $i=0,\ldots ,m-1$, $m=1000$. a The minimum of set $\delta _{\nu _{i} } ( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{U_{k} ,i} \right) )$ (red solid line). b The resulting $\Delta _{\sigma _{\omega _{i} }^{2} }$ variance correction, $i=0,\ldots ,m-1$, $m=1000$ determined from the $\delta _{\nu _{i} } \left( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{U_{k} ,i} \right) \right)$ elements

In a low-SNR setting due to the value range of $\delta _{\nu _{i} } \left( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{U_{k} ,i} \right) \right)$, $i=0,\ldots ,m-1$, the required $\Delta _{\sigma _{\omega _{i} }^{2} }$ variance correction for the subcarriers is, therefore, negligible.

The $x_{U_{k} ,i}$, $i=0,\ldots ,m-1$ input quadratures of user $U_{k}$ with a constant variance $\sigma _{\omega }^{2}$ are illustrated in Fig. 5a. Applying the result of $\Delta _{\sigma _{\omega _{i} }^{2} }$, the $\tilde{x}_{U_{k} ,i}$, $i=0,\ldots ,m-1$ input quadratures of user $U_{k}$ at the $\tilde{\sigma }_{\omega _{i} }^{2} =\sigma _{\omega }^{2} +\Delta _{\sigma _{\omega _{i} }^{2} }$ increased variance are depicted in Fig. 5b.

Fig. 5

a The $x_{U_{k} ,i}$, $i=0,\ldots ,m-1$, $m=1000$ input quadratures of user $U_{k}$ at a constant variance $\sigma _{\omega }^{2} =64$. b The $\tilde{x}_{U_{k} ,i}$, $i=0,\ldots ,m-1$, $m=1000$ input quadratures of user $U_{k}$ at increased variance $\tilde{\sigma }_{\omega _{i} }^{2} =\sigma _{\omega }^{2} +\Delta _{\sigma _{\omega _{i} }^{2} }$

The variance adaption of $x_{U_{k} ,i}$, $i=0,\ldots ,m-1$ requires only a moderate $\Delta _{\sigma _{\omega _{i} }^{2} }$ for all subcarriers to achieve an equalized, significantly lower error rate through the sub-channels.

SNR Differences

The effects of the $\Delta _{\sigma _{\omega _{i} }^{2} }$ variance correction and the resulting $\varphi _{\delta _{\nu _{i} } } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right)$ can be expressed in terms of the resulting SNR change.

The $\Delta _{\mathrm{SNR}} \left( \tilde{\sigma }_{\omega _{i} }^{2} \right) =\mathrm{SNR}\left( \tilde{\sigma }_{\omega _{i} }^{2} \right) -\mathrm{SNR}\left( \sigma _{\omega }^{2} \right)$, $i=0,\ldots ,m-1,$ SNR difference for the input quadratures $\left\{ x_{U_{k} ,i} ,\tilde{x}_{U_{k} ,i} \right\}$ at $\sigma _{\omega }^{2}$ and $\tilde{\sigma }_{\omega _{i} }^{2} =\sigma _{\omega }^{2} +\Delta _{\sigma _{\omega _{i} }^{2} }$ is depicted in Fig. 6a. The $\Delta _{\mathrm{SNR}} \left( \varphi _{\delta _{\nu _{i} } } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) \right)$ SNR differences (see (41)) achieved at a given $\varphi _{\delta _{\nu _{i} } } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right)$, $i=0,\ldots ,m-1,$ are illustrated in Fig. 6b.

Fig. 6

a The $\Delta _{\mathrm{SNR}} \left( \tilde{\sigma }_{\omega _{i} }^{2} \right)$, $i=0,\ldots ,m-1$, $m=1000$ parameter for $\left\{ x_{U_{k} ,i} ,\tilde{x}_{U_{k} ,i} \right\}$ at $\sigma _{\omega }^{2}$ and $\tilde{\sigma }_{\omega _{i} }^{2}$. b The $\Delta _{\mathrm{SNR}} \left( \varphi _{\delta _{\nu _{i} } } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) \right)$ parameter, $i=0,\ldots ,m-1$, $m=1000$

The $\Delta _{\mathrm{SNR}} \left( \tilde{\sigma }_{\omega _{i} }^{2} \right)$ input SNR difference results in an improved $\Delta _{\mathrm{SNR}} \left( \varphi _{\delta _{\nu _{i} } } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) \right)$ parameter via $\varphi _{\delta _{\nu _{i} } } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right)$ for all i.

Error Rate Minimization

The BER values for the initial low-SNR set and for the set of $\varphi _{\delta _{\nu _{i} } } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right)$ are compared in Fig. 2. The BER of ${\mathcal {N}}_{U_{k} ,i}$ at the initial low-SNR set of $\delta _{\nu _{i} } \left( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{U_{k} ,i} \right) \right)$, $i=0,\ldots ,m-1,$ is illustrated in Fig. 7a. The BER of the m sub-channels ${\mathcal {N}}_{U_{k} ,i}$, $i=0,\ldots ,m-1,$ at $\varphi _{\delta _{\nu _{i} } } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right)$, is depicted in Fig. 7b.

Fig. 7

a The BER for the initial low-SNR set $\delta _{\nu _{i} } \left( \mathop {R}\limits _{\smile }\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) ,i=0,\ldots ,m-1,m=1000$ (the minimum of the set is depicted by the green solid line). b The BER values for $\varphi _{\delta _{\nu _{i} } } \left( R\left( {\mathcal {N}}_{U_{k} ,i} \right) \right) ,i=0,\ldots ,m-1,m=1000$

As follows, as $\xi _{U_{k} }$ is determined and applied in the iteration procedure, the resulting BER is equally minimized for all ${\mathcal {N}}_{U_{k} ,i}$ sub-channels of user $U_{k}$.

Conclusions

We defined an iterative secret key adaption method for multicarrier CVQKD. The scheme provides a minimized error rate using the utilization of an adaptive private classical information transmission through the sub-channels. The private classical transmission is realized through pre-defined private rate curves, which characterize an adaption region for each sub-channel to find the best conditions for the transmission at a given private classical rate. The method allows us to reach a given target secret key rate with optimal transmit conditions and minimized error rate for all sub-channels.

Appendix

Multicarrier CVQKD

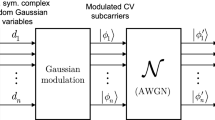
First, we summarize the basic notations of AMQD [15]. The following description assumes a single user, and the use of n Gaussian sub-channels ${\mathcal {N}}_{i}$ for the transmission of the subcarriers, from which only l sub-channels will carry valuable information.

In the single-carrier modulation scheme, the jth input single-carrier state ${\left| \varphi _{j} \right\rangle } ={\left| x_{j} +\mathrm{i}p_{j} \right\rangle }$ is a Gaussian state in the phase space ${\mathcal {S}}$, with i.i.d. Gaussian random position and momentum quadratures $x_{j} \in {\mathcal {N}}\left( 0,\sigma _{\omega _{0} }^{2} \right)$, $p_{j} \in {\mathcal {N}}\left( 0,\sigma _{\omega _{0} }^{2} \right)$, where $\sigma _{\omega _{0} }^{2}$ is the modulation variance of the quadratures. (For simplicity, $\sigma _{\omega _{0} }^{2}$ is referred to as the single-carrier modulation variance, throughout.) Particularly, this Gaussian single carrier is transmitted through a Gaussian quantum channel ${\mathcal {N}}$. In the multicarrier scenario, the information is carried by Gaussian subcarrier CVs, ${\left| \phi _{i} \right\rangle } ={\left| x_{i} +\mathrm{i}p_{i} \right\rangle }$, $x_{i} \in {\mathcal {N}}\left( 0,\sigma _{\omega }^{2} \right)$, $p_{i} \in {\mathcal {N}}\left( 0,\sigma _{\omega }^{2} \right)$, where $\sigma _{\omega }^{2}$ is the modulation variance of the subcarrier quadratures, which are transmitted through a noisy Gaussian sub-channel ${\mathcal {N}}_{i}$. Each ${\mathcal {N}}_{i}$ Gaussian sub-channel is dedicated for the transmission of one Gaussian subcarrier CV from the n subcarrier CVs. (Note: index i refers to the subcarriers, while index j to the single carriers throughout the manuscript.) The single-carrier state ${\left| \varphi _{j} \right\rangle }$ in the phase space ${\mathcal {S}}$ can be modeled as a zero-mean, circular symmetric complex Gaussian random variable $z_{j} \in {\mathcal {CN}}\left( 0,\sigma _{\omega _{z_{j} } }^{2} \right)$, with variance $\sigma _{\omega _{z_{j} } }^{2} ={\mathbb {E}}\left[ \left| z_{j} \right| ^{2} \right]$, and with i.i.d. real and imaginary zero-mean Gaussian random components $\text {Re}\left( z_{j} \right) \in {\mathcal {N}}\left( 0,\sigma _{\omega _{0} }^{2} \right)$, $\text {Im}\left( z_{j} \right) \in {\mathcal {N}}\left( 0,\sigma _{\omega _{0} }^{2} \right)$.

In the multicarrier CVQKD scenario, let n be the number of Alice’s input single-carrier Gaussian states. The n input coherent states are modeled by an n-dimensional, zero-mean, circular symmetric complex random Gaussian vector

$$\begin{aligned} \mathbf {z}=\mathbf {x}+i\mathbf {p}={{\left( {{z}_{1}},\ldots , {{z}_{n}} \right) }^\mathrm{T}}\in \mathcal {CN}\left( 0,{{\mathbf {K}}_{\mathbf {z}}} \right) \end{aligned}$$

(47)

where each $z_{j}$ can be modeled as a zero-mean, circular symmetric complex Gaussian random variable

$$\begin{aligned} z_{j} \in {\mathcal {CN}}\left( 0,\sigma _{\omega _{z_{j} } }^{2} \right) , z_{j} =x_{j} +\mathrm{i}p_{j} . \end{aligned}$$

(48)

Specifically, the real and imaginary variables (i.e., the position and momentum quadratures) formulate n-dimensional real Gaussian random vectors, $\mathbf {x}={{\left( {{x}_{1}},\ldots , {{x}_{n}} \right) }^\mathrm{T}}$ and $\mathbf {p}={{\left( {{p}_{1}},\ldots , {{p}_{n}} \right) }^\mathrm{T}}$, with zero-mean Gaussian random variables with densities $f(x_{j})$ and $f(p_{j})$ as

$$\begin{aligned} f\left( x_{j} \right) ={\frac{1}{\sigma _{\omega _{0} } \sqrt{2\pi } }} e^{{\frac{-x_{j} ^{2} }{2\sigma _{\omega _{0} }^{2} }} }, f\left( p_{j} \right) ={\frac{1}{\sigma _{\omega _{0} } \sqrt{2\pi } }} e^{{\frac{-p_{j} ^{2} }{2\sigma _{\omega _{0} }^{2} }} }, \end{aligned}$$

(49)

where ${{\mathbf {K}}_{\mathbf {z}}}$ is the $n\times n$ Hermitian covariance matrix of $\mathbf {z}$:

$$\begin{aligned} {{\mathbf {K}}_{\mathbf {z}}}=\mathbb {E}\left[ \mathbf {z}{{\mathbf {z}}^{\dagger }} \right] , \end{aligned}$$

(50)

while ${{\mathbf {z}}^{\dagger }}$ is the adjoint of $\mathbf {z}$.

For vector $\mathbf {z}$,

$$\begin{aligned} \mathbb {E}\left[ \mathbf {z} \right] =\mathbb {E}\left[ {{e}^{i\gamma }}\mathbf {z} \right] =\mathbb {E}{{e}^{i\gamma }}\left[ \mathbf {z} \right] \end{aligned}$$

(51)

holds, and

$$\begin{aligned} \mathbb {E}\left[ \mathbf {z}{{\mathbf {z}}^{T}} \right] =\mathbb {E}\left[ {{e}^{i\gamma }}\mathbf {z}{{\left( {{e}^{i\gamma }}\mathbf {z} \right) }^\mathrm{T}} \right] =\mathbb {E}{{e}^{i2\gamma }}\left[ \mathbf {z}{{\mathbf {z}}^\mathrm{T}} \right] , \end{aligned}$$

(52)

for any $\gamma \in \left[ 0,2\pi \right]$. The density of $\mathbf {z}$ is as follows (if ${{\mathbf {K}}_{\mathbf {z}}}$ is invertible):

$$\begin{aligned} f\left( \mathbf {z} \right) =\tfrac{1}{{{\pi }^{n}}\det {{\mathbf {K}}_{\mathbf {z}}}}{{e}^{-{{\mathbf {z}}^{\dagger }}{{\mathbf {K}}_{\mathbf {z}}}^{-1}\mathbf {z}}}. \end{aligned}$$

(53)

A n-dimensional Gaussian random vector is expressed as $\mathbf {x}=\mathbf {As}$, where $\mathbf {A}$ is an (invertible) linear transform from ${\mathbb {R}}^{n}$ to ${\mathbb {R}}^{n}$, and $\mathbf {s}$ is an n-dimensional standard Gaussian random vector ${\mathcal {N}}\left( 0,1\right) _{n}$. This vector is characterized by its covariance matrix ${{\mathbf {K}}_{\mathbf {x}}}=\mathbb {E}\left[ \mathbf {x}{{\mathbf {x}}^\mathrm{T}} \right] =\mathbf {A}{{\mathbf {A}}^\mathrm{T}}$, and has density

$$\begin{aligned} f(\mathbf {x})=\tfrac{1}{{{\left( \sqrt{2\pi } \right) }^{n}}\sqrt{\det \left( \mathbf {A}{{\mathbf {A}}^\mathrm{T}} \right) }}{{e}^{-\tfrac{{{\mathbf {x}}^\mathrm{T}}\mathbf {x}}{2\left( \mathbf {A}{{\mathbf {A}}^\mathrm{T}} \right) }}}. \end{aligned}$$

(54)

The Fourier transformation $F\left( \cdot \right)$ of the n-dimensional Gaussian random vector $\mathbf {v}=\left( v_{1}, \ldots , v_{n} \right) ^\mathrm{T}$ results in the n-dimensional Gaussian random vector $\mathbf {m}={{\left( {{m}_{1}},\ldots , {{m}_{n}} \right) }^{T}}$, as:

$$\begin{aligned} \mathbf {m}=F\left( \mathbf {v} \right) ={{e}^{\tfrac{-{{\mathbf {m}}^{T}}\mathbf {A}{{\mathbf {A}}^{T}}\mathbf {m}}{2}}}={{e}^{\tfrac{-\sigma _{{{\omega }_{0}}}^{2}\left( m_{1}^{2}+\ldots +m_{n}^{2} \right) }{2}}}. \end{aligned}$$

(55)

In the first step of AMQD, Alice applies the inverse FFT (fast Fourier transform) operation to vector $\mathbf {z}$ (see (47)), which results in an n-dimensional zero-mean, circular symmetric complex Gaussian random vector $\mathbf {d}$, $\mathbf {d}\in \mathcal {CN}\left( 0,{{\mathbf {K}}_{\mathbf {d}}} \right)$, $\mathbf {d}={{\left( {{d}_{1}},\ldots , {{d}_{n}} \right) }^\mathrm{T}}$, as

$$\begin{aligned} \mathbf {d}={{F}^{-1}}\left( \mathbf {z} \right) ={{e}^{\tfrac{{{\mathbf {d}}^{T}}\mathbf {A}{{\mathbf {A}}^\mathrm{T}}\mathbf {d}}{2}}}={{e}^{\tfrac{\sigma _{{{\omega }_{0}}}^{2}\left( d_{1}^{2}+\ldots +d_{n}^{2} \right) }{2}}}, \end{aligned}$$

(56)

where

$$\begin{aligned} d_{i} =x_{d_{i} } +\mathrm{i}p_{d_{i} }, d_{i} \in {\mathcal {CN}}\left( 0,\sigma _{d_{i} }^{2} \right) , \end{aligned}$$

(57)

where $\sigma _{\omega _{d_{i} } }^{2} ={\mathbb {E}}\left[ \left| d_{i} \right| ^{2} \right]$ and the position and momentum quadratures of ${\left| \phi _{i} \right\rangle }$ are i.i.d. Gaussian random variables

$$\begin{aligned} \text {Re}\left( d_{i} \right) =x_{d_{i} } \in {\mathcal {N}}\left( 0,\sigma _{\omega _{i} }^{2} \right) , \text {Im}\left( d_{i} \right) =p_{d_{i} } \in {\mathcal {N}}\left( 0,\sigma _{\omega _{i} }^{2} \right) , \end{aligned}$$

(58)

where ${{\mathbf {K}}_{\mathbf {d}}}=\mathbb {E}\left[ \mathbf {d}{{\mathbf {d}}^{\dagger }} \right]$, $\mathbb {E}\left[ \mathbf {d} \right] =\mathbb {E}\left[ {{e}^{i\gamma }}\mathbf {d} \right] =\mathbb {E}{{e}^{i\gamma }}\left[ \mathbf {d} \right]$, and $\mathbb {E}\left[ \mathbf {d}{{\mathbf {d}}^{T}} \right] =\mathbb {E}\left[ {{e}^{i\gamma }}\mathbf {d}{{\left( {{e}^{i\gamma }}\mathbf {d} \right) }^\mathrm{T}} \right] =\mathbb {E}{{e}^{i2\gamma }}\left[ \mathbf {d}{{\mathbf {d}}^\mathrm{T}} \right]$, for any $\gamma \in \left[ 0,2\pi \right]$.

The $\mathbf {T}\left( \mathcal {N} \right)$ transmittance vector of ${\mathcal {N}}$ in the multicarrier transmission is

$$\begin{aligned} \mathbf {T}\left( {\mathcal {N}}\right) =\left[ T_{1} \left( {\mathcal {N}}_{1} \right) ,\ldots , T_{n} \left( {\mathcal {N}}_{n} \right) \right] ^\mathrm{T} \in {\mathcal {C}}^{n}, \end{aligned}$$

(59)

where

$$\begin{aligned} T_{i} \left( {\mathcal {N}}_{i} \right) =\text {Re}\left( T_{i} \left( {\mathcal {N}}_{i} \right) \right) +\mathrm{i}\text {Im}\left( T_{i} \left( {\mathcal {N}}_{i} \right) \right) \in {\mathcal {C}}, \end{aligned}$$

(60)

is a complex variable, which quantifies the position and momentum quadrature transmission (i.e., gain) of the ith Gaussian sub-channel ${\mathcal {N}}_{i}$, in the phase space ${\mathcal {S}}$, with real and imaginary parts

$$\begin{aligned} 0\le \text {Re}T_{i} \left( {\mathcal {N}}_{i} \right) \le {1 / \sqrt{2} }, \end{aligned}$$

(61)

and

$$\begin{aligned} 0\le \text {Im}T_{i} \left( {\mathcal {N}}_{i} \right) \le {1 / \sqrt{2} }. \end{aligned}$$

(62)

Particularly, the $T_{i} \left( {\mathcal {N}}_{i} \right)$ variable has the squared magnitude of

$$\begin{aligned} \left| T_{i} \left( {\mathcal {N}}_{i} \right) \right| ^{2} =\text {Re}T_{i} \left( {\mathcal {N}}_{i} \right) ^{2} +\text {Im}T_{i} \left( {\mathcal {N}}_{i} \right) ^{2} \in {\mathbb {R}}, \end{aligned}$$

(63)

where

$$\begin{aligned} \text {Re}T_{i} \left( {\mathcal {N}}_{i} \right) =\text {Im}T_{i} \left( {\mathcal {N}}_{i} \right) . \end{aligned}$$

(64)

The Fourier-transformed transmittance of the ith sub-channel ${\mathcal {N}}_{i}$ (resulted from CVQFT operation at Bob) is denoted by

$$\begin{aligned} \left| F\left( T_{i} \left( {\mathcal {N}}_{i} \right) \right) \right| ^{2} . \end{aligned}$$

(65)

The n-dimensional zero-mean, circular symmetric complex Gaussian noise vector $\Delta \in {\mathcal {CN}}\left( 0,\sigma _{\Delta }^{2} \right) _{n}$ of the quantum channel ${\mathcal {N}}$, is evaluated as

$$\begin{aligned} \Delta ={{\left( {{\Delta }_{1}},\ldots , {{\Delta }_{n}} \right) }^\mathrm{T}}\in \mathcal {C}\mathbb {N}\left( 0,{{\mathbf {K}}_{\Delta }} \right) , \end{aligned}$$

(66)

where

$$\begin{aligned} {{\mathbf {K}}_{\Delta }}=\mathbb {E}\left[ \Delta {{\Delta }^{\dagger }} \right] . \end{aligned}$$

(67)

with independent, zero-mean Gaussian random components

$$\begin{aligned} \Delta _{x_{i} } \in {\mathcal {N}}\left( 0,\sigma _{{\mathcal {N}}_{i} }^{2} \right) , \end{aligned}$$

(68)

and

$$\begin{aligned} \Delta _{p_{i} } \in {\mathcal {N}}\left( 0,\sigma _{{\mathcal {N}}_{i} }^{2} \right) , \end{aligned}$$

(69)

with variance $\sigma _{{\mathcal {N}}_{i} }^{2}$, for each $\Delta _{i}$ of a Gaussian sub-channel ${\mathcal {N}}_{i}$, which identifies the Gaussian noise of the ith sub-channel ${\mathcal {N}}_{i}$ on the quadrature components in the phase space ${\mathcal {S}}$.

The CVQFT-transformed noise vector can be rewritten as

$$\begin{aligned} F\left( \Delta \right) =\left( F\left( \Delta _{1} \right) ,\ldots , F\left( \Delta _{n} \right) \right) ^\mathrm{T}, \end{aligned}$$

(70)

with independent components $F\left( \Delta _{x_{i} } \right) \in {\mathcal {N}}\left( 0,\sigma _{F\left( {\mathcal {N}}_{i} \right) }^{2} \right)$ and $F\left( \Delta _{p_{i} } \right) \in {\mathcal {N}}\left( 0,\sigma _{F\left( {\mathcal {N}}_{i} \right) }^{2} \right)$ on the quadratures, for each $F\left( \Delta _{i} \right)$. It also defines an n-dimensional zero-mean, circular symmetric complex Gaussian random vector $F\left( \Delta \right) \in {\mathcal {CN}}\left( 0,\mathbf {K}_{F\left( \Delta \right) } \right)$ with a covariance matrix

$$\begin{aligned} \mathbf {K}_{F\left( \Delta \right) } ={\mathbb {E}}\left[ F\left( \Delta \right) F\left( \Delta \right) ^{\dag } \right] , \end{aligned}$$

(71)

where $\mathbf {K}_{F\left( \Delta \right) } =\mathbf {K}_{\Delta }$, by theory. At a constant subcarrier modulation variance $\sigma _{\omega _{i} }^{2}$ for the n Gaussian subcarrier CVs, the corresponding relation is

$$\begin{aligned} {\frac{1}{n}} \sum _{i=1}^{n}\sigma _{\omega _{i} }^{2} =\sigma _{\omega }^{2}, \end{aligned}$$

(72)

where $\sigma _{\omega _{i} }^{2}$ is the modulation variance of the quadratures of the subcarrier ${\left| \phi _{i} \right\rangle }$ transmitted by sub-channel ${\mathcal {N}}_{i}$. Assuming l good Gaussian sub-channels from the n with constant quadrature modulation variance $\sigma _{\omega _{i} }^{2}$, where $\sigma _{\omega _{i} }^{2} =0$ for the ith unused sub-channel

$$\begin{aligned} \sum _{i=1}^{l}\sigma _{\omega _{i} }^{2} =l\sigma _{\omega }^{2} <n\sigma _{\omega _{0} }^{2} . \end{aligned}$$

(73)

In particular, from the relation of (73), for the transmittance parameters the following relation follows at a given modulation variance $\sigma _{\omega _{0} }^{2}$, precisely,

$$\begin{aligned} \left| T_\mathrm{AMQD} \left( {\mathcal {N}}_{i} \right) \right| ^{2} \sigma _{\omega _{0} }^{2} >\left| T\left( {\mathcal {N}}\right) \right| ^{2} \sigma _{\omega _{0} }^{2}, \end{aligned}$$

(74)

where $\left| T\left( {\mathcal {N}}\right) \right| ^{2}$ is the transmittance of ${\mathcal {N}}$ in a single-carrier scenario, and

$$\begin{aligned} \left| T_\mathrm{AMQD} \left( {\mathcal {N}}_{i} \right) \right| ^{2} ={\frac{1}{l}} \sum _{i=1}^{l}\left| F\left( T_{i} \left( {\mathcal {N}}_{i} \right) \right) \right| ^{2} . \end{aligned}$$

(75)

For the method of the determination of these l Gaussian sub-channels, see [15]. Alice’s ith Gaussian subcarrier is expressed as

$$\begin{aligned} {\left| \phi _{i} \right\rangle } ={\left| d_{i} \right\rangle } ={\left| F^{-1} \left( z\right) \right\rangle } . \end{aligned}$$

(76)

A.2 Notations

The notations of the manuscript are summarized in Table 1.

Table 1 Summary of notations